Abstract
The age of industrialization and modernization has increased energy demands globally. Solar energy has been recognized as an inexhaustible source of energy and has been applied for desalination and electricity generation. Among different non-conventional energy resources, Solar Energy (SE) is one of the main contributors to the global energy system. A photovoltaic system (PS) is applied to produce SE using photovoltaic cells. The selection of a solar panel includes many intricate factors involving both subjective and quantifiable parameters; therefore, it can be regarded as a complex Multi-Criteria Decision-Making (MCDM) problem. As the uncertainty commonly occurs in the selection of an ideal solar panel, the theory of Pythagorean fuzzy sets has been proven as one of the flexible and superior tools to deal with the uncertainty and ambiguity that arise in real-life applications. The aim of the study is to present an MCDM framework for solving the Solar Panel Selection (SPS) problem within the Pythagorean fuzzy (PF) environment. For this, first, a new integrated method is proposed based on the Stepwise Weight Assessment Ratio Analysis (SWARA) and VlseKriterijumska Optimizcija I Kaompromisno Resenje (VIKOR) approaches in the Pythagorean fuzzy sets (PFSs) context. In the proposed approach, subjective weights of the evaluation criteria are calculated by the SWARA method, and the preference order of alternatives is decided by the VIKOR method in the PF context. The criteria weights evaluated by this approach involve the imprecision of experts’ opinions, which makes them more comprehensible. The computational procedure of the proposed methodology is established through a case study of the SPS problem under PF environment, which proves the applicability and efficiency of the proposed method. Furthermore, this study performs sensitivity analysis to reveal the stability of the developed framework. This analysis signifies that the solar panel option R4 constantly secures its highest ranking despite how the parameter values vary. In addition, a comparative study is discussed to analyze the validity of the obtained result. The results show that the proposed approach is more efficient and applicable with previously developed methods in the PFS environment.
1. Introduction
Sustainability is defined as an integrated economic, social, environmental, and technological development that meets the needs of the present without compromising the ability of future generations to meet their own needs [1]. The basic principle of sustainable development is that natural resources can be exploited only to the level that provides their reproduction. To ensure a sustainable future, there is an increasing awareness in the world for the development of sustainable energy resources. Sustainable energy is a form of energy that is non-polluted and long-lasting with much less emission of carbon and greenhouse gases. It includes solar, hydroelectricity, geothermal, biomass, wind, wave, and tidal energies. Solar energy is one of the most emerging alternative sources of energy that is widely available, environmentally friendly, and can be used indefinitely without diminishing its future availability [2,3]. Nowadays, solar energy has been recognized as an important sector to support the sustainable development of various countries.
Photovoltaic (PV) systems, which contain photovoltaic cells, are known as a method for generating power in an efficient way. One of the most imperative modules of a solar power plant is the solar panel (SP). SPs have usually been utilized for lower-scale energy production, predominantly for business or residential utilization in multiplexes or individual buildings. They collect clean renewable energy in the form of sunlight and convert that light into electricity, which can be employed to supply power for electrical loads [4]. Solar panels are comprised of several individual solar cells, which are themselves composed of layers of silicon, phosphorous (which provides the negative charge), and boron (which provides the positive charge). The cost of an SP varies with reference to its size, dimension, and strength. As the SP selection (SPS) depends on several tangible and intangible factors/criteria, therefore, it can be scrutinized as a Multi-Criteria Decision-Making (MCDM) problem. Thus, the selection of most suitable solar panel is one of the most significant decisions in the photovoltaic system design. In the recent past, several studies have established diverse decision support systems (DSS) to evaluate solar energy systems. For instance, Ramachandra et al. [5] developed an adaptable DSS to evaluate the solar system potential. Charabi and Gastli [6] proposed an integrated technique to assess the solar PV power plant location selection problem in Oman. Cavallaro [7] established a Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS)-based framework to assess the thermal storage of solar PV plants. Beltran [8] studied an analytic network process for selecting solar projects. Khan and Rathi [9] introduced a method for assessing solar PV plant locations. Kowalski et al. [10] discussed an innovative MCDM procedure for energy problems. Tavana et al. [11] proposed a framework to evaluate the solar farm site selection problem. Ozdemir and Sahin [12] developed an MCDM model to solve the solar PV power plant location assessment problem. Wang et al. [13] studied an MCDM framework to evaluate the SPS problem in Vietnam. The evaluation of the SPS problem involves several uncertain characteristics and a lack of information/data. The conception of fuzzy sets (FSs) originated with Zadeh [14]; they have been widely applied to deal with uncertainties that arise in practical problems. Many scholarly studies have utilized the concept of FSs in order to cope with uncertainties that arise in the ranking of solar panels [15,16,17].
FS theory has successfully been applied in MCDM problems because human judgments are generally imprecise when selecting an alternative concerning multiple criteria with different levels of significance. Later, Atanassov [18] generalized the conception of FSs to intuitionistic fuzzy sets (IFSs), depicted by membership degree (MD) and non-membership degree (ND); this satisfies a constraint that the addition of its MD and ND is less than or equal to 1. After they came into existence, researchers have made their efforts to develop new information measures [19,20,21] and aggregation operators [22,23,24] within the context of IFSs. Due to their potential for solving uncertain real-world problems, IFSs have been broadly utilized in medical diagnosis [25,26], image processing [27,28], and decision-making problems [20,29].
However, there may be a case in the MCDM approach wherein the decision experts (DEs) may give a value, to which an option holds the attribute of , and the value of an option that nullifies the attribute is As a result, it can be simply observed that , and thus, the IFS failed to deal with these circumstances. Recently, Refs. [4,5] introduced the notion of Pythagorean fuzzy sets (PFSs), depicted by the MD and ND, which satisfies the requirement that the square sum of MD and ND is less than or equal to 1 [30]. Therefore, the above-mentioned situation can be systematically handled by PFSs. Due to the increasing complexity and time limitations, the theory of PFSs has been taken into account by several researchers for handling uncertainty and imprecision in a more adaptable way. Yager [31] and Yager and Abbasov [32] studied the fundamental concepts associated with PFSs and explained a relation between complex numbers and Pythagorean fuzzy numbers (PFNs). Zhang and Xu [33] presented the addition, multiplication, union, and intersection operations for PFNs. Gou et al. [34] defined the subtraction and division operations of PFNs and also studied their properties. Apart from them, several researchers have incorporated the idea of PFS theory into information measures [35,36] and aggregation operators [37,38] and have utilized them to handle real-life MCDM problems. In a similar way, there is no study in the literature regarding the assessment of the solar panel selection problem using PFSs.
The significance degrees/weights of the criteria are one of the important concerns during the process of MCDM. In the literature, two types of criteria weights are discussed, which are objective and subjective weights [39]. The objective weights are obtained from the information of decision matrices, while the subjective weights are assessed through the knowledge presented by the DEs [40]. For evaluating objective criteria weights, various authors have developed different procedures [41,42,43]. For determining subjective criteria weights, Kersuliene et al. [44] proposed a new efficient method, named the Stepwise Weight Assessment Ratio Analysis (SWARA) approach. Karabasevic et al. [45] discussed a structure for the assessment of personnel based on the Additive Ratio Assessment (ARAS) and SWARA approaches within the FS context. Mardani et al. [46] discussed a thorough review of the SWARA and Weighted Aggregated Sum Product Assessment (WASPAS) approaches and their applications in diverse fuzzy environments. Maghsoodi et al. [47] suggested a hybrid approach by combining the SWARA and Multi-Objective Optimization on the basis of Ratio Analysis plus full multiplicative form (MULTIMOORA) methods for the evaluation of the renewable energy technology selection problem. Ghorabaee et al. [48] introduced a fuzzy hybrid method based on the SWARA, Criteria Importance Through Intercriteria Correlation (CRITIC) method, and Evaluation Based on Distance from Average Solution (EDAS) techniques to handle MCDM problems and then them applied to assess construction equipment in view of sustainability dimensions. Rani and Mishra [49] studied a hybrid method by employing the SWARA and VlseKriterijumska Optimizcija I Kaompromisno Resenje (VIKOR) approaches to deal with the eco-industrial thermal power plant selection problem within a single-valued neutrosophic fuzzy environment.
The VIKOR approach, which originated with Opricovic [6], is a useful and flexible compromise programming-based framework to tackle MCDM problems. The main objective of the VIKOR technique is to present compromise solution(s) from the metric, utilized as an aggregation function [50]. Numerous authors have applied the conventional VIKOR approach in various fields [51,52,53]. Mardani et al. [54] presented a comprehensive review on the VIKOR method and also discussed its applications. To deal with the uncertainty that arises in MCDM problems, Zhang and Xing [55] suggested an innovative probabilistic linguistic VIKOR methodology to evaluate green supply chain initiatives. Suh et al. [56] discussed an innovative fuzzy VIKOR model to solve the mobile service quality assessment problem. Krishankumar et al. [57] studied a transformation-procedure-based VIKOR method and applied it to solve a personnel selection problem in an IFS context. Rani et al. [43] presented an integrated VIKOR framework based on entropy and divergence measures within a PFSs environment and then employed it in renewable energy technology selection in India. Phochanikorn and Tan [58] suggested a hybrid approach based on the Decision-Making Trial and Evaluation Laboratory (DEMATEL), Analytic Hierarchical Process (AHP), and VIKOR methods, and applied it to evaluate a sustainable supplier selection problem within an intuitionistic fuzzy environment. Salimi et al. [59] recommended an integrated AHP- and VIKOR-based approach to explore the role of mass media advertising types in improving the water consumption pattern in Iran. Recently, several existing studies [60,61,62,63] have extended the VIKOR technique in different fuzzy environments.
Nevertheless, the VIKOR technique has not been combined with the SWARA method within the context of PFSs, though PFSs have been proven as one of the valuable tools to handle with the uncertainty and vagueness that occur in real-life concerns. Consequently, the present study focuses on PFSs. Though various authors have concentrated on the selection of renewable energy resources in PFS contexts, none have studied the SPS problem in this environment. Existing literature shows that there is a need to select the appropriate type of solar panel to generate electricity. The solar panel selection process consists of many objective and subjective attributes that have conflicting goals. In addition, the precision of the assessment procedure is dependent on the nature of the solution methodology implemented. Thus, the above-mentioned problem requires a systematic and suitable approach to evaluate the solar panels. To address this concern, an integrated PF–SWARA–VIKOR method is developed that can successfully tackle the inherent uncertainty and the hesitancy in DEs’ opinions in the evaluation of the solar panel selection problem. The contributions of the present study are:
- (a)
- An integrated Pythagorean fuzzy–SWARA–VIKOR (PF–SWARA–VIKOR) framework is proposed.
- (b)
- The PFS-based SWARA method is utilized to assess the criteria weights.
- (c)
- A problem regarding the selection of solar panels is presented and evaluated by utilizing the proposed PF–SWARA–VIKOR method, which reveals the applicability of the introduced approach.
- (d)
- A comparative study and sensitivity analysis are also discussed to show the usefulness of the introduced approach.
The rest of the work is constructed as follows. Section 2 describes the elementary concepts associated with PFSs. Section 3 proposes the new PF–SWARA–VIKOR framework to tackle the MCDM problems with PFSs. Section 4 implements the developed framework in an empirical study of solar panel selection, which shows the applicability and strength of the developed framework. In addition, sensitivity analysis and a comparative study are presented to validate the stability of the outcomes. Section 5 discusses the concluding remarks of the whole study.
2. Preliminaries
Research manuscripts reporting large datasets that are deposited in a publicly available database should specify where the data have been deposited and provide the relevant accession numbers. If the accession numbers have not yet been obtained at the time of submission, please state that they will be provided during review. They must be provided prior to publication.
Here, we mention some essential definitions of PFSs.
Definition 1 [30,31].
A PFSin a finite universal setis presented as
whereandrepresent the MD and ND of an objecttorespectively, which satisfies a conditionFor eachthe functionis called the hesitation degree. The Pythagorean fuzzy number (PFN) [33] is defined by, which holdsand
Definition 2 [33].
Supposeto be a PFN. The score function and the accuracy function ofis described as
Sincetherefore, an improved score function of PFN is presented.
Definition 3.
Assume thatis a PFN. Then,the normalized score and uncertainty functions ofare described as
For any two PFNsand
ifthen
ifthen
ifthen
ifthen
Definition 4 [30,31].
Let, andbe the PFNs. Then, the following expressions are defined as
Definition 5 [33].
Letandbe the PFNs. Then, the distance betweenandis given by
3. Proposed Pythagorean Fuzzy–SWARA–VIKOR Method
Decision-making processes comprise a logical and scientific way for choosing a feasible course of action among multiple options. When we consider only one criterion for each alternative, the problem is referred to as single-criterion decision-making (SCDM); SCDM turns out to be less complicated because the decision can be constructed implicitly by choosing the optimal one under the best single criterion. Nevertheless, numerous real-life decision-making problems are evaluated under multiple criteria. Such problems turn into MCDM processes, where various MCDM approaches utilize the importance (i.e., weights) vectors of criteria.
Next, an integrated framework based on SWARA and VIKOR methods is introduced in a PFS environment and is named as the PF–SWARA–VIKOR method. In this framework, the subjective criteria weights are estimated by the SWARA method. The main advantage of the SWARA procedure is its ability to estimate the accuracy of the opinions of decision experts (DEs) regarding the weights assigned by the SWARA procedure. The VIKOR method [50] is a compromise programming-based technique to evaluate the compromise solution. Thus, the proposed study combines these two methods within the concept of PFSs, which determines the subjective criteria weights and then evaluates the preference order of the options, respectively. Brief descriptions of PF–SWARA–VIKOR are presented below:
Step I: Construct a decision matrix.
In the MCDM procedure, assume that is a set of ‘m’ alternatives and is a set of ‘n’ criteria. A set of DEs has been formed to obtain desirable alternative(s). Let be a decision matrix expressed by the DEs, wherein presents the evaluation of an alternative Ri concerning the criteria for the kth DE.
Step II: Evaluate the DEs’ weights.
The computation of the significance degrees of the DEs is an important concern in the process of MCDM. For evaluation of the kth DE, let be the Pythagorean fuzzy number, then the weight computation formula for kth DE is presented as follows:
Step III: Construct the aggregated Pythagorean fuzzy decision (APF-D) matrix.
To form the APF-D matrix, each single decision matrix is required to be united in one decision matrix by using the DEs’ opinions. To do this, a Pythagorean fuzzy weighted averaging (PFWA) [31] operator is utilized, and then is the APF-D matrix, where
Step IV: Evaluate the normalized APF-D matrix.
In the decision-making process, the APF-D matrix is converted into a normalized APF-D matrix where
where Tb and Tn denote the beneficial and non-beneficial criterion sets, respectively.
Step V: Calculate the criteria weights.
The SWARA procedure starts to rank the criteria, and directly compares the upper- to lower-ranking criteria pair-wise. Then, a comparative coefficient is evaluated, and the weight is decided and measured for handling decision-making problems. Estimation of criteria weights using SWARA is done using the following steps:
Step V-A: Calculate the crisp values. Score values of PFNs are computed by Equation (3) given in Definition 3.
Step V-B: Preference order of the criteria. The criteria are arranged according to the DE’s preferences from the most to the least significant criterion.
Step V-C: Evaluate the comparative significance of score value. The comparative significance is determined from the criteria that are preferred in the second place, and successive comparative significance is evaluated by differencing criterion j and j − 1.
Step V-D: Compute the comparative coefficient. The coefficient is given by
where sj presents the comparative significance of score value [41].
Step V-E: Estimate the weight. The recalculated weight pj is defined by
Step V-F: Evaluate the criteria weights. The criteria weights are defined by
Step VI: Find the best and worst values.
In the developed framework, the best and worst values are computed in terms of the PF-ideal solution (PF-IS) and the PF-anti-ideal solution (PF-AIS). Let and denote the PF-IS and PF-AIS, respectively; they are calculated as follows:
Step VII: Calculate the group utility, individual regret, and compromise measure.
In the present method, the group utility and individual regret of each alternative Ri are evaluated by employing the Hamming distance measure given in Equation (4). The group utility, individual regret, and compromise degree of the options are computed by using the following procedures:
where , and is the coefficient of the strategy of the majority of criteria (or maximum group utility), while is the coefficient of the strategy of the individual regret.
Step VIII: Estimate the ranking of the options.
On the basis of decreasing values of and determine the preference values of the alternatives. The minimum value of denotes the most desirable choice.
Step IX: Find the compromise solution.
For the uniqueness of the desirable solution, we have to check the following conditions:
(C1): Acceptable advantage:
where and are the options with the initial and subsequent positions in the ranking list, respectively, and m is the number of options.
(C2): Adequate stability: The option must also be ranked by and The compromise solution is stable within an MCDM procedure, which can be selected with “voting by majority rule ”, “by consensus ”, or “by veto ”.
If the acceptable advantage (C1) is not fulfilled, then the extreme value should be inspected by the given relation:
In this case, all of the options are the compromise solutions.
The options and are compromise solutions if the adequate stability (C2) is not fulfilled.
Step X: End.
4. An Empirical Study: Performance Evaluation of Solar Panel Selection
Here, the developed PF–SWARA–VIKOR framework is implemented to select the most suitable solar panel within the PFS context, which demonstrates the usefulness and feasibility of the introduced approach.
For this, we have selected a decision-making evaluation and selection problem of the performance of five typical solar panel alternatives, which are R1, R2, R3, R4 and R5. A team of three DEs is selected to process this solar panel selection problem. This problem associated with the performances of solar panels includes eight attributes or criteria. The facts of the criteria are given in Table 1.

Table 1.
Descriptions of considered criteria for solar panel selection.
To start the PF–SWARA–VIKOR approach, first, we assume the weights of the DEs are PFNs, which are given as {Y(0.75, 0.35, 0.5612), Y(0.60, 0.50, 0.6245), Y(0.65, 0.45, 0.6124)}. The PFN decision matrices given by DEs can be obtained in Table 2 in the form of as follows.

Table 2.
Linguistic values with different experts for solar panel selection.
Step I: Since the DEs’ weights as given by the experts are expressed in terms of PFNs, the crisp Des’ weights have been computed using Equation (5) as {, }.
Steps II–IV: Judgments provided by three DEs have been aggregated into an APF-D matrix by utilizing Equation (6) and are provided in Table 3.

Table 3.
Aggregated Pythagorean fuzzy (PF) decision matrix for solar panel evaluation.
As the criteria and are of cost type and the remaining are of benefit type, it is therefore necessary to form a normalized APF-D matrix using Equation (7). The normalized APF-D matrix is given in Table 4. The linguistic ratings of the criteria are given in Table 5.

Table 4.
Normalized aggregated PF decision matrix for solar panel selection.

Table 5.
Linguistic scale for the rating of criteria.
Steps V–IX: In the SWARA approach, the role of the DEs is an important part of the process of evaluation and criteria weighting. Each DE decides the significance of each criterion. Then, the DE provides the rankings of all the criteria based on their own implicit understanding, information, and experiences (see Table 6). From Table 7, the most important criterion is presented as rank 1 and the least important criterion is presented as the last one. Then, the final criteria weights are evaluated and given in Table 7 as follows:

Table 6.
Criteria weights given by the decision experts (DEs) in terms of LVs for solar panel evaluation.

Table 7.
Results obtained by the Stepwise Weight Assessment Ratio Analysis (SWARA) method for solar panel selection.
By employing Equations (11)–(12), the best and worst values of the solar panel alternatives are estimated as follows:
With the use of Equations (13)–(15), the values of Si, Ii, and Qi are calculated. The obtained results are given in Table 8. By employing the decreasing values of Si, Ii, and Qi, the preference order of the solar panel alternatives is acquired in Table 8. The lowest value of Qi denotes the optimal solar panel, i.e., R4 is the best solar panel alternative.

Table 8.
Group utility, individual regret, and compromise measure of each solar panel selection.
4.1. Sensitivity Analysis
This section discusses sensitivity analysis over different values of parameter . The values of vary from 0.0 to 1.0, but the preference order of the five preferred solar panel alternatives is the same in each case. Consequently, this study proves that the obtained outcome by employing PF–SWARA–VIKOR is more consistent and effective.
It can also be observed from Figure 1 that the compromise solution Qi of R1 decreases when the value of increases, while R2, R3, and R5 increases when the value of increases. Meanwhile, the fourth alternative R4 is stable in each set. Accordingly, despite the change of weights in the criterion set, the preference order of the five solar power alternatives remains the same. The final ranking of solar panel alternatives is presented with respect to following performance scores in Table 9, and it is observed that solar panel R4 is best of all options.
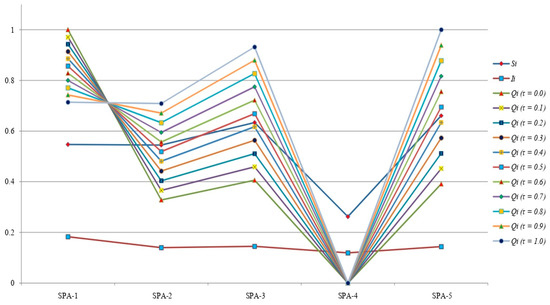
Figure 1.
Sensitivity analysis of the value for each alternative.

Table 9.
Different values of compromise solutions over various values of parameter .
4.2. Comparative Study
Here, a comparison was done between the results attained from the PF–SWARA–VIKOR method and those of another approach. To show the efficiency and display the irreplaceable merits of the PF–SWARA–VIKOR framework, the PF–TOPSIS method [33] is implemented to handle the decision-making problem.
PF-TOPSIS Method
Steps I–VI: Same as the previous method.
Step VII: Compute the degree of distances from PF-PIS and PF-NIS.
With the use of Equation (1), calculate the degree of weighted distance among the alternatives and the PF-IS
Usually, the smaller is, the better the alternative and let
and the degree of distance among the alternatives and the PF-AIS is given as follows:
The bigger the the better the alternative and let
Step VIII: Evaluate the relative closeness coefficient (CC).
The formula for the computation of the relative CC of each solar panel alternative is given as
In accordance with the closeness index the suitable solar panel alternative and the rankings of all options are decided. However, Hadi-Vencheh and Mirjaberi [64] explained that, in many circumstances, the relative CC cannot attain the goal that the most suitable solution should have the minimum distance from the PF-IS and the maximum distance from the PF-AIS, concurrently. Therefore, the revised CC of each alternative is defined by
Step IX: Choose the highest value, among the values Hence, is the optimal choice.
From Table 3 and Equations (11) and (12), PF-IS and PF-AIS are evaluated. Now, all computational results of the PF–TOPSIS [33] method are depicted in Table 10.

Table 10.
Computational results of the PF–Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS) method for solar panel selection.
Finally, the final ranking of the solar panel alternative is obtained as and Therefore, the most suitable solar panel alternative is Obviously, the results slightly vary with different types of methods. To this point, the PF–SWARA–VIKOR method is more robust than the PF–TOPSIS method [33] and thus has wider applicability.
From Figure 2, it is determined that the developed framework is highly consistent with the existing method with PFSs. To retain homogeneity in the method-related comparison, we consider the methods of Zhang and Xu [33] and Hadi-Vencheh and Mirjaberi [64]. The Spearman correlation values with the compromise solution are given by (0.70, 0.90, 1.00, 0.70, 0.825). Spearman correlation is utilized for these rank values to determine the consistency of the developed framework. In addition, Figure 3 depicts the prioritization orders of different methods with PFSs and makes a discussion of different factors to understand the strengths of the proposed framework.
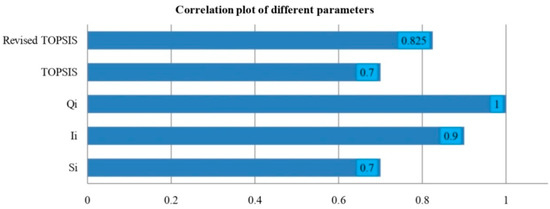
Figure 2.
Correlation plot of various measures of the VIKOR approach with existing approaches.
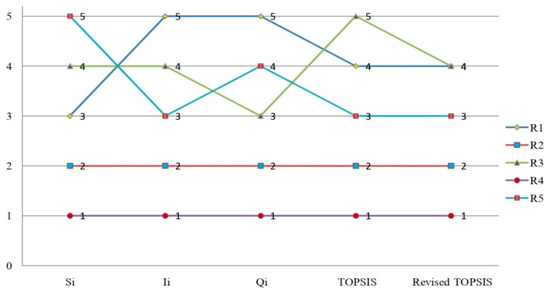
Figure 3.
Comparison of preference order of the Solar Panel Selection (SPS) alternatives with various approaches.
Furthermore, compared with the PF–TOPSIS method, the PF–SWARA–VIKOR approach has the following advantages:
- (a)
- The PF–SWARA–VIKOR method represents the Pythagorean fuzzy information, which can depict the MD, ND, and hesitation degree with an effortless mathematical description. Based on it, we can determine the significance degree of the DEs without any modification and, therefore, the developed method can successfully avoid the loss of information.
- (b)
- As some of the previous measures under the PFSs [33] have been incapable of providing the preference order of the alternatives accurately, thus, their consequent methods may not present relevant outcomes. Alternatively, the proposed approach has the capability to prevail over their limitations and is therefore able to order the alternatives appropriately, which makes it a more desirable approach to solving MCDM problems.
- (c)
- The SWARA approach is utilized to compute the subjective weights of criteria in the process of performance evaluation of solar panels, which makes the developed PF–SWARA–VIKOR approach more sensible, flexible, and efficient.
- (d)
- The developed framework has the following benefits when choosing solar panels:
- An innovative procedure is utilized to enumerate tangible sub-criteria successfully.
- The integrated approach eradicates the subjective estimation of indistinct sub-criteria.
- Pythagorean fuzzy SWARA is used to achieve appropriate harmonizing of criteria.
5. Conclusions
Recently, the selection of most appropriate solar panel has been a significant concern in the development of the sustainable era [65,66,67,68]. Owing to the occurrence of multiple conflicting criteria, the SPS problem can be considered as a complex MCDM problem. To handle this problem, an integrated decision-making framework has been introduced based on the SWARA and VIKOR approaches within a PFS context. In the developed framework, the criteria weights are computed by aggregating the subjective weights calculated by the SWARA method. Next, the VIKOR approach is used to evaluate the preference order of the alternatives. To exemplify the applicability and feasibility of the developed framework, a case study of solar panel selection has been presented, which confirmed its effectiveness and usefulness. Sensitivity analysis has also been discussed to show the stability of the introduced approach with respect to different sets of criteria weights. A comparative analysis has been presented to prove the strength of the outcomes obtained by the developed approach. In the future, we will expand our research by integrating objective and subjective criteria weight information within PFSs and q-rung orthopair fuzzy environments. Apart from the criteria used in this approach, the proposed model will be implemented in various selection scenarios, such as suitable locations of plants, sustainable suppliers, green suppliers, healthcare management, and others.
Author Contributions
P.R., A.R.M., F.C., D.Š., and A.M. conceived and worked together to achieve this work, P.R. and A.R.M. developed the method and worked on computational and comparative discussion, F.C. worked on the literature review, D.Š. worked on the case study and conclusion, and A.M. worked on the introduction. Finally, all the authors have read and approved the final manuscript. S.A.R.K. edited the final draft. All authors have read and agreed to the published version of the manuscript.
Funding
There is no funding for this research.
Conflicts of Interest
All authors declare that there is no conflict of interest.
References
- Streimikiene, D.; Balezentis, T.; Krisciukaitiene, I.; Balezentis, A. Prioritizing sustainable electricity production technologies: MCDM approach. Renew. Sustain. Energy Rev. 2012, 16, 3302–3311. [Google Scholar] [CrossRef]
- Dehghani, E.; Jabalameli, M.S.; Jabbarzadeh, A. Robust design and optimization of solar photovoltaic supply chain in an uncertain environment. Energy 2018, 142, 139–156. [Google Scholar] [CrossRef]
- Alblawi, A.; Elkholy, M.H.; Talaat, M. ANN for assessment of energy consumption of 4 kW PV modules over a year considering the impacts of temperature and irradiance. Sustainability 2019, 11, 6802. [Google Scholar] [CrossRef]
- Wang, T.-C.; Tsai, S.-Y. Solar Panel Supplier Selection for the Photovoltaic System Design by Using Fuzzy Multi-Criteria Decision Making (MCDM) Approaches. Energies 2018, 11, 1989. [Google Scholar] [CrossRef]
- Ramachandra, T.V.; Jha, R.K.; Vamsee Krishna, S.; Shruthi, B.V. Solar energy decision support system. Int. J. Sustain. Energy 2005, 24, 207–224. [Google Scholar] [CrossRef]
- Charabi, Y.; Gastli, A. GIS assessment of large CSP plant in Duqum, Oman. Renew. Sustain. Energy Rev. 2010, 14, 835–841. [Google Scholar] [CrossRef]
- Cavallaro, F. Fuzzy TOPSIS approach for assessing thermal-energy storage in concentrated solar power (CSP) systems. Appl. Energy 2010, 87, 496–503. [Google Scholar] [CrossRef]
- Beltran, P. An AHP (analytic hierarchy process)/ANP (analytic network process)-based multi-criteria decision approach for the selection of solar-thermal power plant investment project. Energy 2013, 17, 645–658. [Google Scholar]
- Khan, G.; Rathi, S. Optimal site selection for solar PV power plant in an Indian state using geographical information system (GIS). Int. J. Emerg. Eng. Res. Technol. 2014, 2, 260–266. [Google Scholar]
- Kowalski, K.; Stagl, S.; Madlener, R.; Omann, I. Sustainable energy futures: Methodological challenges in combining scenarios and participatory multi-criteria analysis. Eur. J. Oper. Res. 2017, 197, 1063–1074. [Google Scholar] [CrossRef]
- Tavana, M.; Arteaga, F.J.S.; Mohammadi, S.; Alimohammadi, M. A fuzzy multi-criteria spatial decision support system for solar farm location planning. Energy Strategy Rev 2017, 18, 93–105. [Google Scholar] [CrossRef]
- Ozdemir, S.; Sahin, G. Multi-criteria decision-making in the Location Selection for a Solar PV Power Plant using AHP. Measurement 2018, 129, 218–226. [Google Scholar] [CrossRef]
- Wang, C.-N.; Nguyen, V.T.; Thai, H.T.N.; Duong, D.H. Multi-Criteria Decision Making (MCDM) Approaches for Solar Power Plant Location Selection in Viet Nam. Energies 2018, 11, 1504. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control. 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Kengpol, A.; Rontlaong, P.; Tuominen, M. A decision support system for selection of solar power plant locations by applying fuzzy AHP and TOPSIS: An empirical study. J. Softw. Eng. Appl. 2013, 6, 470–481. [Google Scholar] [CrossRef]
- Sindhu, S.; Nehra, V.; Luthra, S. Investigation of feasibility study of solar farms deployment using hybrid AHP-TOPSIS analysis: Case study of India. Renew. Sustain. Energy Rev. 2017, 73, 496–511. [Google Scholar] [CrossRef]
- Sasikumar, G.; Ayyappan, S. Multi-criteria Decision Making for Solar Panel Selection Using Fuzzy Analytical Hierarchy Process and Technique for Order Preference by Similarity to ideal Solution (TOPSIS): An Empirical Study. J. Inst. Eng. (India) Ser. C 2019, 100, 707–715. [Google Scholar] [CrossRef]
- Atanassov, K. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Xia, M.; Xu, Z.S. Entropy/cross entropy-based group decision making under intuitionistic fuzzy environment. Inf. Fusion 2012, 13, 31–47. [Google Scholar] [CrossRef]
- Mishra, A.R. Intuitionistic fuzzy information with application in rating of township development. Iran. J. Fuzzy Syst. 2016, 13, 49–70. [Google Scholar]
- Mishra, A.R.; Rani, P. Shapley divergence measures with VIKOR method for multi-attribute decision-making problems. Neural Comput. Appl. 2019, 31, 1299–1316. [Google Scholar] [CrossRef]
- Xu, Z.S.; Yager, R.R. Some geometric aggregation operators based on intuitionistic fuzzy sets. Int. J. Gen. Syst. 2006, 35, 417–433. [Google Scholar] [CrossRef]
- Gumus, S.; Bali, O. Dynamic Aggregation Operators Based on Intuitionistic Fuzzy Tools and Einstein Operations. Fuzzy Inf. Eng. 2017, 9, 45–65. [Google Scholar] [CrossRef]
- Garg, H.; Rani, D. Some Generalized Complex Intuitionistic Fuzzy Aggregation Operators and Their Application to Multicriteria Decision-Making Process. Arab. J. Sci. Eng. 2019, 44, 2679–2698. [Google Scholar] [CrossRef]
- Dhivya, J.; Sridevi, B. A novel similarity measure between intuitionistic fuzzy sets based on the mid points of transformed triangular fuzzy numbers with applications to pattern recognition and medical diagnosis. Appl. Math. —A J. Chin. Univ. 2019, 34, 229–252. [Google Scholar] [CrossRef]
- Dutta, P.; Goala, S. Fuzzy decision making in medical diagnosis using an advanced distance measure on intuitionistic fuzzy sets. Open Cybern. Syst. J. 2018, 12, 136–149. [Google Scholar] [CrossRef]
- Yu, H.; Fan, J. A novel segmentation method for uneven lighting image with noise injection based on non-local spatial information and intuitionistic fuzzy entropy. Eurasip J. Adv. Signal Process. 2017. [Google Scholar] [CrossRef]
- Ansari, M.D.; Mishra, A.R.; Ansari, F.T. New divergence and entropy measures for intuitionistic fuzzy sets on edge detection. Int. J. Fuzzy Syst. 2018, 20, 474–487. [Google Scholar] [CrossRef]
- Mishra, A.R.; Kumari, R. Multi-criteria COPRAS Method Based on Parametric Measures for Intuitionistic Fuzzy Sets: Application of Green Supplier Selection. Iran. J. Sci. Technol. Trans. Electr. Eng. 2020. [Google Scholar] [CrossRef]
- Yager, R.R. Pythagorean Fuzzy Subsets. In Proceedings of the 2013 Joint IFSA World Congress and NAFIPS Annual Meeting, Edmonton, AB, Canada, 24–28 June 2013; pp. 57–61. [Google Scholar]
- Yager, R.R. Pythagorean membership grades in multicriteria decision making. IEEE Trans. Fuzzy Syst. 2014, 22, 958–965. [Google Scholar] [CrossRef]
- Yager, R.R.; Abbasov, A.M. Pythagorean membership grades, complex numbers and decision making. Int. J. Intell. Syst. 2013, 28, 436–452. [Google Scholar] [CrossRef]
- Zhang, X.L.; Xu, Z.S. Extension of TOPSIS to Multicriteria Decision Making with Pythagorean Fuzzy Sets. Int. J. Intell. Syst. 2014, 29, 1061–1078. [Google Scholar] [CrossRef]
- Gou, X.; Xu, Z.S.; Ren, P. The Properties of Continuous Pythagorean Fuzzy Information. Int. J. Intell. Syst. 2016, 31, 401–424. [Google Scholar] [CrossRef]
- Rani, P.; Mishra, A.R.; Razaei, G.; Liao, H.; Mardani, A. Extended Pythagorean Fuzzy TOPSIS Method Based on Similarity Measure for Sustainable Recycling Partner Selection. Int. J. Fuzzy Syst. 2019. [Google Scholar] [CrossRef]
- Rani, P.; Mishra, A.R.; Pardasani, K.R. A novel WASPAS approach for multi-criteria physician selection problem with intuitionistic fuzzy type-2 sets. Soft Comput. 2020, 24, 2355–2367. [Google Scholar] [CrossRef]
- Ma, Z.M.; Xu, Z.S. Symmetric Pythagorean Fuzzy Weighted Geometric/Averaging Operators and Their Application in Multicriteria Decision-Making Problems. Int. J. Intell. Syst. 2016, 31, 1198–1219. [Google Scholar] [CrossRef]
- Khan, A.A.; Ashraf, S.; Abdullah, S.; Qiyas, M.; Luo, J.; Khan, S.U. Pythagorean fuzzy Dombi aggregation operators and their application in decision support system. Symmetry 2019, 11, 383. [Google Scholar] [CrossRef]
- Liu, J.; Liu, P.; Liu, S.F.; Zhou, X.Z.; Zhang, T. A study of decision process in MCDM problems with large number of criteria. Int. Trans. Oper. Res. 2015, 22, 237–264. [Google Scholar] [CrossRef]
- Diakoulaki, D.; Mavrotas, G.; Papayannakis, L. Determining objective weights in multiple criteria problems: The CRITIC method. Comput. Oper. Res. 1995, 22, 763–770. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Podvezko, V. Integrated determination of objective criteria weights in MCDM. Int. J. Inf. Technol. Decis. Mak. 2016, 15, 267–283. [Google Scholar] [CrossRef]
- Mishra, A.R.; Rani, P.; Pardasani, K.R.; Mardani, A. A Novel Hesitant Fuzzy WASPAS Method for Assessment of Green Supplier Problem Based on Exponential Information Measures. J. Clean. Prod. 2019. [Google Scholar] [CrossRef]
- Rani, P.; Mishra, A.R.; Pardasani, K.R.; Mardani, A.; Liao, H.; Streimikiene, D. A novel VIKOR approach based on entropy and divergence measures of Pythagorean fuzzy sets to evaluate renewable energy technologies in India. J. Clean. Prod. 2019, 238. in press. [Google Scholar] [CrossRef]
- Kersuliene, V.; Zavadskas, E.K.; Turskis, Z. Selection of rational dispute resolution method by applying new step-wise weight assessment ratio analysis (SWARA). J. Bus. Econ. Manag. 2010, 11, 243–258. [Google Scholar] [CrossRef]
- Karabasevic, D.; Paunkovic, J.; Stanujkic, D. Ranking of companies according to the indicators of corporate social responsibility based on SWARA and ARAS methods. Serb. J. Manag. 2016, 11, 43–53. [Google Scholar] [CrossRef]
- Mardani, A.; Nilashi, M.; Zakuan, N.; Loganathan, N.; Soheilirad, S.; Saman, M.Z.M.; Ibrahim, O. A systematic review and meta-analysis of SWARA and WASPAS methods: Theory and applications with recent fuzzy developments. Appl. Soft Comput. 2017, 57, 265–292. [Google Scholar] [CrossRef]
- Maghsoodi, A.I.; Maghsoodi, A.I.; Mosavi, A.; Rabczuk, T.; Zavadskas, E.K. Renewable Energy Technology Selection Problem Using Integrated H-SWARA-MULTIMOORA approach. Sustainability 2018, 10, 4481. [Google Scholar] [CrossRef]
- Ghorabaee, M.K.; Amiri, M.; Zavadskas, E.K.; Turskis, Z.; Antuchevicience, J. An extended step-wise weight assessment ratio analysis with symmetric interval type-2 fuzzy sets for determining the subjective weights of criteria in multi-criteria decision-making problems. Symmetry 2018, 10, 91. [Google Scholar] [CrossRef]
- Rani, P.; Mishra, A.R. Single-valued neutrosophic SWARA-VIKOR framework for performance assessment of eco-industrial thermal power plants. ICSES Trans. Neural Fuzzy Comput. 2020, 3, 1–9. [Google Scholar]
- Opricovic, S. Multicriteria optimization of civil engineering systems. Fac. Civ. Eng. Belgrade 1998, 2, 5–21. [Google Scholar]
- Opricovic, S.; Tzeng, G.H. Multicriteria planning of post-earthquake sustainable reconstruction. Comput Aided Civ. Infrastruct. Eng 2002, 17, 211–220. [Google Scholar] [CrossRef]
- Opricovic, S.; Tzeng, G.H. Compromise solution by MCDM methods: A comparative analysis of VIKOR and TOPSIS. Eur. J. Oper. Res. 2004, 156, 445–455. [Google Scholar] [CrossRef]
- Tzeng, G.H.; Lin, C.W.; Opricovic, S. Multi-criteria analysis of alternative-fuel buses for public transportation. Energy Policy 2005, 33, 1373–1383. [Google Scholar] [CrossRef]
- Mardani, A.; Zavadskas, E.K.; Govindan, K.; Senin, A.A.; Jusoh, A. VIKOR Technique: A Systematic Review of the State of the Art Literature on Methodologies and Applications. Sustainability 2016, 8, 37. [Google Scholar] [CrossRef]
- Zhang, X.; Xing, X. Probabilistic linguistic VIKOR method to evaluate green supply chain initiatives. Sustainability 2017, 9, 1231. [Google Scholar] [CrossRef]
- Suh, Y.; Park, Y.; Kang, D. Evaluating mobile services using integrated weighting approach and fuzzy VIKOR. PloS ONE 2019, 14, e0222312. [Google Scholar]
- Krishankumar, R.; Premaladha, J.; Ravichandran, K.S.; Sekar, K.R.; Manikandan, R.; Gao, X.Z. A novel extension to VIKOR method under intuitionistic fuzzy context for solving personnel selection problem. Soft Comput. 2020, 24, 1063–1081. [Google Scholar] [CrossRef]
- Phochanikorn, P.; Tan, C. A new extension to a multi-criteria decision-making model for sustainable supplier selection under an intuitionistic fuzzy environment. Sustainability 2019, 11, 5413. [Google Scholar] [CrossRef]
- Salimi, A.H.; Noori, A.; Bonakdari, H.; Samakosh, J.M.; Sharifi, E.; Hassanvand, M.; Gharabaghi, B.; Agharazi, M. Exploring the Role of Advertising Types on Improving the Water Consumption Behavior: An Application of Integrated Fuzzy AHP and Fuzzy VIKOR Method. Sustainability 2020, 12, 1232. [Google Scholar] [CrossRef]
- Taylan, O.; Alamoudi, R.; Kabli, M.; AlJifri, A.; Ramzi, F.; Herrera-Viedma, E. Assessment of energy systems using extended fuzzy AHP, fuzzy VIKOR, and TOPSIS approaches to manage non-cooperative opinions. Sustainability 2020, 12, 2745. [Google Scholar] [CrossRef]
- Chen, T.-Y. A novel VIKOR method with an application to multiple criteria decision analysis for hospital-based post-acute care within a highly complex uncertain environment. Neural Comput. Appl. 2019, 31, 3969–3999. [Google Scholar] [CrossRef]
- Rani, P.; Jain, D. Information measures-based multi-criteria decision-making problems for interval-valued intuitionistic fuzzy environment. Proc. Natl. Acad. Sci. India Sect. A: Phys. Sci. 2019, in press. [Google Scholar] [CrossRef]
- Pérez-Velázquez, A.; Oro-Carralero, L.L.; Moya-Rodríguez, J.L. Supplier selection for photovoltaic module installation utilizing fuzzy inference and the VIKOR method: A green approach. Sustainability 2020, 12, 2242. [Google Scholar] [CrossRef]
- Hadi-Vencheh, A.; Mirjaberi, M. Fuzzy inferior ratio method for multiple attribute decision making problems. Inf. Sci. 2014, 277, 263–272. [Google Scholar] [CrossRef]
- Cavallaro, F.; Marino, D.; Streimikiene, D. Environmental Assessment of a Solar Tower Using the Life Cycle Assessment (Lca); Springer International Publishing: Cham, Switzerland, 2019; pp. 621–628. [Google Scholar]
- Cavallaro, F.; Zavadskas, E.K.; Streimikiene, D. Concentrated solar power (csp) hybridized systems. Ranking based on an intuitionistic fuzzy multi-criteria algorithm. J. Clean. Prod. 2018, 179, 407–416. [Google Scholar] [CrossRef]
- Cavallaro, F.; Zavadskas, E.K.; Streimikiene, D.; Mardani, A. Assessment of concentrated solar power (csp) technologies based on a modified intuitionistic fuzzy topsis and trigonometric entropy weights. Technol. Forecast. Soc. Chang. 2019, 140, 258–270. [Google Scholar] [CrossRef]
- Cavallaro, F.; Ciraolo, L. Sustainability Assessment of Solar Technologies Based on Linguistic Information. In Assessment and Simulation Tools for Sustainable Energy Systems. Theory and Application; Green Energy and Technology; Cavallaro, F., Ed.; Springer: London, UK, 2013; pp. 3–25. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).