Modeling and Simulation of Pedestrian Movement Planning Around Corners
Abstract
1. Introduction
2. Model Framework
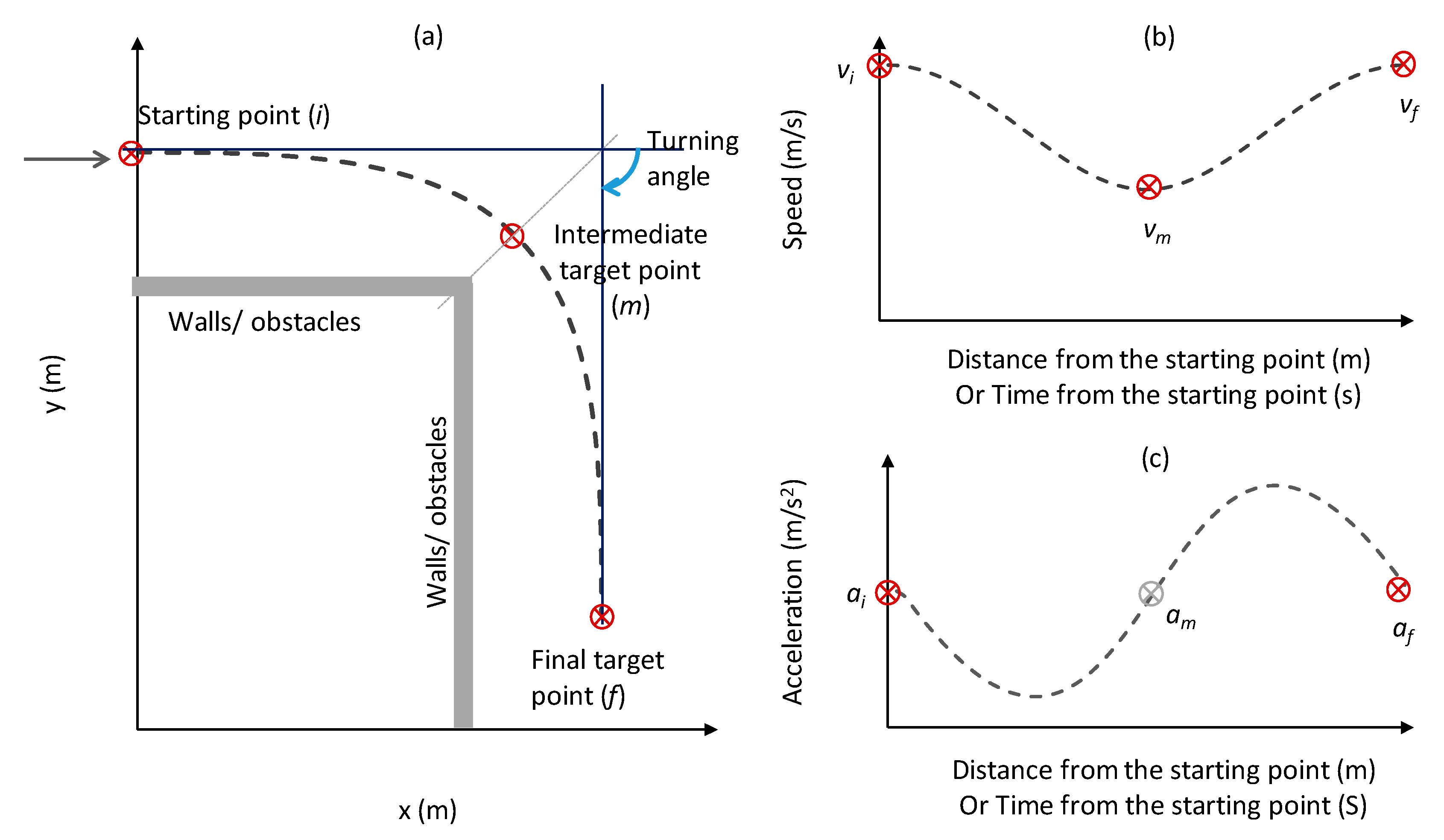
2.1. Problem Description
2.2. Minimum-Jerk Concept
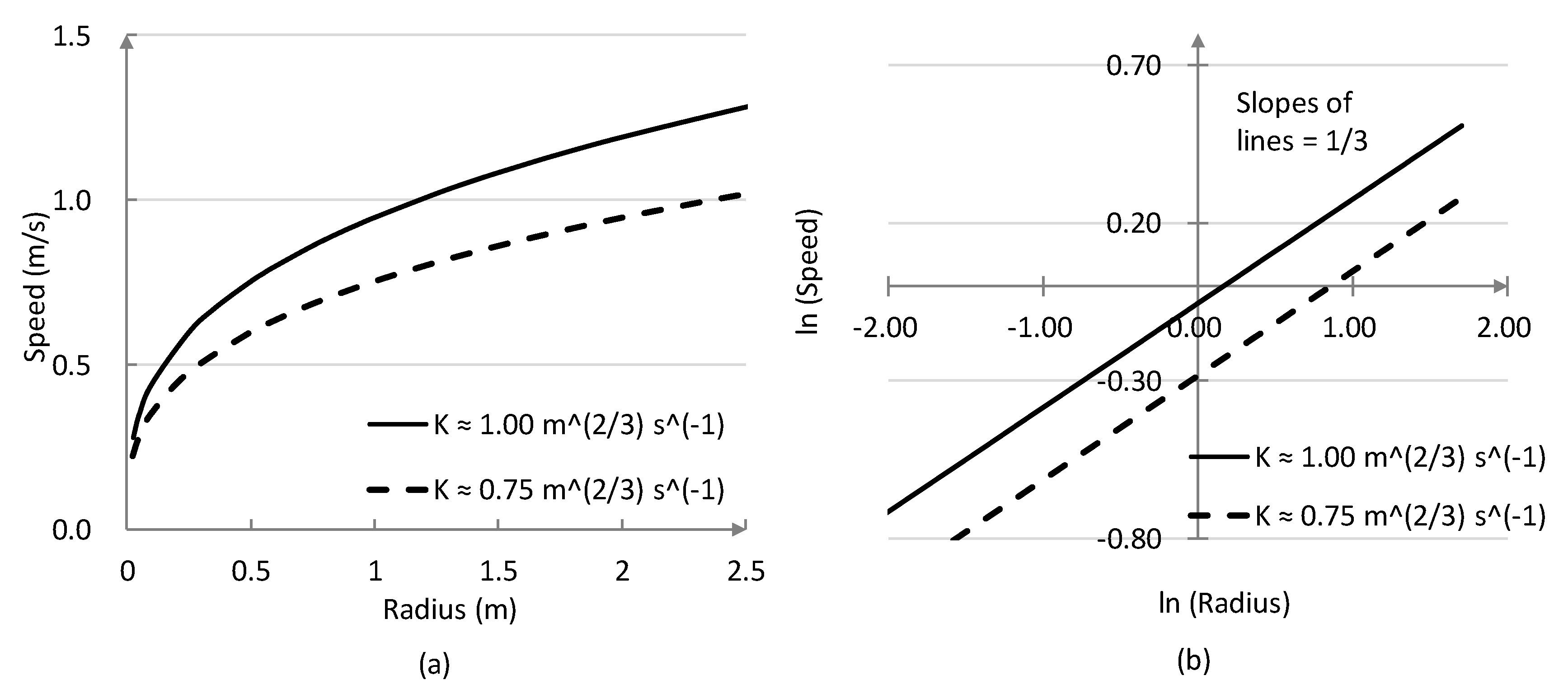
2.3. One-Thirds Power Law Concept
2.4. Model Formulation
3. Model Verification
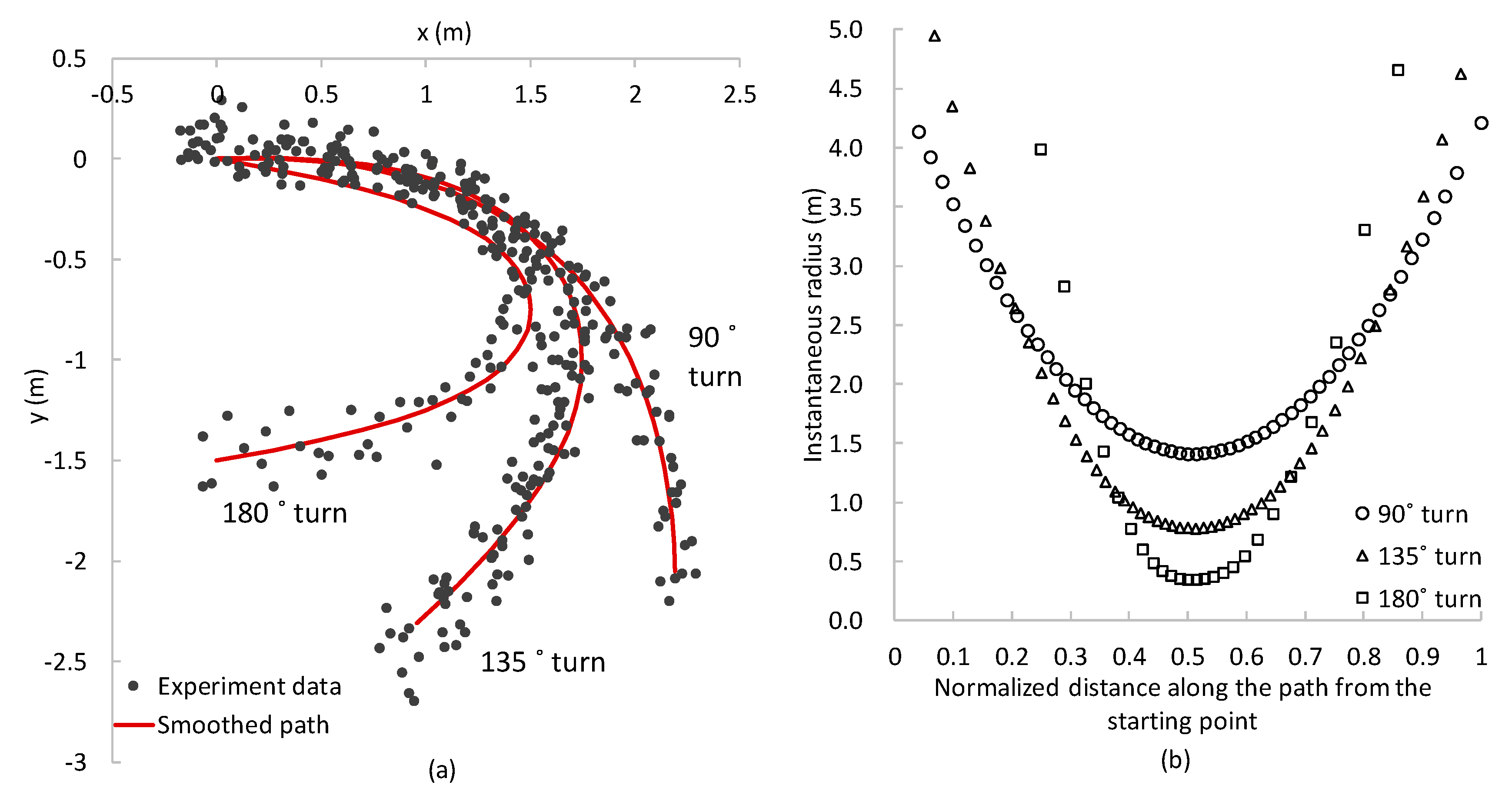
3.1. Estimating Instantaneous Radius of the Path
3.2. Power Law Parameters
3.3. Results
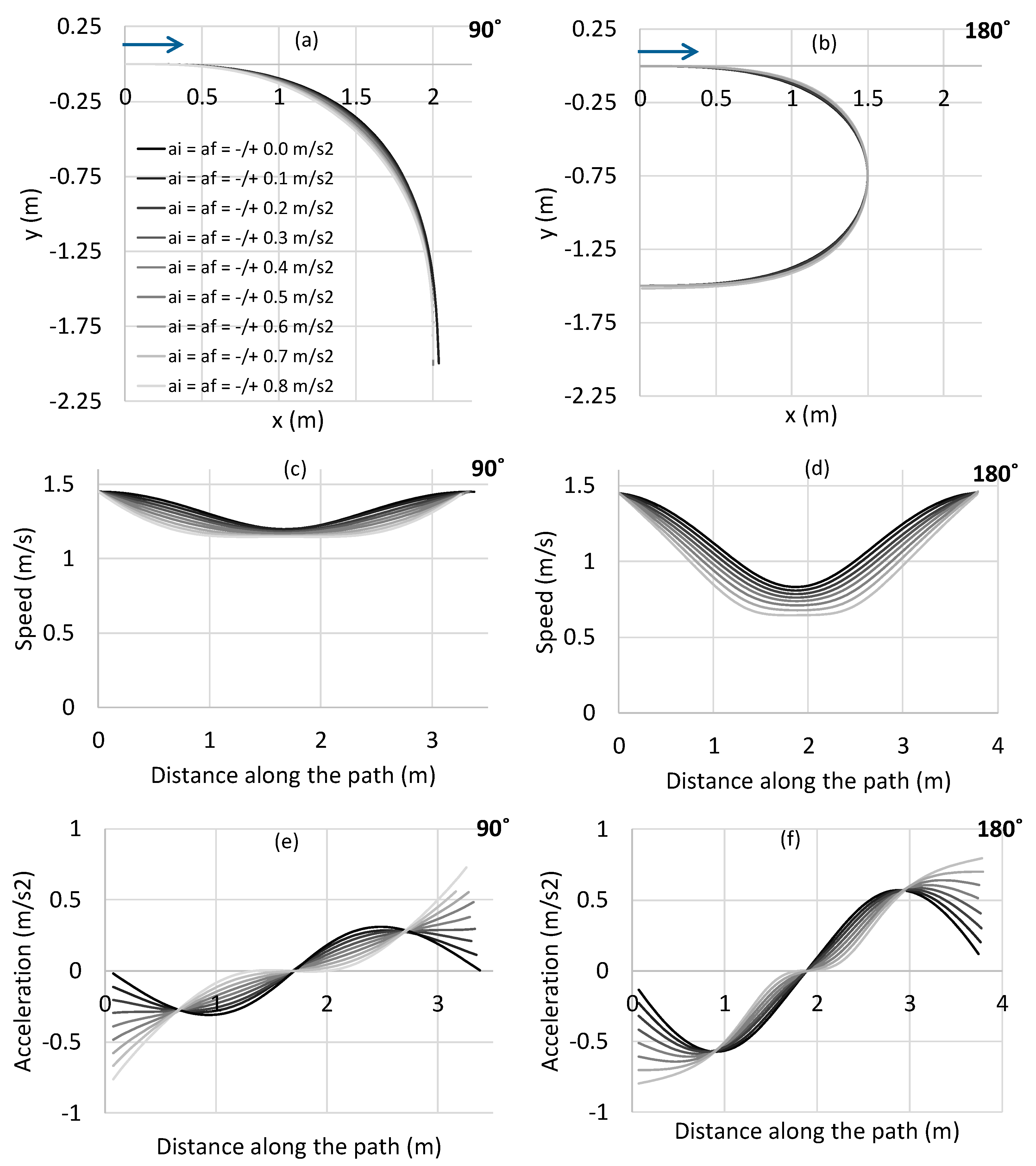
4. Sensitivity Analysis
4.1. Entry and Exit Acceleration
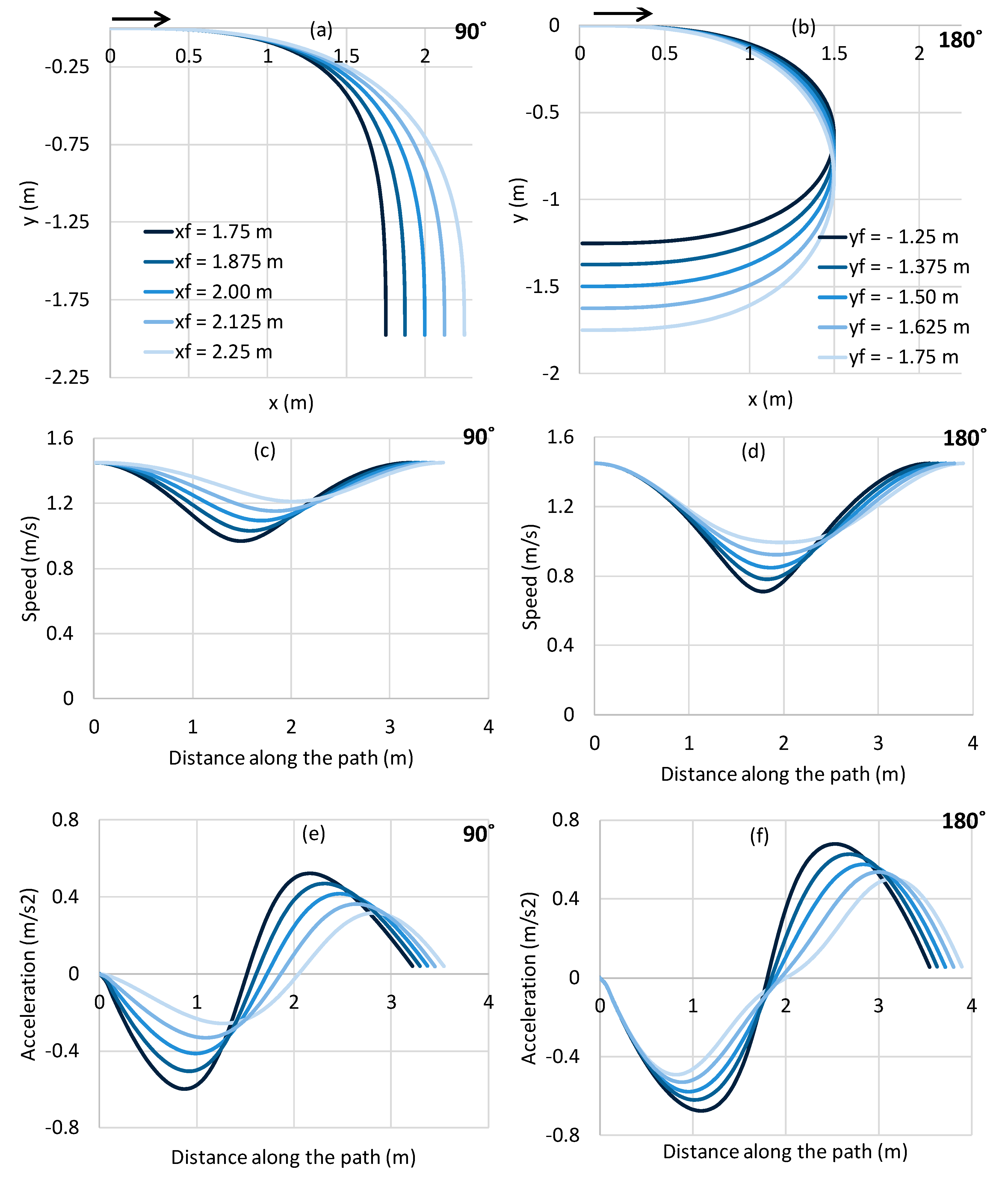
4.2. Exit Location
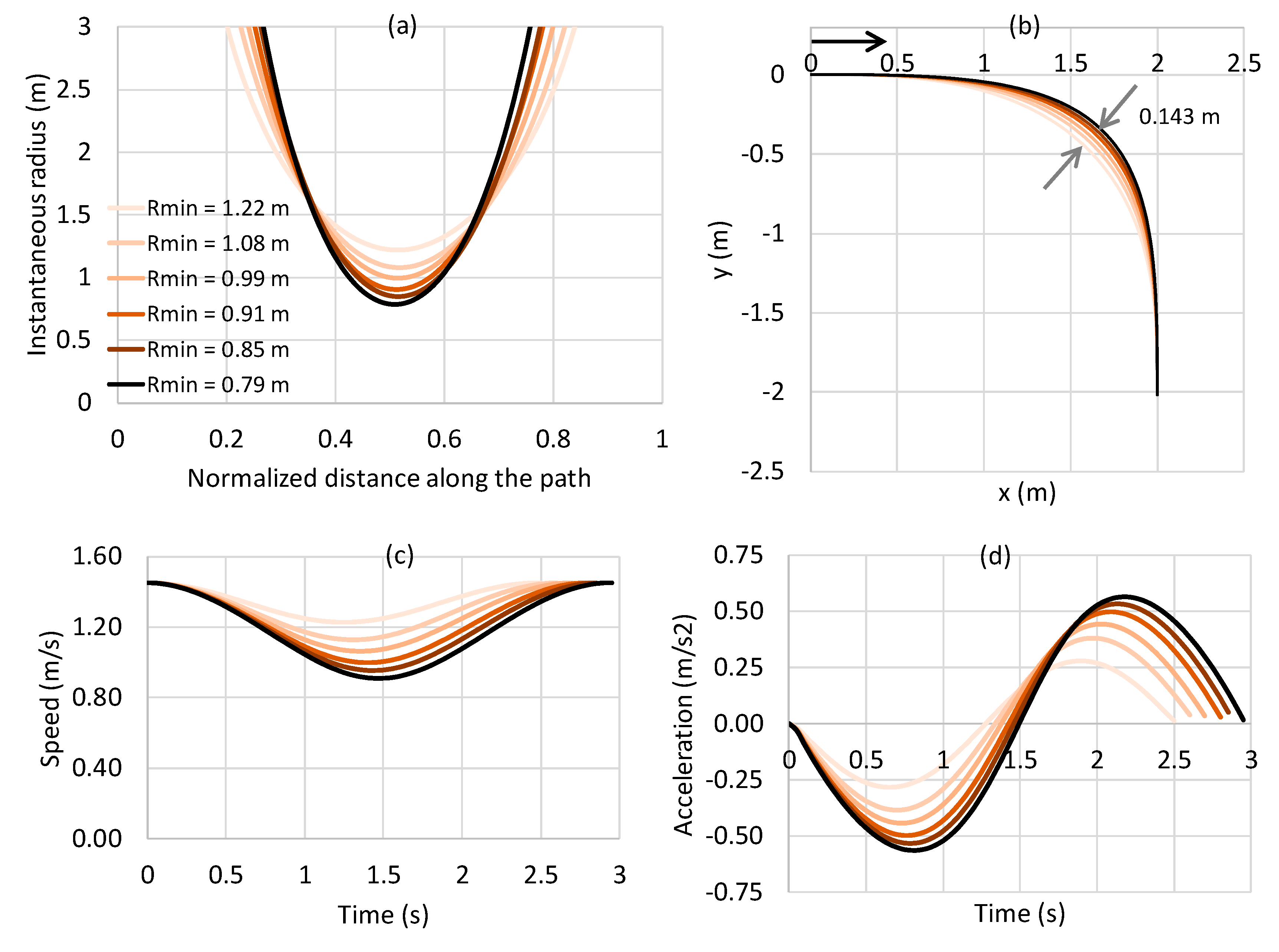
4.3. Radius of the Walking Path
5. Conclusions and Further Studies
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Sedgman, R.; Goldie, P.; Iansek, R. Development of a measure of turning during walking. In Proceedings of the Advancing Rehabilitation: Inaugural Conference of the Faculty of Health Sciences, Bundoora, Australia, 2–4 November 1994. [Google Scholar]
- Morris, M.E.; Huxham, F.; McGinley, J.; Dodd, K.; Iansek, R. The biomechanics and motor control of gait in Parkinson disease. Clin. Biomech. 2001, 16, 459–470. [Google Scholar] [CrossRef]
- Odonkor, C.A.; Thomas, J.C.; Holt, N.; Latham, N.; Van Swearingen, J.; Brach, J.S.; Leveille, S.G.; Jette, A.; Bean, J. A comparison of straight-and curved-path walking tests among mobility-limited older adults. J. Gerontol. A Biomed. Sci. Med. Sci. 2013, 68, 1532–1539. [Google Scholar] [CrossRef] [PubMed]
- Patla, A.E.; Prentice, S.D.; Robinson, C.; Neufeld, J. Visual control of locomotion: Strategies for changing direction and for going over obstacles. J. Exp. Psychol. Hum. Percept. Perform. 1991, 17, 603. [Google Scholar] [CrossRef] [PubMed]
- Hase, K.; Stein, R.B. Turning strategies during human walking. J. Neurophysiol. 1999, 81, 2914–2922. [Google Scholar] [CrossRef] [PubMed]
- Taylor, M.J.; Dabnichki, P.; Strike, S.C. A three-dimensional biomechanical comparison between turning strategies during the stance phase of walking. Hum. Mov. Sci. 2005, 24, 558–573. [Google Scholar] [CrossRef] [PubMed]
- Courtine, G.; Schieppati, M. Human walking along a curved path. II. Gait features and EMG patterns. Eur. J. Neurosci. 2003, 18, 191–205. [Google Scholar] [CrossRef]
- Akiyama, Y.; Okamoto, S.; Toda, H.; Ogura, T.; Yamada, Y. Gait motion for naturally curving variously shaped corners. Adv. Robot. 2018, 32, 77–88. [Google Scholar] [CrossRef]
- Shiwakoti, N.; Sarvi, M.; Rose, G.; Burd, M. Consequence of turning movements in pedestrian crowds during emergency egress. Transp. Res. Rec. J. Transp. Res. Board 2011, 2234, 97–104. [Google Scholar] [CrossRef]
- Dias, C.; Sarvi, M.; Shiwakoti, N.; Ejtemai, O.; Burd, M. Investigating collective escape behaviours in complex situations. Saf. Sci. 2013, 60, 87–94. [Google Scholar] [CrossRef]
- Kretz, T. The use of dynamic distance potential fields for pedestrian flow around corners. In Proceedings of the First International Conference on Evacuation Modeling and Management (ICEM 09), TU Delft, The Netherlands, 23–25 September 2009. [Google Scholar]
- Guo, R.Y.; Tang, T.Q. A simulation model for pedestrian flow through walkways with corners. Simul. Model. Pract. Theory 2012, 21, 103–113. [Google Scholar] [CrossRef]
- Dias, C.; Ejtemai, O.; Sarvi, M.; Burd, M. Exploring pedestrian walking through angled corridors. Transp. Res. Procedia 2014, 2, 19–25. [Google Scholar] [CrossRef]
- Li, S.; Li, X.; Qu, Y.; Jia, B. Block-based floor field model for pedestrian’s walking through corner. Phys. A Stat. Mech. Appl. 2015, 432, 337–353. [Google Scholar] [CrossRef]
- Dias, C.; Lovreglio, R. Calibrating cellular automaton models for pedestrians walking through corners. Phys. Lett. A 2018, 382, 1255–1261. [Google Scholar] [CrossRef]
- Dias, C.; Ejtemai, O.; Sarvi, M.; Shiwakoti, N. Pedestrian walking characteristics through angled corridors: An experimental study. Transp. Res. Rec. J. Transp. Res. Board 2014, 2421, 41–50. [Google Scholar] [CrossRef]
- Grasso, R.; Ivanenko, Y.P.; McIntyre, J.; Viaud-Delmon, I.; Berthoz, A. Spatial, not temporal cues drive predictive orienting movements during navigation: A virtual reality study. Neuroreport 2000, 11, 775–778. [Google Scholar] [CrossRef]
- Prévost, P.; Yuri, I.; Renato, G.; Alain, B. Spatial invariance in anticipatory orienting behaviour during human navigation. Neurosci. Lett. 2003, 339, 243–247. [Google Scholar] [CrossRef]
- Flash, T.; Hogan, N. The coordination of arm movements: An experimentally confirmed mathematical model. J. Neurosci. 1985, 5, 1688–1703. [Google Scholar] [CrossRef]
- Bratt, M.; Smith, C.; Christensen, H.I. Minimum jerk based prediction of user actions for a ball catching task. In Proceedings of the 2007 IEEE/RSJ International Conference on Intelligent Robots and Systems, San Diego, CA, USA, 29 October–2 November 2007; pp. 2710–2716. [Google Scholar]
- Pham, Q.C.; Hicheur, H.; Arechavaleta, G.; Laumond, J.P.; Berthoz, A. The formation of trajectories during goal-oriented locomotion in humans. II. A maximum smoothness model. Eur. J. Neurosci. 2007, 26, 2391–2403. [Google Scholar] [CrossRef]
- Shamir, T. How should an autonomous vehicle overtake a slower moving vehicle: Design and analysis of an optimal trajectory. IEEE Trans. Autom. Control 2004, 49, 607–610. [Google Scholar] [CrossRef]
- Wada, Y.; Kawato, M. A via-point time optimization algorithm for complex sequential trajectory formation. Neural Netw. 2004, 17, 353–364. [Google Scholar] [CrossRef]
- Dias, C.; Oguchi, T.; Wimalasena, K. Drivers’ Speeding Behavior on Expressway Curves: Exploring the Effect of Curve Radius and Desired Speed. Transp. Res. Rec. 2018, 2672, 48–60. [Google Scholar] [CrossRef]
- Lacquaniti, F.; Terzuolo, C.; Viviani, P. The law relating the kinematic and figural aspects of drawing movements. Acta Psychol. 1983, 54, 115–130. [Google Scholar] [CrossRef]
- Viviani, P.; Schneider, R. A developmental study of the relationship between geometry and kinematics in drawing movements. J. Exp. Psychol. Hum. Percept. Perform. 1991, 17, 198. [Google Scholar] [CrossRef] [PubMed]
- Gribble, P.L.; Ostry, D.J. Origins of the power law relation between movement velocity and curvature: Modeling the effects of muscle mechanics and limb dynamics. J. Neurophysiol. 1996, 76, 2853–2860. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Vieilledent, S.; Kerlirzin, Y.; Dalbera, S.; Berthoz, A. Relationship between velocity and curvature of a human locomotor trajectory. Neurosci. Lett. 2001, 305, 65–69. [Google Scholar] [CrossRef]
- Hicheur, H.; Vieilledent, S.; Richardson, M.J.E.; Flash, T.; Berthoz, A. Velocity and curvature in human locomotion along complex curved paths: A comparison with hand movements. Exp. Brain Res. 2005, 162, 145–154. [Google Scholar] [CrossRef] [PubMed]
- Fay, M.P.; Proschan, M.A. Wilcoxon-Mann-Whitney or t-test? On assumptions for hypothesis tests and multiple interpretations of decision rules. Stat. Surv. 2010, 4, 1–39. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dias, C.; Abdullah, M.; Sarvi, M.; Lovreglio, R.; Alhajyaseen, W. Modeling and Simulation of Pedestrian Movement Planning Around Corners. Sustainability 2019, 11, 5501. https://doi.org/10.3390/su11195501
Dias C, Abdullah M, Sarvi M, Lovreglio R, Alhajyaseen W. Modeling and Simulation of Pedestrian Movement Planning Around Corners. Sustainability. 2019; 11(19):5501. https://doi.org/10.3390/su11195501
Chicago/Turabian StyleDias, Charitha, Muhammad Abdullah, Majid Sarvi, Ruggiero Lovreglio, and Wael Alhajyaseen. 2019. "Modeling and Simulation of Pedestrian Movement Planning Around Corners" Sustainability 11, no. 19: 5501. https://doi.org/10.3390/su11195501
APA StyleDias, C., Abdullah, M., Sarvi, M., Lovreglio, R., & Alhajyaseen, W. (2019). Modeling and Simulation of Pedestrian Movement Planning Around Corners. Sustainability, 11(19), 5501. https://doi.org/10.3390/su11195501






