Abstract
With fast-growing interest in sustainable healthcare management, proper selection and evaluation of hospitals become highly essential. Generally, experts/decision-makers (DMs) prefer qualitative information for rating objects. Motivated by this idea, in this paper, a linguistic hesitant fuzzy set (LHFS) is adopted for elicitation of preference information. The LHFS provides qualitative preferences of DMs as well as reflects their hesitancy, inconsistency, and vagueness. Motivated by the power of LHFS, in this paper we present a new decision framework that initially presents some operational laws and properties. Further, a new aggregation operator called simple linguistic hesitant fuzzy weighted geometry (SLHFWG) is proposed under the LHFS context that uses the strength of power operators. Some properties of SLHFWG are also investigated. Criteria weights are estimated using a newly proposed linguistic hesitant fuzzy statistical variance (LHFSV) method, and objects are ranked using the newly proposed linguistic hesitant fuzzy VIKOR (visekriterijumska optimizacijai kompromisno resenje) (LHFVIKOR) method, which is an extension of VIKOR under the LHFS context. The practicality and usefulness of the proposal are demonstrated by using a hospital evaluation example for sustainable healthcare management. Finally, the strengths and weaknesses of the proposal are realized by comparison with other methods.
1. Introduction
The WHO (World Health Organization) conducted a survey recently and predicted that by 2050, seven out of ten people would live in cities [1]. Along with such high demand for city lives, the risks and hazards also grow. To better circumvent the issue, there is an urgent need for proper and sustainable healthcare management. The AIMA (All India Management Association) [2] claimed that among various stages in sustainable healthcare management, the suitable selection of a hospital is highly substantial. Motivated by this claim, many scholars came up with different methods [3,4,5] for the proper evaluation and selection of hospitals. Based on the analysis, it is clear that decision maker(s)(DMs) prefer qualitative preference information for rating objects and the research on linguistic decision making is an attractive and hot topic for exploration in the present scenario. Due to factors such as lack of experience, time pressure, nature of objects, etc., DMs are unable to express their preferences quantitatively. To better circumvent this issue, Zadeh [6] introduced the idea of qualitative decision-making, where the preferences are given as linguistic terms. After the advent of the linguistic term set (LTS) [7], many scholars put forward different theories and concepts [8,9,10]. However, in many practical applications, expressing the viewpoints using the single linguistic term is unreasonable and impractical.
With a view of alleviating such an issue, Rodriguez et al. [11] put forward the concept of a hesitant fuzzy linguistic term set (HFLTS), which combines a hesitant fuzzy set (HFS) [12] with an LTS, where multiple terms are used by the DMs for expressing their viewpoints. Later, Rodriguez et al. [13] presented a study on different fuzzy linguistic models and claimed that HFLTS is a powerful concept for modeling uncertainty in preference elicitation. Further, motivated by the ability of HFLTS (as discussed in Reference [13]) in modeling complex linguistic terms, many scholars [14,15,16,17,18,19,20,21,22,23] presented new theories and concepts under the HFLTS context. Though the HFLTS circumvents the issue of LTS, it is not able to properly reflect the hesitancy and vagueness of the DM. Rodriguez et al. [24] conducted a survey on HFS along with some of its variants and claimed that HFS is a powerful tool for reflecting the hesitation of the DM and presented some future directions. Recently, Liao et al. [25] conducted a deep analysis on HFLTS and presented some challenges and future scope of HFLTS. Attracted by these surveys, and with a view of alleviating the challenge (discussed above), Meng et al. [26] proposed a new concept called a linguistic hesitant fuzzy set (LHFS), which addresses the qualitative preferences of DMs and also reflects the hesitancy and vagueness of the DMs. Inspired by the power of LHFS, Yu et al. [27] extended the Heronian arithmetic and geometric mean operators for LHFS and applied the same for the decision-making process. Zhou et al. [28] extended the Hamming distance and proposed new order relations under an LHFS environment. They also applied the genetic algorithm for a criteria weight calculation and used evidential reasoning for aggregation. Liu et al. [29] extended the linear programming technique for the multi-dimensional analysis of preferences (LINMAP) method for LHFS and used it for solving multi-criteria group decision-making (MCGDM) problems. Further, Zhu et al. [30] developed a new concept called a comprehensive cloud for unifying LHFSs of different lengths. They also extended power operators under an LHFS and applied the same for decision-making. Guan et al. [31] extended different distance and correlation measures under an LHFS environment for the decision-making process. Recently, Dong et al. [32] extended the popular VIKOR method to an LHFS environment and applied the same for intelligent transport system selection. Yuan et al. [33] extended the Choquet integral for LHFS and applied the same for the selection of renewable energy sources. Meng et al. [34] extended the idea of an LHFS by using interval numbers for membership values and put forward a new similarity measure for solving decision-making problems.
Based on the review conducted above, it is clear that the LHFS is an attractive concept for decision-making and the exploration of this concept has just begun. Also from the review, we identify some potential challenges, which are listed below:
- The primary challenge encountered is that there is an urgent need for a scientific decision-making framework under an LHFS to utilize the potential power of an LHFS.
- Following this, the idea of aggregation of LHFS-based preference information has just begun and there is a good scope for exploration. The claim by Xu and Liao [35] to produce consistent aggregated preference information is an interesting challenge to be addressed.
- Another challenge is the calculation of criteria weights using the systematic procedure for obtaining sensible weight values.
- Further, ranking of objects by using LHFS-based preference information is another interesting challenge to address for better decision-making under uncertain situations. Though Dong et al. [32] extended the popular VIKOR method to an LHFS, the challenge of using the method for MCGDM still needs to be addressed.
- Finally, comprehensive comparison of the proposed framework with other methods for realizing the strength and weakness of the proposal is an attractive challenge for exploration.
Motivated by these challenges, some genuine contributions of the proposal are presented in a nutshell below:
- (1)
- With a view of alleviating the primary challenge, a new decision framework is proposed under an LHFS context to utilize the potential power of an LHFS.
- (2)
- Following this, a new aggregation operator called simple linguistic hesitant fuzzy weighted geometry (SLHFWG) is presented with the view of producing consistent aggregated preference information by extending the operator discussed in Reference [35] under an LHFS context. This operator also uses the idea of a power geometry operator for sensible aggregation. He et al. [36] claimed that “whenever the relationship between the objects and criteria are to be aggregated, some unduly high and low information may have some bad impact on the aggregation process. In order to mitigate the effect, support measures are to be used which assign weights to information. This showcases the urge need for power operators during aggregation”. Motivated by this claim, we set our focus in this direction.
- (3)
- Further, a new method for criteria weight estimation is presented which is an extension to standard variance (SV) under an LHFS context. Previous studies on weight estimation have predominantly used entropy measures [37], optimization models [38,39,40], analytic hierarchy process (AHP) [41] method, and decision making trial and evaluation laboratory (DEMATEL) [42], etc., which often yields unreasonable and irrational weight values. Motivated by this challenge, we set our proposal towards this direction.
- (4)
- Also, the popular linguistic hesitant fuzzy visekriterijumska optimizacijai kompromisno resenje (LHFVIKOR) method is adopted for selecting a suitable hospital from a set of hospitals. This example is an MCGDM problem that clarifies the practicality and usefulness of the proposed decision framework and addresses the challenge mentioned by Dong et al. [32].
- (5)
- Finally, the strengths and weaknesses of the proposed framework is realized by comparison with other methods.
The remainder of the paper is organized as Section 2 for preliminaries, Section 3 for the LHFS and its basic concepts, where some operational laws and properties are presented, along with a new aggregation operator, criteria weight estimation method, and ranking method. Following this, in Section 4, a numerical example for hospital evaluation is demonstrated to realize the practicality and usefulness of the proposal, Section 5 presents a comparative study of the proposal with other methods, and finally, Section 6 gives the concluding remarks.
2. Preliminaries
Let us review some basics of LTS, PLTS, and HFS.
Definition 1
[7]: Let be a linguistic term set that is of the form , where n is a positive integer, and and are the lower and upper bounds of the term set. The linguistic term has the following properties:
- andare two linguistic term sets, and the relationholds true, if.
- Negation ofis given by, such that.
Definition 2
[12]: Let be a reference set, and HFS on is a function that maps every element of Y to a subset [0,1]. Mathematically, it is given by:
where is a set of values in the range [0,1] that represent the membership values of the element to the set E.
Definition 3
[12]: Let , and be three hesitant fuzzy elements, where some basic operational laws are given by,
Definition 4
[26]: Consider an LTS of the form , then, the LHFS is a set that when applied to the linguistic terms of yields a subset with many values in [0,1] and is mathematically defined by:
where is the kth linguistic term with its corresponding possible membership degrees, is the number of linguistic term(s), and m is the number of possible membership degrees for each linguistic term.
Remark 1:
For ease of representation, we represent the linguistic hesitant fuzzy element (LHFE) as, whereis the kth subscript of the linguistic term andis the possible membership degrees of.
3. Proposed Decision Framework under LHFS Context
3.1. Some Operational Laws and Properties of LHFS
Let us now present some properties and basic operational laws.
Definition 5:
Consider an LTSthat is of the form, then the empty LHFS and full LHFS is given by:
- Empty LHFS;
- Full LHFS;
Definition 6:
Consider an LHFSthat is of the form, then the complement of LHFSis given bywith.
Proposition 1:
The complement of a LHFS is involutive.
Proof:
If , then complement of is given by with . ☐
Definition 7:
Consider an LTSthat is of the form, then the lower and upper bounds of LHFS are given by:
whereis the score measure for the kth instance preference values.
Definition 8:
Consider two LHFSandof the formand, then:
Whenever the result from Definition 8 goes out of bounds, the procedure suggested in Remark 2 is followed.
Remark 2:
From Definition 8, it is clear that sometimes the linguistic part becomes out of bounds and to transform these terms within the bounds, the procedure discussed in Reference [43] is adapted.
Since the LTS defined in this paper follows Definition 1, the conditions 1 and 3 will hold true. On the other hand, when LTS, then all three conditions mentioned above will hold true.
Property 1:
Commutative
Property 2:
Associative
Property 3:
Boundary
Here,is of the formandis of the form.
Example 1:
Letbe a LTS given by. Consider two LHFEsandof the form (discussed in Remark 1)anddefined over an LTS. Then,,,,, and(at) are given by:
;
;
;
;
.
Theorem 1:
Consider two LHFSsandthat are of the formand, then:
- (1)
- ;
- (2)
- .
Proof:
The proof of this theorem is direct and straightforward and hence we present only the theorem.
Before getting into further discussion of the proposed concepts, it is essential that we present a flowchart representation of the proposed framework. This enhances the understanding of the framework and gives a clear idea of the decision-making process. Figure 1 depicts the flowchart of the proposed decision-making framework under an LHFS context.
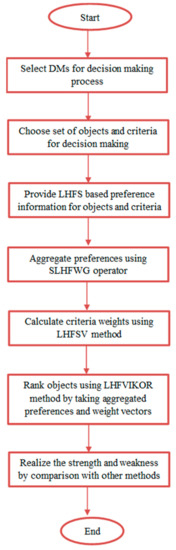
Figure 1.
Flowchart of the proposed decision-framework.
3.2. Proposed SLHFWG Aggregation Operator
In this section, we present a new aggregation operator called SLHFWG that aggregates the DMs viewpoints under an LHFS context. The aggregation is carried out in two phases viz. (a) aggregation of linguistic term, and (b) aggregation of possible membership degrees. We now formally present the definition of an SLHFWG operator.
Definition 9:
Consider an LHFSthat is of the formwithlinguistic terms andpossible membership degrees, then the aggregation is a mappingdefined by:
whereis the weight of the tth DM and m is the total number of DMs.
Scheme 1: When the linguistic term from each DM is unique for a specific instance (i.e., frequency of occurrence is 1), average of the subscript is calculated.
Scheme 2: When linguistic terms are not unique, the term with the highest frequency is chosen as an aggregated value.
where is the distance between the possible membership degrees of two DMs m and n, is the support measure, and is the total support measure.
Some advantages of the proposed aggregation operator are presented here:
- (1)
- The aggregation of linguistic terms using an SLHFWG operator yields a much more sensible term with no virtual set. This can be easily realized from the formulation given in Equation (14). This ensures that the aggregation of the linguistic term is consistent and rational.
- (2)
- Similarly, for the aggregation of the membership degrees, the motivation is gained from the power operator [44,45] and from the work of Xu and Liao [35]. As mentioned earlier by He et al. [34], the unduly high and low values cause bad effects in the aggregation process and the support measure (in formulation of power operator) is used to mitigate the same. Also, they claimed that the relationship between objects and criteria can be realized with the help of a support measure. Further, Xu and Liao [33] proposed a variant of the weighted geometry operator and claimed that the aggregation of preferences by this operator yields consistent values. The second phase of the aggregation applies the idea of a power operator to determine the relative importance of each DM, and these values are further used for aggregating the membership degrees (motivated by the operator proposed in [33]).
- (3)
- Finally, the proposed SLHFWG operator produces consistent non-virtual aggregated values of LHFS preferences and also helps DMs to better understand the relationship between objects and criteria.
Property 4:
(Idempotency)If all values of LHFSare equal, then:
Property 5:
(Boundedness)For all values of, the aggregation operator yields values that are of the form:
Property 6:
(Monotonicity)Letbe an LHFSof the formand, then:
Property 7:
(Commutative)Consideras any permutation of, then:
Proof:
The proof for these properties is straightforward and hence we confine our discussion with the elicitation of properties.
Theorem 2:
The aggregation of LHFSs by using the proposed SLHFWG operator is also an LHFS.
Proof:
The proof for the theorem is considered in two-fold viz. linguistic aggregation and possible membership aggregation. In linguistic aggregation, the linguistic information is collected from each DM for a particular instance and SLHFWG operator is applied to aggregate the information. Clearly, the operator yields no virtual set, and hence, the aggregation of linguistic terms also forms a linguistic term which is within the defined LTS. Thus, the first fold of the theorem is proved. Following this, in the next fold, possible membership degrees are aggregated using an SLHFWG operator that gains motivation from Reference [35] and power operators. Here, we need to show that the aggregation of hesitant fuzzy values is also hesitant fuzzy in nature. For this, we consider the lemma discussed in Reference [46] that states that, for any with , . Motivated by this lemma, we focus the proof in this direction. . Since the possible membership degrees are within the range [0,1] and , we clearly show that the aggregation of possible membership degrees by using an SLHFWG operator also yields a membership degree. Thus, the aggregation of LHFS information by using the proposed SLHFWG operator is also an LHFS in nature.
Example 2:
Consider a LTS of the form. The snippet of LHFS information is given by,, and. When an SLHFWG operator is applied, the aggregated LHFS information is calculated with DMs’ weight values as. The distance values between,and,as,. Similarly,,,, and. Thus,,, and. We apply these values to Equation (16) and we get. Finally, these estimated values are applied to Equation (15) and the aggregated values are given by.
3.3. Proposed LHFSV Method
In this section, criteria weights are estimated using the newly proposed LHFSV method, which is an extension to the standard variance (SV) method under an LHFS context. Motivated by the idea of Liu et al. [47], we set our focus in this direction. Further, the SV method enjoys the following advantages:
- (1)
- Unlike previous studies on criteria weight estimation (for example analytical hierarchy process (AHP) [41], decision making trial and evaluation laboratory (DEMATEL) [42], entropy based method [37], optimization model [36,37,38], etc.), the proposed method does not produce unrealistic and unreasonable weight values.
- (2)
- Also, the proposed method is simple and straightforward, and pays significant attention to those data points (criteria) that are highly conflicting. This property of SV further motivated our focus in this direction.
- (3)
- Rao et al. [48] pointed out that unlike other statistical methods that concentrate only on the boundary points, the SV method concentrates on every data point for determining the distribution. This property of SV helps DMs to estimate criteria weights in a rational manner.
- (4)
- Generally, relative importance is interpreted as the importance of a criterion relative to the hesitation that exists among DMs during preference elicitation. Thus, DMs’ personal characteristics and stimuli play a significant role in the interpretation of relative importance [49]. Thus, criteria with a high variation in preferences are given high importance and the SV method captures and reflects this idea in a better way. Further, Kao [50] presented a geometric proof for the same claim by using the idea of frontiers and projection. This work provides sufficient mathematical justification for realizing the strength of the SV method.
Motivated and attracted by these advantages, we put forward an extension of SV method under an LHFS context. The procedure of the proposal is given below:
Step 1:
Construct a weight evaluation matrix of order with m DMs and n criteria. The LHFS information is used for evaluation.
Step 2:
Calculate the score of the preference values using Equation (6) and convert the LHFS information into a single term by using Equation (20).
where is the subscript of the kth linguistic term and is the score of the kth probability instance.
Step 3:
Calculate the variance by using Equation (21) which considers the values from Step 2.
Step 4:
Normalize these variance values to calculate the relative importance of each criterion by using Equation (22).
where is the weight of the jth criterion with .
Example 3:
Consider the process of evaluation of two criteria by two DMs using LHFS information. The values are given by, and, . By applying Equation (20), we get, and, . Now, from Equation (21), variance is calculated and is given by and . Finally, criteria weight is calculated using Equation (22) and it is given by and .
3.4. Procedure for LHFVIKOR Method
In this section, a new ranking method is presented which is an extension of the classical VIKOR over an LHFS context. VIKOR [51] is a compromise ranking method that is based on the principle of an metric. Further, the VIKOR method finds a suitable alternative based on the closeness to an ideal solution and considers conflicting and non-commensurable criteria for evaluation. Some reasons for considering an extension of the popular VIKOR under an LHFS context are presented below:
- (1)
- Based on the work of Opricovic and Tzeng [51], it can be clearly observed that both VIKOR and TOPSIS (technique for order preference by similarity to ideal solution) are compromise ranking methods. However, VIKOR performs better than TOPSIS in the following ways: (i) The VIKOR method considers a relative distance measure that is much more rational than the rank index of the TOPSIS method. (ii) The VIKOR method considers the attitude of the DM as a key parameter in its formulation, which is missing in TOPSIS.
- (2)
- Further, from the work of Opricovic and Tzeng [52], it can be observed that the ranking order from PROMETHEE (preference ranking organization method for enrichment evaluation) and ELECTRE (ELimination Et Choix Traduisant la REalité) can be easily realized from the S and R parameters of the VIKOR method respectively.
- (3)
- The VIKOR method also selects the compromise solution based on two conditions viz. acceptable stability and acceptable advantage. Also, along with the ranking order, the VIKOR method provides a rank value set (advantage rate) for backup management during uncertain situations.
Motivated by the power of the VIKOR method, in this paper efforts are made to extend the VIKOR method under an LHFS context.
The systematic procedure for the proposed LHFS-based VIKOR is presented below:
Step 1:
Calculate the positive ideal solution and negative ideal solution (PIS, NIS) using Equations (23,24).
where is PIS, is NIS, is the subscript of the kth linguistic term, and is the score of the possible membership degrees for the kth linguistic term.
Step 2:
Calculate the parameters group utility (S) and individual regret (R) using Equations (25,26).
where the weight of the jth criterion, is the distance between two LHFEs a and b and is given by Equation (27).
Step 3:
Calculate the merit function (Q) using Equation (28) to determine the final ranking order of the alternatives. Choose a suitable compromise solution to form the obtained ranking order. The parameters obtained from step 2 are used for the estimation of the merit function.
where , , , , and is the strategy of the DM, which ranges from [0,1].
Step 4:
The final ranking order is obtained by arranging the merit function (Q) in the ascending order. The alternative that has the smaller Q value is preferred more. Also, a compromise solution is selected based on the two conditions viz. acceptable advantage and acceptable stability [44].
Before demonstrating the practicality and usefulness of the proposal, it is worth discussing some intricacies of the proposal.
- (1)
- The proposed LHFS concept extends the HFLTS concept by reflecting the hesitancy and vagueness of the DM by using possible membership degrees. This concept allows DMs to associate possible membership degrees for each linguistic term, which motivates sensible and rational decision making. Moreover, the concept circumvents the drawback of HFLTS by handling uncertainty and vagueness to a reasonable extent.
- (2)
- Following this, a new decision framework is put forward under an LHFS context that uses LHFS information for rating objects. Initially, a new aggregation operator called SLHFWG is proposed that sensibly aggregated DMs’ viewpoints without producing virtual sets.
- (3)
- Further, a new criteria weight estimation method is proposed which is an extension to the SV method under an LHFS context. The LHSV method produces reasonable criteria weights by focusing on every data point rather than only the extreme values.
- (4)
- Finally, a new ranking method is presented, which is an extension to the VIKOR method under an LHFS context. The method does the following: (a) PIS and NIS are calculated by using Equations (23) and (24), which identify a suitable LHFS value for each criterion and hence, the PIS and NIS is a vector of order , where n is the number of criteria. (b) The parameters , , and are estimated using Equations (25)–(28), which is of order where m is the number of alternatives. (c) The stability of the ranking method is realized by performing a sensitivity analysis by varying the strategy parameter ().
4. Numerical Example
This section put forwards a numerical example to demonstrate the practicality and usefulness of the proposal. Motivated by the work of Liao et al. [53] and Roy et al. [54] in the systematic evaluation of hospitals, in this paper, efforts are made to evaluate hospitals in India in a systematic manner. A survey report by IBEF (Indian Brand Equity Foundation) in August 2015 showed that India is expected to be ranked third in the global healthcare sectors with respect to incremental growth by 2020. Also, the report suggested that Indian healthcare is expected to reach USD$280 billion by 2020. With a high attraction and focus on healthcare, it becomes substantial to adopt a systematic scientific method for the rational evaluation of hospitals in India. This not only helps patients to understand hospitals better, but also helps management to improve hospitals’ performance.
With this backdrop, a multi-criteria decision-making problem for hospital evaluation in India is presented which considers four hospitals rated with respect to four criteria by three DMs. The four criteria taken for evaluation were quality of doctors , reputation of the hospital , cost , and environmental risk . Among these, criteria , were benefits, and , were costs. The three DMs adopted LHFS information for ratings, and were advised to use the LTS as mentioned by Reference [53]. Let us now put forward the procedure for evaluation:
Step 1:

Construct three decision matrices of order with LHFS information. This is shown in Table 1.

Table 1.
Decision matrix with LHFS information.
Step 2:
Aggregate these matrices into a single matrix of order by using the SLHFWG operator (refer to Section 3).
The relative importance of the DM was calculated separately for each linguistic term and this is given by Table 2. The reason for calculating the different relative importance of DM for each term is evident from the varying cognition/hesitation that the DM might have while providing the preference information. Motivated by this reason, support was calculated for each instance.

Table 2.
Calculation of weights instance-wise for different DMs.
Based on the support value obtained from Table 2, the aggregated decision matrix was constructed with the LHFS information by using the SLHFWG operator and is presented in Table 3.

Table 3.
Aggregation of LHFS information using the SLHFWG operator.
Step 3:
Construct criteria weight evaluation matrix and apply the LHFSV method (refer Section 3) to determine the weights of the criteria.
The LHFS information (from Table 4) was converted into single value by using the procedure from the LHFSV method. Also, from these single-valued terms, the variance was calculated and it was given by (0.49,0.19,0.45,0.50) and the weight value was further calculated and it was given by .

Table 4.
Evaluation of criteria weights.
Step 4:
Finally rank the hospitals by using the proposed LHFS-based VIKOR method and choose a suitable hospital as a compromise solution from the set of hospitals.
Table 5 shows the PIS and NIS values for each criterion, which is calculated using Equations (23,24). The LHFS information corresponding to the determined value were chosen as PIS and NIS. Table 6 shows the values for the parameters S and R, which were calculated by using Equations (25,26). From these values, we observed that the order was given by for both S and R under biased and unbiased weighting conditions.

Table 5.
Ideal solution.

Table 6.
Group utility and individual regret.
Further, we estimated the Q values under biased and unbiased weighting conditions by using Equations (28). The stability of the proposal was also realized by sensitivity analysis and it is shown in Table 7. From Table 7, we observe that the ranking order was and the suitable hospital was (compromise solution determined using acceptable advantage and acceptable stability conditions [44]). We also inferred that the proposed framework was unaffected and stable against uncertainty and vagueness.

Table 7.
Sensitivity analysis of merit function.
Step 5:
Compare the strengths and weaknesses of the proposal with other methods (refer Section 5).
5. Comparative Analysis: Proposed Versus others
In this section, we make efforts to realize the strengths and weaknesses of the proposal under the realm of both theoretical and numerical aspects. The factors considered for theoretic investigation were obtained from intuition and factors considered for numerical analysis were taken from Reference [55]. With a view of maintaining homogeneity in the comparison process, we considered state of the art methods like LHFS-based aggregation [30], HFLTS-based TOPSIS [16], and HFLTS-based VIKOR [21]. The same aggregated matrix was given as input to these methods, and the ranking order was investigated. Table 8 shows the ranking order obtained by different methods. From Figure 2, it can be observed that the proposed method was highly consistent with other state-of-the-art methods. Also, the HFLTS-based TOPSIS and VIKOR methods produced negative correlation values, which signify the fact that these methods used a different data structure for preference information. The LHFS information was informative and reflected the hesitation and vagueness of the DM in a better way. We further investigated the theoretic and numeric aspects of the proposal with other methods (see Table 9).

Table 8.
Different ranking order from different methods.
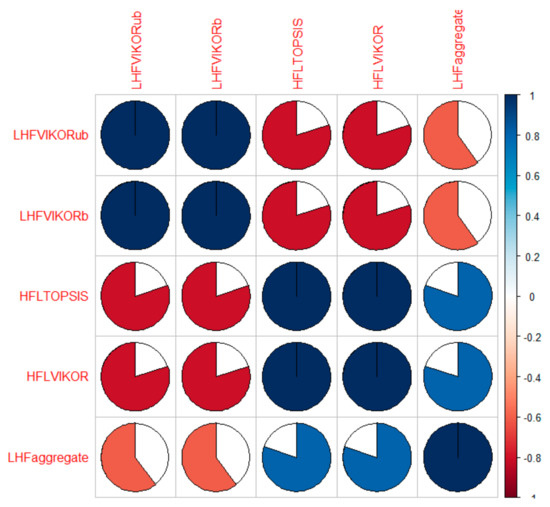
Figure 2.
Spearman correlation plot.

Table 9.
Investigation of different features.
From Table 8, we clearly observe that the proposed method produced a unique ranking order with a broad and sensible rank value set that is much more sensible and reasonable as it considered both the linguistic terms and its corresponding membership degrees to properly reflect the hesitancy in the process. In contrary, the HFLTS-based methods (discussed in Table 8) failed to properly reflect the hesitation of the DM. Further, the consistency of the proposal was realized by using the Spearman correlation method [56]. From Figure 2, it can be clearly observed that the proposed LHFS-based VIKOR method produced a correlation value of with respect to the LHFS-based VIKOR (unbiased), HFLTS-based TOPSIS, HFLTS-based VIKOR, and LHFS-based aggregation methods. This showed that the proposed method was not relatively consistent (negative relation) with other methods and it produced a unique ranking order. Though, readers question this aspect, the reason for such values can be easily realized from the loss of information that was incurred during the process of evaluation. The methods discussed in References [16,21] miss the membership values that are highly important to reflect the hesitation of the DM. Also, method [30] loses a certain amount of information during the process of aggregation.
To enrich our clarity further on the proposal, we make the following discussion:
- The proposal presented a new concept (structure) to the decision-making context by extending HFLTS with possible membership degrees to better reflect hesitation and vagueness. We also investigated some attractive properties of LHFS.
- A two-phase scientific decision-making framework was further presented under an LHFS context for rational decision-making. The framework put forward a new aggregation operator that was motivated from the work in Reference [35] and power operators for the sensible aggregation of DMs’ preference information. Following this, a new criteria weight estimation method was presented for the reasonable estimation of criteria weights, which is an extension of SV method under an LHFS environment. Finally, the framework presented an extension to the popular VIKOR ranking method for MCGDM problems to select a suitable object from the set of objects.
- As mentioned earlier, the superiority of the proposal was realized from theoretic and numerical perspectives. Clearly, Table 9 brought out the superiority of the proposal and showed that the proposed framework was a powerful aid for critical and rational decision-making.
- Certain key factors discussed in Table 9 are: stability, which is ensured by sensitivity analysis on parameters (like weights, strategy etc.); consistency, which is ensured from Spearman correlation; robustness, which is realized from an adequacy test motivated by Reference [55]; and scalability, which is motivated by Reference [57].
- In order to demonstrate the practicality and usefulness of the proposal, an interesting hospital evaluation problem was presented. From Table 8, we observed that the ranking order obtained from the proposal was consistent with its close counterpart. The compromise solution selected by the proposal and its close counterpart were the same and was given by . Though the order coincides, the proposed LHFS-based decision framework was much superior in various factors discussed in Table 9 and also, the proposal handled the weakness of HFLTS in a much better manner.
6. Concluding Remarks
In this paper, efforts were made to present a flexible and reasonable data structure for properly reflecting DMs’ hesitation and vagueness. Motivated by the power of HFLTS and possible membership degrees, we set our research focus in this direction. Some attractive operational laws, properties, etc., were also investigated. Further, a new decision framework was put forward that consisted of a new aggregation method for aggregating DMs’ preference information. Some properties of the operator were also admired in this paper. A new method for the criteria weight estimation was also presented under the LHFS context for the effective and reasonable calculation of weights. Finally, the proposed framework presented an extension to the popular VIKOR method under an LHFS context for an MCGDM problem. With a view of giving a proper realization of the practicality, strength, and weakness of the proposal, a hospital evaluation problem was illustrated and a comparative study (from both a theoretic and numerical perspective) was put forward with other methods.
As a part of the future scope, weaknesses discussed in Table 9 for the proposal will be addressed; also new structures for proper and flexible representation of preference information will be presented by extending HFLTS with soft sets. Also, plans are made to automate the membership degrees for each linguistic term to better reflect the hesitation of DMs. We have also planned to combine hot concepts like machine learning, artificial intelligence, granular computing, etc., with these structures for effective decision-making in uncertain and critical situations.
Author Contributions
The individual contribution and responsibilities of the authors were as follows: Author(s) R.K., K.S.R., and J.P. designed the model for research, collected, pre-processed, and analyzed the data and the obtained inferences, and worked on the development of the paper. Author(s) S.K., E.K.Z. and J.A. provided good advice throughout the research by giving suggestions on model design, methodology, and inferences, and refined the manuscript. All the authors have read and approved the final manuscript.
Acknowledgments
The authors thank the editor and the anonymous reviewer(s) for their insights that helped improve the quality of the research. The authors also thank the funding agencies University Grants Commission (grant no. F./2015-17/RGNF-2015-17-TAM-83) and Department of Science and Technology, Ministry of Science and Technology (grant no. SR/FST/ETI-349/2013) for their financial aid.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Kim, J.L.; Senaratna, D.M.; Ruza, J.; Kam, C.; Ng, S. Feasibility study on an evidence-based decision-support system for hospital site selection for an aging population. Sustainability 2015, 7, 2730–2744. [Google Scholar] [CrossRef]
- Charu, S.; Priya, C.; Sowmya, R. Innovative and Sustainable Healthcare Management: Strategies for Growth, 2nd ed.; Deloitte: India, 2012; pp. 1–20. [Google Scholar]
- Wang, J.; Chen, X. Method for hospital selection considering patients’ expectations. In Proceedings of the 7th International Joint Conference on Computational Sciences and Optimization, CSO 2014, Beijing, China, 4–6 July 2014; pp. 361–365. [Google Scholar] [CrossRef]
- Arasteh, M.A.; Shamshirband, S.; Yee, P.L. Using multi-attribute decision-making approaches in the selection of a hospital management system. Technol. Health Care 2017, 1, 1–17. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.; Chan, C.M.; Lee, H.C.; Chung, Y.; Lai, F. Development of a decision support engine to assist patients with hospital selection topical collection on patient facing systems. J. Med. Syst. 2014, 38, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Zadeh, L.A. The concept of a linguistic variable and its application to approximate reasoning-I. Inf. Sci. 1975, 8, 199–249. [Google Scholar] [CrossRef]
- Herrera, F.; Herrera-Viedma, E.; Verdegay, J.L. A sequential selection process in group decision making with a linguistic assessment approach. Inf. Sci. 1995, 85, 223–239. [Google Scholar] [CrossRef]
- Herrera, F.; Herrera-Viedma, E.; Verdegay, J.L. Linguistic measures based on fuzzy coincidence for reaching consensus in group decision making. Int. J. Approx. Reason. 1997, 16, 309–334. [Google Scholar] [CrossRef]
- Herrera, F.; Herrera-Viedma, E.; Verdegay, J.L. A model of consensus in group decision making under linguistic assessments. Fuzzy Sets Syst. 1996, 78, 73–87. [Google Scholar] [CrossRef]
- Xu, Z. An approach based on the uncertain LOWG and induced uncertain LOWG operators to group decision making with uncertain multiplicative linguistic preference relations. Decis. Support Syst. 2006, 41, 488–499. [Google Scholar] [CrossRef]
- Rodriguez, R.M.; Martinez, L.; Herrera, F. Hesitant fuzzy linguistic term sets for decision making. IEEE Trans. Fuzzy Syst. 2012, 20, 109–119. [Google Scholar] [CrossRef]
- Torra, V.; Narukawa, Y. On hesitant fuzzy sets and decision. In Proceedings of the 2009 IEEE International Conference on Fuzzy System, Jeju Island, Korea, 20–24 August 2009; pp. 1378–1382. [Google Scholar] [CrossRef]
- Rodríguez, R.M.; Labella, A.; Martínez, L. An overview on fuzzy modelling of complex linguistic preferences in decision making. Int. J. Comput. Intell. Syst. 2016, 9, 81–94. [Google Scholar] [CrossRef]
- Chang, K.H. Enhanced assessment of a supplier selection problem by integration of soft sets and hesitant fuzzy linguistic term set. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2015, 229, 1635–1644. [Google Scholar] [CrossRef]
- Wei, C.; Zhao, N.; Tang, X. Operators and comparisons of hesitant fuzzy linguistic term sets. IEEE Trans. Fuzzy Syst. 2014, 22, 575–585. [Google Scholar] [CrossRef]
- Beg, I.; Rashid, T. TOPSIS for hesitant fuzzy linguistic term sets. Int. J. Intell. Syst. 2014, 29, 495–524. [Google Scholar] [CrossRef]
- Zhu, B.; Xu, Z. Consistency measures for hesitant fuzzy linguistic preference relations. IEEE Trans. Fuzzy Syst. 2014, 22, 35–45. [Google Scholar] [CrossRef]
- Liao, H.; Xu, Z.; Zeng, X.J.; Merigo, J.M. Qualitative decision making with correlation coefficients of hesitant fuzzy linguistic term sets. Knowl.-Based Syst. 2015, 76, 127–138. [Google Scholar] [CrossRef]
- Wu, Z.; Xu, J. Possibility distribution-based approach for MAGDM with hesitant fuzzy linguistic information. IEEE Trans. Cybern. 2016, 46, 694–705. [Google Scholar] [CrossRef] [PubMed]
- Liao, H.; Xu, Z.; Zeng, X.J. Distance and similarity measures for hesitant fuzzy linguistic term sets and their application in multi-criteria decision making. Inf. Sci. 2014, 271, 125–142. [Google Scholar] [CrossRef]
- Liao, H.; Xu, Z.; Zeng, X.J. Hesitant fuzzy linguistic VIKOR method and its application in qualitative multiple criteria decision making. IEEE Trans. Fuzzy Syst. 2014, 23, 1–14. [Google Scholar] [CrossRef]
- Wu, Z. A consensus process for hesitant fuzzy linguistic preference relations. In Proceedings of the 2015 IEEE International. Conference on Fuzzy System, Istanbul, Turkey, 2–5 August 2015; pp. 1–7. [Google Scholar] [CrossRef]
- Liao, H.; Wu, D.; Huang, Y.; Ren, P.; Xu, Z.; Verma, M. Green logistic provider selection with a hesitant fuzzy linguistic thermodynamic method integrating cumulative prospect theory and PROMETHEE. Sustainability 2018, 10, 1291. [Google Scholar] [CrossRef]
- Rodríguez, R.M.; Martínez, L.; Torra, V.; Xu, Z.S.; Herrera, F. Hesitant Fuzzy Sets: State of the Art and Future Directions. Int. J. Intell. Syst. 2014, 29, 495–524. [Google Scholar] [CrossRef]
- Liao, H.; Xu, Z.; Herrera-Viedma, E.; Herrera, F. Hesitant Fuzzy Linguistic Term Set and Its Application in Decision Making: A State-of-the-Art Survey. Int. J. Fuzzy Syst. 2017, 1–27. [Google Scholar] [CrossRef]
- Meng, F.; Chen, X.; Zhang, Q. Multi-attribute decision analysis under a linguistic hesitant fuzzy environment. Inf. Sci. 2014, 267, 287–305. [Google Scholar] [CrossRef]
- Yu, S.M.; Zhou, H.; Chen, X.H.; Wang, J.Q. A multi-criteria decision-making method based on heronian mean operators under a linguistic hesitant fuzzy environment. Asia Pac. J. Oper. Res. 2015, 32, 1–35. [Google Scholar] [CrossRef]
- Zhou, H.; Wang, J.; Zhang, H.; Chen, X. Linguistic hesitant fuzzy multi-criteria decision-making method based on evidential reasoning. Int. J. Syst. Sci. 2016, 47, 314–327. [Google Scholar] [CrossRef]
- Liu, Y.Z.; Fan, Z.P.; Gao, G.X. An extended LINMAP method for MAGDM under linguistic hesitant fuzzy environment. J. Intell. Fuzzy Syst. 2016, 30, 2689–2703. [Google Scholar] [CrossRef]
- Zhu, C.; Zhu, L.; Zhang, X. Linguistic hesitant fuzzy power aggregation operators and their applications in multiple attribute decision-making. Inf. Sci. 2016, 367, 809–826. [Google Scholar] [CrossRef]
- Guan, J.; Zhou, D.; Meng, F. Distance measure and correlation coefficient for linguistic hesitant fuzzy sets and their application. Informatica 2017, 28, 237–268. [Google Scholar] [CrossRef]
- Dong, J.Y.; Yuan, F.F.; Wan, S.P. Extended VIKOR method for multiple criteria decision-making with linguistic hesitant fuzzy information. Comput. Ind. Eng. 2017, 112, 305–319. [Google Scholar] [CrossRef]
- Yuan, J.; Li, C.; Li, W.; Liu, D.; Li, X. Linguistic hesitant fuzzy multi-criterion decision-making for renewable energy: A case study in Jilin. J. Clean. Prod. 2018, 172, 3201–3214. [Google Scholar] [CrossRef]
- Meng, F.; Tang, J.; Li, C. Uncertain linguistic hesitant fuzzy sets and their application in multi-attribute decision making. Int. J. Intell. Syst. 2018, 33, 586–614. [Google Scholar] [CrossRef]
- Liao, H.; Xu, Z. Consistency of the fused intuitionistic fuzzy preference relation in group intuitionistic fuzzy analytic hierarchy process. Appl. Soft Comput. J. 2015, 35, 812–826. [Google Scholar] [CrossRef]
- He, Y.; He, Z. Hesitant fuzzy power bonferroni means and their application to multiple attribute decision making. IEEE Trans. Fuzzy Syst. 2015, 23, 1655–1668. [Google Scholar] [CrossRef]
- Hashemi, H.; Mousavi, S.M.; Zavadskas, E.K.; Chalekaee, A.; Turskis, Z. A new group decision model based on grey-intuitionistic fuzzy-ELECTRE and VIKOR for contractor assessment problem. Sustainability 2018, 10, 1635. [Google Scholar] [CrossRef]
- Wan, S.; Xu, G.; Dong, J. A novel method for group decision making with interval-valued Atanassov intuitionistic fuzzy preference relations. Inf. Sci. 2016, 372, 53–71. [Google Scholar] [CrossRef]
- Xu, Y.; Da, Q. A method for multiple attribute decision making with incomplete weight information under uncertain linguistic environment. Knowl.-Based Syst. 2008, 21, 837–841. [Google Scholar] [CrossRef]
- Xu, Z.; Zhang, X. Hesitant fuzzy multi-attribute decision making based on TOPSIS with incomplete weight information. Knowl.-Based Syst. 2013, 52, 53–64. [Google Scholar] [CrossRef]
- Sharma, H.K.; Roy, J.; Kar, S.; Prentkovskis, O. Multi criteria evaluation framework for prioritizing Indian railway stations using modified rough AHP-MABAC method. Transp. Telecommun. 2018, 19, 113–127. [Google Scholar] [CrossRef]
- Debnath, A.; Roy, J.; Kar, S.; Zavadskas, E.K.; Antucheviciene, J. A hybrid MCDM approach for strategic project portfolio selection of agro by-products. Sustainability 2017, 9, 1302. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, Z.; Liao, H. A consensus process for group decision making with probabilistic linguistic preference relations. Inf. Sci. 2017, 414, 260–275. [Google Scholar] [CrossRef]
- Yager, R.R. The power average operator. IEEE Trans. Syst. Cybernatics-Part A Syst. Hum. 2001, 31, 724–731. [Google Scholar] [CrossRef]
- Xu, Z.; Yager, R.R. Power-geometric operators and their use in group decision making. IEEE Trans. Fuzzy Syst. 2010, 18, 94–105. [Google Scholar]
- Xia, M.; Xu, Z. Entropy/cross entropy-based group decision making under intuitionistic fuzzy environment. Inf. Fusion. 2012, 13, 31–47. [Google Scholar] [CrossRef]
- Liu, S.; Chan, F.T.S.; Ran, W. Decision making for the selection of cloud vendor: An improved approach under group decision-making with integrated weights and objective/subjective attributes. Expert Syst. Appl. 2016, 55, 37–47. [Google Scholar] [CrossRef]
- Rao, R.V.; Patel, B.K.; Parnichkun, M. Industrial robot selection using a novel decision making method considering objective and subjective preferences. Rob. Auton. Syst. 2011, 59, 367–375. [Google Scholar] [CrossRef]
- Goldstein, W.M.; Beattie, J. Judgments of Relative Importance in Decision Making: The Importance of Interpretation and the Interpretation of Importance, 1st ed.; Springer: New York, NY, USA, 1991; pp. 110–137. [Google Scholar]
- Kao, C. Weight determination for consistently ranking alternatives in multiple criteria decision analysis. Appl. Math. Model. 2010, 34, 1779–1787. [Google Scholar] [CrossRef]
- Opricovic, S.; Tzeng, G.H. Compromise solution by MCDM methods: A comparative analysis of VIKOR and TOPSIS. Eur. J. Oper. Res. 2004, 156, 445–455. [Google Scholar] [CrossRef]
- Opricovic, S.; Tzeng, G.H. Extended VIKOR method in comparison with outranking methods. Eur. J. Oper. Res. 2007, 178, 514–529. [Google Scholar] [CrossRef]
- Liao, H.; Jiang, L.; Xu, Z.; Xu, J.; Herrera, F. A probabilistic linguistic linear programming method in hesitant qualitative multiple criteria decision making. Inf. Sci. 2017, 416, 341–355. [Google Scholar] [CrossRef]
- Roy, J.; Adhikary, K.; Kar, S. A rough strength relational DEMATEL model for analysing the key success factors of hospital service quality. Decis. Mak. Appl. Manag. Eng. 2018, 1, 121–142. [Google Scholar] [CrossRef]
- Lima Junior, F.R.; Osiro, L.; Carpinetti, L.C.R. A comparison between fuzzy AHP and fuzzy TOPSIS methods to supplier selection. Appl. Soft Comput. J. 2014, 21, 194–209. [Google Scholar] [CrossRef]
- Spearman, C. The proof and measurement of association between two things. Am. J. Psychol. 1904, 15, 72–101. [Google Scholar] [CrossRef]
- Saaty, T.L.; Ozdemir, M.S. Why the magic number seven plus or minus two. Math. Comput. Model. 2003, 38, 233–244. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).