A Decision-Making Model for Evaluating and Selecting Suppliers for the Sustainable Operation and Development of Enterprises in the Aerospace Industry

Abstract

Due to rigorous quality requirements and high unit prices, the manufacture of machines used in the aerospace industry is characterized by a high entry threshold, high risk and a long payback period. A good decision-making model for evaluating and selecting suppliers is vital for sustainable enterprise development. Therefore, this study presents a new two-stage model for evaluating and selecting suppliers in the aerospace industry. In the first stage, a hierarchical structure is built with five main and 16 sub-criteria for supplier evaluation and selection following the modified Delphi method; in the second stage, the best alternative solution is selected following the analytic network process (ANP) method. Finally, this study verifies the feasibility of the above model based on the purchase of high-precision and high-cost 3D measuring tools by Aerowin Technology Corporation, which is listed on the Taiwan Stock Exchange. The results show that the five criteria in the above model are ranked by their degree of importance, as follows: quality > cost > delivery > marketing > organizational planning. The findings of this research can be used as a reference for decision-making during the purchase of high-precision and high-priced machine tools in the aerospace industry.

1. Introduction

The International Air Transport Association states that China will become the world’s largest air passenger transport market by approximately 2024, ahead of the US and the air passenger capacity within and outside China is expected to reach 1,300,000,000 person-times by approximately 2035, which is also ahead of the US (1,100,000,000 person-times) [1]. To account for the large air passenger transport market, two major manufacturers of large civil aircrafts (Boeing and Airbus) have successively released business jet aircrafts. Boeing predicts that within the next 20 years, China will require 6810 passenger aircrafts, valued at over 1 trillion US dollars, thus becoming the world’s largest business aircraft market. Therefore, Boeing predicts that airlines will require 36,770 aircrafts, valued at 5.2 trillion US dollars, within the next 20 years.

Jiang [2] predicts that Taiwan’s aerospace industry will generate 133,500,000,000 New Taiwan Dollars (NTDs), accounting for approximately 0.56% of Taiwan’s GDP and 0.4% of the total output of the global aerospace industry in 2020 and create almost 140,000 job opportunities. Consequently, Taiwan’s aerospace industry still has great potential for growth. Today, aerospace has become an emerging strategic industry. Characterized by a high degree of technology integration, strong industrial correlation and high added value, the aerospace industry is also a comprehensive and innovative technology-intensive industry, which can advance and strengthen the competitiveness of traditional industries. Due to rigorous quality requirements, new entrants to this industry are faced with a high entry threshold and long payback period. Considering this, AIDC Communications [3] stated that the Taiwan government developed the Aerospace Team 4.0 industrial program to meet fierce international competition. The program is intended to fulfill the following purposes: (1) conduct vertical integration of the industrial supply chain and horizontal labor division; (2) establish a cross-industry alliance and develop a pattern of labor division characterized by external competition and internal collaboration; (3) jointly reduce the risks of investment in and quality certification of new products; and (4) strengthen industrial competitiveness and increase industrial output. Therefore, vendors in the aerospace supply chain system must aim for economic, environmental and social sustainability and create long-term partnerships with their customers and social groups. Creating a decision-making model for supplier evaluation and selection that is suited to the aerospace industry is key to achieving sustainable development.

This study presents a new decision-making model for evaluating and selecting suppliers of high-precision machine tools in the aerospace industry. The first part builds an analytic network process (ANP) hierarchy following the modified Delphi method and the second part selects the best alternative solution. Finally, the feasibility of the proposed model is verified and sensitivity analysis is conducted based on the purchase of high-precision and high-priced 3D measuring tools produced by the Aerowin Technology Corporation in 2017. The findings can be used as a reference for decision-making during the purchase of high-precision and high-priced machine tools in the aerospace industry, as well as for formulating sustainable operation strategies.

2. Literature Review

2.1. Criteria for Supplier Evaluation and Selection

In the context of globalization, global manufacturers attach much importance to partnerships between suppliers. They successively integrate upstream and downstream supply chains to more efficiently reduce costs. When evaluating and selecting suppliers, manufacturers typically use the four criteria specified by Donald and O’Shaughnessy [4], including price, quality, delivery and services. Within the framework of the four criteria, scholars subsequently develop diverse criteria and models for supplier evaluation and selection within different industries. McCutcheon et al. [5] argue that a good partnership between purchasers and suppliers will facilitate information flow and enhance environmental adaptability and elasticity of organizations. Goffin et al. [6] contend that, in addition to costs, quality and delivery, the criteria for supplier evaluation and selection should include technical capability, financial capacity, after-sale services and strategies. Byun [7] used the analytic hierarchy process (AHP) to develop a model for evaluating and selecting new automobiles so that consumers could make optimal purchase decisions and ensure that the best consumer services could be provided when there is business competition. Bharadwaj [8] stated the following: (1) if enterprises select qualified suppliers that can satisfy their needs, their competitiveness will be strengthened; (2) otherwise, delivery and supply could be delayed, resulting in reputational and financial losses. To measure small but diverse usage in the aerospace industry, Liao [9] used the AHP to develop eight main criteria (quality capacity, delivery capability, price responsiveness, technical capability, financial and credit standing, after-sale service and partnership and elastic utilization and innovation capability) and 40 sub-criteria for evaluating and selecting suppliers in the aerospace industry. The Supply Chain Council [10] proposed the supply chain operations reference model (SCOR), which comprises five main criteria (reliability, responsiveness, elasticity, costs and asset management) and 13 sub-criteria (punctual delivery, supply rate, perfect order fulfillment, order fulfillment lead-time, responsiveness of the supply chain, output elasticity, management cost of the supply chain, sales cost, added value of productivity, warranty and return process cost, cash cycle time, supply inventory days and asset turnover). Ávila et al. [11] proposed five supplier evaluation and selection criteria (including quality, finance, collaboration, costs and production system) and used the AHP to evaluate and select suppliers. Syu [12] argued that supplier evaluation and selection criteria should include their ability to fulfill orders, financial standing, cost, quality system, lead time and organizational management. Using the fuzzy AHP (FAHP) combined with fuzzy TOPSIS, Francisco et al. [13] developed a supplier evaluation and selection model. Jafar et al. [14] proposed a two-stage supplier evaluation and selection model for Europe’s largest airline: (1) the conjunctive screening method is used first; (2) and the FAHP is used second so that decision-makers determine main and sub-criteria for supplier evaluation and selection, rank suppliers and accordingly make optimal decisions. Lin and Huang [15] used the ANP to evaluate the low-cost purchase intentions of operators for existing and potential customers and found that reliability and image are two important factors within their purchase intentions. Introducing parameters such as the weight of criteria, cost, calibration time, demand, technical capability and number of experts, Erginel and Gecer [16] used the fuzzy multi-objective linear programming model to evaluate and select the suppliers of 20 different types of measuring and calibration devices and 161 measuring devices. Seyyed et al. [17] proposed a model using the Delphi method in the first stage and the AHP in the second stage to evaluate key competitiveness indices and driving factors for airline companies. Using AHP combined with the “vise kriterijumska optimizacija kompromisno resenje (VIKOR),” Luthra et al. [18] created a supplier evaluation and selection model, using three main criteria (economy, environment and society) and 22 sub-criteria to verify the evaluation and selection of suppliers in India’s automation industry. Using DEMATEL combined with the ANP, Chou et al. [19] developed six main and 24 sub-criteria to evaluate supply chain management, based on the management of sustainable green projects.

This study presents a two-stage supplier evaluation and selection model for the aerospace industry. In the first stage, a hierarchical structure is built using supplier evaluation and selection criteria and sub-criteria following the modified Delphi method; and, in the second stage, the weights of the criteria and sub-criteria are calculated following the ANP and the best alternative solution is selected.

2.2. Analytic Network Process

Saaty [20] proposed the ANP method, which is an extension of the AHP method. Specifically, a feedback mechanism was introduced to the AHP method and the feedback is presented in network form to offer a solution to interdependence between criteria. The ANP method includes four steps: (1) building a hierarchical structure; (2) creating a pairwise matrix and calculating the eigenvectors; (3) forming supermatrices and calculating the weights; and (4) selecting the best alternative solution [21,22]. The steps are detailed as follows:

Step 1: Build a hierarchical structure.

This study sets goals according to the nature of the problem, defines the evaluation and sub-criteria and ascertains mutual influences among the criteria. If the criteria are influenced by each other, there is an outer dependence among them. If the sub-criteria are influenced by each other, there is an interdependence among them. This study generates the overall decision-making hierarchy according to all mutual influence results (as shown in Figure 1).

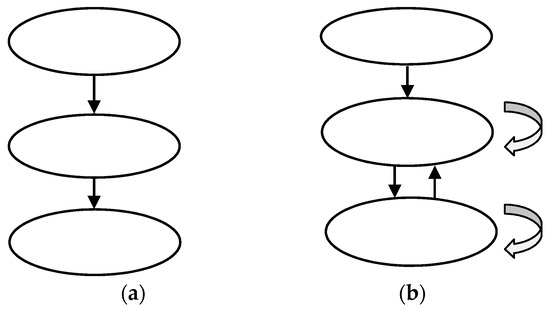
Figure 1. Differences in the architecture of the analytic hierarchy process (AHP) and the analytic network process (ANP); (a) AHP architecture (b) ANP architecture [20].

Step 2: Create a pairwise comparison matrix and calculate the eigenvectors.

For the ANP, comparative evaluation is conducted following the 1–9 scale method specified by Saaty [23]. For example, the 1/9 scale indicates that the vertical criteria are far more important than the horizontal criteria. This study calculates the eigenvectors through a pairwise comparison to estimate the relative importance of each criterion and uses the eigenvectors as the values of the supermatrices. The eigenvector is calculated according to each comparative matrix and used as the value of the supermatrices to reflect interdependence and relative importance.

The computational ANP involves three matrices, including the unweighted, weighted and limit supermatrices. They are formularized as follows:

A × w = λ_max × w

(1)

where A indicates an n × n pairwise comparison matrix, w is the eigenvector and λ_max is the maximum eigenvalue of Matrix A. A consistency test is then conducted according to the maximum eigenvalue; in other words, it calculates the CI and CR to judge the decision-makers’ consistency (as expressed in Equations (2) and (3)).

$$\mathit{C}\mathit{I}=\frac{{\mathit{\lambda }}_{\mathbf{max}}-\mathit{n}}{\mathit{n}-\mathbf{1}}$$

(2)

$$\mathit{C}\mathit{R}=\frac{\mathit{C}\mathit{I}}{\mathit{R}\mathit{I}}$$

(3)

If 0 ≤ CR ≤ 0.1, the judgments of experts are consistent [20].

Step 3: Form the supermatrices.

A supermatrix is divisible; the eigenvector calculated by pairwise comparison is used as the weight value of each submatrix and each submatrix value indicates the relationship and intensity between two nodes (such as criteria or groups) in the decision-making system [21]. It is assumed that decision-making system C_i comprises (i = 1, 2, ∙∙∙, n) criteria and each criterion C_i comprises n_i sub-criteria. This study uses Equation (4) to calculate the eigenvector of each submatrix to be used as its weight value and then transforms the submatrix into a supermatrix in the permutation mode specified by Equation (5) [20]. If the matrix elements are dependent on each other, a fixed convergence extremum will be obtained after the matrix is subjected to repeated multiplication.

$$\mathit{W}=\begin{array}{ccc}& & \begin{array}{cccc}{\mathit{C}}_{\mathbf{1}}& {\mathit{C}}_{\mathbf{2}}& \cdots & {\mathit{C}}_{\mathit{i}}\end{array}\\ & & \begin{array}{cccc}{\mathit{e}}_{\mathbf{11}}{\mathit{e}}_{\mathbf{12}}\cdots {\mathit{e}}_{\mathbf{1}\mathit{n}\mathbf{1}}& {\mathit{e}}_{\mathbf{21}}{\mathit{e}}_{\mathbf{22}}\cdots {\mathit{e}}_{\mathbf{2}\mathit{n}\mathbf{2}}& \cdots & {\mathit{e}}_{\mathit{i}\mathbf{1}}{\mathit{e}}_{\mathit{i}\mathbf{2}}\cdots {\mathit{e}}_{\mathit{i}\mathit{n}\mathit{i}}\end{array}\\ \begin{array}{c}\\ {\mathit{C}}_{\mathbf{1}}\\ \\ \\ \\ {\mathit{C}}_{\mathbf{2}}\\ \\ \\ ⋮\\ \\ \\ {\mathit{C}}_{\mathit{i}}\\ \end{array}& \begin{array}{c}\begin{array}{c}{\mathit{e}}_{\mathbf{11}}\\ {\mathit{e}}_{\mathbf{12}}\\ ⋮\\ {\mathit{e}}_{\mathbf{1}\mathit{n}\mathbf{1}}\end{array}\\ \begin{array}{c}{\mathit{e}}_{\mathbf{21}}\\ {\mathit{e}}_{\mathbf{22}}\\ ⋮\\ {\mathit{e}}_{\mathbf{2}\mathit{n}\mathbf{2}}\end{array}\\ ⋮\\ \begin{array}{c}{\mathit{e}}_{\mathit{i}\mathbf{1}}\\ {\mathit{e}}_{\mathit{i}\mathbf{2}}\\ ⋮\\ {\mathit{e}}_{\mathit{i}\mathit{n}\mathit{i}}\end{array}\end{array}& \left[\begin{array}{cccc}& & & \\ {\mathit{w}}_{\mathbf{11}}& {\mathit{w}}_{\mathbf{12}}& \cdots & {\mathit{w}}_{\mathbf{1}\mathit{i}}\\ & & & \\ & & & \\ & & & \\ {\mathit{w}}_{\mathbf{21}}& {\mathit{w}}_{\mathbf{22}}& \cdots & {\mathit{w}}_{\mathbf{2}\mathit{i}}\\ & & & \\ & & & \\ ⋮& ⋮& \ddots & ⋮\\ & & & \\ & & & \\ {\mathit{w}}_{\mathit{i}\mathbf{1}}& {\mathit{w}}_{\mathit{i}\mathbf{2}}& \cdots & {\mathit{w}}_{\mathit{i}\mathit{i}}\\ & & & \end{array}\right]\end{array}$$

(4)

The computational ANP involves three matrices. Specifically, the weight of the unweighted supermatrix is the weight calculated through the original pairwise comparison, the weight of the weighted supermatrix is that of the same criterion in the unweighted supermatrix multiplied by the related group weight and the limit supermatrix squares the weighted supermatrix several times until the numbers in all columns are equal. Saaty [20] argues that, if supermatrix W is irreducible, all column vectors in the supermatrix share the same values; in other words, the convergence effect is attained.

Equation (5) is a supermatrix with a three-layer hierarchy, as indicated by W_h [20]:

$${\mathit{W}}_{\mathit{h}}=\left[\begin{array}{ccc}\mathbf{0}& \mathbf{0}& \mathbf{0}\\ {\mathit{W}}_{\mathbf{21}}& \mathbf{0}& \mathbf{0}\\ \mathbf{0}& {\mathit{W}}_{\mathbf{32}}& \mathit{I}\end{array}\right]$$

(5)

where W₂₁ is the eigenvector of a criterion under the decision-making goals, W₃₂ is the pairwise comparison matrix of the alternative solution under each criterion, I is the unit matrix and 0 is the independence of the same criterion or between sub-criteria. The primary function of this matrix is to evaluate outer and inner dependence. If there is dependence between criteria, a network structure needs to be used instead of the hierarchical structure. Then, W₂₂ indicates the dependence between these criteria and the supermatrix can be expressed by Equation (6) [20]:

$${\mathit{W}}_{\mathit{n}}=\left[\begin{array}{ccc}\mathbf{0}& \mathbf{0}& \mathbf{0}\\ {\mathit{W}}_{\mathbf{21}}& {\mathit{W}}_{\mathbf{22}}& \mathbf{0}\\ \mathbf{0}& {\mathit{W}}_{\mathbf{32}}& \mathit{I}\end{array}\right]$$

(6)

Any “0” in supermatrix W_n can be replaced with a matrix based on the dependence relationship between criteria or groups. There is typically a dependence relationship between groups in a network structure; therefore, the supermatrix usually contains the weights of multiple interdependent columns. Such a supermatrix is then referred to as an unweighted supermatrix; in other words, the weights are obtained by combining and permutating the eigenvectors of the original pairwise comparison matrix. To meet the mathematical reasoning logic, the supermatrix must first be normalized so that the sum of the weight values of each column is equal to 1. Such a supermatrix is then referred to as a weighted supermatrix. If the sum of the weight values in each column of an unweighted supermatrix is equal to 1, it becomes a weighted supermatrix. This study uses the ANP method to calculate the weights of main and sub-criteria. Therefore, the unweighted supermatrix W_n needs to be modified into a weighted supermatrix W′_n, as expressed by Equation (7):

$${\mathit{W}}^{\prime }{}_{\mathit{n}}=\left[\begin{array}{ccc}\mathbf{0}& \mathbf{0}& \mathbf{0}\\ {\mathit{W}}_{\mathbf{21}}& {\mathit{W}}_{\mathbf{22}}& \mathbf{0}\\ \mathbf{0}& {\mathit{W}}_{\mathbf{32}}& {\mathit{W}}_{\mathbf{33}}\end{array}\right]$$

(7)

where W₂₂ and W₃₃ indicate the weight of dependence between criteria and sub-criteria, respectively.

To attain convergence, the weighted supermatrix W_n is multiplied to the power of 2k + 1 (k→∞), as expressed in Equation (8). Finally, this study obtains a new limit supermatrix W_ANP [20].

$${\mathit{W}}_{\mathit{A}\mathit{N}\mathit{P}}=\underset{\mathit{k}\to \infty }{\mathbf{lim}}{\left({\mathit{W}}^{\prime }{}_{\mathit{n}}\right)}^{\mathbf{2}\mathit{k}+\mathbf{1}}$$

(8)

Step 4: Select the best alternative solution.

The weights of the limit supermatrix W_ANP obtained in Step 3 can be used as the basis for ranking the alternative solutions.

3. Building a Model for Supplier Evaluation and Selection

This study presents a new two-stage supplier evaluation and selection model for the aerospace industry. In the first stage, the model builds a network hierarchy and uses the modified Delphi method to define the main and sub-criteria for supplier evaluation and selection and to determine interdependence between sub-criteria. In the second stage, this model follows the ANP method to select the best alternative solution. Figure 2 contains the flowchart of the two-stage model.

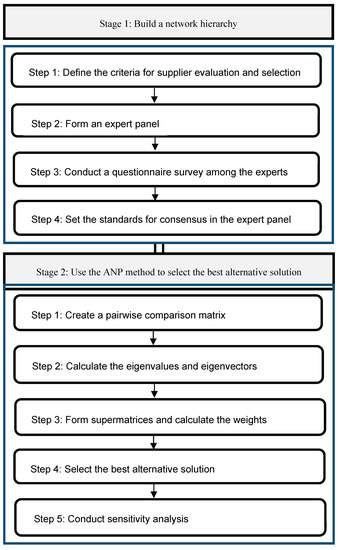
Figure 2. Supplier evaluation and selection model for the aerospace industry.

Stage 1: Build a network hierarchy.

Use the modified Delphi method to perform the following four steps [24,25]:

• Step 1: Define the criteria for supplier evaluation and selection.
• Step 2: Form an expert panel.
• Step 3: Conduct a questionnaire survey among the experts.
• Step 4: Set the standards for consensus in the expert panel.

Stage 2: Use the ANP to select the best alternative solution.

Use the ANP method to conduct the following five steps [20]:

• Step 1: Create a pairwise comparison matrix.
• Step 2: Calculate the eigenvalues and eigenvectors.
• Step 3: Form supermatrices and calculate the weights.
• Step 4: Select the best alternative solution.
• Step 5: Conduct sensitivity analysis.

4. Application of the Model to Aerowin

The Aerowin Technology Corporation is a company listed on the Taiwan Stock Exchange with a registered capital of 685,000,000 NTDs. It manufactures key parts of aircraft engines and is one of the few certified Taiwanese suppliers to major aircraft engine manufacturers worldwide, including Snecma (France) and affiliated with SAFRAN, PRATT & WHITNEY (US) and MHI (Japan).

To manufacture key parts for new aircraft engines, Aerowin needs to purchase high-precision, high-performance and high-priced machines. Taking the purchase of 3D measuring devices with a unit price of approximately 350,000 USD (shown in Figure 3) as an example, this study describes the procedure for evaluating and selecting suppliers when the three alternative solutions include Company A (Japan), Company B (US) and Company C (Germany).

Figure 3. 3D measuring devices [26,27,28].

Stage 1: Build a network hierarchy.

Step 1: Define the criteria for supplier evaluation and selection.

This study selects 6 criteria and 38 sub-criteria from Aerowin’s routine purchase-related documents (as described in Table 1).

Table 1. Definition and documentation of main and sub-criteria.

Criteria	Definition	Documentation	Sub-criteria
Market factors	Manufacturer evaluation involves factors such as brand image, manufacturing cost, delivery schedule and performance-cost ratio.	[17,29,30,31]	Product type Industry trends Competitors’ technologies Governmental industrial planning
Cost	Costs refer to expenses that are incurred by the production department for manufacturing products or providing services, including various direct and manufacturing expenses.	[10,30,32,33]	After-sale service Performance-cost ratio Safety devices Added value of productivity Component acquisition Reduction in labor time Requirements for manufacturing processes Degree of automation Equipment compatibility Warranty cost
Delivery	Delivery involves the lead time of administrative operations, purchase of raw materials, manufacture, transport, inspection and acceptance and contingency handling.	[10,12]	Export license Delivery time Punctual delivery Ordered quantity Delivery schedule Order fulfillment Response speed Terms of trade
Organizational planning	According to the actual conditions of the workshops, the company’s manufacture procedure and quality assurance departments, the fitness for use is evaluated and the requirements for manufacture and maximum equipment load in respect of the machines to be purchased are determined.	[33]	Fitness for use Return on assets Product selection Organizational technology
Information factors	Regarding new machines to be purchased, the company evaluates the reduction in labor time, industry status, maintainability and serviceability according to information provided by the manufacturers.	[17,34]	Information acquisition Industry status Equipment status Support from the information system
Quality	Quality assurance is to define, create and control quality-related costs and evaluate and determine whether products or services meet the requirements for quality, reliability and safety and control the costs incurred in the factory or by the customers in respect of non-conforming products or services.	[35,36,37,38]	Client certification Dynamic acceptance Brand appraisal Precision of equipment Industrial safety specifications Differences in equipment between Taiwan and overseas countries/regions Maximum load of equipment Reliability

Step 2: Form an expert panel.

This study uses Parente and Anderson’s [39] proposition, which states that there should be no upper limit for the number of experts (excluding dropouts) and that there should be at least ten experts who continuously participate in the whole research project until its end. Therefore, a total of 28 available experts were selected, including 14 from the industrial circle (leaders of the production, quality assurance, technological and purchase departments of well-known enterprises in Taiwan’s aerospace sector), 6 from the governmental circle (senior officials of the competent authorities of Taiwan’s aerospace sector) and 8 from the academic circle (professors of aerospace mechanics-related departments or faculties of colleges, or senior administrators of Taiwan’s aerospace research institutes). Table 2 describes the distribution of available experts from the industrial, governmental and academic circles.

Table 2. Statistics regarding the experts from industrial, governmental and academic circles.

Source of Experts	Members	Quantity	Percentage
Industrial circle	Three members of Aerowin, two members of AirAsia, two members of Magnate Technology, two members of GMTC, three members of AIDC and two members of Drewloong	14	50.00
Government circle	Four members of the Ministry of Economic Affairs and two members of the National Development Council	6	21.43
Academic circle	Three members of academic institutions, two members from the Metal Industries Research & Development Center and three members of the Industrial Technology Research Institute	8	28.57
Total		28	100

Step 3: Conduct a questionnaire survey among the experts.

Among the 28 experts, 16 were surveyed by email and 12 by fax. For the first survey, 28 questionnaires were distributed and 25 were returned, creating a return rate of 89.29%. For the second survey, 28 questionnaires were distributed and 28 were returned, creating a return rate of 100%.

Step 4: Set the standards for consensus among the expert panel.

In this study, consensus among the expert panel was measured in terms of the importance of main and sub-criteria (a value of 5 means “very important” and 1 means “very unimportant”) under Likert’s five-point scale and the quartile method proposed by Faherty [40]. The expert panel reaches a consensus when quartile deviation regarding an opinion towards an item is less than or equal to 0.50 and the importance measured by the Likert Scale is less than 4.00. The item should then be deleted. According to the results of the first questionnaire survey, criteria or sub-criteria that the expert panel reached a consensus on were deleted. As a result, five criteria and 16 sub-criteria were retained, as described in Table 3. This study analyzes the interdependence between criteria and sub-criteria for evaluating and selecting suppliers of 3D measuring devices according to expert opinions. Figure 4 shows the interdependence between criteria, Figure 5 shows that between sub-criteria and Figure 6 shows the ANP infrastructure for evaluating and selecting 3D measuring device suppliers.

Table 3. Statistics regarding consensus among the expert panel.

Criteria	Importance	Quartile Deviation	Delete if Reaching a Consensus	Sub-Criteria	Importance	Quartile Deviation	Delete if Reaching a Consensus
Market factors	4.37	0.61	Consensus not reached	Product type	3.89	0.48	Delete
				Industry trend	4.29	0.72	Delete
				Competitors’ technologies	4.78	0.79	Consensus not reached
				Government’s industrial planning	3.86	0.46	Consensus not reached
Cost	4.67	0.76	Consensus not reached	After-sale service	4.52	0.76	Consensus not reached
				Performance-cost ratio	4.81	0.81	Consensus not reached
				Safety device	4.21	0.49	Delete
				Added value of productivity	3.81	0.43	Delete
				Component acquisition	4.82	0.83	Consensus not reached
				Reduction in labor time	4.11	0.44	Delete
				Requirements for manufacture procedure	3.96	0.48	Delete
				Degree of automation	4.28	0.71	Consensus not reached
				Equipment compatibility	3.36	0.43	Delete
				Warranty cost	3.92	0.45	Delete
Delivery	4.42	0.66	Consensus not reached	Export license	4.98	0.93	Consensus not reached
				Delivery time	3.97	0.48	Delete
				Punctual delivery	3.57	0.37	Delete
				Ordered quantity	4.87	0.87	Consensus not reached
				Delivery schedule	4.79	0.85	Consensus not reached
				Order fulfillment	3.89	0.47	Delete
				Response speed	3.77	0.45	Delete
				Terms of trade	3.76	0.47	Delete
Organizational planning	4.27	0.54	Consensus not reached	Fitness for use	3.32	0.32	Delete
				Return on assets	4.38	0.67	Consensus not reached
				Product selection	3.61	0.36	Delete
				Organizational technology	4.52	0.74	Consensus not reached
Information factors	3.89	0.48	Delete	Information acquisition	3.13	0.35	Delete
				Industry status	3.26	0.37	Delete

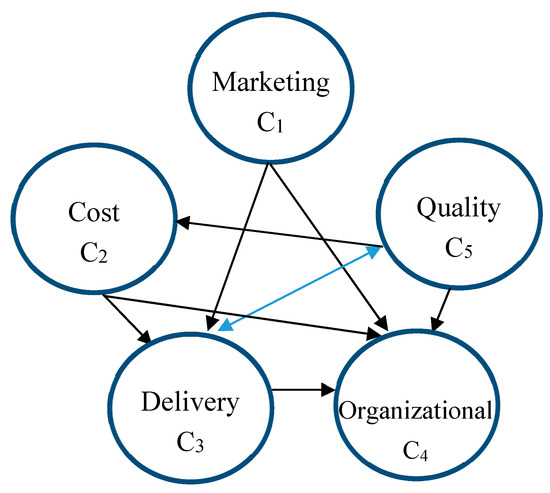
Figure 4. Interdependence among the criteria for evaluating and selecting 3D measuring device suppliers.

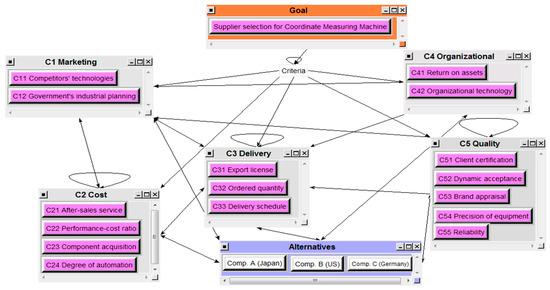
Figure 5. Interdependence among the sub-criteria for evaluating and selecting 3D measuring device suppliers.

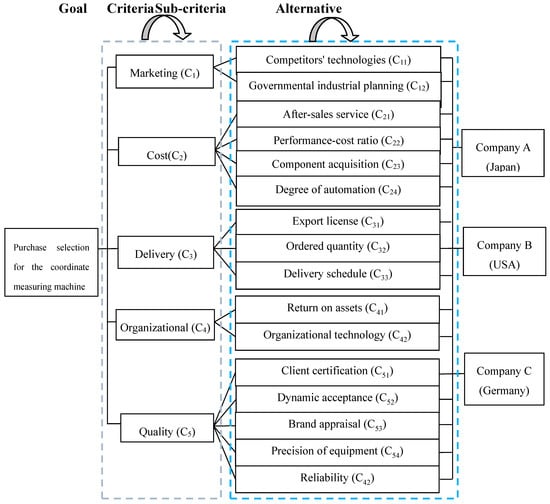
Figure 6. ANP infrastructure for evaluating and selecting 3D measuring device suppliers indicates interdependence between criteria.

Stage 2: Use the ANP method to select the best alternative solution.

Step 1: Create a pairwise comparison matrix.

Based on the results of the questionnaires completed by 28 experts, the pairwise comparison matrix A W₂₁ is completed (as described in Table 4):

Table 4. W₂₁ pairwise comparison matrix and eigenvectors (weights).

Criteria	Marketing (C1)	Cost (C2)	Delivery (C3)	Organizational Planning (C4)	Quality (C5)	Weight
Marketing (C1)	1	2.195	1.266	0.922	2.711	0.110
Cost (C2)	0.456	1	0.576	0.420	1.235	0.242
Delivery (C3)	0.790	1.735	1	0.728	2.142	0.139
Organizational planning (C4)	1.085	2.381	1.373	1	2.941	0.101
Quality (C5)	0.369	0.810	0.467	0.340	1	0.298

λ_max = 5.000; CI = 0; CR = 0.000 ≤ 0.1 consistency.

Step 2: Calculate the eigenvalues and eigenvectors.

According to Equation (1) and SuperDecision, the maximum eigenvalue of Matrix A (λ_max = 5) and corresponding eigenvector (x = (0.110, 0.242, 0.139, 0.101, 0.298)) are calculated. The weight values are shown in the rightmost column.

Step 3: Conduct a consistency test.

According to Equations (2) and (3), the CI and CR values (CI = 0 and CR = 0) are obtained, thus reaching the consistency standard. Table 4 describes the pairwise comparison matrix and weights in respect to the criteria.

Step 4: Form the supermatrices.

After calculating each eigenvector (weight) of W₂₁, this study creates the eigenvector matrix W₃₂. Taking sub-criterion C₁₁ under criterion C₁ as an example, Table 5 lists the calculation results. Table 6 lists the weights of the criteria and sub-criteria of W₂₁ and W₃₂.

Table 5. Pairwise comparison matrix and eigenvectors (weights) for sub-criteria under criterion C₁.

Sub-Criteria under Criterion C1	Competitor’s Technologies (C11)	Governmental Industrial Planning (C12)	Weight
Competitor’s Technologies (C11)	1	1.214	0.548
Government’s Industrial Planning (C12)	0.824	1	0.452

λ_max = 2.000; CI = 0; CR = 0.000 ≤ 0.1 consistency.

Table 6. Weights of criteria and sub-criteria.

Criteria	Criterion Weight (w21)	Sub-Criteria	Sub-Criterion Weight (w32)
C1	0.110	C11	0.548
		C12	0.452
C2	0.242	C21	0.290
		C22	0.365
		C23	0.190
		C24	0.156
C3	0.139	C31	0.650
		C32	0.214
		C33	0.136
C4	0.101	C41	0.556
		C42	0.444
C5	0.298	C51	0.343
		C52	0.221
		C53	0.106
		C54	0.167
		C55	0.162

The supermatrix regarding interdependence can then be obtained by combining the results obtained from w₂₁, w₂₂, w₃₂ and w₃₃, as expressed in Equations (9) and (10). The interdependence of criteria and sub-criteria are calculated, as described in Table 7, which presents an unweighted supermatrix, in addition to the respective vectors and matrices that were previously obtained. As the supermatrix includes interactions between clusters, such as the interdependence among criteria, not all the columns total to one. Additionally, dependence between selection criteria and sub-criteria was considered and analyzed and ANP was introduced within this framework to obtain the criteria weights. The experts separately examined the impact of all criteria via pairwise comparison. The normalized weights for these matrices are calculated and presented as w₂₂ and w₃₃, where zeros correspond to the weights of the criteria and sub-criteria on which a given criterion is based. Then, a weighted supermatrix is formed, as described in Table 8. Table 9 describes a limit supermatrix and W_ANP in Equation (11) indicates the overall weight of each sub-criterion.

$$\begin{array}{l}\begin{array}{ccccc}{ \mathrm{C}}_1& {\mathrm{C}}_2& {\mathrm{C}}_3& {\mathrm{C}}_4& {\mathrm{C}}_5\end{array}\\ {\mathit{w}}_{\mathbf{22}}=\begin{array}{c}{\mathrm{C}}_1\\ {\mathrm{C}}_2\\ {\mathrm{C}}_3\\ \begin{array}{c}{\mathrm{C}}_4\\ {\mathrm{C}}_5\end{array}\end{array}\left[\begin{array}{ccccc}0& 0& 0& 0& 0\\ 0& 0& 0& 0.226& 0.499\\ 0.583& 0.430& 0& 0.349& 0.321\\ 0.417& 0& 0.350& 0& 0.180\\ 0& 0.570& 0.650& 0.424& 0\end{array}\right]\end{array}$$

(9)

$${\mathit{w}}_{\mathbf{33}}=\begin{array}{c}{\mathrm{C}}_{11}\\ {\mathrm{C}}_{12}\\ {\mathrm{C}}_{21}\\ \begin{array}{c}{\mathrm{C}}_{22}\\ {\mathrm{C}}_{23}\\ {\mathrm{C}}_{24}\\ \begin{array}{c}{\mathrm{C}}_{31}\\ {\mathrm{C}}_{32}\\ {\mathrm{C}}_{33}\\ \begin{array}{c}{\mathrm{C}}_{41}\\ {\mathrm{C}}_{42}\\ {\mathrm{C}}_{51}\\ \begin{array}{c}{\mathrm{C}}_{52}\\ {\mathrm{C}}_{53}\\ {\mathrm{C}}_{54}\\ {\mathrm{C}}_{55}\end{array}\end{array}\end{array}\end{array}\end{array}\left[\begin{array}{cccccccccccccccc}0& 0& 0.500& 0.250& 0.167& 0.200& 0.167& 0.200& 0.167& 0.750& 0.200& 0.200& 0.167& 0.167& 0.200& 0.143\\ 0& 0& 0.500& 0.750& 0.833& 0.800& 0.833& 0.800& 0.833& 0.250& 0.800& 0.800& 0.833& 0.833& 0.800& 0.857\\ 0.288& 0.334& 0& 0& 0& 0& 0.323& 0.510& 0.508& 0& 0& 0& 0& 0& 0& 0\\ 0.381& 0.224& 0.750& 0& 0.800& 0& 0.214& 0.221& 0.270& 0& 0& 0& 0& 0& 0& 0\\ 0.059& 0.274& 0& 0& 0& 0& 0.059& 0.063& 0.049& 0& 0& 0& 0& 0& 0& 0\\ 0.273& 0.168& 0.250& 0& 0.200& 0& 0.404& 0.206& 0.173& 0& 0& 0& 0& 0& 0& 0\\ 0.510& 0.497& 0.492& 0.125& 0.085& 0.085& 0& 0& 0.250& 0.069& 0.208& 0.429& 0.167& 0.240& 0.143& 0\\ 0.200& 0.212& 0.159& 0.125& 0.177& 0.177& 0& 0& 0.750& 0.191& 0.131& 0.429& 0.167& 0.210& 0.143& 0\\ 0.291& 0.291& 0.349& 0.750& 0.738& 0.738& 1& 1& 0& 0.741& 0.661& 0.143& 0.667& 0.550& 0.714& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0.169& 0.121& 0& 0.250\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0.251& 0& 0.575& 0.200& 0.750\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0.673& 0.469& 0& 0.800& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0.308& 0.304& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0.075& 0.055& 0& 0& 0\end{array}\right]$$

(10)

Table 7. Unweighted supermatrix used for the ANP.

	Goal	C1	C2	C3	C4	C5	C11	C12	C21	C22	C23	C24	C31	C32	C33	C41	C42	C51	C52	C53	C54	C55	A	B	C
Goal	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
C1	0.128	0	0	0	0	0	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0	0	0
C2	0.281	0	0	0	0.226	0.499	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0	0	0
C3	0.162	0.583	0.430	0	0.349	0.321	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.548	0.167	0.200
C4	0.118	0.417	0	0.350	0	0.180	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.452	0.833	0.800
C5	0.311	0	0.570	0.650	0.424	0	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.553	0.176	0.188
C11	0.000	0.548	0	0	0	0	0	0	0.500	0.250	0.167	0.200	0.167	0.200	0.167	0.750	0.200	0.200	0.167	0.167	0.200	0.143	0.202	0.349	0.428
C12	0.000	0.452	0	0	0	0	0	0	0.500	0.750	0.833	0.800	0.833	0.800	0.833	0.250	0.800	0.800	0.833	0.833	0.800	0.857	0.062	0.056	0.055
C21	0.000	0	0.290	0	0	0	0.288	0.334	0	0	0	0	0.323	0.510	0.508	0	0	0	0	0	0	0	0.183	0.420	0.330
C22	0.000	0	0.365	0	0	0	0.381	0.224	0.750	0	0.800	0	0.214	0.221	0.270	0	0	0	0	0	0	0	0.131	0.094	0.195
C23	0.000	0	0.190	0	0	0	0.059	0.274	0	0	0	0	0.059	0.063	0.049	0	0	0	0	0	0	0	0.208	0.184	0.088
C24	0.000	0	0.156	0	0	0	0.273	0.168	0.25	0	0.200	0	0.404	0.206	0.173	0	0	0	0	0	0	0	0.661	0.722	0.717
C31	0.000	0	0	0.650	0	0	0.510	0.497	0.492	0.125	0.085	0.085	0	0	0.250	0.069	0.208	0.429	0.167	0.240	0.143	0	0.800	0.750	0.333
C32	0.000	0	0	0.214	0	0	0.200	0.212	0.159	0.125	0.177	0.177	0	0	0.750	0.191	0.131	0.429	0.167	0.210	0.143	0	0.200	0.250	0.667
C33	0.000	0	0	0.136	0	0	0.291	0.291	0.349	0.750	0.738	0.738	1	1	0	0.741	0.661	0.143	0.667	0.550	0.714	0	0.247	0.218	0.223
C41	0.000	0	0	0	0.556	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0.234	0.180	0.231
C42	0.000	0	0	0	0.444	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0.148	0.173	0.159
C51	0.000	0	0	0	0	0.343	0	0	0	0	0	0	0	0	0	0	0	0	0.169	0.121	0	0.250	0.144	0.190	0.190
C52	0.000	0	0	0	0	0.221	0	0	0	0	0	0	0	0	0	0	0	0.251	0	0.575	0.200	0.750	0.227	0.239	0.196
C53	0.000	0	0	0	0	0.106	0	0	0	0	0	0	0	0	0	0	0	0.673	0.469	0	0.800	0	0	0	0
C54	0.000	0	0	0	0	0.167	0	0	0	0	0	0	0	0	0	0	0	0	0.308	0.304	0	0	0	0	0
C55	0.000	0	0	0	0	0.162	0	0	0	0	0	0	0	0	0	0	0	0.075	0.055	0	0	0	0	0	0
A	0	0	0	0.361	0.400	0.403	0.395	0.388	0.405	0.387	0.377	0.367	0.388	0.393	0.382	0.382	0.357	0.430	0.376	0	0	0	0	0	0
B	0	0	0	0.308	0.267	0.257	0.264	0.273	0.234	0.281	0.280	0.287	0.271	0.272	0.266	0.275	0.303	0.232	0.269	0	0	0	0	0	0
C	0	0	0	0.330	0.333	0.340	0.341	0.339	0.361	0.331	0.342	0.346	0.341	0.335	0.352	0.344	0.340	0.338	0.355	0	0	0	0	0	0

Table 8. Weighted supermatrix used for ANP.

	Goal	C1	C2	C3	C4	C5	C11	C12	C21	C22	C23	C24	C31	C32	C33	C41	C42	C51	C52	C53	C54	C55	A	B	C
Goal	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
C1	0.128	0	0	0	0	0		0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
C2	0.281	0	0	0	0.117	0.133		0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
C3	0.162	0.290	0.133	0	0.181	0.086		0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
C4	0.118	0.207	0	0.154	0	0.048		0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
C5	0.311	0	0.177	0.285	0.220	0		0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
C11	0	0.276	0	0	0	0	0	0	0.092	0.069	0.031	0.055	0.028	0.034	0.028	0.252	0.067	0.035	0.029	0.029	0.035	0.039	0.085	0.026	0.031
C12	0	0.227	0	0	0	0	0	0	0.092	0.207	0.153	0.220	0.141	0.135	0.141	0.084	0.269	0.140	0.146	0.146	0.140	0.236	0.070	0.129	0.124
C21	0	0	0.200	0	0	0	0.102	0.119	0	0	0	0	0.140	0.221	0.221	0	0	0	0	0	0	0	0.141	0.045	0.048
C22	0	0	0.251	0	0	0	0.135	0.080	0.250	0	0.267	0	0.093	0.096	0.117	0	0	0	0	0	0	0	0.052	0.089	0.109
C23	0	0	0.131	0	0	0	0.021	0.097	0	0	0	0	0.026	0.027	0.021	0	0	0	0	0	0	0	0.016	0.014	0.014
C24	0	0	0.107	0	0	0	0.097	0.060	0.083	0	0.067	0	0.176	0.089	0.075	0	0	0	0	0	0	0	0.047	0.107	0.084
C31	0	0	0	0.365	0	0	0.173	0.169	0.148	0.057	0.026	0.039	0	0	0.085	0.033	0.100	0.156	0.061	0.087	0.052	0	0.025	0.018	0.038
C32	0	0	0	0.120	0	0	0.068	0.072	0.048	0.057	0.053	0.080	0	0	0.255	0.092	0.063	0.156	0.061	0.076	0.052	0	0.040	0.036	0.017
C33	0	0	0	0.076	0	0	0.099	0.099	0.105	0.339	0.222	0.334	0.340	0.340	0	0.357	0.318	0.052	0.242	0.200	0.260	0	0.128	0.140	0.139
C41	0	0	0	0	0.268	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0.089	0.084	0.037
C42	0	0	0	0	0.214	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0.022	0.028	0.074
C51	0	0	0	0	0	0.252	0	0	0	0	0	0	0	0	0	0	0	0	0.070	0.050	0	0.163	0.070	0.062	0.064
C52	0	0	0	0	0	0.162	0	0	0	0	0	0	0	0	0	0	0	0.104	0	0.238	0.083	0.488	0.066	0.051	0.066
C53	0	0	0	0	0	0.078	0	0	0	0	0	0	0	0	0	0	0	0.279	0.194	0	0.331	0	0.042	0.049	0.045
C54	0	0	0	0	0	0.122	0	0	0	0	0	0	0	0	0	0	0	0	0.128	0.126	0	0	0.041	0.054	0.054
C55	0	0	0	0	0	0.119	0	0	0	0	0	0	0	0	0	0	0	0.031	0.023	0	0	0	0.065	0.068	0.056
A	0	0	0	0	0	0	0.110	0.122	0.073	0.108	0.070	0.110	0.022	0.022	0.021	0.071	0.072	0.018	0.018	0.017	0.020	0.028	0	0	0
B	0	0	0	0	0	0	0.094	0.081	0.047	0.072	0.049	0.064	0.016	0.016	0.016	0.049	0.049	0.013	0.013	0.014	0.011	0.020	0	0	0
C	0	0	0	0	0	0	0.101	0.102	0.062	0.093	0.062	0.098	0.019	0.020	0.020	0.062	0.061	0.017	0.016	0.016	0.016	0.026	0	0	0

Table 9. Limit supermatrix used for ANP.

	Goal	C1	C2	C3	C4	C5	C11	C12	C21	C22	C23	C24	C31	C32	C33	C41	C42	C51	C52	C53	C54	C55	A	B	C
Goal	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
C1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
C2	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
C3	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
C4	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
C5	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
C11	0.055	0.055	0.055	0.055	0.055	0.055	0.055	0.055	0.055	0.055	0.055	0.055	0.055	0.055	0.055	0.055	0.055	0.055	0.055	0.055	0.055	0.055	0.055	0.055	0.055
C12	0.037	0.037	0.037	0.037	0.037	0.037	0.037	0.037	0.037	0.037	0.037	0.037	0.037	0.037	0.037	0.037	0.037	0.037	0.037	0.037	0.037	0.037	0.037	0.037	0.037
C21	0.048	0.048	0.048	0.048	0.048	0.048	0.048	0.048	0.048	0.048	0.048	0.048	0.048	0.048	0.048	0.048	0.048	0.048	0.048	0.048	0.048	0.048	0.048	0.048	0.048
C22	0.042	0.042	0.042	0.042	0.042	0.042	0.042	0.042	0.042	0.042	0.042	0.042	0.042	0.042	0.042	0.042	0.042	0.042	0.042	0.042	0.042	0.042	0.042	0.042	0.042
C23	0.120	0.120	0.120	0.120	0.120	0.120	0.120	0.120	0.120	0.120	0.120	0.120	0.120	0.120	0.120	0.120	0.120	0.120	0.120	0.120	0.120	0.120	0.120	0.120	0.120
C24	0.098	0.098	0.098	0.098	0.098	0.098	0.098	0.098	0.098	0.098	0.098	0.098	0.098	0.098	0.098	0.098	0.098	0.098	0.098	0.098	0.098	0.098	0.098	0.098	0.098
C31	0.092	0.092	0.092	0.092	0.092	0.092	0.092	0.092	0.092	0.092	0.092	0.092	0.092	0.092	0.092	0.092	0.092	0.092	0.092	0.092	0.092	0.092	0.092	0.092	0.092
C32	0.023	0.023	0.023	0.023	0.023	0.023	0.023	0.023	0.023	0.023	0.023	0.023	0.023	0.023	0.023	0.023	0.023	0.023	0.023	0.023	0.023	0.023	0.023	0.023	0.023
C33	0.065	0.065	0.065	0.065	0.065	0.065	0.065	0.065	0.065	0.065	0.065	0.065	0.065	0.065	0.065	0.065	0.065	0.065	0.065	0.065	0.065	0.065	0.065	0.065	0.065
C41	0.075	0.075	0.075	0.075	0.075	0.075	0.075	0.075	0.075	0.075	0.075	0.075	0.075	0.075	0.075	0.075	0.075	0.075	0.075	0.075	0.075	0.075	0.075	0.075	0.075
C42	0.083	0.083	0.083	0.083	0.083	0.083	0.083	0.083	0.083	0.083	0.083	0.083	0.083	0.083	0.083	0.083	0.083	0.083	0.083	0.083	0.083	0.083	0.083	0.083	0.083
C51	0.174	0.174	0.174	0.174	0.174	0.174	0.174	0.174	0.174	0.174	0.174	0.174	0.174	0.174	0.174	0.174	0.174	0.174	0.174	0.174	0.174	0.174	0.174	0.174	0.174
C52	0.010	0.010	0.010	0.010	0.010	0.010	0.010	0.010	0.010	0.010	0.010	0.010	0.010	0.010	0.010	0.010	0.010	0.010	0.010	0.010	0.010	0.010	0.010	0.010	0.010
C53	0.006	0.006	0.006	0.006	0.006	0.006	0.006	0.006	0.006	0.006	0.006	0.006	0.006	0.006	0.006	0.006	0.006	0.006	0.006	0.006	0.006	0.006	0.006	0.006	0.006
C54	0.013	0.013	0.013	0.013	0.013	0.013	0.013	0.013	0.013	0.013	0.013	0.013	0.013	0.013	0.013	0.013	0.013	0.013	0.013	0.013	0.013	0.013	0.013	0.013	0.013
C55	0.020	0.020	0.020	0.020	0.020	0.020	0.020	0.020	0.020	0.020	0.020	0.020	0.020	0.020	0.020	0.020	0.020	0.020	0.020	0.020	0.020	0.020	0.020	0.020	0.020
A	0.018	0.018	0.018	0.018	0.018	0.018	0.018	0.018	0.018	0.018	0.018	0.018	0.018	0.018	0.018	0.018	0.018	0.018	0.018	0.018	0.018	0.018	0.018	0.018	0.018
B	0.012	0.012	0.012	0.012	0.012	0.012	0.012	0.012	0.012	0.012	0.012	0.012	0.012	0.012	0.012	0.012	0.012	0.012	0.012	0.012	0.012	0.012	0.012	0.012	0.012
C	0.010	0.010	0.010	0.010	0.010	0.010	0.010	0.010	0.010	0.010	0.010	0.010	0.010	0.010	0.010	0.010	0.010	0.010	0.010	0.010	0.010	0.010	0.010	0.010	0.010

The italic values represent the final weights W_ANP and the weight of each sub-criterion

$${\mathit{W}}_{\mathit{A}\mathit{N}\mathit{P}}=\begin{array}{c}{\mathrm{C}}_{11}\\ {\mathrm{C}}_{12}\\ {\mathrm{C}}_{21}\\ \begin{array}{c}{\mathrm{C}}_{22}\\ {\mathrm{C}}_{23}\\ {\mathrm{C}}_{24}\\ \begin{array}{c}{\mathrm{C}}_{31}\\ {\mathrm{C}}_{32}\\ {\mathrm{C}}_{33}\\ \begin{array}{c}{\mathrm{C}}_{41}\\ {\mathrm{C}}_{42}\\ {\mathrm{C}}_{51}\\ \begin{array}{c}{\mathrm{C}}_{52}\\ {\mathrm{C}}_{53}\\ {\mathrm{C}}_{54}\\ {\mathrm{C}}_{55}\end{array}\end{array}\end{array}\end{array}\end{array}\left[\begin{array}{c}0.055\\ 0.037\\ 0.048\\ 0.042\\ 0.120\\ 0.098\\ 0.092\\ 0.023\\ 0.065\\ 0.075\\ 0.083\\ 0.174\\ 0.010\\ 0.006\\ 0.013\\ 0.020\end{array}\right]$$

(11)

Table 10 presents the pairwise comparison matrices for the sub-criteria of level 3 (C₁₁) to compute the weights of three alternatives.

Table 10. Pairwise comparison matrices for sub-criterion (C₁₁) to compute the weights of three alternative solutions.

C11	Japan Brand (A1)	US Brand (A2)	Germany Brand (A3)	Weight
Japan Brand (A1)	1	1.172	1.095	0.361
US Brand (A2)	0.853	1	1.070	0.308
Germany Brand (A3)	0.913	0.935	1	0.331

λ_max = 3.000; CI = 0.000; CR = 0.000 ≤ 0.1 consistency.

Similarly, the remaining relative weights of level 3 sub-criteria and alternatives can be obtained by pairwise comparison matrices, as presented in Table 11.

Table 11. Aggregate weights of pairwise comparison matrices for the sub-criteria of level 3 and alternative solutions.

Alternatives	Sub-Criteria of Level 3
	C11	C12	C21	C22	C23	C24	C31	C32	C33	C41	C42	C51	C52	C53	C54	C55
A1	0.361	0.400	0.403	0.395	0.388	0.405	0.387	0.377	0.367	0.388	0.393	0.382	0.382	0.357	0.430	0.376
A2	0.308	0.267	0.256	0.264	0.273	0.234	0.281	0.280	0.287	0.271	0.272	0.266	0.275	0.303	0.232	0.289
A3	0.330	0.333	0.340	0.341	0.339	0.361	0.331	0.342	0.346	0.341	0.335	0.352	0.344	0.340	0.338	0.355

Step 4: Select the best alternative solution.

According to Equation (10) and Table 11, calculate the preponderant vectors of three alternative solutions, as expressed in Equation (12):

$$\begin{array}{c}{\mathrm{A}}_1\\ {\mathrm{A}}_2\\ {\mathrm{A}}_3\end{array}\left[\begin{array}{cccccccccccccccc}0.361& 0.400& 0.403& 0.395& 0.388& 0.405& 0.387& 0.377& 0.367& 0.388& 0.393& 0.382& 0.382& 0.357& 0.430& 0.376\\ 0.308& 0.267& 0.256& 0.264& 0.273& 0.234& 0.281& 0.280& 0.287& 0.271& 0.272& 0.266& 0.275& 0.303& 0.232& 0.289\\ 0.330& 0.333& 0.340& 0.341& 0.339& 0.361& 0.331& 0.342& 0.346& 0.341& 0.335& 0.352& 0.344& 0.340& 0.338& 0.355\end{array}\right]\left[\begin{array}{c}0.055\\ 0.037\\ 0.048\\ 0.042\\ 0.120\\ 0.098\\ 0.092\\ 0.023\\ 0.065\\ 0.075\\ 0.083\\ 0.174\\ 0.010\\ 0.006\\ 0.013\\ 0.020\end{array}\right]=\left[\begin{array}{c}0.392\\ 0.267\\ 0.341\end{array}\right]$$

(12)

The three alternative solutions to Aerowin’s purchase of high-precision and high-priced 3D measuring devices are ranked according to Equation (12), as follows: Japanese Company A (0.392), German Company C (0.341) and US Company B (0.267).

Step 5: Conduct sensitivity analysis.

To verify the stability of the above two-stage decision-making model, sensitivity analysis is conducted for the overall evaluation architecture regarding Japanese Company A, US Company B and German Company C.

When the weight parameter of the adjusted purchase decision-making scheme is equal to 0.5, it represents the original weight of the three alternative solutions calculated by the ANP method. The three alternative solutions can then be ranked as follows: Japanese Company A (0.392), German Company C (0.341) and US Company B (0.267), as shown in Figure 7.

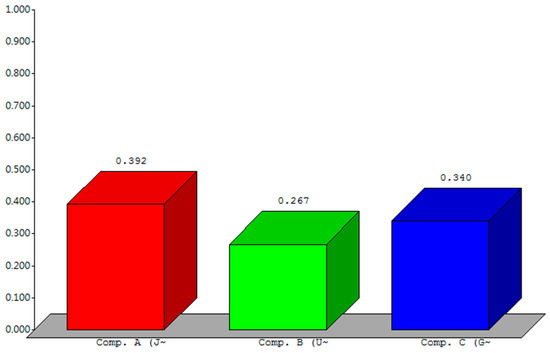
Figure 7. Ranking of three alternative solutions within the original supplier evaluation and selection framework.

When the adjusted weight of German Company C increases from 0.5 to 0.507, the three alternative solutions are ranked as follows: German Company C (0.378), Japanese Company A (0.370) and US Company C (0.252), as shown in Figure 8.

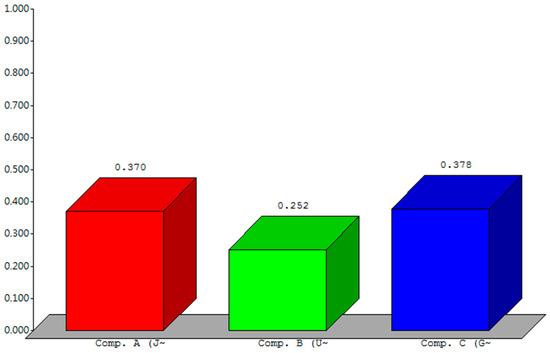
Figure 8. Ranking of three alternative solutions when the weight of German Company C increases from 0.5 to 0.507.

This study provides an in-depth analysis of the properties of the machine tools supplied by Japanese Company A, US Company B and German Company C. The tools are high-precision and high-priced critical machines under military control, so they are manufactured on a made-to-order basis. Based on the sensitivity analysis, Aerowin decided to purchase the machine tools supplied by Japanese Company A for the following reasons: (1) the machine tools of Company A will entail great capital expenditures but they possess high stability and precision; even if they are used for a long time, the produced products will be highly precise and produce a high pass yield. (2) Company A allows Aerowin the maximum elasticity for its current status and future development and provides the highest specifications in the fitness for use, manufacturing procedure and maximum equipment load. (3) The machine tools of Company A are less expensive than those of the other suppliers in terms of maintenance, component acquisition and after-sale services. Therefore, they can help Aerowin reduce their production costs after they are used over a certain period.

5. Conclusions

The aerospace industry has the most rigorous requirements for components and parts. Even small screw spikes need to be produced by mechanical equipment according to the processing conditions of workpieces. Only certified technical personnel can engage in production, quality inspection and worktable operation and maintenance to ensure machining quality and precision of workpieces. This is of critical importance to ensure that suppliers can be certified by the original manufacturers of aircraft engines. The above supplier evaluation and selection model for the aerospace industry is not only suitable for the purchase of general high-precision and high-priced products but can also conduct sensitivity analysis for various products pursuant to the three criteria (quality, cost and delivery) with varying weights to identify the best alternative solution and provide a company with greater elasticity for supplier selection. The findings are of referential value for supplier evaluation and selection policies for high-precision and high-priced machine tools in the aerospace industry. This study makes the following contributions:

(1) Several experts from industrial, governmental and academic circles constitute an expert panel who use the modified Delphi method to develop the criteria and sub-criteria for the ANP architecture. The intent of this is to make conducting ANP questionnaires more practical.

(2) The new purchase model contains five criteria and 16 sub-criteria. The five criteria are ranked by their degree of importance as follows: quality > cost > delivery > marketing > organizational planning. Among the 16 sub-criteria in Table 6, the top three are export license, return on assets and competitors’ technologies, in that order.

(3) Regarding the purchase of high-precision and high-priced 3D measuring devices, this study conducts sensitivity analysis and re-ranks the alternative solutions to verify the stability of the proposed two-stage decision-making model. Based on the sensitivity analysis for the three suppliers, the ranking of alternative solutions changes. The findings are of referential value for flexible purchasing decision-making.

(4) This study presents a new supplier evaluation and selection model for the aerospace industry. According to the empirical results, the new model is of high practical value and enables enterprises to consider and evaluate alternative solutions from multiple perspectives, thus facilitating sustainable operation and development.