Abstract
The growing demand for reliable and secure vehicle-to-vehicle (V2V) communication in next-generation intelligent transportation systems has accelerated the adoption of reconfigurable intelligent surfaces (RIS) as a means of enhancing link quality, spectral efficiency, and physical layer security. In this paper, we investigate the problem of secrecy rate maximization in a cooperative dual-RIS-aided V2V communication network, where two cascaded RISs are deployed to collaboratively assist with secure data transmission between mobile vehicular nodes in the presence of eavesdroppers. To address the inherent complexity of time-varying wireless channels, we propose a novel evolutionary transformer-gated recurrent unit (Evo-Transformer-GRU) framework that jointly learns temporal channel patterns and optimizes the RIS reflection coefficients, beam-forming vectors, and cooperative communication strategies. Our model integrates the sequence modeling strength of GRUs with the global attention mechanism of transformer encoders, enabling the efficient representation of time-series channel behavior and long-range dependencies. To further enhance convergence and secrecy performance, we incorporate an improved gray wolf optimizer (IGWO) to adaptively regulate the model’s hyper-parameters and fine-tune the RIS phase shifts, resulting in a more stable and optimized learning process. Extensive simulations demonstrate the superiority of the proposed framework compared to existing baselines, such as transformer, bidirectional encoder representations from transformers (BERT), deep reinforcement learning (DRL), long short-term memory (LSTM), and GRU models. Specifically, our method achieves an up to 32.6% improvement in average secrecy rate and a 28.4% lower convergence time under varying channel conditions and eavesdropper locations. In addition to secrecy rate improvements, the proposed model achieved a root mean square error (RMSE) of 0.05, coefficient of determination () score of 0.96, and mean absolute percentage error (MAPE) of just 0.73%, outperforming all baseline methods in prediction accuracy and robustness. Furthermore, Evo-Transformer-GRU demonstrated rapid convergence within 100 epochs, the lowest variance across multiple runs.
1. Introduction
Vehicular communication networks are foundational to the development of intelligent transportation systems (ITS), enabling continuous and reliable wireless communication between vehicles, infrastructure, pedestrians, and cloud services [,,,]. These networks form the technological backbone for a wide range of applications, including advanced driver-assistance systems (ADAS), real-time traffic monitoring, autonomous driving, and in-vehicle infotainment [,,]. With the rise of connected and automated vehicles, the demand for high-throughput, low-latency, and ultra-reliable vehicular communication has become more critical than ever []. Projections indicate that, by 2030, over 75% of vehicles globally will be equipped with communication capabilities, allowing for seamless data exchange in dense urban areas, highways, and smart mobility hubs [,,]. Vehicular networks also serve as an essential enabler for broader smart city ecosystems, where mobility, energy, and communication systems are deeply interwoven [,,]. Notably, the integration of vehicular networks with smart grid infrastructure supports emerging services such as vehicle-to-grid (V2G) energy trading, electric vehicle (EV) scheduling, and energy-aware routing, fostering a sustainable and efficient transportation-energy landscape [,,,,].
Among the various communication paradigms, vehicle-to-vehicle (V2V) communication plays a pivotal role in realizing cooperative and decentralized driving strategies [,,]. V2V enables vehicles to share key information, such as velocity, position, and driving intentions, which is vital for collision avoidance, coordinated lane-merging, and real-time hazard warnings. However, despite its criticality, V2V communication faces several technical challenges that hinder its practical deployment [,,]. One major limitation is signal blockage due to dynamic or static obstacles such as large vehicles, buildings, or terrain irregularities, which can disrupt line-of-sight (LoS) paths and introduce severe shadowing effects []. Additionally, the limited transmission range of onboard antennas becomes problematic in high-mobility and dense environments, leading to unreliable and intermittent connectivity [,,]. More importantly, the open nature of wireless V2V links makes them susceptible to passive eavesdropping and active attacks []. Ensuring the confidentiality and integrity of V2V messages is therefore a non-trivial task that requires new physical layer techniques to enhance the resilience and security of the network without compromising latency or efficiency [,,,,].
With the advent of 5G and the emergence of 6G, vehicular networks are expected to undergo a transformative shift in their capabilities, achieving ultra-reliable low-latency communication (URLLC), enhanced mobile broadband (eMBB), and support for massive machine-type communications (mMTC). These technologies serve as the foundational enablers of connected and automated mobility (CAM), where V2V communication plays a central role in cross-border transportation, traffic management, and autonomous driving scenarios [,]. Moreover, 5G-V2X and 6G-V2X architectures increasingly incorporate network slicing and edge computing to manage diverse service requirements, including real-time safety and infotainment []. Despite these advances, physical layer security remains crucial, as higher-layer protections alone cannot fully mitigate the eavesdropping or signal manipulation risks inherent in wireless channels. Thus, this work proposes a PLS-aware framework aligned with the trajectory of future V2X systems.
Reconfigurable intelligent surfaces (RISs) have recently emerged as a transformative technology capable of significantly improving wireless communication performance through smart propagation control [,,]. An RIS consists of a large number of passive, electronically tunable elements that can reflect incident radio waves with adjustable phase shifts, thereby enabling the fine-grained manipulation of the wireless environment. In the context of vehicular networks, especially V2V systems, RISs offer a practical means to overcome common limitations, such as blockage, fading, and weak direct links [,,]. By intelligently configuring the reflection coefficients, RISs can create alternate paths around obstacles, enhance the received signal power, and reduce interference. Furthermore, due to their nearly passive operation, RISs consume very little power, making them particularly attractive for energy-constrained deployments along roadsides or urban infrastructure. Beyond performance gains, RISs also contribute to communication security by shaping wavefronts to minimize signal leakage toward potential eavesdroppers [,,]. As such, RIS-assisted architectures are rapidly gaining attention for their potential to improve spectral efficiency, energy consumption, and physical layer security (PLS) in next-generation vehicular communication networks [,,].
1.1. Related Works
Recent research has explored the integration of RISs into vehicular networks to address various communication and security challenges. In [], the authors studied socially aware RIS-aided V2X networks, where the joint optimization of power allocation, spectrum management, and RIS configurations was used to maximize the sum capacity of vehicle-to-infrastructure (V2I) links while ensuring stable V2V communication. Chen et al. [] developed robust transmission strategies for RIS-assisted mmWave vehicular systems that rely on statistical channel state information (CSI), significantly reducing signaling overhead in high-mobility environments. Chapala and Zafaruddin [] analyzed the impact of vehicle mobility and phase errors on RIS channels and derived closed-form average bit error rate (BER) expressions under generalized-K fading conditions. Security concerns have also been addressed through RIS-enhanced physical layer solutions. Kavaiya and Patel [] derived secrecy outage probability (SOP) metrics to evaluate the effectiveness of RIS in mitigating passive attacks in 6G-enabled V2I communications. Their findings demonstrated that RIS outperforms conventional access points in terms of secrecy enhancement. In [], Mensi and Rawat compared partial RIS selection with partial relay selection and provided analytical expressions for ergodic and secrecy capacities. Their results indicated that partial RIS schemes are particularly advantageous in high-mobility vehicular environments. The work in [] investigated both V2V and V2I links in RIS-assisted networks, confirming through closed-form SOP analysis that RIS can strengthen secrecy to protect against passive eavesdropping. Similarly, [] studied two scenarios involving eavesdropper proximity and RIS orientation, evaluating SOP and average secrecy capacity (ASC) for each case.
In [], the authors examined a secure STAR-RIS-aided NOMA network under both full and statistical CSI assumptions, formulating problems to jointly maximize the sum rate and minimize the SOP. A multi-RIS architecture was explored in [] to improve user coverage and quality-of-service (QoS), where approximate closed-form outage and capacity metrics were derived using the central limit theorem (CLT). In [], the authors formulated an optimization problem to minimize the mean square error (MSE) in multi-RIS systems, accounting for timing and phase distortions. Phan et al. [] analyzed symbol error probability (SEP) under Nakagami-m fading in multi-RIS-assisted scenarios with direct transmitter–receiver links, showing performance gains compared to single-antenna setups. Further, the benefits of RIS diversity were examined in D2D-NOMA systems under Rician fading in [], where multi-RIS architectures significantly outperformed single-RIS counterparts in outage and throughput. A UAV-based transmitter setup was considered in [], where compact expressions for outage probability (OP) and achievable data rate (ADR) were obtained for RIS-aided NOMA links. Lastly, Tran et al. [] studied multi-RIS systems in the presence of hardware impairments, deriving expressions for OP, SEP, ADR, and throughput under Nakagami-m fading, further confirming the resilience and utility of RIS in realistic deployments.
While many prior works have focused on performance analysis and optimization in single-RIS or non-cooperative dual-RIS settings, cooperative RIS architectures have more recently gained interest due to their potential to expand coverage and support edge users. In [], a cooperative multi-RIS downlink model was considered, where beamforming was optimized to maximize the sum rate. The authors showed that coordinated RIS reflection can enhance multiuser downlink communication by intelligently aligning passive elements. Building upon this model, Zhang et al. [] investigated a dual-RIS-aided MIMO system in which active beamforming, receive filtering, and passive RIS configuration were jointly optimized to minimize the mean square error (MSE). Similarly, the work in [] explored a multiuser mmWave uplink scenario assisted by two cooperating RISs, with the objective of maximizing system throughput through joint optimization of transmit power and active/passive beamforming. In [], a cooperative dual-RIS-assisted uplink NOMA system was introduced, incorporating inter-RIS reflections and formulating a total transmit power minimization problem. From an analytical perspective, Shaikh et al. [] studied a dual-RIS V2I communication model and derived closed-form expressions for OP, energy efficiency (EE), and spectral efficiency (SE) under Nakagami-m fading. Their findings confirmed the superior performance of cooperative RIS designs in vehicular contexts.
Additionally, Ghadi et al. [] evaluated the performance of RIS and STAR-RIS in cooperative V2V scenarios under both NOMA and OMA schemes. Their analysis yielded closed-form expressions for OP, ergodic capacity (EC), and EE under Fisher–Snedecor F fading using CLT-based approximations. The results showed that the NOMA configuration with STAR-RIS offers notable gains over its OMA counterpart in ITS environments. In a recent study, the authors in [] examined the PLS performance of a cooperative dual-RIS-assisted V2V communication system operating under the NOMA protocol. The proposed model places one RIS near the transmitter vehicle and another near the legitimate receiver vehicles, while accounting for the presence of an eavesdropper. To characterize the channel behavior between the RISs, the authors adopted the Fisher–Snedecor F fading model. Using the CLT, they derived the marginal distributions of the equivalent cascaded channels and presented closed-form expressions for key PLS metrics, including ASC, SOP, and secrecy energy efficiency (SEE). Furthermore, an asymptotic analysis was conducted to provide deeper insights into system performance. The simulation results demonstrated that cooperative dual-RIS deployment under NOMA significantly improves security and transmission reliability in ITS.
1.2. Research Gaps and Motivations
According to the literature, RISs have emerged as a transformative solution for improving PLS and signal propagation in vehicular communication networks. However, a significant portion of the existing literature has focused primarily on single-RIS or non-cooperative multi-RIS deployments. While these architectures offer improvements in reliability and spectral efficiency, they often fall short in dynamic vehicular scenarios with severe line-of-sight obstructions and strict security requirements. Moreover, many existing approaches rely on static or limited-scope optimization methods, which are inadequate for adapting to the fast-varying nature of vehicular channels and the presence of mobile eavesdroppers. The lack of dynamic coordination between multiple RISs further restricts their performance benefits, especially in realistic cooperative V2V settings. Additionally, most related works do not account for the spatio-temporal variability in V2V environments or leverage dual-RIS architectures in a coordinated manner for secure communication. Another gap lies in the limited integration of deep learning-based optimization frameworks for joint beamforming and RIS configuration in secure vehicular networks. The joint design of transmit beamforming and RIS phase control in such cascaded setups is highly non-convex and computationally intensive.
Furthermore, only a few prior studies address the modeling of time-varying channels and the impact of vehicular mobility, especially at different speeds, on secrecy performance and system stability. Existing approaches typically assume either quasi-static or simplified mobility models, limiting their real-world applicability.
The absence of end-to-end learning-driven frameworks that can jointly optimize secrecy rate, temporal channel dynamics, and mobility-aware beamforming creates a substantial research gap.
These limitations motivate the need for intelligent, evolution-driven models capable of adapting to mobility-induced channel fluctuations while ensuring secure, stable communication in dual-RIS-assisted cooperative V2V systems.
1.3. Paper Contributions
To bridge the aforementioned research gaps, this paper presents a novel framework that integrates cooperative RIS-assisted V2V communication with learning-based optimization techniques to enhance secrecy rate performance. The key contributions are summarized as follows:
- We propose a secure cooperative dual-RIS-aided V2V communication system that jointly optimizes the secrecy rate, transmit beamforming vector, and phase shifts of two RISs under a realistic vehicular environment with blocked direct links.
- A novel Evolutionary Transformer-GRU (Evo-TST-GRU) model is developed, which combines the sequential modeling strength of gated recurrent units (GRUs) with the global attention mechanism of Transformer encoders to learn temporal channel behavior.
- An improved gray wolf optimizer (IGWO) is employed to adaptively tune the beamforming vector and RIS phase shifts, addressing the non-convex secrecy rate maximization problem with high convergence efficiency.
- Extensive simulations validate that the proposed framework significantly outperforms state-of-the-art schemes, achieving higher secrecy rate and faster convergence across various vehicular scenarios.
1.4. Paper Organization
The remainder of this paper is organized as follows: Section 2 describes the system model and problem formulation for SEE maximization in CF m-MIMO-enabled IoT networks. Section 3 presents the materials and methodology of the proposed hybrid DL framework. Section 4 provides the simulation results, assessing the performance of the proposed solution. Section 5 presents the discussion and comparison of the results with benchmark approaches, and finally, Section 6 concludes the paper.
2. System Model and Problem Formulation
We consider a secure wireless vehicle-to-vehicle (V2V) communication network, as depicted in Figure 1, where a source vehicle intends to transmit confidential data to a legitimate receiver vehicle , while an unauthorized eavesdropping vehicle attempts to intercept the transmission. To enhance communication security, two reconfigurable intelligent surfaces (RISs) are deployed to assist in steering the signal towards the intended receivers and mitigating exposure to the eavesdropper. In practical V2V scenarios, the nature of sensitive information transmitted over such networks depends on the application context. Nonetheless, typical confidential messages include safety-related warnings, traffic congestion updates, cooperative maneuver instructions (e.g., merging or lane changes), and privacy-preserving location information. Protecting this data from unauthorized interception is vital to prevent malicious exploitation or interference.
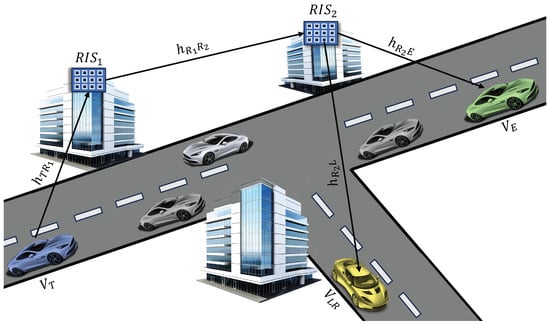
Figure 1.
The proposed system model for secure dual-RIS-aided V2V communication.
Due to the presence of environmental obstacles, such as tall buildings, parked trucks, roadside infrastructure, or even terrain elevation changes, the direct line-of-sight (LoS) paths between and both and are assumed to be blocked. This assumption is particularly valid in urban, suburban, or highly dynamic V2V scenarios, where LoS connectivity is often intermittent or entirely unavailable. To circumvent this, , composed of reflecting elements, is positioned near , while , consisting of elements, is installed closer to and . We consider that all vehicles move at either low or nearly constant speeds, typical in urban traffic, which results in approximately constant Doppler shifts. Consequently, the effect of vehicle mobility on channel variation is considered negligible, as supported in prior studies [,]. Furthermore, we assume that the distances between and , , between and , , between and , , and between the two RISs, , are all sufficiently large. Therefore, the wireless links between the vehicles and RISs, and between the kth element of and the ℓth element of , are modeled as quasi-static fading channels.
Let denote the confidential information symbol transmitted by the source vehicle , with average power , P represent the transmit power, and denote the beamforming vector applied at the multi-antenna transmitter , such that the transmit signal is expressed as with . The channel between and is denoted by , while the channel between and is modeled as . The channels from to the legitimate receiver and the eavesdropper are denoted by and , respectively. The diagonal reflection coefficient matrices of and are represented as and , where each element represents a controllable phase shift. The received signal at the legitimate receiver is then given by
where is the additive white Gaussian noise (AWGN) at . Similarly, the received signal at the eavesdropper is expressed as
where denotes the AWGN at . The entire transmission path includes double reflections via and , and both and observe the same cascaded link, except for the final hop, which differs spatially.
In this study, we consider, without loss of generality, that an advanced synchronization mechanism is employed at both RISs. This mechanism is capable of adaptively updating the phase shifts in real time according to variations in the wireless channel, thereby maintaining alignment even under fast-changing propagation conditions []. Based on the received signals at and , the instantaneous signal-to-noise ratio (SNR) at each receiver can be expressed as follows. For the legitimate receiver , the SNR is given by
where denotes the noise power at . Similarly, the SNR at the eavesdropper is expressed as
where is the noise power at . These expressions represent the effective SNRs experienced by each node through the double-reflected RIS-assisted paths.
To account for a more realistic configuration where the RIS phase shifts are not assumed to perfectly align with the composite channel phases, we explicitly model the received SNRs at the legitimate receiver and the eavesdropper by incorporating the phase differences between the channel coefficients and the adjustable RIS elements. Let and denote the respective distances between the transmitter, , , the legitimate receiver, and the eavesdropper. Assuming a common path loss exponent for all links, the large-scale attenuation is modeled by the product of inverse-distance terms raised to the power . Accordingly, the received SNR at the legitimate receiver is expressed as
and similarly, the SNR at the eavesdropper is given by
The RIS phase shifts and , as well as the transmit beamforming vector , are left as free parameters to be optimized in the subsequent secrecy rate maximization framework.
Based on the received SNRs at the legitimate receiver and the eavesdropper, the instantaneous secrecy rate of the system is defined as
where ensures the secrecy rate remains non-negative. This expression captures the rate at which confidential information can be securely transmitted from the source to the legitimate receiver without being decoded by the eavesdropper. The secrecy performance depends jointly on the transmit beamforming vector and the phase shift configurations of and , which will be jointly optimized in the next section.
We now formulate the secrecy rate maximization problem by jointly optimizing the beamforming vector at the transmitter and the phase shift configurations of the two RISs. Let , , and denote the optimization variables. The optimization problem is formulated as:
This problem is highly non-convex due to the multiplicative coupling between the beamforming vector and the RIS phase shifts, as well as the unit-modulus constraints imposed on the RIS elements. To efficiently solve this problem, we adopt a hybrid evolutionary learning framework. Specifically, we employ an improved gray wolf optimizer (IGWO) to optimize the beamforming vector and RIS phase shifts and , while the temporal dependencies in channel dynamics are captured using a transformer-enhanced gated recurrent unit (Evo-TST-GRU) model.
3. Materials and Methods
This section provides a comprehensive description of the components that form the core of the proposed Evo-Transformer-GRU framework. It begins by detailing the structure and function of the transformer encoder, emphasizing its role in capturing global contextual dependencies. Next, it outlines the design of the basic GRU and its effectiveness in modeling temporal sequences. The IGWO is then introduced as a meta-heuristic approach for hyper-parameter optimization. Finally, the integration of these components into a unified hybrid model is presented, highlighting the complete architecture and operational flow of the proposed learning framework.
3.1. Transformer Encoder
The Transformer architecture, originally introduced by Vaswani et al., has emerged as a pivotal innovation in the field of sequence modeling. Unlike conventional models such as the recurrent neural network (RNN) and the long short-term memory (LSTM), which rely on the iterative processing of sequential data through recurrent connections, the Transformer eliminates recurrence altogether. Instead, it employs a self-attention mechanism that allows the model to process entire input sequences in parallel. This parallelism leads to significantly faster training times and better scalability, particularly when dealing with large datasets or long sequences []. The Transformer’s ability to compute attention weights across all positions simultaneously enables it to capture global contextual information more efficiently than sequential models.
One of the key advantages of the Transformer lies in its capacity to model long-range dependencies without the vanishing gradient problems typically associated with recurrent architectures. In RNNs, each time step relies on the output of the previous step, which makes it difficult to learn dependencies over long intervals. While the LSTM architecture introduces gating mechanisms to mitigate this issue, it still processes sequences in a strictly sequential manner, limiting its capacity for parallelization and often requiring careful tuning to achieve stability. In contrast, the transformer uses Multi-Head Self-Attention to compute the contextual relationships between all input tokens simultaneously, allowing it to attend to both short-term and long-term dependencies within a single layer. This not only improves the representational capacity of the model but also simplifies training and makes it more robust across diverse tasks [].
Although the original Transformer was designed as a full encoder–decoder framework for machine translation, many contemporary applications, particularly those related to feature extraction, classification, or time-series analysis, utilize only the encoder portion. This encoder consists of a stack of identical layers, each comprising a multi-head attention mechanism followed by a feed-forward neural network (FFNN), interleaved with residual connections and layer normalization. In this work, we exclusively employ the transformer encoder to extract dynamic temporal patterns from wireless communication channels.
Since our objective is not to generate sequences but rather to learn meaningful spatio-temporal features for optimization in Vehicle-to-Vehicle communication, the encoder component provides a compact and efficient backbone for integrating attention-driven representation learning with downstream processing modules. To provide the encoder with temporal information, positional encodings are added to the input embeddings. As defined in Equations (9) and (10), sinusoidal functions are used to encode positional indices for each dimension []:
Here, pos is the position index, i is the dimension index, and d is the embedding size. The sinusoidal formulation ensures unique and smooth positional information, enabling the model to learn token order without recurrence. The input, after positional encoding, enters the first sub-layer of the encoder, which is the multi-head self-attention module. As shown in Equations (11)–(13), the input sequence Z is linearly projected into three matrices: queries Q, keys K, and values V.
where are learned projection weights, and Z is the input from the previous encoder layer (or the embedding if it is the first layer). The attention mechanism computes the relevance between each query–key pair, scales the dot product by the square root of the key dimension to stabilize gradients, and applies a softmax operation. This is formalized in Equation (14) []:
Here, is the dimensionality of each attention head. The softmax assigns higher weights to tokens with higher similarity, and the output is a weighted sum of values. Instead of a single head, multiple attention heads are used in parallel. As defined in Equations (15) and (16), each head performs its own attention operation, and the results are concatenated and passed through a linear layer:
is the final output projection. The output from the attention block is then passed through a FFNN, as shown in Equation (17):
where x is the input vector corresponding to a single token or position in the sequence, W is the weight matrix, and b is the bias vector. This fully connected network applies two linear transformations with a ReLU activation in between. It is applied independently to each token.
To stabilize training and retain the original input, both the attention and FFN modules are wrapped with residual connections and layer normalization. These operations are given by Equations (18) and (19) []:
These residual paths allow gradients to flow more easily across layers, enabling deeper stacking and better convergence. Figure 2 illustrates the architecture of the transformer encoder, broken into three conceptual stages. The first block on the left shows the input embedding combined with positional encoding, which is then fed into a stack of encoder layers. Each encoder layer contains two main sub-components: multi-head attention and an FFNN network. Both sub-components include residual connections and are normalized using layer normalization to ensure stability across training iterations.
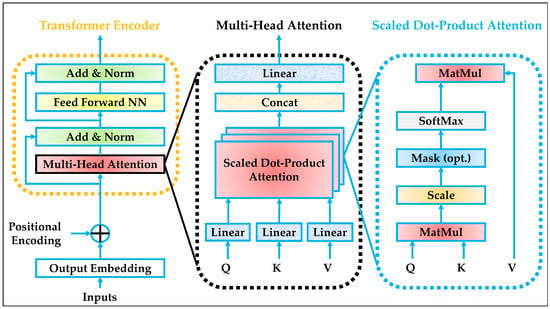
Figure 2.
The transformer encoder architecture.
The central part of Figure 2 expands on the structure of the multi-head attention module, showing how queries, keys, and values are computed via linear projections and used to derive attention scores. These scores are used to aggregate the value vectors, and outputs from all heads are concatenated and projected to produce the final attention output. The rightmost section of the figure provides a detailed look at the scaled dot-product attention mechanism, illustrating how attention weights are derived through matrix multiplications, scaling, softmax normalization, and weighted summation. This visualization emphasizes how global interactions are computed in parallel across the sequence, allowing the encoder to capture deep contextual dependencies efficiently [,,].
3.2. Basic GRU
The gated recurrent unit (GRU) was first introduced by Cho et al. [] in 2014 as a simplified alternative to the LSTM model for sequence learning and RNN training. Designed to mitigate the vanishing gradient problem inherent in vanilla RNNs, the GRU retains the ability to model sequential dependencies over long temporal ranges while reducing the computational complexity associated with LSTM architectures. By utilizing fewer gates and parameters, GRUs enable faster convergence and more efficient training without significantly sacrificing performance. Unlike LSTM, which employs separate memory cells and three gating mechanisms, the GRU integrates memory and gating into a single unit using only two gates: the update gate and the reset gate. This reduction in complexity leads to a more lightweight recurrent unit that is especially advantageous in low-latency or real-time systems. GRUs also avoid the full exposure of internal states, reducing memory overhead, and have shown competitive or superior performance in tasks involving speech, language modeling, and time-series prediction [].
In the context of secure vehicular communication, the GRU’s ability to capture temporal dependencies with a reduced computational load is highly relevant. The rapidly changing nature of wireless channels in high-mobility V2V scenarios requires efficient recurrent models that can operate under tight time constraints. In our framework, the GRU is employed to model the temporal dynamics of input sequences derived from transformer-encoded representations, ensuring that both long-range structure and time-local behavior are learned effectively for optimization purposes. Figure 3 illustrates the overall architecture of a standard GRU model. The structure operates sequentially across time steps, where at each time t, the input vector and the previous hidden state are processed to generate the current hidden state . This recurrent chain is composed of a series of GRU cells, each of which encapsulates the gating and update mechanism internally [].
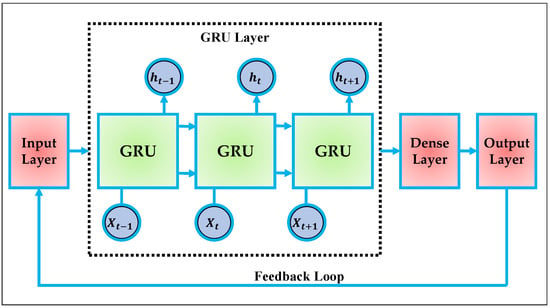
Figure 3.
Standard GRU model.
The outputs of the GRU layer are then passed through a dense layer and an output layer, which are typically connected to a task-specific head such as regression or classification. The input–output feedback loop, as shown in the figure, enables the architecture to operate over sequences with temporal consistency and dynamic memory propagation. At the core of each GRU cell lies the gating mechanism that controls the flow of information. As shown in Equation (20), the update gate determines how much of the previous state should be retained []:
where and are learnable weight matrices, and is the bias term. The sigmoid function squashes the gate output between 0 and 1, effectively controlling memory flow. Simultaneously, the reset gate , defined in Equation (21), determines how much of the previous hidden state to forget when computing the candidate activation:
where and are learnable weight matrices, and is the bias term. The reset gate allows the model to discard irrelevant historical information depending on the current context, enabling dynamic adaptation to changing input distributions. Using the reset gate, a candidate hidden state is computed as shown in Equation (22):
where and are learnable weight matrices, and is the bias term. This equation candidate state incorporates both the current input and a gated version of the previous hidden state, filtered by the reset gate. The Hadamard product ⊙ denotes element-wise multiplication. Finally, the new hidden state is calculated as a convex combination of the previous hidden state and the candidate activation, regulated by the update gate, as expressed in Equation (23):
Equation (14) enables the GRU to maintain and update memory content adaptively across time, blending old and new information based on the learned gating dynamics. Figure 4 provides a detailed visualization of the internal operations of a single GRU cell. The input and previous hidden state are used to compute both the reset gate and the update gate, each governed by a separate sigmoid unit. The reset gate influences how much historical information contributes to the computation of the candidate hidden state, while the update gate controls how much of replaces the existing memory. The final hidden state results from a weighted combination of the previous hidden state and the candidate state. The modular and efficient structure of the GRU cell, as shown in Figure 4, makes it a highly effective component for learning compact temporal representations within deep sequential models [,,].
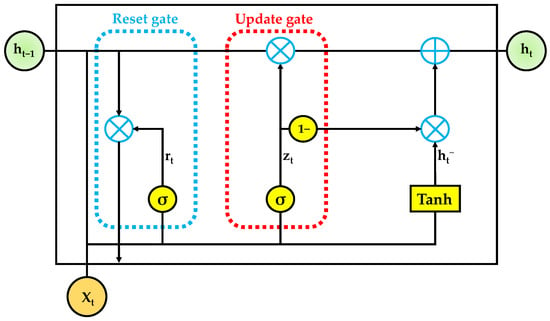
Figure 4.
Internal architecture of a standard GRU cell.
3.3. IGWO
The GWO is a nature-inspired meta-heuristic algorithm introduced by Mirjalili et al. [] to mimic the leadership hierarchy and cooperative hunting behavior of grey wolves in the wild. The population is divided into four hierarchical roles: alpha, beta, delta, and omega, where alpha is considered the dominant leader responsible for decision-making. The beta and delta wolves support the alpha and guide the rest of the population. The search agents update their positions relative to these leaders during the optimization process, creating a collective and adaptive exploration strategy. The core of the GWO lies in its ability to balance exploration and exploitation through the control of coefficient vectors. During the early stages of iteration, the wolves explore the search space by moving more randomly. As the optimization progresses, this exploration gradually transitions into exploitation. This dynamic shift is driven by a time-varying parameter, allowing wolves to first search globally and later converge locally. The transition from exploration to exploitation is essential for avoiding local minima and ensuring convergence to global optima.
The hunting process is mathematically modeled using a set of position update rules. As shown in Equations (24) and (25), the wolf computes its distance from the prey, updates its coefficients, and shifts position accordingly based on attraction and randomness []:
where
and is the position vector of a gray wolf, is the prey (optimal solution), and , are coefficient vectors. , are random vectors in the interval [0, 1], and the control parameter a is linearly reduced from 2 to 0 throughout the iterations.
To improve convergence in later stages, the influence of the three best-ranked wolves is considered. As shown in Equations (27)–(29), the distances to alpha, beta, and delta wolves are computed and used to derive intermediate positions, which are then averaged to update the wolf’s location []:
Here, are the positions of the three leading wolves, are respective distances to each leader, are updated coefficient vectors, and are intermediate candidate positions.
Figure 5 illustrates the geometric interpretation of movement toward each leader. Using vector projections and probabilistic weights, the wolf calculates how far and in what direction to move based on the attraction to each leader. This structure visualizes the core philosophy of the GWO algorithm: leadership-guided cooperation. By triangulating between the three best solutions, the algorithm leverages both convergence and diversity []. Many meta-heuristic algorithms, including the original GWO, are often limited by their exploitation capability and convergence reliability in complex, multimodal search spaces. While GWO balances exploration and exploitation through its control parameters, it still suffers from premature convergence, especially in later iterations. This often results from a lack of sufficient diversity in the influence pool (where only three elite wolves guide the rest of the population). As the algorithm progresses, these wolves may cluster too closely and fail to direct the population toward unexplored optima, reducing the global search effectiveness. Additionally, the exploitation power of GWO (especially in the neighborhood of promising solutions) is sometimes insufficient. The convergence process overly depends on the alpha wolf and the average of three fixed leadership influences. When these solutions are not representative of the global optimum, the algorithm may stagnate or become trapped in local optima. This leads to a narrow exploitation phase that lacks the adaptive flexibility needed for precise fine-tuning, particularly in high-dimensional or rugged search landscapes.
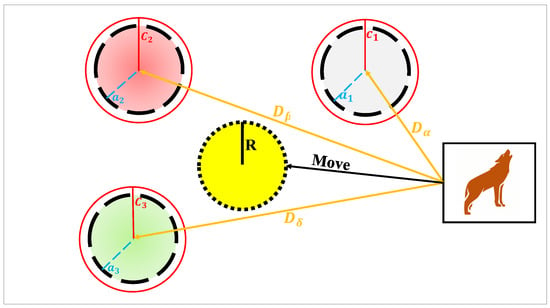
Figure 5.
Position update in the standard GWO algorithm.
To enhance both exploitation and convergence strength, we introduce an auxiliary guiding agent referred to as the -wolf. Positioned immediately below the alpha, beta, and delta wolves in the hierarchy, the -wolf represents the fourth-best solution in the population. This wolf is not an equal leader but acts as a strategic supporter, extending the information pool used to guide the pack. The -wolf is selected for its strong fitness and spatial proximity to the leaders, making it an ideal candidate for supporting convergence toward promising regions without introducing disruptive randomness. By integrating the -wolf into the decision-making structure, the GWO algorithm gains a more robust mechanism for averaging multiple elite perspectives. This mitigates the risk of following a misleading local optimum and enhances the pack’s ability to converge more precisely toward the true optimum. The -wolf also contributes to stronger exploitation by exerting directional influence closer to the pack’s central trajectory, helping to refine solution quality during the later stages of optimization. Furthermore, in high-dimensional problems, where gradient landscapes are complex and noisy, the -wolf acts as a stabilizing intermediary, reducing oscillations and improving convergence smoothness.
To incorporate the -wolf’s influence, a new set of equations is appended to the original GWO formulation. These additions define the distance between a search agent and the -wolf, compute an intermediate candidate position based on ’s guidance, and extend the original average update rule to include a fourth influence. This extension preserves the structure of the original algorithm while enriching it with additional directional information that significantly boosts precision and convergence without adding notable computational overhead. The newly introduced -wolf is integrated into the optimization process through Equations (30)–(32), which define its distance interaction, influence-based candidate position, and extended averaging mechanism for position updates:
where is the position of the -wolf, is the respective distance to the -wolf, and are the updated coefficient vectors, and is the intermediate candidate position. These additions enhance the guidance quality and convergence depth of the original GWO framework.
3.4. Proposed Evo-Transformer-GRU
In this work, we propose a novel hybrid learning architecture, termed Evo-Transformer-GRU, designed to address the problem of secure and efficient V2V communication in the presence of dynamic channel variations and adversarial eavesdropping. In the proposed Evo-Transformer-GRU framework, the input vector at each time step is constructed from real-valued features that characterize the wireless channel and system state. Specifically, the input features include (1) instantaneous SNR values at both RIS1 and RIS2, (2) estimated large-scale fading coefficients for all cascaded links (VT–RIS1, RIS1–RIS2, RIS2–VLR/VE), (3) relative distances , (4) phase misalignment factors between RIS elements and the composite channel, and (5) vehicle mobility context (e.g., static or slowly varying). These features are sequentially fed into the transformer encoder and GRU layers to capture spatio-temporal dependencies in the wireless environment. The model’s output is a scalar prediction of the achievable instantaneous secrecy rate , which is then used as the objective in the IGWO-driven optimization loop for adjusting beamforming vectors and RIS phase shifts. The complete structure of the proposed model is illustrated in Figure 6, which presents the end-to-end pipeline, combining a transformer encoder for spatial and temporal attention modeling, a GRU layer for sequential learning, and an IGWO for hyper-parameter tuning.
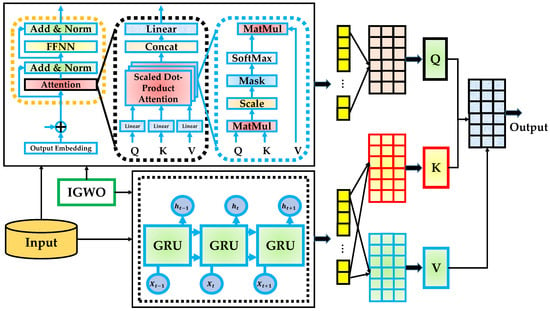
Figure 6.
The overall architecture of the proposed Evo-Transformer-GRU model.
This architecture is constructed to learn complex spatio-temporal patterns, maintain robust generalization, and adaptively optimize performance in the secrecy rate maximization task. The transformer encoder component is employed to extract global dependencies from the sequence of input features. Its core advantage lies in its self-attention mechanism, which enables the model to attend to all positions in the sequence simultaneously, capturing both short-term and long-range interactions. This is particularly important in vehicular networks, where the relevance of a signal can depend on both recent and distant temporal behaviors. Moreover, the parallelizable structure of the transformer encoder significantly reduces training time and allows for efficient gradient propagation, especially in high-dimensional sequence learning tasks. Internally, the transformer encoder uses multi-head attention and a position-wise FFNN network to construct rich, contextualized representations of the input. By incorporating positional encoding, the encoder can also maintain awareness of sequence ordering, compensating for its lack of recurrence. As depicted in the left block of Figure 6, the transformer processes embedded input tokens and produces contextual attention vectors that are used to guide further temporal modeling.
Following the transformer stage, a GRU layer is integrated to capture fine-grained temporal dependencies and hidden transitions across sequential data. GRUs are well-suited for modeling time-varying wireless channels because they effectively filter out irrelevant history while retaining useful long-term memory. Each GRU unit utilizes reset and update gates to control the flow of information, as discussed in Section 3.2. These mechanisms allow the model to dynamically adjust to new channel states and evolving interference patterns in real time. The GRU layer, shown in the center of Figure 6, takes the contextual outputs from the transformer and processes them across time steps to generate sequential hidden states. These hidden states represent the temporal evolution of encoded features and are used to generate query, key, and value matrices that participate in the final attention-based output prediction. This combination ensures that both temporal and contextual information is jointly considered during decision-making.
The strength of combining a transformer encoder with GRU lies in their complementary capabilities. While the transformer focuses on global attention across all tokens, the GRU handles the temporal ordering and time-local dependencies. As visualized in the flowchart, input features pass through the transformer encoder, are optimized using IGWO-guided hyper-parameters, and are then temporally processed by the GRU. These outputs are further refined via attention-based mechanisms and fed to a prediction layer to derive the final output, such as a secrecy-aware decision or a communication signal. In DL architectures, hyper-parameters play a critical role in determining both convergence behavior and generalization performance. Parameters such as learning rate, weight initialization, number of hidden units, number of GRU layers, and dropout rates significantly affect the model’s ability to learn robust representations and avoid overfitting. Manual tuning of these parameters is often time-consuming and suboptimal, especially in dynamically varying environments like vehicular networks.
To address this challenge, the proposed framework incorporates a novel IGWO for hyper-parameter optimization. IGWO not only enhances the traditional GWO with a stronger exploitation capability and convergence stability (as detailed in Section 3.3), but also efficiently explores the hyper-parameter space to find optimal configurations. As shown in Figure 6, IGWO is applied to adaptively adjust the transformer and GRU settings, including the learning rate, weight and bias initialization, number of attention heads, GRU neuron counts, and the number of stacked layers. By integrating IGWO, the Evo-Transformer-GRU model achieves better convergence and more stable training dynamics without exhaustive grid search or manual intervention. The optimizer continually evaluates different parameter combinations based on validation performance, guiding the learning architecture toward optimal solutions in fewer epochs. This adaptive tuning mechanism is essential for maximizing performance under varying channel conditions and ensuring high secrecy capacity in real-time communication scenarios.
4. Results
In this section, we present the simulation results to evaluate the performance of the proposed Evo-TST-GRU-based secure cooperative dual-RIS-aided V2V communication system. The primary objective is to validate the effectiveness of our framework in maximizing the secrecy rate while adapting to vehicular dynamics and potential eavesdropping. Unless otherwise specified, the following system parameters were used throughout the simulations. The distance between the transmitter vehicle and the first RIS, denoted as , was set to 50 m, which is also equal to the distance between the second RIS and the legitimate receiver vehicles; that is, m. The eavesdropper was located closer to the second RIS, with a distance of m. The separation between the two RISs was fixed at m. The noise power levels at the legitimate receiver and the eavesdropper were dBm and dBm, respectively. A uniform path loss exponent of was considered for all wireless links. The target secrecy rate threshold was set at bits per channel use, and the vehicle transmit power was set to dBm to ensure adequate signal strength under realistic operating conditions. All simulations were conducted on a MacBook Air equipped with an Apple M1 processor and 16 GB of RAM. The entire simulation framework was implemented using Python 3.9.13. The reinforcement learning model was built and trained using the TensorFlow library, which enabled the efficient handling of deep neural network computations and real-time policy updates. Numerical computations, such as matrix operations and stochastic sampling, were performed using NumPy, while Matplotlib 3.5.2 was used to generate the performance plots and visualize the results in a clear and reproducible manner.
To rigorously assess the performance of the proposed Evo-Transformer-GRU architecture, we compare it with several well-established baseline models. These include the standard transformer encoder and the bidirectional encoder representations from transformers (BERT), both of which are renowned for their ability to model long-range dependencies and capture contextual relationships through self-attention mechanisms. In addition, we evaluate classical recurrent models such as the GRU and the LSTM, which are frequently used for sequential data processing in wireless communication tasks. To provide a learning-based optimization agent for use as a benchmark, we also include a deep reinforcement learning (DRL) model, trained to maximize the secrecy rate under the same simulation conditions.
The selection of these baseline models was based on their relevance to different aspects of our problem. Transformer and BERT serve as strong attention-based encoders, enabling a direct comparison with the transformer component of our proposed hybrid architecture. GRU and LSTM allow us to isolate the effectiveness of memory-based temporal modeling in capturing vehicular channel dynamics. The DRL model provides an adaptive baseline, demonstrating how policy-based decision-making alone performs without architectural enhancements or optimization. Collectively, these models offer a diverse and meaningful reference set, allowing us to highlight the advantages of the Evo-Transformer-GRU framework in terms of secrecy performance, convergence behavior, and robustness in dynamic vehicular environments.
In order to evaluate the quantitative performance of the proposed Evo-Transformer-GRU model and compare it against the baseline approaches, we utilized a comprehensive set of performance metrics. These included the root mean square error (RMSE), the coefficient of determination (), mean absolute percentage error (MAPE), variance, execution time, convergence behavior, and statistical significance through the t-test. Together, these metrics provide insights into the accuracy, stability, computational efficiency, and statistical reliability of the results across different methods. The RMSE was used to measure the absolute prediction error between the model’s output and the true target value. As defined in Equation (33), RMSE penalizes larger deviations more heavily, making it a robust indicator of prediction quality:
where is the observed value and is the calculated value. A lower RMSE value indicates a more accurate model with fewer large errors.
To complement RMSE, we also report the coefficient of determination, which assesses how well the predictions approximate the actual values. As shown in Equation (34), it represents the proportion of variance in the ground truth that is captured by the predictions:
where and denote the means of the actual and predicted values, respectively, and , are their standard deviations. An value close to 1 implies strong predictive power. We also incorporated the MAPE as a supplementary metric to evaluate prediction accuracy. MAPE provides a normalized, percentage-based measure of prediction error, which is particularly useful when comparing across datasets or models with varying output scales. It expresses the average absolute difference between predicted and true values as a percentage of the true values:
MAPE is especially valuable when interpretability is needed—e.g., an MAPE of 5% means that the model’s predictions are off by 5% on average. In our context, this helps to quantify how closely the predicted secrecy rates match the actual values under varying vehicular communication conditions.
Variance was employed to evaluate the stability of the secrecy rate achieved across multiple independent runs. A lower variance suggests that the model consistently converges to similar performance levels and is not sensitive to random initialization or environmental dynamics. In scenarios involving stochastic learning, variance is critical for assessing robustness. Execution time is reported to demonstrate the computational efficiency of the training process. It provides an important practical dimension, especially in real-time or resource-constrained vehicular systems. Faster convergence with competitive accuracy highlights the scalability of the model. To further analyze convergence behavior, we present a learning curve showing the secrecy rate versus training iterations. This allows us to compare how quickly different models approached their optimal performance. A steeper convergence curve indicates faster learning, while a smooth plateau suggests stability and avoidance of overfitting. Lastly, to ensure that observed improvements are statistically significant and not due to chance, we performed a paired two-tailed t-test on the results of the proposed model and each baseline. A p-value less than 0.01 is considered statistically significant, confirming that the Evo-Transformer-GRU outperforms the competing methods with high confidence.
The selection and tuning of hyper-parameters play a critical role in determining the learning efficiency, convergence stability, and generalization capability of DL models. Inappropriately chosen parameters can lead to under-fitting, over-fitting, slow convergence, or unstable training dynamics—especially in highly dynamic environments such as V2V communication. Key parameters such as learning rate, number of layers, hidden units, dropout rate, and batch size directly influence how well the model captures temporal and spatial features while maintaining robustness under real-time constraints. Therefore, the careful and problem-specific optimization of these parameters is essential to extract the full potential of any deep model. In the proposed Evo-Transformer-GRU framework, hyper-parameters are optimized using the IGWO, which adaptively explores the parameter space to identify the best configuration for maximizing secrecy rate. This evolutionary approach allows the model to self-adjust critical values such as learning rate, attention heads, hidden units, and GRU depth without requiring manual intervention. In contrast, baseline models rely on conventional grid search, a brute-force method that evaluates all possible parameter combinations within a predefined range. While grid search is straightforward, it becomes computationally expensive and less effective in capturing non-linear interdependencies among parameters, especially when the search space is large.
The specific hyper-parameter settings for each model are presented in Table 1. The Evo-Transformer-GRU uses a learning rate of 0.002, batch size of 64, and a transformer encoder with eight layers and 10 attention heads. The GRU subcomponent comprises two layers with 32 hidden units each, and a dropout rate of 0.2. These values were derived through IGWO to strike a balance between model expressiveness and training efficiency. The population size and number of iterations for IGWO were set to 100 and 300, respectively, reflecting a moderate search depth and computational budget. By comparison, the baseline models exhibited a range of manually selected or grid-searched values. For example, the Transformer baseline uses a higher learning rate of 0.003 and 12 attention heads, while the GRU and LSTM models have deeper recurrent structures with four layers and larger hidden sizes (64 units). BERT uses a longer input window (64 time steps), consistent with its architecture’s reliance on longer context. DRL, meanwhile, includes reinforcement-specific parameters such as discount factor () and -greedy value (0.45). These differences underscore the necessity of tailored parameter tuning for each architecture and highlight the advantage of the IGWO-driven adaptive optimization used in the proposed model.

Table 1.
Parameter setting of proposed algorithms.
Figure 7 illustrates the impact of varying the transmit power of the source vehicle on the secrecy rate under different RIS configurations. It can be clearly observed that increasing the transmit power P from dBm to 20 dBm consistently improves the secrecy rate across all configurations. This trend reflects the fundamental relationship between transmit power and the received signal strength at both legitimate and illegitimate receivers. As the transmit power increases, the signal quality at the intended receiver improves, thereby enhancing the secrecy capacity, provided that the eavesdropper does not benefit from the same gain due to channel asymmetry and RIS-based redirection. The presence and configuration of RISs play a critical role in further boosting the secrecy performance. Compared to the baseline case without any RIS deployment, all RIS-assisted configurations demonstrate substantial improvements in secrecy rate. This clearly demonstrates the benefit of leveraging RISs to strengthen the channel to legitimate receivers while weakening the signal path toward potential eavesdroppers. According to the results obtained with the RIS-assisted setups, using a larger number of reflecting elements at both and results in consistently higher achieved secrecy rates. For instance, the configuration outperforms all others, achieving a secrecy rate of nearly 16 bps/Hz at 20 dBm, while the setup reaches approximately 11 bps/Hz. Furthermore, by comparing mixed-element configurations, i.e., vs. , it becomes evident that increasing the number of elements at yields greater secrecy rate gains compared to increasing the size of . This observation highlights the dominant role of , which is placed closer to both the legitimate receiver and the eavesdropper. Since directly influences the final signal path in both the constructive (to ) and destructive (to ) directions, its ability to steer and phase-align signals has a more pronounced impact on the overall secrecy performance. In contrast, mainly serves as an intermediate reflecting surface in the cascaded channel; thus, its influence, while still beneficial, is relatively limited.
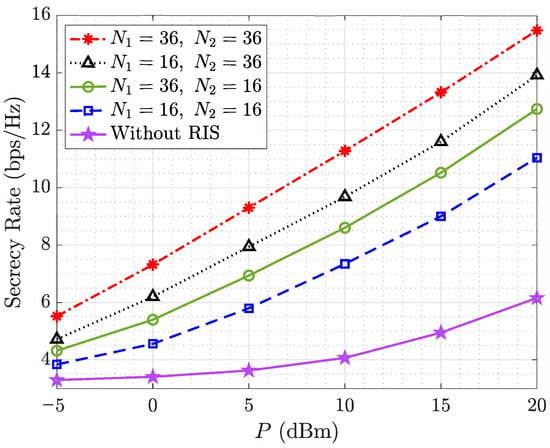
Figure 7.
Secrecy rate vs. the transmit power of for different reflective elements of and .
Figure 8 presents the impact of increasing the distance between and the eavesdropper , denoted as , on the secrecy rate under four different RIS configurations. As expected, increasing leads to a noticeable improvement in the secrecy rate across all scenarios. This behavior aligns with PLS principles, where enlarging the spatial separation between the RIS and the eavesdropper reduces the signal strength at the unintended node due to the higher path loss, thereby decreasing the likelihood of successful eavesdropping. All configurations with RIS deployment consistently outperform the baseline with fewer reflecting elements, demonstrating the significance of RIS-aided cascaded links in shaping the propagation environment. The highest secrecy rate is achieved when both and are equipped with 36 elements, confirming that increasing the number of passive reflecting elements enhances signal strength toward the legitimate receiver while allowing for better suppression or redirecting the signal to prevent it from reaching the eavesdropper. A closer comparison between the asymmetric setups, i.e., and , again emphasizes the dominant role of in secrecy enhancement. The configuration with more elements at yields superior secrecy performance for the same values, particularly at shorter distances. This is attributed to being directly responsible for shaping the signal incident on both the legitimate vehicle and the eavesdropper. As increases beyond 60 m, the performance gap among configurations narrows, since the ’s received power diminishes significantly and the secrecy rate becomes more dominated by the LR’s channel quality.
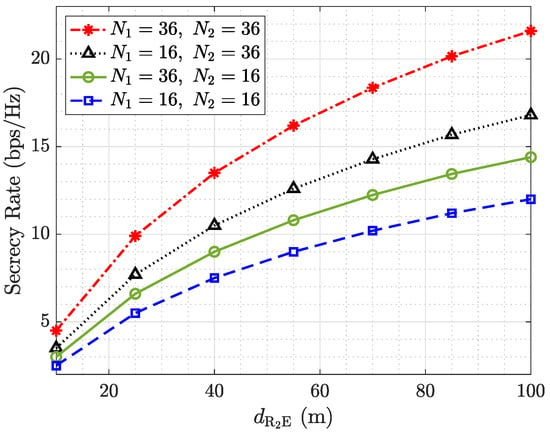
Figure 8.
Secrecy rate vs. for different reflective elements of and .
Figure 9 compares the secrecy rate performance of various algorithms as a function of the transmit power P of the source vehicle under a fixed RIS configuration with . As the transmit power increases from dBm to 20 dBm, all methods demonstrate improved secrecy rates, which is expected due to the higher SNR at the legitimate receiver. However, the rate of improvement varies notably among the different techniques. Among all compared methods, the proposed Evo-TST-GRU model consistently achieves the highest secrecy rate at all levels of transmit power. This superiority stems from its hybrid architecture, which combines the temporal modeling capabilities of GRUs with the global attention mechanism of Transformers, and is further enhanced by the adaptive optimization of beamforming and RIS phase shifts via IGWO. Notably, Evo-TST-GRU exhibits a considerable performance margin over the standalone Transformer and GRU models, indicating the advantage of learning both short- and long-term dependencies in the cascaded dual-RIS environment. The BERT and DRL-based models also perform well, with BERT slightly outperforming DRL, particularly at higher power levels. These results highlight the effectiveness of attention-based mechanisms in capturing contextual channel dynamics. Traditional recurrent architectures like LSTM and GRU exhibit a relatively reduced performance, which is attributed to their limited ability to model long-range dependencies and their lack of reinforcement-based policy updates. The GRU model, while simpler and efficient, provides the lowest secrecy rate among the learning-based approaches, reinforcing the need for more expressive and adaptive frameworks in RIS-aided secure vehicular communication. As a result, these findings demonstrate the clear advantage of the Evo-TST-GRU approach in maximizing the secrecy rate under dynamic conditions in secure V2V communications.
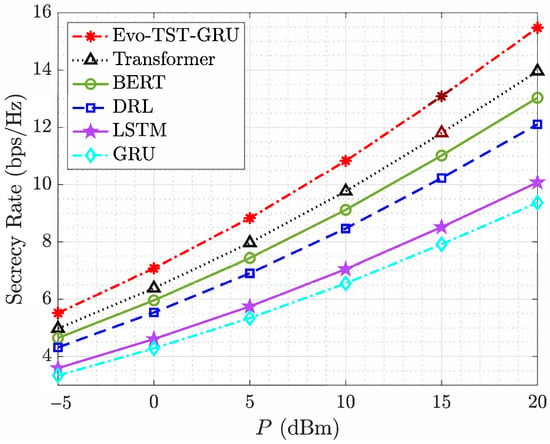
Figure 9.
Secrecy rate vs. the transmit power of for different algorithms and .
Figure 10 illustrates the variation in achievable secrecy rate as a function of vehicular velocity for multiple baseline algorithms, including Transformer, BERT, DRL, LSTM, and GRU, with both RIS units being configured as . As expected, all models experienced a degradation in secrecy performance with increasing velocity due to intensified Doppler effects, faster time-variations in the channel, and reduced coherence time, which together hinder optimal beamforming and phase adaptation. However, the proposed Evo-TST-GRU model consistently outperforms the alternatives across all speed regimes. Notably, at 5 m/s, it achieves a secrecy rate exceeding 11 bps/Hz, while at 25 m/s, it maintains a performance above 4 bps/Hz, well ahead of the next-best method, Transformer. This resilience highlights the model’s superior temporal modeling capacity, enabled by the Transformer-GRU synergy, and its adaptivity via IGWO-based evolutionary tuning. In contrast, DRL, LSTM, and GRU-based baselines show a sharper decline in secrecy rate as velocity increases, underlining their limitations in capturing long-range dependencies and maintaining robustness under rapid environmental fluctuations. These results demonstrate that Evo-TST-GRU is not only effective in static or quasi-static scenarios, but also maintains high confidentiality under mobility-induced dynamics, a critical requirement for real-world vehicular communications.
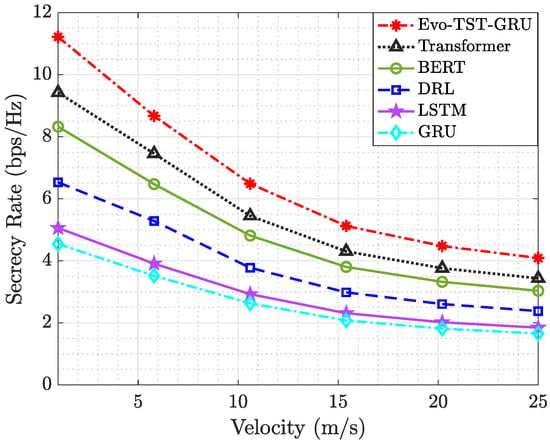
Figure 10.
Secrecy rate vs. vehicles’ velocity for different algorithms and .
Table 2 presents the comparative evaluation of the proposed Evo-Transformer-GRU model against five baseline architectures based on three widely used regression metrics: RMSE, , and MAPE. These metrics collectively assess each model’s accuracy, stability, and reliability in predicting the secrecy rate under the vehicular communication scenario defined in our simulation setup. The proposed Evo-Transformer-GRU achieves a remarkably low RMSE of 0.05, significantly outperforming all baseline models. This low error value demonstrates the model’s ability to closely track the true secrecy rate values with minimal deviation. In contrast, Transformer and BERT show higher RMSE values of 3.86 and 5.41, respectively, while the purely recurrent models (LSTM and GRU) perform notably worse, with RMSEs of 10.29 and 12.33. This indicates that traditional sequential models are less capable of capturing the complex spatio-temporal dependencies required for effective secure communication in dynamic vehicular environments.

Table 2.
Quantitative comparison of prediction performance across models.
In terms of , Evo-Transformer-GRU again leads with a value of 0.96, indicating that it explains 96% of the variance in the ground truth secrecy rates. This reflects high model fidelity and alignment with actual system behavior. In comparison, Transformer and BERT achieve values of 0.89 and 0.87, while DRL, LSTM, and GRU progressively decline to 0.86, 0.83, and 0.81, respectively. These results highlight the importance of combining attention-based encoding with memory-aware sequential modeling, as neither component alone yields the same level of predictive precision. The MAPE scores further validate these findings. Evo-Transformer-GRU registers an MAPE of only 0.73%, confirming its outstanding generalization and low relative error. In contrast, all other models exceed 5%, with GRU reaching as high as 15.70%. Since MAPE provides an intuitive percentage-based interpretation of error, these values reinforce the notion that the proposed model maintains consistent accuracy across different sample points and is robust to local fluctuations in secrecy rate. Taken together, the quantitative results confirm both numerically and conceptually that the Evo-Transformer-GRU architecture is uniquely well-suited to modeling secrecy rate dynamics in V2V communication scenarios. Its hybrid structure enables it to extract rich contextual features via attention mechanisms while preserving temporal dependencies through GRU memory units. Moreover, the IGWO-driven hyper-parameter tuning contributed to optimal architectural balance, providing it a clear edge over models with static or manually tuned configurations.
Figure 11 illustrates a radar plot that visually compares the R2 scores achieved by the six evaluated models. Each axis of the radar corresponds to one model, and the radial value on each axis indicates the respective R2 score obtained in Table 2. The radar plot provides a compact and intuitive visualization of model performance in terms of predictive accuracy, where higher values closer to the outer edge indicate a stronger correlation with ground truth data. The plot clearly highlights the superiority of the proposed Evo-Transformer-GRU model, which achieves the highest R2 score of near 0.96, forming a dominant peak at the top of the radar. Transformer and BERT exhibit relatively strong but lower R2 scores around 0.89 and 0.87, respectively, indicating a moderate capacity to capture underlying data variance. On the other hand, DRL, LSTM, and GRU show progressively weaker performance, with GRU reaching the lowest point at around 0.81. This visual confirms the quantitative results from Table 2 and reinforces the effectiveness of combining transformer attention with recurrent learning and evolutionary hyper-parameter tuning for modeling secrecy rate dynamics in vehicular communication systems.
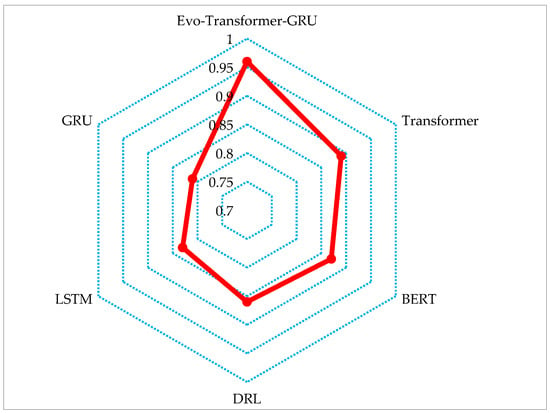
Figure 11.
Radar plot visualization of the R2 scores for all evaluated models.
Figure 12 provides a visual representation of the RMSE and MAPE scores for each of the six models analyzed, offering a clear comparative perspective on prediction accuracy and relative error. The bar chart groups the results by metric, allowing for a side-by-side inspection of how each model performs with respect to absolute prediction error (RMSE) and percentage deviation from the ground truth (MAPE). The Evo-Transformer-GRU model achieves the lowest values across both metrics, with an RMSE close to zero and an MAPE under 1%, clearly setting it apart from the other methods. Transformer and BERT follow at a considerable distance, while DRL, LSTM, and GRU demonstrate visibly poorer performance. This visual contrast underscores the critical importance of combining attention-based context modeling with temporal memory and optimized hyper-parameter tuning.
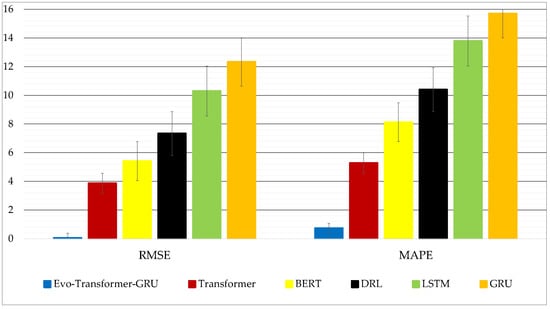
Figure 12.
Bar chart comparison of RMSE and MAPE values for all evaluated models.
Table 3 presents the results of statistical significance tests conducted using paired two-tailed t-tests between the proposed Evo-Transformer-GRU model and each of the baseline architectures. This test evaluates whether the observed performance improvements are statistically meaningful or could have occurred due to random variation. The p-values are compared against a significance threshold of , with lower values indicating stronger evidence against the null hypothesis; that is, the assumption that there is no meaningful performance difference between the compared models. The t-test is particularly relevant in this context because performance metrics like RMSE and MAPE can vary slightly across multiple runs due to randomness in model initialization, optimization, and data shuffling. The t-test allows us to assess whether the differences in these metrics are consistent and reproducible. By confirming statistical significance, we can substantiate that Evo-Transformer-GRU provides not just better average results but also reliably superior outcomes compared to competing models.

Table 3.
Statistical significance analysis of the Evo-Transformer-GRU compared to other models.
As shown in Table 3, all comparisons yield p-values significantly below the 0.01 threshold, indicating that the improvements achieved by Evo-Transformer-GRU are statistically significant across all baselines. For instance, the comparison with Transformer yields a p-value of 0.0007, confirming that the hybrid architecture’s advantage in modeling secrecy rate is not incidental. The results regarding BERT and DRL show even lower p-values (0.0003 and 0.00008, respectively), further emphasizing the model’s consistent superiority in both attention-based and reinforcement learning comparisons. The strongest statistical distinction is observed in comparisons with LSTM and GRU, where p-values drop to 0.00005 and 0.00002, respectively. These results underscore the limitations of traditional recurrent models in capturing complex spatio-temporal patterns in dynamic V2V communication scenarios. Overall, the t-test analysis validates the robustness and reliability of the proposed model’s improvements and provides compelling evidence that Evo-Transformer-GRU consistently outperforms its counterparts with high statistical confidence.
Figure 13 illustrates the RMSE-based convergence behavior of the proposed Evo-Transformer-GRU model in comparison with five baseline architectures across 300 training epochs. This figure provides critical insight into the training dynamics of each model, allowing us to evaluate how quickly and effectively each approach minimizes prediction error over time. The lower RMSE values and steeper descent curves indicate faster and more stable convergence during training. As shown in the figure, the Evo-Transformer-GRU model achieves a significantly faster convergence rate compared to all baselines, reducing its RMSE sharply within the first 50 epochs and approaching near-zero error by epoch 100. In contrast, models such as GRU and LSTM converge much more slowly and still maintain high error levels even beyond 300 epochs. BERT and DRL exhibit intermediate convergence, while the standard Transformer shows better performance but still lags behind the proposed method. This indicates that Evo-Transformer-GRU not only learns more effectively but also requires fewer iterations to stabilize, making it highly suitable for real-time or latency-sensitive applications like secure V2V communication.
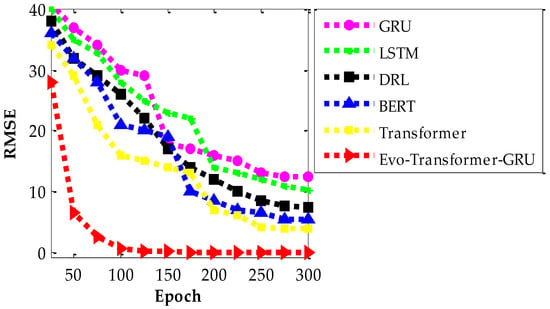
Figure 13.
Convergence curves of RMSE for all evaluated models.
The improved convergence speed can be largely attributed to the role of the IGWO in optimizing critical hyper-parameters such as learning rate, hidden units, and layer configurations. By adaptively tuning these parameters during the training process, IGWO ensures that the model operates in a well-balanced regime that promotes fast learning without overfitting or oscillation. The search agents in IGWO, enhanced by the inclusion of the wolf, maintain a dynamic equilibrium between exploration (searching globally for better configurations) and exploitation (refining known good regions), allowing the model to efficiently descend the error surface. In the context of this problem, where secrecy rate prediction under dynamic vehicular conditions is highly sensitive to feature timing and attention accuracy, the rapid and smooth convergence of Evo-Transformer-GRU is particularly valuable. The model is able to quickly extract meaningful temporal and contextual dependencies, optimize them through recurrent feedback and attention, and stabilize its output. This efficiency directly translates into reduced computational cost and improved responsiveness, which are both essential in the deployment of secure learning-based strategies in vehicular networks where decision latency can compromise security.
5. Discussion
The discussion section provides a deeper analytical reflection on the broader implications of the results presented so far. Beyond reporting superior accuracy and convergence metrics, this section critically examines the real-world applicability of the proposed Evo-Transformer-GRU model by addressing three vital aspects: stability, scalability, and computational feasibility. In practical vehicular communication environments, where decisions must be both secure and time-sensitive, high accuracy alone is insufficient: models must also be consistent, efficient, and robust under varying system loads and channel dynamics. Accordingly, this section explores how the proposed model behaves in terms of output stability under multiple simulation runs, how it scales computationally with respect to system parameters, and how it performs in terms of training efficiency and runtime cost. These aspects are crucial for assessing the operational viability of the model in real-time, latency-constrained V2V communication scenarios, where fluctuating environments and mobile nodes introduce a high degree of uncertainty.
In addition, we compare the computational footprint of Evo-Transformer-GRU with other baseline models, analyzing not just how fast the model learns, but also how efficiently it utilizes resources. We argue that for a model to be realistically deployable in on-board vehicular processors or edge AI platforms, it must strike a balance between predictive strength and computational economy. Hence, this section bridges the gap between experimental performance and practical implementation. The goal of this discussion is not only to validate the technical superiority of the proposed framework but also to evaluate its long-term adaptability in next-generation vehicular networks. By highlighting its performance consistency, runtime profile, and scalability characteristics, we aim to provide a comprehensive picture of how Evo-Transformer-GRU can serve as a foundation for future secure and intelligent wireless systems.
Table 4 presents a quantitative comparison of the evaluated models in terms of stability and computational efficiency. Stability is measured using the statistical variance of output secrecy rates across multiple Monte Carlo simulations, while average run time reflects the time required to complete the training process under consistent hardware and software conditions. These two dimensions provide insight into each model’s practical viability in real-world deployments, where both output consistency and time-to-convergence are crucial. As shown in the table, the proposed Evo-Transformer-GRU model achieves a remarkably low variance of just 0.00008, indicating extremely stable performance across all runs. This stability far surpasses that of all other models, with Transformer and BERT exhibiting significantly higher variances (1.86 and 2.28, respectively), and LSTM and GRU showing the highest instability (5.08 and 6.48). The reduced variance of the proposed model underscores the reliability of its predictions under channel randomness and network dynamics, which is vital in secure V2V communication systems.

Table 4.
Comparative analysis of model stability and computational cost for all architectures.
In terms of average runtime, Evo-Transformer-GRU completes training in 159 s, taking longer than GRU and Transformer but still being significantly more efficient than DRL (306 s), LSTM (259 s) and BERT (218 s). This suggests a balanced trade-off between computational cost and learning complexity. These findings reinforce the notion that Evo-Transformer-GRU is not only accurate and fast-converging but also robust and scalable, qualities that are essential for real-time vehicular applications. Its ability to maintain low variance demonstrates a high degree of generalization and insensitivity to initialization or random environmental shifts. Meanwhile, its moderate runtime, especially compared to DRL and deep recurrent networks, indicates its suitability for deployment on onboard vehicle processors or edge nodes without significant latency penalties.
Table 5 presents a comparative evaluation of algorithm efficiency based on the runtime required to achieve predefined RMSE thresholds (i.e., RMSE < 15, <10, <5, and <2.5). This table illustrates how rapidly each model converges to a certain level of prediction precision, providing a deeper perspective of learning efficiency and training scalability. The presence or absence of values across thresholds highlights not only the speed of convergence but also whether a model is capable of reaching high-precision performance at all. The Evo-Transformer-GRU model significantly outperforms all baselines in convergence efficiency, reaching RMSE < 15 in only 30 s and achieving RMSE < 2.5 in just 169 s—an outcome no other model accomplishes. While the Transformer and BERT models eventually attain RMSE < 5, they require substantially longer training durations (432 s and 269 s, respectively). Models like DRL, LSTM, and GRU struggle to cross the RMSE < 10 threshold and never reach higher-precision targets. These results validate that Evo-Transformer-GRU not only delivers better final accuracy but also requires significantly less time to reach those levels, demonstrating exceptional learning dynamics.

Table 5.
Comparative runtime analysis of algorithms under varying RMSE thresholds.
This performance advantage reflects the synergy between transformer attention, GRU-based temporal encoding, and hyper-parameter tuning via IGWO. The fast convergence of Evo-Transformer-GRU suggests that it can deliver accurate secrecy rate predictions under tight timing constraints, which is crucial for real-time vehicular communication scenarios. Furthermore, the ability to reach lower RMSE thresholds while others stall indicates robustness and efficiency in navigating complex error landscapes—making the proposed model a reliable solution for high-assurance, low-latency intelligent wireless systems. In light of these results, Evo-Transformer-GRU proves to be a strong candidate for future integration into 6G-era vehicular communication systems. Its combination of predictive accuracy, learning stability, and computational tractability positions it as a practical and forward-compatible solution. Such characteristics are critical not only for secure message transmission but also for enabling intelligent decision-making in autonomous and cooperative mobility ecosystems.
Moreover, the proposed Evo-Transformer-GRU model can be deployed in real-time vehicular systems by embedding it into edge units or vehicular onboard units (OBUs), leveraging model compression or quantization for latency reduction. Due to its modular design and reliance on physical-layer inputs, the framework can be integrated into existing V2X protocol stacks such as DSRC or C-V2X, supporting adaptive beamforming and RIS coordination under the constraints of current vehicular communication standards. In terms of deployment cost, the proposed Evo-Transformer-GRU model exhibits low inference latency due to its lightweight GRU structure and Transformer encoder with limited depth, making it feasible for execution on vehicular edge units with moderate computational capabilities. Although the training process is performed offline, energy-aware quantization and model compression techniques can be applied post-training to reduce runtime power consumption and memory footprint in real-world deployments.
6. Conclusions
In this work, we proposed a novel learning-based framework (referred to as Evo-Transformer-GRU) that combines the spatial attention modeling capability of a transformer encoder with the temporal sequence learning strength of GRU. To further enhance adaptability and learning efficiency, we integrated an IGWO to automatically tune critical hyper-parameters such as learning rate, architecture depth, and neuron configuration. The hybrid architecture was evaluated in the context of secrecy rate maximization within a cooperative dual-RIS-aided V2V communication system, offering an end-to-end solution tailored to secure and efficient vehicular wireless scenarios. The experimental evaluations clearly demonstrated the superiority of the proposed Evo-Transformer-GRU model across a diverse range of metrics. It achieved the lowest RMSE value of 0.05, indicating its exceptionally high prediction accuracy in modeling the secrecy rate under dynamic V2V conditions. The model also recorded the highest R2 score of 0.96, reflecting its ability to capture and explain nearly all the variance in the target outputs. In terms of robustness, Evo-Transformer-GRU showed a variance of only 0.00008 across multiple runs, which is significantly lower than all baseline models, confirming its stability and consistency under channel randomness and stochastic initialization. Furthermore, it achieved an MAPE of just 0.73%, highlighting its ability to deliver highly reliable predictions with minimal relative error. From a convergence and computational standpoint, the model consistently outperformed alternatives by converging within 100 epochs and achieving a secrecy rate prediction with RMSE below 2.5 in less than 170 s, something no other model accomplished. The convergence curve demonstrated both speed and smoothness, attributable to the integration of IGWO, which dynamically optimized the model’s hyper-parameters to balance exploration and exploitation. Compared to BERT, DRL, and deep recurrent models, Evo-Transformer-GRU required less training time while delivering more accurate and stable results, validating its practical applicability in latency-sensitive, resource-constrained vehicular systems.
The findings of this study highlight the critical importance of hybrid architectures that can jointly capture spatial attention and temporal dependencies for complex, security-sensitive wireless systems. By leveraging the transformer encoder’s ability to model global contextual interactions and integrating it with the sequential memory structure of GRUs, the proposed Evo-Transformer-GRU framework bridges two complementary learning paradigms. This fusion enables the model to operate effectively under the rapid channel variations and structural uncertainties inherent in V2V networks, offering a robust approach to physical-layer security optimization. The incorporation of IGWO further enhances this architecture by enabling dynamic, problem-specific hyper-parameter tuning—an often overlooked but essential aspect for achieving stable and efficient learning in real-world conditions. Beyond its strong performance in conventional metrics, the proposed framework demonstrates a compelling balance between accuracy, training efficiency, and system robustness, three pillars that are often difficult to optimize simultaneously. The model’s ability to converge quickly, remain stable under varying simulation runs, and maintain a low computational footprint suggests that it is not only theoretically sound but also practically viable. These characteristics make Evo-Transformer-GRU a promising candidate for deployment in next-generation vehicular communication systems where secure, real-time learning is indispensable. The framework also lays the groundwork for broader research into adaptive learning strategies that can generalize across varying network topologies and attack surfaces in future 6G ecosystems.
Limitations and Future Research Directions
One promising direction for future research is to extend the current framework toward online or continual learning under non-stationary channel environments. In real-world vehicular systems, channel conditions and network topology evolve rapidly due to mobility, interference, and environmental dynamics. Adapting the Evo-Transformer-GRU model to support real-time model updates without full retraining would significantly improve its practicality in large-scale deployments. This may involve integrating meta-learning or lightweight incremental update mechanisms, as well as exploring adversarial training schemes to further enhance resistance to active eavesdropping or jamming. On the architectural side, future work could explore multi-agent extensions of the proposed model, where each vehicle or node trains and shares its own Evo-Transformer-GRU instance in a federated or cooperative manner. This would be particularly beneficial in dense vehicular networks, where distributed security-aware optimization must occur under limited communication and computational budgets. Additionally, the IGWO component can be evolved into a self-adaptive, layer-specific optimizer, enabling fine-grained control over deeper transformer or GRU blocks.
Moreover, while the proposed Evo-Transformer-GRU framework demonstrates strong performance and adaptability for secure dual-RIS-aided V2V communication, several limitations remain, which warrant further exploration: (1) Channel Modeling and Mobility Assumptions: The model assumes quasi-static channels based on low or nearly constant vehicular speeds, which is realistic in urban environments but may not capture the full dynamics of high-speed highway or platooning scenarios. Although we included a sensitivity analysis under varying speeds, real-time Doppler effects, frequent handovers, and abrupt channel variations in highly mobile environments require more advanced modeling and adaptive strategies. (2) Input Sequence Length and Temporal Depth: The architecture is trained on short input sequences (length = 4), which may limit the richness of the temporal context available to the model. Although regularization, early stopping, and validation-based optimization help mitigate overfitting, extending the sequence horizon or incorporating memory-aware structures (e.g., attention buffers) may further improve temporal generalization. (3) Simulation-Based Evaluation: All evaluations are currently based on simulated channel conditions and synthetic mobility profiles. While these are grounded in realistic assumptions, real-world vehicular datasets and over-the-air testing would offer a more rigorous validation of the model’s practical effectiveness and robustness. (4) Real-Time Feasibility and Deployment Constraints: The computational requirements of the Transformer-GRU model and the IGWO-based optimization may cause challenges in its real-time deployment on resource-constrained vehicular nodes or roadside units. Future work will focus on model compression, quantization, and distributed edge inference techniques (e.g., MEC-based offloading) to improve practical scalability. (5) Generalization Across Diverse V2X Environments: Although the model performs well across varied simulations, additional testing across diverse V2X communication scenarios, such as mixed V2I/V2P/V2N networks, multi-eavesdropper settings, and non-line-of-sight topologies, would help validate its versatility and identify potential bottlenecks. Future research will extend this work by integrating online learning for adaptive retraining under evolving conditions, developing lightweight variants of the model for onboard inference, and validating the system on public vehicular communication datasets and testbeds. Moreover, we plan to explore reinforcement learning-based strategies to enable real-time policy adaptation in non-stationary vehicular environments.
In addition, it is worth noting that while the proposed cooperative dual-RIS-aided framework shows significant gains in secrecy rate at different speeds (as shown in Figure 10), it assumes the presence of two RIS units with reliable LoS to both the source and destination vehicles for the duration of the transmission session. However, in real vehicular environments, particularly at normal driving speeds, this LoS condition may only hold for a few seconds due to the rapid displacement of vehicles and limited spatial coverage of each RIS. This temporal limitation introduces practical challenges for maintaining sustained RIS-assisted communication, as the physical alignment between the vehicle and RISs can quickly degrade or disappear. Without a dense deployment of RIS elements along the roadway or an RIS handover mechanism, the proposed setup may not maintain continuous performance over long vehicular trajectories. To address this concern, future work may explore dynamic RIS topologies, including RIS meshes along roadside infrastructure, vehicular-mounted RIS units, or drone-assisted RIS deployment. These approaches could ensure the spatial continuity of the reflective paths and support seamless handover between RIS nodes. Incorporating predictive mobility models and handover-aware optimization algorithms would also be essential for extending RIS-aided PLS to large-scale vehicular scenarios. We emphasize that the current study focuses on a single cooperative RIS-pair coverage window, and this broader generalization is left for future investigation.
Author Contributions
Conceptualization, E.B., F.H.-G., D.M. and F.S.; methodology, E.B., F.H.-G. and D.M.; software, E.B. and F.H.-G.; validation, E.B., D.M. and F.S.; formal analysis, E.B. and F.S.; investigation, E.B., F.H.-G., D.M. and F.S.; resources, F.H.-G. and D.M.; data curation, E.B. and F.S.; writing–original draft preparation, E.B., F.H.-G., D.M. and F.S.; visualization, E.B. and F.H.-G.; supervision, D.M.; project administration, D.M.; funding acquisition, D.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Singh, A.K.; Pamula, R.; Akhter, N.; Battula, S.K.; Naha, R.; Chowdhury, A.; Kaisar, S. Intelligent Transportation System for Automated Medical Services during Pandemic. Future Gener. Comput. Syst. 2025, 163, 107515. [Google Scholar] [CrossRef]
- Behura, A.; Kumar, A.; Jain, P.K. A Comparative Performance Analysis of Vehicular Routing Protocols in Intelligent Transportation Systems. Telecommun. Syst. 2025, 88, 26. [Google Scholar] [CrossRef]
- Najafi, F.; Kaveh, M.; Mosavi, M.R.; Brighente, A.; Conti, M. EPUF: An Entropy-Derived Latency-Based DRAM Physical Unclonable Function for Lightweight Authentication in Internet of Things. IEEE Trans. Mob. Comput. 2024, 24, 2422–2436. [Google Scholar] [CrossRef]
- Wazid, M.; Singh, J.; Pandey, C.; Sherratt, R.S.; Das, A.K.; Giri, D.; Park, Y. Explainable Deep Learning-Enabled Malware Attack Detection for IoT-Enabled Intelligent Transportation Systems. IEEE Trans. Intell. Transp. Syst. 2025, 26, 7231–7244. [Google Scholar] [CrossRef]
- Neumann, T. Analysis of Advanced Driver-Assistance Systems for Safe and Comfortable Driving of Motor Vehicles. Sensors 2024, 24, 6223. [Google Scholar] [CrossRef] [PubMed]
- Ghadi, F.; Kaveh, M.; Wong, K.K. Performance Analysis of FAS-Aided Backscatter Communications. IEEE Wirel. Commun. Lett. 2024, 13, 2412–2416. [Google Scholar] [CrossRef]
- Barbosa, R.; Ogobuchi, O.D.; Joy, O.O.; Saadi, M.; Rosa, R.L.; Al Otaibi, S.; Rodríguez, D.Z. IoT-Based Real-Time Traffic Monitoring System Using Image Sensors by Sparse Deep Learning Algorithm. Comput. Commun. 2023, 210, 321–330. [Google Scholar] [CrossRef]
- Biswas, P.; Rashid, A.; Habib, A.K.M.A.; Mahmud, M.; Motakabber, S.M.A.; Hossain, S.; Rokonuzzaman, M.; Molla, A.H.; Harun, Z.; Khan, M.M.H.; et al. Vehicle to Grid: Technology, Charging Station, Power Transmission, Communication Standards, Techno-Economic Analysis, Challenges, and Recommendations. World Electr. Veh. J. 2025, 16, 142. [Google Scholar] [CrossRef]
- Guo, H.; Zhou, X.; Liu, J.; Zhang, Y. Vehicular Intelligence in 6G: Networking, Communications, and Computing. Veh. Commun. 2022, 33, 100399. [Google Scholar] [CrossRef]
- Adhikari, M.; Hazra, A.; Menon, V.G.; Chaurasia, B.K.; Mumtaz, S. A Roadmap of Next-Generation Wireless Technology for 6G-Enabled Vehicular Networks. IEEE Internet Things Mag. 2022, 4, 79–85. [Google Scholar] [CrossRef]
- Ghadi, F.R.; Kaveh, M.; Wong, K.K.; Jäntti, R.; Yan, Z. On Performance of FAS-Aided Wireless Powered NOMA Communication Systems. In Proceedings of the 2024 IEEE 20th International Conference on Wireless and Mobile Computing, Networking and Communications (WiMob), Vilamoura, Portugal, 14–16 October 2024; pp. 496–501. [Google Scholar]
- Inci, M.; Çelik, Ö.; Lashab, A.; Bayındır, K.Ç.; Vasquez, J.C.; Guerrero, J.M. Power System Integration of Electric Vehicles: A Review on Impacts and Contributions to the Smart Grid. Appl. Sci. 2024, 14, 2246. [Google Scholar] [CrossRef]
- Rani, P.; Sharma, R. Intelligent Transportation System for Internet of Vehicles Based Vehicular Networks for Smart Cities. Comput. Electr. Eng. 2023, 105, 108543. [Google Scholar] [CrossRef]
- Kaveh, M.; Mosavi, M.R. A Lightweight Mutual Authentication for Smart Grid Neighborhood Area Network Communications Based on Physically Unclonable Function. IEEE Syst. J. 2020, 14, 4535–4544. [Google Scholar] [CrossRef]
- Wu, Y.; Wang, Z.; Huangfu, Y.; Ravey, A.; Chrenko, D.; Gao, F. Hierarchical Operation of Electric Vehicle Charging Station in Smart Grid Integration Applications—An Overview. Int. J. Electr. Power Energy Syst. 2022, 139, 108005. [Google Scholar] [CrossRef]
- Kaveh, M.; Mosavi, M.R.; Martin, D.; Aghapour, S. An Efficient Authentication Protocol for Smart Grid Communication Based on On-Chip-Error-Correcting Physical Unclonable Function. Sustain. Energy Grids Netw. 2023, 36, 101228. [Google Scholar] [CrossRef]
- Dik, A.; Omer, S.; Boukhanouf, R. Electric Vehicles: V2G for Rapid, Safe, and Green EV Penetration. Energies 2022, 15, 803. [Google Scholar] [CrossRef]
- İnci, M.; Savrun, M.M.; Çelik, Ö. Integrating Electric Vehicles as Virtual Power Plants: A Comprehensive Review on Vehicle-to-Grid (V2G) Concepts, Interface Topologies, Marketing and Future Prospects. J. Energy Storage 2022, 55, 105579. [Google Scholar] [CrossRef]
- Kaveh, M.; Martin, D.; Mosavi, M.R. A Lightweight Authentication Scheme for V2G Communications: A PUF-Based Approach Ensuring Cyber/Physical Security and Identity/Location Privacy. Electronics 2020, 9, 1479. [Google Scholar] [CrossRef]
- Shurrab, M.; Singh, S.; Otrok, H.; Mizouni, R.; Khadkikar, V.; Zeineldin, H. An Efficient Vehicle-to-Vehicle (V2V) Energy Sharing Framework. IEEE Internet Things J. 2021, 9, 5315–5328. [Google Scholar] [CrossRef]
- Tahir, M.N.; Leviäkangas, P.; Katz, M. Connected Vehicles: V2V and V2I Road Weather and Traffic Communication Using Cellular Technologies. Sensors 2022, 22, 1142. [Google Scholar] [CrossRef] [PubMed]
- Das, D.; Banerjee, S.; Chatterjee, P.; Ghosh, U.; Biswas, U. A Secure Blockchain Enabled V2V Communication System Using Smart Contracts. IEEE Trans. Intell. Transp. Syst. 2022, 24, 4651–4660. [Google Scholar] [CrossRef]
- Fan, W.; Su, Y.; Liu, J.; Li, S.; Huang, W.; Wu, F.; Liu, Y.A. Joint Task Offloading and Resource Allocation for Vehicular Edge Computing Based on V2I and V2V Modes. IEEE Trans. Intell. Transp. Syst. 2023, 24, 4277–4292. [Google Scholar] [CrossRef]
- Khan, W.U.; Jameel, F.; Kumar, N.; Jäntti, R.; Guizani, M. Backscatter-Enabled Efficient V2X Communication with Non-Orthogonal Multiple Access. IEEE Trans. Veh. Technol. 2021, 70, 1724–1735. [Google Scholar] [CrossRef]
- Kaveh, M.; Ghadi, F.R.; Jäntti, R.; Yan, Z. Secrecy Performance Analysis of Backscatter Communications with Side Information. Sensors 2023, 23, 8358. [Google Scholar] [CrossRef] [PubMed]
- Gaitán, M.G.; Javanmardi, G.; Sámano-Robles, R. Orthogonal Space-Time Block Coding for Double Scattering V2V Links with LOS and Ground Reflections. Sensors 2023, 23, 9594. [Google Scholar] [CrossRef] [PubMed]
- Saraydar, S.; Tabataba, F.S.; Omidi, M.J. Improving Network Performance and Coverage Using Contract-Based Incentivized V2V Communications. IEEE Trans. Intell. Transp. Syst. 2024, 25, 16574–16583. [Google Scholar] [CrossRef]
- Ozpolat, M.; Bhargava, K.; Kampert, E.; Higgins, M.D. Multi-Lane Urban mmWave V2V Networks: A Path Loss Behaviour Dependent Coverage Analysis. Veh. Commun. 2021, 30, 100348. [Google Scholar] [CrossRef]
- Miri, S.; Kaveh, M.; Shahhoseini, H.S.; Mosavi, M.R.; Aghapour, S. On the Security of “An Ultra-Lightweight and Secure Scheme for Communications of Smart Meters and Neighborhood Gateways by Utilization of an ARM Cortex-M Microcontroller”. IET Inf. Secur. 2023, 17, 544–551. [Google Scholar] [CrossRef]
- Zhang, S.; Xiao, T.; Wang, B. A Communication Scheme with Privacy Protection in V2V Power Transaction Based on Linkable Ring Signature. World Electr. Veh. J. 2025, 16, 141. [Google Scholar] [CrossRef]
- Muslam, M.M.A. Enhancing Security in Vehicle-to-Vehicle Communication: A Comprehensive Review of Protocols and Techniques. Vehicles 2024, 6, 450–467. [Google Scholar] [CrossRef]
- Gupta, H.; Nayak, A. Publish Subscribe System Security Requirement: A Case Study for V2V Communication. IEEE Open J. Comput. Soc. 2024, 5, 389–405. [Google Scholar] [CrossRef]
- Fard, S.; Kaveh, M.; Mosavi, M.R.; Ko, S.B. An Efficient Modeling Attack for Breaking the Security of XOR-Arbiter PUFs by Using the Fully Connected and Long-Short Term Memory. Microprocess. Microsyst. 2022, 94, 104667. [Google Scholar] [CrossRef]
- Xie, Q.; Ding, Z.; Zheng, P. Provably Secure and Anonymous V2I and V2V Authentication Protocol for VANETs. IEEE Trans. Intell. Transp. Syst. 2023, 24, 7318–7327. [Google Scholar] [CrossRef]
- Kaveh, M.; Aghapour, S.; Martin, D.; Mosavi, M.R. A Secure Lightweight Signcryption Scheme for Smart Grid Communications Using Reliable Physically Unclonable Function. In Proceedings of the 2020 IEEE International Conference on Environment and Electrical Engineering and 2020 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Madrid, Spain, 9–12 June 2020; pp. 1–6. [Google Scholar]
- Mun, H.; Seo, M.; Lee, D.H. Secure Privacy-Preserving V2V Communication in 5G-V2X Supporting Network Slicing. IEEE Trans. Intell. Transp. Syst. 2021, 23, 14439–14455. [Google Scholar] [CrossRef]
- Rizopoulos, D.; Laskari, M.; Kouloumbis, G.; Fergadiotou, I.; Durkin, P.; Kaare, K.K.; Alam, M.M. 5G as an Enabler of Connected-and-Automated Mobility in European Cross-Border Corridors—A Market Assessment. Sustainability 2022, 14, 14411. [Google Scholar] [CrossRef]
- Mande, S.; Ramachandran, N. A Comprehensive Survey on Challenges and Issues in V2X and V2V Communication in 6G Future Generation Communication Models. Ing. Des Syst. D’Information 2024, 29, 951. [Google Scholar] [CrossRef]
- Mu, X.; Xu, J.; Liu, Y.; Hanzo, L. Reconfigurable Intelligent Surface-Aided Near-Field Communications for 6G: Opportunities and Challenges. IEEE Veh. Technol. Mag. 2024, 19, 65–74. [Google Scholar] [CrossRef]
- Ghadi, F.R.; Wong, K.K.; New, W.K.; Xu, H.; Murch, R.; Zhang, Y. On Performance of RIS-Aided Fluid Antenna Systems. IEEE Wirel. Commun. Lett. 2024, 13, 2175–2179. [Google Scholar] [CrossRef]
- Liang, J.C.; Zhang, L.; Luo, Z.; Jiang, R.Z.; Cheng, Z.W.; Wang, S.R.; Sun, M.K.; Jin, S.; Cheng, Q.; Cui, T.J. A Filtering Reconfigurable Intelligent Surface for Interference-Free Wireless Communications. Nat. Commun. 2024, 15, 3838. [Google Scholar] [CrossRef] [PubMed]
- Shi, W.; Jiang, H.; Xiong, B.; Chen, X.; Zhang, H.; Chen, Z.; Wu, Q. RIS-Empowered V2V Communications: Three-Dimensional Beam Domain Channel Modeling and Analysis. IEEE Trans. Wirel. Commun. 2024, 23, 15844–15857. [Google Scholar] [CrossRef]
- Ghadi, F.R.; López-Martínez, F.J.; Wong, K.K. Analytical Characterization of Coverage Regions for STAR-RIS-Aided NOMA/OMA Communication Systems. IEEE Commun. Lett. 2023, 27, 3063–3067. [Google Scholar] [CrossRef]
- Ji, B.; Wang, S.; Zhang, G.; Liu, J.; Mumtaz, S. Performance Analysis of RIS-Assisted V2V Communication under Multipath Interference. Veh. Commun. 2024, 45, 100696. [Google Scholar] [CrossRef]
- Shang, Y.; Peng, Y.; Ye, R.; Lee, J. RIS-Assisted Secure UAV Communication Scheme Against Active Jamming and Passive Eavesdropping. IEEE Trans. Intell. Transp. Syst. 2024, 25, 16953–16963. [Google Scholar] [CrossRef]
- Kaveh, M.; Ghadi, F.R.; Li, Z.; Yan, Z.; Jäntti, R. Secure Backscatter Communications Through RIS: Modeling and Performance. arXiv 2024, arXiv:2410.01829. [Google Scholar]
- Shi, W.; Xu, J.; Xu, W.; Yuen, C.; Swindlehurst, A.L.; Zhao, C. On Secrecy Performance of RIS-Assisted MISO Systems Over Rician Channels with Spatially Random Eavesdroppers. IEEE Trans. Wirel. Commun. 2024, 23, 8357–8371. [Google Scholar] [CrossRef]
- Naaz, F.; Nauman, A.; Khurshaid, T.; Kim, S.W. Empowering the Vehicular Network with RIS Technology: A State-of-the-Art Review. Sensors 2024, 24, 337. [Google Scholar] [CrossRef] [PubMed]
- Kaveh, M.; Yan, Z.; Jäntti, R. Secrecy Performance Analysis of RIS-Aided Smart Grid Communications. IEEE Trans. Ind. Inform. 2024, 20, 5415–5427. [Google Scholar] [CrossRef]
- Alsenwi, M.; Abolhasan, M.; Lipman, J. Intelligent and Reliable Millimeter Wave Communications for RIS-Aided Vehicular Networks. IEEE Trans. Intell. Transp. Syst. 2022, 23, 21582–21592. [Google Scholar] [CrossRef]
- Gu, X.; Duan, W.; Zhang, G.; Ji, Y.; Wen, M.; Ho, P.-H. Socially Aware V2X Networks with RIS: Joint Resource Optimization. IEEE Trans. Veh. Technol. 2022, 71, 6732–6737. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, Y.; Jiao, L. Robust Transmission for Reconfigurable Intelligent Surface Aided Millimeter Wave Vehicular Communications with Statistical CSI. IEEE Trans. Wirel. Commun. 2022, 21, 928–944. [Google Scholar] [CrossRef]
- Chapala, V.K.; Zafaruddin, S. Intelligent Connectivity through RIS-Assisted Wireless Communication: Exact Performance Analysis with Phase Errors and Mobility. IEEE Trans. Intell. Veh. 2023, 8, 4445–4459. [Google Scholar] [CrossRef]
- Kavaiya, S.; Patel, D.K. Restricting Passive Attacks in 6G Vehicular Networks: A Physical Layer Security Perspective. Wirel. Netw. 2023, 29, 1355–1365. [Google Scholar] [CrossRef]
- Mensi, N.; Rawat, D.B. On the Performance of Partial RIS Selection vs. Partial Relay Selection for Vehicular Communications. IEEE Trans. Veh. Technol. 2022, 71, 9475–9489. [Google Scholar] [CrossRef]
- Ai, Y.; de Figueiredo, F.A.P.; Kong, L.; Cheffena, M.; Chatzinotas, S.; Ottersten, B. Secure Vehicular Communications through Reconfigurable Intelligent Surfaces. IEEE Trans. Veh. Technol. 2021, 70, 7272–7276. [Google Scholar] [CrossRef]
- Gu, X.; Duan, W.; Zhang, G.; Sun, Q.; Wen, M.; Ho, P.-H. Physical Layer Security for RIS-Aided Wireless Communications with Uncertain Eavesdropper Distributions. IEEE Syst. J. 2023, 17, 848–859. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, R.; Wu, Y.; Ding, Z. STAR-RIS Assisted Secure Transmission for Downlink Multi-Carrier NOMA Networks. IEEE Trans. Inf. Forensics Secur. 2023, 18, 5788–5803. [Google Scholar] [CrossRef]
- Do, T.N.; Kaddoum, G.; Nguyen, T.L.; Da Costa, D.B.; Haas, Z.J. Multi-RIS-Aided Wireless Systems: Statistical Characterization and Performance Analysis. IEEE Trans. Commun. 2021, 69, 8641–8658. [Google Scholar] [CrossRef]
- Zhao, Y.; Xu, W.; Sun, H.; Ng, D.W.K.; You, X. Cooperative Reflection Design with Timing Offsets in Distributed Multi-RIS Communications. IEEE Wirel. Commun. Lett. 2021, 10, 2379–2383. [Google Scholar] [CrossRef]
- Phan, V.-D. Performance of Cooperative Communication System with Multiple Reconfigurable Intelligent Surfaces over Nakagami-m Fading Channels. IEEE Access 2022, 10, 9806–9816. [Google Scholar] [CrossRef]
- Kumar, P.; Bhowmick, A.; Choukiker, Y.K. Performance of Multi-RIS-Assisted D2D Communication Using NOMA. IEEE Access 2023, 11, 109603–109616. [Google Scholar] [CrossRef]
- Nguyen, B.C.; Xuan, N.T.; Manh, H.T.; Thanh, H.L.T.; Hiep, P.T. Performance Analysis for Multi-RIS UAV NOMA mmWave Communication Systems. Wirel. Netw. 2023, 29, 761–773. [Google Scholar] [CrossRef]
- Tran, P.T.; Nguyen, M.H.; Dao, N.M.; Duong, T.Q.; Shin, H. Exploiting Multiple RISs and Direct Link for Performance Enhancement of Wireless Systems with Hardware Impairments. IEEE Trans. Commun. 2022, 70, 5599–5611. [Google Scholar] [CrossRef]
- Ma, X.; Fang, Y.; Zhang, H.; Guo, S.; Yuan, D. Cooperative Beamforming Design for Multiple RIS-Assisted Communication Systems. IEEE Trans. Wirel. Commun. 2022, 21, 10949–10963. [Google Scholar] [CrossRef]
- Zhang, P.; Gong, S.; Ma, S. Double-RIS Aided Multi-User MIMO Communications: Common Reflection Pattern and Joint Beamforming Design. IEEE Trans. Veh. Technol. 2024, 73, 4418–4423. [Google Scholar] [CrossRef]
- Xue, Q.; Wei, R.; Ma, S.; Xu, Y.; Yan, L. Multi-User mmWave Uplink Communications Based on Collaborative Double-RIS: Joint Beamforming and Power Control. IEEE Commun. Lett. 2023, 27, 2702–2706. [Google Scholar] [CrossRef]
- Ma, H.; Wang, H.; Zhao, H.; Fu, S. Power Minimization for Double Cooperative-RIS-Assisted Uplink NOMA System. IEEE Wirel. Commun. Lett. 2023, 12, 1946–1950. [Google Scholar] [CrossRef]
- Shaikh, M.H.N.; Rabie, K.; Li, X.; Tsiftsis, T.; Nauryzbayev, G. On the Performance of Dual RIS-Assisted V2I Communication under Nakagami-m Fading. In Proceedings of the 2022 IEEE 96th Vehicular Technology Conference (VTC2022-Fall), London, UK, 26–29 September 2022; pp. 1–5. [Google Scholar]
- Ghadi, F.R.; Kaveh, M.; Martín, D. Performance Analysis of RIS/STAR-IOS-Aided V2V NOMA/OMA Communications over Composite Fading Channels. IEEE Trans. Intell. Veh. 2024, 9, 279–286. [Google Scholar] [CrossRef]
- Ghadi, F.R.; Kaveh, M.; Wong, K.K.; Martín, D. Physical Layer Security Performance of Cooperative Dual-RIS-Aided V2V NOMA Communications. IEEE Syst. J. 2024, 18, 2074–2084. [Google Scholar] [CrossRef]
- Huang, C.; Zappone, A.; Alexandropoulos, G.C.; Debbah, M.; Yuen, C. Reconfigurable Intelligent Surfaces for Energy Efficiency in Wireless Communication. IEEE Trans. Wirel. Commun. 2019, 18, 4157–4170. [Google Scholar] [CrossRef]
- Zhang, X.; Lin, M.; Hong, Y.; Xiao, H.; Chen, C.; Chen, H. MSFT: A Multi-Scale Feature-Based Transformer Model for Arrhythmia Classification. Biomed. Signal Process. Control 2025, 120, 106968. [Google Scholar] [CrossRef]
- Jiang, J.; Ke, L.; Chen, L.; Dou, B.; Zhu, Y.; Liu, J.; Wei, G.W. Transformer Technology in Molecular Science. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2024, 14, e1725. [Google Scholar] [CrossRef]
- Wang, C.; Chen, Y.; Zhang, S.; Zhang, Q. Stock Market Prediction Using Deep Transformer Model. Expert Syst. Appl. 2022, 208, 118128. [Google Scholar] [CrossRef]
- Ławryńczuk, M.; Zarzycki, K. LSTM and GRU type recurrent neural networks in model predictive control: A Review. Neurocomputing 2025, 632, 129712. [Google Scholar] [CrossRef]
- Mateus, B.C.; Mendes, M.; Farinha, J.T.; Assis, R.; Cardoso, A.M. Comparing LSTM and GRU models to predict the condition of a pulp paper press. Energies 2021, 14, 6958. [Google Scholar] [CrossRef]
- Liu, J.; Wu, C.; Wang, J. Gated recurrent units based neural network for time heterogeneous feedback recommendation. Inf. Sci. 2018, 423, 50–65. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Khatami, S.S.; Shoeibi, M.; Oskouei, A.E.; Martín, D.; Dashliboroun, M.K. 5DGWO-GAN: A Novel Five-Dimensional Gray Wolf Optimizer for Generative Adversarial Network-Enabled Intrusion Detection in IoT Systems. Comput. Mater. Contin. 2025, 82, 881–911. [Google Scholar] [CrossRef]
- Khatami, S.S.; Shoeibi, M.; Salehi, R.; Kaveh, M. Energy-Efficient and Secure Double RIS-Aided Wireless Sensor Networks: A QoS-Aware Fuzzy Deep Reinforcement Learning Approach. J. Sens. Actuator Netw. 2025, 14, 18. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the World Electric Vehicle Association. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).