Numerical Simulation of Hydrogen Leakage from Fuel Cell Vehicle in an Outdoor Parking Garage
Abstract
:1. Introduction
2. Numerical Simulation
2.1. FLACS-Hydrogen Code
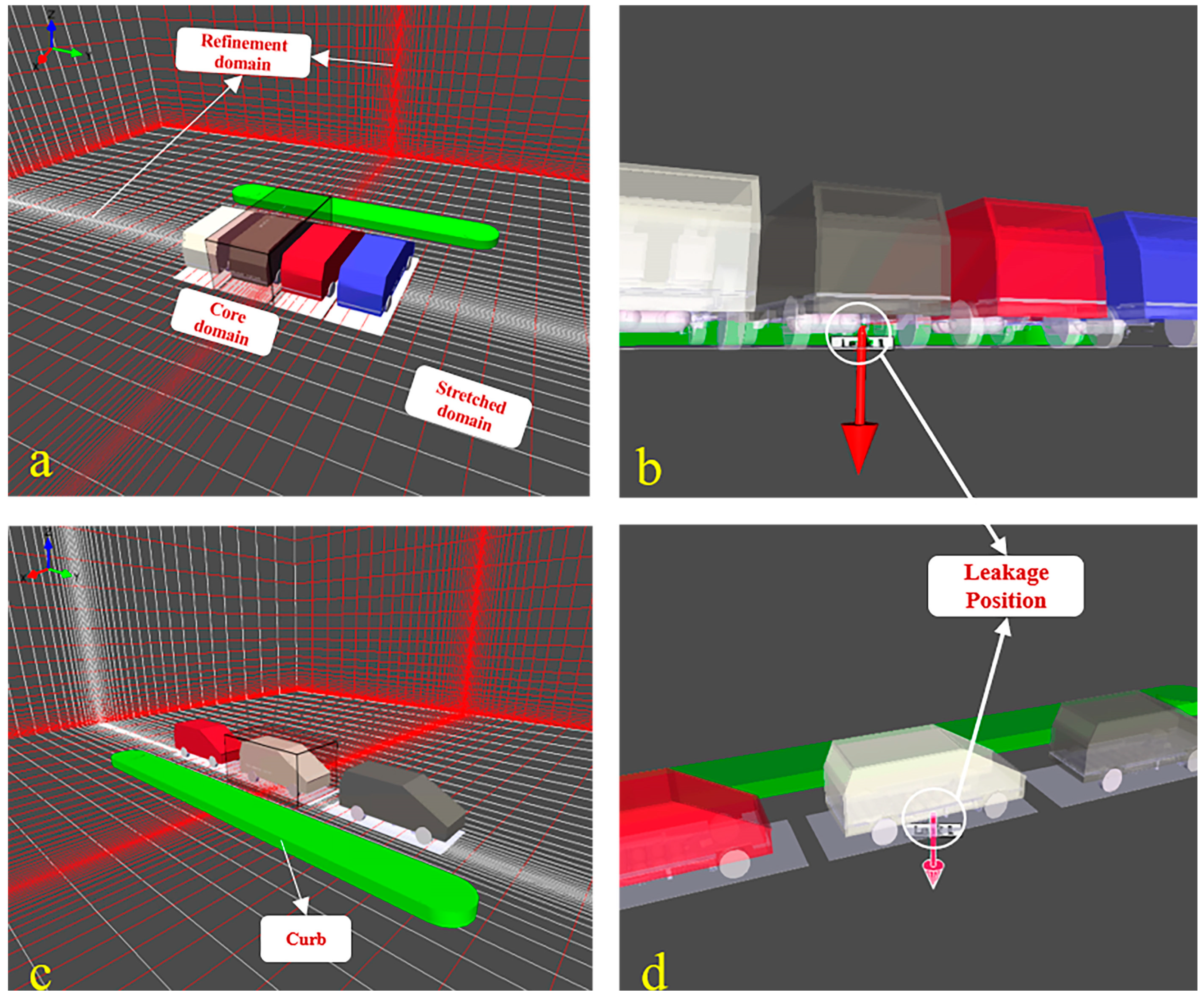
2.2. Geometry Configuration and Grids
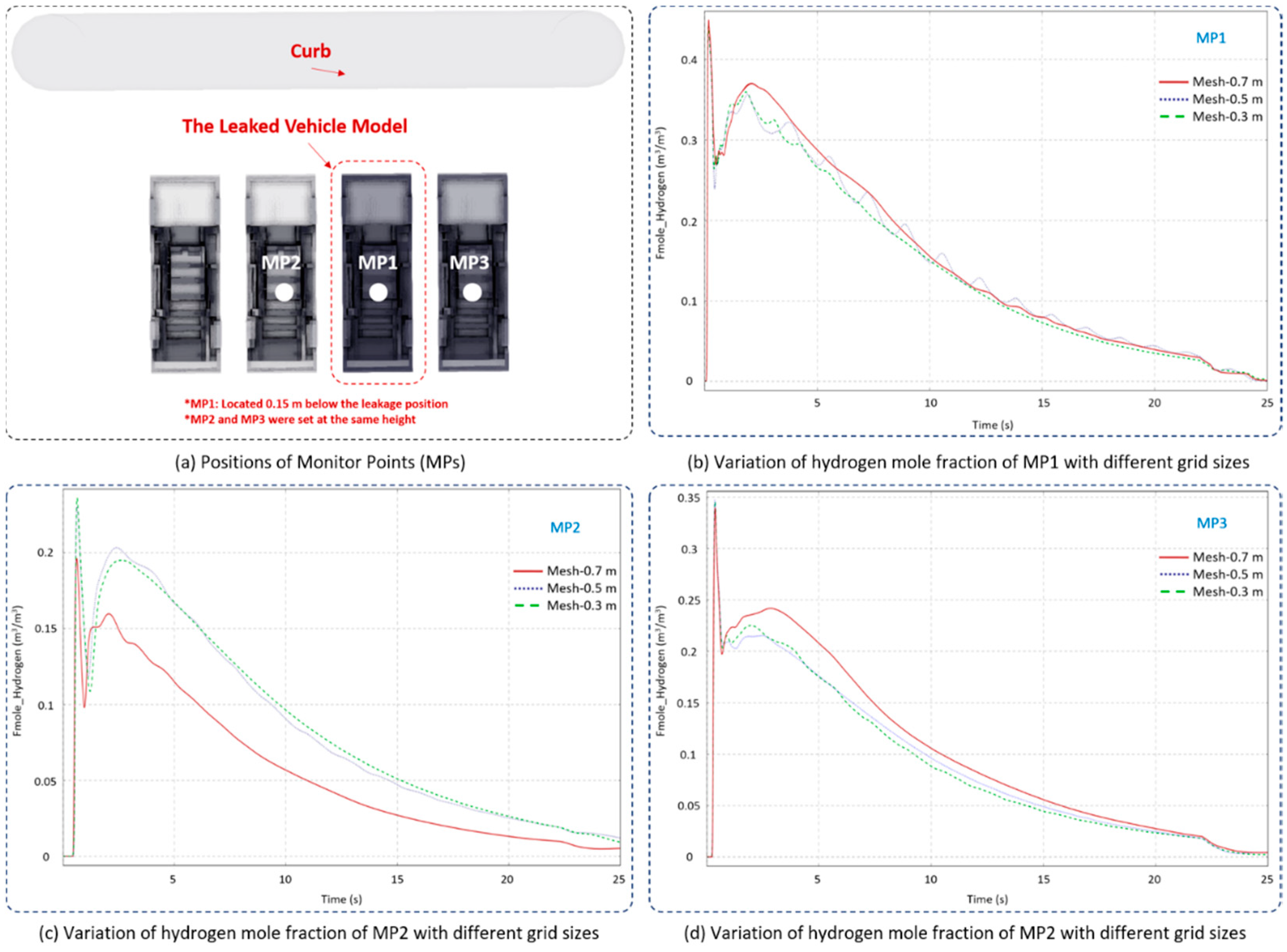
2.3. Grid Independency Validation
2.4. Determination of Hydrogen Leakage Rate
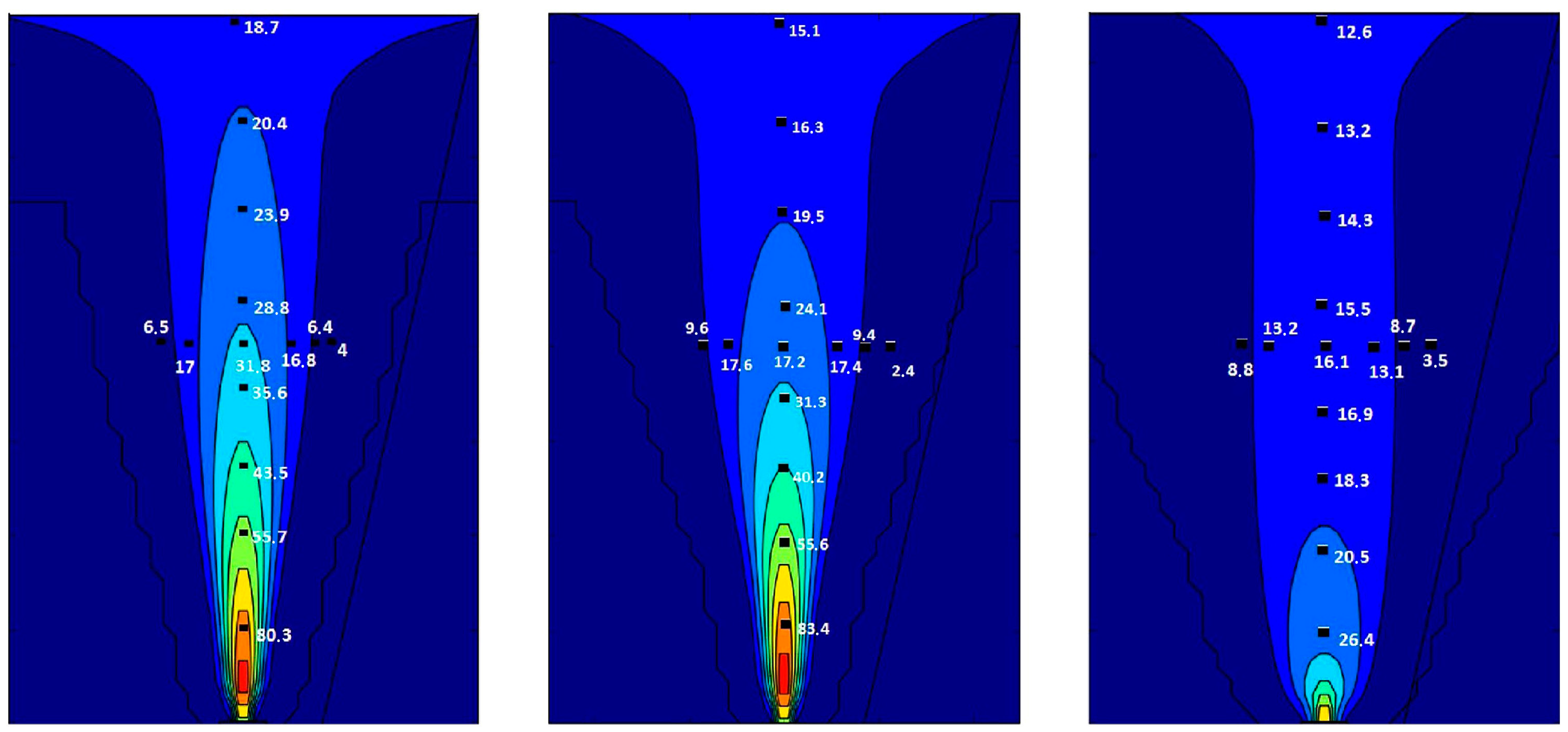
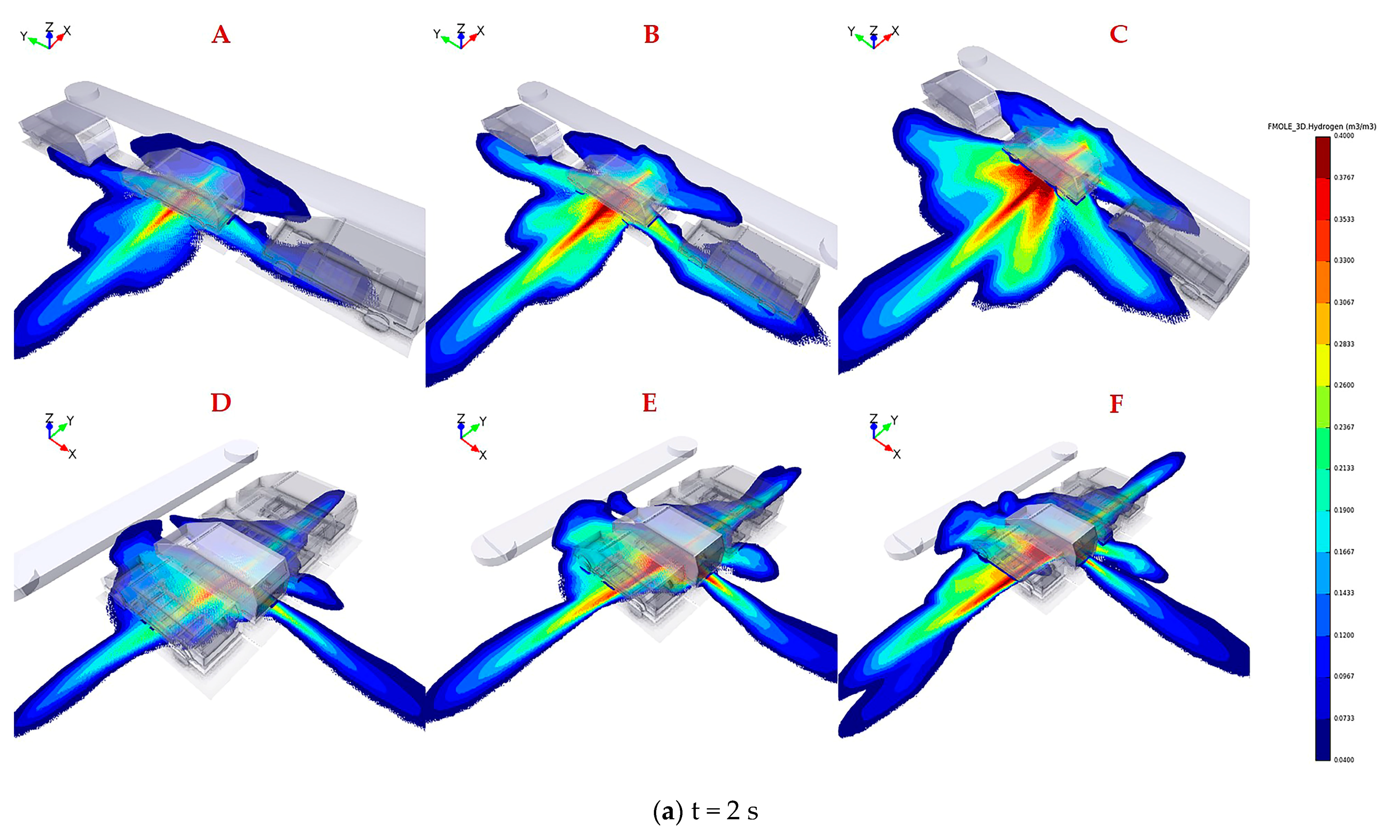
3. Results and Discussions
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Coward, H.F.; Jones, G.W. Limits of Flammability of Gases and Vapors; US Government Printing Office: Washington, DC, USA, 1952; Volume 503.
- San Marchi, C.; Hecht, E.S.; Ekoto, I.W.; Groth, K.M.; LaFleur, C.; Somerday, B.P.; Mukundan, R.; Rockward, T.; Keller, J.; James, C.W. Overview of the DOE hydrogen safety, codes and standards program, part 3: Advances in research and development to enhance the scientific basis for hydrogen regulations, codes and standards. Int. J. Hydrogen Energy 2017, 42, 7263–7274. [Google Scholar] [CrossRef] [Green Version]
- Houf, W.G.; Evans, G.H.; Ekoto, I.W.; Merilo, E.G.; Groethe, M.A. Hydrogen fuel-cell forklift vehicle releases in enclosed spaces. Int. J. Hydrogen Energy 2013, 38, 8179–8189. [Google Scholar] [CrossRef]
- Tamura, Y.; Takeuchi, M.; Sato, K. Effectiveness of a blower in reducing the hazard of hydrogen leaking from a hydrogen-fueled vehicle. Int. J. Hydrogen Energy 2014, 39, 20339–20349. [Google Scholar] [CrossRef]
- Liu, W.; Christopher, D.M. Dispersion of hydrogen leaking from a hydrogen fuel cell vehicle. Int. J. Hydrogen Energy 2015, 40, 16673–16682. [Google Scholar] [CrossRef]
- Yu, X.; Wang, C.; He, Q. Numerical study of hydrogen dispersion in a fuel cell vehicle under the effect of ambient wind. Int. J. Hydrogen Energy 2019, 44, 22671–22680. [Google Scholar] [CrossRef]
- Chen, M.; Zhao, M.; Huang, T.; Ji, S.; Chen, L.; Chang, H.; Christopher, D.M.; Li, X. Measurements of helium distributions in a scaled-down parking garage model for unintended releases from a fuel cell vehicle. Int. J. Hydrogen Energy 2020, 45, 22166–22175. [Google Scholar] [CrossRef]
- Hao, D.; Wang, X.; Zhang, Y.; Wang, R.; Chen, G.; Li, J. Experimental Study on Hydrogen Leakage and Emission of Fuel Cell Vehicles in Confined Spaces. Automot. Innov. 2020, 3, 111–122. [Google Scholar] [CrossRef]
- Tolias, I.C.; Venetsanos, A.G.; Markatos, N.; Kiranoudis, C.T. CFD modeling of hydrogen deflagration in a tunnel. Int. J. Hydrogen Energy 2014, 39, 20538–20546. [Google Scholar] [CrossRef]
- Bie, H.Y.; Hao, Z.R. Simulation analysis on the risk of hydrogen releases and combustion in subsea tunnels. Int. J. Hydrogen Energy 2017, 42, 7617–7624. [Google Scholar] [CrossRef]
- Seike, M.; Kawabata, N.; Hasegawa, M.; Tanaka, H. Heat release rate and thermal fume behavior estimation of fuel cell vehicles in tunnel fires. Int. J. Hydrogen Energy 2019, 44, 26597–26608. [Google Scholar] [CrossRef]
- LaFleur, C.B.; Bran Anleu, G.A.; Muna, A.B.; Ehrhart, B.D.; Blaylock, M.L.; Houf, W.G. Hydrogen Fuel Cell Electric Vehicle Tunnel Safety Study; Sandia National Lab. (SNL-NM): Albuquerque, NM, USA, 2017. [Google Scholar]
- Li, Y.; Xiao, J.; Zhang, H.; Breitung, W.; Travis, J.; Kuznetsov, M.; Jordan, T. Numerical analysis of hydrogen release, dispersion and combustion in a tunnel with fuel cell vehicles using all-speed CFD code GASFLOW-MPI. Int. J. Hydrogen Energy 2021, 46, 12474–12486. [Google Scholar] [CrossRef]
- Hussein, H.G.; Brennan, S.; Shentsov, V.; Makarov, D.; Molkov, V. Numerical validation of pressure peaking from an ignited hydrogen release in a laboratory-scale enclosure and application to a garage scenario. Int. J. Hydrogen Energy 2018, 43, 17954–17968. [Google Scholar] [CrossRef]
- Malakhov, A.A.; Avdeenkov, A.V.; du Toit, M.H.; Bessarabov, D.G. CFD simulation and experimental study of a hydrogen leak in a semi-closed space with the purpose of risk mitigation. Int. J. Hydrogen Energy 2020, 45, 9231–9240. [Google Scholar] [CrossRef]
- De Stefano, M.; Rocourt, X.; Sochet, I.; Daudey, N. Hydrogen dispersion in a closed environment. Int. J. Hydrogen Energy 2019, 44, 9031–9040. [Google Scholar] [CrossRef]
- Giannissi, S.G.; Tolias, I.C.; Venetsanos, A.G. Mitigation of buoyant gas releases in single-vented enclosure exposed to wind: Removing the disrupting wind effect. Int. J. Hydrogen Energy 2016, 41, 4060–4071. [Google Scholar] [CrossRef]
- Dadashzadeh, M.; Ahmad, A.; Khan, F. Dispersion modelling and analysis of hydrogen fuel gas released in an enclosed area: A CFD-based approach. Fuel 2016, 184, 192–201. [Google Scholar] [CrossRef]
- Zhao, M.; Huang, T.; Liu, C.; Chen, M.; Ji, S.; Christopher, D.M.; Li, X. Leak localization using distributed sensors and machine learning for hydrogen releases from a fuel cell vehicle in a parking garage. Int. J. Hydrogen Energy 2021, 46, 1420–1433. [Google Scholar] [CrossRef]
- He, J.; Kokgil, E.; Wang, L.L.; Ng, H.D. Assessment of similarity relations using helium for prediction of hydrogen dis-persion and safety in an enclosure. Int. J. Hydrogen Energy 2016, 41, 15388–15398. [Google Scholar] [CrossRef] [Green Version]
- Hajji, Y.; Bouteraa, M.; Elcafsi, A.; Belghith, A.; Bournot, P.; Kallel, F. Natural ventilation of hydrogen during a leak in a residential garage. Renew. Sustain. Energy Rev. 2015, 50, 810–818. [Google Scholar] [CrossRef]
- Xie, H.; Li, X.; Christopher, D.M. Emergency blower ventilation to disperse hydrogen leaking from a hydrogen-fueled vehicle. Int. J. Hydrogen Energy 2015, 40, 8230–8238. [Google Scholar] [CrossRef]
- Ehrhart, B.D.; Harris, S.R.; Blaylock, M.L.; Muna, A.B.; Quong, S.; Olivia, D. Risk Assessment and Ventilation Modeling for Hydrogen Vehicle Repair Garages; Sandia National Lab. (SNL-NM): Albuquerque, NM, USA, 2019. [Google Scholar]
- Choi, J.; Hur, N.; Kang, S.; Lee, E.D.; Lee, K.-B. A CFD simulation of hydrogen dispersion for the hydrogen leakage from a fuel cell vehicle in an underground parking garage. Int. J. Hydrogen Energy 2013, 38, 8084–8091. [Google Scholar] [CrossRef]
- Hussein, H.; Brennan, S.; Molkov, V. Dispersion of hydrogen release in a naturally ventilated covered car park. Int. J. Hydrogen Energy 2020, 45, 23882–23897. [Google Scholar] [CrossRef]
- Saffers, J.-B.; Makarov, D.; Molkov, V. Modelling and numerical simulation of permeated hydrogen dispersion in a garage with adiabatic walls and still air. Int. J. Hydrogen Energy 2011, 36, 2582–2588. [Google Scholar] [CrossRef]
- Moen, A.; Mauri, L.; Narasimhamurthy, V.D. Comparison of k-ε models in gaseous release and dispersion simulations using the CFD code FLACS. Process. Saf. Environ. Prot. 2019, 130, 306–316. [Google Scholar] [CrossRef]
- Friedrich, A.; Grune, J.; Kotchourko, N.; Kotchourko, A.; Stern, G.; Sempert, K.; Kuznetsov, M. Experimental Study of Jet-Formed Hydrogen-Air Mixtures and Pressure Loads from Their Deflagrations in Low Confined Surroundings. In Proceedings of the 2nd International Conference on Hydrogen Safety, San Sebastian, Spain, 11–13 September 2007. [Google Scholar]
- Hisken, H. Investigation of Instability and Turbulence Effects on Gas Explosions: Experiments and Modelling; Department of Physics and Technology, University of Bergen: Bergen, Norway, 2018. [Google Scholar]
- Li, J.; Hernandez, F.; Hao, H.; Fang, Q.; Xiang, H.; Li, Z.; Zhang, X.; Chen, L. Vented methane-air explosion overpressure calculation—A simplified approach based on CFD. Process. Saf. Environ. Prot. 2017, 109, 489–508. [Google Scholar] [CrossRef] [Green Version]
- Hjertager, B.H. Computer modelling of turbulent gas explosions in complex 2D and 3D geometries. J. Hazard. Mater. 1993, 34, 173–197. [Google Scholar] [CrossRef]
- Jian-ping, Y.; Zheng, F.; Zhi, T.; Jia-Yun, S. Numerical simulations on sprinkler system and impulse ventilation in an underground car park. Procedia Eng. 2011, 11, 634–639. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.; Makarov, D.; Keenan, J.; Molkov, V.V. CFD Study of the Unignited and Ignited Hydrogen Releases from Trpd under a Fuel Cell Car. In Proceedings of the 6st International Conference on Hydrogen Safety, Yokohama, Japan, 14–17 October 2015; Volume 131. [Google Scholar]
- Groth, K.M.; Hecht, E.S. HyRAM: A methodology and toolkit for quantitative risk assessment of hydrogen systems. Int. J. Hydrogen Energy 2017, 42, 7485–7493. [Google Scholar] [CrossRef] [Green Version]
- Alcock, J.; Shirvill, L.; Cracknell, R. Compilation of Existing Safety Data on Hydrogen and Comparative Fuels. European Integrated Hydrogen Project. 2001. Available online: http://www.eihp.org/public/documents/CompilationExistingSafetyData_on_H2_and_ComparativeFuels_S..pdf (accessed on 10 July 2021).
- Molkov, V. Fundamentals of Hydrogen Safety Engineering (Part 1 and 2). In Proceedings of the 4th European Summer School on Hydrogen Safety. 2012, pp. 114–124. Available online: www.bookboon.com (accessed on 10 July 2021).
| Initial Reservoir Condition | Nozzle Conditions | Jet Conditions |
|---|---|---|
| Pressure: p0 | Effective nozzle area: A1 | Velocity: |
| Temperature: T0 | Temperature: | Enthalpy: |
| Volume: V0 | Pressure: | Temperature: |
| Density: | Density: | Pressure: |
| Total mass: | Sound speed: | Density: |
| Heat exchange coefficient: hwall | Velocity: | Effective outlet area: |
| Enthalpy: | Mass flow: | |
| Mass flow: |
| Case Number | Parking Configuration | Release Diameter (mm) | Initial Hydrogen Leakage Rate (kg/s) | Leakage Time (s) | by HyRAM(s) |
|---|---|---|---|---|---|
| A | Parallel Parking | 2 | 0.126 | 166 | 164 (1.2%) |
| B | Parallel Parking | 3 | 0.283 | 70.5 | 72.9 (3.3%) |
| C | Parallel Parking | 4 | 0.428 | 44 | 41 (6.8%) |
| D | Vertical Parking | 2 | 0.126 | 166 | 164 (1.2%) |
| E | Vertical Parking | 3 | 0.283 | 70.5 | 72.9 (3.3%) |
| F | Vertical Parking | 4 | 0.428 | 44 | 41 (6.8%) |
| G | — | 4.2 mm, 171 L at 35 MPa | 102.5 | 100.66 (1.8%) | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, Y.; Zheng, T.; Lv, H.; Zhou, W.; Zhang, C. Numerical Simulation of Hydrogen Leakage from Fuel Cell Vehicle in an Outdoor Parking Garage. World Electr. Veh. J. 2021, 12, 118. https://doi.org/10.3390/wevj12030118
Shen Y, Zheng T, Lv H, Zhou W, Zhang C. Numerical Simulation of Hydrogen Leakage from Fuel Cell Vehicle in an Outdoor Parking Garage. World Electric Vehicle Journal. 2021; 12(3):118. https://doi.org/10.3390/wevj12030118
Chicago/Turabian StyleShen, Yahao, Tao Zheng, Hong Lv, Wei Zhou, and Cunman Zhang. 2021. "Numerical Simulation of Hydrogen Leakage from Fuel Cell Vehicle in an Outdoor Parking Garage" World Electric Vehicle Journal 12, no. 3: 118. https://doi.org/10.3390/wevj12030118
APA StyleShen, Y., Zheng, T., Lv, H., Zhou, W., & Zhang, C. (2021). Numerical Simulation of Hydrogen Leakage from Fuel Cell Vehicle in an Outdoor Parking Garage. World Electric Vehicle Journal, 12(3), 118. https://doi.org/10.3390/wevj12030118






