Abstract
The present work focuses on an aerodynamic and heat transfer study of a battery powered vehicle moving in a vacuum tunnel. The conducted research was based on analytical analysis and numerical calculations. Four different vacuum levels in the tunnel were considered—100 Pa, 1 kPa, 10 kPa and 100 kPa—and two distinct velocities of the vehicle—125 and 166 m/s—to address subsonic and supersonic conditions. It allowed defining limitations related to vacuum transportation in terms of velocity of the vehicle and a blocking ratio of the tunnel. Power consumption and drag coefficient for the considered tunnel pressures were analyzed. The cooling analysis of the batteries by passing air was performed numerically and analytically in the function of flow conditions in the tunnel. It gave some insight into main problems related to cooling of the batteries under low pressure and possible directions to solve it. It was shown that the proposed analytical model compared satisfactorily with the numerical results.
1. Introduction
The beginning of the 19th century was a breakthrough time for transportation. The operation of steam trains began. Researchers dealt with the development of the train transport and looked for innovative solutions, including tunnel railways. Research on cost reduction began, which was largely associated with research on vehicle resistance and aerodynamics [1,2,3,4]. These works led to the derivation of the quadratic function determining the relationship between train resistance and its shape. The quadratic resistance function, called the Davis equation, is defined in Equation (1) [5,6,7,8]. The Davis relation shows that the total resistance depends on three coefficients which are related to rolling resistance (A), mechanical resistance (B) and aerodynamic resistance (C). The aerodynamic resistance grows very fast with the velocity and shows that velocities above 400 km/h are impractical for high-speed trains. This motivates the development of an idea of a vacuum transport, where a vehicle is moving in a low-pressure environment.
The SWISS metro project [9,10] considered a train moving on rails in a vacuum tunnel. The work of Vardy [11,12], Bakre and Brockie [13] showed that the skin friction drag and pressure drag are larger in the tunnel compared to an open space. This motivates a need for research into the most optimal pressure level in the tunnel. Additionally, the vehicle moving in the tunnel creates a compression wave which increases the drag as well [9,10,14,15,16,17]. A tunnel effect promotes the establishment of sonic velocity in narrow passages between the tunnel and the vehicle and can create a shock wave [18,19]. This results in an even larger increase in the pressure drag [20].
Development of modern computers and numerical algorithms allowed using numerical modelling for the railway industry and it was successfully used in train aerodynamic simulations [21,22]. In the case of a train moving inside of a tunnel, a major problem is related to the impact of the tunnel effect on the drag force of the moving train [23,24,25]. It becomes more severe for higher velocities and the blocking ratio must be adequately increased to prevent the development of sonic velocities in the bypass between the vehicle and the tunnel.
The very challenging aspect of the considered vacuum tunnel transport is power supply. The solutions based on magnetic levitation or pantograph need a number of additional and very complicated instruments to be installed in the tunnel. This motivates the current research on the possibility to use batteries to power the vacuum vehicle. The capacities of the modern batteries are improving very fast [26,27]. Moreover, battery production is rising and, consequently, their prices are getting lower. This stimulates the development of the transport industry [28,29]. However, the batteries can work only in a specific range of temperatures. High temperature causes a higher degradation of materials and has a negative impact on the cell’s capacity [30,31] and lifetime [32].
In the current study, twofold analysis was performed. The first was related to the aerodynamics of vehicles moving in the tunnel. A comparison between numerical and analytical calculations was done. The influence of the blocking ratio on the drag coefficient of the vehicle was studied and drag coefficient components for different pressure in the tunnel was calculated. This study allows for the estimation of the optimal vacuum level in the tunnel resulting in minimal energy consumption.
The second part of the research focused on detailed analysis of the cooling of the vehicle batteries. The results are presented for different vacuum levels in the tunnel for a vehicle moving with velocity equal to 125 m/s. This analysis was made to estimate if the flowing air could cool down the batteries to working temperature (55 °C) in the considered pressures. The performed numerical calculations were compared with analytical analysis to confirm the results.
2. Methodology
2.1. Vacuum Vehicle Geometry
The geometry of the considered vehicle was based on an airfoil shape to grant good aerodynamic properties. Consequently, a half-streamline body, N-10, was used to optimally fit to the tunnel, Figure 1.
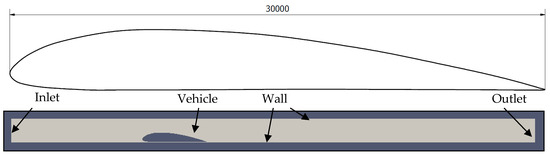
Figure 1.
The N-10 airfoil shape used as a base for the considered vacuum vehicle and its position in the tunnel. Numerical geometry used for the aerodynamic calculations.
The selection of an airfoil shape of the vehicle has two main expected advantages. Its optimal aerodynamic properties assure the minimization of drag forces, especially in the case of subsonic conditions. Second, it substantially reduces an aerodynamic shade (the wake) behind the vehicle. In case of an airfoil with a small angle of attack, a separation point, leading to an eruption of a boundary layer [33] and enhancement of turbulence, does not occur or is shifted to the far end of a trailing edge. The proposed vehicle can be seen as an airfoil with zero angle of attack. Consequently, it assures minimization of the turbulence production in the wake. This can have a direct and positive influence on the reduction in the required minimal distance for the second launched vehicle.
The proposed vehicle is approximately 30 m long and 3.5 m high. Its main purpose would be the transportation of around 20 people or small cargo over a distance comparable to the distance between major European cites (order of several hundred kilometers). In general, the vehicle is assumed to be powered by batteries and its design should allow for a fast exchange of the battery stack.
2.2. Analytical Study
2.2.1. Analytical Analysis of Aerodynamics
The numerical calculations were performed in the OpenFOAM CFD toolbox. In the considered flow, supersonic velocities were expected. To properly address the numerical difficulties related to steep gradients and shocks, two dedicated solvers implemented in OpenFOAM were used: the sonicFoam and the rhoCentralFoam. The first one is a transient solver for trans-sonic/supersonic, turbulent flow of a compressible gas and the second one is a density-based compressible flow solver based on central-upwind schemes of Kurganov and Tadmor [34,35]. Additionally, the SpallartAllmaras turbulence model was used, which was specially developed for aerodynamics-related calculations. [36,37].
The analytical calculations were based on an isentropic flow through a nozzle [37]. This theory was used to estimate speed limits in the bypass between the vehicle and the wall of the tunnel. The flow around the vehicle changes from a stagnation pressure () to a free stream pressure (). Knowing the Mach number in the freestream (), the following formula can estimate a ratio between the stationary and freestream pressure [38]:
where is a specific heat ratio of air. In the considered case, the air in the tunnel is additionally squeezed in the gap between the tunnel and the vehicle. Due to the mass conservation law, the velocity in the gap increases significantly and it affects pressure as well. Based on Equation (2), the change in the air pressure between the stationary point and some point above the vehicle () can be written as:
Combining the Equations (2) and (3) allows us to calculate the air properties in the gap:
The blocking ratio (/), where is cross-section area in the bypass and is cross-section area of the tunnel, can be used to estimate the ratio of the Mach number in the bypass and freestream in a function of the blocking ratio:
To estimate the pressure dependence in the smallest cross-section of the bypass on Mach number, Equation (4) was used. The following values were considered in the calculations: = 100 Pa, 1 kPa, 10 kPa, 100 kPa and ≈ 0.5 and ∈ <0.5; 1.8>.
Based on Equations (4) and (5), the following characterizations were made:
- Isentropic characterization of a Mach number equal to 1 for different freestream velocity and blocking ratio.
- The critical blocking ratio characterization for = 0.5 in freestream (see Figure 3b).
2.2.2. Analytical Analysis for Heat Transfer
In the second part of the work, the increase in temperature of batteries that supply the vehicle was calculated. The thermodynamic properties of air were calculated for two different models: the validation model where the air is cooling only the batteries and the vacuum vehicle model were the batteries are located inside the vehicle and cooled by flowing air in the duct under the vehicle and through the vehicle. Based on the Reynolds number () of each considered case, the Nusselt number () was estimated [39,40]. These calculations provided the estimation of the heat transfer coefficient and gave the possibility to compare the theory with numerical results.
In the case of the validation model with batteries placed in freestream, the Nu number was estimated based on Equation (7). The Prandtl number () was estimated using the dynamic viscosity coefficient (), specific heat capacity () and thermal conduction coefficient ():
The value of the Re number depends on the initial freestream pressure and the Nu number can be calculated accordingly. For = 100 Pa, the Re number is below , for = 1 kPa the Re number is in the range of and for the high pressure cases = 10 kPa and = 100 kPa the Re number was above .
In the vacuum vehicle model with batteries and = (1, 10, 100) kPa, the heat transfer calculations were made using the turbulent flow formula for Nu number and for = 100 Pa the Nu number was calculated as for laminar forced convection:
where is the length of the heat transfer area, is a hydraulic diameter of the duct, and is a reference dynamic viscosity coefficient. Based on calculated Nu numbers, a heat transfer coefficient () was estimated. Based on the batteries’ properties and assumption of inlet temperature ( = 300 K), the temperature after heat exchange was calculated ():
where is the heat flux emitted by the batteries. In the current study, a lithium polymer battery was assumed for charging the vehicle with the following parameters: maximal internal resistance 4 μΩ and current 39 A. It was assumed that the stack of batteries had a rectangular shape and was 1.85 m long, 1 m wide and 12 mm high. Its dimensions were dictated by the geometry of the vehicle and the required power. The stack was placed 7 m behind the leading edge of the vehicle and can be seen in Figure 2b.
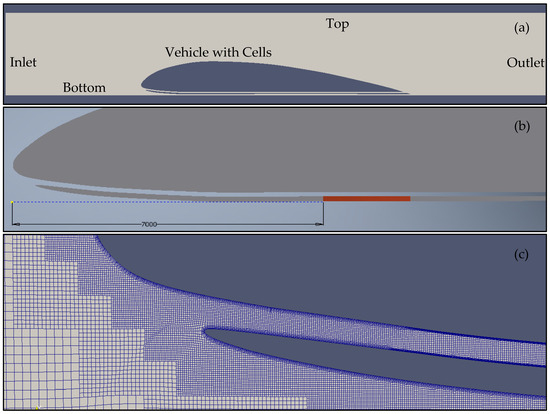
Figure 2.
Numerical domain for the vehicle with batteries and heat transfer calculations: (a) numerical geometry and boundary conditions, (b) position of the batteries in the vehicle (red), (c) detail of the numerical mesh in the vicinity of the cooling ducts (the inner duct and the duct below the tunnel).
Consequently, the Joule’s heating of the batteries under full load was 3215 W/m2. Based on the specifications of the available lithium polymer batteries, the maximum allowed temperature was assumed as 55 °C. The calculations were based on the air properties at reference temperature equal to 0 °C and Sutherland’s law was used for dynamic viscosity estimation.
2.3. Numerical Model
The numerical domain for aerodynamic calculations is shown in Figure 1. The length of free space before the vehicle is equal to 2 and behind the vehicle 5, where = 30 m is the vehicle length. The height of the tunnel is 8.47 m, which gives the blocking ratio = 0.6. The mesh was generated using snappyHexMesh utility provided by OpenFoam. The developed mesh had six levels of gradation. Most of the grid had the fourth level of refinement and was additionally refined around the vehicle and a boundary layer with 5 mesh cells was added. In Figure 2c, the mesh near the vehicle surface is shown. Following the methodology for train drag coefficient calculation [15], the reference area was assumed to be the frontal area of the vehicle = 3.3 m2. During the aerodynamic calculations, the heat flux emitted by the batteries was not included.
For comparison purposes, reference calculations in open space were conducted. To simulate the open space conditions of the vehicle motion, a domain without the top wall was made by setting the height above the vehicle as 15 m (eight times higher than vehicle) and slip boundary conditions. The outside pressure was 1 bar and the vehicle velocity was set to 125 m/s. Due to the unsteady character of the considered flow the PIMPLE algorithm was used to assure better numerical stability.
In the case of the heat transfer calculations, the numerical domain was smaller to ensure faster calculations (Figure 2). Additional boundary conditions to consider were the heat flux emitted from the batteries to the environment. In both cases, the Spalart–Allmaras turbulent model was used, which is a suitable model for aerodynamic calculations [36,37].
3. Results and Discussion
3.1. Aerodynamic Analytical Results
Figure 3a shows the blocking ratio in the function of the vehicle velocity for the Mach number in the bypass equal to 1. These calculations were based on Equations (4) and (5). It can be noticed that for the blocking ratio = 0.6, the Ma = 1 in the bypass can be reached for the velocity of the vehicle around 128 m/s. For 166 m/s, the minimum blocking ratio should be around 0.75 to assure Ma < 1.
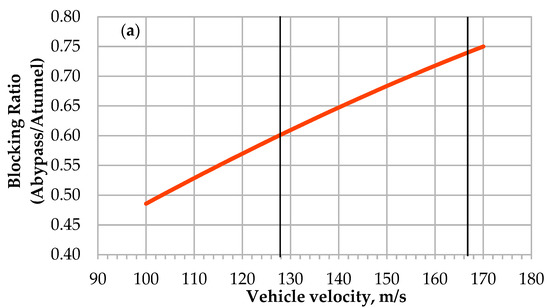
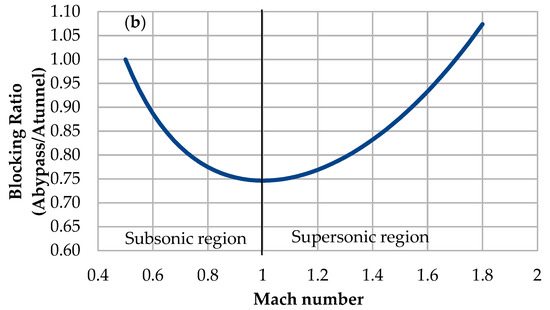
Figure 3.
(a) Isentropic characteristic of blocking ratio in function of the vehicle velocity, with the assumption Ma = 1 in bypass between the vehicle and the tunnel; (b) isentropic characteristic of blocking ratio in function of Mach number for 166 m/s velocity of the vehicle.
Figure 3b shows the change of Ma number in the function of the blocking ratio for the vehicle moving at 166 m/s. These calculations were based on Equations (4) and (5), the assumption of the isentropic state. Due to the compressibility of the fluid, the curve has a minimum in the critical point. It agrees with the De Laval nozzle theory [38]. Analysis for 166 m/s in freestream confirms that critical cross-section occurs for blocking ration around 0.75.
Below the critical point, the air expands due to the design of the vehicle. The distance between the tunnel and the vehicle increases and the velocity of the fluid can increase only if the critical point would have been reached before. Consequently, it can be concluded that the airfoil shape of the vehicle moving in the tunnel is more optimal for subsonic conditions. In the case of supersonic state, the fluid will be accumulated in front of the vehicle due to choking in the bypass, which is known as the Kantrowitz limit [25,37]. Consequently, the static pressure would increase in front of the vehicle.
3.2. Aerodynamic Numerical Results
Aerodynamic calculations were made for two values of the vehicle velocity: 166 and 125 m/s. The first one is based on the initial assumption of the vehicle velocity, while the second one results from the analysis performed above. Each case was calculated for the pressure in the tunnel: 100 Pa, 1 kPa, 10 kPa, and 100 kPa.
3.2.1. Pressure, Velocity and Drag Coefficient.
Based on Equations (2) and (3), the plot in Figure 4a was created. This shows the dependence on Mach number and the pressure in the bypass. It can be noticed that Ma = 1 in the bypass corresponds to approximately 5000 Pa in the bypass. Figure 4b shows the pressure plot along the tunnel and corresponds to the time 0.15 s when the sonic state is established in the bypass. Figure 4c shows the pressure along the tunnel after 4.65 s. It can be noticed that the pressure increased significantly in front of the vehicle. This is a result of the air accumulation in front of the vehicle as a consequence of a choked flow in the bypass. It should be noted that the pressure behind the vehicle increases as well, but with time the difference between the inlet and the outlet pressure gets higher. This confirms that for the blocking ratio 0.6 and freestream velocity 166 m/s, the Kantrowitz limit occurs. Figure 5a,b show that the pressure behaves in the same way for high-pressure and low-pressure cases, respectively.
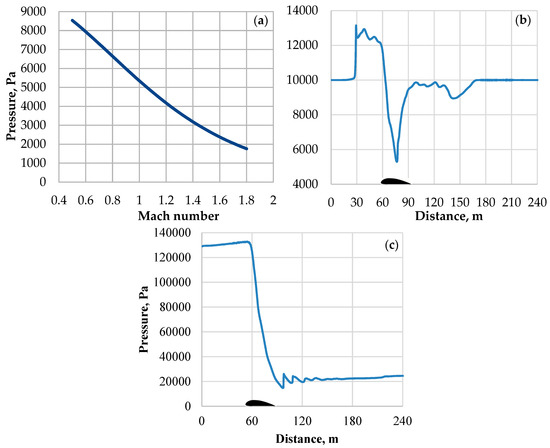
Figure 4.
(a) Change in the pressure in the bypass in the function of Mach number in the bypass for a fixed free stream pressure 10 kPa and = 0.5; (b) pressure distribution in the tunnel after 0.15 s—the value of pressure is equal to the sonic state pressure; (c) pressure distribution after 4.65 s.
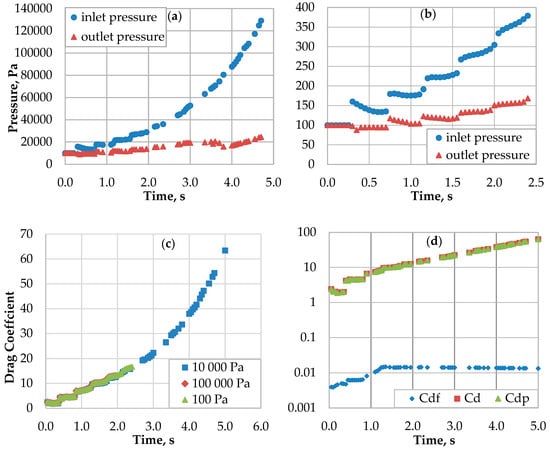
Figure 5.
(a) The average pressure at the inlet and outlet from the tunnel for 10 kPa; (b) for 100 Pa. Results for 166m/s freestream air velocity. The effect of the increasing pressure due to the collection of air in front of the vehicle is visible. (c) Drag coefficient for vehicle velocity 166 m/s and various initial tunnel pressure. (d) Total drag coefficient and their components, the impact of the skin-friction drag is negligibly small.
Figure 5 shows the change in the tunnel pressure and drag coefficients in time due to the vehicle movement. It can be noticed that the drag coefficient increases with time with similar dynamics for each considered case. The increase in the pressure in front of the vehicle is caused by the establishment of supersonic flow in the bypass [9]. The results from Figure 5d show that the total drag coefficient () is mostly due to the pressure drag coefficient (), and the skin friction () component is negligibly small. This confirms that a piston effect has the predominant effect on the total drag. The pressure increases faster on the stagnation point (at the leading edge of the vehicle) than above the vehicle due to the choking. When the choked flow occurs, the drag coefficient is independent of the pressure in the freestream, but on the difference of the pressure in front and behind the vehicle.
The next set of figures show the results for the vehicle at velocity 125 m/s. This value of velocity is a result of the analysis shown in Figure 3a,b, and is 3 m/s below the speed of sound in the bypass for the tunnel with a blocking ratio 0.6. Figure 6 shows that at the beginning of the movement, 0.05 s, and after 4.65 s, the pressure in the bypass is higher than the critical pressure. Consequently, the supersonic state was not established in this case. As opposed to the cases with 166 m/s velocity, the values of the pressure in front of and behind the vehicle are on the same level. Choked flow and the piston effect do not occur.
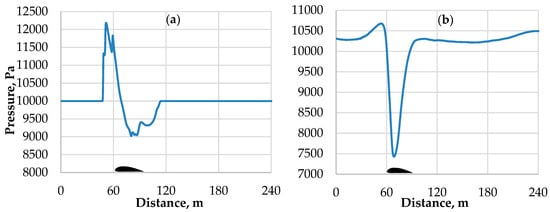
Figure 6.
Pressure distribution along the tunnel 4 m above the ground and 0.7 m above the thickest section of the vehicle: (a) shows the state after 0.05 s and (b) shows the state after 4.65 s.
Table 1 shows the average values of the drag coefficients for the vehicle moving at 125 m/s. It can be noticed that constant values were reached. Similarly, as before, the skin friction drag is negligible. The total drag coefficient and pressure drag coefficient decrease with increasing pressure from approximately 0.3 to 0.5. This is related to the different Reynolds numbers [41,42,43].

Table 1.
Average values of drag coefficient components and power related to the drag force. Ratio of drag acting on a moving vehicle in the tunnel to the drag in open space.
For comparison with the vehicle movement without tunnel effect, the drag coefficient () for open space model was calculated. Table 1 also shows the results of the ratio between the tunnel and open space models. It can be seen that the pressure drag can be 10 to 20 times higher in the tunnel than in the open space. The power needed to overcome the aerodynamic drag force can be calculated using Equation (11) [20] and for the tunnel with 10 kPa it is higher than for the vehicle moving in open space. Consequently, this value can be seen as an upper limit of a tunnel pressure above which energy consumption is higher than in open space.
Comparing the results from Table 1 with Figure 4 and Figure 5, it can be concluded that the supersonic conditions should be avoided to prevent an excessive and rapid growth of the drag force in the tunnel. Figure 4 and Figure 5 show the consequences of establishment of supersonic conditions in the bypass. It can be seen that the pressure in front of the vehicle and the drag coefficient rapidly grows with time, regardless of the initial pressure in the tunnel. The drag coefficient reaches two orders of magnitude higher values that in the case of subsonic conditions. The same is true for the drag force, which depends linearly on the drag coefficient and density. Contrary to this, the subsonic conditions allow keeping the drag force steady and decreasing it substantially with the decrease in the pressure in the tunnel. A substantial reduction in the power consumption can be seen already for the pressure 1 kPa, which is nearly six times lower than for the open space case. In the case of 100 Pa, the power consumption is more than 50 times lower as compared to the open space case.
Figure 7a–c show the distribution of the Mach number in the vicinity of the vehicle for times 0.15, 0.50 and 4.65 s. The formation of the shock wave is visible.
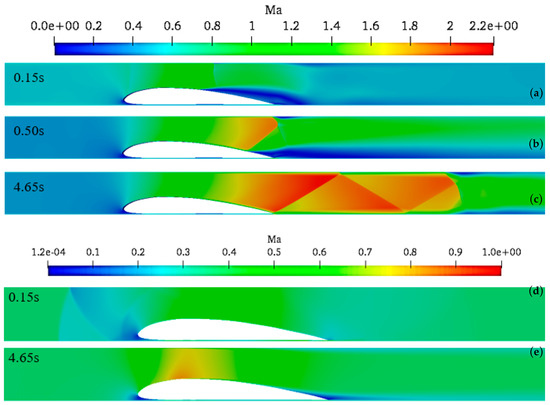
Figure 7.
Mach number field visualization: (a–c) results for = 100 Pa and 166 m/s velocity of the vehicle; (d,e) results for = 10 kPa and 125 m/s velocity of the vehicle.
Figure 7d,e show the distribution of Mach number in the vicinity of the moving vehicle after 0.15 and 4.65 s, respectively. It can be noticed that after a short time, the velocity of air in the bypass get smaller than the velocity of the sound and the conditions are subsonic in the whole tunnel. Figure 8 shows the recirculation zone and corresponding separation points established on the top surface of the vehicle. It can be seen, that the recirculation zone gets smaller and moves downward for the higher pressures in the tunnel.
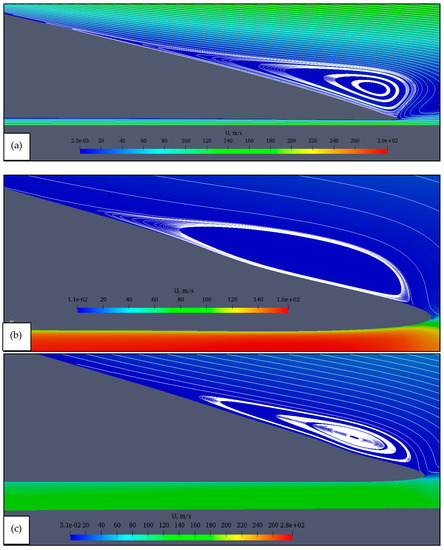
Figure 8.
Recirculation zone and separation point for: (a) 100 Pa, (b) 10 kPa, (c) 1 bar in the tunnel.
3.2.2. Boundary Layer Separation, Back Flow and Velocity Profiles
The numerical investigation for 125 m/s shows that there is a separation in the boundary layer [33]. Figure 8 shows the difference between the recirculation zone for different pressures for the vehicle moving at 125 m/s. It can be noticed that the largest zone is established for 100 Pa and it reaches 8.5 m. For 10 kPa, the zone reaches approximately 2 m, and for 100 kPa it is smaller than 1 m. This zone has a significant impact on the increase in the value of the drag coefficient, as the reversed air collides with the upcoming air.
Figure 9 shows an exemplary velocity profile at 29 m of the vehicle’s top wall for different pressures in the tunnel. For 100 Pa, the backflow is clearly visible and reaches up to 0.5 m above the vehicle. The highest velocity of the backflow is around 20 m/s. For 100 kPa pressure in the tunnel, there is no backflow at the considered location. Prediction and control of the separation occurrence [33] can help to minimize the energy consumption of the vehicle moving in the tunnel by appropriate change in the shape.
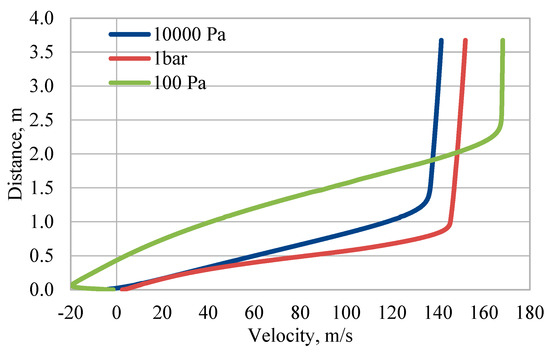
Figure 9.
The velocity profile at 29 m of the vehicle length for 100 Pa, 10 kPa, and 1 bar. There is no separation for 1 bar pressure in the tunnel at this location.
3.3. Heat Transfer
3.3.1. Validation – Battery Cooling in Freestream Flow
Analytical calculations of batteries cooling in a freestream flow were made to validate the mathematical model used in numerical calculations. As it was mentioned in Section 2.2.2, due to the Joule’s heating, the assumed stack of batteries emits 3215 W/m2. It was assumed that the whole emitted heat power was transferred to the passing air. Every considered case in the analysis is characterized by an order of magnitude difference in Reynolds number and is directly related to the value of the considered tunnel pressure. Consequently, Equation (7) was used to calculate the Nusselt number and Equation (9) was used to calculate the heat transfer coefficient.
For small Reynolds numbers, α ≈ 1 W/m2/K and increases with Reynolds number. For very high Reynolds numbers, higher than 107, α ≈ 350 W/m2/K. The received values of α compare well with values reported in [38,44]. Consequently, the temperature of the batteries after cooling was calculated using Equation (10). Table 2 contains the analytical results of heat transfer calculations for the freestream velocity of 166 and 125 m/s. It can be noticed that is higher for 166 m/s and the average temperature for the operating batteries is smaller for the 125 m/s velocity. It should be noted that, only for 100 kPa, the temperature was set below 55 °C (309 K) and stayed in the range of the recommended working temperature of the considered batteries.

Table 2.
Thermo-physical properties for 166 and 125m/s and comparison of analytical temperature results after cooling with numerical results for 166m/s.
Based on the batteries’ properties and conditions in the tunnel, a heat transfer model was developed. The comparison between CFD numerical calculations based on the rhoCentralFoam solver of OpenFoam and analytical analysis described above is satisfactory. For = 0.1, 1, 10, and 100 kPa, the temperature from the analytical model is 2935, 682, 363, and 309 K and from the CFD is 2498, 553, 409, and 339 K, respectively, and the relative error is 14.9%, 19%, 12.7%, and 10%, respectively. The discrepancy between the analytical and CFD results can be related to some impact of natural convection which can intensify the heat transfer in the numerical calculations. Figure 10 shows the temperature distribution in the vicinity of the batteries in freestream cooling.
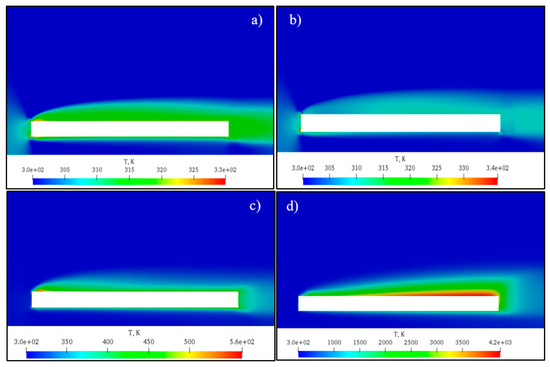
Figure 10.
Temperature distribution around the batteries for pressure: (a) 100 kPa, (b) 10 kPa, (c) 1 kPa and (d) 100 Pa.
3.3.2. Analytical Analysis of Heat Transfer for Vehicle with Batteries
Analytical prediction of an average battery’s temperature in the vehicle cooled by air flowing in the ducts shows that, for 125 m/s, the temperature of batteries is smaller than for the same velocity but in the freestream case. This happens because the Reynolds number and the heat transfer coefficient are higher in the duct. Batteries in the vehicle are cooled by two independent flow streams located above and below the batteries (see Figure 2). Table 3 shows the heat transfer properties and results for air in the duct for the considered tunnel pressures. In the case of 1, 10 and 100 kPa, the Nusselt number was calculated using the turbulent formula (8), and for 100 Pa calculations were made assuming laminar forced convection, using Equation (8).

Table 3.
Analytical and numerical results for the vehicle moving at 125 m/s and thermo-physical properties of air in the cooling duct estimated by analytical calculations and average hydraulic diameter of the duct dh = 0.115 m.
Table 3 present the batteries’ temperature when cooled by freestream flow in open space and by air flowing through the ducts of the vehicle and cooling the batteries from below and above for a velocity of 125 m/s. It can be noticed that the cooling is more efficient for the second case. The difference gets higher for lower pressure. In the case of two ducts for 10 kPa, the temperature is only 11 degrees higher than the safe working temperature of batteries.
3.3.3. Numerical Results—Vehicle with Batteries
The numerical model of the vehicle with batteries is focused on the cooling process of batteries by air flowing in the ducts located below and inside the vehicle (Figure 2b). Figure 11 shows the velocity profiles in the inside duct. They are laminar (parabolic) for 100 Pa and turbulent for the other considered tunnel pressures. It is worth noting that for 1 kPa, the profile can indicate a transition state. In the duct below the vehicle, the velocities are higher than in the duct inside the vehicle.
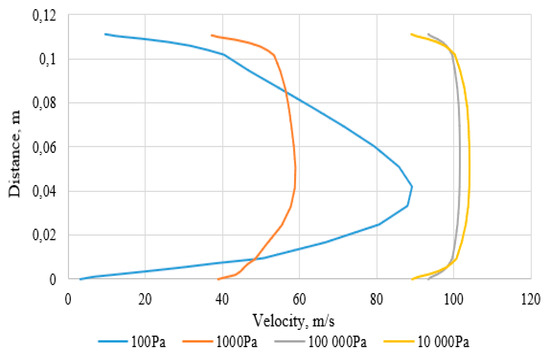
Figure 11.
Velocity profiles of the cooling air in the duct above the batteries.
Figure 12 shows the velocity and temperature distribution in the vicinity of the batteries placed in the vehicle. It can be noticed that the streamlines are going upward due to natural convection. As was mentioned before, this can explain the differences between the numerical and analytical results.
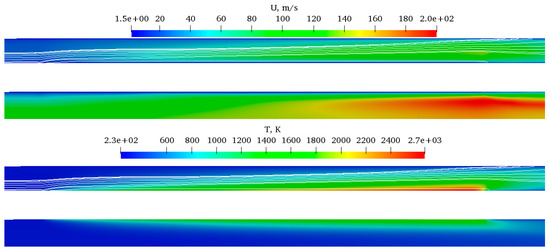
Figure 12.
Temperature and velocity distribution around the batteries in the duct for the 100 Pa case.
Table 2 and Table 3 show the numerical and analytical results of final temperature saturated in the batteries for the vehicle velocity of 125 m/s. It can be noticed that the agreement is satisfactory, both in a qualitative and quantitative way. As was mentioned before, the differences can be caused by an occurrence of natural convection which is excluded from the analytical model. The relative error is not larger than 10% and is the highest for low-pressure cases, namely 100 Pa and 1 kPa.
It is worth mentioning that for the vehicle velocity of 166 m/s, the batteries’ temperature is decreasing continuously and for 100 Pa the temperature of 320K was reached after 4s of calculations. This can be explained by the establishment of the choked flow and continuous increase in pressure in the vicinity of the vehicle. Consequently, the air density was increased and better heat transfer was achieved. Although cooling properties were improved, the drag was significantly higher and not acceptable from an energy consumption point of view. This suggests that better cooling properties could be achieved by the higher compression of the air in the vicinity of batteries.
4. Conclusions
The presented study focused on an aerodynamic and heat transfer analysis of a battery powered vehicle moving in a vacuum tunnel. Analytical and numerical models were created and used to study a wide parameter space of the considered problem, including various pressures in the tunnel, vehicle velocities and blocking ratios of the tunnel. The parameters were chosen to address subsonic and supersonic conditions. It was shown that development of the supersonic conditions in the bypass between the tunnel and the vehicle can increase drag forces significantly due to the establishment of a choked flow around the moving vehicle. Consequently, it caused a significant increase in energy consumption and it should be avoided.
The conducted research clearly showed that occurrence of supersonic conditions in the tunnel should be avoided. This can be achieved either by reducing the velocity of the vehicle or by increasing the size of the bypass between the vehicle and the tunnel. The first option seems to be contradictory from the point of view of the main requirement of fast transportation. The second option can be analyzed in Figure 3. It can be seen that the size of the tunnel should be carefully designed to assure the Mach number in the bypass is less than one but as close as possible to one. Consequently, this would allow minimizing the costs of the tunnel and maximizing the permissible velocity of the vehicle. Based on the De Laval nozzle theory, it was shown that the distance between the vehicle and the wall of the tunnel would have to be increased if supersonic state was reached for a given velocity.
The results of the vehicle moving in the tunnel were compared to the motion of the vehicle in the open space. It was shown that the pressure drag could be 10 to 20 times higher in the tunnel than in the open space. The analyses allowed defining an upper limit of the pressure in the tunnel above which the drag was higher than in the open space. It was shown that for the velocity 125 m/s and blocking ratio 0.6, the upper limit was 10 kPa.
The conducted heat transfer analysis focused on the possibility of cooling batteries using passing air for various conditions in the tunnel. Both analytical and numerical models were developed and compared. Satisfactory comparison was achieved, and the relative error was not larger than 10% and was the highest for the low-pressure cases, namely 100 Pa and 1 kPa. It was shown that the differences could have been caused by an occurrence of natural convection which was excluded from the analytical model. It allowed estimating a final temperature of the batteries under full load. The conducted calculations revealed that the cooling of batteries could be the major difficulty in the considered transportation system. Additionally, it was shown that the numerical results for 100 Pa and 1 kPa were closer to being in the laminar forced convection regime than in the mixed convection. Moreover, the numerical calculations showed that the cooling effect of air flowing through the vehicle was higher than for the batteries placed in freestream flow for the same conditions. This was confirmed by the analytical calculations as well. This was related to the higher velocity of air in the ducts of the vehicle than in the vicinity of the batteries’ walls placed in the freestream. Moreover, it was shown that better cooling properties could be achieved by higher compression of the air in the vicinity of the batteries.
Author Contributions
Conceptualization, K.M., P.W. and Z.M.; methodology, K.M. validation, K.M. and Z.M.; investigation, K.M.; writing—original draft preparation, K.M., Z.M. and P.W.; writing—review and editing, Z.M. and K.M.; visualization, K.M.; supervision, Z.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
The authors would like to thank the 4P group (Pierwszy Polski Pociąg Próżniowy—First Polish Vacuum Train) from Wroclaw University of Science and Technology for inspiration for this research.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Clark, D.K. Railway Machinery; Blackie and Son: Glasgow, UK; Edinburgh, UK; London, UK; New York, NY, USA, 1855. [Google Scholar]
- Harding, W. On the resistances to railway trains at different velocities. Minutes Proc. Inst. Civ. Eng. 1846, 5, 369–411. [Google Scholar] [CrossRef]
- Gooch, D. Observations on the resistances to railway trains at different velocities. Minutes Proc. Inst. Civ. Eng. 1848, 7, 292–294. [Google Scholar] [CrossRef]
- Buhle, M.; Pfitzner, W. Die Schnellbahnwagen der Studiengesellschaft für elektrische Schnellbahnen in Berlin. Polytech. J. 1904, 85, 449–452. [Google Scholar]
- Davis, W.J. The tractive resistance of electric locomotives and cars. Gen. Electr. Rev. 1926, 29, 685–708. [Google Scholar]
- Baker, C.J.; Brockie, N.J. The aerodynamic drag of high speed trains. J. Wind Eng. Ind. Aerodyn. 1990, 34, 273–290. [Google Scholar] [CrossRef]
- Rochard, B.P.; Schmid, F. A review of methods to measure and calculate train resistances. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2000, 214, 185–199. [Google Scholar] [CrossRef]
- Schetz, J.A. Aerodynamics of high-speed trains. Annu. Rev. Fluid Mech. 2001, 33, 371–414. [Google Scholar] [CrossRef]
- Mossi, M.; Sibilla, S. Swissmetro: Aerodynamic Drag and Wave Effects in Tunnels Under Partial Vacuum. 2002. Available online: https://www.semanticscholar.org/paper/Swissmetro-%3A-aerodynamic-drag-and-wave-effects-in-Mossi-Sibilla/a6d97c409f9a24e4f51239dafd9ccb506bbbc49b (accessed on 13 March 2020).
- Cassat, A.; Bourquin, V.; Mossi, M.; Badoux, M.; Vernez, D.; Jufer, M.; Macabrey, N.; Rossel, P. D504 SWISSMETRO-Project Development Status; Swissmetro—Project Development Status: Tokyo, Japan, 2003; pp. 453–460. [Google Scholar]
- Vardy, A.E. Aerodynamic drag on trains in tunnels part 1: Synthesis and definitions. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 1996, 210, 29–38. [Google Scholar] [CrossRef]
- Vardy, A.E. Aerodynamic drag on trains in tunnels part 2: Prediction and validation. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 1996, 210, 39–49. [Google Scholar] [CrossRef]
- Baker, C.J.; Brockie, N.J. Wind tunnel tests to obtain train aerodynamic drag coefficients: Reynolds number and ground simulation effects. J. Wind Eng. Ind. Aerodyn. 1991, 38, 23–28. [Google Scholar] [CrossRef]
- Bourquin, V.; Béguin, C.; Monkewitz, P.A. Aerodynamic Effects in Railway Tunnels as Speed is Increased. In The Aerodynamics of Heavy Vehicles: Trucks, Buses, and Trains. Lecture Notes in Applied and Computational Mechanics; McCallen, R., Browand, F., Ross, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; Volume 19. [Google Scholar]
- Yang, Y.; Ma, D.; Mei, Y. Numerical Simulation of Aerodynamic Drag of Single High-Speed Train Passing through a Tunnel. In Proceedings of the 2nd International Conference on Industrial Aerodynamics (ICIA 2017), Qingdao, China, 18–20 October 2017; ISBN 978-1-60595-481-3. [Google Scholar]
- Raghunathan, R.S.; Kim, H.-D.; Setoguchi, T. Aerodynamics of high-speed railway train. Prog. Aerosp. Sci. 2002, 38, 469–514. [Google Scholar] [CrossRef]
- Faramehr, S.; Hemida, H. Aerodynamics of trains in tunnels. In Proceedings of the Third International Conference on Railway Technology: Research, Development and Maintenance, Cagliari, Sardinia, Italy, 5–8 April 2016. [Google Scholar]
- Jiang, Z.; Matsuoka, K.; Sasoh, A.; Takayama, K. Investigation of Shock-Wave Generation by a High-Speed Rain Running into a Tunnel. In Proceeding of the 7th ISCFD, Beijing, China, 4–8 September 1997; pp. 779–784. [Google Scholar]
- Liu, T.; Jiang, Z.; Chen, X.; Zhang, J.; Liang, X. Wave effects in a realistic tunnel induced by the passage of high-speed trains. Tunn. Undergr. Space Technol. 2019, 86, 224–235. [Google Scholar] [CrossRef]
- Houghton, E.L.; Carpenter, P.W. Aerodynamics for Engineering Students, 5th ed.; Butterworth-Heinemann: Burlington, MA, USA, 2003. [Google Scholar]
- Wang, J.; Gao, G.; Li, X.; Liang, X.; Zhang, J. Effect of bogie fairings on the flow behaviours and aerodynamic performance of a high-speed train. Veh. Syst. Dyn. 2019. Available online: https://www.tandfonline.com/doi/abs/10.1080/00423114.2019.1607400 (accessed on 13 March 2020). [CrossRef]
- Niu, J.Q.; Zhou, D.; Liu, T.H.; Liang, X.F. Numerical simulation of aerodynamic performance of a couple multiple units high-speed train. Veh. Syst. Dyn. 2017, 55, 681–703. [Google Scholar] [CrossRef]
- Decker, K.; Chin, J.; Peng, A.; Summers, C.; Nguyen, G.; Oberlander, A.; Sakib, G.; Sharifrazi, N.; Heath, C.; Gray, J.S.; et al. Conceptual feasibility study of the hyperloop vehicle for next-generation transport. In Proceedings of the 55th AIAA Aerospace Sciences Meeting, AIAA SciTech Forum (2017), Grapevine, TX, USA, 9–13 January 2017. [Google Scholar]
- Mok, J.K.; Yoo, J. Numerical study on high speed train and tunnel hood interaction. J. Wind Eng. Ind. Aerodyn. 2001, 89, 17–29. [Google Scholar] [CrossRef]
- Chin, J.C.; Gray, J.S. Open-Source Conceptual Sizing Models for the Hyperloop Passenger Vehicle. In Proceedings of the 56th AIAA/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Kissimmee, FL, USA, 5–9 January 2015. [Google Scholar] [CrossRef]
- Blomgren, G.E. The Development and Future of Lithium Ion Batteries. J. Electrochem. Soc. 2017, 164, A5019–A5025. [Google Scholar] [CrossRef]
- Yoshino, A. Development of the Lithium-Ion Battery and Recent Technological Trends. In Lithium-Ion Batteries; Pistoia, G., Ed.; Elsevier: Amsterdam, The Netherlands, 2014; pp. 1–20. [Google Scholar] [CrossRef]
- Mohammadi, F. Electric Vehicle Battery Market Analysis: Lithium-Ion. In Proceedings of the 1st International Conference on Modern Approaches in Engineering Science (ICMAES), Tbilisi, Georgia, 21 November 2018. [Google Scholar]
- Budde-Meiwes, H.; Drillkens, J.; Lunz, B.; Muennix, J.; Rothgang, S.; Kowal, J.; Sauer, D.U. A review of current automotive battery technology and future prospects. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2013, 227, 761–776. [Google Scholar] [CrossRef]
- Agwu, D.D.; Opara, F.; Chukwuchekwa, N.; Dike, D.; Uzoechi, L. Review of Comparative Battery Energy Storage Systems (Bess) for Energy Storage Applications in Tropical Enviroments. In IEEE 3rd International Conference on Electro-Technology for National Development; IEEE: Danvers, MA, USA, 2018. [Google Scholar]
- Leng, F.; Tan, C.M.; Pecht, M. Effect of Temperature on the Aging rate of Li Ion Battery Operating above Room Temperature. Sci. Rep. 2015, 5, 12967. [Google Scholar] [CrossRef]
- Ma, S.; Jiang, M.; Tao, P.; Song, C.; Wu, J.; Wang, J.; Deng, T.; Shang, W. Temperature effect and thermal impact in lithium-ion batteries: A review. Prog. Nat. Sci. Mater. Int. 2018, 28, 653–666. [Google Scholar] [CrossRef]
- Kudela, H.; Malecha, Z.M. Investigation of unsteady vorticity layer eruption induced by vortex patch using vortex particles method. J. Theor. Appl. Mech. 2007, 45, 785–800. [Google Scholar]
- Marcantoni, L.F.G.; Tamagno, J.P.; Elaskar, S.A. High speed flow simulation using openfoam. Mec. Comput. 2012, 16, 2939–2959. [Google Scholar]
- Kraposhin, M.; Bovtrikova, A.; Strijhak, S. Adaptation of Kurganov-Tadmor Numerical Scheme for Applying in Combination with the PISO Method in Numerical Simulation of Flows in a Wide Range of Mach Numbers. Procedia Comput. Sci. 2015, 66, 43–52. [Google Scholar] [CrossRef]
- Spalart, P.; Allmaras, S. A One-Equation Turbulence Model for Aerodynamic Flows. In Proceedings of the 30th Aerospace Sciences Meeting and Exhibit (AIAA), Reno, NV, USA, 6–9 January 1992. [Google Scholar] [CrossRef]
- Winter, M. Benchmark and Validation of Open Source CFD Codes, with Focus on Compressible and Rotating Capabilities, for Integration on the SimScale Platform. Master’s Thesis, Department of Applied Mechanics Chalmers, University of Technology, Gothenburg, Sweden, 2013. [Google Scholar]
- Yanus, A.C.; Michale, A.B. Thermodynamics—An Engineering Approach, 5th ed.; McGraw Hill: New York, NY, USA, 2006. [Google Scholar]
- Rohsenow, W.M.; Harnett, J.P.; Cho, Y.I. Handbook of Heat Transfer, 3rd ed.; McGraw-Hill: New York, NY, USA, 1998. [Google Scholar]
- Keith, F. The CRC Handbook of Thermal Engineering; CRC Press LLC: Boca Raton, FL, USA, 2000. [Google Scholar]
- Nagib, H.; Christophorou, C.; Ruedi, J.D.; Monkewitz, P.; Osterlund, J.; Gravante, S.; Chauhan, K.; Pelivan, I. Can We Ever Rely on Results from Wall-Bounded Turbulent Flows Without Direct Measurements of Wall Shear Stress? In Proceedings of the 24th AIAA Aerodynamic Measurement Technology and Ground Testing Conference, Portland, OR, USA, 28 June–1 July 2004. [Google Scholar] [CrossRef]
- Schultz, M.P.; Flack, K.A. Reynolds-number scaling of turbulent channel flow. Phys. Fluids 2013, 25, 025104. [Google Scholar] [CrossRef]
- Manceau, R.; Carlson, J.R.; Gatski, T.B. A rescaled elliptic relaxation approach: Neutralizing the effect on the log layer. Phys. Fluids 2002, 14, 3868–3879. [Google Scholar] [CrossRef]
- Moran, M.J.; Shapiro, H.N.; Boettner, D.D.; Bailey, M.B. Fundamentals of Engineering Thermodynamics; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).