Learning a Hierarchical Global Attention for Image Classification

Abstract

To classify the image material on the internet, the deep learning methodology, especially deep neural network, is the most optimal and costliest method of all computer vision methods. Convolutional neural networks (CNNs) learn a comprehensive feature representation by exploiting local information with a fixed receptive field, demonstrating distinguished capacities on image classification. Recent works concentrate on efficient feature exploration, which neglect the global information for holistic consideration. There is large effort to reduce the computational costs of deep neural networks. Here, we provide a hierarchical global attention mechanism that improve the network representation with restricted increase of computation complexity. Different from nonlocal-based methods, the hierarchical global attention mechanism requires no matrix multiplication and can be flexibly applied in various modern network designs. Experimental results demonstrate that proposed hierarchical global attention mechanism can conspicuously improve the image classification precision—a reduction of 7.94% and 16.63% percent in Top 1 and Top 5 errors separately—with little increase of computation complexity (6.23%) in comparison to competing approaches.

1. Introduction

To classify the image material on the internet, the deep learning/neural network methodology is the most optimal but also the costliest of all computer vision methods. Convolutional neural network (CNN) has been proved as a powerful tool for different computer vision tasks [1]. In CNN, filters extract the information from features with learned adaptive weights and bias [2]. By building the network deeper or wider, the accumulation of filters demonstrates a significant improvement in feature representation. Different from fully connection networks, the filters in CNN have fixed receptive fields to concentrate on the local information from features, saving the parameters and making it possible to build the network deeper [3]. Recently, researchers concentrate on well-designed network architectures for efficient feature exploration [4,5]. The elaborate network designs are composed of depth-wise and channel-wise convolutional layers and effectively exploit the features with modified filters [6]. As the receptive fields and network depths are fixed, these works almost neglect the global information for holistic consideration.

Attention mechanism has been introduced to address this issue [7,8]. As a weighting component for importance distribution, attentions are usually calculated as non-negative feature maps from a Sigmoid activation. To consider the global information, global average pooling is introduced to measure the information from the entire feature map [7]. After pooling, the feature maps will be compressed into a fixed size vector according to the channels. Then, fully connection layers with activation functions are utilized for nonlinear exploration. This channel-wise attention mechanism applies pooling to information evaluation, which treats the spatial information of features equally. In fact, the intrinsic property of pooling operation neglects the diversity of spatial information. Another global attention mechanism termed as non-local attention is proposed based on the matrix multiplication [9]. Due to the characteristic of matrix multiplication, all the spatial information will be considered for holistic consideration. Non-local attention has been proved as an effective design for network representation improvement. However, the matrix multiplication will result in a large memory consumption and high computation complexity. All of this will be further elaborated/introduced in the Related Works.

To reduce the CNN costs and provide better classification performance, we devise an improvement of attention mechanism for comprehensive information consideration. In the proposed hierarchical global attention (HGA) mechanism, multi-scale structure has been proved as an effective mechanism for hierarchical information exploration. We hold to the notion that features from different scales obtain various information, and the multi-scale structure can comprehensively exploit the features for better representation. Global average pooling is a suitable operation to estimate the information from different feature maps, which lacks the spatial-wise consideration. By combining the global average pooling and multi-scale structure, the attention mechanism can learn a comprehensive relations among different feature maps. Then, the nonlinear exploration will find a more adaptive representation of features. The holistic design of proposed HGA mechanism is shown in Figure 1. There are few parameters and restricted computation complexity in HGA, which makes it possible for flexible plug-and-play in exist effective network structures. To address this point, we provide several patterns for flexibly applying HGA to the existing network backbones. Experimental results shows HGA can boost the image classification capacity for different advanced network structures.

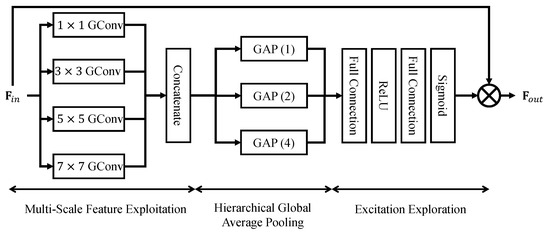
Figure 1. Structure of proposed hierarchical global attention mechanism (HGA). There are three modules in our proposed HGA: Multi-Scale Feature Exploitation (MFE), Hierarchical Global Average Pooling (HAP), and Excitation Exploration (EE).

The contributions of our work can be summarized as follows.

• We propose a hierarchical global attention (HGA) mechanism for comprehensive information consideration. The HGA hierarchically finds the spatial-wise relations among features with multi-scale structure design and utilizes nonlinear exploration to learn an adaptive attention.
• We provide several patterns for applying HGA to exist network backbones, which demonstrates its flexible applications for different structures.
• Experimental results show HGA can boost the image classification capacity for different advanced network structures with restricted computation complexity and parameters.

2. Related Works

2.1. CNN-Based Image Classification

Image classification is one of the classical computer vision issue. In recent years, CNN has demonstrate its superior performance on image classification issue due to the amazing capacity of feature representation. To the best of our knowledge, LeCun et al. first introduced LeNet [1] to handwritten numeral recognition and achieved great success. There are convolution, pooling, and full connection layers in LeNet for mapping an input digital image with size $32\times 32$ to a specific output. There are several benchmarks for image classification, such as MNIST [1], CIFAR-10, and CIFAR-100 [10]. However, the image resolutions of these datasets are small, which cannot sufficiently demonstrate the performance of various networks. ImageNet [11], proposed by Deng et al., is one of the most famous benchmarks for image classification task with large resolution images, and has become one of the most famous competitions in computer vision area. To our best knowledge, the first most famous CNN-based winner of ImageNet is AlexNet [12]. In AlexNet, GPU was firstly utilized to boost the training phase. Furthermore, ReLU activation, dropout, and normalization strategies were utilized in AlexNet, which provided an improvement on classification performance, and were widely considered by later works. After AlexNet, VGGNet [13] has proven to be another milestone of ImageNet competition. Different from AlexNet, VGGNet introduced a well-designed network structure with $3\times 3$ convolutional layers, which could preserve the receptive field with fewer parameters and deeper networks. Because of its superior feature representation capacity, VGGNet has also been utilized in different computer vision tasks, such as object detection, semantic segmentation, and GAN-based applications. However, there is an critical issue that when the networks are deeper, the gradient will vanish, which restricts the network depth. To address this issue, GoogLeNet [14] and ResNet [15] proposed two different style networks. GoogLeNet introduces $1\times 1$ convolutional layers to build a shortcut for efficient transmission. Besides the $1\times 1$ convolution, different scales of convolutions are utilized to find the suitable feature representation. With the deeper network structure and elaborate block design, GoogLeNet achieved better performance than VGGNet. In ResNet, a more suitable and efficient identical shortcut is introduced to build the network, which can efficiently solve the information transmission and gradient vanishing issues. In ResNet, the identical shortcut provides an information and gradient transmission pathway to build the network deeper. The features from shortcut and main path are aggregated as the final output. With the residual connection, ResNet could build the network much deeper than before, and achieved state-of-the-art performance much superior than previous works.

As ResNet has proved to be a success network design, there is a network family based on the ResNet backbone with different elaborate block designs. Res2Net [16], proposed by Gao et al., utilized the granular level to present the multi-scale features and achieved better performance. In Res2Net, the feature maps are separated into several groups. Different groups hold different receptive fields which provide a comprehensive consideration of feature representation. With this substitution, there is a large improvement for Res2Net. Another elaborate designed network is ResNext [17]. ResNext integrated the advantages of ResNet and GoogLeNet and proposed a new concept termed cardinality. In ResNext, the cardinalities are implemented by group convolutions and point-wise convolutions. Recently, another derivative was investigated with split attention mechanism, which is named as ResNeSt [18], has become one of the state-of-the-arts.

Besides ResNet, there are also well-designed networks with amazing performance. DenseNet [19] has proved to be another success network design pattern for efficient gradient and information transmission. In DenseNet, densely connection has been firstly proposed to concentrate features from all convolutional layers. WRN [20], proposed by Zagoruyko et al., introduced a wide residual network for image classification. In PyramidNet [21], Han et al. designed a pyramidal residual network inspired by Pyramid structure from classical computer vision methods. Based on fractal design, Larsson et al. proposed FractalNet [22] with good performance. Recently, IGCV family [23,24,25], Xception [26], PolyNet [27], and other elaborate designs have also achieved state-of-the-art performances.

Handcrafted network designs concentrate on reasonable information transmission. In recent years, network architecture search (NAS) has become a spotlight for researchers. As far as we know, GeneticCNN [28] is the first work using genetic algorithm to find a suitable structure with better performance. After GeneticCNN, there are works concentrating on different restrictions [29,30,31]. Reinforcement learning, which is another method for finding solutions, has also been applied to NAS [32,33]. Recently, Differentiable NAS has been proposed in DARTS [34].

2.2. Attention Mechanism for Image Classification

Attention mechanism, which is first proposed in natural language processing (NLP), has become one of the effective components for improving network representation capacity. Attention mechanism aims to find the inherent correlation among features. CNN-based methods focus on the image feature and try to find a better feature exploration way. It is true that a better network architecture will hold superior performance, but it is challenging to find a distinguished design. Attention mechanism can be considered as an enhancement component to improve the performance of an existed network. With a small cost on parameters and computation complexity, attention can provide an indeed improvement on the network representation. From this point of view, the attention mechanism is important. In attention mechanism, global information has attracted researchers’ eyes and various methods have been proposed for finding the global inherent correlations. To our best knowledge, SENet [7], which is the champion of 2017 ImageNet competition, is the first attention mechanism proposed for image classification. In SENet, global average pooling is utilized to measure the information from different channels. After pooling, squeezing-and-excitation structure is devised to explore the nonlinear relations among channels. Finally, a sigmoid activation is introduced for non-negativity. There are several deviations based on SENet. SKNet [35], which is another effective attention mechanism, was proposed for weighted inherent correlations. Furthermore, ResAttentionNet [8] is another image classification network with attention mechanism.

3. Hierarchical Global Attention

As shown in Figure 1, there are three modules for proposed HGA. First, the multi-scale information will be extracted by convolutional layers with different kernel sizes. After exploitation, the feature maps will be concatenated for a comprehensive consideration. Global average pooling operations with different window sizes provide another multi-scale way for hierarchical global attention, which act as an pyramid structure. Finally, a squeezing-and-excitation way is regarded for adaptive information learning. Herein, the three modules are termed as multi-scale feature exploitation (MFE), hierarchical global average pooling (HAP), and excitation exploration (EE).

3.1. Multi-Scale Feature Exploitation

Let us denote the input tensor of HGA as ${\mathbf{F}}_{in}\in {\mathbb{R}}^{H\times W\times C}$. The MFE module extracts local information with four convolutional layers. For each convolutional kernel $f_i$, where i denotes the kernel size, the exploited multi-scale features are

$$[{\mathbf{F}}_1,{\mathbf{F}}_3,{\mathbf{F}}_5,{\mathbf{F}}_7]=[{\mathbf{F}}_{in}\otimes f_1,{\mathbf{F}}_{in}\otimes f_3,{\mathbf{F}}_{in}\otimes f_5,{\mathbf{F}}_{in}\otimes f_7],$$

(1)

where ⊗ denotes the group convolution operation. After the exploitation, these multi-scale features will be concatenated as one tensor, where

$${\mathbf{F}}_{MFE}=Concat\left([{\mathbf{F}}_1,{\mathbf{F}}_3,{\mathbf{F}}_5,{\mathbf{F}}_7]\right).$$

(2)

${\mathbf{F}}_{MFE}$ holds the shape ${\mathbb{R}}^{H\times W\times 4C}$, which holds the same resolution ${\mathbf{F}}_{in}$, and four times channels from different scales.

3.2. Hierarchical Global Average Pooling

After exploitation, the multi-scale features contain various information for adaptive learning. These features concentrate on the diversity of local spatial signals, while the global information is omitted. Global average pooling (GAP) has proved to be an efficient method for the global signal measurement [7]. To address the global multi-scale information, HAP module applies GAP layers with different window sizes to information extraction. The multi-scale feature ${\mathbf{F}}_{MFE}$ will be processed as

$$[{\mathbf{F}}_{G1},{\mathbf{F}}_{G2},{\mathbf{F}}_{G4}]=GA{P}_1\left({\mathbf{F}}_{MFE}\right),GA{P}_2\left({\mathbf{F}}_{MFE}\right),GA{P}_4\left({\mathbf{F}}_{MFE}\right),$$

(3)

where $GA{P}_j(·)$ denotes the GAP layer with windows size as j.

Notice that ${\mathbf{F}}_{G1}$, ${\mathbf{F}}_{G2}$, and ${\mathbf{F}}_{G4}$ holds the different sizes. The channel number of three tensors are same, while the spatial resolutions vary. To jointly consider the multi-scale global information, ${\mathbf{F}}_{G1}$, ${\mathbf{F}}_{G2}$, and ${\mathbf{F}}_{G4}$ will be resized as $1\times 1\times (j\ast C)$ separately. The resized tensors will be concatenated as a joint vector ${\mathbf{F}}_G$, which contains the multi-scale global information.

3.3. Excitation Exploration

EE module is designed to explore the correlations among multi-scale global information. In the vector ${\mathbf{F}}_G$, each value denotes the global information measurement from different scales. To find the correlations, two fully connection layers with a ReLU activation is utilized to suppress the information distribution, and explore the importance of different channels. The operations can be demonstrated as

$${\mathbf{F}}_{suppress}=F{C}_{21c\to \frac{1}{4}c}\left({\mathbf{F}}_G\right),$$

(4)

$${\mathbf{F}}_{excitation}=F{C}_{\frac{1}{4}c\to c}\left(ReLU\left({\mathbf{F}}_{supress}\right)\right),$$

(5)

where $F{C}_{c_{in}\to c_{out}}(·)$ denotes the fully connection layer with input channel size $c_{in}$ and output channel size $c_{out}$. The suppressed channel number is set as $\frac{1}{4}c$, which is smaller than c for analyzing the computation complexity and representation performance. ReLU activation is applied for introducing the nonlinear relation. After suppression, the vector ${\mathbf{F}}_{suppress}$ will be excited to the same channel size as the input tensor ${\mathbf{F}}_{in}$. Finally, a Sigmoid activation is applied for the non-negativity. The attention vector after EE module is considered as

$${\mathbf{F}}_{attention}=\sigma \left({\mathbf{F}}_{suppress}\right),$$

(6)

where $\sigma$ denotes the Sigmoid activation. Finally, the output after HGA is

$${\mathbf{F}}_{out}={\mathbf{F}}_{in}\odot {\mathbf{F}}_{in},$$

(7)

where ⊙ denotes the channel-wise multiplication.

4. Implementation and Discussion

As an efficient component, HGA can be flexibly applied in different network designs. ResNet [18] and InceptionNet [14] are two classical network design patterns from which most recent networks are derived. From this point of view, we provide the applications of HGA on the two patterns, which are demonstrated in Figure 2. Figure 2a,c denotes the vanilla block designs in ResNet and Inception Net. Figure 2b,d denotes the applications of HGA. In ResNet, HGA is applied in the main path after the ResBlock processing. On one hand, this pattern could find the inherent correlations after feature exploration. On the other hand, applying HGA on main path could preserve the identical information and gradient transmission on the shortcut. Different from ResNet, in Inception Net, the HGA is applied after the Inception Block. In Inception Block, the identical information transmission is utilized by $1\times 1$ convolutional layer. The HGA does not omit the identical transmission in Inception Net. It is because the $1\times 1$ convolution will change the distribution of information from different channels.

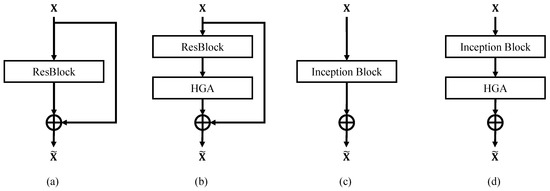
Figure 2. Applications of HGA on different network designs. (a) The vanilla ResBlock [15]. (b) The application of HGA on ResBlock. (c) The vanilla Inception Block [14]. (d) The application of HGA on Inception Block.

From the design, HGA is an efficient component with restricted parameters and computation complexity. Suppose the input ${\mathbf{F}}_{in}$ is with size $H\times W\times C$, then the FLOPs cost on MFE module is

$$FLO{P}_{MFE}=2HWC(1^2+3^2+5^2+7^2).$$

(8)

After concatenation, there are three GAP layers for global information measurement. The FLOPs cost on HAP module is

$$FLO{P}_{HAP}=3HWC.$$

(9)

Finally, there are two full connection layers and two activation functions in EE module. The FLOPs cost on EE module is

$$FLO{P}_{EE}=\frac{85}{2}{C}^2.$$

(10)

The entire FLOP cost of HGA is,

$$FLO{P}_{HGA}=FLO{P}_{MFE}+FLO{P}_{HAP}+FLO{P}_{EE}.$$

(11)

Notice that there is no bias in both group convolutions and the full connection layers. On one hand, it will save the parameters and computation cost. On the other hand, the bias setting will modify the distribution of feature maps.

The parameters of HGA are

$$Para{m}_{HGA}=(1^2+3^2+5^2+7^2)C+\frac{11}{2}{C}^2.$$

(12)

The left-hand side of Equation (12) denotes the parameters of MFE module and the right-hand side denotes the EE module. There is no parameter in HAP module, where only the GAP layers exist.

5. Experiments

5.1. Results

To demonstrate the capacity of HGA, we evaluate the image classification performance on ImageNet [11] 2012 dataset. The ImageNet dataset contains 1.28 million images for training and around 50,000 images for validation, which cover 1000 different classes. Top-1 and top-5 error are considered as the indicators of classification capacity. The images are augmented by randomly cropping, flipping, and rotation. Training data are resized as $224\times 224$ to suit the origin settings of baseline network. The parameters are updated by SGD optimizer with learning rate as $lr=0.6$ and shrunk 10 times for every 30 epochs. We totally update the model for 100 epochs.

For a better representation of the HGA embedding method, we provide the details on two modern backbones, which is shown in Table 1. As there are a large number of filters in the deeper layers, a linear transformation is applied for dimension reduction. In the table, $HGA(a,b,c)$ denotes a three-step operation. First, a full connection (FC) layer is conducted to shrink the dimension from a to b, then an HGA attention with b channels is utilized. After the attention mechanism, the dimension will be restored from b to c with a FC layer.

Table 1. The embedding methods of HGA for different modern backbones.

Output Size	ResNet-50 [15]	HGA-ResNet-50	HGA-ResNeXt-50
$112\times 112$	$conv,7\times 7,64,stride=2$	$conv,7\times 7,64,stride=2$	$conv,7\times 7,64,stride=2$
$56\times 56$	$maxpool,3\times 3,stride=2$	$maxpool,3\times 3,stride=2$	$maxpool,3\times 3,stride=2$
	$\left[\begin{array}{c}conv,1\times 1,64\\ conv,3\times 3,64\\ conv,1\times 1,256\end{array}\right]\times 3$	$\left[\begin{array}{c}conv,1\times 1,64\\ conv,3\times 3,64\\ conv,1\times 1,256\\ HGA(256,32,256)\end{array}\right]\times 3$	$\left[\begin{array}{c}conv,1\times 1,128\\ conv,3\times 3,128\\ conv,1\times 1,256\\ HGA(256,32,256)\end{array}\right]\times 3$
$28\times 28$	$\left[\begin{array}{c}conv,1\times 1,128\\ conv,3\times 3,128\\ conv,1\times 1,512\end{array}\right]\times 4$	$\left[\begin{array}{c}conv,1\times 1,128\\ conv,3\times 3,128\\ conv,1\times 1,512\\ HGA(512,32,512)\end{array}\right]\times 4$	$\left[\begin{array}{c}conv,1\times 1,256\\ conv,3\times 3,256\\ conv,1\times 1,512\\ HGA(512,32,512)\end{array}\right]\times 4$
$14\times 14$	$\left[\begin{array}{c}conv,1\times 1,256\\ conv,3\times 3,256\\ conv,1\times 1,1024\end{array}\right]\times 6$	$\left[\begin{array}{c}conv,1\times 1,256\\ conv,3\times 3,256\\ conv,1\times 1,1024\\ HGA(1024,32,1024)\end{array}\right]\times 4$	$\left[\begin{array}{c}conv,1\times 1,512\\ conv,3\times 3,512\\ conv,1\times 1,1024\\ HGA(1024,32,1024)\end{array}\right]\times 4$
$7\times 7$	$\left[\begin{array}{c}conv,1\times 1,512\\ conv,3\times 3,512\\ conv,1\times 1,2048\end{array}\right]\times 6$	$\left[\begin{array}{c}conv,1\times 1,512\\ conv,3\times 3,512\\ conv,1\times 1,2048\\ HGA(2048,32,2048)\end{array}\right]\times 4$	$\left[\begin{array}{c}conv,1\times 1,1024\\ conv,3\times 3,1024\\ conv,1\times 1,2048\\ HGA(2048,32,2048)\end{array}\right]\times 3$
$1\times 1$	GAP, 1000-d fc, softmax	GAP, 1000-d fc, softmax	GAP, 1000-d fc, softmax

Herein, we consider the error rate as the indicator for different networks. In fact, statistically significant is a less concerned indicator for deep learning-based image classification. On one hand, Top-1 and Top-5 error (%) can well describe the performance for practical applications. On the other hand, CNN has a good generalization ability and performs well on different classification datasets. Usually when a network works well on one class, it will also work well on another one. In this situation, Analysis of Variance (ANOVA) may be not useful for evaluating the network performance. From this point of view, we only compare the numeric values but not perform the statistically significant test.

We compare the single-crop error rates on the ImageNet validation set and adopt better values between the reported results from their origin papers and our reproduction version. The results are shown in Table 2. We apply the HGA to five modern backbones: ResNet-50, ResNet-101, ResNet-152, ResNeXt-50, and ResNeXt-101, which have proved to be remarkable design patterns. From the results, HGA provides a significant performance improvement with restricted increase on FLOPs and parameters. Notice that the accuracy rates from vanilla models are reported from the origin paper, and the HGA versions are trained by ourselves. From the numerical comparison with vanilla models, HGA achieves average 7.94% improvement on Top 1 error and 16.63% on Top 5 error. The FLOPs of HGA version only increases 6.23% on average. Furthermore, we also compare our HGA with recent elaborate attention mechanism SENet [7] and SKNet [35]. The results are shown in Table 3. From the results, HGA achieves better classification accuracy than other attention mechanisms. To demonstrate the generalization ability of HGA, we perform the comparisons on CIFAR-10 and CIFAR-100 dataset in Table 4, which shows the superior capacity of our HGA.

Table 2. Single-crop error rates of different models on ImageNet dataset.

Model		ResNet-50	ResNet-101	ResNet-152	ResNeXt-50	ResNeXt-101
Vanilla	Top 1 err.(%)	24.80	23.17	22.42	22.11	21.18
	Top 5 err.(%)	7.48	6.52	6.34	5.90	5.57
	FLOPs(G)	4.11	7.83	11.55	4.25	8.01
	Params(M)	25.55	44.54	60.19	25.02	44.17
HGA	Top 1 err.(%)	22.48 (−2.32)	21.50 (−1.67)	20.63 (−1.79)	20.22 (−1.89)	19.82 (−1.36)
	Top 5 err.(%)	6.22 (−1.26)	5.60 (−0.92)	5.23 (−1.11)	4.88 (−1.02)	4.59 (−0.98)
	FLOPs(G)	4.38	8.23	12.13	4.53	8.71
	Params(M)	26.73	47.07	63.92	26.21	46.70

Table 3. Comparisons of different attention mechanism on ImageNet dataset.

Model		ResNet-50	ResNet-101	ResNet-152	ResNeXt-50	ResNeXt-101
Vanilla	Top 1 err.(%)	24.80	23.17	22.42	22.11	21.18
SENet [7]	Top 1 err.(%)	23.29 (−1.51)	22.38 (−0.79)	21.57 (−0.85)	21.10 (−1.01)	20.70 (−0.48)
	FLOPs(G)	4.11	7.83	11.56	4.26	8.01
SKNet [35]	Top 1 err.(%)	-	-	-	20.79 (−1.23)	20.19 (−0.84)
	FLOPs(G)	-	-	-	4.47	8.46
HGA	Top 1 err.(%)	22.48 (−2.32)	21.50 (−1.67)	20.63 (−1.79)	20.22 (−1.89)	19.82 (−1.36)
	FLOPs(G)	4.38	8.23	12.13	4.53	8.71

Table 4. Top 1 error(%) of different attention mechanism on CIFAR-10 and CIFAR-100 dataset.

Model	R-110 [15]	R-164 [15]	SE-R-110 [7]	SE-R-164 [7]	HGA-R-110	HGA-R-164
CIFAR-10	6.37	5.46	5.21	4.39	4.52	3.98
CIFAR-100	26.88	24.33	23.85	21.31	22.02	20.82

5.2. Ablation Study

Investigation on different modules. To demonstrate the effectiveness of three different modules, we rebuild the HGA with different module combinations. The results are shown in Table 5. From the table, we can find that MFE plays as a critical role for performance improvement. On one hand, MFE extracts the multi-scale information from input features which provides a diverse comprehension. On the other hand, the MFE module increases the network depth, which helps to enhance the representation.

Table 5. Comparisons of different module combinations.

MFE	HGA	EE	ResNet-101		ResNeXt-101
			Top 1 err.(%)	Top 5 err.(%)	Top 1 err.(%)	Top 5 err.(%)
✓	✓	✓	21.50	5.60	19.82	4.59
✗	✓	✓	21.91	5.73	20.22	4.81
✓	✗	✓	21.58	5.63	19.92	4.62
✓	✓	✗	21.63	5.69	20.01	4.69
✓	✗	✗	21.85	5.69	20.03	4.63
✗	✓	✗	22.40	6.20	20.48	5.09
✗	✗	✓	22.00	5.75	20.34	4.88
✗	✗	✗	23.17	6.52	21.18	5.57

Investigation on HGA module. To further explore the capacity of HGA module, we modify the multi-scale extraction with different convolutional layers, which are shown in Table 6. From the result, we can find that the larger filters will help more on the accuracy improvement. Different filter sizes will exploit different scale information, and the HGA module can comprehensively exploit the multi-scale feature for better representation and semantic understanding.

Table 6. Investigation on HGA module.

$1\times 1$	$3\times 3$	$5\times 5$	$7\times 7$	ResNet-101		ResNeXt-101
				Top 1 err.(%)	Top 5 err.(%)	Top 1 err.(%)	Top 5 err.(%)
✓				21.88	5.72	20.19	4.79
	✓			21.76	5.69	20.11	4.71
		✓		21.70	5.67	20.08	4.69
			✓	21.67	5.66	20.01	4.66
✓	✓	✓	✓	21.50	5.60	19.82	4.59

6. Conclusions

In this paper, we introduced a hierarchical global attention mechanism termed HGA for the image classification issue, considering the multi-scale correlations between different feature maps. There are three modules in HGA for adaptive multi-scale information exploration and finding the attention among features. As an efficient network component, HGA could be flexibly applied in various network design patterns, which was demonstrated in both computational complex analysis and the experimental results. We performed the experiments with several modern network design patterns, the experiment results showed HGA as an effective component for better image classification performance.