Abstract
Volunteer computing (VC) is a distributed computing paradigm, which provides unlimited computing resources in the form of donated idle resources for many large-scale scientific computing applications. Task scheduling is one of the most challenging problems in VC. Although, dynamic scheduling problem with deadline constraint has been extensively studied in prior studies in the heterogeneous system, such as cloud computing and clusters, these algorithms can’t be fully applied to VC. This is because volunteer nodes can get offline whenever they want without taking any responsibility, which is different from other distributed computing. For this situation, this paper proposes a dynamic task scheduling algorithm for heterogeneous VC with deadline constraint, called deadline preference dispatch scheduling (DPDS). The DPDS algorithm selects tasks with the nearest deadline each time and assigns them to volunteer nodes (VN), which solves the dynamic task scheduling problem with deadline constraint. To make full use of resources and maximize the number of completed tasks before the deadline constraint, on the basis of the DPDS algorithm, improved dispatch constraint scheduling (IDCS) is further proposed. To verify our algorithms, we conducted experiments, and the results show that the proposed algorithms can effectively solve the dynamic task assignment problem with deadline constraint in VC.
1. Introduction
In recent years, volunteer computing (VC) [1] has supported diverse large-scale scientific research applications using idle resources from a large number of heterogeneous volunteer computers. VC provides not only almost free unlimited computing resources for scientific research projects, such as SETI@home [2], Folding@home [3], and ATLAS@Home [4], but also opportunities for volunteers to participate in scientific research. At the same time, increasingly more researchers have extended the unlimited computing resources provided by VC to cloud computing [5] and big data fields [6]. The network structure of VC is a master-slave distributed network computing model [7], as shown in Figure 1. The computers that provide resources are called volunteer nodes (VN), and the server is responsible for assigning tasks and collecting results.
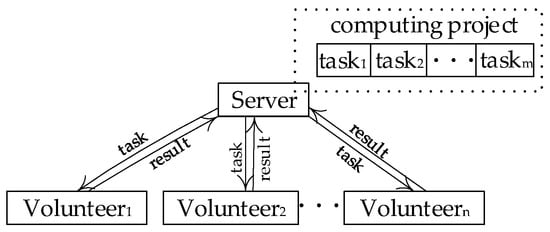
Figure 1.
Master-slave model.
In volunteer computing platforms, the computing power of VN is different. One of the challenges is to the algorithm of scheduling parallel tasks in such heterogeneous and dynamic platforms. At the same time, although studies have shown that assigning parallel tasks to multiple processors are NP-hard, because of its importance, many researchers have done lots of work for this problem [8,9,10,11]. However, these scheduling algorithms can’t be fully applied to volunteer computing, because VN may quit at any time without any responsibility.
Generally speaking, volunteer computing applications are so complex that they are divided into many tasks and assigned to volunteer nodes with a hard deadline constraint [12]. If a task misses its deadline, the completion time of the whole project will be affected. For example, during the production of a chemical product, the delay of a certain ingredient will not only cause the waste of raw materials, but also postpone the delivery time. Therefore, the research on task scheduling with the deadline has great significance.
In addition, since there are not enough resources to complete all tasks in volunteer computing platforms, we mainly focus on the algorithm of completing as many tasks as possible before the deadline for each task. Similarly, Salehi et al. proposed a maximum on-time completions (MOC) [13] algorithm for task scheduling with deadline constraint for heterogeneous distributed platforms. In the MOC algorithm, a stochastic robustness measure is defined to assign tasks, and the algorithm discards tasks that miss their deadlines to maximize the number of the completed tasks. However, the MOC algorithm cannot be fully applied to the volunteer computing platform, because it does not consider suddenly offline nodes. Therefore, it is indispensable to study the dynamic task scheduling for VC platforms.
To tackle the aforementioned problems, this paper proposes two novel dynamic task scheduling algorithms with deadline constraint in heterogeneous VC platforms. To the best of our knowledge, it is the first attempt to study dynamic task scheduling with deadline constraint in the volunteer computing platform. The main contributions of this paper are summarized as follows:
- (1)
- A formal definition of the task assignment problem with deadline constraint in heterogeneous VC platforms for the first time.
- (2)
- A basic deadline preference dispatch scheduling algorithm (DPDS) that can guarantee the task with minimum deadline constraint will be computed first, a match function to select the most suitable VN in task assignment, and an improved dispatch constraint scheduling algorithm (IDCS) that selects tasks according to their priorities and utilizes a risk prediction model to improve the execution efficiency of the application.
- (3)
- A comprehensive evaluation of the proposed algorithms and a comparison with existing algorithms.
The remainder of this paper is organized as follows: The next section presents the related work. Section 3 introduces the definition of the problems. Section 4 illustrates our task scheduling algorithms. Section 5 gives the experimental results and analysis of the proposed task scheduling algorithms. Section 6 concludes this paper.
2. Related Work
In this section, we summarize the related work of task scheduling algorithm. Firstly, we introduce task scheduling algorithms in other distributed computing systems. Secondly, we introduce task assignment algorithms in volunteer computing platforms.
2.1. Task Scheduling Algorithms in Other Distributed Computing Systems
Because effective task allocation algorithm can improve the performance of distributed systems, many researchers have done a lot of works in this area. These task scheduling algorithms can be roughly divided into two categories, static scheduling algorithms and dynamic scheduling algorithms.
Generally speaking, static algorithms use directed acyclic graphs (DAG) [14] to represent task priorities in task scheduling. Topcuoglu et al. [15] proposed two static task scheduling algorithms for heterogeneous distributed computing, which are called earliest-finish-time (HEFT) algorithm and the critical-path-on-a-processor (CPOP) algorithm. The HEFT algorithm chooses tasks with the highest priority at each step to allocate tasks and the CPOP algorithm calculates task priority according to DAG. The ultimate goal of the HEFT is to minimize the completion time of all tasks. The Min-min algorithm [16] extends the HEFT algorithm and uses sophisticated heuristics at each level to reduce the probability of catching local minima. Poola et al. [17] proposed a robust task scheduling algorithm based on deadline and budget constraints for cloud computing, which can minimize the total completion time and the cost under deadline constraint. However, the key issue of these prior studies is that they didn’t consider the dynamic of distributed computing. Because of the dynamic characteristics of volunteer computing platforms, the static scheduling algorithms can’t be fully applied to such platforms, and cannot make full use of the computing resources of the system.
To improve the utilization rate of system resources, researchers have proposed many dynamic scheduling algorithms. Zomaya et al. [18] proposed a dynamic load-balancing algorithm to improve the utilization of computing resources; the experimental results show that their algorithm can achieve a near-optimal task allocation. On this basis, Page et al. [19] proposed an improved dynamic scheduling algorithm which operates in a batch fashion and uses a genetic algorithm to minimize the total completion time. In addition, the greedy algorithm [20] is used to task allocation. However, these algorithms did not take the deadline into account, so it is necessary to design a heterogeneous dynamic scheduling algorithm with the deadline.
The MOC algorithm [13] was proposed to solve the dynamic scheduling problem with deadline constraint in heterogeneous distributed computing, as mentioned before. However, the objective of MOC is that each task must be completed before its deadline, which is different from our work: To complete as many tasks as possible within their respective deadline constraints. Moreover, there are some dynamic task assignment methods with deadline constraints for special application scenarios [21,22,23]. Since application scenarios differ from volunteer computing, these algorithms can’t be applied to volunteer computing.
2.2. Task Scheduling Algorithms in Volunteer Computing Platforms
Anderson et al. [24,25] introduced the dynamic of volunteer computing systems, and they proposed a basic task scheduling algorithm according to the attributes of the tasks and computing resources, such as deadline of the tasks, computing power of volunteer nodes, and the number of tasks to arrive, etc. The system constraints proposed in their system are the same as our work. In contrast to their work, the objective of our work is to maximize the number of completed tasks.
To improve the performance of volunteer computing, it is necessary to design an appropriate task scheduling algorithm to complete as many tasks as possible. This type of algorithms is called throughput driven task scheduling algorithm, which has been extensively studied in previous work. For example, Guler et al. [26] proposed a task allocation algorithm to maximize the number of task completions under monetary budget constraint. They also verify the effectiveness of their algorithm under the price of the electricity consumed by their peers. To make full use of computing resources and increase the percentage of workflows that meet the deadline, Ghafarian et al. [27,28] proposed a workflow scheduling algorithm. The proposed workflow scheduling algorithm partitions a workflow into sub-workflows to minimize data dependencies among the sub-workflows. At the same time, the experimental results show that the proposed algorithm increases the percentage of workflow that meets the deadline with a factor of 75%. Sebastio et al. [29] proposed a framework to allocate tasks according to different policies in volunteer cloud systems. To maximize the number of the completed tasks, they take into account several different aspects. Then they provided a distributed optimization approach relying on the alternating direction method of Multipliers algorithm (ADMM) and the results show that the ADMM algorithm has a good performance in a real environment.
By comparing the above studies, we conclude that algorithms mainly focus on maximizing the number of task completions under different constraints. In contrast to prior works, this paper focuses on dynamic task scheduling which can react quickly in some situations, such as suddenly offline, new arrivers etc. At the same time, this paper intends to maximize the number of task completions considering the deadline for each task.
3. Problem Description
This paper studies the dynamic task allocation method with deadline constraint in the volunteer computing platforms. The notations used in the paper are summarized in Table 1.

Table 1.
Summary of notations.
Given a number of tasks in VC platforms, denoted by the set T = {t1, t2, …, tm}. Suppose that each task ti can be completed by any node nj or several other nodes in the VC platforms. For easy expression, two unified concepts are first introduced in the VC platforms. The server hour means the unit time of the server. One unit means the number of tasks completed within one server hour.
The concepts of task and node are given as follows:
Definition 1
(task).Task ti is a double dimension array that is denoted by (ti.cost,ti.deadline). The unit of ti.cost is called server hour, meaning that ti can be finished on the server for ti.cost hours; ti.deadline means the constraint of task ti, whose unit is hours. If the task ti begins at time l1, the deadline constraint of task ti means that task ti must be completed before l1 + ti.deadline.
For example, as shown in Figure 2a, t3.cost = 5, which means that it will take five server hours to complete the task t3. If the deadline constraint of task t3 is three hours and begins at time l1, it means that task t3 must be finished before l1 + 3.
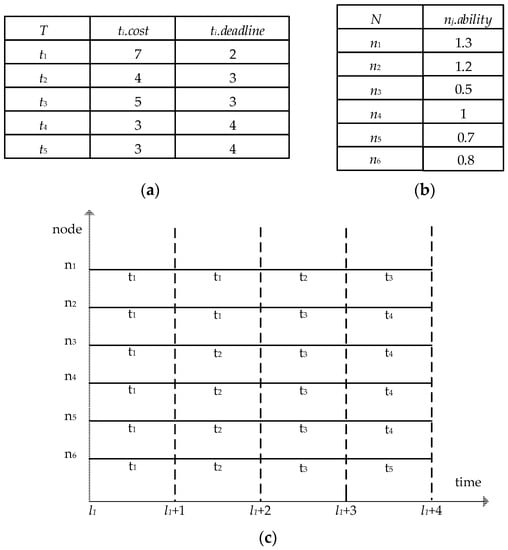
Figure 2.
An example of task scheduling at time l1. (a) List of tasks at time l1; (b) list of volunteer nodes at time l1; (c) task allocation process at time l1.
Definition 2
(node).Given a volunteer node set, denoted by the set N = {n1, n, …, nj}, the computing power of each volunteer node nj is denoted by nj.ablitlity, it means that the number of tasks the node nj can complete in an hour is nj. ability units.
For example, as shown in Figure 2b, n1. ability = 1.3, which means that the volunteer node n1 can complete the number of tasks in an hour is 1.3 times unit.
A dynamic task scheduling with deadline constraint at l1 moment can be denoted by ti. assign = {(n1, t1, l1), (n2, t1, l1), … (ns, t1, l1)}.
List of tasks at time l1 is shown in Figure 2a, List of volunteer nodes at time l1 is shown in Figure 2b and the task allocation process is shown in Figure 2c. Task t1 is taken as an example: The server starts to allocate computing resource to the task t1 at the initial time l1 and the task t1’s allocation is denoted by t1.assign = {(n1, t1, l1), (n2, t1, l1), (n3, t1, l1), (n4, t1, l1), (n5, t1, l1), (n6, t1, l1), (n1, t1, l1 + 1), (n2, t1, l1 + 1)}.
The calculation cost of t1 is seven units and n1 is scheduled to complete two-hour task t1 by the server. It is known that the number of tasks n1 can complete in an hour is 1.3 times unit. So, n1 can complete 2.6 units in two hours. By analogy, the total computing resources allocated to t1 can complete a total of eight units, which are more than seven units of t1. Furthermore, because the deadline constraint of t1 is two hours, so, t1 can be completed. Similarly, the computing resources allocated to t2 is t2.assign = {(n3, t2, l1 + 1), (n4, t2, l1 + 1), (n5, t2, l1 + 1), (n6, t2, l1 + 1), (n1, t2, l1 + 2)}. The calculation cost of t2 is four units, and the deadline constraint of t2 is three hours, so t2 can be completed. The computing resources allocated to t3 is t3.assign = {(n2, t3, l1 + 2), (n3, t3, l1 + 2), (n4, t3, l1 + 2), (n5, t3, l1 + 2), (n6, t3, l1 + 2), (n1, t3, l1 + 3)}. The calculation cost of t3 is five units and the deadline constraint of t3 is three hours. The deadline constraint of t3 cannot be satisfied, therefore t3 cannot be completed. By analogy, it can be concluded that t4 can be completed and t5 cannot be completed. Finally, according to the task allocation of Figure 2c, the tasks that can be completed before deadline constraint are t1, t2 and t4.
In a dynamic network environment, the volunteer nodes are updated hourly. List of tasks at time l1 + 1 is shown in Figure 3a, and the list of volunteer nodes at time l1 + 1 is shown in Figure 3b. At time l1 + 1, the node n2 goes offline, the node n7 goes online. Obviously, the task assignment process in Figure 2c cannot meet the requirements of dynamics, so it is necessary to design a corresponding dynamic task assignment algorithm. The task scheduling algorithm of this paper will be described in the following section.
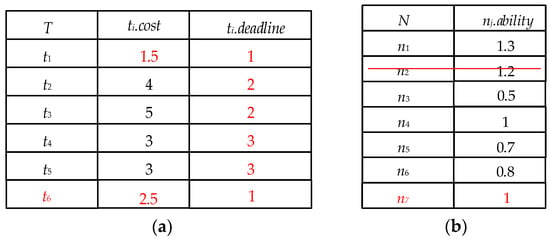
Figure 3.
Task list and volunteer nodes list at time l1 + 1. (a) List of tasks at time l1 + 1; (b) list of volunteer nodes at time l1 + 1.
In VC platforms, the set of volunteer nodes and task sets are updated dynamically over time. In this paper, the objective of the task allocation is to solve the dynamic task scheduling problem and maximize the number of completed tasks before deadline constraint.
4. Algorithm Description
In this section, we introduce the DPDS algorithm and the IDCS algorithm in detail.
4.1. The Deadline Preference Dispatch Scheduling (DPDS) Algorithm
The DPDS algorithm is a dynamic task scheduling algorithm based on deadline constraint priority. Firstly, the DPDS algorithm sorts the tasks in ascending order according to their deadline and sorts the VN in descending order according to their computing power. Secondly, the DPDS algorithm adopts a matching function to select the most suitable volunteer node to assign a task, which make the computing resource will be freed in the least possible amount of time. Consequently, the DPDS algorithm can ensure that the task with nearest deadline constraint is completed first, and free computing resource in the least possible amount of time. The DPDS algorithm is described in detail in Algorithm 1.
Significantly, in the DPDS algorithm, we use a monitoring mechanism, which is triggered to meet the following two conditions simultaneously.
- The volunteer computing platform has been running for an hour.
- There are new nodes or tasks arrived at the VC platform.
| Algorithm 1. The DPDS Algorithm Taskassign(Tl,Nl,l) |
| Input: task set Tl, volunteer nod set Nl, the current time l |
| Output: final task assignment set T.assign. |
|
If the monitoring mechanism is triggered, to make full use of the computing resources provided by the idle VN, we adopt the match function to select the suitable VN that wastes the least amount of computing resources in the DPDS algorithm. The match function is described in detail in Algorithm 2.
For example, the list of tasks at time l1 is shown in Figure 2a and list of volunteer nodes at time l1 is shown in Figure 2b. According to the first to fourth lines of Algorithm 1, at time l1, Tl = {t1, t2, t3, t4, t5}, Nl = {n1, n2, n4, n6, n5, n3}. Take t1 as an example, according to the sixth line of Algorithm 1, it can be seen that t1 is allocated first. According to Algorithm 2, at time l1, t1.assign = {(n1, t1, l1), (n2, t1, l1), (n3, t1, l1), (n4, t1, l1), (n5, t1, l1), (n6, t1, l1)}. As can be seen from the task assignment above, there is still 1.5 units left in task t1, which needs to be allocated at time l1 + 1. At time l1 + 1, both the task list and the node list are updated, which are shown in Figure 3a and Figure 3b, so the monitoring mechanism is triggered. According to the first to fourth lines of Algorithm 1, at time l1 + 1, Tl = {t1, t6, t2, t3, t4, t5}, Nl = {n1, n4, n7, n6, n5, n3}. According to the sixth line of Algorithm 1, it can be seen that t1 is allocated first. According to Algorithm 2, at time l1 + 1, t1.assign = {(n1, t1, l1 + 1), (n3, t1, l1 + 1) }. By analogy, we assume that tasks and nodes are updated only at time l1 + 1, so the rest of the task assignments are shown in Figure 4. Figure 4 shows t3 and t5 cannot be completed within the deadline.
| Algorithm 2. The Match(t’, Nl, l) |
| Input: the task t’, volunteer node set Nl, the current time l |
| Output: task assignment set t’.assign |
|
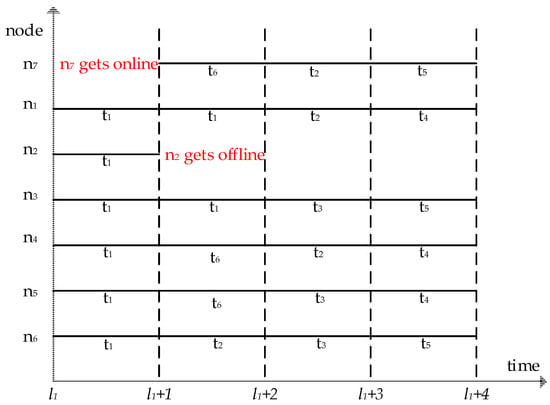
Figure 4.
The execution processes of the deadline preference dispatch scheduling (DPDS) algorithm.
4.2. The Improved Dispatch Constrain Scheduling (IDCS) Algorithm
The DPDS algorithm is a deadline priority allocation method, which can ensure that the most urgent tasks are given the highest priority in dynamic allocation. However, it cannot guarantee the largest number of tasks to be completed. And we find that the task cannot be completed within deadline constraint is still assigned, which causes a waste of computing resources. On this basis, this paper proposes an improved IDCS algorithm. The IDCS algorithm uses a risk prediction model to reduce the waste of computing resources. Before introducing the IDCS algorithm, we introduce the risk prediction model firstly.
4.2.1. The Risk Prediction Model
In this paper, we propose a risk prediction model that can predict the completion risk of each task, which is described in Algorithm 3. In VC platforms, VN is constantly updated at every moment. Although, it is impossible to accurately determine the number of updated nodes and their computing power, the range of the number of possible online nodes at each time can be estimated based on historical data. For easy calculation, we assume that the computing power of all predicted online VN is 1 unit, and the probability of the number of possible VN at each time is the same. On this basis, we calculate the completion risk of each task by completion probability. We will introduce the definition of the completion probability below.
Definition 3
(Completion probability).Given a possible world [30] set W and a task t’ at time l, the completion probability of t’ at time l is defined as follows:
where w represents a possible world in a possible world set W, W’ is a possible world set which is composed of a possible world that can complete t’ within the deadline, and Pr(w) represents the possible probability of w.
| Algorithm 3. The Risk Prediction Model Risk(t,W,l) |
| Input: the task t, possible world set W, the current time l |
| Output: the completion risk R of the task t |
|
For example, at time l1, the task t6 is allocated at time l1 + 3, and the deadline of t6 is l1 + 4. Figure 5a shows that the number of possible VN at time l1 + 3 is 3, 4, and 5, and the number of possible VN at time l1 + 4 is 3, 4, and 5. The possible world set W of t6 is shown in Figure 5c. The completion probability Prl1(t6) of t6 is 66.7%, which is calculated by Equation (1), so the completion risk of the task t6 is 33.3%.
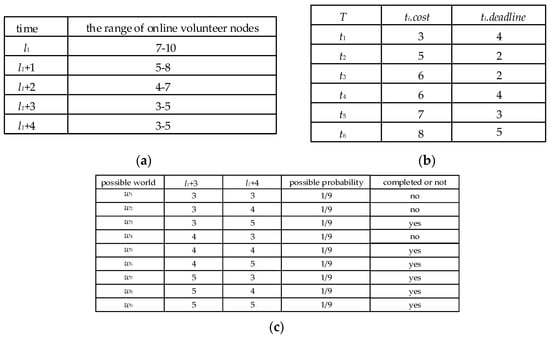
Figure 5.
An example of using a risk prediction model to predict completion risk of the task. (a) The range of online volunteer nodes from time l1 to time l1 + 4; (b) list of tasks at time l1; (c) the possible world set W of the task t6.
4.2.2. The Description of the IDCS Algorithm
The IDCS algorithm is a dynamic allocation method based on the objective of maximizing the number of tasks completed. To achieve the objective of completing the maximum number of tasks with limited computing resources, the IDCS algorithm chooses the task to assign based on task priority and completion risk of the task.
Task partitioning is divided into simple and urgent tasks, simple tasks, complex tasks and complex and urgent tasks according to their computational cost and the size of deadline constraints, which correspond to different task priority, as shown in Figure 6.
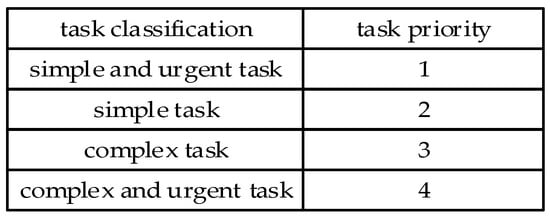
Figure 6.
Task classification and corresponding priority.
The specific ways of division are as follows:
If the computational cost of task t is less than the average computational cost of all tasks in the task list, and t. deadline is less than the middle time of the whole computing time, it is considered that the task t is simple and urgent, and the task priority corresponding to t is 1. If the computational cost of the task t is less than the average computational cost of all tasks in the task list, and t. deadline is greater than the middle time of the whole computing time, it is considered that task t is a simple task, and the task priority corresponding to t is 2. If the computational cost of task t is greater than the average computational cost of all tasks in the task list and t. deadline is greater than the middle time of the whole computing time, it is considered that t is a complex task, and the task priority corresponding to t is 3. If the computational cost of task t is greater than the average computational cost of all tasks in the task list, and t. deadline is less than the middle time of the whole computing time, it is considered that task t is complex and urgent, and the task priority corresponding to t is 4.
For example, as shown in Figure 5b, the average computational cost of all tasks is 5.8 and the middle time of the whole computing time is 2.5. Therefore, according to the division criteria mentioned above, the task t1 is a simple task and the task priority of t1 is 2. The task t2 is a simple and urgent task, and the task priority of t2 is 1. The task t3 is a complex and urgent task, and the task priority of t3 is 4. The task t4, t5, t6 are complex tasks, and their task priority is 3.
In the IDCS algorithm, firstly, the task priority and the completion risk are calculated as described above. Secondly, the IDCS algorithm deletes tasks that cannot be completed based on task priority and completion risk. Finally, Algorithm 1 is called to allocate tasks. The IDCS algorithm is described in detail in Algorithm 4.
| Algorithm 4. The IDCS Algorithm |
| Input: task set Tl, volunteer node set Nl, threshold θ, the current time l, possible world W |
| Output: task assignment set T.assign. |
|
For example, the list of tasks at time l1 is shown in Figure 2a, and the list of volunteer nodes at time l1 is shown in Figure 2b. List of tasks at time l1 + 1 is shown in Figure 3a, and the list of volunteer nodes at time l1 + 1 is shown in Figure 3b. For the easy calculation, we assume that the nodes and tasks are not updated at other times, and the value of θ is 0.5. The completion risk of t3 is 0.67 according to Algorithm 3, which is assigned at time l1 + 3. According to Algorithm 4, t3 is deleted from the task set Tl. According to Algorithm 1, the assignment of the remaining tasks is shown in Figure 7. According to the task allocation of Figure 7, the tasks can be completed within deadline constraint are t1, t2, t4 and t5. Figure 7 shows that the IDCS algorithm can maximize the number of the completed tasks within deadline constraint.
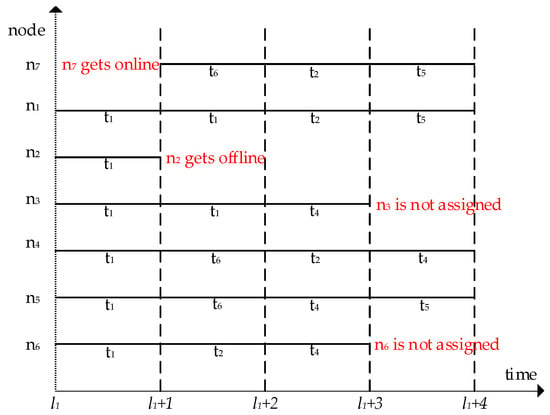
Figure 7.
The execution processes of the improved dispatch constraint scheduling (IDCS) algorithm.
5. Experimental Evaluation
In this section, we first implement the DPDS algorithm and the IDCS algorithm, and use static task set and dynamic task set to compare the performance between the MOC algorithm and our proposed algorithms. The volunteer computing used in the experiment consists of one master node and fifty volunteer nodes. All nodes are configured with Intel Core i7 4790 CPU@3.4GHZ, 8GB DDR3 memory, 1TB hard disk and Windows 10 operating system. To be closer to the real volunteer computing environment and meet the heterogeneity of volunteer computing, 10–20 threads are opened on each host to simulate volunteer nodes, thus, whose number will be between 500 and 1000. Task data fragmentation size is 64 MB, and the parameter nj.ability is tested by the server sending the applet to the node before assigning tasks.
Specifically, to achieve the heterogeneity of nodes, we use a program to specify different CPU cores for some specific threads. In this way, scheduling delays can be reduced by specifying the CPU core for some specific threads. Thus, the performance of some specific threads will be improved.
5.1. Experimental Results and Analysis of the Static Task Sets
In the experiment of the static task set, three common tasks are used: Word frequency statistics, inverted index and distributed Grep. The input files are the data and dump files provided by Wikipedia (the main contents are entries, templates, picture descriptions and basic meta-pages, etc.). We mainly consider the influence of three main parameters as follows:
- The task set scale which is the number of tasks included in the task set T.
- The average size of tasks in task set T is measured by the number of task input file fragments.
- The average completion time of tasks in T.
We assume that the size of a task set fragment is 64 MB, the threshold θ is 0.5 and the completion time of each task fragment is 70 s. The task amount of word frequency statistics for a fragment (unit) is 40 s, the task amount of inverted index for a fragment (unit) is 80 s, and the task amount of distributed Grep for a fragment (unit) is 120 s. The average completion time of the tasks in T is 80 s, denoted by L. For any task in T, t. deadline is a random value in the interval [0.5L, 1.5L]. Table 2 shows the default values and ranges of the main parameters. Table 2 shows the default values and ranges of the main parameters.

Table 2.
Experimental default parameters.
In this paper, the number of the completed tasks is the primary performance index. In addition, this paper also uses the completion rate to measure the performance of the algorithm more comprehensively. The completion rate is defined as follows:
completion rate = number of tasks completed on time/number of tasks in the task set T,
5.1.1. The Impact of Average Size of Tasks
As shown in Figure 8, we test the impact of the different average size of tasks on the performance of the algorithms. It can be seen that IDCS perform the best among the three algorithms in both the number of the completed tasks and completion rate, and the MOC algorithm is slightly worse than the IDCS algorithm. The DPDS algorithm is much less efficient. This is because the IDCS algorithm divides the task priority, which can ensure that the IDCS algorithm completes the less expensive task first, and discards the risky task. In contrast, the DPDS algorithm can’t fully utilize the computing power of the volunteer computing system. Even if it encounters the task that is expensive, the DPDS algorithm will also calculate it, which causes a waste of computing resources. Since the objective of MOC is complete each task before its deadline, it is less efficient than the IDCS algorithm. Moreover, since the computing power of the system is fixed in a certain period of time, the performance of three algorithms decreases as the average size of tasks increases.
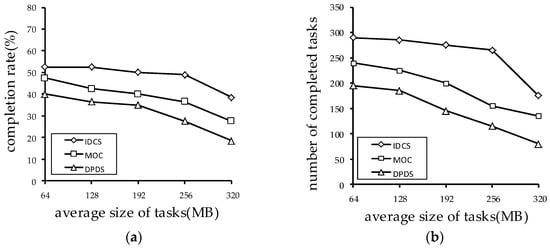
Figure 8.
The impact of the average size of the tasks on the performance of the algorithms: (a) The impact of average size of tasks on task completion rate; (b) the impact of the average size of tasks on number of the tasks completed.
5.1.2. The Impact of Task Set Scale
In Figure 9, we analyze the impact of task set scale. It can be seen that with the increase of the task set scale, the number of the completed task of the three algorithms finally tends to be stable. This is because the number of nodes does not increase, but the number of tasks increases. Therefore, the number of the completed tasks by VN is changeless.
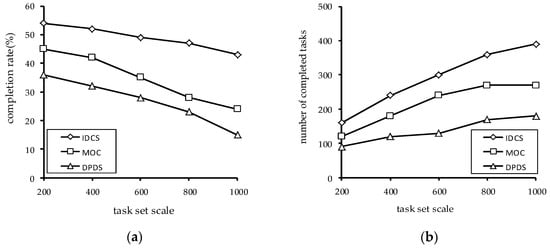
Figure 9.
The impact of task set scale on the performance of the algorithms: (a) The impact of task set scale on task completion rate; (b) the impact of the task set scale on the number of tasks completed.
At the same time, it can be seen from Figure 9b that the larger the size of the task set scale is, the more the number of tasks completed by the IDCS algorithm is. This is mainly because IDCS can make full use of computing resources to discards the tasks with high risks, which improves the number of tasks completed.
The task completion rate of the three algorithms decreases with the task set scale increase. This is because the number of tasks has increased, but there has been no relative increase in computing resources. In Figure 9a, it is obvious that the increase of task set scale has the least impact on IDCS algorithm.
5.1.3. The Impact of the Number of Volunteer Nodes
Figure 10 shows the impact of the number of volunteer nodes on the performance of the algorithms. It can be seen that the task completion rate increases when the number of volunteer nodes increases, and the number of the completed tasks also increases. This is because the more nodes there are, the more computing power there is. At the same time, the IDCS algorithm is superior to the MOC algorithm and DPBS algorithm in both task completion rate and the number of the completed tasks.
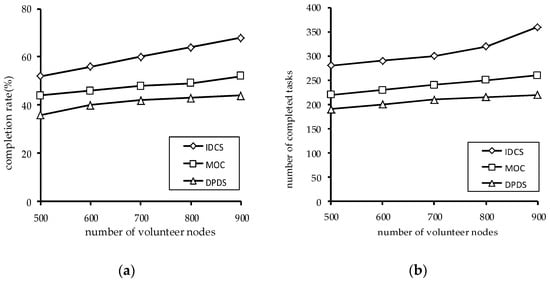
Figure 10.
The impact of the number of volunteer nodes on the performance of the algorithms: (a) The impact of the number of volunteer nodes task completion rate; (b) the impact of the number of volunteer nodes on the number of tasks completed.
5.2. Experimental Results and Analysis of Dynamic Task Sets
In order to be closer to the real application scenario, this section uses a dynamic set of application tasks. The experiment generated five task sets, and each task set has an average of 100 tasks. The average size of each task is four units. The deadline for each task is set to a random value within 200–400 s after the task arrives. Other parameters settings are the same as the Section 5.1. In the experiment, we assume a task request was submitted to the server every two minutes and the task completion status is tested every 100 min. Figure 11 shows the number of the completed tasks and the task completion rate of the three algorithms.
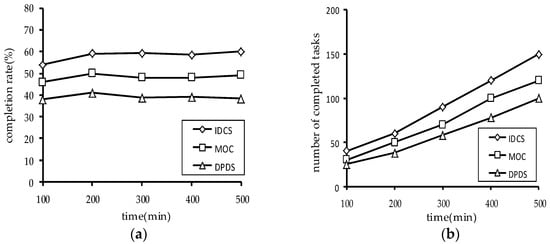
Figure 11.
Performance comparisons of the three algorithms on the dynamic task set: (a) Comparison of task completion rate; (b) comparison of the number of tasks completed.
Figure 11 shows the experimental results. It can be seen that the IDCS algorithm has obvious advantages on dynamic task sets, regardless of the number of the completed tasks or the task completion rate. Through the above experimental results, the validity of the IDCS algorithm proposed in this paper is further proved.
6. Conclusions
In this paper, we propose two novel dynamic task scheduling algorithms to solve the task scheduling problem with deadline constraint in VC platforms. One is the DPDS algorithm, and the other is the IDCS algorithm. In addition, by analyzing the characteristics of tasks and volunteer nodes in VC platforms, this paper uses a new risk prediction model in IDCS algorithm, which can predict the completion risk of each task. A lot of experiments based on a real-world dataset demonstrate that our proposed algorithms can solve the dynamic task scheduling problem with deadline constraint. And compared to the existing algorithms, the IDCS algorithm can maximize the number of task completions within the deadline. The task scheduling problem in VC platforms is very important, and further study should be done to improve the scheduling algorithm. In future, we will consider more factors that may affect task scheduling in VC platforms.
Author Contributions
L.X. designed and wrote the paper; J.Q. supervised the work; L.X. and W.Z. performed the experiments; S.L. analyzed the data. All authors have read and approved the final manuscript.
Acknowledgments
This work was supported by the National Social Science Foundation of China (No. 15BYY028) and Dalian University of Foreign Languages Research Foundation (No. 2015XJQN05).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Anderson, D.P. Volunteer computing: The ultimate cloud. ACM Crossroads 2010, 16, 7–10. [Google Scholar] [CrossRef]
- Anderson, D.P.; Cobb, J.; Korpela, E.; Lebofsky, M.; Werthimer, D. SETI@home: An experiment in public-resource computing. Commun. ACM 2002, 45, 56–61. [Google Scholar] [CrossRef]
- Beberg, A.L.; Ensign, D.L.; Jayachandran, G.; Khaliq, S.; Pande, V.S. Folding@home: Lessons from Eight Years of Volunteer Distributed Computing. In Proceedings of the 23rd IEEE International Symposium on Parallel & Distributed Processing (IPDPS 2009), Rome, Italy, 23–29 May 2009; pp. 1–8. [Google Scholar]
- Adambourdarios, C.; Wu, W.; Cameron, D.; Lancon, E.; Filipčič, A. ATLAS@Home: Harnessing Volunteer Computing for HEP. J. Phys. Conf. Ser. 2015, 664, 022009. [Google Scholar]
- Cunsolo, V.D.; Distefano, S.; Puliafito, A.; Scarpa, M. Cloud@Home: Bridging the Gap between Volunteer and Cloud Computing. In Proceedings of the Emerging Intelligent Computing Technology and Applications: 5th International Conference on Intelligent Computing (ICIC 2009), Ulsan, South Korea, 16–19 September 2009; pp. 423–432. [Google Scholar]
- Li, W.; Guo, W. The Competence of Volunteer Computing for MapReduce Big Data Applications. In Proceedings of the 4th International Conference of Pioneering Computer Scientists, Engineers and Educators (ICPCSEE 2018), Zhengzhou, China, 21–23 September 2018; pp. 8–23. [Google Scholar]
- Filep, L. Model for Improved Load Balancing in Volunteer Computing Platforms. In Proceedings of the 15th European, Mediterranean, and Middle Eastern Conference on Information Systems (EMCIS 2018), Limassol, Cyprus, 4–5 October 2018; pp. 131–143. [Google Scholar]
- Chen, C.H.; Lin, J.W.; Kuo, S.Y. MapReduce scheduling for deadline-constrained jobs in heterogeneous cloud computing systems. IEEE Trans. Cloud Comput. 2018, 6, 127–140. [Google Scholar] [CrossRef]
- Xiao, M.; Wu, J.; Huang, L. Multi-task assignment for crowdsensing in mobile social networks. In Proceedings of the 2015 IEEE Conference on Computer Communications (INFOCOM 2015), Hong Kong, China, 26 April–1 May 2015; pp. 2227–2235. [Google Scholar]
- Buyya, R.; Murshed, M. Gridsim: A toolkit for the modeling and simulation of distributed resource management and scheduling for grid computing. Concurr. Comput. Pract. Exp. 2002, 14, 1175–1220. [Google Scholar] [CrossRef]
- Guo, F.; Yu, L.; Tian, S. A workflow task scheduling algorithm based on the resources’ fuzzy clustering in cloud computing environment. Int. J. Commun. Syst. 2015, 28, 1053–1067. [Google Scholar] [CrossRef]
- Anderson, D.P. Emulating volunteer computing scheduling policies. In Proceedings of the 25th IEEE International Parallel and Distributed Processing Symposium Workshops and PhD Forum, Anchorage, AK, USA, 16–20 May 2011; pp. 1839–1846. [Google Scholar]
- Amini Salehi, M.; Smith, J.; Maciejewski, A.A. Stochastic-based robust dynamic resource allocation for independent tasks in a heterogeneous computing system. J. Parallel Distrib. Comput. 2016, 97, 96–111. [Google Scholar] [CrossRef]
- Maheswaran, M.; Siegel, H.J. A dynamic matching and scheduling algorithm for heterogeneous computing systems. In Proceedings of the 7th Heterogeneous Computing Workshop (HCW’98), Orlando, FL, USA, 30 March 1998; pp. 57–69. [Google Scholar]
- Topcuoglu, H.; Hariri, S.; Wu, M.Y. Performance-effective and low-complexity task scheduling for heterogeneous computing. IEEE Trans. Parallel Distrib. Syst. 2002, 13, 260–274. [Google Scholar] [CrossRef]
- Blythe, J.; Jain, S.; Deelman, E.; Gil, Y.; Vahi, K.; Mandal, A.; Kennedy, K. Task scheduling strategies for workflow-based applications in grids. In Proceedings of the IEEE International Symposium on Cluster Computing and the Grid, Cardiff, Wales, 9–12 May 2005; pp. 759–767. [Google Scholar]
- Poola, D.; Garg, S.K.; Buyya, R.; Yang, Y.; Ramamohanarao, K. Robust Scheduling of Scientific Workflows with Deadline and Budget Constraints in Clouds. In Proceedings of the 28th IEEE International Conference on Advanced Information Networking & Applications, Victoria, BC, Canada, 13–16 May 2014; pp. 858–865. [Google Scholar]
- Zomaya, A.Y.; Teh, Y. Observations on Using Genetic Algorithms for Dynamic Load-Balancing. IEEE Trans. Parallel Distrib. Syst. 2001, 12, 899–911. [Google Scholar] [CrossRef]
- Page, A.J.; Naughton, T.J. Dynamic Task Scheduling using Genetic Algorithms for Heterogeneous Distributed Computing. In Proceedings of the 18th IEEE International Parallel and Distributed Processing Symposium, Denver, CO, USA, 4–8 April 2005; p. 8. [Google Scholar]
- Kang, Q.; He, H.; Wei, J. An effective iterated greedy algorithm for reliability-oriented task allocation in distributed computing systems. J. Parallel Distrib. Comput. 2013, 73, 1106–1115. [Google Scholar] [CrossRef]
- Sahni, J.; Vidyarthi, D. A Cost-Effective Deadline-Constrained Dynamic Scheduling Algorithm for Scientific Workflows in a Cloud Environment. IEEE Trans. Cloud Comput. 2015, 6, 2–18. [Google Scholar] [CrossRef]
- Cheng, D.; Rao, J.; Jiang, C.; Zhou, X.B. Resource and Deadline-Aware Job Scheduling in Dynamic Hadoop Clusters. In Proceedings of the 30th IEEE International Parallel and Distributed Processing Symposium, Chicago, IL, USA, 23–27 May 2015; pp. 956–965. [Google Scholar]
- Coninck, E.D.; Verbelen, T.; Vankeirsbilck, B.; Bohez, S.; Simoens, P.; Dhoedt, B. Dynamic Auto-scaling and Scheduling of Deadline Constrained Service Workloads on IaaS Clouds. J. Syst. Softw. 2016, 108, 101–114. [Google Scholar] [CrossRef]
- Kondo, D.; Anderson, D.P.; Vii, J.M. Performance Evaluation of Scheduling Policies for Volunteer Computing. In Proceedings of the 15th IEEE International Conference on E-science and Grid Computing, Bangalore, India, 10–13 December 2007; pp. 1–10. [Google Scholar]
- Anderson, D.P.; McLeod, J. Local scheduling for volunteer computing. In Proceedings of the 21th IEEE International Parallel and Distributed Processing Symposium, Long Beach, CA, USA, 26–30 March 2007; pp. 1–8. [Google Scholar]
- Guler, H.; Cambazoglu, B.B.; Ozkasap, O. Task allocation in volunteer computing networks under monetary budget constraint. P2P Netw. Appl. 2015, 8, 938–951. [Google Scholar] [CrossRef]
- Ghafarian, T.; Deldari, H.; Javadi, B. Cycloid Grid: A proximity-aware P2P-based resource discovery architecture in volunteer computing systems. Future Gener. Comput. Syst. 2013, 29, 1583–1595. [Google Scholar] [CrossRef]
- Ghafarian, T.; Javadi, B. Cloud-aware data intensive workflow scheduling on volunteer computing systems. Future Gener. Comput. Syst. 2015, 51, 87–97. [Google Scholar] [CrossRef]
- Sebastio, S.; Gnecco, G.; Bemporad, A. Optimal Distributed Task Scheduling in Volunteer Clouds. Comput. Oper. Res. 2016, 81, 231–246. [Google Scholar] [CrossRef]
- Lu, Y.; Wang, L.Z.; Chen, H.M.; Zhao, L.H. Spatial Co-Location Patterns Mining over Uncertain Data Based on Possible Worlds. J. Comput. Res. Dev. 2010, 47, 215–221. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).