Abstract
Afforestation has been a popular restoration procedure for spoil heaps in the sites affected by coal open-cast mining in the Czech Republic. Forest replantation is a frequent restoration variant when spoil heaps are recovered, but unreclaimed sites are often left to spontaneous succession. Studies on the dynamics of such restored forests are missing, and the evidence of restored forests with respect to their recreation value is also sporadic. To study the dynamics and management of restored forests—both replanted and recovered by spontaneous succession—on spoil heaps, we used a matrix growth model, which accounts for harvest, artificial and natural regeneration, and recreation value of these forest stands. The model calibration was performed on data from 250 inventory plots distributed across the Velká Podkrušnohorská spoil heap and the Matyáš spoil heap in the Sokolov brown-coal mining area. The growth model was applied on six restored forest types to simulate—over 65 years with a 10-year cutting cycle—the effect of various management regimes of thinning on their recreation value and aboveground biomass (AGB). The results indicate that initial planting density and stand type have an effect on the dynamics of restored forest stands in the short-term horizon. Applying the thinning management resulted in an increase in recreation value for all types of restored stands, while AGB decreased.
1. Introduction
Surface mining causes extensive changes in land cover and biodiversity and forms a completely new landscape in the area affected by mining. The ecosystems in the whole mining area, not just in the mine, are covered up with overburden material excavated from the mine. During the operation of open-cast coal mines, the overlying spoil material above the coal layer is removed and deposited in spoil heaps. Therefore, the rehabilitation of the post-mining landscape is crucial not only for restoring biomass production, but also for the restoration of both the ecosystem structure and functions of such areas [,].
Extensive areas where mining activity terminates are usually transformed into forests, agricultural land, and artificial lakes. A technical reclamation is a traditional approach to restoration, which is focused on the restoration of soil productivity and production functions of the landscape (forestry, agriculture), or in the case of hydric reclamation, to the landscaping importance of water bodies []. From an ecological perspective, reclamation should enable the restoration of original ecosystems, as well as their functions and services. In this way, there is a strong relation between reclamation and ecosystem services [,].
The concept of ecosystem services can be used as an evaluation framework and for identification of the appropriate methods of landscape restoration in order to achieve targets related to both ecosystem health and the provision of ecosystem services to society [,]. In recent decades, a number of studies have looked at reclamation from a broader perspective, taking into account one or more aspects of ecosystem services. In addition to restoring productivity, they also consider other functions and important ecosystem services that the restored sites are to perform, in particular soil protection, climate regulation, carbon sequestration, water retention, biodiversity, or cultural functions such as recreation [,,,,,,,,,,].
Especially when post-mining areas are located in the immediate vicinity of human settlements, the recreation functions of the restored ecosystems become more important. This is the case of the post-mining area of the Sokolov brown-coal basin—the region in the west of the Czech Republic, where mining and subsequent reclamation of the affected land has been carried out since the 1960s and is going to continue as a result of the legal obligation of mining companies to recultivate the land before it is handed over for further use []. Because afforestation has been a popular reclamation practice for almost six decades, there are abundant reclaimed forests in the vicinity of several towns and villages in the Sokolov mining area that are particularly suitable for short-term recreation.
However, many of these restored forests were left to grow without appropriate forest management, therefore, they are little used for recreation. As found by Braun Kohlová et al. [,], the attractiveness of the restored forests on the Sokolov spoil heaps for recreation is significantly lower than conventionally managed forest stands. As implied by Braun Kohlová et al. [], to increase the recreation value of restored forest ecosystems, it is necessary to implement suitable silvicultural treatment at a young and middle age of these stands.
An appropriate way to address this problem is to develop a forest growth model—and calibrate it using empirical data—that allows the study of the dynamics of restored forests and the evaluation of the thinning management alternative, including the effect of harvesting on the recreation value of these reclaimed stands. Although Frouz et al. [,] carried out the vegetation surveys with the basic dendrometric measurement at the largest Sokolov spoil heap—Velká Podkrušnohorská heap—in 2006 and in 2015, respectively, the small sample of plots—28 sampling plots in 2006 and 8 plots in 2015—was not sufficient for the parametrization of the growth model. In 2018, Cienciala et al. [] conducted a representative one-time forest survey on 250 inventory plots at the Velká Podkrušnohorská heap and the adjacent Matyáš heap. As the inventory survey was stratified according to three growth stages and seven forest stand types, the data are applicable to a growth model that allows the prediction of stand characteristics structured according to its stages or sizes.
A matrix model of forest growth—firstly elaborated in the seminal works of M.B. Usher [,]—is a common approach when the stand-level dynamics on a size-structured population is simulated. Matrix growth models with the Usher matrix are among the empirical dynamic models that are widely used in forest growth modeling because of their ability to provide accurate and detailed simulations of forest stand dynamics structured according to tree-size distribution [].
Compared to the stand-level and size-structured models, individual-based models are applied when the trajectories, spatial heterogeneity of individual trees, and inter-tree competition are accounted for []. However, individual-based models require a lot more data than stand-based models []. On the contrary, the shortcomings of matrix models are seen in the arbitrary division of size classes and the inability to incorporate the variability between trees of the same size class []. Detailed comparison and classification of growth models can be found in Liang and Picard [] and Vanclay [].
Many different types of matrix growth models were developed—with a wide range of forestry applications and across various types of forest ecosystems—and their linear and non-linear specifications from constant-parameter matrices to matrix models with stochastic vital rates or a geospatial dependence [,,]. More recently, matrix growth models, due to their accuracy in predicting forest population dynamics, have been adjusted to account for climate variability, various forest management practices, and environmental disturbances (see []). An example of natural or anthropogenic disturbances are wild or managed fires. A matrix model was used in several applications to study forest restoration and dynamics of forest stands subject to fire [,]. Nevertheless, a study of the forest dynamics of restored forest stands on spoil heaps in the post-mining areas—as an example of anthropogenic disturbance—by matrix growth models is missing.
To expand the existing applications of matrix growth models to restored forest ecosystems on spoil heaps, we adopt a density-dependent matrix growth model with harvest previously developed by Buongiorno and Michie [] and Liang et al. [] and with its extension by artificial regeneration made by Liang []. More specifically, we applied the matrix growth model calibrated on forest inventory data [] from the Velká Podkrušnohorská and Matyáš spoil heaps in order to explore the short-term dynamics of seven types of restored forests—alder, deciduous, larch, pine, spruce, and mixed coniferous-deciduous replantation, and spontaneous succession that represent predominant forest types in the Sokolov mining area. Subsequently, we used the growth model to evaluate various management options (initial planting, thinning regime) and investigate how the respective management regime affects the recreation value and aboveground biomass of restored forest. Here, we hypothesize that thinning will increase the recreation value of the forest regardless of the restored stand type and the intensity of thinning without any significant decrease in the stock of aboveground tree biomass in the short-term at the same time.
2. Materials and Methods
2.1. Study Area
The Sokolov brown-coal mining area is situated in the western part of the Czech Republic, near the German border. The areas of interest are spoil heaps situated in the neighborhood of Sokolov town, which began to be created during the 1960s by the deposition and shaping of the overburden material excavated from up to 200 m during brown-coal open-cast mining. The geographical location of the Sokolov spoil heaps in the Czech Republic is illustrated in Figure 1. So far, about 7000 ha of land on 10 main spoil heaps in the Sokolov mining area have been recultivated, which accounts for 75% of the area affected by coal mining there. The spoil heaps are different in size; the smallest Velký Riesl heap occupies the area of 16 ha, while the largest Velká Podkrušnohorská heap occupies 1900 ha []. The geographical distribution of the Sokolov spoil heaps can be found in Braun Kohlová et al. [] (p. 4).
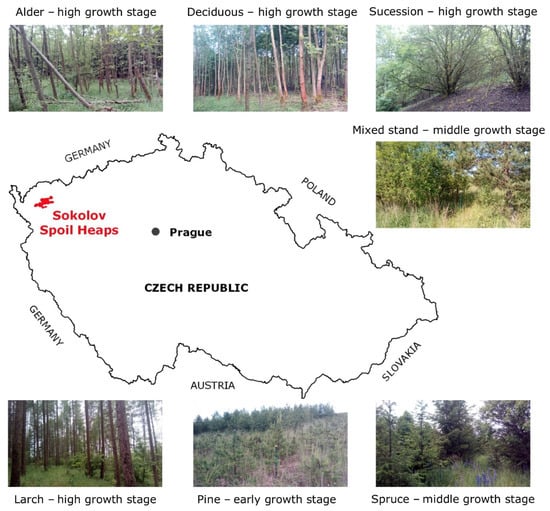
Figure 1.
The geographical location of the Sokolov spoil heaps in the Czech Republic and the visualization of seven types of restored forest stands.
The heaps’ substrate is composed of alkaline tertiary clays—so-called cypris formation—mostly consisting of clay minerals such as illite, kaolinite, and montmorillonite; non-clay minerals such as siderite and calcite are also often present.
More than 53 thousand inhabitants live in the vicinity of the spoil heaps, namely, in three towns, including the town of Sokolov with 23 thousand inhabitants and 14 villages.
Restored forests on the spoil heaps are mainly even-aged with stands represented by one dominant tree species; there is also a mosaic of deciduous and coniferous stands, and some stands are also mixed. The restored forest stands on spoil heaps are either replanted forests with one dominant tree species or some spots are unreclaimed and left for spontaneous succession. Heaps with filled overburden were usually leveled and compacted before stands were replanted, while the terrain of unreclaimed sites was left unleveled. The surface of unreclaimed sites is characterized by numerous ridges and depressions and a series of parallel waves with a 2 m height originally created by heaping machinery during the depositing overburden on the heap [].
Inventory plot data [] measured at two Sokolov spoil heaps—Matyáš heap and Velká Podkrušnohorská heap—were used to calibrate the growth matrix model for a subsequent simulation of forest dynamics with respect to various forest restoration managements. The Matyáš heap with an area of 167 ha is the smaller one of both soil heaps, the neighboring Velká Podkrušnohorská heap—as the largest spoil heap in the Sokolov brown-coal mining district—has an area of 1939 ha and is about 10 km long and 2.5 km wide with a height up to 200 m above the original terrain. The altitude of the study site is in the range of 409–604 m a.s.l. The mean annual precipitation and temperature are 800 mm and 7 °C, respectively []. The geographical distribution of the Matyáš heap and Velká Podkrušnohorská heap is shown in Figure 2.
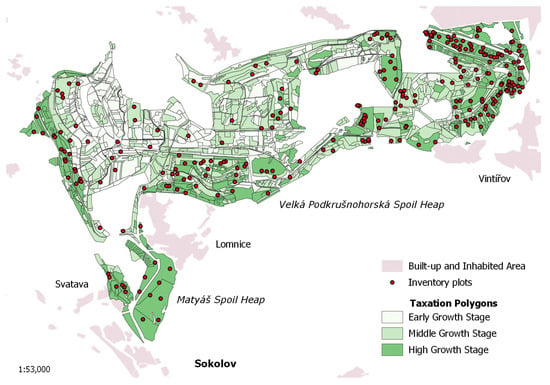
Figure 2.
The geographical distribution of inventory plots and taxation polygons with corresponding growth stages of restored forest stands on the Velká Podkrušnohorská spoil heap and Matyáš spoil heap.
Replanted forest stands on the Velká Podkrušnohorská and Matyáš heap mainly consist of one tree species or two tree species of the same genus that were combined during replantation. Mostly, tree species such as Black alder (Alnus glutinosa (L.) Gaertn.), Norway spruce (Picea abies (L.) H. Karst.), European ash (Fraxinus excelsior L.), Scotch pine (Pinus sylvestris L.), European larch (Larix decidua Mill.), European aspen (Populus tremula L.), Austrian pine (Pinus nigra J. F. Arnold), English oak (Quercus robur L.), and small-leaved linden (Tilia cordata Mill.) have been used for replanting. Silver birch (Betula Pendula Roth) and goat willow (Salix caprea L.) are successional trees that predominate on unreclaimed sites. The overview of the relative representation of individual tree species determined from forest inventory on the investigated spoil heaps is shown in Table A1 in Appendix A.
Restored forest stands growing on the Velká Podkrušnohorská and Matyáš heaps are young and middle-aged forests. Therefore, for the forest inventory purposes, we categorized these stands according to three growth stages: early growth stage with a height of up to 2 m (10–15 years old), middle growth stage of a height from 2 to 10 m (10–30 years old), and high growth stage of a height above 10 m (30–60 years old). The geographical distribution of forest stands on the Velká Podkrušnohorská and Matyáš heap corresponding to their growth stages is illustrated in Figure 2. As prevailing stand types, stands with a dominant representation of alder, larch, pine, spruce, long-lived deciduous trees, mixed coniferous–deciduous stands, and stands with a spontaneous succession are present on the heaps (see their visualization in Figure 1). The classification of individual tree species into the prevailing stand types is given in Table A2 in Appendix A.
In addition to trees, there are also shrubs and herbaceous vegetation in the stands. Among shrub species, European black elder (Sambucus nigra L.), European hawthorn (Crataegus oxyacantha L.) and common snowberry (Symphoricarpos albus L.) are the most widespread species in the shrub understory of restored forest stands. Other shrub species are also present, such as wild privet (Ligustrum vulgare L.), alder buckthorn (Frangula alnus Mill.), dog rose (Rosa canina L.), guelder rose (Viburnum opulus L.), common dogwood (Cornus sanguinea L.), Turkish hazel (Corylus colurna L.), bird cherry (Prunus padus L.), blackthorn (Prunus spinosa L.), common ninebark (Physocarpus opulifolius Maxim.), European buckthorn (Rhamnus cathartica), and cornelian cherry (Cornus mas L.), but their occurrence is rather rare. Most plant species, and at the same time the largest coverage of the herbaceous layer (e. g. Festuca ovina agg., Pastinaca sativa, Festuca gigantea, Crepis biennis, Epipactis helleborine, Melilotus albus), are in the alder, larch, and pine stands (see [] for more details).
2.2. Forest Inventory Data
The matrix growth model was calibrated on data from a forest inventory survey—conducted by Cienciala et al. []—with a sample of 250 inventory plots (see Figure 2), which were randomly distributed across the Velká Podkrušnohorská and Matyáš heap. The inventory plots included restored forests, both stands established by planting and those created by spontaneous succession. In both cases, the stands were unmanaged—left to grow without appropriate forestry management since the planting or colonization with successional trees—forests until the time of inventory.
The inventory survey was planned as a single survey, i.e., with one-time dendrometric measurement on each plot. Each inventory plot was a circular plot composed of three circular zones with the following size criteria that a tree had to meet in order to be subject to a dendrometric measurement. Trees with DBH (diameter at breast height) below 7 cm and with tree height above 25 cm were measured in the zone delimited by the inner circle (radius of 2 m, area 12.6 m2). The trees above DBH > 7 cm were measured in the zone bounded by the middle cycle (radius of 5 m, area 78.5 m2) and trees above DBH > 15 cm were measured in the zone delimited by the outer circle (radius of 10 m, area 314.2 m2).
Tree and stand characteristics on the sample plots were measured throughout the year 2018. On each sample plot, the basic dendrometric measurement was taken for each individual tree that corresponded to the sampling design. Tree data collected include species, diameter, height, status (type of recruitment—natural or artificial, live, or dead standing tree), basal area, and dry matter of aboveground tree biomass. On the plot-level, stem density, natural and artificial recruitment density, total basal area, total AGB, number of tree and shrub species, total cover of shrub understory on a plot, and the age of the stand in years were derived for each plot. The list of stand characteristics and their description is provided for illustration in Table A3 in Appendix B.
Each plot was assigned to one of three growth phases: (i) early—stand up to a height of 1.5–2 m, (ii) middle—stand in the range of height of 2–10 m, and (iii) high—stand above 10 m in height (alder stand above 6 m in height). In addition to the growth stage differentiation, the plot was classified with respect to the seven forest stand types, i.e., according to the dominant tree species prevailing on the given inventory plot. The assignment of individual tree species to the appropriate forest type category is defined in Table A2 in Appendix A. Specifically, the following categories of forest types were defined—the conditions for classifying the inventory plots to the defined forest types are given in parentheses: (i) alder (alder representation of 70% and more in the stand), (ii) long-lived deciduous (≥70%), (iii) spontaneous succession (representation of succession trees >50%), (iv) larch (≥70%), (v) pine (≥70%), (vi) spruce (≥70%), and (vii) mixed coniferous–deciduous stands (if none of the above conditions are met).
While the inventory plots assigned to early and middle growth stages made up 7% and 29% of the sample, respectively, plots with trees in high growth stage accounted for 64% of the sample. The most frequent in the sample were the plots classified as mixed coniferous–deciduous, succession, and pine stand with 22%, 20%, and 15%, respectively. Plots classified as alder and long-lived deciduous stand equally accounted for 12%, plots with spruce and larch stands made up 11% and 8%, respectively.
Summary statistics of stand characteristics for plot-level variables are given in Table A4 and mean values for other stand characteristics are presented in Table A5 in Appendix B. At the same time, statistics are presented for individual forest types. At the plot-level, mean tree density was highest for spruce forest stands (6300 trees∙ha−1), the density of succession, pine, and larch stands was very similar. The mean stand recruitment was the highest for succession; this also applies for natural recruitment. Spruce stands had the highest mean artificial recruitment. Deciduous forest stands had on average the largest both basal area and aboveground tree biomass, while spruce stands had the lowest values of these stand characteristics. Deciduous stands were the oldest on average (34 years), while pine stands were the youngest (17 years). Spontaneous succession stands had the highest tree diversity on average, while alder stands had the lowest. The mean shrub species diversity was highest in deciduous stands and lowest in spruce stands. The coverage of shrub understory exceeding 22%, was measured in alder stands.
Summary statistics of tree characteristics for tree-level variables for all stands and according to forest type category are given in Table A6 in Appendix B. At the tree-level, succession stands had the largest mean values of DBH and aboveground biomass, while pine stands had the lowest. The average tree height was the highest for deciduous stands (14.4 m); pine stands were the lowest (8.5 m). In contrast, pine stands had the lowest mortality rate on average, while mixed coniferous–deciduous stands had the highest mortality.
Mean values of stem density per hectare based on inventory plot data differentiated according to the DBH classes—we implemented 4 DBH classes in the growth model with the first DBH class representing recruitment: (i) 0–2 cm, (ii) 2–7 cm, (iii) 7–14 cm, and (iv) 14 cm and more—and with respect to three growth stages and seven forest types are shown in the three graphs in Figure 3. Across all inventory plots, tree density decreases with diameter classes. Similarly, a decreasing tree density was observed for succession, deciduous, and spruce stands. In contrast, alder and pine stands reached the highest stem density in the second diameter class; larch stands had the highest density in the first two classes. Differentiation according to the growth stages shows that the stem density was the highest in the first diameter class for the early growth stage. Trees in the third and fourth DBH class are no longer observed for this growth stage. Plots of the middle growth stage reached maximum density in the second diameter class. The number of trees inventoried in the fourth DBH class was negligible for this growth stage. As with all forest stands, the distribution of tree density shows a decreasing trend for the high growth stage.
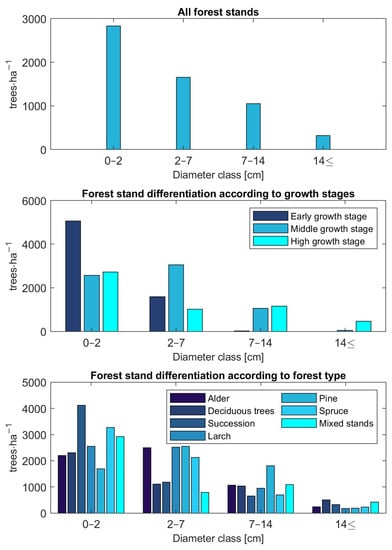
Figure 3.
Tree density distribution by diameter classes and growth stages and forest types.
2.3. Data on Attractiveness for Recreation
Data on the recreation value of restored forest sites came from an environmental preference study [], in which several representative reclaimed forest stands, including spontaneous succession stands, located on spoil heaps in the Sokolov brown-coal basin were evaluated for their recreational values. The study used a discrete choice experiment (DCE), in which the participants evaluated restored stands in response to the particular photography of a given stand as perceptual stimuli. In the DCE, the measure of recreation value was represented by a person’s choice of a location with restored forests for walking in response to particular visual stimuli. The design of choice task in the DCE consisted of two hypothetical localities for recreation represented by different types of restored forest stands and a reference option of staying at home.
The survey was carried out in 2016 as an online questionnaire, which included the DCE. The resulting sample of 869 respondents consisted of the residents living in the neighborhood of spoil heaps and open-cast mines (n = 629) and residents from the Central Bohemian region (n = 240), which represented a control population [].
The questionnaire used photographs of seven forest stands representing different reclamation practices and different growth phases. Spruce, pine, and alder replantation at the age of 35 years represented the plantation practice and stands of the middle growth stage. A 15-year-old spruce replantation was also included in the DCE as the plantation of the early growth stage. Spontaneous succession as an example of an unreclaimed forest site was another type of restored forest included in the DCE and was represented by three age and growth stage classes (15, 35, 55 years, and early, middle, high growth phase, respectively).
The mean recreation values—attractiveness for recreation—expressed as the mean probability of a person’s choice of a given type of restored forest for a one-hour walk are presented in Table A5 in Appendix B, with the highest recreation value for pine replantation and sites restored with spontaneous succession. Conversely, alder stands had a very low recreation value.
2.4. Matrix Growth Model and its Structure
The model used for the simulation of the dynamics of restored forests growing at the Sokolov spoil heaps is a density-dependent matrix growth model developed by Liang []. This growth model is an extension of previous models [,] and takes into account not only harvest and natural regeneration, but also artificial recruitment. To express the dependence of the projection matrix on stand density, the tree growth, mortality, and artificial recruitment are functions of the stand basal area [].
In the subsequent notations, t refers to time in years (, to a type of restored forest stand, and to a diameter class. We consider the model accounting for seven types of restored forests , as they are defined in the description of forest inventory survey. Specifically, we distinguish between alder, long-lived deciduous, spontaneous succession, larch, pine, spruce, and mixed coniferous–deciduous stands. Each stand is structured into four diameter classes specified as follows: (i) 0–2 cm, (ii) 2–7 cm, (iii) 7–14 cm, and (iv) above 14 cm.
At the stand level, the state of forest according to its diametric structure is represented by a column vector that expresses the number of live trees per hectare of restored forest type and diameter class at time . The matrix growth model predicts the state of forest stand in year with respect to the state of forest stand (e.g., tree density per hectare) in year [,]. The growth model [] noticed in a matrix form is as follows:
where is an Usher projection matrix or also growth matrix, is a vector of harvest, is a vector of natural regeneration, is a vector of artificial recruitment, and is a vector of random errors. The initial state of forest stand is given by a vector .
The state-dependent growth matrix is a block matrix:
with seven submatrices on the main diagonal. Each block of the growth matrix represents the projection matrix of order 4 × 4 for a given type of restored forest stand , where:
that describes how the trees of each restored forest type grow or die between and .
The parameters and of are vital rates representing the transition probability of ingrowth and upgrowth, respectively. The parameter of ingrowth is the probability that a tree of restored forest type and diameter class survives and stays in the same diameter class j between and . The parameter of upgrowth is the probability that a tree of restored forest type and diameter class survives and grows into the diameter class between and .
Let the parameter denote the mortality rate representing the probability that a tree of forest stand and diameter class dies between and . Then, the transition parameters and are related as follows:
Vector represents natural recruitment between time and . Vector is a subvector of with zero elements except the first one . This regeneration parameter defines the annual number of trees of restored forest type naturally recruited in the first DBH class (0–2.0 cm) between and , where:
Vector represents state-dependent artificial regeneration between time and . Similar to natural regeneration, vector is a subvector of with zero elements except the replanting parameter in the first position. This parameter expresses the annual number of trees of restored forest type artificially recruited in the smallest diameter class between and , where:
Column vector is a harvest vector formed by subvectors . Vector consists of elements representing the number of harvested alive trees per hectare for restored forest type and diameter class at time :
2.5. Parametrization of Vital Rates and Projected Variables of Restored Stands
The matrix growth model (Equation (1)) is a density-dependent type of the model, of which vital rates—transition, mortality, and recruitment parameters—are dependent on the stand state , thus, the model is non-linear. The vital rates are hypothesized to be functions of stand density, respectively, stand basal area.
The vital rates were parametrized as empirical functions of tree- and stand-level variables from forest inventory data measured at the Sokolov spoil heaps []. The notation of all variables is defined in Table A3, and their summary statistics are given in Table A4, Table A5 and Table A6 in Appendix B. Both the functions of —derived from the annual diameter growth , see Equation (8)—and were formulated based on individual tree-level data, together with stand-level (plot-level) data from the inventory plot in which each individual tree was growing. Conversely, the natural regeneration and artificial recruitment were developed as empirical functions based on stand-level data.
The aboveground tree biomass and recreation value were formulated as other empirical functions that were further used when the dynamics of restored forests were evaluated for different thinning scenarios. These functions were parametrized by stand variables—such as stand density and stand basal area—that the growth model (Equation (1)) enables us to predict. As growth rate and mortality function, the parameters of the tree biomass equation were estimated with individual tree-level data together with stand-level data. The recreation value equation was estimated with stand-level data only.
As explanatory variables, the diameter of an individual tree () and total stand basal area () were used in the annual tree diameter growth, mortality, and aboveground biomass equations. Stem density () was used in both recruitment equations to represent the seed abundance. Total stand basal area () was used in the artificial recruitment equation only. In addition to stem density, age of the dominant tree species and total cover of shrub understory () were used in the recreation value equation. Apart from tree diameter measured at the tree-level, the other explanatory variables were defined at the stand-level.
The regression parameters of all empirical functions, except mortality function, were estimated with the maximum likelihood procedure using Matlab function ‘fitnlm’. Mortality was estimated as a probit function with the generalized least squares using Matlab function ‘fitglm’.
2.5.1. Growth Function
The transition probability of upgrowth is computed as follows [,]:
where is the annual tree diameter growth [cm] of a tree of restored forest type in diameter class and in year , and is the width of the corresponding diameter class [cm]. It is assumed that trees are uniformly distributed within each diameter class [].
The diameter growth [cm∙year−1] is a function of tree diameter and its square ( [cm] and stand basal area, its squared and cubed form [m2∙ha−1], with parameters and error term . The specification of non-linear diameter growth model is as follows:
According to prior biological knowledge, the tree diameter parameter is expected to have a positive sign and to have a negative sign. The stand basal area parameter is expected to be negative; the parameters and of its squared and cubed term, and should be positive and negative, respectively. Therefore, the growth rate is supposed to increase with tree diameter, and the slower growth is expected in denser forests [,].
The total stand basal area for each forest type is defined at the stand-level as follows:
where corresponds to the average basal area of trees growing in the stand of forest type and diameter class .
When predicting during the simulations of the matrix model, was replaced by , the midpoint of the corresponding DBH class , in Equation (9).
In the absence of permanent plot data in the study site, we used one-time plot data, the proposed method for the calculation of the yearly diameter growth is based on the following observations and assumptions: (a) afforested forests on spoil heaps by plantation or spontaneous succession are newly formed stands on sites that previously had no tree cover; (b) the age of the stand, and thus, main trees initially planted or established by spontaneous succession, represents the time since the afforestation of the site; (c) the age of the dominant tree species that represents a given forest type is used to determine the stand age. Table A2 in Appendix A shows the assignment of individual tree species to a given forest type. (d) The trees that played roles in the stand initiation are determined according to their diameter and growth phase of the stand as follows: (i) trees of the first and second DBH class of forest stands in the early growth phase, (ii) trees of the third and fourth DBH class of stands in the middle growth phase, and (iii) trees of the fourth DBH class of stands in the high growth phase.
Under these observations, the annual growth rate of an individual tree was derived with tree-level data such as tree diameter () and age of the dominant tree () with respect to the growth phase of the inventory plot on which the tree was located. Three growth phases are classified: early, middle, and high, denoted by subindexes , , and , respectively. The yearly diameter growth is calculated as follows:
where and are the diameter and age, respectively, of the tree of forest type , diameter class , and growth phase . This means that the tree diameter growth per year is equal to DBH divided by the age of dominant tree growing on the plot. While was computed for trees with DBH below 7 cm—1st and 2nd DBH class—for the inventory plots of the early growth phase, trees with DBH above 7 cm—3rd and 4th diameter class—and trees with DBH above 14 cm—4th diameter class—were considered when the growth rate was calculated for trees growing on the inventory plots of the middle and high growth phases, respectively.
2.5.2. Mortality Function
In the studies [,,] with permanent plot data, the probability of annual tree mortality is derived from the inventory records representing the state whether a tree died or remained alive between two inventories. In our study with cross-section inventory data without periodic measurement, we used the individual tree records indicating the health status of a tree. We constructed a binary variable representing tree mortality , which equals to 1 if a standing tree of forest type and diameter class is dead or a standing tree is otherwise damaged, e.g., a tree with a break, and 0 if it is a live tree without visible damage. Mean values of according to forest type are presented in Table A6 in Appendix B.
We used the time interval parameter with respect to the forest type and diameter class to convert state-based mortality on the probability of annual tree mortality as follows:
The time interval parameter is set with inventory plot age () as:
where is the average age of forest stands represented by inventory plots by growth phases and forest types . The annual mortality rates derived from according to Equations (12) and (13) are roughly similar to those mortality estimates obtained from the permanent plot data in other studies [,,].
The probability of tree mortality is a probit function of tree diameter , stand basal area , its squared and cubed form , with parameters and error term . The specification of mortality model is as follows:
where is the standard normal cumulative function. The tree diameter parameter is expected to be negative. Conversely, the stand basal area parameter is supposed to have a positive sign, the parameters of its squared and cubed term, and should be negative and positive, respectively. Therefore, smaller trees are supposed to have higher mortality than larger ones, and the higher mortality rate will be in denser forest stands.
Knowing and , the transition probability of ingrowth is computed according to the relation in Equation (4).
2.5.3. Recruitment Functions
Dissimilar to growth rate and mortality, both natural regeneration and artificial recruitment, and [trees∙ha−1∙year−1], are developed as stand-based functions, and they are specified as linear functions of stand density, [trees∙ha−1∙year−1]. Specifically, natural regeneration is a function of stand density with parameter and error term , and has the following form:
The stand density parameter is expected to have a positive sign, so that more trees increase the abundance of seeds and cause a higher rate of regeneration.
Artificial recruitment is a function of stand density and stand basal area, with parameters and error term and has the following specification:
One would expect both parameters of stand density and stand basal area to be negative. Therefore, a smaller number of trees in the stand would require a higher intensity of artificial planting. However, the larger the stand basal area is, and thus, stand density, the higher the competition between trees will be.
Data for the recruitment, and , i.e., the number of trees per hectare entering yearly the smallest diameter class as natural regeneration and artificial planting, respectively, were computed from the inventory data measured on individual trees of up to 2.0 cm DBH. First, a tree from recruitment was assigned to either (1) the natural or (2) the artificial recruitment category based on the regeneration origin determined during the inventory survey. Furthermore, the average annual height increment of recruitment () for each restored forest type was derived with tree-level data such as tree height () and age of the dominant tree () measured on inventory plots of the early growth phase—trees up to 2 m height—as follows:
where and are the tree height and age, respectively, of the average tree of forest type , diameter class , and growth phase . The annual height increment of recruitments was from 9 cm for deciduous, larch, and mixed stands to 28 cm for succession stands. The height increment of spruce, pine, and alder stands amounted to 15 cm, 18 cm, and 24 cm, respectively.
The parameter was then used to measure the annual recruitment —both natural and artificial recruitment —on each inventory plot as follows:
where and are, respectively, the tree height of the average tree and the number of trees of forest type , diameter class , and recruitment type , on a given plot.
2.5.4. Function of Aboveground Tree Biomass
The volume of aboveground tree biomass of individual trees [tonnes∙tree−1] is a function of tree diameter , stand basal area , its squared and cubed form , with parameters and error term . The specification of tree biomass model is as follows:
Since the tree volume is related to the tree diameter, the parameter should be positive. The stand basal area reflects possible effect of stand density, so that tree volume should be higher in a less dense stand. Therefore, the stand basal area parameter is expected to be negative, the parameters of its squared and cubed term, and , should be positive and negative, respectively.
The data for in Equation (19) were determined using the allometric equations, which were predominantly derived for main tree species and different tree components in the central Europe [,,,,,,,]. Specifically, the calculation of aboveground tree biomass consisted of deriving the volume of following tree component: coarse wood (≥7 cm in diameter), bark of coarse wood, small wood (<7 cm in diameter) including bar, and needles (in conifers). Individual tree inventory data such as DBH and tree height were used as explanatory variables in the component biomass functions.
2.5.5. Function of Attractiveness for Recreation
The recreation value [probability] as attractiveness of restored forest stands for recreation, is a function of the proportion of stem density () to age of the dominant tree species , and total cover of shrub understory , with parameters and error term The model on recreation value is specified as linear-log model:
The shrub understory parameter is supposed to have a negative sign, so that shrubs detract from scenic beauty of forest stands, as found by Brown and Daniel []. The parameter is assumed to be negative, since increasing stand age should have positive scenic impact, thus, increasing recreation value of the stand. The effect of tree density on recreation value is opposite. As found by Hull et al. [], the age of stand has a positive effect on scenic beauty, but in interaction with tree density, since increasing density weakens the age effect.
The parameters of the recreation value model were estimated with forest inventory data [] and with the estimates of recreation value derived in the environmental preference study []. The data for recreation value, in Equation (20), were represented by mean recreation values predicted by the DCE model for seven restored forest stands at the Sokolov spoil heaps in the environmental preference study. Forest inventory data—such as tree density, age of stand, shrub coverage—from seven inventory plots geographically corresponding to the restored forest stands, where photographs were taken in 2016 for the assessment of the attractiveness for recreation in the environmental preference study, was subsequently attached to the data on recreation value.
2.6. Verification of the Growth Model
The matrix growth model (Equation (1)) with empirical functions (Equations (9), (14)–(16), (19)) representing individual variables in the matrix model was calibrated on inventory plot data from the Velká Podkrušnohorská and Matyáš heap. Verification—accuracy of the calibrated growth model was determined based on the prediction errors, the differences between the observed values of stand characteristics—stem density, density according to the DBH classes, basal area, and AGB—and the predicted values of these simulated forest characteristics.
The observed values of stand characteristics were expressed as 5-year averages. In the given 5-year average, only those inventory plots whose age was within the given 5-year interval were included. At the same time, a 95% confidence interval was determined with the 5-year average of the observed forest characteristic.
The accuracy of the model was verified on 250 inventory plots. The growth model was used to simulate the dynamics of restored forest stands on each inventory plot in a one-year time step up to the age of 59 years. This age corresponds to the maximum age that was determined during the forest inventory survey for the dominant tree growing on the inventory plot. The initial state of forest stand used for simulation corresponds to the observed state of the restored forest on the given inventory plot.
2.7. Application of the Model to Differenct Thinning Managements
The matrix growth model calibrated on inventory plot data from the Sokolov spoil heaps—Velká Podkrušnohorská and Matyáš heap—was applied to study the dynamics of six types of restored forests—alder, deciduous, successional, larch, pine, and spruce stands—with and without the management of various regimes of thinning. The simulation was mainly focused on the prediction of the recreation value and aboveground biomass under different thinning regimes, which correspond to a given type of restored forest stand. The simulation was run in a one-year time step for each thinning scenario for 65 years with a 5-year cutting cycle up to 20 years of stand age and a 10-year cutting cycle in the rest of the simulated period. The simulation period up to 65 years represents the age range of restored forests of early, middle, and high growth stage that are present in the study site. Older restored stands are absent in the Sokolov mining area, because the first forest reclamations were started here only at the beginning of the 1970s.
The parameters of thinning measures considered in the simulation are based on the framework guidelines for the management of reclaimed forests [], which were drawn up for the Sokolov spoil heaps within this study. For each stand type and age, the guidelines propose the state of the forest stand, which corresponds to the minimum target numbers of trees per hectare after thinning in a given cutting year. The minimum target numbers of trees per hectare are given in Table A7 in Appendix C.
3. Results
3.1. Estimates of Parameters
Individual tree data were used for the estimation of the regression coefficients of the diameter growth model (Equation (9)), mortality model (Equation (14)), and aboveground tree biomass model (Equation (19)); the parameters of the recruitment models (Equations (15) and (16)) and the model of forest attractiveness for recreation (Equation (20)) were estimated with inventory plot data.
The diameter growth, mortality, recruitment, aboveground tree biomass model was compiled and estimated both as a common model for all forest types and separately for each type of forest stand. The estimates of regression parameters of the diameter growth, mortality, recruitment, AGB model, and the model on prediction of recreation value are given in Table 1, Table 2, Table 3, Table 4 and Table 5.

Table 1.
Estimated regression parameters of the diameter growth model (Equation (9)).

Table 2.
Estimated regression parameters of the probit mortality model (Equation (14)).

Table 3.
Estimated regression parameters of the recruitment model with artificial regeneration (Equation (16)) and the recruitment model with natural regeneration (Equation (15)).

Table 4.
Estimated regression parameters of the aboveground tree biomass model (Equation (19)).

Table 5.
Estimated regression parameters of the recreation value model (Equation (20)).
The parameter estimates of regression models for both all stands and individual forest types are statistically significant for most of the explanatory variables. The regression coefficients in the estimated models also have the expected direction of the effect on response variable and are consistent across models for individual forest stand types.
Specifically, diameter growth increases at a decreasing rate with tree diameter for all types of restored forests, more so for the pine stand. Diameter growth is positively affected by stand basal area, except the pine stands with a negative effect (Table 1). Mortality declines with tree diameter across all stand types but increases with stand basal area with the only exception of the joint model (Table 2). Both artificial and natural recruitment of each stand type increases with its tree density. However, the negative effect of tree density was expected for artificial recruitment. Moreover, artificial recruitment significantly declines with stand basal area for all stands together (Table 3). In the aboveground tree biomass model, AGB increases with increasing tree diameter and declines with stand basal area for all stand types. Basal area squared and cubed also affects AGB, the quadratic term positively and cubic term negatively, except for in the pine stand (Table 4). The attractiveness for recreation is negatively affected by the logarithm of the tree density-to-age ratio. Moreover, attractiveness declines with increasing cover of the shrub understory (Table 5).
The regression model explaining the variability of recreation value (attractiveness of restored forest stands for recreation) depending on the stem density, its age, and shrub cover was used to predict the recreation value of all inventory areas in the Velká Podkrušnohorská and Matyáš heap, based on inventory plot data. The mean values of the predicted attractiveness by growth stages and forest types with a 95% confidence interval are depicted in the following graphs in Figure 4. The difference in the mean recreation is statistically significant between the individual growth stages at the 5% level. The high growth stage has the highest recreation value; conversely, the early growth stage has the lowest. Furthermore, the mean recreation value differs between alder and deciduous stands and alder and mixed stands, with alder stands having the lowest recreation value.
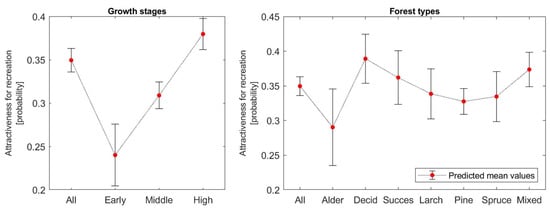
Figure 4.
Mean values of the predicted recreation value (attractiveness for recreation) with a 95% confidence interval according to growth stages and forest types.
3.2. Prediction Errors
The calibrated matrix growth model was tested to be accurate between the observed values of stand characteristics and the predicted ones. The graphs in Figure 5 and Figure 6 present the observed 5-year averages for stands of all forest types with 95% confidence intervals and predicted values by the matrix growth model (Equation (1)), parametrized by empirical functions (Equations (9), (14)–(16), (19)) of stand characteristics, such as total stem density, total basal area, total aboveground tree biomass, and stem density for each DBH class. Harvest was fixed at .
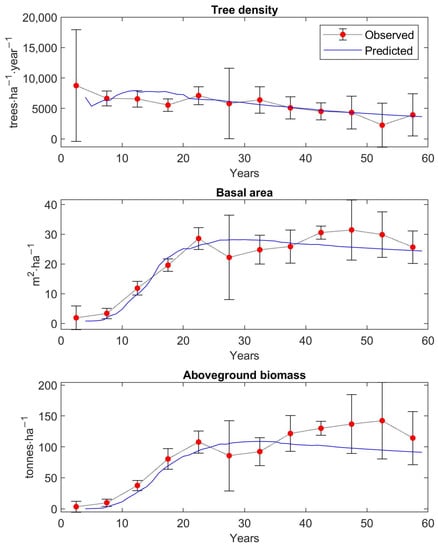
Figure 5.
Verification of the model by the comparison of the observed 5-year average values with average predicted values of stem density, basal area, and AGB, with a 95% confidence interval, over 250 inventory plots.
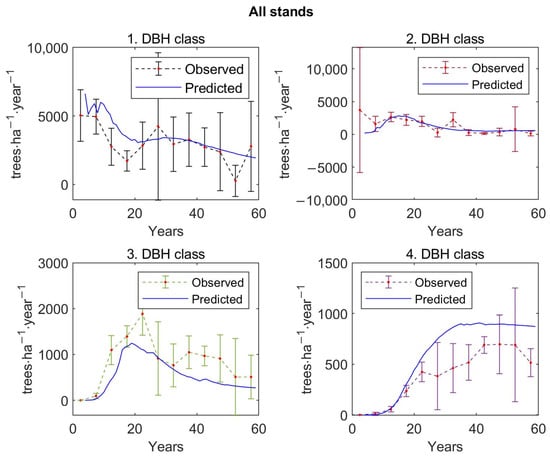
Figure 6.
Verification of the model by the comparison of the observed 5-year average values with average predicted values of stem density distributed according to DBH classes, with a 95% confidence interval, over 250 inventory plots.
The predicted values of stand characteristics pass through almost all 95% confidence intervals, and therefore, the predicted states of forest stands fit well the mean observed states of the 250 inventory plots.
The graphs of Figure A1, Figure A2, Figure A3 and Figure A4 in Appendix D show similarly the observed 5-year averages for individual forest types with 95% confidence intervals and predicted values of basal area (Figure A1), aboveground tree biomass (Figure A2), stem density (Figure A3), and stem density distributed according to DBH classes (Figure A4). The predicted stand states, especially for stem density, basal area, and AGB, match the observed ones.
3.3. Application of Thinning Managements
Various thinning schemes proposed in the framework guidelines [] for six types of restored forest stands including spontaneous succession result in different volumes of the aboveground biomass removed during 65 years. Total amount of the harvested stock is sensitive to the thinning intensities, target numbers of trees per hectare in each cutting year, the initial size of replantation, and also to the restored type of forest. Table A7 in Appendix C shows the predicted stock of aboveground biomass harvested according to different thinning managements for each stand type over 65 years.
The thinning intensity is increasing over time for all restored forests, except for the even harvesting intensity of pine and spruce in the second part of the simulated period. Alder and larch stands have the highest total volume harvested with 65.6 and 65.4 t∙ha−1, respectively. Conversely, pine stands have the lowest AGB removed in total with 1.7 t∙ha−1.
The graphs in Figure 7 and Figure 8 present the simulated dynamics of aboveground tree biomass and recreation values of restored forest types with and without thinning management, respectively. The graphs of Figure A5 and Figure A6 in Appendix E show similarly the simulated dynamics of basal area, and tree density and tree density distributed according to DBH classes of restored forest types without harvesting and with thinning, respectively.
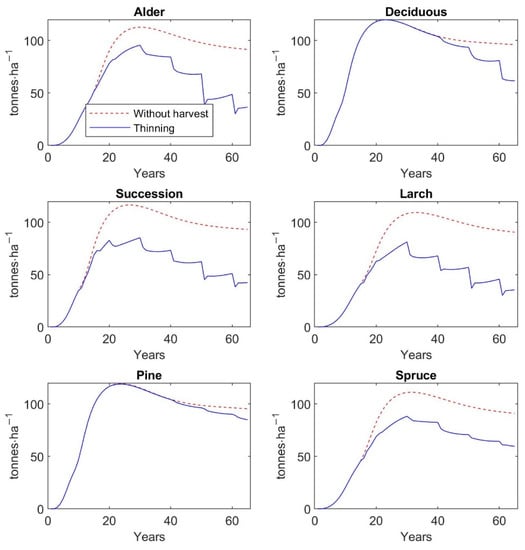
Figure 7.
Predicted aboveground tree biomass over 65 years without harvest and under different thinning regimes and forest types.
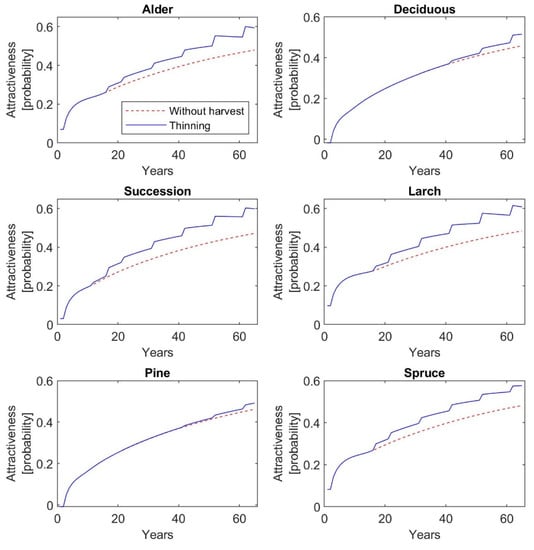
Figure 8.
Predicted recreation value over 65 years without harvest and under different thinning regimes and forest types.
The results indicate that initial planting density and stand type have an effect on the dynamics of restored forest stands in the short-term horizon (up to 65 years). Applying the different thinning practices resulted in an increase in recreation value for all types of restored forest stands, while aboveground tree biomass decreased. When the simulations of AGB and recreation value with and without harvest are compared at the final stand state (65-year-old stand), the highest decrease in AGB of 61% in response to the thinning management is observed for larch stands. At the same time, the recreation value of larch is increased by 26% due to the thinning harvest. The similar changes in AGB and recreation value are observed for alder replantation and spontaneous succession. The lowest decrease in AGB of 11% and the lowest increase in recreation value of 6% due to the thinning is seen for pine replantation.
4. Discussion
Following the findings of previous studies [,], the results have shown that restored forest stands—both replanted and sites with succession—at the Velká Podkrušnohorská and Matyáš spoil heaps in the Sokolov brown-coal mining area, which are left to grow without appropriate silvicultural management, have a lower recreation value than forest stands with targeted after-care such as thinning and pruning. This is consistent with the findings of the study on perceived beauty of various restored forest stands in the North-West Bohemian brown-coal basin in the Czech Republic realized by Sklenicka and Molnarova [], in which managed coniferous forest received higher preferences than wild, unmanaged, deciduous forest. On the other hand, the wilderness element of the forest landscape was not significant in the study by Svobodova et al. [], in which visual preferences of different type of restored landscape were evaluated in the same brown-coal district as in the previous study.
In the matrix growth model (Equation (1)), the recreation value of the restored forests is parametrized apart from the stand age and shrub cover by tree density (Equation (20)) with its negative effect on recreation value, when the decreasing tree density increases the attractiveness of reclaimed forests for recreation. The tree density effect reflects well the stand conditions after the thinning selections in the long-term horizon when the direct remnants of logging are no longer visible. However, the model does not reflect the short-term post-thinning stand conditions, with slash piles, small diameter downed wood, and other visible harvest effects detracting from the scenic beauty and recreation value of managed stands [].
In addition to the tree density, the results indicate that the recreation value of restored forests increases with the age of the stand. The positive effect of stand age on the attractiveness of reclaimed forests for recreation or on their perceived beauty was previously confirmed by Braun Kohlová et al. [,], and Sklenicka and Molnarova [], respectively, for restored forest sites in the Sokolov and North-Bohemian mining area. This means that the restored forest stands of an early (<2 m) and middle (2–10 m) growth stage are characterized by low recreation value; this was confirmed for both successional stands [,] and replantations []. Interestingly, the significantly lower recreation value of early-stage restored stands was observed for spruce plantation compared to spontaneous succession []. This can be explained by a lower density of successional stands in their initial phase, while the spruce is planted in high seedling densities (10,000 seedlings per hectare).
The level of shrub and herbaceous understory and ground deformations are among other stand-level attributes that affect peoples’ preferences towards recreation in restored forests. While the effect of shrubs—the presence of shrub layer detracts from visual attractivity of restored stands—was taken into account in the model on recreation value (Equation (20)), the cover of the herbaceous understory was not measured on the inventory plots, and therefore, the presence of herbaceous vegetation was not considered in the model. This may result in higher estimates of the recreation value of restored stands, especially those with a thick herbaceous vegetation. This is particularly problematic in alder stands with a high fixation of natural nitrogen that supports the spreading of grasses such as Calamagrostis epigejos or Arrhenatherum elatius []. It was alder stands with a large understory vegetation of C. epigejos that were perceived as less attractive than other restored forest stands [].
Ground deformations caused by the conveyor belt dumping and layering of overburden material into 1–2 m high waves during the technical reclamation of the spoil heap are a suitable place for the development of spontaneously emerging ecosystems and the growth of succession tree species [,]. However, visible ground unevenness present at unreclaimed places left to spontaneous succession detract from the attractiveness of successional stands for recreation, as proven by Braun Kohlová et al. []. The highest growth phase of succession (B. pendula) was perceived as more attractive than the early (B. Pendula, P. sylvestris, P. abies) or middle (S. caprea) growth phases. In part, this may be influenced by less visible geomorphological irregularities in high growth stage stands due to geophysical processes. This might partially overestimate the predicted recreation value of successional forests in their early and middle growth stages.
From the long-term perspective, we can, therefore, recommend the formation of numerous ridges and depressions when a spoil heap is created, supporting the emergence and growth of successional forests. At suitable places on the spoil heap, strongly deformed terrain with spontaneous succession can be carefully combined with a phytotoxic surface. This will create future open areas with scenic landscape views and a habitat for rare plant species []. Deeper deformities give birth to ponds and pools suitable for amphibians. After opening these locations with spontaneous succession to visitors, we can inform the public about the importance of habitats for biodiversity and its origins. This information can take many forms, such as information boards or natural trails.
Furthermore, the findings of the current study indicate that thinning of different intensities increases the recreation value of restored forests, but at the same time the aboveground tree biomass significantly decreases, except on pine plantations. AGB and recreation value—measured as mean probability of a person’s choice of a given forest type for a one-hour walk—of a 65-year-old pine stand is 84.9 t∙ha−1 and 0.49, if thinning management is regularly realized. On the other hand, larch plantations at the same age reach 35.6 t∙ha−1 AGB, but recreation value amounts to 0.61. In comparison to unmanaged stands, the AGB of 65-year-old larch stands due to thinning operations is decreased by 61%, while recreation value is increased by 26%. The similar values and dynamics in AGB and recreation value as for larch stands are observed for alder plantations. Deciduous and spruce stands at the age of 65 reach 61.8 and 59.2 t∙ha−1 AGB, and their recreation value is 0.52 and 0.58, respectively. The regular thinning and, thus, subsequent decrease in AGB by 35% in both types of plantations will increase recreation value by 12% for deciduous stands and by as much as 20% for spruce stands. The highest increase in recreation value by 27% is observed for successional stands, which is accompanied by a 54% decrease in AGB. A 65-year-old successional stand reaches 42.5 t∙ha−1 AGB with recreation value at 0.60.
From the timber production perspective of the individual forest types of restored stands, pine forests (usually P. sylvestris or P. nigra) created by plantation have an above-average wood yield, especially if the thinning interventions are regularly realized in the middle and high growth phase. This is consistent with the findings of the study by Vacek et al. [], which proved high productivity and stand volume of P. sylvestris on the reclaimed forest site at the Antonín spoil heap in the Sokolov mining area, even though the pine restored stand was insufficiently thinned out. At the same time, P. sylvestris was found to be very adaptive towards climate change. However, pine forests have worse pedogenetic characteristics than alder or succession forests, as confirmed by Melichar et al. [] at the Velká Podkrušnohorská and Matyáš spoil heaps.
The successional forests have an average wood yield, as was also confirmed by Vacek et al. [] at the Antonín spoil heap. The mean stand volume of successional stands (Populus tremula, S. caprea, or B. pendula) were significantly lower than on afforested stands by Q. robur, B. pendula, or Alnus glutinosa. However, the reclaimed sites colonized with successional trees are significant for their pedogenetic process and tree and herbaceous diversity []. The higher species richness and total stand diversity of successional sites compared to replanted stands were also proven by Vacek et al. [] for the Antonín heap.
Forest plantations predominantly with alder have a lower-than-average wood yield; wood volume per hectare is less than for successional forests. This was confirmed at the Velká Podkrušnohorská heap by Frouz et al. [], when woody biomass was significantly greater on successional sites (P. tremula and S. caprea) than on replanted sites by A. glutinosa at their high growth stages. Nevertheless, woody biomass was greater for alder stands than for successional sites at their early and middle growth stages. The stand volume of alder plantation at the high growth stage was also lower compared to replanted stands with Q. robur and B. pendula and the successional stand with P. tremula at the Antonín heap []. However, successional forests with S. caprea, or B. pendula had a lower stand volume than the alder plantation. Nonetheless, alder planting at spoil heaps is mainly motivated by its suitability as a preparatory tree species. The pedogenetic role of alder stands is crucial, even though natural conditions on soil heaps are less favorable for alders and, thus, cause its premature aging []. The species diversity of alder stands is also relatively high compared to spruce, pine, long-term deciduous, or silver birch plantations [,].
One of the limitations of the matrix growth model is the fact that the model is calibrated on the inventory data of the restored forests from early to high growth stage up to the age of 60 years at maximum, because older forest reclamations are absent in the Sokolov mining area and also in other coal mining areas in the Czech Republic. Therefore, we have used the model to simulate the forest dynamics and evaluate the effects of the thinning interventions for a period of 65 years. Beyond this time horizon, we would not be able to evaluate the errors between the predicted and actual stand states. The possible improvement of the model would be to establish the inventory system of permanent plots capturing a wide range of restored forest types, soil, and geomorphological conditions in the study site and to extend the simulation period beyond the current time horizon of 65 years. In addition, the vital rates including the diameter growth, mortality, and both artificial and natural recruitment rates were parametrized with one-time inventory plot data. Second forest inventory with dendrometric measurements on the same inventory plots as in 2018 could greatly enhance the validity of the estimated parameters of the matrix growth model (Equation (1)).
Finally, in addition to the biomass production and recreation function, the restored forest ecosystems positively influence the properties of reclaimed soil, store carbon in AGB and in soil organic matter, and create the habitat conditions favoring herbaceous species diversity. Given the availability of data from pedological and phytocenological surveys [,] realized at the Sokolov spoil heaps in recent past, the opportunity exists to further extend the matrix model with the soil properties, carbon storage, tree and herbaceous diversity, and to study the stand dynamics from the perspective of the multifunctional use of restored forest ecosystems.
5. Conclusions
This study has shown that the state of restored forest stands established at the Velká Podkrušnohorská and Matyáš spoil heaps in the Sokolov brown-coal mining district is influenced, apart from forest type, by initial planting density and thinning intensity. On average for all growth phases, a higher aboveground biomass production was observed for long-lived deciduous plantations in comparison to half biomass production of spruce plantations on the forest inventory data from 2018. At the same time, larch plantations and forest stands originated by spontaneous succession showed a higher production compared to alder and pine reclamations. The simulations of the matrix growth model calibrated on the inventory data showed that the initial size of afforestation affects the size of biomass production until about 30 years of stand age, when AGB culminates. After that, the difference in tree biomass volume between stands with various seedling rate decreases. However, if we adopt thinning operations in the short-term horizon, the biomass production will decline, especially when thinning management is more intensive. On the other hand, the recreation value of restored stands is increasing with thinning interventions. Specifically, the greater the intensity of the thinning management that is carried out, the higher the increase in recreation value of restored forests is, as it was observed, for example, in larch plantations and successional stands. The possible future improvement of the matrix growth model would be to include, apart from biomass production and recreation function, the other important functions of reclaimed forest ecosystems as pedogenic function, carbon storage, or tree and herbaceous diversity restoration.
Author Contributions
Conceptualization, J.M.; methodology, J.M., E.C. and M.B.K.; validation, J.M., J.A. and V.M.; investigation, E.C., J.A., J.M. and M.B.K.; data curation, J.M., V.M., M.B.K. and J.A.; writing—original draft preparation, J.M., E.C., J.A., M.B.K., V.M. and P.P.; writing—review and editing, P.P.; visualization, J.M. and J.A.; supervision, E.C.; project administration, J.M.; funding acquisition, J.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received funding from the Ministry of Agriculture of the Czech Republic (grant number QK1710241, Optimization of management of forest restoration on sites affected by surface mining) and from the European Commission (grant number LIFE17 IPE/CZ/00005, Integrated LIFE project for the Natura 2000 network in the Czech Republic).
Acknowledgments
The authors thank their colleagues Jana Beranová, Vladimír Zatloukal, and Jan Tumajer for the coordination, work on the collection, and processing of forest inventory data.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Appendix A. Forest Types and Tree Species Occurring in the Study Area

Table A1.
Relative frequencies of tree species growing on the inventory plots of the Matyáš a Velká Podkrušnohorská spoil heaps.
Table A1.
Relative frequencies of tree species growing on the inventory plots of the Matyáš a Velká Podkrušnohorská spoil heaps.
| Common Name | Scientific Name | No. of Trees | Relative Frequency [%] |
|---|---|---|---|
| Black alder | Alnus glutinosa (L.) Gaertn. | 8180 | 17.81 |
| Norway spruce | Picea abies (L.) H. Karst. | 5681 | 12.37 |
| European ash | Fraxinus excelsior L. | 4178 | 9.10 |
| Silver birch | Betula pendula Roth | 3750 | 8.17 |
| Scotch pine | Pinus sylvestris L. | 3305 | 7.20 |
| European larch | Larix decidua Mill. | 3027 | 6.59 |
| European aspen | Populus tremula L. | 2739 | 5.96 |
| Austrian pine | Pinus nigra J. F. Arnold | 2463 | 5.36 |
| English oak | Quercus robur L. | 2158 | 4.70 |
| Small-leaved linden | Tilia cordata Mill. | 1891 | 4.12 |
| Goat willow | Salix caprea L. | 1633 | 3.56 |
| Gray alder | Alnus incana (L.) Moench | 1329 | 2.89 |
| European mountain ash | Sorbus aucuparia L. | 1150 | 2.50 |
| Sycamore maple | Acer pseudoplatanus L. | 877 | 1.91 |
| Douglas fir | Pseudotsuga menziesii (Mirb.) Franco var. menziesii | 804 | 1.75 |
| European field elm | Ulmus minor Mill. | 429 | 0.93 |
| Serbian spruce | Picea omorika (Pančić) Purk. | 353 | 0.77 |
| Sessile oak | Quercus petraea (Matt.) Liebl. | 352 | 0.77 |
| Blue spruce | Picea pungens Engelm. | 293 | 0.64 |
| Field maple | Acer campestre L. | 250 | 0.54 |
| Wild cherry | Prunus avium L. | 238 | 0.52 |
| Box elder | Acer negundo L. | 215 | 0.47 |
| European wild pear | Pyrus pyraster | 157 | 0.34 |
| Other pines (1) | - | 154 | 0.34 |
| Other willows (2) | - | 117 | 0.25 |
| Eastern white pine | Pinus strobus L. | 77 | 0.17 |
| European beech | Fagus sylvatica L. | 75 | 0.16 |
| Norway maple | Acer platanoides L. | 25 | 0.05 |
| Black poplar | Populus nigra L. | 15 | 0.03 |
| Black locust | Robinia pseudoacacia L. | 5 | 0.01 |
| Total | 45,920 | 100.00 |
Note: (1) Other pines are Lodgepole pine (Pinus contorta Douglas ex Loudon), Macedonian pine (Pinus peuce Griseb.), Ponderosa pine (Pinus ponderosa), Jeffrey pine (Pinus jeffreyi), Western white pine (Pinus monticola). (2) Other willows are Bay willow (Salix pentandra L.), Crack willow (Salix euxina I. V. Belyaeva), Basket willow (Salix viminalis L.).

Table A2.
Assignment of individual tree species to the defined categories of forest types.
Table A2.
Assignment of individual tree species to the defined categories of forest types.
| Forest Type Name | Tree Species |
|---|---|
| Alder | A. glutinosa |
| A. incana | |
| Deciduous | Q. robur |
| Q. petraea | |
| F. sylvatica | |
| A. platanoides | |
| A. pseudoplatanus | |
| A. campestre | |
| A. negundo | |
| S. aucuparia | |
| U. minor | |
| R. pseudoacacia | |
| P. avium | |
| P. pyraster | |
| T. cordata | |
| Succession | B. pendula |
| F. excelsior | |
| P. tremula | |
| P. nigra | |
| S. caprea | |
| Other willows | |
| Larch | L. decidua |
| Pine | P. sylvestris |
| P. nigra | |
| P. strobus | |
| Other pines | |
| Spruce | P. abies |
| P. pungens | |
| P. omorika | |
| P. menziesii |
Appendix B. List of Variables Used in the Study and Their Descriptive Statistics

Table A3.
Summary of stand variables and their definitions.
Table A3.
Summary of stand variables and their definitions.
| Type of Variable | Variable | Unit | Definition |
|---|---|---|---|
| Tree-level variables | D | cm | Diameter of a live tree at breast height |
| G | cm∙year−1 | Annual diameter growth of a live tree | |
| M | {0,1} | Mortality: 1 = dead standing tree, 0 = live tree | |
| H | m | Tree height | |
| AGBtree | tonnes∙tree−1 | Dry matter of aboveground tree biomass of individual tree | |
| Plot-level variables | N | trees∙ha−1 | Number of trees per hectare |
| R | trees∙ha−1∙year−1 | Recruitment—the number of trees per hectare growing into the first DBH class in a year | |
| RA | trees∙ha−1∙year−1 | Artificial recruitment—the number of seedlings planted in a year | |
| RN | trees∙ha−1∙year−1 | Natural recruitment—the number of trees per hectare naturally regenerated in the first DBH class in a year | |
| B | m2∙ha−1 | Total stand basal area per hectare | |
| DT | n | Number of tree species growing on a plot | |
| DS | n | Number of shrub species growing on a plot | |
| CS | % | Total cover of shrub understory on a plot | |
| AGBplot | tonnes∙ha−1 | Total dry matter of aboveground tree biomass of all trees on a plot | |
| A | years | Age represented by the dominant tree species on a plot | |
| AR | probability | Attractiveness for recreation expressed as the mean probability of a person’s choice of a given type of restored forest for a one-hour walk |

Table A4.
Descriptive statistics of stand characteristics for inventory plot data.
Table A4.
Descriptive statistics of stand characteristics for inventory plot data.
| Variable | Statistics | All Stands | Alder | Deciduous | Succession | Larch | Pine | Spruce | Mixed Stands |
|---|---|---|---|---|---|---|---|---|---|
| Stem density [trees∙ha−1] | Mean | 5847 | 6004 | 4954 | 6283 | 6192 | 6243 | 6324 | 5235 |
| S.D. | 4224 | 5609 | 2631 | 5883 | 3314 | 2659 | 3435 | 3817 | |
| Min | 32 | 1210 | 1019 | 32 | 1783 | 1751 | 1432 | 382 | |
| Max | 29,316 | 26,261 | 11,077 | 29,316 | 12,955 | 12,350 | 13,528 | 16,329 | |
| n | 250 | 29 | 31 | 51 | 19 | 38 | 27 | 55 | |
| Recruitment [trees∙ha−1∙year−1] | Mean | 367 | 320 | 406 | 648 | 301 | 175 | 320 | 289 |
| S.D. | 663 | 570 | 605 | 1109 | 439 | 236 | 580 | 377 | |
| Min | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| Max | 6565 | 2387 | 2653 | 6565 | 1592 | 1061 | 2785 | 1790 | |
| Basal area [m2∙ha−1] | Mean | 19.90 | 17.54 | 25.08 | 17.60 | 17.48 | 20.91 | 15.01 | 22.90 |
| S.D. | 11.95 | 10.36 | 12.11 | 9.77 | 10.94 | 10.78 | 14.09 | 13.08 | |
| Min | 0.06 | 0.06 | 0.14 | 0.50 | 0.30 | 0.36 | 0.53 | 0.23 | |
| Max | 48.39 | 36.01 | 48.39 | 33.41 | 37.68 | 37.29 | 45.23 | 47.43 |

Table A5.
Mean value of other stand characteristics for inventory plot data and attractiveness for recreation.
Table A5.
Mean value of other stand characteristics for inventory plot data and attractiveness for recreation.
| Variable | Unit | All Stands | Alder | Deciduous | Succession | Larch | Pine | Spruce | Mixed Stands |
|---|---|---|---|---|---|---|---|---|---|
| RA | trees∙ha−1∙year−1 | 65 | 17 | 109 | 23 | 92 | 78 | 154 | 43 |
| RN | trees∙ha−1∙year−1 | 312 | 303 | 315 | 632 | 234 | 103 | 174 | 256 |
| DT | n | 3.08 | 1.93 | 3.16 | 3.65 | 1.89 | 2.68 | 2.52 | 4.07 |
| DS | n | 1.16 | 1.66 | 1.81 | 1.37 | 0.95 | 0.55 | 0.44 | 1.16 |
| CS | % | 7.36 | 22.52 | 7.18 | 9.14 | 2.79 | 0.68 | 0.89 | 7.19 |
| AGBplot | t∙ha−1 | 79.40 | 67.52 | 110.18 | 80.74 | 93.27 | 60.90 | 49.86 | 89.58 |
| A | years | 24 | 24 | 34 | 25 | 21 | 17 | 19 | 28 |
| AR | probability | 0.4006 | 0.1681 | - | 0.4474 | - | 0.4870 | 0.4036 | - |

Table A6.
Descriptive statistics of tree characteristics for individual tree data.
Table A6.
Descriptive statistics of tree characteristics for individual tree data.
| Variable | Statistics | All Stands | Alder | Deciduous | Succession | Larch | Pine | Spruce | Mixed Stands |
|---|---|---|---|---|---|---|---|---|---|
| Diameter [cm] | Mean | 14.4 | 13.1 | 15.6 | 16.5 | 14.3 | 10.9 | 14.2 | 15.3 |
| S.D. | 6.5 | 5.0 | 5.9 | 7.2 | 7.7 | 4.4 | 7.2 | 6.5 | |
| Min | 0.4 | 0.5 | 0.4 | 1.0 | 0.9 | 0.7 | 0.7 | 0.4 | |
| Max | 52.1 | 33.2 | 42.0 | 52.1 | 36.3 | 29.2 | 34.9 | 45.6 | |
| n | 4323 | 427 | 711 | 718 | 255 | 755 | 349 | 1108 | |
| Diameter growth [cm∙year−1] | Mean | 0.53 | 0.45 | 0.42 | 0.65 | 0.53 | 0.57 | 0.52 | 0.52 |
| S.D. | 0.25 | 0.23 | 0.17 | 0.34 | 0.21 | 0.19 | 0.24 | 0.25 | |
| Min | 0.02 | 0.12 | 0.02 | 0.11 | 0.10 | 0.04 | 0.09 | 0.03 | |
| Max | 2.61 | 1.66 | 1.37 | 2.61 | 1.40 | 1.38 | 1.93 | 1.93 | |
| n | 4323 | 427 | 711 | 718 | 255 | 755 | 349 | 1108 | |
| Dead tree {0,1} | Mean | 0.037 | 0.036 | 0.039 | 0.038 | 0.008 | 0.006 | 0.050 | 0.058 |
| S.D. | 0.188 | 0.187 | 0.194 | 0.190 | 0.091 | 0.075 | 0.218 | 0.234 | |
| Min | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| Max | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| n | 4186 | 415 | 690 | 720 | 242 | 710 | 321 | 1088 | |
| Tree height [m] | Mean | 12.00 | 11.40 | 14.39 | 12.57 | 13.31 | 8.52 | 10.80 | 12.72 |
| S.D. | 5.33 | 3.80 | 5.06 | 5.96 | 5.89 | 3.34 | 5.05 | 5.31 | |
| Min | 0.13 | 0.30 | 0.25 | 0.25 | 0.30 | 0.25 | 0.25 | 0.13 | |
| Max | 29.40 | 20.40 | 24.37 | 28.27 | 24.70 | 19.10 | 20.77 | 29.40 | |
| n | 4646 | 445 | 742 | 833 | 269 | 789 | 372 | 1196 | |
| Aboveground biomass [t∙tree−1] | Mean | 0.080 | 0.063 | 0.097 | 0.115 | 0.085 | 0.028 | 0.074 | 0.089 |
| S.D. | 0.104 | 0.052 | 0.082 | 0.167 | 0.104 | 0.030 | 0.077 | 0.101 | |
| Min | 3.8 × 10−6 | 1.7 × 10−4 | 1.6 × 10−5 | 5.3 × 10−6 | 5.4 × 10−5 | 3.0 × 10−5 | 6.5 × 10−5 | 3.8 × 10−6 | |
| Max | 1.871 | 0.349 | 0.539 | 1.871 | 0.488 | 0.217 | 0.404 | 1.575 | |
| n | 4403 | 429 | 713 | 763 | 256 | 762 | 350 | 1130 |
Appendix C. Thinning Management Scenarios

Table A7.
Target number of trees and predicted stock of aboveground biomass harvested according to different thinning managements over 65 years.
Table A7.
Target number of trees and predicted stock of aboveground biomass harvested according to different thinning managements over 65 years.
| Forest Stand Type | Age of Stand | Target No. of Trees | Removed AGB |
|---|---|---|---|
| [trees∙ha−1] | [t∙ha−1] | ||
| Alder | seedlings | 4000 | - |
| 5 | 4000 | 0.0 | |
| 10 | 3000 | 0.0 | |
| 15 | 2500 | 1.7 | |
| 20 | 2000 | 1.1 | |
| 30 | 1200 | 5.1 | |
| 40 | 800 | 10.3 | |
| 50 | 430 | 29.2 | |
| 60 | 310 | 18.1 | |
| Total | - | 65.6 | |
| Deciduous | seedlings | 10,000 | - |
| 5 | 9000 | 0.0 | |
| 10 | 8000 | 0.0 | |
| 15 | 7000 | 0.0 | |
| 20 | 6000 | 0.0 | |
| 30 | 2000 | 0.1 | |
| 40 | 1300 | 0.7 | |
| 50 | 1000 | 5.8 | |
| 60 | 700 | 16.7 | |
| Total | - | 23.3 | |
| Succession | seedlings | 6000 | - |
| 5 | 5000 | 0.0 | |
| 10 | 3000 | 1.1 | |
| 15 | 1500 | 3.0 | |
| 20 | 1200 | 6.3 | |
| 30 | 900 | 9.0 | |
| 40 | 700 | 9.6 | |
| 50 | 500 | 16.7 | |
| 60 | 400 | 12.4 | |
| Total | - | 58.0 | |
| Larch | seedlings | 3000 | - |
| 5 | 2500 | 0.0 | |
| 10 | 2250 | 0.0 | |
| 15 | 2000 | 1.4 | |
| 20 | 1200 | 3.2 | |
| 30 | 800 | 12.1 | |
| 40 | 600 | 13.5 | |
| 50 | 400 | 19.7 | |
| 60 | 300 | 15.5 | |
| Total | - | 65.4 | |
| Pine | seedlings | 9000 | - |
| 5 | 8000 | 0.0 | |
| 10 | 7000 | 0.0 | |
| 15 | 5500 | 0.0 | |
| 20 | 3500 | 0.1 | |
| 30 | 2500 | 0.0 | |
| 40 | 1700 | 0.3 | |
| 50 | 1500 | 0.5 | |
| 60 | 1200 | 0.7 | |
| Total | - | 1.7 | |
| Spruce | seedlings | 3500 | - |
| 5 | 3000 | 0.0 | |
| 10 | 2500 | 0.0 | |
| 15 | 2000 | 1.9 | |
| 20 | 1600 | 1.4 | |
| 30 | 1200 | 2.8 | |
| 40 | 900 | 5.1 | |
| 50 | 800 | 2.6 | |
| 60 | 700 | 2.7 | |
| Total | - | 16.3 |
Appendix D. Verification of the Model for Investigated Stand Characteristics According to Forest Types
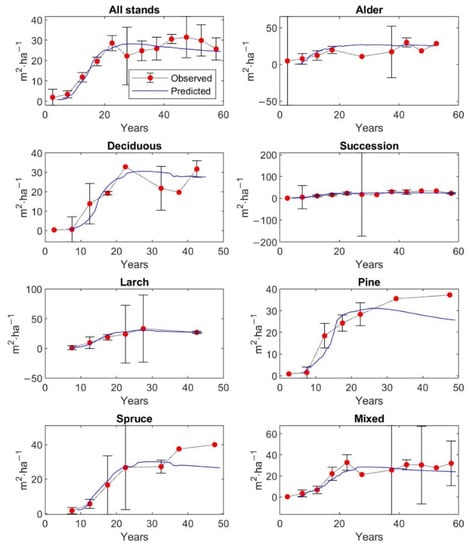
Figure A1.
Verification of the model by the comparison of the observed 5-year average values with average predicted values of basal area, with a 95% confidence interval, according to individual forest types.
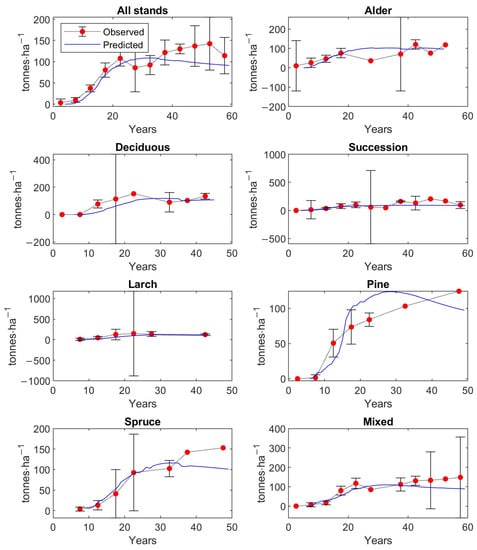
Figure A2.
Verification of the model by the comparison of the observed 5-year average values with average predicted values of AGB, with a 95% confidence interval, according to individual forest types.
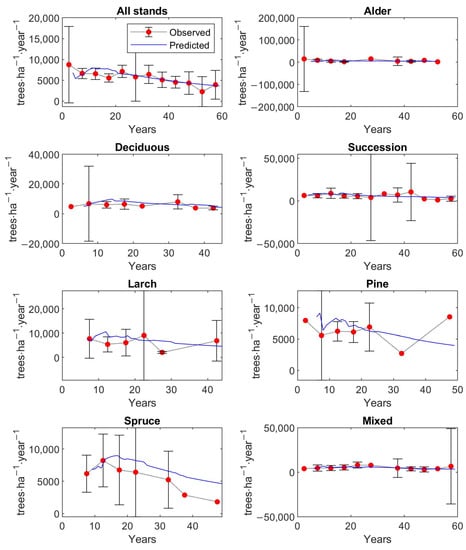
Figure A3.
Verification of the model by the comparison of the observed 5-year average values with average predicted values of stem density, with a 95% confidence interval, according to individual forest types.
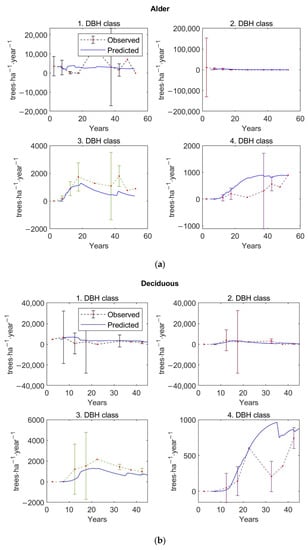
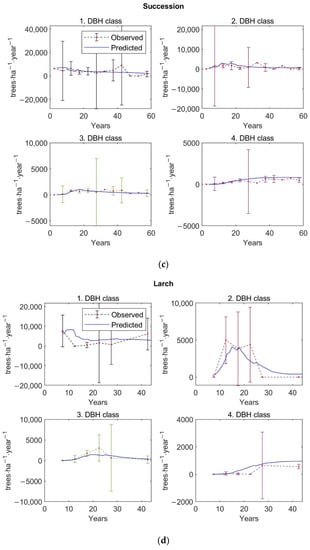
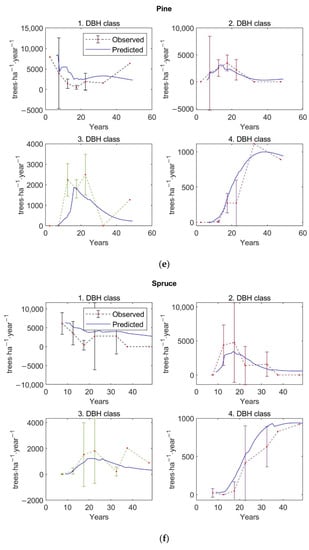
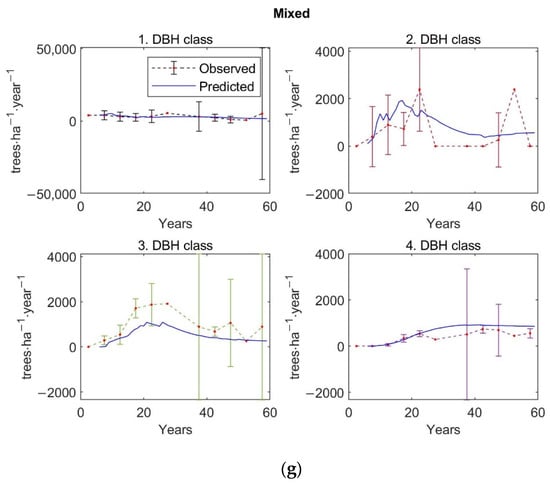
Figure A4.
Verification of the model by the comparison of the observed 5-year average values with average predicted values of stem density distributed according to DBH classes, with a 95% confidence interval, according to individual forest types: (a) alder stand; (b) long-lived deciduous stand; (c) spontaneous succession; (d) larch stand; (e) pine stand; (f) spruce stand; (g) mixed coniferous–deciduous stand.
Appendix E. Simulated Dynamics of Restored Forest Stands under Different Thinning Scenarios
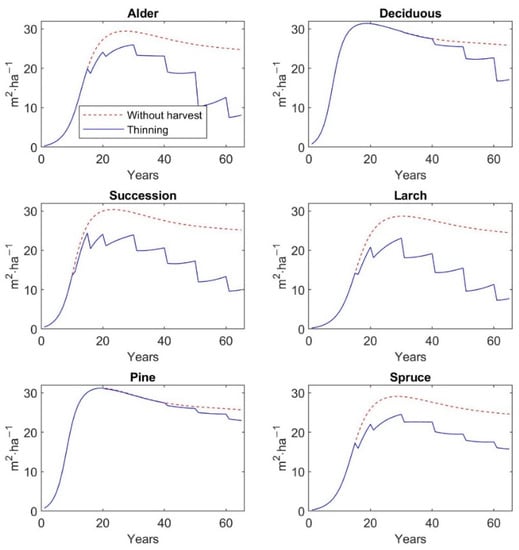
Figure A5.
Predicted basal area over 65 years without harvest and under different thinning regimes and forest types.
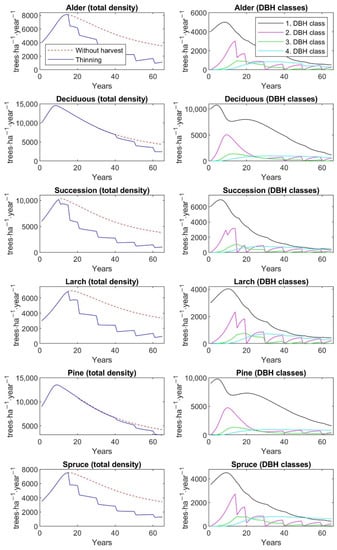
Figure A6.
Predicted stem density and stem density distributed according to DBH classes over 65 years under different thinning regimes and forest types. The total stand density is also predicted without harvest.
References
- Bradshaw, A.D. The reconstruction of ecosystems. J. Appl. Ecol. 1983, 20, 1–17. [Google Scholar] [CrossRef]
- Macdonald, S.E.; Landhausser, S.M.; Skousen, J.; Franklin, J.; Frouz, J.; Hall, S.; Jacobs, D.; Quideau, S. Forest restoration following surface mining disturbance: Challenges and solutions. New Forest. 2015, 46, 703–732. [Google Scholar] [CrossRef]
- Chuman, T. Restoration Practices Used on Post Mining Sites and Industrial Deposits in the Czech Republic with an Example of Natural Restoration of Granodiorite Quarries and Spoil Heaps. J. Landsc. Ecol. 2015, 8, 29–46. [Google Scholar] [CrossRef]
- Zipper, C.E.; Burger, J.; Skousen, J.G.; Angel, P.N.; Barton, C.D.; Davis, V.; Franklin, J. Restoring forests and associated ecosystem services on appalachian coal surface mines. Environ. Manag. 2011, 47, 751–765. [Google Scholar] [CrossRef] [PubMed]
- Alexander, S.; Aronson, J.; Whaley, O.; Lamb, D. The relationship between ecological restoration and the ecosystem services concept. Ecol. Soc. 2016, 21, 34. [Google Scholar] [CrossRef]
- Tolvanen, A.; Aronson, J. Ecological restoration, ecosystem services, and land use: A European perspective. Ecol. Soc. 2016, 21, 47. [Google Scholar] [CrossRef]
- Gurung, K.; Yang, J.; Fang, L. Assessing Ecosystem Services from the Forestry-Based Reclamation of Surface Mined Areas in the North Fork of the Kentucky River Watershed. Forests 2018, 9, 652. [Google Scholar] [CrossRef]
- Larondelle, N.; Haase, D. Valuing post-mining landscapes using an ecosystem services approach—An example from Germany. Ecol. Indic. 2012, 18, 567–574. [Google Scholar] [CrossRef]
- Maiti, S.K.; Ahirwal, J. Ecological restoration of coal mine degraded lands: Topsoil management, pedogenesis, carbon sequestration, and mine pit limnology. In Phytomanagement of Polluted Sites; Elsevier: Amsterdam, The Netherlands, 2019; pp. 83–111. [Google Scholar]
- Mudrák, O.; Frouz, J.; Velichová, V. Understory vegetation in reclaimed and unreclaimed post-mining forest stands. Ecol. Eng. 2010, 36, 783–790. [Google Scholar] [CrossRef]
- Pietrzykowski, M. Soil and plant communities development and ecological effectiveness of reclamation on a sand mine cast. J. Forest Sci. 2008, 54, 554–565. [Google Scholar] [CrossRef]
- Walmsley, A.; Vachová, P.; Hlava, J. Tree species identity governs the soil macrofauna community composition and soil development at reclaimed post-mining sites on calcium-rich clays. Eur. J. For. Res. 2019, 138, 753–761. [Google Scholar] [CrossRef]
- Gypser, S.; Veste, M.; Fischer, T.; Lange, P. Infiltration and water retention of biological soil crusts on reclaimed soils of former open-cast lignite mining sites in Brandenburg, north-east Germany. J. Hydrol. Hydromech. 2016, 64, 1–11. [Google Scholar] [CrossRef]
- Pietrzykowski, M. Tree species selection and reaction to mine soil reconstructed at reforested post-mine sites: Central and Eastern European experiences. Ecol. Eng. X 2019, 3, 100012. [Google Scholar] [CrossRef]
- Sena, K.; Agouridis, C.; Miller, J.; Barton, C. Spoil type influences soil genesis and forest development on an Appalachian surface coal mine ten years after placement. Forests 2018, 9, 780. [Google Scholar] [CrossRef]
- Frouz, J.; Pižl, V.; Cienciala, E.; Kalčík, J. Carbon storage in post-mining forest soil, the role of tree biomass and soil bioturbation. Biogeochemistry 2009, 94, 111–121. [Google Scholar] [CrossRef]
- Frouz, J.; Pöpperl, J.; Přikryl, I.; Štrudl, J. Tvorba Nové Krajiny na Sokolovsku; Sokolovská Uhelná a.s.: Sokolov, Czech Republic, 2007. [Google Scholar]
- Braun Kohlová, M.; Nepožitková, P.; Melichar, J. How Do Observable Characteristics of Post-Mining Forests Affect Their Attractiveness for Recreation? Land 2021, 10, 910. [Google Scholar] [CrossRef]
- Braun Kohlová, M.; Máca, V.; Melichar, J.; Pavelčík, P. How High Is the Recreation Value of Successional Forests Growing Spontaneously on Coal Mine Spoil Heaps? Forests 2021, 12, 160. [Google Scholar] [CrossRef]
- Frouz, J.; Mudrák, O.; Reitschmiedová, E.; Walmsley, A.; Vachová, P.; Šimáčková, H.; Albrechtová, J.; Moradi, J.; Kučera, J. Rough wave-like heaped overburden promotes establishment of woody vegetation while leveling promotes grasses during unassisted post mining site development. J. Environ. Manag. 2018, 205, 50–58. [Google Scholar] [CrossRef]
- Cienciala, E.; Tumajer, J.; Beranová, J.; Zatloukal, V.; Albert, J. Database of Allometric Relationships; IFER–Institute of Forest Ecosystem Research Ltd.: Jílové u Prahy, Czech Republic, 2019; Available online: https://drive.google.com/file/d/102pRwvEK_nDmfVKSbCoXHuBtaztFmGaY/view (accessed on 3 May 2022). (In Czech)
- Usher, M.B. A Matrix Approach to the Management of Renewable Resources, with Special Reference to Selection Forests. J. Appl. Ecol. 1966, 3, 355–367. [Google Scholar] [CrossRef]
- Usher, M.B. A Matrix Model for Forest Management. Biometrics 1969, 25, 309–315. [Google Scholar] [CrossRef]
- Liang, J. Dynamics and management of Alaska boreal forest: An all-aged multi-species matrix growth model. Forest Ecol. Manag. 2010, 260, 491–501. [Google Scholar] [CrossRef]
- Choi, J.; An, H. A Forest Growth Model for the Natural Broadleaved Forests in Northeastern Korea. Forests 2016, 7, 288. [Google Scholar] [CrossRef]
- Pyy, J.; Ahtikoski, A.; Laitinen, E.; Siipilehto, J. Introducing a Non-Stationary Matrix Model for Stand-Level Optimization, an Even-Aged Pine (Pinus sylvestris L.) Stand in Finland. Forests 2017, 8, 163. [Google Scholar] [CrossRef]
- Pyy, J.; Laitinen, E.; Ahtikoski, A. Demonstrating the Effect of Height Variation on Stand-Level Optimization with Diameter-Structured Matrix Model. Forests 2020, 11, 226. [Google Scholar] [CrossRef]
- Liang, J.; Picard, N. Matrix model of forest dynamics: An overview and outlook. Forest Sci. 2013, 59, 359–378. [Google Scholar] [CrossRef]
- Vanclay, J.K. Modeling Forest Growth and Yield: Applications to Mixed Tropical Forests; CAB International: Wallingford, UK, 1994. [Google Scholar]
- Buongiorno, J.; Michie, B.R. A matrix model of uneven-aged forest management. Forest Sci. 1980, 26, 609–625. [Google Scholar]
- Liang, J.; Buongiorno, J.; Monserud, R.A. Growth and yield of all-aged Douglas-fir–western hemlock stands: A matrix model with stand diversity effects. Can. J. For. Res. 2005, 35, 2369–2382. [Google Scholar] [CrossRef]
- Namaalwa, J.; Eid, T.; Sankhayan, P. Amulti-species density-dependent matrix growth model for the dry woodlands of Uganda. For. Ecol. Manag. 2005, 213, 312–327. [Google Scholar] [CrossRef]
- Cropper, W.P., Jr.; Loudermilk, E.L. The interaction of seedling density dependence and fire in a matrix population model of longleaf pine (Pinus palustris). Ecol. Model. 2006, 198, 487–494. [Google Scholar] [CrossRef]
- Price, O.; Bowman, D.M.J.S. Fire-stick forestry: A matrix model in support of skilful fire management of Callitris intratropica R.T. Baker by north Australian Aborigines. J. Biogeogr. 1994, 21, 573–580. [Google Scholar] [CrossRef]
- Melichar, J.; Braun Kohlová, M.; Kaprová, K.; Pavelčík, P.; Frouz, J.; Karel, J.; Krkošková, N. Specialized Map of Production and Non-Production Functions of the Reclaimed Sites for the Mining Site of the Sokolov Coal Basin; Charles University, ATEM–Studio of Ecological Models: Prague, Czech Republic, 2017; Available online: https://drive.google.com/file/d/1FQxHRwMh6I-puwe8ChAc7zqD9obQrMQA/view (accessed on 22 August 2022). (In Czech)
- Vachova, P.; Vach, M.; Skalicky, M.; Walmsley, A.; Berka, M.; Kraus, K.; Hnilickova, H.; Vinduskova, O.; Mudrak, O. Reclaimed Mine Sites: Forests and Plant Diversity. Diversity 2022, 14, 13. [Google Scholar] [CrossRef]
- Lin, C.R.; Buongiorno, J.; Vasievich, M. A multi-species, density-dependent matrix growth model to predict tree diversity and income in northern hardwood stands. Ecol. Model. 1996, 91, 193–211. [Google Scholar] [CrossRef]
- Ralston, R.; Buongiorno, J.; Schulte, B.; Fried, J. Non-linear matrix modeling of forest growth with permanent plot data: The case of uneven-aged Douglas-fir stands. Int. Trans. Oper. Res. 2003, 10, 461–482. [Google Scholar] [CrossRef]
- Ma, W.; Zhou, X.; Liang, J.; Zhou, M. Coastal Alaska forests under climate change: What to expect? For. Ecol. Manag. 2019, 448, 432–444. [Google Scholar] [CrossRef]
- Vonderach, C.; Kändler, G.; Dormann, C.F. Consistent set of additive biomass functions for eight tree species in Germany fit by nonlinear seemingly unrelated regression. Ann. For. Sci. 2018, 75, 49. [Google Scholar] [CrossRef]
- Bronisz, K.; Strub, M.; Cieszewski, C.; Bijak, S.; Bronisz, A.; Tomusiak, R.; Wojtan, R.; Zasada, M. Empirical equations for estimating aboveground biomass of Betula pendula growing on former farmland in central Poland. Silva Fenn. 2016, 50, 1559. [Google Scholar] [CrossRef]
- Cienciala, E.; Černý, M.; Tatarinov, F.; Apltauer, J.; Exnerová, Z. Biomass functions applicable to Scots pine. Trees 2006, 20, 483–495. [Google Scholar] [CrossRef]
- Cienciala, E.; Apltauer, J.; Exnerová, Z.; Tatarinov, F. Biomass functions applicable to oak trees grown in Central-European forestry. J. For. Sci. 2008, 54, 109–120. [Google Scholar] [CrossRef]
- Čihák, T.; Hlásny, T.; Stolariková, R.; Vejpustková, M.; Marušák, R. Functions for the aboveground woody biomass in Small-leaved lime (Tilia cordata Mill.). Lesn. Časopis–For. J. 2014, 60, 150–158. [Google Scholar]
- Johansson, T. Biomass equations for determining fractions of common and grey alders growing on abandoned farmland and some practical implications. Biomass Bioenergy 2000, 18, 147–159. [Google Scholar] [CrossRef]
- Wirth, C.; Schumacher, J.; Schulze, E.-D. Generic biomass functions for Norway spruce in Central Europe—A meta-analysis approach toward prediction and uncertainty estimation. Tree Physiol. 2004, 24, 121–139. [Google Scholar] [CrossRef] [PubMed]
- Wutzler, T.; Wirth, C.; Schumacher, J. Generic biomass functions for Common beech (Fagus sylvatica L.) in Central Europe–predictions and components of uncertainty. Can. J. For. Res. 2008, 38, 1661–1675. [Google Scholar] [CrossRef]
- Brown, T.C.; Daniel, T.C. Modeling Forest Scenic Beauty: Concepts and Application to Ponderosa Pine; Research Paper RM-256. USDA Forest Service: Fort Collins, CO, USA, 1984. [Google Scholar]
- Hull, R.B., IV; Buhyoff, G.J.; Cordell, H.K. Psychophysical Models: An Example with Scenic Beauty Perceptions of Roadside Pine Forests. Landsc. J. 1987, 6, 113–122. [Google Scholar] [CrossRef]
- Cienciala, E.; Zatloukal, V.; Albert, J.; Beranová, J.; Melichar, J. Framework Guidelines for the Management of Reclaimed Forests; IFER–Institute of Forest Ecosystem Research Ltd.: Jílové u Prahy, Czech Republic, 2021; Available online: https://drive.google.com/file/d/10vcA8OTwOwG6yXnwB2RKOlKrRT9lIuw3/view (accessed on 10 June 2022). (In Czech)
- Sklenicka, P.; Molnarova, K. Visual Perception of Habitats Adopted for Post-Mining Landscape Rehabilitation. Environ. Manag. 2010, 46, 424–435. [Google Scholar] [CrossRef] [PubMed]
- Svobodova, K.; Sklenicka, P.; Molnarova, K.; Salek, M. Visual Preferences for Physical Attributes of Mining and Post-Mining Landscapes with Respect to the Sociodemographic Characteristics of Respondents. Ecol. Eng. 2012, 43, 34–44. [Google Scholar] [CrossRef]
- Vacek, Z.; Linda, R.; Cukor, J.; Vacek, S.; Šimůnek, V.; Gallo, J.; Vančura, K. Scots pine (Pinus sylvestris L.), the suitable pioneer species for afforestation of reclamation sites? For. Ecol. Manag. 2021, 485, 118951. [Google Scholar] [CrossRef]
- Melichar, J.; Walmsley, A.; Cienciala, E.; Beranová, J.; Berka, M.; Braun Kohlová, M.; Černý, M.; Holá, Š.; Nepožitková, P.; Pavelčík, P.; et al. Optimization of Management of Forest Restoration on Sites Affected by Surface Mining; Research Report; Project No. QK1710241; Ministry of Agriculture of the Czech Republic; Charles University, Czech University of Life Sciences Prague, IFER–Institute of Forest Ecosystem Research Ltd.: Prague, Czech Republic, 2020. [Google Scholar]
- Vacek, Z.; Cukor, J.; Vacek, S.; Podrázský, V.; Linda, R.; Kovařík, J. Forest biodiversity and production potential of post-mining landscape: Opting for afforestation or leaving it to spontaneous development? Cent. Eur. For. J. 2018, 64, 116–126. [Google Scholar] [CrossRef]
- Frouz, J.; Dvoršík, P.; Vávrová, A.; Doušová, O.; Kadochová, Š.; Matějíček, L. Development of canopy cover and woody vegetation biomass on reclaimed and unreclaimed post-mining sites. Ecol. Eng. 2015, 84, 233–239. [Google Scholar] [CrossRef]
- Jačka, L.; Walmsley, A.; Kovář, M.; Frouz, J. Effects of different tree species on infiltration and preferential flow in soils developing at a clayey spoil heap. Geoderma 2021, 403, 115372. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).