Abstract
Oscillation drying is one of the possible approaches for reducing drying time and limiting drying defects of hardwood timber. This study aimed to design oscillation-drying schedules for beech (Fagus sylvatica L.) timber using the response surface methodology (RSM) and to develop an empirical model describing relationships between drying time, drying rate, moisture content gradient after drying, and the parameters of oscillation drying, i.e., dry-bulb temperature increase, equilibrium moisture content (EMC) decrease, and the duration of phase #1 in the drying schedule. The design employed 8 unique drying schedules for which early stage of drying was studied. The Gompertz model was used to describe the change in moisture flux as a function of moisture content, with estimated parameters of the model used to determine relations between the maximum flux at the initial moisture content, the maximum rate of flux change, and the critical moisture content for the maximum rate of flux change for each oscillation-drying schedule. Analysis of variance (ANOVA) revealed that the decrease in EMC was the only factor significantly influencing oscillation drying. For the most intense oscillation-drying schedule, maximum moisture flow was ca. 75% higher compared with the control drying schedule. Drying processes that accounted for a decrease of EMC from 15% to 12% were characterized by significantly shorter drying time (by 35.8%), 52.6% higher drying intensity, and ca. two times larger moisture content gradient. These results confirm theoretical findings relating the increase of oscillation-drying intensity with the difference in wet-bulb temperature between phases of the drying processes.
1. Introduction
Hardwood sawn timber is attractive material for high-value end-use products, such as furniture and flooring. Beech and oak are considered to be among the most difficult European species to dry as they are especially prone to drying defects, such as checking, case-hardening, warping, honeycomb, discoloration, etc. The basic principle for drying hardwood sawn timber is to reduce drying intensity at early stages of the process, i.e., for the mean moisture content higher than ca. 30% [1,2,3,4]. The use of low temperature and high relative humidity of drying air reduces moisture content differences between the outer and core layers of boards, as well as decreasing drying stress [5]. Mild drying conditions also preserve natural wood color [6]. Although such conditions reduce drying defects, they also entail longer drying times and increased energy consumption. Reductions in drying time are usually obtained by modifying conventional drying schedules [7,8,9]. Aquino-González et al. [10] studied drying time and drying quality using a 22 factorial design (response surface methodology (RSM)). Their analysis evaluated kiln-drying of chalamite (Pinus pseudostrobus Lindl.) wood, using two drying schedules, i.e., accelerated and mild, in combination with two options of air velocity. Multifactor analysis of variance (ANOVA) revealed that drying time was affected by drying schedule options, while drying quality depended both on drying schedule and air-velocity options. The accelerated drying schedule at higher air velocity reduced both drying time and wood defects. The reported results on improved drying quality were obtained for intensive drying processes of easy-to-dry softwood timber.
Langrish et al. [11] stated that the interlaced drying conditions result in better wood quality compared with continuous drying. When they dried red beech at a dry-bulb temperature of 45 °C and wet-bulb depression of 10 K, it took longer to obtain final moisture content than continuous drying under the same conditions, but produced timber without the honeycomb or severe case-hardening observed with continuous drying. Chadwick and Langrish [12] analyzed the drying time and timber quality of red mahogany (Eucalyptus pellita) timber in continuous versus oscillating drying climates. Dry-bulb temperature during continuous drying ranged from 50 to 70 °C, while oscillation drying was characterized by dry- and wet-bulb temperature values that were 5 and 3 K higher, respectively, as well as by interlaced phases of drying and relaxation. Oscillation-drying time was 20% shorter than with continuous drying. Furthermore, there was no significant difference in drying defects between continuous and oscillation drying. Moreover, Sackey et al. [13] found that the positive impact of oscillation drying of 105 mm-square Pacific coast hemlock was more distinct during the early stages of drying for moisture content values above the fiber saturation point (FSP) as a drying time reduction of 10%–14% was observed.
Riehl and Welling [14] found that oscillation drying produces lower stress in timber compared with continuous drying, as the oscillating climate promotes mechano-sorptive creep in surface layers of timber, resulting in stress relaxation. Tomad et al. [15] similarly concluded that oscillation drying produced stress relaxation as a result of mechano-sorptive creep, and that shorter oscillation cycles produced lower levels of stress after stress reversal. According to Salin [16], shorter drying time and better lumber quality using an oscillation processes depend on wet-bulb temperature. Sackey et al. [13] analyzed the effect of dry-bulb and wet-bulb temperature oscillations on hemlock kiln drying. The impact of oscillation-drying schedules on drying rate was the result of faster moisture loss in the early stages of drying. In addition, a large amplitude in dry-bulb temperature produced less case-hardening, reduced variation of the target moisture content and gave a lower difference between core and shell moisture contents. Another issue related to oscillation drying was energy consumption. Milić et al. [9] found that oscillation of drying air parameters had only a small influence on total energy consumption, but concluded that energy consumption could be lowered further compared with conventional drying processes if oscillation drying shortened drying time.
The objectives of the present study were to: (a) determine and model the kinetics of oscillation drying with regard to variation of drying air parameters and drying phase durations, (b) design schedules for oscillation drying of beech timber, and (c) apply the response surface modeling method to identify optimal oscillation-drying schedule and to find the factors that most significantly influence oscillation drying.
2. Materials and Methods
2.1. Sample Preparation
European beech (Fagus sylvatica L.) wood was used in the study due to difficulties in its drying, i.e., long drying times and susceptibility to defects. Wood was obtained from green logs, i.e., the initial moisture content was ca. 90%. The mean oven-dry density of the material was 710 kg/m3. A total of 24 quarter-sawn strips with green dimensions of 100—30—500 mm (for the radial, tangential and longitudinal directions, respectively) were first sawn from the logs according to the pattern depicted in Figure 1a. Prior to drying experiments, the strips were prevented from uncontrolled moisture content changes. Each strip provided two sub-samples for determining initial moisture content with the oven-dry method (Figure 1b), made according to procedures for preparing kiln sample boards used in controlling timber moisture content in drying [2,17]. The initial moisture content was estimated for each strip as the mean of readings obtained from the sub-samples. The main samples were 400 mm long (Figure 1b) and were subjected to drying in a laboratory-scale convective kiln. Three individual samples were used to study each drying process. The kiln-drying parameters, i.e., dry-bulb temperature and relative humidity, were computer monitored and controlled [18]. Air velocity was constant in all drying experiments and equal to 2.0 m/s. The main samples were periodically weighed to determine mass loss during drying and estimate moisture content changes over time. Immediately after the full drying was completed, each main sample was cut into sub-samples to determine thickness variation of the final moisture content (Figure 1c). Variation was estimated as the maximum difference in the final moisture content between the core and shell of each sample.
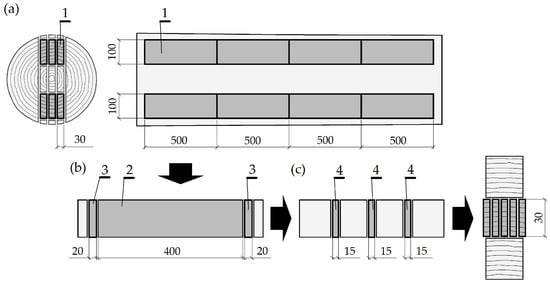
Figure 1.
Scheme of sample preparation: (a) initial sawing of boards from a log (1—strip with green dimensions), (b) cutting pattern of samples before drying (2—main sample, 3—sub-samples to determine initial moisture content), (c) cutting pattern of samples after drying (4—additional sub-samples for determining in thickness variation of final moisture content).
2.2. Design of Oscillation-Drying Schedules and Processes
Air parameters during kiln drying are meant to provide mild drying intensity so that the risk of drying wood defects is reduced. However, in the interest of reducing drying time, kiln parameters are adjusted to speed drying, although this usually results in lower drying quality due to the development of stresses in the wood and surface checks. Therefore, modified drying schedules should account for cycling changes of drying air parameters, i.e., more intensive drying should be interlaced with drying ensuring a phenomenon of mechano-sorptive creep, leading to stress relaxation and a reduced likelihood of drying defects [8,15,16,19]. In this study, a reference non-oscillation drying schedule with constant dry-bulb temperature of 40 °C and equilibrium moisture content (EMC) of 15% until the target moisture content was achieved. RSM was used to design oscillation-drying schedules and processes. A two-level (23) factorial experimental design was used to generate data for a response surface statistical model [20]. The oscillation-drying schedules consisted of a number of interlaced two phases, i.e., phase #1 was characterized by a possible decrease of EMC from 15% to 12%, while during phase #2, an increase of the dry-bulb temperature from 40 to 50 °C was accounted. Two durations of phase #1 were evaluated, i.e., 2 or 4 h, while the duration of phase #2 was always 2 h. Dry-bulb temperature increase, the EMC decrease, and phase #1 duration were considered as three independent variables, designated , and , respectively (Table 1).

Table 1.
Levels of independent variables used for the design of oscillation-drying schedules and processes.
The independent variables were coded according to the following formulas: , , and . The design resulted in 8 schedules for which drying was studied (in Table 2, schedules #1 and #5 are conventional reference schedules). Target moisture content was 30% in all studied options of drying due to the fact that the greatest influence of oscillation drying was expected to occur in the early stages of drying, i.e., for timber moisture content above FSP [13].

Table 2.
Independent and coded variables together with oscillation-drying schedules based on the two-level (23) factorial design.
3. Results and Discussion
3.1. Drying Curve Analysis
The drying processes were performed according to the oscillation-drying schedules resulting from the two-level (23) factorial design (Table 2). The mass of the main samples was weighed at selected time instants and recalculated as moisture content at the end of each drying process. The resulting drying curves relate moisture content to drying time (Figure 2).
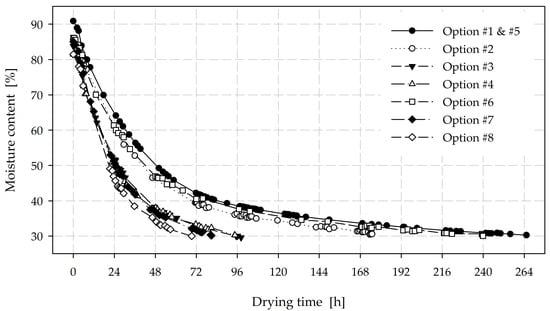
Figure 2.
Comparison of drying curves for various drying schedules.
Moisture flux () was calculated for each process according to Equation (1):
where: m (g)—mass of main sample, A (m2)—sample surface area for water evaporation (here 0.0934 m2), τ (h)—drying time, and i—time instants of mass measurement.
Moisture flux values were estimated with the asymmetrical sigmoid Gompertz model of the form [21]:
where: α; (g/(m2·h))—horizontal asymptote, here the maximum flux at the initial moisture content, κ; (1/%)—the maximum rate of flux change, γ (%)—the inflection point of the Gompertz model, here the critical moisture content (MCC) at the maximum rate of flux change.
Drying curves were also analyzed by calculating the first derivative of the Gompertz model at the inflection point (γ) and constructing tangent lines to the curves. The tangent lines and the horizontal asymptotes (the maximum flux at the initial moisture content) were used to find their intersections, indicating transition points at which a significant decrease in moisture flux was observed [22,23]. Moisture content (MCT) was determined for each transition point.
The estimated parameters of the Gompertz model, as well as the quantities derived from the model, are given in Table 3. High values of the coefficient of determination (from 0.785 to 0.991) were obtained for all drying processes. This clearly shows that the Gompertz model accurately predicted changes in moisture flux with moisture content. The parameters of the model were related to the independent variables used, i.e., dry-bulb temperature increase, EMC decrease, and duration of phase #1. The critical moisture content (MCC) values at the inflection point (γ) of the model were always lower for oscillation-drying schedules compared with the reference-drying schedules (options #1 and #5). The lowest critical moisture contents were found for the processes accounting for simultaneous dry-bulb temperature increase and EMC decrease (options #4 and #8). The critical moisture content value can be interpreted as being the state at which water diffusion starts to be the dominating mechanism of drying. Therefore, the lower the critical moisture content, the longer the phase of intensive capillary transport. This clearly shows that the oscillation schedules allow faster drying. This conclusion is also supported by the analysis of the values of the derivative of the flux with respect to moisture content at the critical moisture content, i.e., the maximum moisture flow. It was found for the oscillation-drying process option #8, the maximum moisture flow was ca. 75% higher compared with the reference-drying processes (options #1 and #5).

Table 3.
Estimated parameters of the Gompertz model together with the quantities derived from the model.
The change in moisture flux with moisture content is also shown in Figure 3a (upper left plot) for the most intensive oscillation-drying process (option #8) and the reference-drying processes (option #1 and #5). The discreet flux data and the model results were supplemented by horizontal asymptotes (the maximum flux at the initial moisture content), the inflection point (the critical moisture content) and the transition moisture content. Comparison of all drying processes estimated with the Gompertz model is also given Figure 3b (upper right plot). The moisture flow as a function of moisture content, calculated from the first derivative of the fitted Gompertz model, is shown in Figure 3 (bottom right plot), with maximum moisture flow marked with symbols for each drying process.
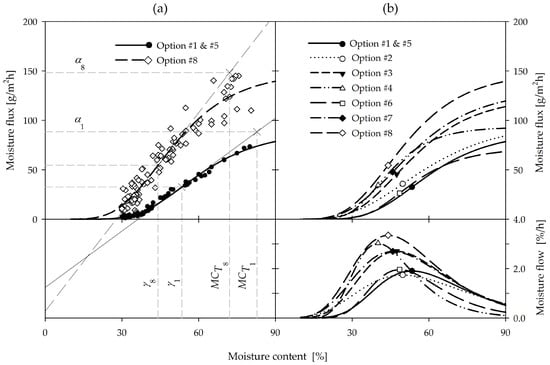
Figure 3.
Moisture flux changes with moisture content (upper plots) for the most intensive oscillation- and reference-drying schedules (a) as well as all analyzed schedules (b) together with moisture flow (bottom right plot).
3.2. Designing Oscillation Drying
RSM was applied to describe the influence of coded variables, i.e., dry-bulb temperature increase (x1), EMC decrease (x2), and phase #1 duration (x3) on drying time (y1), moisture flow (y2) and moisture content gradient (y3). A first order polynomial with the following form was fitted:
where y is the predicted response (i.e., drying time, moisture flow or moisture content gradient), is the y-intercept, and , and are first-order effects. The input data for RSM modeling are presented in Table 4.

Table 4.
Experimental (input) data for the response surface methodology (RSM) model.
The results of ANOVA of the responses are presented in Table 5. Calculated F values are higher than the critical values of the F-distribution (Fcrit) for the drying time (y1) and moisture flow (y2). Therefore, we reject the null hypothesis that all independent variables fail to improve the model (). In the case of the moisture content gradient (y3), the value of F was higher than Fcrit for a lower confidence interval, i.e., 0.90. When the condition F > Fcrit is satisfied it is possible to construct an alternative hypothesis that at least one of the independent variables of the model significantly influenced the dependent variable. The rejection of the null hypothesis made it possible to perform a more detailed analysis of the model to verify the significance of independent variables, i.e., dry-bulb temperature increase, EMC decrease and phase #1 duration, on the progress and effects of oscillation drying of beech timber.

Table 5.
Results from analysis of variance (ANOVA) for the RSM model.
The results of model estimation are given in Table 6. The coefficients to were determined by the least squares method using STATISTICA v.13.3 software (TIBCO Software Inc., Palo Alto, CA, USA). Due to possible linear dependence of the variables, backward stepwise regression was applied to exclude statistically insignificant model terms at a confidence level of 0.95 [24]. It was found for all modeled responses, i.e., drying time (y1), drying rate (y2) and moisture content gradient (y3), that the estimations were characterized by high R2 values of 0.993, 0.928 and 0.864, respectively. Backward stepwise analysis clearly showed that only the intercept () and coefficient were significantly (p < 0.05) related to the independent variable x2, i.e., EMC decrease. Other model coefficients, i.e., and that are related to dry-bulb temperature (x1) and phase #1 duration (x3) are statistically non-significant (p > 0.05). Therefore, the original model (Equation (3)) was reduced to a simpler form (Equation (4)):

Table 6.
Estimated coefficients of the RSM model.
The simplified model in all cases provided good fit (R2 > 0.8) (Table 6).
Statistical analysis indicates that the decrease of EMC (x2) is the only factor significantly influencing the oscillation drying of beech timber. Moreover, the simplified model (Equation (4)) clearly indicates the linear relationship between responses (drying time, moisture flow, moisture content gradient) and the EMC decrease in both phases of oscillation drying. In comparison, dry-bulb temperature increase (x1) and phase #1 duration (x3) have no significant influence on drying. The substantial influence of the EMC decrease (x2) supports the theoretical findings reported by Salin [16], who stated that reduced drying time during oscillation processes is attributable to increased wet-bulb depression. The present analysis clearly shows that the largest reduction in drying time and the greatest drying intensity were obtained with oscillation drying schedule #8. This schedule was characterized by decrease in dry-bulb temperature from 50 to 40 °C and reduced EMC from 15% to 12%, for phases #1 and #2, respectively. Schedule #8 resulted in the highest difference in wet-bulb temperature between the phases, i.e., from 46.4 to 34.5 °C.
The fitted simplified model was used to test the influence of the independent variable on drying progress and the effects of oscillation drying. It was found for the reference process, i.e., drying without a decrease in EMC (ξ2 = 0%; x2 = −1), that drying time (y1) was 236.2 h (for moisture content range 80%–30%), the moisture flow (y2) amounted to 1.9%/h, and the moisture content gradient (y3) was 4.5%. The drying processes accounting for the decrease of EMC from 15% to 12% (ξ2 = 3%; x2 = 1) were characterized by significantly shorter drying time by 35.8% (i.e., y1 = 85.5 h), higher drying intensity by 52.6% (y2 = 2.9%/h) and almost twice the moisture content gradient (y3 = 8.8%).
Surface checks were not observed at the end of the most intensive drying process (option #8). This supports the positive influence of the oscillation of wet-bulb temperature on stress relaxation as a result of mechano-sorptive creep [13,15]. Thus, the intensification of mechano-sorptive creep reduced a risk of checks despite the high moisture content gradient. Tomad et al. [15] stated that wet-bulb temperature oscillation in the early stage of drying had no negative influence on stress development during the second stage, i.e., for moisture content below 30% and intensive drying.
4. Conclusions
- 1.
- The Gompertz model was able to describe the kinetics of oscillation drying, i.e., changes in moisture flux in relation to moisture content. The model developed using the RSM approach allowed determination of relations between maximum flux at the initial moisture content, maximum rate of flux change and critical moisture content at the maximum rate of the flux change for each oscillation-drying schedule.
- 2.
- The critical moisture content was interpreted as the state at which water diffusion starts to be the dominant mechanism of drying. The critical moisture content was thus recognized as an indicator of duration of capillary transport during drying, i.e., the lower the critical moisture content, the longer the capillary drying phase. The lowest values of critical moisture content were found for drying schedules with simultaneous dry-bulb temperature increase and EMC decrease (schedules #4 and #8). Oscillation-drying schedule #8 resulted in the faster drying.
- 3.
- Statistical analysis indicated that EMC decrease (x2) was the only parameter significantly influencing the oscillation-drying processes of beech timber. The derived empirical model quantified linear relations between drying time, moisture flow, moisture content gradient and the EMC decrease in both phases of oscillation drying.
- 4.
- The theoretical findings reported by Salin [16] were confirmed by the present analysis. It was deduced that drying time reduction and increased oscillation-drying intensity were influenced by the difference in wet-bulb temperature between phases #1 and #2 during drying.
Author Contributions
Conceptualization, J.M.; methodology, J.M.; validation, J.M.; formal analysis, J.M.; investigation, J.M. and W.O.; writing—original draft preparation, J.M. and W.O; writing—review and editing, W.O and J.M..; preparing tables and figures, J.M.; performing statistical analysis, J.M.; discussing the results, J.M. and W.O. The authors have read and agreed to the published version of the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
The paper was financed within the framework of the Ministry of Science and Higher Education programme “Regional Initiative of Excellence” in years 2019–2022, Project No. 005/RID/2018/19.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Boone, R.S.; Kozlik, C.J.; Bois, P.J.; Wengert, E.M. Dry Kiln Schedules for Commercial Woods-Temperate and Tropical. General Technical Report FPL-GTR-57; Forest Products Laboratory: Madison, WI, USA, 1988. [Google Scholar]
- Simpson, W.T. Dry Kiln Operator’s Manual. U.S. Department of Agriculture, Forest Service; Forest Products Laboratory: Madison, WI, USA, 1991. [Google Scholar]
- Denig, J.; Wengert, E.M.; Simpson, W.T. Drying Hardwood Lumber. General Technical Report FPL-GTR-118; Forest Products Laboratory: Madison, WI, USA, 2000. [Google Scholar]
- Keey, R.B.; Langrish, T.A.G.; Walker, J.C.F. Kiln-Drying of Lumber; Springer: Berlin, Germany, 2000. [Google Scholar]
- McMillen, J.M. Stresses in Wood during Drying. Report 1652; Forest Products Laboratory: Madison, WI, USA, 1958. [Google Scholar]
- Dzurenda, L.; Deliiski, N. Convective drying of beech lumber without color changes of wood. Drvna Ind. 2012, 63, 95–103. [Google Scholar] [CrossRef][Green Version]
- Scholl, M.S.; Blankenhorn, P.R.; Stover, L.R.; Ray, C.D. Reduction in kiln-drying time for black cherry lumber. For. Prod. J. 2005, 55, 77–82. [Google Scholar]
- Milić, G.; Kolin, B.; Lovrić, A.; Todorović, N.; Popadić, R. Drying of beech (Fagus sylvatica L.) timber in oscillation climates: Drying time and quality. Holzforschung 2013, 67, 805–813. [Google Scholar] [CrossRef]
- Milić, G.; Kolin, B.; Todorović, N.; Gorišek, Ž. Energy consumption of beech timber drying in oscillation climates. Drvna Ind. 2014, 64, 309–314. [Google Scholar] [CrossRef]
- Aquino-González, L.A.; Rodríguez-Ramírez, J.; Méndez-Lagunas, L.L.; Sandoval-Torres, S. Evaluation of drying schedules for chalamite wood (Pinus pseudostrobus). Madera Bosques 2010, 16, 35–46. [Google Scholar] [CrossRef][Green Version]
- Langrish, T.A.G.; Keey, R.B.; Kumar, M. Improving the quality of timber from red beech (N. fusca) by intermittent drying. Dry Technol. 1992, 10, 947–960. [Google Scholar] [CrossRef]
- Chadwick, W.B.; Langrish, T.A.G. A comparison of drying time and timber quality in the continuous and cyclic drying of Australian turpentine timber. Dry Technol. 1996, 14, 895–906. [Google Scholar] [CrossRef]
- Sackey, E.; Avramidis, S.; Oliveira, L. Exploratory evaluation of oscillation drying for thick hemlock timbers. Holzforschung 2004, 58, 428–433. [Google Scholar] [CrossRef]
- Riehl, T.; Welling, J. Taking advantage from oscillating climate conditions in industrial timber drying processes. In Proceedings of the 8th International IUFRO Wood Drying Conference, Brasov, Romania, 24–29 August 2003; pp. 171–177. [Google Scholar]
- Tomad, S.; Matan, N.; Diawanich, P.; Kyokong, B. Internal stress measurement during drying of rubberwood lumber: Effects of wet-bulb temperature in various drying strategies. Holzforschung 2012, 66, 645–654. [Google Scholar] [CrossRef]
- Salin, J.-G. A theoretical analysis of timber drying in oscillating climates. Holzforschung 2003, 57, 427–432. [Google Scholar] [CrossRef]
- Taylor, A.M.; Young, T.M.; Maschl, G. Error in estimates of the moisture content of white oak kiln sample boards. Dry Technol. 2009, 27, 1235–1239. [Google Scholar] [CrossRef]
- Raczkowski, J.; Olek, W.; Guzenda, R. Moisture evaporation rates from sapwood and heartwood samples of Douglas fir (Pseudotsuga menziesii Franco) green wood. Holz Roh Werkst 2000, 58, 247–252. [Google Scholar] [CrossRef]
- Hanhijärvi, A. Creep deformation in drying wood. In Fundamentals of Wood Drying; Perré, P., Ed.; A.R.BO.LOR.: Nancy, France, 2007; pp. 157–174. [Google Scholar]
- Box, G.E.P.; Draper, N.R. Response Surfaces, Mixtures, and Ridge Analyses; Willey: Hoboken, NJ, USA, 2007. [Google Scholar]
- Seber, G.A.F.; Wild, C.J. Nonlinear Regression; John Wiley & Sons: Hoboken, NJ, USA, 2003. [Google Scholar]
- Straže, A.; Gorišek, Ž. Research on internal and external mass transfer at convective drying of European beechwood (Fagus sylvatica L.). In Proceedings of the COST E53 “Quality Control for Wood and Wood Products” Meeting and EDG Drying Seminar “Improvement of Wood Drying Quality by Conventional and Advanced Drying Techniques”, Bled, Slovenia, 21–23 April 2009; pp. 93–102. [Google Scholar]
- Rajewska, K.; Smoczkiewicz-Wojciechowska, A.; Majka, J. Intensification of beech wood drying process using microwaves. Chem. Process. Eng. 2019, 40, 179–187. [Google Scholar]
- Chatterjee, S.; Hadi, A.S. Regression Analysis by Example, 5th ed.; Wiley: Hoboken, NJ, USA, 2012. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).