Uniform Page Migration Problem in Euclidean Space

Abstract

The page migration problem in Euclidean space is revisited. In this problem, online requests occur at any location to access a single page located at a server. Every request must be served, and the server has the choice to migrate from its current location to a new location in space. Each service costs the Euclidean distance between the server and request. A migration costs the distance between the former and the new server location, multiplied by the page size. We study the problem in the uniform model, in which the page has size $D=1$. All request locations are not known in advance; however, they are sequentially presented in an online fashion. We design a $2.75$-competitive online algorithm that improves the current best upper bound for the problem with the unit page size. We also provide a lower bound of $2.732$ for our algorithm. It was already known that 2.5 is a lower bound for this problem.

1. Introduction

The page migration problem is a classical formulation of efficient memory management in a shared memory multiprocessor system comprising a network of processors having their own local memories. In this problem, we are given a sequence of requests issued by processors to access a single shared data object, called a page. Each request must be served via communication between the processor issuing the request and the processor holding the page at the time of the request. The service for the request costs the distance of the communication. After each service, the page is allowed to migrate from the current processor to a new processor before the next request is issued. The migration of the page costs the distance of the migration multiplied by the page size. The objective of the page migration problem is to minimize the total costs of services and migrations (see Section 2 for a formal definition of this problem). This problem can also be viewed as a formulation of general situations for managing shared information in a distributed network, such as the efficient allocation of each shared data object to be accessed by a distributed program running on the network [1].

Black and Sleator [2] first studied online algorithms for the page migration problem via competitive analysis. Some basic notions of competitive analysis are given in Section 2. Chrobak, Larmore, Reingold, and Westbrook [3] studied this problem on continuous metric spaces as well as networks. They proposed a $\left(2+1/2D\right)$-competitive randomized algorithm on trees against oblivious adversaries, together with the same lower bound as this competitiveness even at two points, where $D$ is a positive integer representing the page size. They also proved that any randomized page migration algorithm on ${\text{ℝ}}^n$ can be derandomized while preserving its competitiveness. As any page migration algorithm on a space can be generalized on Cartesian products of the space [2], a $\left(2+1/2D\right)$-competitive deterministic algorithm on ${\text{ℝ}}^n$ under $L^1$ norm can be obtained through generalizing the algorithm on trees in ${\text{ℝ}}^n$ [3]. For general metric spaces, Westbrook [4] proposed a $c\left(D\right)$-competitive randomized algorithm against oblivious adversaries, where $c\left(D\right)$ is a function defined in [4] that tends toward $2.618$ as $D$ grows large. Derandomizing this algorithm on ${\text{ℝ}}^n$, we have a $c\left(D\right)$-competitive deterministic algorithm on ${\text{ℝ}}^n$ under any norm [3].

Moreover, $2+1/2D$ is a lower bound for any randomized or deterministic algorithm in the interval $\left[0, 1\right]$ [3]. This lower bound is also admitted on ${\text{ℝ}}^n$ under $L^p$ norm. This is because, for the interval $I=\left[0, 1\right]$ on a dimension $k$ in ${\text{ℝ}}^n$, any online algorithm A locating its server in ${\text{ℝ}}^n\setminus I$ for requests only in $I$ has a cost of at least that of a certain algorithm locating its server only in $I$, i.e., projection on the kth coordinate of A’s server location if the projection is in $I$, and the closer endpoint of $I$ otherwise. It is a longstanding open question whether we can close the gap of $c\left(D\right)$ and $2 + 1/2D$ under $L^p$ norm even with any $p\ge 2$.

In this paper, we partially answer this question by proposing a $2.75$-competitive deterministic algorithm on ${\text{ℝ}}^n$ under $L^2$ norm for the case $D=1$. We note that the competitiveness improves $c\left(1\right)$, which is equal to $2.8$ as mentioned in [4]. We also provide a lower bound of $2.732$ for our algorithm. Our algorithm is extremely simple: it maintains the page at the center of two special points, both initially located at the initial location of the server. Upon each request, the algorithm chooses one of the points farther from the requested location and moves the point to the requested location; the other point does not move. This algorithm can be viewed as a natural extension of the $\left(2 + 1/2D\right)$-competitive algorithm under $L^1$ norm of [3]. We note that if there exists a $\left(2 + 1/2D\right)$-competitive algorithm under $L^2$ norm, then it would have to behave on any line in the same way as the $\left(2 + 1/2D\right)$-competitive algorithm of [3]. The setting of the unit page size, i.e., $D=1$ is called the uniform model in the context of data management problems including the page migration problem [1,5,6,7].

Other previous results for the page migration problem are as follows. Bartal, Charikar, and Indyk [8] proposed a $4.086$-competitive deterministic algorithm for general networks. For trees and uniform networks, Black and Sleator [2] presented 3-competitive deterministic algorithms, together with the lower bound of 3 even at two points. The first deterministic lower bound larger than 3 for general networks was $3.148$ [3], which was improved to $3.168$ by Matsubayashi [5]. Although these lower bounds, larger than $3$, were proved only for $D=1$, the first lower bound of $3+\Omega \left(1\right)$ was recently proved [9], where $\Omega$ notation is with respect to $D$. For three points, $3$-competitive deterministic algorithms with $D\in \left\{1,2\right\}$ [3,10] and a $\left(3+1/D\right)$-competitive deterministic algorithm with $D\ge 3$ [10] were proposed. The latter algorithm asymptotically matches the lower bound of $3+\Omega \left(1/D\right)$ on three points for every $D\ge 3$ [10]. As for randomized algorithms against adaptive online adversaries, a $3$-competitive algorithm for general metric spaces was proposed in [4] and the upper bound of $3$ is also a lower bound on two points [11]. As for a randomized algorithm against oblivious adversaries, Lund, Reingold, Westbrook, and Yan [12] proved that the optimal competitiveness of $2+1/2D$ can be achieved even on uniform networks.

The rest of this paper is organized as follows. Some preliminaries are given in Section 2. We define our algorithm on ${\text{ℝ}}^n$ under $L^2$ norm and prove its $2.75$ competitiveness in Section 3. In Section 4, we prove a lower bound of $2.732$ for our algorithm. We conclude the paper with remarks and future works in Section 5.

2. Preliminaries

Let $M$ be a metric space with a distance function $\delta$. For a given initial page location $s_0\in M$, a sequence of requests $r_1,\dots ,r_n\in M$, and a page size $D\in {\text{ℤ}}^{+}$, the page migration problem is to compute page locations $s_1,\dots ,s_n\in M$ such that the cost function ${\sum }_{i=1}^n\left(\delta \left(s_{i-1},r_i\right)+D·\delta \left(s_{i-1},s_i\right)\right)$ is minimized. We call $s_i$ a server.

An online algorithm must compute $s_i$ without any information regarding $r_{i+1},\dots ,r_n$, whereas an offline algorithm may compute $s_i$ using the entire sequence of requests $r_1,\dots ,r_n$. An adversary against an online algorithm A generates a sequence of requests given to A and computes an output sequence for the generated requests. If A is deterministic, then the adversary generates requests using the definition of A, or equivalently, the information of the actual behavior of A, and computes its own output according to an optimal offline algorithm OPT. The deterministic algorithm A is $\mathrm{c}$-competitive if $cos{t}_A\left(s_0,\sigma \right)\le c·cos{t}_{OPT}\left(s_0,\sigma \right)+\alpha$ for the initial server $s_0$ and any sequence $\sigma$ of requests, where $cos{t}_A$ and $cos{t}_{OPT}$ are costs of A and OPT, respectively, and $\alpha$ is a constant. For randomized online algorithms, there are two types of adversaries. An adversary is said to be oblivious if it generates requests in advance only using the definition of A, i.e., without any information about the random behavior of A and computes its own output according to OPT. In contrast, an adaptive online adversary generates requests using information of the random behavior of A and computes its own output in an online fashion. The competitiveness of a randomized online algorithm against oblivious or adaptive online adversaries is defined in a similar way to that of a deterministic online algorithm, except that expected values are used for randomized costs.

One commonly used technique for proving the competitiveness of an online algorithm A is to utilize a potential function $\Phi$, which typically maps the situation at a point of time, such as the page locations of A and OPT, to a real value. More specifically, we suitably divide the sequence of the online processes of A and OPT into certain events. Our goal is to define the value of $\Phi$ in such a way that the initial value of $\Phi$ is at most some constant $\beta$, $\Phi$ is always at least some constant $-\gamma$ and that $\Delta cos{t}_A+\Delta \Phi \le c·\Delta cos{t}_{OPT}$ for any event, where $\Delta$ denotes the change of values by the event. Summing the inequality over all events for an initial server $s_0$ and a request sequence $\sigma$, we have $cos{t}_A\left(s_0,\sigma \right)\le c·cos{t}_{OPT}\left(s_0,\sigma \right)+\beta +\gamma$, which means that A is $c$-competitive.

3. Algorithm and Its Upper Bound Analysis

We focus on the page size $D=1$ and the metric space ${\text{ℝ}}^n$ under $L^2$ norm $\delta$ for $n\ge 1$. We state our deterministic algorithm, called PQ, in the following paragraph. Intuitively, the algorithm determines the location of the page using two locations from previous requests. We prove the competitiveness of $2.75$, claimed in Theorem 1, using a potential function $\Phi$. As mentioned in Section 2, defining suitable events and showing that $\Delta cos{t}_{PQ}+\Delta \Phi \le 2.75\Delta cos{t}_{OPT}$ for any defined event is sufficient. For the proof of the theorem, we need to show an inequality different from a triangle inequality. We separately provide a technical part for that inequality as Lemma 1. The lemma is about points computed by the algorithm.

Algorithm PQ. 

This algorithm maintains the server at the center of two points $p$ and $q$, both of which are initially located at the initial server location. Upon each request at location $r$, if $\delta \left(p,r\right)\ge \delta \left(q,r\right)$, then $p$ moves to $r$; otherwise, $q$ moves to $r$. The algorithm migrates its server to $s=\frac{p+q}{2}$ after $p$ or $q$ moves.

Lemma 1. 

For any $\rho >2$ and $p,q,r,s\in {\text{ℝ}}^2$ such that $p\ne q$, $\delta \left(p,r\right)\ge \delta \left(q,r\right)>0$, and $s$ is the center of $p$ and $q$, $g=\delta \left(s,r\right)-\left(\frac{\rho }{2}-\frac{1}{2}\right)·\delta \left(p,r\right)-\left(\frac{\rho }{2}-1\right)·\left(\delta \left(q,r\right)-\delta \left(p,q\right)\right)$ is maximized if $\delta \left(p,r\right)=\delta \left(q,r\right)$, or $\delta \left(p,q\right)=\delta \left(p,r\right)+\delta \left(q,r\right)$, or $\delta \left(p,r\right)=\delta \left(p,q\right)+\delta \left(q,r\right)$.

Proof. 

We may assume without loss of generality that $p=\left(-1,0\right), s=\left(0,0\right), q=\left(1,0\right),$ and $r=\left(\ell \cos \theta , \ell \sin \theta \right)$ with $0\le \theta \le \pi /2$. Moreover, we fix $\delta \left(s,r\right)=\ell$ and regard $g$ as a function of $\theta$. The aim is to prove that $g$ is maximized at $\theta =0$ or $\theta =\pi /2$.

It follows that:

$$\delta \left(p,r\right)=\sqrt{{\left(\ell \cos \theta +1\right)}^2+{\ell }^2{\sin }^2\theta }=\sqrt{{\ell }^2+2\ell \cos \theta +1}$$

$$\delta \left(q,r\right)=\sqrt{{\left(\ell \cos \theta -1\right)}^2+{\ell }^2{\sin }^2\theta }=\sqrt{{\ell }^2-2\ell \cos \theta +1}$$

$$\frac{d\delta \left(p,r\right)}{d\theta }=\frac{-\ell \sin \theta }{\sqrt{{\ell }^2+2\ell \cos \theta +1}}=-\frac{\ell \sin \theta }{\delta \left(p,r\right)}$$

and

$$\frac{d\delta \left(q,r\right)}{d\theta }=\frac{\ell \sin \theta }{\sqrt{{\ell }^2-2\ell \cos \theta +1}}=\frac{\ell \sin \theta }{\delta \left(q,r\right)}$$

Therefore, we have

$$\frac{dg}{d\theta }=\ell \sin \theta \left\{\frac{\rho -1}{2}·\frac{1}{\delta \left(p,r\right)}-\left(\frac{\rho }{2}-1\right)·\frac{1}{\delta \left(q,r\right)}\right\}=\frac{\left(\rho -1\right)·\ell ·\sin \theta }{2\delta \left(q,r\right)}\left\{\frac{\delta \left(q,r\right)}{\delta \left(p,r\right)}-\frac{\rho -2}{\rho -1}\right\}$$

$\frac{\delta \left(q,r\right)}{\delta \left(p,r\right)}=\sqrt{\frac{{\ell }^2-2\ell \cos \theta +1}{{\ell }^2+2\ell \cos \theta +1}}$ monotonically increases from $\frac{\left|\ell -1\right|}{\ell +1}$ to 1 as $\theta$ changes from $0$ to $\pi /2$. If $\frac{\left|\ell -1\right|}{\ell +1}\ge \frac{\rho -2}{\rho -1}$, then $\frac{dg}{d\theta }\ge 0$ for any $\theta$. Therefore, $g$ is maximized at $\theta =\pi /2$. Otherwise, since $0<\frac{\rho -2}{\rho -1}<1$, there exists $0<t<\pi /2$ such that $\sqrt{\frac{{\ell }^2-2\ell \cos t+1}{{\ell }^2+2\ell \cos t+1}}=\frac{\rho -2}{\rho -1}$. Since $\frac{dg}{d\theta }\ge 0$ for $\theta \ge t$ and $\frac{dg}{d\theta }\le 0$ for $\theta <t$, $g$ is maximized at $\theta =0$ or $\theta =\pi /2$. ☐

Theorem 1. 

PQ is $\rho$-competitive for $\rho =\frac{11}{4}$ and the page size $D=1$.

Proof. 

We use the following potential function for OPT’s server location $t$, PQ’s server $s$, and point locations $p$ and $q$:

$$\Phi =\frac{\rho }{2}·\left(\delta \left(p,t\right)+\delta \left(q,t\right)\right)-\frac{\rho -2}{2}·\delta \left(p,q\right)$$

We separate the online events into two parts. The first is to consider only the migration costs incurred by OPT’s server, and the second is to consider the service costs incurred by OPT together with the migration and service costs incurred by PQ. It is sufficient to show that the inequality $\Delta cos{t}_{PQ}+\Delta \Phi \le \rho ·\Delta cos{t}_{OPT}$ follows in both parts, upon each request located at $r$.

Part 1. 

The migration of OPT’s server from $t$ to $t\prime$ induces a change of $\delta \left(t,t\prime \right)$ to the total cost of the optimal algorithm OPT but no change to the cost incurred by PQ. The total change of $\Phi$ is then $\frac{\rho }{2}·\left(\delta \left(p,t^{\prime }\right)-\delta \left(p,t\right)+\delta \left(q,t^{\prime }\right)-\delta \left(q,t\right)\right)$. Therefore, it is sufficient to show the following inequality:

$$\frac{\rho }{2}\delta \left(p,t^{\prime }\right)-\frac{\rho }{2}\delta \left(p,t\right)+\frac{\rho }{2}\delta \left(q,t^{\prime }\right)-\frac{\rho }{2}\delta \left(q,t\right)\le \frac{\rho }{2}\delta \left(t,t^{\prime }\right)+\frac{\rho }{2}\delta \left(t,t^{\prime }\right)$$

This follows by the symmetry of the distance function ($\delta \left(a,b\right)=\delta \left(b,a\right)$) and the triangle inequalities $\delta \left(p,t^{\prime }\right)\le \delta \left(t,t^{\prime }\right)+\delta \left(p,t\right)$ and $\delta \left(q,t^{\prime }\right)\le \delta \left(t,t^{\prime }\right)+\delta \left(q,t\right)$.

Part 2. 

We may assume, without loss of generality, that $\delta \left(p,r\right)\ge \delta \left(q,r\right)$. By this assumption, PQ moves $p$ to $r$. Since PQ maintains its server at the center of $p$ and $q$, the migration cost incurred by PQ is then $\frac{1}{2}\delta \left(p,r\right)$. For this part, we have the following equalities:

$$\Delta cos{t}_{PQ}=\delta \left(s,r\right)+\frac{1}{2}\delta \left(p,r\right)$$

$$\Delta \Phi =\frac{\rho }{2}·\left(\delta \left(r,t\right)-\delta \left(p,t\right)\right)+\left(\frac{\rho }{2}-1\right)·\left(\delta \left(p,q\right)-\delta \left(q,r\right)\right)$$

$$\Delta cos{t}_{OPT}=\delta \left(t,r\right)$$

Therefore, we shall show the following inequality:

$$\delta \left(s,r\right)+\frac{1}{2}\delta \left(p,r\right)+\frac{\rho }{2}·\left(\delta \left(r,t\right)-\delta \left(p,t\right)\right)+\left(\frac{\rho }{2}-1\right)·\left(\delta \left(p,q\right)-\delta \left(q,r\right)\right)-\rho \delta \left(t,r\right)\le 0$$

Since $\delta \left(r,t\right)+\delta \left(p,t\right)\ge \delta \left(p,r\right)$, it is sufficient to show:

$$\delta \left(s,r\right)-\left(\frac{\rho }{2}-\frac{1}{2}\right)·\delta \left(p,r\right)-\left(\frac{\rho }{2}-1\right)·\left(\delta \left(q,r\right)-\delta \left(p,q\right)\right)\le 0.$$

(1)

This follows for the cases $p=q$ and $q=r$, because $s=p=q$ and $\delta \left(s,r\right)=\frac{1}{2} \delta \left(p,r\right)$, respectively. We assume $p\ne q$ and $q\ne r$. It is sufficient to show that the maximum value of the left-hand side of Equation (1) is less than or equal to zero. If we regard $p$, $q$, $r$, and $s$ as vectors in ${\text{ℝ}}^n$, then at most three vectors of them, say $p$, $q$, and $r$, are independent. Therefore, the points $p$, $q$, $r$, and $s$ are on a plane in ${\text{ℝ}}^n$. Applying Lemma 1 on this plane, the left-hand side of Equation (1) is maximized in one of three situations. Situation 1: $\delta \left(p,r\right)=\delta \left(q,r\right)$, Situation 2: $\delta \left(p,q\right)=\delta \left(p,r\right)+\delta \left(r,q\right)$, or Situation 3: $\delta \left(p,r\right)=\delta \left(p,q\right)+\delta \left(q,r\right)$. We proceed to show inequality (1) for each of these three situations.

Situation 1: 

Substitution of $\delta \left(p,q\right)$ by $2·\delta \left(s,q\right)$ in Equation (1) reveals the following inequality.

$$\delta \left(s,r\right)+\left(\rho -2\right)·\delta \left(s,q\right)\le \left(\rho -\frac{3}{2}\right)·\delta \left(q,r\right)$$

By applying $\rho =\frac{11}{4}$ and dividing both sides by $\frac{5}{4}$, it is sufficient to show

$$\frac{4}{5} \delta \left(s,r\right)+\frac{3}{5} \delta \left(s,q\right)\le \delta \left(q,r\right)$$

(2)

Since ${\left(\delta \left(q,r\right)\right)}^2={\left(\delta \left(s,r\right)\right)}^2+{\left(\delta \left(s,q\right)\right)}^2$, Equation (2) can be written as:

$$\frac{4}{5} \delta \left(s,r\right)+\frac{3}{5} \sqrt{{\left(\delta \left(q,r\right)\right)}^2-{\left(\delta \left(s,r\right)\right)}^2}\le \delta \left(q,r\right).$$

By taking the derivative with respect to $\delta \left(s,r\right)$ on the plane containing $q$, $r$, and $s$, the left-hand side of Equation (2) is maximized at $\delta \left(s,r\right)=\frac{4}{5} \delta \left(q,r\right)$ and $\delta \left(s,q\right)=\frac{3}{5}\delta \left(q,r\right)$. Therefore, Equation (2) follows.

Situation 2: 

The inequality in Equation (1) can be rewritten as:

$$\delta \left(s,r\right)-\left(\frac{\rho }{2}-1\right)\left(\delta \left(p,r\right)+\delta \left(q,r\right)-\delta \left(p,q\right)\right)\le \frac{1}{2}\delta \left(p,r\right)$$

(3)

In this situation, we recall that $p,s,r,$ and $q$ are all located on the same line segment. Since $\delta \left(p,q\right)\ge \delta \left(p,r\right)$, and $s$ is located at the center of $p$ and $q$, it follows that $\frac{1}{2}\delta \left(p,r\right)=\delta \left(p,s\right)=\delta \left(s,q\right)=\delta \left(s,r\right)+\delta \left(r,q\right)\ge \delta \left(s,r\right)$. Since $\delta \left(p,r\right)+\delta \left(q,r\right)-\delta \left(p,q\right)=0$, the inequality in Equation (3) follows.

Situation 3: 

Since $\rho =\frac{11}{4}$, we rewrite Equation (1) as:

$$\delta \left(s,r\right)-\frac{7}{8}\delta \left(p,r\right)-\frac{3}{8}\delta \left(q,r\right)+\frac{3}{8}\delta \left(p,q\right)\le 0$$

The points $p,s,r,$ and $q$ are also located on the same line segment in this situation. By $\delta \left(p,r\right)=\delta \left(p,q\right)+\delta \left(q,r\right)$, we have $\delta \left(s,r\right)-\frac{1}{2}\delta \left(p,q\right)-\frac{5}{4}\delta \left(q,r\right)\le 0$. By $\delta \left(p,q\right)=2\delta \left(s,q\right)$ we have $\delta \left(s,r\right)-\delta \left(s,q\right)-\frac{5}{4}\delta \left(q,r\right)\le 0$. In addition, by $\delta \left(s,r\right)=\delta \left(s,q\right)+\delta \left(q,r\right)$ we have $\delta \left(q,r\right)-\frac{5}{4}\delta \left(q,r\right)\le 0$.

Therefore, the proof completes. ☐

4. A Lower Bound for PQ

In this section, we show that the exact competitiveness of the algorithm is greater than $2.732$. We introduce an adversary through Theorem 2 and prove the existence of such a lower bound. The adversary makes a special sequence of requests on ${\text{ℝ}}^2$ against the proposed algorithm. The requests are given at vertices of a triangle that tends to be equilateral. After the second request, the server repeatedly migrates between the center points of two sides of the triangle.

Theorem 2. 

For a sufficiently large integer $n$, there exist a request sequence $\sigma =r_1,\dots ,r_{2n+1}$, three request locations $a,b,$ and $s$ on a plane, and the initial server location $s$, such that $cos{t}_{PQ}\left(s,\sigma \right)\ge \rho ·cos{t}_{OPT}\left(s,\sigma \right)$ for $\rho =1+\sqrt{3}\approx 2.732$.

Proof. 

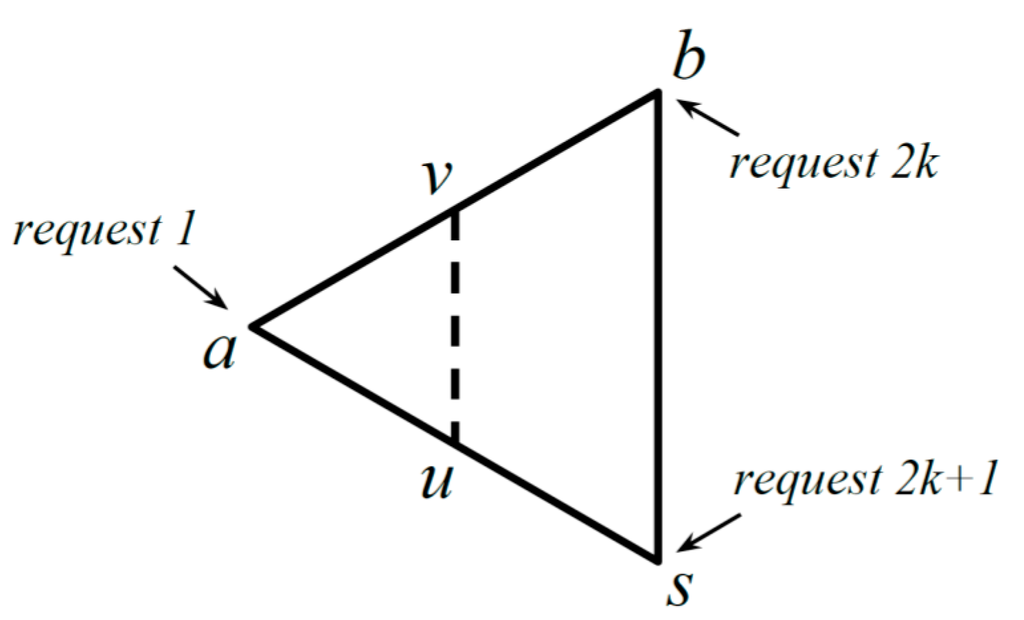
We describe our approach before more technical discussion in the subsequent paragraphs. In Figure 1, we illustrate the behavior of PQ against requests by our adversary. We assume that $\delta \left(s,b\right)$ is slightly larger than $\delta \left(s,a\right)=\delta \left(b,a\right)$. Points $u$ and $v$ are the centers of $a$ and $s$, and $a$ and $b$, respectively. For requests $a, b, s, b, s, b, s, \dots$, PQ migrates its server along the dashed line, because $p$ does not move from $a$. A request occurs at $b$ when the server is at $u$, and a request occurs at $s$ when the server is at $v$. Note that $a$, $b$, and $s$ tend to be the vertices of an equilateral triangle as $\delta \left(s,b\right)$ approaches $\delta \left(s,a\right)=\delta \left(b,a\right)$.

Figure 1. The request sequence $a,b,s,b,s,b,s,\dots$ to access the page at the server; $k\ge 1$.

For $r_1=a$, $r_{2\mathrm{k}}=b$, and $r_{2\mathrm{k}+1}=s$, where $1\le k\le n$ and $a$, $b$, and $s$ are the vertices of an equilateral triangle with a unit side length, the cost of the optimal algorithm $cos{t}_{OPT}\left(s,\sigma \right)$ is at most $n+1$ by keeping the server at the initial location $s$.

The adversary infinitesimally perturbs the distances by slightly increasing the distance between $s$ and $b$. Upon the first request at $a$, PQ serves the request by the cost of $\delta \left(s,a\right)$ and migrates the server to $u$, which is the center of $s$ and $a$, by the cost of $\delta \left(s,u\right)$. This is because point $p$ at $s$ moves to $a$. The $2k$th request at $b$ is served with the cost of $\delta \left(u,b\right)$, causing point $q$ at $s$ to move to $b$, and the server migrates to $v$, which is at the center of $a$ and $b$, with the cost of $\delta \left(u,v\right)$. The $\left(2k+1\right)$st request at $s$ is served with the cost of $\delta \left(v,s\right)$. The point $q$ at $b$ moves to $s$; hence, the server migrates to $u$ with the cost of $\delta \left(u,v\right)$.

We compute the total cost of PQ by using the distances of the unperturbed triangle, since the actual distances (and hence the actual costs of PQ and OPT) may differ by an infinitesimally small amount from these computations. Therefore, we have

$$cos{t}_{PQ}\left(s,\sigma \right)=\delta \left(s,a\right)+\delta \left(s,u\right)+n·\left(\delta \left(u,b\right)+\delta \left(u,v\right)+\delta \left(v,s\right)+\delta \left(v,u\right)\right)\approx 1.5+\left(\sqrt{3}+1\right)n$$

Since

$$\underset{n\to \infty }{\lim }\frac{1.5+\left(\sqrt{3}+1\right)n}{n+1}=\sqrt{3}+1$$

then $\frac{cos{t}_{PQ}\left(s,\sigma \right)}{cos{t}_{OPT}\left(s,\sigma \right)}$ is at least $2.732$. This completes the proof. ☐

5. Concluding Remarks

In this paper, we proposed a deterministic algorithm for the page migration problem in Euclidean space with a page size $D=1$. The $2.75$-competitiveness of the algorithm is an improvement on the former $2.8$ ratio. An adversary was found to express a lower bound of $2.732$ for the algorithm. If possible, one could seek to find an algorithm to cover a larger $D$ with better competitiveness than $2.618$. Another area of improvement is to narrow the upper and lower bounds of the algorithm. Moreover, the generalization of the algorithm under norms other than the Euclidean and Manhattan ones remains an open problem in this research area.