Abstract
The performance of Radio-Isotope Identification (RIID) algorithms using NaI-based γ spectroscopy is increasingly important. For example, sensors at locations that screen for illicit nuclear material rely on isotope identification using NaI detectors to distinguish innocent nuisance alarms, arising from naturally occurring radioactive material, from alarms arising from threat isotopes. Recent data collections for RIID testing consist of repeat measurements for each of several measurement scenarios to test RIID algorithms. It is anticipated that vendors can modify their algorithms on the basis of performance on chosen measurement scenarios and then test modified algorithms on data for other measurement scenarios. It is therefore timely to review the current status of RIID algorithms on NaI detectors. This review describes γ spectra from NaI detectors, measurement issues and challenges, current RIID algorithms, data preprocessing steps, the role and current quality of synthetic spectra, and opportunities for improvements.
1. Introduction
Radioactive isotopes produce characteristic γ−rays of various energies and intensities that are measured by γ spectrometers. Such spectra serve as fingerprints that are typically used to estimate the identity and quantity of γ emitters in the source. Example scaled spectra from high resolution (high purity Germanium, HpGe) and low resolution (Sodium Iodide, NaI) detectors are shown in Figure 1 for 235U and 239Pu. The scaling was done by first converting counts C to square root of counts, and then dividing the values by the maximum value of so the plotted result lies in the interval [0,1].
There are many applications for γ spectroscopy. Our focus is isotope identification in the context of nuclear nonproliferation. For example, securing national borders against terrorist threats such as dirty bombs regularly makes the news [1], as sensors at various locations screen for illicit nuclear material. Many of these sensors rely on Radio-Isotope Identification (RIID) algorithms using γ spectroscopy to distinguish innocent nuisance alarms arising from naturally occurring radioactive material (NORM) from alarms arising from threat isotopes. NORM examples include 40K from cat litter and 232Th in soil. Threat isotopes include special nuclear material (SNM) isotopes such as isotopes of U and Pu. Currently, most alarms are nuisance alarms due to innocent NORM or due to medical or industrial radioactive isotopes. Consequently, assessing and improving the performance of RIID algorithms is an important activity.
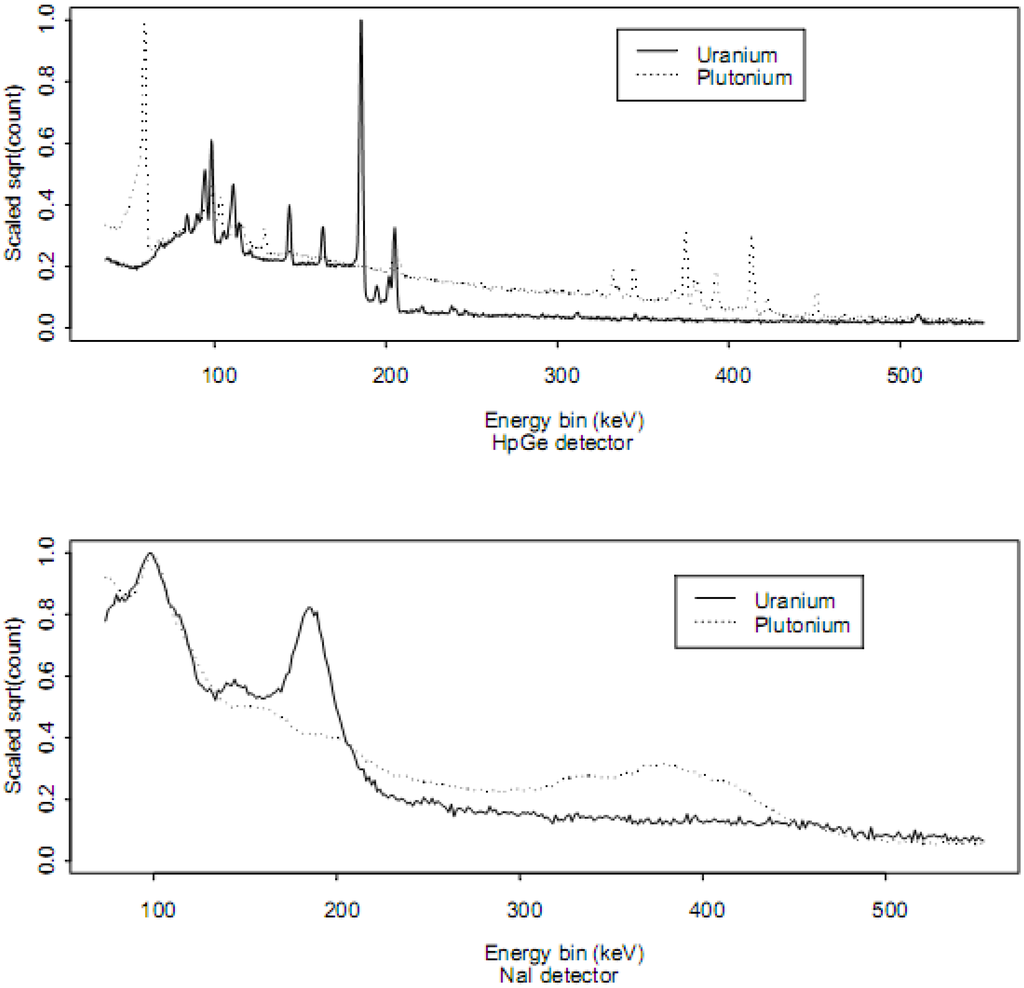
Figure 1.
High resolution (HpGe) and low resolution (NaI) scaled spectra for 235U and 239Pu.
Conventional wisdom is that increasing energy resolution as defined by peak widths improves isotope identification (see Figure 1). However, higher resolution detectors typically have lower overall efficiency, and are more costly to buy, operate and maintain. Furthermore, increasing resolution beyond some amount will not improve isotope identification, particularly if RIID algorithms are effectively tuned to each candidate resolution. Studies comparing low, medium, and high energy resolution detectors have suggested that relatively low resolution detectors, such NaI detectors will continue to play a key role [2]. Although current RIID algorithm performance is worse than desired [3], the fact that expert spectroscopists using NaI detectors can perform well suggests there is room to improve existing RIID algorithms.
Recent data collections for RIID testing consist of repeat measurements for each of several measurement scenarios using NaI detectors typically having 512 or 1,024 calibrated energy channels to test RIID algorithms. Each channel corresponds to a particular energy range of the incident detected γ−ray. It is anticipated that vendors can modify their algorithms on the basis of performance on chosen measurement scenarios and then test modified algorithms on data for other measurement scenarios. It is therefore timely to review the status of RIID algorithms. This review describes γ spectra from NaI detectors, measurement issues and challenges, current RIID algorithms, data preprocessing steps, the role and current quality of synthetic spectra, and opportunities for improvements.
2. Background
γ-Ray detectors generally belong to one of three broad categories: gas-filled, solid state, and scintillators. We focus here on NaI-based scintillator detectors, which are widely used because of the large variety of shapes, sizes, types, and low cost.
γ-Ray spectroscopy using scintillation detectors is a relatively mature subject, dating to the demonstration in 1948 [4] that crystalline NaI with a trace of thallium iodide produces an exceptionally large scintillations light output. Although experiments continue using other light scintillation materials, NaI detectors continue to dominate in practical applications. In scintillation detectors, light of a characteristic spectrum is emitted following the absorption of radiation.
Because this review focuses on RIID algorithms, we omit detailed discussion of the physical processes except to point out that γ s and their energies are indirectly detected in NaI scintillator detectors via voltage bursts arising from detected charged particles that arise from any of the three main γ−ray interactions: photoelectric effects, Compton scattering, and pair production, which are described next.
In photoelectric absorption, which dominates at low γ−ray energies, an incident γ−ray is absorbed by an atom, ejecting a bound electron. This process can also release characteristic photons (x-rays) due to rearrangement of electrons from other energy levels of the atom. Compton scattering is the most frequent interaction for γ−rays in the 30 keV to 3,000 keV range, which is characteristic of most isotopes of interest in our context. In Compton scattering, the incident γ−ray is deflected rather than absorbed, transferring some of its energy to the recoiled electron. In pair production, which can only occur above 1,020 keV, the incident γ-ray disappears and is replaced by an electron-positron pair.
One important feature that results from the voltage bursts is that high count rates can lead to voltage gain shifts. As described below, voltage must be calibrated to infer the energy of the incident γ-ray, and high count rates are known to shift the calibration relation (often referred to as the “gain”) between energy and voltage [5,6].
The pulse shaping photomultiplier tube (PMT), which amplifies the signal from the incident γs, is another important aspect of NaI spectroscopy. PMTs consist of a glass vacuum tube that contains a photocathode material that produces photoelectric effect electrons, plus several dynodes and an anode that together amplify the signal from an incident γ by approximately a factor of 106. Partly due to this amplification and largely due to the fact that a random number of initial electrons is created by each “detected” γ-ray leads to pulse broadening, or “Gaussian energy broadening.” Many peaks in NaI spectra are approximately Gaussian in shape [7], so peak fitting methods often assume a symmetric, Gaussian shape around the peak centroid.
3. Problem Statement
The most general challenging problem in our context of screening for threat isotopes requires an isotope library of approximately 200 radio-isotopes and contains several unknown factors, including an unknown source (single or multiple isotopes) in unknown form (gas, liquid, solid) in unknown geometry with unknown shielding, unknown distance between the source and detector, and unknown potential for electronics drifting. Most RIID algorithms insist that the detector properties are known as specified by standard vendor specifications, and so the detector’s energy resolution, efficiency at a given distance from the source, and calibration are at least fairly well known.
The main inference goal is to identify all isotopes present in the source, and also quantify the isotopes. Absorbing materials between the source and detector and in the detector distort peak shapes and overall spectral shape which complicates the main inference task. Typically, inferring the type and amount of shielding is not a primary goal but instead is a secondary goal because an estimate of shielding material can improve source identification.
Many screening locations apply RIID algorithms using hand-held NaI detectors scanning only those cases (vehicles, people, cargo, containers, etc., depending on specific application) that were found in initial gross-count screening to have significantly higher-than-background radiation [8]. The measurement protocol for such hand-held detectors can vary depending on operations at each deployment. Therefore, special cases of the general problem are of interest in which some of these factors are known. For example, the source might be known to be a solid in a vehicle at a known distance from a hand-held NaI detector. Also, in some applications, the inference goal is to infer whether the source isotopes belong to medical, industrial, NORM, or SNM categories. Medical isotopes include 67Ga, 51Cr, 75Se, 99mTc, 103Pd, 111In, 123I, 125I, 131I, 201Tl, and 133Xe. Industrial isotopes include 57Co, 60Co, 133Ba, 137Cs, 192Ir, 204Tl, 226Ra, and 241Am. NORM isotopes include 40K, 226Ra, 232Th and its daughters, and 238U and its daughters. SNM isotopes include 233U, 235U, 237Np, and Pu isotopes.
Whenever any of the factors such as source-to-detector distance, shielding materials, number of source isotopes, identity of possible source isotopes, or degree of electronic stability, is known, one can tailor the RIID algorithm accordingly for improved results. For example [9], requires an instrument vendor’s RIID algorithm to specify what isotopes it can identify and their category. Reference [9] also requires the RIID algorithm to recognize each isotope in a specific list of approximately 20 isotopes including some of those listed above. Note that if a RIID algorithm must only recognize 20 isotopes, then custom isotope libraries could be extracted from the more complete library of approximately 200 isotopes.
As a qualitative example of how distinguishable various isotopes are, Figure 2 plots two example scaled NaI detector spectra from each of 239Pu, 235U, and 137Cs. A small 137Cs check source is present in this detector, so the 239Pu and 235U spectra have peaks near 662 keV associated with a 662keV γ emitted from 137Cs. The same scaling as in Figure 1 was used.
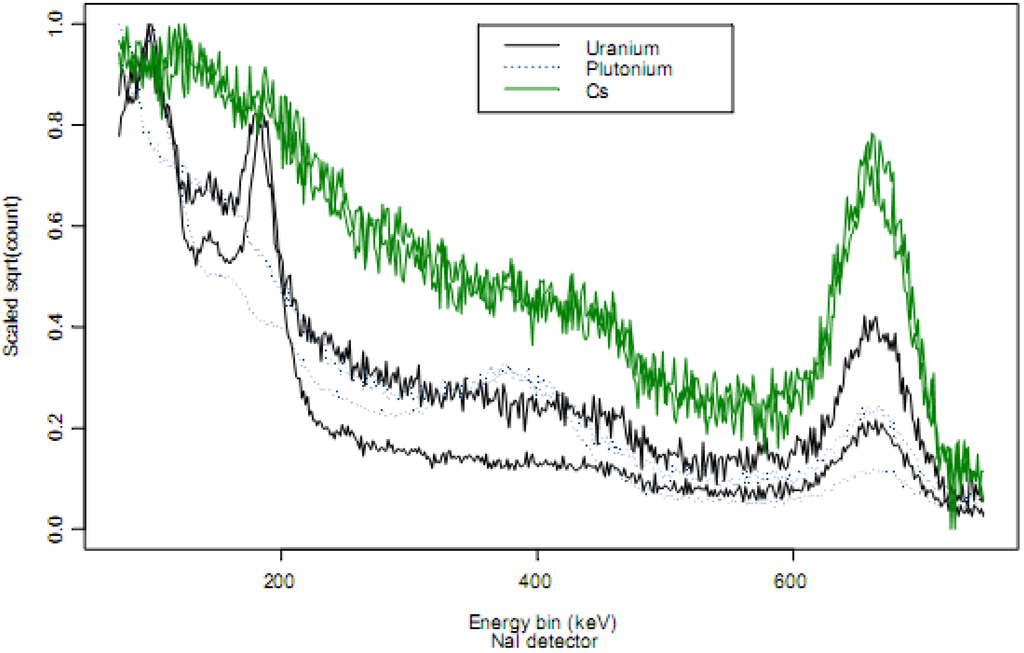
Figure 2.
Two example scaled spectra from each of 239Pu , 235U, and 137Cs. A small 137Cs check source is present in this detector, so the 239Pu and 235U spectra have peaks near 662 keV associated with a 662keV γ emitted from 137Cs.
4. Challenges in NaI Spectroscopy
In general, RIID algorithms measure the degree of similarity between measured characteristics of the test spectrum and reference spectra for an isotope library of a few hundred isotopes. Essentially all challenges in NaI spectroscopy involve perturbations in test spectra compared to corresponding reference spectra.
Challenges include:
- Absorbers attenuate peak counts but also attenuate counts differentially with respect to energy, causing distorted pulse height distributions;
- The calibration of detected voltage to incident γ energy can be nonlinear, and electronic gain shift effects can be nonlinear and unstable over time as environmental effects change;
- Isotope mixtures can result in ambiguous spectra, particularly when absorbers attenuate and/or broaden peaks;
- Measurement protocols can modify the challenge depending on the specific protocols. For example, temperature and other factors impact the calibration of spectral channel to γ energy, and some protocols control the temperature to within a narrow range to minimize gain shifts. As another example, the source-detector distance can sometimes be known and spectra from multiple distances can be compared.
- There are several challenge problems, including the “general problem” described in the problem statement above and its various sub-problems depending on what can be controlled and/or known for a given application. For example, some applications monitor only for specific isotopes, and other applications require only outlier detection in the context of recognizing non-NORM isotopes without distinguishing specific isotopes;
- There can be hundreds of isotopes in the isotope library, each with numerous example spectra that often depend in important ways on the detector and on the absorbers.
- Detector issues such as dead time and pulse pileup can distort test spectra.
Although recognizing what radioactive isotopes are present in a source might appear to be a standard pattern recognition problem [10], these challenges combine to make isotope identification using NaI spectra difficult.
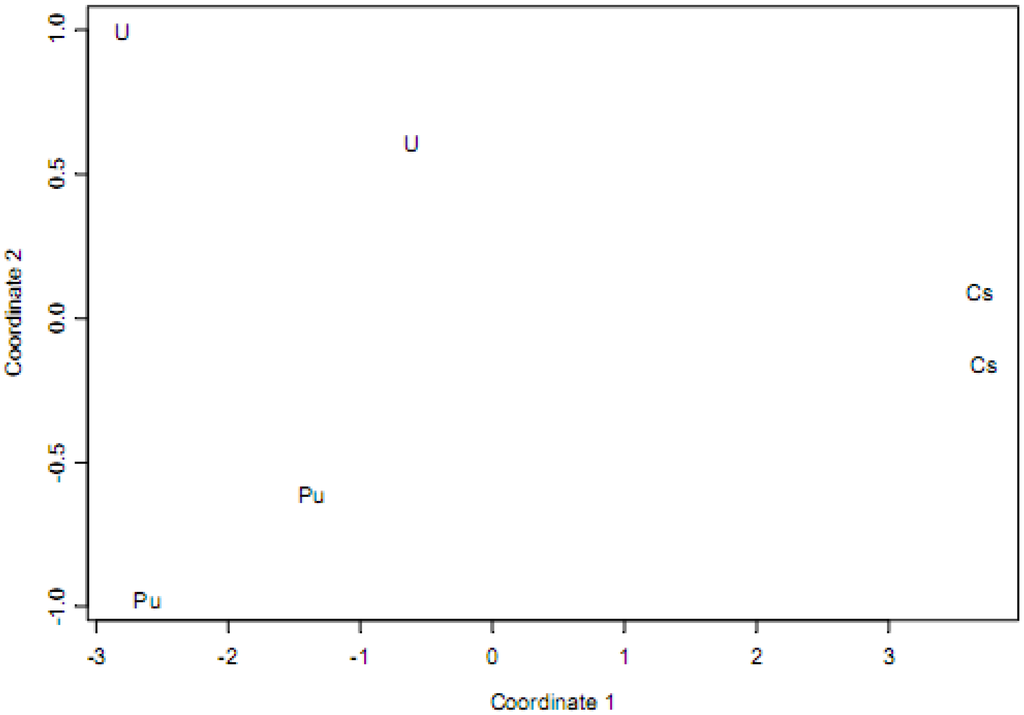
Figure 3.
A principal coordinates plot of the three spectral pairs from Figure 2.
Figure 3 is an example of the challenge confronted by pattern recognition arising from relatively large “within isotope” variability compared to “between isotope” variability. Figure 3 corresponds to the same three pairs of spectra shown in Figure 2. The values of the two coordinates in Figure 3 are chosen so that distances between each of the 15 (i.e., combinations) spectral pairs are very closely approximated (using multi-dimensional scaling, [11]) by the distances as computed using the ordinary Euclidean distance applied to the 2-component values. In this case, each isotope has a unique “signature” that can be regarded as a cluster of points in the 2-component space. As more isotopes are added, the “between isotope” distances will decrease, eventually resulting in ambiguous isotopic signatures.
5. Data Model
Clarifying the impact of the challenges described in the previous section on RIID algorithm performance requires a model for the data. Under standard assumptions, the counts C in a given energy channel that does not drift in calibration over the repeats will be distributed as Poisson (μ). Repeat measurements vary because of this Poisson variation and also because the detected counts will be less than the true counts in a given time period because the efficiency ε of any detector will be less than 1. The efficiency ε at a given channel is the probability that a γ-ray incident on the detector will be detected.
Given C, the simplest effective model for the detected counts D in time t is therefore D|C ~ Binomial(C, ε) and C ~ Poisson(μ), where D|C denotes the conditional distribution of D given C. Although it appears to not be well known in the literature, it is not difficult to then show that D|μ ~ Poisson(με). To simplify notation, we will write C for the detected counts and include the efficiency term ε in the term μ, so C ~ Poisson(μ).
The simple model C ~ Poisson(μ) has often been found to adequately describe detected counts at a given energy channel in NaI spectral data, even after effects such as Gaussian broadening [12]. If C ~ Poisson(μ), then variance(C) = μ, so a simple check for the Poisson assumption is to compare the sample variance across measurement repeats to the sample mean at each energy channel. Overdispersion, defined as , typically occurs when the mean μ is not constant across repeat measurements. Underdispersion, defined as , can occur, for example, at high values of μ due to detector dead time effects [12].
Following the notation in [13] for an unshielded source, the mean count rate at channel i can be expressed as for isotopic composition vector describing the activity in decays per second of each isotope present and response matrix . The response matrix either is or can be thought of as a representative reference spectra for each unshielded isotope in the library. When attenuating absorbers are present or could be present, the response matrix with matrix elements is modified to with matrix elements where is the density of absorber z (the relative amount of the zth absorber), , and the sum is over absorbers z in a library of absorbers. The multiple-isotope material basis set approach described in Section 9 typically allows only up to three to five representative absorbers such as Pu, Steel, and Fe to fit the spectral effects of arbitrary absorber mixtures. Without such a reduction in the absorber library, the number of unknowns could be quite large, with approximately 200 possible source isotopes and approximately 100 absorbers.
The RIID algorithms described in Section 9 each assume that all relevant isotopes, including all possible NORM isotopes of interest are in the spectral library. One practical challenge in constructing such a comprehensive spectral library is that each measurement scenario and detector could require its own library, particularly if effects such as secondary interactions leading to minor peaks and backscatter from nearby structures are nonnegligible and dependent on the measurement scenario.
6. Noise Sources and Identification Performance
Each of the challenges described above impact the noise sources in the task to identify all radio-isotopes present in a sample. For example, to address issue (1), Figure 4 (top plot) is where C is the measured counts per second by a GR135 NaI detector for a 239Pu spectra without shielding and when shielded by 0.5 inches of Pb or 4.0 inches of polyethylene. In the bottom plot, the measured ratio is plotted, which estimates the true count rate for each of the two shielded measurements of the 239Pu spectra. Recall that the term refers to the measured count rate for isotope j, shielded by absorber z in channel i. The term refers to the reference, which is the no-absorber case.
In Figure 4, the measurements were made by different models of the GR135 NaI detector [14]. Clearly the absorbers attenuate the peak counts, as described above by Beer’s Law [15], which is an approximation. Beer’s Law ignores the fact that when an incident γ undergoes an interaction, one result is a lower-energy γ. In the case of the polyethylene shielding, notice the region where the ratio exceeds one. In effect, the shielding material acts as a source of lower energy γ s, thus modifying spectral shape.
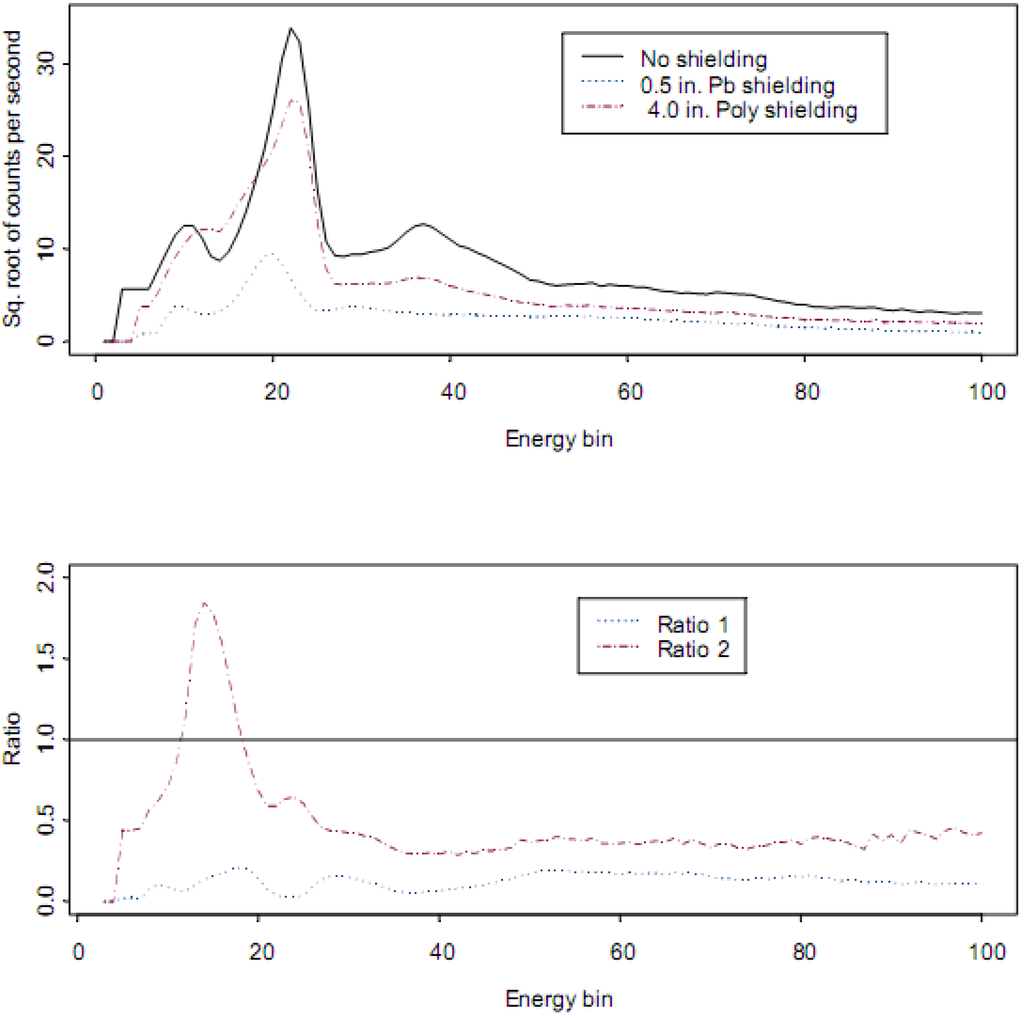
Figure 4.
Example effects of Pb shielding on low-energy counts in 239Pu spectra. Ratio 1 is , for the 0.5 in. of Pb shielding, which estimates for isotope j (239Pu), channel i, where is the unshielded true count rate and is the shielded true count rate. The counts are noticeably smaller in Ratio 1, but the ratio is not constant, indicating a distortion of spectral shape. Ratio 2 is the same, but for the 4.0 in. of polyethylene shielding. There is a region of low energy counts that noticeably larger than one in Ratio 2.
Regarding issue (2), nonlinear calibration requires multi-line sources and calibration drift is an important noise source. For example [3] and [16] showed that a typical peak centroid can shift by tens of keV in either direction. If in a given spectum, all peak centroids shift in the same direction, then corrections such as those in [16] can be effective. Nevertheless, such adjustments cannot be expected to be perfect. Imperfections in estimated peak centroids will clearly impact any method that identifies peak locations. Figure 5 is an example using two different NaI models of the same detector (the GR135) of shifting peak centroids in which the peak centroid shifts are not all in the same direction.
Isotope mixtures [issue (3)] can result in ambiguous spectra, so isotope identification performance will degrade. One reasonable strategy is to eliminate redundant spectra from the algorithm’s library; however, a statistical assessment is required to identify “redundant” spectra as those having shapes that are “too similar” to distinguish.
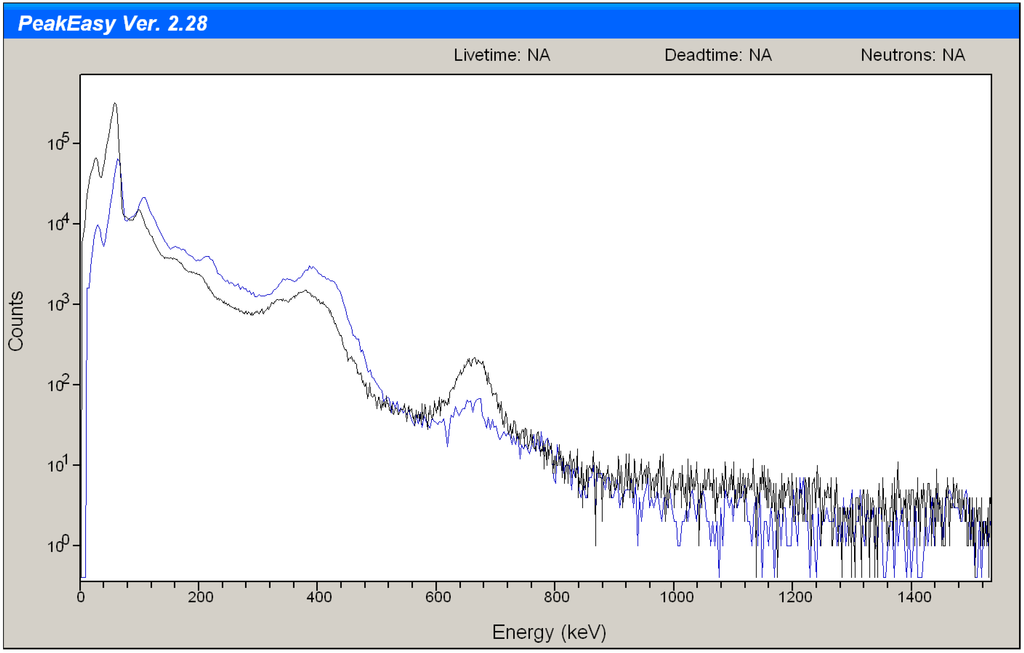
Figure 5.
Two measurements of 239Pu illustrating calibration drifting.
Issue (4) involving measurement protocols is an ongoing challenge. For example, temperature variation impacts the calibration of spectral channel to γ energy, and some protocols control the temperature to within a narrow range to minimize calibration shifts. The measurement standard [9] requires only that the instrument be operational at -20°C to 50°C, but calibration stabilization is not required. Even if calibration stabilization were required, such stabilization will never work perfectly, so that noise will be introduced by temperature variation.
Each of several challenge problems [issue (5)], including the “general problem” described in the problem statement above has unique noise sources. For example, any application that monitors only for specific isotopes will have effectively “less noise” and better RIID algorithm performance, particularly if the challenge problem modified ths isotope library size [issues (5) and (6)]. As another example, if the application only requires outlier detection in the context of recognizing non-NORM isotopes without distinguishing specific isotopes [17,18] then the noise associated with characterizing the background is very different than if a single background measurement is compared to a “background plus source” measurement .
Any effect that distorts test spectra either randomly or systematically is a noise source (issue (7)). Performance degradation can occur due to noise introduced by detector issues such as dead time and pulse pileup. Detector dead time occurs when an incident γ temporarily locks the detector into a “cannot detect at present” mode. Detector live time is the actual clock time of the assay minus the dead time. Dead time effects are a function of count rate.
Pulse pileup or peak summing occurs when two (or more) incident γs arrive essentially simultaneously, resulting in a peak at an energy equal to the sum of the two incident γ energies. Such a peak is sometimes considered an artifact peak and regardless of whether data preprocessing attempts to remove such peaks or if the peak library is modified to anticipate them, peak summing is expected to degrade identification performance. Other characteristic peaks include a single escape peak, annihilation peak, and double-escape peak. These peaks are all the result of pair production in the crystal detector. The annihilation peak is at 510 keV and is the result of absorption of one of the two 510 keV γs. When one of the two annihilation γs escapes without detection, the single-escape peak is produced at the original γ energy minus 510 keV. Or, both the annihilation γs can escape the detector without interaction and produce the double escape peak at the original γ energy minus 1,020 keV.
7. General Approaches in RIID Algorithms
Current RIID algorithms can be categorized into a few distinct approaches, each of which involves at least implicitly a spectral library [5,6,19]. Algorithm categories include: expert interactive, simple library comparisons, region of interest (ROI) methods, template matching, and variable subset selection.
Expert interactive methods often look at largest peak(s) and seek corroborating γ-rays within the library. A user should correct each peak area to compensate for differences in the branching ratio for γ-ray and the detector’s efficiency as a function of energy. This approach is best for HpGe or high resolution detectors; however, expert spectroscopists can accomplish the same goal with NaI detectors.
Library comparison methods often use the centroid of each peak but not the peak area or branching ratio of candidate sources. Slight drifts or inaccuracies in the energy calibration can lead to incorrect identifications. Complications of this approach include a significant number of low-energy lines being shielded and missing due to absorbers, or numerous nuclides emitting γ−rays of similar energy.
ROI methods develop one or more ROIs for every nuclide in the library and need to avoid overlap of ROIs. This is difficult as the library size grows. An example challenge are the 177Lu peaks at 378.502 keV and 413.658 keV, and 239Pu peaks at 375.018 keV and 413.691 keV, so other energies would need to be used to distinguish 177Lu and 239Pu because of the closeness of these two pairs of peaks.
Template matching methods quantify the quality of the fit between the test spectrum and each member of a spectral template library. The library consists of several templates for each isotope, varying the detecting medium, intervening materials, and source-to-detector spacings. It is possible to infer source(s) and absorber(s), but source mixtures are problematic, although additive combinations can be considered. Often decay chains are used that include daughter products as precomputed mixtures.
In template matching, the correlation coefficient r between two measured spectra and or between a library spectra and a test spectra is also often used, defined as . Also, a standard chi-squared goodness of fit is used, defined as where ci is the number of counts in channel i, TPi is the expected number of counts in channel i with T the total counts in the entire spectrum, Pi the relative probability of observing a count in channel i, and σi the standard deviation in the number of counts in the histogram at channel i. Because of the Poisson assumption previously described, σI is typically estimated as the mean, which is written here as TPi.
Peak finding and characterization methods often apply spectral smoothing [20,21] followed by peak fitting and corresponding peak area estimation. Peak area estimation is useful because each radio-isotope in the library has known γ-emission energies and relative intensities. For example, [22] proposed the first practical method for measuring the isotopic composition of an arbitrary (in size, shape, composition, and measurement geometry) plutonium sample by an analysis of its γ-ray spectrum from a relatively high resolution detector such as HpGe. The key to their method as described in [23] was the incorporation of an internal, or intrinsic, self-determination of the relative efficiency curve from the γ-ray spectrum of each unknown sample using published values for emission probabilities. An expression for the photopeak counts from a specific γ-ray emitted from a given isotope in a sample of arbitrary configuration is:
where
- is the photopeak area of the γ-ray j with energy Ej emitted from the isotope;
- is the decay constant of the isotope i, = ( is the half-life of the isotope i);
- is the number of atoms of the isotope;
- is the branching ratio or emission probability (γ-rays/disintegration) of the γ-ray j from the isotope;
- is the absolute efficiency of photopeak detection of the γ-ray with energy . The absolute efficiency includes detector efficiency, geometry (solid angle), sample self-absorption, and attenuation in absorbers between the sample and the detector.
A combination of equations 1 for γ-ray l from isotope k and γ-ray j from isotope i gives Equation (2) for calculating the atom ratio of the isotope i to the isotope k from measurements of the areas of the corresponding photopeaks:
In going from Equation 1, the absolute efficiency has been rewritten in terms of the relative efficiency RE. All constant geometric factors that are associated with the absolute efficiency cancel in the ratio in Equation 2. The relative efficiency RE reflects all energy-dependent effects, including those due to sample self-absorption, attenuation in materials between the sample and the detector, detector efficiency, and any energy-dependent effects relating to the finite sample-detector geometry. The half-lives and the emission probabilities (branching ratios, BR) are known (published) nuclear data, which is a key feature of this measurement technique [23]. Although (2) is currently used [23] for higher resolution spectra, branching ratios and relative efficiencies can in principle be also used for NaI spectra.
8. Spectral Data Preprocessing Steps
The noise sources described above can be mitigated to varying degrees by various data preprocessing. Preprocessing options depend on the measurement protocol, such as whether multiple detector positions are used, whether a check-source calibration is available for each background and source measurement, etc.
The first preprocessing step is to obtain a background spectrum, preferably using the same detector as for the source plus background measurement. Archived background measurements or calculated background measurements [24] could also be used. Then, either the net counts calculated by background subtraction can be analyzed, or the background and source plus background can be separately analyzed. If a mixture of a few common background isotopes such as 232Th and 226Ra fit the measured background well, then a constrained fit to the source plus background spectrum could force the background fit into the final fit, avoiding the need to subtract the background and perhaps more naturally leading to a non-negativity constraint on the source plus background fit.
A second preprocessing step that can be applied before each measurement or much less frequently is the energy calibration. Calibration is required to map the measured test spectrum to the reference spectra. Typically the energy E in keV for a given channel is calibrated to voltage bin x using a simple relatively low-order polynomial such as E = a0 + a1 x + a2 x2 + a3 x3 + error [5]. Other functional forms have also been applied.
Recall that Figure 5 shows an example of peak centroid drifting between two measurements of 239Pu from two models of the same GR135 detector. This can be regarded as a shift or drift in the calibration constants. Counts from a very small 137Cs check-source are also evident due to the peak near 662 keV. Notice that the drift in peak centroid locations is not consistently in the same direction. If instead two repeated measurements of the same source were made using the same detector and model, we expect peak centroid locations shifts to be in the same direction. One option to align such shifted spectra requires making multiple measurements of the source, each from a different detector location to map the effect of high count rate (for small source-detector distances) on calibration- shift-related peak centroid shifting [16].
An intriguing possible preprocessing step attempts to mimic higher resolution spectra from NaI spectra by using highly accurate estimates of the detector response function (DRF), which specifies the probability density function for detected γ energies for any incident γ energy [25] This is sometimes called spectrum unfolding. Because estimation errors in the DRF are amplified during the unfolding process of matrix inversion, the estimated DRFs must have negligible error for using unfolded NaI spectra rather than the NaI spectra in the context of RIID algorithms. This DRF-inversion method is relatively untested although the peak recovery reported in [25] is promising.
Other possible preprocessing steps include spectral smoothing [20,21], and peak area and centroid estimation [7]. To locate peaks, sometimes a second derivative method first attempts to locate the centroid of each peak, by finding the location where the spectrum is most concave down (as defined by the spectrum’s second derivative). Typically, a rolling window smooths the spectrum and isolates the second derivative calculation within each window [5].
9. Specific RIID Algorithm Examples
Isotope identification relies on quantifying the similarity between the measured test spectrum and reference isotope information. Algorithms differ in how they represent the measured data, the reference data, and the comparison method.
9.1. GADRAS
Development of the γ detector response and analysis software (GADRAS) at Sandia National Laboratory began in 1986 [24,26] focusing on DRF estimation using relatively simple 1-dimensional geometric model. GADRAS currently includes several RIID algorithms, and perhaps the most extensive uses multiple linear regression with backward variable elimination to find the best fitting subset of library isotopes. A key requirement is to characterize each detector and measurement scenario with measured spectra that are used to form the spectral library described in Section 5.
Backward elimination is a search strategy that in this case begins by fitting a large model that contains all isotopes in the library and then successively omitting isotopes whose presence in the model does not significantly improve the fit. The best fitting subset is then the predicted isotope subset.
Multiple linear regression is a standard technique [10] that we will not fully describe here. See, for example, [10,15]. Briefly, using the notation from the Data Model section, with , if the measured counts satisfy Ci ~ Poisson(μι) and μι is large enough (20 or larger) for the Poisson distribution to be well approximated by the Gaussian, then the weighted least squares (WLS) solution might be competitive with a more correct maximum likelihood approach that relies on the Poisson likelihood. The WLS solution is , where is the estimated variance-covariance matrix of the count vector, which would be estimated using the fact that variance of Ci is μι. The WLS approach is nearly the optimal method and is more easily implemented than a technically more correct approach that uses the Poisson likelihood. Because there will be measurement errors in the R matrix, the most appropriate approach requires both Poisson likelihood for the measured counts and a measurement error model for R (see the Future Directions section).
9.2. MIMBS
The multiple-isotope material basis set (MIMBS) method arose from an active tomographic γ scanning method using higher resolution spectroscopy such as HpGe [27]. MIMBS uses an iterative application of multiple regression using the model given in the Data Model section [13]. Its key strategy is to fit the unknown absorber effects using only two to five representative “basis” absorbers vectors.
Recall that the mean count rate at channel i can for an unshielded source be expressed as and the response matrix has entries and in MIMBS, the sum is over absorbers z in a very small set of representative absorbers, selected so that linear combinations of these “basis set” absorbers can adequately represent the effect of arbitrary absorbers and absorber combinations.
Because the MBS composition typically requires only two or three components to fit nearly any absorber’s effects, the values are iteratively varied and the isotopic composition vector is the WLS solution for a given value. Several trial values of are evaluated, with coefficients representing isotopic quantities constrained to be nonnegative, requiring specialized constrained least squares software. To date, most performance claims have been on simulated data, but [28] also has results for real data.
9.3. LibCorNID
Any library correlation or template method requires the measured spectrum, standard energy, peak shape, and peak efficiency calibrations. The LibCorNID approach is somewhat unusual in that it includes both peak fitting and template matching with tolerances for variations in the calibrations [29]. Its key steps are:
- Estimate the continuum background by peak erosion after background compensation to isolate the peaks. If available, a scaled background spectrum is subtracted from the measured spectrum.
- Apply nuclide filtering in which candidate nuclide peak spectra are constructed in accordance with line abundances and energy, shape, and efficiency calculations. Nuclides that cannot meet the identification criteria for amplitude do not need to be made candidates, thus reducing the search space during the shape matching step. The percent gain shift tolerance is the maximum gain shift considered during analysis, expressed as the percentage change in the energy calibration slope. The sensitivity threshold is the minimum nuclide spectral area required for identification, as a percentage of the measured peak spectrum. The percent gain shift tolerance and sensitivity thresholds are used along with the residual peak spectrum after baseline estimation to filter out non-candidates from the library.
- Simultaneously fit constructed spectra to the isolated measured peak data while allowing tolerance for calibration errors. Calibration compensation includes fitting gain shift and an effective thickness of absorbers to account for shielding not considered in the default efficiency. Only iron shielding is considered to modify the peak efficiency calibration.
- Match shapes by calculating the normalized correlation coefficient between the theoretical shape and the interference corrected measured shape and applying a threshold.
9.4. Other Algorithms
There are several other RIID algorithm options, many of which are available in commercial detectors. For example, [30] describes a few methods and distinguished between estimation and classification applications.
10. Current Performance
Performance is defined in various ways [3], but most simply by how far the algorithm deviates from perfect performance. Perfect performance of an algorithm on a test problem means that an algorithm detects all isotopes that are present in the source and does not detect any isotope that is not in the source. An example of a more specific performance metric is “conditionally correct,” which means that at least one of the most abundant isotopes in the sample was correctly identified, but with less confidence than some isotope that was not in the source.
Several studies have demonstrated lower-than-desired performance as characterized by various measures of correct isotope identification. For example, [3] reported only approximately 30%-50% correction identification among medical, industrial, NORM, and threat isotopes and [31] reported a high rate of correct identification for several RIID algorithms for bare sources, but a very low rate of correct identification when the same sources where shielded by 2 mm of steel.
Largely because of inadequate RIID algorithm performance, the U.S. Department of Energy (DOE) has created a program requiring trained γ -ray spectroscopists to be on call every day all day to resolve alarms as rapidly as possible. That is, human experts outperform the best RIID algorithm. The Domestic Nuclear Detection Office and the Department of Homeland Security within the DOE, and other interested organizations continue to sponsor dedicated experiments to evaluate NaI γ detectors as well as lower and higher resolution detectors.
10.1. Experiments to Assess Performance
Reference [31] describes aspects of the measurement protocols used for the RIID algorithm comparisons. One important task is to choose the number of repeat measurements per scenario, where a measurement scenario is defined by the source, geometry, shielding, and count time. There is a tradeoff between how many measurement scenarios can be assessed with how many repeat measurements. Options to augment real repeat measurements with synthetic (using MCNP-X for example, or simply using Poisson random numbers using estimated energy channel means) should be evaluated in performance assessments. Our view is that until simulated data is sufficiently realistic, the potential for algorithm improvements is not fully understood.
Section 6 mentioned a measurement protocol that requires measurements of the source at several distances between the source and detector as a way to correct for gain shift. RIID algorithm performance assessments should provide a convenient repository of data for evaluating candidate measurement protocols.
11. The Role and Quality of Synthetic Spectra
RIID algorithm performance assessment is currently based on real data collections such as those described in the previous section. Because computer models such as MCNP-X [32] and GEANT4 [33] can model the source, geometry, and shielding with high fidelity, it is likely that synthetic spectra can augment real data for algorithm testing and improvement. The main research area remaining in generating high-fidelity synthetic spectra is the DRF. Various aspects of NaI detectors such as the scintillator crystal imperfections and PMT electronics are very difficult to model using first principles. Therefore, various empirical or semi-empirical options are being developed [34].
Regarding the DRF, there are three key features of the spectra to consider, including the Gaussian broadening due to various physical effects such as the PMT as previously described; the exponential tails associated with peaks, and the “flat continua” that are often called the “Compton” continua. As an aside, a first principles physics model of the associated background counts (that must be added to the source counts in order to mimic real spectra) is difficult to model in general. In principle, one could assess the particular background sources, shielding, and geometries and attempt to model the background, but this would involve too large an effort for practical use. In practice, software such as GADRAS instead allows the user to fit the measured background using a small collection of isotopes that are ubiquitous in the environment, such as 232Th and 226Ra.
It is currently believed that accurate background simulation is less important for low resolution detectors (NaI) than for relatively high resolution detectors such as HpGe detectors. Qualitatively, this is because NaI detectors smooth/average over closely-separated peaks and therefore are not as likely to mistake a background-radiation-induced peak for a source peak. Also, the background need not always be modeled; for example, the effects of a relevant measured background could in many contexts be combined with the modeled source spectrum.
Figure 7 is an example of real and simulated NaI spectra (real or simulated counts recorded in one second) for 60Co. The simulation used MCNP-X, and either small, medium, or large strength background was assumed, while normalizing the simulated counts to roughly match the real counts in one region of interest. Details of this simulation are available in [35] and available by request. We are not aware of any numerical studies that compare RIID algorithm performance on real spectra to performance on corresponding simulated spectra. Instead, studies make qualitative comparisons such as visual inspection of Figure 7 to assess simulation quality.
Reference [34] reviews three options to estimate DRFs: experimental, computer model, or semi-empirical involving the use of both real and model results to characterized the three key features mentioned above (Gaussian broadening, exponential tails of peaks, and flat continua). Because RIID algorithms must essentially solve the “inverse DRF” problem by mapping a measured spectrum to an estimated “true” spectrum at the detector surface arising from the source of interest, improved DRF models should lead to improved isotope ID algorithms.
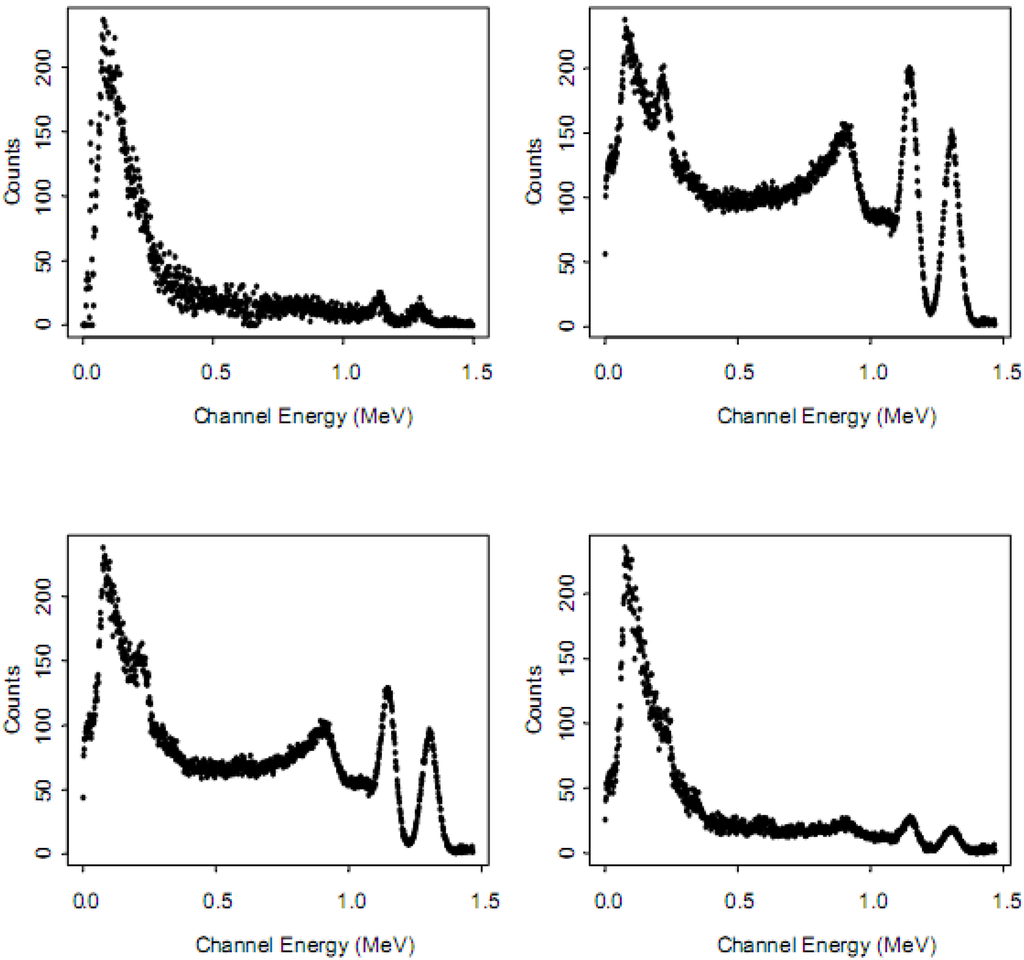
Figure 7.
Example Co-60 spectra from a 1,024 channel NaI detector. (top left) real spectra; (top right, bottom left, bottom right) synthetic spectra from MCNP with large, medium, and small background counts, respectively.
12. Future Directions
Although NaI detectors have been fielded for decades, RIID algorithms continue to improve, and next we describe two specific recommendations for future work. The first is Bayesian variable selection and the second is a comprehensive treatment of all noise sources along with possible mitigation strategies in the context of the Bayesian variable selection strategy.
12.1. Bayesian Variable Selection
By “variable selection,” we mean to choose the subset of isotopes from the chemical library that are thought to be present in the source. Bayesian Model Averaging (BMA) is one option to implement variable selection. BMA refers to averaging over subsets of candidate radio-isotopes. Variable selection continues to generate research [36,37] in a wide variety of applications. To infer which isotopes are present in a source, one implementation of BMA consists of the following steps.
- Define an upper bound Nmax for the number of isotopes that could be present in a source, such as Nmax = 5.
- Fit the background spectrum using a library of isotopes that are commonly found in the relevant background. Assume that background measured without the source is negligibly different than the background measured with the source so that the fitted background can effectively be “subtracted out” from the background plus source spectrum. Because of background suppression by the source, this “negligibly different assumption” is not exactly correct ([5],[18]), and the impact of this assumption should be the subject of additional study.
- Evaluate the likelihood for each subset consisting of 0, 1, 2, 3, …, Nmax isotopes for given data D. We write D to represent either the measured spectrum or perhaps a processed spectrum that extracts peak information, and/or smooths the measured spectrum, etc. There are possible subsets, where L is the size of the isotope library, which is approximately 200 in the broadest challenge problem. The effects of absorbers can be treated using the MBS [13] approach by having a representative library of approximately 3 to 5 absorbers.
- Apply BMA to evaluate the probability that isotope C is present, using , where equals 1 if its argument is true. That is, to estimate P(C|D), we simply sum the model probabilities for each subset that includes isotope C.
Although the estimated probabilities P(Mj|D) have varying accuracy depending on the data D, BMA is one of the most effective strategies for variable subset selection, particularly when prior information such as some isotope combinations being unlikely is available. For data D and a probability model for the data, it would be ideal if we could calculate the exact probability of each isotope subset. By Bayes theorem, where P(M1) is the prior probability for subset M1. This calculation requires calculation of where is the coefficient vector for the isotopes in model M1. Such integrals are notoriously difficult in most real problems requiring either numerical integration, analytical approximation, or Markov chain Monte Carlo (MCMC) methods [36,37]. Even if the integral could be computed accurately, we would rarely know the exact subset probabilities because real data never follows any probability model exactly. Therefore, various approximations are in common usage, with the BIC (Bayesian Information Criterion) being perhaps the most common [36,37,38]. We therefore suggest approximating using the approximate result that where will depend on the type of data D used (either the raw spectrum or a the spectrum following pre-processing as described), but will always involve a penalty term to make larger subsets less likely than smaller subsets, and a goodness of fit terms such as the weighted residuals around the fitted values. Particularly if the number M of possible subsets is large and each is evaluated, then MCMC might be too slow to run for each subset and a BIC-type approximation to quickly approximate the probability of each subset should be considered.
It is likely that variable selection methods customized for realistic Poisson likelihood regression with nonnegativity constraints can be most effectively treated using Bayesian variable selection. Because the MBS method [13] implies that the number of parameters (material basis vectors) required to fit the absorber effect is only three to five, the total number of required parameters is relatively small compared to the number of energy channels. One aspect of modern Bayesian methods is that a single best fitting model is rarely the final summary. Instead, for example, BMA is used to combine information from all of the evaluated models. Confidence measures from such a Bayesian strategy are directly available, which is one of the compelling reasons to favor a Bayesian approach. Alternatively, the assumption that at most five to ten unique isotopes will be present in a source of interest can be treated using a very strong penalty for model size (having more than 10 isotopes) or by simply trying all subsets up to size 10 as described above if that search is feasible [37,39].
12.2. Comprehensive Assessment of all Noise Sources
We are not aware of a comprehensive treatment of all noise sources and possible mitigation strategies. The published literature on RIID algorithms using NaI spectra, much of which is referenced here, tends to isolate one or a few noise sources and evaluate mitigation strategies, such as the peak alignment strategy described in [16]. Therefore, in conjunction with the Bayesian variable selection approach, a combination of real and simulated spectra should be used in extensive testing to assess the individual impact of all noise sources and potential noise mitigation strategies as measurement protocols are varied.
One noise source that is especially important to model is the error in the reference spectra and associated response matrix so that techniques from the errors in predictors literature [40] could be applied. For example, the MCMC approach to implement the Bayesian variable selection can easily accommodate errors in predictors, particularly if combined with a MIMBS-type approach that reduces the number of possible absorbers to a representative basis set. Specifically, in the model the response matrix will have errors that can be assessed and properly treated using MCMC to generate samples from the posterior distribution for both the isotopic composition vector aj and the values that characterize the absorber effects. That is, the values that impact can be treated as unknown parameters in MCMC so that both and aj are included in the unknown parameter vector in the MCMC search space. Two attractive features of the MCMC approach are that it easily handles nonnegativity constraints on both and aj and easily handles appropriate likelihoods such as the Poisson likelihood in this case.
It would be straightforward in simulation data to systematically eliminate or amplify each noise source, define “cases” by which noise sources are present in what amounts, and repeat the inference for the isotopic composition vector aj using Bayesian variable selection in each case.
13. Summary
RIID algorithm performance using relatively low resolution NaI detectors is currently considerably worse than the performance of expert spectroscopists, whose performance is typically judged by a consensus of experts that defines the correct result. In the past few years there has been growing interest in improving automated RIID algorithms so that the time burden on the on-call expert spectroscopists can be reduced. This review has described the current status of RIID algorithms for NaI detectors, the issues and related noise sources, and two main areas for potential improvements.
Acknowledgements
We acknowledge the Department of Homeland Security for partly funding the production of this material under DOE Contract Number DE-AC52-06NA25396 for the management and operation of Los Alamos National Laboratory.
References and Notes
- Redeker, W. New Dirty Bomb Detection Equipment Boosts Port, Border Security, ABC News, October 9, 2005, Albuquerque, NM.
- Stromswold, D.; Carkoch, J.; Ely, J.; Hansen, R.; Kouzes, R.; Milbath, B.; Runkle, R.; Sliger, W.; Smart, J.; Stephens, D.; Todd, L.; Woodring, M. Field Tests of a NaI(T1)-Based Vehicle Portal Monitor at Border Crossings. In Proceedings of IEEE Nuclear Science Symposium Conference, Rome, Italy, Oct 16-22, 2004; 1, pp. 196–200. http://ieeexplore.ieee.org/iel5/9892/31433/ 01462180.pdf.
- Blackadar, J.; Garner, S.; Bounds, J.; Casson, W.; Mercer, D. Evaluation of Commercial Detectors. In Proceedings of the Annual Meeting of the Institute of Nuclear Materials Management, Phoenix, AZ, July 13-17, 2003.
- Hofstadter, R. Alkali Halide Scintillation Counters. Phys. Rev. 1948, 74, 100–106. [Google Scholar] [CrossRef]
- Sullivan, C. Isotope identification algorithms. In Nuclear Reachback Reference Manual; Cason, W., Sullivan, C., Blackadar, J., Paternoster, R., Matzki, J., Eds.; Los Alamos National Laboratory Unrestricted Release Publication, LAUR-06-0504: Los Alamos, NM, USA, 2006; pp. 75–90. [Google Scholar]
- Sullivan, C.; Garner, S.; Lombardi, M.; Butterfield, K.; Smith-Nelson, M. Evaluation of key detector parameters for isotope identification. IEEE Nuclear Science Symposium Conference Record 2007, 1181–1184. [Google Scholar]
- Zhang, W.; Zahringer, M.; Ungar, K.; Hoffman, I. Statistical analysis of uncertainties of γ peak identification and area calculation in particulate air-filter environment radionuclide measurements using the results of a comprehensive nuclear-test-ban treaty organization organized intercomparison. Appl. Radiat. Isotopes 2008, 66, 1695–1701. [Google Scholar]
- Picard, R.; Burr, T. Networked Sensors for Cargo Screening. IEEE Sensors J. 2008, 8, 1389–1396. [Google Scholar] [CrossRef]
- American National Standard Performance Criteria for Hand-held Instruments for the Detection and Identification of Radionuclides, N42.34. 2003. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=4079480 access date 11/22/08.
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of statistical learning; Springer: New York, 2001. [Google Scholar]
- Venables, W.; Ripley, B. Modern applied statistics with S-plus; Springer: New York, 1999. [Google Scholar]
- Knoll, G. Radiation Detection and Measurement. 2nd edition; Wiley: New York, 1989. [Google Scholar]
- Estep, R.; McCluskey, C.; Sapp, B. The multiple isotope material basis set (MIMBS) method for isotope identification with low- and medium-resolution γ-ray detectors. J. Radioanal. Nucl. Chem. 2008, 276, 737–741. [Google Scholar] [CrossRef]
- GR135 detector; http://www.holger.se/pdf/gr_135.pdf access date 11/22/08.
- Burr, T.; Hengartner, N. Overview of Physical Models and Statistical Approaches for Weak Gaseous Plume Detection Using Infrared Hyperspectral Imagery. Sensors 2006, 6, 1721–1715. [Google Scholar] [CrossRef]
- Robinson, S.; Kiff, S.; Ashbaker, E.; Bender, S.; Flumerfelt, E.; Salvitti, M.; Borgardt, J.; Woodring, M. Effects of high count rate and gain shift on isotope identification algoritms. IEEE Nuclear Science Symposium Conference Record 2007, 2, 1152–1156. [Google Scholar]
- Runkle, R.; Tardiff, M.; Anderson, K.; Carlson, D.; Smith, E. Analysis of Spectroscopic Radiation Portal Monitor Data using Principal Components Analysis. IEEE Transactions on Nuclear Science 2006, 53, 1418–1423. [Google Scholar] [CrossRef]
- Burr, T.; Myers, K. Signatures for Several Types of Naturally Occurring Radioactive Material. Appl. Radiat. Isotopes 2008, 66, 1250–1261. [Google Scholar] [CrossRef] [PubMed]
- Blackadar, J. Automatic isotope identifier and their features. IEEE Sensors J. 2005, 5, 589–592. [Google Scholar] [CrossRef]
- Garner, S. PeakDoctor Analysis Software. IEEE Nuclear Science Symposium 2004. Rome, Italy. [Google Scholar]
- Sullivan, C.; Martinez, M.; Garner, S. Wavelet Analysis of NaI Spectra. IEEE Transactions on Nuclear Science 2006, 53, 2916–2922. [Google Scholar] [CrossRef]
- Parker, J.; Reilly, D. Plutonium Isotopic determination by γ-ray Spectroscopy. In Nuclear Analysis Research and Development Program Status Report; January-April 1974; Robert Keepin, G., Ed.; Los Alamos Scientific Laboratory report LA-5675-PR. Similar and more recent publications are available from tburr@lanl.gov upon request. [Google Scholar]
- Burr, T.; Sampson, T.; Vo, D. Statistical evaluation of FRAM γ -ray isotopic analysis data. Appl. Radiat. Isotopes 2005, 62, 931–940. [Google Scholar] [CrossRef] [PubMed]
- Mitchell, D. γ detector response and analysis software (GADRAS). Sandia Report SAND88-2519; Sandia National Laboratories: Albuquerque, New Mexico, 1988. [Google Scholar]
- LaVigne, E.; Sjoden, G.; Backiak, J.; Detwiler, R. Extraordinary improvement in scintillation detectors via post-processing with ASEDRA- solution to a 50-year-old problem. In Proceedings of SPIE, Orlando, FL, USA, March 18, 2008.
- GADRAS. http://ipal.sandia.gov/ip_details.php?ip=7530 access date 11/22/08.
- Miko, D.; Estep, R.; Rawool-Sullivan, M. An innovative method for extracting isotopic information from low-resolution γ spectra. Nucl. Instrum. Meth. Phys. Res. A 1999, 422, 433–437. [Google Scholar] [CrossRef]
- Estep, R.; Rawool-Sullivan, M.; Miko, D. A Method for correcting NaI spectra for attenuation losses in hand-held instrument applications. IEEE Transactions on Nuclear Science 1998, 45, 1022–1028. [Google Scholar] [CrossRef]
- Russ, W. Library correlation nuclide identification algorithm. Nucl. Instrum. Meth. Phys. Res. A 2007, 579, 288–291. [Google Scholar] [CrossRef]
- Labov, S.; Pleasance, L.; Sokkappa, P.; Craig, W.; Chapline, G.; Frank, M.; Gronberg, J.; Jernigan, J.; Johnson, S.; Kammeraad, J.; Lange, D.; Meyer, K.; Nelson, K.; Pohl, B.; Wright, D.; Wurtz, R. Foundations for Improvements to Passive Detection Systems- Final Report, UCRL-TC-207129. 2004. available as http://www.llnl.gov/tid/lof/documents/pdf/312592.pdf access date 11/22/08. [Google Scholar]
- Pibida, L.; Unterweger, M.; Karam, L. Evaluation of Handheld Radionuclide Identifiers. Journal of Research of the National Instisute of Standards and Technology 2004, 109, 451–456. [Google Scholar] [CrossRef]
- MCNP-X (Monte Carlo N-Particle Transport Code). http://www-xdiv.lanl.gov/x5/MCNP/ access date 11/22/08.
- GEANT4:. http://wwwasd.web.cern.ch/wwwasd/geant/ access date 11/22/08.
- Sood, A.; Gardner, R. A new Monte Carlo assisted approach to detector response functions. Nucl. Instrum. Meth. Phys. Res. B 2004, 213, 100–104. [Google Scholar] [CrossRef]
- Burr, T.; Myers, S.; Sood, A. Sources of uncertainty in computer models for the detected γ radiation emitted from naturally occurring radioactive materials. Los Alamos National Laboratory unrestricted release report, LA-UR-07-2867.
- Raftery, A.; Madigan, D.; Hoeting, J. Bayesian Model Averaging for Linear Regression Models. J. Amer. Statist. Assn. 1997, 92, 179–191. [Google Scholar]
- Burr, T.; Fry, H.; McVey, B.; Sander, E.; Cavenaugh, J.; Neath, A. Performance of variable selection methods in regression using variations of the Bayesian Information Criterion. Comm. in Stat- Simulation 2008, 37, 507–520. [Google Scholar] [CrossRef]
- Kass, R.; Raftery, A. Bayes Factors. J. Amer. Statist. Assn. 1995, 90, 773–795. [Google Scholar] [CrossRef]
- Burr, T.; Foy, B.; Fry, H.; McVey, B. Characterizing Clutter in the Context of Detecting Weak Gaseous Plumes in Hyperspectral Imagery. Sensors 2006, 6, 1587–1615. [Google Scholar] [CrossRef]
- Davies, R.; Hutton, B. The effect of errors in the independent variables in linear regression. Biometrika 1975, 62, 383–391. [Google Scholar] [CrossRef]
© 2009 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).