Algorithm for Active Suppression of Radiation and Acoustical Scattering Fields by Some Physical Bodies in Liquids
Abstract
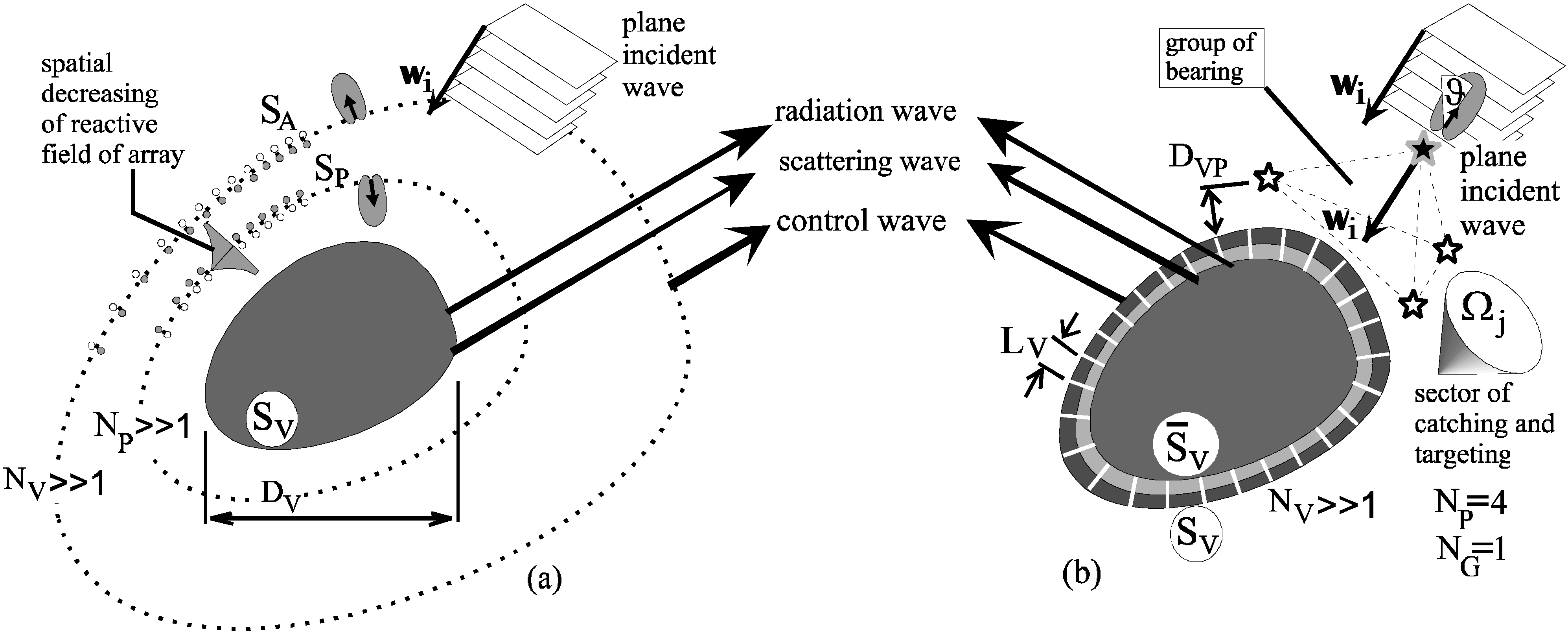
:1. Introduction
1.1. Passive Methods (Passive Coatings)

1.1.1. Absorbing Coatings
1.1.2. Coatings Based on Interference
1.1.3. Coatings Based on Metamaterials
1.2. Active Methods
1.2.1. Malyuzhinets’ Method
1.2.2. Bobrovnitskii’s Active Method
1.2.3. Joint Suppression of Radiating and Scattering Field by a Coating of Controlled Thickness
1.2.4. Rules of Chain Substitution
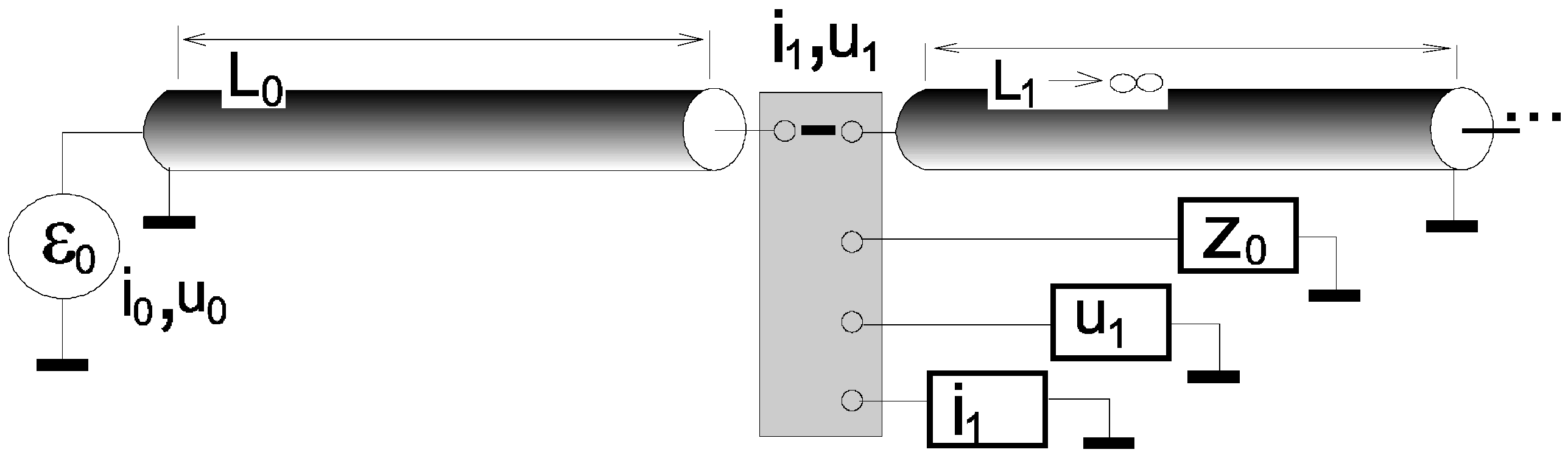
1.2.5. Choice of Velocity or Displacement Control (Nonequivalence of Velocity and Pressure Control)
2. Features of the Statement of the Problem
- a)
- simultaneous suppression of radiation and scattering fields of the protected body;
- b)
- wide frequency range of suppression;
- c)
- minimum prior and current information on the incident waves and radiation waves;
- d)
- minimum prior and current information on the vibroacoustical characteristics of protected body;
- c)
- neutral floatability of protected body in liquid;
- d)
- quick response of active system, caused by changes of the incident wave field.
3. The Control of Normal Velocities (Displacements) of the Body’s Surface
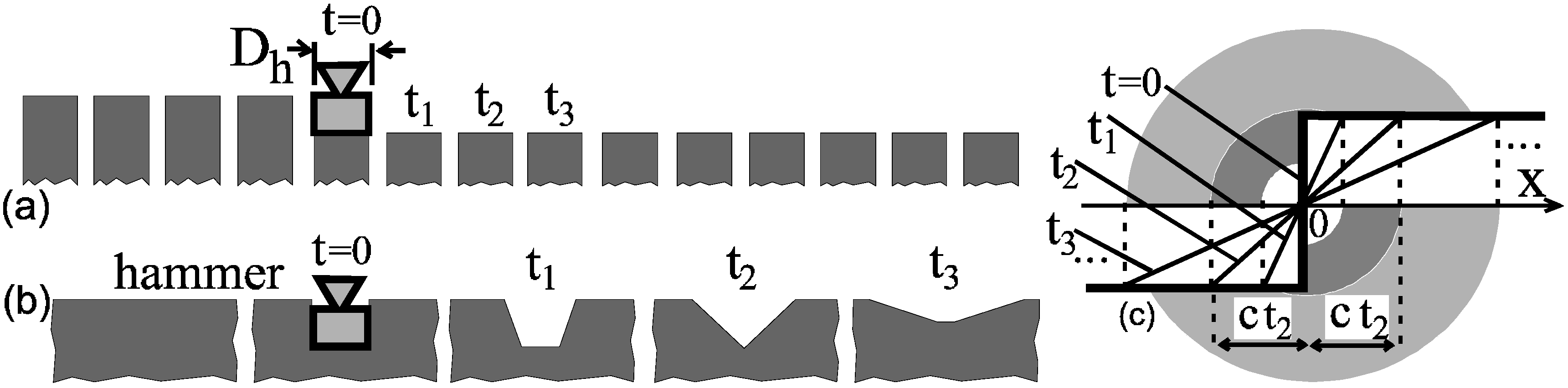
4. Prior Information About the Construction of the Protected Body
4.1. The Construction of the Protected Body

4.1.1. Ringingness of the Protected Body
4.1.2. Smoothness of Vibrational Fields on the Protected Body
4.1.3. Constancy of Parameters of the Protected Body
4.1.4. Layer of Dissipative Polymer
5. Active Coating and its Control Algorithm
5.1. The Discrete Representation of the Body Protection Surface
5.2. Active Coating

5.3. The Cross-Section Structure of the Protected Body
5.4. The Control Algorithm for the Synthesis of DNOV
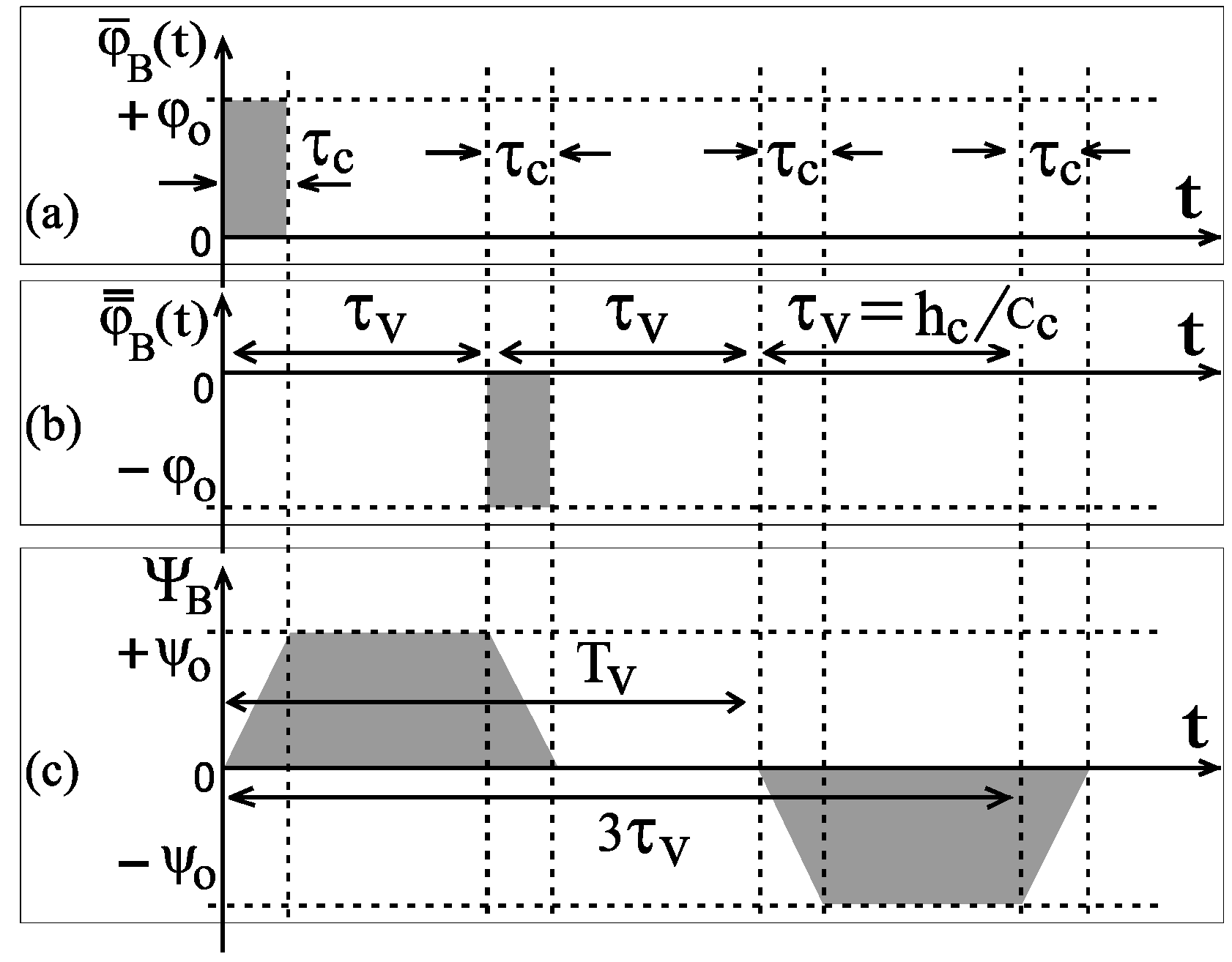
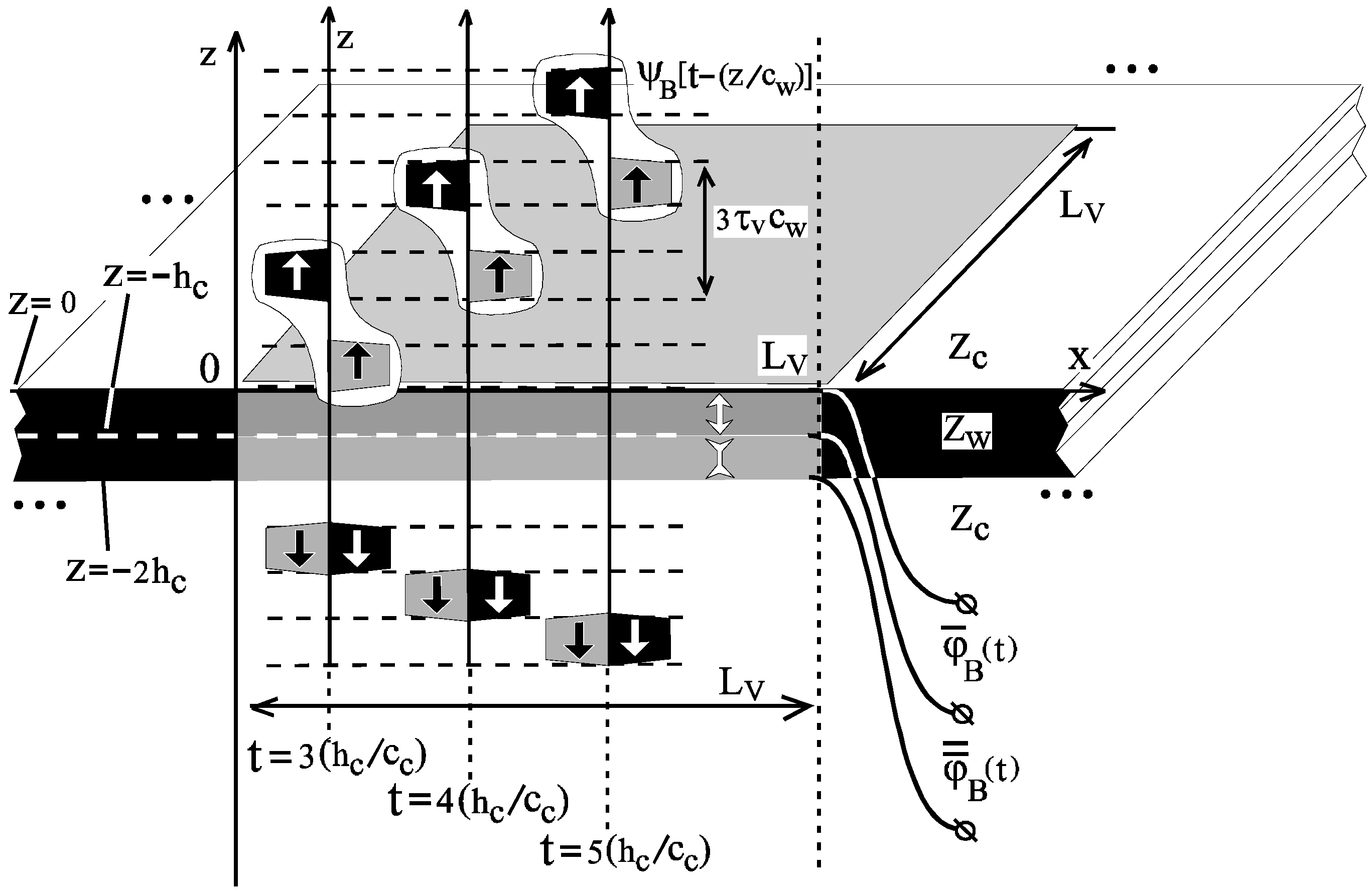
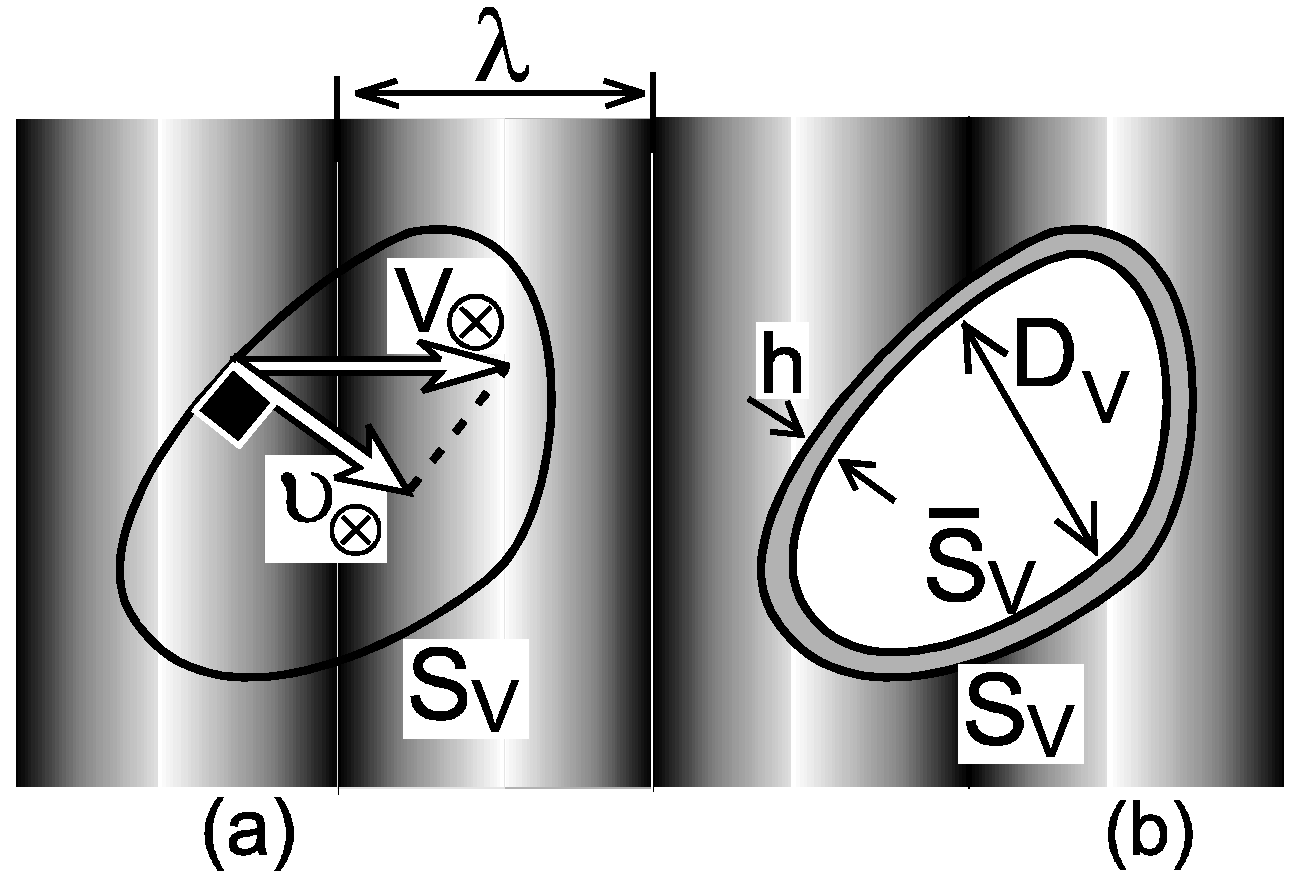
5.5. Some Notes about the Stability of the Synthesis of DNOV (DNOD)
5.5.1. Interaction Between Adjacent Pistons
5.5.2. Synthesis of One-Dimensional DNOD in a Three-Dimensional Case

5.5.3. Formation of Step-Like DNOD
5.5.4. Formation of Strip-Like Piston DNOD
5.5.5. About Ringingness of a Body
5.5.6. Hierarchy of Scales in the Active Coating
5.6. The Measuring Section of the Active Control Damping System
6. Suppression of the Scattering Field
6.1. Incident Wave Field
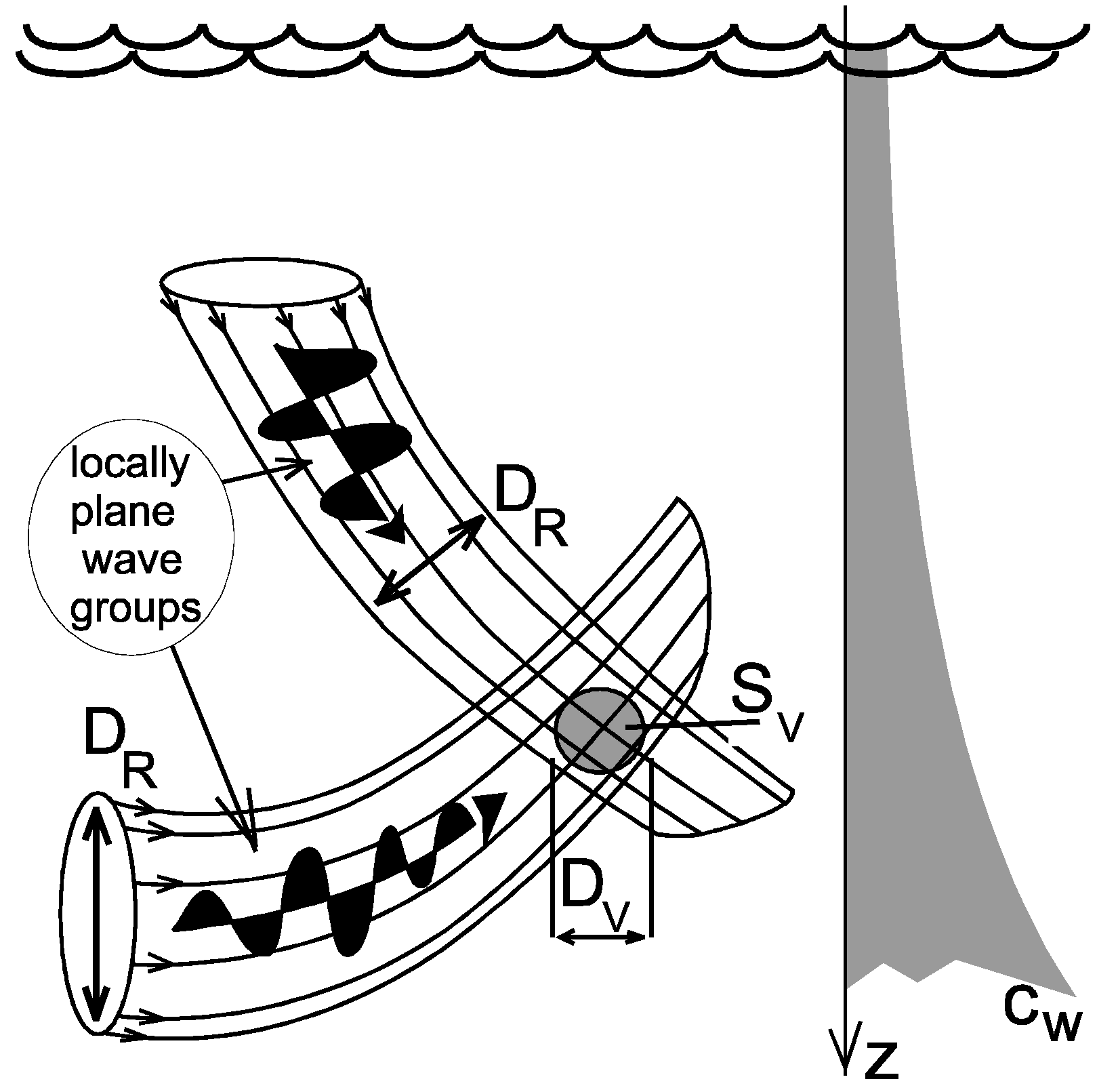
6.2. The Scattering Suppression System and Algorithm
6.2.1. Targeting of One Incident Wave

6.2.2. Vector Microphone
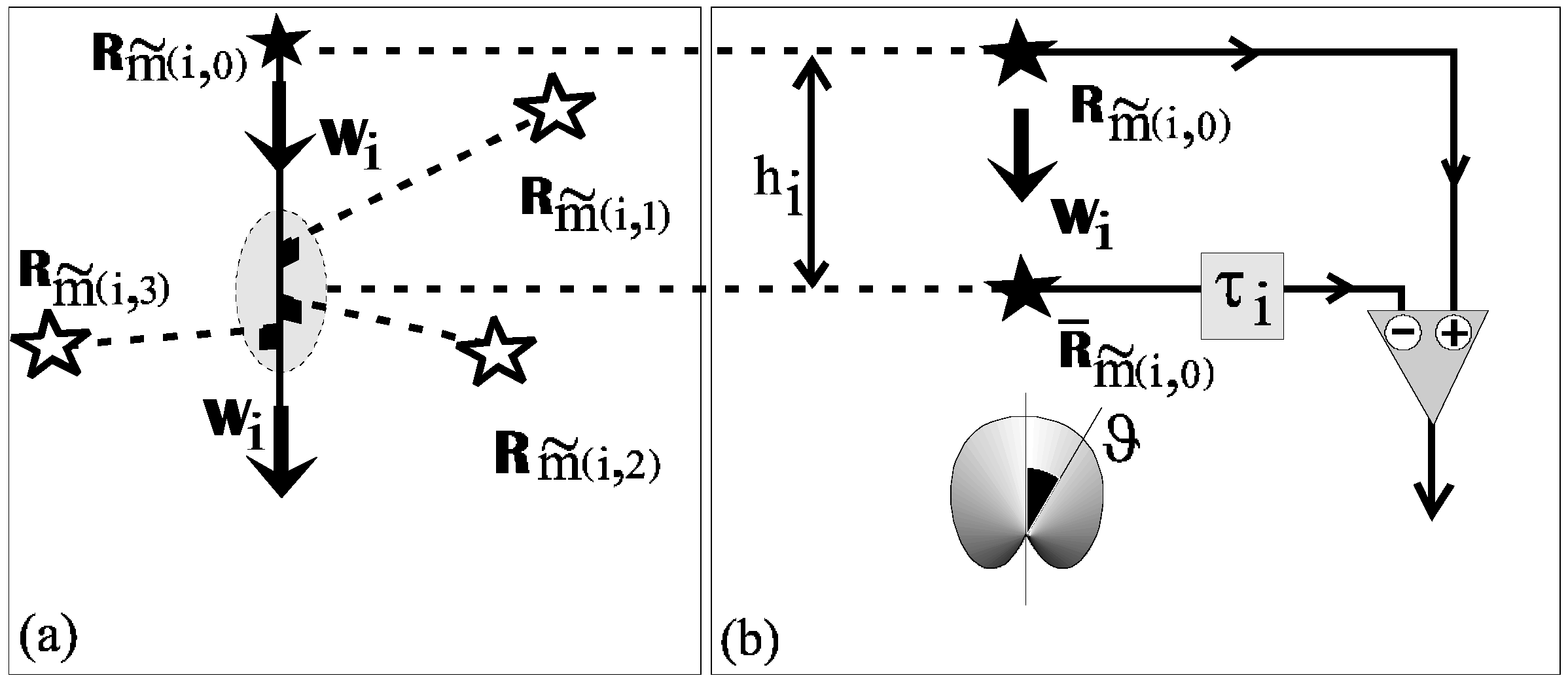
6.2.3. Renovation of DNOV on for the First Incident Wave
6.2.4. Microphone Signal Renovation for Catching the Second Incident Wave.
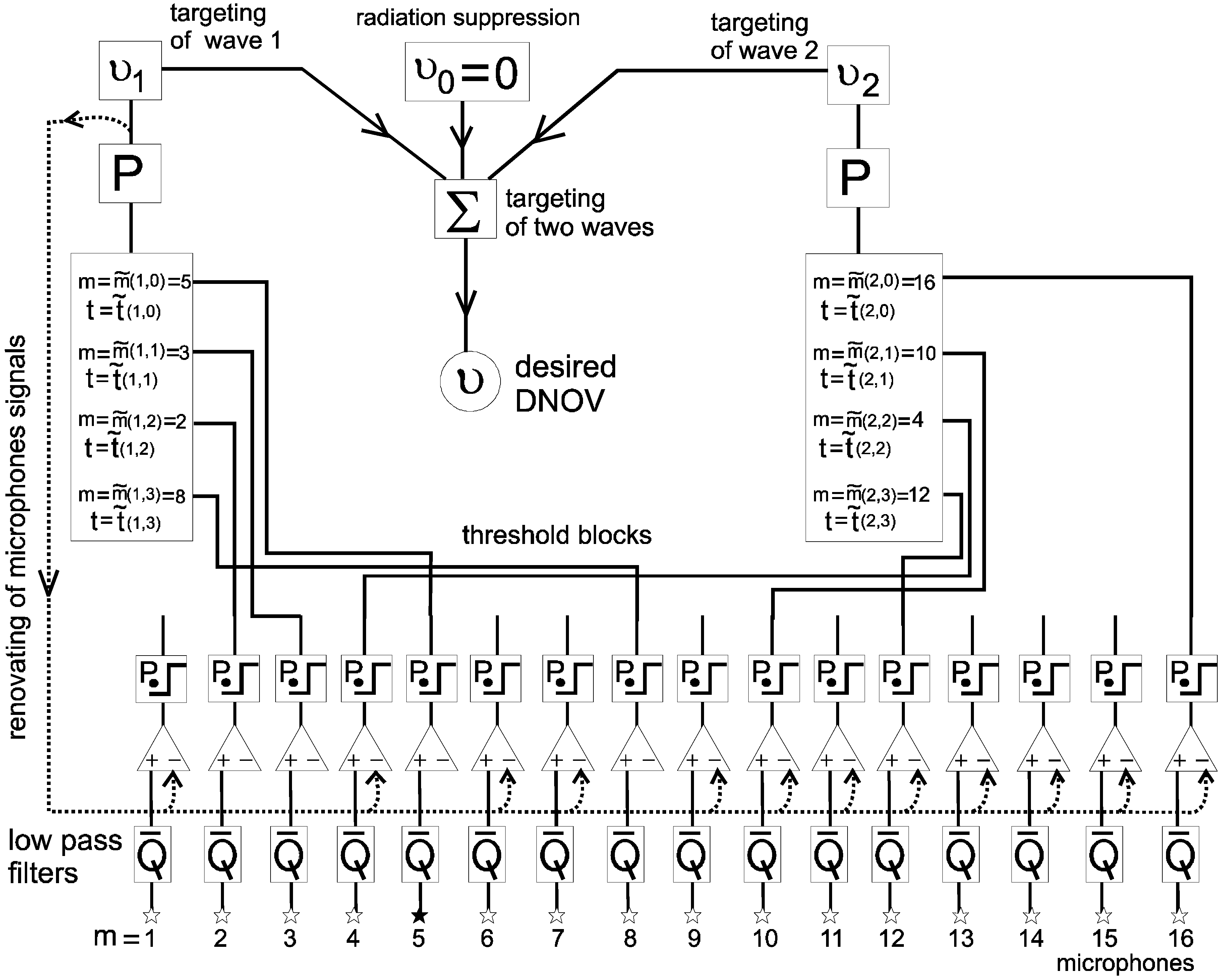
6.2.5. Two Incident Wave Targeting
6.2.6. Renovation of DNOV on for Two Incident Waves
6.2.7. Microphone Signal Renovation for Catching the Third Incident Wave
6.2.8. Calibration
6.2.9. Reset of Active System
6.3. Notes about the Stability of an Active System with Microphones
6.4. Hierarchy of Scales in the System of Scattering Suppression
6.5. Placement of Microphones

6.5.1. Geometry of the Microphone Grid

6.5.2. Total Number of Microphones
6.6. Microphone Noise
6.6.1. Noise of a Vector Microphone
7. Conclusions
Acknowledgements
References and Notes
- Rozanov, N.N. Invisibility: “pro” and “contra”. Priroda 2008, 6, 3–10. [Google Scholar]
- Bobrovnitski, Yu.I. A nonscattering coating for a cylinder. Acoustical Physics 2008, 6, 879–889. [Google Scholar] [CrossRef]
- Alu, A.; Engheta, N. Achieving transparency with plasmonic and metamaterial coatings. Physical Review 2005, E72, 0166623. [Google Scholar]
- Shurig, D.; Mock, J.; Justice, B.; Cummer, S.; Pendry, J.; Starr, A.; Smith, D. Metamaterial electromagnetic cloak at microwave frequencies. Science 2006, 314, 977–980. [Google Scholar] [CrossRef] [PubMed]
- Torrent, D.; Sanchez-Dehesa, J. Acoustic metamaterials for two-dimensional sonic devices. New Journal of Physics 2007, 9, 323–335. [Google Scholar] [CrossRef]
- Kerker, M. Invisible bodies. Journal of the Optical Society of America 1975, 65, 376–379. [Google Scholar] [CrossRef]
- Cummer, S.A.; Popa, B.I.; Shuring, D.; Smith, D.R.; Pendry, J.; Rahm, M.; Starr, A. Scattering theory derivation of a 3D acoustic cloaking shell. Physical Review Letter 2008, 100, 024301. [Google Scholar] [CrossRef]
- Leonhard, U. Notes on conformal invisibility devices. New Journal of Physics 2006, 8, 118–123. [Google Scholar] [CrossRef]
- Jessel, M.; Mangiante, G. Active sound absorbers in an air ducts. Sound and Vibration 1973, 6, 383–390. [Google Scholar] [CrossRef]
- Zhu, H.; Raymany, R; Stelson, K.A. Active control of acoustic reflection, absorption and transmission using thin panel speakers. Journal of the Acoustical Society of America 2003, 2, 852–870. [Google Scholar] [CrossRef]
- Elliott, S.J.; Joseph, P.; Nelson, P.A.; Johnson, M.E. Active output absorption in the active control sound. Journal of the Acoustical Society of America 1993, 5, 2501–2512. [Google Scholar]
- Premount, A. Vibration Control of Active Structures, an Introduction; Kluwer Academic Publishers: New York, NY, USA, 2002. [Google Scholar]
- Fuller, C.R.; Elliott, S.J.; Nelson, P.A. Active Control of Vibration; Academic Press: London, UK, 1996. [Google Scholar]
- Nelson, P.A.; Elliott, S.J. Active control of Sound; Academic Press: London, UK, 1993. [Google Scholar]
- Furstoss, M.; Thenail, D.; Galland, M.A. Surface impedance control for absorption: direct and hybrid passive-active strategies. Journal of Sound and Vibration 2003, 6, 219–236. [Google Scholar] [CrossRef]
- Hansen, C.H.; Snyder, S.D. Active Control of Noise and Vibration; E&FN: London, UK, 1997. [Google Scholar]
- Lasiecka, I.; Morton, B. Control Problems in Industry; Birkhauser: London UK, 1995. [Google Scholar]
- Avalos, G.; Lasiecka, I. Exact controllability of structural acoustic interactions. Journal de Matematiques Pure et Applique 2003, 82, 1074–1073. [Google Scholar] [CrossRef]
- Lasiecka, I. Triggiani. In Research Monograph: Deterministic Control Theory for Infinite Dimensional Systems; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Bobrovnitski, Yu.I. A new solution to the problem of an acoustically transparent body. Acoustical Physics 2004, 6, 647–651. [Google Scholar] [CrossRef]
- Arabadzhi, V.V. Suppression of the sound field of a vibrating body by monopoles attached to its surface. Acoustical Physics 2006, 5, 505–512. [Google Scholar] [CrossRef]
- Bobrovnitski, Yu.I. Active control of sound in a room: method of global impedance matching. Acoustical Physics 2003, 6, 731–737. [Google Scholar] [CrossRef]
- Widrow, B; Mc Cool, J.M. A comparison of adaptive alforithms based on the methods of steepest descent and random search. IEEE Transactions on Antennas & Propagation 1976, 5, 615–637. [Google Scholar]
- Babasova, E.M.; Zavadskaya, M.P.; Egelski, B.L. Active Methods of Acoustic Field Suppression (Based on Huygens Surfaces); Tyutekin, V.V., Fedoryuk, M.V., Eds.; TsNII Rumb: Moscow, USSR, 1982. [Google Scholar]
- Malyuzhinets, G.D. Nonstationary diffraction problems for a wave equation with finite right parts. Proceedings of Acoustical Institute 1971, 15, 124–139. [Google Scholar]
- Mazanikov, A.A.; Tyutekin, V.V. Investigation of active autonomic sound absorption system in multimode waveguide. In Presented at the 9th International Congress of Acoustics, Madrid, Spain, June 1977; p. 260.
- Friot, E.; Bordier, C. Real-time active suppression of scattered acoustic radiation. Journal of Sound and Vibration 2004, 3, 563–580. [Google Scholar] [CrossRef]
- Friot, E.; Guillermin, R.; Winninger, M. Active control of scattered acoustic radiation: a real-time implementation for a three-dimensional object. Acustica Acta 2006, 2, 278–288. [Google Scholar]
- Miller, D.A.B. On perfect cloaking. Optic Express 2006, 25, 12457–12466. [Google Scholar] [CrossRef]
- Junger, M.C.; Feit, D. Sound, Structure, and Their Interaction; ASA Publications: New York, NY USA, 1993. [Google Scholar]
- Premount, A. Mechatronics. In Dynamics of Electromechanical and Peizoelectric Systems; Springer: New York, NY USA, 2006. [Google Scholar]
- Howarth, T.R.; Varadan, V.K.; Bao, X.; Varadan, V.V. Piezocomposite coating for active underwater sound reduction. Journal of the Acoustical Society of America 1992, 2, 823–831. [Google Scholar] [CrossRef]
- Lusheikin, G.A. New piezoelectric materials, containing polymers. Physics of Solid State 2006, 6, 963–964. [Google Scholar]
- Deu, J.-F.; Larbi, W.; Ohayon, R. Piezoelectric structural acoustic problems: symmetric variational formulations and finite element result. Computer Methods in Applied Mechanics and Engineering 2008, 197, 1715–1724. [Google Scholar] [CrossRef]
- Gentilman, R; Fiore, D.; Torri, R.; Glynn, J. Piezocomposite smart panels for active control of underwater vibration and noise. In Proceedings of 5th SPIE International Symposium on Smart Structures and Materials, San Diego, CA, USA, August 1998; pp. 1–7.
- Arabadzhi, V.V. Active control of normal particle velocity at a boundary between two media. Acoustical Physics 2005, 2, 139–146. [Google Scholar] [CrossRef]
- Arabadzhi, V.V. Conversion of acoustically hard body into an acoustically transparent one in an initial value problem. Acoustical Physics 2008, 6, 869–878. [Google Scholar] [CrossRef]
- Arabadzhi, V.V. Supportless Unidirectional Acoustic Sources. Acoustical Physics 2009, 1, 104–116. [Google Scholar] [CrossRef]
- Virovlyansky, A.L. Ray Theory of Long-Range Sound Propagation in Ocean; Institute of Applied Physics (RAS): Nizhny Novgorod, Russia, 2006. [Google Scholar]
© 2009 by the authors licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Arabadzhi, V.V. Algorithm for Active Suppression of Radiation and Acoustical Scattering Fields by Some Physical Bodies in Liquids. Algorithms 2009, 2, 361-397. https://doi.org/10.3390/a2010361
Arabadzhi VV. Algorithm for Active Suppression of Radiation and Acoustical Scattering Fields by Some Physical Bodies in Liquids. Algorithms. 2009; 2(1):361-397. https://doi.org/10.3390/a2010361
Chicago/Turabian StyleArabadzhi, Vladimir V. 2009. "Algorithm for Active Suppression of Radiation and Acoustical Scattering Fields by Some Physical Bodies in Liquids" Algorithms 2, no. 1: 361-397. https://doi.org/10.3390/a2010361
APA StyleArabadzhi, V. V. (2009). Algorithm for Active Suppression of Radiation and Acoustical Scattering Fields by Some Physical Bodies in Liquids. Algorithms, 2(1), 361-397. https://doi.org/10.3390/a2010361



