GLADC: Global Linear Attention and Dual Constraint for Mitigating Over-Smoothing in Graph Neural Networks

Abstract

Graph Convolutional Networks (GCNs) enhance node representations by aggregating information from neighboring nodes, but deeper layers often suffer from over-smoothing, where node embeddings become indistinguishable. Transformers enable global dependency modeling on graphs but suffer from high computational costs and can exacerbate over-smoothing when multiple attention layers are stacked. To address these issues, we propose GLADC, a novel framework designed for semi-supervised node classification. It integrates global linear attention for efficient long-range dependency capture and a dual constraint module for local propagation. The dual constraint consists of (1) column-wise random masking on the representation matrix to dynamically limit redundant information aggregation, and (2) row-wise contrastive constraint to explicitly increase inter-node distance and preserve distinctiveness. This design achieves linear-complexity global mixing while effectively countering representation homogenization. Extensive evaluations on seven real-world datasets demonstrate that GLADC delivers competitive performance and maintains robustness in deep architectures (up to 32 layers). An ablation study further confirms the synergistic effect of both constraints in alleviating over-smoothing and preventing premature convergence.

1. Introduction

Graph Convolutional Networks (GCNs) [1,2] have become a mainstream approach for processing relational data, with successful applications in protein function prediction [3], recommendation systems [4], traffic flow analysis [5], and social network modeling [6]. This process involves iteratively aggregating information from neighboring nodes, which effectively summarizes large amounts of data into concise representations and facilitates efficient learning [7,8]. Through this mechanism, GCNs integrate both structural and attribute information into node representations, thereby improving performance on various downstream tasks.

However, as the number of layers increases, repeated message passing causes node embeddings to become increasingly homogeneous, rapidly diminishing their discriminative power. This phenomenon, known as over-smoothing [9], has been widely recognized as a key bottleneck limiting the scalability and effectiveness of deep GCNs. As illustrated in Figure 1, although nodes P and Q have distinct first-order neighbors, they share many overlapping neighbors at the third-order level, leading to highly similar node representations.

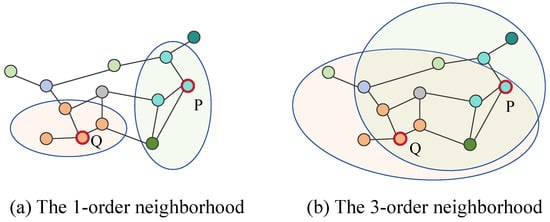
Figure 1. The neighboring nodes vary with different orders. Nodes P and Q have different first-order neighbors. In the third-order neighborhood, nodes P and Q share overlapping neighbors, and the number of neighboring nodes increases substantially.

Existing methods to mitigate over-smoothing can be broadly categorized into neighbor filtering and individuality enhancement. The former aims to reduce redundant information injection by randomly dropping edges, messages, or nodes, or by modifying normalization weights, as seen in methods like DropEdge [10], DropMessage [11], and ContraNorm [12]. However, as shown in Figure 2, while DropMessage and ContraNorm can maintain accuracy up to 8 layers, their performance sharply declines beyond 16 layers due to the excessive aggregation of information from exponentially growing neighbors. Thus, neighbor filtering struggles to counter the exponential growth of neighbors as depth increases, which leads to feature homogenization. The latter category, individuality enhancement, aims to preserve node-specific characteristics via techniques such as residual connections, skip-layer aggregation, or contrastive learning. For instance, AIR [13] incorporates shallow representations into new layer embeddings and introduces inter-layer contrastive losses. Nevertheless, individuality enhancement alone is insufficient to address the information redundancy caused by high-order neighbor overlap. To synergistically overcome the limitations of both strands, we propose a Dual Constraint module, composed of random masking and contrastive constraint. The random masking strategy acts as a dynamic neighbor filter by selectively discarding a subset of feature dimensions from the aggregated neighborhood information and replacing them with the node’s own representations from the previous layer. This technique effectively limits the influx of redundant information from high-order neighbors during aggregation, thereby mitigating feature homogenization. Similarly, the contrastive constraint serves as an individuality enhancement technique by minimizing the distance between representations of the same node across layers while maximizing the distance between different nodes, thereby explicitly reinforcing inter-node discriminability.

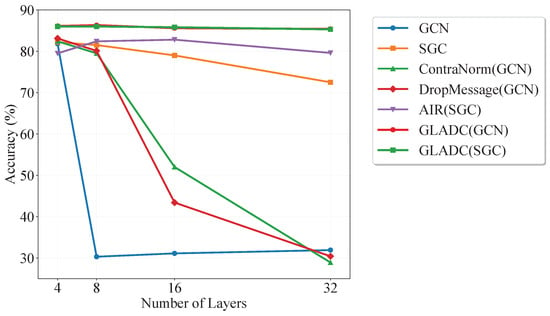
Figure 2. Accuracy comparison across varying depths on the Cora dataset.

In recent years, Transformer-based models [14] have emerged as powerful encoders for graph-structured data by representing nodes as input tokens, demonstrating competitive performance on both graph-level and node-level tasks. The global attention mechanism inherent in Transformers enables the modeling of implicit dependencies between nodes beyond explicit topological connections, which may reflect essential correlations in the underlying data generation process. However, prevailing Transformer architectures often inherit design principles from the computer vision and natural language processing, typically stacking multiple layers of multi-head attention. This design results in high computational complexity, as both time and memory costs grow quadratically with the number of nodes. To address this, we adopt a global linear attention mechanism, which reduces complexity to $\mathcal{O}\left(N\right)$, thereby significantly decreasing computational runtime. Furthermore, the global linear attention mechanism facilitates direct interaction and information mixing among all nodes in the graph, overcoming the limitation of traditional GNNs that aggregate information only from first-order or limited-order neighbors. This global interactive capability allows the model to capture potential long-range dependencies between distant nodes. In contrast, GNNs based on local neighborhood aggregation focus more on excavating the local topological properties of the graph structure. Therefore, the integration of global linear attention with local GNN propagation naturally establishes an effective global–local synergistic constraint within the model: the former is responsible for integrating global information to enrich node representations, while the latter ensures that the learned representations remain faithful to the local graph structure. This synergy collectively enhances the model’s expressive power and helps mitigate the over-smoothing issue in deep networks.

In summary, we propose a novel scheme termed GLADC, which integrates global linear attention and dual constraint.

• Global linear attention, which captures long-range dependency across all nodes with linear complexity, enabling efficient global information mixing;
• Dual constraint applied during local propagation to synergistically mitigate over-smoothing:

  –

  Column-wise random masking acts as a dynamic neighbor filter. It randomly freezes a subset of feature channels during aggregation, limiting the influx of redundant information from high-order neighbors and preserving the node’s intrinsic features from the previous layer.

  –

  Row-wise contrastive constraint explicitly maximizes the distance between representations of different nodes while minimizing the distance for the same node across layers, thereby enhancing inter-node discriminability.

Our main contributions are summarized as follows:

• We propose GLADC, a novel scheme that integrates global linear attention and dual constraint to achieve efficient long-range modeling while effectively resisting over-smoothing.
• Extensive experiments on multiple real-world graph datasets demonstrate that GLADC significantly alleviates over-smoothing, prevents performance degradation in deep architectures, and achieves state-of-the-art performance on multiple real-world graph datasets.

2. Related Work

2.1. Over-Smoothing Phenomenon and Mitigation Strategies

The over-smoothing phenomenon was first systematically analyzed by [9], who observed that as the number of graph convolutional layers increases, node embeddings progressively converge into a homogeneous subspace, leading to a significant loss of node discriminability. This issue primarily arises from two underlying causes: (1) redundant information introduced by overlapping high-order neighbors, and (2) the exponential growth in neighbor count, which drives individual node characteristics toward homogenization. Existing mitigation strategies addressing these challenges can be broadly categorized into two groups: neighbor filtering and individuality enhancement.

Neighbor filtering methods selectively aggregate neighbor information to prevent node representations from becoming indistinguishable. They can be divided into explicit and implicit approaches. Explicit methods such as APPNP [15], DropEdge [10], DropNode [16], and DropMessage [11] randomly remove edges, nodes, or messages to reduce the volume of information propagation, thereby alleviating over-smoothing. Implicit methods include PairNorm [17], NodeNorm [18], and ContraNorm [12], which regulate the embedding distribution without altering the graph structure. Specifically, PairNorm normalizes layer-wise mean and variance, NodeNorm performs per-node normalization, and ContraNorm introduces contrastive normalization to counteract embedding collapse. However, such normalization techniques may shift the embedding distribution away from class boundaries due to biases introduced by class-level statistics.

Individuality enhancement methods, on the other hand, aim to preserve node-specific features by incorporating self-representations (e.g., from the first or last layer) into the new layer embeddings. JKNet [19], for example, uses jump connections to aggregate features across all layers, while DeepGCNs [20] borrows the residual structure of ResNet to inject shallow information into deeper layers, and GCNII [21] further incorporates the initial input features into every subsequent layer to strengthen information preservation. However, over-reliance on shallow representations may hinder the integration of high-order neighbor information. Recent approaches, such as AIR [13], introduce shallow information and inter-layer contrastive losses to explicitly amplify differences between node representations. Similarly, TSC [22] constrains information propagation and enlarges the distance between node representations by employing a masking matrix and introducing inter-layer loss. Although incorporating shallow information helps avoid degeneration, it can also obstruct the capture of global dependencies.

2.2. Graph Transformers and Scalability

Transformer models, originally developed for natural language processing, have been successfully adapted to graph representation tasks and have become a promising direction for graph neural networks. Representative models such as Graphormer [23] and GraphTrans [24] integrate structural encoding (e.g., shortest path distance, centrality) into attention weights to enhance structural awareness. These models have shown strong performance in graph classification and node prediction tasks. However, they often rely on deep stacks of multi-head attention layers, which are computationally expensive and highly sensitive to node count and batch size during training. SGFormer [14] proposes a simple yet effective graph Transformer architecture that combines single-head attention with lightweight GNN layers to achieve efficient global modeling. However, SGFormer does not introduce any optimization or improvement to the GNN component itself.

3. Preliminaries

3.1. Problem Definition

We focus on an unweighted and undirected graph $\mathcal{G}=(\mathcal{V},\mathcal{E})$, where $\mathcal{V}=\{v_1,\dots ,v_n\}$ denotes a set of n nodes, and $\mathcal{E}$ represents the edge set defined over $\mathcal{G}$. Let $\mathbf{A}\in {\{0,1\}}^{n\times n}$ denote the symmetric adjacency matrix (with ${\mathit{A}}_{i,i}=0$ indicating no self-edges), satisfying ${\mathit{A}}_{i,j}={\mathit{A}}_{j,i}$. The degree of each node $v_i$ is defined as $d_i={\sum }_{j\ne i}{\mathit{A}}_{i,j}$, and the degree matrix $\mathbf{D}\in {\mathbb{R}}^{n\times n}$ is a diagonal matrix with entries ${\mathit{D}}_{i,i}=d_i$ for $i=1,\dots ,n$. The normalized Laplacian matrix is defined as $\mathbf{P}={\mathbf{D}}^{-\frac{1}{2}}(\mathbf{A}+\mathbf{I}){\mathbf{D}}^{-\frac{1}{2}}$, where $\mathbf{I}$ is the identity matrix.

The node feature matrix $\mathbf{X}\in {\mathbb{R}}^{n\times w}$ encodes the input features for all nodes, where w is the feature dimension. The node representation matrix $\mathbf{H}\in {\mathbb{R}}^{n\times d}$ is used for both message propagation and node classification. In our setting, only a subset of nodes is labeled, and the goal is to predict the class labels of the remaining nodes. This task is commonly referred to as semi-supervised node classification.

3.2. Graph Convolutional Networks

Graph Convolutional Networks (GCNs) [1] are a representative class of graph neural networks, which propagate node features guided by the adjacency structure to aggregate information from neighboring nodes. At the l-th layer, the feature update can be formulated as follows:

$${\mathbf{H}}^{(l+1)}=\sigma \left(\mathbf{P}{\mathbf{H}}^{\left(l\right)}{\mathbf{W}}^{\left(l\right)}\right),$$

(1)

where $\sigma (·)$ denotes a non-linear activation function, ${\mathbf{H}}^{\left(l\right)}$ is the node representation matrix at the l-th layer, ${\mathbf{W}}^{\left(l\right)}$ is the trainable weight matrix, and $\mathbf{P}$ represents the normalized Laplacian matrix.

Although deep GCN models possess strong expressive power and can capture complex structural dependencies, they often suffer from the over-smoothing problem: as the number of layers increases, the representations of different nodes tend to become indistinguishable, thereby undermining the model’s ability to discriminate among them.

3.3. Simplified Graph Convolutional Networks

Simplified Graph Convolutional Networks (SGC) [25] represent a simplified form of traditional GCNs. This method streamlines the architecture by removing non-linear activation functions and intermediate linear transformations, retaining only the linear propagation operation based on the graph structure. The node representation at the l-th layer can be concisely expressed as:

$${\mathbf{H}}^{\left(l\right)}={\mathbf{P}}^l\mathbf{X}\mathbf{W},$$

(2)

where ${\mathbf{P}}^l$ denotes the l-th power of the Laplacian matrix, $\mathbf{X}$ is the node feature matrix, and $\mathbf{W}$ represents the trainable weight matrix. SGC performs multi-order neighborhood propagation in a single linear operation, significantly reducing computational cost and training time while preserving graph information. This minimalist design improves training efficiency on large-scale graphs and alleviates issues such as vanishing gradients and overfitting. Compared to standard GCNs, SGC better preserves original node feature distinctions and reduces feature homogenization, thereby mitigating over-smoothing to some extent.

4. Methods

GLADC consists of a global linear attention mechanism and a dual constraint module, as illustrated in Figure 3. The global linear attention mechanism enables efficient propagation of information across the entire graph, while the dual constraint module incorporates both random masking and contrastive constraint to mitigate over-smoothing and enhance local feature discrimination. Specifically, random masking is applied along the column-wise dimension of the representation matrix, while contrastive constraint is imposed along the row-wise dimension. These mechanisms are integrated into both SGC and GCN backbones to promote diverse and stable node representations.

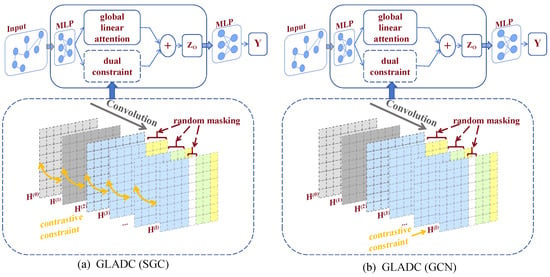
Figure 3. Architecture of GLADC, composed of a global linear attention mechanism for efficient whole-graph message propagation and a dual constraint module incorporating random masking (column-wise) and contrastive constraint (row-wise) to mitigate over-smoothing and enhance representational independence.

4.1. Input Layer

We first project the node features $\mathbf{X}={\left[{\mathbf{x}}_u\right]}_{u=1}^n$ into a latent node embedding space through a neural network layer: ${\mathbf{H}}^{\left(0\right)}=ML{P}_1\left(\mathbf{X}\right)$, where $ML{P}_1$ is implemented as a multi-layer perceptron (MLP). The initial embedding ${\mathbf{H}}^{\left(0\right)}\in {\mathbb{R}}^{n\times d}$ serves as input for subsequent attention computation and message passing.

4.2. Global Linear Attention

The global interaction in our model is realized through an attention mechanism that covers all node pairs, enabling the computation of mutual influence between any two nodes. Unlike traditional Transformer architectures, we perform a single-layer propagation over a fully connected attention graph, allowing each node to adaptively exchange information with any other node in the same batch. Despite its structural simplicity, this design effectively captures potential dependencies between arbitrary node pairs while substantially reducing computational overhead. In practice, we adopt an attention function with linear computational complexity, defined as follows:

$$\begin{array}{cc}\hfill \mathbf{Q}& =f_Q\left({\mathbf{H}}^{\left(0\right)}\right),\tilde{\mathbf{Q}}={\displaystyle \frac{\mathbf{Q}}{{\parallel \mathbf{Q}\parallel }_{\mathcal{F}}}},\mathbf{K}=f_K\left({\mathbf{H}}^{\left(0\right)}\right),\tilde{\mathbf{K}}={\displaystyle \frac{\mathbf{K}}{{\parallel \mathbf{K}\parallel }_{\mathcal{F}}}},\mathbf{V}=f_V\left({\mathbf{H}}^{\left(0\right)}\right),\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill \mathbf{D}& =\mathrm{diag}\left(1+{\displaystyle \frac{1}{N}}\tilde{\mathbf{Q}}\left({\tilde{\mathbf{K}}}^{\top }\mathbf{1}\right)\right),\mathbf{Z}=\beta {\mathbf{D}}^{-1}\left[\mathbf{V}+{\displaystyle \frac{1}{N}}\tilde{\mathbf{Q}}\left({\tilde{\mathbf{K}}}^{\top }\mathbf{V}\right)\right]+(1-\beta ){\mathbf{H}}^{\left(0\right)},\hfill \end{array}$$

(4)

where $f_Q$, $f_K$, and $f_V$ are shallow neural network layers (e.g., linear in our implementation). ${\parallel ·\parallel }_{\mathcal{F}}$ denotes the Frobenius norm, $\tilde{\mathbf{Q}}$ and $\tilde{\mathbf{K}}$ are normalized using the Frobenius norm to stabilize their magnitudes and ensure consistent attention scaling across batches. $\mathbf{1}$ is an N-dimensional column vector of ones, $\mathrm{diag}$ transforms a vector into a diagonal matrix, $\mathbf{D}$ denotes a diagonal matrix used for scaling and residual balancing, and $\beta$ is a residual weight hyperparameter.

In Equation (4), the representation $\mathbf{Z}$ integrates both attention-based propagation across all node pairs and self-loop information preservation. The former allows the model to capture information from other nodes, while the latter preserves the features of the central node itself. This formulation avoids explicitly constructing the full $N\times N$ attention matrix by computing the term $\tilde{\mathbf{Q}}\left({\tilde{\mathbf{K}}}^{\top }\mathbf{V}\right)$ in a right-to-left manner, the product ${\tilde{\mathbf{K}}}^{\top }\mathbf{V}$ is first obtained and then multiplied by $\tilde{\mathbf{Q}}$. Such an implementation ensures that intermediate results remain in linear scale with respect to the number of nodes, thereby maintaining the overall computational complexity at $\mathcal{O}\left(N\right)$, significantly reducing training time and effectively mitigating overfitting and vanishing gradient issues.

4.3. Dual Constraint

After obtaining the initial global representation ${\mathbf{H}}^{\left(0\right)}$, we stack L layers with the dual constraint module to refine local representations.

(a)

Random Masking (Column-wise Masking)

A column-wise binary mask matrix ${\mathbf{M}}^{\left(l\right)}\in {\{0,1\}}^{n\times d}$ is applied to the input ${\mathbf{H}}^{\left(l\right)}$ at the l-th layer:

$${\mathbf{H}}^{(l+1)}=\mathbf{P}{\mathbf{H}}^{\left(l\right)}\circ {\mathbf{M}}^{\left(l\right)}+{\mathbf{H}}^{\left(l\right)}\circ (1-{\mathbf{M}}^{\left(l\right)}),l=0,1,2,\dots ,L-1,$$

(5)

where ${\mathbf{M}}^{\left(l\right)}\in {\{0,1\}}^{n\times d}$ is a binary mask matrix, and ${\mathbf{M}}_{i,:}^{\left(l\right)}$ is a d-dimensional row vector with each element is either 0 or 1. The size of the mask matrix is $n\times d$ with a masking ratio initially set to 1. The operator ∘ denotes element-wise matrix multiplication. If ${\mathit{M}}_{i,j}^{\left(l\right)}=1$, the corresponding element is updated by neighborhood aggregation; otherwise, it retains its value from the previous layer.

Specifically, random masking is a dynamic, column-wise feature dropout technique applied to the node representation matrix during the local propagation phase. It acts as a form of “neighbor filtering” by randomly and temporarily deactivating a subset of feature dimensions from being updated by the neighborhood aggregation. The masked features are replaced with the node’s own representations from the previous layer, which preserves the node’s individuality and prevents it from being overly influenced by redundant information from its neighbors in a single update step.

In graph neural networks, the excessive aggregation of high-order neighbor information often leads to the over-smoothing problem. The random masking strategy alleviates this issue by applying column-wise masking to the representation matrix during aggregation, thereby selectively updating only a subset of node features. This selective update module prevents premature convergence of node representations and effectively mitigates over-smoothing.

Given that shallow-layer neighbors tend to retain higher discriminative power and contribute more effectively to representation learning, our approach applies the masking strategy starting from the third layer onward (i.e., $l\ge 3$). As the network depth increases, neighboring nodes become more similar, intensifying the over-smoothing effect. To counteract this, we gradually reduce the masking rate in deeper layers. The masking rate is defined as:

$$\mathrm{MaskingRate}\left({\mathbf{M}}_{i,:}^{\left(l\right)}=0\right)=\left\{\begin{array}{cc}0\hfill & ,l\le 2\hfill \\ 1-log(\lambda /l+1)\hfill & ,l\ge 3\hfill \end{array}\right.$$

(6)

where l denotes the current layer of the network, and $\lambda >0$ is a hyperparameter that controls the decay rate of the masking ratio. A smaller $\lambda$ leads to a faster decay. To prevent representation stagnation as the network deepens, we enforce that at least one column is masked in each masking operation, ensuring continual representation updates.

(b)

Contrastive Constraint (Row-wise Constraint)

While the random masking strategy effectively slows feature updates and alleviates representation convergence, it does not actively enhance the distinctiveness of node representations. To address this limitation, we introduce a contrastive constraint mechanism designed to preserve intra-node consistency across layers while simultaneously enhancing inter-node discrimination.

Specifically, in the context of SGC, the representations of the same node in two consecutive layers are treated as a positive pair, and their similarity is encouraged through a contrastive loss. In contrast, representations of different nodes are regarded as negative pairs and are pushed apart. This explicit separation of node features effectively alleviates the over-smoothing by reinforcing inter-node discriminability. The corresponding formulation is as follows:

$$\begin{array}{c}\hfill L_{SGC}=-\sum _{l=0}^{L-1}\sum _{i=1}^{n}log{\displaystyle \frac{e^{(s(h_i^{(l+1)},h_i^{\left(l\right)})/\tau )}}{{\sum }_{\begin{array}{c}j\ne i\end{array}}^n{e}^{(s(h_i^{(l+1)},h_j^{\left(l\right)})/\tau )}+e^{(s(h_i^{(l+1)},h_i^{\left(l\right)})/\tau )}}},\end{array}$$

(7)

where n denotes the total number of nodes, l indicates the layer index ($l\ge 0$), $\tau$ is the temperature coefficient, and $s(·)$ represents the cosine similarity function. The numerator and denominator correspond to the positive and negative sample constraints, respectively.

Compared with SGC, GCN involves higher computational complexity. Applying the contrastive constraint to every layer would significantly increase computational cost. To address this issue, we apply dropout twice to the final-layer representation. Nodes that are the same across both subgraphs are treated as positive pairs, while nodes that differ are regarded as negative pairs. Introducing negative samples enhances the diversity among node representations and strengthens the distinction between them. Specifically, we apply dropout twice to the final-layer representation $H^{\left(L\right)}$, yielding ${\tilde{H}}^{\left(L\right)}$ and ${\widehat{H}}^{\left(L\right)}$. We then apply a contrastive constraint similar to that used in SGC to enhance the distinctiveness of node embeddings. The following three equations are derived as:

$${\tilde{\mathbf{H}}}^{\left(L\right)}=\mathrm{dropout}\left({\mathbf{H}}^{\left(L\right)}\right),$$

(8)

$${\widehat{\mathbf{H}}}^{\left(L\right)}=\mathrm{dropout}\left({\mathbf{H}}^{\left(L\right)}\right),$$

(9)

$$\begin{array}{c}\hfill L_{GCN}=-\sum _{i=1}^{n}log{\displaystyle \frac{e^{(s({\widehat{h}}_i^{\left(L\right)},{\tilde{h}}_i^{\left(L\right)})/\tau )}}{{\sum }_{j\ne i}^n{e}^{(s({\widehat{h}}_i^{\left(L\right)},{\tilde{h}}_j^{\left(L\right)})/\tau )}+e^{(s({\widehat{h}}_i^{\left(L\right)},{\tilde{h}}_i^{\left(L\right)})/\tau )}}},\end{array}$$

(10)

where L is the number of layers.

4.4. Overall Training Procedure

To provide a clearer view of the overall training process, the complete workflow of GLADC is summarized in Algorithm 1. It sequentially describes the feature projection, global linear attention, dual constraint optimization, and final prediction steps.

Algorithm 1: Training procedure of GLADC

4.5. Structural Information Fusion

The output of the dual constraint (DC) module is linearly combined with the global linear attention output $\mathbf{Z}$ as follows:

$$\begin{array}{c}\hfill {\mathbf{Z}}_o=(1-\alpha )\mathbf{Z}+\alpha \mathrm{DC}({\mathbf{H}}^{\left(0\right)},\mathbf{A}),\widehat{\mathbf{Y}}={\mathrm{MLP}}_o\left({\mathbf{Z}}_o\right),\end{array}$$

(11)

where $\alpha$ controls the balance between global and local contributions, ${\mathbf{H}}^{\left(0\right)}$ denotes the initial node features, and $\mathbf{A}$ represents the adjacency matrix. Here, $\mathrm{DC}({\mathbf{H}}^{\left(0\right)},\mathbf{A})$ denotes the output of the Dual Constraint module after L layers of propagation (i.e., ${\mathbf{H}}^{\left(L\right)}$). The function $ML{P}_o$ maps the final representation ${\mathbf{Z}}_o$ to the predictions. In our implementation, $ML{P}_o$ is implemented as a multi-layer perceptron (MLP) that produces the final classification results.

For model optimization, we adopt the cross-entropy loss $L_{\mathrm{CE}}$ for the semi-supervised node classification task. In addition, during the contrastive constraint stage, the model incorporates an auxiliary loss determined by the chosen convolutional backbone. Specifically, when Simplified Graph Convolution (SGC) is employed, the auxiliary loss is $L_{\mathrm{SGC}}$; when Graph Convolutional Network (GCN) is used, the auxiliary loss becomes $L_{\mathrm{GCN}}$. The overall loss is defined as:

$$Loss=L_{\mathrm{CE}}+L_{\mathrm{Constraint}},$$

(12)

where $L_{\mathrm{Constraint}}\in \{L_{\mathrm{SGC}},L_{\mathrm{GCN}}\}$ is selected according to the underlying propagation scheme.

5. Results

We evaluated the effectiveness of GLADC on the semi-supervised node classification task. To provide a comprehensive assessment, we compared GLADC with eight recently developed representative models specifically designed to alleviate the over-smoothing problem. Model performance is assessed using classification accuracy (ACC), while the degree of feature smoothness is quantified using the Mean Average Distance (MAD) [26] metric. Moreover, all experiments are conducted on a single NVIDIA RTX 4090 GPU with 24 GB of memory.

5.1. Experimental Setups

Datasets. To comprehensively evaluate the performance of our proposed method across diverse graph structures, we conducted experiments on seven datasets with varying scales and topological characteristics. These datasets include three classic citation networks: Cora [27], Citeseer [27], and Pubmed [27]; two co-authorship and product graphs with high homophily ratios: Coauthor CS [28] and Amazon Photo [28]; and two well-known heterophilous graphs: Actor [29] and Squirrel [30]. We selected 20 nodes from each class in the datasets for training; the dataset statistics are summarized in Table 1.

Table 1. Statistics of the benchmark datasets used for node classification.

Dataset	Cora	Citeseer	Pubmed	CoauthorCS	AmazonPhoto	Actor	Squirrel
Nodes	2708	3327	19,717	18,333	7650	7600	2223
Edges	5429	4732	44,338	81,894	119,043	29,926	46,998
Classes	7	6	3	15	8	5	5
Train	140	120	60	300	160	100	100
Validate	500	500	500	500	500	500	500
Test	1000	1000	1000	1000	1000	1000	1000

Baselines. We compared GLADC with a suite of representative GNN models, including classical baselines and recent state-of-the-art approaches. First, we selected standard GNN baseline models, including Graph Convolutional Networks (GCN) [1] and Simplified Graph Convolutional Networks (SGC) [25]. Building upon this, we further compared several advanced GNN models such as APPNP [15], AIR [13], ContraNorm [12], DropMessage [11], and TSC [22]. Furthermore, to provide a more comprehensive evaluation of GLADC’s capabilities, we also compared it with SGFormer [14], a node classification model based on the Transformer architecture. Through extensive validation, we set parameter $\beta$ to 0.8, parameter $\tau$ to 0.4, parameter $\lambda$ to 0.5, and parameter $\alpha$ to 0.7.

5.2. Experimental Results

We evaluated the overall performance of GLADC against all baseline models on the node classification task, and the results are presented in Table 2. Our proposed GLADC model consistently achieves superior performance across six datasets. Specifically, GLADC (SGC) achieves the highest classification accuracy on Cora, Citeseer, Pubmed, and Squirrel, and GLADC(GCN) achieves the best performance on AmazonPhoto and Actor, respectively.

Table 2. Node classification performance (Accuracy %) on benchmark datasets. Results are reported as mean ± standard deviation based on ten independent runs. The best and second-best results are highlighted in bold and underlined, respectively.

Dataset	Cora	Citeseer	Pubmed	CoauthorCS	AmazonPhoto	Actor	Squirrel
GCN	$83.2\pm 0.4$	$71.5\pm 0.4$	$79.1\pm 0.6$	$90.5\pm 0.3$	$91.1\pm 0.3$	$30.2\pm 0.7$	$39.5\pm 1.5$
SGC	$82.3\pm 0.2$	$73.7\pm 0.3$	$78.6\pm 0.3$	$91.1\pm 0.4$	$90.2\pm 0.4$	$30.6\pm 0.3$	$40.2\pm 0.9$
APPNP	$83.2\pm 0.6$	$72.1\pm 0.5$	$80.1\pm 0.2$	$91.4\pm 0.8$	$91.6\pm 0.5$	$32.0\pm 0.4$	$37.3\pm 1.1$
AIR (SGC)	$82.2\pm 0.6$	$74.1\pm 0.4$	$79.0\pm 0.5$	$\mathbf{92}.\mathbf{9}\pm \mathbf{0}.\mathbf{2}$	$93.0\pm 0.5$	$38.1\pm 0.8$	$39.9\pm 2.1$
ContraNorm (GCN)	$83.4\pm 0.8$	$72.6\pm 0.5$	$79.6\pm 0.3$	$91.2\pm 0.3$	$92.0\pm 0.7$	$37.1\pm 1.1$	$40.5\pm 1.9$
DropMessage (GCN)	$83.2\pm 0.1$	$72.1\pm 0.2$	$79.5\pm 0.3$	$91.8\pm 0.1$	$91.5\pm 0.4$	$36.6\pm 1.2$	$39.8\pm 1.5$
TSC (GCN)	$85.1\pm 0.3$	$74.3\pm 0.3$	$\underline{80.7\pm 0.6}$	$91.6\pm 0.5$	$93.1\pm 0.4$	$38.0\pm 0.7$	$\underline{43.5\pm 1.6}$
SGFormer	$84.9\pm 0.4$	$72.7\pm 0.5$	$80.2\pm 0.3$	$91.6\pm 0.3$	$93.1\pm 0.4$	$38.1\pm 1.1$	$42.6\pm 1.1$
GLADC (GCN)	$\underline{86.3\pm 0.3}$	$\underline{75.6\pm 0.3}$	$\underline{80.7\pm 0.5}$	$92.7\pm 0.2$	$\mathbf{94}.\mathbf{6}\pm \mathbf{0}.\mathbf{4}$	$\mathbf{40}.\mathbf{0}\pm \mathbf{0}.\mathbf{7}$	$43.4\pm 0.8$
GLADC (SGC)	$\mathbf{86}.\mathbf{8}\pm \mathbf{0}.\mathbf{2}$	$\mathbf{75}.\mathbf{9}\pm \mathbf{0}.\mathbf{4}$	$\mathbf{81}.\mathbf{9}\pm \mathbf{0}.\mathbf{1}$	$\underline{92.8\pm 0.4}$	$\underline{93.9\pm 0.2}$	$\underline{39.8\pm 0.9}$	$\mathbf{44}.\mathbf{6}\pm \mathbf{1}.\mathbf{1}$

Further analysis shows that GLADC achieves the best performance across all datasets except for CoauthorCS, where it obtains the second-best result, slightly behind AIR (SGC). We attribute this to the distinctive characteristics of the CoauthorCS graph. As a co-authorship network, it exhibits exceptionally high homophily and dense connectivity, where an author’s local neighborhood is often highly informative and predictive of their research areas. In such a context, the strong local propagation of AIR (SGC) may be nearly sufficient. While our global linear attention mechanism is designed to enrich node representations with long-range dependencies, its effect on a graph where local signals are already very strong might be less pronounced compared to its significant benefits on heterophilic or sparser graphs (e.g., Actor and Squirrel). Nevertheless, GLADC’s performance on CoauthorCS remains highly competitive and superior to a wide range of other baselines, demonstrating its overall robustness.

Beyond accuracy improvements, GLADC also exhibits stronger robustness and generalization. On heterophilic datasets (e.g., Actor and Squirrel), the performance margin over existing GNN and Transformer-based models exceeds 2%, demonstrating its superior capability to preserve discriminative representations even under weak homophily. Moreover, the consistent improvement across both SGC-based and GCN-based backbones demonstrates that the proposed global linear attention and dual constraint are model-agnostic and can be seamlessly integrated into different GNN architectures. These results collectively confirm that GLADC not only mitigates over-smoothing but also alleviates premature convergence, leading to more stable and expressive node representations.

5.3. Over-Smoothing Analysis

To evaluate the effectiveness of the proposed dual constraint in mitigating the over-smoothing problem, we reported classification accuracy (ACC) as the model depth increased through 4, 8, 16, and 32 layers. Specifically, we conducted experiments on two representative datasets: Cora and Actor, with the results presented in Table 3 and Table 4. In these tables, “OOM” indicates an out-of-memory error. The best performance in each table is highlighted in red, From the results presented in Table 3 and Table 4, we draw the following key observations:

Table 3. Accuracy comparison across varying depths on the Cora dataset. Results are reported as mean ± standard deviation over ten runs. Red indicates the best overall performance. Bold and underline denote the best and second-best performance at the same layer.

Model	Layer 4	Layer 8	Layer 16	Layer 32
GCN	$81.8\pm 0.5$	$30.3\pm 0.6$	$31.1\pm 0.8$	$31.9\pm 1.0$
SGC	$82.2\pm 0.3$	$81.5\pm 0.4$	$79.0\pm 0.5$	$72.5\pm 0.9$
ContraNorm (GCN)	$82.4\pm 0.6$	$79.5\pm 0.7$	$52.0\pm 1.3$	$28.9\pm 1.0$
DropMessage (GCN)	$83.1\pm 0.4$	$80.1\pm 0.5$	$43.4\pm 0.7$	$30.4\pm 1.1$
AIR (SGC)	$79.5\pm 0.5$	$82.4\pm 0.3$	$82.8\pm 0.4$	$79.6\pm 0.6$
TSC (GCN)	$84.5\pm 0.2$	$84.7\pm 0.3$	$85.1\pm 0.2$	$84.8\pm 0.3$
GLADC (GCN)	$\mathbf{86}.\mathbf{1}\pm \mathbf{0}.\mathbf{3}$	86.3 ± 0.2	$\underline{85.6\pm 0.3}$	$\mathbf{85}.\mathbf{4}\pm \mathbf{0}.\mathbf{4}$
GLADC (SGC)	$\underline{86.0\pm 0.3}$	$\underline{86.0\pm 0.2}$	$\mathbf{85}.\mathbf{8}\pm \mathbf{0}.\mathbf{3}$	$\underline{85.3\pm 0.3}$

Table 4. Accuracy comparison across varying depths on the Actor dataset. Results are reported as mean ± standard deviation over ten runs. Red indicates the best overall performance. Bold and underline denote the best and second-best performance at the same layer.

Model	Layer 4	Layer 8	Layer 16	Layer 32
GCN	$30.1\pm 0.7$	$25.8\pm 0.6$	$21.3\pm 0.9$	$16.2\pm 1.0$
SGC	$30.5\pm 0.5$	$29.9\pm 0.5$	$29.6\pm 0.6$	$28.7\pm 0.8$
ContraNorm (GCN)	$36.8\pm 0.8$	$31.5\pm 0.9$	OOM	OOM
DropMessage (GCN)	$36.1\pm 0.7$	$35.8\pm 0.6$	$30.7\pm 0.7$	$30.1\pm 0.8$
AIR (SGC)	$38.1\pm 0.5$	$37.8\pm 0.6$	OOM	OOM
TSC (GCN)	$38.0\pm 0.5$	$37.5\pm 0.4$	$37.7\pm 0.6$	$37.3\pm 0.6$
GLADC (GCN)	$\underline{38.9\pm 0.4}$	40.4 ± 0.3	$\mathbf{39}.\mathbf{1}\pm \mathbf{0}.\mathbf{4}$	$\mathbf{38}.\mathbf{6}\pm \mathbf{0}.\mathbf{5}$
GLADC (SGC)	$\mathbf{39}.\mathbf{3}\pm \mathbf{0}.\mathbf{3}$	$\underline{39.8\pm 0.4}$	$\underline{38.8\pm 0.5}$	$\underline{38.5\pm 0.4}$

Existing over-smoothing mitigation methods only partially improve stability. ContraNorm and DropMessage alleviate over-smoothing at shallow depths but suffer from significant performance degradation or even out-of-memory (OOM) issues in deeper configurations. AIR(SGC) performs better but fails to maintain scalability at large depths. TSC(GCN) demonstrates more stable performance, yet its improvements remain limited compared to our method.

GLADC achieves superior and stable performance across depths. Both GLADC (GCN) and GLADC (SGC) maintain high accuracy even in very deep configurations (16–32 layers). For instance, on Cora, GLADC (GCN) peaks at 86.3% with 8 layers and still preserves 85.4% at 32 layers, while GLADC (SGC) consistently stays within 85.3–86.0% across all depths. Similarly, on Actor, both variants achieve the best or second-best results across all depths without noticeable performance degradation.

In terms of the optimal depth range, traditional GCN/SGC typically reach their best accuracy at 4–8 layers and rapidly degrade afterward. In contrast, GLADC maintains near-optimal performance at 16–32 layers, clearly demonstrating its ability to overcome the depth-induced performance collapse. These findings confirm that GLADC not only alleviates the over-smoothing problem but also enables GNNs to scale to deeper architectures while preserving or even improving classification accuracy.

5.4. Efficiency Analysis

To assess the computational efficiency of GLADC, we compared its total training time against several baseline models on the Cora dataset across varying depths (2, 4, 8, 16, and 32 layers). The results are visualized in Figure 4.

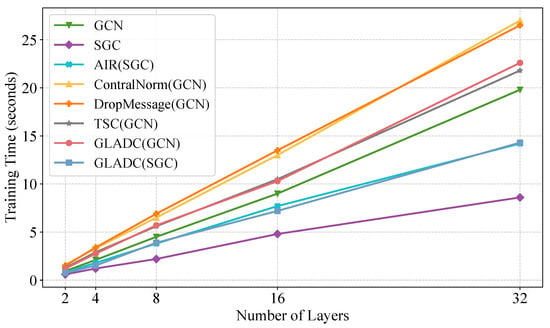
Figure 4. Scalability of total training time with respect to the number of layers for various models on the Cora dataset.

The analysis of computational efficiency yields several key conclusions. Primarily, the runtime of all evaluated models demonstrates approximately linear scaling with increasing network depth, thereby confirming the practical scalability inherent in our linear-complexity design. As anticipated, the GLADC framework introduces a modest computational overhead relative to the vanilla GCN and SGC architectures, which is directly attributable to the incorporation of its global attention and dual constraint mechanisms. Crucially, when evaluated against contemporary advanced models, GLADC proves to be highly efficient. Specifically, the GLADC (SGC) variant emerges as the fastest method within this category across all tested depths, while the GLADC (GCN) variant also exhibits competitive efficiency, operating notably faster than normalization-heavy approaches such as ContraNorm and DropMessage and demonstrating comparable speed to TSC (GCN). Collectively, these findings substantiate the superiority of GLADC, as it achieves its enhanced performance without incurring disproportionate computational costs, ultimately presenting a highly favorable performance–efficiency trade-off.

5.5. Ablation Study

To rigorously evaluate the contribution of each component and validate their synergistic integration, we conducted extensive ablation study on GLADC (SGC) using the Cora and Actor datasets. We compared the complete model against systematically designed variants, with experimental configurations including:

• SGC: The baseline model without our proposed components.
• W/O dual constraint: Only global linear attention active.
• Only random masking: Solely with random masking mechanism.
• Only contrastive constraint: Solely with contrastive constraint.
• W/O random masking: Without random masking.
• W/O contrastive constraint: Without contrastive constraint.
• GLADC (SGC): Our complete proposed model.

The experimental results are comprehensively analyzed in Figure 5. The results, measured by classification accuracy (ACC) and Mean Average Distance (MAD, where MAD = 0 indicates complete over-smoothing), yield the following critical insights.

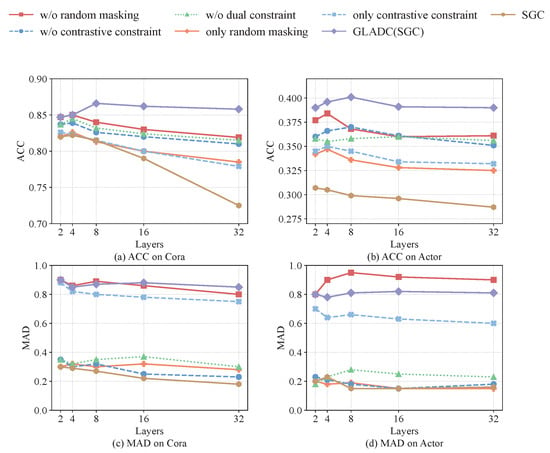
Figure 5. The ablation analysis: the first row shows results based on the ACC metric, while the second row presents outcomes for MAD.

The ablation analysis reveals that the global attention mechanism provides a fundamental foundation for mitigating over-smoothing. The “w/o dual constraint” variant significantly outperforms the SGC baseline across all configurations, maintaining substantially higher accuracy and MAD values even in deep layers. This demonstrates that global linear attention alone substantially alleviates over-smoothing through effective long-range dependency modeling.

While individual constraint mechanisms offer measurable benefits, they provide only incomplete protection against over-smoothing. The “only contrastive constraint” variant maintains relatively better MAD values but suffers significant accuracy degradation in deeper layers, whereas the “only random masking” variant shows more stable accuracy preservation but achieves limited feature distinctiveness. This performance pattern clearly indicates that neither constraint mechanism alone is sufficient for achieving optimal performance in deep graph networks.

Our experiments further reveal the complementary nature of the two constraint mechanisms. Random masking primarily functions as a stabilizer in the learning process by selectively preventing redundant feature aggregation, thereby maintaining baseline accuracy during deep propagation. In contrast, the contrastive constraint explicitly enforces representation diversity by separating node embeddings in the feature space, thus directly preserving feature distinctiveness. This complementary relationship allows the combined approach to address both key aspects of over-smoothing simultaneously.

Finally, the synergistic integration of these components proves crucial for achieving optimal performance. The complete GLADC model demonstrates clear synergistic advantages, substantially exceeding all partial configurations in both accuracy and feature distinctiveness. The performance gap is particularly pronounced in deeper layers (16–32 layers) where over-smoothing effects are most severe, providing strong validation that the integrated design produces emergent benefits that extend beyond simple additive effects of individual components.

In conclusion, the factorial ablation analysis provides definitive evidence that GLADC’s robustness stems from the synergistic integration where global attention enriches representations with long-range dependencies while the complementary dual constraints ensure these representations maintain both accuracy and distinctiveness during deep propagation.

5.6. Hyperparameter Sensitivity Analysis

To further evaluate the robustness of GLADC, we conducted a systematic sensitivity analysis on three key hyperparameters: $\beta$ (global attention residual weight in Equation (4)), $\lambda$ (masking decay rate in Equation (6)), and $\tau$ (contrastive temperature in Equation (7)). We focused on two representative datasets, Cora and Actor, to examine the influence of these parameters on the GLADC(SGC) model. The evaluation metrics include test classification accuracy (ACC) and Mean Average Distance (MAD), which jointly reflect the model’s classification performance and its resistance to over-smoothing.

As illustrated in Figure 6, the sensitivity analysis of the global attention residual weight $\beta$ reveals its distinct impact on model performance. The classification accuracy (ACC) on both Cora and Actor datasets shows a clear upward trend as $\beta$ increases from 0.1 to 0.9, with optimal performance achieved when $\beta$ falls within the range of 0.7 to 0.9. This pattern suggests that strengthening the residual connection between the global attention output and the original node features significantly enhances feature propagation and optimization stability. In contrast, the Mean Average Distance (MAD) metric remains largely unaffected by variations in $\beta$, maintaining consistently high values across the entire parameter range. This divergence indicates that while $\beta$ plays a crucial role in determining classification performance, the mitigation of over-smoothing is primarily governed by the Dual Constraint mechanism rather than the residual weight configuration. Consequently, setting $\beta$ between 0.7 and 0.9 provides an optimal balance that leverages the benefits of global attention while maintaining robust resistance to over-smoothing.

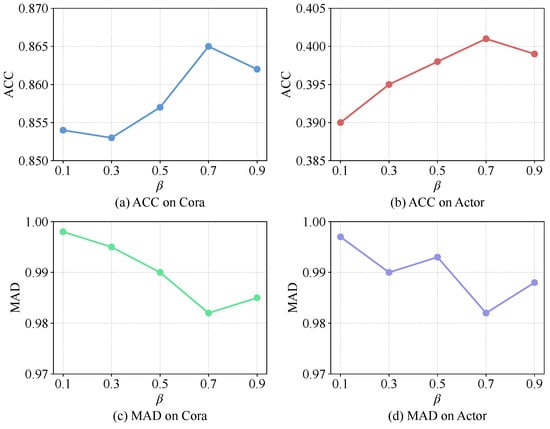
Figure 6. Sensitivity analysis of the global attention residual weight $\beta$.

Figure 7 illustrates the impact of the masking decay rate $\lambda$ on model performance across network depths. The analysis reveals a clear trend where increasing $\lambda$ values lead to progressive degradation in classification accuracy on both Cora and Actor datasets, particularly evident in deeper architectures beyond 16 layers. This performance decline becomes more pronounced with larger $\lambda$ values, suggesting that slower decay of masking rates may overly restrict information flow and hinder effective feature learning. Conversely, the MAD metric shows an opposite pattern, with higher $\lambda$ values generally corresponding to improved feature distinctiveness. This divergence indicates that while stronger masking constraints enhance resistance to over-smoothing by preserving feature diversity, they simultaneously impair the model’s discriminative capacity for classification tasks. The observed trade-off underscores the importance of selecting an intermediate $\lambda$ value that balances smoothing prevention with maintained predictive performance, with $\lambda$ around 0.6 providing the most favorable compromise across both evaluation metrics.

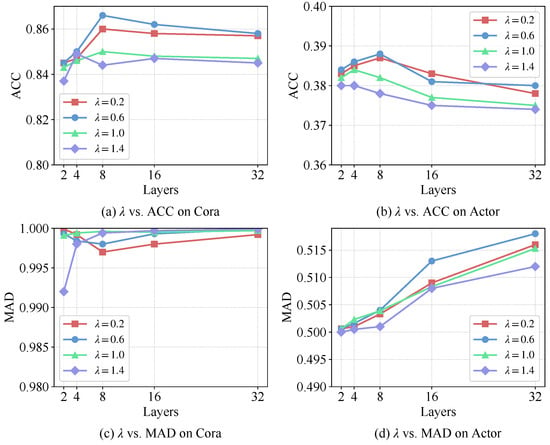
Figure 7. Sensitivity analysis of the masking decay rate $\lambda$.

Figure 8 presents the sensitivity analysis of the temperature coefficient $\tau$ in the contrastive constraint, revealing its crucial role in balancing model performance across different depths. The results demonstrate that moderate $\tau$ values around 0.4–0.6 achieve optimal performance on both datasets, maintaining stable accuracy throughout all network depths while ensuring robust feature distinctiveness. Specifically, lower $\tau$ values ($\tau =0.2$) tend to over-sharpen the similarity distribution, leading to suboptimal accuracy in shallow layers, while higher $\tau$ values ($\tau =1.0$) over-smooth the contrastive objective, resulting in gradual performance degradation in deeper architectures. The MAD metric further confirms that intermediate $\tau$ values best preserve feature diversity across layers, effectively preventing over-smoothing without compromising discriminative power. This analysis validates $\tau =0.4$ as the optimal setting, providing the best trade-off between classification accuracy and representation quality throughout the entire depth spectrum.

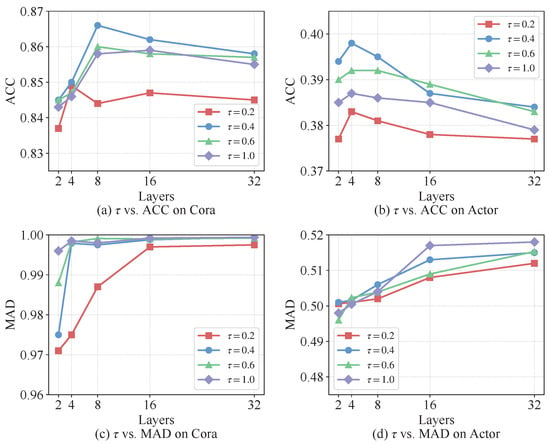
Figure 8. Sensitivity analysis of the contrastive temperature coefficient $\tau$.

6. Conclusions and Outlooks

In this paper, we propose GLADC, a novel Graph Neural Network scheme designed to effectively tackle the pervasive over-smoothing problem in deep graph architectures. By integrating a global linear attention mechanism and a dual constraint strategy, GLADC effectively captures long-range dependencies while preserving node-level distinctiveness. The proposed column-wise random masking and row-wise contrastive constraint operate synergistically to control information propagation and enhance inter-node discriminability, thereby mitigating the homogenization of node representations in deeper layers. Extensive experiments conducted on seven diverse real-world graph datasets demonstrate that GLADC achieves competitive or superior performance compared to state-of-the-art baselines in semi-supervised node classification tasks. Furthermore, both the ablation study and over-smoothing analysis confirm the crucial roles of both the random masking and contrastive constraint mechanisms in delaying premature convergence and maintaining representational diversity. With its linear computational complexity and lightweight architecture, GLADC provides a scalable and efficient solution for graph representation learning, paving the way for more effective modeling of complex relational structures in diverse applications.

Despite its strengths, GLADC has certain limitations that point to promising directions for future work. First, while the global linear attention reduces complexity to $\mathcal{O}\left(N\right)$, processing the entire graph in memory can still be challenging for web-scale graphs with billions of nodes. Extending GLADC to a more distributed or sub-sampling-based framework would be a critical step for such scenarios. Second, our current work is focused on static graphs. Investigating how to effectively integrate the global–local synergy of GLADC into dynamic graph settings, where the graph structure and node features evolve over time, presents a compelling and challenging research direction.