Hybrid Geoid Modelling with AI Enhancements: A Case Study for Almaty, Kazakhstan

Abstract

Developing a high-precision regional geoid model is a key element in modernizing Kazakhstan’s vertical reference framework and ensuring consistent GNSS-based height determination. However, the mountainous terrain of southeastern Kazakhstan, characterized by strong topographic gradients and sparse terrestrial gravity coverage, poses significant modelling challenges. This study presents the first AI-enhanced hybrid geoid model developed for the Almaty region, integrating classical gravimetric modelling with modern machine-learning simulation. The baseline solution was computed using the Least-Squares Modification of Stokes’ Formula with Additive Corrections, combining digitized Soviet-era terrestrial gravity data, the global geopotential model XGM2019e_2159, and the FABDEM 30 m digital elevation model. Validation using GNSS/levelling benchmarks revealed a systematic bias of −0.06 m and an RMS of 0.08 m. To improve the fit between modelled and observed undulations, three machine-learning regressors—Gaussian Process Regression (GPR), Support Vector Regression (SVR), and LSBoost—were applied to model the residual correction surface. Among them, SVR provided the best held-out performance (RMSE = 0.04 m), while LOOCV, 10-fold and spatial CV confirmed stable generalization across terrain regimes. The resulting hybrid model, designated N_ALM2025, achieved centimetre-level consistency with GNSS/levelling data. The results demonstrate that integrating classical geoid computation with AI-based residual modelling provides an efficient computational framework for high-precision geoid determination in complex mountainous environments.

1. Introduction

The creation of a precise geoid model is one of the most important tasks of modern geodesy, as it forms the foundation for establishing a unified national height system. This is particularly relevant for countries with vast territories and complex topography. The Republic of Kazakhstan, the ninth largest country in the world by area, is characterized by pronounced elevation contrasts, ranging from the Caspian Lowland to the mountain ranges of the Tien Shan and Altai. Under such conditions, the use of global geopotential models (GGMs), such as EGM2008 or XGM2019e, provides only an averaged description of the gravity field and does not allow achieving the high accuracy level required for engineering and geodetic applications. Therefore, a tailored and customized model is required for such terrains. Conventionally, geodetic data obtained using levelling techniques and the global navigation satellite system (GNSS) is used for geoid modelling. However, they do have some disadvantages: field surveying is expensive, especially in remote and difficult-to-access areas, there are very few GNSS stations, and it is time consuming to level up after each levelling operation. Also, data gaps might result from the processes [1,2].

The development of a high precision model is one of the key tasks within the framework of an ongoing national programme on the establishment of a state coordinate and height system. This will enable the replacement of labour-intensive and expensive geometric levelling with GNSS technologies, where the orthometric height is determined as the difference between the ellipsoidal height and the geoid height. Such a transition will ensure a significant reduction in costs while maintaining high accuracy and efficiency of geodetic works.

Over the last two decades, significant progress has been made in developing refined gravimetric geoid determination methods. The Least-Squares Modification of Stokes’ Formula with Additive Corrections (LSMSA, also known as the KTH method) has become a widely accepted framework for regional geoid modelling [3,4,5,6,7,8,9]. This method rigorously integrates heterogeneous data-gravity anomalies, DEM-derived terrain corrections, and GGMs while accounting for truncation and spectral errors. However, residual discrepancies between gravimetric solutions and GNSS/levelling observations often remain due to datum inconsistencies, measurement noise, or local heterogeneities [10]. Traditionally, such residuals have been minimized using different parametric methods; yet these approaches may overfit and cannot adequately represent complex local biases.

Recent advances in machine learning (ML) have opened new opportunities for geodetic modelling, offering flexible, data-driven alternatives for residual correction in geoid and quasigeoid computation. Early studies already demonstrated that Support Vector Machines can be used to model GPS/levelling-based geoid undulations with competitive accuracy [11], while Artificial Neural Networks were successfully applied to regional geoid mapping from GNSS observations [12]. Later works introduced more sophisticated regression schemes, including heuristic and ensemble-type models, to optimize local geoid undulation surfaces derived from GPS/levelling data [13,14,15]. Generalized regression neural networks and related architectures have also been compared with classical interpolation techniques, typically yielding improved fit to observations in local test areas [16]. More recent contributions have focused on Gaussian Process Regression (GPR) and other kernel-based methods for predicting geoid undulations [17,18], as well as on hybrid regional geoid/quasigeoid models in which global geopotential models are combined with ML-based residual modelling, including rugged mountainous terrain and explicit use of neighbourhood characteristics [1,19]. In parallel, ML techniques have been applied to gravity anomaly prediction and gravity-field recovery in data-sparse regions [20,21], and their broader role in geodesy has been synthesized in a dedicated survey [22].

Across these studies, ML methods consistently demonstrate several advantages over traditional deterministic interpolators and purely stochastic approaches. First, they are able to capture complex, nonlinear relationships between geoid/quasigeoid heights, gravity anomalies, global geopotential models, and terrain-related predictors without imposing a fixed parametric form. Second, they can assimilate heterogeneous data with irregular spatial sampling, which is typical for GPS/levelling and terrestrial gravity networks. Third, many case studies report lower root-mean-square errors and reduced residual dispersion for ML-based corrector surfaces compared with inverse-distance weighting, kriging, or purely GGM-based solutions, especially in regions with strong topographic gradients or sparse control [1,11,12,13,14,15,16,18,19,20,21]. In other words, AI-based regressors do not simply reproduce existing interpolators; they provide alternative solutions that can better exploit auxiliary information and mitigate systematic distortions in physically based models.

From an algorithmic perspective, the most frequently used regressors in geodetic applications are Support Vector Regression (SVR), Gaussian Process Regression, and ensemble learners such as gradient boosting (e.g., LSBoost). SVR offers good control of model complexity through the penalty parameter and ε-insensitive loss, and, with a radial basis function kernel, it has shown robust performance in the presence of noise and outliers [11,13,14,15,16]. GPR provides a probabilistic framework with explicit prediction variances, which is attractive for uncertainty assessment [17,18], but its cubic scaling with the number of training points can become a practical limitation for dense geodetic datasets. Ensemble methods such as LSBoost are computationally efficient and handle mixed-scale predictors well, yet their performance can be sensitive to the depth and number of trees, and they tend to behave more like black-box interpolators with less transparent control of smoothness. In most published case studies, hyperparameters are tuned by grid search or Bayesian optimization with k-fold cross-validation, balancing bias, and variance while keeping computational costs manageable [1,13,14,15,16,17,18,19,20,21].

In the present study, ML regressors are not intended to replace the physical gravimetric model but to complement it. We adopt an LSMSA-type gravimetric solution as the baseline geoid and use ML only as a compact correction layer that models residual discrepancies with respect to GNSS/levelling. SVR is selected as the primary regressor because it provides a favourable trade-off between accuracy, stability, and computational cost in our data regime. Compared with GPR, it scales better to larger training sets, and compared with LSBoost, it yields smoother, more physically plausible corrector fields, while achieving similar or lower RMS values in validation. In this hybrid setting, the ML-based corrector surface systematically reduces remaining biases and improves the consistency of the LSMSA geoid with GPS/levelling across the complex mountainous terrain of the Almaty region, thereby addressing the limitations highlighted in previous work and responding to the need for algorithmically robust, high-accuracy hybrid geoid models.

In this study we aim to develop a high-resolution hybrid geoid model for the Almaty region of southeastern Kazakhstan using the LSMSA method and machine learning. We integrate digitized terrestrial gravity data, the global model XGM2019e_2159, the FABDEM 30 m DEM, and a network of GNSS/levelling benchmarks. The geoid is first computed using the LSMSA method to obtain a physically consistent gravimetric baseline. Subsequently, residual corrections are modelled using both classical Helmert fitting and advanced machine-learning regressors (GPR, SVR, LSBoost), enabling a comparative assessment of accuracy, robustness, and generalization. The final outcome is a refined hybrid geoid surface (N_ALM2025), designed to support precise geodetic, engineering, and scientific applications in one of the most challenging regions of Kazakhstan.

2. Study Area

The study area lies between latitudes 42.5–44° N and longitudes 76–77.5° E, covering the southeastern part of Kazakhstan, specifically the Almaty region (Figure 1). This area includes the Zailiyskiy Alatau Range, a prominent subrange of the northern Tien Shan Mountains. The region is characterized by highly variable topography, with elevations ranging from approximately 600 m in the lowlands to over 5000 m in the high mountain peaks. Such dramatic elevation differences within a relatively small spatial extent create a complex geophysical environment.

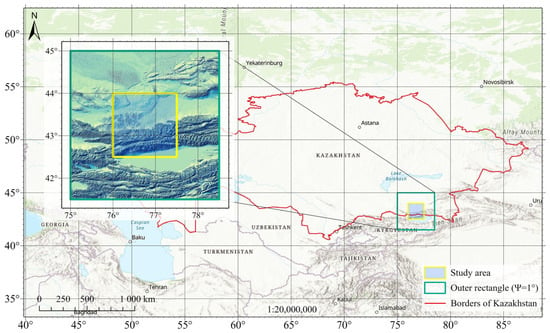
Figure 1. Location and topography of the study area.

Geologically, the study area belongs to the northern Tien Shan, a highly seismically active intracontinental mountain belt formed by the ongoing convergence between the Eurasian and Indian plates [23,24]. Active faulting and present-day crustal shortening along the northern Tien Shan range front near Almaty give rise to significant crustal deformation, steep and highly dissected relief with pronounced elevation differences, and localized gravity anomalies [25,26]. The combined effect of rugged topography and active tectonics introduces substantial challenges for geoid determination, particularly when relying solely on global geopotential models (GGMs). Previous validation studies have shown that in mountainous regions the short-wavelength gravity and topographic signal is only partially resolved by high-degree GGMs such as EGM2008, leaving residuals at the several-decimetre level unless regional refinement is applied [27,28,29,30]. These limitations motivate the use of regional hybrid geoid modelling techniques, in which a physically based gravimetric solution is further refined using terrestrial gravity and GNSS/levelling data to capture the complex gravity field of the northern Tien Shan more accurately.

Furthermore, the Almaty region holds strategic importance for geodetic and surveying activities due to its urban expansion, infrastructure development, and the presence of numerous scientific institutions. Accurate geoid models are critical for precise height systems and geospatial applications in such a topographically and geophysically complex region. Therefore, this area serves as an ideal testbed for evaluating the performance of hybrid geoid modelling methods that integrate satellite-based models, terrestrial gravity data, and digital elevation models (DEMs).

3. Information Base, Required for Local Geoid Modelling

The hybrid geoid model in this study is constructed using four complementary datasets: terrestrial gravity measurements, a global geopotential model (GGM), a high-resolution digital elevation model (DEM), and GNSS/levelling points. In the present study, the long-wavelength component of the gravity field is represented by the global gravity model XGM2019e_2159, since it is one of the most up-to-date combined models integrating satellite (GRACE, GOCE) and terrestrial gravity data [31,32]. Topographic information and terrain corrections are derived from the FABDEM 30 m dataset, offering improved representation of bare-earth elevations [33]. The primary sources of information, however, are the gravity data—compiled from digitized historical surveys, validated by modern ground measurements, and harmonized with global models–and the GNSS/levelling data, which serve both for AI-supported geoid correction and independent validation of the geoid.

3.1. Gravity Data

For this study, gravimetric data are sourced from Soviet-era gravity anomaly maps at a scale of 1:200,000. These maps provide extensive coverage and detailed gravity information across Kazakhstan. In priority regions, higher-resolution surveys (1:50,000 or finer) were conducted [34,35]. The maps are based on Bouguer anomaly reductions using densities of 2.30 g/cm³ and 2.67 g/cm³ and include associated metadata such as free-air anomalies, elevation values, and terrain corrections. A historical gravity database was created by digitizing 14,061 gravity observation points from the following nomenclature sheets: L-43-XXVIII, L-43-XXIX, L-43-XXX, L-44-XXV, L-43-XXXIV, L-43-XXXV, L-44-XXXI, K-43-IV, K-43-V, K-43-VI, K-44-I, K-43-X, K-43-XI, K-43-XII, and K-44-VII. (Figure 2).

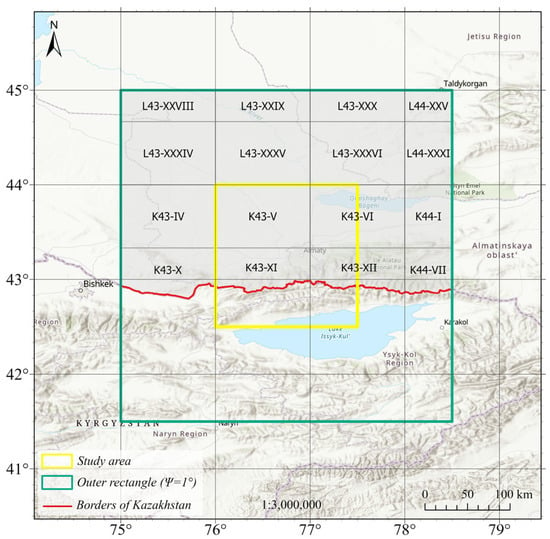
Figure 2. Cartogram of digitized gravimetric maps at a scale of 1:200,000 for the study area.

The digitization process includes the scanning of original paper maps and georeferencing to the WGS84 coordinate system. The georeferencing was initially performed in the Pulkovo 1942 datum within the relevant Gauss–Krüger projection zone. After georeferencing, terrain corrections, and elevations–were entered into structured at-tribute tables. Priority was given to maps with Bouguer reductions using 2.67 g/cm³ with terrain correction. Maps with 2.30 g/cm³ density reductions were used only in areas lacking higher-quality datasets.

A quality control procedure was implemented by generating a digital gravity anomaly surface using Kriging interpolation (250 × 250 m grid) and comparing it to the original raster images. Any discrepancies, often due to digitization errors, were corrected, and affected points were flagged in the database. Kriging method was used solely as a quality-control tool to identify digitization outliers; the interpolated gravity anomaly surface was not used in any subsequent computations. Ordinary Kriging was chosen because its variogram based formulation provides statistically consistent local predictions and is more sensitive to anomalous values than purely distance-based methods such as IDW or smooth spline surfaces. Since the objective was only to detect inconsistent points rather than to generate a final interpolated model, alternative methods (e.g., Spline or IDW) were not employed. Final data transformation from Gauss–Krüger coordinates to WGS84 was conducted using the transformation parameters Pulkovo 1942 to WGS 84 EPSG:15865. All digitized sheets were then merged into a unified spatial dataset.

To address data gaps in remote or mountainous areas lacking terrestrial surveys, global gravity data from the WGM2012 model (5′ × 5′ resolution) were integrated (Figure 3). These supplementary data enhanced the spatial continuity of the gravity field and were essential for accurate interpolation in regions where local measurements were unavailable.

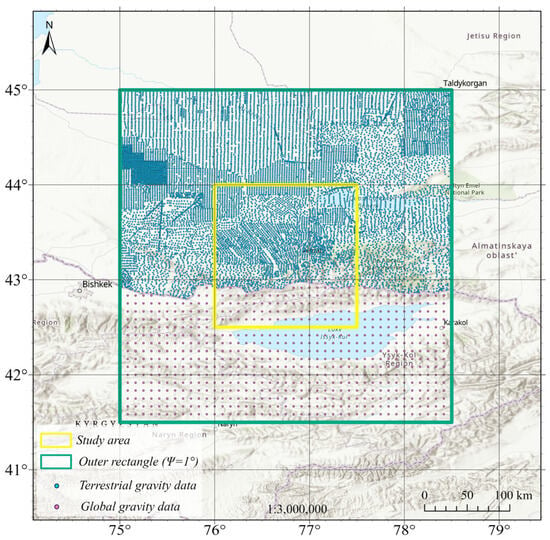
Figure 3. Integration of ground-based gravity data with the global WGM2012 model.

To assess the reliability of the gravity data, a comparison was conducted with modern absolute gravity measurements from QazGRF (Kazakhstan Gravimetric Reference Frame) stations [36,37] (Figure 4). Bouguer anomaly values were interpolated from the gravity data and corrected to estimate absolute gravity, which was then compared against observed values.

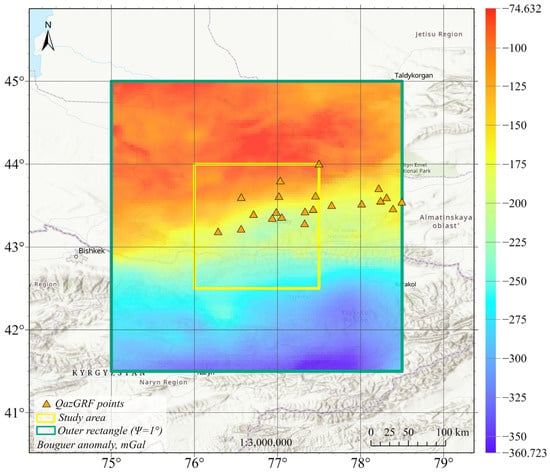
Figure 4. Spatial distribution of QazGRF stations and Bouguer gravity anomalies over the study area, mGal.

The statistical evaluation shows a mean difference of 3.23 mGal and a standard deviation of 2.95 mGal, with over 90% of discrepancies within ±5 mGal. This indicates the absence of systematic bias and confirms the generally high quality of the gravity data. The dataset was subsequently converted into a free-air gravity anomaly grid, which served as the primary input for the LSMSA method in local geoid determination.

3.2. GNSS/Levelling Data

A hybrid geoid model was derived and validated from a combined dataset of GNSS observations levelling benchmarks with integrated geodetic points (Figure 5).

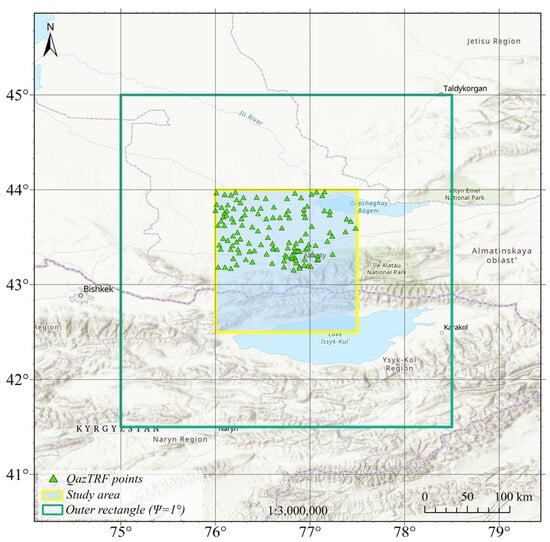
Figure 5. Spatial distribution of GNSS/levelling benchmarks of national levelling network.

The network covers both lowland and mountainous areas in southeastern Kazakhstan, which allows for accounting the diversity of topographic and geophysical conditions essential for precise geoid modelling. Normal heights, defined in the BHS-77 system, range from approximately 626 m to 1466 m and were compared with ellipsoidal heights derived from GNSS measurements, providing a basis for quantifying and minimizing systematic differences between the physical and geometric height systems. The GNSS surveys were conducted in static mode using dual-frequency GPS/GLONASS receivers, with observation sessions lasting no less than 24 h to suppress atmospheric effects, including ionospheric and tropospheric delays. The raw data were collected in RINEX format and processed with the GAMIT/GLOBK software package. The GAMIT module applied precise IGS orbits, atmospheric delay models, and multipath corrections based on double-difference carrier phase solutions, while GLOBK was used for network adjustment and integration into the global IGS reference frame through nearby permanent stations (BADG, LHAZ, URUM, NOVM). The full GNSS post-processing cycle is summarized in four main stages: synchronization of data to a single time scale, elimination of atmospheric distortions, construction of baseline vectors between observation points, and least squares adjustment of coordinates to minimize random errors (Figure 6).

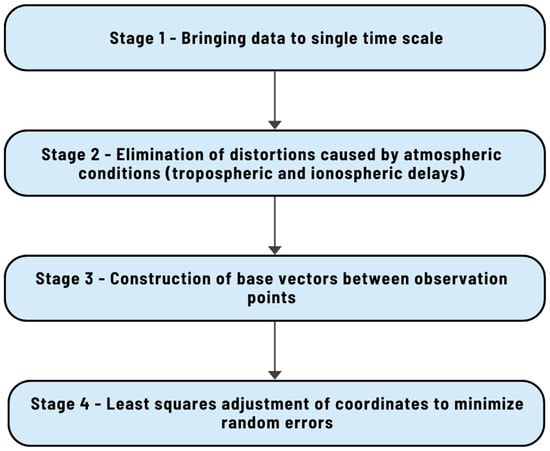
Figure 6. Stages of the full GNSS post-processing cycle.

The quality of the adjusted solution was assessed using weighted root-mean-square (WRMS) values for the east, north, and vertical components, which in most cases were below 0.050 m, with the most stable stations, such as KOTU and KURS, achieving WRMS values as low as 0.004 m. Although some sites initially exhibited higher RMS values due to multipath effects, the final adjusted coordinates remained well within accepted geodetic precision. The control dataset comprises 131 GNSS/levelling points distributed across the Almaty region.

4. Methods of the Local Geoid Modelling

The proposed methodology integrates the classical Least-Squares Modification of Stokes’ Formula with Additive Corrections (LSMSA, also known as the KTH method) and advanced machine learning techniques to improve the accuracy of local geoid determination. The workflow is divided into three main stages (Figure 7).

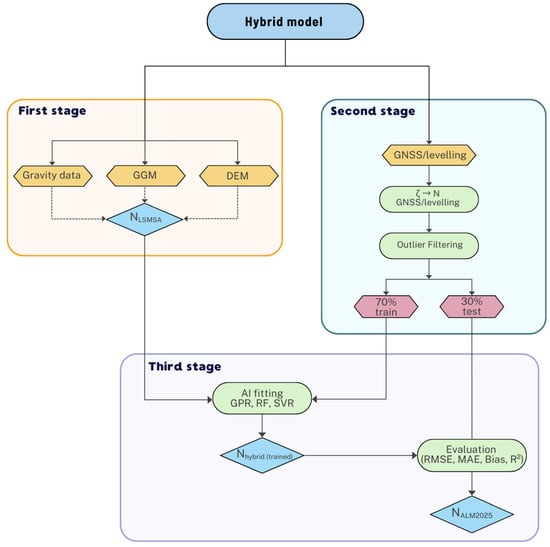
Figure 7. Workflow of the hybrid geoid modelling.

The first stage of our workflow follows the classical LSMSA method [38]. This approach provides a rigorous theoretical framework to integrate heterogeneous datasets—terrestrial gravity anomalies, global geopotential models (GGMs), digital elevation models, and GNSS/levelling observations—into a single regional geoid model.

The LSMSA method optimizes modification parameters of the Stokes kernel in a least-squares sense, thereby minimizing the mean square error of the derived geoid heights [39]. It accounts for:

–

truncation and spectral errors of gravity anomalies;

–

regularization of the poorly conditioned system for high-degree harmonics; and

–

additive corrections for topography, atmosphere, ellipsoidal effects, and downward continuation.

The output is a gravimetric geoid model $N_{LSMSA}$, which serves as the baseline solution for further refinement.

In the second stage, GNSS/levelling observations are preprocessed to geoid undulations compatible with the gravimetric baseline. Kazakhstan’s national height system is realized in normal heights. We first form height anomalies ζ and convert them to geoid undulations $N_{\mathrm{G}\mathrm{N}\mathrm{S}\mathrm{S}/\mathrm{L}\mathrm{e}\mathrm{v}}$ via the Moritz [40] geoid–quasigeoid separation formula, ensuring strict commensurability with the gravimetric geoid $N_{LSMSA}$ and an unbiased assessment of GNSS/levelling results.

$$N_{\mathrm{G}\mathrm{N}\mathrm{S}\mathrm{S}/\mathrm{L}\mathrm{e}\mathrm{v}}=\zeta +{\delta N}_{Moritz}.$$

(1)

where ${\delta N}_{Moritz}$-Moritz geoid–quasigeoid separation correction.

The GNSS/levelling points undergo an outlier detection procedure using a robust z-filter. The purpose of this step is to ensure the statistical consistency of the height anomalies that will subsequently be used for training the AI-based models. The robust-z approach reliably identifies and removes measurements that deviate substantially from the typical behaviour of the dataset, while remaining insensitive to non-Gaussian error characteristics and the presence of large outliers [41,42,43].

The resulting $N_{\mathrm{G}\mathrm{N}\mathrm{S}\mathrm{S}/\mathrm{L}\mathrm{e}\mathrm{v}}$ values are then split into training (70%) and test (30%) subsets for subsequent Helmert and AI comparisons. A 70/30 hold-out split is widely used for small-to-moderate GNSS/levelling datasets and is consistent with recent geoid-modelling studies that employ similar proportions [1,17,19].

The third stage consists of building a data-driven corrector surface from the pointwise residuals between GNSS/levelling undulations and the gravimetric baseline and then superimposing this field on the LSMSA surface to obtain the final hybrid geoid. Traditionally, this is achieved with a 3-, 5-, 7-parameters Helmert transformation, which aligns the two datasets by modelling shifts, rotations, and scale distortions. However, Helmert fitting can introduce systematic errors when datasets use different vertical datums or contain topographic inconsistencies. To improve the flexibility and accuracy of residual modelling, we propose the use of AI-based regression methods to approximate the difference between GNSS/levelling values and the gravimetric LSMSA model.

Specifically, let $\chi =\left[E,\hspace{0.17em}N,{\hspace{0.17em}N}_{LSMSA}\right]$ denote the feature vector composed of local east–north coordinates (in kilometres) and the baseline LSMSA undulation interpolated at the point location (in metres). For each control point, pointwise residuals are formed as

$$y\left(\chi \right)=\Delta N\left(\chi \right)=N_{GNSS/Lev}\left(\chi \right)-N_{LSMSA}\left(\chi \right),$$

(2)

And learn a data-driven regressor $\widehat{f}\left(\chi \right)$ such that $\widehat{f}\left(\chi \right)\approx \Delta N\left(\chi \right)$. The final hybrid geoid is then obtained by superimposition,

$$N_{hyb}\left(\chi \right)=N_{LSMSA}\left(\chi \right)+f\left(\chi \right).$$

(3)

To approximate $\Delta N$ over the study area we evaluate three complementary regression families: Gaussian Process Regression (GPR), Least-Squares Boosting (LSBoost), and Support Vector Regression (SVR). These methods are trained on 70% of the GNSS/levelling dataset and validated on the remaining 30%. To further reduce sensitivity to a single data split, we complement the hold-out approach with LOOCV, 10-fold, and spatial cross-validation.

GPR was implemented using an Automatic Relevance Determination Squared Exponential (ARD) kernel (GPR, ARD kernel). We place a Gaussian process prior on the latent field $f(\cdot )$ with i.i.d. Gaussian observation noise,

$$f\left(\chi \right)\sim \mathcal{G}\mathcal{P}\left(0, k_{\theta }\left(\chi ,\chi \prime \right)\right), y_i=f\left({\chi }_i\right)+{\epsilon }_i, {\epsilon }_i\sim \mathcal{N}\left(0, {\sigma }_n^2\right).$$

(4)

An automatic relevance determination (ARD) kernel is used so that the model learns separate length-scales for E, N, and N_LSMSA. In practice, a Matérn-3/2 covariance is adopted (with fallbacks to Matérn-5/2 or squared-exponential when required). Writing

$$r\left(\chi ,\chi \prime \right)=\sqrt{{\sum }_j{\displaystyle \frac{{(x_j-{x\prime }_j)}^2}{l_j^2}}}.$$

(5)

The kernel read:

$$k_{Matèrn-3/2}={\sigma }_{f }^2\left(1+\sqrt{3}r\right)e^{-\sqrt{3}r}, k_{SE}= {\sigma }_f^2\mathrm{e}\mathrm{x}\mathrm{p}(-{\displaystyle \frac{1}{2}}{\sum }_j{\displaystyle \frac{{(x_j-x_j^{\prime })}^2}{l_j^2}}).$$

(6)

Given training inputs X and targets y, the posterior predictor at x^∗ has mean and variance.

$${\mu }_{\ast }\left(x_{\ast }\right)=k_{\ast }^T{\left(K+{\sigma }_n^{2}I\right)}^{-1}y, {\sigma }_{\ast }^2\left(x_{\ast }\right)=k_{\ast \ast }-{k_{\ast }^T\left(K+{\sigma }_n^{2}I\right)}^{-1}{k}_{\ast },$$

(7)

With hyperparameters $\theta =\left\{{\mathsf{\sigma }}_f\right.,\left\{l_j\right\},\left.{\mathsf{\sigma }}_n\right\}$ fitted by maximizing the log marginal likelihood. Using heterogeneous units (E, N in km; $N_{LSMSA}$ in m) is handled by z-standardization and ARD.

Support Vector Regression (SVR, RBF kernel)

SVR seeks a function with small RKHS norm while keeping residuals within an ε-insensitive tube:

$$\begin{array}{c}min\\ w,b,\mathsf{\xi },{\mathsf{\xi }}^{\ast }\end{array}{\displaystyle \frac{1}{2}}{‖w‖}^2+C{\sum }_{i=1}^n({\mathsf{\xi }}_i+{\mathsf{\xi }}_i^{\ast }) s.t. \left\{\begin{array}{c}{y}_i-f\left({\chi }_i\right)\le \epsilon +{\mathsf{\xi }}_i,\\ f\left({\chi }_i\right)-y_i\le {\mathsf{\xi }}_i^{\ast },\\ {\mathsf{\xi }}_i,{\mathsf{\xi }}_i^{\ast }\ge 0.\end{array}\right.$$

(8)

By the representer theorem,

$$f\left(x\right)={\sum }_{i=1}^n\left(a_i-a_i^{\ast }\right)k\left({\chi }_i,\chi \right)+b,$$

(9)

With an RBF kernel $k\left(\chi ,\chi \prime \right)=\mathrm{e}\mathrm{x}\mathrm{p}(-{‖\chi -\chi \prime ‖}^2/(2{\mathsf{\sigma }}^2\left)\right)$. The hyperparameters C, ε, and σ (KernelScale) govern smoothness and robustness. As with GPR, inputs (E, N,${\hspace{0.17em}N}_{LSMSA}$) are kept in their standard units and standardized prior to training.

Least-Squares Boosting (LSBoost)

We fit an additive ensemble of regression trees by steepest descent on the squared loss. Starting from

$$f_0\left(\chi \right)=\begin{array}{c}arg \mathrm{m}\mathrm{i}\mathrm{n}\\ c\end{array}{\sum }_i(y_i-c{)}^2=\overline{y},$$

(10)

We iterate for m = 1, …, M:

$$r_{im}=y_i-f_{m-1}\left({\chi }_i\right), h_m\leftarrow tree fit to\left\{\left({\chi }_i\right)\}, r_{im})\},\right. f_m\left(\chi \right)=f_{m-1}\left(\chi \right)+\nu h_m\left(\chi \right),$$

(11)

With learning rate $\mathsf{\nu }\in \left(\mathrm{0,1}\right]$. Regularization is controlled by (M,ν) and tree complexity (e.g., minimum leaf size). This yields a flexible, piecewise-smooth approximation of ΔN (E, N, N_LSMSA) that complements the smooth, kernel-based GPR/SVR models.

Data preprocessing and validation for machine-learning regressors. We used GNSS/levelling control points covering the Almaty. For each control point, we first interpolated the baseline LSMSA geoid undulation to the point location and formed residuals $\mathrm{r}=N_{\mathit{GNSS}/\mathit{Lev}}-N_{\mathit{LSMSA}}$. To improve numerical conditioning and enable spatial validation, geographic coordinates $(\mathsf{\phi },\mathsf{\lambda })$ were converted to local east–north coordinates $\left(E,N\right)$ in kilometres using a tangent-plane approximation centred at the dataset centroid. The feature vector supplied to the regressors is $\mathrm{x}=[E,N,N_{\mathit{LSMSA}}]$(with $N_{\mathit{LSMSA}}$ in metres).

Data transformation and cleaning. Raw tables were cast to numeric types, duplicate grid nodes and rows with missing core fields were removed. If the baseline undulation at a point was absent, it was filled by interpolation from the LSMSA grid. A robust-z screening flagged potential outliers. All kernel-based models (SVR/GPR) used internal standardization of predictors/targets; tree-boosting did not require feature scaling.

Primary hold-out and additional cross-validation (CV). In addition to the reproducible 70/30 split, we report three complementary validation protocols to assess generalization and guard against spatial leakage [44]: leave-one-out CV (LOOCV), 10-fold CV, and spatial CV, in which points are partitioned by k-means clustering in the $(E,N)$ plane to create geographically coherent folds. For each protocol we summarize RMSE (primary), and MAE, bias (mean error), and $R^2$.

Hyperparameter selection. SVR (RBF) and LSBoost hyperparameters were selected via nested $\mathrm{k}$-fold cross-validation on the training portion (outer split as above; inner $\mathrm{k}=5$), using small discrete grids for $\mathrm{C}$/KernelScale/$\mathsf{\epsilon }$ (SVR) and cycles/learning-rate/min-leaf (LSBoost). GPR employed an ARD kernel (squared-exponential or Matérn) with automatic length-scale adaptation. Final models were refitted on the full training set and evaluated on the untouched test set and under the CV protocols listed above.

Model interpretability and complexity control. Interpretability is addressed with model-aware diagnostics: for GPR (ARD), predictor-specific length-scales ${\mathcal{l}}_{\mathrm{j}}$ quantify relative sensitivity to $(E,N,N_{LSMSA})$; for SVR, capacity is summarized by the fraction of support vectors and margin parameters $(\mathrm{C},\mathsf{\epsilon })$; for LSBoost, effective complexity is governed by $\left(\mathrm{M},\mathsf{\nu }\right)$ and tree depth/leaf size, and can be summarized by split-gain/frequency profiles. These diagnostics are reported alongside errors to verify that improvements are physically plausible and not due to uncontrolled model capacity.

To assess the effectiveness of the proposed approach, we perform a comparative analysis of Helmert 7-parameter fitting versus AI-based regression fitting (GPR, LSBoost, SVR).

Comparisons use the 30% hold-out together with LOOCV, 10-fold, and spatial CV, reporting RMSE (primary), MAE, bias, and $R^2$. The final regressor for constructing $N_{\mathrm{A}\mathrm{L}\mathrm{M}2025}$ is selected based on held-out performance and cross-validated generalization.

Error metrics and interpretation. Let $y_i$ denote the observed residual at control point $i$ (i.e., $y_i=\Delta N_i=N_{\mathit{GNSS}/\mathit{leveling},i}-N_{\mathit{LSMSA},i}$, in metres), and ${\widehat{y}}_i$ the model prediction. Define the error $e_i=y_i-{\widehat{y}}_i$. Metrics are computed on the hold-out TEST set and across CV folds.

(1) 

Root-Mean-Square Error (RMSE, primary).

$$RMSE=\sqrt{{\displaystyle \frac{1}{n}} {\sum }_{i=1}^n{e}_i^2}.$$

(12)

RMSE measures the energy of the errors and penalizes large deviations more strongly than MAE. For (approximately) stationary errors, $RMS{E}^2\approx {\mathrm{bias}}^2+\mathrm{Var}\left(e\right)$; therefore, reporting bias and a dispersion metric alongside RMSE helps separate systematic vs. random components.

(2) 

Mean Absolute Error (MAE).

$$MAE={\displaystyle \frac{1}{n}}{\sum }_{i=1}^n\left|e_i\right|.$$

(13)

MAE is the typical absolute error (metres) and is less sensitive to single outliers than RMSE. If $RMSE\gg MAE$, the error distribution likely has heavy tails (a few large misses); if $RMSE\approx MAE$, residuals are more homogeneous. MAE is often used as an intuitive “expected absolute correction error” for engineering applications.

(3) 

Bias (mean error).

$$bias=\overline{e}={\displaystyle \frac{1}{n}}{\sum }_{i=1}^n{e}_i.$$

(14)

Bias quantifies the systematic offset relative to GNSS/levelling. The sign matters: $bias<0$ indicates systematic overestimation of the corrected geoid (model above observations), $bias>0$ indicates underestimation. For a hybrid geoid, bias should be statistically indistinguishable from zero (e.g., confidence interval includes 0), especially on TEST and in spatial CV, to exclude datum-related drifts and global tilts.

(4) 

Coefficient of determination ($R^2$).

$$R^2=1-{\displaystyle \frac{\sum _{i=1}^n{e}_i^2}{\sum _{i=1}^n{\left(y_i-\overline{y}\right)}^2}}, \overline{y}={\displaystyle \frac{1}{n}}{\sum }_{i=1}^n{y}_i$$

(15)

$R^2$ reports the fraction of the variance in the target residuals explained by the model. In spatial regression, $R^2$ can be sensitive to the spread of $y$ and sampling density, so it serves as a supporting metric and should be read together with RMSE/MAE. An increase in $R^2$ without deterioration in RMSE/MAE indicates better capture of the residual field’s structure.

5. Results

5.1. Classical Geoid Modelling by LSMSA Method

Geoid model calculations included the use of XGM2019 spherical harmonic coefficients to powers of 120, 200, 300, 400, 500, 630, and 760 with a combination of ground gravity data error variance C (0)—0.5, 1, 3, 6, 9, and 16 mGal². The results are presented in Table 1.

Table 1. Statistics for fitting a combination of spherical harmonic coefficients with error variance of ground gravity data (m).

	C(0), mGal2
	16		9		6		3		1
Mmax	STD	RMSE	STD	RMSE	STD	RMSE	STD	RMSE	STD	RMSE
760	0.279	0.474	0.231	0.382	0.197	0.337	0.153	0.273	0.111	0.195
630	0.217	0.348	0.182	0.313	0.161	0.284	0.131	0.241	0.102	0.182
500			0.126	0.194	0.109	0.179	0.099	0.168	0.087	0.140
400							0.094	0.144	0.083	0.103
300									0.079	0.095
200									0.112	0.156
180									0.121	0.219

The initial parameters for calculating the modification parameters were a. Degree of modification L = M = 300; b. Variance of errors in ground gravity data C (0) = 1 m Gal²; c. The size of the integration coverage is Ѱ = 1.

In the computational scheme of the LSMSA method for determining the geoid, the surface gravity anomalies and the GGM are used to determine N_app (Figure 8), and then necessary corrections are added (Figure 9, Table 2).

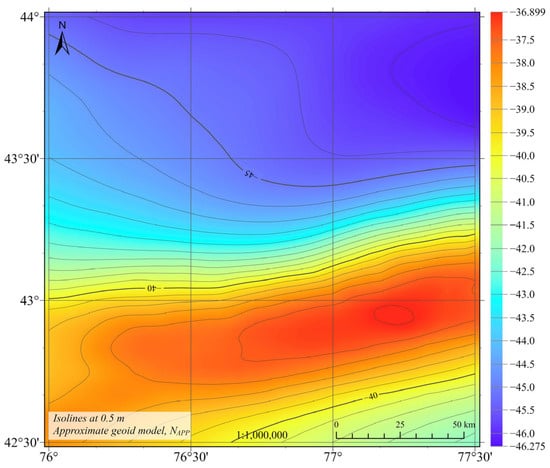
Figure 8. Approximate geoid heights without corrections Napp, m.

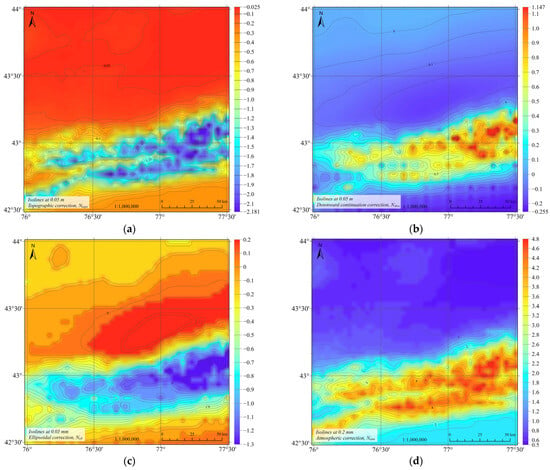
Figure 9. Corrections to approximate geoid heights using: (a) topographic correction, m; (b) correction for analytical downward continuation, m; (c) ellipsoidal correction, mm; (d) atmospheric correction, mm.

Table 2. Statistics of applied additive corrections.

Correction Type	Min	Max	Mean	STD
Topographic	−2.181 m	−0.025 m	−0.421 m	0.534 m
DWC reduction	−0.255 m	1.147 m	0.042 m	0.245 m
Ellipsoidal	−1.3 mm	0.2 mm	−0.3 mm	0.3 mm
Atmospheric	0.5 mm	4.8 mm	1.7 mm	1.2 mm
Sum of all corrections	−1.652 m	−0.020 m	−0.378 m	0.331 m

Figure 10 shows the result of calculating the geoid heights for the study area using the Least-Squares Modification of Stokes’ Formula with Additional Corrections (LSMSA) method.

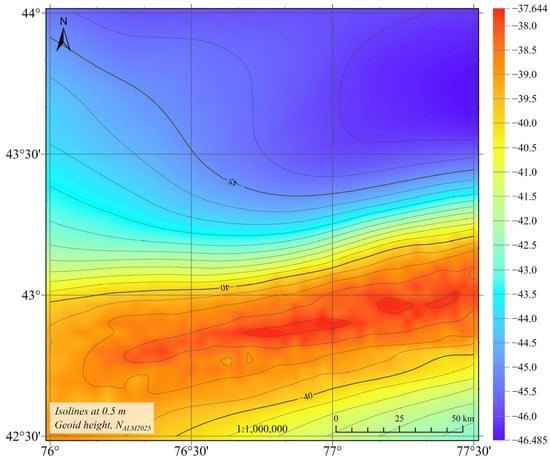
Figure 10. Geoid height by the method of Least-Squares Modification of Stokes’ Formula with Additional Corrections N_LSMS, m.

The calculated geoid heights for Almaty region using the LSMSA method vary in the range from −46.485 m to −37.644 m, the average value is −42.577 m, and the standard deviation is 2.873 m.

5.2. GNSS/Levelling Data Preprocessing

To obtain a consistent and reliable GNSS/levelling dataset for subsequent AI-based model training, the height anomalies were converted into geoid undulations using the Moritz geoid–quasigeoid separation formula (Equation (1)). For the study area, the Moritz separation correction ranges from 0.05 to 0.31 m.

Application of the robust-z filtering procedure removed 12 statistically inconsistent observations, leading to a clear reduction in residual dispersion and an improvement in the internal consistency of the dataset: the RMSE decreased from 0.095 m to 0.081 m, and the residual distribution became more symmetric and closer to normal (Figure 11).

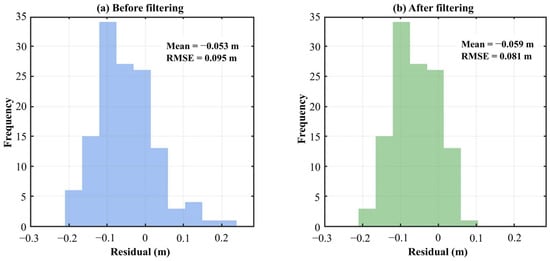
Figure 11. Distribution of residuals before and after outlier filtering in GNSS/levelling geoid comparison, m.

Following the filtering step, the cleaned dataset was randomly divided into a training subset (83 points, 70%) and a test subset (36 points, 30%), ensuring that both subsets preserved the spatial distribution and statistical characteristics of the original data.

5.3. Corrector Surface by AI

We evaluated residuals between observed geoid undulations $N_{GNSS/Lev}$ and the $N_{LSMSA}$ grid interpolated to 119 control points (train = 83, test = 36). Table 3 summarizes distributional statistics for the baseline (“Before”) and for four fitted models (“After”).

Table 3. Residual error statistics for geoid correction across ALL/TRAIN/TEST.

Method	Split	N	Mean, m	Median, m	STD, m	RMS, m	MAE, m	IQR, m	MIN, m	MAX, m
BEFORE
None	ALL	119	−0.059	−0.063	0.056	0.081	0.068	0.079	−0.187	0.068
	TRAIN	83	−0.061	−0.064	0.055	0.082	0.069	0.080	−0.187	0.068
	TEST	36	−0.053	−0.057	0.059	0.079	0.066	0.084	−0.186	0.058
AFTER
Helmert	ALL	119	0.004	0.006	0.058	0.058	0.048	0.084	−0.129	0.128
	TRAIN	83	0.002	0.002	0.057	0.057	0.047	0.077	−0.129	0.128
	TEST	36	0.010	0.010	0.070	0.072	0.059	0.102	−0.135	0.129
GPR (ARD)	ALL	119	0.001	−0.001	0.043	0.043	0.034	0.060	−0.099	0.107
	TRAIN	83	0.000	0.000	0.042	0.042	0.033	0.060	−0.099	0.095
	TEST	36	0.005	−0.001	0.046	0.045	0.036	0.058	−0.093	0.107
SVR (RBF)	ALL	119	0.000	−0.001	0.043	0.043	0.035	0.065	−0.094	0.109
	TRAIN	83	−0.001	−0.003	0.044	0.043	0.036	0.070	−0.094	0.099
	TEST	36	0.003	−0.004	0.042	0.040	0.034	0.056	−0.055	0.101
LSBoost	ALL	119	0.003	0.000	0.028	0.028	0.013	0.000	−0.101	0.116
	TRAIN	83	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
	TEST	36	0.010	0.021	0.051	0.051	0.042	0.064	−0.101	0.116

The residual statistics of the GNSS/levelling control points with respect to the initial gravimetric geoid (Table 3) reveal a pronounced systematic bias and relatively large noise: before any corrections, the RMS reaches 0.081 m with a mean of −0.059 m, corresponding to a downward offset of about 6 cm. The Helmert regression reduces the RMS to 0.058 m and almost completely removes the systematic shift; however, the remaining standard deviation and interquartile range at the level of 6–7 cm indicate that a more flexible modelling approach is required.

The application of machine-learning regressors leads to a further, robust improvement. Both GPR (ARD) and SVR (RBF) achieve RMS values of about 0.043 m over all points and ~0.04–0.05 m on the independent TEST subset, with nearly zero bias and clearly reduced interquartile ranges. Thus, they almost halve the RMS compared with the original gravimetric solution and significantly outperform the Helmert model. In contrast, LSBoost nearly interpolates the training data (zero residuals on TRAIN) but yields higher errors on the TEST subset (RMS ≈ 0.05 m), indicating pronounced overfitting.

The cross-validation results (Table 4) corroborate these findings. Under both LOOCV and 10-fold CV, SVR consistently attains the lowest RMSE and highest R², followed closely by GPR, whereas LSBoost exhibits larger errors and negative R², i.e., it generalizes worse than a trivial mean model. Spatial group cross-validation, mimicking extrapolation to new areas, leads to an expected increase in errors for all models; however, SVR remains comparable to the Helmert noise level, while LSBoost shows a strong deterioration (RMSE ~0.10 m and strongly negative R²). Overall, SVR with an RBF kernel offers the best compromise between accuracy and robustness, with GPR providing slightly inferior but comparable performance, and LSBoost being of limited practical use due to its tendency to overfit and its poor spatial generalization.

Table 4. Comparative cross-validation statistics for GPR (ARD), SVR (RBF), and LSBoost using LOOCV, 10-fold, and spatial CV.

Method	Protocol	RMSE, m	MAE, m	Bias, m	R2, -
GPR (ARD)		0.048	0.039	0.002	0.267
SVR (RBF)	LOOCV	0.044	0.035	0.000	0.380
LSBoost		0.057	0.045	0.001	−0.047
GPR (ARD)		0.049	0.039	0.003	0.246
SVR (RBF)	10-fold	0.046	0.036	0.001	0.343
LSBoost		0.060	0.047	0.003	−0.150
GPR (ARD)		0.063	0.052	−0.014	−0.260
SVR (RBF)	spatial CV	0.056	0.044	−0.002	0.020
LSBoost		0.100	0.086	−0.023	−2.195

The terrain-stratified statistics on the TEST points (Table 5) show that the linear Helmert transformation exhibits increasing RMS from flat to hilly and mountainous areas, whereas GPR and especially SVR provide lower and more homogeneous errors across all three terrain classes. For GPR/SVR, biases on TEST remain small (on the order of ±0.03 m), confirming good generalization of the correctors and the absence of systematic accuracy degradation in mountainous regions.

Table 5. Residual error statistics for geoid correction across ALL/TRAIN/TEST (m).

Method	Terrain Type	N	Mean, m	Median, m	STD, m	RMS, m	MAE, m	IQR, m	MIN, m	MAX, m
Helmert	Flat	15	0.011	0.008	0.052	0.056	0.038	0.069	−0.056	0.098
	Hilly	15	0.032	0.028	0.065	0.070	0.061	0.111	−0.065	0.119
	Mountainous	6	−0.047	−0.047	0.058	0.071	0.063	0.050	−0.126	0.046
GPR (ARD)	Flat	15	0.003	0.002	0.031	0.030	0.025	0.050	−0.047	0.063
	Hilly	15	0.021	0.026	0.055	0.057	0.049	0.072	−0.057	0.107
	Mountainous	6	−0.032	−0.023	0.035	0.046	0.032	0.041	−0.093	−0.002
SVR (RBF)	Flat	15	−0.002	−0.005	0.032	0.031	0.025	0.043	−0.048	0.065
	Hilly	15	0.019	0.026	0.052	0.054	0.046	0.067	−0.053	0.109
	Mountainous	6	−0.023	−0.029	0.024	0.032	0.027	0.023	−0.055	0.011
LSBoost	Flat	15	0.002	0.017	0.047	0.046	0.039	0.068	−0.092	0.077
	Hilly	15	0.028	0.029	0.052	0.057	0.048	0.052	−0.093	0.116
	Mountainous	6	−0.014	−0.013	0.051	0.048	0.037	0.045	−0.101	0.041

5.4. Hybrid Geoid (LSMSA + AI)

Given its superior held-out performance and balanced residual distribution, SVR (RBF) was selected for the final hybrid grid.

$$N_{ALM2025} =N_{LSMSA} + f_{SVR}\left(∆X\right),$$

(16)

The resulting grid, computed at 2′ × 2′ resolution, preserves the long-wavelength physical consistency of LSMSA while effectively removing local biases.

Compared with the original LSMSA solution and the intermediate Helmert fit, the hybrid surface provides a substantial reduction in residual scatter at GNSS/levelling control points: the all-point RMS decreases from 0.081 m (baseline) and 0.058 m (Helmert) to ≈0.04–0.05 m for the SVR–LSMSA hybrid, with biases remaining statistically indistinguishable from zero. Figure 12 illustrates the transition from a biased, dispersed residual distribution to a more centred and compact one after SVR-based adjustment; quantitative values are reported in Table 3.

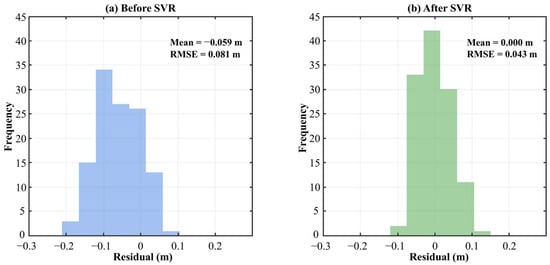
Figure 12. Histograms of geoid residuals before and after SVR-based correction, m.

6. Discussion

The LSMSA results confirm that a physically rigorous gravimetric approach can provide a stable and internally consistent baseline geoid for the Almaty region. However, the residual statistics in Table 3 show that, without additional local correction, its accuracy remains insufficient for demanding engineering and geodetic applications. The baseline LSMSA solution exhibits a systematic offset of about −0.06 m and an RMS of 0.081 m relative to GNSS/levelling, which is a typical decimetre-level mismatch observed in mountainous regions with strong topographic gradients and heterogeneous gravity coverage. Similar initial discrepancies between gravimetric geoids and GNSS/levelling (RMS ≈ 0.08–0.12 m) have been reported in recent hybrid-geoid case studies for rugged areas, including parts of Turkey, Brazil, and the Andes, prior to the application of hybrid corrections [45,46,47,48,49].

The 7-parameter Helmert transformation reduces these discrepancies by removing the mean bias and decreasing the RMS to 0.058 m, but the remaining 6–7 cm scatter highlights the limitations of global affine models. Terrain-stratified statistics indicate that the Helmert fit performs reasonably well over flat and gently undulating terrain but deteriorates in mountainous zones, where short-wavelength gravity and topographic effects generate spatially structured residuals that cannot be captured by a single linear transformation. This behaviour is consistent with previous studies, where Helmert-type adjustments improved global alignment but left residual tilts and curvature that required more flexible correction schemes [45,46,47,48,49].

In contrast, the machine-learning regressors achieve a substantially higher level of fit while preserving physical consistency through residual learning. By training on the feature vector x = (E, N, N_LSMSA) and modelling only ΔN = N_GNSS/Lev − N_LSMSA, the ML models keep the long- and medium-wavelength structure fixed by LSMSA and allocate their capacity to local systematic effects and datum inconsistencies. Both GPR and SVR reduce the overall RMS to ≈0.043 m with near-zero bias at the control points, effectively halving the misfit relative to the LSMSA baseline and clearly outperforming both the uncorrected solution and the Helmert adjustment (Table 3). These values fall within the 0.04–0.06 m range reported for state-of-the-art hybrid geoid/quasigeoid models in similarly complex mountainous regions [45,46,47,48,49], indicating that the proposed framework reaches a competitive accuracy level.

The choice of SVR with an RBF kernel as the operational corrector for NALM2025 is supported by several lines of evidence. First, according to Table 4, SVR attains the lowest RMSE and highest R² in LOOCV and 10-fold CV and maintains a lower RMSE than GPR in spatial cross-validation, which is the most demanding protocol from a geographic-generalization perspective. Second, terrain-stratified statistics (Table 5) show that SVR yields more homogeneous errors across flat, hilly, and mountainous regimes, reducing RMS in the mountainous subset to ≈0.03 m, whereas the Helmert model degrades most strongly there. Third, from a computational standpoint, SVR offers compact inference and favourable scaling with sample size, making it suitable for dense gridding at 2′ × 2′ resolution and for potential regional or national extensions.

LSBoost, while achieving RMS values comparable to GPR on the full dataset, exhibits a larger train–test spread and a pronounced degradation under spatial CV, indicating a higher variance component under the current sample size. This behaviour is characteristic of over-parameterised ensemble models trained on limited data. Inspection of tree depth and split frequencies confirms a complex and difficult-to-interpret structure, supporting the decision to exclude LSBoost as an operational corrector and to use it instead as a diagnostic tool for exploring small-scale patterns in the residual field.

The discussion also underscores the importance of data preprocessing for successful ML-based hybrid geoid modelling. Robust-z filtering removed 12 inconsistent GNSS/levelling observations and reduced RMS from 0.095 m to 0.081 m, while coordinate transformation to a local east–north frame improved numerical conditioning and facilitated spatial clustering for cross-validation. Normalization of predictors and careful feature design ensured that the regressors focused on geophysically meaningful structures rather than artefacts of scale or coordinate representation. These steps are consistent with recent ML-oriented geodetic studies, where outlier handling, coordinate normalization, and robust validation strategies are considered essential for reliable model construction.

Finally, several limitations should be acknowledged. The control network, although spanning both lowlands and high mountains, remains moderate in size and may not fully resolve small-scale heterogeneities, particularly in remote high-altitude areas. Part of the gravity input originates from digitized historical surveys, which may contain residual local biases despite quality checks. Cross-validated performance additionally depends on fold design in spatial CV, and extrapolation beyond the Almaty region should therefore be carried out with caution. These limitations motivate future work aimed at densifying the control network, integrating new gravity and GNSS/levelling data, and exploring physics-informed ML architectures that more tightly couple data-driven residuals with underlying geophysical processes.

7. Conclusions

This study developed and assessed a high-resolution hybrid geoid model for the Almaty region of southeastern Kazakhstan by combining a physically rigorous LSMSA baseline with machine-learning-based residual correction. The integration of digitized Soviet-era gravity data, the global geopotential model XGM2019e_2159, high-resolution DEMs, and a carefully processed GNSS/levelling network allowed the construction of a consistent gravimetric geoid and an information base suitable for data-driven refinement.

The LSMSA method successfully captured the long- and medium-wavelength structure of the regional gravity field but left decimetre-level discrepancies with GNSS/levelling benchmarks (RMS ≈ 0.081 m, bias ≈ −0.06 m), especially in rugged mountainous terrain. A classical Helmert transformation reduced the mean bias and lowered the RMS to 0.058 m but could not fully represent the complex spatial structure of the residuals. By contrast, residual learning with SVR and GPR, trained on the feature vector x = (E, N, N_LSMSA), and evaluated under a nested cross-validation framework, reduced the RMS to ≈0.043 m with near-zero bias, effectively halving the misfit relative to the baseline solution and eliminating the systematic offset.

Among the tested regressors, SVR provided the most favourable balance between accuracy, robustness, and scalability, achieving the best combination of RMSE and R² across validation protocols and yielding homogeneous errors across flat, hilly, and mountainous terrain. The resulting hybrid geoid N_ALM2025, computed on a 2′ × 2′ grid, preserves the physical consistency of the LSMSA solution while removing local biases and achieving centimetre-level agreement with GNSS/levelling data. This performance is comparable to that of state-of-the-art hybrid geoids in other mountainous regions and is adequate for many geodetic and engineering applications in southeastern Kazakhstan.

Future work will focus on extending the LSMSA–SVR framework to a national scale by incorporating additional GNSS/levelling networks and newly acquired gravity data, improving the spatial density of control points in high-relief areas, and assessing uncertainty propagation when deploying AI-based correctors within height-system modernisation programmes. In this way, the proposed methodology can contribute to the development of a robust, high-accuracy geoid infrastructure for Kazakhstan and to the broader advancement of AI-assisted hybrid geoid modelling in complex mountainous environments.