Cover Edge-Based Novel Triangle Counting

Abstract

Counting and listing triangles in graphs is a fundamental task in network analysis, supporting applications such as community detection, clustering coefficient computation, k-truss decomposition, and triangle centrality. We introduce the cover-edge set, a novel concept that eliminates unnecessary edges during triangle enumeration, thereby improving efficiency. This compact cover-edge set is rapidly constructed using a breadth-first search (BFS) strategy. Using this concept, we develop both sequential and parallel triangle-counting algorithms and conduct comprehensive comparisons with state-of-the-art methods. We also design a benchmarking framework to evaluate our sequential and parallel algorithms in a systematic and reproducible manner. Extensive experiments on the latest Intel Xeon 8480+ processor reveal clear performance differences among algorithms, demonstrate the benefits of various optimization strategies, and show how graph characteristics, such as diameter and degree distribution, affect algorithm performance. Our source code is available on GitHub.

1. Introduction

Triangle listing and counting is a well-established problem in computer science and forms a key foundation for many graph analysis methods, such as clustering coefficients [1], k-truss decomposition [2], and triangle centrality [3]. Its significance is further demonstrated by its inclusion in high-performance computing benchmarks like Graph500 [4] and the MIT/Amazon/IEEE Graph Challenge [5], as well as its role in influencing the design of future computing architectures (e.g., IARPA AGILE [6]).

A graph $G=(V,E)$ with $n=\left|V\right|$ vertices and $m=\left|E\right|$ edges can contain at most $\left({\displaystyle \genfrac{}{}{0pt}{}{n}{3}}\right)=\mathsf{\Theta }\left(n^3\right)$ triangles. The naive approach—checking every triple $(u,v,w)$ via triple-nested loops—requires $\mathcal{O}\left(n^3\right)$ time, which is prohibitively slow for sparse graphs. It is known that listing all triangles in G requires at least $\mathsf{\Omega }\left(m^{3/2}\right)$ time [7,8]. To address this, Cohen [9] introduced a map-reduce-based parallel technique that generates open wedges between triples of vertices and then checks for the existence of a closing edge, avoiding redundant counts while improving load balancing. Many parallel approaches [10,11] adopt this wedge-generation strategy, partitioning the graph across multiple compute nodes and communicating wedge data to detect closing edges. However, in large-scale settings, this communication cost often dominates the total runtime.

In this work, we introduce a novel approach for triangle counting that reduces unnecessary edge checks by operating on a smaller subset of edges, which we call the cover-edge set. This reduced set preserves all triangles in the graph, while significantly reducing the computational workload. The cover-edge set is constructed efficiently using a breadth-first search (BFS) to orient vertices into levels.

The main contributions of this paper are as follows:

• We propose a new triangle counting algorithm, Cover-Edge Triangle Counting (CETC), based on the concept of the cover-edge set. This approach identifies all triangles using only the cover-edge set instead of the full edge set, ensuring correctness while reducing computation. Several sequential variants of CETC are also presented.
• We release open-source software containing implementations of over 22 sequential triangle counting algorithms and 11 OpenMP parallel algorithms, all written in C.
• We perform a comprehensive experimental evaluation on both real-world and synthetic graphs, comparing our proposed algorithms against state-of-the-art methods and analyzing how graph properties affect performance.

2. Notations and Definitions

For an undirected graph $G=(V,E)$ with $n=\left|V\right|$ vertices and $m=\left|E\right|$ edges, a triangle is a set of three distinct vertices $\{v_a,v_b,v_c\}\subseteq V$ such that all three edges $\{(v_a,v_b),(v_b,v_c),(v_c,v_a)\}$ belong to E. For any vertex $v\in V$, its neighborhood is defined as

$$N\left(v\right)=\{u\in V\mid (u,v)\in E\},$$

and its degree is $d\left(v\right)=\left|N\right(v\left)\right|$. We denote by $d_{\max }$ the maximum degree among all vertices in G.

With these notations, the total number of triangles in graph G is denoted as $|\Delta (G\left)\right|$. Specifically, $\Delta \left(G\right)=\left\{\right(u,v,w\left)\right|u,v,w$ are different vertices of V and $(u,v),$$(v,w),$$(w,u)$ are edges of $E\}$.

The triangle counting problem can be expressed in two ways, based on edges and vertices:

• For any edge $(u,v)\in E$, the number of triangles that include $(u,v)$ is $|\Delta (u,v\left)\right|$, where $\Delta (u,v)=N\left(u\right)\cap N\left(v\right)$. Since each triangle edge will count the same triangle and we will count both $\Delta (u,v)$ and $\Delta (v,u)$, the total number of triangles is computed as $|\Delta \left(G\right)|=\frac{{\sum }_{(u,v)\in E}|\Delta (u,v)|}{6}$, using the edge-iteration-based method.
• For any vertex $v\in V$, the number of triangles including v is $|\Delta (v\left)\right|$, where $\Delta \left(v\right)=\left\{\right(u,w\left)\right|u,w\in N\left(v\right)\wedge (u,w)\in E\}$. The total number of triangles is computed as $|\Delta \left(G\right)|=\frac{{\sum }_{v\in V}|\Delta \left(v\right)|}{6}$, using the vertex-iteration-based method.

3. Related Work

3.1. Existing Sequential Algorithms

For triangle counting, the obvious algorithm is brute-force search (see Algorithm 1), enumerating over all $\mathsf{\Theta }$$\left(n^3\right)$ triples of distinct vertices, and checking how many of these triples are triangles. Faster algorithms that rely on representing the input graph using an adjacency matrix exist and employ fast matrix multiplication techniques, such as the method proposed by Alon, Yuster, and Zwick [12]. In fact, if A is the adjacency matrix of G, for any vertex v, the value $A_{vv}^3$ on the diagonal of $A^3$ is twice the number of triangles to which v belongs. So, the number of triangles is ${\displaystyle \frac{1}{6}}\sum tr\left(A^3\right)$. Triangle counting problems can therefore be solved in $\mathcal{O}\left(n^{\omega }\right)$, where $\omega <2.732$ is the exponent of the fast matrix product [13,14]. Alon et al. [12] also show that it is possible to solve the triangle counting problem in $\mathcal{O}\left(m^{\frac{2\omega }{\omega +1}}\right)$⊂$\mathcal{O}\left(m^{1.41}\right)$ time. However, the implementation is infeasible for large, sparse graphs, and certain matrix multiplication methods fall short of listing all the triangles. For these reasons, despite their evident theoretical strength, these algorithms have limited practical impact.

Algorithm 1 Triples

Require:  Graph $G=(V,E)$ Ensure:  Triangle Count T  1: $T\leftarrow 0$  2: $\forall u\in V$  3:    $\forall v\in V$  4:      $\forall w\in V$  5:        if $(u,v)\in E\wedge (v,w)\in E\wedge (u,w)\in E$  6:          $T\leftarrow T+1$  7: return $T/6$

Another category of fundamental problem formulation is called a subgraph query, which aims to identify instances of a triangle subgraph within the input graph. It is crucial to emphasize that determining the presence of a specific subgraph in a graph is an NP-hard problem. Although various methods, including the backtracking strategy [15], have been introduced, they are not preferred choices for the triangle counting problem, particularly for large-scale graphs.

Latapy [8] presents a comprehensive survey of triangle-counting algorithms designed for very large and sparse graphs. One of the earliest methods, known as the tree-listing algorithm, was introduced by Itai and Rodeh in 1978 [7]. The algorithm begins by constructing a rooted spanning tree of the graph. It then iterates over the non-tree edges, applying specific criteria to detect triangles. Afterward, the corresponding tree edges are removed, and the process is repeated until no edges remain (see Algorithm 2). The algorithm runs in $\mathcal{O}\left(m^{\frac{3}{2}}\right)$ time, or $\mathcal{O}\left(n\right)$ for planar graphs.

Algorithm 2 Tree-listing (IR) [7]

Require:  Graph $G=(V,E)$ Ensure:  Triangle Count T  1: $T\leftarrow 0$  2: while E is not empty  3:    $K\leftarrow$ Covering tree(G)  4:    $\forall (u,v)\in E\wedge (u,v)\notin K$  5:      if $\left(\mathrm{parent}\right(u),v)\in E$  6:        $T\leftarrow T+1$  7:      elif $\left(\mathrm{parent}\right(v),u)\in E$  8:        $T\leftarrow T+1$  9:    $E\leftarrow E-K$  10: return $T/2$

The most widely used triangle-counting algorithms in the literature are the vertex-iterator [7,8] and edge-iterator [7,8] approaches, both of which have a time complexity of $\mathcal{O}(m·d_{\max })$.

In the vertex-iterator approach (see Algorithm 3), for each vertex $u\in V$, the algorithm inspects the adjacency list $N\left(v\right)$ of every vertex $v\in N\left(u\right)$. If there exists a vertex w in the intersection of $N\left(u\right)$ and $N\left(v\right)$, then the triplet $(u,v,w)$ forms a triangle. Arifuzzaman et al. [16] investigate several variants of the vertex-iterator algorithm that employ different vertex ordering strategies to improve performance.

Algorithm 3 Vertex-Iterator [7,8]

Require:  Graph $G=(V,E)$ Ensure:  Triangle Count T  1: $T\leftarrow 0$  2: $\forall u\in V$  3:    $\forall v\in N\left(u\right)$  4:      $X=Intersection\left(N\right(u),N(v\left)\right)$  5:      $T\leftarrow T+X$  6: return $T/6$

In the edge-iterator approach (see Algorithm 4), each edge $(u,v)$ in the graph is examined, and the intersection of $N\left(u\right)$ and $N\left(v\right)$ is computed to identify triangles. A common optimization is the direction-oriented method, which only considers edges $(u,v)$ where $u<v$.

Algorithm 4 Edge-Iterator [7,8]

Require:  Graph $G=(V,E)$ Ensure:  Triangle Count T  1: $T\leftarrow 0$  2: $\forall (u,v)\in E$  3:    $X=Intersection\left(N\right(u),N(v\left)\right)$  4:    $T\leftarrow T+X$  5: return $T/6$

Variants of the edge-iterator algorithm differ primarily in how they perform the intersection $Intersection\left(N\right(u),N(v\left)\right)$. When the two adjacency lists are sorted, MergePath and BinarySearch methods can be applied. The MergePath algorithm performs a linear scan through both lists, counting common elements; Makkar, Bader, and Green [17] present an efficient GPU implementation of this approach. Mailthody et al. [18] further optimize the set intersection using a two-pointer (MergePath) technique.

In contrast, the BinarySearch method uses binary search to check whether each element of the smaller adjacency list appears in the larger one. Another option, Hash, performs set intersection without requiring sorted adjacency lists. A typical implementation initializes a Boolean array of size m with all entries set to false. For each vertex in $N\left(u\right)$, the corresponding position in the array is set to true, and then $N\left(v\right)$ is scanned to check in $\mathsf{\Theta }\left(1\right)$ time whether a match exists.

Chiba and Nishizeki [19] proposed one of the earliest edge-iterator algorithms using hashing for triangle enumeration. Its runtime is $\mathcal{O}\left(a\right(G\left)m\right)$, where $a\left(G\right)$ denotes the arboricity of G, bounded by $a\left(G\right)\le \lceil {(2m+n)}^{\frac{1}{2}}/2\rceil$ [19]. In 2018, Davis [20] rediscovered this method—referred to as tri_simple—in his comparison using SuiteSparse GraphBLAS. Mowlaei [21] introduced a variant of the edge-iterator algorithm employing vectorized sorted set intersection and vertex reordering based on the reverse Cuthill–McKee heuristic.

In 2005, Schank and Wagner [22,23] proposed a fast triangle-counting algorithm called forward (see Algorithm 5), which refines the edge-iterator approach. Rather than computing intersections of full adjacency lists, the forward algorithm uses a dynamic data structure $A\left(v\right)$ to store a subset of the neighborhood $N\left(v\right)$ for each vertex $v\in V$. Initially, all sets $A\left(v\right)$ are empty. For each edge $(u,v)$ with $u<v$, the algorithm computes the intersection of $A\left(u\right)$ and $A\left(v\right)$ to identify triangles and then adds u to $A\left(v\right)$. This strategy significantly reduces the size of the intersections required to find triangles. The algorithm has a running time of $\mathcal{O}(m·d_{\max })$. However, if the vertices are preprocessed and reordered in decreasing order of their degrees—a $\mathsf{\Theta }$$\left(n\log n\right)$ step—the running time of the forward algorithm improves to $\mathcal{O}\left(m^{\frac{3}{2}}\right)$. Ortmann and Brandes [24] provide a survey of triangle-counting algorithms, propose a unifying framework for efficient implementations, and conclude that nearly all triangle-listing variants achieve a running time of $\mathcal{O}(m·a(G\left)\right)$, where $a\left(G\right)$ denotes the arboricity of the graph.

Algorithm 5 Forward Triangle Counting (F) [22,23]

Require:  Graph $G=(V,E)$ Ensure:  Triangle Count T  1: $T\leftarrow 0$  2: $\forall v\in V$  3:    $A\left(v\right)\leftarrow \varnothing$  4: $\forall (u,v)\in E$  5:    if $(u<v)$ then  6:      $\forall w\in A\left(u\right)\cap A\left(v\right)$  7:        $T\leftarrow T+1$  8:      $A\left(v\right)\leftarrow A\left(v\right)\cup \left\{u\right\}$  9: return T

The forward-hashed algorithm [22,23] (also referred to as compact-forward [8]) is a variant of the forward algorithm that employs the hashing technique described earlier to compute intersections of the $A\left(v\right)$ sets (see Algorithm 6). Low et al. [25] propose a linear algebra–based method for triangle counting that avoids matrix multiplication; their approach effectively produces the forward-hashed algorithm.

Algorithm 6 Forward-Hashed Triangle Counting (FH) [22,23]

Require:  Graph $G=(V,E)$ Ensure:  Triangle Count T  1: $T\leftarrow 0$  2: $\forall v\in V$  3:    $A\left(v\right)\leftarrow \varnothing$  4: $\forall (u,v)\in E$  5:    if $(u<v)$ then  6:      $\forall w\in A\left(u\right)$  7:        Hash[w] ← true  8:      $\forall w\in A\left(v\right)$  9:        if Hash[w] then  10:          $T\leftarrow T+1$  11:      $\forall w\in A\left(u\right)$  12:        Hash[w] ← false  13:      $A\left(v\right)\leftarrow A\left(v\right)\cup \left\{u\right\}$  14: return T

3.2. Existing Parallel Algorithms

Although most sequential algorithms tend to run quickly on graphs that fit in main memory, the expansion of the size of the graphs, driven by ongoing technological advancements, presents a challenge. To further accelerate the emergence of parallel version algorithms is inevitable. Algorithms 7–9 are parallel versions of the three most common intersection-based triangle counting methods.

Algorithm 7 Parallel Edge Iterator with Merge Path (EMP)

Require:  Graph $G=(V,E)$ Ensure:  Triangle Count T  1: $T\leftarrow 0$  2: $\forall (u,v)\in E$ do in parallel  3:    $A\leftarrow N\left(u\right)$, $B\leftarrow N\left(v\right)$  4:    $x\leftarrow 0$, $y\leftarrow 0$  5:    while $x<\left|A\right|\wedge y<\left|B\right|$  6:      if $A\left[x\right]==B\left[y\right]$  7:        $T\leftarrow T+1$;  8:        $x\leftarrow x+1$, $y\leftarrow y+1$  9:      else  10:        if $A\left[x\right]<B\left[y\right]$  11:          $x\leftarrow x+1$  12:        else  13:          $y\leftarrow y+1$  14: return $T/6$

Algorithm 8 Parallel Edge Iterator with Binary Search (EBP)

Require:  Graph $G=(V,E)$ Ensure:  Triangle Count T  1: $T\leftarrow 0$  2: $\forall (u,v)\in E$ do in parallel  3:    for $l\in N\left(u\right)$ do  4:      $K\leftarrow N\left(v\right)$  5:      $bottom\leftarrow 0$, $top\leftarrow \left|K\right|$  6:      while $bottom<top$  7:        $mid\leftarrow bottom+(top-bottom)/2$  8:        if $K\left[mid\right]==l$  9:          $T\leftarrow T+1$  10:          break  11:        elif $K\left[mid\right]<l$  12:          $bottom\leftarrow mid+1$  13:        else  14:          $top=mid$  15: return $T/6$

Algorithm 9 Parallel Edge Iterator with Hash (EHP)

Require:  Graph $G=(V,E)$ Ensure:  Triangle Count T  1: $T\leftarrow 0$  2: $\forall (u,v)\in E$ do in parallel  3:    for $w\in N\left(u\right)$  4:      hash(w) = True  5:    for $w\in N\left(v\right)$  6:      if hash(w)  7:        $T\leftarrow T+1$  8:    for $w\in N\left(u\right)$  9:      hash(w) = False  10: return $T/6$

In addition to intersection-based methods, there are several optimized parallel algorithms in the literature. Shun et al. [26] gives a multi-core parallel algorithm for shared memory machines. The algorithm has two steps: in the first step, each vertex is ranked based on degree, and a ranked adjacency list of each vertex is generated, which contains only higher-ranked vertices than the current vertex; the second step counts triangles from the ranked adjacency list for each vertex using merge-path or hash. Parimalarangan et al. [27] present variations of triangle counting algorithms and how they relate to performance on shared-memory platforms. TriCore [28] partitions the graph held in a compressed-sparse row (CSR) data structure for multiple GPUs and uses stream buffers to load edge lists from CPU memory to GPU memory on the fly and then uses binary search to find the intersection. Hu et al. [29] employ a “copy-synchronize-search” pattern to improve the parallel threads efficiency of GPU and mix the computing and memory-intensive workloads together to improve the resource efficiency. Zeng et al. [30] present a triangle counting algorithm that adaptively selects a vertex-parallel and edge-parallel paradigm.

4. Cover-Edge Based Triangle Counting Algorithms

4.1. Cover-Edge Set

Definition 1

(Cover-Edge, Cover-Edge Set, and Covering Ratio). In a graph G, an edge e belonging to a triangle Δ is called a cover edge of Δ. An edge set $S\subseteq E$ is a cover-edge set if it contains at least one cover edge from every triangle in G. The covering ratio is defined as $c=\left|S\right|/\left|E\right|$.

From the above definition, it is clear that the full edge set E trivially qualifies as a cover-edge set. Nevertheless, our objective is to count all triangles more efficiently by considering only a smaller subset of edges. The main challenge, therefore, is to construct a compact cover-edge set that minimizes c. In this work, we propose generating such a set using a breadth-first search (BFS) traversal.

Definition 2

(BFS-Edge). Let r be a designated root vertex of an undirected graph G. The level $L\left(v\right)$ of any vertex v is defined as the distance from r computed via BFS. Based on BFS, edges are classified into three categories:

• Tree-Edges: edges that are part of the BFS tree.
• Strut-Edges: non-tree edges connecting vertices on consecutive levels.
• Horizontal-Edges: non-tree edges connecting vertices on the same level.

Figure 1 shows an example of this edge classification in a BFS tree.

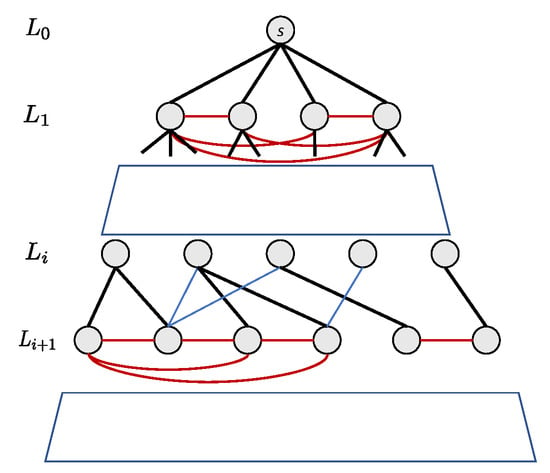
Figure 1. Illustration of edge classification in a BFS spanning tree. Tree-edges are black, strut-edges are blue, and horizontal-edges are red.

Lemma 1.

Every triangle $\{u,v,w\}$ in a graph contains at least one horizontal edge in a BFS tree rooted at any vertex.

Proof. 

Assume, for the sake of contradiction, that a triangle contains no horizontal edges. Then all edges are either tree edges or strut edges, which change the BFS level by $\pm 1$.

For the triangle to form a closed cycle, the number of edges that increase the level must equal the number that decrease it. This implies the cycle length must be even. Since a triangle has length 3, this is a contradiction.

Hence, each triangle must include at least one horizontal edge.    □

Theorem 1

(Cover-Edge Set Construction). The set of all horizontal edges in a BFS tree forms a valid cover-edge set.

Proof. 

By Lemma 1, each triangle contains at least one horizontal edge. Therefore, collecting all horizontal edges from a BFS traversal ensures that every triangle in the graph has at least one of its edges in this set, satisfying the definition of a cover-edge set.    □

Accordingly, we define the BFS-CES cover-edge set as the collection of all horizontal edges obtained from a BFS traversal. This set is a subset of E and is generally significantly smaller than the full edge set, enabling more efficient triangle counting.

4.2. Cover-Edge Triangle Counting (CETC)

In this subsection, we describe the CETC algorithm, which identifies all triangles in a graph by leveraging a cover-edge set generated via breadth-first search.

Lemma 2.

Every triangle $\{u,v,w\}$ contains either one or three horizontal edges.

Proof. 

From Lemma 1, the triangle’s three edges consist of an even number of tree-edges and strut-edges. This implies that each triangle contains either 0 or 2 tree/strut edges.

If there are 0 tree/strut edges, all three edges are horizontal, as no tree or strut edges are present. If there are 2 tree/strut edges, then exactly one edge must be horizontal to connect the remaining two vertices.

Therefore, each triangle contains either one or three horizontal edges.    □

The sequential triangle counting method, CETC-Seq, is outlined in Algorithm 10. The algorithm maintains a counter T (line 1) to store the total number of triangles. To generate the cover-edge set, a BFS is performed from any unvisited vertex, determining the level $L\left(v\right)$ of each vertex in its connected component (lines 2–3).

Next, the algorithm iterates over all edges, selecting horizontal edges in a direction-oriented manner (lines 4–8, line 5). For each vertex w in the intersection of the neighborhoods of the horizontal edge’s endpoints (line 6), two conditions are checked to ensure the triangle $(u,v,w)$ is counted only once (line 7):

• If $L\left(u\right)\ne L\left(w\right)$, then $(u,v)$ is the single horizontal edge in the triangle.
• If $L\left(u\right)=L\left(w\right)$, then $(u,v)$ is one of three horizontal edges in the triangle.

An additional ordering constraint $v<w$ guarantees uniqueness. When these conditions are satisfied, T is incremented (line 8).

This procedure ensures that every triangle is counted exactly once without redundancy.

Theorem 2

(Correctness). Algorithm 10 correctly counts all triangles in a graph G.

Algorithm 10 CETC: Cover-Edge Triangle Counting (CETC-Seq)

Require:  Graph $G=(V,E)$ Ensure:  Triangle Count T  1: $T\leftarrow 0$  2: $\forall v\in V$  3:    if v unvisited, then BFS(G, v)  4: $\forall (u,v)\in E$  5:    if $\left(L\right(u)\equiv L(v\left)\right)\wedge (u<v)$                                ▹$(u,v)$ is horizontal  6:      $\forall w\in N\left(u\right)\cap N\left(v\right)$  7:        if $(L\left(u\right)\ne L\left(w\right))\vee \left(\left(L\right(u)\equiv L(w\left)\right)\wedge (v<w)\right)$ then  8:          $T\leftarrow T+1$  9: return T

Proof. 

Lemma 2 classifies triangles into two types: (1) triangles with one horizontal edge whose endpoints share a level while the apex is at a different level, and (2) triangles where all three vertices lie on the same level.

Consider a triangle $\{v_a,v_b,v_c\}$. Without loss of generality, let $(v_a,v_b)$ be horizontal. In the first case, the triangle is uniquely determined by this horizontal edge and an apex vertex from the intersection of the endpoints’ neighborhoods. Algorithm 10 increments T by 1 when such a triangle is found.

In the second case, all vertices are at the same level ($L\left(v_a\right)=L\left(v_b\right)=L\left(v_c\right)$). The algorithm increments T only when $v_a<v_b<v_c$, ensuring each triangle is counted exactly once.

Thus, Algorithm 10 accurately counts all triangles in G.    □

The time complexity of Algorithm 10 can be analyzed as follows. BFS computation, including determining vertex levels and identifying horizontal edges, requires $\mathcal{O}(n+m)$ time.

Since there are at most $\mathcal{O}\left(m\right)$ horizontal edges, computing the intersection of neighborhoods for each horizontal edge can be done in $\mathcal{O}\left(d_{\max }\right)$ time, where $d_{\max }$ is the maximum degree of any vertex.

Hence, the overall time complexity of CETC-Seq is $\mathcal{O}(m·d_{\max })$.

4.3. Variants of CETC-Seq

4.3.1. CETC Forward Exchanging Triangle Counting Algorithm (CETC-Seq-FE)

The overall performance of CETC-Seq is closely related to the coverage ratio c. A higher coverage ratio results in fewer reduced edges, which will increase the actual running time of the algorithm. Therefore, after completing BFS, the selection of an appropriate algorithm can be based on c. Algorithm 11 presents the variant of CETC-Seq that dynamically selects the most suitable approach based on c, called CETC-Seq-FE. Initially, it calculates c using the results of BFS if the value of c is below a specified threshold (the value of c should be at least less than $\left(\frac{m-n+1}{m}\right)$. After comparing the performance of Algorithms 5 and 10, we set this threshold at 0.7 in our experiments), and we continued using Algorithm 10; otherwise, Algorithm 5 was chosen. Taking into account the analyses presented in Algorithms 5, 10 and 11 maintains a time complexity of $\mathcal{O}\left(m^{1.5}\right)$.

Algorithm 11 CETC Forward Exchanging (CETC-Seq-FE)

Require: Graph $G=(V,E)$ Ensure: Triangle Count T  1: $T\leftarrow 0$  2: $\forall v\in V$  3:    if v unvisited, then BFS(G, v)  4: Calculate c based on the BFS results  5: If $(c<threshold)$  6:   $T\leftarrow CETC-Seq\left(G\right)$                                 ▹ Algorithm 10  7: Else  8:    $T\leftarrow TC\_forward\left(G\right)$                                 ▹ Algorithm 5  9: return T

4.3.2. CETC Split Triangle Counting Algorithm (CETC-Seq-S)

Algorithm 12 presents a variant of CETC-Seq, denoted CETC-Seq-S. Like Algorithm 10, this algorithm uses BFS to assign a level to each vertex (lines 2–3).

Algorithm 12 CETC Split Triangle Counting (CETC-Seq-S)

Require:  Graph $G=(V,E)$ Ensure:  Triangle Count T  1: $T\leftarrow 0$  2: $\forall v\in V$  3:    if v unvisited, then BFS(G, v)  4: $\forall (u,v)\in E$  5:    if $\left(L\right(u)\equiv L(v\left)\right)$ then                         ▹$(u,v)$ is horizontal  6:      Add $(u,v)$ to $G_0$  7:    else  8:      Add $(u,v)$ to $G_1$  9: $T\leftarrow TC\_forward-hashed\left(G_0\right)$                     ▹ Algorithm 6  10: $\forall u\in V_{G_1}$  11:    $\forall v\in N_{G_1}\left(u\right)$  12:      Hash[v] ← true  13:    $\forall v\in N_{G_0}\left(u\right)$  14:      if $(u<v)$ then  15:        $\forall w\in N_{G_1}\left(v\right)$  16:          if Hash[w] then  17:            $T\leftarrow T+1$  18:    $\forall v\in N_{G_1}\left(u\right)$  19:      Hash[v] ← false  20: return T

In lines 4–8, the edge set E is partitioned into two disjoint subsets: $E_0$, containing horizontal edges with both endpoints on the same level, and $E_1$, consisting of the remaining edges that span levels. This defines two subgraphs: $G_0=(V,E_0)$ and $G_1=(V,E_1)$, where $E=E_0\cup E_1$ and $E_0\cap E_1=\varnothing$. Triangles fully contained in $G_0$ are counted using one method, while triangles involving edges in $G_1$ are counted using another.

For $G_0$, the subgraph of horizontal edges, triangles are efficiently counted using the forward-hashed method (line 9). For triangles not entirely in $G_0$, the algorithm relies on $G_1$ and a hash-based intersection of adjacency lists (lines 10–19). Specifically, edges in $G_0$ are used to select candidate triangles, and intersections are performed using the adjacency lists in $G_1$. The correctness of this approach follows directly from the proof of cover-edge triangle counting given in Section 4.2.

Thus, Algorithm 12 is a hybrid algorithm: it partitions the edge set and applies two different counting strategies, while maintaining the correctness guarantees of the original CETC approach.

Regarding time complexity, the running time is dominated by the maximum of the forward-hashed method and Algorithm 10. For each edge $(u,v)$, hash-based intersections require $min\left(d\right(u),d(v\left)\right)$ time, where $d\left(u\right)$ and $d\left(v\right)$ are the vertex degrees. Across all edges, this results in an expected running time of $\mathcal{O}\left(m·a\left(G\right)\right)$, where $a\left(G\right)$ denotes the arboricity of G.

As with the forward-hashed approach, preprocessing the graph by reordering vertices in decreasing degree order in $\mathsf{\Theta }\left(n\log n\right)$ time often improves performance in practice.

4.3.3. CETC-Split Recursive Triangle Counting Algorithm (CETC-Seq-SR)

Algorithm 13 is similar to Algorithm 12. The only difference is that for the subgraph $G_0$ consisting of the horizontal edges, if its size is larger than the given threshold value, we will recursively call the algorithm to further reduce the graph size (line 9). If the size of $G_0$ is not larger than the given threshold value, we will directly call Algorithm 6 to obtain the total number of triangles in $G_0$ (line 11). We used the same threshold value of 0.7 in the experiment as described in Algorithm 11. The idea behind the recursive call is that we can quickly count the triangles containing edges across both $G_0$ and $G_1$, and then we can safely remove all the edges in $G_1$ to reduce the graph size. Finally, Algorithm 6 will focus on a smaller graph whose edges may contain multiple triangles.

Algorithm 13 CETC-Split Recursive Triangle Counting (CETC-Seq-SR)

Require:  Graph $G=(V,E)$ Ensure:  Triangle Count T  1: $T\leftarrow 0$  2: $\forall v\in V$  3:    if v unvisited, then BFS(G, v)  4: $\forall (u,v)\in E$  5:    if $\left(L\right(u)\equiv L(v\left)\right)$ then                                           ▹$(u,v)$ is horizontal  6:      Add $(u,v)$ to $G_0$  7:    else  8:      Add $(u,v)$ to $G_1$  9: if (size of $G_0>$ threshold) then  10:    $T\leftarrow CESR\left(G_0\right)$  11: else  12:    $T\leftarrow TC\_forward-hashed\left(G_0\right)$                                   ▹ Algorithm 6  13: $\forall u\in V_{G_1}$  14:    $\forall v\in N_{G_1}\left(u\right)$  15:      Hash[v] ← true  16:    $\forall v\in N_{G_0}\left(u\right)$  17:      if $(u<v)$ then  18:        $\forall w\in N_{G_1}\left(v\right)$  19:          if Hash[w] then  20:            $T\leftarrow T+1$  21:    $\forall v\in N_{G_1}\left(u\right)$  22:      Hash[v] ← false  23: return T

4.4. Parallel CETC Algorithm on Shared-Memory (CETC-SM)

In Section 3, we introduced three commonly employed intersection-based methods: merge-path, binary search, and hash, alongside their corresponding parallel version as outlined in Algorithms 7–9.

The fundamental concept behind the proposed parallel algorithms is to calculate the intersection of neighbor lists of two endpoints of any $(u,v)$ in parallel, which will significantly increase the performance.

Algorithm 14 demonstrates the parallelization of the Covering-Edge triangle counting algorithm for shared-memory. In the context of the PRAM (Parallel Random Access Machines) model, both parallel BFS and parallel sorting have been shown to achieve scalable performance [31]. For set intersection operations on a single edge, it is imperative that the computation remains well below $m^{0.5}$ [23], particularly when dealing with large input graphs, where p represents the total number of processors. Consequently, the total work, which is $\mathcal{O}\left(m^{1.5}\right)$, can be evenly distributed among p processors. As a result, CETC-SM exhibits a parallel time complexity of $\mathcal{O}\left(\frac{m^{1.5}}{p}\right)$, ensuring scalability as the number of parallel processors increases.

Algorithm 14 Shared Memory Parallel Cover-Edge Triangle Counting (CETC-SM)

Require:  Graph $G=(V,E)$ Ensure:  Triangle Count T  1: $c_1,c_2\leftarrow 0$  2: Run Parallel BFS on G and mark the level.  3: $\forall (u,v)\in E$ do in parallel  4:    if $\left(L\right(u)\equiv L(v\left)\right)\wedge (u<v)$                                                        ▹$(u,v)$ is horizontal  5:      $\forall w\in N\left(u\right)\cap N\left(v\right)$  6:        if ($L\left(w\right)\ne L\left(u\right)$) then  7:          $c_1\leftarrow c_1+1$  8:        else  9:          $c_2\leftarrow c_2+1$  10: $T\leftarrow c_1+c_2/3$  11: return T                                                                                    ▹ See Algorithm 10

5. Open-Source Evaluation Framework

In the preceding sections, we presented all sequential and shared-memory algorithms from the literature known to the authors, plus our novel approaches. In this section, we introduce our open-source framework designed to integrate comprehensive triangle counting implementations.

There is a lack of a unified framework that encompasses all implementations, which is important for researchers to conduct performance comparisons between existing algorithms and to assess their efficacy against newly proposed methods. Consequently, we have developed a comprehensive open-source framework to solve this problem. This framework is designed to ensure a thorough evaluation of triangle counting algorithms. It includes implementations of 22 sequential methods and 11 parallel methods on shared-memory, as a complete set of what is found in the literature.

Each triangle counting routine takes a single argument: a pointer to the graph stored in compressed sparse row (CSR) format. The input graph is treated as read-only. Any auxiliary arrays, pre-processing steps, or additional data structures required by an implementation are fully accounted for in its cost. Implementations must handle memory carefully, ensuring that all dynamically allocated memory is properly freed before returning the result, so as to avoid memory leaks.

The output of each routine is an integer representing the total number of triangles detected in the graph. Each algorithm is executed ten times, and the mean running time is reported. To minimize variance in experiments on random graphs, the same graph instance is used across all trials. Sequential algorithms are implemented in plain C without explicit parallelization, whereas parallel algorithms leverage OpenMP for concurrency. Equal coding effort and style are applied across all implementations to ensure a fair comparison.

Here, we list algorithms subjected to the experiments given in the next section, including both established methods and newly proposed algorithms. Algorithms ending with P indicate that we have also developed parallel versions.

• W/WP: Wedge-checking/Parallel version
• WD/WDP: Wedge-checking (direction-oriented)/Parallel version
• EM/EMP: Edge Iterator with MergePath for set intersection/Parallel version
• EMD/EMDP: Edge Iterator with MergePath for set intersection (direction-oriented)/Parallel version
• EB/EBP: Edge Iterator with BinarySearch for set intersection/Parallel version
• EBD/EBDP: Edge Iterator with BinarySearch for set intersection (direction-oriented)/Parallel version
• ET/ETP: Edge Iterator with partitioning for set intersection/Parallel version
• ETD/ETDP: Edge Iterator with partitioning for set intersection (direction-oriented)/Parallel version
• EH/EHP: Edge Iterator with Hashing for set intersection/Parallel version
• EHD/EHDP: Edge Iterator with Hashing for set intersection (direction-oriented)/Parallel version
• F: Forward method
• FH: Forward method with hashing
• FHD: Forward method with hashing and degree-based vertex ordering
• TS:tri_simple (Davis [20])
• LA: Linear algebra-based method (CMU [25])
• IR: Treelist from Itai-Rodeh [7]
• CETC-Seq/CETC-SM: Cover Edge Triangle Counting (Bader [32])/Parallel version on shared-memory
• CETC-Seq-D: Cover Edge Triangle Counting with degree-ordering (Bader [32])
• CETC-Seq-FE: Cover Edge Forward Exchanging Triangle Counting
• CETC-Seq-S: Cover Edge Split Triangle Counting (Bader [33])
• CETC-Seq-SD: Cover Edge Split Triangle Counting with degree-ordering (Bader [33])
• CETC-Seq-SR: Cover Edge-Split Recursive Triangle Counting

6. Experimental Results

In our experiments, we conducted a comprehensive evaluation of both sequential and shared-memory parallel triangle counting algorithms across 24 diverse graphs, including real-world datasets from SNAP and synthetic RMAT graphs. The sequential experiments analyzed the effects of direction-oriented (DO) optimization, hash-based methods, forward algorithms and variants, and the novel cover-edge sequential algorithms (CETC-Seq and its extensions).

DO optimization consistently reduced redundant operations, yielding up to $3.6\times$ speedup, while hash-based methods further improved performance, with speedups up to $5.4\times$. The forward algorithm and its hashed and degree-ordered variants demonstrated exceptional efficiency, achieving speedups as high as $29.1\times$. Our novel CETC-Seq variants, especially CETC-Seq-S and CETC-Seq-SD, combined BFS-based preprocessing, hash-based set intersections, degree ordering, and recursive strategies to further minimize unnecessary checks, achieving speedups up to $24\times$.

Analysis revealed that the algorithm’s performance is closely related to the covering ratio c, although low-degree, large-diameter road networks showed limited gains. These results suggest that graph topology plays a major role in determining the effectiveness of each optimization, with dense and highly clustered graphs benefiting most from the proposed techniques.

For shared-memory parallelization, we evaluated algorithms using 32 to 224 threads. Binary search and hash-based methods achieved the highest scalability, with EBP and EHDP showing superior speedups, up to $233\times$ on large graphs. Optimal performance depended on graph topology, size, and the number of threads, with smaller graphs favoring sequential methods due to parallelization overhead.

Overall, the experiments highlight that combining algorithmic optimizations—DO, hashing, degree ordering, forward methods, and CETC-Seq variants—can significantly enhance triangle counting performance. Parallelization benefits are maximized when algorithm structures and graph characteristics align with the available hardware resources.

In the following subsections, we will give the details of the experimental results.

6.1. Platform Configuration

We use the Intel Development Cloud for benchmarking our results on a GNU/Linux node. The compiler is Intel(R) one API DPC++/C++ Compiler 2023.1.0 (2023.1.0.20230320), and ‘-O2’ is used as a compiler optimization flag. We use a high-core-count Intel Xeon processor (Sapphire Rapids launched Q1’23) with DDR5 memory for both sequential and parallel implementations. The node is a dedicated 2.00 GHz 56-core (112 thread) Intel(R) Xeon(R) Platinum 8480+ processor (formerly known as Sapphire Rapids) with 105M cache and 1024 GB of DDR5 RAM.

6.2. Data Sets

We utilize a diverse set of graphs in our experiments. The real-world datasets are sourced from the Stanford Network Analysis Project (SNAP) (available from http://snap.stanford.edu/) while the synthetic graphs are generated using large Graph500 RMAT graphs [34] with parameters $a=0.57$, $b=0.19$, $c=0.19$, and $d=0.05$, following the IARPA AGILE benchmark configuration. An overview of all 24 graphs in our collection is provided in Table 1.

Table 1. Data sets for the experiments.

Graph Name	n	m	# Triangles	c (%)
RMAT 6	64	1024	9100	93.8
RMAT 7	128	2048	18,855	90.9
RMAT 8	256	4096	39,602	87.6
RMAT 9	512	8192	86,470	87.2
RMAT 10	1024	16,384	187,855	82.8
RMAT 11	2048	32,768	408,876	81.1
RMAT 12	4096	65,536	896,224	77.5
RMAT 13	8192	131,072	1,988,410	74.9
RMAT 14	16,384	262,144	4,355,418	70.5
RMAT 15	32,768	524,288	9,576,800	68.4
RMAT 16	65,536	1,048,576	21,133,772	65.5
RMAT 17	131,072	2,097,152	46,439,638	62.8
karate	34	78	45	35.9
amazon0302	262,111	899,792	717,719	44.2
amazon0312	400,727	2,349,869	3,686,467	52.4
amazon0505	410,236	2,439,437	3,951,063	52.7
amazon0601	403,394	2,443,408	3,986,507	52.8
loc-Brightkite	58,228	214,078	494,728	43.2
loc-Gowalla	196,591	950,327	2,273,138	50.8
roadNet-CA	1,971,281	2,766,607	120,676	14.5
roadNet-PA	1,090,920	1,541,898	67,150	14.6
roadNet-TX	1,393,383	1,921,660	82,869	14
soc-Epinions1	75,888	405,740	1,624,481	53.3
wiki-Vote	8297	100,762	608,389	54.3

The values of c exhibit substantial variation across different graphs, ranging from 0.90 to 0.14. Smaller c values signify a higher potential for avoiding fruitless searches, thereby enhancing the efficiency of our approach.

6.3. Results and Analysis of Sequential Algorithms

6.3.1. Effect of Direction-Oriented Method on Sequential Algorithms

The DO performance optimization is a pivotal strategy in triangle counting, designed to mitigate redundant calculations. In this section, we explore five distinct duplicate counting algorithms, each accompanied by its corresponding DO variant. The results presented in Figure 2 vividly demonstrate the speedup achieved by the DO counterparts compared to their duplicate counting versions.

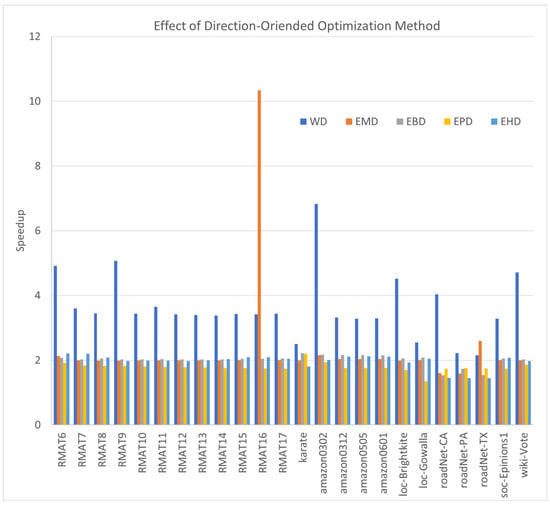
Figure 2. The speedups of direction-oriented optimization compared with the duplicate counting counterparts.

Evidently, across all scenarios, the majority of DO algorithms yield a speedup of at least two-fold. Particularly, the WD algorithm stands out with a higher average speedup of 3.637, surpassing the performance gains of other algorithms. EBD exhibits a speedup of $2.015\times$, closely followed by EMD at $2.005\times$, EHD at $1.965\times$, and ETD at $1.784\times$.

DO optimization primarily constitutes an algorithmic enhancement, resulting in a reduction in the overall number of operations. So, for any graph, it can improve the performance, and our experimental results also confirm its efficiency. However, the practical performance gains can be impacted by various factors, including memory access patterns and cache utilization. Our comprehensive experiments, conducted on diverse graphs using a range of algorithms, underscore the substantial performance enhancements achievable through DO optimization.

In summary, as a Pareto optimization, DO optimization is efficient for eliminating duplicate triangle counting and significantly improving overall performance.

6.3.2. Effect of Hash Method on Sequential Algorithms

Similar to the DO optimization, the hash-based optimization proves highly efficient in most scenarios. In Figure 3, we illustrate the speedup achieved by Hash methods compared to non-hash implementations. The first comparison showcases the speedup of the Hash set intersection (EH) compared with the non-hashed method (EM), while the second presents the speedup of (FH) compared with (F).

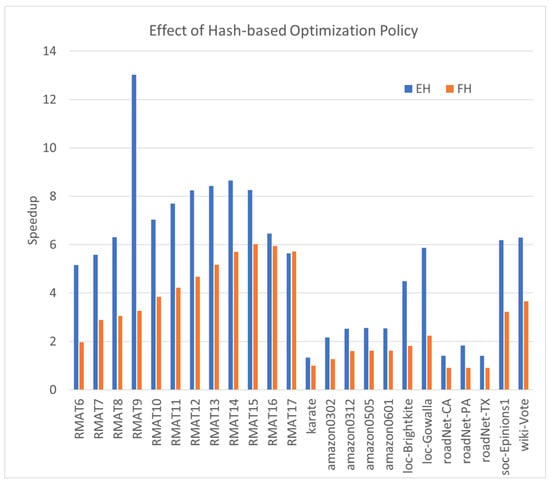
Figure 3. The speedups of hash-based optimization compared with the MergePath method.

The average speedup of EH is $5.4\times$, and for FH, it is $3.0\times$, underscoring the effectiveness of the hash-based optimization. Notably, the results reveal that, for more efficient algorithms, like F, the speedup is slightly lower than that of less efficient algorithms, such as EM.

However, we observe several exceptions. For roadNet-CA, roadNet-PA, and roadNet-TX, the Hash algorithm FH performs worse than the non-hashed algorithm F. This is attributed to the unique topologies of these graphs, characterized by relatively long diameters and very few neighbors for each vertex. As the intersection sets are relatively small, the MergePath operation on small sets proves more efficient than the Hash method, given the relatively high hash table overhead for very small sets. Therefore, the Hash optimization method remains efficient, but not for some special topologies and diameter graphs, as the hash table overhead may not compensate for small intersection sets.

6.3.3. Effect of Forward Algorithm and Its Variants

Our experimental results underscore the effectiveness of the Forward algorithm and its variants as robust algorithms for enhancing the performance of triangle counting. In Figure 4, we present the speedup achieved by three algorithms—namely, the forward algorithm (F), the hashed forward algorithm (FH), and the hashed forward algorithm with degree ordering (FHD)—in comparison with the traditional MergePath algorithm.

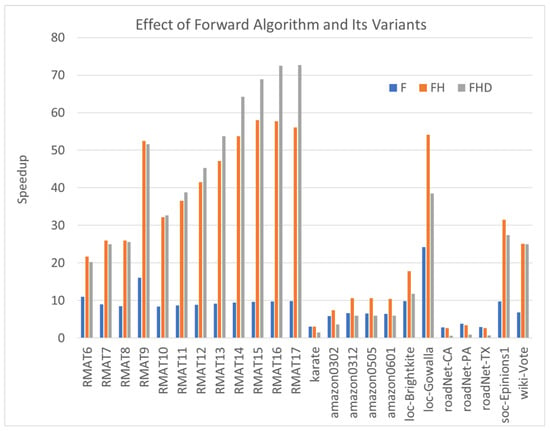
Figure 4. The speedups of Forward algorithm and its variants compared with the MergePath method.

The observed performance improvement is remarkably significant. Specifically, F achieves a $8.6\times$ speedup, while FH and FHD achieve even more substantial speedups at $28.7\times$ and $29.1\times$, respectively. These results indicate that reducing the sizes of intersection sets and employing hash functions and degree ordering can collectively contribute to performance enhancements.

Similar to the hash method, degree ordering demonstrates substantial performance improvements across various scenarios. However, for roadNet-CA, roadNet-PA, and roadNet-TX, the hash-based algorithm FH performs worse than the non-hashed algorithm F, and the performance of degree ordering FD is inferior to that of MergePath. This arises from the fact that most vertices in these graphs possess similar and small numbers of degrees. Consequently, reordering the vertices has minimal impact on intersection performance and introduces additional overhead. Despite these exceptions, the combined approach of reducing intersection set sizes, hash functions, and degree ordering consistently enhances performance for a wide range of cases.

6.3.4. Effect of CETC-Seq Algorithm and Its Variants

The fundamental principle underlying the cover-edge method is minimizing unnecessary set intersection operations. In Figure 5, we illustrate the impact of the CETC-Seq algorithm and its variants, namely CETC-Seq-D, CETC-Seq-FE, CETC-Seq-S, CETC-Seq-SD, CETC-Seq-SR.

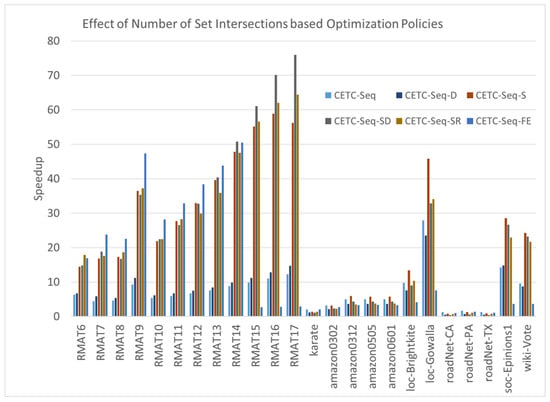
Figure 5. The speedups of CETC-Seq and its variants compared with the MergePath method.

Compared to the MergePath method, CETC-Seq demonstrates an average speedup of $7.4\times$. CETC-Seq-D achieves a slightly lower average speedup of $7.39\times$, mainly due to its low performance on the road networks.

CETC-Seq-FE combines CETC-Seq and F in a unique manner. It employs CETC-Seq for large graphs or when the c value is small; otherwise, it uses F. This switching approach yields an average speedup of $14.6\times$. The rationale behind CETC-Seq-FE lies in dynamically selecting the most suitable algorithm based on its compatibility with the characteristics of the graphs.

CETC-Seq-S splits a graph into two parts based on the vertex levels marked by a BFS pre-processing and applies CETC-Seq and F on each part. The performance of CETC-Seq-S achieves a speedup of $23.4\times$. This represents a more efficient combination method. Additionally, when we integrate degree ordering into CETC-Seq-S, the resulting CETC-Seq-SD algorithm performs slightly better than CETC-Seq-S, achieving a speedup of $24.0\times$. This result highlights that degree ordering works well with the F algorithm. The reason is that degree ordering can further reduce the size of intersecting sets of the F algorithm. CETC-Seq-SR employs the recursive method to simplify the problem. For a large graph, it recursively applies CETC-Seq to minimize set intersections, counting only triangles including non-horizontal edges, and finally applies F to the smaller graph consisting of all horizontal edges that are known to include all the other triangles. CETC-Seq-SR achieves an average speedup of $22.7\times$.

Notably, CETC-Seq exhibits low performance on certain graphs compared to other methods. The relatively high overhead of BFS preprocessing in CETC-Seq, compared with set intersection, contributes to the low efficiency. A breakdown time analysis reveals that the percentages of BFS processing time are 60% of the total execution time. In the case of a long-diameter graph where each vertex has a small number of neighbors, the overhead of BFS becomes large despite its time complexity of $\mathcal{O}\left(m\right)$ compared to the time complexity of total set intersections at $\mathcal{O}\left(m^{1.5}\right)$. This overhead becomes particularly impactful when the neighbors of each vertex are limited, and the graph diameter is large. For road networks characterized by very small vertex degrees, where degree ordering introduces additional overhead without providing any significant benefit, CETC-Seq-D experiences further performance degradation.

6.3.5. Comprehensive Sequential Algorithms Comparison

The execution times of the sequential algorithms (in seconds) are presented in Figure 6.

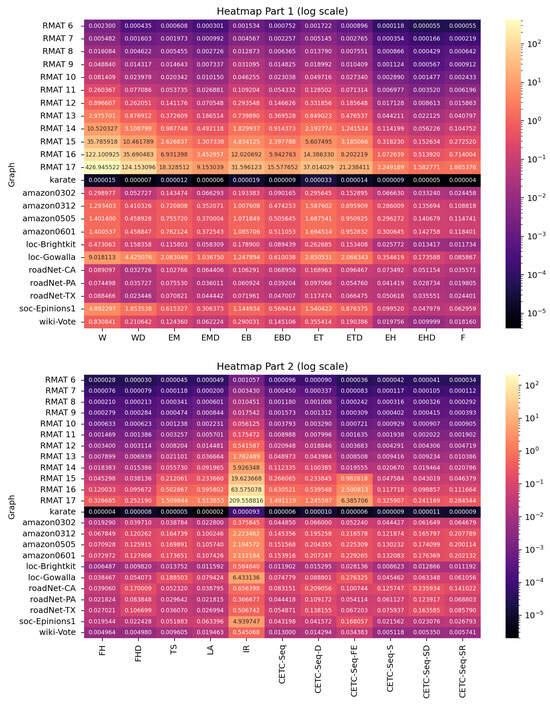
Figure 6. Execution time (in seconds) for sequential algorithms.

While optimal in time complexity, the IR spanning tree-based triangle counting algorithm exhibits nearly the slowest performance among all the compared algorithms. This is due to the involvement of spanning tree generation, removal of tree edges, and regeneration of a smaller graph in each iteration. Although these operations can be completed in $\mathcal{O}\left(m\right)$ time, the cost is relatively high in terms of practical performance.

The W wedge-checking-based triangle counting algorithm often performs poorly. This is primarily because most graphs are sparse, resulting in most wedge-checking operations being fruitless, or most wedges cannot form a triangle. For example, for the RMAT 6 graph, the percentage of wedges/triangles is 0.53%. For the RMAT 14 graph, the percentage reduces to 0.009%. This makes most of the checks useless for counting triangles. W can demonstrate better performance only when most of the graph’s wedges can form triangles. This scenario is not common in most practical applications.

The algorithmic structures of EM (Edge Merge Path), EB (Edge Binary Search), ET (Edge Partitioning), and EH (Edge Hash) are very similar to each other, differing primarily in the set intersection methods they employ. Merge path requires pre-sorted adjacency lists, enabling it to compare the two adjacency lists of a given edge $(u,v)$ in $d\left(u\right)+d\left(v\right)$ time. This is optimal because we have to check every neighbor. Binary search method EB searches each vertex in a small adjacency list (e.g., $N\left(u\right)$) in a larger adjacency list (e.g., $N\left(v\right)$) in $d\left(u\right)\times \log \left(d\right(v\left)\right)$ time. ET is a specific case of EB and involves additional operations to find the midpoint of the two adjacency lists. Thus, from an algorithmic analysis perspective, ET’s performance will always be worse than EB’s. However, EB and ET can leverage parallelism effectively to improve performance. Our parallel results demonstrate that they may outperform EM. EH takes $min\left(d\right(u),d(v\left)\right)<d\left(u\right)+d\left(v\right)$ operations to find triangles, and the Hash method does not require pre-sorting adjacency lists, making it better than EM and often the best performer among the four methods.

TS (Triangle Summation) and LA (Linear Algebra) are two linear algebra-based methods. They can count the total number of triangles, but cannot list all the triangles. Their performance improvements depend on optimizing formulas and architecture-related methods. The advantage of such methods lies in their ability to directly apply results from linear algebra theory and leverage highly optimized numerical techniques integrated into linear algebra libraries. Their performance is often superior to that of the EM method.

F (Forward) often demonstrates excellent performance in most scenarios but is inherently sequential. As we discussed earlier, F dynamically generates two sets that are much smaller than the size of the original adjacency lists. It is based on the DO method, which further reduces the fruitless checks in triangle counting operations. Additionally, pre-sorting vertices in non-increasing degrees enhances memory access locality and cache hit ratios. As one can observe, F effectively reduces the operations that cannot find new triangles. The results of FH and FHD show that the performance is further improved when Hash is used.

CETC-Seq and its variants introduce another perspective for eliminating fruitless searches in triangle counting. First, it skips unnecessary edge searches based on a quick BFS operation that can be completed in $\mathcal{O}(m+n)$ time. By leveraging the directed-oriented technique, CETC-Seq achieves a further significant reduction in the fruitless searches during triangle counting. It is competitive with the fastest approaches and may be useful when the BFS preprocessing overhead can be negligible. CETC-Seq-S and its variants further optimize the performance with Hash, degree ordering and recursive method.

We assigned rank values to each test case and calculated the average rank value. The performance from high to low are FH, CETC-Seq-S, FHD, CETC-Seq, LA, F, EHD, TS, CETC-Seq-SR, CETC-Seq-SD, CETC-Seq-FE, EH, CETC-Seq-D, EMD, EBD, ET, WD, EB, EM, ETD, W, IR.

We can say the top four set intersection-based triangle counting algorithms include our novel CETC-Seq-S and CETC-Seq algorithms. The performance of CETC-Seq-S with an average rank of 2.80 is slightly worse than that of FH with an average rank of 2.0. The average rank of FHD is 4.6 and CETC-Seq is 6.4.

6.3.6. Influence of the c Value on the Performance of the Novel Algorithm

Building upon the definition of our novel algorithm, its performance should be highly related to the covering ratio c.

A noteworthy trend is identified when evaluating the results, particularly concerning the RMAT graphs. Our finding reveals that the forward algorithm and its variants tend to perform the fastest. As the scale of the RMAT graph increases, the parameter c decreases, indicating a more substantial removal of fruitless checks after BFS. Under these conditions, our novel method demonstrates greater efficiency compared to the F algorithms.

These observations validate our hypothesis that the performance of our new algorithm is significantly correlated with the covering ratio c. As c decreases, performance improves.

A closer examination of the road network graphs (roadNet-CA, roadNet-PA, roadNet-TX) highlights their distinct behavior compared to the other datasets. Unlike social networks, road networks typically consist of low-degree vertices (e.g., many vertices with degree four) and have large diameters. Although the covering ratio for these graphs is below 15%, the performance gains from our approach are limited due to this low value of c. This observation indicates that a smaller covering ratio does not necessarily translate into higher performance.

6.4. Results and Analysis of Parallel Algorithms on Shared-Memory

The execution times of the parallel algorithms (in seconds) are presented in Figure 7 for 32 threads and in Figure 8 for 224 threads.

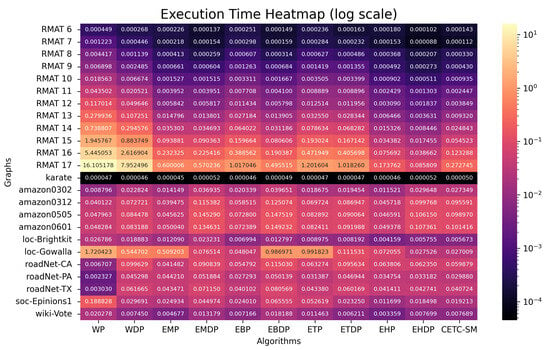
Figure 7. Execution time (in seconds) for shared-memory parallel algorithms (32 threads).

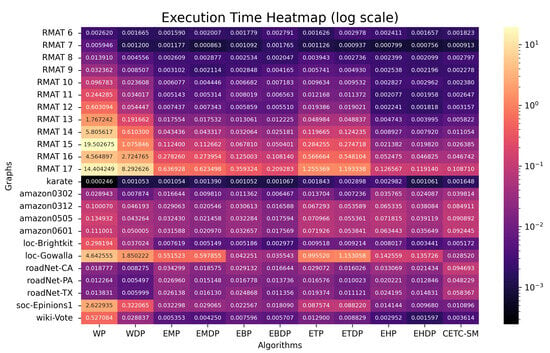
Figure 8. Execution time (in seconds) for shared-memory parallel algorithms (224 threads).

6.4.1. Performance Utilizing 32 Threads

While F and its variants excel as sequential algorithms, they are inherently sequential and cannot be parallelized. In this section, we focus on algorithms conducive to parallelization to showcase the speedups achieved with parallel methods. Figure 9 illustrates the speedups of various parallel algorithms compared to their corresponding sequential counterparts, employing 32 threads.

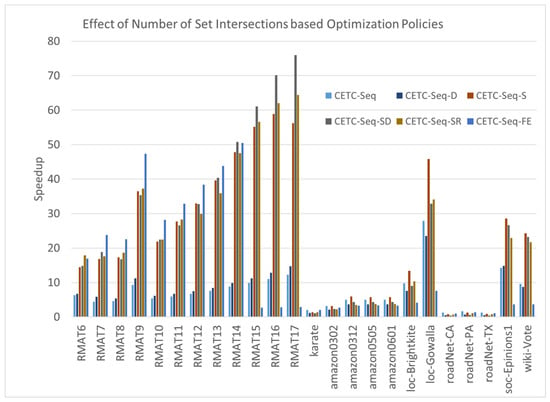
Figure 9. The speedups of parallel optimization methods compared with their sequential counterparts using 32 threads.

The average speedups are as follows: WP is $10.5\times$; WDP is $7.5\times$; EMP is $13.6\times$; EMDP is $8.3\times$; EBP is $23.3\times$; EBDP is $19.3\times$; ETP is $16.2\times$; ETDP is $10.8\times$; EHP is $6.6\times$; EHDP is $5.0\times$; CETC-SM is $3.9\times$. The results affirm that parallel optimization significantly improves performance.

However, certain scenarios highlight limitations. For instance, in the case of the small-sized graph “karate”, all parallel algorithms fail to exhibit performance improvements. This can be attributed to the inherent overhead of the OpenMP parallel method, which outweighs the benefits for very small graphs. A similar pattern is observed for the graph RMAT 6, where three parallel methods—EHP, EHDP, and CETC-SM—show no performance improvement. As previously mentioned, the baseline algorithms EH, EHD, and CETC-Seq have already demonstrated high performance, and the parallel overhead for small graphs nullifies the potential benefits of parallelization.

6.4.2. Performance Utilizing All System Threads

When we harness our experimental system’s full parallel processing capacity, we can execute our OpenMP parallel programs with 224 threads. Based on the results in Figure 8, the performance from high to low are EHDP, EBDP, EMDP, EHP, EBP, CETC-SM, EMP, ETDP, WDP, ETP, WP.

The presented results highlight that not only can hash and binary search deliver commendable parallel performance by minimizing operations per parallel thread, but also the application of degree ordering proves effective in improving the performance of individual threads.

6.4.3. Scalable Performance

This subsection delves into the performance of these algorithms in response to varying thread counts. We use RMAT 15 as an illustrative example of a synthetic graph and Amazon0312 as a representative instance of a real graph. By progressively increasing the number of threads to 2, 4, 8, 16, 32, 64, 128, and 224, we seek to identify changes in speedup corresponding to increasing thread counts.

Figure 10 illustrates the change in speedup with the increasing number of threads on RMAT15. For most algorithms, a bottleneck emerges starting from 64 threads, with no discernible speedup observed with the continued increase in thread count. Notably, the WP algorithm exhibits a degradation in performance with the incorporation of additional parallel threads. The only algorithm demonstrating notable scalability is EBP, showcasing consistent performance improvement with the increasing number of threads. A similar observation is made for the real graph (see Figure 11), where most algorithms encounter a bottleneck at 64 threads. However, EBP and EBDP exhibit good scalability, indicating that binary search-based methods possess superior scalability compared to other approaches.

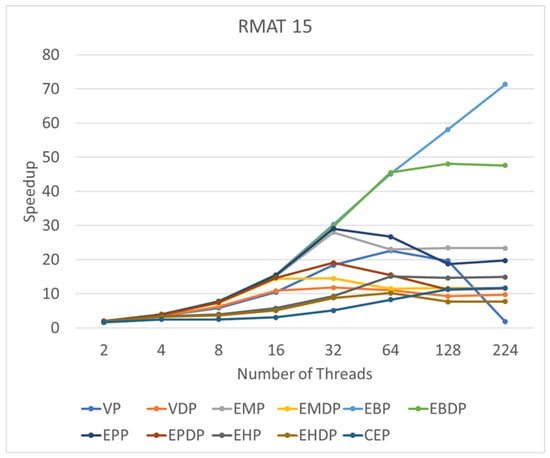
Figure 10. Speedups of various algorithms on RMAT15 compared with a single-thread setup.

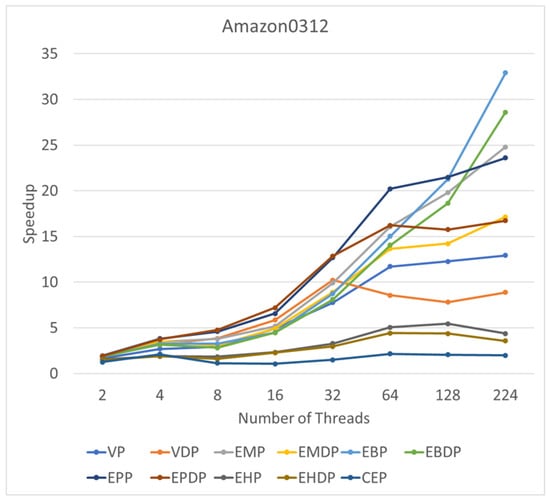
Figure 11. Speedups of various algorithms on Amazon0312 compared with a single-thread setup.

6.4.4. Best Performance on Different Graphs

In this section, we use EM as the performance baseline to evaluate the best speedup achieved by different algorithms. The results are summarized in Table 2. The number following a specific algorithm name indicates how many parallel threads are used.

Table 2. Best performance and algorithms for different graphs (second).

Graph	RMAT6	RMAT7	RMAT8	RMAT9	RMAT10	RMAT11	RMAT12	RMAT13	RMAT14	RMAT15	RMAT16	RMAT17
Baseline Time	0.0006080	0.0019730	0.0054550	0.0146430	0.0203420	0.0537350	0.1411760	0.3726090	0.9877480	2.6268370	6.9313980	18.3285120
Best Time	0.0000280	0.0000760	0.0002070	0.0002170	0.0003830	0.0008570	0.0014210	0.0029630	0.0066920	0.0150250	0.030892	0.078430
Algorithm	FH	FH	EHDP32	EHDP64	EHDP64	EHDP128	EHDP64	EHDP128	EHDP64	EHDP64	EHDP64	EHDP64
Speedup	21.7	26.0	26.4	67.5	53.1	62.7	99.3	125.8	147.6	174.8	224.4	233.7
Graph	karate	amazon0302	amazon0312	amazon0505	amazon0601	loc-Brightkite	loc-Gowalla	roadNet-CA	roadNet-PA	roadNet-TX	soc-Epinions1	wiki-Vote
Baseline Time	0.0000120	0.1434740	0.7208080	0.7557200	0.7621240	0.1158030	2.0830490	0.1027660	0.0755300	0.0708210	0.6153270	0.1243600
Best Time	0.0000020	0.0064670	0.0165880	0.0175940	0.0175690	0.0028280	0.0200290	0.002870	0.001671	0.003030	0.0088180	0.0015570
Algorithm	LA	EBDP224	EBDP224	EBDP224	EBDP224	EHDP64	CETC-SM128	WDP128	WDP64	WDP32	EHDP128	EHDP128
Speedup	6.0	22.2	43.5	43.0	43.4	40.9	104.0	35.8	45.2	23.4	69.8	79.9

Integrated optimization methods demonstrate a substantial speedup, averaging at 75.8. Examining various algorithms on different graphs unveils insights into optimization methods.

Firstly, for small graphs like RMAT 6, RMAT 7, and karate, parallel optimization techniques fail to outperform the sequential FH and linear algebra LA methods. Practical performance considerations suggest that employing multiple parallel threads might introduce overhead for small graphs, making sequential methods more efficient.

Secondly, as the graph size increases, optimal performance often requires more parallel resources. However, beyond a critical point, additional parallel resources may lead to decreased performance. For example, RMAT 8 and roadNet-TX achieve peak performance with 32 threads. In contrast, RMAT 9 to RMAT 10, RMAT 12, RMAT 14 to RMAT 17, loc-Brightkite, and roadNet-PA require 64 threads. Certain graphs, such as RMAT 11, RMAT 13, loc-Gowalla, roadNet-CA, soc-Epinions1, and wiki-Vote, demand 128 threads. Larger graphs, such as amazon0302, amazon0312, amazon0505, and amazon0601, leverage the whole system’s parallel resources (224 threads). Notably, graph size alone does not determine parallel resource needs, as topology plays a crucial role in parallel performance. At the same time, the parallel algorithms that achieve the best performance vary. Among them, EHDP achieves the best performance 13 times, EBDP 4 times, WDP 3 times, and CETC-SM once.

Thirdly, the various sequential and parallel optimizations needed for better performance can differ. For instance, WD might not be ideal in a sequential scenario due to checking numerous wedges, many of which are not fruitful for sparse graphs. However, in a parallel scenario, WDP64 excels with 64 threads on roadNet-PA, surpassing other algorithms. The efficiency arises from the smaller number of wedges when vertex degrees are low, coupled with DO optimization method that reduces fruitless searches. Another case is EBD, which may not be favorable in sequential algorithms due to increased total operations compared to EMD. However, in parallel algorithms, EBDP could outperform MergePath by distributing work more efficiently through parallel binary searches.

In conclusion, our results highlight that different algorithms find their optimal scenarios based on specific graph topology and hardware configurations. Graph topology and available hardware resources are pivotal factors in selecting the most efficient triangle counting algorithm.

7. Conclusions

In this paper, we present CETC, a novel and efficient triangle-counting algorithm that introduces the concept of a cover-edge set to significantly enhance performance. Unlike prior approaches, which are primarily refinements of the classic vertex-iterator and edge-iterator paradigms, CETC provides a fundamentally new perspective by reducing the computational cost of set intersections through selective edge coverage. To the best of our knowledge, this is the first triangle-counting algorithm in decades to employ such a conceptually distinct approach, bridging structural graph insights with algorithmic optimization.

We performed extensive, uniform performance evaluations across 24 diverse real-world and synthetic graphs, encompassing both sequential and shared-memory parallel implementations. The results demonstrated that CETC and its sequential variants, particularly CETC-Seq-S and CETC-Seq-SD, consistently outperform traditional methods by leveraging BFS-based preprocessing, degree ordering, and hash-based set intersections. When combined with direction-oriented (DO) optimization, the proposed methods achieved speedups of up to $24\times$ compared to baseline algorithms. The forward-hashed and degree-ordered versions also performed remarkably well, confirming that structural awareness—through vertex ordering and selective edge coverage—is key to achieving scalability on large, sparse graphs.

For shared-memory parallelization, we implemented OpenMP-based versions of several algorithms and evaluated their performance on Intel’s latest Sapphire Rapids architecture (Platinum 8480+). The results highlight that binary search and hash-based variants of CETC (EBP and EHDP) exhibit excellent scalability, achieving speedups of up to $233\times$ on large graphs with 224 threads. These experiments underscore that algorithmic design and graph structure jointly determine scalability and that parallel efficiency is maximized when computation, memory access, and graph topology are jointly optimized.

Beyond its empirical performance, the CETC framework offers conceptual generality. Because it relies on the notion of a cover-edge set, the same principle can be extended to related graph analytics tasks, such as motif enumeration, subgraph matching, and community detection, where overlapping local structures play a key role. Furthermore, CETC is particularly advantageous when BFS traversal data is already available—an increasingly common situation in network science, brain connectomics, and social graph analytics workloads—allowing it to reuse precomputed structures with minimal overhead.

In future work, we plan to extend CETC to distributed memory systems and heterogeneous architectures, including GPU and multi-GPU environments. Incorporating hybrid task parallelism and asynchronous data exchange will be crucial to maintaining high performance at scale. Another promising direction is to integrate CETC into dynamic graph processing frameworks, enabling efficient triangle maintenance under edge insertions and deletions. We also envision applying the cover-edge principle to broader classes of subgraph counting and pattern discovery problems.

We believe that this work will inspire renewed interest within the Graph Challenge community and the broader graph analytics research field in exploring structural optimizations that go beyond traditional iterator-based paradigms. Our complete source code is publicly available at https://github.com/Bader-Research/triangle-counting (accessed on 10 September 2025), facilitating reproducibility, community benchmarking, and future extensions.