Abstract
Graph Neural Networks (GNNs) capture complex information in graph-structured data by integrating node features with iterative updates of graph topology. However, they inherently rely on the homophily assumption—that nodes of the same class tend to form edges. In contrast, real-world networks often exhibit heterophilous structures, where edges are frequently formed between nodes of different classes. Consequently, conventional GNNs, which apply uniform smoothing over all nodes, may inadvertently aggregate both task-relevant and task-irrelevant information, leading to suboptimal performance on heterophilous graphs. In this work, we propose TRed-GNN, a novel end-to-end GNN architecture designed to enhance both the performance and robustness of node classification on heterophilous graphs. The proposed approach decomposes the original graph into a task-relevant subgraph and a task-irrelevant subgraph and employs a dual-channel mechanism to independently aggregate features from each topology. To mitigate the interference of task-irrelevant information, we introduce a reverse process mechanism that, without compromising the main task, extracts potentially useful information from the task-irrelevant subgraph while filtering out noise, thereby improving generalization and resilience to perturbations. Theoretical analysis and extensive experiments on multiple real-world datasets demonstrate that TRed-GNN not only achieves superior classification performance compared to existing methods on most benchmarks, but also exhibits strong adaptability and stability under graph structural perturbations and over-smoothing scenarios.
1. Introduction
Graph-structured data are ubiquitous in real-world scenarios. Examples include social networks, which store and represent interpersonal relationships, interactions, and information flow [], as well as biological networks, which describe complex relationships and interactions within biological systems []. Due to the inherent complexity of graph structures and the irregularity of relationships between nodes, learning from graph data has long been an important research focus. Graph Neural Networks (GNNs), particularly Graph Convolutional Networks (GCNs) have emerged as powerful algorithms for processing graph-structured data, capable of capturing rich graph representations by aggregating information from neighboring nodes. Owing to their remarkable performance, GNNs have been widely applied to a variety of graph-based learning tasks, such as node classification [], link prediction [], and graph classification [].
However, many GCNs are designed under the homophily assumption, wherein nodes of the same class tend to be connected by edges. Some studies have shown that GCNs can also perform well on heterophilous graphs with low homophily rates. To learn node representations in heterophilous graphs, GNNs often need to capture long-range interactions between nodes, which typically require stacking multiple message-passing layers []. Nevertheless, both empirical and theoretical studies have demonstrated that GNNs tend to over-smooth node representations across layers, significantly limiting their generalization ability beyond homophily []. Recently, GCNs have been extended to heterophilous graphs. For example, GCN-IED updates the graph topology to introduce direct edges and employs scalable neighborhood aggregation to explore latent edges from multi-hop neighbors []. Similarly, LAAH leverages label information from different neighborhoods to guide adaptive aggregation. However, such approaches cannot fully avoid the influence of inter-class information, which may be inadvertently aggregated into the representations of nodes from different classes, thereby causing class indistinguishability [].
One potential reason for the suboptimal performance of GNNs on heterophilous graphs lies in the mismatch between node labels and graph links. The former serves as the target for the classification task that GNNs aim to predict, while the latter determines how messages are propagated between nodes to achieve this objective. In homophilous graphs, the two are closely aligned, as most connected nodes belong to the same class. However, in heterophilous graphs, the motivation for establishing connections between nodes may be ambiguous with respect to the classification task. For example, in social networks, numerous connections exist between users with different interests, backgrounds, or professions []. This means that, during information propagation over the network, harmful or distracting information may be introduced. Existing state-of-the-art GCN models often fail to fully identify and differentiate such irrelevant or harmful information in the local neighborhood, making node representations prone to entanglement with incorrect signals and thus reducing robustness. An effective classification design should be able to identify task-irrelevant connections while extracting the most relevant information for prediction. However, in real-world datasets, node features are often noisy, and the connections between nodes may not reflect their class relationships. Existing techniques typically parameterize the weights of node pairs to indicate similarity or dissimilarity, but such approaches do not effectively assess the correlation between node connections and downstream task objectives.
In this paper, we propose an end-to-end node classification framework named TRed-GNN. We assume that the primary reason two nodes are connected is their similarity in features, and such features are not necessarily related to the target task. Some studies have divided the edges of a graph into two complementary sets, each representing potential relationships between nodes []. However, this division is not entirely accurate, as there may still exist useful information in connections between two task-irrelevant nodes. Therefore, we categorize node connections as task-relevant or task-irrelevant. In the implementation, we design a residual mechanism to distinguish between these types of edges. Node features are then aggregated separately over these connections to produce disentangled representations. Furthermore, a reverse process is introduced to extract latent information from task-irrelevant connections. To theoretically support our proposed algorithm, we conduct extensive experiments on real-world datasets and provide a detailed analysis of the feasibility of our model. In summary, the main contributions of this work are as follows:
- We propose TRed-GNN, a novel framework for node classification. By disentangling graph edges into task-relevant and task-irrelevant subgraphs, TRed-GNN mitigates noise from edge heterogeneity and processes information through independent channels. This dual-path design improves classification accuracy, especially on graphs with complex heterogeneous structures.
- To handle edge heterogeneity and node-level noise, TRed-GNN introduces a reverse process on the task-irrelevant subgraph. This mechanism recovers useful information while suppressing noise, effectively alleviating over-smoothing.
- We conducted systematic experiments on multiple real-world datasets (e.g., Cora, Citeseer, Chameleon) to evaluate TRed-GNN, demonstrating its superior performance over existing graph neural network methods across graphs with varying levels of homogeneity and heterogeneity.
2. Related Work
In this section, we review the fundamental research on Graph Neural Networks (GNNs) and their extensions to heterophilous graph scenarios. We also discuss recent advances in task-relevance modeling and disentangled representation learning and analyze the causes of the over-smoothing problem along with existing mitigation strategies. These studies lay the theoretical foundation for the proposed TRed-GNN framework and highlight our innovations in task-relevance modeling and robustness enhancement. As shown in Table 1, by comparing with existing methods, we clearly demonstrate the unique mechanism and advantages of the TRed GNN model in dealing with these problems.

Table 1.
Comparative table: task relevance, heterophily handling, and over-smoothing mitigation.
2.1. Graph Neural Networks
GNNs are a class of neural networks that operate directly on graph structures. The core idea of most GNNs is to utilize the information from a node’s neighborhood to construct its task-specific representation. Based on this principle, numerous variants have been developed, such as GCN [], GAT [], and GraphSAGE []. Among them, Graph Convolutional Networks primarily operate in the spectral and spatial domains. The spectral approach defines graph convolution as a filtering operation on graph signals in the frequency domain [], while the spatial approach interprets it as an aggregation operation between nodes []. In the spectral domain, convolution operations are defined via the graph Fourier transform based on spectral graph theory. For example, BernNet employs Bernstein polynomials to construct graph filters capable of learning arbitrary filter types, enabling convolution to better adapt to different graph structures []. ChebNet further approximates graph convolution using Chebyshev polynomials, which allows efficient signal processing in the frequency domain while avoiding the computationally expensive eigen-decomposition operation []. On the other hand, spatial-based GNNs perform convolution operations directly on the spatial structure of the graph. For instance, GAT applies an attention mechanism to learn the weights between each node and its neighbors, automatically assigning importance to different neighbors []. GraphSAGE proposes a framework for sampling and aggregating neighbor features []. However, these methods are generally designed under the homophily assumption and largely ignore the structural relationships in heterophilous graphs, which can lead to non-smooth variations of node features and labels across the graph.
2.2. GNN for Heterophilous Graphs
In recent years, GCNs have been increasingly extended to heterophilous graphs, where nodes tend to connect with others that have dissimilar features. Heterophilous graphs emphasize the dissimilarity between a node and its neighbors, indicating that edges may form between nodes of different types. To adapt GNNs to heterophilous graphs, several studies have exploited remote information beyond the immediate neighborhood. For example, Geom-GCN proposes a two-level aggregation method that leverages geometric neighborhood selection and multi-region information aggregation to address the issue of information mixing in conventional GNNs on heterophilous graphs []. H2GCN incorporates higher-order neighborhood aggregation and skip connections to better accommodate heterophilous structures []. ACM-GNN enhances the flexibility of convolution through an adaptive channel-mixing mechanism, enabling the model to select appropriate information propagation strategies based on the characteristics of the graph, thereby improving performance across different types of graphs []. GEN estimates a graph structure suitable for GNN learning to compute node embeddings, incorporating multi-order neighborhood information and using Bayesian inference as guidance [].
However, these methods often overlook the underlying motivation for the connection between two nodes and fail to associate such connections with the learning task. This motivates the need for a model that explicitly distinguishes between task-relevant and task-irrelevant connections. Such a design would allow us to leverage this information as guidance, separating and extracting additional information from task-irrelevant connections with respect to the final prediction objective, thereby improving the performance of GNNs on heterophilous graphs.
2.3. Consider Task Relevance and Disentanglement Representation Learning
The concept of task relevance has been employed in many areas of GNN research to address various problems, such as contrastive learning [], structure learning [,], and topology denoising [,]. Given that this work focuses on classification tasks, we next review studies in this domain to highlight the unique contribution of TRed-GNN to task-relevance modeling in GNN development. For example, GCN-LPA introduces task-relevant structural information via label propagation to improve classification performance and interpretability []. PGIB incorporates prototype learning into the information bottleneck framework to identify critical subgraphs in the input graph that are relevant to the classification task, using them as key prototypes []. These methods focus on selecting task-relevant edges to facilitate the extraction of task-related information, but they lack mechanisms to handle task-irrelevant information, and their modeling of task relevance is typically one-sided and static. In contrast, TRed-GNN adopts a disentangled paradigm that separates both the network topology and node features into task-relevant and task-irrelevant components. Specifically, it explicitly models task-irrelevant information to reduce noise while enhancing feature extraction within task-relevant information. By analyzing the graph topology from a more comprehensive perspective, our approach improves classification performance.
Disentangled representation learning aims to learn interpretable and independent representations, where each dimension or subspace corresponds to a distinct factor of the data []. In recent years, disentangled representation learning has been increasingly applied to GNNs to address graph-related tasks. For example, IPGDN enhances model performance by promoting independence among decomposition factors and integrating global graph information []. DisenGCN introduces a neighborhood routing mechanism that iteratively partitions each node’s neighborhood into different segments, thereby disentangling node information []. FactorGNN takes a generative perspective, decoupling node representations into multiple factor graphs to capture higher-order semantics []. IDGCL employs multi-channel disentangled modeling to accurately distinguish multiple independent factors in a graph, effectively improving interpretability in graph classification tasks []. It is worth noting that our model shares certain similarities with FactorGNN in that both decompose the original network topology into multiple subgraphs. However, there are fundamental differences between the two. First, FactorGNN merely partitions neighboring nodes into multiple semantic factors without explicitly modeling task relevance. Second, it allows an edge to belong to multiple subgraphs, which may lead to potential overlaps. In contrast, TRed-GNN adopts an edge-separation strategy to generate two complementary subgraphs representing task-relevant and task-irrelevant topologies. It then introduces a reverse process mechanism within the subgraphs to enhance classification capability and generalization.
2.4. The Problem of Over-Smoothing in GNNs
Many empirical and theoretical studies have shown that GNNs tend to smooth node representations across layers, ultimately leading to learned representations that become overly similar. During the aggregation process, information from neighboring nodes becomes increasingly alike, and as this balance is reached, node representations become indistinguishable. However, existing studies have proposed various hypotheses to address this issue. For instance, CPGNN introduces a learnable compatibility matrix to capture information from non-adjacent but label-consistent nodes []. FSGNN proposes soft feature selection, which adaptively aggregates features from neighboring and multi-hop nodes []. LRGNN employs a low-rank approximation to compute a label relationship matrix, which is then used for signed message passing []. Despite these advances, many methods still cause global node representations to converge toward similarity, which degrades classification performance. To address this, Ordered GNN retains non-aggregated information by extracting and preserving it separately and proposes ordering message passing to prevent the mixing of messages from different hops []. FAGCN introduces a self-gating mechanism that adaptively leverages both low-frequency and high-frequency signals []. ACM-GCN uses a combination of low-pass and high-pass filters to adaptively capture node-level local information []. GRAND strengthens the understanding of over-smoothing by drawing analogies between GNN architectures and the heat diffusion equation []. DropEdge randomly removes edges from the graph to cut off message propagation between adjacent nodes []. While these methods may mitigate the over-smoothing problem to some extent, learning discriminative representations between adjacent nodes remains challenging. In our approach, we introduce a reverse process mechanism to alleviate over-smoothing. Notably, we apply this mechanism only to the task-irrelevant subgraph. This is because the task-relevant subgraph is used for the main task learning and should directly participate in forward information propagation, whereas the task-irrelevant subgraph is not intended to enhance classification performance directly. Instead, it serves to extract useful information from the latent structure and filter out noise without interfering with the main task learning, thereby improving robustness and generalization.
3. Notations and Preliminaries
In this section, we represent an undirected graph as , where V denotes the set of nodes and denotes the set of edges. Let denote the node feature matrix, where d is the dimensionality of node features and n is the number of nodes. We use to denote the i-th row of X, corresponding to node . Let be the adjacency matrix of G, where indicates that there exists an edge between node i and node j, and otherwise. The degree matrix D is obtained by summing each row of A and placing the results along the diagonal. The adjacency matrix with self-loops is defined as , and the corresponding degree matrix is . In this paper, we decompose the original graph into two subgraphs: a task-relevant subgraph and a task-irrelevant subgraph, whose adjacency matrices are denoted as and , respectively. For node classification tasks, each node is assigned with a label out of classes and have a ground truth one-hot vector . In this context, real-world graphs can be divided into homophilous and heterophilous ones based on the extent of similarity in class labels among connected nodes. The homophily ratio is shown in Table 2.

Table 2.
Statistics of experimental datasets.
4. The Proposed Method
In this section, we present an end-to-end graph learning framework, TRed-GNN, which extends Graph Neural Networks to heterophilous graphs. An overview of the model is shown in Figure 1. The core idea is to decompose the original GNN graph structure into two subgraphs and process them separately, using the graph topology to guide task-relevant and task-irrelevant node features.
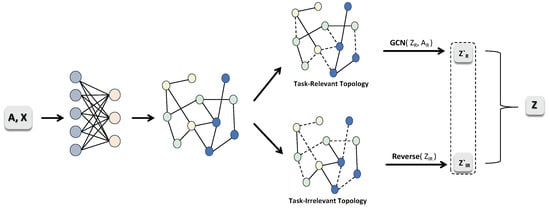
Figure 1.
Illustration of TRed-GNN framework where A and X denote the adjacency matrix and feature matrix of nodes, respectively. First, X is passed through a fully connected layer to learn node representations more suitable for the task. Then, it is mapped to different latent subspaces via separate channels, R and . Next, an edge splitting operation is performed to divide the original graph edges into two complementary sets. Node information can then be aggregated separately on the different edge sets to produce disentangled representations for the subsequent edge splitting in the next layer. By extracting latent information from , the task is then predicted by combining it with .
4.1. Dynamically Update Graph Topology
Before updating the graph topology, the original node features X may be irregularly distributed and not directly related to the task. Therefore, we first apply a fully connected layer to learn node representations that are more suitable for the task. Specifically, the feature matrix X is passed through a fully connected neural network (FCNN) parameterized by , as formulated below:
where denotes a FCNN, which is then applied to the feature matrix using the ReLU activation function.
Next, the updated feature matrix is fed into two separate channels to extract task-relevant and task-irrelevant information from the nodes. We project the above feature matrix into different subspaces:
where and are learnable parameters in channel , d denotes the dimension of the node hidden states, and represents the non-linear activation function.
First, we assume that the connection between two nodes is primarily due to their similarity in certain features. However, such feature similarity may be relevant to the current learning task, irrelevant, or even harmful. Based on this assumption, we can adopt a flexible approach by assigning continuous weights ranging from 0 to 1 to soften the node connections, reflecting the varying degrees of task relevance or irrelevance of each edge. However, determining and independently based on node similarity metrics may fail to fully capture the complex interactions between the two channels and may reduce attention to topological distinctions. To address this issue, for an edge , we parameterize the difference between and by solving the following equation:
where and , with . To effectively quantify the interaction between the task-relevant and task-irrelevant aspects of each edge, we introduce a residual mechanism:
where g is a learnable convolution function, and tanh is the hyperbolic tangent activation function, which constrains the output within the range .
4.2. Neighborhood Aggregation
Since the split graph topologies reveal partial relationships between nodes in different latent spaces, they can be used to aggregate information between different nodes. Specifically, we first use GCN to aggregate task-relevant node information, as given by the following equation:
where and are learnable weight matrix, is the activation function, and D is the degree matrix associated with the adjacency matrix A.
Next, we aim to learn to recover the information from the input space based on a certain output space. However, in traditional GNNs, node representations are typically obtained by aggregating information from neighboring nodes through message passing. This process tends to push the representations of adjacent nodes toward similarity, and the over-smoothing phenomenon becomes more severe as the number of graph layers increases. To alleviate this issue, we propose using a reverse diffusion model, whose core idea is to invert the diffusion process in traditional GNNs. Specifically, the reverse diffusion process attempts to “trace back” the node representations to their pre-diffusion state, thereby avoiding over-smoothing. Based on this idea, we apply the reverse diffusion process to the task-irrelevant graph topology so that it can re-extract useful information from the topological structure. The formula is as follows:
where is a reverse-process function. In this paper, we implement it by using an MLP as the reverse mapping function through structural design.
Next, we incorporate the useful information from task-irrelevant nodes into the task-relevant node representations through weighted fusion, as expressed by the following equation:
where and denote the task-relevant and task-irrelevant representations, respectively, and are hyperparameters controlling their weights.
Finally, we use the cross-entropy loss function to compute the loss and improve the model performance by minimizing the following training objective.
where denotes a training node, is the number of training nodes, is the ground-truth label of the i-th node (one-hot encoded), and is the predicted probability distribution of the i-th node (typically obtained via softmax), where C is the number of classes.
4.3. Computational Complexity Analysis
Let the graph be , where the adjacency matrix and the feature matrix . In each layer, TRed-GNN requires the following operations: (1) feature projection and the reverse process MLP with complexity ; (2) edge disentanglement with residual coefficient computation , costing ; (3) message passing on both task-relevant and task-irrelevant subgraphs, with a total cost of ; (4) weighted fusion, which costs only and can be neglected in asymptotic analysis. Therefore, the overall time complexity per layer of TRed-GNN is . To assess the computational efficiency of all compared methods, we provide a comparison for the time complexities of the compared algorithms, outlined in Table 3.

Table 3.
A comparison for computational complexity of all compared methods, where |E| is the number of edges.
5. Experiments
- Datasets: In this section, we evaluate TRed-GNN on real-world datasets. We use the following real-world datasets: Cora, Citeseer, Cornell, Chameleon, Squirrel, Wisconsin, Texas, and Film.
- Data Splits: For homophilous graphs, we follow the standard setting of selecting 20 nodes per class for training, 500 nodes for validation, and 1500 nodes for testing. For heterophilous graphs, we split the data into training, validation, and test sets with ratios of 60%, 20%, and 20%, respectively.
- Baselines and Implementation Details: To assess the performance of our model, we compare it against several state-of-the-art GNN models and task-specific models. Specifically, the baseline models include GCN [], GAT [], SGC [], GraphSAGE [], APPNP [], Geom-GCN [], ACM-GCN [], H2GCN [], FAGCN [], GPR-GNN [], LRGNN [], and MixHop []. For all baselines and TRed-GNN, we set as the number of hidden units to ensure a fair comparison, use Adam as the optimizer, and tune hyperparameters for each dataset using Optuna on the validation set. For the multi-layer perceptron, the hidden feature dimension is set to 512, and training is performed for 200 runs. After obtaining the optimal hyperparameters, we train the model for 1000 epochs with an early stopping strategy of 100 epochs patience. The final performance is reported as the average over 10 runs with different random data splits on the test set.
5.1. Classification Results
Table 4 presents the node classification accuracy of various models on real-world datasets. We observe that, compared to the strongest baseline model, TRed-GNN achieves improvements of 4.62 percentage points, 7.85 percentage points, 4.00 percentage points, and 6.56 percentage points on the Citeseer, Wisconsin, Texas, and Squirrel datasets, respectively. On the Cora, Chameleon, and Film datasets, it yields smaller gains of 2.03 percentage points, 2.47 percentage points, and 0.57 percentage points, respectively. However, on the Cornell dataset, its performance is lower than that of the ACM-GNN model, which we attribute to the relatively low edge density and sparser topology of Cornell, limiting our model’s ability to extract sufficient useful information when partitioning the graph topology.

Table 4.
Performance (%) comparison of 8 real heterophilous datasets. The best and second-best results are highlighted in bold and underlined, respectively. Error reduction gives the average improvement of TRed-GNN upon baselines w/o Basic GNNs.
Importantly, beyond mean accuracy, we also report 95% confidence intervals across 10 random runs to ensure fairness and statistical robustness in Table 5. The intervals show that the improvements in TRed-GNN over baselines are consistent and remain significant within the estimated uncertainty ranges. For example, on Citeseer and Texas, TRed-GNN not only achieves higher mean accuracy but also exhibits tighter confidence intervals, indicating both stability and reliability. This further demonstrates that the observed performance gains are not due to randomness but reflect the inherent advantage of disentangling task-relevant and task-irrelevant structures.

Table 5.
Accuracy (%) with 95% confidence intervals across 10 runs. Bold indicates the best performance.
Overall, TRed-GNN demonstrates superior and statistically robust performance on most datasets, strongly indicating that our model can effectively reduce inter-class edge noise propagation during node classification.
5.2. Ablation Experiment
To evaluate the effectiveness of each module in our model, we conducted ablation experiments on TRed-GNN and its variants across eight real-world datasets. Specifically, we define two variants: (1) “w/o ZIR”: without the task-irrelevant channel, and (2) “w/o ”: without the reverse process. From Figure 2, we can draw the following conclusions. First, when the distinction between task-relevant and task-irrelevant graph topologies is removed, the model’s performance drops significantly. This confirms that incorporating the classification task into the topology design helps reduce the interference of irrelevant information, thereby improving the model’s ability to focus on task-relevant information. Second, removing the reverse process also leads to a noticeable drop in accuracy, which validates that the reverse process effectively enhances graph structure learning.
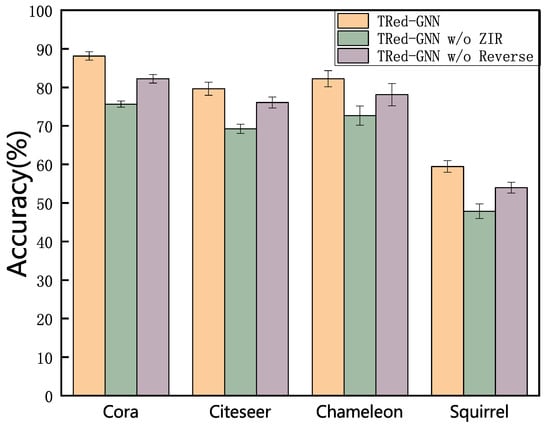
Figure 2.
Ablation study of TRed-GNN on four datasets in node classification.
5.3. Robustness Analysis
To assess the robustness of our model under graph structural perturbations, we conducted structure corruption experiments on standard datasets (Cora, Citeseer, Chameleon, and Squirrel). Specifically, we randomly rewired different proportions of edges in the original graph structure, with perturbation rates ranging from 0 percentage point to 100 percentage point in increments of 20 percentage point. This setup simulates real-world scenarios where graph structures may be incomplete, noisy, or dynamically evolving. As shown in Figure 3, we compare our model against GCN, GAT, ACM-GNN, H2GCN, and LRGNN. The results show that our model consistently exhibits superior performance. With increasing random perturbations, false edges are more likely to connect nodes from different labels, leading to erroneous message passing in conventional methods. This provides strong evidence for the ability of TRed-GNN to distinguish between task-relevant and task-irrelevant connections. Consequently, even when a large number of false edges are present in the graph topology, our model can still effectively gather neighborhood information to predict node labels. These results further demonstrate that our model has a stronger capacity to remove irrelevant edges while preserving task-relevant structures, thereby enhancing both robustness and stability.
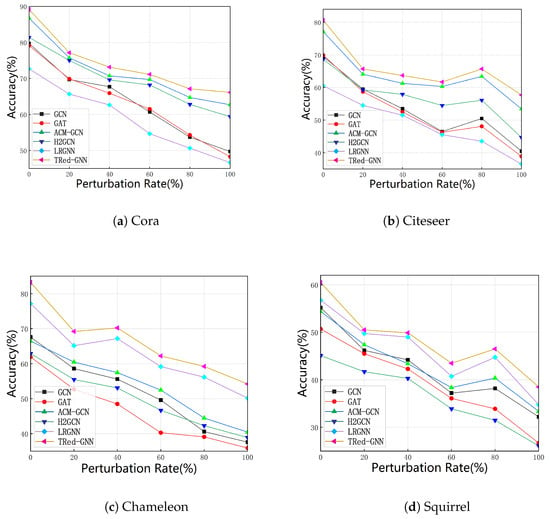
Figure 3.
Results of different models on perturbed homophilous graphs. TRed-GNN exhibits superior robustness against disturbances compared to other models. The line charts display the accuracy of different models under varying levels of perturbed rates in (a) the Cora dataset, (b) the Citeseer dataset, (c) the Chameleon dataset, and (d) the Squirrel dataset. TRed-GNN is able to identify the falsely injected (the task-irrelevant) graph edges, and exclude these connections from the final predictive learning, thereby displaying relative robust performance against adversarial edge attacks.
5.4. Relieve the Problem of Excessive Smoothness
To evaluate the over-smoothing behavior of TRed-GNN, we varied the number of layers in the model and compared its performance with GCN and GAT. As shown in Figure 4, when the number of layers reaches two, both GCN and GAT achieve their highest performance. However, as the number of layers increases, their accuracy gradually declines. In contrast, TRed-GNN exhibits a curve that rises steadily before leveling off. Although it starts with relatively lower accuracy, the performance of TRed-GNN improves consistently as the number of layers increases, ultimately achieving accuracy significantly higher than that of GCN and GAT. We attribute this to the fact that TRed-GNN can adaptively utilize edges from different layers to produce results aligned with the target task. Furthermore, by incorporating the reverse process to gather hidden node information, the model enriches node representations and thereby alleviates the over-smoothing problem.
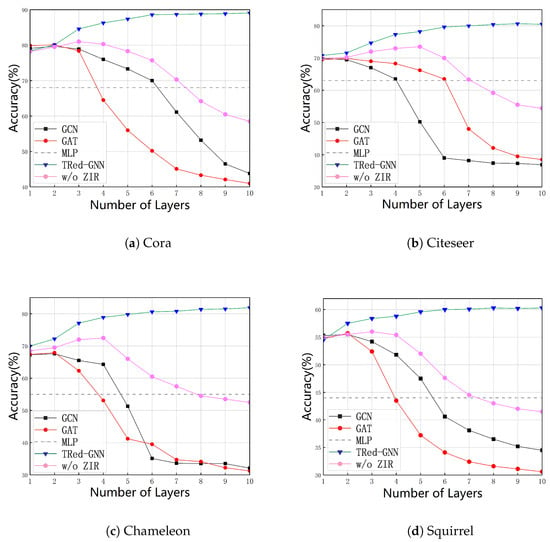
Figure 4.
Accuracy comparison of GCN, GAT, MLP, TRed-GNN, and its variant w/o ZIR on four datasets ((a) Cora, (b) Citeseer, (c) Chameleon, and (d) Squirrel) as the number of layers increases, illustrating the impact of model depth on performance and over-smoothing.
In addition, we include the variant “w/o ZIR”, which removes the dual-channel disentanglement and propagates messages over a single graph structure. As illustrated in the figure, “w/o ZIR” performs similarly to GCN in the shallow regime, but its accuracy stabilizes at a slightly higher level when the depth increases, showing that the reverse process can still alleviate part of the over-smoothing. However, compared with the full TRed-GNN, the gap is significant, especially on heterophilous datasets such as Chameleon and Squirrel, where dual-channel disentanglement is crucial. This clearly demonstrates that separating task-relevant and task-irrelevant edges plays an indispensable role in enhancing model robustness against over-smoothing.
5.5. Limitations
While TRed-GNN demonstrates robust performance in classification tasks, several limitations and challenges must be considered when deploying the model in practical scenarios. Many real-world graph datasets exhibit sparse connectivity between nodes, particularly in highly heterogeneous graphs where limited edge connectivity may lead to less pronounced performance of TRed-GNN compared to its performance on conventional graphs. A key limitation is the model’s performance degradation on highly sparse graphs, such as the Cornell dataset. In graphs with limited edges, the model struggles to effectively distinguish between task-relevant and task-irrelevant edges due to insufficient structural information. The reverse-process mechanism may not fully compensate for this connectivity sparsity, potentially resulting in suboptimal performance, as observed in our experiments. Future work will focus on enhancing the model’s capability to handle sparse graphs by incorporating additional structural priors or refining the reverse-processing mechanism for graphs with deficient edge structures.
6. Conclusions
In this paper, we proposed a novel TRed-GNN model that leverages task-relevant and task-irrelevant graph topologies, together with a reverse process mechanism, to effectively address noise interference in node representations, insufficient generalization, and the over-smoothing problem in heterophilous graphs. Extensive experiments demonstrate that the proposed method achieves excellent performance on a variety of both homophilous and heterophilous graph datasets. Furthermore, ablation studies confirm the necessity of task-relevance modeling and the reverse process mechanism. For future work, we plan to explore more fine-grained edge separation strategies and extend the framework to graph-level tasks and dynamic scenarios.
Author Contributions
Conceptualization, M.X. and Z.Z.; methodology, M.X.; software, Z.Z.; validation, M.X., Q.W. and Y.Y.; formal analysis, Y.Y.; investigation, M.X.; resources, H.C.; data curation, M.X.; writing—original draft preparation, M.X.; writing—review and editing, M.X.; visualization, M.X.; supervision, Y.Y.; project administration, H.C.; funding acquisition, H.C. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Open Research Fund of Fujian Key Laboratory of Financial Information Processing, Putian University (NO. JXJS202507).
Data Availability Statement
Data derived from public domain resources. The data supporting this study are openly available at https://lig-membres.imag.fr/grimal/data.html.
Conflicts of Interest
The authors declare that they have no known competing financial interests or personal relationships that could be construed as influencing the work reported in this paper.
References
- Costa, A.R.; Ralha, C.G. AC2CD: An actor–critic architecture for community detection in dynamic social networks. Knowl.-Based Syst. 2023, 261, 110202. [Google Scholar] [CrossRef]
- Li, D.X.; Zhou, P.; Zhao, B.W.; Su, X.R.; Li, G.D.; Zhang, J.; Hu, P.W.; Hu, L. Biocaiv: An integrative webserver for motif-based clustering analysis and interactive visualization of biological networks. BMC Bioinform. 2023, 24, 451. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Lin, B.; Luo, B.; Gui, N. Graph representation learning beyond node and homophily. IEEE Trans. Knowl. Data Eng. 2022, 35, 4880–4893. [Google Scholar] [CrossRef]
- Zheng, Q.; Zhang, Y. Tagnn: Time adjoint graph neural network for traffic forecasting. In Proceedings of the International Conference on Database Systems for Advanced Applications, Tianjin, China, 17–20 April 2023; Springer: Cham, Switzerland, 2023; pp. 369–379. [Google Scholar]
- Li, W.; Wang, C.h.; Cheng, G.; Song, Q. Optimum-statistical Collaboration Towards General and Efficient Black-box Optimization. arXiv 2021, arXiv:2106.09215. [Google Scholar]
- Rusch, T.K.; Bronstein, M.M.; Mishra, S. A survey on oversmoothing in graph neural networks. arXiv 2023, arXiv:2303.10993. [Google Scholar] [CrossRef]
- Chen, D.; Lin, Y.; Li, W.; Li, P.; Zhou, J.; Sun, X. Measuring and relieving the over-smoothing problem for graph neural networks from the topological view. Proc. AAAI Conf. Artif. Intell. 2020, 34, 3438–3445. [Google Scholar] [CrossRef]
- He, L.; Bai, L.; Yang, X.; Liang, Z.; Liang, J. Exploring the role of edge distribution in graph convolutional networks. Neural Netw. 2023, 168, 459–470. [Google Scholar] [CrossRef]
- Liu, L.; Wang, Y.; Xie, Y.; Tan, X.; Ma, L.; Tang, M.; Fang, M. Label-aware aggregation on heterophilous graphs for node representation learning. Displays 2024, 84, 102817. [Google Scholar] [CrossRef]
- Chen, Y.; Jiang, D.; Tan, C.; Song, Y.; Zhang, C.; Chen, L. Neural moderation of ASMR erotica content in social networks. IEEE Trans. Knowl. Data Eng. 2023, 36, 275–280. [Google Scholar] [CrossRef]
- Guo, J.; Huang, K.; Zhang, R.; Yi, X. ES-GNN: Generalizing graph neural networks beyond homophily with edge splitting. IEEE Trans. Pattern Anal. Mach. Intell. 2024, 46, 11345–11360. [Google Scholar] [CrossRef]
- Kipf, T. Semi-Supervised Classification with Graph Convolutional Networks. arXiv 2016, arXiv:1609.02907. [Google Scholar]
- Veličković, P.; Cucurull, G.; Casanova, A.; Romero, A.; Lio, P.; Bengio, Y. Graph attention networks. arXiv 2017, arXiv:1710.10903. [Google Scholar]
- Hamilton, W.; Ying, Z.; Leskovec, J. Inductive representation learning on large graphs. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Bruna, J.; Zaremba, W.; Szlam, A.; LeCun, Y. Spectral networks and locally connected networks on graphs. arXiv 2013, arXiv:1312.6203. [Google Scholar]
- Gilmer, J.; Schoenholz, S.S.; Riley, P.F.; Vinyals, O.; Dahl, G.E. Neural message passing for quantum chemistry. In Proceedings of the International Conference on Machine Learning, Sydney, NSW, Australia, 6–11 August 2017; PMLR. pp. 1263–1272. [Google Scholar]
- He, M.; Wei, Z.; Huang, z.; Xu, H. Bernnet: Learning arbitrary graph spectral filters via bernstein approximation. Adv. Neural Inf. Process. Syst. 2021, 34, 14239–14251. [Google Scholar]
- Defferrard, M.; Bresson, X.; Vandergheynst, P. Convolutional neural networks on graphs with fast localized spectral filtering. In Proceedings of the 30th International Conference on Neural Information Processing System, Barcelona, Spain, 5–10 December 2016. [Google Scholar]
- Pei, H.; Wei, B.; Chang, K.C.C.; Lei, Y.; Yang, B. Geom-gcn: Geometric graph convolutional networks. arXiv 2020, arXiv:2002.05287. [Google Scholar] [CrossRef]
- Zhu, J.; Yan, Y.; Zhao, L.; Heimann, M.; Akoglu, L.; Koutra, D. Beyond homophily in graph neural networks: Current limitations and effective designs. Adv. Neural Inf. Process. Syst. 2020, 33, 7793–7804. [Google Scholar]
- Luan, S.; Hua, C.; Lu, Q.; Zhu, J.; Zhao, M.; Zhang, S.; Chang, X.W.; Precup, D. Revisiting heterophily for graph neural networks. Adv. Neural Inf. Process. Syst. 2022, 35, 1362–1375. [Google Scholar]
- Wang, R.; Mou, S.; Wang, X.; Xiao, W.; Ju, Q.; Shi, C.; Xie, X. Graph structure estimation neural networks. In Proceedings of the Web Conference 2021, Ljubljana, Slovenia, 19–23 April 2021; pp. 342–353. [Google Scholar]
- Xu, D.; Cheng, W.; Luo, D.; Chen, H.; Zhang, X. Infogcl: Information-aware graph contrastive learning. Adv. Neural Inf. Process. Syst. 2021, 34, 30414–30425. [Google Scholar]
- Sun, Q.; Li, J.; Peng, H.; Wu, J.; Fu, X.; Ji, C.; Yu, P.S. Graph structure learning with variational information bottleneck. Proc. AAAI Conf. Artif. Intell. 2022, 36, 4165–4174. [Google Scholar] [CrossRef]
- Yang, M.; Shen, Y.; Qi, H.; Yin, B. Soft-mask: Adaptive substructure extractions for graph neural networks. In Proceedings of the Web Conference 2021, Ljubljana, Slovenia, 19–23 April 2021; pp. 2058–2068. [Google Scholar]
- Zheng, C.; Zong, B.; Cheng, W.; Song, D.; Ni, J.; Yu, W.; Chen, H.; Wang, W. Robust graph representation learning via neural sparsification. In Proceedings of the International Conference on Machine Learning, Virtual Event, 13–18 July 2020; PMLR. pp. 11458–11468. [Google Scholar]
- Luo, D.; Cheng, W.; Yu, W.; Zong, B.; Ni, J.; Chen, H.; Zhang, X. Learning to drop: Robust graph neural network via topological denoising. In Proceedings of the 14th ACM International Conference on Web Search and Data Mining, Virtual Event, 8–12 March 2021; pp. 779–787. [Google Scholar]
- Wang, H.; Leskovec, J. Unifying graph convolutional neural networks and label propagation. arXiv 2020, arXiv:2002.06755. [Google Scholar] [CrossRef]
- Seo, S.; Kim, S.; Park, C. Interpretable prototype-based graph information bottleneck. Adv. Neural Inf. Process. Syst. 2023, 36, 76737–76748. [Google Scholar]
- Higgins, I.; Amos, D.; Pfau, D.; Racaniere, S.; Matthey, L.; Rezende, D.; Lerchner, A. Towards a definition of disentangled representations. arXiv 2018, arXiv:1812.02230. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, X.; Wu, S.; Xiao, Z. Independence promoted graph disentangled networks. Proc. AAAI Conf. Artif. Intell. 2020, 34, 4916–4923. [Google Scholar] [CrossRef]
- Ma, J.; Cui, P.; Kuang, K.; Wang, X.; Zhu, W. Disentangled graph convolutional networks. In Proceedings of the International Conference on Machine Learning, Long Beach, CA, USA, 9–15 June 2019; PMLR. pp. 4212–4221. [Google Scholar]
- Yang, Y.; Feng, Z.; Song, M.; Wang, X. Factorizable graph convolutional networks. Adv. Neural Inf. Process. Syst. 2020, 33, 20286–20296. [Google Scholar]
- Li, H.; Zhang, Z.; Wang, X.; Zhu, W. Disentangled graph contrastive learning with independence promotion. IEEE Trans. Knowl. Data Eng. 2022, 35, 7856–7869. [Google Scholar] [CrossRef]
- Zhu, J.; Rossi, R.A.; Rao, A.; Mai, T.; Lipka, N.; Ahmed, N.K.; Koutra, D. Graph neural networks with heterophily. Proc. AAAI Conf. Artif. Intell. 2021, 35, 11168–11176. [Google Scholar] [CrossRef]
- Maurya, S.K.; Liu, X.; Murata, T. Simplifying approach to node classification in graph neural networks. J. Comput. Sci. 2022, 62, 101695. [Google Scholar] [CrossRef]
- Liang, L.; Hu, X.; Xu, Z.; Song, Z.; King, I. Predicting global label relationship matrix for graph neural networks under heterophily. Adv. Neural Inf. Process. Syst. 2023, 36, 10909–10921. [Google Scholar]
- Song, Y.; Zhou, C.; Wang, X.; Lin, Z. Ordered gnn: Ordering message passing to deal with heterophily and over-smoothing. arXiv 2023, arXiv:2302.01524. [Google Scholar] [CrossRef]
- Bo, D.; Wang, X.; Shi, C.; Shen, H. Beyond low-frequency information in graph convolutional networks. Proc. AAAI Conf. Artif. Intell. 2021, 35, 3950–3957. [Google Scholar] [CrossRef]
- Chamberlain, B.; Rowbottom, J.; Gorinova, M.I.; Bronstein, M.; Webb, S.; Rossi, E. Grand: Graph neural diffusion. In Proceedings of the International Conference on Machine Learning, Virtual, 18–24 July 2021; PMLR. pp. 1407–1418. [Google Scholar]
- Rong, Y.; Huang, W.; Xu, T.; Huang, J. Dropedge: Towards deep graph convolutional networks on node classification. arXiv 2019, arXiv:1907.10903. [Google Scholar]
- Wu, F.; Souza, A.; Zhang, T.; Fifty, C.; Yu, T.; Weinberger, K. Simplifying graph convolutional networks. In Proceedings of the International Conference on Machine Learning, Long Beach, CA, USA, 9–15 June 2019; PMLR. pp. 6861–6871. [Google Scholar]
- Gasteiger, J.; Bojchevski, A.; Günnemann, S. Predict then propagate: Graph neural networks meet personalized pagerank. arXiv 2018, arXiv:1810.05997. [Google Scholar]
- Chien, E.; Peng, J.; Li, P.; Milenkovic, O. Adaptive universal generalized pagerank graph neural network. arXiv 2020, arXiv:2006.07988. [Google Scholar]
- Abu-El-Haija, S.; Perozzi, B.; Kapoor, A.; Alipourfard, N.; Lerman, K.; Harutyunyan, H.; Ver Steeg, G.; Galstyan, A. Mixhop: Higher-order graph convolutional architectures via sparsified neighborhood mixing. In Proceedings of the International Conference on Machine Learning, Long Beach, CA, USA, 9–15 June 2019; PMLR. pp. 21–29. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).