Perfect Roman Domination: Aspects of Enumeration and Parameterization ^†

Abstract

Perfect Roman Dominating Functions and Unique Response Roman Dominating Functions are two ways to translate perfect code into the framework of Roman Dominating Functions. We also consider the enumeration of minimal Perfect Roman Dominating Functions and show a tight relation to minimal Roman Dominating Functions. Furthermore, we consider the complexity of the underlying decision problems Perfect Roman Domination and Unique Response Roman Domination on special graph classes. For instance, split graphs are the first graph class for which Unique Response Roman Domination is polynomial-time solvable, while Perfect Roman Domination is NP-complete. Beyond this, we give polynomial-time algorithms for Perfect Roman Domination on interval graphs and for both decision problems on cobipartite graphs. However, both problems are NP-complete on chordal bipartite graphs. We show that both problems are $\mathsf{W}\left[1\right]$-complete if parameterized by solution size and FPT if parameterized by the dual parameter or by clique width.

1. Introduction

There are many ways to get along with NP-complete problems. For example, you could consider exponential-time algorithms or approximation algorithms. Here, we want to deal with Perfect Roman Domination and Unique Response Roman Domination by looking into enumeration, into the complexity of related decision problems in special graph classes, and into parameterized complexity.

We only consider simple undirected graphs $G=(V,E)$ throughout this paper. We recall some notions next. $N_G\left(v\right):=\{u\in V\mid uv\in E\}$ describes the open neighborhood of $v\in V$ with respect to G. The closed neighborhood of $v\in V$ with respect to G is defined by $N_G\left[v\right]:=N_G\left(v\right)\cup \left\{v\right\}$. $D\subseteq V$ is a dominating set (or a perfect code, respectively) of G if each vertex v finds a (unique) vertex u in $D\cap N_G\left[v\right]$. A function $f:V\to \{0,1,2\}$ is called a Roman dominating function (Rdf for short) if each $v\in V$ with $f\left(v\right)=0$ is adjacent to a $u\in V$ with $f\left(u\right)=2$. The weight of a function $f:V\to \{0,1,2\}$ is defined by $\omega \left(f\right)={\sum }_{v\in V}f\left(v\right)$. The decision problem Roman Domination has as input a graph G and a positive number k, and the question is whether there exists a Roman dominating function such that the weight of the function is at most k. Roman Domination is a well-studied variation of the dominating set. It is motivated by a defense strategy of the Roman Empire. The idea is to position the armies in regions in such a way that either (1) one army is in this region or (2) two armies are in one neighbored region. We model the distribution of the armies on the region (viewed as vertices of the graph) by a function that maps each region to the number of armies placed on this region.

In recent years, this problem received notable attention [1,2,3,4,5,6,7]. As for the dominating set, there are also many variants of Roman Dominating Functions considered in the literature. Examples are Roman-$\left\{2\right\}$-domination (also known as Italian domination) [8] or double Roman Domination [9,10,11]. Clearly, as testified by books written on this topic [12,13,14], there are even more variations of the basic concept of domination in graphs.

Here, we will consider two further variations of Roman Domination, perfect and Unique Response Roman Domination. A perfect Roman dominating function (pRdf for short) (introduced by Henning et al. [15]) is a Roman Dominating Function where each vertex with value 0 has exactly one neighbor with value 2. If, moreover, all vertices with at least 1 as a value have no neighbor with value 2, then we have a unique response Roman dominating function (urRdf for short) (as introduced in [16]). Both variations can be seen as a way to translate the idea of perfect code into the realm of Roman dominating function. A further motivation can also be the idea of positioning armies in regions: if the armies are placed according to a perfect Roman dominating function and a region without any army is attacked, then it is clear from which region an army moves to secure the attacked region, so no time is wasted to first agree on who is the one to take action and move to the endangered region. This article is a revised and expanded version of a paper entitled “Perfect Roman Domination: Aspects of Enumeration and Parameterization”, which was presented at the 35th International Workshop Combinatorial Algorithms, IWOCA 2024, which took place on the island of Ischia, Italy, 1–3 July 2024. An extended abstract of this paper has appeared in the proceedings of IWOCA 2024; see [17]. More formally, the decision problems sketched so far are given as follows:

Problem name: Unique Response Roman Domination (URRD) Given: A graph $G=(V,E)$ and $k\in \mathbb{N}$ Question: Is there a unique response Roman dominating function f on G with $\omega \left(f\right)\le k$?

Problem name: Perfect Roman Domination (PRD) Given: A graph $G=(V,E)$ and $k\in \mathbb{N}$ Question: Is there a perfect Roman dominating function f on G with $\omega \left(f\right)\le k$?

Let $u_R\left(G\right)$ denote the smallest weight of any unique response Roman dominating function f on G. Furthermore, ${\gamma }_R^p\left(G\right)$ denotes the smallest weight of any perfect Roman dominating function on G. The following is known about the complexity of these decision problems. Unique Response Roman Domination is NP-complete on regular bipartite graphs [18]. Banerjee et al. [19] showed that it is NP-complete on chordal graphs, and polynomial-time solvable on distance-hereditary and interval graphs. They also proved that there is no Unique Response Roman Domination polynomial-time approximation algorithm within a factor of $n^{1-ϵ}$ for any constant $ϵ>0$ and any n-vertex input graph, if $\mathsf{NP}\ne \mathsf{P}$. Perfect Roman Domination is NP-complete on chordal graphs, planar graphs, and bipartite graphs, and polynomial-time solvable on block graphs, cographs, series-parallel graphs, and proper interval graphs as shown in [20]. These results are complemented by our complexity results in this paper as surveyed in Table 1 that presents the main classical complexity results of our paper. Notice that, in particular, our results concerning split and chordal bipartite graphs solve questions posed as open in [19] (Table 1). We complement the NP-hardness results by providing FPT-algorithms for the parameters treewidth and solution size, as well as for the dual parameter, both for Perfect Roman Domination and for Unique Response Roman Domination. Also, if the clique decomposition is explicitly given, the problems can be solved in FPT-time when parameterized by the clique width of this decomposition.

Table 1. Survey of basic complexity results of Perfect Roman Domination (PRD) and of Unique Response Roman Domination (URRD) on graph various classes.

Graph Class	PRD	URRD
chordal	NP-complete [20]	NP-complete [19]
interval	P Theorem 6	P [19]
split	NP-complete Theorem 8	P Theorem 7
cobipartite	P Theorem 10	P Lemma 2
bipartite	NP-complete [20]	NP-complete [18]
chordal bipartite	NP-complete Theorem 13	NP-complete Theorem 13
distance-hereditary	P Theorem 14	P [19]
cographs	P [20]	P [19]
bounded treewidth	P Theorem 15	P Theorem 17

Enumeration is a wide area of research as testified by specialized workshops like [21]. For some examples, we refer to the survey [22]. From a practical point of view, enumeration can be interesting if not all aspects of the problem have been satisfactorily modeled. This also makes sense for the motivation of Roman Domination (variants). It could be the case that between neighbored regions, there is a conflict unknown to the strategic planner of the army deployment. Such a conflict could be a reason why the regions do not want to defend each other. Enumerating minimal Roman dominating functions was considered by Abu-Khzam et al. [23]. There, it was shown that all pointwise (i.e., for $f,g:V\to \{0,1,2\}$, $f\le g$ if and only if $f\left(v\right)\le g\left(v\right)$ for all $v\in V$) minimal Roman dominating functions of a graph of order n can be enumerated in time $\mathcal{O}\left({1.9332}^n\right)$ with polynomial delay. An enumeration algorithm has polynomial delay if the time between two subsequent outputs of the algorithm can be bounded by some polynomial, as well as the time from the start to the first output and the time between the last output and the termination of the algorithm. This property is interesting if a user (or another program) processes the results in a pipeline fashion. Also, it is not known if there is such an algorithm for enumerating (inclusion-wise) minimal dominating sets. In this context, we remark the following.

Observation 1.

Unless $\mathsf{P}=\mathsf{NP}$, there exists no polynomial-delay enumeration algorithm for (inclusion-wise minimal) perfect codes.

Namely, such a polynomial-delay enumeration algorithm could also be used to decide (in polynomial time) if a perfect code exists in a given graph, a problem known to be NP-hard; see [24]. This contrasts with the polynomial-delay algorithms that we develop in this paper for enumerating minimal unique response and Perfect Roman Dominating Functions. We also obtain input-sensitive enumeration results in this way.

We now collect more notation that we will use in the paper. Let $\mathbb{N}$ denote the set of all non-negative integers (including 0). For $n\in \mathbb{N}$, we will use the notation $\left[n\right]:=\{1,\dots ,n\}$. Let $A,B$ be two sets. $B^A$ is the set of all total functions $f:A\to B$. Likewise, $\left({\displaystyle \genfrac{}{}{0pt}{}{A}{2}}\right)$ is the set of all 2-element subsets of A. For $A\subseteq B$, ${\chi }_A:B\to \mathbb{N}$ denotes the characteristic function (${\chi }_A\left(a\right)=1$ if and only if $a\in A$; ${\chi }_A\left(a\right)=0$, otherwise). Let $G=(V,E)$ be a graph. For a set $A\subseteq V$, the open neighborhood is defined as $N_G\left(A\right):=\left({\bigcup }_{v\in A}{N}_G\left(v\right)\right)$. The closed neighborhood of A is given by $N_G\left[A\right]:=N_G\left(A\right)\cup A$. The private neighborhood of a vertex $v\in A$ with respect to G and A is denoted by $P_{G,A}\left(v\right):=N_G\left[v\right]\backslash N_G[A\backslash \left\{v\right\}]$. Let $G=(V,E)$ be a graph and $f:V\to \{0,1,2\}$. We define $V_i\left(f\right):=\{v\in V\mid f\left(v\right)=i\}$ for $i\in \{0,1,2\}$. If $v\in V$ obeys $f\left(v\right)=2$, then $u\in N_G\left(v\right)$ with $f\left(u\right)=0$ is called a private neighbor of v (with respect to f) if $|N_G\left(u\right)\cap V_2\left(f\right)|=1$. In the previous notation, we dropped the subscript G if it was clear from the context.

Observation 2.

Let $G=(V,E)$ be a graph and $f:V\to \{0,1,2\}$. (1) If f is a perfect Roman dominating function, then for all $v\in V_2\left(f\right)$ and $u\in N\left(v\right)\cap V_0\left(f\right)$, u is a private neighbor of v. (2) If f is a Roman dominating function such that for all $v\in V_2\left(f\right)$ and $u\in N\left(v\right)\cap V_0\left(f\right)$, u is a private neighbor of v, then f is a perfect Roman dominating function.

Observation 3.

Each unique response Roman dominating function on a graph without isolated vertices is a minimal Roman dominating function.

A final note on parameterized complexity: If P is some problem and $\kappa$ is some parameter, we write $\kappa \text{-}P$ to denote the problem P parameterized by $\kappa$.

2. Enumerating Minimal Perfect Roman Domination

The main goal of this section is to find a polynomial-delay algorithm to enumerate all minimal perfect Roman dominating functions even when solving the extension problem is hard, which blocks the standard approach to obtaining such enumeration algorithms.

Remark 1.

It should be mentioned that there are graphs $G=(V,E)$ such that the set of perfect Roman dominating functions on G is not closed under ≤. This means that there exists a perfect Roman dominating function $f\in {\{0,1,2\}}^V$ and a $g\in {\{0,1,2\}}^V$ with $f\le g$ such that g is no perfect Roman dominating function. One example of this is the 4-cycle

$$C_4=(\{v_1,v_2,v_3,v_4\},\{\{v_1,v_2\},\{v_2,v_3\},\{v_3,v_4\},\{v_4,v_1\}\})$$

with the two functions

$$\begin{array}{cccc}\hfill f\left(v_1\right)=0,& f\left(v_2\right)=2,& f\left(v_3\right)=0,\hfill & f\left(v_4\right)=1,\\ \hfill g\left(v_1\right)=0,& g\left(v_2\right)=2,& g\left(v_3\right)=0,\hfill & g\left(v_4\right)=2.\end{array}$$

This contradicts the idea of extension problems as they are defined in [25] because this violates the so-called upward closedness condition, but this condition is a matter of debate even in [25].

We often employ the following characterization result that is of independent interest.

Theorem 1.

Let $G=(V,E)$ be a graph. A function $f:V\to \{0,1,2\}$ is a minimal perfect Roman dominating function if and only if the following conditions are true:

1.

$\forall v\in V_0\left(f\right):|N_G\left(v\right)\cap V_2\left(f\right)|=1$.

2.

$\forall v\in V_1\left(f\right):|N_G\left(v\right)\cap V_2\left(f\right)|\ne 1$.

3.

$\forall v\in V_2\left(f\right):|N_G\left(v\right)\cap V_0\left(f\right)|\ne 0$.

Proof. 

Let f be a minimal perfect Roman dominating function. This implies the first condition. If there exists a $v\in V_1\left(f\right)$ with $|N_G\left(v\right)\cap V_2\left(f\right)|=1$, then $f-{\chi }_{\left\{v\right\}}$ is also a perfect Roman dominating function, cf. Observation 2. For each $v\in V_2\left(f\right)$, $|N_G\left(v\right)\cap V_0\left(f\right)|\ne 0$, as, otherwise, $f-{\chi }_{\left\{v\right\}}$ is also a perfect Roman dominating function.

Now assume f is a function that fulfills these conditions. By Condition 1, we know f is a perfect Roman dominating function. Let g be a minimal perfect Roman dominating function with $g\le f$. Thus, $V_0\left(f\right)\subseteq V_0\left(g\right)$ and $V_2\left(g\right)\subseteq V_2\left(f\right)$ hold. Assume there exists a $v\in V$ with $g\left(v\right)<f\left(v\right)=2$. By Condition 3, there exists some $u\in N_G\left(v\right)\cap V_0\left(f\right)$. Because of condition 1, v is the only neighbor of u with value 2. Hence, $N_G\left(u\right)\cap V_2\left(g\right)\subseteq N_G\left(u\right)\cap (V_2\left(f\right)\backslash \left\{v\right\})=\varnothing$. This contradicts the construction of g as a perfect Roman dominating function. Therefore, $V_2\left(g\right)=V_2\left(f\right)$. If there were a $v\in V$ with $g\left(v\right)=0<1=f\left(v\right)$, then this would contradict that g is a perfect Roman dominating function since $|N_G\left(v\right)\cap V_2\left(g\right)|=|N_G\left(v\right)\cap V_2\left(f\right)|\ne 1$. □

Remark 2.

This result implies that the constant function ${\chi }_V:V\to \{0,1,2\},v\mapsto 1$ is the maximum minimal perfect Roman dominating function with respect to ω for each graph $G=(V,E)$, similar to maximum minimal Roman dominating functions as discussed in [26]. The reason is simple: if there exists a vertex $v\in V$ of value 2, then this vertex needs a neighbor u with value 0. Since u has exactly one neighbor in $V_2\left(f\right)$, $\omega \left(f\right)\le \left|V\right|$ for each perfect Roman dominating function f.

Problem name: Extension Perfect Roman Domination (Ext PRD) Given: A graph $G=(V,E)$ and $f\in {\{0,1,2\}}^V$. Question: Is there a minimal perfect Roman dominating function g on G with $f\le g$?

For the NP-hardness proof, we use Monotone 3-Sat-(2,2). This is a variant of 3-Sat where each clause includes only positive or negative literals and each variables appears twice positive and twice negative in clauses. It is known by [27] that also this restriction of 3-Sat is NP-complete.

Theorem 2.

Extension Perfect Roman Domination is NP-complete even on bipartite graphs of maximum degree 4.

Proof. 

For the NP-hardness result, we employ Monotone 3-Sat-(2,2). So, let $X:=\{x_1,\dots ,x_n\}$ be the set of variables and $C:=\{c_1,\dots ,c_m\}$ the set of clauses. To simplify the notation, denote $X^{\prime }=\{x_i,\overline{x_i}\mid i\in \left[n\right]\}$. For each $j\in \left[m\right]$, let $c_j=l_{j,1}\vee l_{j,2}\vee l_{j,3}\in C$ with $l_{j,1},l_{j,2},l_{j,3}\in X^{\prime }$.

Define $G=(V,E)$ with

$$\begin{array}{cc}\hfill V:=& \{v_i,\overline{v_i},w_i,y_i,z_i\mid i\in \left[n\right]\}\cup \{p_j,q_j,r_j\mid j\in \left[m\right]\}\hfill \\ \hfill E:=& \{\{v_i,w_i\},\{\overline{v_i},w_i\},\{v_i,y_i\},\{\overline{v_i},y_i\},\{z_i,y_i\}\mid i\in \left[n\right]\}\cup \hfill \\ \hfill & \{\{v_i,p_j\}\mid j\in \left[m\right],k\in \left[3\right],i\in \left[n\right],x_i=l_{j,k}\}\cup \hfill \\ \hfill & \{\{\overline{v_i},p_j\}\mid j\in \left[m\right],k\in \left[3\right],i\in \left[n\right],\overline{x_i}=l_{j,k}\}\cup \hfill \\ \hfill & \{\{q_j,p_j\},\{q_j,r_j\}\mid j\in \left[m\right]\}.\hfill \end{array}$$

The gadgets are also depicted in Figure 1. Furthermore, let

$$f:=2·{\chi }_{\{q_j\mid j\in \left[m\right]\}\cup \{y_i\mid i\in \left[n\right]\}}+{\chi }_{\{p_j\mid j\in \left[m\right]\}}\in {\{0,1,2\}}^V.$$

Figure 1. Construction for Theorem 2.

Clearly, G can be constructed in polynomial time. Furthermore, the sets $A:=\{v_i,\overline{v_i},z_i\mid i\in \left[n\right]\}\cup \{q_j\mid j\in \left[m\right]\}$ and $B:=\{w_i,y_i\mid i\in \left[n\right]\}\cup \{p_j,r_j\mid j\in \left[m\right]\}$ are partition classes. This is easy to observe, as in each of the edges, we mention first the element of A and then the one of B. Since we consider Monotone 3-Sat-(2,2), for all $i\in \left[n\right],j\in \left[m\right]$

$$\begin{array}{cc}\hfill & deg\left(r_j\right)=deg\left(z_i\right)=1<deg\left(w_i\right)=deg\left(q_j\right)=2<deg\left(y_i\right)=3\hfill \\ \hfill <& deg\left(v_i\right)=deg\left(\overline{v_i}\right)=deg\left(p_j\right)=4.\hfill \end{array}$$

Claim 1.

There is an assignment ϕ satisfying C if and only if there is a minimal perfect Roman dominating function $g\in {\{0,1,2\}}^V$ with $f\le g$.

Proof. 

Let $\varphi$ be an assignment satisfying the clauses. Then, define

$$g:=f+2·{\chi }_{\{v_i\mid \varphi \left(x_i\right)=1\}\cup \{\overline{v_i}\mid \varphi \left(x_i\right)=0\}}.$$

Trivially, $f\le g$. For $j\in \left[m\right]$, $r_j\in V_0\left(g\right)$ is only dominated by $q_j\in V_2\left(g\right)$. Let $i\in \left[n\right]$. Observe that $z_i\in V_0\left(g\right)$ and that $N\left(z_i\right)\cap V_2\left(g\right)=\left\{y_i\right\}$. The last type of vertex to discuss in $V_0\left(g\right)$ is $w_i$. If $\varphi \left(x_i\right)=1$, $w_i$ is only dominated by $v_i$. For $\varphi \left(x_i\right)=0$, $N\left(w_i\right)\cap V_2\left(g\right)=\left\{\overline{v_i}\right\}$. Hence, the first condition of Theorem 1 is fulfilled.

In order to see the validity of the second condition, let $j\in \left[m\right]$. Assume $c_j$ includes only positive literals (otherwise, the proof is analogous). Since $\varphi$ is a solution to the SAT instance, there exists $x_i\in c_j$ with $\varphi \left(x_i\right)=1$, which implies $|N\left(p_j\right)\cap V_2\left(g\right)|\ge 2$. As $V_1\left(g\right)=\{p_j\mid j\in \left[m\right]\}$, the second condition is also satisfied.

This leaves us to show the last condition. For each $j\in \left[m\right]$, $N\left(r_j\right)\cap V_2\left(g\right)=\left\{q_j\right\}$. Let $i\in \left[n\right]$. The vertex $z_i$ is a private neighbor of $y_i\in V_2\left(g\right)$. Since $\varphi$ is an assignment, $w_i$ is the private neighbor of the vertex in $V_2\left(g\right)\cap \{v_i,\overline{v_i}\}$. Hence, g is a minimal perfect Roman dominating function.

For the reverse direction, assume there is a minimal perfect Roman dominating function $g\in {\{0,1,2\}}^V$ with $f\le g$. Observe that $V\backslash N\left(V_2\left(f\right)\right)=\{w_i\mid i\in \left[n\right]\}$. Because each vertex in $V_2\left(g\right)$ needs to have a private neighbor, $V_2\left(g\right)\backslash V_2\left(f\right)\subseteq \{v_i,\overline{v_i}\mid i\in \left[n\right]\}$. For any $i\in \left[n\right]$, $\{v_i,\overline{v_i}\}⊈V_2\left(g\right)$. Otherwise, $v_i$ would not have a private neighbor.

Define $\varphi :={\chi }_{\{x_i\mid i\in \left[n\right],g\left(v_i\right)=2\}}$. Assume there is a clause $c_j$ which is not satisfied by $\varphi$. Then, $q_j$ is the only neighbor of $p_j$ in $V_2\left(g\right)$. Since $g\left(p_j\right)=1$, this contradicts Condition 2 of Theorem 1 and g is not a minimal perfect Roman dominating function. Hence, $\varphi$ is a solution to the Sat instance. □

This proves that we have described a valid polynomial-time computable reduction and hence we have shown NP-hardness. Membership in NP is easy by a guess-and-check approach. This concludes the proof of Theorem 2. □

We use Theorem 1 also to obtain the announced polynomial-delay enumeration algorithm. This algorithm uses the idea that there is a bijection between all minimal perfect Roman dominating functions and all minimal Roman dominating functions of a graph. To show this bijection, we need the following characterization theorem from [23].

Theorem 3.

Let $G=\left(V,E\right)$ be a graph, $f:V\to \{0,1,2\}$ be a function and let $G^{\prime }:=G\left[V_0\left(f\right)\cup V_2\left(f\right)\right]$. Then, f is a minimal Roman dominating function if and only if the following holds:

1.

$N_G\left[V_2\left(f\right)\right]\cap V_1\left(f\right)=\varnothing$.

2.

$\forall v\in V_2\left(f\right):P_{G^{\prime },V_2\left(f\right)}\left(v\right)⊈\left\{v\right\}$.

3.

$V_2\left(f\right)$ is a minimal dominating set on $G^{\prime }$.

Let $G=(V,E)$ be a graph. Define the following sets of functions:

$\mu \text{-}\mathcal{RDF}\left(G\right)=\{f:V\to \{0,1,2\}\mid f$ is a minimal Roman dominating function} and

$\mu \text{-}\mathcal{PRDF}\left(G\right)=\{f:V\to \{0,1,2\}\mid f$ is a minimal perfect Roman dominating function}.

Theorem 4.

Let $G=(V,E)$ be a graph. There is a bijection $B:\mu \text{-}\mathcal{RDF}\left(G\right)\to \mu \text{-}\mathcal{PRDF}\left(G\right)$. Furthermore, $B\left(f\right)$ and $B^{-1}\left(g\right)$ can be computed in polynomial time (with respect to G) for each $f\in \mu \text{-}\mathcal{RDF}\left(G\right)$ and $g\in \mu \text{-}\mathcal{PRDF}\left(G\right)$.

Proof. 

Let $f\in \mu \text{-}\mathcal{RDF}\left(G\right)$ and $g\in \mu \text{-}\mathcal{PRDF}\left(G\right)$. Define $B\left(f\right)$ by the three sets

$$\begin{array}{cc}\hfill V_0\left(B\left(f\right)\right)=& \{v\in V_0\left(f\right)\mid |N_G\left(v\right)\cap V_2\left(f\right)|=1\},\hfill \\ \hfill V_1\left(B\left(f\right)\right)=& \{v\in V_0\left(f\right)\mid |N_G\left(v\right)\cap V_2\left(f\right)|\ge 2\}\cup V_1\left(f\right),V_2\left(B\left(f\right)\right)=V_2\left(f\right).\hfill \end{array}$$

By the definition of B, $|N_G\left(v\right)\cap V_2\left(f\right)|=1$ holds for all $v\in V_0\left(B\left(f\right)\right)$. Since each $v\in V$ with $f\left(v\right)=2$ needs a private neighbor except itself by Theorem 3, $N_G\left(v\right)\cap V_0\left(B\left(f\right)\right)\ne \varnothing$ holds. As any $v\in V_1\left(f\right)$ has no neighbor in $V_2\left(f\right)$ and any $v\in V_1\left(B\left(f\right)\right)\backslash V_1\left(f\right)$ has at least two neighbors in $V_2\left(f\right)$, all conditions of Theorem 1 are met. Therefore, $B\left(f\right)\in \mu \text{-}\mathcal{PRDF}\left(G\right)$.

Define $B^{-1}\left(g\right)$ by the three sets

$$\begin{array}{cc}\hfill V_0\left(B^{-1}\left(g\right)\right)=& V_0\left(g\right)\cup \{v\in V_1\left(g\right)\mid |N_G\left(v\right)\cap V_2\left(g\right)|\ge 2\},\hfill \\ \hfill V_1\left(B^{-1}\left(g\right)\right)=& \{v\in V_1\left(g\right)\mid |N_G\left(v\right)\cap V_2\left(g\right)|=0\},V_2\left(B^{-1}\left(g\right)\right)=V_2\left(f\right).\hfill \end{array}$$

By the definition of $B^{-1}$, $N_G\left(v\right)\cap V_2\left(B^{-1}\left(g\right)\right)=\varnothing$ for each $v\in V_1\left(B^{-1}\left(g\right)\right)$. By Theorem 1, each $v\in V_0\left(g\right)$ has exactly one neighbor in $V_2\left(g\right)$. Therefore, each vertex in $V_0\left(B^{-1}\left(g\right)\right)$ has a neighbor in $V_2\left(B^{-1}\left(g\right)\right)$, and $V_2\left(B^{-1}\left(g\right)\right)$ is a dominating set on $G[V_0\left(B^{-1}\left(g\right)\right)\cup V_2\left(B^{-1}\left(g\right)\right)]$. Theorem 1 implies that each $v\in V_2\left(g\right)$ has a $u\in N_G\left(v\right)\cap V_0\left(g\right)$ with $\left\{v\right\}=N_G\left(u\right)\cap V_2\left(g\right)$. Hence, u is a private neighbor of v and $B^{-1}\left(g\right)\in \mu \text{-}\mathcal{RDF}\left(G\right)$. This leaves to show that $B^{-1}\left(B\left(f\right)\right)=f$ and $B\left(B^{-1}\left(g\right)\right)=g$. Trivially,

$$V_2\left(B^{-1}\left(B\left(f\right)\right)\right)=V_2\left(f\right)\mathrm{and}{V}_2\left(B\left(B^{-1}\left(g\right)\right)\right)=V_2\left(g\right)$$

holds. Let $v\in V_1\left(f\right)$. By Theorem 3, we know $N_G\left(v\right)\cap V_2\left(f\right)=\varnothing$. This implies $v\in V_1\left(B\left(f\right)\right)\cap V_1\left(B^{-1}\left(B\left(f\right)\right)\right)$. Let $v\in V_0\left(f\right)$ with $|N_G\left(v\right)\cap V_2\left(f\right)|=1$. Thus, $v\in V_0\left(B\left(f\right)\right)\cap V_0\left(B^{-1}\left(B\left(f\right)\right)\right)$. Let $v\in V_0\left(f\right)$ with $|N_G\left(v\right)\cap V_2\left(f\right)|\ge 2$. Therefore, $v\in V_1\left(B\left(f\right)\right)$ holds. The definition of $B^{-1}$ implies $v\in V_0\left(B^{-1}\left(B\left(f\right)\right)\right)$. Hence, $B^{-1}\left(B\left(f\right)\right)=f$. Assume $v\in V_0\left(g\right)$. Theorem 1 implies $|N_G\left(v\right)\cap V_2\left(f\right)|=1$. Therefore, $v\in V_0\left(B\left(B^{-1}\left(f\right)\right)\right)\cap V_0\left(B^{-1}\left(f\right)\right)$. For $v\in V_1\left(g\right)$ with $N_G\left(v\right)\cap V_2\left(g\right)=\varnothing$, the construction of the functions $B,B^{-1}$ implies $v\in V_1\left(B\left(B^{-1}\left(f\right)\right)\right)\cap V_1\left(B^{-1}\left(f\right)\right)$. Let $v\in V_1\left(g\right)$ with $|N_G\left(v\right)\cap V_2\left(g\right)|\ge 2$. This leads to $v\in V_0\left(B^{-1}\left(g\right)\right)$ and $v\in V_1\left(B\left(B^{-1}\left(g\right)\right)\right)$. Hence, $B\left(B^{-1}\left(g\right)\right)=g$. Therefore, the theorem holds. □

This bijection is a so-called parsimonious reduction. This is a class of reductions designed for enumeration problems. For more information, we refer to [28]. Even without this paper, Theorem 4 implies some further results thanks to [23].

Corollary 1.

There are graphs of order n that have at least ${\sqrt[5]{16}}^n\in \Omega \left({1.7441}^n\right)$ many minimal perfect rdf.

Theorem 5.

There is a polynomial-space, polynomial-delay algorithm that enumerates all minimal perfect Roman dominating functions of a given graph of order n in time ${\mathcal{O}}^{*}\left({1.9332}^n\right)$.

Remark 3.

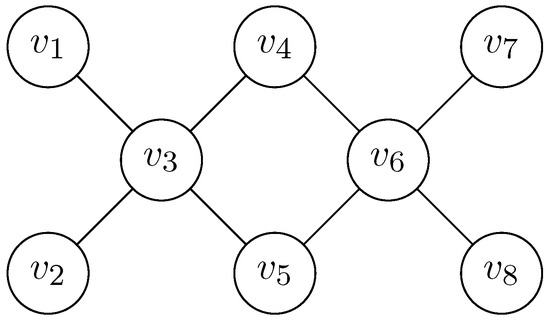
It should be mentioned that the function B defined in the proof of Theorem 4 inherits inclusion-wise minimality, but this does not mean that, if f is a minimum Roman Dominating Function, then $B\left(f\right)$ is a minimum perfect Roman dominating function. To see this, we consider the graph $G=(V,E)$ with $V:=\{v_1,\dots ,v_8\}$ and

$$E:=\{\{v_1,v_3\},\{v_2,v_3\},\{v_4,v_3\},\{v_5,v_3\},\{v_4,v_6\},\{v_5,v_6\},\{v_7,v_6\},\{v_8,v_6\}\}.$$

The graph is visualized in Figure 2. Since $v_1,v_2$ and $v_7,v_8$ are pairs of false twins and $v_1,v_7$ have no common neighbors, for each Roman dominating function f on G, $\omega \left(f\right)\ge 4$. Therefore, $f\in {\{0,1,2\}}^V$ with $V_0\left(f\right)=\{v_1,v_2,v_4,v_5,v_7,v_8\}$, $V_1\left(f\right)=\varnothing$, and $V_2\left(f\right)=\{v_3,v_6\}$ is a minimum Roman dominating function. $B\left(f\right)$ is given by $V_0\left(B\left(f\right)\right)=\{v_1,v_2,v_7,v_8\}$, $V_1\left(B\left(f\right)\right)=\{v_4,v_5\}$, and $V_2\left(f\right)=\{v_3,v_6\}$. The weight is $\omega \left(B\left(f\right)\right)=6$. The minimal perfect Roman dominating function $g\in \{0,1,2\}$ with $V_0\left(g\right)=\{v_1,v_2,v_4,v_5\}$, $V_1\left(g\right)=\{v_6,v_7,v_8\}$ and $V_2\left(g\right)=\left\{v_3\right\}$ fulfills $\omega \left(g\right)=5$. Hence, $B\left(f\right)$ is no minimum perfect Roman dominating function.

Figure 2. Counter-example of Remark 3.

Let $h\in {\{0,1,2\}}^V$ be a minimal perfect Roman dominating function. For $h\left(v_3\right)=h\left(v_6\right)=2$, $h=B\left(f\right)$, as $v_1,v_2,v_7,v_8\in N\left(V_2\left(h\right)\right)$ are pendant. Assume $h\left(v_3\right)=2\ne h\left(v_6\right)$. If $h\left(v_4\right)=2$ (respectively, $h\left(v_5\right)=2$), then $h\left(v_7\right)=h\left(v_8\right)=1$ and $\omega \left(h\right)\ge 6$. For $h\left(v_7\right)=2$ (respectively, $h\left(v_8\right)=2$), $h\left(v_8\right)=1$ (respectively, $h\left(v_7\right)=1$) and $\omega \left(g\right)=5\ge \omega \left(h\right)$. As $v_1,v_2\notin V_2\left(h\right)$ for $h\left(v_3\right)=2$, the remaining possibility is $h=g$. Thus, $\omega \left(g\right)=5\le \omega \left(h\right)$ holds for each minimal perfect Roman dominating function with $h\left(v_3\right)=2\ne h\left(v_6\right)$. Analogously, for perfect Roman dominating functions h with $h\left(v_6\right)\ne 2=h\left(v_3\right)$, $\omega \left(g\right)=5\le \omega \left(h\right)$. Let $h\left(v_3\right)\ne 2$ and $h\left(v_6\right)\ne 2$. Since $N\left(v_i\right)\subseteq \{v_3,v_6\}$ for $i\in \{1,2,4,5,7,8\}$, $v_1,v_2,v_4,v_5,v_7,v_8\notin V_0\left(h\right)$. Hence, $\omega \left(h\right)\ge 6$ and g is a minimum perfect Roman dominating function. Furthermore, $B^{-1}\left(g\right)=g$ is not a minimum Roman dominating function.

According to [29], we obtain some further results for special graph classes: Let $G=(V,E)$, with $n:=\left|V\right|$ being of the order of G. If G is a forest or interval graph, then there is a perfect Roman dominating function enumeration algorithm that runs in time ${\mathcal{O}}^{*}\left({\sqrt{3}}^n\right)$ with polynomial delay. For both graph classes, a graph with many isolated edges is an example of a graph with ${\sqrt{3}}^n$ many minimal perfect Roman dominating function. This is also the worst-case example for chordal graphs which is known so far. We can enumerate all perfect Roman dominating functions of these graphs in time $\mathcal{O}(1.{8940}^n)$. If G is a split or cobipartite graph, then we can enumerate all perfect Roman dominating functions of G in ${\mathcal{O}}^{*}\left({\sqrt[3]{3}}^n\right)$ with polynomial delay. Further, both classes include graphs of order n with $\Omega \left({\sqrt[3]{3}}^n\right)$ many perfect Roman dominating functions. There is also a polynomial-time recursive algorithm to count all perfect Roman dominating functions of paths. The enumeration of unique response Roman dominating functions in split graphs is considered in Section 3.4.

3. Complexity and Enumeration in Special Graph Classes

In this section, we consider the complexity of our problems Perfect Roman Domination and Unique Response Roman Domination on different graph classes: interval, split, cobipartite, and chordal bipartite graphs. Perfect Roman Domination is known to be NP-complete on chordal graphs [20].

3.1. Interval Graphs

We first start with a polynomial-time algorithm for Perfect Roman Domination for interval graphs. A graph $G=(V,E)$ is called an interval graph (see [30]) if, for $v\in V$, there is an interval $I_v=[l_v,r_v]$ such that $\{v,u\}\in E$ if and only if $I_v\cap I_u\ne \varnothing$. We can assume that the interval representation obeys $\forall u,v\in V:r_u=r_v\Rightarrow u=v$.

Theorem 6.

Perfect Roman Domination is polynomial-time solvable on interval graphs.

Proof. 

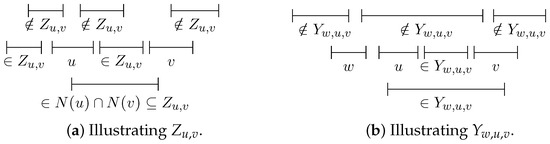
Let $G=(V,E)$ be an interval graph such that $I_v=[l_v,r_v]$ is the interval representation of $v\in V$. The dynamic programming works from “left to right” according to some linear extension of the partial order defined as $w\le v$ if and only if $l_w\le l_v\wedge r_w\le r_v$. For $v\in V$, $L_v:=\{w\in V\mid l_w\le r_v\}$ denotes the set of vertices which are dominated by v or “to the left” of $I_v$. To simplify our notation, we define $P_v:=\{w\in V\backslash \left\{v\right\}\mid w\le v\}$ to easily refer to the already considered vertices in the dynamic program. $W_v:=\{w\in V\mid r_v<r_w\}$ is the set of not yet considered vertices. For $v\in V$, $u\in P_v$ and $w\in P_u$, define $Z_{u,v}:=\left(L_v\backslash (N\left[u\right]\cup N\left[v\right])\right)\cup (N\left(u\right)\cap N\left(v\right))$ and $Y_{w,u,v}:=\left(\left(N\left(u\right)\cap N\left(v\right)\right)\backslash N\left[w\right]\right)\cup \left(L_v\backslash (L_u\cup N\left[v\right])\right)$; see Figure 3. All these sets and their cardinalities can be computed before the actual dynamic programming starts. Also, we can compute the perfect Roman dominating functions that set at most one vertex to 2 and store their minimum weight in ${min}_{\le 1}$.

Figure 3. Examples illustrating our notions.

We need some more notation to formulate the dynamic programming algorithm and prove its correctness. For $v\in V$ and $u\in P_v$, define ${\Gamma }_{u,v}:=\{f\in {\{0,1,2\}}^V\mid f{|}_{L_v}\in \mathcal{PRDF}\left(G\left[L_v\right]\right)\wedge f\left(u\right)=f\left(v\right)=2\wedge \forall w\in W_u\backslash \left\{v\right\}:f\left(w\right)\ne 2\}$ and ${\gamma }_{u,v}={min}_{f\in {\Gamma }_{u,v}}\omega \left(f\right)$. In the following, $f_{u,v}^{\prime }$ will denote one function from ${\Gamma }_{u,v}$ that attains this minimum, i.e., $\omega \left(f_{u,v}^{\prime }\right)={\gamma }_{u,v}$. For the inductive computation, we will reuse the values ${\gamma }_{w,u}$ with $w\in P_u$. For the correctness of this approach, the following observations are helpful.

• $Z_{u,v}$ is connected to the function $f_{u,v}\in {\Gamma }_{u,v}$ by setting $V_2\left(f_{u,v}\right)=\{u,v\}$ and $V_1\left(f_{u,v}\right)=Z_{u,v}$.
• $Y_{w,u,v}=V_1\left(f_{w,u,v}\right)\backslash V_1\left(f_{w,u}^{\prime }\right)$, where $f_{w,u,v}$ is the auxiliary perfect Roman dominating function which we will construct from $f_{w,u}^{\prime }$ in the induction step.
• If $f\in {\Gamma }_{u,v}$, then $\tilde{f}:=f+{\chi }_{V\backslash L_v}$ is a perfect Roman dominating function on G. If f is a minimum, then $\tilde{f}$ is a minimum perfect Roman dominating function on G.

By the third property, after the inductive computations,

$$min\left\{{\min }_{\le 1},min\{{\gamma }_{u,v}+|V\backslash L_v\left|\right|v\in V,u\in P_v\}\right\}$$

gives the minimum weight of any perfect Roman dominating function for G.

Assume now that v is a vertex for which we want to compute all relevant ${\gamma }_{u,v}$ next, with $u\in P_v$. The following claim contains a formula that describes how to do this. It implicitly also covers the initial step: then, ${\gamma }_{u,v}=4+\left|Z_{u,v}\right|$ since $P_u=\varnothing$.

Claim 2.

Let $v\in V$ and $u\in P_v$. Then,

$${\gamma }_{u,v}=min\{4+|Z_{u,v}|,2-|\left\{v\right\}\cap N\left(u\right)\cap N\left(w\right)|+{\gamma }_{w,u}+|Y_{w,u,v}|\mid w\in P_u\}.$$

Proof. 

Let $f_{w,u}^{\prime }\in {\Gamma }_{w,u}$ for $w\in P_u$ such that $\omega \left(f_{w,u}^{\prime }\right)={\gamma }_{w,u}$. Define

$$f_{w,u,v}:=f_{w,u}^{\prime }+(2-{\chi }_{N\left(u\right)\cap N\left(w\right)})·{\chi }_{\left\{v\right\}}+{\chi }_{Y_{w,v,u}}.$$

Clearly, $\omega \left(f_{w,u,v}\right)={\gamma }_{w,u}+2-|\left\{v\right\}\cap N\left(u\right)\cap N\left(w\right)|+|Y_{w,u,v}|$ and $f_{w,u,v}\left(x\right)=f_{w,u}^{\prime }\left(x\right)\in \{0,1,2\}$ for $x\in V\backslash (\left\{v\right\}\cup Y_{w,u,v})$. In particular, $f_{w,u,v}\left(u\right)=f_{w,u}^{\prime }\left(u\right)=2$. (More generally, $V_2\left(f_{w,u,v}\right)\supseteq V_2\left(f_{w,u}^{\prime }\right)$.) Now we consider $x\in Y_{w,u,v}$. For $x\in L_v\backslash (L_u\cup N\left(v\right))\subseteq V\backslash L_u$, $f_{w,u}^{\prime }\left(x\right)=0$. Otherwise, $f_{w,u}^{\prime }-{\chi }_{\left\{x\right\}}$ would belong to ${\Gamma }_{w,u}$ with $\omega \left(f_{w,u}^{\prime }-{\chi }_{\left\{x\right\}}\right)<\omega \left(f_{w,u}^{\prime }\right)$. So assume $x\in \left(N\left(v\right)\cup N\left(u\right)\right)\backslash N\left(w\right)$. Since $w\in P_u$, $r_w<l_x<r_u<r_v$. If $\varnothing \ne (V_2\left(f_{w,u}^{\prime }\right)\backslash \left\{u\right\})\cap N\left(x\right)$, this would contradict the fact that $f_{w,u}^{\prime }\left(z\right)\ne 2$ for all $z\in W_w\backslash \left\{u\right\}$. Hence, $f_{w,u}^{\prime }\left(z\right)=0$ because of minimality. Hence, $Y_{w,u,v}\subseteq V_0\left(f_{w,u}^{\prime }\right)$ and $f_{w,u,v}\left(x\right)\in \{0,1,2\}$ for $x\in Y_{w,u,v}$.

Now consider $f_{w,u,v}\left(v\right)$. As $f_{w,u}^{\prime }\left(v\right)\ne 2$, $v\notin Y_{w,u,v}$ and $f_{w,u}^{\prime }\left(v\right)+1\le f_{w,u,v}\left(v\right)\le f_{w,u}^{\prime }\left(v\right)+2$, i.e., $1\le f_{w,u,v}\left(v\right)\le 3$. We will next show that $1\le f_{w,u,v}\left(v\right)\le 2$. For the sake of contradiction, assume $f_{w,u,v}\left(v\right)=3$. Then, $f_{w,u}^{\prime }\left(v\right)=1$ and $v\notin N\left(u\right)\cap N\left(w\right)$. As (in addition) $r_w<r_u<r_v$ and $l_w\le l_u\le l_v$, we must have $r_w<l_v$. Hence, $\{w,v\}\notin E$. If $N\left(v\right)\cap V_2\left(f_{w,u}^{\prime }\right)\subseteq \left\{u\right\}$, then $f_{w,u}^{\prime }-{\chi }_{\left\{v\right\}}\in {\Gamma }_{w,u}$, contradicting minimality of $f_{w,u}^{\prime }$ in ${\Gamma }_{w,u}$. If $\varnothing \ne (V_2\left(f_{w,u}^{\prime }\right)\cap N\left(v\right))\backslash \{u,w\}$, this would contradict the construction of ${\Gamma }_{w,u}$, as $r_w<l_v<r_x$. Hence, $f_{w,u,v}\left(v\right)\in \{1,2\}$. If $f_{w,u,v}\left(v\right)=1$, then $v\in N\left(u\right)\cap N\left(w\right)\subseteq L_u$ and $f_{w,u}^{\prime }\left(v\right)=0$. But then $f_{w,u}^{\prime }{|}_{L_u}$ would not be a perfect Roman dominating function. Therefore, $f_{w,u,v}\left(v\right)=2$.

Now we want show that $f_{w,u,v}{|}_{L_v}$ is a perfect Roman dominating function on $G\left[L_v\right]$. Since $f_{w,u}^{\prime }$ is a Roman dominating function on $G\left[L_u\right]$ and $L_v=L_u\cup N\left[v\right]\cup (L_v\backslash (L_u\cup N\left[v\right]))\subseteq L_u\cup N\left[v\right]\cup Y_{w,u,v}$, $f_{w,u,v}{|}_{L_v}$ is a Roman dominating function on $G\left[L_v\right]$. Assume there is an $x\in V_0\left(f_{w,u,v}{|}_{L_v}\right)$ with $|V_2\left(f_{w,u,v}{|}_{L_v}\right)\cap N\left(x\right)|>1$. Since $V_2\left(f_{w,u,v}\right)=V_2\left(f_{w,u}^{\prime }\right)\cup \left\{v\right\}$ (also implying that for all $y\in W_u\backslash \left\{v\right\}$, $f_{w,u,v}\left(y\right)\ne 2$), $x\in N\left(v\right)$. For each $x\in N\left(v\right)\cap N\left(u\right)$, either $x\in Y_{w,u,v}$ or $x\in N\left(u\right)\cap N\left(w\right)\subseteq V_1\left(f_{w,u}^{\prime }\right)\cup V_2\left(f_{w,u}^{\prime }\right)$. Hence, $x\in N\left(v\right)\backslash N\left(u\right)$ and $N\left(x\right)\subseteq W_u\subseteq W_w$ (otherwise $u\notin P_v$). By definition of ${\Gamma }_{w,u}$, $N\left(x\right)\cap V_2\left(f_{w,u,v}\right)=\left\{v\right\}$. In total, $f_{w,u,v}\in {\Gamma }_{u,v}$.

By the definition of ${\Gamma }_{u,v}$, $\{u,v\}\subseteq V_2\left(f_{u,v}^{\prime }\right)$. (a) Assume $\{u,v\}=V_2\left(f^{\prime }\right)$. Since $f_{u,v}^{\prime }{|}_{L_v}$ is a perfect Roman dominating function on $G\left[L_v\right]$, $L_v\backslash (N\left[u\right]\cup N\left[v\right])\subseteq V_1\left(f_{u,v}^{\prime }\right)$, as these vertices are not dominated. Further, $N\left(u\right)\cap N\left(v\right)\subseteq V_1\left(f_{u,v}^{\prime }\right)$ because these vertices have two neighbors in $V_2\left(f_{u,v}^{\prime }\right)$. So $f:=2·{\chi }_{\{u,v\}}+{\chi }_{Z_{u,v}}\le f_{u,v}^{\prime }$. As $f\in {\Gamma }_{u,v}$, $f=f_{u,v}^{\prime }$ with $\omega \left(f\right)=4+\left|Z_{u,v}\right|$. (b) Assume $\{u,v\}⊊V_2\left(f_{u,v}^{\prime }\right)$. Then, let $w\in V_2\left(f_{u,v}^{\prime }\right)\backslash \{u,v\}$ with maximal $r_w$. Since $w\notin W_u\backslash \left\{v\right\}$, $r_w<r_u$. If $l_u<l_w$, $f_{u,v}^{\prime }-{\chi }_{\left\{w\right\}}\in {\Gamma }_{u,v}$ with $\omega \left(f_{u,v}^{\prime }-{\chi }_{\left\{w\right\}}\right)<f_{u,v}^{\prime }$. Therefore, $w\in P_u$ and for each $y\in V_2\left(f_{u,v}^{\prime }\right)\backslash \left\{v\right\}$, $N\left(y\right)\subseteq L_u$. Hence, $x\in L_v\backslash \left(L_u\cup N\left[v\right]\right)$ has no neighbor in $V_2\left(f_{u,v}^{\prime }\right)$ and $L_v\backslash \left(L_u\cup N\left[v\right]\right)\subseteq V_1\left(f_{u,v}^{\prime }\right)$. Consider a $x\in \left(N\right(u)\cap N(v\left)\right)\backslash N\left(w\right)$. Since x has more than one neighbor in $V_2\left(f_{u,v}^{\prime }\right)$, $f_{u,v}^{\prime }\left(x\right)>0$. Clearly, $r_w<l_x<r_u$ holds. By the definition of w, $f_{u,v}^{\prime }\left(x\right)\ne 2$. Define $f^{″}:=f_{u,v}^{\prime }-{\chi }_{Y_{w,u,v}}-(2-{\chi }_{N\left(u\right)\cap N\left(u\right)})·{\chi }_{\left\{v\right\}}$. Clearly, $\omega \left(f^{\prime \prime }\right)=\omega \left(f_{u,v}^{\prime }\right)-2+|\left\{v\right\}\cap N\left(u\right)\cap N\left(w\right)|-|Y_{w,u,v}|$. We want to show that $f^{″}\in {\Gamma }_{w,u}$ to obtain ${\gamma }_{w,u}<\omega \left(f^{\prime \prime }\right)$ and

$$min\{4+|Z_{u,v}|,2-|\left\{v\right\}\cap N\left(u\right)\cap N\left(w\right)|+{\gamma }_{w,v}+|Y_{w,u,v}|\mid w\in P_u\}\le \omega \left(f_{u,v}^{\prime }\right).$$

By the definition of w, $f^{\prime \prime }\left(y\right)\ne 2$ for all $y\in W_w\backslash \left\{u\right\}$. Further, $f^{″}\left(w\right)=f^{″}\left(u\right)=2$. This leaves us to show that $\tilde{f}=f^{\prime \prime }{|}_{L_u}\in \mathcal{PRDF}\left(G\left[L_u\right]\right)$. Assume there is a $x\in V_0\left(\tilde{f}\right)$ with $|N\left(x\right)\cap V_2\left(\tilde{f}\right)|\ne 1$. As $V_2\left(f^{\prime \prime }\right)=V_2\left(f_{u,v}^{\prime }\right)\backslash \left\{v\right\}$, for $x\in V_0\left(f_{u,v}^{\prime }\right)\backslash (N\left[v\right]\cup Y_{u,v,w})$, $|N\left(x\right)\cap V_2\left(\tilde{f}\right)|=1$. Since $L_u\cap \left(L_v\backslash \left(L_u\cup N\left[v\right]\right)\right)=\varnothing$, we can assume $x\in N\left[v\right]\cap L_u$. For $y\in N\left(v\right)\cup N\left(u\right)\cup N\left(w\right)$, $\tilde{f}\left(y\right)=f^{″}\left(y\right)=1$ and $w\in V_2\left(\tilde{f}\right)$. Let $x\in N\left(u\right)\backslash N\left[w\right]$. Hence, $|N\left(x\right)\cap V_2\left(\tilde{f}\right)|>1$. This contradicts the definition of w, as there is a $z\in V_2\left(\tilde{f}\right)\backslash \left\{u\right\}=V_2\left(f_{u,v}^{\prime }\right)\backslash \{u,v\}$ with $r_w<l_x<r_z$. If $x\in N\left(v\right)\backslash N\left(u\right)$, then $r_u<l_x$ and $x\in L_u$, since $l_u<l_v$ and $r_u<r_v$. Now consider $x=v$. For $v\in N\left(u\right)\cap N\left(w\right)$, $\tilde{f}\left(v\right)=1$. If $v\notin N\left(u\right)$, then $r_u<l_v$ and $v\notin L_u$. Since the case $v\in N\left(u\right)\backslash N\left(w\right)$ is discussed above, this completes the proof of the claim. □

Let f be a minimum perfect Roman dominating function on G. If there is a $u\in V$ with $V_2\left(f\right)=\left\{u\right\}$, then $\omega \left(u\right)=|V\backslash N\left[u\right]|+2$. So assume $|V_2\left(f\right)|>1$. Then, let $u,v\in V_2\left(f\right)$ such that for all $w\in V_2\left(f\right)\backslash \{v,u\}$, $r_w<r_u<r_v$. Therefore, $N\left(x\right)\backslash L_v=\varnothing$ for each $x\in V_2\left(f\right)$. So f is perfect Roman dominating function on $L_v$. Further $V\backslash L_v\subseteq V_1\left(f\right)$. Because f is also minimal, $l_u<l_v$. Hence, ${\gamma }_{v,u}+|V\backslash L_v|\le \omega \left(f\right)$. Since $f_{u,v}+{\chi }_{V\backslash L_v}$ is also a perfect Roman dominating function for $f_{u,v}\in {\Gamma }_{u,v}$, equality holds.

In total, an algorithm only has to compute ${\gamma }_{u,v}+|V\backslash L_v|$ for each $v\in V$ and $u\in P_v$ as explained above. Clearly, ${\gamma }_{u,v}$ can be computed in polynomial time, and as there are at most ${\left|V\right|}^2$ many such pairs, the whole algorithm runs in polynomial time. This concludes the proof of Theorem 6. □

3.2. Split Graphs

A split graph $G=(V,E)$ is a graph in which the vertex set V can be partitioned into $C,I$, where C is a clique and I is an independent set of G. It seems to be open as to which complexity class Perfect Roman Domination and Unique Response Roman Domination belong on split graphs as explicitly asked in [19]. We will answer this question in a somewhat surprising manner: while Unique Response Roman Domination can be solved in linear time, Perfect Roman Domination turns out to be NP-complete. First, we will consider unique response Roman dominating functions on split graphs and prove a combinatorial result.

Lemma 1.

Let $G=(V,E)$ be a connected split graph with a clique C and an independent set I such that $V=C\cup I$ and $C\cap I=\varnothing$. For each unique response Roman dominating function $f:V\to \{0,1,2\}$, one of the following conditions holds:

1.

$V_2\left(f\right)\cap I=\varnothing$ and $|V_2\left(f\right)\cap C|\le 1$;

2.

$V_2\left(f\right)\subseteq I$.

Proof. 

Suppose that $V_2\left(f\right)⊈I$. By the definition of unique response Roman dominating function, two vertices of C cannot have the value 2 since C is a clique. Hence, $|V_2\left(f\right)\cap C|\le 1$. For the sake of contradiction, assume there are $v\in I$ and $u\in C$ with $f\left(u\right)=f\left(v\right)=2$. As the function f is a unique response Roman dominating function, u and v cannot be neighbors. Since G is connected, $\varnothing ⊊N_G\left(v\right)\subseteq C\backslash \left\{u\right\}\subseteq N_G\left(u\right)$. This contradicts the assumption that f is a unique response Roman dominating function. □

This lemma implies that we can solve Unique Response Roman Domination by looking for a vertex v of maximum degree (which must be in an inclusion-wise maximal clique) and setting the value of v to two and the values of the other vertices accordingly. This implies the following.

Theorem 7.

Unique Response Roman Domination can be solved in linear time on split graphs.

Proof. 

How can we find a unique response Roman dominating function of the smallest weight? Let us take a look at the unique response Roman dominating function for the two cases of Lemma 1. Without loss of generality, we can assume that for the given split graph $G=(V,E)$, we have a decomposition $V=C\cup I$ into a clique C and an independent set I such that C is inclusion-wise maximal. Consider the unique response Roman dominating function $f:V\to \{0,1,2\}$.

First, assume f fulfills $V_2\left(f\right)\cap I=\varnothing$ and $|V_2\left(f\right)\cap C|\le 1$. Since $V_2\left(f\right)\cap C=\varnothing$ would imply $f=1$ (constant) and $\omega \left(f\right)=\left|C\right|+\left|I\right|$, let us assume $\left\{v\right\}=V_2\left(f\right)\cap C$. Therefore, $C\cap V_1\left(f\right)=\varnothing$ holds. Hence, $\omega \left(f\right)=2+|I\backslash N_G\left(v\right)|$. This implies $u_R\left(G\right)\le {min}_{v\in C}\left(2+|I\backslash N_G\left(v\right)|\right)\le 2+\left|I\right|$.

Secondly, let us assume $V_2\left(f\right)\subseteq I$. As I is an independent set and there is no vertex in C with the value 2, $f\left(v\right)\ge 1$ for each $v\in I$. This implies

$$\omega \left(f\right)=\left|I\right|+|V_2\left(f\right)|+|C\backslash N_G\left(V_2\left(f\right)\right)|\ge |I|+1.$$

Equality holds if and only if there exists a vertex $v\in I$ with $N_G\left(v\right)=C$ and, for all $u\in I$, $f\left(u\right)=2$ if and only if $u=v$. In this case, C is not maximal, contradicting our assumption. Thus, this second case can never give a smaller value than the first one, i.e., $u_R\left(G\right)={min}_{v\in C}\left(2+|I\backslash N_G\left(v\right)|\right)$. Hence, in order to solve the Unique Response Roman Domination on G, we only have to find the vertex with the highest degree, as it will be in a maximal clique. □

Interestingly, the seemingly very similar problem of Perfect Roman Domination on split graphs is harder to solve. To see this, we will use a problem called Perfect Code that is formally defined next.

Problem name: Perfect Code (PC for short) Given: A graph $G=(V,E)$ and $k\in \mathbb{N}$ Question: Is there a perfect code D on G with $\left|D\right|\le k$?

It is known that Perfect Code is NP-complete, also in restricted graph classes like cubic planar graphs and if $k\ge \left|V\right|$; see [24,31,32].

Theorem 8.

Perfect Roman Domination on split graphs is NP-complete.

Proof. 

Membership follows from Perfect Roman Domination on general graphs. To prove NP-hardness, we will make use of the NP-hardness of Perfect Code. Let $G=(V,E)$ be a graph and $k\in \mathbb{N}$. To avoid trivialities, assume $k\le \left|V\right|$.

Define $t=3·\left|V\right|+4$, $k^{\prime }=k+\left|V\right|+4$ and $G^{\prime }=(V^{\prime },E^{\prime })$ with

$$\begin{array}{cc}\hfill V^{\prime }=& \{x,y\}\cup \{v^{\prime }\mid v\in V\}\cup \{v_i\mid v\in V,i\in \left[t\right]\}\cup \{a_1,b_1,\dots ,a_t,b_t\},\hfill \\ \hfill E^{\prime }=& \{\{x,a_i\},\{y,b_i\}\mid i\in \left[t\right]\}\cup \{\{v^{\prime },u_i\}\mid v,u\in V,u\in N\left[v\right],i\in \left[t\right]\}\cup \hfill \\ \hfill & \left({\displaystyle \genfrac{}{}{0pt}{}{\{x,y\}\cup \{v^{\prime }\mid v\in V\}}{2}}\right).\hfill \end{array}$$

The instance $(G^{\prime },k^{\prime })$ of Perfect Roman Domination can be constructed in polynomial time. Moreover, $G^{\prime }$ is easily seen to be a split graph. We still have to prove that $(G,k)$ is a yes-instance of Perfect Code if and only if $(G^{\prime },k^{\prime })$ is a yes-instance of Perfect Roman Domination.

Let $S\subseteq V$ be a perfect code of G with $\left|S\right|\le k$. Define $f\in {\{0,1,2\}}^V$ by the sets

$$\begin{array}{cc}\hfill V_0\left(f\right)=& \{v_i\mid i\in \left[t\right],v\in V\}\cup \{a_i,b_i\mid i\in \left[t\right]\},\hfill \\ \hfill V_1\left(f\right)=& \{v^{\prime }\mid v\notin S\},\hfill \\ \hfill V_2\left(f\right)=& \{x,y\}\cup \{v^{\prime }\mid v\in S\}.\hfill \end{array}$$

This implies $\omega \left(f\right)=|V\backslash S|+4+2·\left|S\right|=\left|V\right|+4+\left|S\right|\le k^{\prime }.$ The set $\{a_1,\dots ,a_t\}\cup \{v^{\prime }\mid f\left(v\right)\ne 2\}$ is only dominated by x and the vertices $b_1,\dots ,b_t$ are only dominated by y. Assume there are $v\in V$ and $i\in \left[t\right]$ such that $|N_{G^{\prime }}\left(v_i\right)\cap V_2\left(f\right)|\left[4\right]\ne 1$. By $N_{G^{\prime }}\left(v_i\right)=\{u^{\prime }\mid u\in N_G\left[v\right]\}$, this implies $|N_{G^{\prime }}\left(v_i\right)\cap V_2\left(f\right)|=|N_G\left(v\right)\cap S|\left[4\right]\ne 1$. This contradicts that S is a perfect code.

Assume that $f\in {\{0,1,2\}}^{V^{\prime }}$ is a minimum perfect Roman dominating function (so also minimal) with $\omega \left(f\right)\le k^{\prime }$.

Claim 3.

For each $z\in \{v_i,a_i,b_i\mid i\in \left[t\right],v\in V\}$, it holds that $f\left(z\right)=0$.

Proof. 

For the sake of contradiction, assume that there is some $v\in V$ and $i\in \left[t\right]$ with $f\left(v_i\right)=2$. This implies with Theorem 1 that $\{x,y\}\cup \{z^{\prime }\mid z\in V\}\subseteq N_{G^{\prime }}\left(u^{\prime }\right)$ has no vertex with f-value 2. Thus, $N_{G^{\prime }}\left(v_i\right)\cap V_2\left(f\right)=\varnothing$. Therefore, $f\left(v_j\right)\ne 0$ for each $j\in \left[t\right]$. Hence, $\omega \left(f\right)\ge t+1>k^{\prime }$, contradicting the choice of f.

Assume that there are some $v\in V$ and $i\in \left[t\right]$ with $f\left(v_i\right)=1$. Furthermore, we can assume $|N_{G^{\prime }}\left(v_i\right)\cap V_2\left(f\right)|\ne 1$, by Theorem 1. As by construction $N_{G^{\prime }}\left(v_i\right)=N_{G^{\prime }}\left(v_j\right)$ for each $j\in \left[t\right]$, we find $|N_{G^{\prime }}\left(v_i\right)\cap V_2\left(f\right)|=|N_{G^{\prime }}\left(v_j\right)\cap V_2\left(f\right)|$. If $|N_{G^{\prime }}\left(v_i\right)\cap V_2\left(f\right)|=0$, then $f\left(v_j\right)\ne 0$ holds for each $j\in \left[t\right]$ since $v_j$ is not dominated. Hence, $\omega \left(f\right)\ge t·\left|V\right|\ge t>k^{\prime }$, contradicting the choice of f. Assume $|N_{G^{\prime }}\left(v_i\right)\cap V_2\left(f\right)|\ge 2$. Thus, for each $j\in \left[t\right]$, $f\left(v_j\right)\ne 0$, as, otherwise, f is not perfect. This contradicts the construction as above.

We can discuss the claims concerning $a_i$ and $b_i$ along very similar lines. □

Further, we know $f\left(x\right)=f\left(y\right)=2$. Define $S=\{v\mid f\left(v^{\prime }\right)=2\}$. As $f\left(v_i\right)=0$ for each $v\in V,i\in \left[t\right]$, $|N_{G^{\prime }}\left(v_i\right)\cap V_2\left(f\right)|=1$. This implies that $|N_G\left[v\right]\cap S|=1$ for each $v\in V$. Therefore, S is a perfect code.

Since $f\left(x\right)=f\left(y\right)=2$, $f\left(v^{\prime }\right)\ge 1$ for all $v\in V$. This implies that $\omega \left(f\right)=\left|V\right|+|V_2\left(f\right)|+4=|V|+|S|+4\le k^{\prime }$. Hence, $\left|S\right|\le k^{\prime }-4-\left|V\right|=k$. This concludes the proof of Theorem 8. □

We contrast this by giving a branching algorithm for Perfect Roman Domination that yields the following result. Our algorithm relies on combinatorial insights from Theorem 4 and [29], where Roman dominating functions have been discussed on split graphs so that $V_2\left(f^{\prime }\right)\cap I=\varnothing$ or $V_2\left(f^{\prime }\right)\cap C=\varnothing$ for minimum $f^{\prime }$.

Theorem 9.

$\omega \left(f\right)$-Perfect Roman Domination can be solved in time ${\mathcal{O}}^{*}\left({\phi }^{\omega \left(f\right)}\right)$ on split graphs, where φ is the golden ratio.

Proof. 

Let $G=(V,E)$ be a split graph with the vertex set partition $V=C\cup I$, where C is a clique and I an independent set. Let k be the input parameter. Further, let $f^{\prime }:V\to \{0,1,2\}$ be a minimum perfect Roman dominating function on G. Then, by Theorem 4 and [29], where Roman dominating functions have been discussed on split graphs, $V_2\left(f^{\prime }\right)\cap I=\varnothing$ or $V_2\left(f^{\prime }\right)\cap C=\varnothing$. We have to consider these two possibilities for the perfect Roman dominating functions f that we will consider in our algorithm.

For $V_2\left(f\right)\cap C=\varnothing$, we just branch on each vertex in I if it obtains the value 1 or 2. The vertices cannot obtain the value 0, as they cannot be dominated by any other vertex. After deciding this, we can delete the vertex, and the parameter goes down by either 1 or 2. This gives us the branching vector $(1,2)$. When we have branched on each vertex in I, then we assign 0 to each $c\in C$ with $|V_2\left(f\right)\cap N\left(c\right)|=1$, and we assign 1 otherwise (this is important to obtain the perfect Roman dominating function property). Now, we only need to check if any $\omega \left(f\right)$ is at most the given parameter value k.

Now, we consider the perfect Roman dominating functions $f\in {\{0,1,2\}}^V$ with $V_2\left(f\right)\cap I=\varnothing$. As C is a clique, if $|V_2\left(f\right)\cap C|\ge 2$, then $C\subseteq V_1\left(f\right)\cup V_2\left(f\right)$. First, we consider the polynomially many perfect Roman dominating functions with $|V_2\left(f\right)\cap C|=1$. Since these functions are unique response Roman dominating functions, this can be performed in polynomial time. After this, we guess two vertices from C and assign the value 2 to these vertices. Again, there are polynomially many possibilities here. From now on, we can branch on the remaining vertices in C and decide if these will be assigned to 1 or 2. Analogously to $V_2\left(f\right)\cap C=\varnothing$, then we assign 0 to each $v\in I$ with $|V_2\left(f\right)\cap N\left(v\right)|=1$, and we assign 1 otherwise. Again, we also have to check if $\omega \left(f\right)$ is at most the given parameter value k.

Our algorithm obviously runs in time ${\mathcal{O}}^{*}\left({\phi }^k\right)$, where $\phi$ is the golden ratio and k the parameter. □

3.3. Cobipartite Graphs

Now, we consider cobipartite graphs, which are the complementary graphs of bipartite graphs. These graphs can be also characterized as graphs for which the vertex set can be partitioned into two cliques. On this graph class, Perfect Roman Domination is solvable in polynomial time.

Theorem 10.

Perfect Roman Domination  is polynomial-time solvable on cobipartite graphs.

Proof. 

Let $G=(V,E)$ be a cobipartite graph, with V partitioned into the two cliques $C_1,C_2\subseteq V$. For $v\in V$, define the perfect Roman dominating function

$$g_v:V\to \{0,1,2\},x\mapsto \left\{\begin{array}{cc}0,\hfill & x\in N\left(v\right),\hfill \\ 1,\hfill & x\in V\backslash N\left[v\right],\hfill \\ 2,\hfill & x=v.\hfill \end{array}\right.$$

Let $f\in {\{0,1,2\}}^V$ be a perfect Roman dominating function with $|V_2\left(f\right)\cap C_1|\ge 2$ and $v\in C_2$. Next, we prove that $\omega \left(g_v\right)\le \omega \left(f\right)$. For each $u\in C_1\backslash V_2\left(f\right)$, $|V_2\left(f\right)\cap N\left(u\right)|\ge 2$. Hence, $C_1\subseteq V_1\left(f\right)\cup V_2\left(f\right)$. Since $C_2\subseteq N\left[v\right]=V_0\left(g_v\right)\cup \left\{v\right\}$, $\omega \left(g_v\right)\le \left|C_1\right|+2\le \omega \left(f\right)$. Symmetrically, $\omega \left(g_v\right)\le \left|C_1\right|+2\le \omega \left(f\right)$ for $v\in C_1$ and a perfect Roman dominating function f with $|V_2\left(f\right)\cap C_2|\ge 2$.

Let f be a minimum perfect Roman dominating function on G. By the previous considerations, we can assume $|V_2\left(f\right)\cap C_i|\le 1$ for each $i\in \{1,2\}$. This leaves only ${\left|V\right|}^2+\left|V\right|$ many possibilities to check. □

As mentioned before, Cabrera et al. [18] proved that Unique Response Roman Domination is NP-complete on bipartite graphs. For cobipartite graphs, this problem is polynomial-time solvable. For this result, we use the idea of 2-packings; we also refer to the discussion in [33]. Let $G=(V,E)$ be a graph. A set $S\subseteq V$ is called a 2-packing if the distance between two vertices in S is at least 3. Targhi et al. [34] presented a proof for $u_r\left(G\right)=min\left\{2\right|S|+|V\left(G\right)\backslash N_G\left[S\right]|\mid S\mathrm{is}\mathrm{a}2\text{-}\mathrm{packing}\}$. Analogously to this, we can prove that, for each graph $G=(V,E)$, there exists a bijection ${\psi }_G$ between all 2-packings of the graph and all unique response Roman dominating functions. Here, for a 2-packing S and for $x\in V$,

$${\psi }_G\left(S\right)\left(x\right)=\left\{\begin{array}{cc}0,\hfill & x\in N\left(S\right)\backslash S,\hfill \\ 1,\hfill & x\in V\backslash N\left(S\right),\hfill \\ 2,\hfill & x\in S.\hfill \end{array}\right.$$

This also yields that, for each unique response Roman dominating function f, $V_2\left(f\right)$ is a 2-packing. This is the main idea of our algorithm.

Lemma 2.

Unique Response Roman Domination  is polynomial-time solvable on cobipartite graphs. Furthermore, there are at most ${\displaystyle \frac{{\left|V\right|}^2}{4}}$ many 2-packings, or unique response Roman dominating functions, in $G=(V,E)$.

Proof. 

Let $G=(V,E)$ be a cobipartite graph, together with the partition into the two cliques $C_1,C_2\subseteq V$. Two vertices from the same clique cannot be in a 2-packing at the same time. Therefore, from each clique, there can be at most one vertex in a 2-packing. Hence, there are at most $|C_1|·|C_2|$ many 2-packings, or unique response Roman dominating functions. As $C_1,C_2$ is a partition of V, this leads to $|C_1|·|C_2|=|C_1|·|V\backslash C_1|=|C_1|·\left(\left|V\right|-|C_1|\right)$ many 2-packings. This expression is maximal if $|C_1|=|C_2|$, which implies that there are at most ${\displaystyle \frac{{\left|V\right|}^2}{4}}$ many 2-packings, or unique response Roman dominating functions, in G. □

As indicated in the proof, the upper bound ${\displaystyle \frac{{\left|V\right|}^2}{4}}$ is tight: consider the complement of the complete bipartite graph $K_{t,t}$, where both classes have the same size t. This is interesting, as there could be exponentially many unique response Roman dominating functions even on connected split graphs, which is quite a related class of graphs that we consider next.

3.4. Remarks on Enumeration of Unique Response Roman Dominating Functions in Split Graphs

Enumerating 2-packings (corresponding to unique response Roman dominating functions) in general graphs in time $\mathcal{O}\left({1.5399}^n\right)$ was shown in [35].

Corollary 2.

All unique response Roman dominating functions of a connected split graph of order n can be enumerated in time $\mathcal{O}\left({\sqrt[3]{3}}^n\right)\subseteq \mathcal{O}\left({1.4423}^n\right)$.

Proof. 

Non-trivial connected split graphs have no isolates. By Observation 3, we can hence use the enumeration algorithm for minimal Roman dominating functions on split graphs of order n from [29] which runs in time $\mathcal{O}\left({\sqrt[3]{3}}^n\right)$. □

$\Omega \left({\sqrt[3]{3}}^{\left|V\right|}\right)$ is even a tight lower bound for connected split graphs as shown next.

Theorem 11.

There is an infinite family of connected split graphs $G_t=(V_t,E_t)$ with $\Omega \left({\sqrt[3]{3}}^{|V_t|}\right)$ many unique response Roman dominating functions.

Proof. 

We only need to consider the split graph family $G_t=(V_t,E_t)$ with $V_t:=C_t\cup I_t$, $C_t:=\{c_1,\dots ,c_t\}$, $I_t:=\{v_1,\dots ,v_{2t}\}$ and

$$E_t:=\left({\displaystyle \genfrac{}{}{0pt}{}{C_t}{2}}\right)\cup \{\{c_i,v_{2i-1}\},\{c_i,v_{2i}\}\mid i\in \{1,\dots ,t\}\}.$$

Clearly, $|V_t|=3t$. By the arguments from Theorem 7, for each unique response Roman dominating function f on $G_t$ with $|V_2\left(f\right)\cap C_t|=1$, in fact $|V_2\left(f\right)|=1$. There are t many such unique response Roman dominating functions. Let f be a unique response Roman dominating function with $V_2\left(f\right)\cap C_t=\varnothing$. In this situation, for each $i\in \{1,\dots ,t\}$, there are three ways to dominate $c_i$:

• $f\left(c_i\right)=f\left(v_{2i-1}\right)=f\left(v_{2i}\right)=1$;
• $f\left(c_i\right)=f\left(v_{2i}\right)=0$ and $f\left(v_{2i-1}\right)=2$;
• $f\left(c_i\right)=f\left(v_{2i-1}\right)=0$ and $f\left(v_{2i}\right)=2$.

Hence, there are $t+3^t={\displaystyle \frac{\left|V\right|}{3}}+{\sqrt[3]{3}}^{\left|V\right|}$ many unique response Roman dominating functions. □

For general graphs, the best lower bound [35] is $\mathcal{O}\left({1.4970}^n\right)$.

It should be mentioned that the polynomial-delay property of the Roman dominating function-enumeration algorithm from [29] is not inherited for enumerating the unique response Roman dominating function, as each minimal Roman dominating function is not a unique response Roman dominating function. Nonetheless, we present a sketch of a direct polynomial-delay branching enumeration algorithm for enumerating unique response Roman dominating functions that is optimal due to Theorem 11. For this purpose, we consider each 2-packing on a connected split graph and use the bijesction between unique response Roman dominating functions and 2-packings. Our algorithm is a modification of the recursive backtracking algorithm of [36] and has polynomial delay with the same arguments. The algorithm of [36] is a general approach to enumerate all sets of $\mathcal{F}\subseteq 2^U$ for a universe U, where $\mathcal{F}$ fulfills the following downward closure property: if $X\in \mathcal{F}$ and $Y\subseteq X$, then $Y\in \mathcal{F}$.

Theorem 12.

All unique response Roman dominating functions of a connected split graph of order n can be enumerated in time $\mathcal{O}\left({\sqrt[3]{3}}^n\right)$ with polynomial delay and polynomial space.

One of the rather surprising aspects of the proof is that we do not need any sophisticated measure-and-conquer methodology to analyze the run-time of the branching algorithm by a simple case analysis concerning the vertex degrees. In the core part of the algorithm, we decide if a vertex in the independent set is put into the related 2-packing or not; also cf. [36] concerning polynomial delay.

Proof. 

Let $G=(V,E)$ be a connected split graph with the partition $V=C\cup I$, where C is a clique and I is an independent set. With the arguments from Theorem 7, we can first enumerate each of the $\left|C\right|$ many 2-packings S with $S\cap C\ne \varnothing$. From now on, we branch on the vertices in I, deciding if they will be in the 2-packing S or not. If the vertex from I is not put into S, then we delete this vertex. If we put a vertex $v\in I$ into S, then we delete, for each $u\in N\left(v\right)$, the whole set $\left\{u\right\}\cup \left(N\left(u\right)\cap I\right)$. Furthermore, we delete vertices from C which have no neighbors in I. We always branch on a vertex $v\in I$ with the highest degree. If $deg\left(v\right)\ge 3$, then by putting the vertex in S, we delete 4 vertices. This leads to a branching vector $(4,1)$ (the branching value is below 1.3804). For $deg\left(v\right)=2$, we have to make a case distinction in the analysis: if v is the only neighbor in I for each of the neighbors of v, then in both cases, these vertices will be deleted after this branch. This implies the branching vector $(3,3)$ (the branching value is $\sqrt[3]{2}<\sqrt[3]{3}$). Otherwise, at least 4 vertices will be deleted after putting v into S. This would again lead to the branching vector $(4,1)$.

Therefore, we can assume that each vertex in I has exactly one neighbor.Let c be this neighbor. If $\left|N\right(c)\cap I|\ge 3$, after putting v into S, we would delete at least 4 vertices and the branching would be again $(4,1)$. For $N\left(c\right)\cap I=\left\{v\right\}$, we would delete c in each case. This would lead to the branching vector $(2,2)$ (the branching value is $\sqrt{2}\le \sqrt[3]{3}$). The remaining case would be $\left|N\right(c)\cap I|=2$. This case is considered in the $\Omega \left({\sqrt[3]{3}}^n\right)$-example in Theorem 11. Its analysis implies the claimed running time of ${\mathcal{O}}^{*}\left({\sqrt[3]{3}}^n\right)$. □

3.5. Chordal Bipartite Graphs

Chordal bipartite graphs are bipartite graphs where each induced cycle has length 4. Before working on the NP-hardness, we prove the following lemma.

Lemma 3.

Let $G=(V,E)$ be a graph with $v,u\in V$ with $v\ne u$ and $N\left(v\right)=N\left(u\right)$. G is a chordal bipartite graph if and only if $G[V\backslash \{u\left\}\right]$ is one.

Proof. 

Let $G^{\prime }:=G[V\backslash \left\{u\right\}]$. If G is a chordal bipartite graph, $G^{\prime }$ is clearly also one. Now assume $G^{\prime }$ is a chordal bipartite graph with the partition $V\backslash \left\{u\right\}=A\cup B$. W.l.o.g., let $v\in A$. As $N\left(u\right)=N\left(v\right)$, G is a bipartite graph with the partition $V=(A\cup \{u\left\}\right)\cup B$. So let $u,x_1,\dots ,x_{\ell },u$ be a cycle with $\ell >4$. If $v\notin \{x_1,\dots ,x_{\ell }\}$, then $v,x_1,\dots ,x_{\ell },v$ is a cycle in $G^{\prime }$. Hence, there is a chord in $u,x_1,\dots ,x_{\ell },u$. Assume there is an $i\in [\ell ]$ with $x_i=v$. Clearly, $i\notin \{1,\ell \}$. Thus, $u,x_1,v,x_{i+1},u$ a cycle. So, G is chordal bipartite. □

To prove the NP-hardness on Perfect Roman Domination and Unique Response Roman Domination on chordal bipartite graphs, we use the problem One-in-Three 3SAT, with a reduction inspired by [32] (Theorem 2.2) for the NP-hardness of Perfect Code. However, our proof is much more sophisticated in order to deal with the weights of the perfect Roman dominating functions.

Let us define this problem more formally.

Problem name: One-in-Three 3SAT Given: Set X of variables, set C of clauses over X with at most three literals. Question: Is there a truth assignment such that each clause in C has exactly one true literal?

Theorem 13.

Perfect Roman Domination  and  Unique Response Roman Domination  are  NP-complete even on chordal bipartite graphs.

Proof. 

The NP-membership follows as in the general case by guess-and-check. The following NP-hardness proof is inspired by the NP-hardness proof for Perfect Code in [32]. Let $\mathcal{X}=\{x_1,\dots ,x_n\}$ be a set of Boolean variables, and $\mathcal{C}=\{C_1,\dots ,C_m\}$ be a set of clauses over $\mathcal{X}$. Define $k:= 4mn+2n(3m-1)+2m$, $M^{\prime }:=\left[n\right]\times \left[m\right]$, $M:= M^{\prime }\times \left[k\right]$, $\mathcal{A}:= \{a_{i,j},{\overline{a}}_{i,j}\mid (i,j)\in M^{\prime }\}$, $\mathcal{B}:= \{b_{i,j},{\overline{b}}_{i,j}\mid (i,j)\in M^{\prime }\}$. Further define for $(i,j)\in M^{\prime }$:

• ${\mathcal{E}}_{i,j}:= \{e_{i,j,p}\mid p\in \left[k\right]\}$;
• ${\mathcal{F}}_{i,j}:= \{f_{i,j,p}\mid p\in \left[k\right]\}$;
• ${\mathcal{U}}_{i,j}:= \{u_{i,j,p}\mid p\in \left[k\right]\}$ for $j\ne m$.

Also, let ${\mathcal{W}}_j:= \{w_{j,p}\mid p\in \left[k\right]\}$ for $j\in \left[m\right]$. We group these sets into the following:

• $\mathcal{E}:= {\bigcup }_{(i,j)\in M^{\prime }}{\mathcal{E}}_{i,j}$;
• $\mathcal{F}:= {\bigcup }_{(i,j)\in M^{\prime }}{\mathcal{F}}_{i,j}$;
• $\mathcal{U}:= {\bigcup }_{(i,j)\in M^{\prime },j\ne m}{\mathcal{U}}_{i,j}$;
• $\mathcal{W}:= {\bigcup }_{j=1}^m{\mathcal{W}}_j$;
• $\mathcal{V}:= \mathcal{E}\cup \mathcal{F}\cup \mathcal{U}\cup \mathcal{W}$;
• ${\mathcal{V}}^{\prime }:= \{{\mathcal{E}}_{i,j},{\mathcal{F}}_{i,j}\mid (i,j)\in M^{\prime }\}\cup \{{\mathcal{U}}_{i,j}\mid (i,j)\in M^{\prime },j\ne m\}\cup \{{\mathcal{W}}_j\mid j\in \left[k\right]\}$.

For $T\in {\mathcal{V}}^{\prime }$, define

• $V_T:= \left\{r\left[T\right]\right\}\cup \{s\left[T,p\right],q\left[T,p\right]\mid p\in \left[k\right]\}$;
• $E_T:= \{\{r\left[T\right],t\},\{q[T,p],s\left[T,p\right]\},\{r\left[T\right],q\left[T,p\right]\}\mid t\in T,p\in \left[k\right]\}$.

Define $G:=(V,E)$ with

$$\begin{array}{cc}\hfill V:=& \mathcal{A}\cup \mathcal{B}\cup \mathcal{V}\cup \left(\bigcup _{T\in {\mathcal{V}}^{\prime }}{V}_T\right),\hfill \\ \hfill E:=& \{\{a_{i,j},{\overline{b}}_{i,j}\},\{a_{i,j},e_{i,j,p}\},\{{\overline{a}}_{i,j},b_{i,j}\},\{{\overline{a}}_{i,j},e_{i,j,p}\}\mid i\in \left[n\right],j\in \left[m\right],p\in \left[k\right]\}\hfill \\ \hfill & \cup \{\{f_{i,j,p},{\overline{b}}_{i,j}\},\{f_{i,j,p},b_{i,j}\}\mid (i,j,p)\in M\}\cup \left(\bigcup _{T\in {\mathcal{V}}^{\prime }}{E}_T\right)\hfill \\ \hfill & \cup \{\{a_{i,j},w_{j,p}\}\mid (i,j,p)\in M,x_i\in C_i\}\cup \{\{{\overline{a}}_{i,j},w_{j,p}\}\mid (i,j,p)\in M,{\overline{x}}_i\in C_i\}\hfill \\ \hfill & \cup \{\{u_{i,j,p},b_{i,j}\},\{u_{i,j,p},{\overline{b}}_{i,j+1}\}\mid (i,j,p)\in M,j\ne m\}\hfill \\ \hfill & \cup \{\{t_1,t_2\}\mid t_1\in \mathcal{F}\cup \mathcal{U},t_2\in \mathcal{E}\cup \mathcal{W}\}.\hfill \end{array}$$

Claim 4.

G is a chordal bipartite graph.

Proof. 

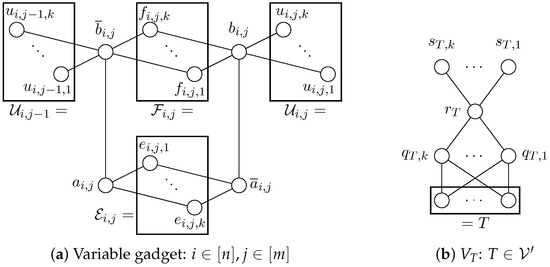
G is bipartite with the partition $A\cup B=V$, where

$$\begin{array}{cc}\hfill A:=& \mathcal{A}\cup \mathcal{F}\cup \mathcal{U}\cup \{r\left[{\mathcal{U}}_{i,j}\right]\mid (i,j)\in M^{\prime },j\ne m\}\hfill \\ \hfill & \cup \{r\left[{\mathcal{F}}_{i,j}\right],q[{\mathcal{E}}_{i,j},p],s[{\mathcal{E}}_{i,j},p],q[{\mathcal{W}}_j,p],s[{\mathcal{W}}_j,p]\mid (i,j,p)\in M\},\hfill \\ \hfill B:=& \mathcal{B}\cup \mathcal{E}\cup \mathcal{W}\cup \{q[{\mathcal{U}}_{i,j},p],s[{\mathcal{U}}_{i,j},p]\mid (i,j,p)\in M,j\ne m\}\hfill \\ \hfill & \cup \{r\left[{\mathcal{E}}_{i,j}\right],r\left[{\mathcal{W}}_j\right],q[{\mathcal{F}}_{i,j},p],s[{\mathcal{F}}_{i,j},p]\mid (i,j,p)\in M\}.\hfill \end{array}$$

To make it easier to recognize each edge (besides the ones in $E_T$), we mention the vertex in A first when talking about edges; see Figure 4 for an illustration of the important aspects of the construction. Observe that for $t_1,t_2\in T^{\prime }$, with

$$T^{\prime }\in \left\{T,\{s[T,p]\mid p\in \left[k\right]\},\{q[T,p]\mid p\in \left[k\right]\}\mid T\in {\mathcal{V}}^{\prime }\}\right\},$$

Figure 4. Constructions for Theorem 13.

$N\left(t_1\right)=N\left(t_2\right)$. Hence, we can use Lemma 3 exhaustively and consider $G^{\prime }:=G\left[V^{\prime }\right]$ with $V^{\prime }:=\mathcal{A}\cup \mathcal{B}\cup {\mathcal{V}}_1\cup {\bigcup }_{T\in {\mathcal{V}}^{\prime }}{V}_T^{\prime }$ with ${\mathcal{V}}_1:=\{e_{i,j,1},f_{i,j,1},u_{i,j^{\prime },1},w_{j,1}\mid (i,j)\in M^{\prime },j^{\prime }\in [m-1]\}$ and $V_T^{\prime }=\{r\left[T\right],q[T,1],s[T,1]\}$. By construction, no vertex in ${\bigcup }_{T\in {\mathcal{V}}^{\prime }}{V}_T^{\prime }$ can be part of an induced cycle. Thus, we can also delete these vertices. The remaining graph is $G^{\prime \prime }=G\left[V^{\prime \prime }\right]$ with $V^{″}:=\mathcal{A}\cup \mathcal{B}\cup {\mathcal{V}}_1.$

Let $c=x_1,\dots ,x_{\ell },x_1$ be a chordless cycle in $G^{\prime \prime }$ with smallest length $\ell >4$. If $a_{i,j},{\overline{b}}_{i,j}$ are on c for $(i,j)\in M^{\prime }$, then either $e_{i,j,1}$ or $w_{j,1}$ and either $f_{i,j,1}$ or $u_{i,j,1}$ are on c. This would give a chord. Hence, $a_{i,j},{\overline{b}}_{i,j}$ cannot be on c at the same time. Analogously, this holds for ${\overline{a}}_{i,j},b_{i,j}$. Therefore, if there are $a\in A$ and $b\in B$ on c, then the neighbors $y_1,y_2$ of a in c are in $\mathcal{E}\cup \mathcal{W}$ and the neighbors $z_1,z_2$ of b in c are in $\mathcal{F}\cup \mathcal{U}$. Hence, $a,y_1,z_1,y_2,a$ is a cycle included in c. If there is an $a\in A$ on c, then its neighbors $x,y$ on the cycle are in $\mathcal{E}\cup \mathcal{W}$. The neighbors of $x,y$ on c are in $\mathcal{F}\cup \mathcal{U}$. Therefore, there also exists a chord between x and the neighbor of y on c and there is no vertex of $\mathcal{A}$ on c. Analogously, this holds for $\mathcal{B}$. So, c is a cycle in $G\left[\mathcal{V}\right]$, which is a complete bipartite graph, contradicting our assumption that c is chordless and of length $\ell >4$. Thus, there exists no such c and $G^{\prime \prime }$, as well as $G^{\prime }$ and G being chordal bipartite. □

For each $T\in {\mathcal{V}}^{\prime }$, $|V_T|=2k+1$. Further $\left|\mathcal{V}\right|=k(m+n(m-1)+2nm)$ and $\left|\mathcal{A}\right|=\left|\mathcal{B}\right|=2nm$. Thus, the graph has

$$\begin{array}{cc}\hfill & \left|A\right|+\left|B\right|+\left|\mathcal{V}\right|+\left|\right\{z_T\mid T\in {\mathcal{V}}^{\prime },z_T\in V_T\left\}\right\}|\hfill \\ \hfill & =4nm+k(m+n(m-1)+2nm)+|{\mathcal{V}}^{\prime }|·(2k+1)\hfill \\ \hfill & =4nm+(3k+1)(m+n(m-1)+2nm)\hfill \end{array}$$

many vertices. Since k is polynomial in $n,m$, the graph can be constructed in polynomial time. This leaves us to show that $(\mathcal{X},\mathcal{C})$ is a yes-instance of the One-in-Three 3SAT if and only if there is a perfect Roman dominating function f on G with $\omega \left(f\right)\le k$. To prove the NP-hardness for Unique Response Roman Domination, we show that if there is such an f, then there is even a unique response Roman dominating function g with $\omega \left(g\right)\le k$.

Let $\varphi$ be a solution of the One-in-Three 3SAT instance. Then, define $f\in {\{0,1,2\}}^V$ with

$$v\mapsto \left\{\begin{array}{cc}2,\hfill & \exists T\in {\mathcal{V}}^{\prime }:v=r_T\hfill \\ 2,\hfill & \exists (i,j)\in M^{\prime }:v\in \{a_{i,j},b_{i,j}\}\wedge \varphi \left(x_i\right)=1\hfill \\ 2,\hfill & \exists (i,j)\in M^{\prime }:v\in \{{\overline{a}}_{i,j},{\overline{b}}_{i,j}\}\wedge \varphi \left(x_i\right)=0\hfill \\ 0,\hfill & \mathrm{else}\hfill \end{array}\right.$$

Clearly, $\omega \left(f\right)=2·(m+n(m-1)+2nm)+4nm=k$. For each $T\in {\mathcal{V}}^{\prime }$ and $p\in \left[k\right]$, $q[T,p],s[T,p]$ are only dominated by $r_T$. By the definition of f, for each $i\in \left[n\right]$, the vertices in $\{a_{i,j},b_{i,j},{\overline{a}}_{i,j},{\overline{b}}_{i,j},e_{i,j,p},f_{i,j,p}\mid j\in \left[m\right],p\in \left[k\right]\}\cup \{u_{i,j,p}\mid j\in [m-1],p\in \left[k\right]\}$ are dominated exactly once by either $a_{i,j},b_{i,j}$, or ${\overline{a}}_{i,j},{\overline{b}}_{i,j}$. Let $j\in \left[m\right]$ and $p\in \left[k\right]$. Since $\varphi$ is a solution, there is exactly one literal which fulfills $C_j$. Hence, there is exactly one neighbor of $w_{j,p}$ in of value 2. Thus, f is a perfect Roman dominating function. Furthermore, it is even a unique response Roman dominating function.

Now, let f be a minimal perfect Roman dominating function with $\omega \left(f\right)=k$. Let $T\in {\mathcal{V}}^{\prime }$ and $p\in \left[k\right]$. Since $s[T,p]$ is pendant, $f\left(s[T,p]\right)\ne 0$ implies $f\left(r\right[T\left]\right)\ne 2$. Otherwise, f would not be minimal (see Theorem 1, conditions 2 and 3). Hence, for each $p^{\prime }\in \left[k\right]$, $f\left(s[T,p]\right)\ne 0$ and $\omega \left(f\right)>k$, as $r\left[T\right]$ has to be dominated. Thus, for each $T^{\prime }\in {\mathcal{V}}^{\prime }$ and $p^{\prime }\in \left[k\right]$, $f\left(s[T^{\prime },p]\right)=0$ and $f\left(r\left[T^{\prime }\right]\right)=2$. If there is a $v\in T$ with $f\left(v\right)=2$, then $f\left(q[T,p^{\prime }]\right)\ne 0$ for each $p^{\prime }\in \left[k\right]$ and $\omega \left(f\right)>k$. Hence, $T\cap V_2\left(f\right)=\varnothing$. For each $t_1,t_2\in T$, $N\left(t_1\right)=N\left(t_2\right)$ and conditions 1 and 2 of Theorem 1 imply $f\left(t_1\right)=f\left(t_2\right)$. Hence, $N(\mathcal{A}\cup \mathcal{B})\backslash \left(\mathcal{A}\cup \mathcal{B}\right)\subseteq \mathcal{V}\subseteq V_0\left(f\right)$ as otherwise $\omega \left(f\right)>k$. Since for each $i\in \left[n\right],j\in \left[m\right]$, $N\left[a_{i,j}\right]\backslash \mathcal{V}=\{a_{i,j},{\overline{b}}_{i,j}\}=N\left[{\overline{b}}_{i,j}\right]\backslash \mathcal{V}$ and $N\left[{\overline{a}}_{i,j}\right]\backslash \mathcal{V}=\{{\overline{a}}_{i,j},b_{i,j}\}=N\left[b_{i,j}\right]\backslash \mathcal{V}$ and we have $2nm$ such pairs, $\omega \left({f|}_{\mathcal{A}\cup \mathcal{B}}\right)\le 4nm$. Hence,

$$\omega \left({f|}_{\mathcal{A}\cup \mathcal{B}\cup \{r\left[T\right]\mid T\in {\mathcal{V}}^{\prime }\}}\right)\le 4nm+2(m+n(m-1)+2nm)=k.$$

Thus, equality has to hold and $\{q_{T,p}\mid T\in {\mathcal{V}}^{\prime },p\in \left[k\right]\}\subseteq V_0\left(f\right)$. Further, for each $i\in \left[n\right],j\in \left[m\right]$, $f\left(a_{i,j}\right)+f\left({\overline{b}}_{i,j}\right)=2=f\left({\overline{a}}_{i,j}\right)+f\left(b_{i,j}\right)$. If there exist $i\in \left[n\right],j\in \left[m\right]$ such that $f\left(a_{i,j}\right)=1=f\left({\overline{b}}_{i,j}\right)$, then $f\left({\overline{a}}_{i,j}\right)=2=f\left(b_{i,j}\right)$ to dominate ${\mathcal{E}}_{i,j}\cup {\mathcal{F}}_{i,j}$. Hence, $V_1\left(f\right)=\varnothing$. For all $i\in \left[n\right],j\in \left[m\right]$, to dominate ${\mathcal{E}}_{i,j}\cup {\mathcal{F}}_{i,j}$, $|V_2\left(f\right)\cap \{a_{i,j},{\overline{a}}_{i,j}\}|=1=|V_2\left(f\right)\cap \{b_{i,j},{\overline{b}}_{i,j}\}|$ and $f\left(a_{i,j}\right)=f\left(b_{i,j}\right)\ne f\left({\overline{a}}_{i,j}\right)=f\left({\overline{b}}_{i,j}\right)$. Let $i\in \left[n\right],j\in [m-1]$. Since $u_{i,j,p}$ must be dominated exactly once, $f\left({\overline{b}}_{i,j+1}\right)\ne f\left(b_{i,j}\right)$. Also, $f\left(b_{i,j}\right),f\left(b_{i,j+1}\right),f\left(b_{i,j+1}\right)\in \{0,2\}$, together with $f\left({\overline{b}}_{i,j+1}\right)\ne f\left(b_{i,j+1}\right)$, implies $f\left(b_{i,j}\right)=f\left(b_{i,j+1}\right)$. So, for each $i\in \left[n\right]$ and $j_1,j_2\in \left[m\right]$, $f\left(a_{i,j_1}\right)=f\left(a_{i,j_2}\right)\ne f\left({\overline{a}}_{i,j_1}\right)=f\left({\overline{a}}_{i,j_2}\right)$.

Define $X_1:=\{x_i\mid i\in \left[n\right],\forall j\in \left[m\right]:f\left(a_{i,j}\right)=2\}$ and the assignment $\varphi :={\chi }_{X_1}\in {\{0,1\}}^{\mathcal{X}}$. Let $j\in \left[m\right]$. Since $j\in \left[m\right]$, $w_{j,p},q[{\mathcal{W}}_j,p]\in V_0\left(f\right)$ for all $p\in \left[k\right]$, $N\left(w_{j,p}\right)\cap \mathcal{A}\cap V_2\left(f\right)$ is not empty. Hence, there is a true literal satisfying $C_j$. So, the given One-in-Three 3SAT instance is a yes-instance. This completes the proof of Theorem 13. □

4. Parameterized Complexity

In this section, we consider the parameterized complexity aspects of Perfect Roman Domination and Unique Response Roman Domination. More precisely, we consider the parameters clique width (cwd for short, originally defined in [37]), treewidth (tw for short, originally defined in several papers at about the same time but nowadays standard; see [38]), solution size, and its dual order minus solution size.

4.1. Clique Width and Treewidth

The clique width of a graph G ($\mathsf{cwd}\left(G\right)$ for short) denotes the minimum number of labels needed to construct G with the following operations:

• Create a graph of one isolate vertex.
• Build the disjoint union of two labeled graphs.
• Connect each vertex with label i with each vertex of label j by an edge.
• Relabel vertices with label i to j.

Recall that $\mathrm{LinEMSOL}\left({\tau }_1\right)$ refers to the possibility to formulate an optimization problem using a linear function of the cardinalities of sets that realize the free set variables, while ${\tau }_1$ restricts the vocabulary of the monadic second-order logic to vertex set variables, with adjacency as the only relation. We want to employ this logic next. First, we give a $\mathrm{LinEMSOL}\left({\tau }_1\right)$ formula for the optimization problems corresponding to Perfect Roman Domination and to Unique Response Roman Domination in order to show that these are linear-time FPT if parameterized by cwd, using now classical results from [39,40]. cwd is an interesting parameter since an FPT algorithm with cwd as the parameter implies FPT algorithms with respect to tw, nd, or vc as parameters. However, the algorithmic results of the previous section do not follow from these considerations, as it is known that even unit interval graphs have unbounded clique width; see [40].

Lemma 4.

Minimum Perfect Roman Domination  on the graph $G=(V,E)$ can be expressed as

$$\underset{X_1\subseteq V,X_2\subseteq V}{argmin}\left\{\right|X_1|+2|X_2|\mid ⟨G,X_1,X_2⟩\vDash \theta (X_1,X_2)\},\mathit{with}\theta (X_1,X_2)\mathit{equal}\mathit{to}$$

$$\forall v\left(X_1\left(v\right)\vee X_2\left(v\right)\vee \exists u\left[X_2\left(u\right)\wedge E(v,u)\wedge \forall w\left(\left[X_2\left(w\right)\wedge E(w,v)\right]\Rightarrow u=w\right)\right]\right).$$

Proof. 

Let $G=(V,E)$ be a graph for which we want to determine the perfect Roman dominating function of the smallest weight. First, if f is some perfect Roman dominating function of G, then $\theta (V_1\left(f\right),V_2\left(f\right))$ is obviously true. Now, we want to show why $X_1,X_2\subseteq V$, as a minimum solution would describe a perfect Roman dominating function. Define $f:={\chi }_{X_1}+2{\chi }_{X_2}$. We can then see that for all $v\in V$, we have either $v\in X_1$, or $v\in X_2$, or there exists a $u\in X_2\cap N\left(v\right)$ such that there is no other neighbor of v in $X_2$. Therefore, we only need to show $X_1\cap X_2=\varnothing$. So, assume there is a $v\in X_1\cap X_2$. Then, for $X_1^{\prime }:=X_1\backslash \left\{v\right\}$, $(X_1^{\prime },X_2)$ is a smaller solution: v is still in $X_2$, which does not change. Hence, f is a perfect Roman dominating function. □

Theorem 14.

$\mathsf{cwd}$-Perfect Roman Domination  is in $\mathsf{FPT}$ if we assume the clique decomposition given as part of the input. Furthermore,  Perfect Roman Domination  can be solved in linear time on distance-hereditary graphs.

Proof. 

As already noted, the first claim follows from Lemma 4. Golumbic and Rotics showed in [40] that distance-hereditary graphs have a clique width bounded by three, which gives the second claim. □

Theorem 15.

$\mathsf{tw}$-Perfect Roman Domination  is in $\mathsf{FPT}$.

Proof. 

First, given a graph $G=(V,E)$, it is possible to compute an optimal tree decomposition in $\mathsf{FPT}$-time, parameterized by the treewidth of the graph. Then, we can apply Courcelle’s theorem that allows to conclude our result, as we have provided an MSO formula for our property. □

With similar techniques, we can also prove an analogous result for Unique Response Roman Domination.

Theorem 16.

$\mathsf{cwd}$-Unique Response Roman Domination is in $\mathsf{FPT}$ if we assume the clique decomposition given as part of the input.

Proof. 

For Unique Response Roman Domination, we have to make sure that there is no vertex of value 1 or 2 in the neighborhood of any vertex of value 2. We do this by adding the following part, connected with a logical conjunction to the formula $\theta (X_1,X_2)$ in Lemma 4: $\forall v\left(X_2\left(v\right)\Rightarrow \forall u\left[E(v,u)\Rightarrow \left(\neg X_1\left(u\right)\wedge X_2\left(u\right)\right)\right]\right).$ □

Theorem 17.

$\mathsf{tw}$-Unique Response Roman Domination  is in $\mathsf{FPT}$.

4.2. Solution Size

Besides the structural parameters, also the solution size is an interesting, often-used parameter. We show next that $\omega \left(f\right)$-Unique Response Roman Domination and $\omega \left(f\right)$-Perfect Roman Domination are $\mathsf{W}\left[1\right]$-complete. We do this by using Steps-Short Non-Deterministic Turing Machine Computation (SNTMC) which is known to be $\mathsf{W}\left[1\right]$-complete (see [38,41,42]), as well as Perfect Code, parameterized by the solution size. So, we cannot expect FPT-results with this natural parameterization. We start our presentation with a $\mathsf{W}\left[1\right]$-membership proof, which is, in a mathematical sense, the most interesting proof. As a side product, we also obtain membership in XP. To this end, we need the following interesting structural characterization lemma that is proven with some double-counting arguments.

Lemma 5.

Let $G=(V,E)$ be a graph and $f\in {\{0,1,2\}}^V$ be a function such that $N\left(u\right)\cap N\left(v\right)\cap V_0\left(f\right)=\varnothing$ for all $u,v\in V_2\left(f\right)$, $u\ne v$. Then, f is a perfect Roman dominating function if and only if

$$\left|V\right|=\left(\sum _{u\in V_1\left(f\right)}(1-|N\left(u\right)\cap V_2\left(f\right)\left|\right)\right)+\left(\sum _{v\in V_2\left(f\right)}\left(\left|N\left[v\right]\right|-|N\left(v\right)\cap V_2\left(f\right)|\right)\right).$$

Proof. 

On $G=(V,E)$, let $f\in {\{0,1,2\}}^V$ be a function such that $N\left(u\right)\cap N\left(v\right)\cap V_0\left(f\right)=\varnothing$ for all $u,v\in V_2\left(f\right)$, $u\ne v$. First, consider

$$\begin{array}{cc}\hfill \sum _{u\in V_1\left(f\right)}(1-|N\left(u\right)\cap V_2\left(f\right)\left|\right)& =|V_1\left(f\right)|-\sum _{u\in V_1\left(f\right)}\sum _{v\in V_2\left(f\right)}{\chi }_E\left(\{u,v\}\right)\hfill \\ \hfill & =|V_1\left(f\right)|-\sum _{v\in V_2\left(f\right)}|N\left(v\right)\cap V_1\left(f\right)|.\hfill \end{array}$$

Furthermore, we can re-write the second sum as follows:

$$\begin{array}{cc}\hfill \sum _{v\in V_2\left(f\right)}\left(\right|N\left[v\right]|-|N\left(v\right)\cap V_2\left(f\right)\left|\right)& =|V_2\left(f\right)|+\sum _{v\in V_2\left(f\right)}|N\left(v\right)\backslash V_2\left(f\right)|.\hfill \end{array}$$

Putting these thoughts together, we observe

$$\begin{array}{cc}\hfill & \left(\sum _{u\in V_1\left(f\right)}(1-|N\left(u\right)\cap V_2\left(f\right)\left|\right)\right)+\left(\sum _{v\in V_2\left(f\right)}\left(\right|N\left[v\right]|-|N\left(v\right)\cap V_2\left(f\right)\left|\right)\right)\hfill \\ \hfill & =|V_1\left(f\right)|+|V_2\left(f\right)|+\sum _{v\in V_2\left(f\right)}\left(\right|N\left(v\right)\backslash V_2\left(f\right)|-|N\left(v\right)\cap V_1\left(f\right)\left|\right)\hfill \\ \hfill & =|V_1\left(f\right)|+|V_2\left(f\right)|+\sum _{v\in V_2\left(f\right)}|N\left(v\right)\backslash (V_1\left(f\right)\cup V_2\left(f\right))|\hfill \\ \hfill & =|V_1\left(f\right)|+|V_2\left(f\right)|+\sum _{v\in V_2\left(f\right)}|N\left(v\right)\cap V_0\left(f\right)|.\hfill \end{array}$$

By the assumption on f, $\{N\left(v\right)\cap V_0\left(f\right)\mid v\in V_2\left(f\right)\}$ is a collection of pairwise disjoint sets, i.e., ${\sum }_{v\in V_2\left(f\right)}|N\left(v\right)\cap V_0\left(f\right)|=|{\bigcup }_{v\in V_2\left(f\right)}(N\left(v\right)\cap V_0\left(f\right))|\le |V_0\left(f\right)|$. This leads us to

$$\left|V\right|\ge \left(\sum _{u\in V_1\left(f\right)}(1-|N\left(u\right)\cap V_2\left(f\right)\left|\right)\right)+\left(\sum _{v\in V_2\left(f\right)}\left(\right|N\left[v\right]|-|N\left(v\right)\cap V_2\left(f\right)\left|\right)\right).$$

Equality holds if and only if $|{\bigcup }_{v\in V_2\left(f\right)}(N\left(v\right)\cap V_0\left(f\right))|=|V_0\left(f\right)|$. Since $(N\left(v\right)\cap V_0\left(f\right))$ are disjoint and subsets of $V_0\left(f\right)$, this is equivalent to the fact that f is a Roman dominating function. With the assumption on f, f would even be a perfect Roman dominating function. □

Theorem 18.

$\omega \left(f\right)$-Perfect Roman Domination  belongs to $\mathsf{W}\left[1\right]$.

Proof. 

(Sketch) We will use Steps-SNTMC. So let $G=(V,E)$ be a graph of order n and $k\in \mathbb{N}$. The reduction will compute a Turing machine M with a tape alphabet containing $V\cup \left\{\zeta \right\}$, with $\zeta \notin V$. In its internal memory, M stores a table T that contains, for $u,v\in V$, $u\ne v$, either $N\left(u\right)\cap N\left(v\right)$ (if $\left|N\right(u)\cap N(v\left)\right|\le k$) or ∞. Moreover, the reduction machine also computes addition and subtraction tables for numbers up to n and the alphabet contains also these numbers so that M can perform basic arithmetic, like reading two number symbols from the tape and printing the result, in constant time. Finally, M has access to a table of the degrees of all vertices in its internal memory. The Turing machine M will work in five phases as follows:

• Guess the vertices in $V_2\left(f\right)$ and then $V_1\left(f\right)$ and write them (as symbols) on the tape. We separate the vertices via the symbol $\zeta$. This takes $\le k+1$ steps.
• Also, in time $\mathcal{O}\left(k\right)$, M can check if twice the number of $V_2$-symbols (left of the separator $\zeta$) plus the number of $V_1$-symbols (right to $\zeta$) is at most k. If not, M stops in a non-final state.
• Check if we enumerated any vertex in $V_1\left(f\right)\cup V_2\left(f\right)$ twice (in $\mathcal{O}\left(k^2\right)$ steps). If this is the case, then the machine stops in a non-final state.
  Otherwise, we know now that the $V_1$-symbols together with the $V_2$-symbols that we guess do define a function f of weight $\omega \left(f\right)\le k$.
• Check for each pair of vertices $u,v\in V_2\left(f\right)$ ($u\ne v$) if $N\left(u\right)\cap N\left(v\right)\subseteq V_1\left(f\right)\cup V_2\left(f\right)$. This condition is clearly necessary if f should be a perfect Roman dominating function. For this check, we need table T. If $T[u,v]=\infty$, $N\left(u\right)\cap N\left(v\right)\subseteq V_1\left(f\right)\cup V_2\left(f\right)$ is impossible and we can stop in a non-final state. Otherwise, M checks element by element of $N\left(u\right)\cap N\left(v\right)$ if it is in $V_1\left(f\right)\cup V_2\left(f\right)$. Altogether, this needs at most $\mathcal{O}\left(k^3\right)$ many steps.
• For each $v\in V_1\left(f\right)\cup V_2\left(f\right)$, M computes $|N\left(v\right)\cap V_2\left(f\right)|$ (at most $\mathcal{O}\left(k^2\right)$ steps). Use these numbers to compute (with basic arithmetics)

  $$n^{\prime }:=\left(\sum _{u\in V_1\left(f\right)}(1-|N\left(u\right)\cap V_2\left(f\right)\left|\right)\right)+\left(\sum _{v\in V_2\left(f\right)}\left(\right|N\left[v\right]|-|N\left(v\right)\cap V_2\left(f\right)\left|\right)\right)$$

  Finally, M uses Lemma 5 to check if f is a perfect Roman dominating function, i.e., if $n=n^{\prime }$. □

Using a construction simpler than the previous one for $\mathsf{W}\left[1\right]$-membership together with a relatively straightforward reduction from Perfect Code for the $\mathsf{W}\left[1\right]$-hardness that basically introduces $2k$ twins per vertex, we can prove the following.

Theorem 19.

$\omega \left(f\right)$-Unique Response Roman Domination  is $\mathsf{W}\left[1\right]$-complete.

Proof. 

For the $\mathsf{W}\left[1\right]$-hardness proof, we use Perfect Code. Let $G=(V,E)$ be a graph and $k\in \mathbb{N}$. Define $V_i:=\{v_i\mid v\in V\}$ for $i\in [2k+1]$ and $\tilde{G}:=(\tilde{V},\tilde{E})$ with

$$\begin{array}{cc}\hfill \tilde{V}:=& \bigcup _{i=1}^{2k+1}{V}_i,\tilde{E}:=\{\{v_i,u_j\}\mid i,j\in [2k+1],v,u\in V,v\in N\left[u\right]\}.\hfill \end{array}$$

This graph has $(2k+1)·\left|V\right|$ many vertices.

Claim 5.

G has a perfect code Dof size $\left|D\right|\le k$ if and only if $\tilde{G}$ has a perfect Roman dominating function f with $\omega \left(f\right)\le 2k$.

Proof. 

Let $D\subseteq V$ be a perfect code. Define $D_1:=\{v_1\mid v\in D\}$, $f_D:=2·{\chi }_{D_1}$. Assume there exists a $v_i\in V_0\left(f_D\right)$ with $N_{\tilde{G}}\left(v_i\right)\cap D_1=N_{\tilde{G}}\left(v_i\right)\cap V_2\left(f_D\right)=\varnothing$. Thus, $v_i$ has no neighbor in $D_1$ and $N_G\left[v\right]\cap D=\varnothing$. Hence, D is no dominating set, which is a contradiction. Assume there is a $v_i\in V_0\left(f_D\right)$ with $|N_{\tilde{G}}\left(v_i\right)\cap D_1|=|N_{\tilde{G}}\left(v_i\right)\cap V_2\left(f_D\right)|\ge 2$. In this case, $|N_G\left[v\right]\cap D|=2$, contradicting the fact that D is a perfect code. If there exists a $v_1\in D_1=V_2\left(f_D\right)$ with $N_{\tilde{G}}\left(v_1\right)\cap V_2\left(f_D\right)\ne \varnothing$, then $v\in D$ would have a neighbor in D, and D would not be a perfect code in G. As even $V_1\left(f_D\right)=\varnothing$, $f_D$ is also a unique response Roman dominating function with $\omega \left(f\right)=2·\left|D\right|\le 2k$.

Let $f\in {\{0,1,2\}}^V$ be a unique response Roman dominating function with $\omega \left(f\right)\le 2k$ and $v\in V$. Since $C_v:=\{v_i\in i\in [2k+1]\}$ is a clique, we can assume $|C_v\cap V_2\left(f\right)|\le 1$. Further, for all $v_i,v_j\in C_v$, $N_{\tilde{G}}\left[v_i\right]=N_{\tilde{G}}\left[v_j\right]$. Therefore, we can assume, without loss of generality, that if $C_v\cap V_2\left(f\right)\ne \varnothing$, then $f\left(v_1\right)=2$. Assume there is a $v_i\in V_1\left(f\right)$. Thus, $N_{\tilde{G}}\left(v_i\right)\cap V_2\left(f\right)=\varnothing$. Since $C_v$ is a clique of true twins, $N_{\tilde{G}}\left(v_j\right)\cap V_2\left(f\right)=\varnothing$ and $f\left(v_j\right)=1$ for each $j\in [2k+1]$. Hence, $|V_1\left(f\right)|>2k$. This contradicts $\omega \left(f\right)\le 2k$. Therefore, $V_1\left(f\right)=\varnothing$.

Define $D:=\{v\in V\mid v_1\in V_2\left(f\right)\}$. If there is a $v\in V$ with $N\left[v\right]\cap D=\varnothing$, f would not be a Roman dominating function, as $v_1$ is not dominated. The existence of a $v\in V$ with $\left|N\right[v]\cap D|\ge 2$ would contradict the fact that f is unique response Roman dominating function, as either $v_1\in V_2\left(f\right)$ and $v_1$ has a neighbor in $V_2\left(f\right)$, or $v_1$ has two neighbors in $V_2\left(f\right)$. In total, D is a perfect code. □

Now, we will sketch the $\mathsf{W}\left[1\right]$-membership proof by using Steps-STMC. To this end, let $G=(V,E)$ be a graph of order n and $k\in \mathbb{N}$. The Turing machine will work in four phases as follows, assuming it was provided with some basic arithmetic capabilities by the reduction machine as detailed in the proof of Theorem 18:

• Guess the vertices in $V_2\left(f\right)$ and then $V_1\left(f\right)$. We split the vertices via a special symbol $\zeta$ (this takes at most $2k+1$ steps).
• Check if vertices in $V_2\left(f\right)$ have distance 2 to the vertices in $V_1\left(f\right)$ and distance 3 to the vertices in $V_2\left(f\right)$ (in at most ${\displaystyle \frac{k(k+1)}{2}}$ steps). If this is the case, then the machine stops in a non-final state.
• Check if we enumerated vertices in $V_1\left(f\right)$ twice (in at most ${\displaystyle \frac{k(k+1)}{2}}$ steps). If this is the case, then the machine stops in a non-final state.
• If $|V_1\left(f\right)|+{\sum }_{v\in V_2\left(f\right)}\left|N\left[v\right]\right|=\left|V\right|$, then f is a minimal unique response Roman dominating function (as each vertex is only dominated once). This can be computed in k steps.

This concludes the proof of Theorem 19. □

The previous $\mathsf{W}\left[1\right]$-hardness result could also be used to show that $\omega \left(f\right)$-Perfect Roman Domination is $\mathsf{W}\left[1\right]$-complete. We can show this type of result even on bipartite graphs.

Theorem 20.

$\omega \left(f\right)$-Perfect Roman Domination  is $\mathsf{W}\left[1\right]$-complete even on bipartite graphs.

Proof. 

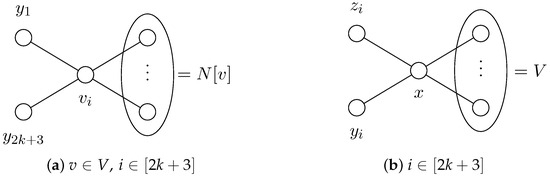
For membership, we refer to Theorem 18. For the hardness, we use Perfect Code. Let $G=(V,E)$ be a graph and $k\in \mathbb{N}$. Define $\tilde{G}:=(\tilde{V},\tilde{E})$ with $V^{\prime }:=\{v_i^{\prime }\mid v\in V,i\in [2k+3]\},Y:=\{y_1,\dots ,y_{2k+3}\},Z:=\{z_1,\dots ,z_{2k+3}\}$, giving

$$\begin{array}{cc}\hfill \tilde{V}:=& V\cup V^{\prime }\cup \left\{x\right\}\cup Y\cup Z,\hfill \\ \hfill \tilde{E}:=& \{\{v,u_i^{\prime }\}\mid \{v,u\}\in E,i\in [2k+3]\}\cup \{\{y_i,x\},\{z_i,x\}\mid i\in [2k+3]\}\cup \hfill \\ \hfill & \{\{v,x\}\mid v\in V\}\cup \{\{y_i,v_i^{\prime }\}\mid v\in V,i\in [2k+3]\}.\hfill \end{array}$$

$\tilde{G}$ is visualized in Figure 5. $\tilde{G}$ is bipartite with the classes $A:=V\cup Y\cup Z$ and $B:=\left\{x\right\}\cup V^{\prime }$ (the edges are written in such a way that the vertices from A are mentioned first). Furthermore, $\tilde{G}$ has $(2k+3)·\left(\right|V|+2)+\left|V\right|+1$ many vertices. This leaves us to show that G has a perfect code of size at most k if and only if $\tilde{G}$ has a perfect Roman dominating function with weight at most $2k+2$.

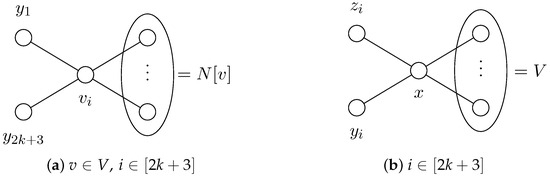
Figure 5. Construction for Theorem 20.

Assume there is a perfect code $D\subseteq V$ with $\left|D\right|\le k$. Then, define $f:=2·{\chi }_{D\cup \left\{x\right\}}$. $V\cup \left\{x\right\}\cup Y\cup Z$ is dominated by x. If there were a $v_i^{\prime }\in V^{\prime }$ which is not dominated by f, then v would not be dominated in G by D. Therefore, f is a Roman dominating function. Further $N(Y\cup Z)\cap V_2\left(f\right)=\left\{x\right\}$. For any $i\in [2k+3]$ and $v\in V$, $v_i^{\prime }$ has only one neighbor in $V_2\left(f\right)$, as $Y\subseteq V_0\left(f\right)$ and, otherwise, v would be dominated twice by D. Thus, f is a perfect Roman dominating function with $\omega \left(f\right)=2·\left|D\right|+2\le 2k+2$.

Let $f\in {\{0,1,2\}}^{\tilde{V}}$ be a minimal perfect Roman dominating function with $\omega \left(f\right)\le 2k+2$. Assume $f\left(x\right)\ne 2$. As $N\left(z_i\right)=\left\{x\right\}$ for each $i\in [2k+3]$, $Z\cap V_0\left(f\right)=\varnothing$. So, $2k+2<2k+3\le \omega \left(f\right)$. Hence, $f\left(x\right)=2$. Since $N\left(v_i^{\prime }\right)\subseteq N\left(x\right)$ for each $i\in \left[2k\right]$ and $v\in V$, $V_2\left(f\right)\cap V^{\prime }=\varnothing$. Otherwise, f is not minimal. Assume there is an $i\in [2k+3]$ with $f\left(y_i\right)=2$. As f is minimal, there must exist a private neighbor in $V_0\left(f\right)$. As $f\left(x\right)=2$, there exists a $v\in V$ such that $v_i^{\prime }$ is the private neighbor. Thus, $\left(N\left(v_j^{\prime }\right)\backslash \left\{y_j\right\}\right)\cap V_2\left(f\right)=N\left[v\right]\cap V_2\left(f\right)=\left(N\left(v_i^{\prime }\right)\backslash \left\{y_i\right\}\right)\cap V_2\left(f\right)=\varnothing$ for $j\in [2k+3]$. Thus, for each $j\in [2k+3]$, $f\left(v_j^{\prime }\right)\ne 0$ or $f\left(y_j\right)=2$. Hence, $2k+2<2k+3+2\le \omega \left(f\right)$. So, $Y\subseteq V_0\left(f\right)$.

Define $D=V_2\left(f\right)\cap V$. Clearly, $\left|D\right|\le k$. Assume that D is not a dominating set. Then, there is a $v\in V$ that is not dominated. Therefore, $N\left(v_i^{\prime }\right)\cap V_2\left(f\right)=\varnothing$ and $f\left(v_i\right)=1$ for each $j\in [2k+3]$. Hence, $\omega \left(f\right)\ge 2k+3$. Therefore, D is a dominating set. Assume D is not perfect. So, there is a $v\in V$ with $2\le |N\left[v\right]\cap D|=|V_2\left(f\right)\cap N\left(v_i^{\prime }\right)|$ for each $i\in [2k+1]$. So, $\omega \left(f\right)\ge 2k+3$. Hence, D is a perfect code. □

4.3. Dual Parameterization

Different from Perfect Code, it makes sense to consider the dual parameterization ($\left|V\right|-k$), as it is even NP-hard to find out if the graph has any perfect code (see [24]). So, the problem is para-NP-hard for the dual parameterization. This is not the case for Perfect Roman Domination and Unique Response Roman Domination since the constant 1 function is always a perfect Roman dominating function/unique response Roman dominating function. Therefore, these problems are trivially solvable if $n-k=0$. We can even see this parameter as a distance from triviality parameter in the sense of [43].

Theorem 21.

$(n-k)$-Perfect Roman Domination, $(n-k)$-Unique Response Roman Domination  $\in \mathsf{FPT}$.

Proof. 

Let $G=(V,E)$ be a graph and $f\in {\{0,1,2\}}^V$. Then,

$$\begin{array}{cc}\hfill n-\omega \left(f\right)& =\sum _{v\in V}(1-f\left(v\right))\hfill \\ \hfill & =\left(\sum _{v\in V_0\left(f\right)}(1-0)\right)+\left(\sum _{v\in V_1\left(f\right)}(1-1)\right)+\left(\sum _{v\in V_2\left(f\right)}(1-2)\right)\hfill \\ \hfill & =|V_0\left(f\right)|-|V_2\left(f\right)|.\hfill \end{array}$$

We will use this equality to bound the diameter and degree by $n-k$.

Assume there is a vertex v with $deg\left(v\right)\ge n-k+1$. Then, $f_v:={\chi }_V+{\chi }_{\left\{v\right\}}-{\chi }_{N\left(v\right)}$ is clearly a unique response Roman dominating function, and therefore a perfect Roman dominating function with

$$n-\omega \left(f_v\right)=|V_0\left(f_v\right)|-|V_2\left(f_v\right)|=deg\left(v\right)-1\ge n-k.$$

Hence, $\omega \left(f_v\right)\le k$, and we observe a yes-instance and can hence use the consideration of a vertex of maximum degree as a reduction rule.

Assume there is a shortest path $p=v_1,\dots ,v_{3·(n-k)}$ of length $3·(n-k)$. Define $f_p:={\chi }_V+{\sum }_{i=0}^{n-k-1}({\chi }_{\left\{v_{3i+2}\right\}}-{\chi }_{N\left(v_{3i+2}\right)})$. Clearly, each vertex in $V_0\left(f\right)$ has at least one neighbor in $V_2\left(f\right)$. Assume there exists a vertex $u\in V_0\left(f\right)$ with $v_{3i+2},v_{3j+2}\in V_2\left(f\right)\cap N\left(u\right)$ with $i\ne j$ (without loss of generality., $i<j$). This would imply that $v_1,\dots ,v_{3i+2},u,v_{3j+2},\dots ,v_{3·(n-k)}$ is a shorter path. Hence, $f_p$ is a perfect Roman dominating function. Analogously, $V_2\left(f_p\right)$ is an independent set. Therefore, $f_p$ is even a unique response Roman dominating function. Further,

$$n-\omega \left(f_p\right)=|V_0\left(f_p\right)|-|V_2\left(f_p\right)|\ge 2·(n-k)-n-k\ge n-k.$$

So, $\omega \left(f\right)\le k$, and we observe a yes-instance and can hence use the consideration of the graph diameter as a reduction rule.

As the maximum degree and diameter are bounded in $n-k$, the number of vertices is bounded by the Moore bound, giving $\mathcal{O}\left({(n-k)}^{3·(n-k)}\right)$ as the kernel size; see [44]. □

5. Final Remarks

We have enhanced the understanding of the combinatorial structure, the algorithmic nature, and the complexity of Perfect Roman Domination and Unique Response Roman Domination in many ways: on certain graph classes, with respect to several parameterizations, and concerning enumeration. But many aspects are still open for exploration. For instance, we did not touch the question of kernel sizes in any of our FPT results. Also, the fact that the ‘bijection approach’ that we took for enumeration necessitates parsimonious reductions, and this could be used towards investigating counting complexities, again, an untouched ground in this area.