Abstract
We consider the problem of determinizing and minimizing automata for nested words in practice. For this we compile the nested regular expressions () from the usual XPath benchmark to nested word automata (). The determinization of these , however, fails to produce reasonably small automata. In the best case, huge deterministic are produced after few hours, even for relatively small of the benchmark. We propose a different approach to the determinization of automata for nested words. For this, we introduce stepwise hedge automata (s) that generalize naturally on both (stepwise) tree automata and on finite word automata. We then show how to determinize s, yielding reasonably small deterministic automata for the from the XPath benchmark. The size of deterministic s automata can be reduced further by a novel minimization algorithm for a subclass of s. In order to understand why the new approach to determinization and minimization works so nicely, we investigate the relationship between and s further. Clearly, deterministic s can be compiled to deterministic in linear time, and conversely can be compiled to nondeterministic s in polynomial time. Therefore, we can use s as intermediates for determinizing , while avoiding the huge size increase with the usual determinization algorithm for . Notably, the obtained from the s perform bottom-up and left-to-right computations only, but no top-down computations. This behavior can be distinguished syntactically by the (weak) single-entry property, suggesting a close relationship between s and single-entry . In particular, it turns out that the usual determinization algorithm for behaves well for single-entry , while it quickly explodes without the single-entry property. Furthermore, it is known that the class of deterministic multi-module single-entry enjoys unique minimization. The subclass of deterministic s to which our novel minimization algorithm applies is different though, in that we do not impose multiple modules. As further optimizations for reducing the sizes of the constructed s, we propose schema-based cleaning and symbolic representations based on apply-else rules that can be maintained by determinization. We implemented the optimizations and report the experimental results for the automata constructed for the XPathMark benchmark.
1. Introduction
Nested words are hierarchical structures that are omnipresent in computer science. They were used to represent sequences of data trees, like XML or JSON documents, and to analyze the call structure of recursive programs. The idea of nested words is to generalize on both words and trees, resulting in sequences of unranked trees that are also known as hedges. Otherwise, nested words can be obtained by enriching Dyck words with internal letters, besides opening and closing parentheses. Furthermore, nested words are the elements of the least set containing internal letters from a given alphabet, triples consisting of an opening parenthesis, a nested word, and a closing parenthesis, and all sequences of nested words. Last but not least, nested words can be seen as words over an alphabet with internal letters, opening parentheses, and closing parentheses, under the conditions that the parenthesis are well nested, so that every opening parenthesis is properly closed and every closing parenthesis properly opened.
From the viewpoint of formal language theory, a natural question is how to lift the notions of finite automata and regular expressions, from words and trees to nested words, while preserving their well-known relationships. Nested word automata () were heavily studied since the 1980s [1,2,3,4], under the name input-driven automata. They are the same as visibly pushdown automata [5], pushdown forest automata [6], and streaming tree automata [7]. can recognize the same languages of unranked trees as hedge automata [8], a generalization of tree automata for ranked trees [9]. are often defined as pushdown automata with visible stacks, meaning that exactly one symbol is pushed when reading an opening parenthesis, and exactly one symbol is popped when reading a closing parenthesis, while the stack is not used otherwise. Their main advantage is a powerful notion of determinism, generalizing both over bottom-up and top-down determinism of tree automata for ranked trees [2,3]. We note that general pushdown automata do not permit determinization in contrast.
Regular expressions for nested words were proposed more recently by Hosoya and Pierce [10] under the name of regular expression types. In the present article, we will call them nested regular expressions () instead. Independently, more complex notions of nested regular expressions were introduced [11,12] in order to deal with generalizations of nested words with dangling opening and closing parentheses, which are not of interest to us. It was already claimed in [10], that our simpler notion of has the same expressiveness as hedge automata [8,9], which in turn have the same expressiveness as [3]. However, the question under which conditions can be compiled to small deterministic has not been studied. For classes of for which deterministic can be computed in polynomial time, we can decide language inclusion or equivalence in polynomial time too. For other classes, these problems may not be feasible since language inclusion for nondeterministic is EXP-complete.
Our concrete interest in the universality of deterministic is motivated by XML stream processing: we want to compute the certain answers of a navigational XPath query on an XML stream [13,14], i.e., those elements that are selected in all possible futures of the stream. Whether an answer is certain is computationally hard, even for tiny syntactic fragments of navigational XPath [14,15], but can be done in polynomial time for queries defined by deterministic [16]. A natural question is, therefore, whether it is possible to compile navigational XPath queries as in the usual benchmark [17] to deterministic of reasonable size. Unfortunately, the existing compilers fail to do so [18], as they are based on determinization for dealing with disjunction, negation, and recursive steps. Thereby, they produce huge deterministic automata even for very simple navigational XPath queries from the benchmark, or do not terminate after some hours.
In this article, we consider for defining queries on nested words. For benchmarking with realistic example, we consider the navigational XPath queries in the XPathMark benchmark with only forwards axis, that we compiled to of the same size up to a constant factor. The question is then whether these can be compiled to reasonably small deterministic .
As a first approach, we distinguish a subclass of “deterministic” that can be compiled in polynomial time to deterministic by generalizing on Glushkov’s construction of deterministic finite-state automata (DFAs) from “deterministic” regular expressions [19,20]. However, the obtained by compilation from navigational XPath queries are rarely deterministic, so neither are the compiled from them. Moreover, as we cannot apply determinization to them in practice as argued above, this first approach has a much too low coverage to reach the objective. Therefore, we will report it only at the end in Section 9.
For our second approach, we propose a novel variant of automata for nested words that we call stepwise hedge automata (s). Even though motivated by the wish to create deterministic automata for the of our benchmark, they are of general interest: they generalize naturally on both (stepwise) tree automata [21] and on finite word automata. In contrast to stepwise tree automata, s can not only recognize unranked trees, but also sequences thereof, i.e., hedges or nested words. Furthermore, s can be determinized in a bottom-up and left-to-right manner by combining in a natural manner the determinization procedures for tree and word automata.
By adapting existing compilers for stepwise tree automata [21], s can be compiled to with the same language in linear time while preserving determinism. Conversely, can be compiled to s in polynomial time, but at the cost of introducing nondeterminism. By compiling to s, determinizing the , and compiling the obtained deterministic back to a deterministic , we can determinize by determinizing the corresponding s. This alternative determinization algorithm for is different from the usual determinization algorithm for [2,3,18]. Indeed, it yields reasonably small deterministic for the from the XPath benchmark.
Yet another alternative algorithm for determinizing can be obtained by compiling to s and back, and then determinizing the obtained in this manner. When applied to back-and-forth converted , the usual determinization algorithm turns out to be well behaved: it produces deterministic of reasonable size for all our benchmark . This might be surprising, given that the same determinization algorithm behaved so poorly for the non-converted that were obtained from the benchmark directly.
We contribute two further solutions for producing deterministic for our benchmark . These are both based on a direct compiler from to s. We can then determinize these s, followed by compilation to deterministic . Otherwise, we can first compile the s to and then determinize these NWAs.
The next question is why the new determinization algorithms for that use s as intermediates work so nicely. In order to understand this, we need to investigate the relationship between and s more deeply. Clearly, the obtained via s do all their work in a bottom-up and left-to-right manner, and nothing when moving top-down. We can characterize the subclass of with this restricted behavior syntactically by the (weak) single-entry property: it requires that all opening rules of the go into into the same target state while popping the sources state onto the stack. Note that our single-entry property is weaker than the (multi-module) single-entry property studied previously [22,23,24], which in addition requires that the automaton can be split into at least 2 modules, one for the top level and one for the nested level. The obtained by compilation from s all have the (weak) single-entry property (but not necessarily multiple modules). Therefore, when compiling to s and back, the resulting also have the (weak) single-entry property. It seems that the usual determinization algorithm from is well-behaved when applied to with the (weak) single-entry property. The relationship between s and (weak) single-entry seems sufficiently close, so that their determinization algorithms seem to operate in somehow similar manners.
It is known that the subclass of deterministic multi-module single-entry (also called call-driven automata) enjoys unique minimization [22,23]. The separation of the module for the top level from the module for the nested level can be obtained w.l.o.g., by building a product with the with two hedge states that distinguishes the two levels. In our application, minimization could thus be used to reduce the size of the deterministic produced by our four algorithms for converting , with the hope to eventually obtain a unique outcome after minimization. However, as we will use some symbolic representations for sets of rules, the uniqueness will hold only for the non-symbolic counterpart. In any case, the number of states of the deterministic minimal obtained for the same could be expected to become unique.
Motivated by our application, we found it more relevant to minimize deterministic s rather than deterministic (weak) single-entry (despite of their close correspondence). As for the class of deterministic (weak) single-entry , a restriction is needed for the class of deterministic s to obtain unique minimization. We could have required the existence of multiple modules as for multi-module single-entry . Instead, we restrict ourselves to deterministic s for which the initial states for trees and hedges coincide. We then show that minimization for such s can be reduced to the minimization of tree automata up to a novel encoding of hedges to binary trees.
We implemented all four algorithms for compiling our benchmark to deterministic and report the experimental results. We have also implemented the novel minimization algorithm for s with equal tree and hedge initial states, and used it in our experiments. We propose two further optimization methods for reducing the sizes of the constructed automata.
First, we introduce schema-based cleaning both for s and . In our application, the schema expresses the Xml data model, stating that hedges must encode valid Xml documents. More generally, an automaton A can be cleaned relative to an automaton S for the schema, if the language of interest is the intersection rather than itself. The idea of schema-based cleaning is to keep only those transition rules of A that are used to recognize some hedge of . These transition rules can be computed from the product of A and S. Note that schema-based cleaning may change the language of the automaton. Only the intersection is preserved, not necessarily .
Second, we propose a symbolic representations for s based on apply-else rules. They help to represent more compactly a large number of apply rules produced by the determinization of s. Before compiling s to , however, we need to eliminate the apply-else rules. This is because we have not developed analogous symbolic representations for so far. A second limitation is that we have not implemented any minimization algorithm for at the time being.
The main improvement of this journal article compared with the conference version [25] is the addition of the minimization algorithm for the subclass of s with equal tree and hedge initial states. Furthermore, we added the idea of schema-based cleaning and the symbolic representations for s by apply-else rules. The experimental results were enhanced with minimization, symbolic representations of rules, and schema-based cleaning. All the nested regular expressions generated for the XPathMark benchmark queries that we consider, as well as their corresponding automata—when we could produce them—can be found at http://researchers.lille.inria.fr/niehren/complementary-material (accessed on 1 February 2021).
Related Work. In the present article, we restrict ourselves to nested words over signatures with a single opening parenthesis, a single closing parenthesis, and possibly many internal letters . This permits us to simplify the presentation of nested regular expressions, the notions of and s, their forth and back compilers, as well as the determinization algorithms. Note that any multi-module for such signatures must have exactly 2 modules. From an application perspective, multiple parentheses can be encoded by using internal letters, that is a named opening parenthesis by the word and a named closing parenthesis by the word . When encoding XML documents as nested words, such some encoding is needed anyway in order to deal with the complex information in XML tags, and also to provide symbolic representations with else rules that are able to deal with infinite signatures.
For the minimization of deterministic , general signatures with multiple parentheses raise additional problems. Chervet and Walukiewicz [23] solved such problems by reducing the minimization for expanded CDAs to the minimization of CDAs. Gauwin, Muscholl, and Raskin [24] showed that the minimization for deterministic is NP-hard in the case with general signatures. Their approach is based on a reduction from the problem of minimal immersion for sequences of Dfas, for which they construct with an unbounded number of opening parenthesis and an unbounded number of entry states. Weak single-entry in our setting do not permit this. Neither do over fixed general signatures with a finite number of opening parenthesis.
Navigational XPath queries on XML documents can be formalized in the language CoreXPath [26], or more generally by nested regular path queries [27] on data trees. Nested regular path queries were introduced earlier under the name of the propositional dynamic logic (PDL) in the 1970s [28], where they are applied to labeled graphs that generalize on data trees.
As certain query answering for XPath was considered difficult, the currently existing approaches to XPath query evaluation on XML streams [13,18] either approximate certain query answers based on nondeterministic machines or restrict the queries so that answer certainty can be decided without latency [15,29]. This also holds for recent streaming algorithms on words without nesting in the context of complex event processing [30].
2. Nested Words
Nested words are words with parentheses that are well nested. They can be identified with hedges, that is, sequences of internal symbols and unranked trees.
Nested words are constructed with opening and closing parentheses, respectively, ⟨ and ⟩. An unranked alphabet is a possibly infinite set of so-called “internal” symbols, that does not contain the two parentheses. The set of nested words over is denoted and is defined by the following abstract syntax:
The empty nested word is denoted by and assumed to be the neutral element of the composition operator , which furthermore is assumed to be associative, i.e., .
Nested words can be identified with hedges, i.e., words of trees and internal symbols. Seen as a graph, the inner nodes are labeled by the tree constructor and the leaves by symbols in or the tree constructor. For instance, corresponds to the hedge in Figure 1. A nested word of type tree has the form .
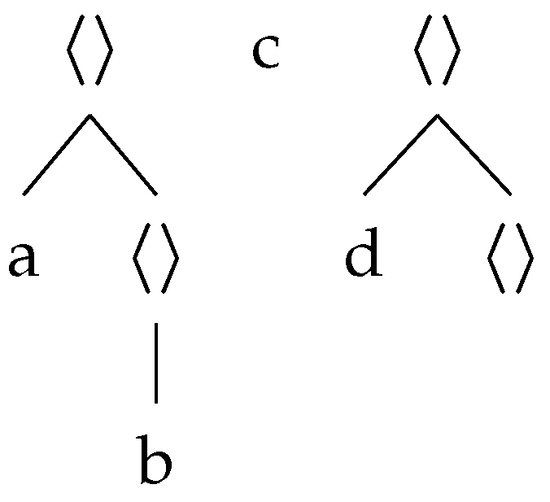
Figure 1.
Nested word seen as a graph.
Variants. Our notion of nested words accepts only well-nested words without dangling opening or closing parentheses in contrast to others [3,5]. This will lead to simpler notion of regular expressions, avoiding the more complex operators as with visibly rational expressions [12,31]. A less important difference is that we do not support labeled parentheses.
Labeled unranked trees. Labeled parentheses can be simulated by using internal letters. For instance, the labeled tree can be represented by the nested word of type tree . In this way, the labeled tree is represented by the nested word , which is of type tree (while the internal letter a alone is not). Unranked sequences of subtrees, often called hedges and sometimes forests, can be composed by using the sequence operator.
XML Documents. Our notion of nested words is sufficiently powerful to express general XML documents. An example of an XML document is given in Figure 2 and the representing nested word in Figure 3.

Figure 2.
An Xml document.

Figure 3.
The corresponding nested word.
We use the names of XML elements as labels of the nested word, as well as the letters of UTF8 for the string data values. Further labels such as doc and elem are added to express the types of the XML data model document and element, respectively.
When it comes to querying for nodes in Xml documents, we will be interested in nested words encoding Xml documents, in which a unique node is marked. We will use the label x to mark the selected node and the label for all others. When marking the date in the XML document of Figure 2, we obtain the nested word in Figure 4.

3. Nested Regular Expressions
We present nested regular expressions (), which were introduced under the name regular expression types in the context of XDuce [10] up to minor details. Note that similar nested regular expressions for ranked trees are folklore in the context of tree automata [32].
3.1. Syntax and Semantics
Let the alphabet be a set. An over is a term describing a language of nested words. It has the following abstract syntax where :
The expressions are the same as in -calculus [33], except that we restrict them such that all occurrences of a in E are nested below parentheses. Otherwise, nonregular languages could be defined such as with whose language would be . We also forbid intersections and complements in expression on all paths between the -operator and the occurrences of a in E that are bound by this operator. The expressions allow for vertical recursion, while the expressions with the Kleene star support horizontal recursion.
Our syntax allows for conjunctions and negations , which are well known to not add expressiveness if is finite. They are still relevant from the viewpoints of modeling, and for the treatment of infinite signatures. This comes at the price of increasing the complexity, as for the well-known case of words [34].
For infinite signatures, we can define for any finite subset of labels the language of single-letter words by some . This can be seen as follows. If , then the expression _ does the job: it matches exactly the set of all labels in . Moreover, if is nonempty then we can use negation. For instance, if then the expression describes the language .
The sets of free and bound letters and are defined as usual. The only binder binds the symbol a with scope E. Note that .
There are three differences with respect to the regular expression types from [10]. First, our treat labels as internal symbols instead of labels of parentheses. Second, they provide recursion through the -operator instead of using recursive equation systems. Third, conjunctions and general negations are not considered there.
Any E describes a language of nested words that we define by induction on the structure of E as follows: is the set of nested words over , as defined in Section 2.
For all expressions—, and , the notation stands for the expression E where all the occurrences of have been replaced by . The semantics of a -operator is then defined using the shortcuts and for all . In particular , so that . The semantics of the complement expression is the complement of in the set of all nested words, that is .
3.2. XPath Example
We now show how to express navigational XPath queries by that are restricted to forward axis. The idea is to adapt the spirit of a generate-and-test algorithm for query answering. The generation produces a nested word from Xml documents by guessing a single node and marking it by x. This node is a candidate for a query answer that is to be tested. The test is done by a .
For expressing XPath queries with child and descendant-or-self axes we will use the following where :
For instance, consider the XPath query A5 from the XPathMark benchmark [17]:
| /site/closed_auctions/closed_auction[descendant::keyword]/date |
Applied to the above Xml document, it selects all date children of closed_auctions nodes that contain at least one keyword descendant. Query A5 can be compiled to the following , which will accept the nested word in Figure 4 in particular:
The only label that the expression _ may match on a document that is properly annotated with the variable x will be the letter . The label x is annotated to the marked node, which is tested for being selected by the query. The label is annotated to all nodes except a unique x-marked node.
Note also that the -operator of the -expression expresses the recursion of the descendant axis. Furthermore, the conjunction permits us to connect the main path of A5 with its only filter.
3.3. XPath Benchmark
For testing , we rely on the usual XPathMark benchmark [17]. We restrict ourselves to navigational path queries with forward axis: child, descendant, and following-sibling. We notice that the following axis is excluded in contrast to following-sibling, as following is not strictly forwards. We can also admit path composition and filters with conjunction, disjunction, and negation.
The XPath queries of the benchmark satisfying these restrictions are the queries A1, …, A8 and B3 given in Figure 5. We developed a more general compiler from navigational forward XPath queries to , which yields the in Figure A1 of the Appendix B for the benchmark XPath queries. The for A1–A3 do have neither conjunctions nor negations, while the queries A4–A8 contain filters, which are mapped to conjunctions in . The compiler uses the -operator to capture the recursion of descendant axis as in A2, A3, and A5. Furthermore, nondeterminism is introduced by disjunctions in filters as in A7 and A8. Conjunction in filters appears in A6 which is mapped to conjunctions in too. A detailed description of this compiler is not in the scope of the present article though.

Figure 5.
XPath benchmark queries.
4. Nested Word Automata
Nested word automata () are pushdown automata reading nested words, whose stacks are visible: they push a single stack symbol when reading an opening parenthesis, pop a single stack symbol when reading a closing parenthesis, and do not alter or inspect the stack otherwise.
Definition 1.
An is a tuple consisting of a possibly infinite set Σ of internal symbols; finite sets and of states of type hedge and tree, respectively; sets of initial and final states ; a finite set Γ of stack symbols; and a finite set Δ of transition rules of the forms:
Our are symbolic, in that they come with else rules, i.e., elements of that we will denote by , for dealing with large or infinite alphabets.
An example for an is given in a graphical syntax in Figure 6. Tree states are drawn in circles that are filled in light gray  , while hedge states are in unfilled circles . Initial states are drawn as and final states as
, while hedge states are in unfilled circles . Initial states are drawn as and final states as  . Hedge rules that have the form where are denoted by , while any tree rule is denoted . Opening rules are represented as and closing rules as .
. Hedge rules that have the form where are denoted by , while any tree rule is denoted . Opening rules are represented as and closing rules as .
 , while hedge states are in unfilled circles . Initial states are drawn as and final states as
, while hedge states are in unfilled circles . Initial states are drawn as and final states as  . Hedge rules that have the form where are denoted by , while any tree rule is denoted . Opening rules are represented as and closing rules as .
. Hedge rules that have the form where are denoted by , while any tree rule is denoted . Opening rules are represented as and closing rules as .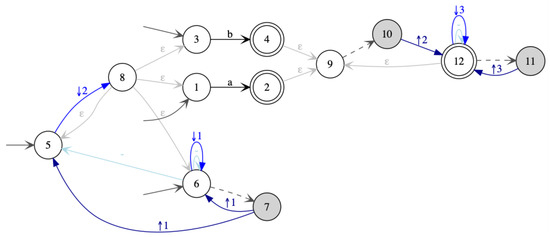
Figure 6.
Nested word automaton .
Our notion of supports factorization in the spirit of the work in [35]. It is obtained by distinguishing two types of states, and , and adding explicit type coercion rules . Semantically, both kinds of states could be merged when replacing the type coercion rules by the epsilon rule , but at the cost of introducing additional nondeterminism. This may lead to quadratically larger deterministic automata, as we will illustrate at the in Figure 20.
The language of nested words between two states is defined as the least language such that
The language of the is then .
4.1. Determinization of
Determinization for was first studied by von Braunmühl and Verbeek [2] in the 1980s, where are named input-driven pushdown automata. We notice that the determinization algorithm was published only in the journal version of this paper, but not in the conference version. Later on, the same algorithm was rediscovered in the context of visibly pushdown automata and republished for nested word automata.
Definition 2.
An A is called deterministic or equivalently a if
- I contains at most one element;
- there is no epsilon rule, i.e., ,
- and are partial functions from to for all , and is a partial function from to ;
- for all and there exists a most one such that ; and
- is a partial function from to for all .
Proposition 1
(von Braunmühl and Verbeek [2]). A with n states can be determinized in time .
Many of our results are based on the determinization algorithm going back to von Braunmühl and Verbeek. For self-containedness, we recall the version of this algorithm that we will use in the Appendix A. For illustrations, the determinization of the in Figure 6 is also presented here too, see Figure A1. It has size 271 while the nondeterministic has size 39 (12 states + 2 letters + 3 stack symbols + 22 rules). The blow-up is even worse in general as our experimental results will show and as noticed earlier by [18].
4.2. Multi-Module
Multi-module will play a prominent role for our constructions and are relevant for minimization [23]. For signatures with a single opening parenthesis, each multi-module has exactly two modules, one for the top level and one for the nested level.
We can define multi-module based on the natural notion of homomorphisms for . A homomorphism from an A to an with the same signature is a triple of functions that maps all concepts of A to the corresponding concepts of . These concepts are hedge initial states, final states, opening, closing, internal, and tree transitions. We do not enforce the preservation of epsilon rules by homomorphisms.
Definition 3.
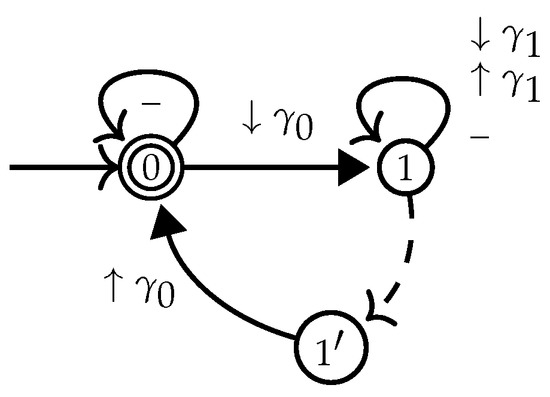
A multi-module A is an for which there exists a homomorphism from A to the in Figure 7.

Figure 7.
The maps top level positions to state 0 and nested positions to 1 or .
The evaluates all top level positions of a nested word to state 0: all those positions that are not between parentheses. All nested positions are evaluated to state 1. The homomorphism of a multi-module A to thus partitions the states of A between those that can be assigned to top level positions, and the others that can be assigned to nested positions.
4.3. Compilation of to
We next discuss a compiler from E to . This compiler extends on the McNaughton–Yamada–Thompson algorithm [36] for regular expressions, which introduces epsilon edges for constructing the automata of composition .
Theorem 1.
For any E, we can construct an A such that . If E contains neither conjunctions nor negations, then the construction is in time .
Proof sketch.
Conjunctions are compiled to products of automata, so repeated conjunctions may lead to an exponential blow up. Negations are computed by complementing automata based on determinization. Each complementation may lead to an exponential blow-up, so when this is repeated, the construction may become non-elementary.
For expressions without conjunction and negation, no such blow-up may arise. As stated by the theorem, we have to show that expressions can be compiled in linear time.
- Case :
- We use the McNaughton–Yamada–Thompson algorithm for composing the of and .
- Case :
- Let , , and be, respectively, the set of hedge states, tree states, and stack symbols of . We consider new hedge states and that are not in , a new tree state p not in and a new stack symbol not in . Then, is constructed by adding to opening rules for all the initial states q of , tree rules for all the final states of and a closing rule . Furthermore, we set as the only initial state of , and as its sole final state.
- Case :
- Special care has to be given to repeat expression . First of all, the naive compilation approach for these expression turns out to be wrong. Second, fixing the problem in the simplest possible manner does not lead to a linear time algorithm.Note that we can assume w.l.o.g. that a occurs at most once in E by using the golden lemma of the calculus [37], stating for all names and expressions in which can appear free that . Our construction guarantees that all transitions of the form in will start with the same state q. The wrong naive construction would remove the transitions from and add -rules from q to all the initial states of , and from all final states of to . Unfortunately, the construction is not correct. For illustration, we consider the . The reader should be warned that constructing an for E is less trivial than it might seem at first sight. One has to start from the for which is given in Figure 8. Simply adding epsilon edges to capture the operator will not work though. It will lead to the wrong automaton in Figure 9. This automaton will wrongly accept the hedge , as this hedge does not belong to .
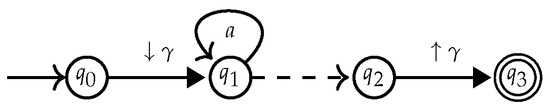 Figure 8. Automaton for the expression.
Figure 8. Automaton for the expression. Figure 9. Wrong naive construction for .If the for E is multi-module, then the naive construction of compiling can be made correct. Therefore, the simplest fix is to make the multi-moduled, before applying the naive construction. This can be achieved by typing the states of the automaton, by states of the in Figure 7. The added types yield the homomorphism of the constructed automaton to .The naive algorithm is then adapted as follows. Let be the multi-module obtained from the product of and . Note that we keep only the accessible top level states (type 0), but all nested states (type 1). In our example, this yields the in Figure 10. We then remove transition and add -rules from state to all states in , and from all states in to , where I and F are, respectively, the set of initial and final states of . Then, recognizes . The result obtained in the example is shown in Figure 11.
Figure 9. Wrong naive construction for .If the for E is multi-module, then the naive construction of compiling can be made correct. Therefore, the simplest fix is to make the multi-moduled, before applying the naive construction. This can be achieved by typing the states of the automaton, by states of the in Figure 7. The added types yield the homomorphism of the constructed automaton to .The naive algorithm is then adapted as follows. Let be the multi-module obtained from the product of and . Note that we keep only the accessible top level states (type 0), but all nested states (type 1). In our example, this yields the in Figure 10. We then remove transition and add -rules from state to all states in , and from all states in to , where I and F are, respectively, the set of initial and final states of . Then, recognizes . The result obtained in the example is shown in Figure 11.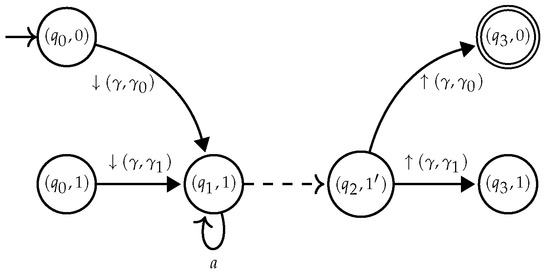 Figure 10. The multi-module for .
Figure 10. The multi-module for .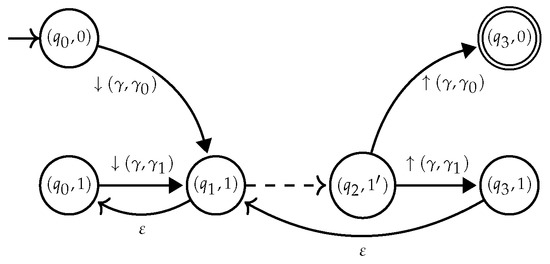 Figure 11. The correctly adapted naive construction for .The algorithm described so far makes the multi-moduled before compiling a -operator. For this, two copies of all states are introduced. This, however, could lead to an exponential construction if multiple -operators are nested. This problem can be avoided by preserving multi-moduledness as an invariant. Whenever a new state is created, it is created twice: once for the top level and once for the nested level. This information is maintained by typing the states, so that no further copies of the same state are produced later on.
Figure 11. The correctly adapted naive construction for .The algorithm described so far makes the multi-moduled before compiling a -operator. For this, two copies of all states are introduced. This, however, could lead to an exponential construction if multiple -operators are nested. This problem can be avoided by preserving multi-moduledness as an invariant. Whenever a new state is created, it is created twice: once for the top level and once for the nested level. This information is maintained by typing the states, so that no further copies of the same state are produced later on.
We omit the correctness proof of this construction. □
4.4. Experimental Results Starting with the Compiler
In the first two column of Figure 12, we report the sizes of the obtained from by our compiler, and the size of the deterministic produced thereof. For each automaton, we give its total size and in parentheses the number of states.
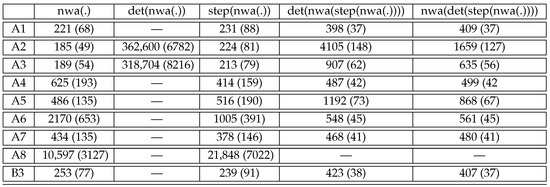
Figure 12.
The size (#states) of the nested word automata () for the benchmark nested regular expressions () and the automata derived thereof.
The sizes of the nondeterministic produced by the compiler for the for A1–A8 and B3 are given in column of Figure 12. Note that the are cleaned so that only accessible and co-accessible states remain. The sizes of the nondeterministic are acceptable for all , except for A8, for which the has more than 3000 states and an overall size greater than . This can be partially explained by the fact that the for A8 contains three conjunctions (one for the filter and two for the conjunctions in the filter). Still, the number of states remains surprising.
The determinized are given in column . It turns out that only A2 and A3 could be determinized successfully with some few hours of computation time on a standard laptop. However, even in the successful cases, the resulting deterministic are simply huge. This confirms similar problems first noticed in [18] and not solved since then.
The remaining columns of Figure 12 based on the back-and-forth compiler from s to from the following Section 6. They show that better determinization algorithms can indeed be obtained, yielding of acceptable size for all benchmark queries, with the exception of A8. The idea of is to compile the obtained from the to stepwise hedge automata and back before applying the above algorithm for . This might be surprising, as this determinization algorithm failed for the original , while it now proves successful on the forth-and-back transformed .
5. Stepwise Hedge Automata
We propose s as an extension of stepwise tree automata [21] that allows to recognize not only unranked trees but also hedges. We avoid more classical hedge automata from [9] that were already introduced in 1967 by Thatcher [8], as their notion of determinism is problematic. For instance, it makes unique minimization fail [38] and universality hard.
Our notion of s will be symbolic in using else rules, and factorized as in [35]: there are two types of states for hedges and trees and an operator for explicit type coercion. We also propose a novel treatment of internal letters inspired by nested word automata, so that s generalize both on stepwise tree automata and on Nfas.
Definition 4.
A is a tuple such that and are finite sets of states of two types: t for tree and h for hedge, respectively; Σ an alphabet of internal letters (that may be infinite); are subsets of hedge initial and final states, respectively; and Δ is a finite set of transition rules such that for all and :
An example for a is given in graphical syntax in Figure 13. It recognizes all hedges that are either just a or b or contain some tree node that contains either just a or b. In the graphical syntax, the states of type tree are drawn in circles filled in light gray  , while the states of type hedge are drawn in unfilled circles . The right part of the graph is an Nfa which uses tree states as additional edge labels, while the left part is a stepwise tree automaton that defines the tree languages of these tree states.
, while the states of type hedge are drawn in unfilled circles . The right part of the graph is an Nfa which uses tree states as additional edge labels, while the left part is a stepwise tree automaton that defines the tree languages of these tree states.
 , while the states of type hedge are drawn in unfilled circles . The right part of the graph is an Nfa which uses tree states as additional edge labels, while the left part is a stepwise tree automaton that defines the tree languages of these tree states.
, while the states of type hedge are drawn in unfilled circles . The right part of the graph is an Nfa which uses tree states as additional edge labels, while the left part is a stepwise tree automaton that defines the tree languages of these tree states.
Figure 13.
Stepwise hedge automaton : the part with the stepwise tree automaton is on the left and middle, and the Nfa part on the right.
Let be the restriction of to the hedge rules. Then, is a standard Nfa with -rules, which is symbolic [39] in providing else rules for dealing with large or infinite alphabets in addition. Therefore, we denote the hedge initial states by and the final states by  . A rule with an internal letter is denoted by stating that a hedge in state can be extended by the internal letter a leading to a hedge in state . Similarly, an epsilon rule is denoted by , and an else rule is denoted by . In the same spirit, a hedge rule —also called apply rule—is denoted by , stating that a hedge in state can be extended by a tree in state q leading to a hedge in state .
. A rule with an internal letter is denoted by stating that a hedge in state can be extended by the internal letter a leading to a hedge in state . Similarly, an epsilon rule is denoted by , and an else rule is denoted by . In the same spirit, a hedge rule —also called apply rule—is denoted by , stating that a hedge in state can be extended by a tree in state q leading to a hedge in state .
 . A rule with an internal letter is denoted by stating that a hedge in state can be extended by the internal letter a leading to a hedge in state . Similarly, an epsilon rule is denoted by , and an else rule is denoted by . In the same spirit, a hedge rule —also called apply rule—is denoted by , stating that a hedge in state can be extended by a tree in state q leading to a hedge in state .
. A rule with an internal letter is denoted by stating that a hedge in state can be extended by the internal letter a leading to a hedge in state . Similarly, an epsilon rule is denoted by , and an else rule is denoted by . In the same spirit, a hedge rule —also called apply rule—is denoted by , stating that a hedge in state can be extended by a tree in state q leading to a hedge in state .A tree initial state is graphically denoted by and a tree final rule by . Intuitively, a tree can be evaluated to state q if h can be evaluated starting with some tree initial state to some state such that . More formally, the hedge languages between any two hedge states are defined as
This definition is mutually recursive with the definition of the tree languages of all tree states :
The hedge language that is recognized by the automaton is . The rules of standard bottom-up tree automata have the form where a is a symbol of arity n. With s, this rule can be encoded by the sequence where the states are all tree states, and new hedge states.
5.1. Determinization of s
We formalize the notion of determinism for stepwise hedge automata and show how determinization works.
Definition 5.
A is deterministic or equivalently a , if it satisfies the following conditions:
- I contains at most one element;
- contains at most one element;
- there is no epsilon transition, i.e., ;
- , are partial functions from to for all and ; and
- is a partial function from to .
Proposition 2.
A of size n can be made deterministic in time while preserving the hedge language.
Proof.
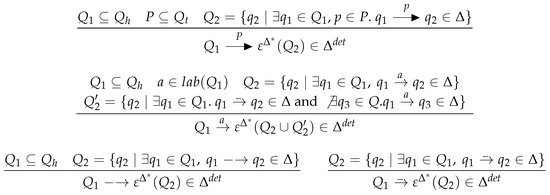
The determinization procedure for s combines the determinization algorithms of word and tree automata in the natural manner, while eliminating epsilon transitions. Let be the reflexive and transitive closure of , and for any subset let . Given a , we define an equivalent deterministic such that , , and . There is a unique tree initial state in and no -rule, that is, . The inference rules in Figure 14 define the missing part of .
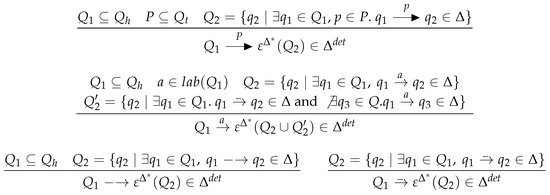
Figure 14.
Determinization of s.
We can show for all and that
so that . Therefore, and thus . □
For illustration, the deterministic in Figure 15 is obtained by determinization of the in Figure 13.
Figure 15.
The determinized .
5.2. Compilation of to s
As for , we introduce the notion of multi-module s for which the sets of hedge states are partitioned between those that can evaluate top level positions and those to which nested positions are assigned. Therefore, multi-module s will have exactly two modules too.
Definition 6.
A is a multi-module if there is a subset of states , that we call top level states, such that
- and
- the states in can reach only other states in via Δ.
For instance, consider the multi-module in Figure 13. The states of module for the top level are . The others belong to the module for the nested level.
Any E can be compiled to a multi-module such that and for all tree states . The can be partitioned into disjoint s such that and for all and . Note that the transitions relation is decomposed thereby into independent connected components. The automaton can be identified with an Nfa with signature given that it has no tree initial states. The automata are stepwise tree automata that recognize the tree language when taking as final state. For this, they may have tree initial states, but will not have any initial nor final states.
Theorem 2.
For any E, we can construct a A such that . If E contains neither conjunctions nor negations, then the construction is in time .
Proof sketch.
For the case of expressions with conjunctions or negations, the construction is analogous to the way it is done for . We next sketch the construction of s for expressions without conjunction and negation.
- Case :
- We use McNaughton–Yamada–Thompson algorithm [36] for composing the multi-module Nfas of and . The stepwise tree automata of the subexpressions of type tree are preserved. For succinctness, if some subexpression occurs more than once, then only a single copy of is kept. References to states of the removed copy should be renamed to their equivalent counterparts.
- Case :
- We construct from . The initial states of are turned into tree initial states. We then add a new tree state and connect it to all final states of by a tree final rule . Furthermore, the previously final state q becomes non final. Finally we add a new initial state , a new final state and a transition rule .
- Case :
- The main idea of the construction is similar to the case of . The correctness argument relies on the invariant that only multi-module s are built.Again by the golden lemma of the -calculus, we can assume w.l.o.g. that a occurs at most once in . By using -rules, we can preserve the invariant that there will be at most one pair such that in . Furthermore, these transitions cannot be on top level, given that the occurrence of a in must be nested below parentheses. The automaton is obtained from by first copying the top level Nfa of , as in Figure 16. We thus obtain two versions for each state of the top level Nfa of : one referred to as the top level copy— and in Figure 16, and another one as the nested level – and in Figure 16. Only top level states may be initial or final. Then, we add -rules from q to the nested states that correspond to the initial states of , and from the nested states corresponding to the final states of to . Finally we remove the rule . The resulting automaton is shown in Figure 17.
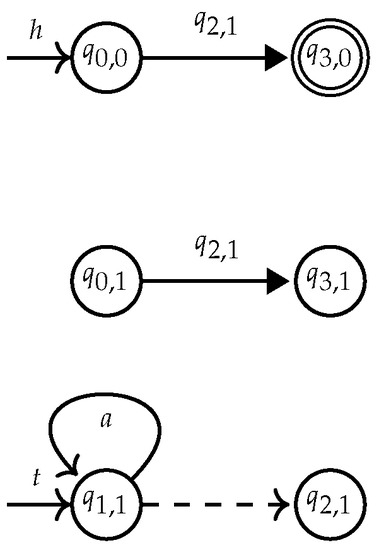 Figure 16. for .
Figure 16. for .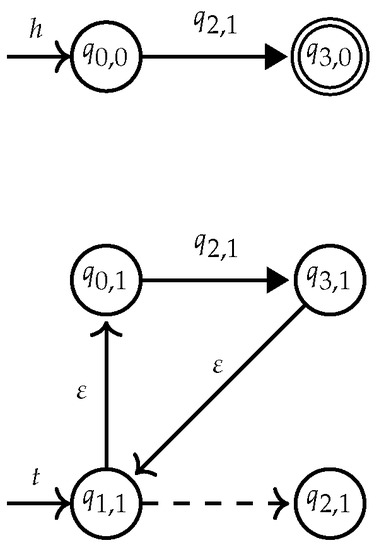 Figure 17. for .Note that every transition added for a state–top level or nested—in a subsequent step of the construction—except the -rules added for -expressions—must also be added for its copy.The construction is correct as the -bound name a is nested below parenthesis in . Therefore, it can be shown that the -edges introduced cannot be used to produce unwanted order in successful runs. Maintaining this invariant in polynomial time requires an additional argument. Instead of copying the top level parts of subexpressions, each state is introduced twice during the construction: one version for nesting, and another one for being part of top level parts. This way the size of the automaton is not doubled at each step, but only once.
Figure 17. for .Note that every transition added for a state–top level or nested—in a subsequent step of the construction—except the -rules added for -expressions—must also be added for its copy.The construction is correct as the -bound name a is nested below parenthesis in . Therefore, it can be shown that the -edges introduced cannot be used to produce unwanted order in successful runs. Maintaining this invariant in polynomial time requires an additional argument. Instead of copying the top level parts of subexpressions, each state is introduced twice during the construction: one version for nesting, and another one for being part of top level parts. This way the size of the automaton is not doubled at each step, but only once.
We omit the correctness proof of this construction. □
Unlike , one cannot preserve the determinism of the expressions of in s, even with Glushkov-like constructions. For instance, for the deterministic , one would have an having a tree initial state for each of the subtree, implying nondeterminism.
5.3. Experimental Results Starting with the Compiler
In the first two columns of Figure 18, we report the size of the s obtained from by our compiler, and the size of the deterministic s produced thereof.
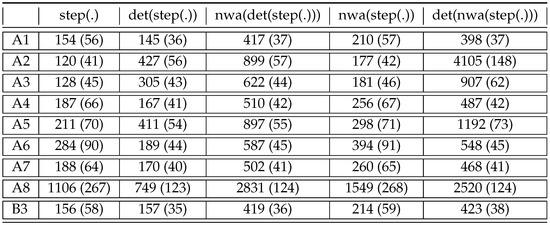
Figure 18.
The s for the benchmark and the automata derived thereof.
The compiler yields automata of acceptable size from the of all benchmark queries. These sizes are given in the first column of Figure 18. This even holds for A8, in contrast to the case where the produced has overall size 1106 and 267 states.
The determinization of the s in the second column even yields smaller automata in all cases. For A8, we obtain a deterministic stepwise automaton of overall size 749 and with 123 states. This might be surprising, in that the determinization algorithm may lead to an exponential blow-up in the worst case. However, it may also clean the automaton, keeping only accessible sets of states. This is what seems to happen systematically on the benchmark with the exception of A2, where the size goes up by a factor of four and A5 where the size doubles. For A2 the number of states grows by one third, while for A5 it decreases by one third.
Based on the back-and-forth compiler from s to from following Section 6, we can obtain deterministic of acceptable size for all benchmark queries. The method yield for A a of size 2831 and with 124 states. The alternative method yields a of size 2520, which is even smaller, and the same number of states.
6. NWAs versus SHAs
We next show how to compile s to such that determinism is preserved, and back while introducing nondeterminism. Thereby, we can obtain small for such as for which blew up in size in a surprising manner (see Figure 12).
6.1. SHAs to NWAs
As a first step, we introduce a transformation on s, so that for any A:
- if A is deterministic, the transformation returns A, and
- if A is nondeterministic with set of hedge states and transition relation , the transformation returns a new with set of hedge states where is a new hedge state, and set of transitions which equals except that and .
Then, we compile any obtained after the above transformation to an such that . We set , , for all , , :
Clearly, if S is deterministic then so is , as p is unique in this case in particular. One might be tempted to skip the first-step transformation and restrict the above construction rule to states p such that . However, this would lead to a huge blow-up when determinizing these , basically as this change spoils the single-entry property discussed in Definition 7.
The conversion of in Figure 13 yields the in Figure 19. Note that the opening rules are deterministic (but not the whole ), as for all tree states q there is at most one hedge state p with such that q is accessible from p. The NWA has size 64, while its determinization has size 159 (see Figure A3 of the Appendix C). The size increase raised by determinization is thus for this .
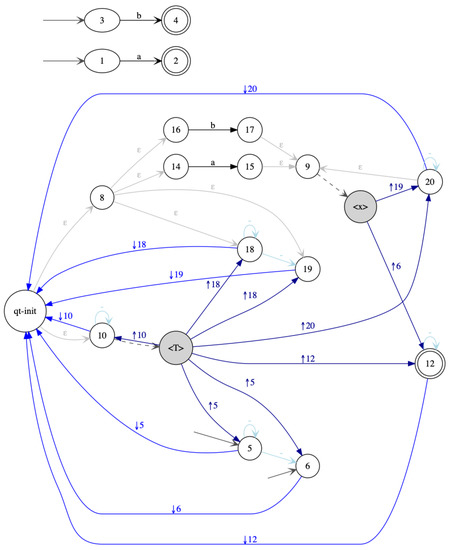
Figure 19.
The single-entry obtained from the .
The size increase for determinization is considerably smaller for the obtained from the regular expressions by indirection via a than for obtained by direct compilation. Indeed, the determinization of blows the size from 39 to 271. The size increase for the determinization of is thus while for it is only .
The experiments will show that this is not an exception but the general rule. Intuitively, the reason is that obtained from s do all the work bottom-up, where obtained directly from the regular expression do a considerable amount of work top-down. In terms of the work in [22], this restriction can be characterized syntactically by the single-entry property:
Definition 7.
A (weak) single-entry is a for which there exists a single state such that all opening rules in Δ have the form .
Note that call-driven automata (CDAs) discussed in [23] coincide with multi-module single-entry and also with (multi-module) single-entry visibly pushdown automata [22,24].
It can be shown that has the (weak) single-entry property for all s S for which the p’s are unique in the above construction rule, i.e., such that . Note that this was not the case for in Figure 13 but could have been imposed w.l.o.g. leading to a slightly different than in Figure 19.
The conversion of the determinization in Figure 15 yields the deterministic in Figure 20. The size goes up slightly from 53 to 73. It should be noticed that factorization avoids a quadratic blow up in this case. This can be observed at state 14, which has 3 incoming tree edges and 10 outgoing closing edges. Without factorization, the 3 tree edges could be replaced by 3 -edges whose elimination would produce 30 closing edges. This would increase the number edges to edges.
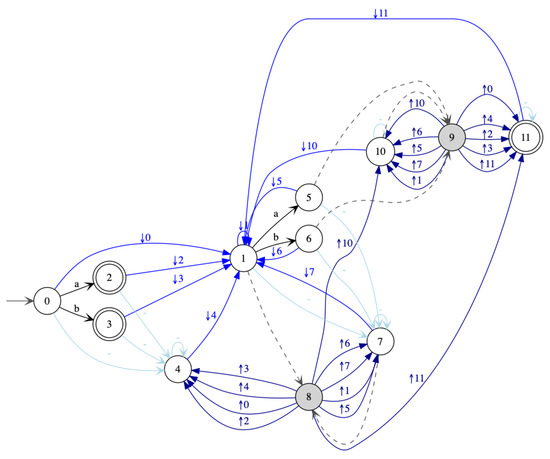
Figure 20.
Deterministic : .
6.2. NWAs to SHAs
Conversely, can be compiled to stepwise hedge automata, but at the cost of introducing nondeterminism, as an may traverse the branches of a tree top-down, while a stepwise must traverse them bottom-up. For this, the stepwise guesses the state in which the will arrive from above and then evaluates the subtree starting with this state, while verifying the correctness of the guess later on. Let be an . We build a where , , , and is the smallest satisfying the following rules:
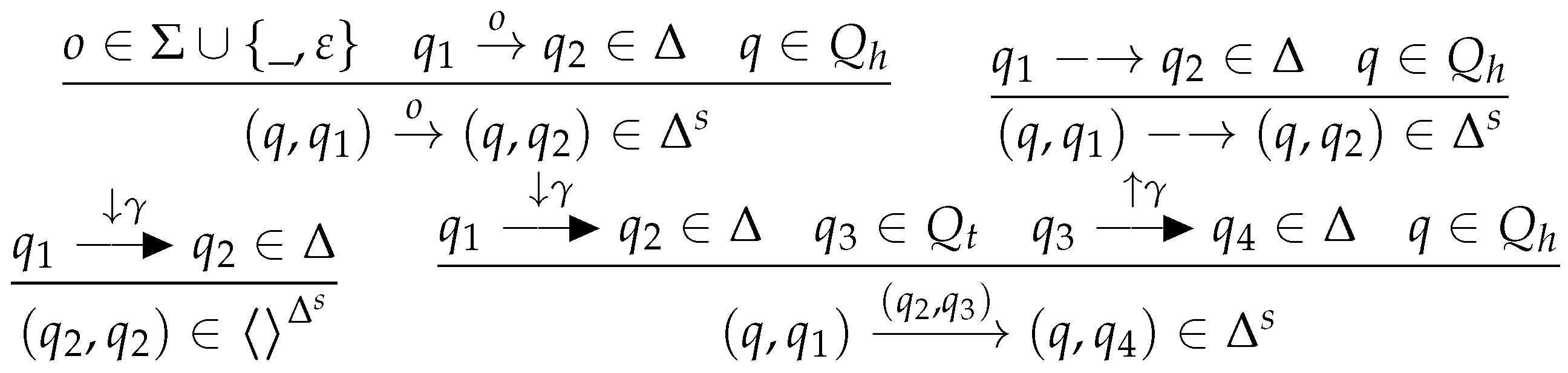
The construction is such that .
7. Optimizations
We will use three optimization methods for constructing smaller s and thus smaller : minimization, symbolic representations of sets of transition rules, and schema-based cleaning.
7.1. Minimization
Our next objective is to reduce the size of deterministic s by developing a minimization algorithm for a subclass of s. Even though our implementation can deal with them, we consider s without symbolic rules for simplicity in this section.
We start with an example that motivates the choice of our subclass. In Figure 21 and Figure 22, two s are given that both recognize the language of all hedges with signature containing exactly one occurrence of the letter x. The in Figure 22 is the recognizing this language which has the minimal number of states. The in Figure 21 is the minimal multi-module for this language. The question is how a minimization algorithm for s could convert the in Figure 21 to this minimal one in Figure 22. In particular, why would it merge the tree initial state and the hedge initial state? We do not see how this could be done based on some Myhill–Nerode-like equivalence relation. This motivates an a priori restriction to s imposing that the tree initial state and hedge initial state must be equal.
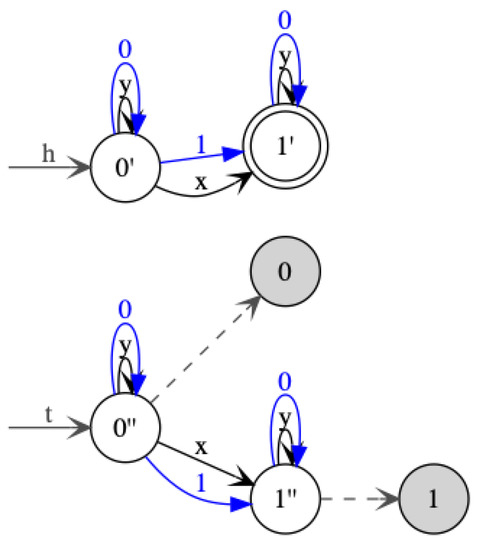
Figure 21.
A for hedges over with single occurrence of x. It is minimal in the class of multi-module s.
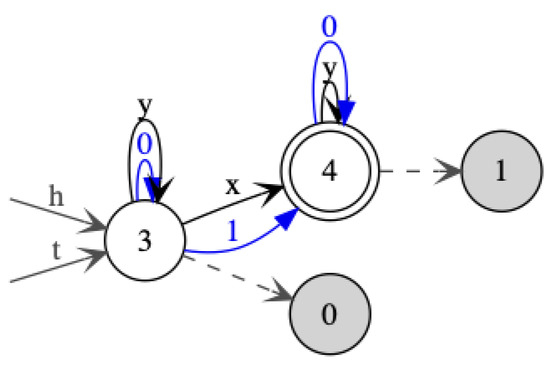
Figure 22.
An equivalent to that in Figure 21 that is minimal in the class of s with equal tree and hedge initial states.
Note that any can be converted into a with equal tree and hedge initial states. For this, it is sufficient to “fuse” these states and then to determinize the obtained. When doing so for the in Figure 21, we indeed obtain the minimal from Figure 23, so no further minimization is needed in this case.
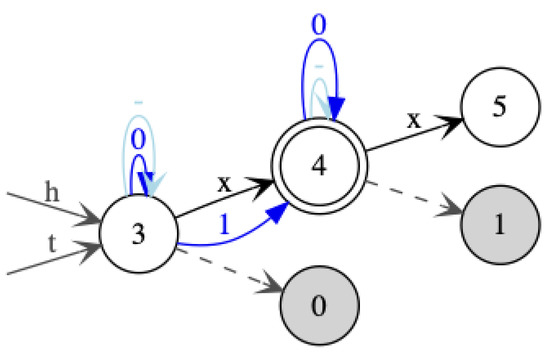
Figure 23.
A single x-marked position.
Given the close relationship between s and weak single-entry , it is instructive to consider the existing results on minimization for . It is known that the class of general does not allow for unique minimization [22] and that the minimization becomes NP-hard when admitting general signatures with multiple parenthesis [24].
On the positive side, the best existing minimization algorithm is due to Chervet and Walukiewicz [23]. It applies to the subclass of multi-module single-entry , called there call-driven automata (CDA) (Chervet and Walukiewicz [23] permit signatures with multiple opening parenthesis. In the case of a single opening parenthesis, the class of CDAs is equal to their subclass of expanded CDAs for which they develop their minimization algorithm in the first place.). They showed that the subclass of multi-module single-entry enjoys unique minimization in polynomial time.
In the case of s, we believe that unique minimization holds for the following two subclasses, and will show it for the second:
- the subclass of multi-module s, and
- the subclass of s where the hedge and tree initial state are the same, i.e., .
The first subclass of multi-module s is motivated by the subclass of multi-module single-entry . Note, however, that the s that are obtained by compilation from single-entry need not be deterministic, so the analogy between both automata classes is not perfect. The in Figure 21 is minimal for the class of multi-module s.
The second subclass of s corresponds to the subclass of single-entry in which the single-entry state is equal to the initial state. The in Figure 22 is minimal for the second subclass. In the remainder of this section, we present a minimization algorithm for the second subclass. For this, we identify s in which tree and hedge initial state coincide with two-sorted deterministic tree automata, so that we can use a minimization algorithm for the latter. Our automaton translation is based on a novel encoding of hedges into ranked well-sorted trees with monadic and binary function symbols, which is inspired by the previous binary encoding of unranked trees known from stepwise tree automata [21]. For any unranked signature , as for the construction of hedges, we consider two sorts: for hedges and for trees. We then consider the following ranked signature with these two sorts:
The well-sorted trees over of both sorts then have the following abstract syntax:
Any hedge over can be encoded into a ranked well-sorted tree of sort with signature . For instance, the hedge
is encoded into the following ranked well-sorted tree of sort over :
Any with equal tree and hedge initial states, that is, , can then be encoded into a two sorted tree automaton by mapping the transition rules in to those in as follows:
We can first note that . Second, the translation function is a bijection between s over and two-sorted tree automata over . Furthermore, this translation preserves determinism. It follows that if A is a with a minimal number of states recognizing then is a deterministic two-sorted tree automaton with a minimal number of states recognizing . Furthermore, the unique minimization of deterministic two-sorted tree automata implies the unique minimization of the class of s with equal tree and hedge initial states.
Using this translation back and forth, we can thus lift the minimization algorithm of deterministic two-sorted tree automata to a minimization algorithm for the subclass of s with equal tree and hedge initial states. This is the minimization algorithm for s that we have implemented. We then used it in our constructions to reduce the size of the s obtained by determinization.
7.2. Symbolic SHAs with Apply-Else Rules
The sizes of the s constructed so far are dominated by the number of transitions. We now propose a class of symbolic s by adding apply-else rules, in order to represent large numbers of apply rules in a more compact and symbolic manner.
An apply-else rule has the form where . It represents the set of apply rules , where can be chosen arbitrarily from a subset of tree states distinguished by the automaton.
We have also adapted our determinization for s so that it preserves apply-else rules. What is missing so far is a concept for that corresponds to the apply-else rules of s. Therefore, we have to eliminate apply-else rules before translating s to .
7.3. Schema-Based Cleaning
Automata for XPath queries recognize nested words that can be obtained by encoding Xml documents with a single x-marked position. The class of such nested words is characterized by a schema that we can define as the intersection of the two s in Figure 23 and Figure 24. The first tests whether there is exactly one occurrence of the internal letter x, and the second one tests that the Xml data model is satisfied, and the node annotations with x and are put at the right positions.
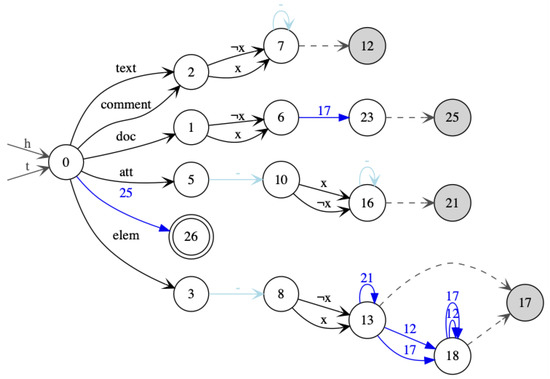
Figure 24.
Nested words of x-marked XML documents.
The automata constructed for the XPath queries may accept some trees that do not satisfy the schema (but will never be evaluated on such trees when answering the query). The idea of schema-based cleaning is to remove all transition rules and states that are not used for recognizing any nested word satisfying the schema. Schema-based cleaning of an automaton can be performed by constructing the product of the automaton with the schema, which is in our case an intersection of two s. We then only keep those states of the original that are used in accessible and co-accessible states of the product with the schema.
Note that schema-based cleaning typically changes the language of the automaton. Different languages may be obtained when cleaning different automata for the same query with respect to the schema. If one is interested in a unique language, then one can choose the intersection of the automaton with the schema. This intersection, however, is usually larger than the automaton obtained by schema-based cleaning.
7.4. Experimental Results for Optimizations
The sizes of optimized automata for the benchmark queries are reported in Figure 25.
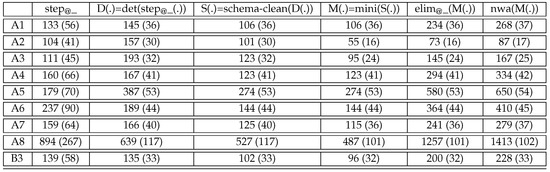
Figure 25.
Optimized automata for derived stepwise automata compiled from .
The function used in the first column compiles to s with apply-else rules. This does not change the number of states, but reduces the number of automata transitions. In the case of A8, the size of the stepwise automaton is reduced from 1106 to 894.
An optimized determinizer is applied by the function in the second column. It preserves apply-else rules in particular. For A8, the size is reduced from 749 to 639 while the number of states is preserved.
Schema-based cleaning is applied by the function in the third column. For A8, the number of rules is reduced further from 639 to 527.
Minimization is applied by the function in the fourth column. In the case of A8, it reduces the number of states from 117 to 101 and the size from 527 to 487.
In order to come back to , we have to eliminate the apply-else rules in column six. For A8 this increases the number of rules back from 527 to 1257.
In the final column, we apply the compiler from s to which preserves determinism. For , this results in a of size 1413 and 102 states. This is better than the previous results, in particular with respect to the number of states.
8. Summary of Experimental Results
We now plug the different compilers and optimization methods all together and compare the sizes of deterministic that we can obtain thereby.
The overall sizes (#states) of the resulting are given in Figure 26. We see that the two methods starting with s and yield reasonably small deterministic for the of all benchmark queries. The methods starting with and provide reasonably small deterministic for queries except for A8.
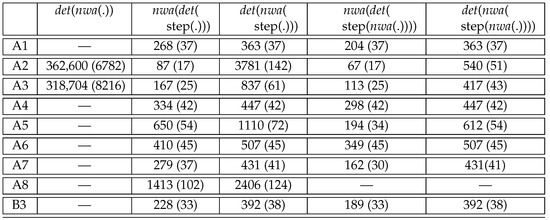
Figure 26.
Deterministic computed with optimizations for the XPath benchmark queries. Note that different for the same query may recognize different languages, due to schema-based cleaning with respect to the Xml data model. Furthermore, our implementation of the minimization algorithm for the subclass of s worked successfully only for s with at most 200 states.
We also tested our algorithms on collections of XPath queries with a scalable parameter, such as the queries for increasing n. This series is known to require automaton with a number of states exponential in n for deterministic bottom-up evaluation. The best methods to produce deterministic in this case is . It works until , leading to an of size with 772 states. The number of states close to doubles when increasing n by 1. The second best method for producing for the series works only until .
For explaining the different size of the for the series , we first note that no schema-based cleaning was applied in this experiment. As a consequence, unique minimal single-entry in which the single-entry state is the initial state should exist. The reason for the larger number of states with the three other methods is that we have not implemented any minimization algorithm for this subclass of single-entry . Furthermore, our implementation of the minimization algorithm for our subclass of s failed for too big s. In this case, the number of states reported in Figure 27 could not be reduced to the minimum. In addition, the number of rules seems to be increased further by the lack of any symbolic representation for rules of that could mimic the apply-else rules for s.
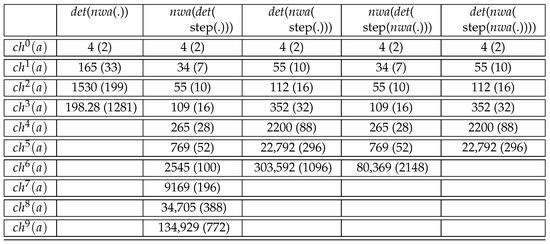
Figure 27.
Deterministic for the queries where : size (#states). There is no schema-based cleaning. Our implementation of the minimization algorithm was applied to all with at most 200 states, as it failed for larger s. No minimization algorithm for subclasses of single-entry was implemented.
9. Deterministic Nested Regular Expressions
We finally show how to distinguish that can be evaluated deterministically in polynomial time, for instance, by compilation to deterministic . For this, we consider the language of that extends the abstract syntax of by a new constant T and a new unary operator .
Definition 8.
An expression of is deterministic if it does not contain a subexpression of any of the forms: , , , .
Note in particular that is a deterministic expression of , as the child operator is added as a primitive there. In contrast, the semantically equivalent expression is not deterministic. Similarly, T is deterministic since it is a primitive expression of , while the equivalent expression is nondeterministic for three different reasons: the -operator, star *, and disjunction +. The recursive expression is nondeterministic: it is not primitive in , and its definition is based on the -operator and disjunction.
The only query of the benchmark for which we can provide a deterministic is the query A1. The for query A1 in Figure A1 is nondeterministic nevertheless, as we replaced with . This is not problematic, given that we can use a decent method for determinization of . For this reason, it does no more seem worth the effort to maintain specialized compilation methods for deterministic . For the same reason, we will not present any experimental results for our specialized compiler from deterministic to deterministic . Instead we use the more general compiler for general nondeterministic .
The compiler from Theorem 1 introduces epsilon rules, and thus it does not preserve determinism: some deterministic will be compiled to nondeterministic . This introduction of nondeterminism can be avoided by eliminating epsilon rules on the fly, that is by using Glushkov’s approach rather than that of Thompson.
Theorem 3.
For any deterministic regular expression E of without conjunction and negation, we can construct in time a recognizing the same language.
Proof sketch.
Theorem 3 uses Glushkov’s construction and thus eliminates -edges on the fly compared to the McNaughton–Yamada–Thompson algorithm. The Glushkov construction is well-known to preserve determinism when compiling regular expressions without nesting to finite state automata [20]. For the additional deterministic expressions , we adapt the deterministic compilation from the work in [18]. This quadratic time result generalizes a previous result for the Glushkov construction [19] from regular expressions without conjunctions and negations to without conjunctions and negations. □
Small deterministic without conjunction and negation can thus be compiled to small . On the benchmark, however, this construction can be applied to the query only, so only a few queries can be covered in this manner.
10. Conclusions and Future Work
We presented s and showed how they can be used to compile to deterministic . When applied to for navigational XPath queries in the usual XPathMark benchmark, we obtained reasonably small deterministic , in contrast to all previous approaches.
The that we obtain by compilation from s all have the weak single-entry property. This property means that the computation of the is done in a purely bottom-up and left-to-right manner, so in the same way as by an . Our experiments show that the usual determinization algorithm for is well-behaved when applied to weak single-entry , while it quickly fails without the weak single-entry property.
We have also stated a unique minimization algorithm for s with the same tree and hedge initial state. It is open whether unique minimization holds for general s. Neither do we know whether minimization is NP-hard. The analogous questions remain open for the class of weak single-entry .
In future work, one needs to tackle the open questions on the minimization of s, weak single-entry , and with fixed general signatures. One has to understand, whether and why unique minimization holds or not, and whether and why minimization is hard or not. Independently, it is interesting to use s in various questions in theory and practice. In particular, we want to develop new algorithms for earliest query answering for s that are more efficient than the existing algorithms for [16] and to see how they behave in practice.
Author Contributions
Conceptualization, J.N.; methodology, J.N.; software, J.N. and M.S.; validation, J.N. and M.S.; formal analysis, J.N. and M.S.; writing—original draft preparation, J.N. and M.S.; writing—review and editing, J.N. and M.S.; visualization, J.N. and M.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially funded by a grant from CPER Nord-Pas de Calais/FEDER DATA Advanced data science and technologies 2015–2020.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The nested regular expressions generated for the queries mentioned in this article and their corresponding automata—when we could produce them—can be found at http://researchers.lille.inria.fr/niehren/complementary-material.
Acknowledgments
It is a pleasure to thank Iovka Boneva for her contributions to the conference version [25] onto which this journal article extends. We are equally grateful to Antonio Al Serhali for implementing the determinization algorithm for s with apply-else rules.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Determinization of NWAs
Let us first introduce some notations. For a transition , we write . Furthermore, we write to denote the reflexive and transitive closure of . Finally, for any set Q, we write to denote the binary relation that relates every element of Q to itself, that is, .
We adapt the usual determinization procedure for [3,18] so that they can account for hedge ending and else rules. Given an , the difficulty is to deal with concurrent opening rules and in during determinization without mixing up the stack symbols and . Therefore, we use transition relations as states of the determinized automaton , , , that is, , . The only initial state is the composition of with , i.e., . The set of final states is . Schemas generating the transition rules in are given below.
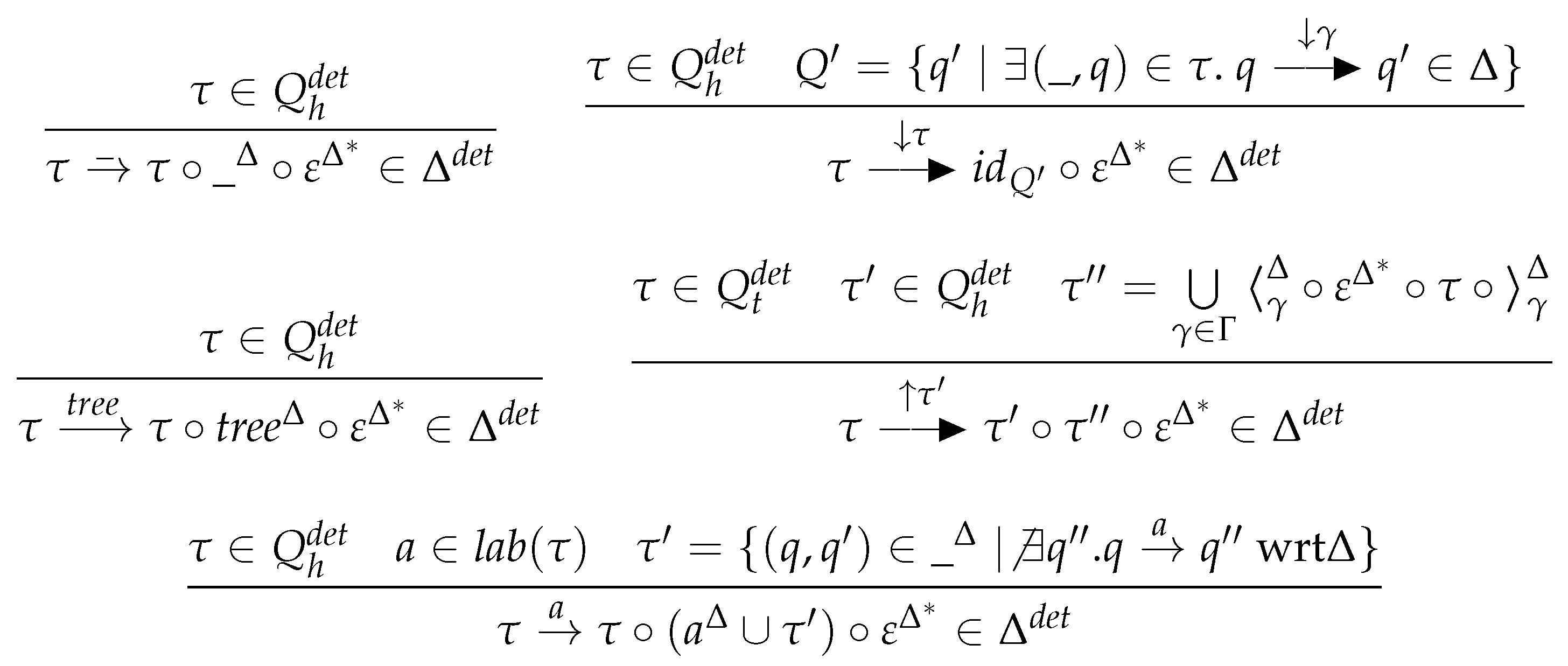
Appendix B. NREs for the XPathMark Benchmark
We compiled navigational XPath queries of the XPathMark benchmark to the given in Figure A1.

Figure A1.
The of the XPath benchmark queries.
Appendix C. Some More Automata
Figure A2.
Deterministic : .
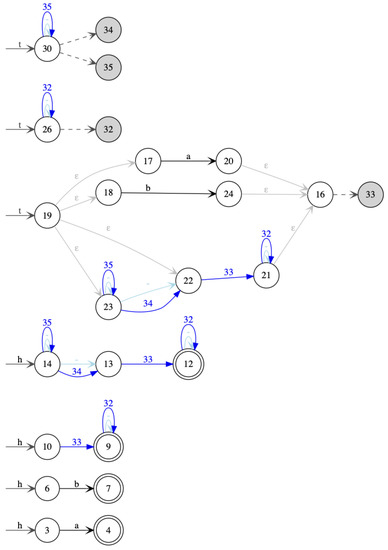
Figure A3.
Stepwise hedge automaton from for .
Figure A4.
Determinization of from stepwise hedge automaton: .
References
- Mehlhorn, K. Pebbling Moutain Ranges and its Application of DCFL-Recognition. In Automata, Languages and Programming, Proceedings of the 7th Colloquium, Noordweijkerhout, The Netherlands, 14–18 July 1980; Lecture Notes in Computer Science; de Bakker, J.W., van Leeuwen, J., Eds.; Springer: Berlin/Heidelberg, Germany, 1980; Volume 85, pp. 422–435. [Google Scholar] [CrossRef]
- Von Braunmühl, B.; Verbeek, R. Input Driven Languages are Recognized in log n Space. North Holl. Math. Stud. 1985, 102, 1–19. [Google Scholar] [CrossRef]
- Alur, R. Marrying Words and Trees. In Proceedings of the 26th ACM SIGMOD-SIGACT-SIGART Symposium on Principles of Database Systems, Paris, France, 14–16 June 2004; ACM-Press: New York, NY, USA, 2007; pp. 233–242. [Google Scholar]
- Okhotin, A.; Salomaa, K. Complexity of input-driven pushdown automata. SIGACT News 2014, 45, 47–67. [Google Scholar] [CrossRef]
- Alur, R.; Madhusudan, P. Visibly pushdown languages. In Proceedings of the 36th ACM Symposium on Theory of Computing, Chicago, IL, USA, 13–16 June 2004; ACM-Press: New York, NY, USA, 2004; pp. 202–211. [Google Scholar]
- Neumann, A.; Seidl, H. Locating Matches of Tree Patterns in Forests. In Proceedings of the Foundations of Software Technology and Theoretical Computer Science, Chennai, India, 17–19 December 1998; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 1998; Volume 1530, pp. 134–145. [Google Scholar]
- Gauwin, O.; Niehren, J.; Roos, Y. Streaming Tree Automata. Inf. Process. Lett. 2008, 109, 13–17. [Google Scholar] [CrossRef]
- Thatcher, J.W. Characterizing derivation trees of context-free grammars through a generalization of automata theory. J. Comput. Syst. Sci. 1967, 1, 317–322. [Google Scholar] [CrossRef][Green Version]
- Comon, H.; Dauchet, M.; Gilleron, R.; Löding, C.; Jacquemard, F.; Lugiez, D.; Tison, S.; Tommasi, M. Tree Automata Techniques and Applications. 2007. Available online: http://tata.gforge.inria.fr (accessed on 1 February 2021).
- Hosoya, H.; Pierce, B.C. XDuce: A statically typed XML processing language. ACM Trans. Internet Technol. 2003, 3, 117–148. [Google Scholar] [CrossRef]
- Mozafari, B.; Zeng, K.; Zaniolo, C. From Regular Expressions to Nested Words: Unifying Languages and Query Execution for Relational and XML Sequences. PVLDB 2010, 3, 150–161. [Google Scholar] [CrossRef]
- Pitcher, C. Visibly Pushdown Expression Effects for XML Stream Processing. Program. Lang. Technol. XML 2005, 1060, 1–14. [Google Scholar]
- Olteanu, D. SPEX: Streamed and Progressive Evaluation of XPath. IEEE Trans. Know. Data Eng. 2007, 19, 934–949. [Google Scholar] [CrossRef]
- Gauwin, O.; Niehren, J. Streamable Fragments of Forward XPath. In Proceedings of the International Conference on Implementation and Application of Automata, Blois, France, 13–16 July 2011; Lecture Notes in Computer Science; Markhoff, B.B., Caron, P., Champarnaud, J.M., Maurel, D., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; Volume 6807, pp. 3–15. [Google Scholar] [CrossRef]
- Benedikt, M.; Jeffrey, A.; Ley-Wild, R. Stream Firewalling of XML Constraints. In Proceedings of the ACM SIGMOD International Conference on Management of Data, Vancouver, BC, Canada, 10–12 June 2008; ACM-Press: New York, NY, USA, 2008; pp. 487–498. [Google Scholar]
- Gauwin, O.; Niehren, J.; Tison, S. Earliest Query Answering for Deterministic Nested Word Automata. In Proceedings of the 17th International Symposium on Fundamentals of Computer Theory, Wroclaw, Poland, 2–4 September 2009; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2009; Volume 5699, pp. 121–132. [Google Scholar]
- Franceschet, M. XPathMark Performance Test. Available online: https://users.dimi.uniud.it/~massimo.franceschet/xpathmark/PTbench.html (accessed on 25 October 2020).
- Debarbieux, D.; Gauwin, O.; Niehren, J.; Sebastian, T.; Zergaoui, M. Early nested word automata for XPath query answering on XML streams. Theor. Comput. Sci. 2015, 578, 100–125. [Google Scholar] [CrossRef]
- Brüggemann-Klein, A. Regular Expressions into Finite Automata. Theor. Comput. Sci. 1993, 120, 197–213. [Google Scholar] [CrossRef]
- Brüggemann-Klein, A.; Wood, D. One-Unambiguous Regular Languages. Inf. Comput. 1998, 142, 182–206. [Google Scholar] [CrossRef]
- Carme, J.; Niehren, J.; Tommasi, M. Querying Unranked Trees with Stepwise Tree Automata. In Proceedings of the 19th International Conference on Rewriting Techniques and Applications, Paris, France, 26–28 June 2004; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2004; Volume 3091, pp. 105–118. [Google Scholar]
- Alur, R.; Kumar, V.; Madhusudan, P.; Viswanathan, M. Congruences for Visibly Pushdown Languages. In Automata, Languages and Programming, Proceedings of the 32nd International Colloquium, Lisbon, Portugal, 11–15 July 2005; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2005; Volume 3580, pp. 1102–1114. [Google Scholar] [CrossRef]
- Chervet, P.; Walukiewicz, I. Minimizing Variants of Visibly Pushdown Automata. In Mathematical Foundations of Computer Science 2007; Kučera, L., Kučera, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; pp. 135–146. [Google Scholar]
- Gauwin, O.; Muscholl, A.; Raskin, M. Minimization of visibly pushdown automata is NP-complete. Log. Methods Comput. Sci. 2020, 16. [Google Scholar] [CrossRef]
- Boneva, I.; Niehren, J.; Sakho, M. Nested Regular Expressions Can Be Compiled to Small Deterministic Nested Word Automata. In Computer Science—Theory and Applications, Proceedings of the 15th International Computer Science Symposium in Russia (CSR 2020), Yekaterinburg, Russia, 29 June–3 July 2020; Lecture Notes in Computer Science; Fernau, H., Ed.; Springer: Cham, Switzerland, 2020; Volume 12159, pp. 169–183. [Google Scholar] [CrossRef]
- Gottlob, G.; Koch, C.; Pichler, R. The complexity of XPath query evaluation. In Proceedings of the 22nd ACM SIGMOD-SIGACT-SIGART Symposium on Principles of Database Systems, San Diego, CA, USA, 9–12 June 2003; pp. 179–190. [Google Scholar]
- Libkin, L.; Martens, W.; Vrgoč, D. Querying Graph Databases with XPath. In Proceedings of the 16th International Conference on Database Theory (ICDT’13), Genoa, Italy, 18–22 March 2013; Association for Computing Machinery: New York, NY, USA, 2013; pp. 129–140. [Google Scholar] [CrossRef]
- Fischer, M.J.; Ladner, R.E. Propositional Dynamic Logic of Regular Programs. J. Comput. Syst. Sci. 1979, 18, 194–211. [Google Scholar] [CrossRef]
- Mozafari, B.; Zeng, K.; Zaniolo, C. High-performance complex event processing over XML streams. In Proceedings of the SIGMOD Conference, Scottsdale, AZ, USA, 20–24 May 2012; Candan, K.S., Chen, Y., Snodgrass, R.T., Gravano, L., Fuxman, A., Eds.; ACM: New York, NY, USA, 2012; pp. 253–264. [Google Scholar] [CrossRef]
- Grez, A.; Riveros, C.; Ugarte, M. A Formal Framework for Complex Event Processing. In Proceedings of the 22nd International Conference on Database Theory (ICDT 2019), Lisbon, Portugal, 26–28 March 2019; Volume 127, pp. 5:1–5:18. [Google Scholar] [CrossRef]
- Bozzelli, L.; Sánchez, C. Visibly Rational Expressions. Acta Inf. 2014, 51, 25–49. [Google Scholar] [CrossRef][Green Version]
- Gécseg, F.; Steinby, M. Tree Automata; Akadémiai Kiadó: Budapest, Hungary, 1984. [Google Scholar]
- Scott, D.; de Bakker, J.W. A Theory of Programs; IBM: Vienna, Austria, 1969; Unpublished Manuscript. [Google Scholar]
- Stockmeyer, L.J.; Meyer, A.R. Word Problems Requiring Exponential Time. In Proceedings of the 5th ACM Symposium on Theory of Computing, Austin, TX, USA, 30 April–2 May 1973; pp. 1–9. [Google Scholar]
- Champavère, J.; Gilleron, R.; Lemay, A.; Niehren, J. Efficient Inclusion Checking for Deterministic Tree Automata and XML Schemas. Inf. Comput. 2009, 207, 1181–1208. [Google Scholar] [CrossRef][Green Version]
- Aho, A.V.; Lam, M.S.; Sethi, R.; Ullman, J.D. Compilers: Principles, Techniques, and Tools, 2nd ed.; Addison Wesley: Reading, MA, USA, 2006. [Google Scholar]
- Arnold, A.; Niwiński, D. Complete lattices and fixed-point theorems. In Rudiments of μ-Calculus; Studies in Logic and the Foundations of Mathematics; Elsevier: Amsterdam, The Netherlands, 2001; Volume 146. [Google Scholar]
- Martens, W.; Niehren, J. On the Minimization of XML-Schemas and Tree Automata for Unranked Trees. J. Comput. Syst. Sci. 2007, 73, 550–583. [Google Scholar] [CrossRef][Green Version]
- D’Antoni, L.; Alur, R. Symbolic Visibly Pushdown Automata. In Computer Aided Verification, Proceedings of the 26th International Conference (CAV, VSL 2014), Vienna, Austria, 18–22 July 2014; Lecture Notes in Computer Science; Biere, A., Bloem, R., Eds.; Springer: Cham, Switzerland, 2014; Volume 8559, pp. 209–225. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).