1. Introduction
The utilization of spatial multiplexed multiple-input multiple-output (MIMO) technology could linearly increase the link capacity of the communication systems without sacrificing spectrum and time resource [
1,
2]. A recent highlight for MIMO technologies is to consider massive number of receiving antennas at base stations and user equipments. In massive MIMO systems, the total number of antenna elements at user terminals are relatively small. This ensures satisfactory performance with simpler signal detection techniques. Massive MIMO is regarded as a core technology for the next generation mobile communication systems [
1]. Harnessing such benefits of large-dimensions in practice, however, is challenging. In particular, with the increasing number of concurrent user data streams, detection complexity could become infeasible [
3,
4].
Several detection algorithms have been proposed in the literature to address the problem of detecting massive MIMO signal. It is well known that maximum likelihood (ML) [
5] is the optimal algorithm for MIMO detection. The core of the ML algorithm is to calculate the respective ML cost for all trasmission combination candidates, and then find the one with the minimum cost. Theoretically, the algorithm provides optimal performance; however, with the increased number of antennas and modulation level, the computational complexity of the algorithm increases exponentially. For practical applications, the minimum mean square error algorithm [
6] is usually low in computational complexity, but it may not obtain full diversity gain and has a performance worse than an ML detector. Sphere decoding (SD) [
7] is an algorithm for searching a space of a multiple dimensional sphere which has a soft complexity may raise exponentially with the increased number of antennas. In addition, tabu search (TS) is a heuristic algorithm which is originally developed to obtain approximate solutions to combinatorial optimization problems [
8]. Recently TS is increasingly being applied to communication problem [
9,
10,
11,
12]. In [
9], a reactive tabu search to seek approximate ML solutions in large dimension is presented. In traditional RTS algorithm, the number of candidates involved in the calculation determines the complexity and the performance of the detection algorithm. However, in this work, we believe not all the candidates are required to perform the ML cost calculation, and many of the candidates can be excluded from the detection procedure and their performance impact on the detection results can be neglected.
The detection complexity of the RTS algorithm is associated with the number of candidates involved in calculating the ML cost for each candidate. A larger number of RTS candidates usually correspond to a higher complexity [
13] for detection. Therefore, in this paper, inspired by [
14,
15], we propose a new scheme which may reducing the RTS complexity by decreasing the searching space of candidates with the help of their estimated reliability. A brief introduction of the proposed algorithm is summarised as follows: First, an initial solution vector is given, and the vector is usually given by an MMSE or ZF filter. Then, with the initial solutions, we separate the reliable decision candidates from the unreliable ones according to the proposed CC structure. Finally, we use the modified RTS algorithm for updating the unreliable candidates with the reliable decisions. The simulation results show that the proposed CC-RTS detection algorithm has a complexity about 50% lower than the traditional RTS with the same target SNR value.
With the help of reliability checking of the proposed CC structure, the RTS candidates with high reliability will be excluded from the neighborhood, and the number of candidates participating the following RTS procedures for evaluating the ML cost will be significantly reduced. Therefore the complexity of the overall detection algorithm is significantly reduced. The contribution of this paper is given as follows:
We propose a scheme, namely Constellation Constraints (CC) algorithm for determining the reliability of the initial vector.
With the proposed CC structure, the algorithm separate the reliable symbol estimates in the initial vector from unreliable symbols.
A algorithm is developed for generating a new candidate set and neighborhood searching space and their implementation with RTS detection.
The simulation results of the proposed scheme are given to verify that similar BER performance can be achieved with significant lower computational complexity.
The rest of this paper is organized as follows. The system model is introduced in
Section 2, while the proposed algorithm in the massive MIMO configuration is described in
Section 3. In
Section 4, the attainable performance of our scheme is verified. Finally, the conclusion is given in
Section 5.
3. CC-RTS Algorithm
Maximum Likelihood (ML): Maximum likelihood detection algorithm calculates the Euclidean distance between the received signal vector and the product of all possible transmitted signal vectors multiplied by channel
H and searching for the one with the minimum distance. Let
denote the whole ML search space with a number of combination candidates which increases exponentially with a raising number of spatial multiplexed transmit antennas modulation level. ML algorithm determines the estimated transmitted signal vector
as:
where
corresponds to the ML metric of the candidate
.
Traditional RTS Algorithm: The implementation of RTS algorithm in massive MIMO [
10,
11,
12] is introduced in the following. With sufficient number of receiving antennas, the RTS algorithm has a performance closes to the ML algorithm, but with significant lower detection complexity. This algorithm use the MMSE output as the initial solution vector, and find the neighborhood candidates of the initial solution vector; Then, the algorithm computes the respective ML cost with these candidates and searching for the one with the minimum cost. If it is the case that the selected candidate does not appear in the tabu list (Tabu list is used to hold the initial solution of the next iterative process. The elements in the list follow first in first out FIFO rules. The tabu length indicates that the element will not be used again as the initial solution vector in the next few iterations. The length of tabu is divided into variable and immutable. If the tabu length is fixed, then the algorithm is called fixed tabu search. If the length is a variable, then the algorithm is termed reactive tabu search), the selected candidate is used as the initial value for the next iteration of searching, meanwhile the algorithm includes this selected candidate into the tabu list; On the other hand, if the candidate is already included in the tabu list, a suboptimal solution outside the tabu list is selected as the initial value for the next iteration of searching, and the suboptimal solution is added to the tabu list. After several iterations, the candidate with the minimum ML cost can be selected as the final output of the RTS algorithm.
RTS neighborhood: The selection criteria of neighborhood candidates in [
9] is the metric of Euclidean distance, that is, to find the nearest constellation candidates from a given point. For example: If we use
to indicate a transmitting signal symbol, and
denotes the neighborhood candidates of
. For QPSK modulation, if we consider a
MIMO model and the initial value is considered to be
, the number of candidates for
is 2, by finding the nearest two candidates, we have
.
For the RTS algorithm, the most expensive step is to find the nearest constellation candidates by measuring Euclidean distance and calculate their respective ML costs [
14,
15,
16,
17].
Table 1 shows the number of nearest candidates in different modulation modes. With the increased number of antennas, the number of candidates for the RTS algorithm is raising. The main contribution of the proposed algorithm is to reduce the computational complexity of the conventional RTS by shorten the candidates list. In below, we will introduce in detail of the proposed CC algorithm, and how the CC algorithm can be used for reducing the number of candidates in each iteration of searching.
CC-RTS: The inspiration to use a CC device to improve traditional RTS algorithm in this paper comes from our previous work [
14,
15,
16,
17]. With the analysis of MMSE filter, theoretical research shows that the estimated symbols gradually converge with an increasing value of signal-to-noise ratio. For each transmission, the distance between an estimated symbol and its nearest constellation point can be regarded as an measurement of the reliability of the estimates. For the RTS algorithm, in this work, the proposed CC algorithm [
17] is used to reduce the computational complexity for traditional reactive tabu search and the algorithm may prevent the search space from growing exponentially with the increased number of transimitting antennas. In [
14,
15,
16,
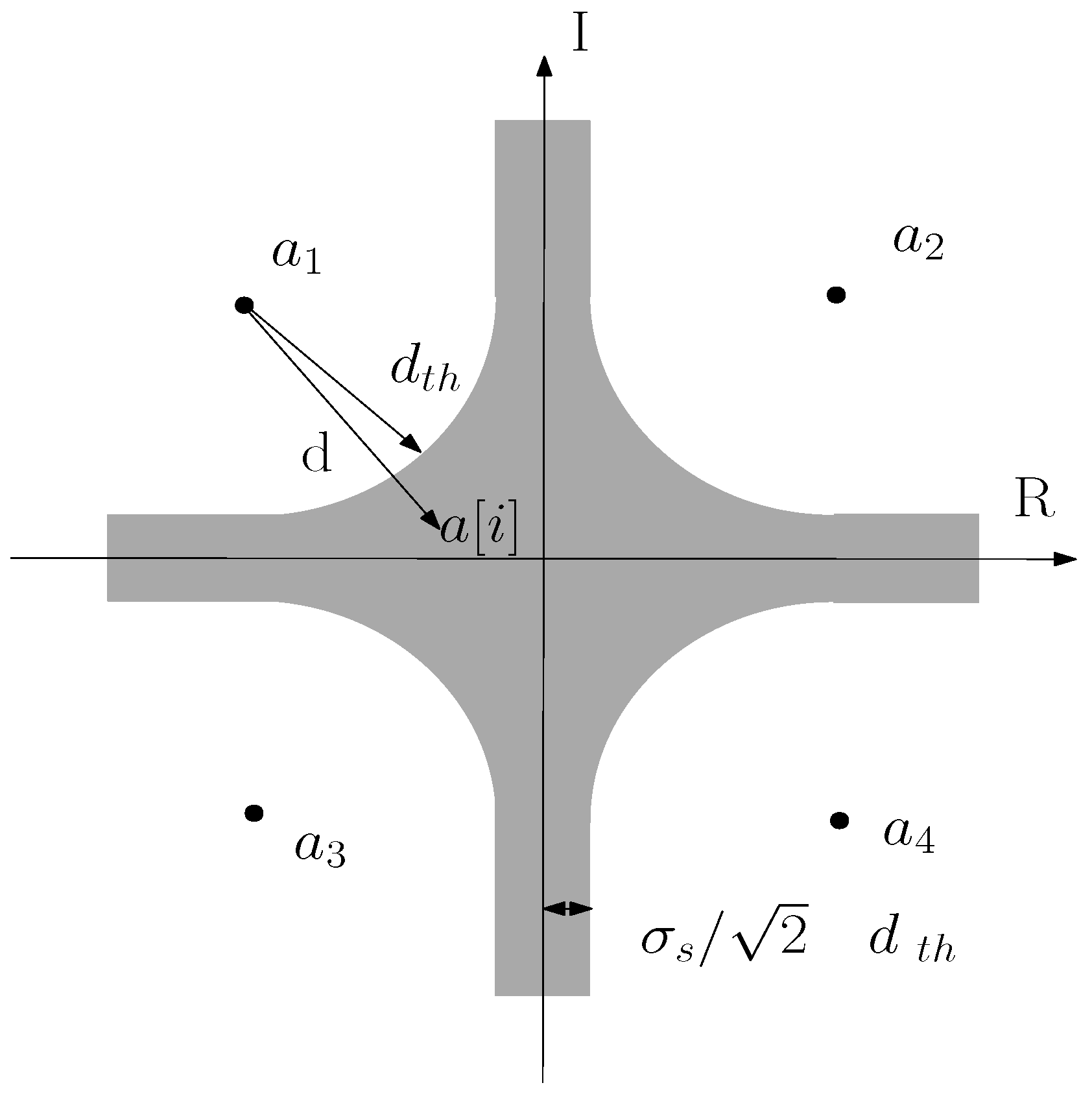
17], an estimation reliability measuring and refining strategy (CC algorithm) is used to detect MIMO signal with nonlinear decision feedback systems. Inspired by its principle of determining reliability, in this paper, we have modified the CC algorithm to improve heuristic neighborhood search algorithms, such as traditional RTS algorithm. A simplification of the proposed CC structure is shown in
Figure 1. The parameters marked in the figure are given as follows,
refers to the signal power, and the threshold
represents the device radius which can control the shaded area. It can be designed as a constant, or a joint function of the signal power
and the noise power
. The value
d represents the distance between the detection signal and its nearest constellation point. The following equation is given to determine the nearest constellation point for a given signal
.
where
represents the selected element of the constellation.
From
Figure 1, we can see that the constellation space is divided into shaded areas and bright areas, we stipulate that if the candidate falls in the shaded area, we determine that this candidate is unreliable. The signal falling in the shadow area to meet the following condition.
If the signal to be detected satisfies the above conditions, the algorithm considers the candidate as unreliable. On the other hand, if the detection signal does not satisfy above conditions, the algorithm considers the candidate as reliable. If it is the case that the proposed CC structure considers the candidate as unreliable, it introduces more candidates as the output for test; While CC structure considers the candidate is reliable, the quantization of the candidate is performed at the output. The detected signals can be MMSE soft output or Zero Force soft output.
The pseudo code of the proposed CC-RTS algorithm is given in
Table 2. In
, we not only consider the hard output of MMSE but also include the soft output, generating the initial value of RTS algorithm; In
, we define a vector
. Through the distribution of
, we divide the signals into reliable signals and unreliable signals. In
, for the distribution of the
, we only look for candidates of the initial value of
is 1, and then execute RTS algorithm for these elements. This reduces the number of candidates in the traditional RTS algorithm, thereby reducing the complexity of the traditional RTS algorithm.
4. Simulation Results
In this part, we will shown the advantages of CC-RTS algorithm in terms of computational complexity and BER performance. The algorithm may approach the original RTS algorithm in terms of BER performance with various MIMO configurations. Meanwhile the proposed algorithm may significantly reduce the detection complexity of the traditional RTS algorithm for massive MIMO systems. To evaluate the achievable performance of the proposed scheme, we present our results based on MATLAB simulations. We set up a simulation model with the following parameters: the system is a MIMO using QPSK modulation with
,
,
,
MIMO antennas. We assume that the transmitted signal encounters independent Rayleigh Fading in the propagation channels. The transmitted
are grouped into frames consisting of 100,000 symbol vectors, and 100,000 Monte Carlo simulation is carried to produce the results. In addition, the following RTS parameters are also used in the simulations: MMSE initial vector, initial tabu length is 3, and Iterations is 20. These parameters are shown in
Table 3.
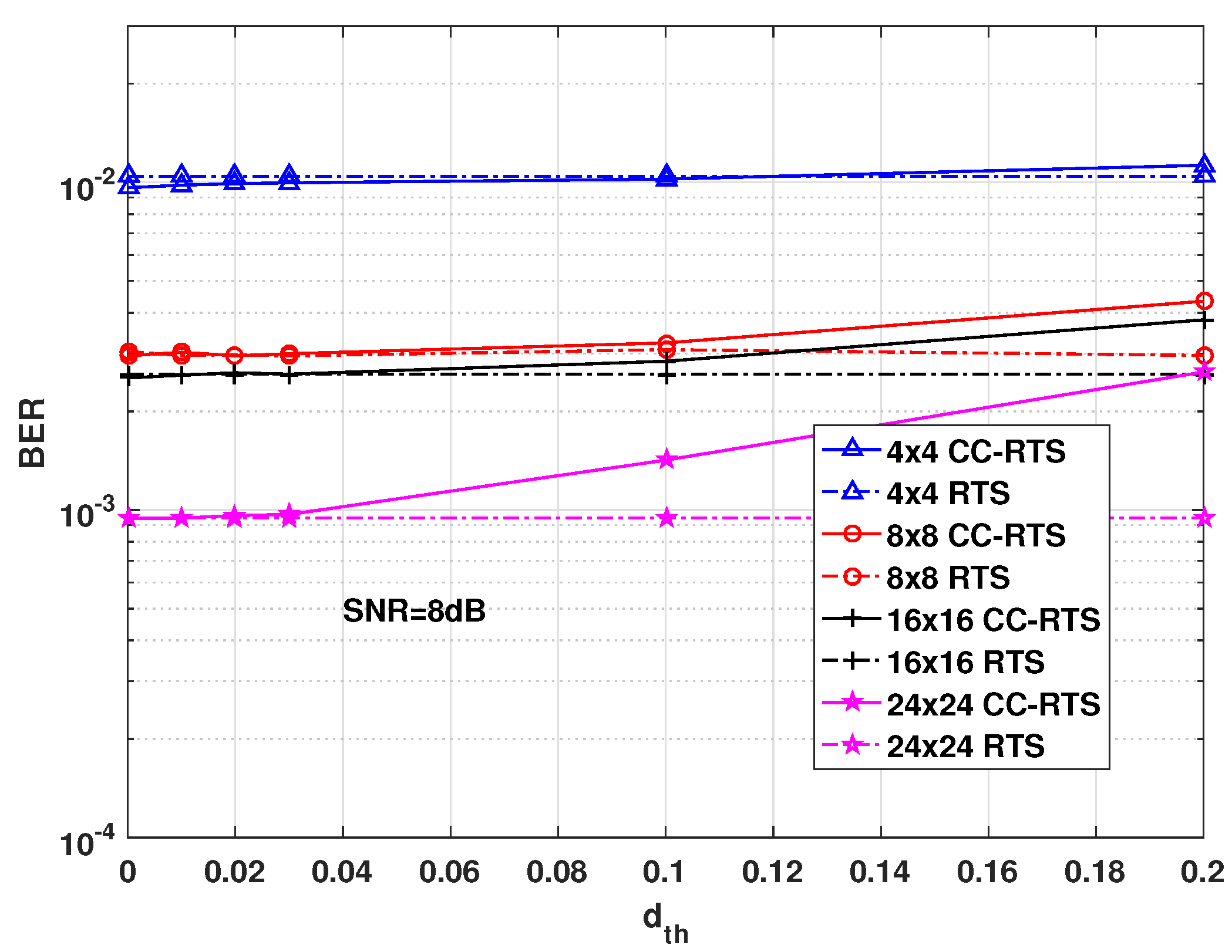
Performance: In
Figure 2 and
Figure 3, we present the simulated BER performance of the proposed CC-RTS algorithm with various selection of
with Rayleigh channel.
Figure 2 shows that the variation of BER as a function of the
, with
=
= 4, 8, 16, 24, respectively, and all the simulations are with SNR = 8dB. It can be observed from
Figure 2 that, depending on the choice of the value of
, BER and
rendering correlation.
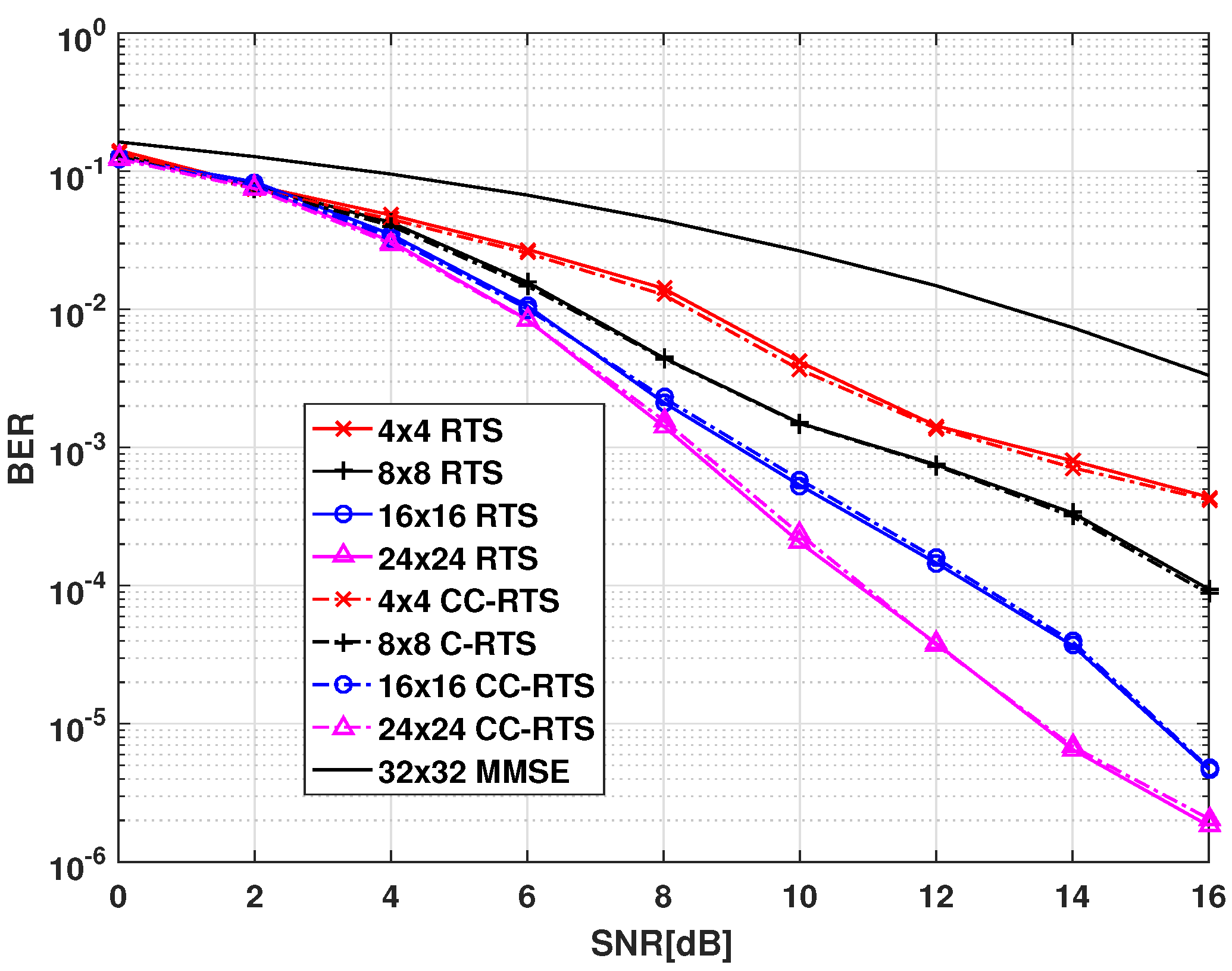
Figure 3 shows the performances of the proposed CC-RTS and reference RTS, with
=
= 4, 8, 16, 24, and
=0.02. It can be seen that the proposed CC-RTS has a performance close to the traditional RTS algorithm.
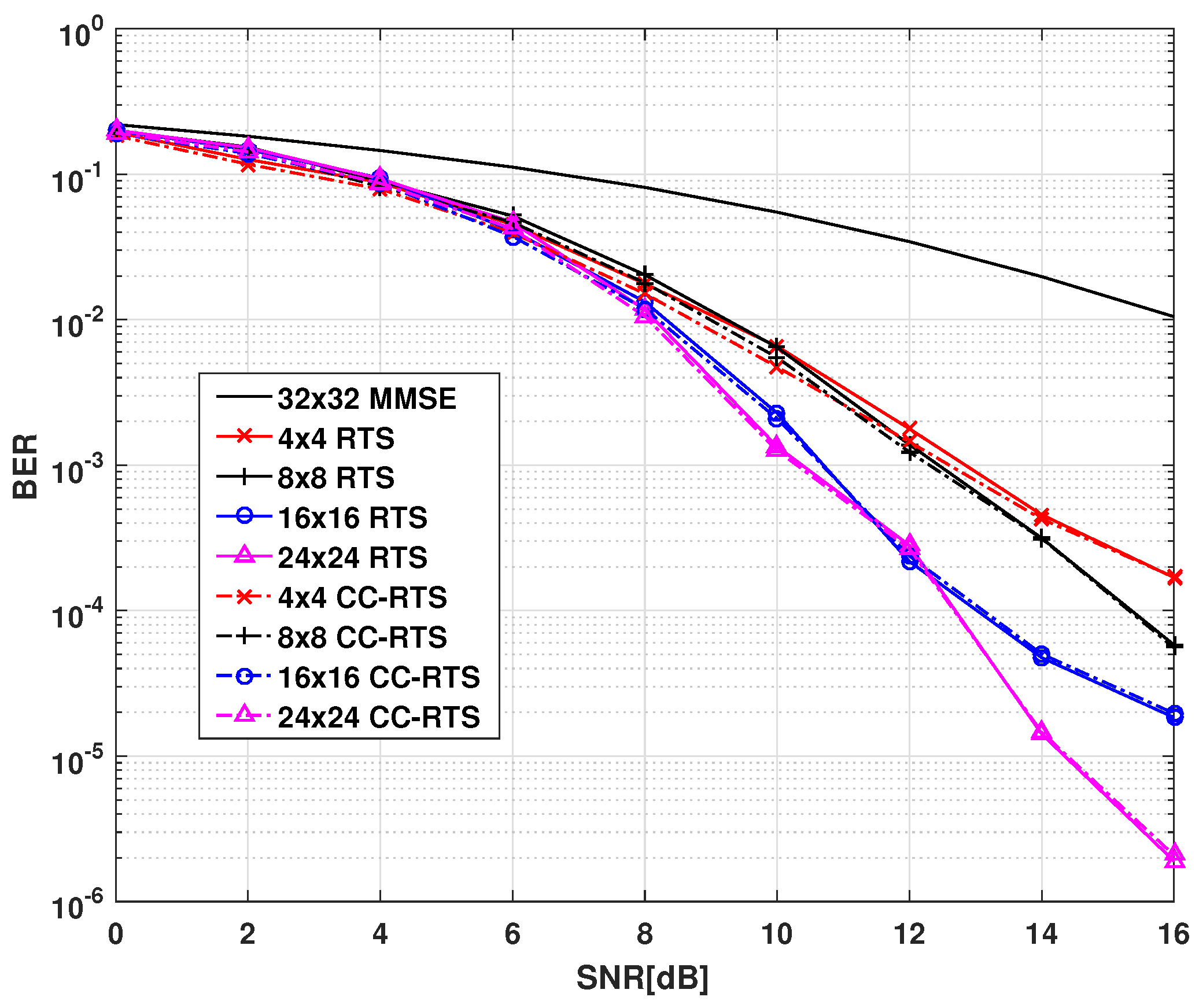
Besides, in the case that the channel is time-varying, we also make a model simulation. The channel model adopted is Doppler Frequency Shift, and the value of
is 0.02. In this simulation process, we used rayleighchan MATLAB build in function to generate channel with Doppler Frequency Shift. The sampling frequency shift was 1/15,000 and the maximum Doppler Frequency Shift is 500. The performance of the proposed CC-RTS and reference RTS with Channel with Doppler Frequency Shift is shown in
Figure 4. From
Figure 4, we can get a conclusion that: With Doppler Frequency Shift, CC-RTS algorithm also have the advantages of greatly reducing the computational complexity of RTS algorithm without affecting the performance of the traditional RTS algorithm, although the bit error rate is slightly different.
Complexity: In order to further verify the proposed algorithm, we exam the complexity reduction over the traditional RTS algorithm. The complexity analysis is based on the assumption that the radius of the CC device is given by 0.02. We can see from
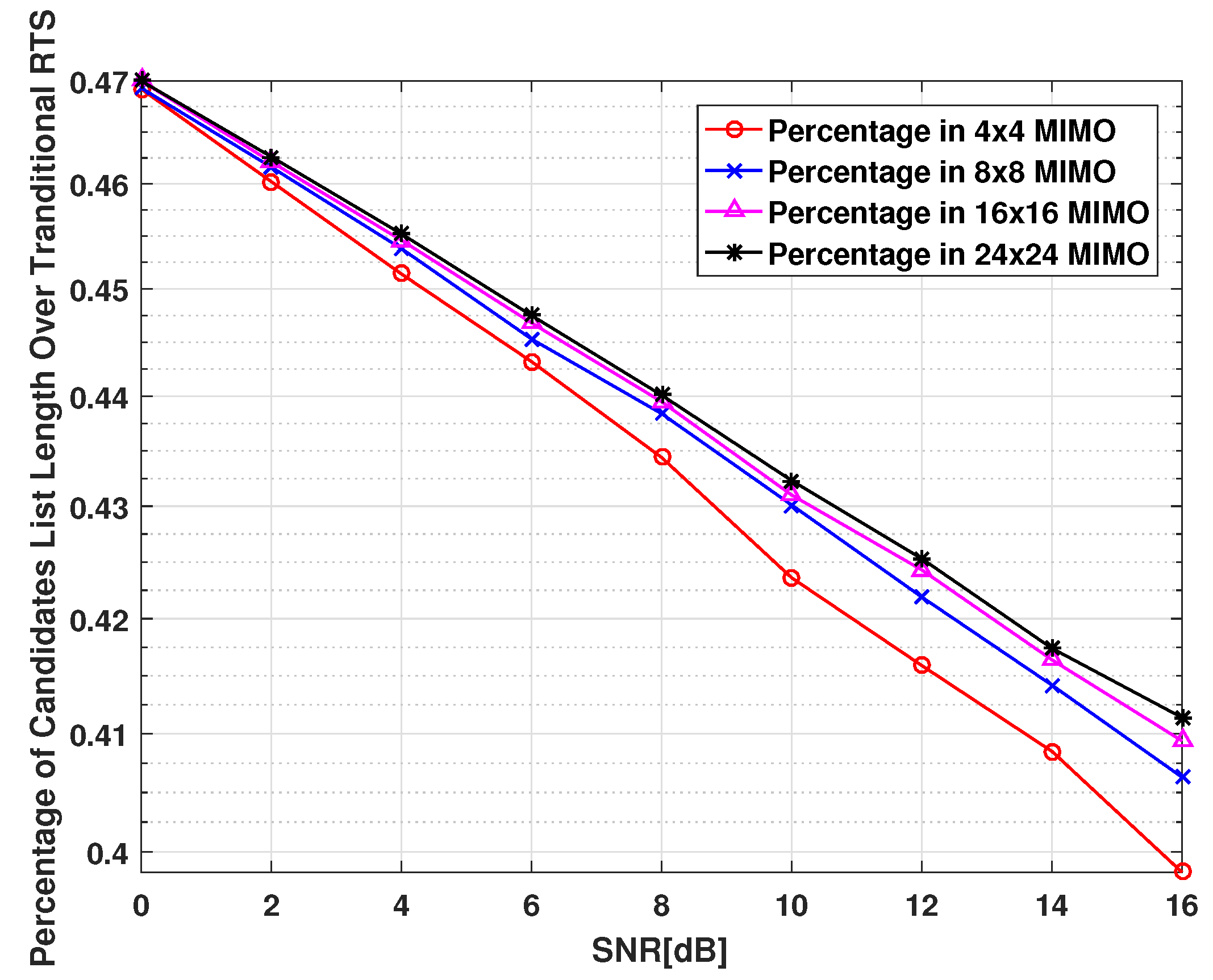
Figure 5 that with the proposed scheme, more than half number of the candidates are excluded under different antenna configurations compare to the traditional RTS algorithm. For same number of antennas, with an increasing value of SNR, the number of candidates is gradually reduced and the subsequently calculation of ML cost and overall detection complexity can be saved. In addition, from
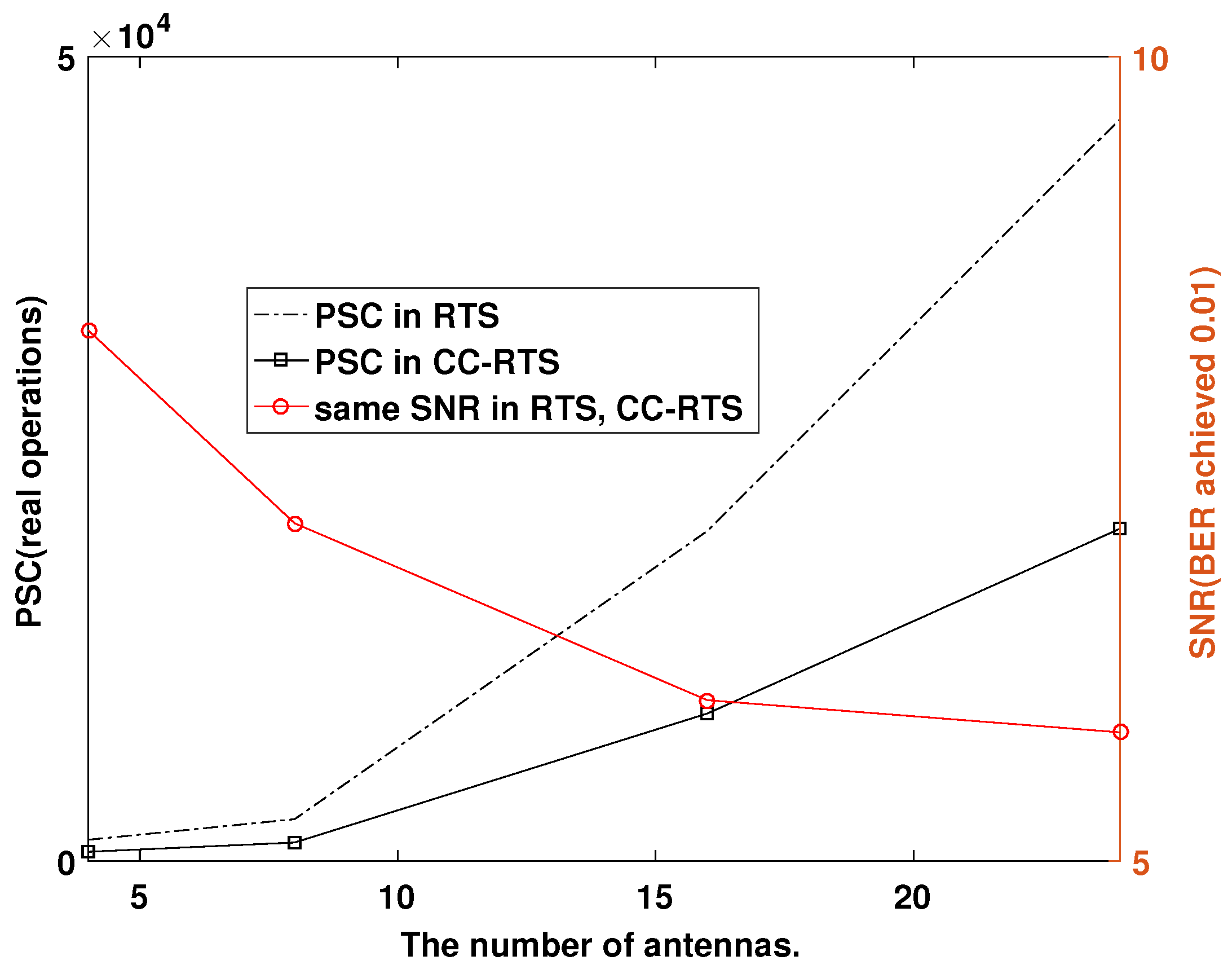
Figure 6 and
Table 4, we can see that for a given target BER performance, such as
, the per-symbol-complexity (PSC) of the CC-RTS algorithm is smaller than that of the traditional RTS algorithm. The following is a detailed derivation of the mathematical expression of PSC:
It is known that the most expensive part of the RTS algorithm is to calculate the Euclidean distance. For the MIMO models, multiplication and addition are needed in this process. If the number of iterations is , each symbol’s neighbor is M, then the computational complexity of each symbol in the RTS algorithm is . As an improvement of RTS algorithm, CC-RTS algorithm could significantly reduce the number of search candidates without reducing the ML cost of each set of candidates. Therefore, the computational complexity of CC-RTS algorithm and RTS algorithm on a vector is consistent, but the overall computational complexity of CC-RTS algorithm is smaller than that of RTS algorithm.