Abstract
This paper creates a bi-directional prediction model to predict the performance of carbon fiber and the productive parameters based on a support vector machine (SVM) and improved particle swarm optimization (IPSO) algorithm (SVM-IPSO). In the SVM, it is crucial to select the parameters that have an important impact on the performance of prediction. The IPSO is proposed to optimize them, and then the SVM-IPSO model is applied to the bi-directional prediction of carbon fiber production. The predictive accuracy of SVM is mainly dependent on its parameters, and IPSO is thus exploited to seek the optimal parameters for SVM in order to improve its prediction capability. Inspired by a cell communication mechanism, we propose IPSO by incorporating information of the global best solution into the search strategy to improve exploitation, and we employ IPSO to establish the bi-directional prediction model: in the direction of the forward prediction, we consider productive parameters as input and property indexes as output; in the direction of the backward prediction, we consider property indexes as input and productive parameters as output, and in this case, the model becomes a scheme design for novel style carbon fibers. The results from a set of the experimental data show that the proposed model can outperform the radial basis function neural network (RNN), the basic particle swarm optimization (PSO) method and the hybrid approach of genetic algorithm and improved particle swarm optimization (GA-IPSO) method in most of the experiments. In other words, simulation results demonstrate the effectiveness and advantages of the SVM-IPSO model in dealing with the problem of forecasting.
1. Introduction
Carbon fibers are produced mainly from polyacrylonitrile (PAN), rayon, and pitch. Attributing to inherent structural composites, the PAN-based carbon fibers have maintained their predominance as engineering materials up to the present. It has been documented that 90% of the world’s total carbon fibers used today are made from the PAN precursor [1]. Their high specific modulus and outstanding fatigue characteristics, combined with their stiffness and lower weight, make these fibers attractive for mass applications ranging from sporting goods to engineering components [2].
Producing a high quality carbon fiber is not an easy thing, since the technological process for carbon fiber is a complex nonlinear system which involves many process parameters that must be carefully optimized and adjusted. Most of the previous work was focused on analyzing the properties of carbon fibers by means of physical or chemical instruments. Liu et al. [3] referred to a surface treatment technique of electrochemical oxidation to improve interfacial bonding strength and tensile strength of carbon fibers. Wang et al. [4] investigated the chemical element potassium permanganate modification for carbon fibers during the heat treatment process by differential scanning calorimetry, infrared spectra, elemental analysis, and X-ray photoelectron spectroscopy. Rahman et al. [5] referred to the residence time of 3 s as being the most suitable residence time for producing carbon fibers in a solvent-free coagulation process. Experimental data suggest that the Young’s modulus of carbon fibers can reach a highest value of 2.55 Gpa. Liang et al. [6] used a bio-inspired intelligent cooperative controller to provide a plan for a stretching process for fiber production. Rennhofer et al. [7] investigated the structural change of carbon fibers with the use of an X-ray testing device at high temperatures under load. Belyaev et al. [8] investigated the kinetics of carbon fibers in oxidative stabilization by differential scanning calorimetry data. Chen et al. [9] proposed a hybrid model of genetic algorithm and improved particle swarm optimization to optimize the radial basis function neural network for real-time predicting of the carbon fiber manufacturing process. According to all the kinds of descriptions mentioned above, we know that they mostly previously analyzed properties with the aid of different instruments [10], considering solely relationship between the productive parameters and the fiber properties in the literature. This situation resulted for two main reasons, on the one hand, numerous researchers in materials science had different perspectives in the study of the productive process, while on the other hand, the technological process for carbon fiber is a nonlinear system, containing a lot of separate processes: polymerization, spinneret, coagulating baths, washing, stretching, applying oil, drying, pre-oxidation, carbonization, and more. These process can be regarded as subsystems, each subsystem has its own control parameters. These parameters affect and restrict the performance of the whole system directly, whereas they are not only affected by interrelation and coupling among subsystems but also by the external environment. Therefore, it is difficult to establish a precise mathematical model to represent linearly the relation between properties indices and productive parameters.
With the rise of intelligent algorithms, the theory of intelligent algorithm has provided a powerful tool of systematic research for analyzing the unknown complex nonlinear system. Among them, artificial neural network (ANN) has proved to be an excellent adaptive method with dark-box operating performance, powerful study and generalized ability to deal with modeling the dynamic process for process control. Kadi [11] used the ANN to predict mechanical modeling for fiber-reinforced composite materials. Yu et al. [12] used a fuzzy ANN to predict the fabric hand in different fabric specimens. However, ANN needs a long training time because its topology is not compact enough. Then RNN was adopted to compensate for the weaknesses of ANN. Du et al. [13] investigated the center selection of multi-output RNN. Roy et al. [14] investigated the learning theory of the RNN. Hong et al. [15] presented a novel topology of the RNN, referred to as the boundary value constraints. Huang et al. [16] investigated the function approximation of the RNN. Qiao et al. [17] presented a self-organizing RNN to identify nonlinear systems and the model. Wang et al. [18] proposed a forecasting method based on self-correcting RNN for adapting changing conditions. However, the training procedure for ANN models is not only time consuming but it is also possible to get trapped in local minima and subjectively in selecting the model architecture [19]. SVM is a relatively new artificial intelligence technique which is increasingly being applied to geotechnical problems and has yielded encouraging results [20,21]. SVM implements the structural risk minimization principle rather than the empirical risk minimization principle implemented by most traditional ANN models [22,23]. Based on this principle, SVM achieves an optimum network structure; meanwhile, it can lower the global error of the model. It raises the generalization capability of the model, which is more prominent in small-sample learning. SVM have found a wide application in the fields of pattern recognition, bio-informatics, and nonlinear regression estimation problems. Particularly, support vector regression (SVR) is an extension of SVM. Wang et al. [24] proposed a hybrid load forecasting model combining differential evolution algorithm and SVR. Gilan et al. [25] developed a hybrid SVR and PSO model to predict the compressive and rapid chloride penetration test (RCPT) results of concretes containing metakaolin. Hong [26] developed a hybrid SVR and chaotic particle swarm optimization model to predict electric load. Kang et al. [27] developed swarm intelligence approaches to optimize power flow problems in power networks. Liang et al. [28] developed an adaptive PSO method based on clustering to solve multimodal function optimization problems.
In this paper, we propose the SVM-IPSO hybrid model to bi-directionally forecast a productive process for carbon fiber. We use IPSO to tune the parameters in SVM. With this model, we can predict the performance of carbon fiber and obtain a design scheme for new carbon fiber.
The main contributions of this article include the following: (1) we propose IPSO, which pushes forward the development of intelligent computing; (2) the hybrid SVM-IPSO model is used to set up a bi-directional prediction approach for carbon fiber; (3) with the proposed model, we can online forecast the productive parameters and the properties of carbon fiber, adjust technical parameters in time, reduce not only wasted time but also energy consumption.
The main structure of this article is organized as follows: The first section describes the research motivation of this paper. The second section introduces the regression algorithm of SVM. The third section introduces the parameters for selecting SVM based on IPSO. The fourth section testifies the performance of the proposed model with the experimental data and compares the results with other methods. The fifth section discusses the research conclusion.
2. Carbon Fiber Production and Its Bi-Directional Optimization
2.1. The Process of Carbon Fiber Production
The technological process for carbon fiber is a sufficiently complex system. It is a very meaningful research subject to control the performance of the carbon fiber process in as small a range as we possibly can. For this purpose, we should observe the parameters of the productive process in real-time, synchronously predict the product properties of the carbon fiber, after which we can determine the defective carbon fiber, timely adjust the parameters of the productive process, avoid reducing the quality of the carbon fiber, and prevent significantly wasting of raw materials. The production of carbon fiber mainly comprises several processes, such as coagulation, stretching, oiling, and heat treatment. Figure 1 shows the main technological process of carbon fiber production.
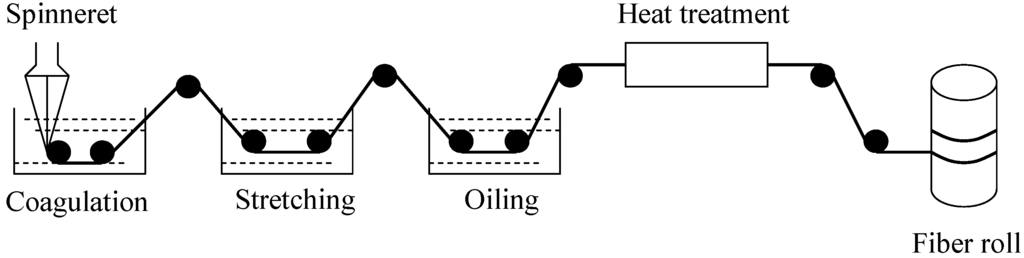
Figure 1.
The technological process of carbon fiber production.
2.2. The Bi-Directional Prediction Methods for Carbon Fiber Production
The bi-directional prediction methods include forward prediction and backward prediction. Forward prediction is the process of predicting property indexes from productive parameters. It means that when the productive parameters of carbon fiber are changed, the corresponding performance of carbon fiber will fluctuate accordingly. In other words, if the productive parameters have little differences, there must be the same among the carbon fiber performances. The backward prediction is a reverse process of the forward prediction, so the process can be seen as a method for designing new types of carbon fiber. In the early stage, we design a new kind of carbon fiber through previous experience, then we test this kind of carbon fiber with chemical and physical instruments to verify its expected performance, get inconsistent results, adjust the corresponding parameters in a new scheme, produce carbon fiber products again, repeat this process of production, testing, and adjusting parameters until we get a satisfactory performance of the carbon fiber. From the foregoing, this method wastes a lot of raw materials, energy, and time. The worst thing is that, if we choose inappropriate parameters for the manufacturing equipment, it will cause damage to the corresponding equipment. For this reason, a better way to solve this problem is to use computer simulation in the whole productive process, avoid unilateral decisions made by workers with interests and experience, and give out more reasonable control parameters based on the actual production process.
In this paper, we propose a bi-directional prediction model of carbon fiber production based on SVM. We adopt IPSO to tune the parameters of the model. The overall chart of bi-directional prediction approaches are as shown in Figure 2.
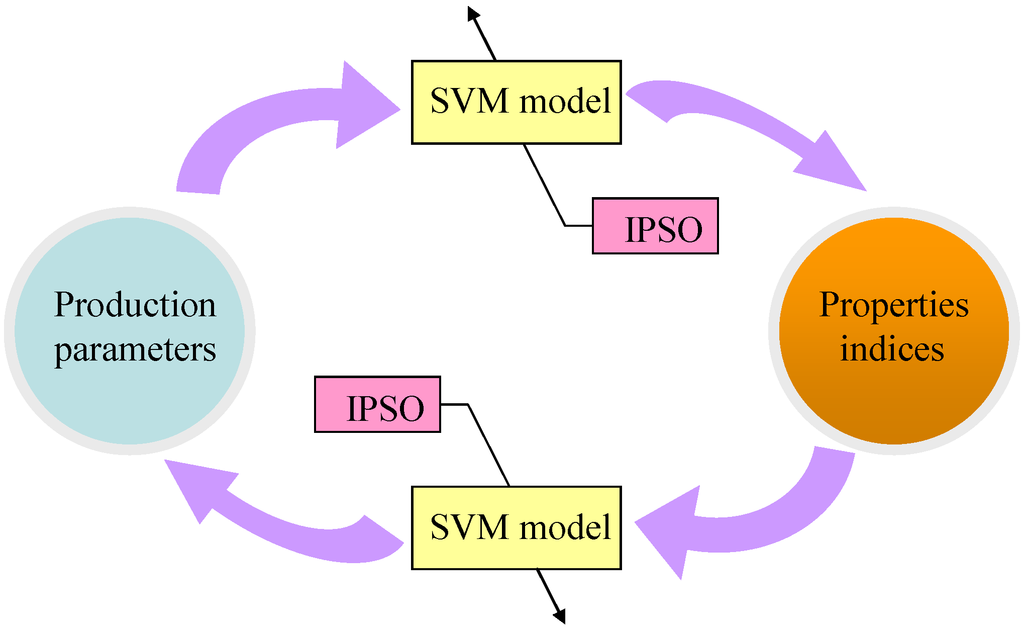
Figure 2.
Bidirectional prediction model of carbon fiber production.
3. Methodology of the SVM-IPSO Model
3.1. The SVM Model
The SVM, proposed by Vapnik in 1995 [29], is widely used for many machine learning problems such as bio-informatics, pattern recognition, linear regression analysis and nonlinear regression estimation problems.
The basic principle is as follows [30]: given a training data
, where
is the input vector and
is the corresponding output of input xi, and N is the total number of the input vectors. By nonlinear mapping φ(x), the data are mapped nonlinearly from the original feature space to a high-dimensional feature space, thus, it can be approximated in a linear way as follows:
where f(x) denotes the regression estimate function; w denotes the weight vector; and b denotes the bias vector.
As mentioned above, the problem of regression approximation is equivalent to minimizing the empirical risk,
where C and ξ are regularized constants; Θξ(yi, f(x)) denotes the ξ-insensitive loss function and is defined as Equation (3)
Then, we introduce two positive slack variables
and εi to simplify the risk function R(f) in Equation (2). Thus, Equation (2) is transformed into the objective function shown as follows:
with the constraints
where εi is the lower training error (
is the upper) subjected to the ξ-insensitive loss function.
After the convex quadratic programming problem with constraints is solved, the weight vector w in Equation (1) is obtained as Equation (6),
where
,
are the Lagrangian multipliers and are obtained by solving a convex quadratic optimization.
Finally, the regression function is obtained as the following equation:
where K(xi, xj) is called the kernel function, which is the inner product of φ(xi) and φ(xj), that is, K(xi, xj)= φ(xi)•φ(xj). The values of φ(xi) and φ(xj) are produced by mapping xi and xj into the higher-dimensional feature space, respectively. It can be shown that any function meeting Mercer’s criteria [29] can be used as the kernel function.
However in general, three different types of kernel functions are commonly used, e.g., the sigmoid kernel function, the polynomial kernel function, and the Gaussian RBF kernel function. The Gaussian RBF is a most used for the kernel function because of the fewer free variables that need to be set and an excellent nonlinear forecasting performance [31]. Therefore, in this study, the Gaussian RBF was selected (as shown in Equation (8)) as the kernel function:
Therefore, there are two variables that need to be selected in the SVM model, which are the constant “C” and the width of the Gaussian RBF kernel “σ”. In this paper, IPSO is used to optimize the parameters of the SVM model.
3.2. Overview of Particle Swarm Optimization
The PSO is inspired by simulation of the behavior of birds flocking in nature [32,33]. It has won high reputation in numerical function optimization due to its precision and efficiency in the fields of stochastic optimization algorithms. It solves a problem by initializing a random population of candidate solutions (particles) and can search for the optimal solution through the search space. Each particle is characterized by a dynamic adjustable velocity, which originates from the momentum of a flying particle. Giving the PSO sufficient numbers of iterations, it is hoped to end up with a global optimal solution. The above-mentioned behavior of the i-th particles can be mathematically expressed as:
In the above formulas, ω denotes the inertia weight,
denotes its velocity vector of the i-th particle on dimension D;
denotes its previously best known position of the i-th particle on dimension D and
denotes its best global position, c1 and c2 are social and personal learning parameters, r1 and r2 are random numbers in the range [0,1]; and
denotes its previous position of the i-th particle at time t.
3.3. Improved Particle Swarm Optimization
3.3.1. The Basic Concept of the Cell Communication
Cell communication refers to a message through a medium to another cell and interacts with the corresponding receptors of target cells, and then through a series of physiological changes inside the cell. Indeed, cells cannot live in isolation, and survive by processing and receiving information from the external environment, whether that information suits the availability of nutrients and change in temperature. Cell to cell communication is essential for orchestration and coordination of cellular events in multi-cellular systems [34]. Intercellular communication has three main ways: gap junction, cell recognition, and chemical communication.
Gap junction: narrow water-filled channels that connect the cytoplasm of adjacent epithelial cells, as well as of some other cell types.
Cell recognition: mutual identification among cells, usually by particular complementary interaction among their separate membrane glycoproteins or surface molecules.
Chemical communication: cells secrete some chemicals (such as hormones) to outside the cell, as a signal molecule in target cells, adjusts its function, is specific and can be divided into four forms: (a) endocrine; (b) paracrine; (c) synaptic; (d) autocrine.
3.3.2. IPSO Based on the Communication Mechanism of Cells
Although PSO has been applied to many kinds of practical problems, PSO still suffers to some degree of premature convergence and poor quality of solution. To overcome the shortcomings, we present IPSO by combining the cell communication mechanism. Based on the three main ways of cell communication, three evolutionary strategies are established. Specifically, the gap junction, the cell recognition, the chemical communication in the mode of cell communication can be replaced by evolutionary strategies, Equations (15)–(17) in the iterative and evolutionary process, respectively. IPSO applies modified update formula to maintain population diversity and enhances the convergence velocity and precision, which by incorporating the information of the global best solution into the search strategy improves the exploitation. In particular, the modified update formulas are determined as follows.
A solution of problem Pi with D variables can be expressed as:
An intuitive illustration of how the Euclidean distance is measured is given in Figure 3. As can be seen from Figure 3, the first line represents the Euclidean distance between the 1-th solution to all solutions, the second line represents the Euclidean distance between the 2-th solution to all solutions, and so forth. The Euclidean distance between solutions of problem can be defined as:
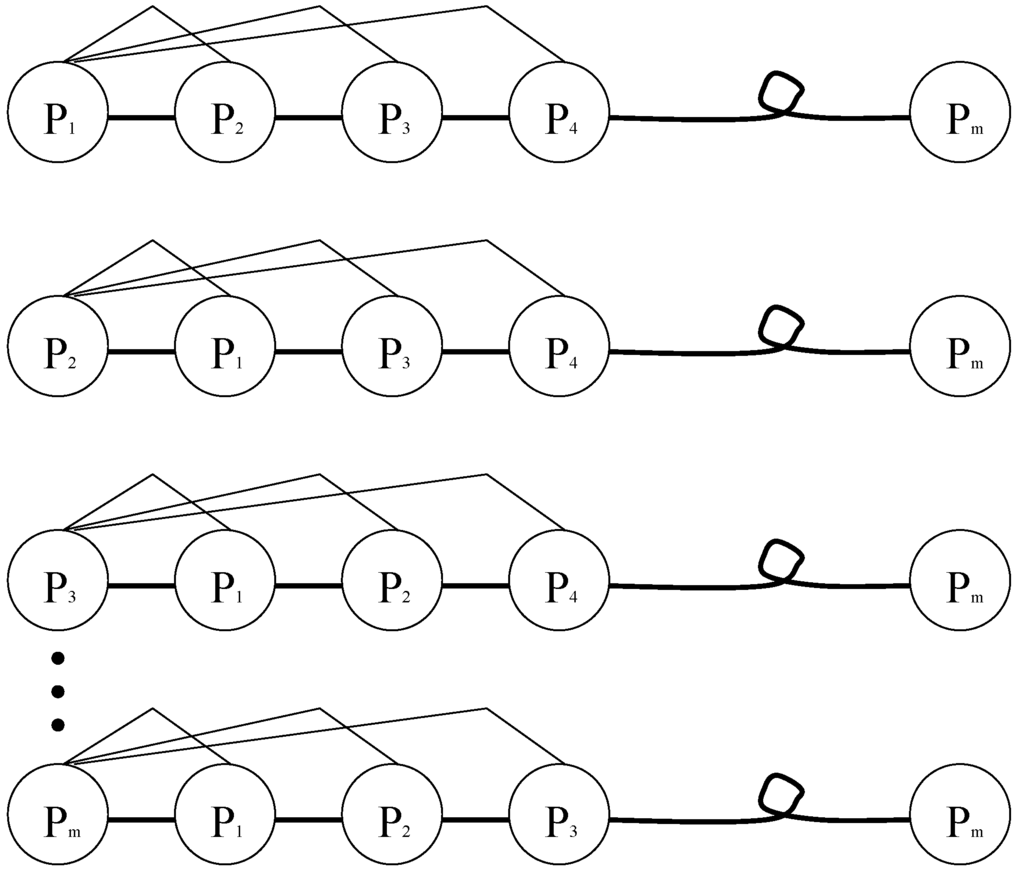
Figure 3.
Schematic drawing to show distances with different solution.
The concentration of the particles can be expressed as:
where Nk denotes the total number of similar particles, and N denotes the total number of particles.
In this paper, two parameters of SVM are optimized, so, each particle’s position is checked using the following formula:
If (Ck > 0.5):
where pi1 denotes the first value of the i-th particle; and xb1 denotes the first value of the best particle.
If ():
where
denotes the fitness function value;
denotes the updated fitness function value; pi2 denotes the second value of the i-th particle, and xb2 denotes the second value of the best particle.
The last particle’s position is checked using the following formula:
where Pi denotes the i-th particle; and xb denotes the best particle of the whole particles.
The values of the aforementioned parameters are usually prescribed to be selected as follows: ω = 0.8 and c1 = c2 = 2. Furthermore, ω denotes the particle’s search capability, and defines the balance between local search capabilities and global search capabilities. Once the velocity of the particle is calculated, its new position is updated according to Equation (10). The range of permissible velocity of the particle is usually restricted in order to eliminate fluctuations and obtain better exploration during the iteration process.
3.4. SVM Based on the IPSO
The diagram of SVM-IPSO forecasting model is illustrated in Figure 4.
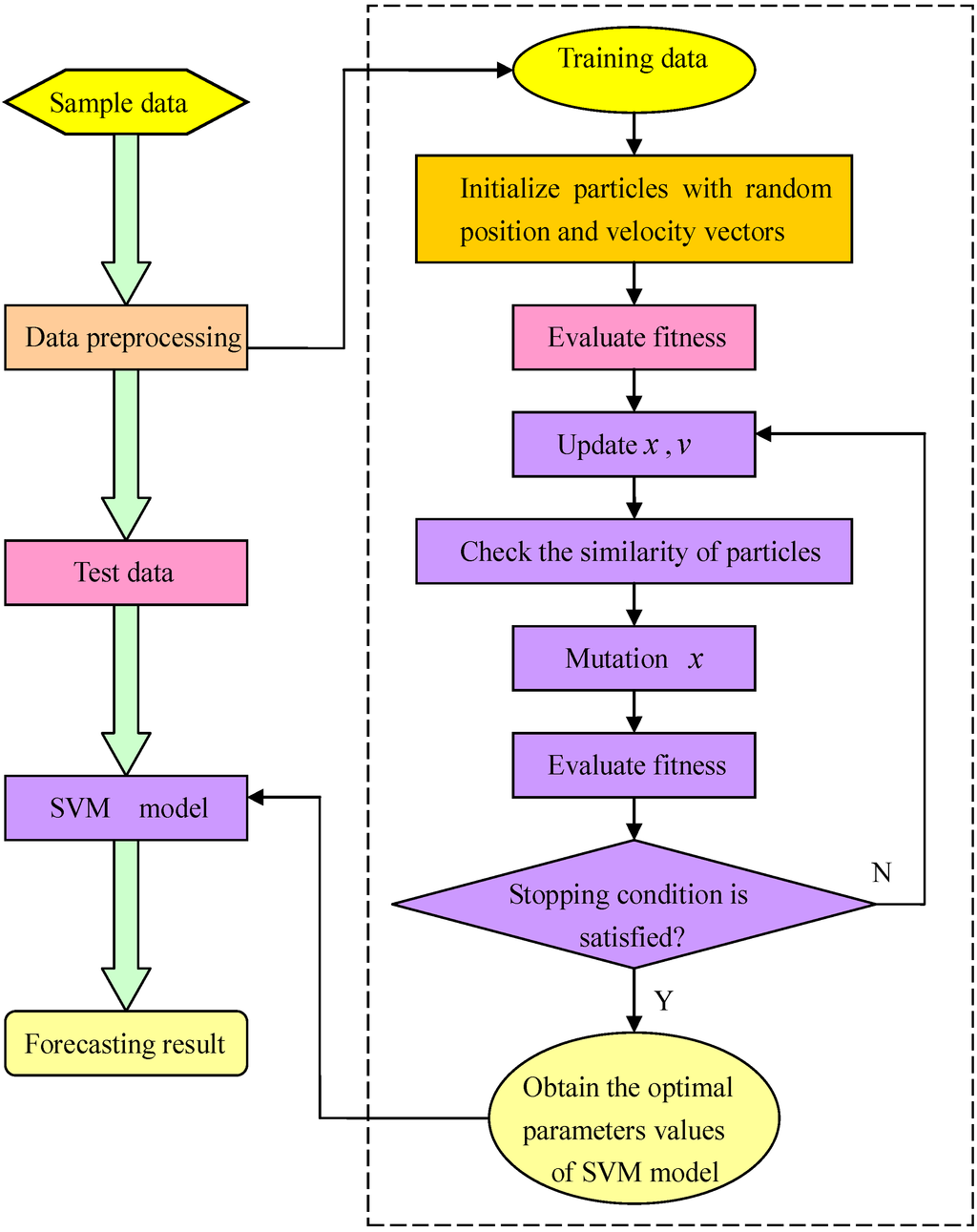
Figure 4.
Diagram of the support vector machine and improved particle swarm optimization (SVM-IPSO) forecasting model.
The details of IPSO for selecting parameters for the SVM model are as follows:
Step 1: Initialization parameters
The population size is 20, the maximum iteration number is 100, the initial particle swarm location is X, and the random flight velocity is V should first be determined. In the SVM-IPSO program, we set X = rand(1,2), where rand() is a random function in the range [0,1].
Step 2: Evolution starts
Set gen = 0, and give the random position and the flight velocity for food finding of an individual particle i. In the SVM-IPSO program, we use two variables [x1,x2] to denote the new position for food finding of an individual particle i.
Step 3: Preliminary calculations
Calculate the new position Xi of an individual particle i, and then input Xi into the SVM model for carbon fiber production forecasting; the parameters [C,σ] of the SVM model are replaced by [Xi(1),Xi(2)]. According to the carbon fiber production forecasting result, the fi can be calculated. The fi is represented by the root-mean-square error, as shown in Equation (18), which calculates the errors between the actual values and the forecasted values:
where n is the number of training input data; yi is the i-th actual value;
denotes the i-th forecasting value.
Step 4: Offspring generation
The global best value is generated according to Equations (15)–(17) after updating the position value according to Equation (10). Then the global best value is inputted into the SVM model and the fitness function value calculated again. Set gen = gen + 1.
Step 5: Circulation stops
When gen is equal to the maximum iteration number, and the stop criterion is met, the optimal parameters of the SVM model are finally obtained. Otherwise, it is necessary to go back to Step 2.
4. Simulation and Discussion
4.1. The Preprocessing of Sample Data
In order to examine the performance of the new prediction model, we used the data organized from experiments in Table 1 [9]. The errors by the proposed method for the below mentioned experimental data, classified into four different types are given in Table 2, where to facilitate comparison the corresponding errors obtained by other methods on the same data are also listed.

Table 1.
Experimental data of carbon fiber in the productive process.
| No. | Viscosity Average Molecular Weight (104) | Conversion Ratio (%) | Solid Content (%) | Spinning Jet Drawing Ratio (%) | Coagulating Bath Temperature (°C) | Total Drawing Ratio | Strength (CN/d) | Structure Parameter |
|---|---|---|---|---|---|---|---|---|
| 1 | 8.9 | 94.5 | 20.8 | −50.3 | 14 | 6.33 | 4.08 | 14.82 |
| 2 | 6.3 | 91.0 | 20.0 | −59.7 | 15 | 5.89 | 3.23 | 12.63 |
| 3 | 11.6 | 92.0 | 20.4 | −50.5 | 14 | 6.03 | 3.76 | 13.24 |
| 4 | 8.8 | 94.8 | 21.8 | −63.4 | 13 | 6.65 | 4.17 | 17.24 |
| 5 | 7.0 | 81.8 | 17.9 | −63.4 | 15 | 6.32 | 3.99 | 15.14 |
| 6 | 8.2 | 85.5 | 21.7 | −59.5 | 15 | 5.49 | 4.58 | 16.61 |
| 7 | 7.2 | 89.8 | 19.5 | −53.1 | 13 | 5.88 | 3.64 | 15.49 |
| 8 | 8.9 | 82.5 | 17.5 | −56.8 | 19 | 6.38 | 4.07 | 17.57 |
| 9 | 8.0 | 83.4 | 18.6 | −62.1 | 17 | 5.72 | 3.18 | 15.48 |
| 10 | 11.7 | 90.6 | 17.9 | −53.8 | 16 | 6.47 | 3.22 | 12.10 |
| 11 | 11.5 | 82.8 | 18.7 | −64.8 | 17 | 5.79 | 3.27 | 12.73 |
| 12 | 6.3 | 95.1 | 19.6 | −54.9 | 16 | 6.37 | 4.36 | 17.18 |
| 13 | 10.4 | 98.6 | 20.2 | −68.3 | 17 | 6.41 | 3.99 | 14.91 |
| 14 | 7.6 | 93.1 | 19.7 | −55.4 | 16 | 5.88 | 3.38 | 17.07 |
| 15 | 8.5 | 84.6 | 22.3 | −65.3 | 18 | 5.04 | 3.99 | 13.26 |
| 16 | 9.3 | 89.8 | 20.1 | −53.8 | 16 | 5.66 | 3.30 | 15.31 |
| 17 | 11.7 | 79.4 | 22.7 | −55.8 | 19 | 5.85 | 3.11 | 15.78 |
| 18 | 8.5 | 96.9 | 20.8 | −51.8 | 14 | 5.54 | 4.70 | 12.19 |
| 19 | 11.9 | 96.4 | 22.7 | −61.5 | 13 | 5.39 | 4.12 | 15.69 |
| 20 | 7.8 | 95.0 | 18.4 | −63.7 | 13 | 6.64 | 4.86 | 14.17 |
| 21 | 10.2 | 82.7 | 21.1 | −60.9 | 13 | 5.86 | 4.39 | 12.30 |
| 22 | 10.0 | 90.1 | 18.7 | −58.5 | 15 | 6.78 | 4.17 | 14.94 |
| 23 | 9.2 | 77.5 | 21.0 | −62.9 | 16 | 5.78 | 4.63 | 13.16 |
| 24 | 10.2 | 86.4 | 21.2 | −63.0 | 15 | 6.54 | 4.76 | 12.74 |
| 25 | 10.0 | 83.9 | 17.4 | −63.6 | 18 | 5.79 | 4.98 | 13.23 |
| 26 | 7.1 | 80.6 | 18.5 | −62.7 | 17 | 6.62 | 3.00 | 12.88 |
| 27 | 6.8 | 80.9 | 18.3 | −68.9 | 18 | 6.51 | 4.73 | 13.13 |
| 28 | 12.0 | 86.3 | 21.0 | −54.2 | 19 | 5.75 | 4.23 | 12.26 |
| 29 | 7.0 | 79.1 | 22.1 | −64.2 | 19 | 5.43 | 4.98 | 15.81 |
| 30 | 6.2 | 90.2 | 19.1 | −54.7 | 14 | 6.58 | 4.06 | 13.69 |
| 31 | 9.4 | 87.4 | 21.7 | −52.4 | 13 | 6.90 | 3.96 | 15.23 |
| 32 | 11.3 | 92.3 | 21.1 | −62.1 | 17 | 5.66 | 4.60 | 16.17 |
| 33 | 10.0 | 92.4 | 17.0 | −59.0 | 13 | 6.34 | 3.46 | 14.99 |
| 34 | 7.1 | 91.0 | 20.6 | −59.2 | 16 | 5.88 | 4.00 | 15.21 |
| 35 | 8.2 | 77.7 | 19.3 | −63.2 | 16 | 6.67 | 4.80 | 14.67 |
| 36 | 8.8 | 78.5 | 22.5 | −65.4 | 19 | 6.54 | 4.15 | 12.74 |
| 37 | 11.9 | 84.0 | 17.0 | −57.0 | 16 | 5.33 | 4.69 | 14.94 |
| 38 | 6.9 | 88.7 | 19.8 | −63.2 | 15 | 6.72 | 4.48 | 17.12 |
| 39 | 11.1 | 91.4 | 19.5 | −58.3 | 17 | 6.98 | 4.17 | 17.24 |
| 40 | 9.9 | 86.0 | 19.8 | −66.8 | 18 | 6.03 | 3.49 | 13.62 |
| 41 | 8.3 | 95.0 | 21.6 | −66.7 | 16 | 6.77 | 4.33 | 13.25 |
| 42 | 7.1 | 92.8 | 18.9 | −55.1 | 15 | 6.18 | 3.17 | 15.39 |
| 43 | 8.6 | 98.3 | 21.7 | −62.3 | 14 | 5.31 | 4.25 | 15.84 |
| 44 | 8.9 | 88.7 | 19.8 | −61.6 | 17 | 5.40 | 4.32 | 14.50 |
| 45 | 6.7 | 84.2 | 17.2 | −60.8 | 14 | 5.81 | 4.46 | 13.24 |
| 46 | 11.0 | 98.0 | 22.7 | −74.6 | 12 | 6.89 | 3.90 | 12.82 |
| 47 | 9.5 | 92.2 | 20.3 | −50.5 | 17 | 5.92 | 3.91 | 13.20 |
| 48 | 7.7 | 78.2 | 17.2 | −63.4 | 19 | 6.17 | 3.99 | 15.19 |
| 49 | 9.5 | 79.3 | 18.1 | −67.4 | 13 | 6.50 | 4.78 | 17.69 |
| 50 | 7.4 | 90.4 | 21.3 | −55.3 | 18 | 6.65 | 4.96 | 12.49 |
Note: sample data sources come from reference [9].

Table 2.
Comparison of errors among the proposed method, the GA-IPSO-RNN [9], the basic PSO-RNN [9], and the conventional RNN [9].
| Algorithms | Conventional RNN | Basic PSO-RNN | GA-IPSO-RNN | Proposed method | |
|---|---|---|---|---|---|
| MAE | 1 | 1.1950 | 0.4818 | 0.4258 | 0.3839 |
| 2 | 3.6827 | 2.0262 | 1.9833 | 1.7821 | |
| Mean | 2.4389 | 1.2540 | 1.2045 | 1.0830 | |
| MRE(%) | 1 | 28.63 | 10.65 | 9.39 | 8.71 |
| 2 | 27.96 | 14.61 | 14.01 | 12.41 | |
| Mean | 28.30 | 12.63 | 11.70 | 10.56 | |
| RMSE | 1 | 1.4843 | 0.5841 | 0.5157 | 0.4076 |
| 2 | 4.5364 | 2.2637 | 2.1177 | 1.9649 | |
| Mean | 3.0104 | 1.4239 | 1.3167 | 1.1863 | |
| TIC | 1 | 0.1675 | 0.0690 | 0.0609 | 0.0481 |
| 2 | 0.1452 | 0.0766 | 0.0727 | 0.0679 | |
| Mean | 0.1563 | 0.0728 | 0.0668 | 0.0580 | |
Notes: 1: strength, 2: structure parameter.
In the SVM modeling, the preprocessing steps are implemented before attempting to calculate, to eliminate any bad data or outliers. These steps guarantee that the raw data retrieved from the database is completely suitable for modeling. In order to improve the accuracy of prediction and smooth the training procedure, all the sample data are normalized to fit them in the interval [0,1] using the following linear mapping formula:
where
is the mapped value;
is the initial value from the experimental data; N is the total number of input data; xmax and xmin denote the maximum and minimum values of initial data, respectively.
In Table 1, the values for the first six columns indicate different parameters, and the values for the last two columns indicate different property indices. These detailed parameters can synthetically represent the whole manufacturing process. Meanwhile, the two kinds of property indices can fully represent the performance of the carbon fiber. In the predictive process, we obtained training sets from the first 45 rows of samples and test sets from the last five rows of samples. Also, to examine the performance of the several algorithms, the mean absolute error, root mean square error, mean relative error and Theil’s inequality coefficient were defined according to the following formulations, respectively:
Mean absolute error:
Root mean square error:
Mean relative error:
Theil’s inequality coefficient:
where yi is the true value;
is the predicted value.
4.2. The Selection of Comparative Models
As mentioned above, the technological process for carbon fiber is a nonlinear system, it involves many process parameters that must be carefully optimized and adjusted. Most of the previous work was focused on analyzing the properties of carbon fibers by means of physical or chemical instruments. However it is a kind of method which wastes time and energy. Thus, we should build the predictive model for the productive process of carbon fiber. In this way, we can effectively predict the properties of carbon fiber in real-time, and thus we can find out inferior carbon fiber with poor quality in advance, timely adjust the process parameters, and avoid wasting raw materials. However, on the contrary, the prediction of productive parameters by the properties of the carbon fiber is a backward reasoning process. Therefore, it is a better idea to analyze all antecedent production schemes through computer simulation. This will avoid partial production schemes created by operational staff who rely on their personal experience and interests.
4.3. Forward Prediction
Carbon fiber production is a positive process, and the predictable performance of carbon fiber by productive parameters is a forward prediction, too. Thus, in forward prediction, we can take the parameters of carbon fiber production as input and the corresponding performance of carbon fiber as output. By employing IPSO to optimize the parameters of SVM, we gain the best parameters for SVM. The training effectiveness of the proposed method is shown in Figure 5.
Comparing performance of the conventional RNN, the basic PSO-RNN, the GA-IPSO-RNN with the SVM-IPSO is carried out in terms of (a) mean absolute error; (b) root mean square error; (c) mean relative error and (d) Theil’s inequality coefficient result. The detailed results are listed in Table 2.
From Table 2, we can see that on the basis of MAE, the proposed SVM-IPSO achieves roughly a decrease of 55.59%, 13.64% and 10.09% compared to the other three methods, respectively. Similar results can be obtained from the other errors such as MRE with a decrease of 62.69%, 16.39% and 9.74%, RMSE with a decrease of 60.59%, 16.69% and 9.90%, and TIC with a decrease of 62.89%, 20.33% and 13.17%. Similar results are obtained on the basis of strength and structure parameters.
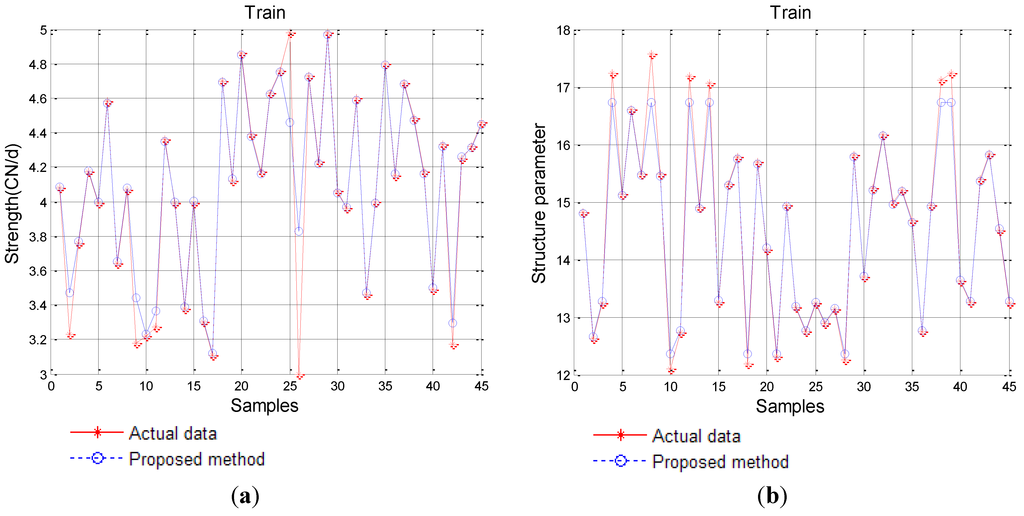
Figure 5.
Training results of the proposed SVM-IPSO model. (a) Strength; (b) Structure parameter.
4.4. Backward Prediction
The productive parameters of carbon fiber forecast by the performance of carbon fiber is a reverse process of forward prediction, so the predictive process can be considered inverse inference. In the backward prediction, we take the performance of carbon fiber as input and the productive parameters as output, which can be considered as a design scheme for a novel style carbon fiber. In order to achieve the above goals, by employing IPSO to optimze the parameters of SVM, we gain the best parameters for SVM. The training effectiveness of the proposed method is shown in Figure 6.
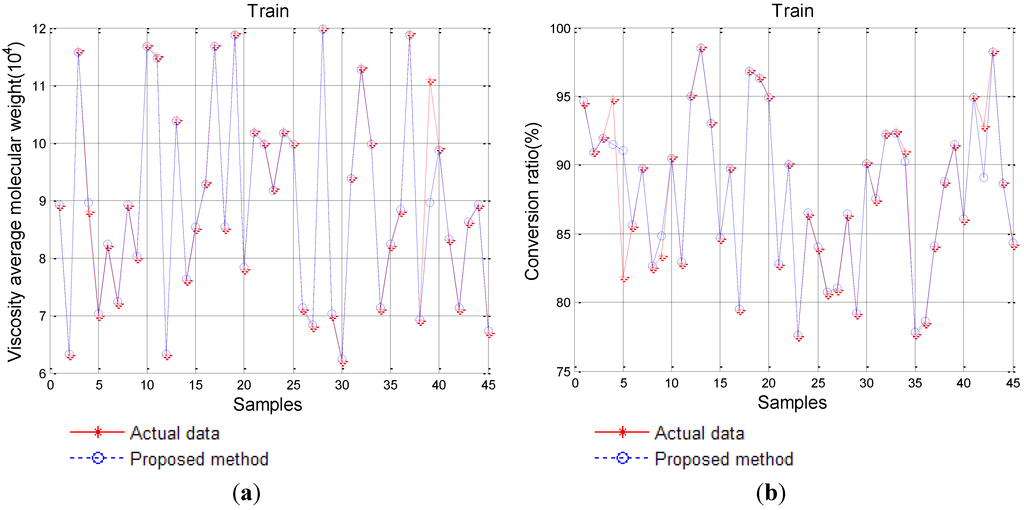
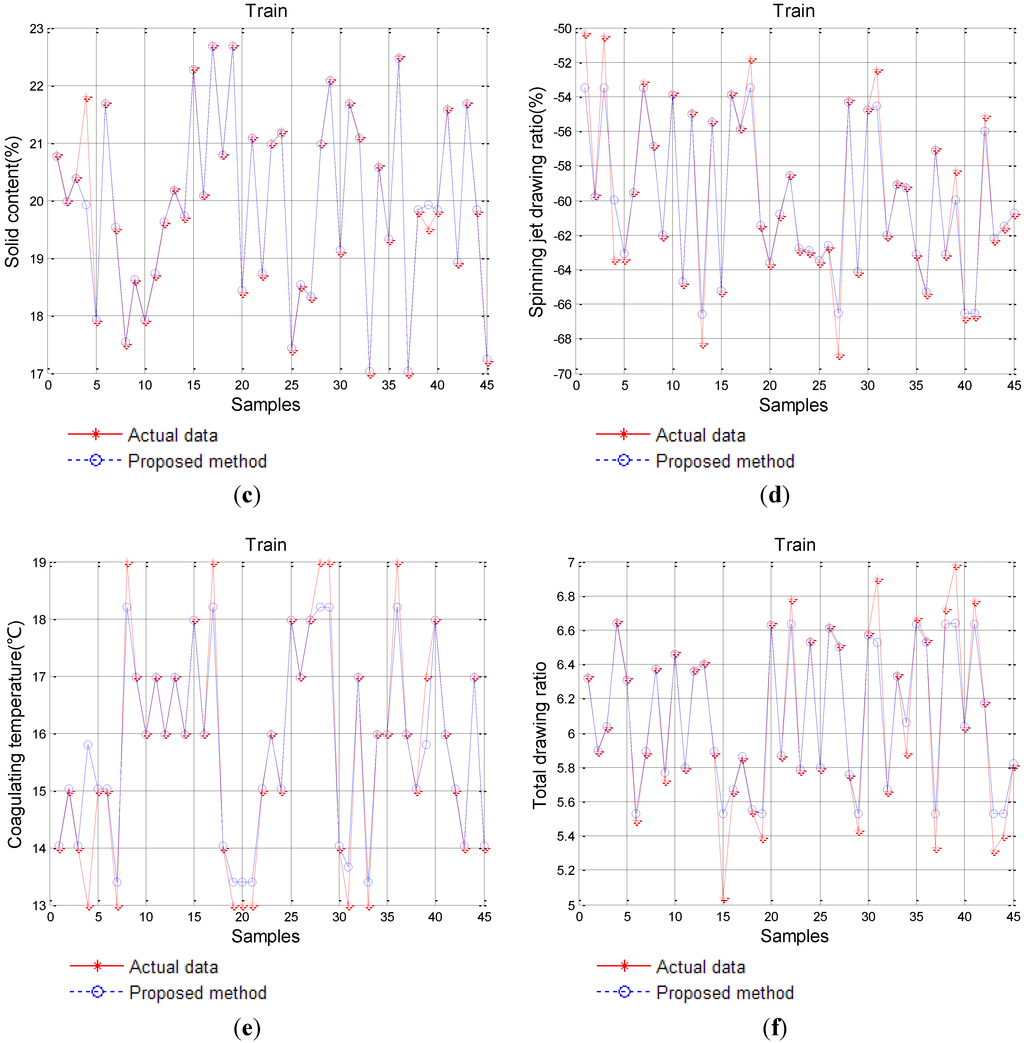
Figure 6.
Training results of the proposed SVM-IPSO model. (a) Viscosity average molecular weight; (b) Conversion ratio; (c) Solid content; (d) Spinning jet drawing ratio; (e) Coagulating temperature; (f) Total drawing ratio.
We compared the effectiveness of SVM-IPSO with that of conventional RNN, the basic PSO-RNN, and the GA-IPSO-RNN optimal schemes. The detailed results are listed in Table 3. In Table 3, (1) is the viscosity average molecular weight; (2) is the conversion ratio; (3) is the solid content; (4) is the spinning jet drawing ratio; (5) is the coagulating bath temperature; (6) is the total drawing ratio.
From Table 3, we can see that on the basis of MAE, the proposed SVM-IPSO achieves roughly a decrease of 98.69%, 19.48% and 6.68% compared to the other three methods, respectively. Similar results can be obtained from the other errors such as MRE with a decrease of 98.72%, 25.78% and 7.51%, RMSE with a decrease of 99.22%, 18.70% and 7.60%, and TIC with a decrease of 93.02%, 23.26% and 11.48%. Similar results are obtained on the basis of viscosity average molecular weight, conversion ratio, solid content, spinning jet drawing ratio, and coagulating bath temperature, respectively.

Table 3.
Comparison of errors among the proposed methods, the GA-IPSO-RNN [9], the basic PSO-RNN [9], and the conventional RNN [9].
| Algorithms | MAE | MRE (%) | RMSE | TIC |
|---|---|---|---|---|
| Conventional RNN | ||||
| 1 | 173.1400 | 1876.58 | 341.7052 | 0.9612 |
| 2 | 1062.8000 | 1310.66 | 2004.3000 | 0.9391 |
| 3 | 151.6600 | 816.09 | 285.3062 | 0.9051 |
| 4 | 171.6800 | 264.56 | 285.1956 | 0.7416 |
| 5 | 62.6800 | 443.07 | 103.5493 | 0.8054 |
| 6 | 34.8800 | 533.97 | 63.3625 | 0.9510 |
| Mean | 276.1367 | 874.16 | 513.9031 | 0.8839 |
| Basic PSO-RNN | ||||
| 1 | 1.9652 | 22.73 | 2.2049 | 0.1138 |
| 2 | 9.7604 | 11.30 | 10.3417 | 0.0590 |
| 3 | 2.5932 | 13.19 | 2.7487 | 0.0690 |
| 4 | 8.9433 | 15.27 | 10.2110 | 0.0806 |
| 5 | 3.2098 | 20.66 | 3.2757 | 0.1054 |
| 6 | 0.4920 | 7.38 | 0.6731 | 0.0544 |
| Mean | 4.4940 | 15.09 | 4.9092 | 0.0804 |
| GA-IPSO-RNN | ||||
| 1 | 1.3996 | 14.37 | 1.7597 | 0.1026 |
| 2 | 8.2660 | 9.61 | 9.1148 | 0.0518 |
| 3 | 2.2693 | 11.04 | 2.5107 | 0.0647 |
| 4 | 8.0976 | 13.47 | 9.1473 | 0.0733 |
| 5 | 2.9085 | 19.20 | 2.9776 | 0.0944 |
| 6 | 0.3260 | 4.94 | 0.4054 | 0.0317 |
| Mean | 3.8778 | 12.11 | 4.3192 | 0.0697 |
| Proposed method | ||||
| 1 | 1.0585 | 11.80 | 1.2290 | 0.0693 |
| 2 | 7.7362 | 9.03 | 8.4285 | 0.0479 |
| 3 | 1.7943 | 9.17 | 1.9964 | 0.0500 |
| 4 | 7.9765 | 12.74 | 8.8876 | 0.0724 |
| 5 | 2.7471 | 18.42 | 2.9189 | 0.0920 |
| 6 | 0.3994 | 6.02 | 0.4855 | 0.0387 |
| Mean | 3.6187 | 11.20 | 3.9910 | 0.0617 |
5. Conclusions
The non-linear relationship of the productive parameters for carbon fiber with its performance makes bi-directional prediction very complicated. Thus, how to improve the bi-directional prediction accuracy is worthy of study. In this paper, we present the SVM-IPSO hybrid algorithm to bi-directionally forecast the productive process for carbon fiber, which can be considered as predicting the performance of carbon fiber and designing a method for new carbon fiber production. By the proposed model, we can online forecast the performance of the carbon fiber, and adjust the productive parameters in time, while reducing time and energy. In addition, this model can provide a means to determine the productive parameters for production to meet the performance requirements of different fibers.
Acknowledgments
This work was supported in part by the Key Project of the National Nature Science Foundation of China (No. 61134009), the National Nature Science Foundation of China (No. 61473077, 61473078), Cooperative research funds of the National Natural Science Funds Overseas and Hong Kong and Macao scholars (No. 61428302), Program for Changjiang Scholars from the Ministry of Education, Specialized Research Fund for Shanghai Leading Talents, Project of the Shanghai Committee of Science and Technology (No. 13JC1407500, 11JC1400200), and Innovation Program of Shanghai Municipal Education Commission (No. 14ZZ067).
Author Contributions
Wrote the paper: Chuncai Xiao and Kuangrong Hao; Conceived and designed the experiments: Yongsheng Ding; Analyzed the data: Kuangrong Hao; Performed the experiments: Chuncai Xiao.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Yusof, N.; Ismail, A.F. Post spinning and pyrolysis processes of polyacrylonitrile (PAN)-based carbon fiber and activated carbon fiber: A review. J. Anal. Appl. Pyrolysis 2012, 93, 1–13. [Google Scholar] [CrossRef]
- Chand, S. Review carbon fibers for composites. J. Mater. Sci. 2000, 35, 1303–1313. [Google Scholar] [CrossRef]
- Liu, J.; Tian, Y.; Chen, Y.; Liang, J.; Zhang, L.; Fong, H. A surface treatment technique of electrochemical oxidation to simultaneously improve the interfacial bonding strength and the tensile strength of PAN-based carbon fibers. Mater. Chem. Phys. 2010, 122, 548–555. [Google Scholar] [CrossRef]
- Wang, Y.; Yin, W. Chemical modification for PAN fibers during heat-treatment process. Phys. Procedia 2011, 18, 202–205. [Google Scholar] [CrossRef]
- Rahman, M.A.; Ismail, A.F.; Mustafa, A. The effect of residence time on the physical characteristics of PAN-based fibers produced using a solvent-free coagulation process. Mater. Sci. Eng. 2007, 448, 275–280. [Google Scholar] [CrossRef]
- Liang, X.; Ding, Y.S.; Ren, L.H.; Hao, K.R.; Wang, H.P.; Chen, J.J. A bio-inspired multi-layered intelligent cooperative controller for stretching process of fiber production. IEEE Trans. Syst. Man Cybern. C 2012, 42, 367–377. [Google Scholar]
- Rennhofer, H.; Loidl, D.; Puchegger, S.; Peterlik, H. Structural development of PAN-based carbon fibers studied by in situ X-ray scattering at high temperatures under load. Carbon 2010, 48, 964–971. [Google Scholar] [CrossRef]
- Belyaev, S.S.; Arkhangelsky, I.V.; Makarenko, I.V. Nonisothermal kinetic analysis of oxidative stabilization processes in PAN fibers. Thermochim. Acta 2010, 507–508, 9–14. [Google Scholar] [CrossRef]
- Chen, J.J.; Ding, Y.S.; Hao, K.R. The bidirectional optimization of carbon fiber production by neural network with a GA-IPSO hybrid algorithm. Math. Probl. Eng. 2013, 2013, 1–16. [Google Scholar]
- Sugimoto, Y.; Shioya, M.; Yamamoto, K.; Sakurai, S. Relationship between axial compression strength and longitudinal microvoid size for PAN-based carbon fibers. Carbon 2012, 50, 2860–2869. [Google Scholar] [CrossRef]
- Kadi, H.E. Modeling the mechanical behavior of fiber-reinforced polymeric composite materials using artificial neural networks—A review. Compos. Struct. 2006, 73, 1–23. [Google Scholar] [CrossRef]
- Yu, Y.; Hui, C.L.; Choi, T.M.; Au, R. Intelligent fabric hand prediction system with fuzzy neural network. IEEE Trans. Syst. Man Cybern. C 2010, 40, 619–629. [Google Scholar] [CrossRef]
- Du, D.; Li, K.; Fei, M. A fast multi-output RBF neural network construction method. Neurocomputing 2010, 73, 2196–2202. [Google Scholar] [CrossRef]
- Roy, A.; Govil, S.; Miranda, R. A neural-network learning theory and a polynomial time RBF algorithm. IEEE Trans. Neural Netw. 1997, 8, 1301–1313. [Google Scholar] [CrossRef]
- Hong, X.; Chen, S. A new RBF neural network with boundary value constraints. IEEE Trans. Syst. Man Cybern. B 2009, 39, 298–303. [Google Scholar] [CrossRef]
- Huang, G.B.; Saratchandran, P.; Sundararajan, N. A generalized growing and pruning RBF (GGAP-RBF) neural network for function approximation. IEEE Trans. Neural Netw. 2005, 16, 57–67. [Google Scholar] [CrossRef]
- Qiao, J.-F.; Han, H.-G. Identification and modeling of nonlinear dynamical systems using a novel self-organizing RBF-based approach. Automatica 2012, 48, 1729–1734. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, G. A forecasting method based on online self-correcting single model RBF neural network. Procedia Eng. 2012, 29, 2516–2520. [Google Scholar] [CrossRef]
- Hong, W.C.; Dong, Y.; Zhang, W.Y.; Chen, L.Y.; Panigrahi, B.K. Cyclic electric load forecasting by seasonal SVR with chaotic genetic algorithm. Int. J. Electr. Power Energy Syst. 2013, 44, 604–614. [Google Scholar] [CrossRef]
- Goh, A.T.C.; Goh, S.H. Support vector machines: Their use in geotechnical engineering as illustrated using seismic liquefaction data. Comput. Geotech. 2007, 34, 410–421. [Google Scholar] [CrossRef]
- Kordjazi, A.; Nejad, F.P.; Jaksa, M.B. Prediction of ultimate axial load-carrying capacity of piles using a support vector machine based on CPT data. Comput. Geotech. 2014, 55, 91–102. [Google Scholar] [CrossRef]
- Lin, J.Y.; Cheng, C.T.; Chau, K.W. Using support vector machines for long-term discharge prediction. Hydrol. Sci. J. 2006, 51, 599–612. [Google Scholar] [CrossRef]
- Niu, D.; Wang, Y.; Wu, D.D. Power load forecasting using support vector machine and ant colony optimization. Expert Syst. Appl. 2010, 37, 2531–2539. [Google Scholar] [CrossRef]
- Wang, J.J.; Li, L.; Niu, D.; Tan, Z.F. An annual load forecasting model based on support vector regression with differential evolution algorithm. Appl. Energy 2012, 94, 65–70. [Google Scholar] [CrossRef]
- Gilan, S.; Jovein, H.B.; Ali, A.R. Hybrid support vector regression-Particle swarm optimization for prediction of compressive strength and RCPT of concretes containing metakaolin. Constr. Build. Mater. 2012, 34, 321–329. [Google Scholar] [CrossRef]
- Hong, W.C. Chaotic particle swarm optimization algorithm in a support vector regression electric load forecasting model. Energy Convers. Manag. 2009, 50, 105–117. [Google Scholar] [CrossRef]
- Kang, Q.; Zhou, M.; An, J.; Wu, Q. Swarm intelligence approaches to optimal power flow problem with distributed generator failures in power networks. IEEE Trans. Autom. Sci. Eng. 2013, 10, 343–353. [Google Scholar] [CrossRef]
- Liang, X.; Li, W.; Zhang, Y.; Zhou, M. An adaptive particle swarm optimization method based on clustering. Soft Comput. 2014. [Google Scholar] [CrossRef]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer: New York, NY, USA, 1995. [Google Scholar]
- Li, X.; Zhang, A.; Li, C.C.; Zhang, L. Rolling element bearing fault detection using support vector machine with improved ant colony optimization. Measurement 2013, 46, 2726–2734. [Google Scholar] [CrossRef]
- Keerthi, S.S.; Lin, C.J. Asymptotic behaviors of support vector machines with Gaussian kernel. Neural Comput. 2003, 15, 1667–1689. [Google Scholar] [CrossRef] [PubMed]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. IEEE Proc. Int. Conf. Neural Netw. 1995, 4, 1942–1948. [Google Scholar]
- Zhu, H.; Wang, Y.; Wang, K.; Chen, Y. Particle Swarm Optimization (PSO) for the constrained portfolio optimization problem. Expert Syst. Appl. 2011, 38, 10161–10169. [Google Scholar] [CrossRef]
- Ahmed, K.A.; Xiang, J. Mechanisms of cellular communication through intercellular protein transfer. J. Cell. Mol. Med. 2011, 15, 1458–1473. [Google Scholar] [CrossRef] [PubMed]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).