Formulation of Hyperelastic Constitutive Model for Human Periodontal Ligament Based on Fiber Volume Fraction
Abstract
1. Introduction
2. Materials and Methods
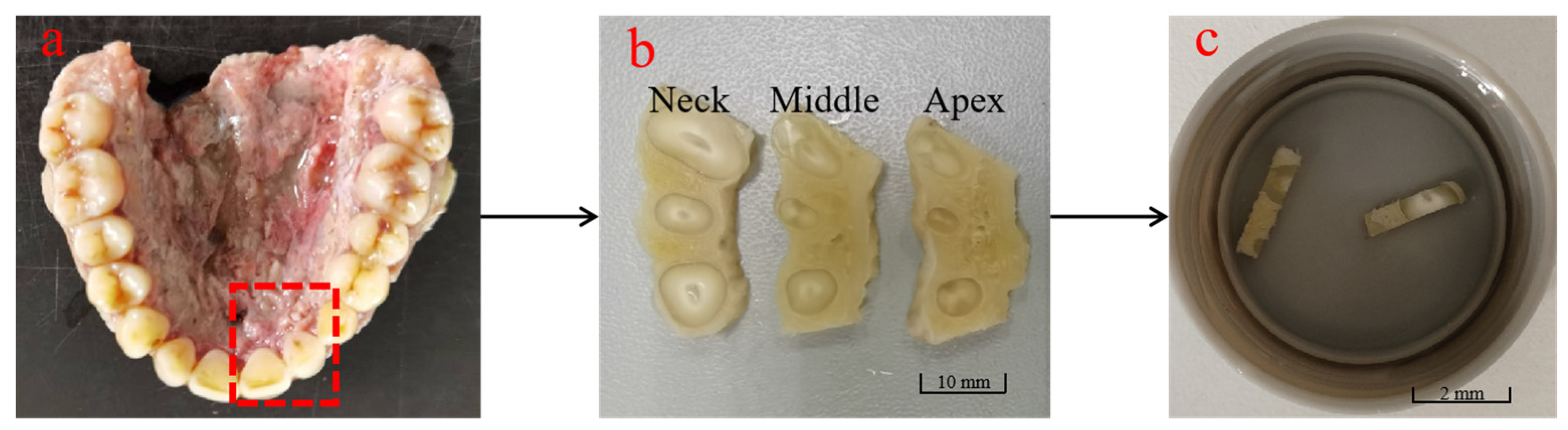
2.1. Sample Preparation
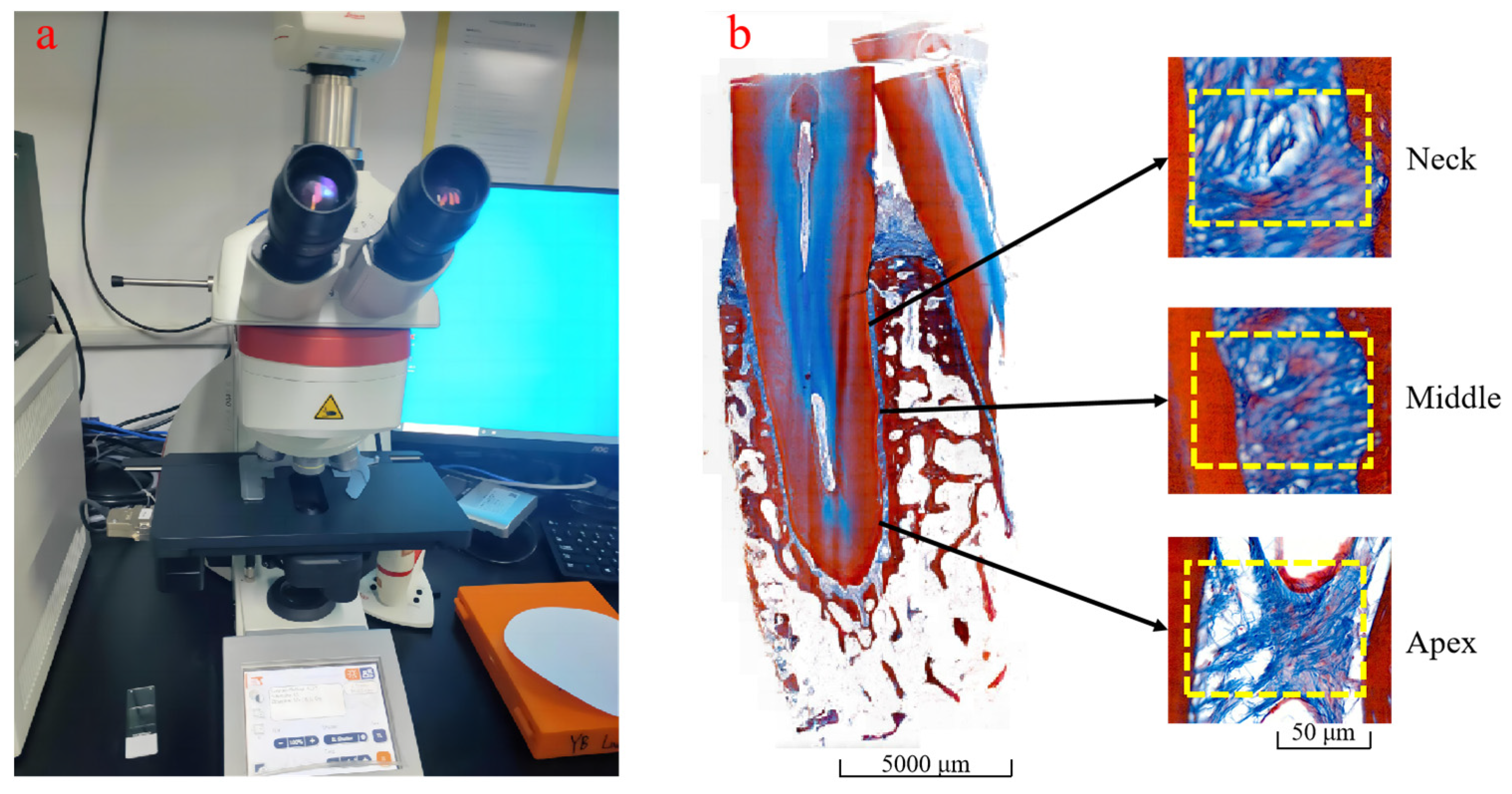
2.2. PDL Section Staining and Collagen Fiber Volume Fraction Measurement
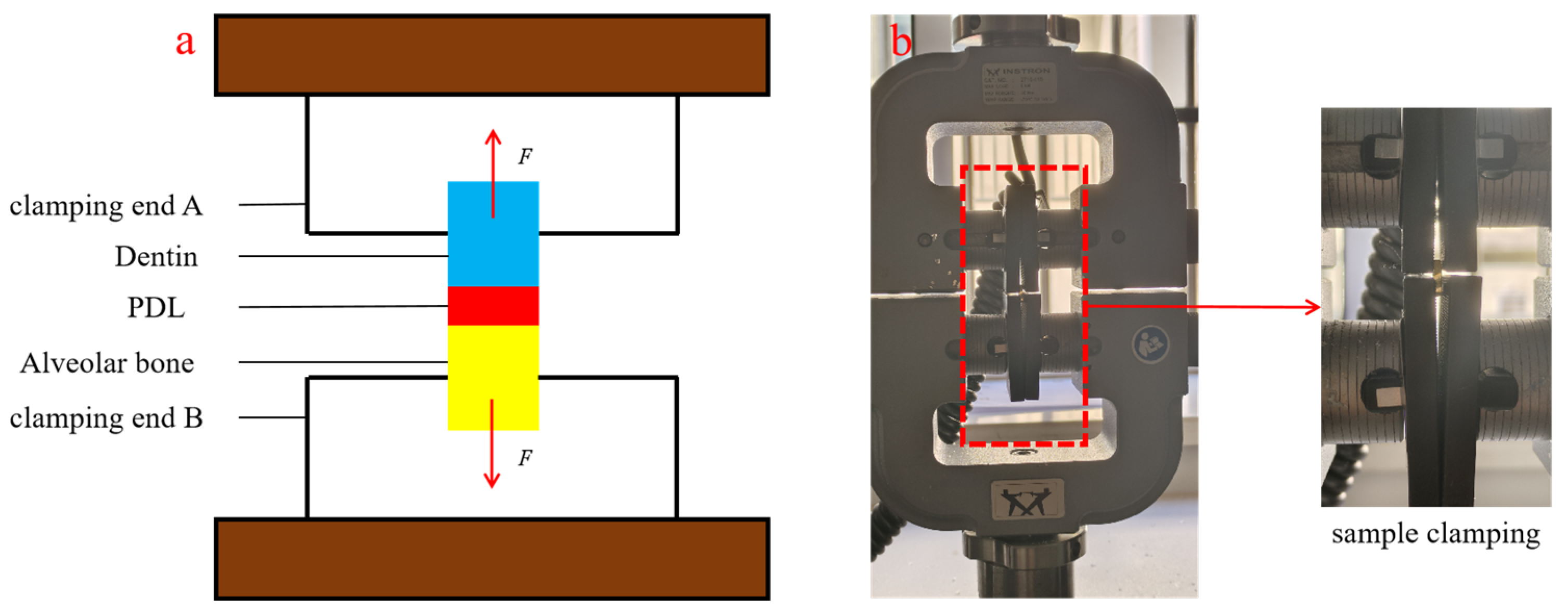
2.3. Uniaxial Tensile Test
3. Constitutive Model Based on the Volume Fraction of Collagen Fibers
4. Results
4.1. Observation Results of Collagen Fiber Volume Fraction
4.1.1. Microscopic Observation of Periodontal Collagen Fibers
4.1.2. Imaging Analysis Results of Collagen Fiber Volume Fraction of PDL
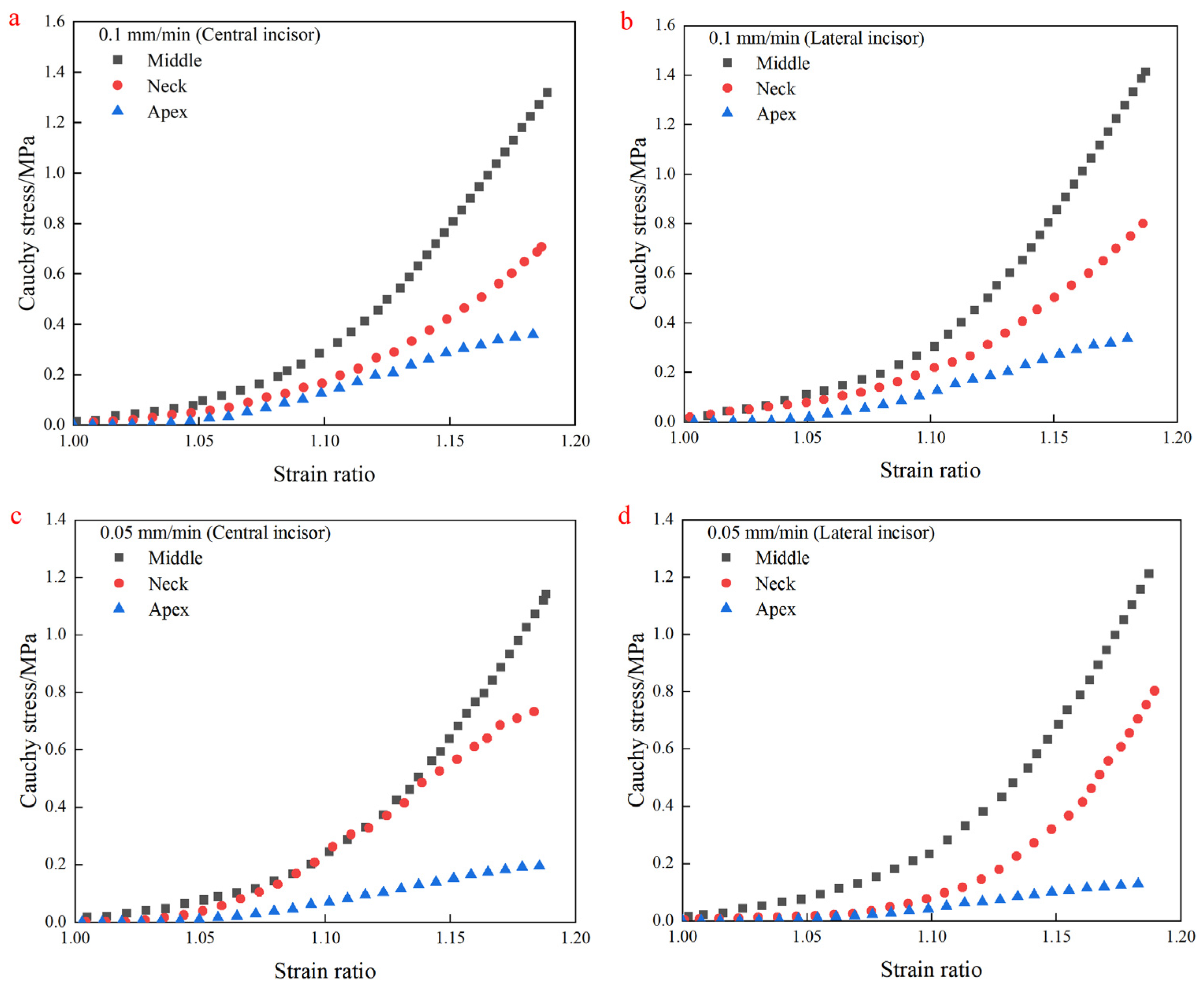
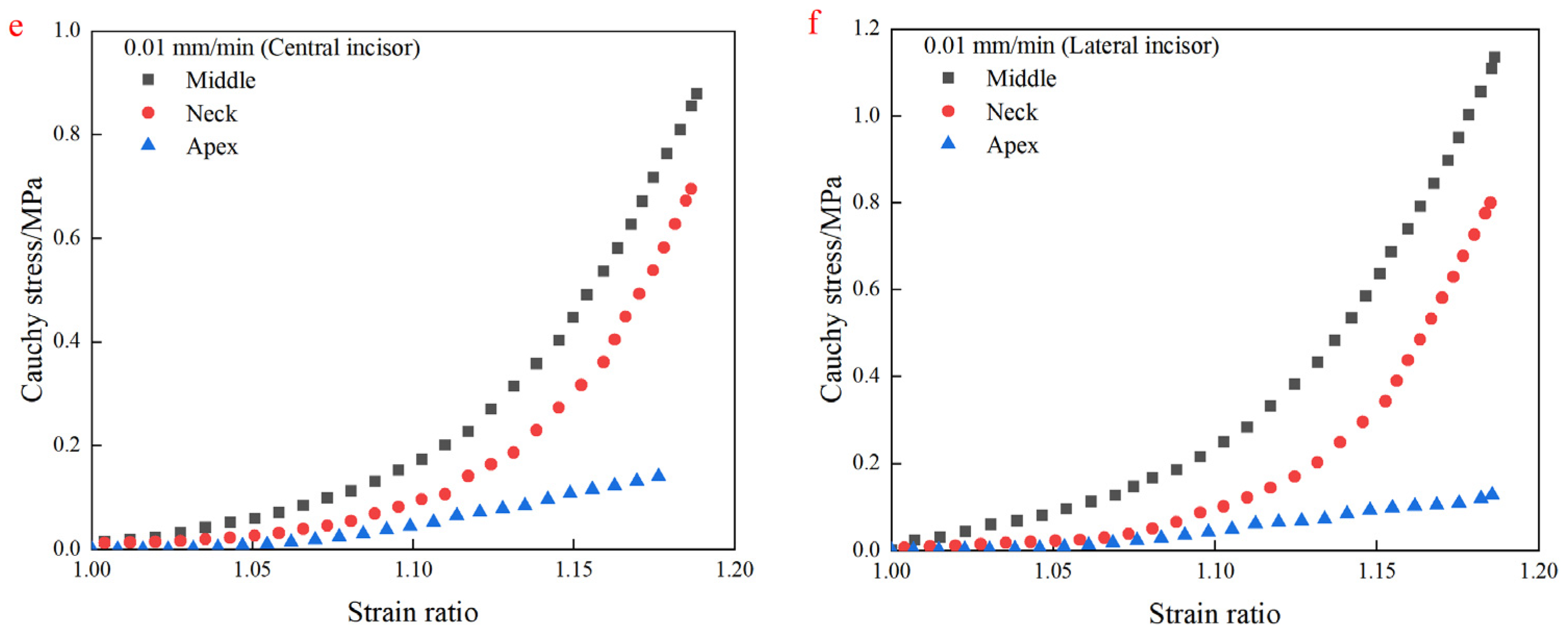
4.2. Uniaxial Tensile Test Results
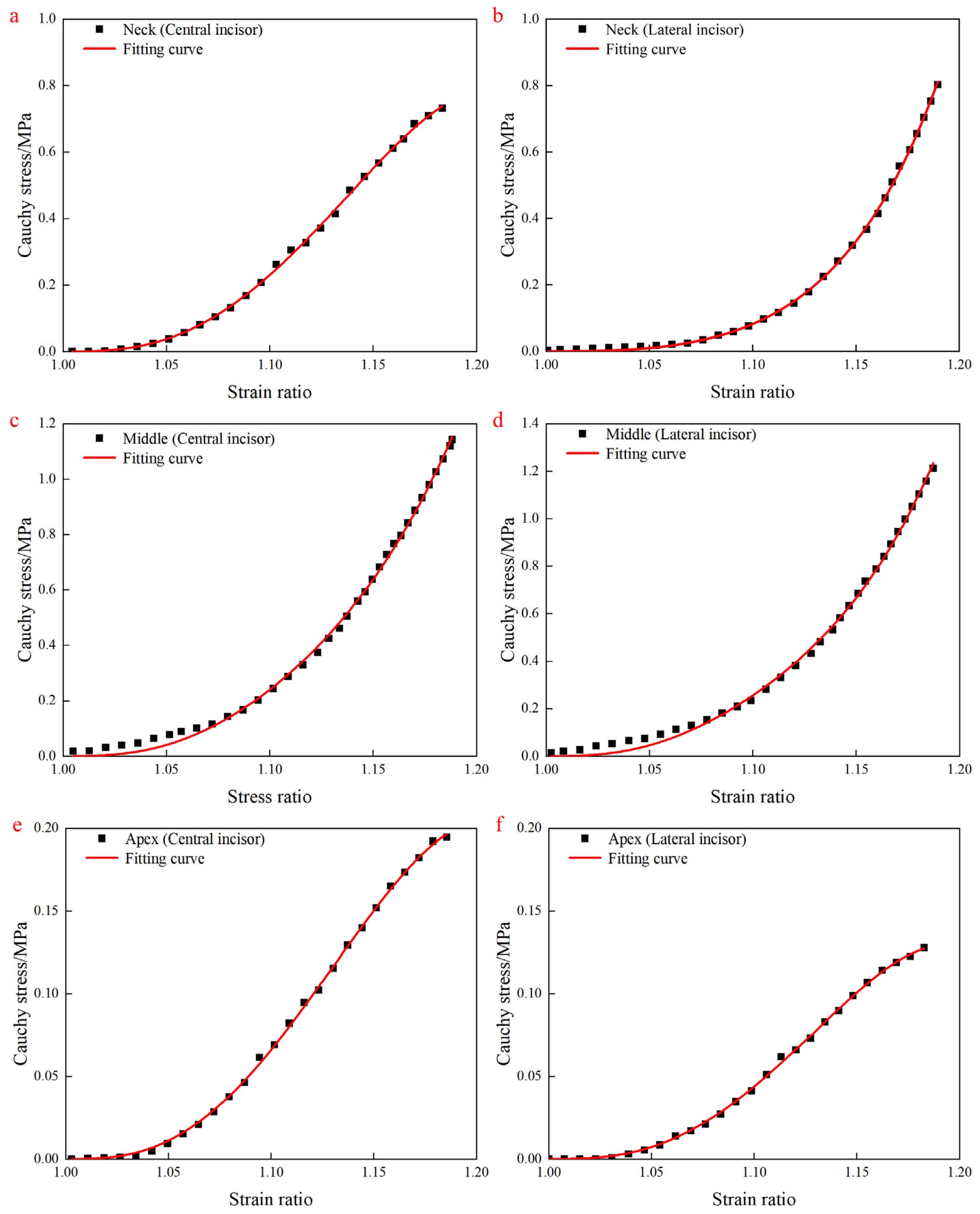
4.3. Fitting Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, S.; Liu, J.; Feng, F.; Jia, Y.; Xu, F.; Wei, Z.; Zhang, M. Rational Design of Viscoelastic Hydrogels for Periodontal Ligament Remodeling and Repair. Acta Biomater. 2024, 174, 69–90. [Google Scholar] [CrossRef]
- Hosiriluck, N.; Kashio, H.; Takada, A.; Mizuguchi, I.; Arakawa, T. The Profiling and Analysis of Gene Expression in Human Periodontal Ligament Tissue and Fibroblasts. Clin. Exp. Dent. Res. 2022, 8, 658–672. [Google Scholar] [CrossRef]
- Wen, S.; Zheng, X.; Yin, W.; Liu, Y.; Wang, R.; Zhao, Y.; Liu, Z.; Li, C.; Zeng, J.; Rong, M. Dental Stem Cell Dynamics in Periodontal Ligament Regeneration: From Mechanism to Application. Stem Cell Res. Ther. 2024, 15, 389. [Google Scholar] [CrossRef] [PubMed]
- Dastgerdi, A.K.; Bavil, A.Y.; Rouhi, G. The Effects of Material and Structural Properties of the Periodontal Ligament in Mechanical Function of Tooth-Pdl-Bone Complex in Dental Trauma: A Sensitivity Study Using Finiteelement Analysis. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 2023, 237, 619–627. [Google Scholar] [CrossRef]
- Mapar, A.; Taheri-Nassaj, N.; Shen, J.; Komari, O.; Sheets, C.G.; Earthman, J.C. Finite Element Study of Periodontal Ligament Properties for a Maxillary Central Incisor and a Mandibular Second Molar Under Percussion Conditions. J. Med. Biol. Eng. 2022, 42, 681–691. [Google Scholar] [CrossRef]
- Moga, R.A.; Olteanu, C.D.; Botez, M.D.; Buru, S.M. Assessment of the Orthodontic External Resorption in Periodontal Breakdown-a Finite Elements Analysis (Part I). Healthcare 2023, 11, 1447. [Google Scholar] [CrossRef] [PubMed]
- Ovy, E.G.; Romanyk, D.L.; Flores, M.C.; Westover, L. Modelling and Evaluating Periodontal Ligament Mechanical Behaviour and Properties: A Scoping Review of Current Approaches and Limitations. Orthod. Craniofac. Res. 2022, 25, 199–211. [Google Scholar] [CrossRef]
- Moga, R.A.; Buru, S.M.; Chiorean, C.G.; Cosgarea, R. Compressive Stress in Periodontal Ligament Under Orthodontic Movements During Periodontal Breakdown. Am. J. Orthod. Dentofacial. Orthop. 2021, 159, e291–e299. [Google Scholar] [CrossRef]
- Wu, C.; Liu, X.; Zhang, H.; Zhang, Q.; Ding, S.; Jin, S.; Zheng, X.; Fu, C.; Han, Q.; Shen, J.; et al. Response of Human Periodontal Ligament to Orthodontic Force Using Superb Microvascular Imaging. Am. J. Orthod. Dentofacial. Orthop. 2022, 162, e257–e266. [Google Scholar] [CrossRef] [PubMed]
- Liang, Y.; Shakya, A.; Liu, X. Biomimetic Tubular Matrix Induces Periodontal Ligament Principal Fiber Formation and Inhibits Osteogenic Differentiation of Periodontal Ligament Stem Cells. ACS Appl. Mater. Interfaces 2022, 14, 36451–36461. [Google Scholar] [CrossRef]
- Zhong, J.; Pierantoni, M.; Weinkamer, R.; Brumfeld, V.; Zheng, K.; Chen, J.; Swain, M.V.; Weiner, S.; Li, Q. Microstructural Heterogeneity of the Collagenous Network in the Loaded and Unloaded Periodontal Ligament and its Biomechanical Implications. J. Struct. Biol. 2021, 213, 107772. [Google Scholar] [CrossRef] [PubMed]
- Poschke, A.; Krahling, B.; Failing, K.; Staszyk, C. Molecular Characteristics of the Equine Periodontal Ligament. Front. Vet. Sci. 2017, 4, 235. [Google Scholar]
- Xu, H.; Lee, A.; Sun, L.; Naveh, G. 3D Imaging of Pdl Collagen Fibers During Orthodontic Tooth Movement in Mandibular Murine Model. J. Vis. Exp. 2021, 170, e62149. [Google Scholar] [CrossRef]
- Zhao, Z.; Tarce, M.; Georgopoulou, M.; Zong, C.; Van Holm, W.; Attanasio, C.; Pedano, M.S.; de Llano-Pérula, M.C. Periodontal Ligament Reactions to Orthodontic Force: A Transcriptomic Study on Maxillary and Mandibular Human Premolars. J. Periodontal Res. 2024. [Google Scholar] [CrossRef] [PubMed]
- Zhou, J.; Song, Y.; Shi, X.; Zhang, C. Tensile Creep Mechanical Behavior of Periodontal Ligament: A Hyper-Viscoelastic Constitutive Model. Comput. Methods Programs Biomed. 2021, 207, 106224. [Google Scholar] [CrossRef]
- Nikolaus, A.; Currey, J.D.; Lindtner, T.; Fleck, C.; Zaslansky, P. Importance of the Variable Periodontal Ligament Geometry for Whole Tooth Mechanical Function: A Validated Numerical Study. J. Mech. Behav. Biomed. Mater. 2017, 67, 61–73. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.; Liu, Y.; Li, B.; Dong, X. Development and Verification of a Constitutive Model for Human Periodontal Ligament Based on Finite Element Analysis. Comput. Methods Biomech. Biomed. Eng. 2022, 25, 1051–1062. [Google Scholar] [CrossRef] [PubMed]
- Karimi, A.; Razaghi, R.; Biglari, H.; Rahmati, S.M.; Sandbothe, A.; Hasani, M. Finite Element Modeling of the Periodontal Ligament Under a Realistic Kinetic Loading of the Jaw System. Saudi Dent. J. 2020, 32, 349–356. [Google Scholar] [CrossRef] [PubMed]
- Liu, M.; Wu, B.; Yang, F.; Jiang, D.; Izadikhah, I.; Chen, Y.; Li, N.; Yan, B. Understanding the Hierarchical Structure of Collagen Fibers of the Human Periodontal Ligament: Implications for Biomechanical Characteristics. Acta Biomater. 2024, 188, 253–265. [Google Scholar] [CrossRef] [PubMed]
- Connizzo, B.K.; Sun, L.; Lacin, N.; Gendelman, A.; Solomonov, I.; Sagi, I.; Grodzinsky, A.J.; Naveh, G. Nonuniformity in Periodontal Ligament: Mechanics and Matrix Composition. J. Dent. Res. 2021, 100, 179–186. [Google Scholar] [CrossRef] [PubMed]
- Hirashima, S.; Kanazawa, T.; Ohta, K.; Nakamura, K. Three-Dimensional Ultrastructural Imaging and Quantitative Analysis of the Periodontal Ligament. Anat. Sci. Int. 2020, 95, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Wu, B.; Li, N.; Liu, M.; Cheng, K.; Jiang, D.; Yi, Y.; Ma, S.; Yan, B.; Lu, Y. Construction of Human Periodontal Ligament Constitutive Model Based on Collagen Fiber Content. Materials 2023, 16, 6582. [Google Scholar] [CrossRef] [PubMed]
- Wu, B.; Cheng, K.; Liu, M.; Liu, J.; Jiang, D.; Ma, S.; Yan, B.; Lu, Y. Construction of Hyperelastic Model of Human Periodontal Ligament Based on Collagen Fibers Distribution. J. Mech. Behav. Biomed. Mater. 2022, 135, 105484. [Google Scholar] [CrossRef] [PubMed]
- Po, J.M.; Kieser, J.A.; Gallo, L.M.; Tesenyi, A.J.; Herbison, P.; Farella, M. Time-Frequency Analysis of Chewing Activity in the Natural Environment. J. Dent. Res. 2011, 90, 1206–1210. [Google Scholar] [CrossRef]
- Parthasarathy, R.; Srinivasan, S.; Vikram, C.; Thanikachalam, Y.; Ramachandran, A. An Interdisciplinary Management of Avulsed Maxillary Incisors: A Case Report. Cureus 2022, 14, e23891. [Google Scholar] [CrossRef] [PubMed]
- Huang, R.; Zhou, C.; Zhan, L.; Liu, Y.; Liu, X.; Du, Q.; Wang, J.; Zhao, W.; Song, G.; Wu, L.; et al. Experts Consensus on Management of Tooth Luxation and Avulsion. Int. J. Oral Sci. 2024, 16, 57. [Google Scholar] [CrossRef]
- Ortun-Terrazas, J.; Cegonino, J.; Santana-Penin, U.; Santana-Mora, U.; Perez, D.P.A. A Porous Fibrous Hyperelastic Damage Model for Human Periodontal Ligament: Application of a Microcomputerized Tomography Finite Element Model. Int. J. Numer. Meth. Biomed. 2019, 35, e3176. [Google Scholar] [CrossRef] [PubMed]
- Otani, T.; Koga, T.; Nozaki, K.; Kobayashi, Y.; Tanaka, M. Mechanical Effects of Distributed Fibre Orientation in the Periodontal Ligament of an Idealised Geometry. Comput. Methods Biomech. Biomed. Eng. 2020, 24, 701–709. [Google Scholar] [CrossRef]
- Sánchez-Molina, D.; García-Vilana, S.; Llumà, J.; Galtés, I.; Velázquez-Ameijide, J.; Rebollo-Soria, M.C.; Arregui-Dalmases, C. Mechanical Behavior of Blood Vessels: Elastic and Viscoelastic Contributions. Biology 2021, 10, 831. [Google Scholar] [CrossRef]
- Liu, X.; Liu, M.; Wu, B.; Tang, W.; Yan, B.; Lu, R. A Novel Method for Monitoring the Maxillary Tooth Movement During Orthodontics in 3D Space. Int. J. Comput. Dent. 2023, 26, 49–60. [Google Scholar] [PubMed]
- Shokrani, P.; Hashemi, A.; Bostan, S.M.; Oskui, I.Z. Effect of Geometric Dimensions and Material Models of the Periodontal Ligament in Orthodontic Tooth Movement. Orthod. Craniofac. Res. 2020, 23, 404–412. [Google Scholar] [CrossRef]
- Roser, C.J.; Rues, S.; Erber, R.; Hodecker, L.; Lux, C.J.; Bauer, C. Tooth Mobility Restriction by Multistranded and CAD/CAM Retainers-an in Vitro Study. Eur. J. Orthod. 2024, 46, cjad076. [Google Scholar] [CrossRef] [PubMed]
- Oskui, I.Z.; Hashemi, A. Dynamic Tensile Properties of Bovine Periodontal Ligament: A Nonlinear Viscoelastic Model. J. Biomech. 2016, 49, 756–764. [Google Scholar] [CrossRef]
- Papadopoulou, K.; Hasan, I.; Keilig, L.; Reimann, S.; Eliades, T.; Jäger, A.; Deschner, J.; Bourauel, C. Biomechanical Time Dependency of the Periodontal Ligament: A Combined Experimental and Numerical Approach. Eur. J. Orthod. 2013, 35, 811–818. [Google Scholar] [CrossRef] [PubMed]

| Neck (Central) | Middle (Central) | Apex (Central) | Neck (Lateral) | Middle (Lateral) | Apex (Lateral) | |
|---|---|---|---|---|---|---|
| Length/mm | 2.53 | 2.60 | 2.23 | 2.27 | 2.40 | 2.57 |
| Width/mm | 2.16 | 2.08 | 2.20 | 2.22 | 1.96 | 2.03 |
| Thickness/mm | 0.25 | 0.25 | 0.25 | 0.25 | 0.25 | 0.25 |
| Area/mm2 | 5.4648 | 5.4080 | 4.9060 | 5.0394 | 4.7040 | 5.2171 |
| (%) | Section 1 | Section 2 | Section 3 | Section 4 | Section 5 | Average |
|---|---|---|---|---|---|---|
| Neck | 60.007 | 51.991 | 53.889 | 67.895 | 67.78 | 60.312 |
| Middle | 58.249 | 65.771 | 65.65 | 61.369 | 64.669 | 63.142 |
| Apex | 62.198 | 59.01 | 41.2 | 51.417 | 46.116 | 51.988 |
| /MPa | /MPa | /MPa | R2 | |
|---|---|---|---|---|
| Neck (central) | 25.57 | 9.76 | −6.61 | 0.998 |
| Neck (lateral) | −7.13 | 40.93 | 55.60 | 0.999 |
| Middle (central) | 24.30 | −15.23 | 18.00 | 0.997 |
| Middle (lateral) | 35.33 | −16.01 | 20.90 | 0.997 |
| Apex (central) | 8.12 | 0.58 | 1.69 | 0.999 |
| Apex (lateral) | 8.31 | 7.05 | −4.27 | 0.999 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, B.; Huang, C.; Li, N.; Lu, Y.; Yi, Y.; Yan, B.; Jiang, D. Formulation of Hyperelastic Constitutive Model for Human Periodontal Ligament Based on Fiber Volume Fraction. Materials 2025, 18, 705. https://doi.org/10.3390/ma18030705
Wu B, Huang C, Li N, Lu Y, Yi Y, Yan B, Jiang D. Formulation of Hyperelastic Constitutive Model for Human Periodontal Ligament Based on Fiber Volume Fraction. Materials. 2025; 18(3):705. https://doi.org/10.3390/ma18030705
Chicago/Turabian StyleWu, Bin, Chenfeng Huang, Na Li, Yi Lu, Yang Yi, Bin Yan, and Di Jiang. 2025. "Formulation of Hyperelastic Constitutive Model for Human Periodontal Ligament Based on Fiber Volume Fraction" Materials 18, no. 3: 705. https://doi.org/10.3390/ma18030705
APA StyleWu, B., Huang, C., Li, N., Lu, Y., Yi, Y., Yan, B., & Jiang, D. (2025). Formulation of Hyperelastic Constitutive Model for Human Periodontal Ligament Based on Fiber Volume Fraction. Materials, 18(3), 705. https://doi.org/10.3390/ma18030705







