Effects of Surface Rearrangement on H and O Adsorption on Cu and Pd Nanoparticles
Abstract
1. Introduction
- (i)
- Calculate the adsorption energy of hydrogen and oxygen atoms on highly symmetric active sites of flat and stepped (kinked) copper and palladium surfaces.
- (ii)
- Calculate the adsorption energy of hydrogen and oxygen atoms both with and without allowing relaxation of the surface atoms.
- (iii)
- Analyze the obtained data and quantify the contribution of atomic deformation to the adsorption energy.
2. Calculation Method
3. Results and Discussion
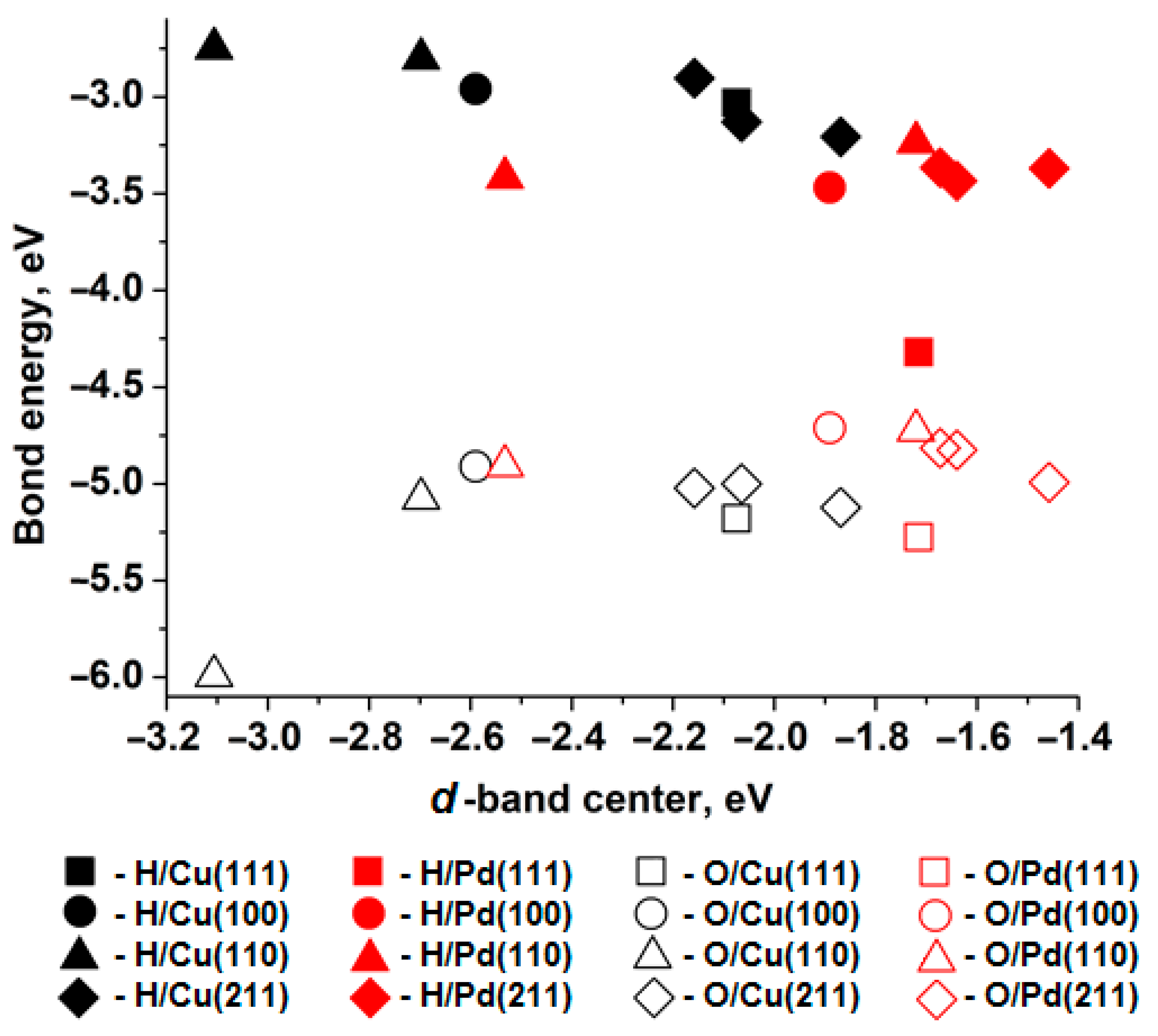
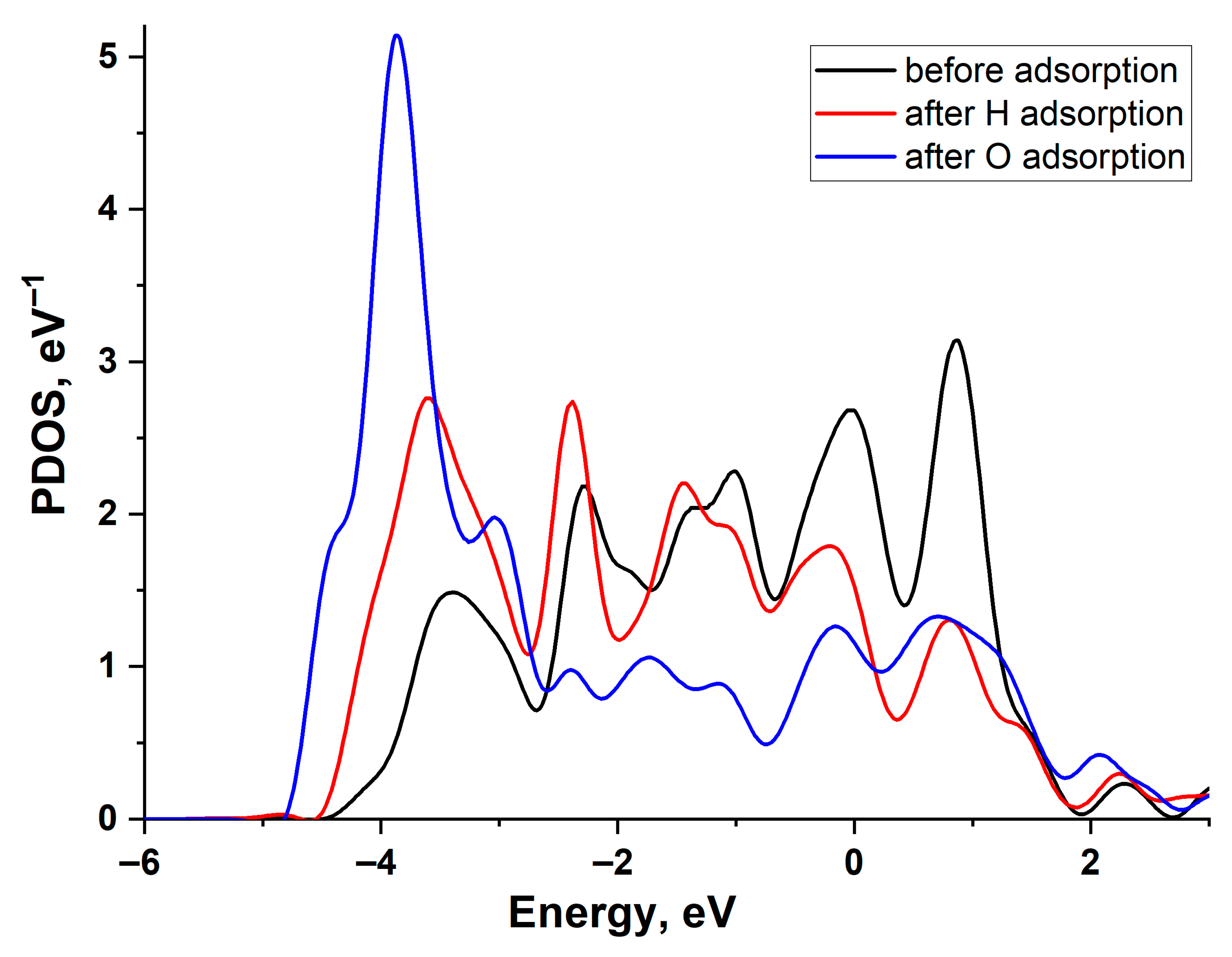
3.1. The Relationship Between Electronic and Atomic Structures
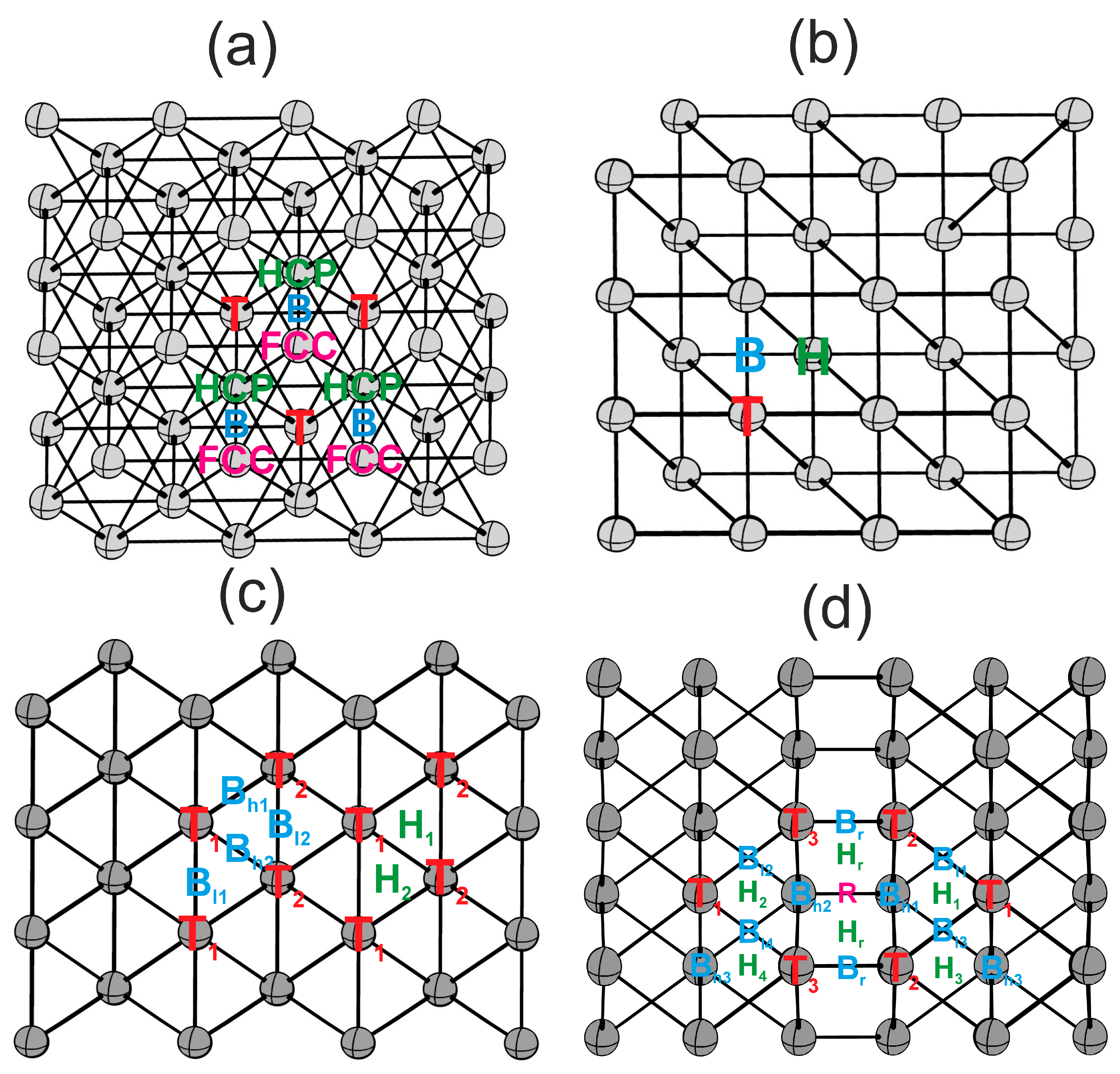
3.2. Atomic Contributions of Highly Symmetric Hydrogen and Oxygen Adsorption Sites on Cu and Pd(111), (100), (110), and (211) Surfaces
3.2.1. Cu(111), Cu(100), Cu(110), Cu(211)
3.2.2. Pd(111), Pd(100), Pd(110), Pd(211)
4. Conclusions
- (i)
- The influence of atomic deformation on adsorption energy is most pronounced for active sites with CN = 3 on flat (111) surfaces and CN = 4 on (100) surfaces. For curved (110) and (211) surfaces, the effect of atomic deformation shows no clear trend. This behavior appears to be governed by surface packing density. Surfaces with higher packing density—and consequently more uniform local environments around each active site—exhibit maximum deformation effects at sites with the highest coordination number. In contrast, surfaces with lower packing density contain active sites with heterogeneous local coordination environments, where the influence of atomic deformation varies even among sites with identical coordination numbers but different atomic arrangements.
- (ii)
- Atomic deformation consistently enhances binding strength across all studied systems.
- (iii)
- The influence of the local atomic environment depends on the adatom type and indirectly correlates with the magnitude of the interaction matrix element. A larger interaction matrix element corresponds to a greater contribution of repulsive interactions in the metal-adsorbate complex. When repulsive interactions have limited influence, the contribution from surrounding atoms is proportional to the active site’s coordination number. Conversely, strong repulsive interactions reverse this dependence. A similar correlation between the local environment effect and the interaction matrix element was also established for gold, platinum, and nickel.
- (iv)
- Our results demonstrate that atomic-scale contributions can play a significant role in determining the reactivity and adsorption properties of nanoscale systems. Consequently, when selecting catalytic systems, not only the chemical composition of the nanophase but also the choice of its support material becomes crucial. This insight opens new possibilities for enhancing and fine-tuning the properties of practical catalytic nanosystems.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lin, C.; Huang, X.; Xue, Y.; Jiang, S.; Chen, C.; Liu, Y.; Chen, K. Advances in medical devices using nanomaterials and nanotechnology: Innovation and regulatory science. Bioact. Mater. 2025, 48, 353–369. [Google Scholar] [CrossRef]
- Zakir, O.; Ait-Karra, A.; Khardazi, S.; Idouhli, R.; Khadiri, M.E.; Dikici, B.; Aboulaich, A.; Outzourhit, A.; Abouelfida, A. Recent progress in nanomaterials for water treatment: A comprehensive review of adsorption, photocatalytic, and antibacterial applications. J. Water Process Eng. 2025, 72, 107566. [Google Scholar] [CrossRef]
- Lambert, R.M.; Pacchioni, G. (Eds.) Chemisorption and Reactivity on Supported Clusters and Thin Films; Springer: Dordrecht, The Netherlands, 1997; p. 532. [Google Scholar] [CrossRef]
- Scheffler, M.; Stampfl, C. Theory of Adsorption on Metal Substrates. In Handbook of Surface Science; Horn, K., Scheffler, M., Eds.; Elsevier Science: Amsterdam, The Netherlands, 2000; Volume 2, p. 1058. [Google Scholar] [CrossRef]
- Piumetti, M.; Bensaid, S. (Eds.) Nanostructured Catalysts for Environmental Applications; Springer International Publishing: Cham, Switzerland, 2021; p. 435. [Google Scholar] [CrossRef]
- Okonkwo, T.P.; Amienghemhen, O.D.; Nkwor, A.N.; Ifijen, I.H. Exploring the versatility of copper-based nanoparticles as contrast agents in various imaging modalities. Nano-Struct. Nano-Objects 2024, 40, 101370. [Google Scholar] [CrossRef]
- Arif, M. A review on copper nanoparticles loaded in smart microgels. Mater. Today Commun. 2023, 36, 106580. [Google Scholar] [CrossRef]
- Katin, K.P.; Kochaev, A.I.; Bereznitskiy, I.V.; Kalika, E.B.; Kaya, S.; Flores-Moreno, R.; Maslov, M.M. Interaction of pristine and novel graphene allotropes with copper nanoparticles: Coupled density functional and molecular dynamics study. Diam. Relat. Mater. 2023, 138, 110190. [Google Scholar] [CrossRef]
- Li, X.; Yang, L.; Zhou, J.; Dai, B.; Gan, D.; Yang, Y.; Wang, Z.; He, J.; Xia, S. Biogenic palladium nanoparticles for wastewater treatment: Formation, applications, limitations, and future directions. J. Water Process Eng. 2024, 64, 105641. [Google Scholar] [CrossRef]
- Yaduvanshi, N.; Jaiswal, S.; Tewari, S.; Shukla, S.; Wabaidur, S.M.; Dwivedi, J.; Sharma, S. Palladium nanoparticles and their composites: Green synthesis and applications with special emphasis to organic transformations. Inorg. Chem. Commun. 2023, 151, 110600. [Google Scholar] [CrossRef]
- Zhao, Q.; Yu, H.; Hu, D.; Li, L.-L.; Jin, J.; Ai, M.-J.; Wei, J.; Song, K. Recent advances in electrochemical sensors based on palladium nanoparticles. Chin. J. Anal. Chem. 2022, 50, 100144. [Google Scholar] [CrossRef]
- Henry, C.R. Morphology of supported nanoparticles. Prog. Surf. Sci. 2005, 80, 92–116. [Google Scholar] [CrossRef]
- Chantaramethakul, J.; Hussakan, C.; Yenmankhong, Y.; Chandeang, P.; Techapiesancharoenkij, R.; Hirunpinyopas, W.; Kasmui Kurniawan, C.; Panomsuwan, G. Effect of carbon black supports on the hydrogen evolution reaction activity of Pd nanoparticle electrocatalysts synthesized via solution plasma sputtering. RSC Adv. 2024, 14, 31648–31654. [Google Scholar] [CrossRef]
- Ngom, N.; Etindele, A.J.; Andriambelaza, N.F.; Nithaya, C.; Wakata, A.S.; Kenmoe, S. Comparative study of CO adsorption on Au, Cu, MoO2 and MoS2 2D Nanoparticles. Comput. Theor. Chem. 2024, 1241, 114877. [Google Scholar] [CrossRef]
- Zhu, M.; Nguyen, M.T.; Sim, W.J.; Yonezawa, T. Co-sputtered CuPt/Ag alloy nanoparticles and comparative catalytic performance of mono-, bi-, and tri-metallic nanoparticles in the oxygen reduction reaction. Mater. Adv. 2022, 3, 8967–8976. [Google Scholar] [CrossRef]
- Güntherodt, H.J.; Wiesendanger, R. (Eds.) Scanning Tunneling Microscopy I: General Principles and Applications to Clean and Absorbate-Covered Surfaces; Springer: Berlin/Heidelberg, Germany, 1994; p. 280. [Google Scholar] [CrossRef]
- Binnig, G.; Rohrer, H.; Berber, C.; Weibel, E. Tunneling through a controllable vacuum gap. Appl. Phys. Lett. 1982, 40, 178–180. [Google Scholar] [CrossRef]
- Meyer, E.; Hug, H.J.; Bennewitz, R. (Eds.) Scanning Probe Microscopy. The Lab on a Tip; Springer International Publishing: Cham, Switzerland, 2021; p. 322. [Google Scholar] [CrossRef]
- Grishin, M.V.; Gatin, A.K.; Dokhlikova, N.V.; Kirsankin, A.A.; Shub, B.R.; Kulak, A.I.; Nikolaev, S.A. Adsorption and interaction of hydrogen and oxygen on the surface of separate crystalline gold nanoparticles. Kinet. Catal. 2015, 56, 532–539. [Google Scholar] [CrossRef]
- Gatin, A.K.; Grishin, M.V.; Sarvadii, S.Y.; Slutskii, V.G.; Kharitonov, V.A.; Shub, B.R.; Kulak, A.I. Physicochemical properties of nanoparticles: Interaction of supported platinum nanoparticles with gaseous reactants. Kinet. Catal. 2018, 59, 196–202. [Google Scholar] [CrossRef]
- Nørskov, J.K. Chemisorption on metal surfaces. Rep. Prog. Phys. 1993, 53, 1253–1295. [Google Scholar] [CrossRef]
- Hammer, B.; Nørskov, J.K. Theory of adsorption and surface reactions. In Chemisorption and Reactivity on Supported Clusters and Thin Films; Lambert, R.M., Pacchioni, G., Eds.; Springer: Dordrecht, The Netherlands, 1997; 532p. [Google Scholar] [CrossRef]
- Dokhlikova, N.V.; Gatin, A.K.; Sarvadii, S.Y.; Tastaibek, D.; Slutskii, V.G.; Grishin, M.V. Surface Structure Effects on H and O Adsorption on Gold, Nickel and Platinum Nanoparticles. Materials 2025, 18, 631. [Google Scholar] [CrossRef]
- Giannozzi, P.; Andreussi, O.; Brumme, T.; Bunau, O.; Buongiorna Nardelli, M.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Cococcioni, M.; et al. Advanced capabilities for materials modelling with Quantum ESPRESSO. J. Phys. Condens. Matter 2017, 29, 465901. [Google Scholar] [CrossRef]
- Perdew, J.P.; Ruzsinszky, A.; Csonka, G.I.; Vydrov, O.A.; Scuseria, G.E.; Constantin, L.A.; Zhou, X.; Burke, K. Restoring the density-gradient expansion for exchange in solids and surfaces. Phys. Rev. Lett. 2008, 100, 136406. [Google Scholar] [CrossRef] [PubMed]
- Vanderbilt, D. Soft self-consistent pseudopotentials in a generalized eigenvalue formalism. Phys. Rev. B 1990, 41, 7892–7895. [Google Scholar] [CrossRef] [PubMed]
- Ozaki, T.; Kino, H. Numerical atomic basis orbitals from H to Kr. Phys. Rev. B 2004, 69, 195113. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H–Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188. [Google Scholar] [CrossRef]
- Methfessel, M.; Paxton, A.T. High-precision sampling for Brillouin-zone integration in metals. Phys. Rev. B Condens. Matter 1989, 40, 3616. [Google Scholar] [CrossRef] [PubMed]
- Hammer, B.; Nørskov, J.K. Theoretical Surface science and catalysis—Calculations and concepts. Adv. Catal. 2000, 45, 71–129. [Google Scholar] [CrossRef]
- Hammer, B.; Nørskov, J.K. Electronic factors determining the reactivity of metal surfaces. Surf. Sci. 1995, 343, 211–220. [Google Scholar] [CrossRef]
- Dokhlikova, N.V.; Grishin, M.V.; Doronin, S.V. Hydrogen diffusion on (100), (111), (110) and (211) gold faces. Int. J. Quant. Chem. 2024, 124, e27242. [Google Scholar] [CrossRef]
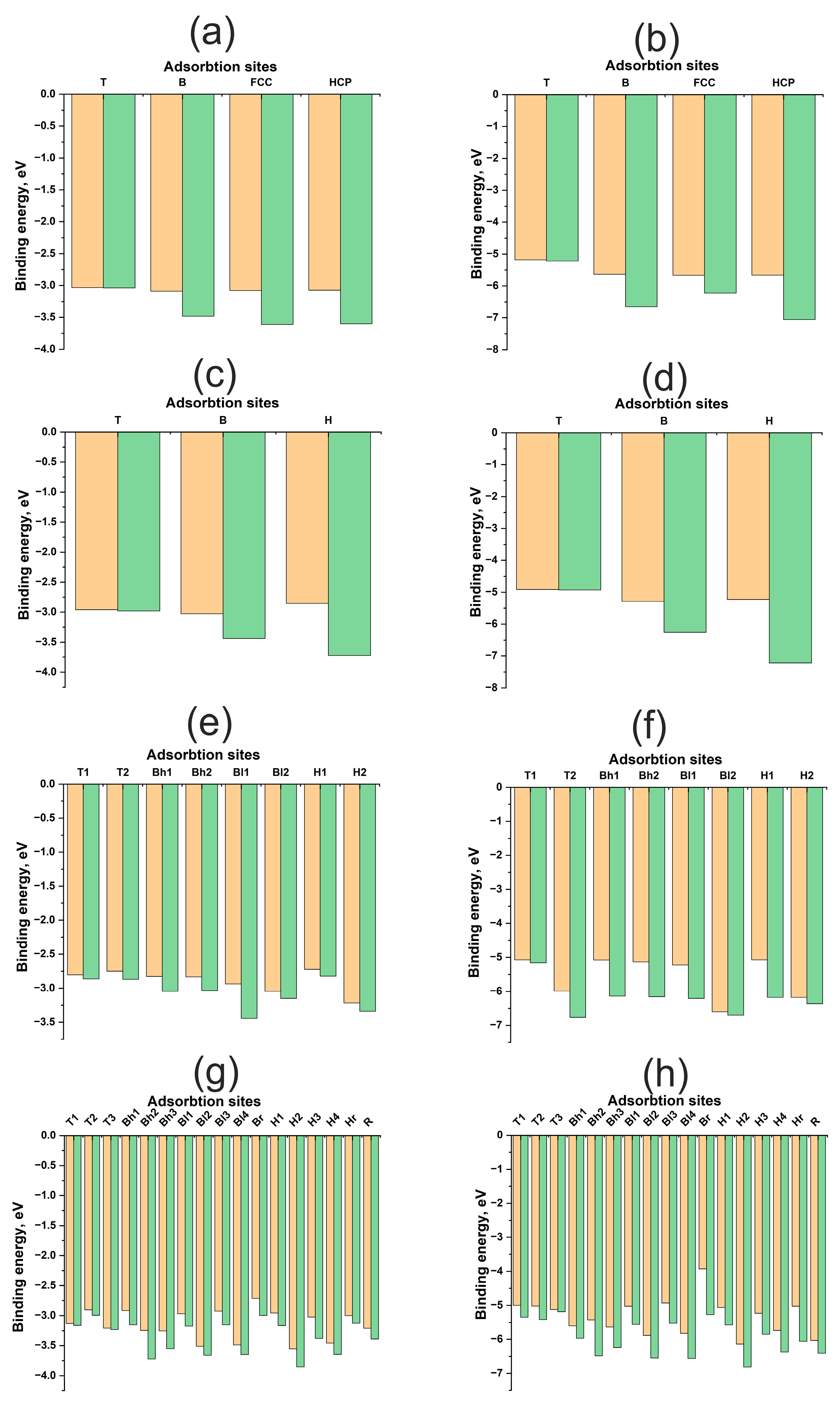

| H | O | |||||||
| Cu(111) | ||||||||
| T | −3.03 | −3.04 | 1.51 | 1.54 | −5.18 | −5.22 | 1.72 | 1.71 |
| B | −3.09 | −3.48 | 1.66 | 1.14 | −5.64 | −6.65 | 1.82 | 1.24 |
| FCC | −3.08 | −3.61 | 1.74 | 1.03 | −5.67 | −6.22 | 1.87 | 1.18 |
| HCP | −3.07 | −3.60 | 1.74 | 1.00 | −5.66 | −7.06 | 1.98 | 1.33 |
| Cu(100) | ||||||||
| T | −2.96 | −2.98 | 1.521 | 1.609 | −4.91 | −4.93 | 1.71 | 1.76 |
| B | −3.03 | −3.44 | 1.642 | 1.179 | −5.29 | −6.26 | 1.80 | 1.36 |
| H | −2.85 | −3.73 | 1.832 | 0.599 | −5.23 | −7.22 | 1.97 | 0.96 |
| Cu(110) | ||||||||
| T1 | −2.80 | −2.86 | 1.52 | 1.595 | −5.08 | −5.16 | 1.70 | 1.67 |
| Bl1 | −2.94 | −3.44 | 1.64 | 1.25 | −5.22 | −6.21 | 1.80 | 1.46 |
| Bh2 | −2.83 | −3.04 | 1.99 | 1.58 | −5.14 | −6.16 | 1.95 | 1.465 |
| Bh1 | −2.83 | −3.05 | 1.995 | 1.62 | −5.08 | −6.14 | 1.96 | 1.50 |
| Bl2 | −3.05 | −3.15 | 1.76 | 1.31 | −6.60 | −6.70 | 2.06 | 1.65 |
| T2 | −2.75 | −2.87 | 1.695 | 1.63 | −5.99 | −6.77 | 2.06 | 1.88 |
| H2 | −3.22 | −3.34 | 1.93 | 1.46 | −6.18 | −6.36 | 1.96 | 1.45 |
| H1 | −2.72 | −2.82 | 1.79 | 1.165 | −5.08 | −6.18 | 1.96 | 1.08 |
| Cu(211) | ||||||||
| Bh1 | −2.92 | −3.15 | 1.69 | 1.15 | −5.60 | −5.97 | 1.97 | 1.45 |
| H1 | −2.96 | −3.16 | 1.74 | 0.997 | −5.06 | −5.57 | 1.91 | 1.30 |
| T1 | −3.13 | −3.16 | 1.53 | 1.52 | −5.00 | −5.35 | 1.81 | 1.67 |
| H2 | −3.55 | −3.85 | 1.75 | 1.06 | −6.14 | −6.81 | 1.89 | 1.31 |
| Bh2 | −3.24 | −3.72 | 1.63 | 1.14 | −5.43 | −6.49 | 1.79 | 1.38 |
| R | −3.21 | −3.39 | 2.15 | 2.79 | −6.03 | −6.41 | 2.17 | 1.31 |
| Bl1 | −2.97 | −3.17 | 1.67 | 1.13 | −5.02 | −5.56 | 1.87 | 1.35 |
| Bl2 | −3.51 | −3.66 | 1.69 | 1.17 | −5.88 | −6.55 | 1.87 | 1.28 |
| Hr | −3.00 | −3.12 | 2.00 | 1.49 | −5.03 | −6.06 | 1.90 | 1.38 |
| T2 | −2.90 | −2.99 | 1.59 | 1.55 | −5.02 | −5.42 | 1.88 | 1.77 |
| H3 | −3.02 | −3.38 | 1.73 | 1.08 | −5.23 | −5.85 | 1.899 | 1.29 |
| Bh3 | −3.25 | −3.55 | 1.69 | 1.17 | −5.63 | −6.24 | 1.89 | 1.42 |
| H4 | −3.46 | −3.64 | 1.79 | 1.09 | −5.73 | −6.37 | 1.91 | 1.24 |
| T3 | −3.21 | −3.23 | 1.50 | 1.52 | −5.12 | −5.19 | 1.69 | 1.73 |
| Br | −2.71 | −3.00 | 2.11 | 1.87 | −3.93 | −5.28 | 1.83 | 1.60 |
| Bl3 | −2.93 | −3.15 | 1.67 | 1.18 | −4.93 | −5.52 | 1.87 | 1.35 |
| Bl4 | −3.49 | −3.65 | 1.69 | 1.17 | −5.83 | −6.56 | 1.87 | 1.27 |
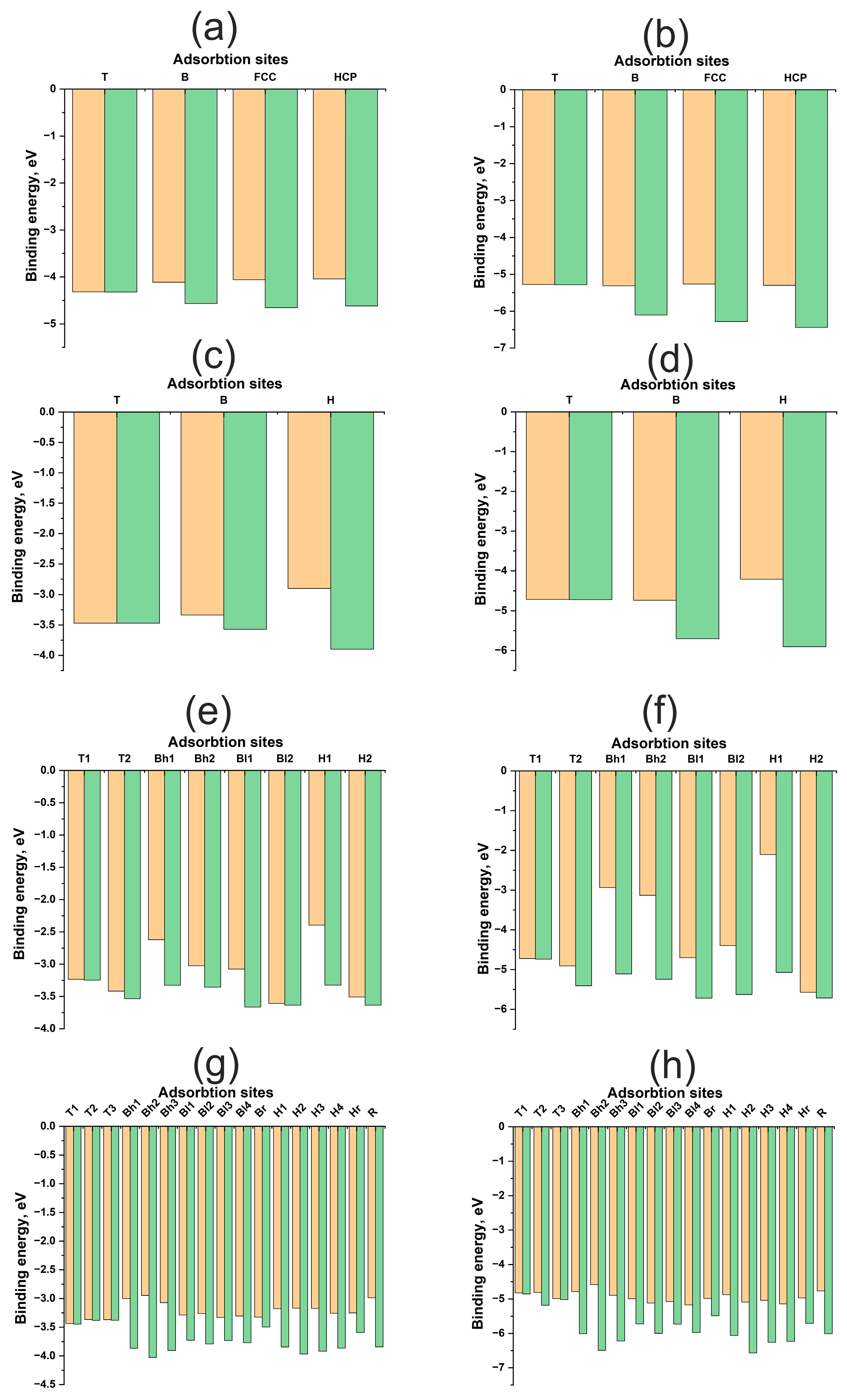
| H | O | |||||||
| Pd(111) | ||||||||
| T | −4.32 | −4.32 | 1.54 | 1.54 | −5.28 | −5.29 | 1.83 | 1.79 |
| B | −4.11 | −4.57 | 1.73 | 1.11 | −5.31 | −6.10 | 1.96 | 1.40 |
| FCC | −4.04 | −4.62 | 1.833 | 0.99 | −5.26 | −6.28 | 2.02 | 1.24 |
| HCP | −4.06 | −4.66 | 1.83 | 1.00 | −5.30 | −6.44 | 2.03 | 1.32 |
| Pd(100) | ||||||||
| T | −3.47 | −3.47 | 1.544 | 1.554 | −4.71 | −4.72 | 1.805 | 1.802 |
| B | −3.34 | −3.89 | 1.709 | 1.083 | −4.74 | −5.70 | 1.917 | 1.389 |
| H | −2.90 | −3.90 | 1.945 | 0.575 | −4.21 | −5.90 | 2.114 | 0.991 |
| Pd(110) | ||||||||
| T1 | −3.24 | −3.25 | 1.537 | 1.475 | −4.72 | −4.74 | 1.788 | 1.79 |
| Bl1 | −3.08 | −3.66 | 1.691 | 1.059 | −4.70 | −5.72 | 1.894 | 1.406 |
| Bh2 | −3.02 | −3.36 | 2.140 | 1.791 | −3.13 | −5.25 | 2.401 | 1.96 |
| Bh1 | −2.62 | −3.33 | 2.198 | 1.87 | −2.94 | −5.11 | 2.447 | 2.05 |
| Bl2 | −3.61 | −3.64 | 2.027 | 1.52 | −4.39 | −5.63 | 2.978 | 2.604 |
| T2 | −3.42 | −3.54 | 1.715 | 1.659 | −4.91 | −5.40 | 2.166 | 2.038 |
| H2 | −3.51 | −3.64 | 1.994 | 1.407 | −5.57 | −5.72 | 2.256 | 1.882 |
| H1 | −2.39 | −3.33 | 2.513 | 1.97 | −2.10 | −5.07 | 2.769 | 2.089 |
| Pd(211) | ||||||||
| Bh1 | −3.00 | −3.87 | 1.705 | 0.771 | −4.79 | −6.01 | 1.962 | 1.228 |
| H1 | −3.18 | −3.85 | 1.799 | 0.809 | −4.88 | −6.06 | 1.974 | 1.11 |
| T1 | −3.44 | −3.45 | 1.543 | 1.996 | −4.82 | −4.85 | 1.812 | 1.793 |
| H2 | −3.19 | −3.97 | 1.790 | 0.794 | −5.09 | −6.57 | 1.975 | 1.128 |
| Bh2 | −2.95 | −4.03 | 1.69 | 0.431 | −4.59 | −6.49 | 1.911 | 0.981 |
| R | −2.99 | −3.84 | 1.996 | 0.348 | −4.77 | −6.01 | 2.22 | 1.004 |
| Bl1 | −3.29 | −3.73 | 1.709 | 1.085 | −5.00 | −5.72 | 1.921 | 1.325 |
| Bl2 | −3.26 | −3.79 | 1.700 | 1.047 | −5.12 | −6.00 | 1.917 | 1.338 |
| Hr | −3.25 | −3.59 | 1.724 | 0.827 | −4.97 | −5.70 | 1.963 | 1.152 |
| T2 | −3.37 | −3.38 | 1.559 | 1.184 | −4.81 | −5.19 | 1.881 | 1.793 |
| H3 | −3.17 | −3.92 | 1.794 | 0.822 | −5.04 | −6.25 | 1.986 | 1.197 |
| Bh3 | −3.07 | −3.91 | 1.702 | 0.744 | −4.89 | −6.22 | 1.95 | 1.124 |
| H4 | −3.28 | −3.86 | 1.813 | 0.858 | −5.14 | −6.23 | 1.983 | 1.097 |
| T3 | −3.37 | −3.38 | 1.546 | 1.989 | −4.99 | −5.02 | 1.789 | 1.852 |
| Br | −3.33 | −3.50 | 1.717 | 1.095 | −4.99 | −5.49 | 1.898 | 1.3 |
| Bl3 | −3.33 | −3.73 | 1.708 | 1.069 | −5.08 | −5.73 | 1.921 | 1.35 |
| Bl4 | −3.31 | −3.77 | 1.704 | 1.056 | −5.17 | −5.97 | 1.917 | 1.321 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dokhlikova, N.V.; Gatin, A.K.; Sarvadiy, S.Y.; Rudenko, E.I.; Tastaibek, D.; Ignat’eva, P.K.; Grishin, M.V. Effects of Surface Rearrangement on H and O Adsorption on Cu and Pd Nanoparticles. Materials 2025, 18, 5047. https://doi.org/10.3390/ma18215047
Dokhlikova NV, Gatin AK, Sarvadiy SY, Rudenko EI, Tastaibek D, Ignat’eva PK, Grishin MV. Effects of Surface Rearrangement on H and O Adsorption on Cu and Pd Nanoparticles. Materials. 2025; 18(21):5047. https://doi.org/10.3390/ma18215047
Chicago/Turabian StyleDokhlikova, Nadezhda Vladimirovna, Andrey Konstantinovich Gatin, Sergey Yurievich Sarvadiy, Ekaterina Igorevna Rudenko, Dinara Tastaibek, Polina Konstantinovna Ignat’eva, and Maxim Vyacheslavovich Grishin. 2025. "Effects of Surface Rearrangement on H and O Adsorption on Cu and Pd Nanoparticles" Materials 18, no. 21: 5047. https://doi.org/10.3390/ma18215047
APA StyleDokhlikova, N. V., Gatin, A. K., Sarvadiy, S. Y., Rudenko, E. I., Tastaibek, D., Ignat’eva, P. K., & Grishin, M. V. (2025). Effects of Surface Rearrangement on H and O Adsorption on Cu and Pd Nanoparticles. Materials, 18(21), 5047. https://doi.org/10.3390/ma18215047








