Highlights
- We conducted a literature review of articles examining the static and dynamic behaviors of functionally graded (FG) microplates and microshells using analytical and numerical methods based on the consistent/modified couple stress theory (CCST/MCST) and consistent/modified strain gradient theory (CSGT/MSGT).
- We categorized the existing methods based on CCST/MCST and CSGT/MSGT for analyzing microplates/microshells into (a) 3D exact and semi-analytical numerical methods, (b) 2D unified shear deformation theory (SDT), and (c) 2D advanced and refined SDT, and reported their applications.
- A comparison study showed that the results from the CCST are nearly the same as those from MCST when estimating deformations, in-plane stresses, and the natural frequency of FG microplates.
- The results showed that material length-scale parameters consistently enhance the FG microplate’s overall stiffness, decreasing its deformations and raising its lowest natural frequency. Their significance is arranged in descending order for flexural mode as the couple stress effect > the deviatoric strain gradient effect > the dilatational strain gradient effect, while for extensional mode, deviatoric strain gradient effect > couple stress effect.
- The results also showed that the applicable ranges of the structural scale for the CCST/MCST and the CSGT/MSGT are approximately within the intervals of 5 × 10−7 m < h < 1 × 10−4 m and 1 × 10−9 m < h < 1 × 10−4 m, respectively.
Abstract
This paper provides an overview of various size-dependent theories based on modified/consistent couple stress and strain gradient theories (CSTs and SGTs), highlighting the development of two-dimensional (2D) refined and advanced shear deformation theories (SDTs) and three-dimensional (3D) pure analytical and semi-analytical numerical methods, including their applications, for analyzing the static and dynamic behaviors of microscale plates and shells made from advanced materials such as fiber-reinforced composites, functionally graded (FG) materials, and carbon nanotube/graphene platelet-reinforced composite materials. The strong and weak formulations of the 3D consistent CST, along with their corresponding boundary conditions for FG microplates, are derived and presented for illustration. A comparison study is provided to show the differences in the results of a simply supported FG microplate’s central deflection, stress, and lowest natural frequency obtained using various 2D size-dependent SDTs and 3D analytical and numerical methods based on the consistent CST. A parametric study is conducted to examine how primary factors, such as the effects of dilatational and deviatoric strain gradients and couple stress, impact the static bending and free vibration behaviors of a simply supported FG microplate using a size-dependent local Petrov–Galerkin meshless method based on the consistent SGT. Influences such as the inhomogeneity index and length-to-thickness ratio are considered. It is shown that the significance of the impact of various material length-scale parameters on the central deflection and its lowest natural frequency (in the flexural mode) of the FG microplate is ranked, from greatest to least, as follows: the couple stress effect, the deviatoric strain gradient effect, and finally the dilatational strain gradient effect. Additionally, when the microplate’s thickness is less than 10−7 m, the couple stress effect on its static and dynamic behaviors becomes saturated. Conversely, the impact of the dilatational and deviatoric strain gradients consistently influences the microplate’s static and dynamic behaviors.
1. Introduction
Functionally graded (FG) material is an emerging industrial material that has been widely used in advanced engineering fields, including aerospace, aeronautical, submarine, electrical, electronic, and communication engineering [1,2,3,4]. Generally, FG material consists of two or more phases of materials with different volume fractions. Because their material properties gradually and smoothly vary within the structural domain, FG structures can eliminate stress concentrations and delamination damage, which often occur in traditional fiber-reinforced composite structures. Additionally, FG structures can achieve specific desirable mechanical properties, including high thermal insulation, a high strength-to-weight ratio, a high stiffness-to-weight ratio, and high corrosion resistance, by optimizing the distribution of the volume fractions of each phase material [5,6,7]. To extend the lifetime of FG structures, developing efficient analytical and numerical methods within the framework of classical continuum mechanics (CCM) and employing them to analyze various mechanical behaviors of FG plate/shell-like structures has gained significant interest. A comprehensive literature review of three-dimensional (3D) and two-dimensional (2D) analytical and numerical methods, along with their applications, can be found in the publications [8,9,10,11,12,13,14,15,16].
Due to the rapid advancements in materials science and manufacturing technology over the past few decades, various components and structures in cutting-edge industries have been miniaturized. However, experimental reports increasingly reveal that when the structure scale approaches the micron level, its mechanical behavior changes significantly from that of macroscale structures. This shift results from size-dependent (or microstructure-dependent) effects caused by notable changes in the microstructure of the constituents. For example, Li et al. [17] and Lei et al. [18] demonstrated through their experiments that the natural frequency of a cantilever nickel microbeam increased by approximately a factor of 2.0 when its thickness decreased from 15 to 2.1 microns. Ince et al. [19] reported that the nominal strength of a concrete specimen increases as its size decreases. Chang et al. [20] found that Young’s modulus of a penta-twinned Ag nanowire increased when its diameter decreased. Using geometrically self-similar indenters, such as cones and pyramids, Pharr et al. [21] observed that the hardness of the specimen increased when the depth of penetration was reduced to less than one micron. In their experimental results, Fleck et al. [22] indicated a significant increase in the torsional hardening of a thin copper wire when its diameter was reduced within the micron-scale range. Lam et al. [23] performed a four-point bending test on an epoxy polymer microbeam, showing a significant increase in its normalized bending rigidity as the microbeam’s thickness decreases within the micron-scale range. McFarland and Colton [24] conducted a static flexural test on a cantilever polypropylene microbeam. They observed notable discrepancies between the experimental results and the predictions obtained from the Euler–Bernoulli beam theory, due to size-dependent effects that occur when the microbeam’s dimensions are reduced within the micron-scale range. These findings indicate that the microstructure’s mechanical behavior is highly dependent on its size. Many classical structural theories based on classical continuum mechanics (CCM) fail to provide precise predictions for the mechanical behavior of microstructures. To address this issue, several higher-order non-CCMs have been developed, including micropolar elasticity [25,26,27], Eringen’s nonlocal elasticity theory (ENET) [28,29,30,31], strain gradient theory (SGT) [23,32,33,34], doublet mechanics [35,36,37], and couple stress theories (CSTs) [38,39,40]. Moreover, Eringen [25] criticized the original CST for having an indeterminacy issue that limited its application. To overcome this, Yang et al. [41] and Hadjesfandiari and Dargush [42,43,44,45] developed the modified CST (MCST) and the consistent CST (CCST), respectively, by deducing that the couple-stress tensor is symmetric and skew-symmetric. This makes MCST and CCST suitable for investigating the various mechanical behaviors of microscale plates and shells, and they are becoming more popular than other non-CCM theories mentioned above because only one material length-scale parameter needs to be calibrated. Subsequently, Yang et al. [41] and Wu and Chang [46] introduced modified and consistent strain gradient theories (MSGT and CSGT), which incorporate the effects of dilatational and deviatoric strain gradients on the MCST and CCST, respectively.
Several review articles on the development of non-CCM theories and their applications have been published [47,48,49,50,51,52,53,54,55,56]. We list these review papers in chronological order, from oldest to newest, in Table 1. These reviews are also categorized based on the theories they explore, the kinematic models they use, the structural types they analyze, and the structural behaviors they examine, helping readers understand the differences among these papers. In this article, we provide a comprehensive review of the development of the MCST, CCST, MSGT, and CSGT, as well as their applications to various mechanical behavior analyses of microscale plates and shells. The current study differs from the review articles mentioned above by focusing on the development of the strong and weak forms of the CCST, MCST, CSGT, and MSGT, along with their relevant 3D semi-analytical and 2D numerical methods, as well as their applications to the static and dynamic behaviors of FG microscale plates and shells, including the significance order for the impact of couple stress and dilatational and deviatoric strain gradients on the static and dynamic behaviors of a simply-supported FG microplate. The purpose of this work is to provide a comprehensive theoretical framework for the CCST, MCST, CSGT, and MSGT, as well as their application scopes, as outlined in the literature. Its layout is organized as follows: In Section 1, we introduce the definition of FG structures, describe the benefits of FG structures, explain size-dependent effects, introduce conventional non-CCM theories, and review relevant existing articles. Section 2 introduces various FG materials, for which the estimates of their effective material properties are presented. In Section 3, we present the strong form of the 3D CCST, including the corresponding Euler–Lagrange equations and associated boundary conditions. We review the relevant 3D analytical and numerical methods based on the strong forms of the 3D MCST, CCST, MSGT, and CSGT, along with their applications to various mechanical behaviors of microscale plates and shells. Additionally, we introduce the weak form of the 3D CCST and review the related semi-analytical numerical methods based on the weak form of the 3D MCST, CCST, MSGT, and CSGT, as well as their applications to different mechanical behaviors of microscale plates and shells. In Section 4, we review several unified 2D size-dependent shear deformation theories (SDTs), based on the MCST, CCST, MSGT, and CSGT, and their applications to various mechanical behaviors of microscale plates and shells. Section 5 conducts a comparative study to illustrate the differences in results obtained using the 3D semi-analytical finite layer method (FLM), the local Petrov–Galerkin meshless (LPGM) method, and 2D advanced and refined SDTs, based on the CCST/MCST. This section also conducts a parametric study to analyze the influence of specific factors on the static and dynamic behaviors of an FG microplate under simply-supported boundary conditions, using the LPGM method based on the CSGT. These factors specifically include the dilatational strain gradient, deviatoric strain gradient, and couple-stress tensors, as well as the inhomogeneity index and the length-to-thickness ratio. Some conclusions from the parametric studies are summarized in Section 6.

Table 1.
A partial list of articles examining the mechanical behaviors of FG microscale plates and shells using non-CCM theories.
2. Material Properties
The constituent materials of FG microscale plates and shells cited in the literature can be categorized as exponentially graded (EG) material, power-law FG material, sigmoid FG material, FG carbon nanotube-reinforced composite (CNTRC) material, and FG graphene platelet-reinforced composite (GPLRC) material. The effective material properties of the FG microscale plates and shells mentioned above are presented below.
2.1. EG Microscale Plates and Shells
For an EG microscale plate and shell, its material properties are assumed to vary exponentially with the thickness coordinate and are expressed as follows:
where the superscript b denotes the microstructure’s bottom surface; z is the thickness coordinate, with values ranging from −h/2 to h/2, where h is the thickness of the microscale plate or shell being considered; is the inhomogeneity index for an EG material, which represents the degree of the material gradient along the thickness and can be determined by the values of the material properties at the top and bottom surfaces, i.e.,
where the superscript t represents the microstructure’s top surface; represents the material-property ratio between the top and bottom surfaces.
2.2. Power-Law FG Microscale Plates and Shells
For a typical FG microscale plate and shell, its material properties are assumed to follow the power-law distribution of the constituents’ volume fraction along the thickness direction and are given by
where the symbol denotes the volume fraction of the material at the top surface and is defined as ; is the inhomogeneity index for a power-law FG material. When = 0 and = , the FG microscale plate and shell reduce to a homogeneous microscale plate and shell with material properties and , respectively.
2.3. Sigmoid FG Microscale Plates and Shells
For a sigmoid FG microscale plate and shell, the material properties are assumed to follow the sigmoid function of the constituents’ volume fractions through the thickness direction and are expressed as follows:
where is the inhomogeneity index for a sigmoid FG material.
2.4. FG-CNTRC Microscale Plates and Shells
Because CNTs have exceptional chemical, physical, and electrical properties, they have been incorporated into the polymer matrix to create the FG-CNTRC material. Five different distribution functions of CNTs, varying in the thickness direction, are commonly discussed in the literature: uniformly distributed (UD), as well as FG A-, O-, V-, and X-type variations.
The through-thickness distributions of the volume fraction of CNTs, , for the five aforementioned types of FG-CNTRC microscale plates and shells are presented as follows:
where denotes the volume fraction index of CNTs and is expressed as
where represents the mass fraction of CNTs in the FG-CNTRC microstructure, and and are the mass densities of the CNTs and the polymer matrix, respectively.
The rule of mixtures [57] has been applied to estimate the effective material properties of an FG-CNTRC microscale plate and shell, which vary through the thickness and are presented as follows.
where , , and represent Young’s moduli and shear modulus of CNTs; and represent Young’s moduli and shear modulus of the polymer matrix; are the CNT efficiency parameters, which are determined by equalizing the material properties of the FG-CNTRC material obtained using the rule of mixtures and molecular dynamics simulation. Shen and Xiang [57] indicated that the value ranges of are related to the value of . For a polymer matrix, when , the values of are reported in the literature as 0.149, 0.934, and 0.934; these values are 0.150, 0.941, and 0.941 for the case of and 0.149, 1.381, and 1.381 for the case of . and are the volume fractions of CNTs and the polymer matrix, respectively, in which .
The Poisson’s ratio of the FG-CNTRC material is determined in the same way, as follows:
where and are Poisson’s ratios of the CNTs and the polymer matrix, respectively. is considered as a constant through the thickness coordinate of the FG-CNTRC material, and .
By utilizing Equations (7a–c) and (8), we can derive the through-thickness distributions of the effective properties of the FG-CNTRC microstructures.
2.5. FG-GPLRC Microscale Plates and Shells
An alternative nanomaterial, GPL, exhibits exceptional chemical, physical, and electrical properties. As a result, it has been incorporated into the polymer matrix to create the FG-GPLRC material. Consequently, five GPL distribution patterns, varying in the thickness direction, have been examined in the relevant literature, including UD and FG A-type, O-type, V-type, and X-type variations. Furthermore, the Halpin–Tsai model [58] is used to estimate the effective Young’s modulus, while the rule of mixtures [58] is applied to calculate the effective Poisson’s ratio and effective mass density. As a result, the following equations are used to describe these material properties.
According to the Halpin–Tsai model, the effective Young’s modulus of the FG-GPLRC microscale plate or shell can be approximated with
where and denote the longitudinal and transverse moduli, respectively, and they are expressed following Song et al. [59] as follows:
where denotes Young’s modulus of the GPLs; is the volume fraction of the GPLs; are the parameters characterizing the geometrical dimensions of the GPLs; are the parameters describing the geometrical dimensions of the GPLs and Young’s modulus ratio between the GPLs and the polymer matrix; and represent the length, width, and thickness of the GPLs, respectively. In a parametric study [59], the size ranges of the geometric parameters of the GPLs are given as , and . A specific set of geometric parameters, and was commonly used in the relevant literature.
Following the rule of mixtures, we express the effective Poisson’s ratio and the effective mass density of the GPLRC material as follows:
where the subscripts GPL and eff denote the GPLs and the GPLRC material, respectively; represents the volume fractions of the GPLs. In the numerical example, with a specific value of , the weight fractions of five relevant distribution patterns of the GPLs varying through the thickness of the microscale shell () are expressed as follows:
where the total volume fraction of the GPLs in each case, given in Equations (13a)–(13e), can be obtained using the relationship between and , which is
3. Consistent Couple Stress Theory
3.1. Strong Form
As mentioned above, Hadjesfandiari and Dargush [42,43] reformulated the original CST by deducing that the couple-stress tensor is skew-symmetric and subsequently proposed the CCST. Within the framework of the CCST, we employ Hamilton’s principle to derive an alternative version of the strong form of the CCST by selecting the displacements and transverse shear and normal stresses as the primary variables subjected to variation. The Euler–Lagrange equations and associated boundary conditions are presented below. By incorporating specific interpolation or approximation functions into the mixed strong form of the 3D CCST, a semi-analytical point collocation method can be developed for analyzing the mechanical behaviors of FG microscale plates and shells.
3.1.1. Fundamental Equations
We consider an elastic isotropic FG microplate, as illustrated in Figure 1. A Cartesian coordinate system, consisting of x, y, and z coordinates, is oriented such that the xy-plane serves as its central plane. The length, width, and thickness of the microplate are defined as Lx, Ly, and h, respectively.
Figure 1.
Schematic diagram of a simply supported FG elastic microplate.
In CCST, Hadjesfandiari and Dargush indicated that, generally speaking, due to the size-dependent effect, when an elastic microscale solid is subjected to applied external loads, the induced force-stress and couple-stress tensors should be asymmetric and skew-symmetric, respectively.
Hadjesfandiari and Dargush distinguished the force-stress and couple-stress tensors by using parentheses and brackets to enclose a pair of indices. Additionally, Hadjesfandiari and Dargush derived a relationship between the skew-symmetric part of the force-stress tensor and the couple-stress tensor, which was expressed as [42,43]
where denotes the skew-symmetric part of the force-stress tensor; and is the couple-stress tensor, such that , and the indices i, j, and k are followed in a right-hand screw rule order.
Based on Equation (14), Hadjesfandiari and Dargush derived a consistent differential operator for the force-stress tensor in classical elasticity theory and the total force-stress tensor in the CCST.
For a typical isotropic microplate, the linear constitutive equations are expressed as follows [42,43]:
where represent the symmetric part of the force-stress components, i.e., ; are the strain components; is the skew-symmetric part of the curvature tensor, such that ; cij represents the elastic coefficients, and and , where represent Young’s modulus, Poisson’s ratio, and shear modulus. For comparison purposes, it is noted that we revise the coupling couple stress–skew-symmetric part of the curvature coefficient from to , where represent the material length-scale parameters for the MCST and CCST, respectively, for which .
The strain tensor is defined as such that the relationship between the strain tensor and the displacement tensor is expressed as follows [42,43]:
where , .
The rotation tensor is defined as and , such that the relationship between the rotation tensor and displacement tensor is expressed as follows [42,43]:
The symmetric part of the curvature tensor is defined as and such that the relationship between the symmetric part of the curvature tensor and the displacement tensor is expressed as follows [42,43]:
As mentioned above, the skew-symmetric part of the curvature tensor is defined as , and , such that the relationship between the skew-symmetric part of the curvature tensor and the displacement tensor is expressed as follows [42,43]:
3.1.2. Hamilton’s Principle
Hamilton’s principle is utilized to derive the Euler–Lagrange equations for the microplate, along with its possible boundary conditions. The corresponding energy functional is expressed as follows:
where L denotes the Lagrange functional, which is defined as follows [60]:
where T, , and W represent the kinetic energy and Reissner’s strain energy of the microplate and the work resulting from the action of the bi-axial compression, and are expressed as follows:
where A represents the microplate domain on the xy-plane, and represents the microplate’s top surface at , upon which the transverse loads () are applied; and represent the portions of the edge boundary, where the surface traction force and moment components and the displacement and rotation components are prescribed, respectively; is the complementary energy density function, in which and ; are the applied resultant forces, and are the von Kármán second-order strains and are expressed as and .
In the mixed formulation, the elastic displacement and transverse force–stress components are taken as the primary variables subject to variation.
3.1.3. Euler–Lagrange Equations and Possible Boundary Conditions
Substituting Equations (23)–(25) into Equation (21), employing Hamilton’s principle (i.e., ), and conducting integration by parts using Green’s theorem, we can finally obtain the Euler–Lagrange equations of the 3D CCST from the resulting domain integral terms and the possible boundary conditions from the resulting boundary integral terms, which are expressed below.
The Euler–Lagrange equations are expressed as follows:
The surface boundary conditions are obtained as follows:
The possible boundary conditions are obtained as follows:
where and represent the components of the unit normal vectors on the edges.
The Euler–Lagrange Equations (26)–(31), along with the possible boundary condition (33a–f), constitute a well-defined mathematical problem and are capable of investigating the static bending, free vibration, and static buckling behaviors of microplates. By incorporating the differential reproducing kernel (DRK) interpolants [61] into the strong form of the CCST, Wu and Chang [62] and Wu and Chou [63] developed a semi-analytical meshless point collocation method to evaluate the static bending, static buckling, and free vibration behaviors of FG microplates. Utilizing the perturbation method, Wu and Lyu [64] presented an asymptotic theory for investigating the free vibration characteristics of FG microplates. On the other hand, based on the strong form of the 3D MCST and utilizing the state-space analytical method, Salehipour et al. [65,66] presented exact closed-form solutions for the free vibration analysis of FG microplates, as well as the static bending and free vibration analyses of porous FG cylindrical microscale shells. Based on the strong form of the MSGT, Salehipour and Shahsavar [67] provided the 3D solutions for the free vibration analysis of FG microplates. The aforementioned 3D analyses [62,63,64,65,66,67], within the framework of the 3D CCST, MCST, and MSGT, are rare and valuable because they provide a reference for assessing the accuracy of size-dependent 2D advanced and refined SDTs. They are listed in Table 2 in chronological order, from oldest to most recent.

Table 2.
A partial list of articles examining the mechanical behaviors of FG microscale plates and shells using the strong formulation of 3D non-CCM theories.
3.2. Weak Form
3.2.1. Hamilton’s Principle
A weak formulation of the 3D CCST can also be derived using the Hamilton principle, for which the displacements are taken as the primary variables subject to variation. Conducting the first-order variation of the kinetic energy, strain energy, and work performed, utilizing the kinematics assumptions provided in Equations (23)–(25), and performing integration by parts, we finally express the resulting equations as follows:
where the superscript T represents the transposition of the matrices or vectors,
where , and .
3.2.2. Galerkin Weak Formulation
Employing Hamilton’s principle and utilizing Equations (34)–(36), we can obtain the Galerkin weak formulation of 3D CCST, which is expressed as follows:
where and .
By incorporating specific kinematic models into Equation (38), Wu and Hsu [68] developed the Lagrangian C0 and Hermitian Cn FLM in 2022 for investigating the static and dynamic behaviors of FG microplates. They indicated that the differences between the formulations of the CCST and MCST are minor, and most of the different terms fall within the extensional stiffness matrix. After a comparison study, they found that the results of deformations and in-plane stresses obtained using the CCST- and MCST-based FLMs are nearly identical in the static bending analysis. In contrast, the transverse stress solutions differ from one another. In the free vibration analysis, it was found that the results of the lowest natural frequency for the microplate’s flexural modes, obtained using the CCST, are nearly the same as those obtained using the MCST. In contrast, those for the extensional modes using the CCST- and MCST-based FLMs are different from each other. Within the framework of the CSGT-based weak formulation, Wu and Chang [46] developed an LPGM method in 2025 for analyzing the 3D static and dynamic behaviors of an FG microplate under simply supported boundary conditions. In their article, Wu and Chang examined the impact of the dilatational strain gradient, deviatoric strain gradient, and couple-stress tensors on the static and dynamic behaviors of the microplate. The CCST-based FLM and CSGT-based LPGM methods mentioned above were shown to converge rapidly and closely agree with the relevant 3D solutions documented in the literature. The applications of the numerical methods discussed above to various mechanical behaviors of microscale plates and shells [46,68,69,70,71,72,73,74] are listed in Table 3 in chronological order from oldest to most recent.

Table 3.
The articles examining the mechanical behaviors of FG microscale plates and shells using the weak formulations of 3D non-CCM theories.
4. Various 2D Shear Deformation Theories
4.1. Unified Size-Dependent SDTs
In a unified 2D formulation, the displacements of a microplate, according to various microplate theories, can be written as follows:
where denote the microplate’s mid-plane displacements in the x, y, and z directions, respectively. are the mid-plane shear rotations of the microplate in the x–z and y–z planes, respectively. represents a specific function of z characterizing the through-thickness distribution of the transverse shear deformations. The displacement fields of various nanoplate theories can be obtained by assigning as follows:
Incorporating the specific kinematic model expressed in Equations (39)–(41) into the MCST and CCST, Lou et al. [75] and Wu and Hu [76] developed a unified size-dependent SDT for analyzing the mechanical behaviors of elastic isotropic microplates in 2015 and 2021, respectively. Various MCST- and CCST-based SDTs can be reproduced by utilizing their specific function f(z). Subsequently, several unified size-dependent SDTs [77,78,79,80,81] for analyzing microscale plates and shells made of advanced materials have also been presented and are listed in Table 4 in chronological order, from oldest to most recent.

Table 4.
Various unified shear deformation theories for analyzing the mechanical behaviors of microscale plates and shells.
4.2. Size-Dependent Advanced and Refined SDTs
The advanced and refined SDTs, based on the MCST, CCST, MSGT, and CSGT mentioned above, have also been employed to analyze the various mechanical behaviors of microscale plates and shells. The relevant articles are categorized by their use of analytical and numerical methods and are described below.
4.2.1. Variational Analytical Methods
Some variational analytical methods, including the Navier, Nevy, Ritz, and Galerkin methods, have been used to obtain results from various mechanical behavior analyses of EG, FG, sigmoid FG, FG-CNTRC, and FG-GPLRC microscale plates and shells, based on the advanced and refined SDTs mentioned above. These analyses include bending, free vibration, buckling, nonlinear bending, force vibration, nonlinear vibration, post-buckling, and dynamic instability behaviors. The effects of several primary factors on the mechanical behaviors of EG, FG, sigmoid FG, FG-CNTRC, and FG-GPLRC microscale plates and shells have also been examined and discussed. These factors include thickness-stretching, rotation, porosity, imperfection, thermal environment, hygrothermal environment, foundation, sandwich structure, piezoelectricity, and magnetostrictive effects. Partially relevant articles based on the MCST/CCST are listed in Table 5 and Table 6, respectively, for microscale plates [82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116] and shells [117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145], while those based on the MSGT/CSGT are listed in Table 7 and Table 8 for microscale plates [146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168] and shells [126,169,170,171,172,173,174,175,176,177,178,179,180,181]. Finally, within the MSGT framework, Ashoori and Mahmoodi [182] derived the Euler–Lagrange equations and possible boundary conditions of an FG microshell in general curvilinear coordinates. Their results were obtained using a tensor notation approach, which is a general and applicable method for a wide range of problems.

Table 5.
A partial list of references on various mechanical behavior analyses of FG microplates using advanced and refined shear deformation theories based on CCST and MCST, implemented using variational analytical methods.

Table 6.
A partial list of references on various mechanical behavior analyses of FG microshells using advanced and refined shear deformation theories based on CCST and MCST, implemented using variational analytical methods.

Table 7.
A partial list of references on various mechanical behavior analyses of FG microplates using advanced and refined shear deformation theories based on CSGT and MSGT, implemented using variational analytical methods.

Table 8.
A partial list of references on various mechanical behavior analyses of FG microshells using advanced and refined shear deformation theories based on CSGT and MSGT, implemented using variational analytical methods.
4.2.2. Numerical Methods
The articles referenced in Section 4.2.1 analyze the mechanical behaviors of microscale plates and shells using various variational analytical methods. These methods are limited to examining microstructures under simply-supported boundary conditions and with regular boundary edges, such as rectangular plates, circular annular plates, cylindrical shells, doubly curved shells, and conical shells. To expand the application range of the CCST/MCST and CSGT/MSGT, several numerical methods have been developed for studying the mechanical behaviors of microscale plates and shells, including the differential quadrature (DQ) method, the finite element method (FEM), and the meshless method, which are described below.
DQ Method
In the DQ method, each primary variable and its derivatives are expressed as a combination of the nodal function value and an undetermined coefficient, as follows:
where np represents the total number of the sampling nodes; and and represent the relevant undetermined coefficients for the function F(x) and its r-order derivatives, respectively.
The undetermined coefficients and , given in Equations (48) and (49), can be obtained using a set of Lagrange polynomials and are expressed as follows:
The derivations for and their applications can be found in Du et al. [183], Bert and Malik [184], and Wu and Lee [185]. Partially relevant articles [141,186,187,188,189,190,191,192,193,194,195,196,197] based on the MCST/CCST and MSGT/CSGT, covering various mechanical behaviors of microscale plates and shells using the DQ method, are listed in Table 9.

Table 9.
A partial list of references on various mechanical behavior analyses of FG microscale plates and shells using advanced and refined shear deformation theories based on CCST/MCST and CSGT/MSGT, implemented using the differential quadrature method.
Finite Element Method
When utilizing an FEM, the physical domain of a structure to be analyzed must be divided into multiple elements, where each primary variable is expressed as a combination of the nodal function value and an undetermined coefficient, as follows:
where (j = 1, 2, …, nd) represent the shape function for the reference node, which is determined using the Lagrange polynomials as the basis functions and satisfies the nodal interpolation properties; x and represent the global and natural coordinates, respectively, and the relationship between them is expressed as for an isoparametric FEM; and nd is the total number of nodes of each element.
The rth-order derivative of each variable is expressed as follows:
where np represents the total number of sampling nodes; and and represent the relevant undetermined coefficients for the function and its r-order derivatives, respectively.
Partially relevant articles [177,184,198,199,200,201,202,203,204,205,206,207,208,209,210,211,212,213,214] based on the MCST/CCST and MSGT/CSGT, covering various mechanical behaviors of microscale plates and shells using the FEM, are listed in Table 10.

Table 10.
A partial list of references on various mechanical behavior analyses of FG microscale plates and shells using advanced and refined shear deformation theories based on CCST/MCST and CSGT/MSGT, implemented using the FEM.
Meshless Method
Unlike the FEM, a pre-divided mesh is necessary before analysis. The meshless method randomly selects specific nodes within the physical domain, and the approximation function of each variable at the reference node is determined using several neighboring nodes and the least squares method, resulting in a more efficient and less time-consuming process. In the meshless method, each variable is expressed as follows:
where represents the approximation or interpolation function for the reference node, depending on whether the Kronecker delta properties are satisfied or not. Additionally, some basis function sets have been used to determine the approximation function, including the reproducing kernel approximation/interpolation function, the multi-quadric basis function, the moving Kriging interpolation function, and the B-spline basis function.
Partially relevant articles [115,215,216,217,218,219,220,221,222,223,224,225] based on the MCST/CCST and MSGT/CSGT for various mechanical behaviors of microscale plates and shells using the meshless method are listed in Table 11.

Table 11.
A partial list of references on various mechanical behavior analyses of FG microscale plates and shells using advanced and refined shear deformation theories based on CCST/MCST and CSGT/MSGT, implemented using the meshless method.
5. Illustrative Examples
5.1. Static Bending Problems
5.1.1. Comparison Studies
Based on the CCST/MCST, we analyze the static bending problem of an FG microplate under simply supported boundary conditions subjected to sinusoidally distributed loads on its top surface, which is expressed as . The constituent materials of the microplate are aluminum (Al), a metal, and alumina (Al2O3), a ceramic. Their material properties are assumed to follow the power-law distributions of the volume fractions of each component through the microplate’s thickness. The effective material properties are expressed in Equation (3), and the ceramic and the metal materials’ volume fractions are provided as follows:
where the subscripts met and cer represent the metal and ceramic materials, respectively. The ceramic and metal materials are fully enriched at the top and bottom surfaces of the microplate, respectively.
The material properties of the metal and ceramic materials are provided as follows [102]:
For the metal material,
For the ceramic material,
For comparison, a set of dimensionless stresses and deflections is defined as follows:
Table 12 compares the results of the microplate’s central deflection and in-plane stress parameters obtained using the 3D CCST-based FEM [68], the Hermitian C2 DRK meshless method [63], and various 2D MCST-/CCST-based plate theories [76,102], where Lx/h = 5, 10, and 20; . As shown in Table 12, the results from the 3D CCST-based FLM [69] and meshless method [62] are nearly identical. Similarly, the results from the CCST/MCST-based advanced and refined SDTs are the same. For the case of the relative errors between the solutions of the microplate’s central deflection obtained using the 3D FLM and the CCST-based RSDT, they are 0.14% and 1.03%, respectively, when the l/h ratio is 0 and 0.8, with Lx/h = 20. However, these two relative errors increase to 0.65% and 5.3% for the moderately thick microplate (Lx/h = 10) and to 2.26% and 12.1% for the thick microplate (Lx/h = 5). This indicates that the impact of the material length-scale parameter on the thick microplate’s deflection is more significant than that on the thin microplate’s deflection due to the effects of 3D couple stress, transverse shear deformation, and transverse normal deformation. Additionally, Wu and Hsu [68] noted that the differences between the weak formulations of the 3D CCST and MCST are very minor. Since all the different terms fall within the extensional stiffness matrix, the displacements and in-plane stresses obtained from the CCST and MCST are nearly identical.

Table 12.
Comparisons of the deflection and stress results induced in a simply-supported FG microplate subjected to the sinusoidally distributed loads obtained using various MCST-/CCST-based microplate theories.
5.1.2. Parametric Studies
Based on the CSGT, we perform a parametric study to examine how certain primary factors affect the microplate’s central deflection, including the impact of material length-scale parameters, the inhomogeneity index, and the length-to-thickness ratio. Table 13 and Table 14 compare the results of the microplate’s central deflection and stresses obtained with the CSGT-based LPGM method [46]. The relevant material and geometric parameters are provided as li/h = 0 and 0.5 (i = 0, 1, and 2); Lx/h = 10 in Table 13, as well as li/h = 0 and 0.5 (i = 0, 1, and 2); Lx/h = 5, 10, and 20 in Table 14.

Table 13.
Comparison of results for the deflections and stresses induced in an FG square microplate with fully simple supports, obtained using the CSGT-based LPGM method, where Lx/h = 10 [46].

Table 14.
Comparison of results for the deflections and stresses induced in an FG square microplate with fully simple supports, obtained using the CSGT-based LPGM method, where .
As shown in Table 13, any material length-scale parameter increases the overall stiffness of the microplate, leading to a decrease in the microplate’s central deflections and in-plane stresses. For a moderately thick microplate with an Lx/h value of 10 and , the microplate’s central deflections decrease by 19.5%, 41.7%, and 55.4% of their original values for the cases of and and and and respectively. The results show that increasing the inhomogeneity index decreases the microplate’s overall stiffness because the volume fraction of the softer metal material rises, leading to greater deflections and stresses.
As shown in Table 14, for a microplate with the value of being three and Lx/h = 5, the microplate’s central deflections decrease by 16.0%, 31.6%, and 54.7% of their original values for the cases of and respectively. When we convert the results of the dimensionless variables to those of the dimensional variables, it is shown that an increase in the Lx/h ratio leads to a decrease in the microplate’s overall stiffness, as the microplate becomes thinner, which increases its deflections and stresses.
Figure 2a,b show how the microplate’s central deflection varies with different l/h ratios for four cases: (a) , considering only the dilatational strain gradient effect; (b) , considering only the deviatoric strain gradient effect; (c) , considering only the couple stress effect; and (d) , considering the dilatational strain gradient, deviatoric strain gradient, and couple stress effects. The relevant material and geometric parameters are provided as and for Figure 2a and for Figure 2b. As shown in Figure 2a,b again, the higher the value, the softer the microplate’s overall stiffness, leading to greater central deflection of the microplate.
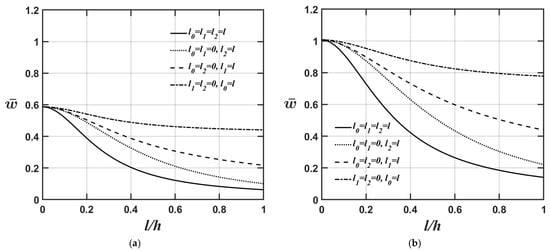
Figure 2.
Variations in the microplate’s central deflection with changing the value of the l/h ratio for different values of the material length-scale parameters, where the relevant geometric and material parameters are and (a) , and (b) .
Figure 3a,b show the variations in the microplate’s central deflection with respect to changes in the l/h ratio for four different values of the material length-scale parameters. The relevant material and geometric parameters are expressed as , and in Figure 3a, and in Figure 3b. As shown in Figure 3a,b again, the higher the value, the softer the microplate’s overall stiffness, leading to greater central deflection of the microplate when we convert the dimensionless microplate’s central deflection to the dimensional microplate’s central deflection. The results shown in Figure 2a,b and Figure 3a,b also demonstrate that the significance of different material length-scale parameters on the microplate’s central deflection is in the following order: couple stress effect > deviatoric strain gradient effect > dilatational strain gradient effect. This is because most of the strain energy contributions from the couple stress effects are associated with the flexural stiffness matrix; however, the contributions from the deviatoric strain gradient effects are associated with the extensional stiffness matrix. Additionally, the strain energy contributions from the dilatational strain gradient effects are smaller, and most of them are associated with the extensional stiffness matrix. This results in the couple stress effects being dominant in the structural behaviors related to the out-of-plane motion and the deviatoric strain gradient effects being dominant in the structural behavior associated with the in-plane motion.
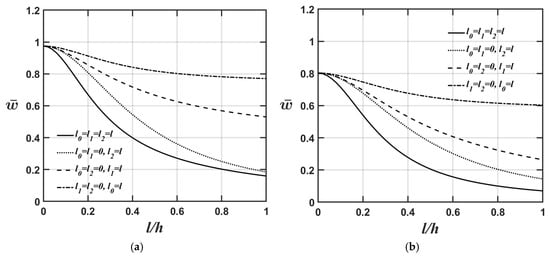
Figure 3.
Variations in the microplate’s central deflection with respect to changes in the l/h ratio for different values of the material length-scale parameters, where the relevant geometric and material parameters are , and (a) (b) .
5.2. Free Vibration Problems
5.2.1. Comparison Studies
Based on the CCST/MCST, this section examines the free vibration problem of a simply-supported EG microplate, where the material properties are defined as an exponential function through the thickness, as follows [65]:
where E, , and represent the Young’s modulus, mass density, and Poisson’s ratio; represents the inhomogeneity index for the EG microplate, and and .
For comparison, a non-dimensional frequency parameter is provided as follows [65]:
Table 15 compares the lowest natural frequency results for the microplate’s flexural modes obtained using the 3D CCST-based Hermitian C1 DRK meshless method [63], the 3D CCST-based FLM [68], the 3D MCST-based state space method [65], and the CCST-based RSDPT and SSDPT [76]. The relevant material and geometric parameters are expressed as Lx = Ly; Lx/h = 5 and 10; .

Table 15.
Comparisons of the results for the lowest frequency parameter solutions of the flexural modes (i.e., the out-of-plane modes) for a simply supported, EG microplate, obtained using various CCST/MCST-based microplate theories.
As shown in Table 15, the results obtained using the 3D CCST-based Hermitian C1 DRK meshless method [63], the FLM [68], and the state space analytical method [65] are nearly identical. Similarly, the results obtained using the CCST-based RSDT and SSDT are similar. For a moderately thick microplate with = 10, the relative errors between the solutions of the microplate’s lowest natural frequency obtained using the 3D MCST and the CCST-based RSDT are 0.05% and 2.9% for the l/h ratio values of 0 and 1.0, respectively, where . However, these two relative errors increase to 0.2% and 9.4% for the thick microplate with Lx/h = 5. This shows that the impact of the material length-scale parameter on the thick microplate’s lowest natural frequency is more significant than that on the thin microplate’s lowest natural frequency, due to the 3D couple stress effect and the transverse shear and normal deformation effects. Additionally, Wu and Hsu [68] noted that the differences between the weak formulations of the 3D CCST and 3D MCST are very minor. The different terms all fall within the extensional stiffness matrix, leading to nearly identical solutions for the lowest natural frequency of the flexural mode obtained using the CCST and MCST. The only difference occurs in the solutions for the lowest natural frequency of the microplate’s extensional mode from the CCST-based and MCST-based theories.
5.2.2. Parametric Studies
Based on the CSGT, we conduct a parametric study examining the impact of specific primary factors on the lowest natural frequency of the FG microplate, including the effects of material length-scale parameters, the inhomogeneity index, and the length-to-thickness ratio. The constituent materials of the FG microplate are the same as those in Section 5.1; the volume fractions and material properties of these materials are given in Equations (55a,b), (56) and (57), respectively; and the effective material properties of the microplate are described in Equation (3). A dimensionless natural frequency is defined as
Table 16 and Table 17 compare the results of the microplate’s lowest natural frequency obtained using the CSGT-based LPGM method [46], with and (1, 2). The relevant material and geometric parameters are expressed as li/h = 0 and 0.5 (i = 0, 1, and 2); and Lx/h = 10, as shown in Table 16, as well as li/h = 0 and 0.5 (i = 0, 1, and 2); and Lx/h = 5, 10, and 20, as shown in Table 17. As shown in Table 16, any material length-scale parameters cause the microplate to become stiffer, increasing the lowest natural frequency of its flexural and extensional modes. For a moderately thick microplate with the value Lx/h equal to 10 and , the lowest natural frequency of the microplate’s flexural mode increases by 11.5%, 31.0%, and 49.8% of its original value for the cases of and respectively. The relative errors for the lowest natural frequency of the microplate’s extensional mode are 0.2%, 1.3%, and 0%, respectively, for the cases of and . This indicates that the material length-scale parameter significantly influences the lowest natural frequency of the microplate’s flexural mode, more than its extensional mode. The results also show that increasing the inhomogeneity index decreases the microplate’s overall stiffness because the volume fraction of the softer metal material increases, which in turn reduces the microplate’s lowest natural frequency.

Table 16.
The results for the natural frequency of an FG square microplate with fully simple supports obtained using the CSGT-based LPGM method, where Lx/h = 10.

Table 17.
The results for the natural frequency of an FG square microplate with fully simple supports obtained using the CSGT-based LPGM method, where .
As shown in Table 17, when the results of dimensionless natural frequency are converted to those of the dimensional natural frequency, the results indicate that an increase in the Lx/h ratio causes a decrease in the microplate’s overall stiffness because the microplate becomes thinner, which lowers the microplate’s lowest natural frequency.
Figure 4a,b and Figure 5a,b show how the lowest natural frequency of the microplate’s flexural and extensional modes varies with respect to changes in the l/h ratio for four different values of the material length-scale parameters. The relevant material and geometric parameters are expressed as ; ; and , as shown in Figure 4a and Figure 5a, and , as shown in Figure 4b and Figure 5b.
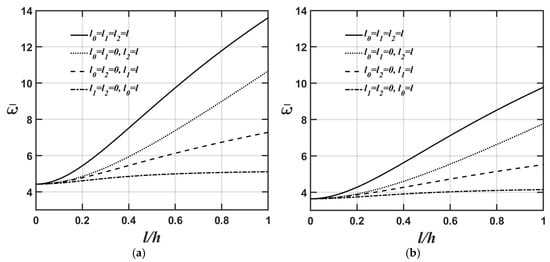
Figure 4.
Variations in the lowest natural frequency of the microplate’s flexural mode with respect to changes in the l/h ratio for different values of the material length-scale parameters, where the relevant geometric and material parameters are and (a) , (b) .
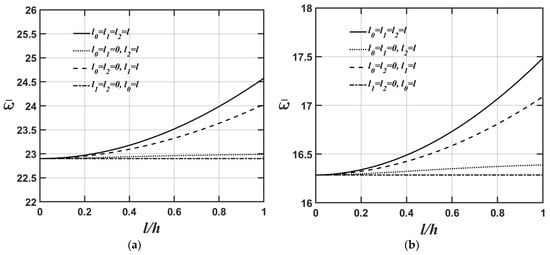
Figure 5.
Variations in the lowest natural frequency of the microplate’s extensional mode with respect to changes in the l/h ratio for different values of the material length-scale parameters, where the relevant geometric and material parameters are and (a) , (b) .
As shown in Figure 4a,b and Figure 5a,b, the higher the value, the softer the microplate’s overall stiffness, leading to a lower value of the microplate’s lowest natural frequency.
Figure 6a,b and Figure 7a,b display the variations in the lowest natural frequency of the microplate’s flexural and extensional modes, respectively, as the value of the l/h ratio changes for four different material length-scale parameters. The relevant material and geometric parameters are expressed as ; ; and as shown in Figure 6a and Figure 7a, and as shown in Figure 6b and Figure 7b.
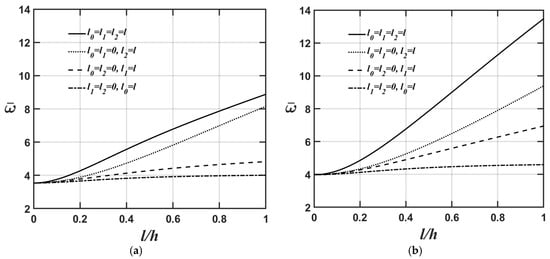
Figure 6.
Variations in the lowest natural frequency of the microplate’s flexural mode with respect to changes in the l/h ratio for different values of the material length-scale parameters, where the relevant geometric and material parameters are , and (a) (b) .
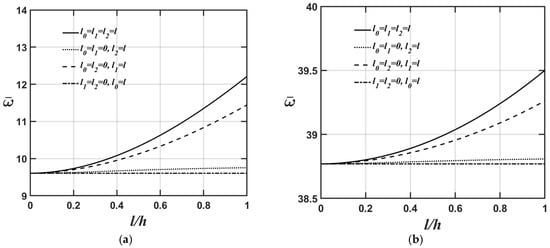
Figure 7.
Variations in the lowest natural frequency of the microplate’s extensional mode with respect to changes in the l/h ratio for different values of the material length-scale parameters, where the relevant geometric and material parameters are , and (a) (b) .
As shown in Figure 6a,b and Figure 7a,b, the higher the value, the softer the microplate’s overall stiffness, leading to a lower value of the microplate’s lowest natural frequency when converting the dimensionless lowest natural frequency to the dimensional lowest natural frequency. Furthermore, the results shown in Figure 4a, Figure 5a, Figure 6a and Figure 7a and Figure 4b, Figure 5b, Figure 6b and Figure 7b demonstrate that the impact of material length-scale parameters on the lowest natural frequency of the microplate’s flexural mode is considerably greater than in the microplate’s extensional mode. Additionally, the importance of different material length-scale parameters on the lowest natural frequency of the microplate’s flexural mode is ranked as follows: couple stress effect > deviatoric strain gradient effect > dilatational strain gradient effect; however, for the lowest natural frequency of the microplate’s extensional mode, the order is as follows: deviatoric effect > couple stress effect > dilatational strain gradient effect. As mentioned above, most of the strain energy contributions from the couple stress effects fall within the flexural stiffness matrix; however, those arising from the deviatoric strain gradient effects fall within the extensional stiffness matrix. This results in the couple stress effects being dominant in the lowest natural frequency of the microplate’s flexural mode and the deviatoric strain gradient effects being dominant in the lowest natural frequency of the microplate’s extensional mode.
Figure 8a,b show variations in the lowest natural frequency of the microplate’s flexural mode with respect to changes in its thickness based on the CCST and CSGT, respectively. The relevant geometric and material parameters are expressed as and . As shown in Figure 8a,b, the impact of the material length-scale parameter l2 on the lowest natural frequency of the microplate’s flexural mode becomes saturated when its thickness is less than ; conversely, the effects of the dilatational and deviatoric strain gradients consistently influence the microplate’s lowest natural frequency of its flexural mode.
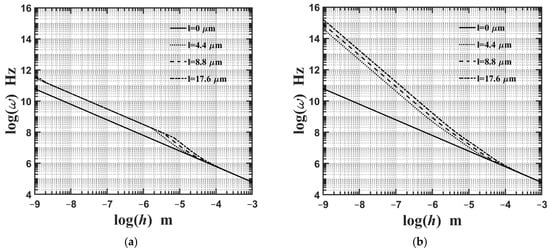
Figure 8.
Variations in the lowest natural frequency of the microplate’s flexural mode with respect to changes in its thickness for different values of the material length-scale parameters, where the relevant geometric and material parameters are and for (a) CCST and (b) CSGT.
5.3. Supplementary Notes
Conducting the comparison and parametric studies, we found that the values of the material length-scale parameters significantly influence the induced deformation results and the lowest natural frequency of the FG microplate. Although the theoretical and numerical methods for analyzing the microplate are well-established, estimating various material length-scale parameters remains a research area with significant potential for development. Additionally, to the best of the authors’ knowledge, the applicable ranges of the structural scale for the CCST/MCST and CSGT/MSGT have not been discussed and recommended. Therefore, a comparison between the results obtained from the experimental test and the theoretical and numerical methods provides another potential research area to be explored.
6. Conclusions
This work provides a comprehensive review of studies examining various mechanical behaviors of FG microscale plates and shells based on the MCST/CCST and MSGT/CSGT. We develop and present the strong and weak forms of the 3D CCST and perform a comparative study on the static and dynamic behaviors of a simply supported FG microplate using a range of 3D CCST/MCST-based exact and numerical methods and 2D CCST/MCST-based SDTs. Additionally, based on the 3D CSGT, we conduct a parametric study to investigate how different primary factors affect the deflection, stress, and lowest natural frequency of the FG microplate. Several conclusions from the parametric analysis are summarized as follows:
- The material length-scale parameters stiffen the FG microplate, resulting in less deflection and an increase in the lowest natural frequency.
- The higher the value of the inhomogeneity index, the softer the overall stiffness of the FG microplate, leading to a higher value of the microplate’s central deflection and a reduction in its lowest natural frequency.
- The higher the length-to-thickness ratio, the softer the overall stiffness of the FG microplate, leading to a greater value of the microplate’s central deflection and a reduction in its lowest natural frequency.
- The importance of the impact of various material length-scale parameters on the FG microplate’s central deflection and the lowest natural frequency of the microplate’s flexural mode is ordered, from greatest to least, as follows: the couple stress effect, the deviatoric strain gradient effect, and finally the dilatational strain gradient effect.
- The importance of the impact of various material length-scale parameters on the lowest natural frequency of the FG microplate’s extensional mode is arranged, in descending order, as follows: deviatoric strain gradient effect > couple stress effect > dilatational strain gradient effect.
- The effect of the material length-scale parameters on the lowest natural frequency of the FG microplate’s flexural mode is significantly greater than in its extensional mode.
- The impact of the material length-scale parameter l2 on the lowest natural frequency of the microplate’s flexural mode becomes saturated when its thickness is less than ; conversely, the effects of the dilatational and deviatoric strain gradients consistently influence the microplate’s lowest natural frequency in its flexural mode.
Since 3D results of deformations, stresses, and natural frequency in an FG microplate are rarely published, the findings in this article can serve as a reference for evaluating the accuracy of the 2D size-dependent advanced and refined SDTs and their relevant numerical methods. Furthermore, the classification of research work provided in the tables will help future scholars gain an overall understanding of related research topics.
Author Contributions
Conceptualization, C.-P.W.; methodology, C.-P.W.; software, T.-Y.C.; validation, C.-P.W. and T.-Y.C.; investigation, C.-P.W. and T.-Y.C.; resources, C.-P.W.; data curation, T.-Y.C.; writing—original draft preparation, C.-P.W.; writing—review and editing, C.-P.W.; supervision, C.-P.W.; project administration, C.-P.W.; funding acquisition, C.-P.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Science and Technology Council of Taiwan, grant number NSTC 114-2221-E-006-010-MY3.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations/Notations
The following abbreviations and notations are used in this manuscript:
| Abbreviations | |
| CCM | Classical continuum mechanics |
| CCST | Consistent couple stress theory |
| CNT | Carbon nanotube |
| CNTRC | Carbon nanotubes-reinforced composite |
| CPT | Classical plate theory |
| CSGT | Consistent strain gradient theory |
| CST | Couple stress theory |
| DQ | Differential quadrature |
| DRK | Differential reproducing kernel |
| EG | Exponentially graded |
| ENET | Eringen’s nonlocal elasticity theory |
| ESDT | Exponential shear deformation theory |
| FEM | Finite element method |
| FG | Functionally graded |
| FLM | Finite layer method |
| FOSDT | First-order shear deformation theory |
| GPL | Graphene platelet |
| GPLRC | Graphene platelet-reinforced composite |
| HOSDT | Higher-order shear deformation theory |
| HSDT | Hyperbolic shear deformation theory |
| LPGM | Local Petrov–Galerkin meshless |
| MCST | Modified couple stress theory |
| MSGT | Modified strain gradient theory |
| RSDT | Refined shear deformation theory |
| SDT | Shear deformation theory |
| SGT | Strain gradient theory |
| SSDT | Sinusoidal shear deformation theory |
| SWCNT | Single-walled carbon nanotubes |
| TOSDT | Third-order shear deformation theory |
| TSNDT | Transverse shear and normal deformation theory |
| UD | Uniformly distributed |
| 2D | Two-dimensional |
| 3D | Three-dimensional |
| Notations | |
| The relevant undetermined coefficients for unknowns and its r-th derivatives for the DQ method | |
| The complementary strain energy | |
| The relevant matrices in the Galerkin weak formulation | |
| The elastic coefficients | |
| The effective Young’s modulus of a typical material | |
| Young’s modulus in the l-direction of a typical material k | |
| The longitudinal modulus of a typical material | |
| The transverse modulus of a typical material | |
| f(z) | A specific function of z characterizing the through-thickness direction of the transverse shear deformations |
| Shear modulus related to the ij-plane of a typical material k | |
| h | The thickness of a microplate |
| The material length-scale parameters for the MCST and CCST | |
| The material length-scale parameters related to the effects of the dilatational and deviatoric strain gradients and couple stress for the CSGT and MSGT | |
| L | The Lagrange functional |
| The length of a microplate | |
| The width of a microplate | |
| A general material property on the bottom surface of a microplate | |
| A general material property on the top surface of a microplate | |
| The components of the unit normal vectors of the edges of a microplate | |
| The shape functions for the reference point l for the finite element method | |
| The applied resultant forces | |
| The magnitude of the applied load | |
| The relevant stiffness matrices | |
| T | The kinetic energy |
| u | The mid-plane displacement in the x-direction of a microplate |
| The displacement tensor | |
| v | The mid-plane displacement in the y-direction of a microplate |
| w | The mid-plane displacement in the z-direction of a microplate |
| The dimensionless deflection of a microplate | |
| W | The work performed |
| The weight fraction of a typical material k | |
| The weight index of a typical material k | |
| The volume fraction of a typical material k | |
| The volume fraction index of a typical material k | |
| The variational operator | |
| The strain tensor | |
| The von Kármán second-order strains | |
| The parameters describing the geometric dimensions of GPLs | |
| The inhomogeneity index for an EG microplate | |
| The inhomogeneity index for the power-law FG microplate | |
| The inhomogeneity index for the sigmoid FG microplate | |
| The material-property ratio between the top and bottom surfaces of a microplate | |
| The skew-symmetric part of the curvature tensor | |
| The CNT efficiency parameters | |
| The couple-stress tensor | |
| The parameters characterizing the geometrical dimensions of GPLs | |
| Reissner’s strain energy | |
| The mass density of a typical material k | |
| The symmetric part of the force-stress tensor | |
| The skew-symmetric part of the force-stress tensor | |
| The dimensionless stress tensor | |
| Poisson’s ratio for transverse strain in the j-direction when stressed in the i-direction | |
| The interpolation function of a reference node j for the meshless method | |
| The mid-plane shear rotation of a microplate | |
| The symmetric part of the curvature tensor | |
| Natural frequency and its dimensionless form | |
| The rotation tensor | |
References
- Koizumi, M. Recent progress of functionally graded materials in Japan. In Proceedings of the 16th Annual Conference on Composites and Advanced Ceramic Materials: Ceramic Engineering and Science Proceedings; Jhon, B.W., Jr., Ed.; The American Ceramic Society: Westerville, OH, USA, 1992; Volume 13, pp. 333–347. [Google Scholar]
- Koizumi, M. FGM activities in Japan. Compos. Part B 1997, 28, 1–4. [Google Scholar] [CrossRef]
- Van Doan, D.; Van Minh, P.; Van Ke, T.; Nhung, N.T.C.; Van Thom, D. An overview of functionally graded materials: From civil applications to defense and aerospace industries. J. Vib. Eng. Technol. 2025, 13, 68. [Google Scholar] [CrossRef]
- Shen, H.S. Functionally Graded Materials: Nonlinear Analysis of Plates and Shells; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Nikbakht, S.; Kamarian, S.; Shakeri, M. A review on optimization of composite structures Part II: Functionally graded materials. Compos. Struct. 2019, 214, 83–102. [Google Scholar] [CrossRef]
- Ding, S.; Wu, C.P. Optimization of material composition to minimize the thermal stresses induced in FGM plates with temperature-dependent material properties. Int. J. Mech. Mater. Des. 2018, 14, 527–549. [Google Scholar] [CrossRef]
- Wu, C.P.; Li, K.M. Multi-objective optimization of functionally graded beams using a genetic algorithm with non-dominated sorting. J. Compos. Sci. 2021, 5, 92. [Google Scholar] [CrossRef]
- Zhang, N.; Khan, T.; Guo, H.; Shi, S.; Zhong, W.; Zhang, W. Functionally graded materials: An overview of stability, buckling, and free vibration analysis. Adv. Mater. Sci. Eng. 2019, 2019, 1354150. [Google Scholar] [CrossRef]
- Ghatage, P.S.; Kar, V.R.; Sudhagar, P.E. On the numerical modelling and analysis of multi-directional functionally graded composite structures: A review. Compos. Struct. 2020, 236, 111837. [Google Scholar] [CrossRef]
- Jha, D.K.; Kant, T.; Singh, R.K. A critical review of recent research on functionally graded plates. Compos. Struct. 2013, 96, 833–849. [Google Scholar] [CrossRef]
- Punera, D.; Kant, T. A critical review of stress and vibration analyses of functionally graded shell structures. Compos. Struct. 2019, 210, 787–809. [Google Scholar] [CrossRef]
- Liew, K.M.; Zhao, X.; Ferreira, A.J.M. A review of meshless methods for laminated and functionally graded plates and shells. Compos. Struct. 2011, 93, 2031–2041. [Google Scholar] [CrossRef]
- Thai, H.T.; Kim, S.E. A review of theories for the modeling and analysis of functionally graded plates and shells. Compos. Struct. 2015, 128, 70–86. [Google Scholar] [CrossRef]
- Chen, D.; Gao, K.; Zhang, L. Functionally graded porous structures: Analyses, performances, and applications—A review. Thin-Walled Struct. 2023, 191, 111046. [Google Scholar] [CrossRef]
- Wu, C.P.; Liu, Y.C. A review of semi-analytical numerical methods for laminated composite and multilayered functionally graded elastic/piezoelectric plates and shells. Compos. Struct. 2016, 147, 1–15. [Google Scholar] [CrossRef]
- Wu, C.P.; Chiu, K.H.; Wang, Y.M. A review on the three-dimensional analytical approaches of multilayered and functionally graded piezoelectric plates and shells. CMC—Comput. Mater. Contin. 2008, 8, 93–132. [Google Scholar]
- Li, Z.; He, Y.; Lei, J.; Han, S.; Guo, S.; Liu, D. Experimental investigation on size-dependent higher-mode vibration of cantilever microbeams. Microsyst. Technol. 2019, 25, 3005–3015. [Google Scholar] [CrossRef]
- Lei, J.; He, Y.; Guo, S.; Li, Z.; Liu, D. Size-dependent vibration of nickel cantilever microbeams: Experment and gradient elasticity. Aip Adv. 2016, 6, 105202. [Google Scholar] [CrossRef]
- Ince, R.; Yalcin, E.; Arslan, A. Size-dependent response of dowel action in R.C. members. Eng. Struct. 2007, 29, 955–961. [Google Scholar] [CrossRef]
- Chang, T.H.; Cheng, G.; Li, C.; Zhu, Y. On the size-dependent elasticity of penta-twinned silver nanowires. Extrem. Mech. Lett. 2016, 8, 177–183. [Google Scholar] [CrossRef]
- Pharr, G.M.; Herbert, E.G.; Gao, Y. The indentation size effect: A critical examination of experimental observations and mechanistic interpretations. Annu. Rev. Mater. 2010, 40, 271–292. [Google Scholar] [CrossRef]
- Fleck, N.A.; Muller, G.M.; Ashby, M.F.; Hutchinson, J.W. Strain gradient plasticity: Theory and experiment. Acta Metall. Mater. 1994, 42, 475–487. [Google Scholar] [CrossRef]
- Lam, D.C.C.; Yang, F.; Chong, A.C.M.; Wang, J.; Tong, P. Experiments and theory in strain gradient elasticity. J. Mech. Phys. Solids 2003, 51, 1477–1508. [Google Scholar] [CrossRef]
- McFarland, A.W.; Colton, J.S. Role of material microstructure in plate stiffness with relevance to microcantilever sensors. J. Micromech. Microeng. 2005, 15, 1060–1067. [Google Scholar] [CrossRef]
- Eringen, A.C. Theory of micropolar elasticity. In Microcontinuum Field Theories; Eringen, A.C., Ed.; Springer: New York, NY, USA, 1999; pp. 101–248. [Google Scholar]
- Fares, M.E.; Salem, M.G.; Atta, D.; Elmarghany, M.K. Mixed variational principle for micropolar elasticity and an accurate two-dimensional plate model. Eur. J. Mech. A/Solids 2023, 99, 104870. [Google Scholar] [CrossRef]
- Athanasiadis, A.E.F.; Budzik, M.K.; Fernando, D.; Dias, M.A. On micropolar elastic foundations. Eur. J. Mech. A/Solids 2024, 105, 105277. [Google Scholar] [CrossRef]
- Eringen, A.C.; Edelen, D.G.B. On nonlocal elasticity. Int. J. Eng. Sci. 1972, 10, 233–248. [Google Scholar] [CrossRef]
- Eringen, A.C. Theory of nonlocal thermoelasticity. Int. J. Eng. Sci. 1974, 12, 1063–1077. [Google Scholar] [CrossRef]
- Eringen, A.C. Theories of nonlocal plasticity. Int. J. Eng. Sci. 1983, 21, 741–751. [Google Scholar] [CrossRef]
- Shaat, M.; Ghavanloo, E.; Fazelzadeh, S.A. Review on nonlocal continuum mechanics: Physics, material applicability, and mathematics. Mech. Mater. 2020, 150, 103587. [Google Scholar] [CrossRef]
- Mindlin, R.D.; Eshel, N.N. On first strain-gradient theories in linear elasticity. Int. J. Solids Struct. 1968, 4, 109–124. [Google Scholar] [CrossRef]
- Polyzos, D.; Fotiadis, D.I. Derivation of Mindlin’s first and second strain gradient elastic theory via simple lattice and continuum models. Int. J. Solids Struct. 2012, 49, 470–480. [Google Scholar] [CrossRef]
- Zhao, J.; Pedroso, D. Strain gradient theory in orthogonal curvilinear coordinates. Int. J. Solids Struct. 2008, 45, 3507–3520. [Google Scholar] [CrossRef]
- Ferrari, M.; Granik, V.T.; Imam, A. Introduction to doublet mechanics. In Advanced in Doublet Mechanics: 45; Ferrari, M., Granik, V.T., Imam, A., Nadeau, J.C., Eds.; Lecture Notes in Physics Monographs; Springer: Berlin/Heidelberg, Germany, 1997. [Google Scholar]
- Mon, K.; Ferrari, M. Doublet thermomechanics. In Advanced in Doublet Mechanics: 45; Ferrari, M., Granik, V.T., Imam, A., Nadeau, J.C., Eds.; Lecture Notes in Physics Monographs; Springer: Berlin/Heidelberg, Germany, 1997. [Google Scholar]
- Granik, V.T. Comparison with other theories. In Advanced in Doublet Mechanics: 45; Ferrari, M., Granik, V.T., Imam, A., Nadeau, J.C., Eds.; Lecture Notes in Physics Monographs; Springer: Berlin/Heidelberg, Germany, 1997. [Google Scholar]
- Mindlin, R.D.; Tierstem, H.F. Effects of couple-stresses in linear elasticity. Arch. Ration. Mech. Anal. 1962, 11, 415–448. [Google Scholar] [CrossRef]
- Toupin, R.A. Theories of elasticity with couple-stress. Arch. Ration. Mech. Anal. 1964, 17, 85–112. [Google Scholar] [CrossRef]
- Koiter, W.T. Couple stresses in the theory of elasticity I and II. Phil. Trans. Roy. Soc. Lond. B 1964, 67, 17–44. [Google Scholar]
- Yang, F.; Chong, A.C.M.; Lam, D.C.C.; Tong, P. Couple stress-based strain gradient theory for elasticity. Int. J. Solids Struct. 2002, 39, 2731–2743. [Google Scholar] [CrossRef]
- Hadjesfandiari, A.R.; Dargush, G.F. Couple stress theory for solids. Int. J. Solids Struct. 2011, 48, 2496–2510. [Google Scholar] [CrossRef]
- Hadjesfandiari, A.R.; Dargush, G.F. Fundamental solutions for isotropic size-dependent couple stress elasticity. Int. J. Solids Struct. 2013, 50, 1253–1265. [Google Scholar] [CrossRef]
- Hadjesfandiari, A.R. Size-dependent thermoelasticity. Latin Amer. J. Solids Struct. 2014, 11, 1679–1708. [Google Scholar] [CrossRef]
- Hadjesfandiari, A.R. Size-dependent piezoelectricity. Int. J. Solids Struct. 2013, 50, 2781–2791. [Google Scholar] [CrossRef]
- Wu, C.P.; Chang, T.Y. A comparative study of consistent couple stress and strain gradient theories on the mechanical behaviors of functionally gradient microplates using the local Petrov-Galerkin meshless method. Thin-Walled Struct. 2025, 215, 113527. [Google Scholar] [CrossRef]
- Askes, H.; Aifantis, E.C. Gradient elasticity in statics and dynamics: An overview of formulations, length scale identification procedures, finite element implementations and new results. Int. J. Solids Struct. 2011, 48, 1962–1990. [Google Scholar] [CrossRef]
- Hassanpour, S.; Heppler, G.R. Micropolar elasticity theory: A survey of linear isotropic equations, representative notations, and experimental investigations. Math. Mech. Solids 2015, 22, 224–242. [Google Scholar] [CrossRef]
- Thai, H.T.; Vo, T.P.; Nguyen, T.K.; Kim, S.E. A review of continuum mechanics models for size-dependent analysis of beams and plates. Compos. Struct. 2017, 177, 196–219. [Google Scholar] [CrossRef]
- Farajpour, A.; Ghayesh, M.H.; Farokhi, H. A review on the mechanics of nanostructures. Int. J. Eng. Sci. 2018, 133, 231–263. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Farajpour, A. A review on the mechanics of functionally graded nanoscale and microscale structures. Int. J. Eng. Sci. 2019, 137, 8–36. [Google Scholar] [CrossRef]
- Wu, C.P.; Yu, J.J. A review of mechanical analysis of rectangular nanobeams and single-, double-, and multi-walled carbon nanotubes using Eringen’s nonlocal elasticity theory. Arch. Appl. Mech. 2019, 89, 1761–1792. [Google Scholar] [CrossRef]
- Wu, C.P.; Hu, H.X. A review of dynamic analyses of single-, and multi-layered graphene sheets/nanoplates using various nonlocal continuum mechanics-based plate theories. Acta Mech. 2021, 232, 4497–4531. [Google Scholar] [CrossRef]
- Kong, S. A review on the size-dependent models of micro-beam and micro-plate based on the modified couple stress theory. Arch. Computat. Methods Eng. 2022, 29, 1–31. [Google Scholar] [CrossRef]
- Roudbari, M.A.; Jorshari, T.D.; Lu, C.; Ansari, R.; Kouzani, A.Z.; Amabili, M. A review of size-dependent continuum mechanics models for micro- and nano-structures. Thin-Walled Struct. 2022, 170, 108562. [Google Scholar] [CrossRef]
- Nuhu, A.A.; Safaei, B. A comprehensive review on the vibration analyses of small-scaled plate-based structures by utilizing the nonclassical continuum elasticity theories. Thin-Walled Struct. 2022, 179, 109622. [Google Scholar] [CrossRef]
- Shen, H.S.; Xiang, Y. Nonlinear vibration of nanotube-reinforced composite cylindrical shells in thermal environments. Comput. Methods Appl. Mech. Eng. 2012, 213, 196–205. [Google Scholar] [CrossRef]
- Zhao, S.; Zhao, Z.; Yang, Z.; Ke, L.; Kitipornchai, S.; Yang, J. Functionally graded graphene reinforced composite structures: A review. Eng. Struct. 2020, 210, 110339. [Google Scholar] [CrossRef]
- Song, M.; Kitipornchai, S.; Yang, J. Free and forced vibrations of functionally graded polymer composite plates reinforced with graphene platelets. Compos. Struct. 2017, 159, 579–588. [Google Scholar] [CrossRef]
- Reddy, J.N. Energy and Variational Methods in Applied Mechanics; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 2017. [Google Scholar]
- Wang, Y.M.; Chen, S.M.; Wu, C.P. A meshless collocation method based on the differential reproducing kernel interpolation. Comput. Mech. 2010, 45, 585–606. [Google Scholar] [CrossRef]
- Wu, C.P.; Chang, R.S. A Hermitian C2 differential reproducing kernel interpolation meshless method for the 3D microstructure-dependent static flexural analysis of simply supported and functionally graded microplates. CMES-Comput. Methods Eng. Sci. 2024, 141, 917–949. [Google Scholar]
- Wu, C.P.; Chou, Y.Q. A size-dependent meshless differential reproducing kernel point method for static buckling and free vibration analyses of functionally graded microplates subjected to bi-axial compression. Acta Mech. 2025. submitted for review. [Google Scholar] [CrossRef]
- Wu, C.P.; Lyu, Y.S. An asymptotic consistent couple stress theory for the three-dimensional free vibration analysis of functionally graded microplates resting on an elastic medium. Math. Methods Appl. Sci. 2023, 46, 4891–4919. [Google Scholar] [CrossRef]
- Salehipour, H.; Nahvi, H.; Shahidi, A.R. Exact closed-form free vibration analysis for functionally graded micro/nano plates based on modified couple stress and three-dimensional elasticity theories. Compos. Struct. 2015, 124, 283–291. [Google Scholar] [CrossRef]
- Salehipour, H.; Shahgholian-Ghahfarokhi, D.; Shahsavar, A.; Civalek, O.; Edalati, M. Static deflection and free vibration analysis of functionally graded and porous cylindrical micro/nano shells based on the three-dimensional elasticity and modified couple stress theories. Mech. Based Des. Struct. Mach. 2020, 50, 2184–2205. [Google Scholar] [CrossRef]
- Salehipour, H.; Shahsavar, A. A three-dimensional elasticity model for free vibration analysis of functionally graded micro/nano plates: Modified strain gradient theory. Compos. Struct. 2018, 206, 415–424. [Google Scholar] [CrossRef]
- Wu, C.P.; Hsu, C.H. A three-dimensional weak formulation for stress, deformation, and free vibration analyses of functionally graded microscale plates based on the consistent couple stress theory. Compos. Struct. 2022, 296, 115829. [Google Scholar] [CrossRef]
- Wu, C.P.; Lu, Y.A. A Hermite-family C1 finite layer method for the three-dimensional free vibration analysis of exponentially graded piezoelectric microplates based on the consistent couple stress theory. Int. J. Struct. Stab. Dyn. 2023, 23, 2350044. [Google Scholar] [CrossRef]
- Wu, C.P.; Tan, T.F.; Hsu, H.T. A size-dependent finite element method for the 3D free vibration analysis of functionally graded graphene platelets-reinforced composite cylindrical microshells based on the consistent couple stress theory. Materials 2023, 16, 2363. [Google Scholar] [CrossRef] [PubMed]
- Wu, C.P.; Wu, M.L.; Hsu, H.T. 3D size-dependent dynamic instability analysis of FG cylindrical microshells subjected to combinations of periodic axial compression and external pressure using a Hermitian C2 finite layer method based on the consistent couple stress theory. Materials 2024, 17, 810. [Google Scholar] [CrossRef]
- Wu, C.P.; Hsu, H.T. A Hermitian Cn finite cylindrical layer method for 3D size-dependent buckling and free vibration analyses of simply supported FG piezoelectric cylindrical sandwich microshells subjected to axial compression and electric voltages. ZAMM-J. Appl. Math. Mech. 2024, 104, e202300472. [Google Scholar] [CrossRef]
- Wu, C.P.; Lu, Y.S. 3D static bending analysis of functionally graded piezoelectric microplates resting on an elastic medium subjected to electro-mechanical loads using a size-dependent Hermitian C2 finite layer method based on the consistent couple stress theory. Mech. Bas. Des. Struct. Mach. 2024, 52, 3799–3841. [Google Scholar] [CrossRef]
- Wu, C.P.; Chang, R.S. Semi-analytical differential reproducing kernel element method for the size-dependent free vibration characteristics analysis of functionally graded doubly curved microscale shells. Int. J. Struct. Stab. Dyn. 2025, 2650260. [Google Scholar] [CrossRef]
- Lou, J.; He, L.; Du, J. A unified higher order plate theory for functionally graded microplates based on the modified couple stress theory. Compos. Struct. 2015, 133, 1036–1047. [Google Scholar] [CrossRef]
- Wu, C.P.; Hu, H.X. A unified size-dependent plate theory for static bending and free vibration analyses of micro- and nano-scale plates based on the consistent couple stress theory. Mech. Mater. 2021, 162, 104085. [Google Scholar] [CrossRef]
- Wang, Y.; Xie, K.; Fu, T.; Zhang, W. A unified modified couple stress model for size-dependent free vibrations of FG cylindrical microshells based on high-order shear deformation theory. Eur. Phys. J. Plus 2020, 135, 71. [Google Scholar] [CrossRef]
- Tran, V.T.; Nguyen, T.K.; Nguyen, P.T.T.; Vo, T.P. Stochastic vibration and buckling analysis of functionally graded microplates with a unified higher-order shear deformation theory. Thin-Walled Struct. 2022, 177, 109473. [Google Scholar] [CrossRef]
- Wu, C.P.; Lin, E.L. Free vibration analysis of porous functionally graded piezoelectric microplates resting on an elastic medium subjected to electric voltages. Arch. Mech. 2022, 74, 463–511. [Google Scholar]
- Shaban, M.; Minaeii, S.; Kalhori, H. Size-dependent flexural analysis of thick microplates using consistent couple stress theory. J. Compos. Sci. 2025, 9, 142. [Google Scholar] [CrossRef]
- Wu, C.P.; Hsu, C.D. A unified size-dependent theory for analyzing the free vibration behavior of an FG microplate under fully simply supported conditions and magneto-electro-thermo-mechanical loads considering couple stress and thickness stretching effects. J. Compos. Sci. 2025, 9, 201. [Google Scholar] [CrossRef]
- Tang, F.; Dong, F.; Guo, Y.; Shi, S.; Jiang, J.; Liu, S. Size-dependent buckling and post-buckling analysis of the functionally graded thin plate Al-Cu material based on a modified couple stress theory. Nanomaterials 2022, 12, 3502. [Google Scholar] [CrossRef]
- Wang, Y.G.; Lin, W.H.; Zhou, C.L. Nonlinear bending of size-dependent circular microplates based on the modified couple stress theory. Arch. Appl. Mech. 2014, 84, 391–400. [Google Scholar] [CrossRef]
- Wang, Y.G.; Lin, W.H.; Liu, N. Large amplitude free vibration of size-dependent circular microplates based on the modified couple stress theory. Int. J. Mech. Sci. 2013, 71, 51–57. [Google Scholar] [CrossRef]
- Thai, H.T.; Choi, D.H. Size-dependent functionally graded Kirchhoff and Mindlin plate models based on a modified couple stress theory. Compos. Struct. 2013, 95, 142–153. [Google Scholar] [CrossRef]
- Simsek, M.; Aydin, M. Size-dependent forced vibration of an imperfect functionally graded (FG) microplate with porosities subjected to a moving load using the modified couple stress theory. Compos. Struct. 2017, 160, 408–421. [Google Scholar] [CrossRef]
- Ke, L.L.; Wang, Y.W.; Yang, J.; Kitipornchai, S. Free vibration of size-dependent Mindlin microplates based on the modified couple stress theory. J. Sound Vib. 2012, 331, 94–106. [Google Scholar] [CrossRef]
- Kim, J.; Zur, K.K.; Reddy, J.N. Bending, free vibration, and buckling of modified couple stress-based functionally graded porous microplates. Compos. Struct. 2019, 209, 879–888. [Google Scholar] [CrossRef]
- Yekani, S.M.A.; Fallah, F. A Levy solution for bending, buckling, and vibration of Mindlin microplates with a modified couple stress theory. SN Appl. Sci. 2020, 2, 2169. [Google Scholar] [CrossRef]
- Tounsi, A.; Kaci, A.; Tounsi, A.; Al-Osta, M.A.; Yaylaci, M.; Mohamed, S.M.Y.; Althobaiti, S.; Selim, M.M. Quasi-3D plate theory for size-dependent static and free vibration analysis of FG microplate with porosities based on a modified couple stress theory. Mech. Adv. Mater. Struct. 2025. [Google Scholar] [CrossRef]
- Jung, W.Y.; Park, W.T.; Han, S.C. Bending and vibration analysis of S-FGM microplates embedded in Pasternak elastic medium using the modified couple stress theory. Int. J. Mech. Sci. 2014, 87, 150–162. [Google Scholar] [CrossRef]
- Beitollahi, A.; Bazargan-Lari, Y.; Janghorban, M. On the variable length scale parameter in functionally graded non-porous and porous microplate/nanoplate. Mech. Adv. Mater. Struct. 2024, 31, 12481–12503. [Google Scholar] [CrossRef]
- Cuong-Le, T.; Hoang-Le, M.; Ferreira, A.J.M.; Wahab, M.A. Small size-effect isogeometric analysis for linear and nonlinear responses of porous metal foam microplate. Compos. Struct. 2022, 285, 115189. [Google Scholar] [CrossRef]
- Arefi, M.; Kiani, M. Magneto-electro-mechanical bending analysis of three-layered exponentially graded microplate with piezomagnetic face-sheets resting on Pasternak’s foundation via MCST. Mech. Adv. Mater. Struct. 2018, 27, 383–395. [Google Scholar] [CrossRef]
- Van Hieu, D.; Hoa, N.T.; Chan, D.Q. Size-dependent mechanical analysis of imperfect FG Mindlin microplate with porosities resting on elastic foundation through the modified couple stress theory. Iran J. Sci. Technol. Trans. Mech. Eng. 2023, 47, 163–185. [Google Scholar] [CrossRef]
- Wang, S.; Hong, J.; Yin, S.; Zhang, G. Isogeometric analysis of magneto-electro-elastic functionally graded Mindlin microplates. Thin-Walled Struct. 2024, 198, 111740. [Google Scholar] [CrossRef]
- Yin, B.; Fang, J. Modified couple stress-based free vibration and dynamic responses of rotating FG multilayer composite microplates reinforced with graphene platelets. Arch. Appl. Mech. 2023, 93, 1051–1079. [Google Scholar] [CrossRef]
- Jung, W.Y.; Han, S.C.; Park, W.T. A modified couple stress theory for buckling analysis of S-FGM nanoplates embedded in Pasternak elastic medium. Compos. Part B 2014, 60, 746–756. [Google Scholar] [CrossRef]
- Trinh, L.C.; Vo, T.P.; Thai, H.T.; Mantari, J.L. Size-dependent behavior of functionally graded sandwich microplates under mechanical and thermal loads. Compos. Part B 2017, 124, 218–241. [Google Scholar] [CrossRef]
- Tranh, C.L.; Nguyen, T.N.; Vu, T.H.; Khatir, S.; Wahab, M.A. A geometrically nonlinear size-dependent hypothesis for porous functionally graded microplate. Eng. Comput. 2022, 38, 449–460. [Google Scholar]
- Lei, J.; He, Y.; Zhang, B.; Liu, D.; Shen, L.; Guo, S. A size-dependent FG microplate model incorporating higher-order shear and normal deformation effects based on a modified couple stress theory. Int. J. Mech. Sci. 2015, 104, 8–23. [Google Scholar] [CrossRef]
- Thai, H.T.; Kim, S.E. A size-dependent functionally graded Reddy plate model based on a modified couple stress theory. Compos. Part B 2013, 45, 1636–1645. [Google Scholar] [CrossRef]
- Fang, J.; Yin, B.; Li, L.; Zhang, D. Thermal buckling and vibration analysis of rotating porous FG GNPs-reinforced Reddy microplates. Aerosp. Sci. Technol. 2023, 137, 108298. [Google Scholar] [CrossRef]
- Arefi, M.; Firouzeh, S.; Bidgoli, M.R.E.; Civalek, O. Analysis of porous microplates reinforced with FG-GNPs based on Reddy plate theory. Compos. Struct. 2020, 247, 112391. [Google Scholar] [CrossRef]
- Coskun, S.; Kim, J.; Toutanji, H. Bending, free vibration, and buckling analysis of functionally graded porous microplates using a general third-order plate theory. J. Compos. Sci. 2019, 3, 15. [Google Scholar] [CrossRef]
- Afshari, H.; Adab, N. Size-dependent buckling and vibration analyses of GNP reinforced microplates based on the quasi-3D sinusoidal shear deformation theory. Mech. Based Des. Struct. Mach. 2020, 50, 184–205. [Google Scholar] [CrossRef]
- Thanh, C.L.; Tran, L.V.; Vu-Huu, T.; Nguyen-Xuan, H.; Abdel-Wahab, M. Size-dependent nonlinear analysis and damping responses of FG-CNTRC micro-plates. Comput. Methods Appl. Mech. Eng. 2019, 353, 253–276. [Google Scholar] [CrossRef]
- Zhang, C.; Eyvazian, A.; Alkhedher, M.; Alwetaishi, M.; Ahammad, N.A. Modified couple stress theory application to analyze mechanical buckling behavior of three-layer rectangular microplates with honeycomb core and piezoelectric face sheets. Compos. Struct. 2022, 292, 115582. [Google Scholar] [CrossRef]
- Sobhy, M.; Zenkour, A.M. A comprehensive study on the size-dependent hygrothermal analysis of exponentially graded microplates on elastic foundations. Mech. Adv. Mater. Struct. 2019, 27, 816–830. [Google Scholar] [CrossRef]
- Arefi, M.; Adab, N. Coupled stress based formulation for static and dynamic analyses of a higher-order shear and normal deformable FG-GPL reinforced microplates. Waves Random Complex Media 2021, 34, 4244–4269. [Google Scholar] [CrossRef]
- Khorasani, M.; Soleimani-Javid, Z.; Arshid, E.; Lampani, L.; Civalek, O. Thermal-elastic buckling of honeycomb micro plates integrated with FG-GNPs reinforced epoxy skins with stretching effect. Compos. Struct. 2021, 258, 113430. [Google Scholar] [CrossRef]
- Mohseni, E.; Saidi, A.R.; Mohammadi, M. Vibration analysis of thick functionally graded microplates using HOSNDPT and modified couple stress theory. Iran J. Sci. Technol. Trans. Mech. Eng. 2019, 43, 641–651. [Google Scholar] [CrossRef]
- Mohseni, E.; Saidi, A.R.; Mohammadi, M. Bending-stretching analysis of thick functionally graded microplates using higher-order shear and normal deformable plate theory. Mech. Adv. Mater. Struct. 2017, 24, 1221–1230. [Google Scholar] [CrossRef]
- Thai, C.H.; Ferreira, A.J.M.; Tran, T.D.; Phung-Van, P. A size-dependent quasi-3D isogeometric model for functionally graded graphene platelet-reinforced composite microplates based on the modified couple stress theory. Compos. Struct. 2020, 234, 111695. [Google Scholar] [CrossRef]
- Radwan, A.F.; Sobhy, M. Transient instability analysis of viscoelastic sandwich CNTs-reinforced microplates exposed 2D magnetic field and hygrothermal conditions. Compos. Struct. 2020, 245, 112349. [Google Scholar] [CrossRef]
- He, L.; Lou, J.; Zhang, E.; Wang, Y.; Bai, Y. A size-dependent four variable refined plate model for functionally graded microplates based on modified couple stress theory. Compos. Struct. 2015, 130, 107–115. [Google Scholar] [CrossRef]
- Mohammadpour, A.; Mehrabadi, S.J.; Yousefi, P.; Mohseni-Monfared, H. Free vibration analysis of functionally graded porous elliptical microshells using modified couple stress theory. Waves Random Complex Media 2022, 35, 947–972. [Google Scholar] [CrossRef]
- Razavi, H.; Babadi, A.F.; Beni, Y.T. Free vibration analysis of functionally graded piezoelectric cylindrical nanoshell based on consistent couple stress theory. Compos. Struct. 2017, 160, 1299–1309. [Google Scholar] [CrossRef]
- Tang, F.; He, S.; Shi, S.; Xue, S.; Dong, F.; Liu, S. Analysis of size-dependent linear static bending, buckling, and free vibration based on a modified couple stress theory. Materials 2022, 15, 7583. [Google Scholar] [CrossRef] [PubMed]
- Zeighampour, H.; Shojaeian, M. Buckling analysis of functionally graded sandwich cylindrical micro/nanoshells based on the couple stress theory. J. Sandw. Struct. Mater. 2017, 21, 917–937. [Google Scholar] [CrossRef]
- Beni, T.; Mehralian, F.; Zeighampour, H. The modified couple stress functionally graded cylindrical thin shell formulation. Mech. Adv. Mater. Struct. 2016, 23, 791–801. [Google Scholar] [CrossRef]
- Farokhi, H.; Ghayesh, M.H. Nonlinear mechanical behavior of microshells. Int. J. Eng. Sci. 2018, 127, 127–144. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Liu, Y.F.; Zu, J.W. Size-dependent vibration of circular cylindrical polymeric microshells reinforced with graphene platelets. Int. J. Appl. Mech. 2019, 11, 1950036. [Google Scholar] [CrossRef]
- Khuat Duc, D.; Nguyen Tuan, L.; Dao Nhu, M.; Hong, N.T.; Van Ke, T.; Minh, P.V. A novel isogeometric model for dynamic buckling analysis of doubly curved two-directional functionally graded porous shallow microshells in thermal environments via variable length-scale parameters. Mech. Based Des. Struct. Mach. 2024, 52, 8610–8638. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, Y. Size-dependent free vibration and buckling of three-dimensional graphene foam microshells based on modified couple stress theory. Materials 2019, 12, 729. [Google Scholar] [CrossRef]
- Abbaspour, F. Free vibration analysis of simply-supported graphene platelets reinforced laminated piezoelectric cylindrical microshells. Int. J. Comput. Methods Eng. Sci. Mech. 2021, 23, 461–474. [Google Scholar] [CrossRef]
- Karami, B.; Ghayesh, M.H.; Hussain, S.; Amabili, M. On the size-dependent vibrations of doubly curved porous shear deformable FGM microshells. Int. J. Mech. Syst. Dyn. 2024, 4, 387–405. [Google Scholar] [CrossRef]
- Lou, J.; He, L.; Wu, H.; Du, J. Pre-buckling and buckling analyses of functionally graded microshells under axial and radial loads based on the modified couple stress theory. Compos. Struct. 2016, 142, 226–237. [Google Scholar] [CrossRef]
- Zeighampour, H.; Shojaeian, M. Size-dependent vibration of sandwich cylindrical nanoshells with functionally graded material based on the couple stress theory. J. Braz. Soc. Mech. Sci. Eng. 2017, 39, 1789–2800. [Google Scholar] [CrossRef]
- Mirfatah, S.M.; Shahmohammadi, M.A.; Salehipour, H. Size-dependent dynamic stability of nanocomposite enriched microshell panels in thermal environment using the modified couple stress theory. Eng. Anal. Bound. Elem. 2022, 143, 483–500. [Google Scholar] [CrossRef]
- Abbaspour, F.; Hosseini, S. Thermal buckling of piezoelectric graphene platelets reinforced cylindrical microshells using Navier’s and meshless methods. Mech. Based Des. Struct. Mach. 2023, 52, 5653–5672. [Google Scholar] [CrossRef]
- SafarPour, H.; Hosseini, M.; Ghadiri, M. Influence of three-parameter viscoelastic medium on vibration behavior of a cylindrical nonhomogeneous microshell in thermal environment: An exact solution. J. Therm. Stress. 2017, 40, 1353–1367. [Google Scholar] [CrossRef]
- Abbaspour, F.; Hosseini, S. Free vibration analyses of graphene platelets reinforced laminated piezoelectric cylindrical microshells using the Chebyshev-Ritz formulation. J. Vib. Eng. Technol. 2022, 10, 2129–2141. [Google Scholar] [CrossRef]
- Veysi, A.; Shabani, R.; Rezazadeh, G. Nonlinear vibration of micro-doubly curved shallow shells based on the modified couple stress theory. Nonlinear Dyn. 2017, 87, 2051–2065. [Google Scholar] [CrossRef]
- Sheng, G.G.; Wang, X. Nonlinear resonance responses of size-depenednt functionally graded cylindrical microshells with thermal effect and elastic medium. Eng. Comput. 2022, 38, 725–742. [Google Scholar] [CrossRef]
- Ghadiri, M.; SafarPour, H. Free vibration analysis of size-dependent functionally graded porous cylindrical microshells in thermal environment. J. Therm. Stress. 2016, 40, 55–71. [Google Scholar] [CrossRef]
- Gholami, R.; Ansari, R.; Darvizeh, A.; Sahmani, S. Axial buckling and dynamic stability of functionally graded microshells based on the modified couple stress theory. Int. J. Struct. Stab. Dyn. 2015, 15, 1450070. [Google Scholar] [CrossRef]
- Beni, Y.T.; Mehralian, F.; Razavi, H. Free vibration analysis of size-dependent shear deformable functionally graded cylindrical shell on the basis of modified couple stress theory. Compos. Struct. 2015, 120, 65–78. [Google Scholar] [CrossRef]
- Ma, H.M.; Gao, X.L.; Reddy, J.N. A non-classical Mindlin plate model based on a modified couple stress theory. Acta Mech. 2011, 220, 217–235. [Google Scholar] [CrossRef]
- Mehditabar, A.; Ansari Sadrabadi, S.; Walker, J. Thermal buckling analysis of a functionally graded microshell based on higher-order shear deformation and modified couple stress theories. Mech. Based. Des. Struct. Mach. 2021, 51, 2812–2830. [Google Scholar] [CrossRef]
- Sahmani, S.; Ansari, R.; Gholami, R.; Darvizeh, A. Dynamic stability analysis of functionally graded higher-order shear deformable microshells based on the modified couple stress theory. Compos. Part B 2013, 51, 44–53. [Google Scholar] [CrossRef]
- Arefi, M. MCST bending formulation of a cylindrical microshell based on TSDT. Earthq. Struct. 2024, 26, 299–309. [Google Scholar]
- Zhang, M.; Jiang, X.; Arefi, M. Dynamic formulation of a sandwich microshell considering modified couple stress and thickness-stretching. Eur. Phys. J. Plus 2023, 138, 227. [Google Scholar] [CrossRef]
- Lori Dehsaraji, M.; Arefi, M.; Loghman, A. Size dependent free vibration analysis of functionally graded piezoelectric micro/nano shell based on modified couple stress theory with considering thickness stretching. Def. Technol. 2021, 17, 119–134. [Google Scholar] [CrossRef]
- Lori Dehsaraji, M.; Loghman, A.; Arefi, M. Three-dimensional thermo-electro-mechanical buckling analysis of functionally graded piezoelectric micro/nano-shells based on modified couple stress theory considering thickness stretching effect. Mech. Adv. Mater. Struct. 2020, 28, 2030–2045. [Google Scholar] [CrossRef]
- Li, A.; Zhou, S.; Zhou, S.; Wang, B. A size-dependent model for bi-layered Kirchhoff micro-plate based on strain gradient elasticity theory. Compos. Struct. 2014, 113, 272–280. [Google Scholar] [CrossRef]
- Movassagh, A.A.; Mahmoodi, M.J. A microscale modeling of Kirchhoff plate based on modified strain-gradient elasticity theory. Eur. J. Mech. A/Solids 2013, 40, 50–59. [Google Scholar] [CrossRef]
- Wang, B.; Zhou, S.; Zhao, J.; Chen, X. A size-dependent Kirchhoff micro-plate model based on strain gradient elasticity theory. Eur. J. Mech. A/Solids 2011, 30, 517–574. [Google Scholar] [CrossRef]
- Hosseini, M.; Bahreman, M.; Jamalpoor, A. Using the modified strain gradient theory to investigate the size-dependent biaxial buckling analyses of an orthotropic multi-microplate system. Acta Mech. 2016, 227, 1621–1643. [Google Scholar] [CrossRef]
- Farahmand, H.; Naseralav, S.S.; Iranmanesh, A.; Mohammadi, M. Navier solution for buckling analysis of size-dependent functionally graded microplates. Lat. Am. J. Solids Struct. 2016, 13, 3161–3173. [Google Scholar] [CrossRef][Green Version]
- Mohammadi, M.; Mahani, M.F. An analytical solution for buckling analysis of size-dependent rectangular micro-plates according to the modified strain gradient and couple stress theories. Acta Mech. 2015, 226, 3477–3493. [Google Scholar] [CrossRef]
- Ansari, R.; Shojaei, M.F.; Mohammsdi, V.; Gholami, R.; Rouhi, H. Size-dependent thermal buckling and postbuckling of functionally graded annular microplates based on the modified strain gradient theory. J. Therm. Stress. 2013, 37, 174–201. [Google Scholar] [CrossRef]
- Ansari, R.; Gholami, R.; Shojaei, M.F.; Mohammadi, V.; Sahmani, S. Bending, buckling and free vibration analysis of size-dependent functionally graded circular/annular microplates based on the modified strain gradient elasticity theory. Eur. J. Mech. A/Solids 2015, 49, 251–267. [Google Scholar] [CrossRef]
- Markolefas, S.; Fafalis, D. Strain gradient theory based dynamic Mindlin-Reissner and Kirchhoff microplates with microstructural and micro-inertial effects. Dynamics 2021, 1, 49–94. [Google Scholar] [CrossRef]
- Ma, B.; Chen, K.Y.; Habibi, M.; Albaijan, I. Static/dynamic analyses of sandwich microplate based on modified strain gradient theory. Mech. Adv. Mater. Struct. 2023, 31, 5760–5767. [Google Scholar] [CrossRef]
- Gholami, R.; Ansari, R. A most general strain gradient plate formulation for size-dependent geometrically nonlinear free vibration analysis of functionally graded shear deformable rectangular microplates. Nonlinear Dyn. 2016, 84, 2403–2422. [Google Scholar] [CrossRef]
- Thai, S.; Thai, H.T.; Vo, T.P.; Patel, V.I. Size-dependent behavior of functionally graded microplates based on the modified strain gradient elasticity theory and isogeometric analysis. Comput. Struct. 2017, 190, 219–241. [Google Scholar] [CrossRef]
- Thai, C.H.; Ferreira, A.J.M.; Phung-Van, P. Size dependent free vibration analysis of multilayer functionally graded GPLRC microplates based on modified strain gradient theory. Compos. Part B 2019, 169, 174–188. [Google Scholar] [CrossRef]
- Wang, J.; Ma, B.; Gao, J.; Liu, H.; Safaei, B.; Sahmani, S. Nonlinear stability characteristics of porous graded composite microplates including various microstructural-dependent strain gradient tensors. Int. J. Appl. Mech. 2022, 24, 2150129. [Google Scholar] [CrossRef]
- Nguyen, L.B.; Thai, C.H.; Duong-Nguyen, N.; Nguyen-Xuan, H. A size-dependent isogeometric approach for vibration analysis of FG piezoelectric porous microplates using modified strain gradient theory. Eng. Comput. 2022, 38, 4415–4435. [Google Scholar]
- Sahmani, S.; Ansari, R. On the free vibration response of functionally graded higher-order shear deformable microplates based on the strain gradient elasticity theory. Compos. Struct. 2013, 95, 430–442. [Google Scholar] [CrossRef]
- Jain, V.; Kumar, R. Geometrically nonlinear dynamic analysis of a damped porous microplate resting on elastic foundations under transverse patch loadings. Mech. Adv. Mater. Struct. 2023, 31, 5454–5477. [Google Scholar] [CrossRef]
- Zhang, B.; He, Y.; Liu, D.; Shen, L.; Lei, J. An efficient size-dependent plate theory for bending, buckling, and free vibration analyses of functionally graded microplates resting on elastic foundation. Appl. Math. Modell. 2015, 39, 3814–3845. [Google Scholar] [CrossRef]
- Hung, P.T.; Thai, C.H.; Phung-Van, P. Isogeometric free vibration of honeycomb sandwich microplates with the graphene nanoplatelets reinforcement face sheets. Eng. Struct. 2024, 305, 117670. [Google Scholar] [CrossRef]
- Thai, C.H.; Ferreira, A.J.M.; Rabczuk, T.; Nguyen-Xuan, H. Size-dependent analysis of FG-CNTRC microplates based on modified strain gradient elasticity theory. Eur. J. Mech. A/Solids 2018, 72, 521–538. [Google Scholar] [CrossRef]
- Akgoz, B.; Civalek, O. A microstructure-dependent sinusoidal plate model based on the strain gradient elasticity theory. Acta Mech. 2015, 226, 2277–2294. [Google Scholar] [CrossRef]
- Farahmand, H. A variational approach for analytical buckling solution of moderately thick microplate using strain gradient theory incorporating two-variable refined plate theory: A benchmark study. J. Braz. Soc. Mech. Sci. Eng. 2021, 43, 125. [Google Scholar] [CrossRef]
- Thai, C.H.; Ferreira, A.J.M.; Nguyen-Xuan, H. Isogeometric analysis of size-dependent isotropic and sandwich functionally graded microplates based on modified strain gradient elasticity theory. Compos. Struct. 2016, 192, 274–288. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Farokhi, H. Nonlinear mechanics of doubly curved shallow microshells. Int. J. Eng. Sci. 2017, 119, 288–304. [Google Scholar] [CrossRef]
- Zeighampour, H.; Beni, Y.T. Cylindrical thin-shell model based on modified strain gradient theory. Int. J. Eng. Sci. 2014, 78, 27–47. [Google Scholar] [CrossRef]
- Qi, L.; Zhou, S. A size-dependent spherical microshell model based on strain gradient elasticity theory. Eur. J. Mech. A/Solids 2020, 84, 104087. [Google Scholar] [CrossRef]
- Tohidi, H.; Hosseini-Hashemi, S.H.; Maghsoudpour, A. Nonlinear size-dependent dynamic buckling analysis of embedded micro cylindrical shells reinforced with agglomerated CNYs using strain gradient theory. Microsyst. Technol. 2017, 23, 5727–5744. [Google Scholar] [CrossRef]
- Gholami, R.; Darvizeh, A.; Ansari, R.; Sadeghi, F. Vibration and buckling of first-order shear deformable circular cylindrical micro-/nano-shells based on Mindlin’s strain gradient elasticity theory. Eur. J. Mech. A/Solids 2016, 58, 76–88. [Google Scholar] [CrossRef]
- Le, T.M.; Vo, D.; Aung, Z.Y.; Atroshchenko, E.; Bui, T.Q.; Rungamornrat, J. Isogeometric analysis of shear-deformable, in-plane functionally graded microplates by Mindlin’s strain gradient theory. Eng. Comput. 2024, 40, 1397–1430. [Google Scholar] [CrossRef]
- Movahedfar, V.; Kheirikhah, M.M.; Mohammadi, Y.; Ebrahimi, F. Modified strain gradient theory for nonlinear vibration analysis of functionally graded piezoelectric doubly curved microshells. Proc. Instit. Mech. Eng. Sci. 2021, 236, 4219–4231. [Google Scholar] [CrossRef]
- Zhang, F.; Bai, C.Y.; Zhang, Y.; Cao, D.Y. Dynamic stability analysis of functionally graded three-dimensional graphene form cylindrical microshells using interior pressure based on modified strain gradient theory. Eur. Phys. J. Plus 2022, 137, 228. [Google Scholar] [CrossRef]
- Gholami, R.; Darvizeh, A.; Ansari, R.; Hosseinzadeh, M. Size-dependent axial buckling analysis of functionally graded circular cylindrical microshells based on the modified strain gradient elasticity theory. Meccanica 2014, 49, 1679–1695. [Google Scholar] [CrossRef]
- Hajilak, Z.E.; Pourghader, J.; Hashmabadi, D.; Bagh, F.S.; Habibi, M.; Safarpour, H. Multilayer GPLRC composite cylindrical nanoshell using modified strain gradient theory. Mech. Based Des. Struct. Mach. 2019, 47, 521–545. [Google Scholar] [CrossRef]
- Le, T.M.; Vo, D.; Rungamornrat, J.; Bui, T.Q. Strain-gradient theory for shear deformation free-form microshells: Governing equations of motion and general boundary conditions. Int. J. Solids Struct. 2022, 248, 111579. [Google Scholar] [CrossRef]
- Krishnan, N.M.A.; Ghosh, D. Buckling analysis of cylindrical thin-shells using strain gradient elasticity theory. Meccanica 2017, 52, 1369–1379. [Google Scholar] [CrossRef]
- Zhang, B.; He, Y.; Liu, D.; Shen, L.; Lei, J. Free vibration analysis of four-unknown shear deformable functionally graded cylindrical microshells based on the strain gradient elasticity theory. Compos. Struct. 2015, 119, 578–597. [Google Scholar] [CrossRef]
- Ashoori, A.; Mahmoodi, M.J. The modified version of strain gradient and couple stress theories in general curvilinear coordinates. Eur. J. Mech. A/Solids 2015, 49, 441–454. [Google Scholar] [CrossRef]
- Du, H.; Lim, M.K.; Lin, R.M. Application of generalized differential quadrature method to structural problems. Int. J. Numer. Methods Eng. 1994, 37, 1881–1896. [Google Scholar] [CrossRef]
- Bert, C.W.; Malik, M. Differential quadrature: A powerful new technique for analysis of composite structures. Compos. Struct. 1997, 3–4, 179–189. [Google Scholar] [CrossRef]
- Wu, C.P.; Lee, C.Y. Differential quadrature solution for the free vibration analysis of laminated conical shells with variable stiffness. Int. J. Mech. Sci. 2001, 43, 1853–1869. [Google Scholar] [CrossRef]
- Ansari, R.; Shojaei, M.F.; Mohammadi, V.; Gholami, R.; Darabi, M.A. Nonlinear vibrations of functionally graded Mindlin microplates based on the modified couple stress theory. Compos. Struct. 2014, 114, 124–134. [Google Scholar] [CrossRef]
- Hosseini-Hashemi, S.; Sharifpour, F.; Ilkhani, M.R. On the free vibrations of size-dependent closed micro/nano-spherical shell based on the modified couple stress theory. Int. J. Mech. Sci. 2016, 115–116, 501–515. [Google Scholar] [CrossRef]
- Zhang, B.; Li, H.; Kong, L.; Zhang, X.; Feng, Z. Strain gradient differential quadrature finite element for moderately thick microplates. Int. J. Numer. Methods Eng. 2020, 121, 5600–5646. [Google Scholar] [CrossRef]
- Ansari, R.; Gholami, R.; Faghih Shojaei, M.; Mohammadi, V.; Darabi, M.A. Thermal buckling analysis of a Mindlin rectangular FGM microplate based on the strain gradient theory. J. Therm. Stress. 2013, 36, 446–465. [Google Scholar] [CrossRef]
- Adab, N.; Arefi, M.; Amabili, M. A comprehensive vibration analysis of rotating truncated sandwich conical microshells including porous core and GPL-reinforced face-sheets. Compos. Struct. 2022, 279, 114761. [Google Scholar] [CrossRef]
- Emdadi, M.; Mohammadimehr, M.; Bargozini, F. Vibration of a nanocomposite annular sandwich microplate based on HSDT using DQM. Multiscale Sci. Eng. 2023, 5, 180–194. [Google Scholar] [CrossRef]
- Yuan, Y.; Zhao, K.; Han, Y.; Sahmani, S.; Safaei, B. Nonlinear oscillations of composite conical microshells with in-plane heterogeneity based upon a couple stress-based shell model. Thin-Walled Struct. 2020, 154, 106857. [Google Scholar] [CrossRef]
- Yang, Y.; Sahmani, S.; Safaei, B. Couple stress-based nonlinear primary resonant dynamics of FGM composite truncated conical microshells integrated with magnetostricitive layers. Appl. Math. Mech. 2021, 42, 209–222. [Google Scholar] [CrossRef]
- Fan, L.; Sahmani, S.; Safaei, B. Couple stress-based dynamic stability analysis of functionally graded composite truncated conical microshells with magnetostrictive facesheets embedded within nonlinear viscoelastic foundations. Eng. Comput. 2021, 37, 1635–1655. [Google Scholar] [CrossRef]
- Suwankornkij, P.; Pulngern, T.; Tangbanjongkij, C.; Chucheepsakul, S.; Jiammeepreecha, W. Static analysis of a hemispherical nanoshell under uniform pressure based on MCST: A comparison of FEM and GDQ solutions. Arch. Appl. Mech. 2025, 95, 85. [Google Scholar] [CrossRef]
- Al-Furjan, M.S.H.; Habibi, M.; Ebrahimi, F.; Chen, G.; Safarpour, M.; Safarpour, H. A coupled thermomechanical approach for frequency information of electrically composite microshell using heat-transfer continuum problem. Eur. Phys. J. Plus 2020, 135, 837. [Google Scholar] [CrossRef]
- Mohammadimehr, M.; Atifeh, S.J.; Rousta, N.B. Stress and free vibration analysis of piezoelectric hollow circular FG-SWBNNTs reinforced nanocomposite plate based on modified couple stress theory subjected to thermo-mechanical loadings. J. Vibr. Control 2017, 24, 3471–3486. [Google Scholar] [CrossRef]
- Mao, Y.H.; Shang, Y.; Cen, S.; Li, C.F. An efficient 3-node triangular plate elementfor static and dynamic analyses of microplates based on modified couple stress theory with micro-inertia. Eng. Comput. 2023, 39, 3061–3084. [Google Scholar] [CrossRef]
- Wang, S.; Qian, Z.; Shang, Y. Size-dependent finite element analysis of FGMs in thermal environment based on the modified couple stress theory. Eng. Comput. 2024, 41, 1035–1066. [Google Scholar] [CrossRef]
- Dehrouyeh-Semnani, A.M.; Mostafaei, H. Vibration analysis of scale-dependent thin shallow microshells with arbitrary planform and boundary conditions. Int. J. Eng. Sci. 2021, 158, 103413. [Google Scholar] [CrossRef]
- Soleimani, I.; Beni, Y.T.; Dehkordi, M.B. Size-dependent two-node axisymmetric shell element for buckling analysis with couple stress theory. Proc. Instit. Mech. Eng. Part C J. Mech. Eng. Sci. 2019, 233, 4729–4741. [Google Scholar] [CrossRef]
- Wang, S.H.; Shang, Y.; Qian, Z.H. Size-dependent analysis of porous multi-directional FG shell structures based on the modified couple stress theory using the unsymmetric finite element method. Acta Mech. 2022, 233, 5105–5136. [Google Scholar] [CrossRef]
- Nguyen, T.C.N.; Le, M.H.; Tran, V.K.; Nguyen, T.D.; Phung, V.M. Static bending analysis of variable thickness microplates using the finite element method and modified couple stress theory. J. Sci. Technol. 2022, 17, 13–26. [Google Scholar] [CrossRef]
- Korayem, M.H.; Hefzabad, R.N. A quadrilateral non-classical microplate element considering the voltage effect. Proc. Instit. Mech. Eng. Part C J. Mech. Eng. Sci. 2024, 238, 9825–9839. [Google Scholar] [CrossRef]
- Zhang, B.; He, Y.; Liu, D.; Gan, Z.; Shen, L. A non-classical Mindlin plate finite element based on a modified couple stress theory. Eur. J. Mech. A/Solids 2013, 42, 63–80. [Google Scholar] [CrossRef]
- Taghizadeh, M.; Askari, A.R.; Farzinpoor, H. Size-dependent finite element buckling analysis of porous cylindrical microshells reinforced by graphene platelets. Mech. Based Des. Struct. Mach. 2024, 53, 2152–2181. [Google Scholar] [CrossRef]
- Genao, F.Y.; Kim, J.; Zur, K.K. Nonlinear finite element analysis of temperature-dependent functionally graded porous microplates under thermal and mechanical loads. Compos. Struct. 2021, 256, 112931. [Google Scholar]
- Karamanli, A.; Aydogdu, M. Vibration of functionally graded shear and normal deformable porous microplates via finite element method. Compos. Struct. 2020, 237, 111934. [Google Scholar] [CrossRef]
- Wu, H.P.; Shang, Y.; Cen, S.; Li, C.F. Penalty C0 8-node quadrilateral and 20-node hexahedral elements for consistent couple stress elasticity based on the unsymmetric finite element method. Eng. Anal. Bound. Elem. 2023, 147, 302–319. [Google Scholar] [CrossRef]
- Wang, S.; Qian, Z.; Shang, Y. Size-dependent vibration analysis of porous 3D-FG microshells in complex thermal environments using a neural network enhanced finite element model. Case Stud. Therm. Eng. 2024, 61, 104887. [Google Scholar] [CrossRef]
- Thai, T.Q.; Zhuang, X.; Rabczuk, T. A nonlinear geometric couple stress-based strain gradient Kirchhoff-Love shell formulation for microscale thin-wall structures. Int. J. Mech. Sci. 2021, 196, 106272. [Google Scholar] [CrossRef]
- Ansari, R.; Shojaei, M.F.; Mohammadi, V.; Bazdid-Vahdati, M.; Rouhi, H. Triangular Mindlin microplate element. Comput. Methods Appl. Mech. Eng. 2015, 295, 56–76. [Google Scholar] [CrossRef]
- Zuo, D.; Safaei, B.; Sahmani, S.; Ma, G. Nonlinear free vibrations of porous composite microplates incorporating various microstructural-dependent strain gradient tensors. Appl. Math. Mech. 2022, 43, 825–844. [Google Scholar] [CrossRef]
- Li, L.; Pan, Y.; Arabmarkadeh, A. Nonlinear finite element study on forced vibration of cylindrical micro-panels based on modified strain gradient theory. Mech. Adv. Mater. Struct. 2021, 29, 3727–3742. [Google Scholar] [CrossRef]
- Roque, C.M.C.; Ferreira, A.J.M.; Reddy, J.N. Analysis of Mindlin micro plates with a modified couple stress theory and a meshless method. Appl. Math. Modell. 2013, 37, 4626–4633. [Google Scholar] [CrossRef]
- Roque, C.M.C.; Zur, K.K. On the static, vibration, and transient responses of micro-plates made of materials with different microstructures. Eng. Anal. Bound. Elem. 2022, 143, 579–590. [Google Scholar] [CrossRef]
- Zhang, Y.; Sahmani, S.; Safaei, B. Meshfree-based applied mathematical modeling for nonlinear stability analysis of couple stress-based lateral pressurized randomly reinforced microshells. Eng. Comput. 2022, 38, 3523–3538. [Google Scholar] [CrossRef]
- Yang, Z.; Safaei, B.; Sahmani, S.; Zhang, Y. A couple-stress-based moving Kriging meshfree shell model for axial postbuckling analysis of random checkerboard composite cylindrical microshells. Thin-Walled Struct. 2022, 170, 108631. [Google Scholar] [CrossRef]
- Liu, H.; Safaei, B.; Sahmani, S. Combined axial and lateral stability behavior of random checkboard reinforced cylindrical microshells via a couple stress-based moving Kriging meshfree model. Arch. Civ. Mech. Eng. 2022, 22, 15. [Google Scholar]
- Liu, S.; Yu, T.; Bui, T.Q.; Xia, S. Size-dependent analysis of homogeneous and functionally graded microplates using IGA and a non-classical Kirchhoff plate theory. Compos. Struct. 2017, 172, 34–44. [Google Scholar] [CrossRef]
- Nguyen, H.X.; Atroshchenko, E.; Nguyen-Xuan, H.; Vo, T.P. Geometrically nonlinear isogeometric analysis of functionally graded microplates with the modified couple stress theory. Comput. Struct. 2017, 193, 110–127. [Google Scholar] [CrossRef]
- Nguyen, H.X.; Nguyen, T.N.; Abdel-Wahab, M.; Bordas, S.P.A.; Nguyen-Xuan, H.; Vo, T.P. A refined quasi-3D isogeometric analysis for functionally graded microplates based on the modified couple stress theory. Comput. Methods Appl. Mech. Eng. 2017, 313, 904–940. [Google Scholar] [CrossRef]
- Fan, F.; Xu, Y.; Sahmani, S.; Safaei, B. Modified couple stress-based geometrically nonlinear oscillations of porous functionally graded microplates using NURBS-based isogeometric approach. Comput. Methods Appl. Mech. Eng. 2020, 372, 113400. [Google Scholar] [CrossRef]
- Thai, C.H.; Nguyen-Xuan, H.; Nguyen, L.B.; Phung-Van, P. A modified strain gradient meshfree approach for functionally graded microplates. Eng, Comput. 2022, 38, 4545–4567. [Google Scholar] [CrossRef]
- Hung, P.T.; Phung-Van, P.; Thai, C.H. Small scale thermal analysis of piezoelectric-piezomagnetic FG microplates using modified strain gradient theory. Int. J. Mech. Mater. Des. 2023, 19, 739–761. [Google Scholar] [CrossRef]
- Thai, H.T.; Vo, T.P. A size-dependent functionally graded sinusoidal plate model based on a modified couple stress theory. Compos. Struct. 2013, 96, 376–383. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).