Detection of Defects in Solid Carbide Cutting Tools During Creep-Feed Flute Grinding (CFG) Using Recurrence Analysis
Abstract
1. Introduction
1.1. Characteristics of Creep-Feed Grinding
1.2. Application of Recurrence Analysis
1.3. Motivation and Aim
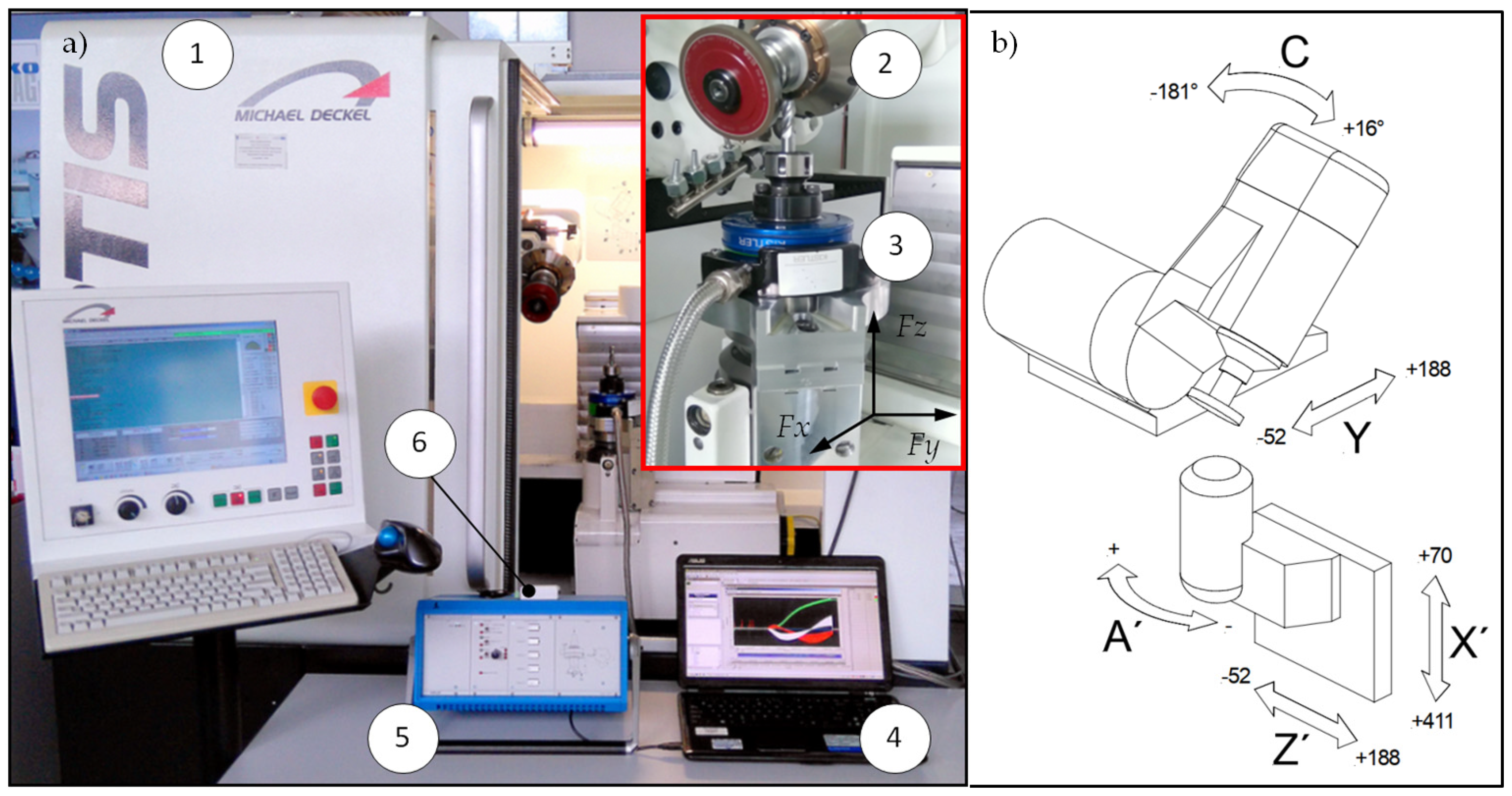
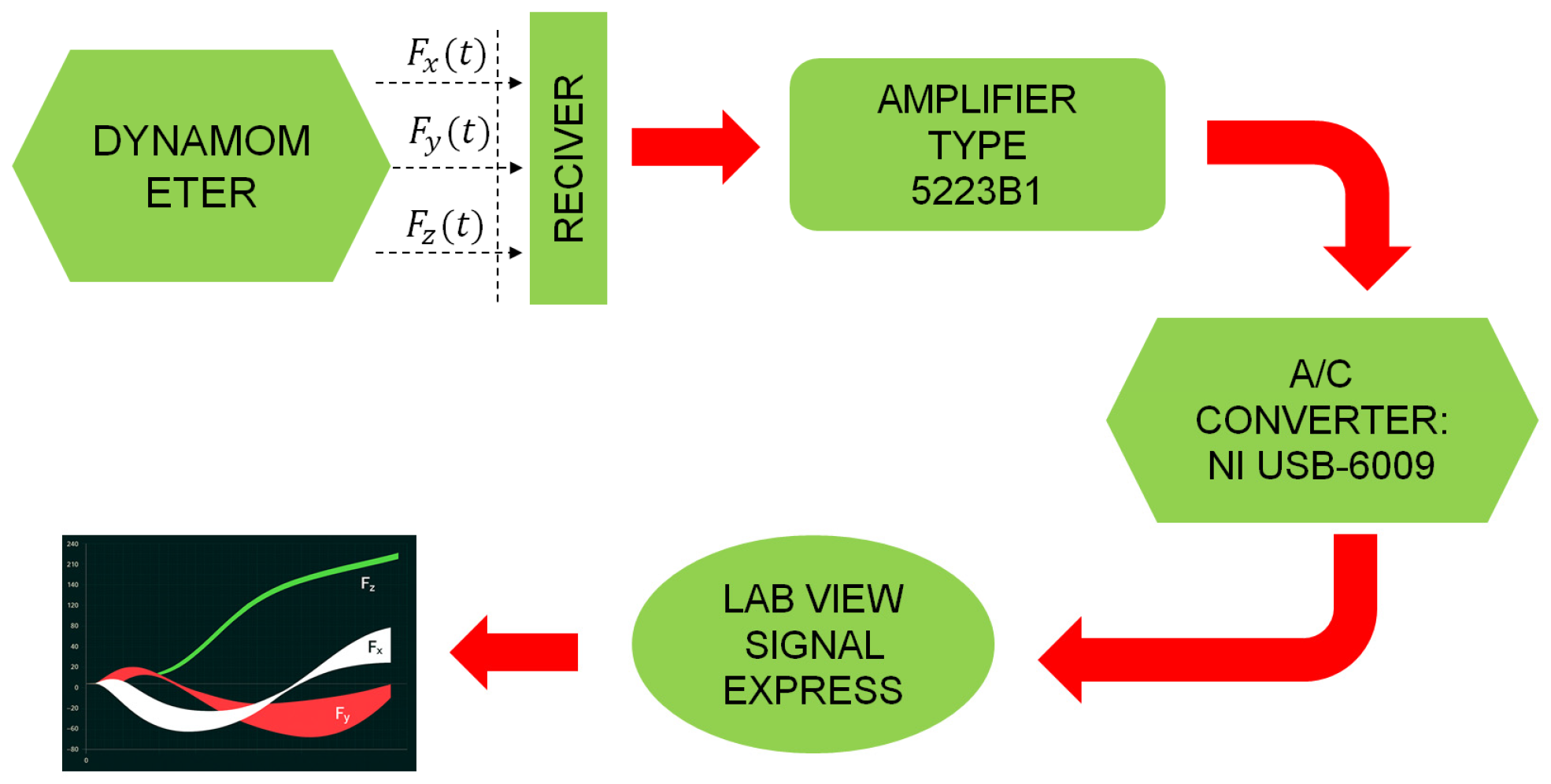
2. Methodology of Experiment
3. Materials and Methods
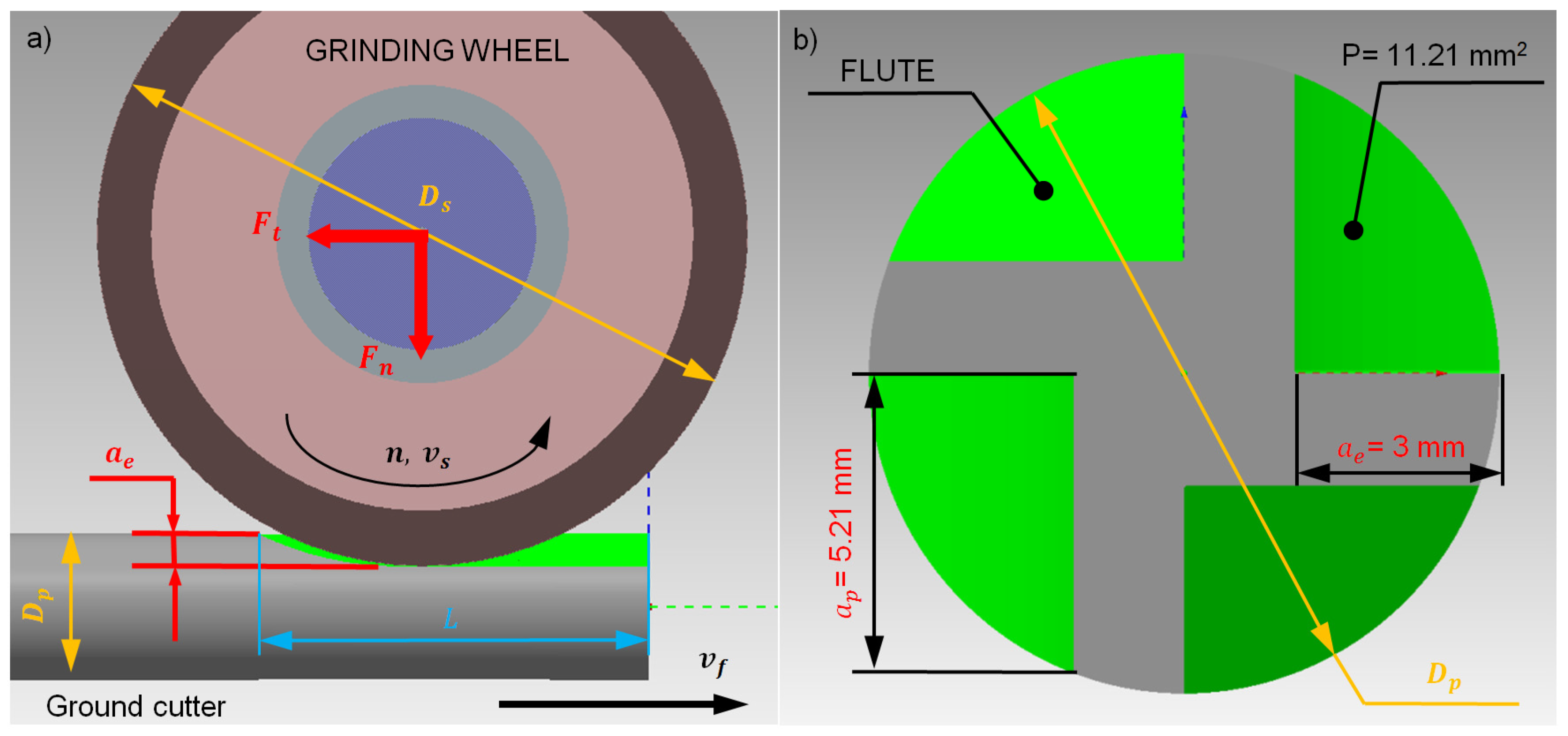
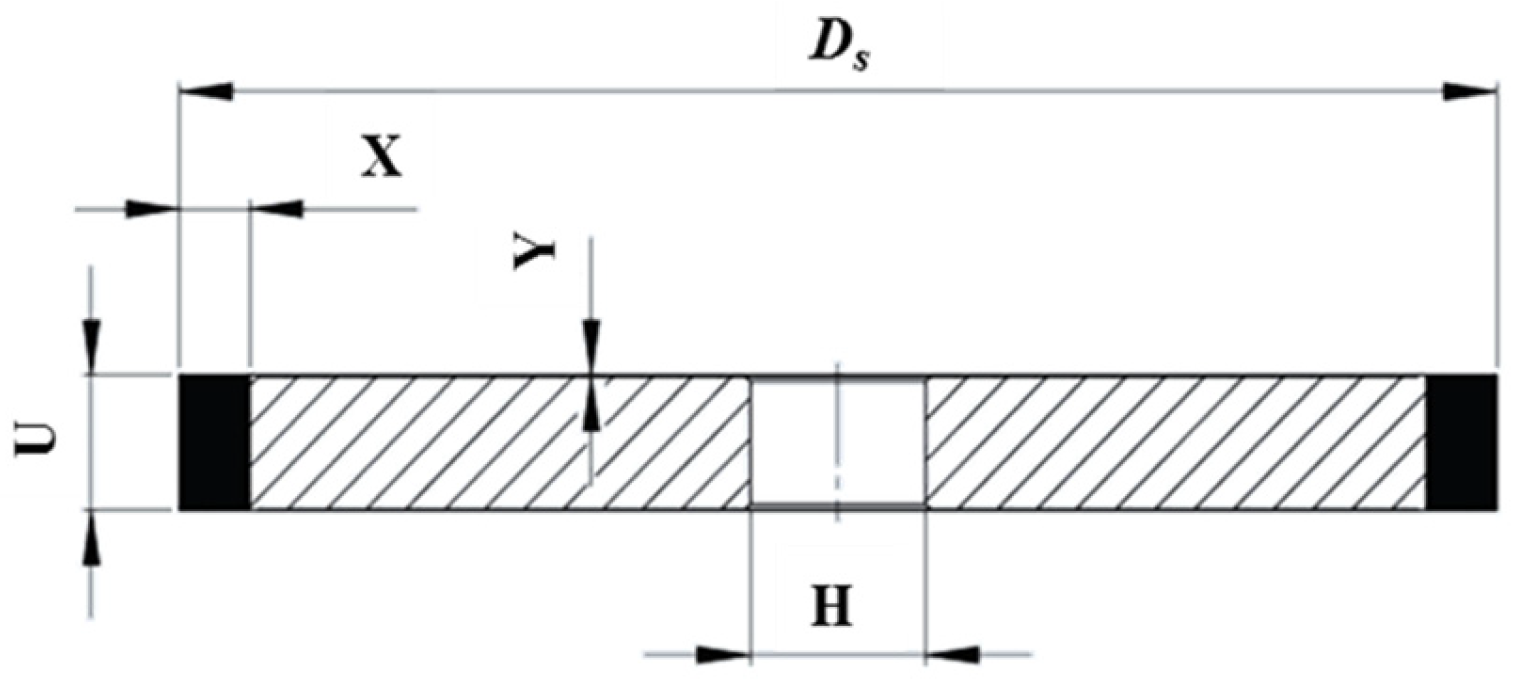
3.1. Characteristics of Tool Grinding Process
3.2. Recurrence Analysis
4. Results and Analysis
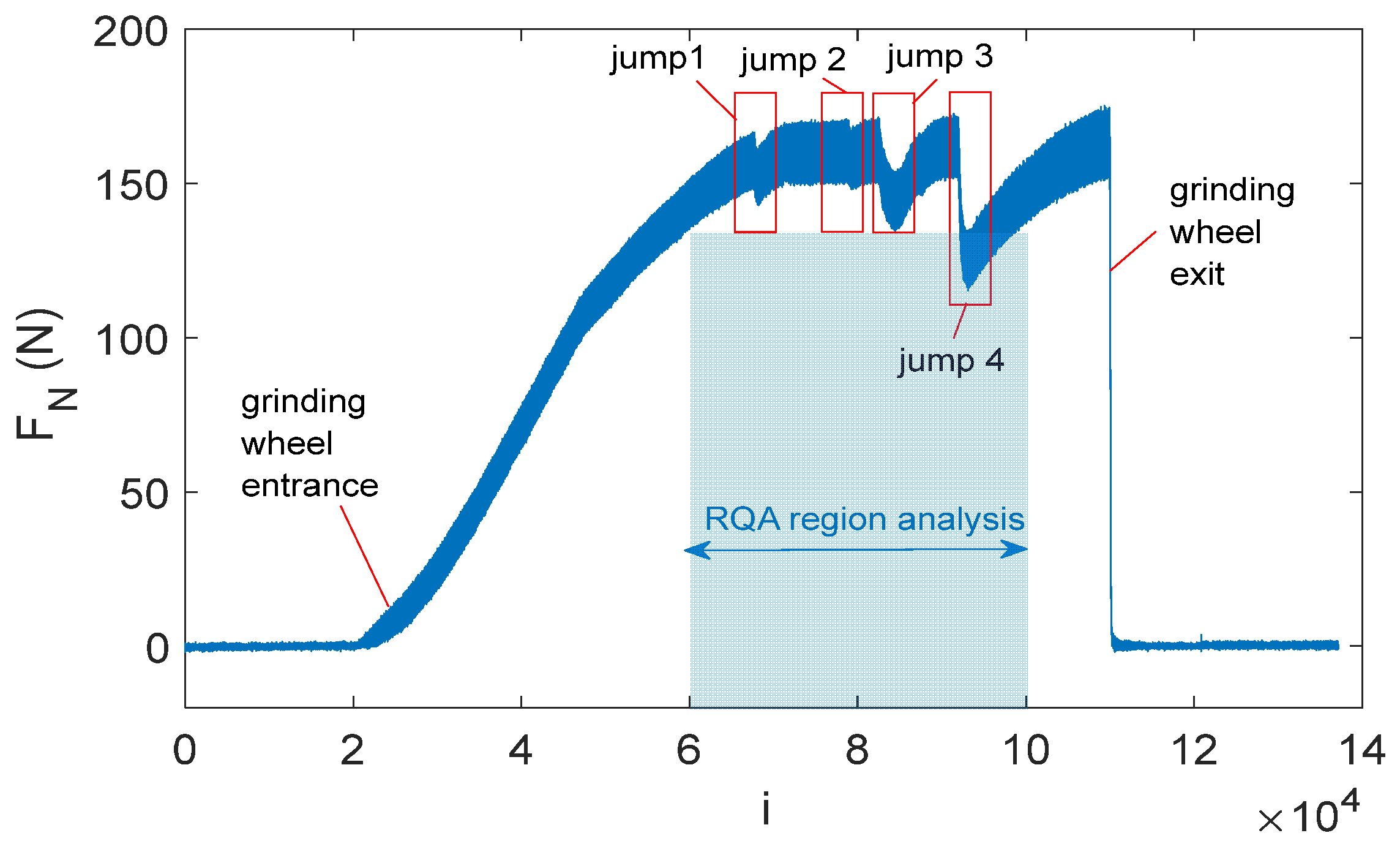
4.1. Measured Grinding Force and Defect Identification
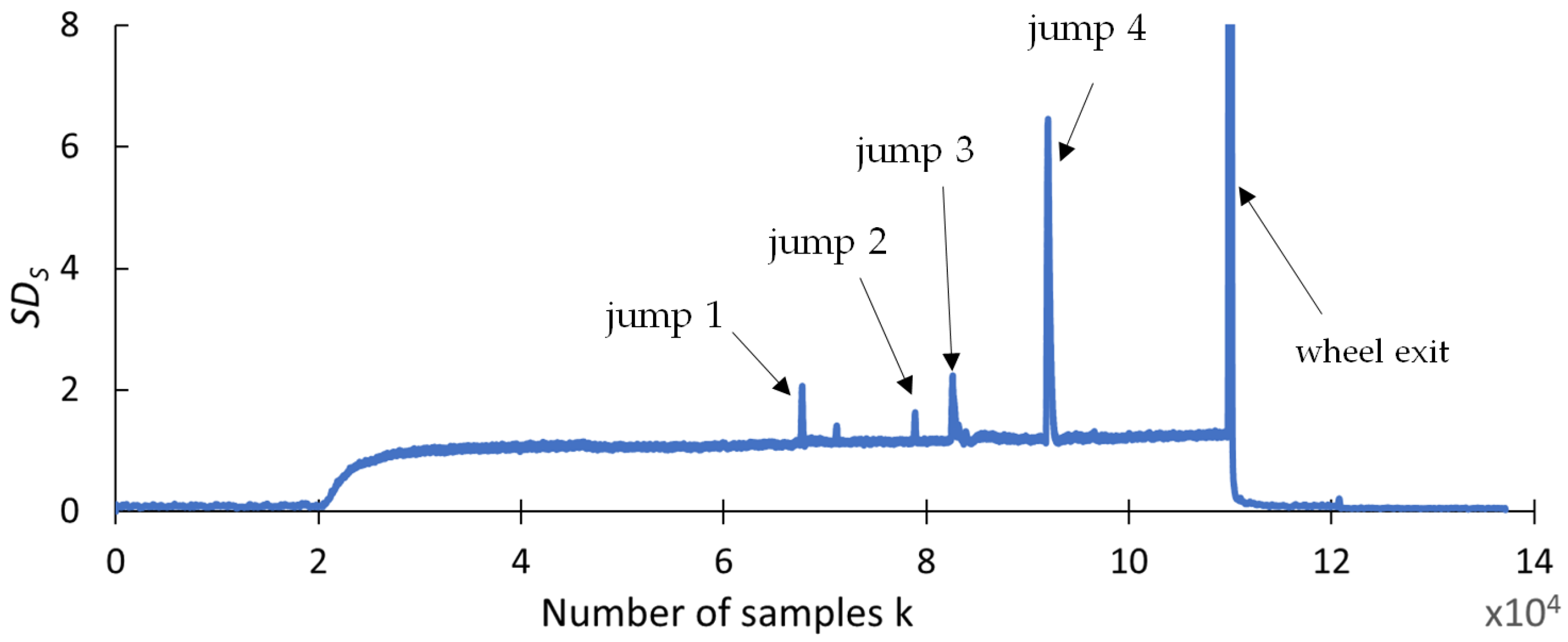
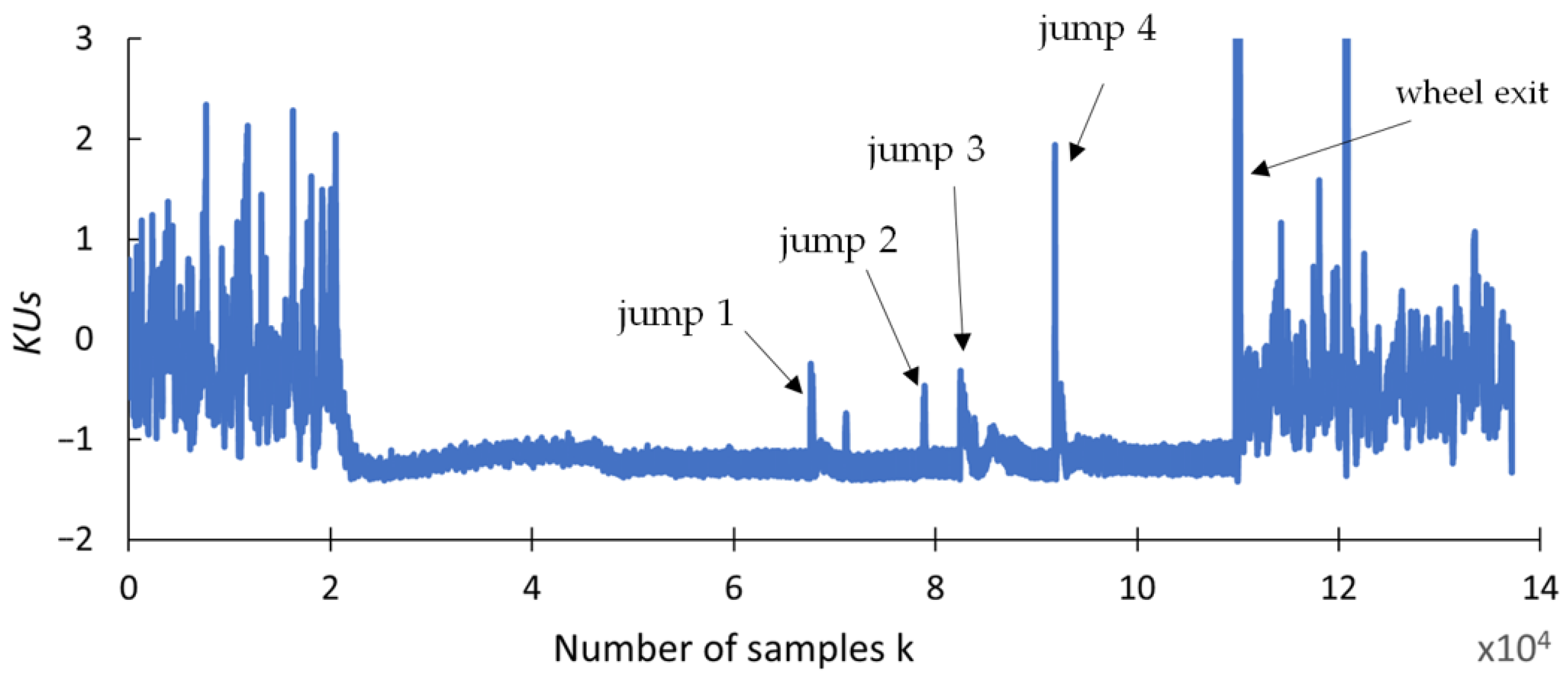
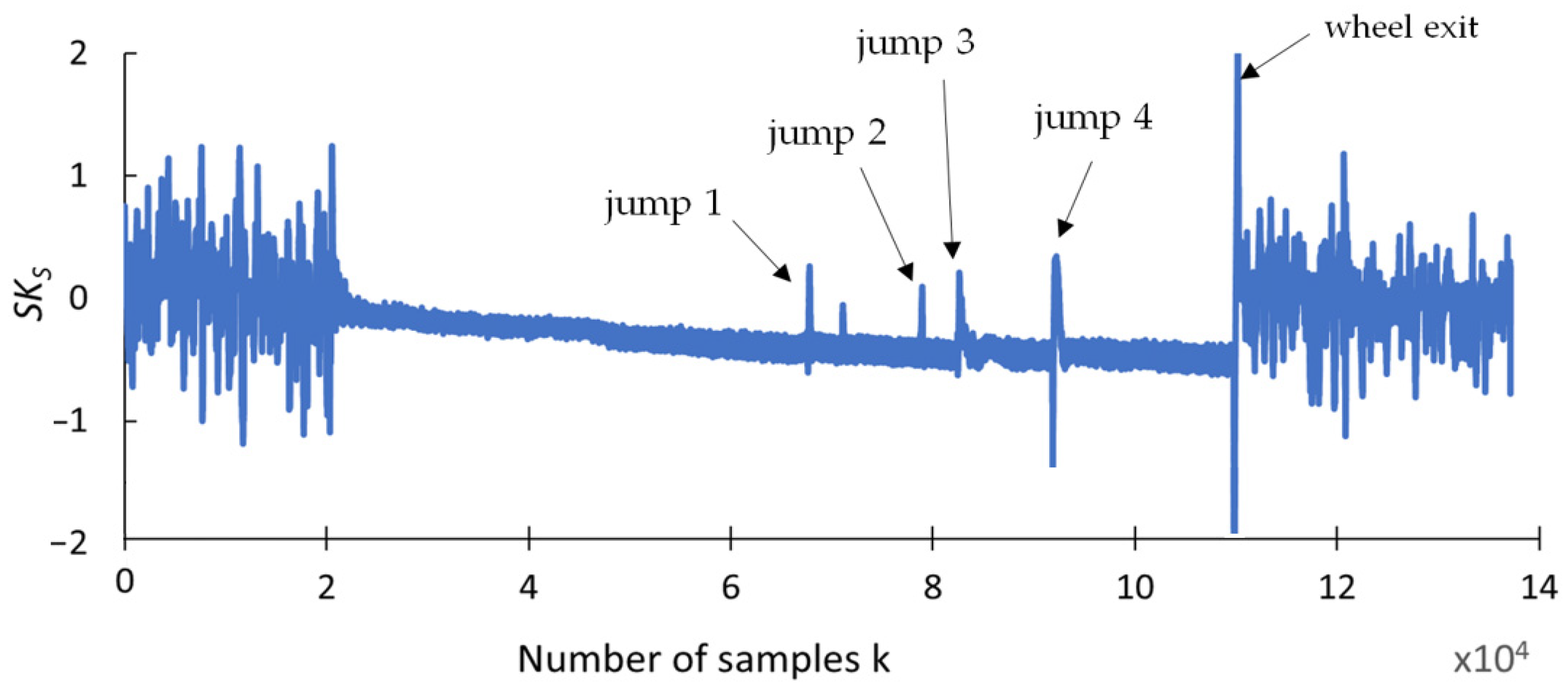
4.2. Statistical Analysis Results
4.3. Recurrence Plot Results
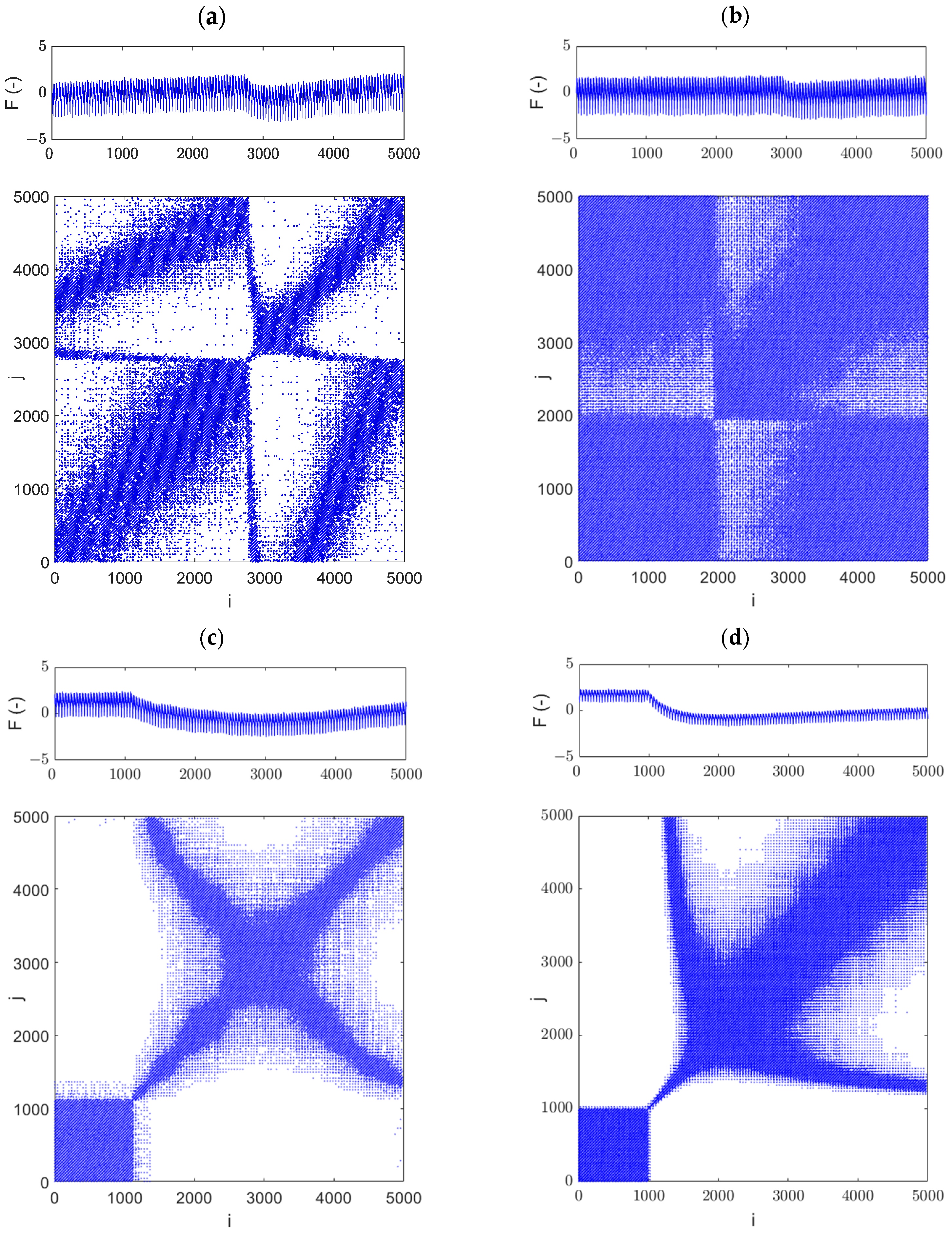
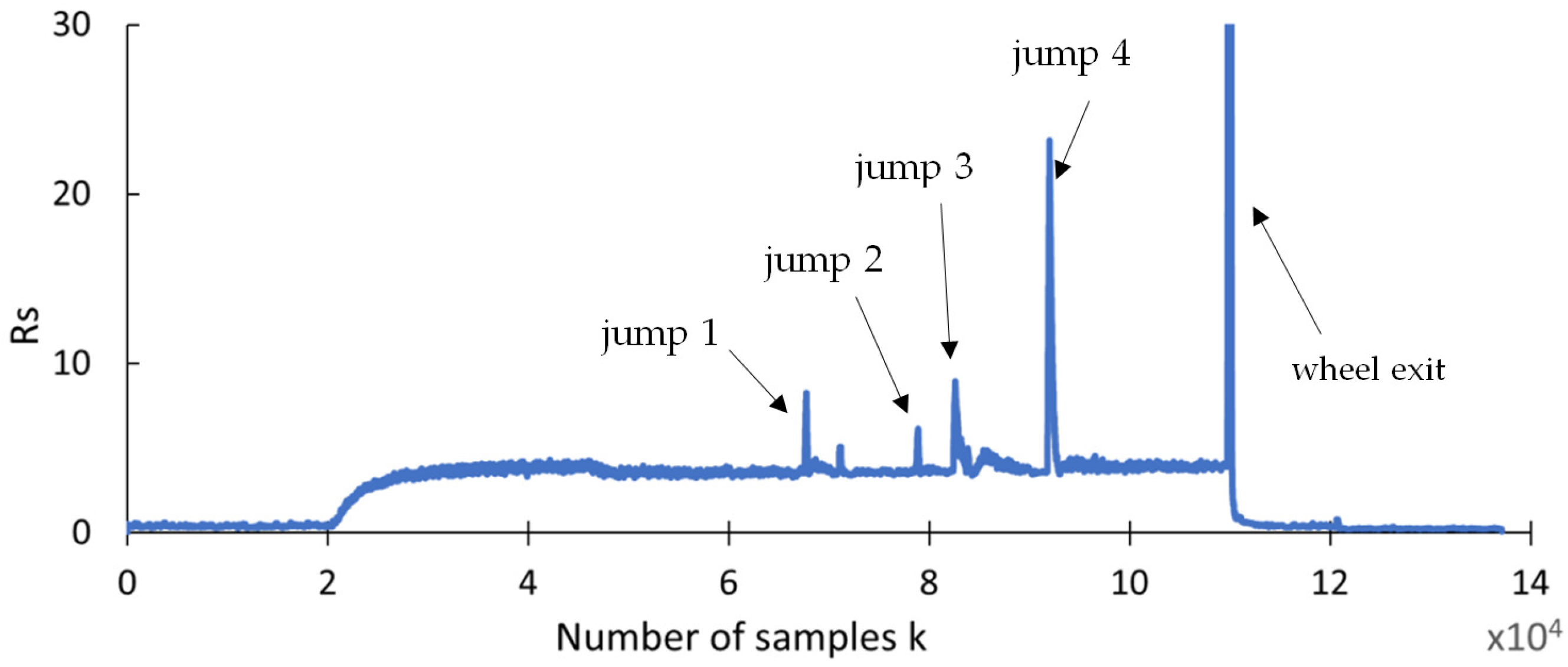
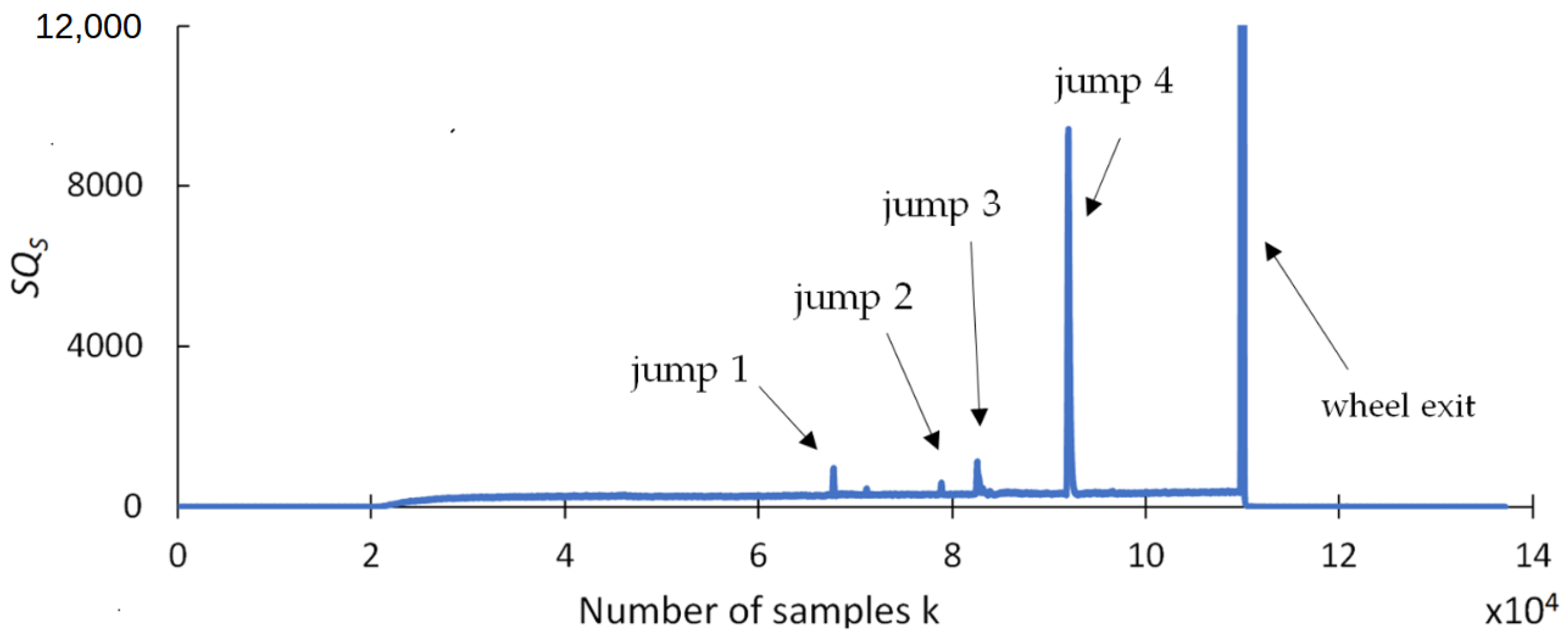
4.4. Recurrence Quantyfication Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Malkin, S.; Guo, C. Grinding Technology: Theory and Application of Machining with Abrasives, 2nd ed.; Industrial Press: New York, NY, USA, 2008. [Google Scholar]
- Hubert, C. Schleifen von Hartmetall-und Vollkeramik–Schaftfräsern. Ph.D. Thesis, Technische Universität Berlin, Berlin, Germany, 2011. [Google Scholar]
- Fujara, M. Methode zur rechnerunterstützten Auslegung und Optimierung der Geometrie des Vollhartmetall-Spiralbohrers. Ph.D. Thesis, Technische Universität Darmstadt, Darmstadt, Germany, 2011. [Google Scholar]
- Li, G.; Sun, J.; Li, J. Modeling and Analysis of Helical Groove Grinding in End Mill Machining. J. Mater. Process. Technol. 2014, 214, 3067–3076. [Google Scholar] [CrossRef]
- Burek, J.; Sałata, M.; Bazan, A. Influence of Grinding Parameters, on the Surface Quality in the Process of Single-Pass Grinding of Flute in Solid Carbide End Mill. Mechanik 2018, 10, 808–810. [Google Scholar] [CrossRef][Green Version]
- Burek, J.; Sałata, M.; Bazan, A. The Influence of the Type of Grinding Wheels Bond on Flute Grinding of Carbide Tools. Mechanik 2016, 8–9, 1130–1131. [Google Scholar] [CrossRef][Green Version]
- Uhlmann, E.; Hübert, C. Tool grinding of end mill cutting tools made from high performance ceramics and cemented carbides. CIRP Ann. Manuf. Technol. 2011, 60, 359–362. [Google Scholar] [CrossRef]
- Badger, J. Grinding of sub-micron-grade carbide: Contact and wear mechanisms, loading, conditioning, scrubbing and resin-bond degradation. CIRP Ann. Manuf. Technol. 2015, 64, 341–344. [Google Scholar] [CrossRef]
- Nadolny, K. A Review on Single-Pass Grinding Processes. J. Cent. South Univ. 2013, 20, 1502–1509. [Google Scholar] [CrossRef]
- Gostimirovic, M.; Sekulic, M.; Rodic, D. Thermal Study of the Creep-Feed Grinding—A Review. J. Prod. Eng. 2020, 23, 1–10. [Google Scholar] [CrossRef]
- Miao, Q.; Lu, M.; Ding, W.; Kuang, W.; Dai, C.; Yin, Z.; Zhang, M. Creep-Feed Grinding of Single Crystal Nickel-Base Turbine Blade Fir-Tree Roots: Tool Wear, Grinding Force, Temperature, and Surface Integrity. Int. J. Adv. Manuf. Technol. 2023, 126, 1453–1470. [Google Scholar] [CrossRef]
- Habrat, W.F. Effect of Bond Type and Process Parameters on Grinding Force Components in Grinding of Cemented Carbide. Procedia Eng. 2016, 149, 122–129. [Google Scholar] [CrossRef]
- Sałata, M. The Analysis of the Influence of Technological Parameters on the Grinding Temperature in the Single-Pass Grinding Process of Solid Carbide End Mill Flutes. Adv. Sci. Technol. Res. J. 2022, 16, 190–202. [Google Scholar] [CrossRef]
- Salmon, S. Creep-feed grinding is surprisingly versatile. Manuf. Eng. 2004, 11, 59–64. [Google Scholar]
- Burek, J.; Sałata, M. Up-Cut and down-Cut Grinding Flute in Solid Carbide End Mills. Mechanik 2015, 8–9, 59–62. [Google Scholar] [CrossRef]
- Żyłka, Ł.; Babiarz, R.; Płodzień, M. Comparison of up-cut and down-cut grinding of CFG (Creep-Feed Grinding) process of Inconel alloy. Mechanik 2014, 9, 349–351. [Google Scholar]
- Buk, J.; Sułkowicz, P.; Szeliga, D. The Review of Current and Proposed Methods of Manufacturing Fir Tree Slots of Turbine Aero Engine Discs. Materials 2023, 16, 5143. [Google Scholar] [CrossRef]
- Sulkowicz, P.; Babiarz, R.; Burek, J.; Buk, J.; Gancarczyk, K. A Method of Increasing the Accuracy of Low-Stiffness Shafts: Single-Pass Traverse Grinding Without Steady Rests. Acta Mech. Autom. 2022, 16, 357–364. [Google Scholar] [CrossRef]
- Zhang, X.; Xu, K.; Chen, P.; Chen, L.; Li, S. Indirect Measurement of Grinding Force in Cemented Carbide Processing Based on SSA-KELM Algorithm. Int. J. Precis. Eng. Manuf. 2024, 26, 849–858. [Google Scholar] [CrossRef]
- García-Ordás, M.; Alegre, E.; Alaiz, R.; González-Castro, V. Tool Wear Monitoring Using an Online, Automatic and Low Cost System Based on Local Texture. Mech. Syst. Signal Process. 2018, 112, 98–112. [Google Scholar] [CrossRef]
- Dai, J.; Su, H.; Wang, Z.; Xu, J.; Fu, Y.; Chen, J. Damage Formation Mechanisms of Sintered Silicon Carbide during Single-Diamond Grinding. Ceram. Int. 2021, 47, 28419–28428. [Google Scholar] [CrossRef]
- Malkin, S. Grinding Technology: Theory and Applications of Machining with Abrasives, 1st ed.; Ellis Horwood Series in Mechanical Engineering; Society of Manufacturing Engineers: Dearborn, MI, USA, 1989; ISBN 9780872634800. [Google Scholar]
- Dieye, M.; D’Acunto, A.; Martin, P. Modelling and Simulation Creep Feed Grinding Process. CISM Int. Cent. Mech. Sci. Courses Lect. 2005, 486, 235–246. [Google Scholar] [CrossRef]
- Ganeshraja, A.; Dheenathayalan, T. Analysis and Control of Vibration in Grinding machines. Int. J. Res. Eng. Technol. 2014, 3, 134–136. [Google Scholar] [CrossRef][Green Version]
- Hou, Z.B.; Komanduri, R. On the Mechanics of the Grinding Process—Part I. Stochastic Nature of the Grinding Process. Int. J. Mach. Tools Manuf. 2003, 43, 1579–1593. [Google Scholar] [CrossRef]
- Oh, J.Y.; Lee, W. Model-Based Tool Wear Detection and Life Prognostics for End-Mill. J. Manuf. Process. 2025, 133, 1086–1099. [Google Scholar] [CrossRef]
- Hirsch, E.; Friedrich, C. Data-Driven Tool Wear Prediction in Milling, Based on a Process-Integrated Single-Sensor Approach. arXiv 2024, arXiv:2412.19950. [Google Scholar] [CrossRef]
- Gao, S.; Duan, X.; Zhu, K.; Zhang, Y. Investigation of the Tool Flank Wear Influence on Cutter-Workpiece Engagement and Cutting Force in Micro Milling Processes. Mech. Syst. Signal Process. 2024, 209, 111104. [Google Scholar] [CrossRef]
- Aldekoa, I.; del Olmo, A.; Sastoque-Pinilla, L.; Sendino-Mouliet, S.; Lopez-Novoa, U.; de Lacalle, L.N.L. Early Detection of Tool Wear in Electromechanical Broaching Machines by Monitoring Main Stroke Servomotors. Mech. Syst. Signal Process. 2023, 204, 110773. [Google Scholar] [CrossRef]
- Hou, W.; Wang, J.; Wang, L.; Zhang, S. Novel Tool Wear Prediction Method Based on Multimodal Information Fusion and Deep Subdomain Adaptation. Mech. Syst. Signal Process. 2025, 224, 112128. [Google Scholar] [CrossRef]
- Wang, S.; Tian, Y.; Hu, X.; Wang, J.; Han, J.; Liu, Y.; Wang, J.; Wang, D. Identification of Grinding Wheel Wear States Using AE Monitoring and HHT-RF Method. Wear 2025, 205668, 562–563. [Google Scholar] [CrossRef]
- Pimenov, D.Y.; Ribeiro da Silva, L.R.; Kuntoğlu, M.; Abrão, B.S.; dos Santos Paes, L.E.; Linul, E. Review of Advanced Sensor System Applications in Grinding Operations. J. Adv. Res. 2025; in press. [Google Scholar] [CrossRef]
- Rusinek, R.; Lajmert, P.; Kecik, K.; Kruszynski, B.; Warminski, J. Chatter identification methods on the basis of time series measured during titanium superalloy milling. Int. J. Mech. Sci. 2015, 99, 196–207. [Google Scholar] [CrossRef]
- Eneyew, E.D.; Ramulu, M. Tool wear monitoring using microphone signals and recurrence quantification analysis when drilling composites. Adv. Mater. Res. 2013, 711, 239–244. [Google Scholar] [CrossRef]
- Mhalsekar, S.D.; Rao, S.S.; Gangadharan, K.V. Investigation on feasibility of recurrence quantification analysis for detecting flank wear in face milling. Int. J. Eng. Sci. Technol. 2010, 2, 23–38. [Google Scholar] [CrossRef]
- Ciecieląg, K.; Skoczylas, A.; Matuszak, J.; Zaleski, K.; Kecik, K. Defect detection and localization in polymer composites based on drilling force signal by recurrence analysis. Measurement 2021, 186, 110126. [Google Scholar] [CrossRef]
- Ciecielag, K.; Kecik, K.; Zaleski, K. Defects detection from time series of cutting force in composite milling process by recurrence analysis. J. Reinf. Plast. Compos. 2020, 39, 890–901. [Google Scholar] [CrossRef]
- Kecik, K.; Ciecielag, K. The effect of cutting parameters on defect detection based on recurrence analysis of cutting force signals obtained from GFRP composite milling. Measurements 2025, 239, 115406. [Google Scholar] [CrossRef]
- Nichols, J.M.; Trickey, S.T.; Seaver, M. Damage detection using multivariate recurrence quantification analysis. Mech. Syst. Signal Process. 2006, 20, 421–437. [Google Scholar] [CrossRef]
- Iwaniec, J. Investigation of selected mechanical systems by recurrence plots method. Int. J. Struct. Stab. Dyn. 2013, 13, 13400087. [Google Scholar] [CrossRef]
- Iwaniec, J.; Uhl, T.; Staszewski, W.J.; Klepka, A. Detection of changes in cracked aluminium plate determinism by recurrence analysis. Nonlinear Dyn. 2012, 70, 125–140. [Google Scholar] [CrossRef]
- Qian, Y.; Yan, R.; Hu, S. Bearing Degradation Evaluation Using Recurrence Quantification Analysis and Kalman Filter. IEEE Trans. Instrum. Meas. 2014, 63, 2599–2610. [Google Scholar] [CrossRef]
- Kecik, K.; Smagala, A.; Ciecielag, K. Diagnosis of angular contact ball bearing defects based on recurrence diagrams and quantification analysis of vibration signals. Measurement 2023, 216, 112963. [Google Scholar] [CrossRef]
- Kecik, K.; Smagala, A.; Lyubitska, K. Ball bearing fault diagnosis using recurrence analysis. Materials 2022, 15, 5940. [Google Scholar] [CrossRef]
- Zylka, L.; Plodzien, M.; Latalski, J.; Lajmert, P.; Rusinek, R. Recurrence Quantification Analysis (RQA) of Toroidal End Tool Milling Process. Appl. Sci. 2025, 15, 1347. [Google Scholar] [CrossRef]
- Lisowicz, J.; Krupa, K.; Leksycki, K.; Rusinek, R.; Wojciechowski, S. Analysis of Tool Wear in Finish Turning of Titanium Alloy Ti-6Al-4V Under Minimum Quantity Lubrication Conditions Observed with Recurrence Quantification Analysis. Materials 2025, 18, 79. [Google Scholar] [CrossRef] [PubMed]
- Eckmann, J.P.; Kamphorst, S.O.; Ruelle, D. Recurrence plots of dynamical systems. Europhys. Lett. 1987, 4, 973–977. [Google Scholar] [CrossRef]
- Goswami, B. A Brief Introduction to Nonlinear Time Series Analysis and Recurrence Plots. Vibration 2019, 2, 332–368. [Google Scholar] [CrossRef]
- Webber, C.L.; Zbilut, J.P. Dynamical assessment of physiological systems and states using recurrence plot strategies. J. Appl. Physiol. 1994, 76, 965–973. [Google Scholar] [CrossRef]
- Marwan, N.; Wessel, N.; Meyerfeldt, U.; Schirdewan, A.; Kurths, J. Recurrence-plot-based measures of complexity and their application to heart-rate-variability data. Phys. Rev. E 2002, 66, 026702. [Google Scholar] [CrossRef]





| Grade | Classification | Grain Size [μm] | Co [%] | Density [g/cm3] | Hardness HV30 | Transverse Rupture Strength [MPa] |
|---|---|---|---|---|---|---|
| TSF22 | Ultrafine | 0.2–0.5 | 8.2 | 14.5 | 1930 | 4400 |
| Workpiece Material | Cutting Speed [m/s] | Feed Rate [mm/min] | Grinding Direction | Grinding Length [mm] | Grinding Depth [mm] | Grinding Width [mm] | Coolant |
|---|---|---|---|---|---|---|---|
| TSF22 | 40 | 100 | Down grinding | 30 | 5.21 | 3 | Grinding oil |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sałata, M.; Babiarz, R.; Kęcik, K. Detection of Defects in Solid Carbide Cutting Tools During Creep-Feed Flute Grinding (CFG) Using Recurrence Analysis. Materials 2025, 18, 2743. https://doi.org/10.3390/ma18122743
Sałata M, Babiarz R, Kęcik K. Detection of Defects in Solid Carbide Cutting Tools During Creep-Feed Flute Grinding (CFG) Using Recurrence Analysis. Materials. 2025; 18(12):2743. https://doi.org/10.3390/ma18122743
Chicago/Turabian StyleSałata, Marcin, Robert Babiarz, and Krzysztof Kęcik. 2025. "Detection of Defects in Solid Carbide Cutting Tools During Creep-Feed Flute Grinding (CFG) Using Recurrence Analysis" Materials 18, no. 12: 2743. https://doi.org/10.3390/ma18122743
APA StyleSałata, M., Babiarz, R., & Kęcik, K. (2025). Detection of Defects in Solid Carbide Cutting Tools During Creep-Feed Flute Grinding (CFG) Using Recurrence Analysis. Materials, 18(12), 2743. https://doi.org/10.3390/ma18122743







