Abstract
We consider the effect of atomic impurities on the energy spectrum and electrical conductance of graphene. As is known, the ordering of atomic impurities at the nodes of a crystal lattice modifies the graphene spectrum of energy, yielding a gap in it. Assuming a Fermi level within the gap domain, the electrical conductance diverges at the ordering of graphene. Hence, we can conclude about the presence of a metal–dielectric transition. On the other hand, for a Fermi level occurring outside of the gap, we see an increase in the electrical conductance as a function of the order parameter. The analytic formulas obtained in the Lifshitz one-electron strong-coupling model, describing the one-electron states of graphene doped with substitutional impurity atoms in the limiting case of weak scattering, are compared to the results of numerical calculations. To determine the dependence of the energy spectrum and electrical conductance on the order parameter, we consider both the limiting case of weak scattering and the case of finite scattering potential. The contributions of the scattering of electrons on a vapor of atoms to the density of states and the electrical conductance of graphene with an admixture of interstitial atoms are studied within numerical methods. It is shown that an increase in the electrical conductance with the order parameter is a result of both the growth of the density of states at the Fermi level and the time of relaxation of electron states. We have demonstrated the presence of a domain of localized extrinsic states on the edges of the energy gap arising at the ordering of atoms of the admixture. If the Fermi level falls in the indicated spectral regions, the electrical conductance of graphene is significantly affected by the scattering of electrons on clusters of two or more atoms, and the approximation of coherent potential fails in this case.
1. Introduction
Modifications of graphene with impurities, defects, and chemical functional groups are of increasing interest, as they change the physical properties of graphene and make it a basic system, generating a new class of functional materials. Such materials can be supposedly used in nanoelectromechanical systems, systems of accumulation of hydrogen, etc. as competitors of silicon in electronic devices, though the quasirelativistic spectrum of charge carriers in graphene hampers its application, for example, in field transistors due to the absence of a gap in its spectrum. However, it is worth noting that the impurities can induce the appearance of such a gap.
Indeed, within the self-consistent meta-gradient approximation and the method of projection of adjoint waves [1], the numerical calculations executed by this method showed the opening of a gap in the energy spectrum of graphene due to the presence of an impurity. The electronic structures of the isolated monolayer of graphene, two- and three-layer graphene, and graphene grown on ultrathin layers of hexagonal boron nitride (h-BN) were calculated in [2] in the frame of the pseudopotential method. It was shown that a forbidden energy band 57 meV in width appears in graphene grown on a monolayer of h-BN.
Similar calculations for graphene with impurities of aluminum, silicon, phosphorus, sulfur, boron, nitrogen, and lithium were executed in works [3,4], where the opening of a gap was demonstrated, in particular.
It is clear that the numerical calculations should be supported by a simple but adequate model presenting the exact analytic solutions. The theory of the modification of the spectrum of graphene caused by an increase in the concentration of point impurities was developed in works [5,6,7], where the possibility of the metal–dielectric transition was predicted, and the dominant role of a quasigap filled by localized states in the scattering by pairs and triples of impurity centers was indicated.
The Kubo–Greenwood quantum-mechanical formalism in the Lifshitz one-band model was applied in [8,9,10,11,12,13] to study the influence of impurity atoms or atoms adsorbed on the surface on the electronic structure and electrical conductance of graphene. There, the method of the reduction of the Hamiltonian to the three-diagonal form was developed to study the influence of completely ordered impurity atoms on the energy spectrum and electrical conductance of graphene. In work [10], it was found that a gap of 0.45 eV in width appears in the energy spectrum of electrons of graphene deposited on a potassium substrate. It was assumed that the appearance of this gap is associated with a change in the symmetry of the crystal. This assumption was confirmed in work [14], where the influence of the atomic ordering on the energy spectrum and electrical conductance of an alloy was analytically studied. It was established [14] that, for a long-range ordering of the alloy, a gap arises in the energy spectrum of electrons. It was also found that, in the case where the Fermi level falls in the domain of the gap and at a long-range atomic ordering, a metal–dielectric transition appears in the alloy.
We note that, having the Fermi level falling in the gap domain, the velocity of an electron can lower its speed on such a level. This leads to a decrease in the mobility of electrons and in the electrical conductance, which can worsen the functional characteristics of graphene.
Introducing the notation as the ordering parameter, . as the difference in the scattering potentials of impurity atoms and carbon, and as the impurity concentration, it was established in Ref. [15] that a gap with width and positioned at point arises in the graphene energy spectrum, as a consequence of the ordering of substitutional atoms at nodes of the crystal lattice. Assuming a Fermi level within the gap domain, at the ordering of graphene, the electrical conductance diverges; hence, we can conclude that we are in the presence of a metal–dielectric transition. On the other hand, for a Fermi level occurring outside of the gap, we see an increase in the electrical conductance as a function of the order parameter . As at the concentration , the electrical conductance of graphene , i.e., graphene transits into the state of ideal conductance.
It is worth indicating the different nature of a gap in the energy spectrum of graphene related to edge effects. Work [16] presents an experimental study of the appearance of the energy gap in armchair-like graphene nanoribbons, which increases as the nanoribbon width decreases. In works [17,18] in the model of strong coupling, selection rules for optical transitions between the valence and the conductance zones were determined for armchair and zigzag graphene nanoribbons. Electron and optical properties of inhomogeneous two-layer graphene nanoribbons in the external magnetic field were considered in [19]. Based on the results of numerical calculations, it was shown there that the electron and optical properties of nanoribbons depend strongly on the competition between the magnetic quantization, width of nanoribbons, and arrangement configuration of such nanoribbons. Work [20] gives a review of the electron and optical properties of graphene nanoribbons in magnetic and electric fields with regard to the effects of side limitation, curvature, and structural inhomogeneities. The theoretically predicted parabolic subzones, edge-localized states, opening of a gap, and Landau’s subzones were identified by various experimental measurements.
In recent times, several tens of works have been published on the influence of various types of deformations on the electron properties of (mainly, defectless) graphene (see, e.g., review [21]). The results of the first calculations within density functional theory [22] asserted that even small deformations can cause the appearance of a forbidden zone. The calculations in the model of strong coupling and linear elasticity theory [23] showed that the forbidden zone appears only at the tensile deformations (~23%) close to the rupture deformation (≈27%). Thus, many questions remain open and require subsequent discussion.
The goal of the present work is to clarify the nature of the influence of the ordering of a substitutional impurity on the appearance of a gap in the energy spectrum and on the electric conductance of graphene.
The conclusions in work [15] were based on the results of analytical studies of the energy spectrum and electrical conductance of graphene performed in the approximation of the coherent potential. However, the domain of convergence of the cluster expansion used in [15] for a Green’s function and the domain of validity of the approximation of the coherent potential were not analyzed.
In the present work, we will consider the interconnection between a change in the electrical conductance, changes in the energy spectrum, and the decay time for electron states under the ordering of impurity atoms in graphene.
2. Theoretical Model
The Hamiltonian in the Lifshitz one-electron strong-coupling model describing the one-electron states of graphene doped with substitutional impurity atoms can be presented in the following form [15]:
where is a nondiagonal matrix element of the Hamiltonian (hopping integral) in the Wannier representation and is independent of the random arrangement of atoms in the approximation of diagonal disorder; is a diagonal matrix element taking the values or depending on that which the atoms or is placed at node ; is the number of an elementary cell, and is the number of a node of the sublattice in the elementary cell.
Let us add to and subtract the translationally invariant operator from Equation (1), where is a diagonal matrix element of the Hamiltonian of some effective ordered medium (coherent potential), depending on the sublattice number. As a result, the Hamiltonian of graphene reads
The formula for the coherent potential will be given below.
The retarded Green’s function of graphene, which is an analytic function in the upper half-plane of values of the complex energy z, is defined as
A Green’s function satisfies the equation
where
is the Green’s function of the effective medium corresponding to the Hamiltonian in Equation (2). The scattering T-matrix can be presented in the form of an infinite series [15]:
Here,
where
is the operator of scattering on one node, and I is the identity operator.
The terms of Equation (6) describe the processes of multiple scattering of electrons on clusters comprising one, two, three, etc. scattering centers.
In work [15], it was shown that the contributions of the processes of the scattering of electrons on clusters to the density of states and to the electrical conductance decrease and are guided by some small parameter [24], as the number of atoms in a cluster increases. The formula for will be presented in the following.
Neglecting the contributions of the processes of scattering on clusters of three or more atoms, which are small due to the parameter , we give the density of one-electron states of graphene in the following form [15]:
where is the number of sublattices of graphene.
Using the Kubo–Greenwood formula [25] and neglecting the contribution of the processes of scattering on clusters of three and more atoms, we write the static electrical conductance of graphene (at T = 0) as [15]
, , , and and are the retarded and advanced Green’s functions, respectively; is the volume of an elementary cell of graphene, is the volume per atom, is Planck’s constant, and
where is the Fourier transform of the Green’s function of an effective medium, and is the radius-vector of node . The wave vector varies in the limits of the Brillouin zone of graphene.
The operator of the electron velocity projection is given by
where is the Fourier transform of the hopping integral. We calculate in the approximation of the nearest neighbors:
where is the hopping integral [26] and is the radius-vector of node .
The Fermi level μ is determined from the relation
where is the mean number of electrons per atom whose energies belong to the energy zone.
In Equations (9) and (10), is the probability of the filling of node of the crystal sublattice by atoms of the sort . We have
where is the concentration of impurity atoms and is the long-range atomic order parameter.
In Equations (9) and (10), is the probability of the filling of node by atoms of the sort under the condition that an atom of the sort occupies node (the parameter of binary interatomic correlations in the filling of nodes of the crystal lattice by impurity atoms).
The probabilities are determined by the interatomic pair correlations via [27,28]
where δ is the Kronecker delta function. Note that the interatomic pair correlations also satisfy the relation
Here, is a random number equal to 1, if an atom of the sort occupies node , or to zero in the opposite case; . The brackets mean the averaging over the distribution of impurity atoms at nodes of the crystal lattice.
The coherent potential can be determined from the condition , which yields the equation [15]
Setting , we obtain
where
is the difference of the scattering potentials for the components of graphene.
Solving the system of Equations (11) and (18), we find the values of the coherent potential
.
In the limiting case of weak scattering , where is the half-width of the energy zone of pure graphene, the given theoretical model admits analytic solutions [14]. It was established that the arising gap in width is centered at the point .
Equation (15) implies that the maximum order parameter . For and , the gap is placed, respectively, to the right and left of the Dirac point on the energy scale.
At the electron concentration (Equation (14)), at which the Fermi level falls in the arising gap, the electrical conductance tends to zero at the ordering of an impurity, , i.e., a metal–dielectric transition occurs [15].
At the electron concentration (Equation (14)) such that the Fermi level is outside the arising gap, the electrical conductance increases with the order parameter [15]. As the order parameter tends to its maximum value , the electrical conductance diverges, , i.e., graphene transits in the state of ideal conductance.
We recall that the contributions of the processes of the scattering of electrons on clusters to the density of states and to the electrical conductance decrease and are guided by some small parameter [24], as the number of atoms in a cluster increases. This parameter is
The parameter can be represented in the form [14]
Using formula obtained in [14] in the limiting case of weak scattering , it can be shown that the parameter takes values in a narrow interval of energies in the energy gap:
The parameter is small except for the narrow energy intervals (Equation (23)) on the gap edges. As the value of the energy tends to the gap edge, [14], whereas the parameter (Equation (22)).
Thus, the processes of scattering on clusters give a significant contribution to the density of states at the energies of electrons lying in interval (Equation (23)). The product σxx·d enters the formula for the electrical resistance of a graphene layer
where l is the length of a graphene layer along the axis x, and L is the layer width. Here, is the thickness of graphene. The axis x is directed from a carbon atom to its nearest neighbor. The values of σxx·d are given in units of .
To establish the nature of the dependence of the electrical conductivity on the order parameter η, we consider both the limiting case of weak scattering, , and the case of a finite value of the scattering potential .
If the order parameter η tends to its maximum value, , the nodes of sublattice 2 are mainly occupied by carbon atoms. In this case, Equations (15) and (18) imply that the imaginary part of the coherent potential for this sublattice tends to zero, , and the formula for the electrical conductance (Equation (10)) in the approximation of coherent potential takes the form
where is the partial density of states for the second sublattice.
For the three-dimensional crystals with a simple lattice in the approximation of effective mass, Equation (25) with the corresponding and takes the well-known form
where is the number of electrons in unit volume with energies less than the Fermi level, is the effective mass of an electron, and is the relaxation time of electron states, which is defined by the relation
3. Results
In Figure 1, we present the results of numerical calculations of the density of states of graphene g(ε) by Equation (9) at the substitutional impurity concentration and different values of the scattering potential [ (a), (b)] and the parameter of binary interatomic correlations on the first coordinate sphere. The energy is given in units of the energy zone half-width .
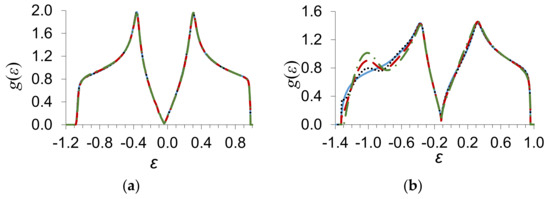
Figure 1.
Dependence of the density of electron states on the energy at the concentration of a substitutional impurity , for different values of the parameter of binary interatomic correlations on the first coordinate sphere , , and values of the scattering potential: (a) , (b) . The density of electron states calculated in the approximation of coherent potential is shown by a continuous curve with regard to the processes of scattering on the pairs of atoms in the limits of the first coordinate sphere; the dotted curve corresponds to , the dashed line to , and the dash-dotted curve to .
It is seen from Figure 1b that the appearance of the interatomic correlations is accompanied by the appearance of a characteristic burst on the curve of the energy dependence of the density of electron states. Its value increases with the parameter of correlations . The curves describing the density of electron states in the approximation of coherent potential with regard to the processes of scattering on the pairs of atoms in Figure 1a practically coincide for small values of the scattering parameter .
In Figure 1b, the continuous curve describes the density of electron states g(ε) of graphene, which is calculated in the approximation of coherent potential according to the first term in Equation (9). The dotted curve gives the density of states g(ε) calculated with regard to the processes of scattering on the pairs of atoms located in the limits of the first coordinate sphere in the case of the completely disordered arrangement of impurity atoms, , . The values of the density of states g(ε), calculated with regard to the processes of scattering on the pairs of atoms in the limits of three coordinate spheres and in the limits of ten coordinate spheres, practically coincide with the results of calculations that consider the scattering on the pairs in the limits of the first coordinate sphere. Thus, we may conclude that the domain of electron states of an impurity in graphene in the model under study is spatially bounded by the first coordinate sphere.
In Figure 2 and Figure 3, we show the density of electron states g(ε) and the electrical conductance σxx(μ) as functions of the energy ε and the Fermi level μ, respectively; d means the thickness of a graphene layer. The calculations of g(ε) and σxx(μ) are carried out by Equations (9) and (10). The values of the energy ε and the Fermi level μ are given in units of the energy zone half-width . The substitutional impurity concentration , the order parameter , the parameter of binary interatomic correlations , the scattering potential (Figure 2), and (Figure 3).
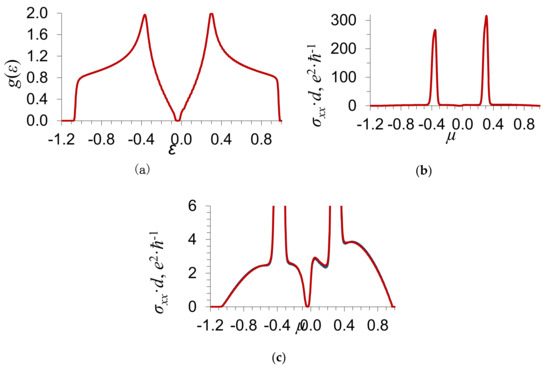
Figure 2.
Dependence of (a) the density of electron states g(ε) on the energy ε; (b) the electrical conductance σxx(μ) on the Fermi level μ, where d is the thickness of a graphene layer; and (c) the electrical conductance σxx(μ) on the Fermi level μ (shown on a larger scale). The substitutional impurity concentration , the scattering potential , the order parameter , and the parameter of binary interatomic correlations . The blue curve shows the results of calculations in the approximation of coherent potential, while the red curve shows those with regard to the processes of the scattering of electrons on the pairs of atoms of the first coordinate sphere.
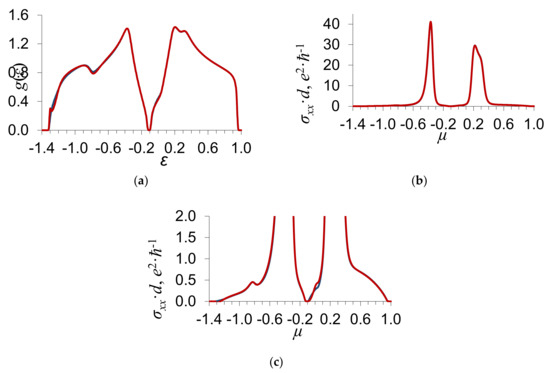
Figure 3.
Dependence of (a) the density of electron states g(ε) on the energy ε; (b) the electrical conductance σxx(μ) on the Fermi level μ, where d is the thickness of a graphene layer; and (c) the electrical conductance σxx(μ) on the Fermi level μ (shown on a larger scale). The substitutional impurity concentration , the scattering potential , the order parameter , and the parameter of binary interatomic correlations . The blue curve shows the results of calculations in the approximation of the coherent potential, while the red curve shows those with regard to the processes of the scattering of electrons on the pairs of atoms of the first coordinate sphere.
Figure 2 and Figure 3 indicate that, at the ordering of impurity atoms, there appears a gap in the energy spectrum of graphene in which the density of states g(ε) = 0 (Figure 2a). The electrical conductance of graphene σxx(μ) for the Fermi level located in the gap is equal to zero. For the Fermi level outside the gap, the electrical conductance of graphene is nonzero and increases with the density of states on the Fermi level.
As distinct from the above-described limiting case of weak scattering , where the gap width increases with the scattering potential , the dependence of the gap width on in the case of strong scattering has a more complex character. As the absolute value of the scattering potential increases from to , the gap width decreases a little. The dependences of the electrical conductance on the scattering potential and the order parameter also have a more complicated character than in the limiting case of weak scattering [14].
With the purpose to clarify the character of the dependence of the electrical conductance σxx on the scattering potential and the order parameter η, we present the dependence of the electrical conductance of graphene σxx on the order parameter of impurity atoms η for different values of the scattering potential in Figure 4 and Figure 5. The number of electrons per atom, whose energies are in the energy zone, is equal to . For such value of , the Fermi level μ(η) calculated by Equation (14) lies to the right of the energy gap. In Figure 4b and Figure 5b, we show the Fermi level μ(η) as a function of the order parameter of an impurity η. In Figure 4c and Figure 5c, we give the dependence of the partial density of states gi(μ) at the Fermi level on the order parameter of an impurity η; i = 1, 2 is the number of a sublattice. Figure 4d and Figure 5d present the dependence of the imaginary part of the coherent potential at the Fermi level on the order parameter of impurity atoms η.
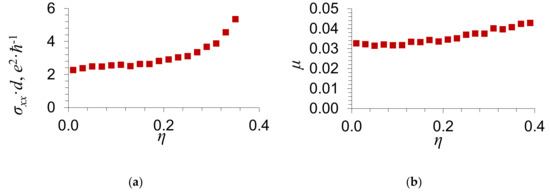
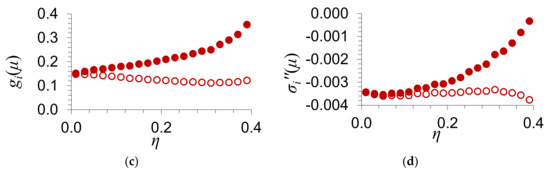
Figure 4.
Dependence of (a) the electrical conductance of graphene σxx; (b) the Fermi level μ; (с) the partial density of states at the Fermi level; and (d) the imaginary part of the coherent potential at the Fermi level on the order parameter of impurity atoms η. The substitutional impurity concentration and the scattering potential . Circles correspond to and of the first sublattice, in which the impurity atoms are located in the case of full order. Filled circles show and for the second sublattice.
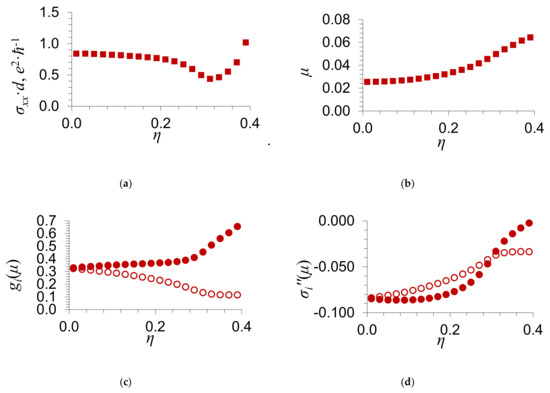
Figure 5.
Dependence of (a) the electrical conductance of graphene σxx; (b) the Fermi level μ; (с) the partial density of states at the Fermi level; and (d) the imaginary part of the coherent potential at the Fermi level on the order parameter of impurity atoms η. The substitutional impurity concentration and the scattering potential . Circles correspond to and of the first sublattice, in which the impurity atoms are located in the case of full order. Filled circles show and for the second sublattice.
It is seen from Figure 4 and Figure 5 that the electrical conductance of graphene increases with the order parameter of an impurity η.
The numerical results presented in Figure 4 and Figure 5 for the electrical conductance σxx agree qualitatively with the formula obtained in the limiting case of weak scattering [14] and with Equation (25). In this case, we took into account that the dependence of the electrical conductance of graphene, which was obtained in the limiting case of weak scattering [14], on the ordering of an admixture is applicable only in the case of such concentration at which the Fermi level lies in the vicinity of the Dirac point. In the present work, we give the results of numerical calculations of the dependence of the electrical conductance of graphene σxx on the ordering parameter η. We have considered such values of concentrations and scattering potentials, at which the Fermi level lies in the vicinity of the Dirac point, as well as outside it.
As the order parameter η tends to the maximum value, , the electrical conductance . As is seen from Equation (25), this is caused by an increase in the density of states at the Fermi level and in the relaxation time with the order parameter [as , the imaginary part of the coherent potential ].
4. Conclusions
We note that values of the density of states and the electrical conductance of graphene cannot be used, if the Fermi level falls in the interval (Equation (23)) of energies at the gap edges. The values of the density of states g(ε) calculated with regard to the processes of scattering on the pairs of atoms located in the limits of three coordinate spheres and in the limits of ten coordinate spheres practically coincide with the results of calculations involving the scattering on the pairs located in the limits of the first coordinate sphere. Thus, we may conclude that the domain of electron states of the impurity in graphene in the model under consideration is spatially bounded by the first coordinate sphere. We showed the existence of domains with localized extrinsic states on the edges of the energy gap arising at the ordering of atoms of the admixture. If the Fermi level falls in the indicated domains, the processes of the scattering of electrons on clusters consisting of at least two atoms contribute essentially to the electrical conductance of graphene, and the approximation of coherent potential fails in this case.
We have established that, at the ordering of impurity atoms, a gap appears in the energy spectrum of graphene. Its width depends on the order parameter η and the difference in the scattering potentials of an impurity atom and a carbon atom.
In the limiting case of weak scattering , we have shown that the gap arising at the ordering of impurity atoms in the energy spectrum of graphene has a width of and is centered at the point , where is the energy zone half-width of pure graphene.
At the electron concentration (Equation (14)), when the Fermi level falls in the arising gap, the electrical conductance tends to zero at the ordering of an impurity, , i.e., a metal–dielectric transition arises.
If the Fermi level lies outside the gap, the electrical conductance σxx increases with the order parameter and tends to infinity, as the order parameter .
An increase in the electrical conductance σxx of graphene with the order parameter η of impurity atoms is caused by an increase in the density of states at the Fermi level, , and by an increase in the relaxation time of electron states, , tending to infinity, as .
Author Contributions
S.P.R. did the calculations.; I.G.V. constructed and optimized the computational models; R.M. responsible for the software; S.K. responsible of methodology and conceptualization; S.B. supervised the work and did main calculation. All authors contributed to manuscript preparation. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the NATO Partnership and Cooperative Security Committee, in the framework of the Science for Peace and Security (SPS) Programme, project SPS G5351—“Nanocomposite Based Photonic Crystal Sensors of Biological and Chemical Agents,” by the Ministry of Education and Science of Ukraine (project No. 19BP07–03), and by the National Academy of Sciences of Ukraine (project No. 0116U002067, KPKVK 6541230).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Sun, J.; Marsman, M.; Csonka, G.I.; Ruzsinszky, A.; Hao, P.; Kim, Y.-S.; Kresse, G.; Perdew, J.P. Self-consistent meta-generalized gradient approximation within the projector-augmented-wave method. Phys. Rev. B 2011, 84, 035117. [Google Scholar] [CrossRef]
- Yelgel, C.; Srivastava, G.P. Ab initio studies of electronic and optical properties of graphene and graphene–BN interface. Appl. Surf. Sci. 2012, 258, 8338–8342. [Google Scholar] [CrossRef]
- Denis, P.A. Band gap opening of monolayer and bilayer graphene doped with aluminium, silicon, phosphorus, and sulphur. Chem. Phys. Lett. 2010, 492, 251. [Google Scholar] [CrossRef]
- Deng, X.; Wu, Y.; Dai, J.; Kang, D.; Zhang, D. Electronic structure tuning and band gap opening of graphene by hole/electron codoping. Phys. Lett. A 2011, 365, 3890–3894. [Google Scholar] [CrossRef]
- Skrypnyk, Y.V.; Loktev, V.M. Impurity effects in a two-dimensional system with the Dirac spectrum. Phys. Rev. B 2006, 73, 241402. [Google Scholar] [CrossRef]
- Zhang, Y.-Y.; Tsai, W.-F.; Chang, K.; An, X.-T.; Zhang, G.-P.; Xie, X.-C.; Li, S.-S. Electron delocalization in gate-tunable gapless silicene. Phys. Rev. B 2013, 88, 125431. [Google Scholar] [CrossRef]
- Pershoguba, S.S.; Skrypnyk, Y.V.; Loktev, V.M. Numerical simulation evidence of spectrum rearrangement in impure graphene. Phys. Rev. B 2009, 80, 214201. [Google Scholar] [CrossRef]
- Radchenko, T.M.; Shylau, A.A.; Zozoulenko, I.V. Influence of correlated impurities on conductivity of graphene sheets: Time-dependent real-space Kubo approach. Phys. Rev. B 2012, 86, 035418. [Google Scholar] [CrossRef]
- Radchenko, T.M.; Tatarenko, V.A.; Sagalianov, I.Y.; Prylutskyy, Y.I.; Szroeder, P.; Biniak, S. On adatomic-configuration-mediated correlation between electrotransport and electrochemical properties of graphene. Carbon 2016, 101, 37–48. [Google Scholar] [CrossRef]
- Radchenko, T.M.; Tatarenko, V.A.; Sagalianov, I.Y.; Prylutskyy, Y.I. Effects of nitrogen-doping configurations with vacancies on conductivity in grapheme. Phys. Lett. A 2014, 378, 2270–2274. [Google Scholar] [CrossRef]
- Radchenko, T.M.; Shylau, A.A.; Zozoulenko, I.V.; Ferreira, A. Effect of charged line defects on conductivity in graphene: Numerical Kubo and analytical Boltzmann approaches. Phys. Rev. B 2013, 87, 195448. [Google Scholar] [CrossRef]
- Radchenko, T.M.; Shylau, A.A.; Zozoulenko, I.V. Conductivity of epitaxial and CVD graphene with correlated line defects. Solid State Commun. 2014, 195, 88–94. [Google Scholar] [CrossRef]
- Radchenko, T.M.; Tatarenko, V.A.; Sagalianov, I.Y.; Prylutskyy, Y.I. Configurations of structural defects in graphene and their effects on its transport properties. In Graphene: Mechanical Properties, Potential Applications and Electrochemical Performance; Edwards, B.T., Ed.; Nova Science Publ.: Hauppauge, NY, USA, 2014; Chapter 7; pp. 219–259. [Google Scholar]
- Los’, V.F.; Repetsky, S.P. A theory for the electrical conductivity of an ordered alloy. J. Phys. Condens. Matter 1994, 6, 1707–1730. [Google Scholar] [CrossRef]
- Repetsky, S.P.; Vyshyvana, I.G.; Kruchinin, S.P.; Bellucci, S. Influence of the ordering of impurities on the appearance of an energy gap and on the electrical conductance of grapheme. Sci. Rep. 2018, 8, 9123. [Google Scholar] [CrossRef]
- Merino-Díez, N.; Garcia-Lekue, A.; Carbonell-Sanroma, E.; Li, J.; Corso, M.; Colazzo, L.; Sedona, F.; Sanchez-Portal, D.; Pascual, J.I.; de Oteyza, D.G. Width-dependent band gap in armchair graphene nanoribbons reveals Fermi level pinning on Au(111). ACS Nano 2017, 11, 11661–11668. [Google Scholar] [CrossRef]
- Saroka, V.A.; Shuba, M.V.; Portnoi, M.E. Optical selection rules of zigzag graphene nanoribbons. Phys. Rev. B 2017, 95, 155438. [Google Scholar] [CrossRef]
- Chung, H.C.; Lee, M.H.; Chang, C.P.; Lin, M.F. Exploration of edge-dependent optical selection rules for graphene nanoribbons. Opt. Express 2011, 19, 23350–23363. [Google Scholar] [CrossRef]
- Chung, H.-C.; Lin, Y.-T.; Lina, S.-Y.; Ho, C.-H.; Chang, C.-P.; Lin, M.-F. Magnetoelectronic and optical properties of nonuniform graphene nanoribbons. Carbon 2016, 109, 883–895. [Google Scholar] [CrossRef][Green Version]
- Chung, H.-C.; Chang, C.-P.; Lin, C.-Y.; Lin, M.-F. Electronic and optical properties of graphene nanoribbons in external fields. Phys. Chem. Chem. Phys. 2016, 18, 7573. [Google Scholar] [CrossRef]
- Si, C.; Sun, Z.; Liu, F. Strain engineering of graphene: A review. Nanoscale 2016, 8, 3207–3217. [Google Scholar] [CrossRef]
- Gui, G.; Li, J.; Zhong, J. Band structure engineering of graphene by strain: First-principles calculations. Phys. Rev. B 2008, 78, 075435. [Google Scholar] [CrossRef]
- Pereira, V.M.; Castro Neto, A.H.; Peres, N.M.R. Tight-binding approach to uniaxial strain in grapheme. Phys. Rev. B 2009, 80, 045401. [Google Scholar] [CrossRef]
- Ducastelle, F. Analytic properties of the coherent potential approximation and its molecular generalizations. J. Phys. C Solid State Phys. 1974, 7, 1795–1816. [Google Scholar] [CrossRef]
- Velicky, B. Theory of electronic transport in disordered binary alloys: Coherent potential approximation. Phys. Rev. 1969, 184, 614–627. [Google Scholar] [CrossRef]
- Slater, J.C.; Koster, G.F. Simplified LCAO method for the periodic potential problem. Phys. Rev. 1954, 9, 1498–1524. [Google Scholar] [CrossRef]
- Repetsky, S.; Vyshyvana, I.; Nakazawa, Y.; Kruchinin, S.; Bellucci, S. Electron transport in carbon nanotubes with adsorbed chromium impurities. Materials 2019, 12, 524. [Google Scholar] [CrossRef]
- Repetsky, S.P.; Shatnii, T.D. Thermodynamic potential of a system of electrons and phonons in a disordered alloy. Theor. Math. Phys. 2002, 131, 832–851. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).