A Two-Stage Algorithm to Estimate the Fundamental Frequency of Asynchronously Sampled Signals in Power Systems

Abstract

A two-stage algorithm is proposed for the estimation of the fundamental frequency of asynchronously sampled signals in power systems. In the first stage, time-domain interpolation reconstructs the power system signal at a new sampling time and the reconstructed signal passes through a tuned sine filter to eliminate harmonics. In the second stage, the fundamental frequency is estimated using a modified curve fitting, which is robust to noise. The evaluation results confirm the efficiency and validity of the two-stage algorithm for accurate estimation of the fundamental frequency even for asynchronously sampled signals contaminated with noise, harmonics, and an inter-harmonic component.

1. Introduction

Sampling-based power measurements are typically carried out using a clock signal that is synchronized with the signal from the power system under analysis. However, often there may be no means of synchronizing the clock signal to the power system signal, and power measurements are instead based on asynchronous sampling of power system signals. These circumstances include industrial measurements and high-precision calibrations in metrology laboratories. Under such circumstances, accurate estimation of the fundamental frequency of power system signals is essential to minimize the errors caused by asynchronous sampling.

Numerous studies have estimated the fundamental frequency of asynchronously sampled signals, and several interesting results have been published in recent decades. Spectral techniques [1,2,3,4,5] are among the most popular approaches because of their low computational burden and feasibility for real-time applications. When asynchronously sampled data are processed using a discrete Fourier transform (DFT) to extract frequency information, the spectral leakage error is appended to the calculated result. Spectral techniques compensate for this leakage error to estimate the fundamental frequency. Orthogonal techniques [6,7,8,9,10,11,12,13,14] are another of the most popular approaches for real-time applications. In this approach, filters generate orthogonal signals and complex vectors, which are used to estimate the fundamental frequency. However, the calculation accuracy of spectral and orthogonal techniques is limited, and does not satisfy the precision required for certain applications.

In contrast, time-domain techniques, such as curve fitting [15,16,17,18,19] and parametric interpolations [20,21,22,23], are capable of highly accurate frequency estimation, at the cost of a higher computational burden. Curve fitting algorithms are commonly used in time-domain techniques because of their robustness to noise. In particular, the four-parameter sine fit (4PSF) algorithm [16] performs close to the Cramer Rao lower bound (CRLB), which is the theoretical limit of variance for an unbiased estimator, for almost all noise levels [24,25]. The 4PSF algorithm is more suited to less distorted steady-state waveforms, since its performance significantly degrades as total harmonic distortion (THD) increases. Parametric interpolations, such as cubic spline interpolations [20,21] and Newton interpolations [22,23], offer an alternative time-domain approach and are used to modify the sampling rate of an analog-to-digital conversion in software. In particular, the time-domain interpolation and scanning (TDIS) algorithm [20] reconstructs a waveform by cubic spline interpolation to find a new sampling rate that is an integer multiple of the fundamental frequency using a scanning procedure. The phase drift in the reconstructed waveform is used to estimate the fundamental frequency and iteratively correct the waveform. The TDIS algorithm gives greater frequency errors in the presence of inter-harmonics. In the opposite sense to the TDIS algorithm, which modifies the sampled signal to synchronize with the estimated frequency, the phase sensitive frequency estimation with interpolated phase (PSFEi) algorithm [26,27] modifies the frequency of the sine waves used in curve fitting to synchronize with the sampled data. The PSFEi algorithm calculates the phase increase of the fundamental component between two groups within the sampled data using the three-parameter sine fit (3PSF) algorithm [28] and then updates the fundamental frequency to be consistent with the phase increase. To minimize the effect of harmonic components, the phase increase in the final iteration is interpolated to an exact integer number of fundamental cycles. The PSFEi gives greater frequency errors in the presence of fluctuating harmonics.

In this paper, a two-stage algorithm is proposed for accurate estimation of the fundamental frequency of asynchronously sampled signals regardless of noise and harmonics. The remainder of the paper is organized as follows: frequency estimation using the two-stage algorithm is formulated in Section 2, and the performance of the algorithm is evaluated in Section 3 using both computer simulations and a hardware implementation. Conclusions are presented in Section 4.

2. Two-Stage Algorithm for Estimating a Fundamental Frequency

Assuming that a power system signal has a purely sinusoidal waveform with a fundamental frequency ω_f (rad/s), amplitude A_f (V or A), and phase θ_f (rad), the N_M-point data uniformly sampled with a sampling time Δt can be described in discrete time steps as follows:

$$y(n)=A_f\cdot \cos ({\text{ω}}_f\cdot n\frac{2\text{π}}{{\text{ω}}_0{N}_0}+{\text{θ}}_f)=A_f\cdot \cos ({\text{ω}}_f\cdot n\Delta t+{\text{θ}}_f)n=1,\cdots ,N_M$$

(1)

where ω₀ (rad/s) is a nominal frequency and N₀ is the number of samples per cycle at ω₀.

2.1. Tuned Sine Filtering Followed by Time-Domain Interpolation

Harmonics within a power system signal make accurate estimation of the fundamental frequency difficult. To eliminate these harmonics from the power system signal, a sine filter is usually used and its reference frequency is typically set to the nominal frequency [11]. When the fundamental frequency is equal to the reference frequency, the sine filter can eliminate harmonics from the power system signal perfectly. However, when the fundamental frequency deviates from the reference frequency, harmonics may not be eliminated effectively. To overcome this drawback, this paper proposes a tuned sine filter that adjusts its reference frequency to synchronize with an estimate of the fundamental frequency. The filter length should be matched to the number of samples per cycle at the reference frequency to keep its ability to eliminate harmonics. To meet this constraint, time-domain interpolation is used to reconstruct the power system signal at a new sampling time corresponding to the reference frequency, prior to applying the tuned sine filter.

Assuming that ${\widehat{\text{ω}}}_f^{(i-1)}$ is an estimate of the fundamental frequency at the previous iteration (i – 1), which will be used as the reference frequency for the tuned sine filter, the new sampling time $\Delta {\widehat{t}}^{(i)}$ is given as:

$$\Delta {\widehat{t}}^{(i)}=\frac{2\text{π}}{{\widehat{\text{ω}}}_f^{(i-1)}{N}_0}$$

(2)

To reconstruct the power system signal at the new sampling time, application of cubic spline interpolation to Equation (1) yields:

$${\widehat{y}}^{(i)}(n)=A_f\cdot \cos ({\text{ω}}_f\cdot n\Delta {\widehat{t}}^{(i)}+{\text{θ}}_f)n=1,\cdots ,{\widehat{N}}_M^{(i)}$$

(3)

where ${\widehat{N}}_M^{(i)}$ is the number of samples in the reconstructed signal and is given as $\lfloor \frac{N_M\Delta t}{\Delta {\widehat{t}}^{(i)}}\rfloor$. The algorithm used to compute the splines and interpolation is taken from [29]. Using the estimate of the fundamental frequency as the reference frequency for the tuned sine filter, the coefficients of the filter are given by:

$$H_S(n)=\frac{2}{N_0}\sin ({\widehat{\text{ω}}}_f^{(i-1)}\cdot n\Delta {\widehat{t}}^{(i)})=\frac{2}{N_0}\sin (2\text{π}\frac{n}{N_0})n=1,\cdots ,N_0$$

(4)

It is noted that the coefficients of the filter are independent of the estimate of the fundamental frequency since this has already been considered in the calculation of the new sampling time, given in Equation (2). Applying Equation (4) to ${\widehat{y}}^{(i)}(n)$ in Equation (3) yields a sine-filtered signal:

$${\widehat{y}}_S^{(i)}(n)=A_f|H_S({\text{ω}}_f)|\cdot \cos ({\text{ω}}_f\cdot n\Delta {\widehat{t}}^{(i)}+{\text{θ}}_f+\angle H_S({\text{ω}}_f))n=N_0,\cdots ,{\widehat{N}}_M^{(i)}$$

(5)

where $|H_{\text{S}}({\text{ω}}_f)|$ and $\angle H_{\text{S}}({\text{ω}}_f)$ are the amplitude and phase response of the tuned sine filter at ω_f, respectively. Some minor calculations yield:

$${\widehat{y}}_S^{(i)}(n)=C_f\cdot \cos ({\text{ω}}_f\cdot n\Delta {\widehat{t}}^{(i)})+S_f\cdot \sin ({\text{ω}}_f\cdot n\Delta {\widehat{t}}^{(i)})n=N_0,\cdots ,{\widehat{N}}_M^{(i)}$$

(6)

where:

$$C_f=A_f|H_S({\text{ω}}_f)|\cdot \cos ({\text{θ}}_f+\angle H_{\text{S}}({\text{ω}}_f))$$

$$S_P=-A_f|H_S({\text{ω}}_f)|\cdot \sin ({\text{θ}}_f+\angle H_S({\text{ω}}_f))$$

2.2. Modified Curve Fitting with an Unknown Frequency

The 3PSF algorithm performs a least-squares curve fitting on the sampled data to find the DC component, and the amplitude and phase of the component at a known frequency [28]. In the 4PSF algorithm, the frequency itself is treated as an unknown parameter to be found. Although the 4PSF algorithm is more computationally complex, this algorithm is recommended for sampled data containing five or more cycles of the power system signal [16,30], because the 4PSF algorithm usually determines the frequency to greater accuracy even if it is accurately known a priori. Since the tuned sine filter, which is used prior to applying the modified curve fitting, can eliminate the DC component, it can be assumed that there is no DC component in the sine-filtered signal given in Equation (6). Therefore, the number of modeling parameters in the 4PSF algorithm can be reduced from four to three: the fundamental frequency, amplitude, and phase. Assuming that ${\widehat{C}}_f^{(i)}$, ${\widehat{S}}_f^{(i)}$, and ${\widehat{\text{ω}}}_f^{(i)}$ are estimates of C_f, S_f, and ω_f in Equation (6) respectively, the sine-filtered signal of Equation (6) can be expressed as:

$${\widehat{y}}_S^{(i)}(n)={\widehat{C}}_f^{(i)}\cdot \cos ({\widehat{\text{ω}}}_f^{(i)}\cdot n\Delta {\widehat{t}}^{(i)})+{\widehat{S}}_f^{(i)}\cdot \sin ({\widehat{\text{ω}}}_f^{(i)}\cdot n\Delta {\widehat{t}}^{(i)})n=N_0,\cdots ,{\widehat{N}}_M^{(i)}$$

(7)

To find an iterative form of Equation (7), a Taylor series expansion of the cosine function in Equation (7) is taken around the previous frequency estimate ${\widehat{\text{ω}}}_f^{(i-1)}$:

$$\begin{array}{ll}\cos ({\widehat{\text{ω}}}_f^{(i)}\cdot n\Delta {\widehat{t}}^{(i)})& =\cos (({\widehat{\text{ω}}}_f^{(i-1)}+\Delta {\widehat{\text{ω}}}_f^{(i)})\cdot n\Delta {\widehat{t}}^{(i)})\\ & =\cos ({\widehat{\text{ω}}}_f^{(i-1)}\cdot n\Delta {\widehat{t}}^{(i)})\cos (\Delta {\widehat{\text{ω}}}_f^{(i)}\cdot n\Delta {\widehat{t}}^{(i)})-\sin ({\widehat{\text{ω}}}_f^{(i-1)}\cdot n\Delta {\widehat{t}}^{(i)})\sin (\Delta {\widehat{\text{ω}}}_f^{(i)}\cdot n\Delta {\widehat{t}}^{(i)})\\ & \cong \cos ({\widehat{\text{ω}}}_f^{(i-1)}\cdot n\Delta {\widehat{t}}^{(i)})-\sin ({\widehat{\text{ω}}}_f^{(i-1)}\cdot n\Delta {\widehat{t}}^{(i)})\Delta {\widehat{\text{ω}}}_f^{(i)}\cdot n\Delta {\widehat{t}}^{(i)}\\ & =\cos (\frac{2\text{π}n}{N_0})-\sin (\frac{2\text{π}n}{N_0})\Delta {\widehat{\text{ω}}}_f^{(i)}\cdot n\Delta {\widehat{t}}^{(i)}\end{array}$$

(8)

Similarly, a Taylor series expansion of the sine function in Equation (7) is taken around ${\widehat{\text{ω}}}_f^{(i-1)}$:

$$\sin ({\widehat{\text{ω}}}_f^{(i)}\cdot n\Delta {\widehat{t}}^{(i)})\cong \sin (\frac{2\text{π}n}{N_0})+\cos (\frac{2\text{π}n}{N_0})\Delta {\widehat{\text{ω}}}_f^{(i)}\cdot n\Delta {\widehat{t}}^{(i)}$$

(9)

Substitution of Equations (8) and (9) into Equation (7) yields:

$$\begin{array}{ll}{\widehat{y}}_S^{(i)}(n)& \cong {\widehat{C}}_f^{(i)}\{\cos (\frac{2\text{π}n}{N_0})-\sin (\frac{2\text{π}n}{N_0})\Delta {\widehat{\text{ω}}}_f^{(i)}\cdot n\Delta {\widehat{t}}^{(i)}\}+{\widehat{S}}_f^{(i)}\{\sin (\frac{2\text{π}n}{N_0})+\cos (\frac{2\text{π}n}{N_0})\Delta {\widehat{\text{ω}}}_f^{(i)}\cdot n\Delta {\widehat{t}}^{(i)}\}\\ & ={\widehat{C}}_f^{(i)}\cos (\frac{2\text{π}n}{N_0})+{\widehat{S}}_f^{(i)}\sin (\frac{2\text{π}n}{N_0})+\Delta {\widehat{\text{ω}}}_f^{(i)}\cdot n\Delta {\widehat{t}}^{(i)}\{{\widehat{S}}_f^{(i)}\cos (\frac{2\text{π}n}{N_0})-{\widehat{C}}_f^{(i)}\sin (\frac{2\text{π}n}{N_0})\}\\ & \cong {\widehat{C}}_f^{(i)}\cos (\frac{2\text{π}n}{N_0})+{\widehat{S}}_f^{(i)}\sin (\frac{2\text{π}n}{N_0})+\Delta {\widehat{\text{ω}}}_f^{(i)}\cdot n\Delta {\widehat{t}}^{(i)}\{{\widehat{S}}_f^{(i-1)}\cos (\frac{2\text{π}n}{N_0})-{\widehat{C}}_f^{(i-1)}\sin (\frac{2\text{π}n}{N_0})\}\end{array}$$

(10)

The successive samples in Equation (10) can be written in matrix form:

$${\widehat{y}}_S^{(i)}={\widehat{A}}^{(i)}{\widehat{x}}^{(i)}$$

(11)

where:

$${\widehat{y}}_S^{(i)}={\left[\begin{array}{ccc}{\widehat{y}}_S^{(i)}(N_0)& \cdots & {\widehat{y}}_S^{(i)}({\widehat{N}}_M^{(i)})\end{array}\right]}^T{\widehat{x}}^{(i)}={\left[\begin{array}{ccc}{\widehat{C}}_f^{(i)}& {\widehat{S}}_f^{(i)}& \Delta {\widehat{\omega }}_f^{(i)}\end{array}\right]}^T$$

$${\widehat{A}}^{(i)}=\left[\begin{array}{ccc}\cos (\frac{2\text{π}{N}_0}{N_0})& \sin (\frac{2\text{π}{N}_0}{N_0})& N_0\Delta {\widehat{t}}^{(i)}\{{\widehat{S}}_f^{(i-1)}\cos (\frac{2\text{π}{N}_0}{N_0})-{\widehat{C}}_f^{(i-1)}\sin (\frac{2\text{π}{N}_0}{N_0})\}\\ ⋮& ⋮& ⋮\\ \cos (\frac{2\text{π}{\widehat{N}}_M^{(i)}}{N_0})& \sin (\frac{2\text{π}{\widehat{N}}_M^{(i)}}{N_0})& {\widehat{N}}_M^{(i)}\Delta {\widehat{t}}^{(i)}\{{\widehat{S}}_f^{(i-1)}\cos (\frac{2\text{π}{\widehat{N}}_M^{(i)}}{N_0})-{\widehat{C}}_f^{(i-1)}\sin (\frac{2\text{π}{\widehat{N}}_M^{(i)}}{N_0})\}\end{array}\right]$$

Since the coefficient matrix ${\widehat{A}}^{(i)}$ with dimensions $({\widehat{N}}_M^{(i)}-N_0+1)\times 3$ is not square, its pseudo inverse with dimensions $3\times 3$ is used to find ${\widehat{x}}^{(i)}$:

$${\widehat{x}}^{(i)}={({({\widehat{A}}^{(i)})}^T{\widehat{A}}^{(i)})}^{-1}{({\widehat{A}}^{(i)})}^T{\widehat{y}}_S^{(i)}$$

(12)

Finally, the frequency estimate is updated using the frequency deviation $\Delta {\widehat{\text{ω}}}_f^{(i)}$ in ${\widehat{x}}^{(i)}$:

$${\widehat{\text{ω}}}_f^{(i)}={\widehat{\text{ω}}}_f^{(i-1)}+\Delta {\widehat{\text{ω}}}_f^{(i)}$$

(13)

2.3. Frequency Estimation Procedure

Figure 1 shows the block diagram for the frequency estimation procedure using the two-stage algorithm. Initial estimates for ${\widehat{C}}_f^{(0)}$, ${\widehat{S}}_f^{(0)}$, and ${\widehat{\text{ω}}}_f^{(0)}$ are obtained using 3pDFT [31], a simple and efficient algorithm for estimating the fundamental frequency. At the first iteration, a new sampling time $\Delta {\widehat{t}}^{(1)}$ is calculated corresponding to ${\widehat{\text{ω}}}_f^{(0)}$ and cubic spline interpolation is applied to reconstruct the power system signal at the new sampling time. The reconstructed signal passes through the tuned sine filter to eliminate harmonics. Prior to performing the modified curve fitting on the sine-filtered signal, the coefficients of ${\widehat{A}}^{(1)}$ are calculated based on ${\widehat{C}}_f^{(0)}$, ${\widehat{S}}_f^{(0)}$, and $\Delta {\widehat{t}}^{(0)}$. After finding the pseudo inverse of ${\widehat{A}}^{(1)}$ as given in Equation (12), the modified curve fitting determines the modeling parameters (${\widehat{C}}_f^{(1)}$, ${\widehat{S}}_f^{(1)}$, and $\Delta {\widehat{\text{ω}}}_f^{(1)}$) and the frequency estimate ${\widehat{\text{ω}}}_f^{(1)}$ is updated using $\Delta {\widehat{\text{ω}}}_f^{(1)}$. The $i^{th}$ iteration is the same as the first iteration, but uses the most recent estimates ${\widehat{C}}_f^{(i-1)}$, ${\widehat{S}}_f^{(i-1)}$, and ${\widehat{\text{ω}}}_f^{(i-1)}$ instead of the initial estimates ${\widehat{C}}_f^{(0)}$, ${\widehat{S}}_f^{(0)}$, and ${\widehat{\text{ω}}}_f^{(0)}$. Since curve fitting algorithms with an unknown frequency double the number of significant digits in the frequency estimate at each iteration and converge very rapidly, six iterations have been considered more than adequate [30]. In this paper, six iterations are repeated to produce an accurate frequency estimate.

Figure 1. Frequency estimation procedure for the two-stage algorithm.

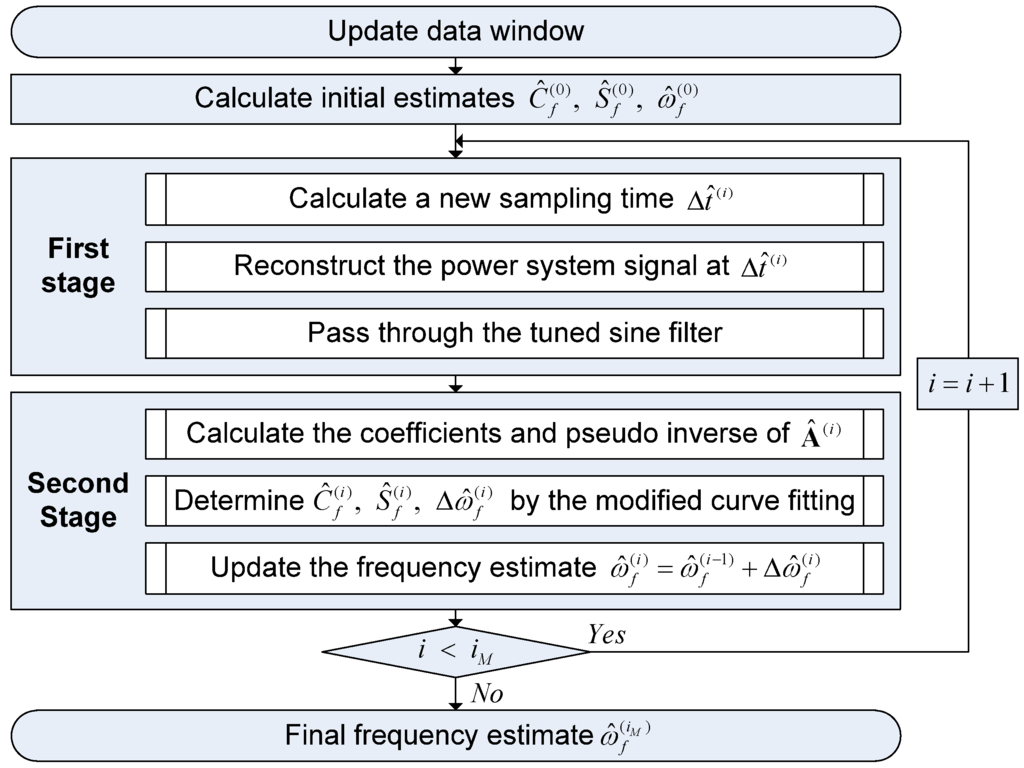
Figure 1. Frequency estimation procedure for the two-stage algorithm.

3. Performance Evaluation

To evaluate the performance of the two-stage algorithm, results were compared with those obtained using the TDIS, 4PSF, and PSFEi algorithms. All four algorithms were tested using two approaches: computer simulations and a hardware implementation.

3.1. Computer Simulations

3.1.1. Number of Cycles in the Data Window

While the sampling time and length of the data window were fixed (i.e., $\Delta t=30us$ and $N_M=8192$), the number of cycles in the data window was varied by varying the fundamental frequency of the test waveform, which consisted of a single-tone sine wave and a 60 dB white noise signal. In the simulations, the number of cycles in the data window was varied between 3 and 20, which corresponds to the fundamental frequencies between 12.207 Hz and 81.380 Hz. The root-mean-square (RMS) error of frequency estimation after 1000 repetitions at each number of cycles is shown in Figure 2, together with the CRLB. The 4PSF and PSFEi algorithms perform close to the CRLB for all numbers of cycles; the TDIS algorithm performs well, but is marginally worse than the 4PSF and PSFEi algorithms for six cycles or more within the data window. It was also found that the two-stage algorithm needs at least eight cycles in the data window to perform close to the CRLB.

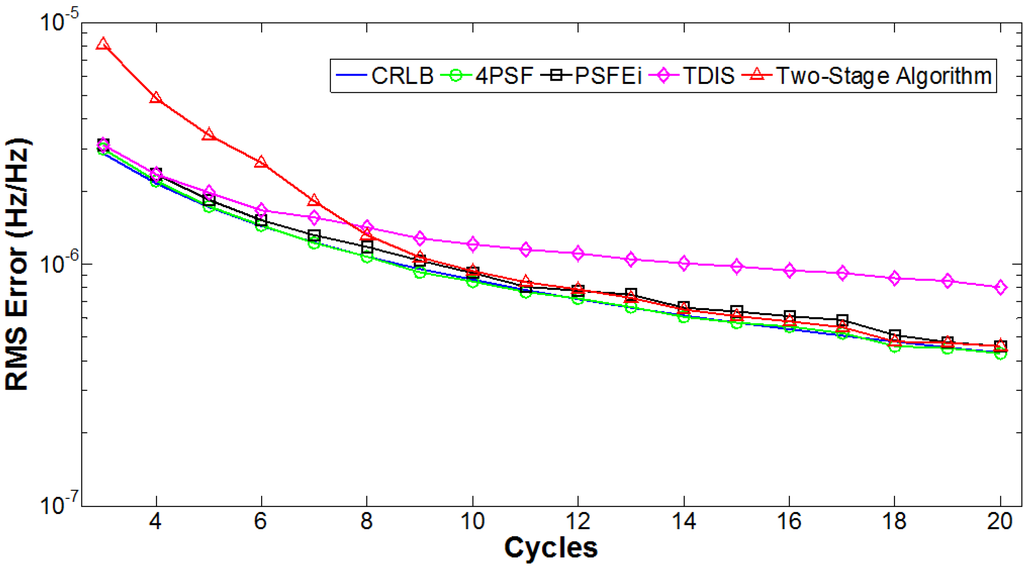
Figure 2. RMS error of frequency estimation with an increasing number of cycles in the data window.

Figure 2. RMS error of frequency estimation with an increasing number of cycles in the data window.

3.1.2. Noise Level

Simulations with noise were performed using a single-tone sine waveform with a random phase and fundamental frequency of 61.2 Hz. The signal-to-noise ratio (SNR) varied from 0 dB to 100 dB with a noise increase of 10 dB. The RMS error of frequency estimation after 1000 repetitions at each SNR level is shown in Figure 3. As with previous tests, the 4PSF and PSFEi algorithms perform close to the CRLB for all noise levels, and the two-stage algorithm also performs close to the CRLB. The TDIS algorithm performs approximately 1.2-fold worse than the others.

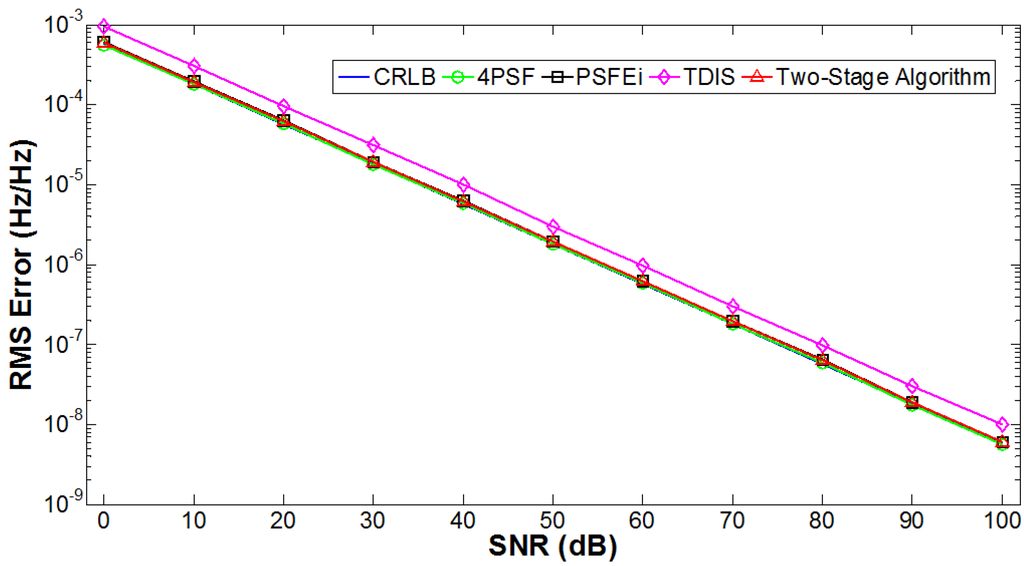
Figure 3. Root-mean-square (RMS) error of frequency estimation with increasing noise level.

Figure 3. Root-mean-square (RMS) error of frequency estimation with increasing noise level.

3.1.3. Harmonics

The simulated test waveforms have the following form:

$$y(n)={\displaystyle \sum _{h=0}^H{A}_h(n)\sin (h\cdot {\text{ω}}_f{t}_n+{\text{θ}}_h)}+e(n)$$

(14)

Tests were run with fundamental frequencies varying within 60 ± 5 Hz, with a random phase ${\text{θ}}_h$ for each harmonic. The other parameters in Equation (14) were set as follows: $e(n)=60\mathrm{dB}$, $H=10$, $A_1(n)=1$, $A_{h\text{,even}}(n)=0.01\times S$, $A_{h\ne 1,\text{odd}}(n)=0.2\times S$, where S was an integer multiplier from 0 to 4 used to increase the amplitudes of the even and odd harmonics. The maximum error of frequency estimation after 1000 repetitions at each level of THD is given in Figure 4. The performance of the 4PSF algorithm significantly degrades as the multiplier S and, therefore, the THD increases. The PSFEi, TDIS, and two-stage algorithms perform with greater accuracy regardless of THD level, with the two-stage algorithm exhibiting slightly improved performance over the PSFEi and TDIS algorithms.

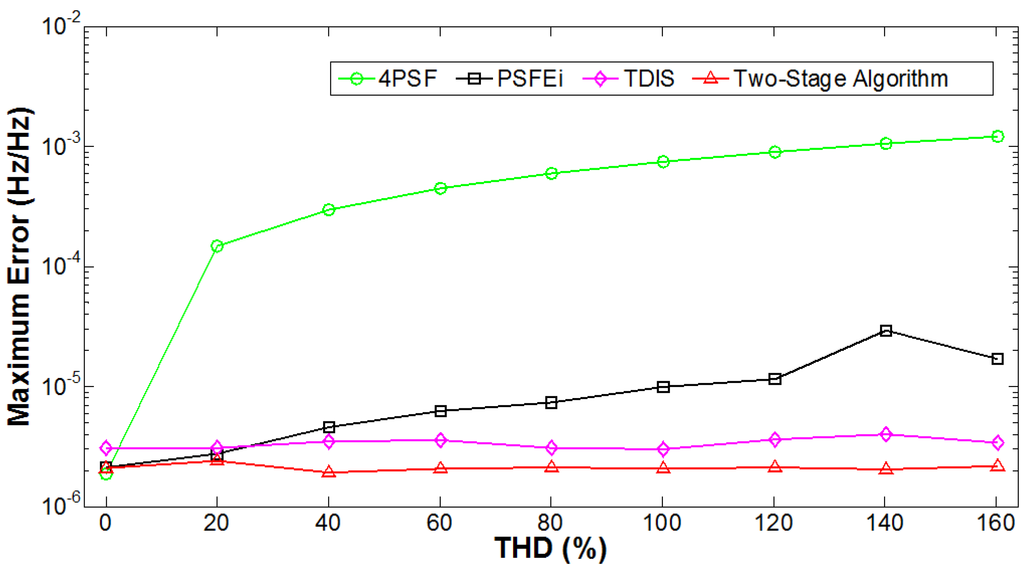
Figure 4. Maximum error of frequency estimation with increasing THD.

Figure 4. Maximum error of frequency estimation with increasing THD.

3.1.4. Fluctuating Harmonic Component

The simulated test waveforms with a fluctuating harmonic component of order k have the following form:

$$y(n)={\displaystyle \sum _{h=0,\ne k}^H{A}_h(n)\sin (h\cdot {\text{ω}}_f{t}_n+{\text{θ}}_h)}+A_k(1+B_k\sin ({\text{ω}}_k{t}_n))\cdot \sin (k\cdot {\text{ω}}_f{t}_n+{\text{θ}}_k)+e(n)$$

(15)

where ω_k is the frequency of fluctuation, which was set to vary randomly within 7 ± 2 Hz; A_k is the amplitude of the fluctuating harmonic component, which was set to 0.5; and B_k is the depth of fluctuation, which was set to 0.1. The other parameters were identical to those used in Section 3.1.3, except that here the integer multiplier S was set to 1. The order of the fluctuating harmonic component was varied from 2 to 10, and the maximum error of frequency estimation after 1000 repetitions for each fluctuating harmonic order is given in Figure 5; comparison between Figure 4 and Figure 5 shows that the maximum errors for most of the algorithms are significantly worse when one of the harmonics fluctuates. Performance slightly improves as the fluctuating harmonic order increases. This is most likely because spectral leakage from a fluctuating harmonic closer to the fundamental frequency has a greater effect on the estimate.

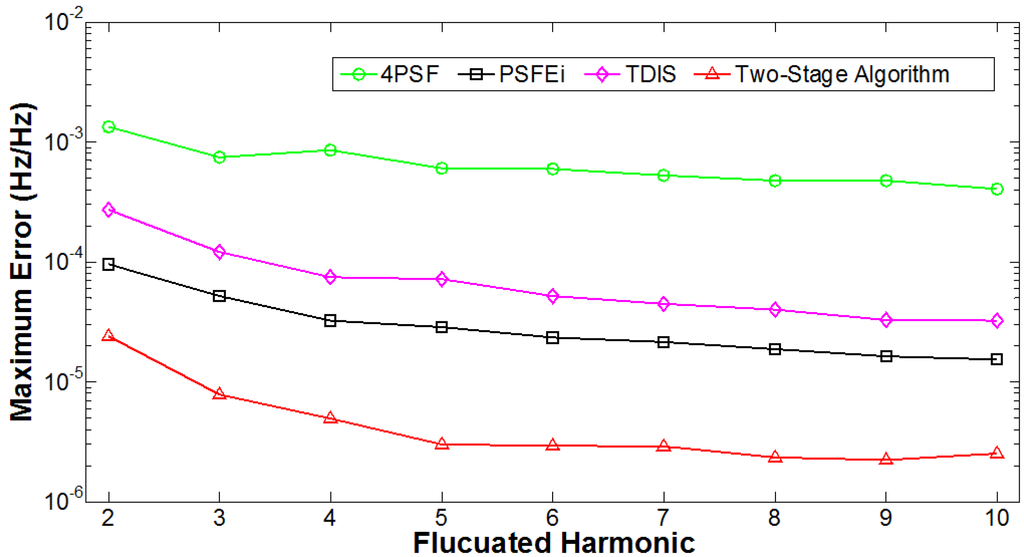
Figure 5. Maximum error of frequency estimation with increasing order of the fluctuating harmonic.

Figure 5. Maximum error of frequency estimation with increasing order of the fluctuating harmonic.

To evaluate the effect of modulation depth, the order of the fluctuating harmonic was set to 3 and B_k was varied from 0 to 1.0 in 0.1 increments. The maximum error of frequency estimation after 1000 repetitions for each modulation depth is shown in Figure 6. Similar to the effect seen when changing the fluctuating harmonic order, an increase in spectral leakage due to greater modulation depth has an adverse effect on the performance of the PSFEi, TDIS and two-stage algorithms. The 4PSF algorithm is more influenced by THD level and a fluctuating harmonic component does not have a significant effect on its performance.

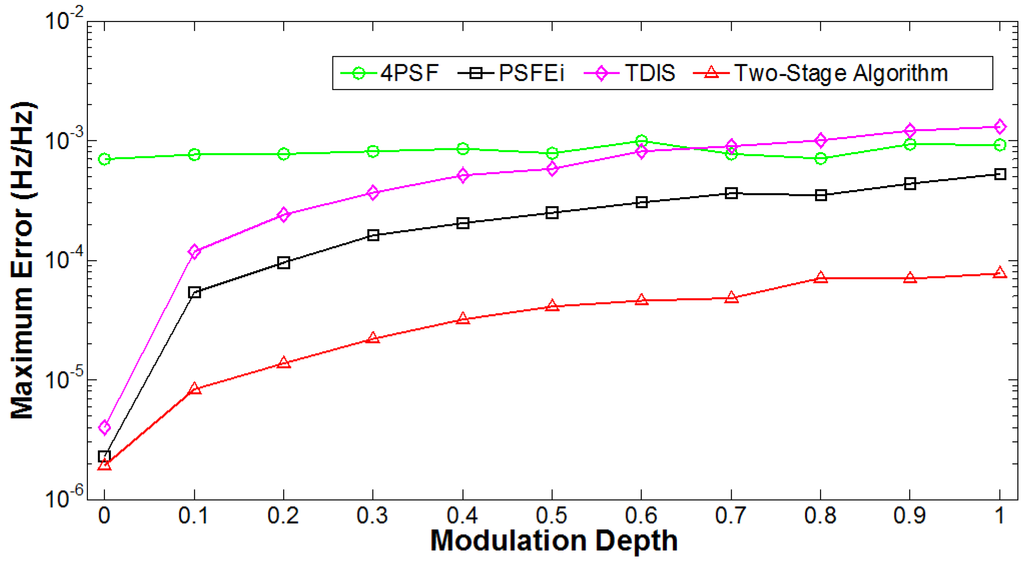
Figure 6. Maximum error of frequency estimation with increasing modulation depth of the third harmonic.

Figure 6. Maximum error of frequency estimation with increasing modulation depth of the third harmonic.

3.1.5. Fluctuating Inter-Harmonic Component

The simulated test waveforms with a fluctuating inter-harmonic component of index x have the following form:

$$y(n)={\displaystyle \sum _{h=0}^H{A}_h(n)\sin (h\cdot {\text{ω}}_f{t}_n+{\text{θ}}_h)}+A_x(1+B_x\sin ({\text{ω}}_x{t}_n))\cdot \sin (x\cdot {\text{ω}}_f{t}_n+{\text{θ}}_x)+e(n)$$

(16)

where ${\text{ω}}_x$ is the frequency of fluctuation, which was set to vary randomly within 7 ± 2 Hz; and $B_x$ is the depth of fluctuation, which was set to 0.1. Other parameters were identical to those used in Section 3.1.3, except that the integer multiplier S was set to 1. The inter-harmonic amplitude A_x was varied from 0 to 0.7 in 0.1 increments. The maximum error of frequency estimation after 1000 repetitions for each of the inter-harmonic amplitude is given in Figure 7. At each repetition, index x was randomly varied from 1.5 to 10. The contamination of the fundamental component caused by the inter-harmonic component leads to increasing estimation errors for the TDIS, PSFEi, and two-stage algorithms with increasing inter-harmonic amplitude. Again, a fluctuating inter-harmonic component does not have a significant effect on the performance of the 4PSF algorithm.

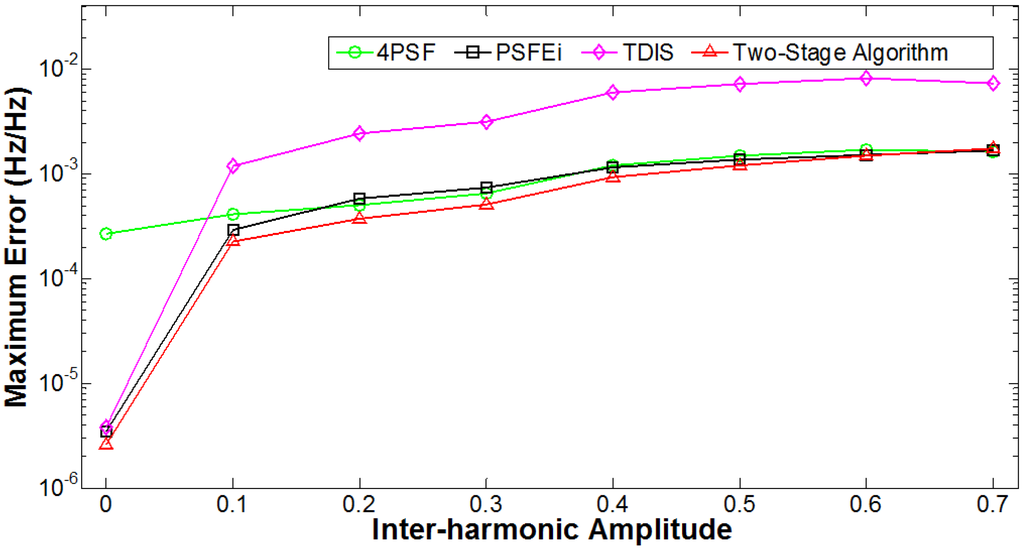
Figure 7. Maximum error of frequency estimation with increasing inter-harmonic amplitude.

Figure 7. Maximum error of frequency estimation with increasing inter-harmonic amplitude.

3.1.6. Computational Burden

Table 1 lists the average time taken to complete a frequency estimate in the simulations for each of the algorithms. The algorithms were implemented in MATLAB, and all simulations were run on a personal computer with an Intel Core i7 processor running at 4.0 GHz. The TDIS and two-stage algorithms required significantly more time than the 4PSF and PSFEi algorithms, which is due to the time-domain interpolation.

Table 1. Average time required for one frequency estimation (ms).

Algorithm	Figure number
	2	3	4	5	6	7
4PSF	8.3337	8.2824	8.1042	8.3044	8.2134	8.5206
PSFEi	12.388	11.279	10.444	11.102	10.710	11.762
TDIS	463.98	465.78	459.23	466.76	462.63	481.13
Two-stage	254.12	348.07	331.07	341.41	339.56	355.14

Table 1. Average time required for one frequency estimation (ms).

Algorithm	Figure number
	2	3	4	5	6	7
4PSF	8.3337	8.2824	8.1042	8.3044	8.2134	8.5206
PSFEi	12.388	11.279	10.444	11.102	10.710	11.762
TDIS	463.98	465.78	459.23	466.76	462.63	481.13
Two-stage	254.12	348.07	331.07	341.41	339.56	355.14

3.2. Hardware Implementation

Tests using real waveforms with known characteristics are a useful indicator of the performance of the algorithms under real conditions. A system for efficient implementation and comparison of the algorithms was developed at Korea Testing Laboratory (KTL), a representative accreditation authority in South Korea for the testing and calibration of measurement equipment. As shown in Figure 8, an electrical power quality calibrator (Fluke 6105A) generates calibration voltage and current signals, which were sampled using the data acquisition system developed for the KTL power measurement calibration service. In the data acquisition system, a current shunt (Fluke A40B) converts the calibration current signal to a shunt voltage signal. Two digitizing multi-meters (Agilent 3458A) encode the calibration voltage signal and the shunt voltage signal into digital outputs at a 16-bit resolution. During the encoding process, a waveform generator (Agilent 33500B) produces an EXT TRIG signal to synchronize the operation of the two multi-meters. Integrated software on a host computer controls the two multi-meters through a GPIB and gathers the sampled data, which are used for power measurement calibration. All four algorithms are implemented as sub-programs to estimate the fundamental frequency of the calibration voltage signal, sampled at 8.192 kS/s for 8192-point data.

Figure 8. Hardware implementation for tests using real waveforms.

Figure 8. Hardware implementation for tests using real waveforms.

No.	Device Name
1	Electrical power quality calibrator (Fluke 6105A)
2	Waveform generator (Agilent 33500B)
3,4	Digitizing multi-meter (Agilent 3458A)
5	Current shunt (Fluke A40B)
6	Host computer

Table 2 summarizes the maximum errors of frequency estimation when tests were run at a fundamental frequency of 60 Hz. Two calibration voltage levels (110 V and 220 V) were used in the tests and all algorithms demonstrated similar performance regardless of the calibration voltage level and harmonic. In particular, the maximum errors of the two-stage algorithm are maintained stably between $9.5416\times {10}^{-6}$ and $9.9564\times {10}^{-6}$.

Table 2. Maximum errors of frequency estimation with a fundamental frequency of 60 Hz (10⁻⁶ × Hz/Hz).

Voltage	H1 = 110 V, θ1 = 0				H1 = 220V, θ1 = 0
Harmonic	H3 = 10%	H3 = 10%	H49 = 10%	H49 = 10%	H3 = 10%	H3 = 10%	H49 = 10%	H49 = 10%
	θ3 = 0	θ3 = π	θ49 = 0	θ49 = π	θ3 = 0	θ3 = π	θ49 = 0	θ49 = π
4PSF	6.6318	12.492	9.9227	9.6065	8.7664	11.733	9.5059	9.7659
PSFEi	9.4811	9.9378	9.9649	9.6864	9.6831	9.4355	9.8214	9.9948
TDIS	11.623	8.4567	9.3250	9.1283	10.472	9.7417	9.0150	9.0917
Two-stage	9.5266	9.8951	9.9366	9.6903	9.5992	9.5416	9.7377	9.9564

Table 2. Maximum errors of frequency estimation with a fundamental frequency of 60 Hz (10⁻⁶ × Hz/Hz).

Voltage	H1 = 110 V, θ1 = 0				H1 = 220V, θ1 = 0
Harmonic	H3 = 10%	H3 = 10%	H49 = 10%	H49 = 10%	H3 = 10%	H3 = 10%	H49 = 10%	H49 = 10%
	θ3 = 0	θ3 = π	θ49 = 0	θ49 = π	θ3 = 0	θ3 = π	θ49 = 0	θ49 = π
4PSF	6.6318	12.492	9.9227	9.6065	8.7664	11.733	9.5059	9.7659
PSFEi	9.4811	9.9378	9.9649	9.6864	9.6831	9.4355	9.8214	9.9948
TDIS	11.623	8.4567	9.3250	9.1283	10.472	9.7417	9.0150	9.0917
Two-stage	9.5266	9.8951	9.9366	9.6903	9.5992	9.5416	9.7377	9.9564

4. Conclusions

A two-stage algorithm is proposed for estimation of the fundamental frequency of asynchronously sampled signals in power systems. In the first stage, time-domain interpolation reconstructs the power system signal at a new sampling time and the reconstructed signal passes through a tuned sine filter. The tuned sine filter retains its ability to eliminate harmonics by adjusting its reference frequency to synchronize with an estimate of the fundamental frequency. Prior to applying the tuned sine filter, time-domain interpolation renders it possible to match the filter length of the tuned sine filter to the number of samples per cycle in the reconstructed signal. In the second stage, the fundamental frequency is estimated using a modified curve fitting, which is robust to noise. Since the tuned sine filter eliminates the DC component in addition to harmonics, the DC component is removed from the modeling parameters of the modified curve fitting.

The performance of the two-stage algorithm was evaluated using computer-simulated signals, which were asynchronously sampled and contaminated with noise, harmonics, and an inter-harmonic component. The comparison showed that the two-stage algorithm required approximately eight cycles within the data window to provide a level of performance similar to CRLB, and enabled estimation of the fundamental frequency accurately under a range of conditions. In particular, the two-stage algorithm could estimate the fundamental frequency with greater accuracy than the other algorithms in the presence of high levels of THD, a fluctuating harmonic component and a fluctuating inter-harmonic component. The two-stage algorithm was then implemented on a KTL data acquisition system with 16-bit resolution. The results of this implementation demonstrate both the efficiency and validity of the two-stage algorithm, and show that it can achieve accurate estimations of the fundamental frequency in practical conditions. Therefore, the two-stage algorithm may be considered useful for high-precision applications, such as calibrations in metrology laboratories.