Abstract
This paper presents a coordinated control method for a doubly-fed induction generator (DFIG)-based wind-power generation system with a series grid-side converter (SGSC) under distorted grid voltage conditions. The detailed mathematical models of the DFIG system with SGSC are developed in the multiple synchronous rotating reference frames. In order to counteract the adverse effects of the voltage harmonics upon the DFIG, the SGSC generates series compensation control voltages to keep the stator voltage sinusoidal and symmetrical, which allows the use of the conventional vector control strategy for the rotor-side converter (RSC), regardless of grid voltage harmonics. Meanwhile, two control targets for the parallel grid-side converter (PGSC) are identified, including eliminating the oscillations in total active and reactive power entering the grid or suppressing the fifth- and seventh-order harmonic currents injected to the grid. Furthermore, the respective PI-R controller in the positive synchronous reference frame for the SGSC voltage control and PGSC current control have been developed to achieve precise and rapid regulation of the corresponding components. Finally, the proposed coordinated control strategy has been fully validated by the simulation results of a 2 MW DFIG-based wind turbine with SGSC under distorted grid voltage conditions.
1. Introduction
With the increased penetration of wind energy into power grids all over the World, more and more large-scale wind turbines and wind power plants have been installed in rural areas or offshore where the grids are generally quite weak. The operation and control of such remote wind turbines under non-ideal voltage conditions, including severe voltage sags, network unbalance, and harmonic voltage distortions, have attracted more and more attention [1,2,3,4,5,6,7,8,9,10,11,12,13,14]. With many excellent merits such as low rating converter capacity, variable speed constant frequency operation and independent power regulation capability, wind turbines based on doubly-fed induction generators (DFIGs) have become one of the mainstream types of variable speed wind turbine in recent years. Unlike wind generators with the full-sized grid-connected converters (such as permanent magnet synchronous generators), DFIG is very sensitive to aforementioned grid disturbances as its stator is directly connected to the grid and the rating of the back-to-back converter is limited.
Recently, some improved operation and control strategies for DFIG were investigated under non-ideal grid voltage conditions. For the severe grid short-circuit fault and unbalanced grid voltage conditions, some improved excitation control strategies or an additional series voltage compensation method using a dynamic voltage restorer (DVR) have been proposed to effectively enhance the low voltage ride through (LVRT) capability of the DFIG system [1,2,15,16,17,18,19]. Besides, the overall operation performance of the whole DFIG system can be improved by coordinately controlling the rotor-side converter (RSC) and parallel grid-side converter (PGSC) during a network unbalance, and some enhanced operation functionalities such as eliminating the oscillations in the active or reactive power from the whole system, or suppressing the negative-sequence currents injected to the grid have been achieved [6,11]. To further improve the operation performance of DFIG system under distorted grid voltage conditions, some enhanced control strategies for the DFIG have been studied in [13,14]. As mentioned in [14], a rotor current PI regulator and a harmonic resonant compensator tuned at six times the grid frequency in the positive (dq)+ reference frame are designed to provide different operation functionalities, i.e., removing the stator or rotor current harmonics, or eliminating the oscillations at six times the grid frequency in the stator output active and reactive powers. However, due to the limited RSC control variables, the proposed method cannot eliminate the stator and rotor current harmonics and the output power pulsations in the DFIG simultaneously under network harmonic distortions. Therefore, harmonic power losses in the stator and rotor windings or the stator power oscillations and torque pulsations in the DFIG still exist, which might degrade the life time of the winding insulation materials or deteriorate the output power quality.
The main reason causing stator and rotor current distortions, electromagnetic torque and power pulsations in the DFIG is harmonically distorted stator voltages, so if the stator voltage harmonics can be eliminated and only the positive-sequence voltage is left, the adverse effects of network voltage distortion upon the DFIG will be removed naturally. As similarly discussed in [20,21,22], the DFIG system with a series grid-side converter (SGSC) can be used to enhance the overall operation performance under distorted voltage conditions. As mentioned in [20,21,22], by coordinately controlling the SGSC, PGSC and RSC, the DFIG system with SGSC has been fully demonstrated to be able to deal with the LVRT operation under severely symmetrical and unsymmetrical grid faults or network unbalance in steady-state operation. However, the operation and control of such a DFIG system under grid voltage harmonic distortion have not been discussed in detail. Unlike other series voltage compensation methods using a DVR mentioned in [15,16,17,18,19], the DFIG system with SGSC can also cope with the case of steady-state grid voltage harmonic distortions as the SGSC is directly connected with the PGSC and RSC through the dc-link.
For the operation and control of SGSC, PGSC and RSC during network harmonic distortions, this paper investigates ways to further improve the operation performance of the DFIG system with SGSC. In the grid voltage-oriented positive (dq)+ and harmonic (dq)5−, (dq)7+ reference frames, the mathematical models of SGSC and PGSC under 5th and 7th grid voltage harmonics are developed. Besides, the control target for the SGSC and different control targets for the PGSC under the distorted voltage conditions are identified, and the reference values of the PGSC’s fundamental and harmonic currents are deduced. Furthermore, a coordinated control of the SGSC, PGSC and RSC and control schemes for SGSC and PGSC using a PI controller and a harmonic resonant regulator tuned at six times the grid frequency in the positive (dq)+ reference frame are developed. Finally, numerical simulations on a 2 MW DFIG system with SGSC are presented to verify the proposed control scheme.
2. Modeling of DFIG System with SGSC during Network Harmonic Distortions
Figure 1 shows the configuration of the DFIG system with SGSC. The stator voltage of DFIG can be flexibly regulated by controlling the series injected voltage of SGSC to improve the operation performance, which can be expressed in the stationary αβ reference frame as:
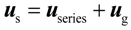
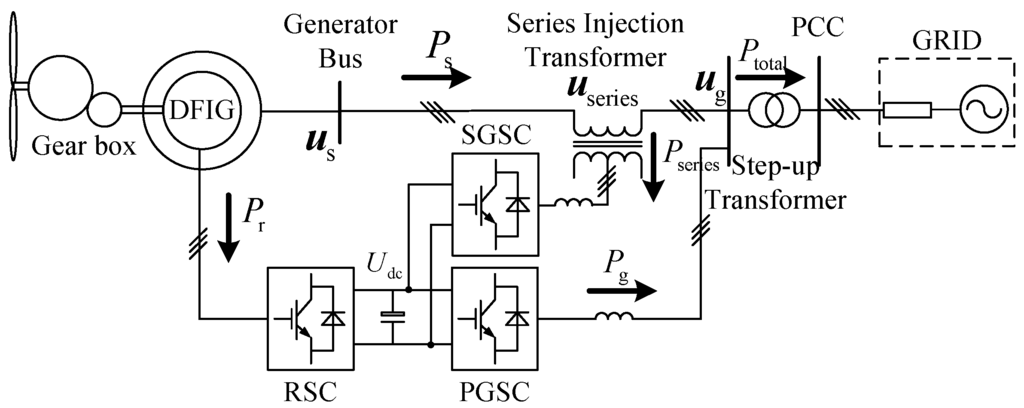
Figure 1.
Configuration of DFIG system with SGSC.
In this paper, only the fundamental component and the low order (fifth- and seventh-order) harmonic components are considered. In the stationary αβ reference frame, the voltage and current vectors can be represented as the combinations of the fundamental positive-sequence vector and the harmonic fifth- and seventh-order vectors. In order to simplify the analysis, the multiple synchronous rotating reference frames are adopted, as shown in Figure 2. For the positive (dq)+ reference frame, the d+-axis is aligned with the positive-sequence grid voltage vector.
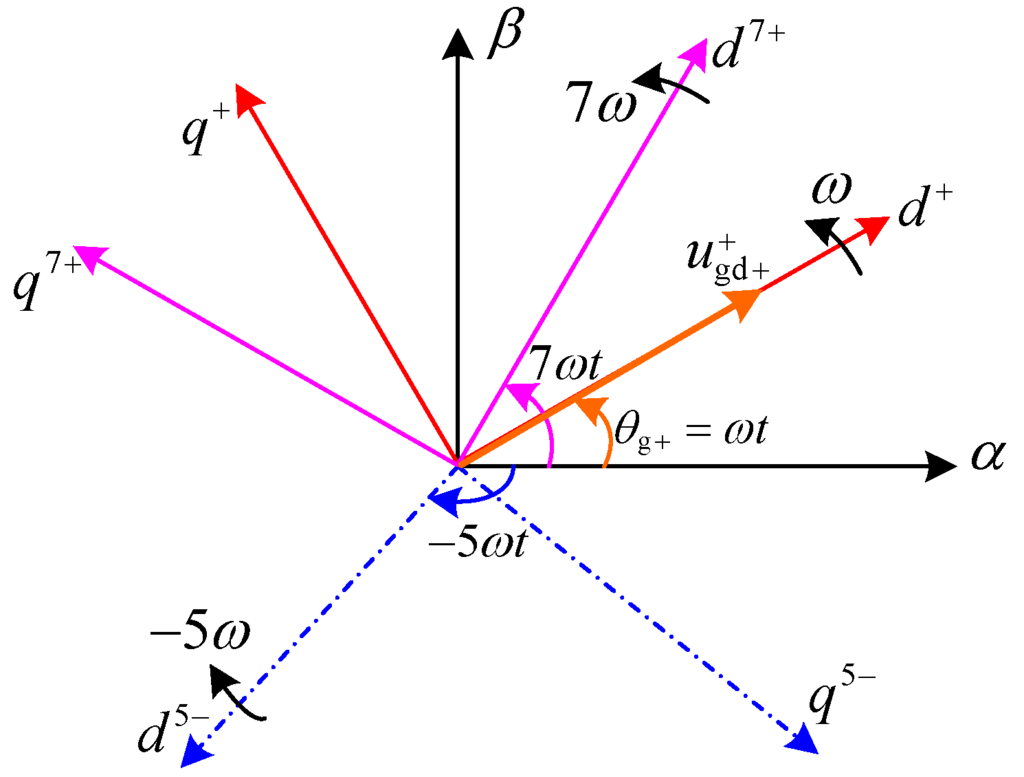
Figure 2.
Multiple synchronous rotating reference frames.
2.1. SGSC
In order to counteract the effect of the 5th and 7th grid voltage harmonic components and compensate the impedance voltage drop of the series transformer, a series compensation voltage vector generated by the SGSC should be injected to keep the DFIG stator voltage in line with the positive-sequence grid voltage, which can be expressed as:
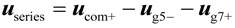 where ucom+ is the positive-sequence voltage vector error which needs to be compensated.
where ucom+ is the positive-sequence voltage vector error which needs to be compensated.
Under distorted grid voltage conditions, the instantaneous active and reactive power flowing through the SGSC can be represented as:
 where:
where:
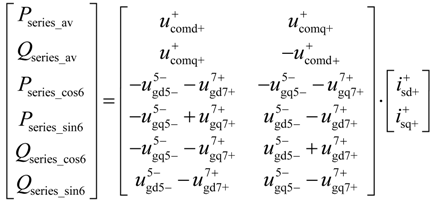
As can be seen from Equation (4), although there are zero oscillations in generator’s power output, the pulsations of six times the grid frequency in SGSC’s active and reactive power still exist due to the interaction between the fifth- and seventh-order harmonic grid voltages and positive-sequence stator currents, which inevitably leads to oscillations of the total output power entering the grid. On the other hand, the oscillating active power from the SGSC is also delivered into the dc-link capacitor, which produces the pulsations in dc-link voltage.
2.2. PGSC
Considering that the PGSC is directly connected to the grid, its operation behavior is similar to a grid-connected voltage-source converter (VSC) system. Unlike the power oscillations in SGSC, due to the existence of fifth- and seventh-order harmonic grid currents, the active and reactive power flowing through the PGSC include three parts, i.e., the dc average power, the pulsations at the six times the grid frequency and the pulsations at the twelve times the grid frequency, which can be expressed as:
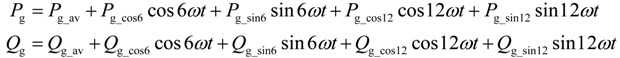 where:
where:
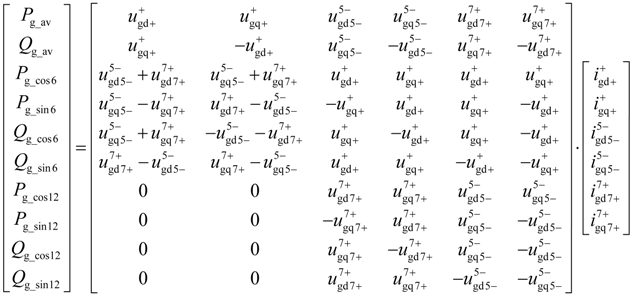
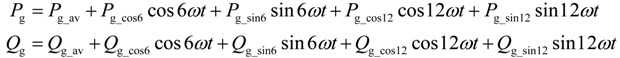
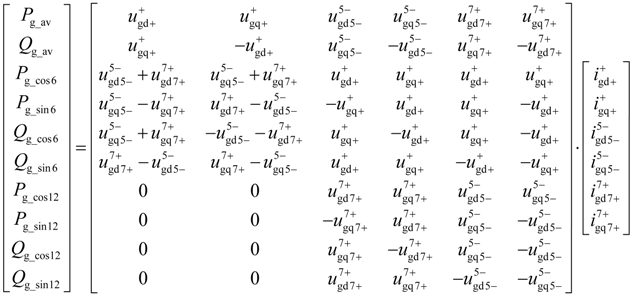
As it can be seen from Equation (6), under distorted grid voltage conditions, the significant active and reactive power oscillations at six times the grid frequency could result from the interactions among the fundamental or harmonic grid voltages and currents. However, it still can be found from Equation (6) that the power pulsations at twelve times the grid frequency are only produced by the fifth- and seventh-order harmonic grid voltages and currents. Compared with the pulsations terms at the 6th grid frequency, the pulsations terms of the 12th grid frequency is relatively small, which could be reasonably neglected for the system control analysis and design.
As shown in Figure 1, the common dc-link voltage can be obtained as:
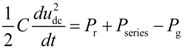
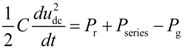
As derived from Equations (6) and (7), like the case illustrated by Equation (4), the power exchanges between the PGSC and grid contain active and reactive power oscillating at the six times the grid frequency, which further leads to pulsations in the dc-link voltage and deteriorates the quality of output powers.
2.3. RSC
By eliminating the fifth- and seventh-order stator voltage harmonics, the DFIG stator voltages become sinusoidal and balanced. As a result, a conventional vector control (VC) strategy or direct power control (DPC) scheme for the RSC remains in full force under distorted grid voltage conditions. With effective control of SGSC, the adverse effects of voltage harmonics upon DFIG such as large stator and rotor current harmonics, electromagnetic torque and power pulsations will be eliminated naturally. Consequently, the enhanced operation performance for the overall DFIG system can be significantly improved. As the operation and control of RSC under normal condition have been well documented in numerous references [23,24], these topics will be not discussed in detail in this paper.
3. Coordinated Control of SGSC, PGSC and RSC
3.1. SGSC
As mentioned in Sections 2.1, the SGSC should be controlled to achieve the following control target:
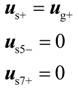
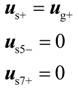
In order to meet the demand of Equation (8), positive-sequence component of stator voltage vector should be controlled to equal to that of grid voltage vector, while the 5th and 7th harmonic component of stator voltage vectors should be controlled to zero.
3.2. PGSC
As it can be seen from Equation (6), under distorted grid voltage conditions, there are six grid current components of PGSC, i.e., , , , , and can be controlled to improve the overall system performance. Therefore, for the PGSC, apart from the average grid-side active and reactive powers Pg_av and Qg_av, shown in Equation (6), there are four more power oscillating terms of the 6th grid frequency can be controlled when ignoring the power pulsations of the 12th grid frequency. It is worth noting that, unlike the PGSC control during a network unbalance mentioned in [22], the simultaneous elimination of the oscillations in total active and reactive power can be realized due to the enough control variables of grid currents, which can also simplify the control target selection and system control design. Consequently, the PGSC may be controlled to achieve one of the following two control targets:
Target 1: to eliminate the oscillations at the six times the grid frequency in the total active and reactive powers entering the grid simultaneously;
Target 2: to suppress the whole system’s fifth- and seventh-order harmonic currents injected to the grid.
3.2.1. Target 1
As shown in Figure 1, in order to eliminate the oscillation of the total powers, the oscillations at the six times the grid frequency in the active and reactive powers flowing through the SGSC should be equal to the corresponding oscillations in the active and reactive powers flowing through the PGSC, i.e.:
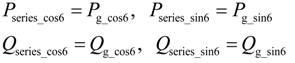
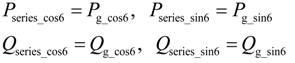
Based on Equations (6) and (9), and taking into account the fact that the d+-axis is aligned with the positive-sequence grid voltage vector, which means = 0, the required current reference values for the PGSC to realize Target 1 can be given as Equation (10), where the oscillating terms of active and reactive power flowing through the SGSC are calculated from Equation (4). The term and represents the dq-axis fundamental component of grid current, respectively:
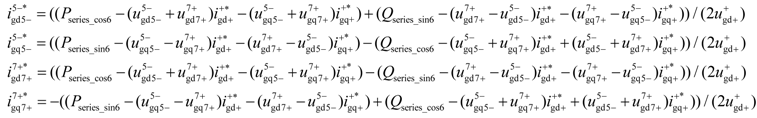
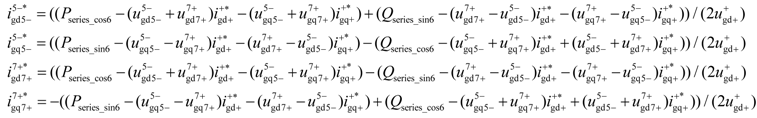
Unlike the unbalanced voltage conditions, considering that the fifth- and seventh-order grid voltage harmonics are much smaller than the fundamental grid voltages, the dc average active and reactive power are mainly determined by the fundamental grid voltage and current. Therefore, under distorted grid voltage conditions, the term and can be assumed to be proportional to the required average active power and reactive power from the PGSC delivered to the grid, respectively. As the required average active power should maintain the constant dc-link voltage, it would be related with the average component of the dc-link voltage. If a conventional dc-link voltage PI regulator is adopted, the average active power reference value can be expressed as:
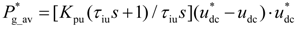 where Kpu and τiu are the proportional and integral time parameters of the PI controller, respectively.
where Kpu and τiu are the proportional and integral time parameters of the PI controller, respectively.
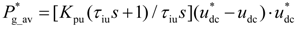
On the other hand, when neglecting the power pulsations of the 12th grid frequency, the common dc-link voltage can be rewritten using the average and oscillation power components as:
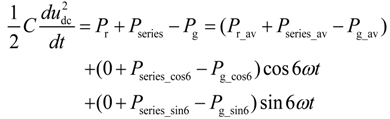 which indicates that the oscillations of the common dc-link voltage can also be diminished when eliminating the total power oscillations of the whole system.
which indicates that the oscillations of the common dc-link voltage can also be diminished when eliminating the total power oscillations of the whole system.
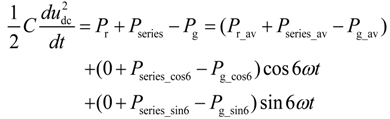
3.2.2. Target 2
As shown in Figure 1, the total current delivered into the grid is the sum of the currents from DFIG stator-side and PGSC. Since the fifth- and seventh-order current harmonics of the DFIG stator are eliminated with the effective control of SGSC, the required current reference for Target 2 thus can be expressed as:
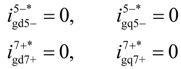
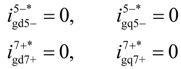
While achieving the goal of no fifth- and seventh-order harmonic currents injected to the grid, Equation (13) also indicates that currents generated from the PGSC are sinusoidal and balanced.
3.3. RSC
For RSC, as the stator voltage of DFIG is still sinusoidal and balanced during network distortions, the conventional vector control strategy or direct power control strategy can be still used without modification.
3.4. System Implementation Using PI-R Controllers
Under distorted grid voltage conditions, several separate dual current PI controllers can be used in the multiple rotating synchronous reference frames to provide the required system response. However, the decomposition of positive-sequence, fifth- and seventh-order feedback components will introduce extra time delays and errors when detecting the amplitude and phase signals, which might degrade the transient performance and stability of the system. In order to avoid such a sequential decomposition, the controllers including a standard proportional-integral (PI) regulator and a resonant (R) compensator tuned at six times the grid frequency in the rotating positive (dq)+ reference frame are developed for the SGSC voltage control and PGSC current control, respectively.
Under distorted grid voltage condition, the voltage and current in the (dq)+ reference frame consist of two parts, i.e., the dc fundamental positive-sequence component and the ac fifth- and seventh-order harmonic components oscillating at the frequencies of ±6ω. As the resonant controller is a generalized double-side ac integrator [25], it can simultaneously eliminate the ac errors of the positive- and negative-sequence components at the frequencies of ±6ω. Therefore, a resonant compensator tuned at six times the grid frequency can be introduced to regulate the fifth- and seventh-order voltages or currents to their reference values in the positive (dq)+ reference frame, while the fundamental positive-sequence voltages or currents can be controlled by using a traditional PI regulator. Consequently, the PI plus R (PI-R) controllers for the SGSC and PGSC in the rotating positive (dq)+ reference frame can be designed to directly regulate both the fundamental positive-sequence component and the harmonic components without involving sequential decomposition, significantly improving the transient performance of the whole system. A detailed study on the PI-R controller has been provided in [14]. Therefore, only a brief description is given in this paper.
The designed transfer function of the PI-R controller is given as:
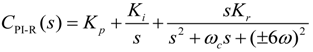 where Kp, Ki and Kr are the proportional, integral and resonant parameters of the PI-R controller, respectively. And ωc is the cutoff frequency used to widen the resonant frequency bandwidth.
where Kp, Ki and Kr are the proportional, integral and resonant parameters of the PI-R controller, respectively. And ωc is the cutoff frequency used to widen the resonant frequency bandwidth.
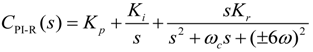
In the positive (dq)+ reference frame, the respective SGSC and PGSC output control voltage can be obtained as:
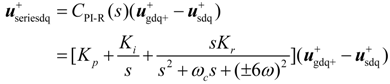
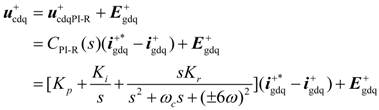 where:
where:
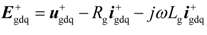 is defined as the feedforward grid voltage of PGSC.
is defined as the feedforward grid voltage of PGSC.
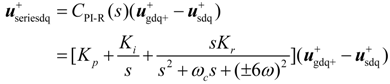
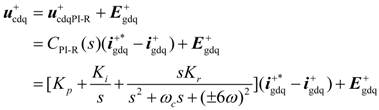
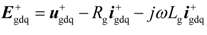
Based on Equations (15) and (16), the control voltages in the positive-sequence reference frames can be transformed into the stationary αβ reference frames, i.e.:
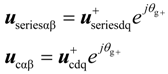
The respective resulting control voltages u seriesαβ and ucαβ for the SGSC and PGSC can be applied by using standard space vector pulse width modulation (SVPWM) techniques.
Figure 3 shows the schematic diagram of the proposed control scheme for the DFIG system with SGSC during network voltage distortions. The reference values for both SGSC and PGSC in the positive-sequence synchronous reference frame are compared with their respective feedback voltage and current signals to generate the final regulating control voltages. It is obvious that the feedback signals need not decomposed into the positive-sequence, fifth- and seventh-order components in both the SGSC and PGSC controllers, which improving the dynamic response performance of the whole system naturally. Furthermore, the conventional vector control strategy for the RSC can be still used without modification.
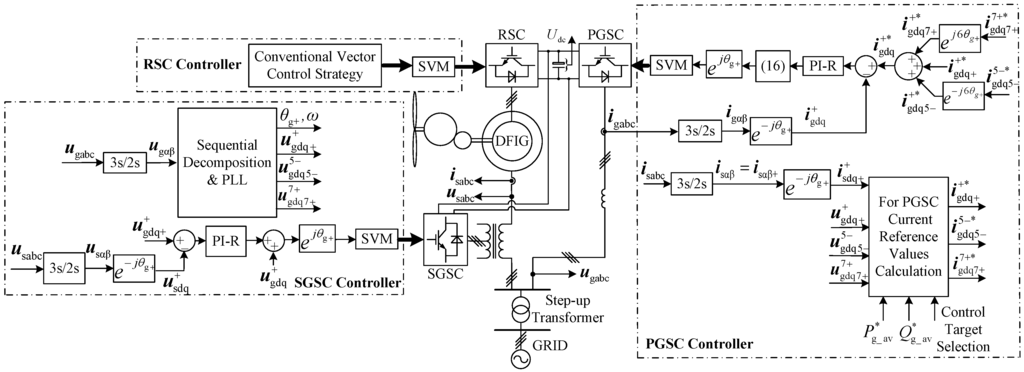
Figure 3.
Schematic diagram of the proposed control scheme for the DFIG system with SGSC.
4. Evaluation Studies
For evaluation of the proposed control strategy, simulations on a 2 MW DFIG-based wind power generation system with SGSC have been conducted by using Matlab/Simulink. Details of the simulated DFIG system are given in the Appendix A. The PI-R controller parameters for both SGSC voltage and PGSC current by using the traditional transfer function design method are listed in Table 1.

Table 1.
Parameters of the PI-R controllers.
| Converter | Kp | Ki | Kr | ωc (rad/s) |
|---|---|---|---|---|
| PGSC | 10 | 200 | 200 | 5 |
| SGSC | 10 | 200 | 200 | 5 |
Figure 4 shows the configuration of the simulated DFIG system with SGSC. In the simulation model, three discrete control systems are built for the SGSC, PGSC and RSC, respectively. The DFIG is rated at 2 MW/690 V, and the dc-link voltage is set at 1200 V. The discrete control periods for the three converters are all 100 μs, and the switching frequency for each converter is 2 kHz. The DFIG system is connected to a programmable power grid rated at 20 MVA via a step-up transformer. The programmable ac voltage source is used to generate the fifth- and seventh-order harmonic grid voltages during the simulation studies, which are set to 4% and 3%, respectively. During the initial simulation, the rotor speed is assumed to be fixed at a normal speed of 1950 r/min (the maximal slip: –0.3). The total active and reactive power outputs of the generation system are 2 MW and zero (rated power and unit power factor), respectively.
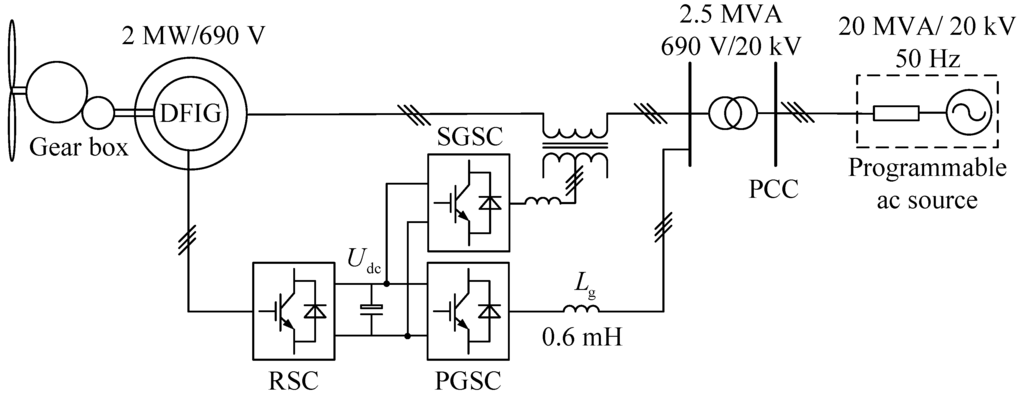
Figure 4.
Configuration of the simulated DFIG system with SGSC.
Figure 5, Figure 6 and Figure 7 show the simulation results of the DFIG system with SGSC under grid voltage harmonics of the aforementioned condition between 1.6 and 1.7 s. Figure 5 shows the simulation results of the system with the conventional control strategy, i.e., no harmonic control for the system during grid voltage harmonics, while the Figure 6 and Figure 7 show the simulation results of the system with the proposed control Targets 1 and 2, respectively. During the simulation process, the RSC is controlled with the conventional vector control strategy to achieve the decoupling control of stator active and reactive powers, while the SGSC is controlled to keep the DFIG stator voltage always in line with the positive-sequence grid voltage and the PGSC is controlled with two different control targets.
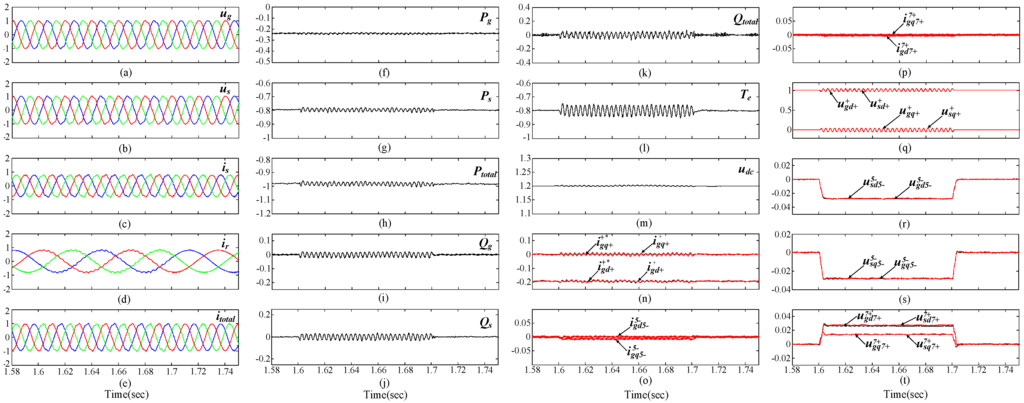
Figure 5.
Simulation results of DFIG system with SGSC under distorted grid voltage condition between 1.6 and 1.7 s without harmonic control. (a) grid voltage (pu); (b) stator voltage (pu); (c) stator current (pu); (d) rotor current (pu); (e) total current (pu); (f) PGSC active power (pu); (g) stator active power (pu); (h) total active power (pu); (i) PGSC reactive power (pu); (j) stator reactive power (pu); (k) total reactive power (pu); (l) electromagnetic torque (pu); (m) common dc-link voltage (V); (n) PGSC positive-sequence dq-axis currents reference and response (pu); (o) PGSC 5th harmonic dq-axis currents (pu); (p) PGSC 7th harmonic dq-axis currents (pu); (q) grid and stator positive-sequence dq-axis voltages (pu); (r) grid and stator 5th harmonic d-axis voltages (pu); (s) grid and stator 5th harmonic q-axis voltages (pu); (t) grid and stator 7th harmonic dq-axis voltages (pu).

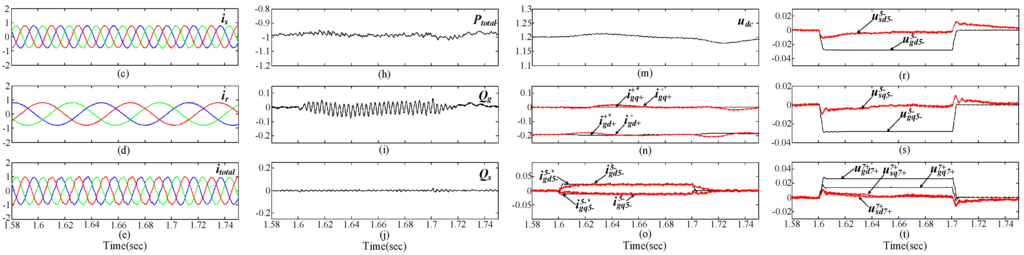
Figure 6.
Simulation results of DFIG system with SGSC under distorted grid voltage condition between 1.6 and 1.7 s with proposed control scheme with Target 1. (a) grid voltage (pu); (b) stator voltage (pu); (c) stator current (pu); (d) rotor current (pu); (e) total current (pu); (f) PGSC active power (pu); (g) stator active power (pu); (h) total active power (pu); (i) PGSC reactive power (pu); (j) stator reactive power (pu); (k) total reactive power (pu); (l) electromagnetic torque (pu); (m) common dc-link voltage (V); (n) PGSC positive-sequence dq-axis currents reference and response (pu); (o) PGSC 5th harmonic dq-axis currents reference and response (pu); (p) PGSC 7th harmonic dq-axis currents reference and response (pu); (q) grid and stator positive-sequence dq-axis voltages (pu); (r) grid and stator 5th harmonic d-axis voltages (pu); (s) grid and stator 5th harmonic q-axis voltages (pu); (t) grid and stator 7th harmonic dq-axis voltages (pu).
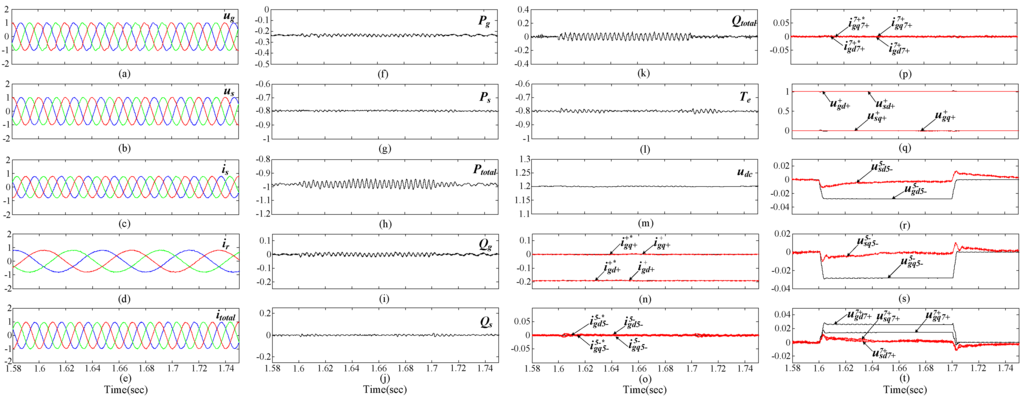
Figure 7.
Simulation results of DFIG system with SGSC under distorted grid voltage condition between 1.6 and 1.7 s with Proposed control scheme with Target 2. (a) grid voltage (pu); (b) stator voltage (pu); (c) stator current (pu); (d) rotor current (pu); (e) total current (pu); (f) PGSC active power (pu); (g) stator active power (pu); (h) total active power (pu); (i) PGSC reactive power (pu); (j) stator reactive power (pu); (k) total reactive power (pu); (l) electromagnetic torque (pu); (m) common dc-link voltage (V); (n) PGSC positive-sequence dq-axis currents reference and response (pu); (o) PGSC 5th harmonic dq-axis currents reference and response (pu); (p) PGSC 7th harmonic dq-axis currents reference and response (pu); (q) grid and stator positive-sequence dq-axis voltages (pu); (r) grid and stator 5th harmonic d-axis voltages (pu); (s) grid and stator 5th harmonic q-axis voltages (pu); (t) grid and stator 7th harmonic dq-axis voltages (pu).
As it can be seen from Figure 5, Figure 6 and Figure 7a, due to the existence of the fifth- and seventh-order harmonic grid voltage components, the grid voltages are obviously distorted between 1.6 and 1.7 s. In a conventional control system, a only single PI controller in the positive (dq)+ synchronous reference frame is used for the SGSC voltage and PGSC current. As the traditional single PI controller of SGSC has limited regulating gain for the fifth- and seventh-order harmonic voltage components which are oscillating at six times the grid frequency in the positive (dq)+ reference frame, the fifth- and seventh-order voltage harmonics in the stator still exist and the stator voltages will contain 300 Hz pulsations in the positive synchronous reference frame, as shown in Figures 5b,q–t. The harmonically polluted stator voltages will lead to badly distorted stator currents, which inevitably make the rotor currents contain both fundamental component of 15 Hz, and harmonic components of 315 Hz (300 + 15 Hz) and 285 Hz (300 – 15 Hz), respectively. Consequently, the significant oscillations at 300 Hz in the electromagnetic torque and instantaneous stator powers of DFIG could occur, as shown in Figure 5g,j,l. In the meanwhile, distorted currents and power pulsations in the PGSC will also result from the failure regulation of harmonic currents in the PGSC when a single current PI controller is used, which further degrading the operation performance of whole system, as shown in Figure 5e,f,h,i,k,n. As it can be seen from Figure 6 and Figure 7b,q–t, when the proposed control strategy for the SGSC under distorted grid voltage condition is implemented, the harmonic voltage at the DFIG’s stator terminal can be eliminated by injecting appropriate series compensation voltages of SGSC to counteract the grid voltage harmonics, although the grid voltage harmonics always exist. Compared with the conventional control method, the fundamental component of the stator voltage is controlled to be equal to the positive-sequence grid voltage, while the harmonic components of the stator voltage are effectively controlled to zero by using the proposed PI-R voltage control strategy. As analyzed in Section 2, once the stator voltage harmonics are suppressed, the stator and rotor current harmonics, electromagnetic torque and power oscillations in the DFIG will be eliminated naturally, which are nicely demonstrated in Figure 6 and Figure 7c,d,g,j,l.
The system performances with the two different control targets for the PGSC are compared in Figure 6 and Figure 7. As seen in these figures, the objectives of the two control targets have been fully achieved. With Target 1, the 300 Hz oscillations in the total active power and reactive power entering the power grid can be eliminated simultaneously, and the pulsation of the common dc-link voltage is also suppressed effectively, as shown in Figure 6h,k,m. When Target 2 is selected, the fifth- and seventh-order harmonic currents of PGSC can be eliminated successfully, as analyzed in Section 3, the total current distortions can also be suppressed, as shown in Figure 7e. With the limited control variables of the PGSC, the oscillation of the total active and reactive power output could not be eliminated simultaneously, as shown in Figures 7h,k, respectively.
Figure 5, Figure 6 and Figure 7 also show the system dynamic responses with the conventional standard PI control scheme and the developed PI-R control method when the voltage distortions occurring between 1.6 and 1.7 s, respectively. As shown, compared with the case without harmonic control, the required voltage and current references can be obtained with the improved control targets, which allow us to achieve the goal of eliminating 300 Hz pulsations in the total output powers entering the grid or removing fifth- and seventh-order harmonic currents injected to the grid. With the proposed PI-R controllers for the SGSC and PGSC, the respective fifth- and seventh-order harmonic voltages or currents oscillating at 300 Hz in the positive (dq)+ reference frame can be tuned to the their references by using the resonance regulator. Consequently, it can be seen that the voltage and current feedback signals of SGSC and PGSC precisely track their corresponding reference values, which indicates that the developed PI-R controllers have excellent dynamic response performance. It is also worth noting that the function of SGSC does not need to be changed during the normal grid condition and the distorted voltage condition for the PGSC’s two control strategies, and the R regulator can eliminate the harmonic voltages or currents when the voltage distortions is cleared, which means that the developed PI-R regulator can work under both distorted grid voltage conditions and the normal conditions, without any modifications.
For detailed comparison, the harmonic spectrums of the grid and stator voltages, the stator and rotor currents are given in Figure 8, and the harmonic and pulsating components are listed in Table 2. As shown, the two control targets have been fully achieved with the proposed control strategies. With the effective control of SGSC, the fifth- and seventh-order voltage harmonics in the stator have been successfully suppressed, reduced to 0.08% and 0.05% with respect to the fundamental component, respectively. As a consequence, not only the stator and rotor current harmonics but also the significant oscillations in the DFIG’s electromagnetic torque and output powers can be avoided simultaneously, which undoubtedly improves the operation performance and stability of the generator under distorted network conditions. With Target 1, the 300 Hz pulsations in both the total active and reactive power entering the grid and dc-link voltage can be eliminated simultaneously. In addition, Target 2 can effectively diminish the total harmonic currents injected to the grid. While for a practical system, the control target can be flexibly selected by considering the operation of the network to meet different requirements.
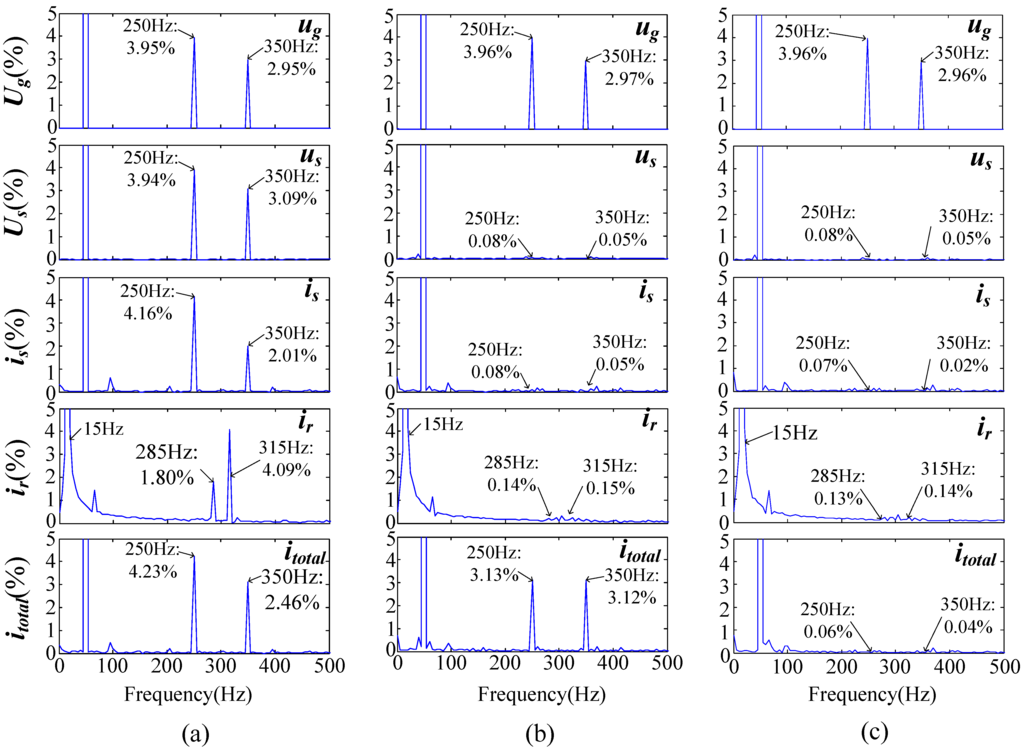
Figure 8.
Harmonic spectrums. (a) No harmonic control; (b) Proposed control scheme with Target 1; (c) Proposed control scheme with Target 2.

Table 2.
Comparisons of different control Targets.
| Measured Parameter | Conventional | Target 1 | Target 2 |
|---|---|---|---|
| us 5th harmonic (%) | 3.94% | 0.08% | 0.08% |
| us 7th harmonic (%) | 3.09% | 0.05% | 0.05% |
| is 5th harmonic (%) | 4.16% | 0.08% | 0.07% |
| is 7th harmonic (%) | 2.01% | 0.05% | 0.02% |
| ir 19th harmonic (%) | 1.80% | 0.14% | 0.13% |
| ir 21st harmonic (%) | 4.09% | 0.15% | 0.14% |
| itotal 5th harmonic (%) | 4.23% | 3.13% | 0.06% |
| itotal 7th harmonic (%) | 2.46% | 3.12% | 0.04% |
| Ps pulsation (pu) | 0.03 | 0.007 | 0.007 |
| Qs pulsation (pu) | 0.06 | 0.012 | 0.01 |
| Ptotal pulsation (pu) | 0.04 | 0.01 | 0.07 |
| Qtotal pulsation (pu) | 0.13 | 0.03 | 0.12 |
| Tem pulsation (pu) | 0.10 | 0.01 | 0.01 |
| udc pulsation (V) | 4.0 | 2.0 | 2.0 |
To further illustrate the robustness of the proposed control strategies, the system responses with both a step change of PGSC’s reactive power and the variations of generator’s speed and active power under 4% 5th and 3% 7th steady-state voltage condition are carried out. Figure 9a,b show the results when a step change of PGSC’s reactive power from 0 to –0.1 pu at 2.0 s. As shown, the dynamic response of the PGSC’s reactive power is relatively satisfactory, which means that the PGSC can participate in the auxiliary reactive power regulation if needed. Meanwhile, the fifth- and seventh- order PGSC current harmonics can accurately track their reference values during the PGSC’s reactive power quick regulation, and the other operation requirements for the DFIG system can also be fully met with the two control targets. Simulations during variable rotor speed and power with the proposed control strategies are shown in Figure 9c,d. During the simulation process, the generator speed is changed from 1.3 to 0.8 pu during 2.0 s to 2.7 s, and the stator active power is changed from –0.8 pu to –0.2 pu with the stator reactive power being zero. It is obvious that the operation performances of the DFIG system with the variations of rotor speed and power are nicely demonstrated. With the developed control strategies, the oscillations in electromagnetic torque, stator active and reactive powers, and total power outputs or total harmonic currents are eliminated during the whole process. In addition, the three phase stator and rotor currents of the DFIG are all sinusoidal and balanced as well. As the power pulsations in PGSC and SGSC are proportional to the stator current, as a consequence, the peak amplitude of oscillating active and reactive power in the PGSC and the DFIG system are all decreased with the reduction of the generator’s output power, as shown in Figure 9c,d.
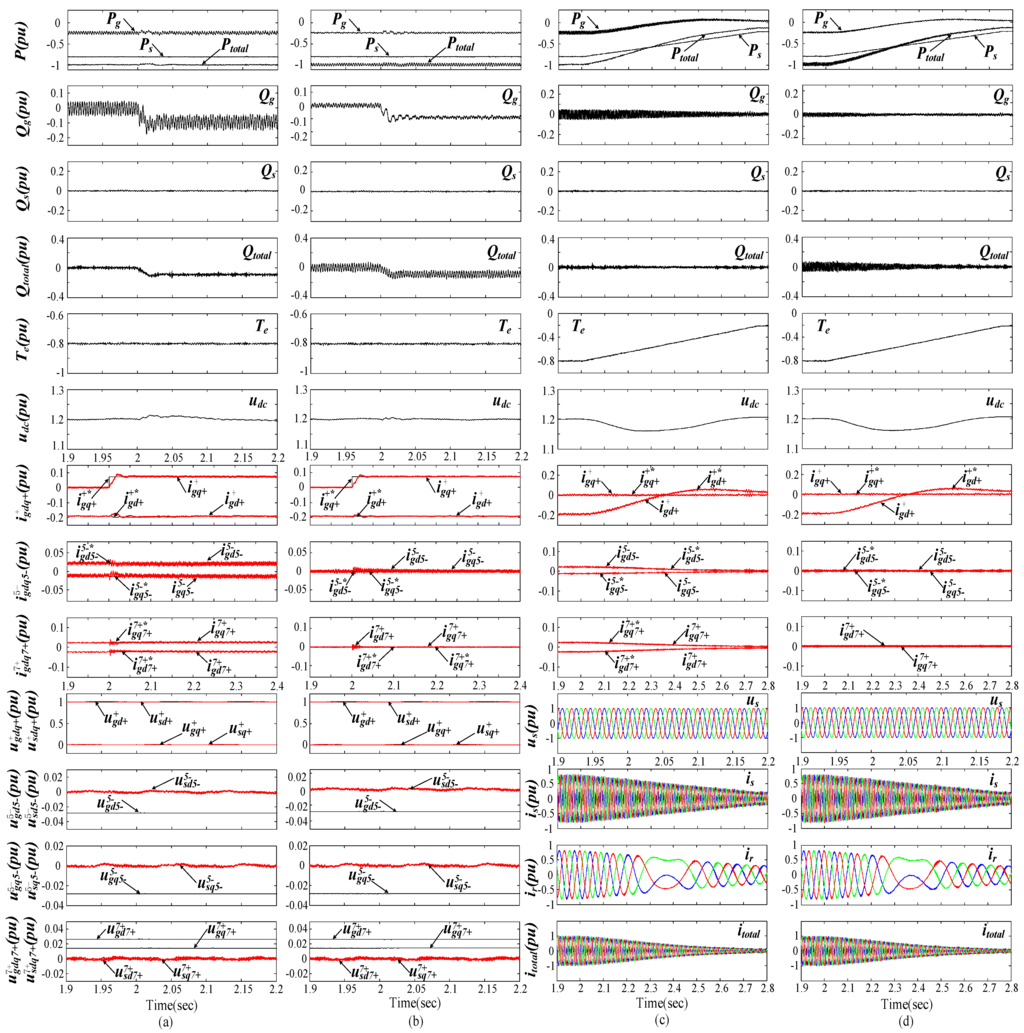
Figure 9.
Simulation results with PGSC’s reactive power step at 2.0 s and generator speed variations during 2.0 s to 2.7 s. (a) Reactive power step with Target 1; (b) Reactive power step with Target 2; (c) Variable rotor speed with Target 1; (d) Variable rotor speed with Target 2.
To further illustrate the robustness of the proposed control strategies, the system responses with both a step change of PGSC’s reactive power and the variations of generator’s speed and active power under 4% 5th and 3% 7th steady-state voltage condition are carried out. Figure 9a,b show the results when a step change of PGSC’s reactive power from 0 to –0.1 pu at 2.0 s. As shown, the dynamic response of the PGSC’s reactive power is relatively satisfactory, which means that the PGSC can participate in the auxiliary reactive power regulation if needed. Meanwhile, the fifth- and seventh- order PGSC current harmonics can accurately track their reference values during the PGSC’s reactive power quick regulation, and the other operation requirements for the DFIG system can also be fully met with the two control targets. Simulations during variable rotor speed and power with the proposed control strategies are shown in Figure 9c,d. During the simulation process, the generator speed is changed from 1.3 to 0.8 pu during 2.0 s to 2.7 s, and the stator active power is changed from –0.8 pu to –0.2 pu with the stator reactive power being zero. It is obvious that the operation performances of the DFIG system with the variations of rotor speed and power are nicely demonstrated. With the developed control strategies, the oscillations in electromagnetic torque, stator active and reactive powers, and total power outputs or total harmonic currents are eliminated during the whole process. In addition, the three phase stator and rotor currents of the DFIG are all sinusoidal and balanced as well. As the power pulsations in PGSC and SGSC are proportional to the stator current, as a consequence, the peak amplitude of oscillating active and reactive power in the PGSC and the DFIG system are all decreased with the reduction of the generator’s output power, as shown in Figure 9c,d.
5. Conclusions
This paper has investigated the dynamic modeling and enhanced control of a grid-connected DFIG-based wind turbine with a series grid-side converter under grid voltage harmonic distortion. Based on the deduced mathematic models of the DFIG system with SGSC, a coordinated control strategy for the SGSC, PGSC and RSC has been proposed to improve the performance of the system. Two alternative control targets for the PGSC, including eliminating the pulsations oscillating at six times of the grid frequency in the total active and reactive power entering the grid or keeping the three phase total current sinusoidal and symmetrical have been achieved by coordinately controlling the SGSC and PGSC, while the RSC is able to be controlled with the conventional vector control strategy regardless of grid voltage harmonics. The respective PI-R regulator in the positive synchronous reference frame for the SGSC voltage control and PGSC current control have been proposed to directly regulate both the fundamental positive-sequence component and the harmonic components, without involving sequential decomposition. Therefore, excellent dynamic response performance can be achieved. The simulation results of a 2 MW DFIG system with SGSC under distorted grid voltage conditions fully demonstrate the effectiveness of the developed control strategies.
Nomenclature
| us and ug | Stator and grid voltage vectors. |
| useires | Series injected voltage vector of SGSC referred to stator-side. |
| is, ir | Stator and rotor current vectors. |
| iseries | SGSC current vector referred to stator-side. |
| itotal | Total current vector of the DFIG system. |
| Ps and Qs | Stator output active and reactive powers. |
| Pr and Qr | Rotor output active and reactive powers. |
| Pg and Qg | PGSC output active and reactive powers. |
| Pseries and Qseries | Active and reactive powers through SGSC. |
| Ptotal and Qtotal | Total output active and reactive powers of the DFIG system with SGSC. |
| Te | Electromagnetic torque. |
| udc | Common dc-link voltage. |
| ω | Synchronous angular speed. |
| θg | Grid voltage angle. |
| s | Slip. |
| C | Common dc-link capacitance. |
Subscripts
| α,β | Stationary α- and β-axis. |
| av | Average component. |
| sin and cos | Sine and cosine oscillating components. |
| abc | Stationary abc-axis. |
| dq | Synchronous dq-axis. |
| s and r | Stator and rotor. |
| g and series | PGSC and SGSC. |
| +, 5– and 7+ | Fundamental, fifth-order and seventh-order components. |
Superscripts
| +, 5– and 7+ | Positive (dq)+, harmonic (dq)5− and (dq)7+reference frames |
| * | Reference value |
| ^ | Conjugate complex |
Acknowledgments
The authors would like to thank the China Scholarship Council for sponsoring Jun Yao to visit Department of Energy Technology, Aalborg University, Denmark, 2012–2013.
Conflict of Interest
The authors declare no conflict of interest.
Appendix A: Simulation System Parameters

Table A1.
Parameters of the simulated DFIG.
| DFIG parameters | Value | DFIG parameters | Value |
|---|---|---|---|
| Rated generator power | 2 MW | Rotor resistance | 0.00549 pu |
| Rated generator voltage | 690 V | Rotor leakage inductance | 0.1493 pu |
| Frequency | 50 Hz | Magnetizing inductance | 3.9527 pu |
| Stator resistance | 0.00488 pu | Stator/rotor turns ratio | 0.45 |
| Stator leakage inductance | 0.1386 pu | Inertia constant H | 3.5 s |

Table A2.
Parameters of Step-up transformer and Series transformer.
| Step-up transformer parameters | Value | Series transformer parameters | Value |
|---|---|---|---|
| Rated capacity | 2.5 MVA | Rated capacity | 200 kVA |
| Frequency | 50 Hz | Frequency | 50 Hz |
| Primary windings | 20 kV-Yg | Stator to SGSC side transformer turns ratio | 1:7 |
| Secondary windings | 690 V-Δ | Sum of transformer and choke resistance | 0.006 pu |
| Short circuit impedance | 0.0098 + j0.09241 pu | Sum of transformer and choke inductance | 0.03 pu |

Table A3.
Parameters of Grid-side converter.
| Grid-side converter parameters | Value | Grid-side converter parameters | Value |
|---|---|---|---|
| Reactor resistance | 6 mΩ | Common dc-link capacitor | 38,000 μF |
| Reactor inductance | 0.6 mH | Common dc-link voltage reference value | 1,200 V |
References
- Morrent, J.; de Haan, S.W.H. Ride-through of wind turbines with doubly-fed induction generator during a voltage dip. IEEE Trans. Energy Convers. 2005, 20, 435–441. [Google Scholar] [CrossRef]
- Seman, S.; Niiranen, J.; Arkkio, A. Ride-through analysis of doubly fed induction wind-power generator under unsymmetrical network disturbance. IEEE Trans. Power Syst. 2006, 21, 1782–1789. [Google Scholar] [CrossRef]
- Brekken, T.A.; Mohan, N. Control of a doubly fed induction wind generator under unbalanced grid voltage conditions. IEEE Trans. Energy Convers. 2007, 22, 129–135. [Google Scholar] [CrossRef]
- Pena, R.; Cardenas, R.; Escobar, E.; Clare, J.; Wheeler, P. Control system for unbalanced operation of stand-alone doubly fed induction generators. IEEE Trans. Energy Convers. 2007, 22, 544–545. [Google Scholar] [CrossRef]
- Xu, L.; Wang, Y. Dynamic modeling and control of DFIG based wind turbines under unbalanced network conditions. IEEE Trans. Power Syst. 2007, 22, 314–323. [Google Scholar] [CrossRef]
- Xu, L. Coordinated control of DFIG’s rotor and grid side converters during network unbalance. IEEE Trans. Power Electron. 2008, 23, 1041–1049. [Google Scholar] [CrossRef]
- Xu, L. Enhanced control and operation of DFIG-based wind farms during network unbalance. IEEE Trans. Energy Convers. 2008, 23, 1073–1081. [Google Scholar] [CrossRef]
- Qiao, W.; Harley, R.G. Improved Control of DFIG Wind Turbines for Operation with Unbalanced Network Voltages. In Proceedings of IEEE Industry Applications Society Annual Meeting (IAS 2008), Edmonton, AB, Canada, 5–9 October 2008; pp. 1–7.
- Pena, R.; Cardenas, R.; Escobar, E.; Clare, J.; Wheeler, P. Control strategy for a doubly-fed induction generator feeding an unbalanced grid or stand-alone load. Electr. Power Syst. Res. 2009, 79, 355–364. [Google Scholar] [CrossRef]
- Hu, J.B.; He, Y.K.; Xu, L.; Williams, B.W.J. Improved control of DFIG systems during network unbalance using PI-R current regulators. IEEE Trans. Ind. Electron. 2009, 56, 439–450. [Google Scholar] [CrossRef]
- Hu, J.B.; He, Y.K. Reinforced control and operation of DFIG-based wind-power-generation system under unbalanced grid voltage conditions. IEEE Trans. Energy Convers. 2009, 24, 905–915. [Google Scholar] [CrossRef]
- Zhou, Y.; Bauer, P.; Ferreira, J.A.; Pierik, J. Operation of grid-connected DFIG under unbalanced grid voltage condition. IEEE Trans. Energy Convers. 2009, 24, 240–246. [Google Scholar] [CrossRef]
- Ramos, C.J.; Martins, A.P.; Carvalho, A.S. Rotor Current Controller with Voltage Harmonics Compensation for a DFIG Operating under Unbalanced and Distorted Stator Voltage. In Proceedings of the 33rd Annual Conference of IEEE Industrial Electronics Society (IECON 2007), Taipei, Taiwan, 5–8 November 2007; pp. 1287–1292.
- Hu, J.B.; Nian, H.; Xu, H.L.; He, Y.K. Dynamic modeling and improved control of DFIG under distorted grid voltage conditions. IEEE Trans. Energy Convers. 2011, 26, 163–175. [Google Scholar] [CrossRef]
- Ibrahim, A.O.; Nguyen, T.H.; Lee, D.C.; Kim, S.C. A fault ride-through technique of DFIG wind turbine systems using dynamic voltage restorers. IEEE Trans. Energy Convers. 2011, 26, 871–882. [Google Scholar] [CrossRef]
- Leon, A.E.; Farias, M.F.; Battaiotto, P.E.; Solsona, J.A.; Valla, M.I. Control strategy of a DVR to improve stability in wind farms using squirrel-cage induction generators. IEEE Trans. Power Syst. 2011, 26, 1609–1617. [Google Scholar] [CrossRef]
- Abdel-Baqi, O.; Nasiri, A. Series voltage compensation for DFIG wind turbine low-voltage ride-through solution. IEEE Trans. Energy Convers. 2011, 26, 272–280. [Google Scholar] [CrossRef]
- Wessels, C.; Gebhardt, F.; Fuchs, F.W. Fault ride-through of a DFIG wind turbine using dynamic voltage restorer during symmetrical and asymmetrical grid faults. IEEE Trans. Power Electron. 2011, 26, 807–815. [Google Scholar] [CrossRef]
- Zhang, S.; Tseng, K.; Choi, S.S.; Nguyen, T.D.; Yao, D. Advanced control of series voltage compensation to enhance wind turbine ride-through. IEEE Trans. Power Electron. 2012, 27, 763–772. [Google Scholar] [CrossRef]
- Flannery, P.S.; Venkataramanan, G. A fault tolerant doubly fed induction generator wind turbine using a parallel grid side rectifier and series grid side converter. IEEE Trans. Power Electron. 2008, 23, 1126–1135. [Google Scholar] [CrossRef]
- Flannery, P.S.; Venkataramanan, G. Unbalanced voltage sag ride-through of a doubly fed induction generator wind turbine with series grid-side converter. IEEE Ind. Appl. 2009, 45, 1879–1887. [Google Scholar] [CrossRef]
- Liao, Y.; Li, H.; Yao, J.; Zhuang, K. Operation and control of a grid-connected DFIG-based wind turbine with series grid-side converter during network unbalance. Electr. Power Syst. Res. 2011, 81, 228–236. [Google Scholar] [CrossRef]
- Pena, R.; Clare, J.C.; Asher, G.M. Doubly fed induction generator using back-to-back PWM converter and its application to variable-speed wind-energy generation. IEEE Proc. Electr. Power Appl. 1996, 143, 231–241. [Google Scholar] [CrossRef]
- Muller, S.; Deicke, M.; De Doncker, R.W. Doubly fed induction generator systems for wind turbines. IEEE Ind. Appl. Mag. 2002, 8, 26–33. [Google Scholar] [CrossRef]
- Yuan, X.; Merk, W.; Stemmler, H.; Allmeling, J. Stationary-frame generalized integrators for current control of active power filters with zero steady-state error for current harmonics of concern current under unbalanced and distorted operating conditions. IEEE Ind. Appl. 2002, 38, 523–532. [Google Scholar] [CrossRef]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).