Abstract
Efficient high speed propulsion requires exploiting the cooling capability of the cryogenic fuel in the propulsion cycle. This paper presents the numerical model of a combined cycle engine while in air turbo-rocket configuration. Specific models of the various heat exchanger modules and the turbomachinery elements were developed to represent the physical behavior at off-design operation. The dynamic nature of the model allows the introduction of the engine control logic that limits the operation of certain subcomponents and extends the overall engine operational envelope. The specific impulse and uninstalled thrust are detailed while flying a determined trajectory between Mach 2.5 and 5 for varying throttling levels throughout the operational envelope.
1. Introduction
The achievement of long-haul supersonic transport entails the development of air-breathing propulsion technologies with acceptable performance in terms of fuel consumption, reliability, safety, environmental impact (noise and pollutants emissions) and cost. Among the various air-breathing engine architectures intended to accomplish those requirements, the rocket and the turbine based combined cycles follow variations of the Brayton cycle. The goal is to extend the engine operational envelope towards the supersonic regime while best fulfilling the mission requirements of thrust to weight ratio and specific impulse. Although these architectures are not new [1,2,3], there is scarce practical knowledge about them and their assessment must be based on numerical simulations. Moreover, the interdependence of the three areas of study—mission, vehicle and power plant—becomes more and more significant for the high speed flight. In particular, the air-breathing engine efficiency becomes a critical factor in determining the overall mission performance, as was pointed out by Schmidt and Lovell [4] when analyzing an air-breathing launch system. Therefore, higher fidelity in the complex numerical model is required to achieve accurate engine predictions. On this line, a hydrogen-fueled aircraft for high speed transport was studied here in the frame of an EU funded program LAPCAT II [5]. The vehicle is powered by a variable cycle engine that combines a turbofan based cycle with an air turbo-rocket cycle (ATR) such that the engine holds high efficiency during the lengthy acceleration phase (Figure 1). The engine, named Scimitar, was conceived by Alan Bond of Reaction Engines Ltd. [6].
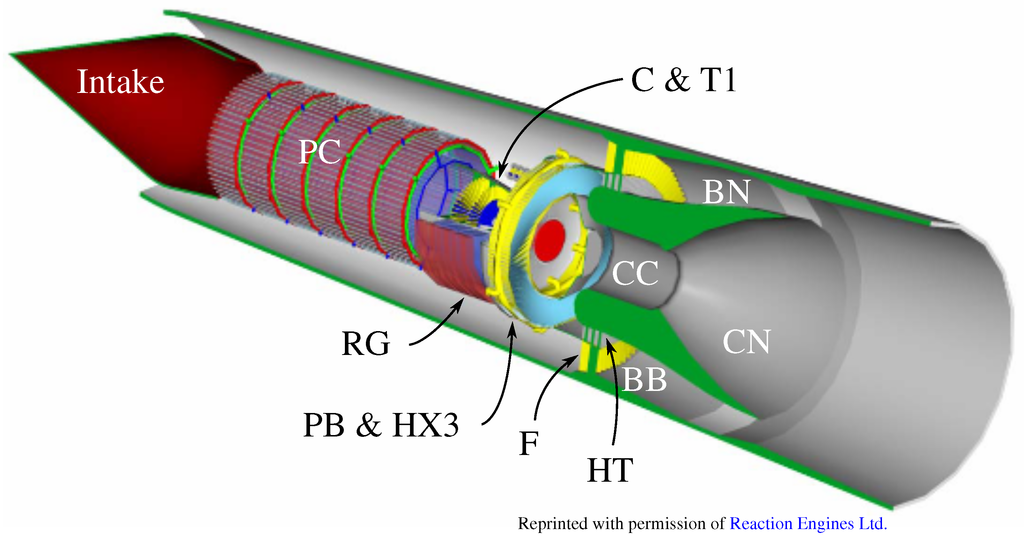
Figure 1.
Three dimensional view of Scimitar engine.
The turbofan based cycle operates from take-off to Mach 2.5. The core flow is diverted towards the hub turbine (HT) that drives the fan (F) (Figure 2). Then it is mixed with the air from the bypass duct. The bypass burner augments (BB) the thrust during the acceleration phase but is not in operation during the subsonic cruise at Mach 0.9. Between Mach 2.5 and Mach 5 the engine has the dual operation of an air turbo-rocket with a ramjet burner in the bypass. The core flow is drawn into the core main combustion chamber and the fan windmills in the bypass, upstream of the ramjet burner that exhausts around the core jet. The speed of the fan is brought down as the bypass nozzle (BN) is progressively closed. During cruise at Mach 5 the bypass is closed and the thrust is solely provided by the engine core, which operates as an air turbo-rocket [6]. Table 1 shows the working mode in function of the flight speed.
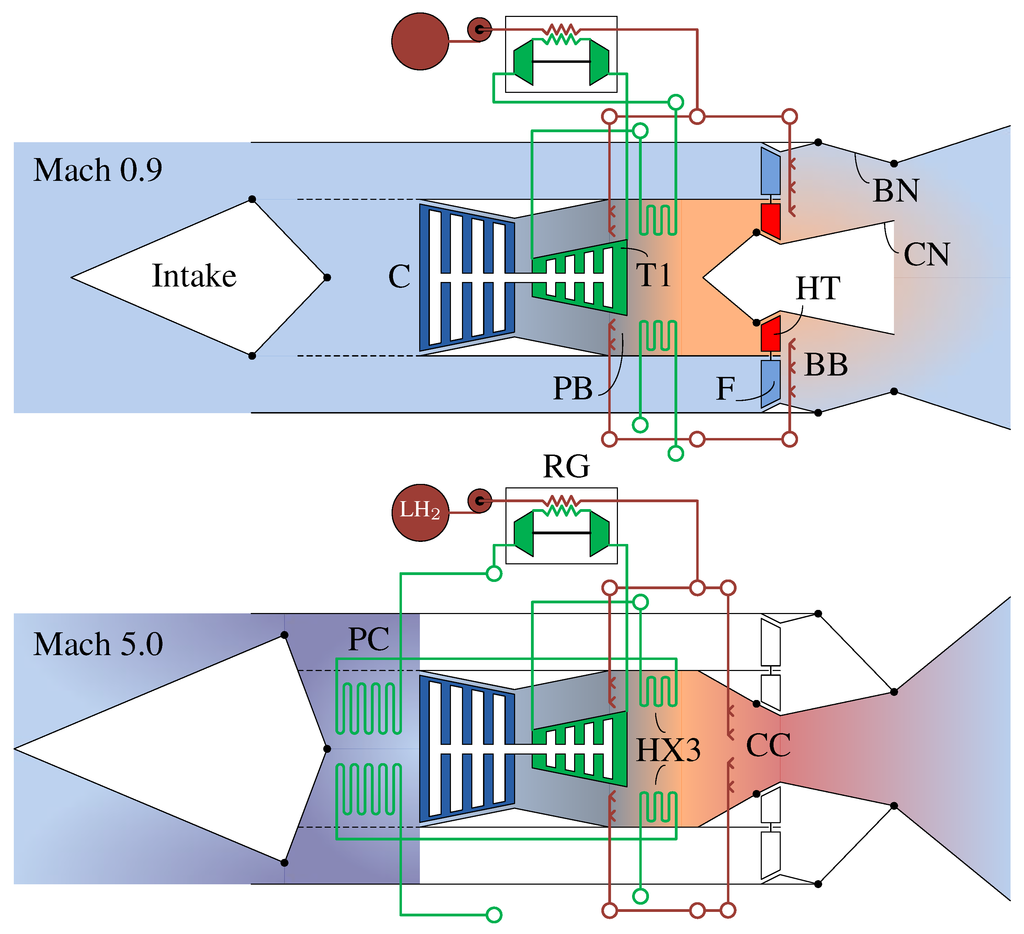
Figure 2.
Turbofan (upper) and air turbo-rocket (lower) configurations of Scimitar engine.

Table 1.
Variable cycle schedule of Scimitar.
| Mach Range | Regime | Mode | Bypass Burner | Bypass Nozzle |
|---|---|---|---|---|
| 0.0–0.9 | Subsonic Acceleration | Turbofan | On | Open |
| 0.9 | Subsonic Cruise | Turbofan | Off | Fully Open |
| 0.9–2.5 | Supersonic Acceleration | Turbofan | On | Open |
| 2.5–5.0 | Supersonic Acceleration | Ramjet + ATR | On | Open |
| 5.0 | Supersonic Cruise | ATR | Off | Closed |
The core consists of an air compressor (C) driven by a helium turbine (T1) that supplies air to the combustion chamber. Contrarily to the turbojet, the air compressor and turbine are not coupled by the same working fluid. Hence the turbine efficiency is maintained near the optimum point independently of the flight condition. The stream of helium follows a closed Brayton cycle between precooler (PC) and the regenerator (RG) and develops mechanical power through the helium turbine. At flight speeds below the cruise at Mach 5, the enthalpy of the incoming air does not suffice to power the air compressor and the preburner (PB) is in operation. The cryogenic hydrogen flowing through the regenerator is the heat sink of the helium loop.
A numerical model of the air turbo-rocket core, i.e., disregarding the bypass while the engine is in ATR configuration (Figure 2, lower), has been developed based on the simulation platform EcosimPro and the set of libraries of the European Space Propulsion System Simulation (ESPSS) [7]. State of the art engine subcomponents are used, the performance of which is known from other applications. The model provided the engine operational envelope and performances along the prescribed vehicle trajectory, in the range of Mach numbers from 2.5 to 5.0, for variable throttling conditions.
2. Numerical Model
The numerical model is programmed by assembling the different engine modules (compressors, turbines, heat exchangers, combustion chambers, nozzles and intake) in EcosimPro, an object oriented simulation environment. Each module encapsulates the mathematical formulation that governs its physical behavior such that the state of the overall model is described by a system of differential-algebraic equations:
The differential-algebraic system solver algorithm DASSL [8] is used to integrate in time the implicit system , given the appropriate initial and boundary conditions. The algorithm consists in replacing the time derivative by a backward differentiation of order and solving the resulting algebraic system at each time step with an implicit Newton–Raphson method. The size of the time steps and order of the time discretization is chosen automatically by DASSL based on the evolution of the integration. The discussion that follows in Section 4 focuses on the steady solutions of Equation (1), which are reached after the initial transient response to changes of engine throttling and flight regime along the vehicle trajectory.
The commonly used elements for the simulation of aerospace propulsion systems as the combustor and nozzles are contained within the set of libraries of the European Space Propulsion System Simulation (ESPSS) [7]. Also included in this framework is an application programming interface to retrieve the fluid properties according to either semi-perfect gas or real fluid models.
The joining elements (manifolds and valves) and the turbomachinery components lack a spatial discretization. In the manifolds, only characterized by their volume, the mass and energy conservation equations are applied to compute fluid velocity v, and the state variables pressure p and enthalpy h. In the valve element, the flow is adiabatic and the mass flow is computed from the momentum equation, considering the discharge characteristic of the valve and accounting for the possible sonic blockage of the section [7]. The turbomachinery components (compressors and turbines) are described by computed or measured performance maps of specific machines that are rescaled to target a specific on-design point.
The flow throughout the piping of the heat exchangers and ducts in the combustors is spatially resolved along the element axis. The one-dimensional form of the conservation equations of mass, energy and momentum are implemented in conservative form:
The conservative variables, flux and source terms are respectively:
In case of the combustor, the fluid is a reactive mixture of S species, which are considered as perfect gases and are formed among E chemical elements. Therefore, the conservation variables and and the molar composition of the mixture determine the fluid state. The gas composition is computed by assuming that the mixture is in thermodynamic equilibrium at the current pressure and temperature, i.e., the gas composition is that for which the Gibbs potential is minimum:
The number of moles of species cannot vary independently because mass conservation must be granted, therefore the minimization problem is constrained by imposing that the total mass of each chemical element j remains constant in the mixture:
The mass of atoms j in the species i is denoted as . The constrained minimization problem defined by Equations (6) and (7) is solved via the Lagrange multipliers method. Further details on the numerical aspects of the calculation method are explained in [10] and the documentation of ESPSS [9].
The expressions for the heat flux and the friction factor ξ provide the closure equations of the system in Equation (2). The heat flux through the wall of a one-dimensional fluid vein is computed by means of the convective heat transfer coefficient :
where the wall and fluid temperatures are respectively and T. The convective heat transfer coefficient is computed based on the Nusselt number (Nu):
where is the hydraulic diameter of the section. Appropriate correlations for the Nusselt number are used for each of the engine modules under consideration, as will be explained throughout this chapter.
The correlation by Churchill [11], valid for laminar, turbulent and transient flows, is used to calculate the pressure loss per unit of length of the duct, designated as friction factor ξ:
where the wall rugosity is and the coefficient serves to scale the pressure loss in case of targeting the specific design conditions and assuming that the off-design behavior is still described by the correlation f.
The fluid model provides the thermodynamical and transport properties. The fluids with working conditions in the vicinity or in the supercritical region (hydrogen, helium) are modeled as real gases according to the NIST properties database [12]. The air is considered as semi-perfect gas and the combustion gases are described as a mixture of perfect gases, as stated previously.
Equation (2) is solved with a centered scheme in a staggered domain, in which the conservation variables and the source terms are evaluated at the cell nodes (i), whereas the fluxes are computed at the cell interfaces () in Figure 3.
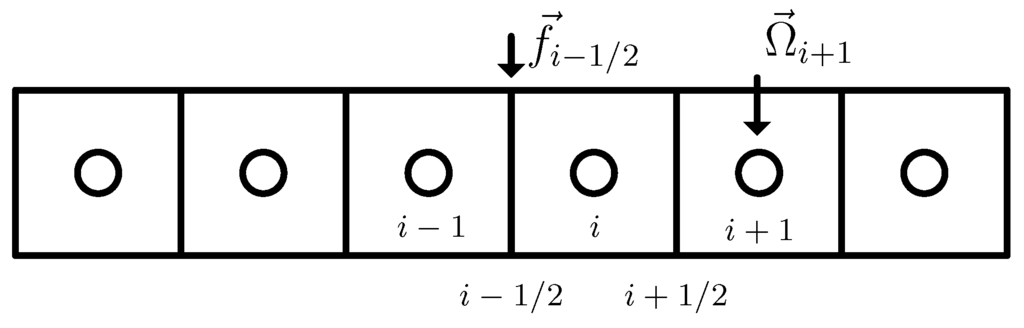
Figure 3.
Staggered grid.
Provided below is a detailed description of the engine sub-components: combustion chamber and nozzle, heat exchangers and turbomachinery used for the modeling of the air-breathing high speed propulsion system.
2.1. Intake
The intake is provided with a variable geometry mechanism such that the throat is wide open at low subsonic speeds and closes progressively towards the supersonic regime. The mismatch between intake and compressor is avoided during the supersonic regime by deviating through the bypass duct and the variable geometry bypass nozzle (BN), the excess of mass flow captured. Hence, it is assumed that the intake delivers the exact mass flow requested by the air compressor.
The selected ceramic composite material for the intake walls is able to withstand the high temperatures during hypersonic flight; hence the flow through the intake is modeled as adiabatic. The total pressure recovery through the intake is the ratio of outlet to inlet stagnation pressures. For air behaving as perfect gas and provided that the flow is adiabatic, the total pressure recovery is related to the intake kinetic efficiency by:
where Ma is the free stream Mach number and γ the ratio of specific heats. The kinetic efficiency is the ratio of kinetic energy of the outlet flow (if expanded to ambient pressure) to the free stream kinetic energy [13]. The calculations are performed assuming a constant kinetic efficiency above Ma and a conservative value of below this flight speed. The atmospheric model in [14] provides the variation of atmospheric pressure and temperature with the altitude for the standard day, with 288.15 K and 1 atm at sea level.
2.2. Combustion Chambers and Nozzle
As previously stated, the flow in the combustor chamber is resolved with Equation (2). For the combustion of air with hydrogen, 19 reacting species formed from hydrogen, nitrogen and oxygen are considered in the calculation of chemical equilibrium. The steady form of Equation (2) resolves the frozen flow throughout the nozzle, downstream of the combustor, assuming that the gas composition is the same as calculated at the combustor outlet. The calculation of the equilibrium composition along the nozzle would slow down the simulation without a reasonable gain in performance accuracy. The geometry of both the combustor and the nozzle is characterized by the cross-sectional area along the axis , in Equations (4) and (5). The combustion chambers feature a heterogeneous combustion zone in order to avoid contact between the flame and the walls. The wall temperature is therefore maintained below the thermal limit of the material and the combustor walls are considered adiabatic in the model.
The nozzle is cooled by radiation to the environment, of which the temperature varies with the flight altitude according to the U. S. Standard Atmosphere of 1976. A uniform view factor of one is considered along the external surface of the nozzle in order to compute the radiated heat using the Stefan–Boltzmann law. With respect to the internal surface of the nozzle, the convective heat transfer coefficient is calculated with the correlation of Bartz [15] and the law of Stefan–Boltzmann for the radiated heat. The heat flux through the wall of the grid node results:
In the above equation, and are respectively the wet perimeter and the wet area associated to the grid node, for which the bulk temperature of the fluid is . The constant of Stefan–Boltzmann is σ and the adiabatic wall temperature is computed as:
The heat transfer coefficient is computed from Bartz correlation as:
In the above expression, the thermal and transport properties of the combustion gases (, and ) are evaluated at the temperature halfway between the bulk and the wall temperatures. The throat mass flow, diameter and curvature radius are respectively , and and is the cross sectional area associated to the grid node.
The uninstalled thrust is computed as:
where the nozzle efficiency is supposed to be . In the case of over-expanded nozzle regime, the criterion of Sommerfield states that the jet separates from the nozzle wall when the jet pressure is as low as 30% of the ambient pressure [16]. The cross sectional area and gas velocity at the separation point are computed with a first order approach from the interpolation in pressure between the adjacent grid nodes i and :
In absence of flow separation, the corresponding values of and are computed at the nozzle exit section.
2.3. Heat Exchangers
The heat exchangers of this air turbo-rocket engine are built in three different configurations, namely the precooler, the reheater and the regenerator modules. The location of the precooler (HX1 and HX2), reheater (HX3) and regenerator (HX4L, HX4H, HX5, HX41-44, HX46-48) modules is shown in Figure 4. A one-dimensional discretization, as described in the foregoing paragraphs, is utilized to resolve the fluid flow along the hot and cold streams inside each of the configurations. The heat transfer performance is characterized by the specific geometry of each configuration.
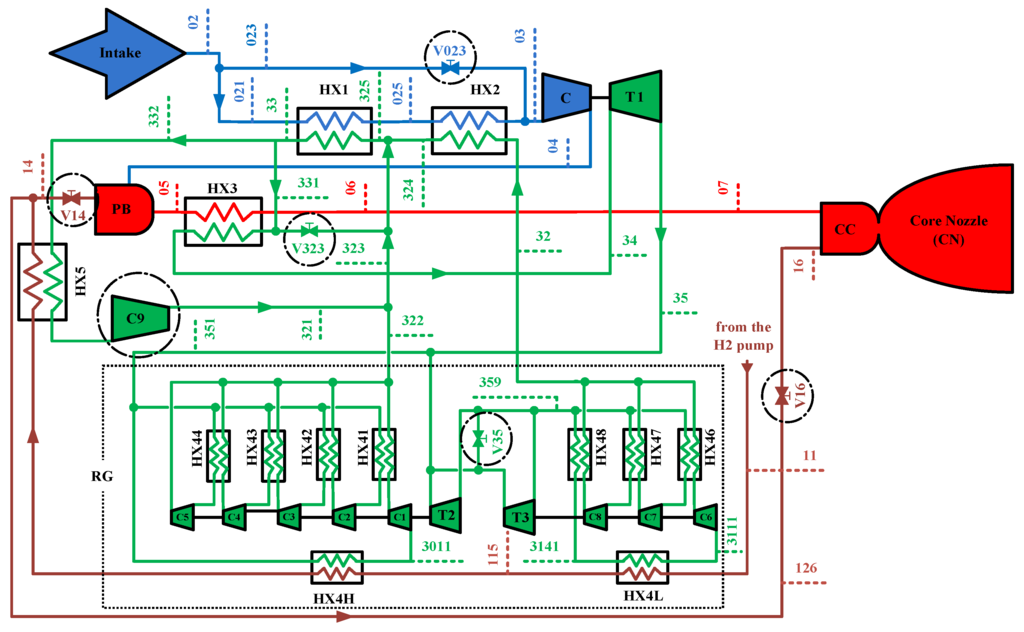
Figure 4.
Scheme of the air turbo-rocket numerical model: the station and component labeling are shown; the engine control devices are enclosed in circles.
2.3.1. Precooler
The precooler contains two modules consisting of a number of tubes tangentially mounted in a spiral around the engine axis. The external diameter of the tubes is μm. The air flows radially inwards across the tubes and the helium inside the tubes follows the spiral path from the internal to the external headers (Figure 5). The low temperature module (HX2) is located coaxially to and inside the high temperature module (HX1), both sharing a common manifold. Any curvature effect can be discarded because the ratio of the module diameter to the tube size are in the order of . The equivalent planar bank of staggered tubes in cross-flow is shown in Figure 6, in which the air flows in the y-direction and the helium flows through the tubes along the direction of decreasing y-coordinate.
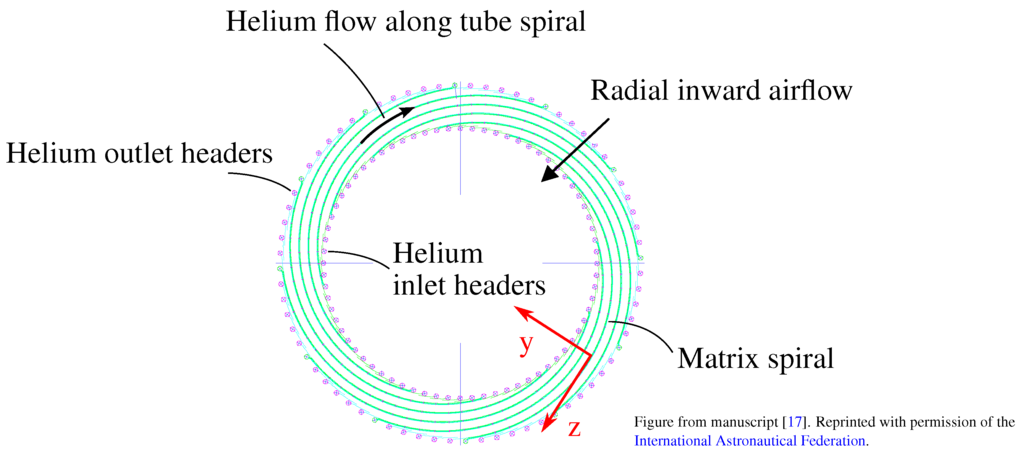
Figure 5.
Frontal view of the precooler module [17].
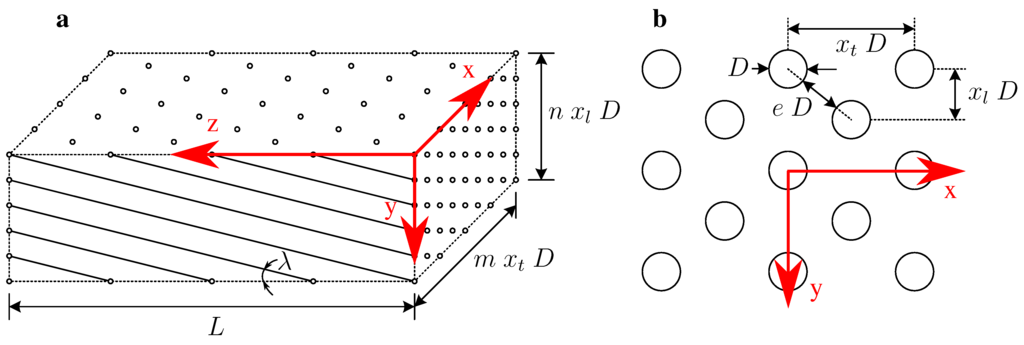
Figure 6.
Equivalent matrix of tubes in cross-flow: bulk matrix (a) and cross sectional view (b).
By assuming uniform boundary conditions at the matrix inlet and outlet surfaces, the flow is periodic on the xz-plane (Figure 7b,c), therefore the thermal field across the shell can be approximated as being one-dimensional along the y-axis. Let us suppose the domain is discretized in a number of cells, each of them containing a tube segment. Figure 7c shows that there are two types of cells depending on whether the tube segments are cell-centered (black tubes) or sliced by the cell lateral boundaries (red tubes). The position of the cell nodes is determined by the indexes related to the x-, y-, z-directions. The one-dimensional discrete temperature field in the shell is . The helium tubes are aligned along the equation (Figure 7b), thus they are contained in the cells and are submitted to an external thermal field . Because the helium flows in the direction of decreasing y-coordinate, the equivalent disposition of the tubes is in counterflow with respect to the shell (Figure 7a). The tube stagger angle λ (Figure 6a) and the tangential tube pitch s (Figure 7b) are:
being n the shell node count in the transversal y-direction and the tube length.
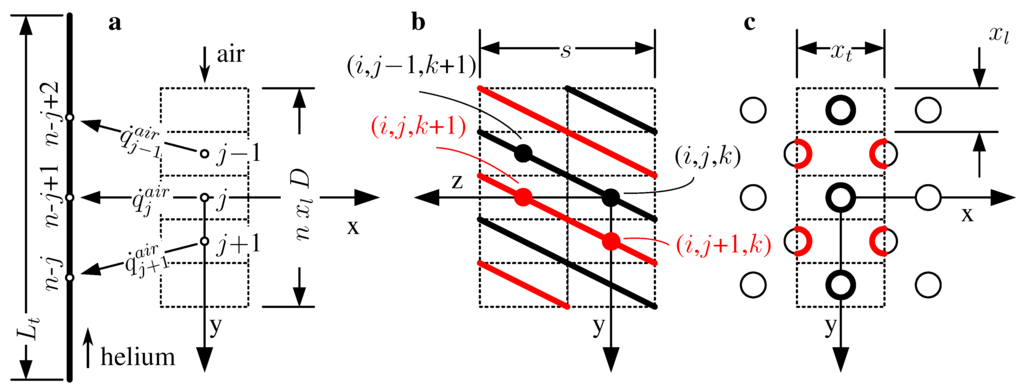
Figure 7.
Computational domain for the periodic flow field: thermal field in counterflow disposition (a), longitudinal cut (b) and transversal cut (c) of the tube matrix.
The flow is resolved with each spatial discretizations of the one dimensional conservation Equation (2) applied to a single helium pipe and to the shell periodic domain in Figure 7 rightmost. The thermal connectivities between both numerical domains are in counterflow disposition. The heat transfer through the wall is not spatially resolved and the energy balance to the wall stands:
where is the heat capacity of the wall of a single pipe. The heat fluxes from the air and to the helium streams are respectively and . The helium-air interface is the pipe external perimeter Γ, which for each cell of the staggered arrangement is the highlighted bold contour in the rightmost plot in Figure 7. The global mass flow and heat flux throughout the entire matrix equal those of a single domain times the total number of tubes contained in the matrix. The n discretization nodes are uniformly spaced.
The helium pipe of the numerical model has the same internal diameter and length as the corresponding tubes of the real module. However, the fluid vein that resolves the air flow has a uniform cross section equal to the passage minimum area of the matrix , which is a conservative account for the blockage incurred by the tubes:
where A is the matrix surface in the direction orthogonal to the airflow. The transversal and longitudinal pitches are respectively 2 and 1.5 tube diameters, which results in an area ratio equal to the tube dimensionless spacing e.
Correlations for most phenomena can be constructed by taking the nth root of the sum of the powers of the limiting solutions of the independent variable [18]. The following ad hoc power-mean combination was used to define the laminar-turbulent transitional zone:
The correlation of Dittus–Boelter for the Nusselt number Nu in turbulent flow throughout a tube is:
where Reynolds and Prandtl numbers are based on the tube hydraulic diameter and bulk properties of the fluid across the section of the tube. The Nusselt number for laminar fully developed flow throughout a tube with constant heat flux across the walls is Nu and, if the temperature of the walls, instead of the heat flux across them, is maintained constant, then the Nusselt number is Nu [19]. The heat transfer coefficient to the helium stream inside the precooler tubes is computed from Equation (9) with the Nusselt number provided by Equation (26).
With respect to the convective heat transfer in the air flow field, Figure 8 summarizes the survey carried out on previous works studying the heat transfer through a bank of staggered tubes in cross-flow. The results shown are for heat transfer across a square bank () under the hypothesis of isothermal boundary condition. The analytical correlation of Khan for steady flow is close to the empirical results by Hausen. The steady quasi-three dimensional numerical calculations of Nakayama were obtained for a bank of square tubes and showed the potentially large improvement of the heat transfer by changing to a square tube section. The results of the unsteady fully developed flow calculations by Beale indicated that the staggered configuration was naturally unstable without any external excitation, hence the averaged Nusselt number is nearly the same for both cases: with a perturbed initial condition with Strouhal number and without perturbation for . The expression provided by Khan [20] was used in the present application for being conservative with respect to the numerical results while retaining the influence of the matrix geometry through the analytical expression:
where the Reynolds number is based on the average speed across the passage minimum section, where the cross sectional area to the flow is , and the external diameter of the tube D.
Figure 9 compares the predictions of Nusselt number obtained by Khan and Hausen for the geometry and operational range ( 300–600) of the current precooler. The analytical expressions of Khan and Hausen, both for a single row of tubes in cross-flow with blockage ratio , highlight the improvement by having a configuration of staggered rows, as predicted by the correlation of Kahn [20].
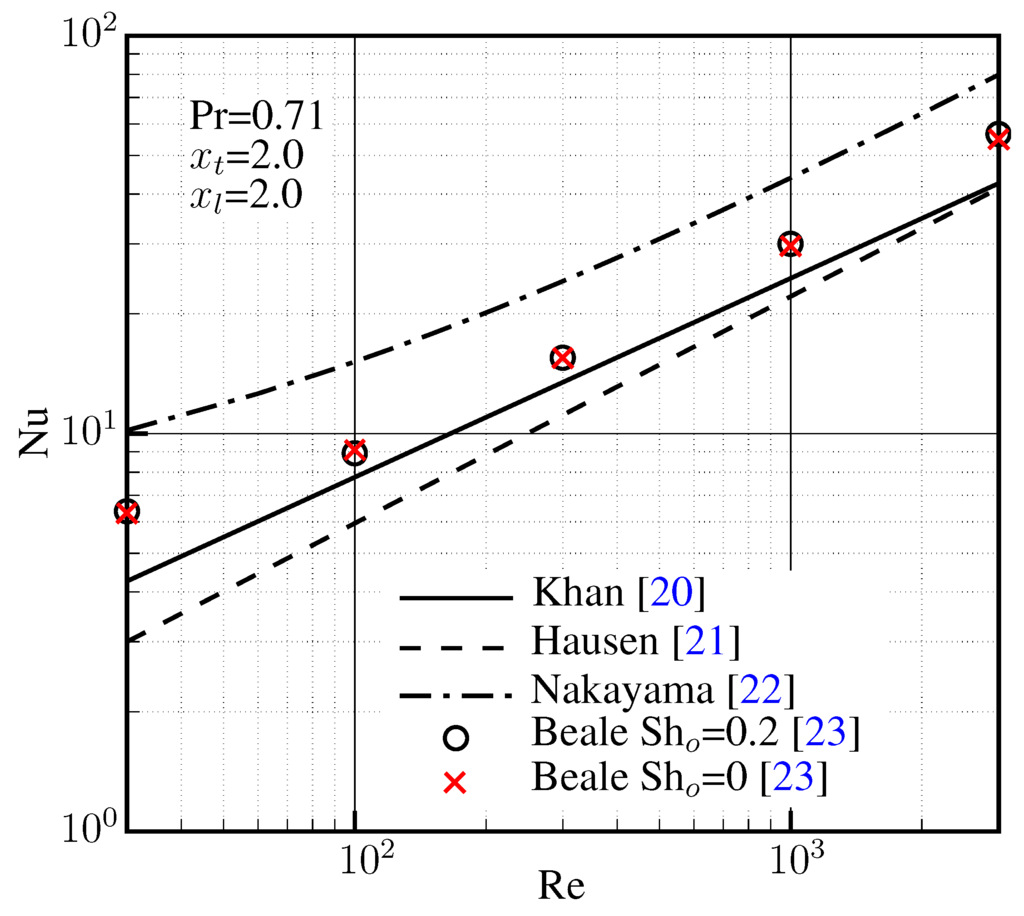
Figure 8.
Comparison of the different Nusselt predictions in the staggered-square tube bank.
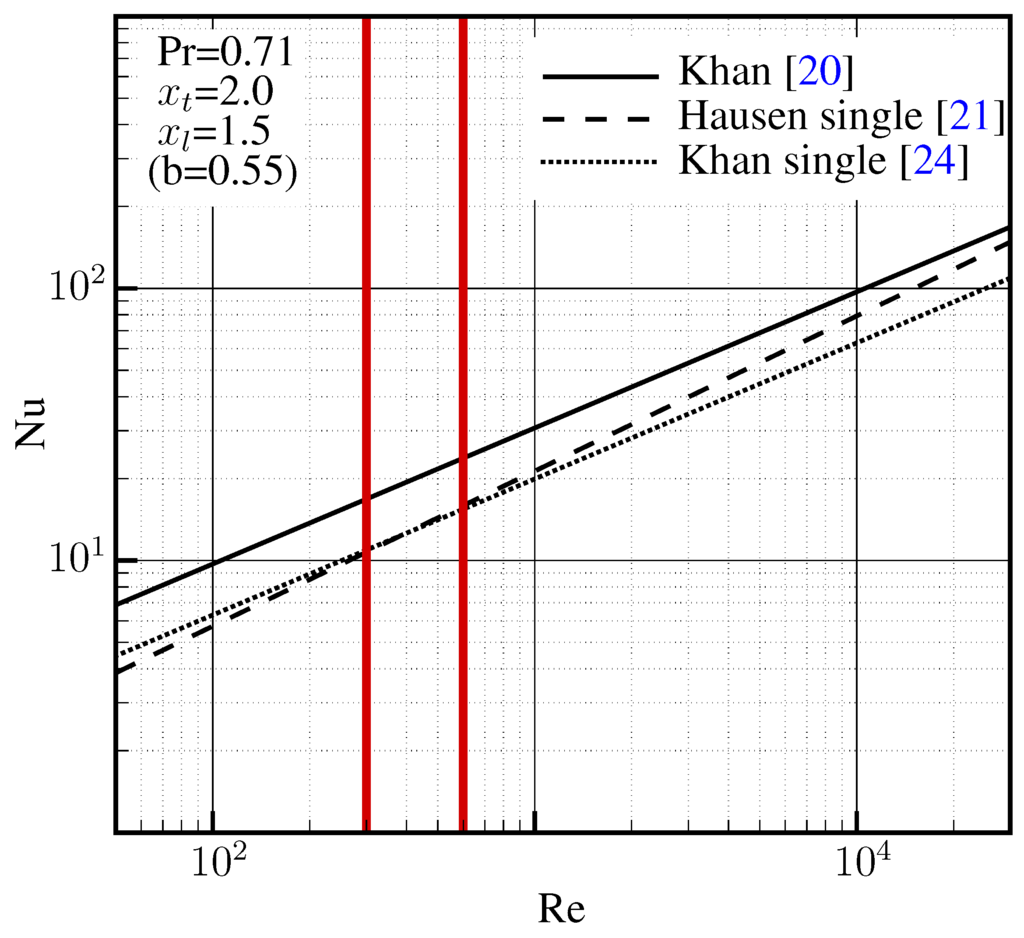
Figure 9.
Comparison of different correlations for the Nusselt number for the precise geometry of the precooler. The operational range of the current application is shown between red lines.
2.3.2. Reheater
The reheater (HX3) is located downstream of the preburner (PB) with the purpose of maintaining a constant inlet temperature to the helium turbine (T1) throughout the engine operation (Figure 4). The assembly in Figure 10 is composed of an inner and an outer cylindrical shroud of respective diameters and with a number of plates disposed in spiral between them. The spiral length of the plates, along the radial direction, is mm.
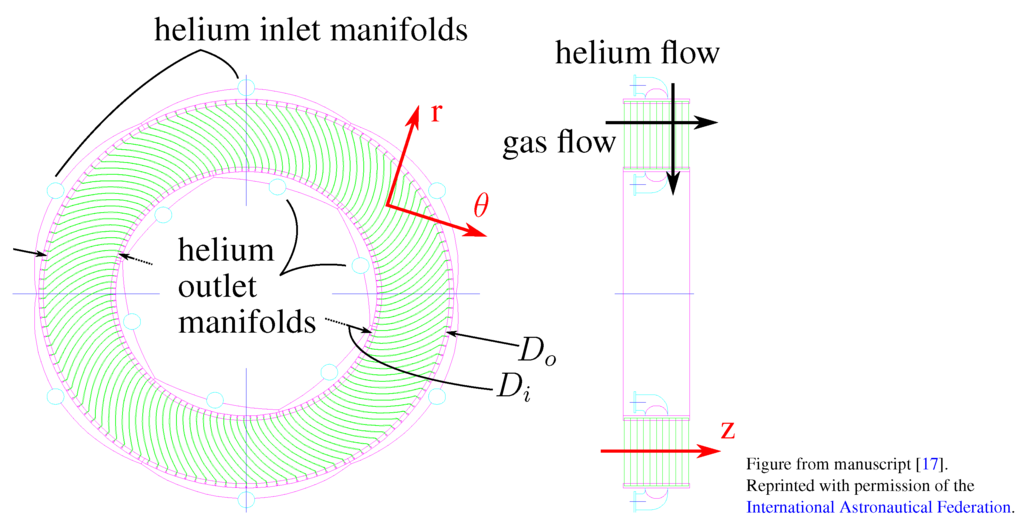
Figure 10.
Frontal and side view of the reheater module [17].
The gas from the preburner flows along the axis, whereas helium flows radially inward from the outer to the inner shroud and through the plates. The ratio of the passage span to mean diameter is 2:5, nonetheless the slenderness of the passage is high (1:120) and the curvature of the inner/outer shroud as well as that of the plates can be disregarded, the passage assumed to be rectangular in Figure 11. The tangential pitch s between plates was computed such that the gas flow area A of the equivalent rectangular and of the real spiral passages are equal:
where the plate thickness is mm and the computed pitch mm. Each plate is divided into a number of strips , each strip having a width mm and containing a number of square channels. The channels have a cross section of 1.5 × 1.5 mm and perimeter Γ of 6 mm. The helium streams flow throughout these channels in opposite direction to the r-axis and the gas flows along the z-direction between the plates.
Assuming uniform boundary conditions at the gas inlet and outlet planes, only one gas passage is modeled. Using the same assumption on the helium side, a single channel characterizes the thermal and fluid fields throughout the channels of the strip. Hence, the one-dimensional flow through the channels is resolved once for each of the strips along the z-direction. The temperature of the wall strip is supposed to be uniform along the r-direction and characterized by the one-dimensional thermal field (Figure 12). The thermal field along the channels is resolved in the radial direction and the energy balance to the wall stands:
where is the heat capacity of a single plate. The corresponding heat fluxes from the gas and to the helium streams are computed from Equations (8) and (9). The Nusselt number is calculated with Equation (26), in which the Reynolds number is based on the hydraulic diameter of the gas or helium channel , whichever applies:
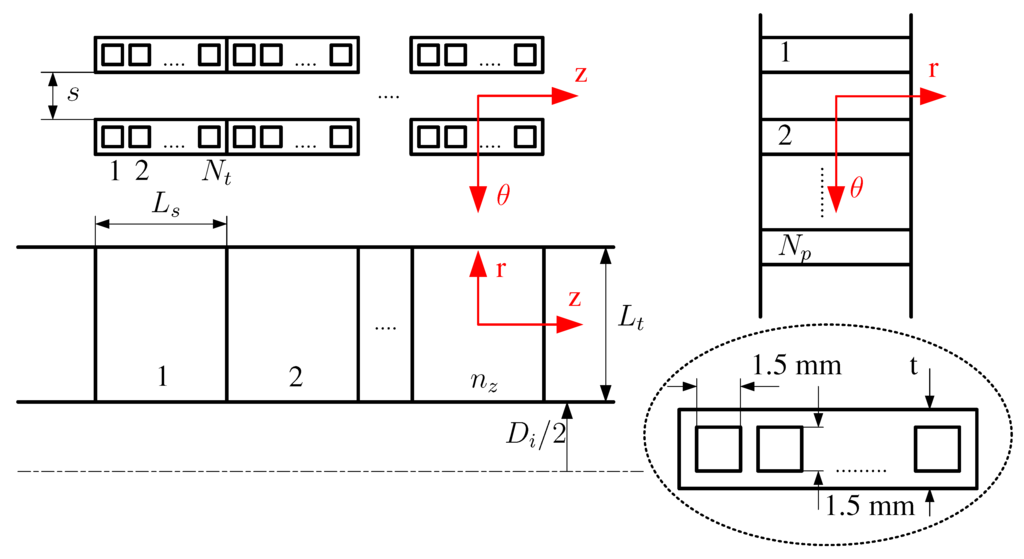
Figure 11.
Reheater module: geometrical definition of the numerical model.
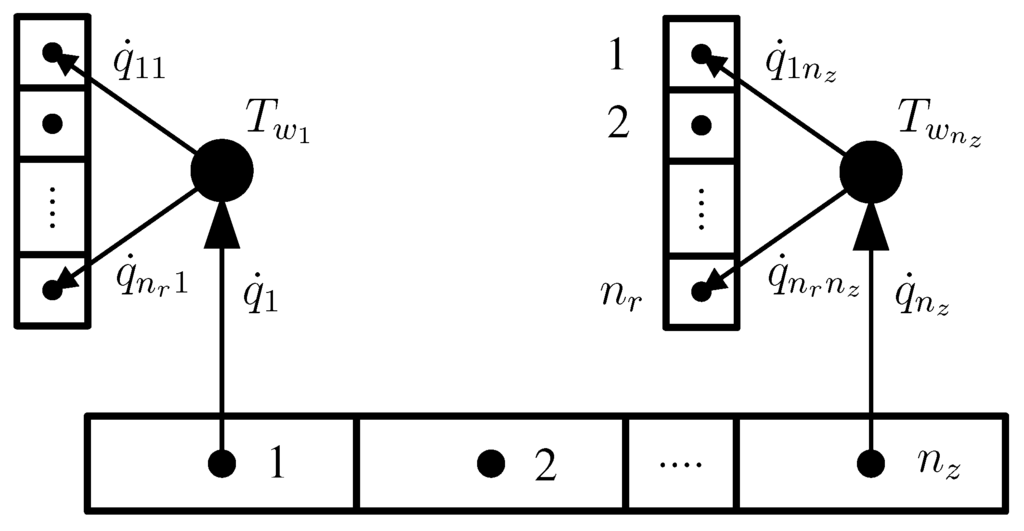
Figure 12.
Reheater module: thermal connectivities between the gas and the helium streams.
2.3.3. Regenerator
The regenerator modules are used in the helium-to-helium (HX41-44 and HX46-48) and the helium-to-hydrogen (HX4H, HX4L and HX5) heat exchanger units (Figure 4). The same geometry consisting of a monolithic structure of alternative layers of heating and cooling micro-channels [25] is used in both configurations and for each unit. Each unit contains a number of modules circumferentially disposed around the engine axis (Figure 13, left). The purpose of such geometry is twofold: firstly, to achieve a laminar regime along the full length of the channels, which minimizes the pressure drop and, secondly, to improve the cooling performance with a large heat exchange area, in the order of m/m.
The curvature effects on the flow field along the channel can be disregarded because the ratio of the channel transversal dimensions to the average diameter of the module is negligible (). Each module contains rows of respectively and heating and cooling channels, being the total number of channels per regenerator unit. The channels are embedded in the same base material with the cooling and heating rows in counterflow disposition. Each of the heating and cooling channels have a cross section of 50 × 50 μm.
Figure 13 (right) shows the cross section of the periodic one-dimensional fluid field representative of the overall module. The periodic field comprises a cold channel, two halved hot channels and a portion of the solid matrix. The respective one-dimensional flow through the cold and hot channels is resolved with each one-dimensional discretizations of Equation (2) along the θ-direction. The energy conservation equation applied to the wall provides the following relationship for the heat fluxes between the hot and cold streams:
where and are the respective heat fluxes from the hot and to the cold streams, n is the number of grid nodes used in the discretization, is the heat capacity of the portion of solid matrix contained in the periodical domain, and the perimeter and length of both the heating and cooling channels are respectively Γ and .
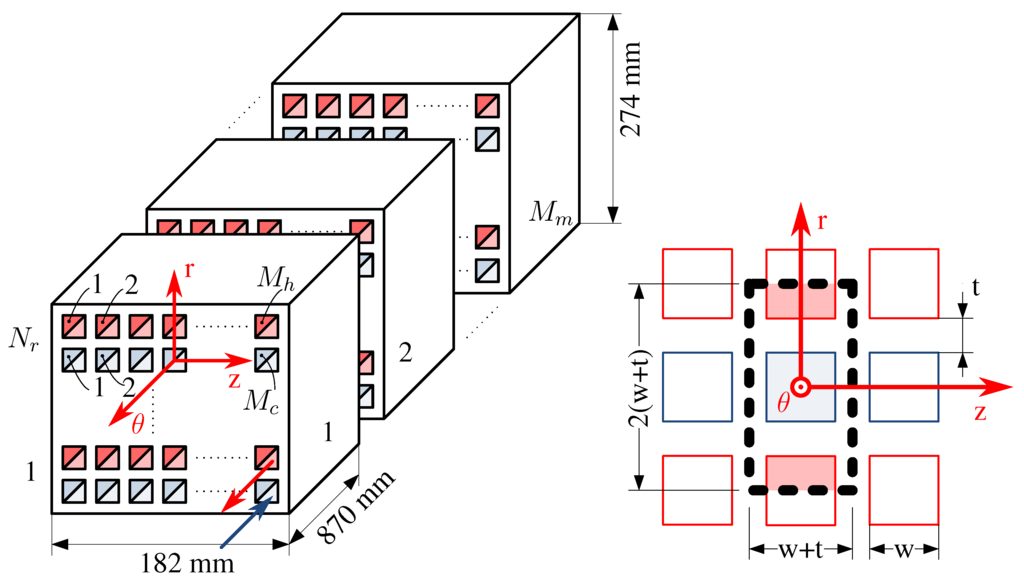
Figure 13.
Geometry of the regenerator units (left) and cross section of the periodic domain representative of the overall unit (right).
The flow regime throughout the regenerator modules for either the helium or the hydrogen streams is always laminar, where the Reynolds number ranges between 200 and 1000. Under these conditions, the thermal entry length to the micro-channels () has a typical value of cm. The measurements done by Colgan report that a Nusselt number of is readily achievable with channel lengths 10 times smaller than the entry length, [26]. He employed manifolded silicon micro-channels with a cross section of 180 × 60 and 180 × 75 μm in a configuration of staggered fins with a length of 60 or 100 μm. However, the heat transfer enhancement was probably caused by the impinging flow on the channel lateral surfaces at the manifolds entry zones.
The calculations made by Kim showed that the channel aspect ratio improves considerably the Nusselt number. He modeled the square micro-channels as a continuous porous medium, for which the Nusselt number in the fully developed flow depends only on the channel aspect ratio [27]. The Nusselt number could be as high as for an aspect ratio of 1:6, with an asymptotic limit of for very high aspect ratios.
The value of the Nusselt number exceeds when wavy channels are used instead of straight ones. In this case the channel aspect ratio is as low as 1:2 and the enhancement phenomena has to do with the generation of vortical structures that improve the mixing of the stream [28]. On the other hand, the study of Gong showed that even when no vortical structure can be formed, in case of very low Reynolds (50–150), high values of the Nusselt number () could be achieved due to the thinning of the boundary layer [29].
Independently of the precise geometry and the flow features, the straight channel geometry of Figure 13 was assumed to be enough representative of the regenerator fluid dynamic performance and a constant Nusselt number was adopted for both the hot and the cold channel fluid streams.
2.4. Turbomachinery
The turbomachinery off-design performances, i.e., pressure ratio π, corrected mass flow and adiabatic efficiency η, are given by the steady characteristic maps, which in turn are expressed in function of the corrected speed and the β-parameter:
The β-lines constitute an arbitrary parameterization that, together with the -lines, define a one-to-one correspondence between performance and operating point [30].
The corrected speed and mass flow are the respective values of shaft speed and mass flow referred to the standard inlet conditions at which the map was obtained:
where is the machine design rotational speed with standard inlet conditions, the ratio of actual to standard inlet pressures is designated as and the temperature correction is done through the variable Θ:
where R is the constant of the working gas and the inlet temperature, each referred to the constant of the gas used to obtain the map and the corresponding standard inlet temperature . The corrected variables are deduced in a natural way from the dimensional analysis of the compressible flow through the turbomachine [31].
The turbomachine is resized applying constant factors () to the characteristic map of a known machine:
The unscaled map of the air compressor (C), i.e., Π, and , was based on an axial multistage high pressure compressor reported by Cumpsty [32]. However, the contra-rotating helium turbine (T1) was specifically designed for the current application [33], therefore the characteristic map was directly obtained from a CFD analysis without the need of rescaling coefficients. The maps of the regenerator compression stages (C1–C8) and turbines (T2 and T3) are rescaled respectively from a radial compressor [34] and a radial turbine [35]. The power demanded by the circulator (C9) (∼223 kW) is an order of magnitude lower than any of the helium compressor stages, therefore the cycle overall performance is rather insensitive to the off-design behavior of the circulator. The circulator was considered to operate constantly on design () and driven by the power of the engine auxiliary systems, which were not included in the numerical model.
As for the helium circulator (C9), the power required by the hydrogen pump, with an assumed efficiency of , does not exceed 173 kW for any of the engine operational points. Therefore the performance of the liquid hydrogen turbo-pump assembly has little effect on the overall engine performance and was not included in the engine model.
The numerical study was focused on the complex interaction between the large number of turbomachinery components (12) and heat exchangers (13), therefore the implementation of more physical map rescaling procedures like the one presented in [36] was considered of secondary importance for the investigation.
The increase of stagnation enthalpy throughout the machine, i.e., the specific power transmitted to the fluid, is computed from the isentropic enthalpy increase as:
The enthalpy increase of the hypothetical isentropic evolution throughout the machine is a function of the inlet and outlet boundary conditions . The power to the shaft equals the power transmitted to the fluid plus the kinetic power required to accelerate the rotor:
where the rotor has inertia and the boundary condition on the torque, assuming that the machine is coupled to other mechanical component, depends from the rotor speed and explicitly from the time: .
In a similar way as the rotor inertia reduces the stiffness of the mechanical constraint in Equation (44), which otherwise is algebraic, an artificial capacity of the discharge duct is introduced to relax the mass flow constraint:
where is the flow rate obtained from the characteristic map and the convective characteristic time throughout the turbomachine, i.e., the ratio of the machine characteristic length to the speed of sound: . The time is much smaller than the characteristic time of the boundary conditions, therefore the error in the mass flow constraint, Equation (45), is damped out quickly during the system initialization [37]. The actual flow rate exhausting the machine through the discharge duct is a general function of the machine outlet conditions and depends explicitly on time, provided that a control mechanism, for instance a control valve, is implemented: .
Based on the previous analysis, the mechanical and the flow constraints in Equation (44) and Equation (45) have the general form:
The transient operating line of the turbomachine is found upon integration of this system of equations and is uniquely determined for the given boundary conditions , the discharge characteristic and the mechanical constraint , for a given machine size .
The system of Equation (46) becomes algebraic under the assumption of steady operation on the design point :
The efficiency rescaling coefficient is computed from the efficiency prescribed by the design cycle , which, invoking Equation (42), equals the machine on-design efficiency:
The solution of the system in Equations (47) and (48) provides the rescaling coefficients for steady on-design operation. The steady form of Equations (43) and (44) defines a relationship for the boundary condition and efficiency under consideration, therefore the sizing of the machine in Equation (47) can be done with the pressure ratio instead of the rotor power or the mass flow . In a machine operating alone, the boundary conditions , design mass flow , efficiency and rotor power are known from the engine thermodynamical cycle on-design and the rotor speed and operating point are the design parameters. Nonetheless, the stationary operation of a turbomachine, which is linked to other dynamic components like pipes, manifolds or heat exchangers, cannot be known a priori unless integrating the system of Equation (46). In this case the rescaling coefficients can still be found from Equations (43) and (47) but is not a stationary point of Equation (46), in general. The drift of the steady operating point from the wanted on-design point depends on the proximity between the initially targeted design cycle and the stationary solution. For more complex systems in which a number m of machines are mounted on the same rigid shaft in equilibrium, the system of Equations (47) and (48) must be solved with the additional constraint:
This constraint is automatically satisfied when the compressors are sized to deliver the design mass flow at the pressure ratio , whereas the turbines are rescaled to deliver the rotor power demanded by all the compressors mounted on the same shaft at the expansion ratio . If several turbines are mounted on the same shaft, the fractional power developed by each one respect to the total power demand is an additional design parameter.
Figure 14 is a graphical representation of the variables in the system of Equations (47–49) when matching a compressor with a turbine on the same shaft. Table 2 shows the turbomachinery design parameters and the corresponding scaling factors for the supersonic cruise regime.
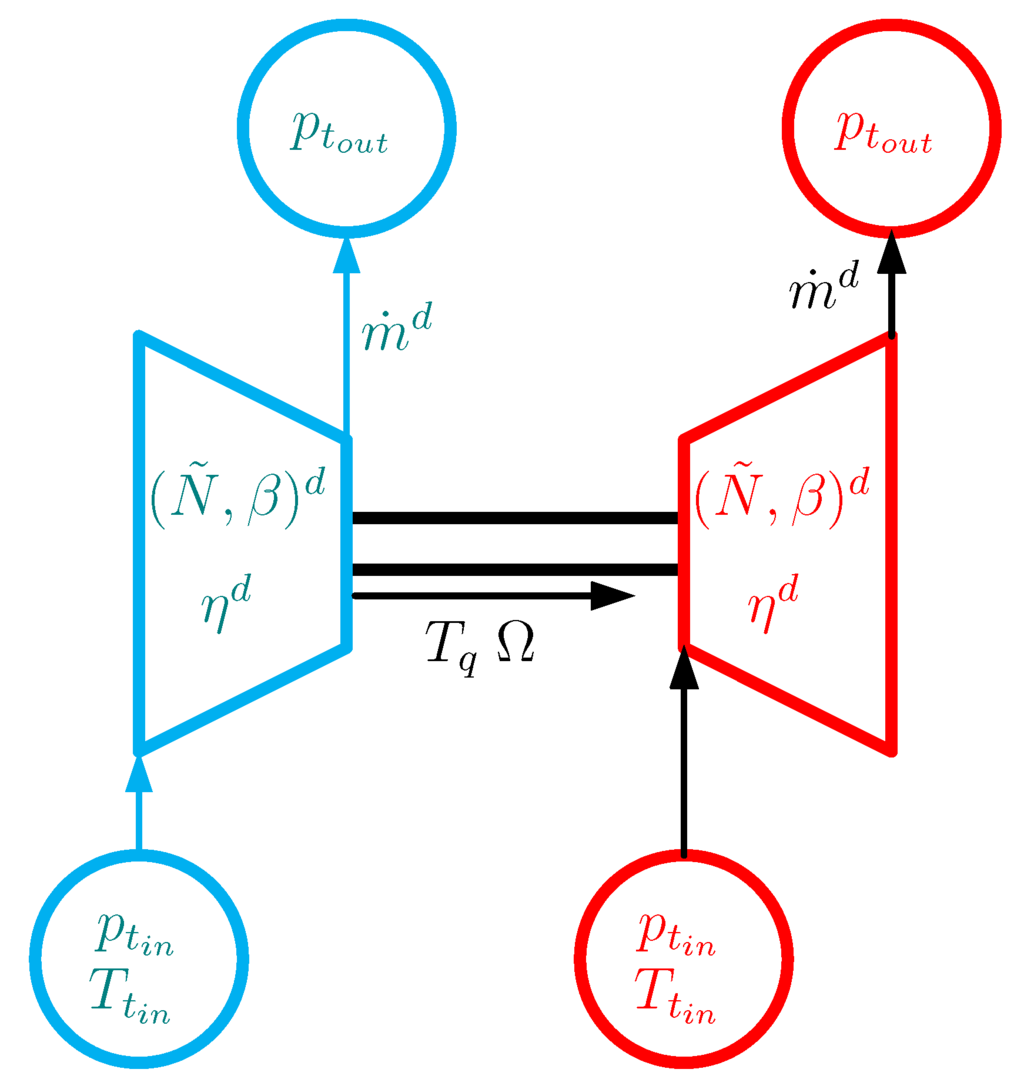
Figure 14.
Compressor-turbine matching: compressor and turbine input data are shown respectively in blue and red, dependent variables are shown in black.

Table 2.
Turbomachinery design parameters and scaling factors.
| Scaling factors | |||||||||||||
| Label | [bar] | [K] | [kg s ] | [%] | [rpm] | [hN m] | [kg m ] | ||||||
| C | 2.9 | 648 | 172.6 | 4.2 | 86 | 0.74 | 0.75 | 10,471 | 594 | 0.51 | 1.54 | 2.27 | 0.99 |
| C1 | 129.6 | 296 | 11.2 | 1.5 | 94 | 0.63 | 0.72 | 48,340 | 7 | 0.01 | 0.40 | 0.39 | 1.11 |
| C2 | 129.5 | 371 | 11.2 | 1.5 | 94 | 0.63 | 0.72 | 48,340 | 9 | 0.01 | 0.45 | 0.39 | 1.11 |
| C3 | 129.4 | 458 | 11.2 | 1.5 | 94 | 0.63 | 0.72 | 48,340 | 11 | 0.01 | 0.50 | 0.39 | 1.11 |
| C4 | 129.3 | 559 | 11.2 | 1.5 | 94 | 0.63 | 0.72 | 48,340 | 13 | 0.01 | 0.55 | 0.39 | 1.11 |
| C5 | 129.2 | 676 | 11.2 | 1.5 | 94 | 0.63 | 0.72 | 48,340 | 16 | 0.01 | 0.61 | 0.39 | 1.11 |
| C6 | 50.9 | 33 | 11.2 | 3.9 | 90 | 0.63 | 0.65 | 48,357 | 4 | 0.01 | 0.45 | 2.71 | 1.08 |
| C7 | 51.4 | 75 | 11.2 | 3.9 | 90 | 0.63 | 0.65 | 48,357 | 8 | 0.01 | 0.62 | 2.67 | 1.08 |
| C8 | 51.3 | 151 | 11.2 | 3.9 | 90 | 0.63 | 0.65 | 48,357 | 15 | 0.01 | 0.86 | 2.68 | 1.08 |
| T1 | 195.7 | 1000 | 89.6 | 1.5 | 91 | 0.20 | 1.00 | 10,471 | 594 | 0.51 | 1.03 | 1.05 | 0.96 |
| T2 | 130.1 | 863 | 22.5 | 2.5 | 89 | 0.35 | 1.00 | 48,340 | 56 | 1.00 | 2.40 | 1.00 | 1.02 |
| T3 | 130.1 | 863 | 11.1 | 2.5 | 88 | 0.35 | 1.00 | 48,357 | 27 | 1.00 | 1.18 | 1.00 | 1.01 |
3. Engine Control
The numerical model of the air turbo-rocket is a dynamic system of which the state depends on the flight regime, i.e., the flight Mach number and altitude, and six control variables—the helium turbine inlet temperature , the opening of each three bypass valves of the precooler , the high temperature module and the high temperature section of the regenerator , the recirculator flow rate and the fuel consumption (see Figure 4 for the schematic representation of the numerical model with the station and component labels). The implementation of an engine control logic, as described in the lines that follow, can be materialized by means of the engine control unit and reduces the number of control variables to one: the fuel consumption , by which the thrust level is controlled throughout the operational range.
The heat power through the reheater (HX3) to the helium stream is set for a constant turbine inlet temperature K by regulating the preburner fuel consumption at each operational regime. The control is done by means of a valve on the hydrogen supply line. The difference between the throttle required and the fuel flow into the preburner is diverted to the combustion chamber (CC). The injection command is proportional to the difference between targeted and sensed temperatures:
The response time to the flow command is s and the sensitivity of the controller is K/(kg/s). Fuel supply pressure and mass flow are related through the injector characteristic . The lumped physical model of the valve, which acts on the flow rate instead of the valve opening, simplifies the formulation without a significant effect on the engine model fidelity. For a control based on the opening area A, with the pressure drop and mass flow through the valve related by the non-linear equation , the numerical simulation was substantially slower.
The air stream captured by the intake bypasses the precooler at low speed. The bypass valve V023 closes when the inlet recovery temperature rises above K, for increasing flight speed. The air stream is then driven through the precooler, of which only the low temperature segment (HX2) is in operation. The high temperature segment (HX1) is traversed by the air stream but the helium supply, which remains hotter than the air stream, is bypassed towards the reheater. The opening law of the bypass valve is proportional to the difference between air and helium temperatures:
The sensitivity of the controller is K and is the cross sectional area of the bypass valve when fully open.
The temperature of the module HX1 is limited by diverting part of the helium stream towards the helium-hydrogen heat exchanger HX5 as the flight speed increases: when the outlet temperature rises above 1000 K, the recirculator (C9) pumps a constant flow of helium kg/s through HX5. For decreasing flight speed, the recirculator is shut down when the temperature falls below 900 K. This hysteretic control avoids the oscillations caused by a transient increase of the helium temperature when the recirculator is shut down.
The increase of fuel flow for a given flight regime augments the cooling capacity of the precooler, hence the power demand of the turbo-compressor (C-T1) diminishes. Meanwhile, the turbine inlet temperature is maintained constant and the working point of the turbine (T1) does not vary appreciably, therefore the mass flow through the turbine is reduced. In order to accommodate the decrease of helium mass flow, the power on the regenerator spool is reduced by opening the bypass valve V35 of the regenerator turbines T2 and T3. The valve opening follows the law:
where the controller sensitivity is . The bypass valve maintains the expansion ratio through the turbines T2 and T3 below and the engine throttling capability is eventually increased.
4. Results
The numerical model of the engine was set to match the design cycle during the supersonic cruise regime presented in [6]. The computed values of stagnation pressure and temperature and mass flow at each engine station during supersonic cruise are shown in Figure 17F. The values corresponding to the other five points (A–E) representative of the engine off-design operation are shown in Figure 15A,B, Figure 16C,D and Figure 17E. The flight regimes and throttling levels at each operational point are identified in Figure 18.
The off-design performance of the engine core was obtained at each flight regime along the vehicle trajectory and for different throttling levels . The mapping of the engine control commands is shown in Figure 18, in which the different zones represent operation for each configuration of: bypassed precooler (V023 Open) and precooler in function (V023 Closed) respectively below and above Mach 3.1, bypass of the regenerator turbines not in operation (V35 Closed) and operating elsewhere, recirculator in operation (C9 On) and precooler module (HX1) in operation (V323 Closed). The preburner regime is indicated by the dotted lines, which represent the ratios of injected to overall fuel consumption of 1%, 10%, 20% and 30%. The operational ranges of the turbomachinery components define the working envelope of the engine, of which each boundary point identifies a regime for which one of the turbomachinery components reaches a limiting operation. At low speed, overspeed of both the air compressor (C) and the helium turbine (T1) narrows the operational envelope to great extent and limits the flight regime to Mach 2.5 (Figure 18). Below Mach 2.5 the Scimitar engine switches to turbofan configuration (Table 1 and Figure 2), in which the reheater (HX3) discharges to the hub turbine (HT) instead of the main combustion chamber (CC). This cycle layout, which is out of the scope of the present study, changes the discharge characteristics of the air compressor (C) and would certainly extend the operational envelope towards lower speeds upon the implementation of the right control logic to adjust the cycle. At high speed and full throttle, the flow demand to the regenerator decreases and drives the compression stage (C8) towards the surge limit. The boundary for high speed and minimum throttle is established by the regenerator turbine (T3), which reaches the minimum rotational speed.
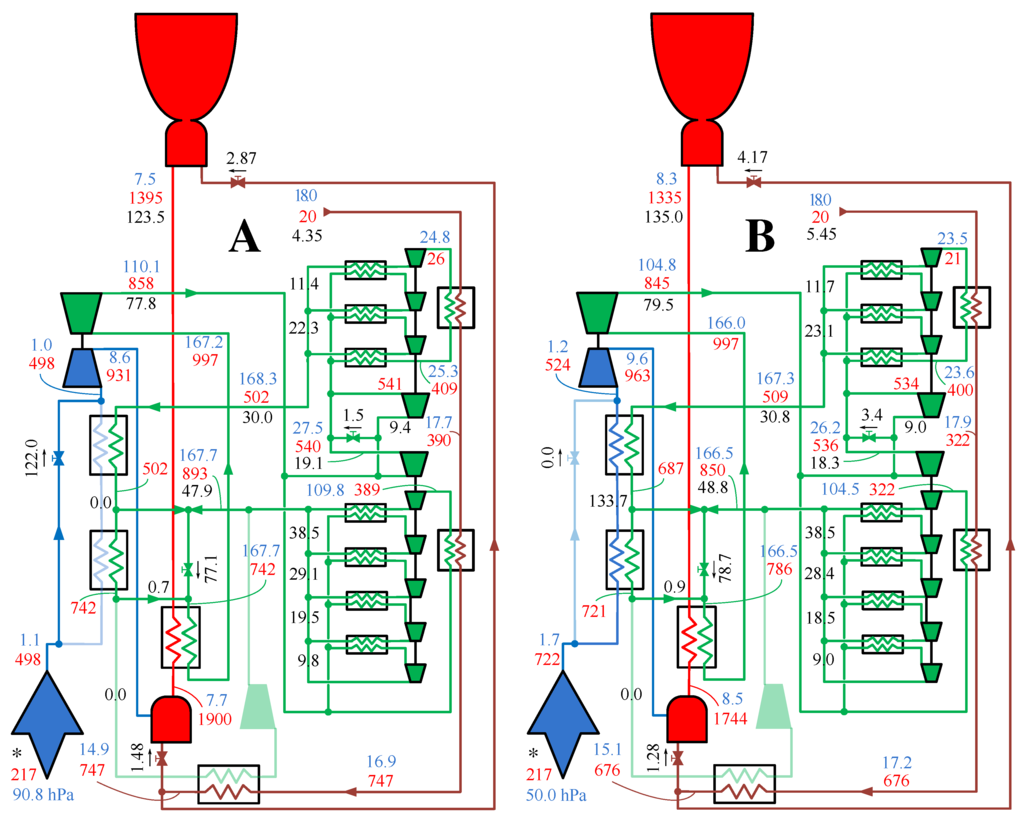
Figure 15.
Station total pressures (), total temperatures () and mass flows (black numerals, kg/s) during acceleration (A and B). Fluid lines and components working with air, helium, hydrogen and combustion gases are drawn respectively in blue, green, brown and red colors. The ambient (static) conditions are labeled with (*).
Figure 19 shows the off-design performance of the air turbo-compressor (C-T1) and the regenerator compression stages (C1–C8) and turbines (T1-2). The machines exhibit optimum efficiency in the surroundings of the cruise point. Nonetheless, the air compressor (C) needs to operate at suboptimal condition during on-cruise regime in order to allow a wide operational range (70 < < 100 and 4 < π < 8). A specific compressor design is needed to cope with the extended operation range while maintaining optimal on-cruise efficiency.
Figure 20 shows the throttling characteristics of the air turbo-rocket engine core at each flight condition of altitude and Mach along the vehicle trajectory. The uninstalled thrust , computed with Figure 19, increases monotonically with the fuel flow, . At the low flight regime of Mach 2.5, the flow in the core nozzle (CN) separates at the axial location where the nozzle cross section is 69% of the nozzle exit area. The separation point moves downstream as the flight speed and altitude increase and the nozzle runs full at flight regimes above Mach 3.5. The specific impulse is the ratio of uninstalled thrust to fuel flow rate: . The mixture ratio and the specific impulse reach their maximum simultaneously at each flight condition. The reason for this same trend in and is that the nozzle exit velocity is very insensitive to the changes in fuel flow and therefore the mixture ratio dominates the trend of the specific impulse . As the flight speed increases, the specific impulse reaches a global maximum around Mach 4 for a lean mixture ratio of (the stoichiometric mixture ratio is around 32) and decreases then towards Mach 5.
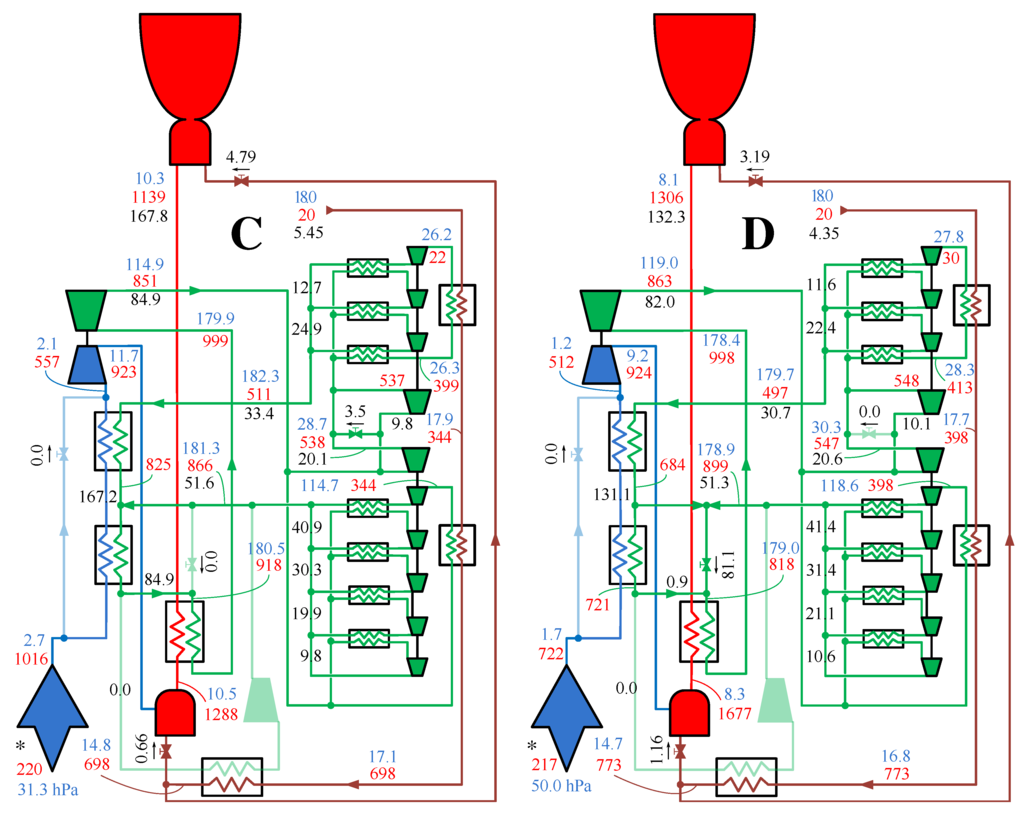
Figure 16.
Station total pressures (), total temperatures () and mass flows (black numerals, kg/s) during acceleration (C and D). Fluid lines and components working with air, helium, hydrogen and combustion gases are drawn respectively in blue, green, brown and red colors. The ambient (static) conditions are labeled with (*).
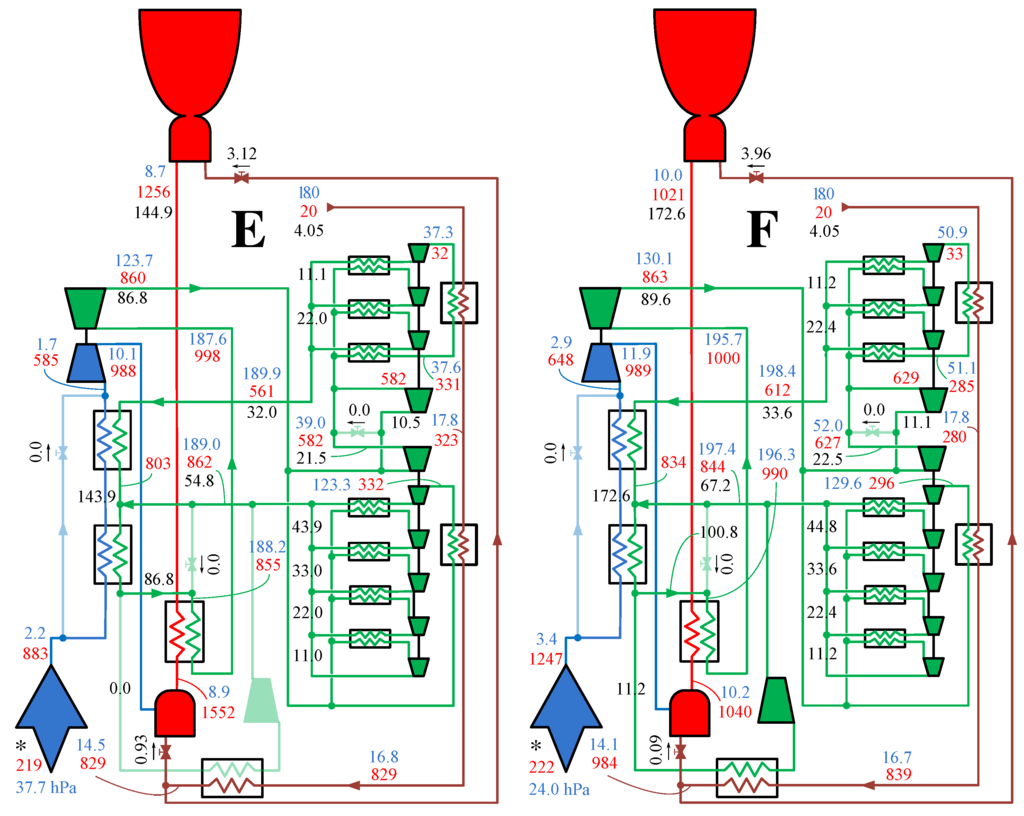
Figure 17.
Station total pressures (), total temperatures () and mass flows (black numerals, kg/s) during acceleration (E) and cruise (F). Fluid lines and components working with air, helium, hydrogen and combustion gases are drawn respectively in blue, green, brown and red colors. The ambient (static) conditions are labeled with (*).
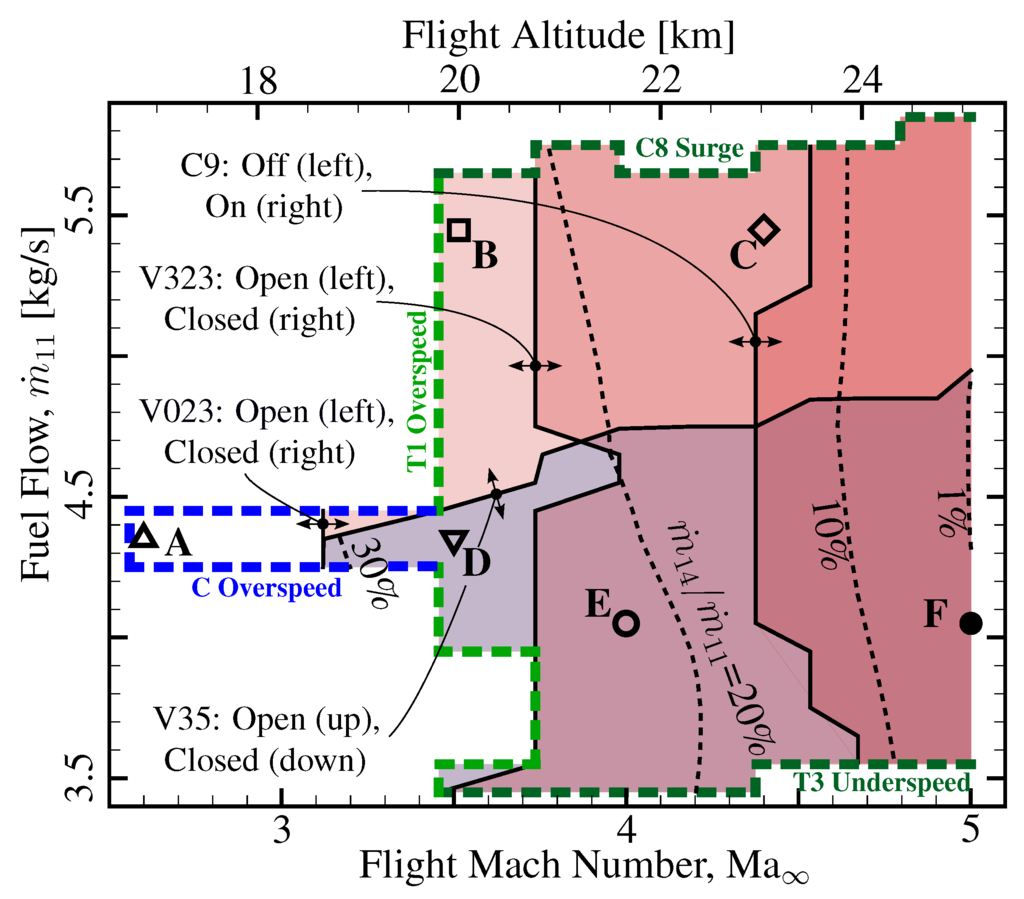
Figure 18.
Mapping of the control commands throughout the operational envelope.
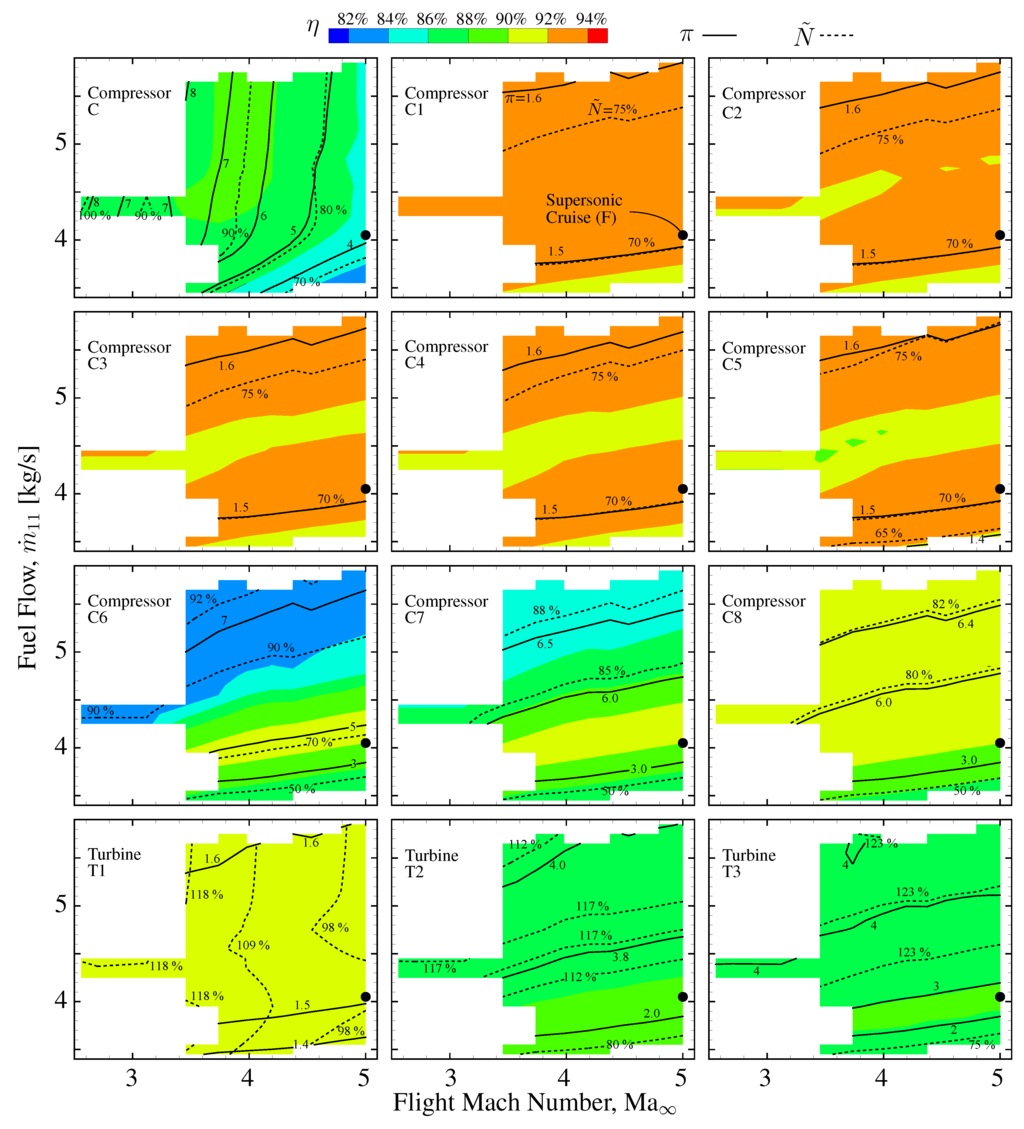
Figure 19.
Turbomachinery performance: adiabatic efficiency (η), pressure ratio (π) and corrected speed () vs. flight Mach number (Ma) and throttling level ().
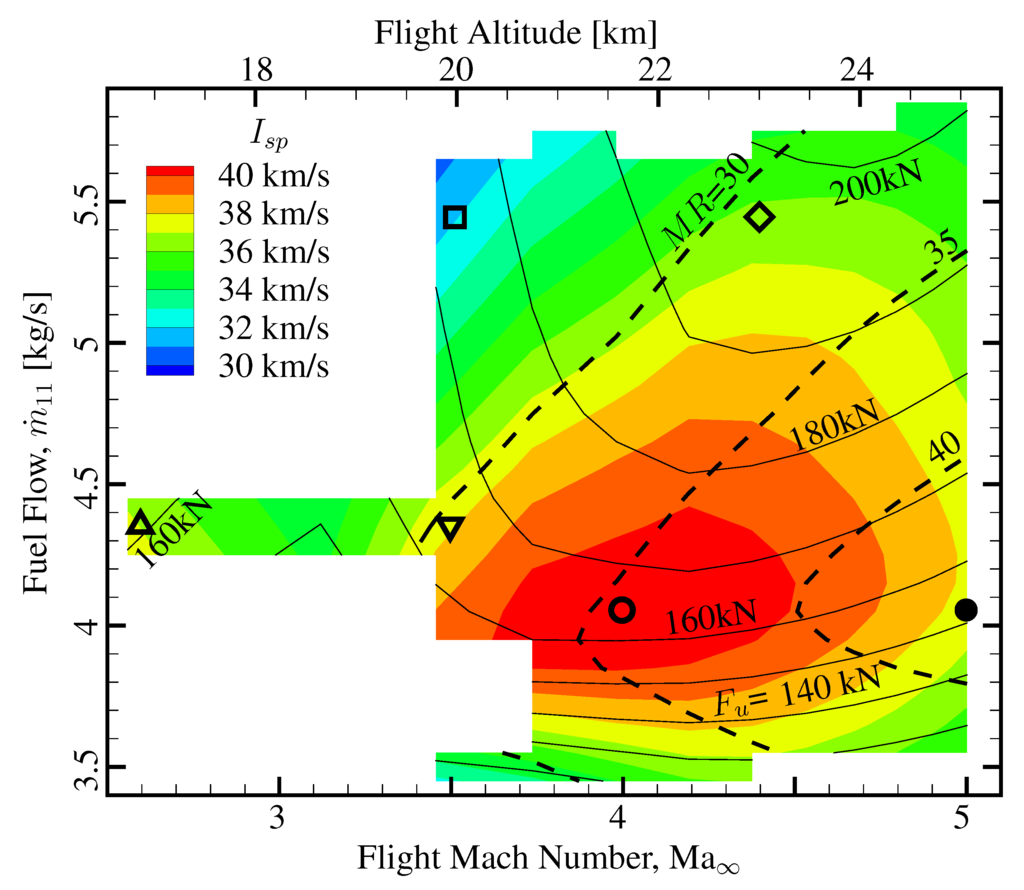
Figure 20.
Scimitar core operational range: uninstalled thrust and specific impulse vs. fuel consumption and flight condition.
5. Conclusions
A dynamic numerical model has been developed for an air turbo-rocket under acceleration and at sustained supersonic cruise at Mach 5. The complexity of the model resides in the use of a large number of heat exchanging units in combination with a considerable sum of turbomachinery components. The numerical model was programmed in EcosimPro based on the capabilities of the European Space Propulsion System Simulation and specific heat exchanger architectures and off-design turbomachinery models based on characteristic maps.
The implementation of the appropriate engine control logic allowed the reduction of the number of engine control variables to a single one: the throttle. In this manner, the engine operational envelope and the performance in terms of specific impulse and uninstalled thrust were obtained along the prescribed aircraft trajectory for various throttling levels.
Acknowledgements
The authors acknowledge the financial support from ESA/ESTEC through the NPI program: TEC-MPA/2006/318, Contract no.: 20366/07/NL/EM, and the continuous support of the technical officer Johan Steelant.
This research was also performed within the Long-Term Advanced Propulsion Concepts and Technologies II project investigating high-speed air-breathing propulsion. LAPCAT II, coordinated by ESA-ESTEC, is supported by the EU within the 7th Framework Programme, Theme 7 Transport, Contract no.: ACP7-GA-2008-21 1485.
Nomenclature:
| A | = transversal area [m] |
= cross section of the reheater helium channels [m] | |
| a | = speed of sound [m s] |
= total mass of chemical element j in the chemical species i | |
| b | = blockage ratio of the tubes in crossflow |
= total mass of chemical element j in the gas mixture | |
| C | = heat capacity [m K s] |
= specific heat at constant pressure [m K s] | |
| D | = diameter [m] |
= hydraulic diameter [m] | |
| e | = tube minimum distance to diameter ratio or total specific energy
() [m s] |
= uninstalled thrust [kg m s] | |
= mathematical function whose root defines the constraint which the turbomachinery design parameters , and must satisfy | |
| G | = Gibbs potential [kg m s] |
= mathematical function whose root defines the locus of turbomachinery operational points which satisfy the fluid dynamical constraint imposed by the turbomachine discharge duct | |
= mathematical function whose root defines the locus of turbomachinery operational points which satisfy the mechanical constraint imposed by the turbomachine shaft | |
= adiabatic efficiency characteristic of the unscaled turbomachine | |
| h | = specific enthalpy [m s] |
= convective heat transfer coefficient [kg K s] | |
= shaft inertia [kg m] | |
= specific impulse [m s] | |
| k | = thermal conductivity [kg K m s] or controller sensitivity |
= mass flow scaling factor | |
= efficiency scaling factor | |
= pressure ratio scaling factor | |
| L | = length [m] |
= characteristic length [m] | |
= axial length of the reheater module strips [m] | |
= characteristic thermal entry length [m] | |
| Ma | = Mach number |
= number of coolant channels per row in the regenerator module | |
= number of heatant channels per row in the regenerator module | |
= number of modules in each regenerator unit | |
= mass flow characteristic of the unscaled turbomachine [kg s] | |
| m | = mass [kg] |
= mass flow rate [kg s] | |
= corrected mass flow rate [Equation (38)] [kg s] | |
| N | = number of mols or rotational speed [rpm] |
= number of plates of the reheater module | |
= number of rows of heatant / coolant channels per regenerator module | |
= number of helium channels per strip of the reheater module | |
= corrected speed [Equation (37)] | |
| n | = number of nodes |
= number of strips per plate of the reheater module | |
| Nu | = Nusselt number |
| Nu | = Nusselt number in turbulent flow |
| Nu | = Nusselt number in laminar fully developed flow with uniform heat flux boundary condition |
| Nu | = Nusselt number in laminar fully developed flow with isothermal boundary condition |
| Pr | = Prandtl number |
| p | = pressure [kg m s] |
= heat flux [kg s] | |
| R | = ideal gas constant [K m s] |
= curvature radius [m] | |
| Re | = Reynolds number |
| Sh | = Strouhal number |
= mathematical function whose root defines the locus of the turbomachinery steady operational points which satisfy the fluid dynamical constraint imposed by the turbomachine discharge duct | |
= mathematical function whose root defines the locus of turbomachinery operational points which satisfy the mechanical constraint imposed by the turbomachine shaft | |
| s | = tangential pitch between the reheater plates [m] |
| T | = temperature [K] |
= torque [kg m s] | |
| t | = reheater plate thickness [m] or time [s] |
= characteristic time [s] | |
| v | = velocity [m s] |
= ratio of precooler tube longitudinal pitch to external diameter | |
= ratio of precooler tube transversal pitch to external diameter |
| Greek | |
|---|---|
| β | = coordinate of the turbomachine map parametrization |
| Γ | = perimeter [m] |
| γ | = ratio of specific heats |
= increment of x | |
| δ | = dimensionless turbomachine equivalent inlet pressure () |
= rugosity [m] | |
| η | = adiabatic efficiency |
= intake kinetic efficiency | |
= nozzle efficiency | |
| Θ | = dimensionless turbomachine equivalent inlet temperature [Equation (39)] |
| λ | = tube stagger angle [rad] |
| μ | = viscosity [kg m s] |
| ξ | = friction factor [m] |
| Π | = pressure ratio characteristic of the unscaled turbomachine |
| π | = turbomachine compression (compressor) or expansion (turbine) ratio |
| ρ | = density [kg m] |
| σ | = constant of Stefan-Boltzmann [kg K s] |
| τ | = valve response time [s] |
| Ω | = rotational speed [rad s] |
| Subscripts | |
|---|---|
| c | = relative to the compressor |
| i | = relative to the ith grid node or element in the set |
= relative to the inlet | |
= relative to the outlet | |
| s | = corresponding to an isentropic evolution |
= relative to the stream tube | |
= standard | |
| t | = stagnation quantity or relative to the turbine |
= relative to the nozzle throat | |
| w | = relative to the wall |
| ∞ | = free stream conditions |
| Superscript | |
|---|---|
= time derivative | |
= design value | |
= reference value | |
| Acronyms | |
|---|---|
| BB | = bypass burner |
| BN | = bypass nozzle |
| CC | = main combustion chamber |
| DASSL | = differential algebraic system solver algorithm |
| ESPSS | = European Space Propulsion System Simulation |
| F | = by-pass fan |
| HT | = hub turbine |
| MR | = mixture ratio, i.e., ratio of air to fuel mass flows |
| NIST | = National Institute of Standards and Technology |
| PB | = preburner |
| PC | = precooler |
| RG | = regenerator |
| TPR | = intake total pressure recovery () |
References
- Luidens, R.W.; Weber, R.J. An Analysis of Air-Turborocket Engine Performance Including Effects of Components Changes; Technical Report RM E55H04a; NACA Lewis Flight Propulsion Laboratory: Cleveland, OH, USA, 1956. [Google Scholar]
- Escher, W.J.D. Cryogenic hydrogen-induced air-liquefaction technologies for combined-cycle propulsion applications. In Proceedings of Rocket-Based Combined-Cycle (RBCC) Propulsion Technology Workshop; NASA Lewis Research Center: Cleveland, OH, USA, March 1992; No. 92N21526. [Google Scholar]
- Balepin, V.; Tanatsugu, N.; Sato, T. Development study of precooling for ATREX engine. In Proceedings of 12th International Symposium on Air Breathing Engines; American Institute of Aeronautics and Astronautics: Melbourne, Australia, September 1995; No. ISABE 95-7015. [Google Scholar]
- Schmidt, D.K.; Lovell, T.A. Mission Performance and Design Sensitivities of Air-Breathing Hypersonic Launch Vehicles. J. Spacecr. Rocket. 1997, 34, 158–164. [Google Scholar] [CrossRef]
- Steelant, J. Sustained Hypersonic Flight in Europe: First Technology Achievements within LAPCAT II. In Proceedings of 17th AIAA International Space Planes and Hypersonic Systems and Technologies Conference; American Institute of Aeronautics and Astronautics: San Francisco, CA, USA, April 2011; No. AIAA-2011-2243. [Google Scholar]
- Jivraj, F.; Varvill, R.; Bond, A.; Paniagua, G. The Scimitar Precooled Mach 5 Engine. In Proceedings of 2nd European Conference for Aerospace Sciences (EUCASS), Brussels, Belgium, July 2007.
- Moral, J.; Pérez Vara, R.; Steelant, J.; de Rosa, M. ESPSS Simulation Platform. In Space Propulsion 2010; European Space Agency: San Sebastian, Spain, May 2010. [Google Scholar]
- Petzold, L.R. DASSL: Differential Algebraic System Solver; Technical Report; Sandia National Laboratories: Livermore, CA, USA, 1983. [Google Scholar]
- ESA; Astrium-Bremen; Cenaero; Empresarios Agrupados Int.; Kopoos. ESPSS EcosimPro Libraries User Manual; Version 2.0; Technical Report TN-4140; ESA European Space Research and Technology Centre: Noordwijk, The Netherlands, 2010. [Google Scholar]
- Gordon, S.; McBride, B.J. Computer Program for the Calculation of Complex Chemical Equilibrium Compositions with Applications; I Analysis; Technical Report RP 1311; NASA Glenn Research Center: Cleveland, OH, USA, 1994. [Google Scholar]
- Churchill, S.W. Friction-Factor Equation Spans All Fluid-Flow Regimes. Chem. Eng. 1977, 84, 91–92. [Google Scholar]
- Lemmon, E.W.; McLinden, M.O.; Friend, D.G. Thermophysical Properties of Fluid Systems. In NIST Chemistry WebBook; NIST Standard Reference Database No. 23; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2007. [Google Scholar]
- Heiser, W.H. Hypersonic Airbreathing Propulsion; American Institute of Aeronautics and Astronautics: Washington, DC, USA, 1994; ISBN 1563470357. [Google Scholar]
- U.S. Standard Atmosphere, 1976; Technical Report NASA-TM-X-74335; NOAA-NASA-USAF: Washington, DC, USA, 1976.
- Bartz, D.R. Turbulent Boundary-Layer Heat Transfer from Rapidly Accelerating Flow of Rocket Combustion Gases and of Heated Air. Adv. Heat Transf. 1965, 2, 1–108. [Google Scholar]
- Martinez-Sanchez, M. Liquid Rocket Propulsion Theory. In Spacecraft Propulsion; Von Karman Institute: Rhode-Saint-Genèse, Belgium, 1993; VKI LS 1993-01. [Google Scholar]
- Varvill, R. Heat Exchanger Development at Reaction Engines Ltd. In Proceedings of 59th International Astronautical Congress; International Astronautical Federation: Glasgow, UK, September–October 2008; IAC-08-C4.5.2.
- Churchill, S.W.; Usagi, R. A general expression for the correlation of rates of transfer and other phenomena. AIChE J. 1972, 18, 1121–1128. [Google Scholar] [CrossRef]
- Bejan, A.; Kraus, A.D. Heat Transfer Handbook; Number ISBN 0-471-39015-1; John Wiley & Sons: Hoboken, NJ, USA, 2003; p. 1480. [Google Scholar]
- Khan, W.A.; Culham, J.R.; Yovanovich, M.M. Convection Heat Transfer from Tube Banks in Crossflow: Analytical Approach. Int. J. Heat Mass Transf. 2006, 49, 4831–4838. [Google Scholar] [CrossRef]
- Hausen, H. Heat Transfer in Counterflow, Parallel Flow and Cross Flow; McGraw-Hill: New York, NY, USA, 1983. [Google Scholar]
- Nakayama, A.; Kuwahara, F.; Hayashi, T. Numerical Modelling for Three-Dimensional Heat and Fluid Flow Through a Bank of Cylinders in Yaw. J. Fluid Mech. 2004, 498, 139–159. [Google Scholar] [CrossRef]
- Beale, S.B.; Spalding, D.B. A Numerical Study of Unsteady Fluid Flow in In-Line and Staggered Tube Banks. J. Fluid. Struct. 1999, 13, 723–754. [Google Scholar] [CrossRef]
- Khan, W.A.; Culham, J.R.; Yovanovich, M.M. Fluid Flow and Heat Transfer from a Cylinder Between Parallel Planes. J. Thermophys. Heat Transf. 2004, 18, 395–403. [Google Scholar] [CrossRef]
- Webber, H.; Feast, S.; Bond, A. Heat Exchanger Design in Combined Cycle Engines. In Proceedings of 59th International Astronautical Congress; International Astronautical Federation; Glasgow, UK, September–October 2008; IAC-08-C4.5.1.
- Colgan, E.G.; Furman, B.; Gaynes, M.; Graham, W.S.; LaBianca, N.C. A Practical Implementation of Silicon Microchannel Coolers for High Power Chips. IEEE Trans. Compon. Packag. Technol. 2007, 30, 218–225. [Google Scholar] [CrossRef]
- Kim, S.J.; Kim, D. Forced Convection in Microstructures for Electronic Equipment Cooling. J. Heat Transf. 1999, 121, 639–645. [Google Scholar] [CrossRef]
- Sui, Y.; Lee, P.S.; Teo, C.J. An Experimental Study of Flow Friction and Heat Transfer in Wavy Microchannels with Rectangular Cross Section. Int. J. Therm. Sci. 2011, 50, 2473–2482. [Google Scholar] [CrossRef]
- Gong, L.; Kota, K.; Tao, W.; Joshi, Y. Parametric Numerical Study of Flow and Heat Transfer in Microchannels with Wavy Walls. J. Heat Transf. 2011, 133, 051702:1–051702:10. [Google Scholar] [CrossRef]
- Riegler, C.; Bauer, M.; Kurzke, J. Some aspects of modeling compressor behavior in gas turbine performance calculations. J. Turbomach. 2001, 123, 372–378. [Google Scholar] [CrossRef]
- Dixon, S.L. Fluid Mechanics, Thermodynamics of Turbomachinery; Butterworth-Heinemann: Oxford, UK, 1998. [Google Scholar]
- Cumpsty, N. Jet Propulsion—A Simple Guide to the Aerodynamic and Thermodynamic Design and Performance of Jet Engines; Cambridge University Press: Cambridge, UK, 1997; p. 115. [Google Scholar]
- Paniagua, G.; Szokol, S.; Kato, H.; Manzini, G. Contrarotating Turbine Aerodesign for an Advanced Hypersonic Propulsion System. J. Propuls. Power 2008, 24, 1269–1277. [Google Scholar] [CrossRef]
- Kurzke, J. Component Map Collection; Joachim Kurzke: Dachau, Germany, 2004; Issue 2. [Google Scholar]
- Coverse, G.L. Extended Parametric Representation of Compressor Fans and Turbines; Technical Report NASA-CR-174646; NASA Lewis Research Center: Cleveland, OH, USA, 1984; Volume 2. [Google Scholar]
- Kurzke, J.; Riegler, C. A New Compressor Map Scaling Procedure for Preliminary Conceptual Design of Gas Turbines; ASME IGTI Turbo Expo: Munich, Germany, 2000; 2000-GT-0006. [Google Scholar]
- Brenan, K.E.; Campbell, S.L.; Petzold, L.R. Numerical Solution of Initial-Value Problems in Differential Algebraic Equations; SIAM: Philadelphia, PA, USA, 1996. [Google Scholar]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).