Thermal CFD Analysis of Tubular Light Guides

Abstract

Tubular light guides are applicable for daylighting of windowless areas in buildings. Despite their many positive indoor climate aspects they can also present some problems with heat losses and condensation. A computer CFD model focused on the evaluation of temperature distribution and air flow inside tubular light guides of different dimensions was studied. The physical model of the tested light guides of lengths more than 0.60 m proves shows that Rayleigh numbers are adequate for a turbulent air flow. The turbulent model was applied despite the small heat flux differences between the turbulent and laminar model. The CFD simulations resulted into conclusions that the growing ratio of length/diameter increases the heat transmission loss/linear transmittance as much as by 50 percent. Tubular light guides of smaller diameters have lower heat transmission losses compared to the wider ones of the same lengths with the same outdoor temperature being taken into account. The simulation results confirmed the thermal bridge effect of the tubular light guide tube inside the insulated flat roof details. The thermal transmittance of the studied light guides in the whole roof area was substituted with the point thermal bridges. This substitution gives possibility for simple thermal evaluation of the tubular light pipes in roof constructions.

1. Introduction

Tubular light guides, or light pipes, are systems that serve for daylighting of internal windowless parts of buildings. They transport light from the outdoors into interiors via multi-reflections on their mirrored internal facings. Typically light pipes consist of roof transparent domes, highly reflective tubes and ceiling transparent covers—the diffusers. The diffusers are used for scattering daylight for more evenly light distribution in the illuminated rooms [1,2]. They represent a possibility of improvement of indoor visual comfort and also an energy savings alternative compared to artificial lighting.

Tubular light guiding systems can consist of tubes with both ventilated and/or non-ventilated air cavities. Research programs have focused on innovative light pipe systems and their evaluation [3]. The EU project Triplesave unit [4] was focused on development and evaluation of an integrated light pipe for a daylighting/passive stack ventilation/solar heating cooling unit.

Tubular light guides have been the subject of increased professional interest since at least the mid-1980s [5]. The guide light transmittance has been studied in experimental and theoretical models [6,7]. Computer simulations focused on thermal and air flow profiles of a special light guide system composed of two concentric tubes which combine daylighting and ventilation functions were run [8,9,10]. In a double shell light guide model for light/vent pipes, both stack and external wind effects were studied [11,12]. Specific studies on rectangular light guide ducts integrated with ventilation systems and solar water heaters [13] and a computer fluid dynamic (CFD) model of internal helically finned tubes for parabolic trough design by CFD tools [14] were also published.

This article is aimed at the thermal evaluation of common tubular light guides that serve for daylighting without the ventilation effect, as shown in Figure 1. The thermal properties of light pipes were noted in [15,16]. Installation of the light guides in insulated roofs could produce thermal bridges and water vapour condensation problems. These problems depend on many factors, but mainly on the hydrothermal properties of materials and on indoor and outdoor air temperatures and relative humidity. Building construction thermal bridging has been topic of many investigations [17,18,19] but the common tubular light guides have not been studied in detail in terms of temperature and air flow profiles.

Figure 1. Common tubular light guide and its components.

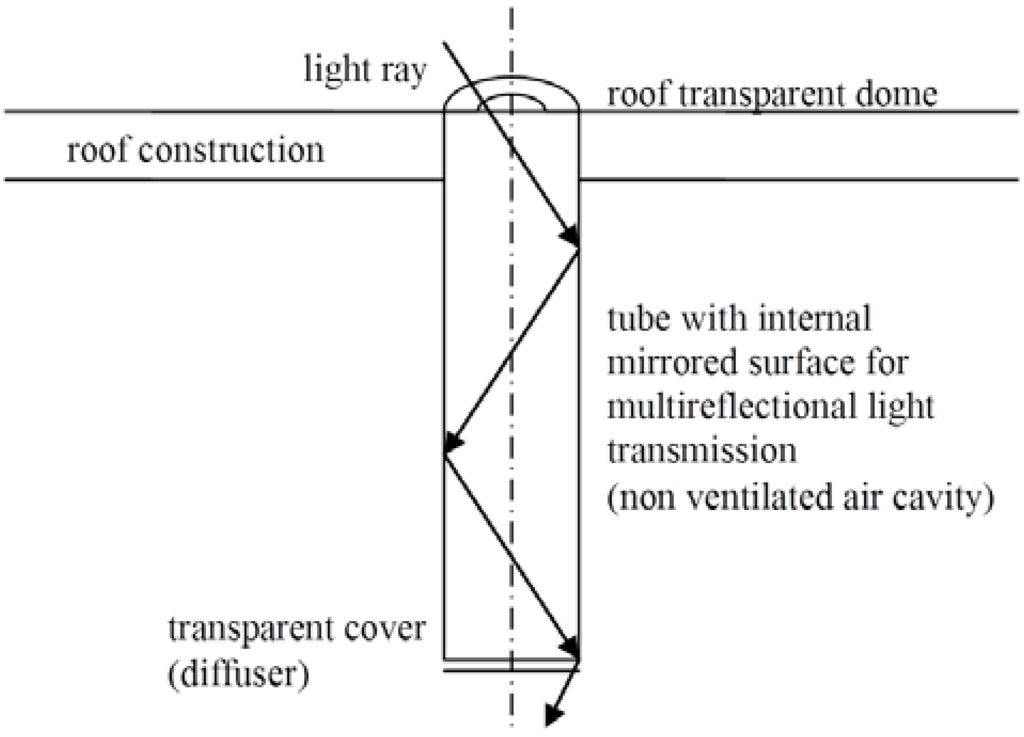
Figure 1. Common tubular light guide and its components.

2. CFD Model

Tubular light guide CFD simulation models have been studied for prediction of temperature distribution and air flow computational methods [20,21,22]. For the purposes of the simulations of temperature profiles and air flow patterns within tubular light guides of different dimensions the software ANSYS Fluent [22] was used. The simulation models are based on the assumption of perfectly sealed tubular light guide systems without air exchange by infiltration or exfiltration.

Results of our former simulations, published in [23], were for a 3D model of a roof segment with a tubular light guide installation, as shown in Figure 2. The simulation confirmed the thermal bridge area with the low internal surface between the light pipe and insulated roof construction.

Figure 2. Result of the CFD simulation of a tubular light guide [23].

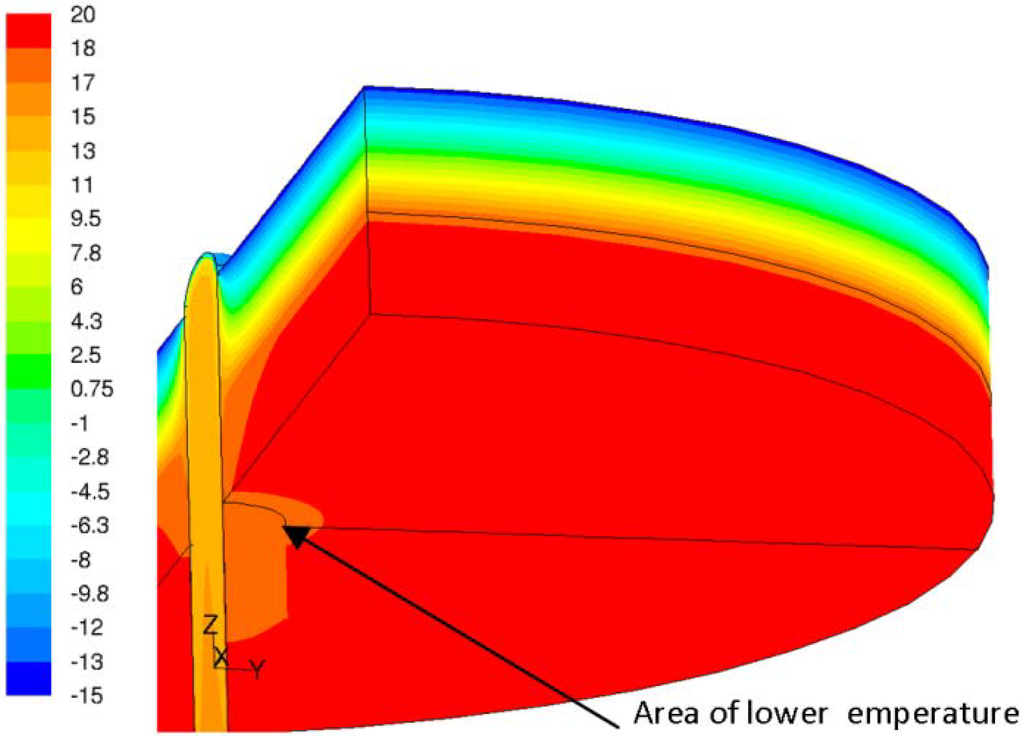
Figure 2. Result of the CFD simulation of a tubular light guide [23].

The CFD simulation study is focused on the:

• Simulation of thermal profile and determination of heat loss through tubular light guides;
• Specification of potential condensation risks on internal surface of the light guide tube at the interface between the tube and the roof construction;
• Simulation of air flow within tubular light guides under specified boundary conditions.

The evaluation is carried out for the following boundary conditions:

• Outdoor temperature interval is set to −15 °C and +15 °C to correspond with the winter and spring/autumn seasons of the temperate climate of the Central Europe region;
• Indoor temperature +20 °C and relative humidity of indoor air 50%.

2.1. Physical Models

Physical models of heat conduction, natural convection and radiation transfer within the tubular light guide were studied. Two models, of laminar convection and a two-equation turbulence model k−ω Shear Stress Transport (SST) model [24] were compared [22,25]. The laminar model gives sufficiently correct results for lower Rayleigh numbers <10⁹. The laminar model was created in accordance with the already published articles focused on the laminar convection in air cavities [26,27].

The SST model is an advanced turbulence model. It is a hybrid version of the k−ε model and k–ω models. It combines the k−ω model for the near wall region and the k−ε model in the outer region. This means that the model reduces the deficiency of the k−ω model in the outer region [28]. The laminar and turbulent (SST) models were compared for the tested tubular light guide simulation.

All simulations were run for steady state conditions. The air within the light guide was considered to be incompressible and diathermal, which means permeable to thermal radiation. The optical thickness of the air equals to zero. The Discrete Ordinates Model was selected, as it solves heat transfer in rotation symmetrical geometric models with semi-transparent materials and partially-specular reflection surfaces [22].

2.2. Geometric Models

Several geometric models and their meshing were compared because of optimization of the simulation results with respect to accuracy and the simulation time. First of all, the 3D model of the tubular light guide was determined [23] (Figure 3). The model consists of insulated roof segment with the tubular light guide. In the following step the cylindrical 3D model was separated by adiabatic walls, which divide it into four identical quadrants. A one quadrant segment was selected for the meshing as shown in Figure 4. The cross section of the segment was used for presentation of simulation results as shown in Figure 5a.

The computational mesh substantially influences results. The meshing presents a rather complicated task because of the light guide geometry wide air cavity rounded by a very thin metal sheet. The initial regular meshing, shown in Figure 5a, was adapted for boundary layers on the light guide perimeter as shown in Figure 5b.

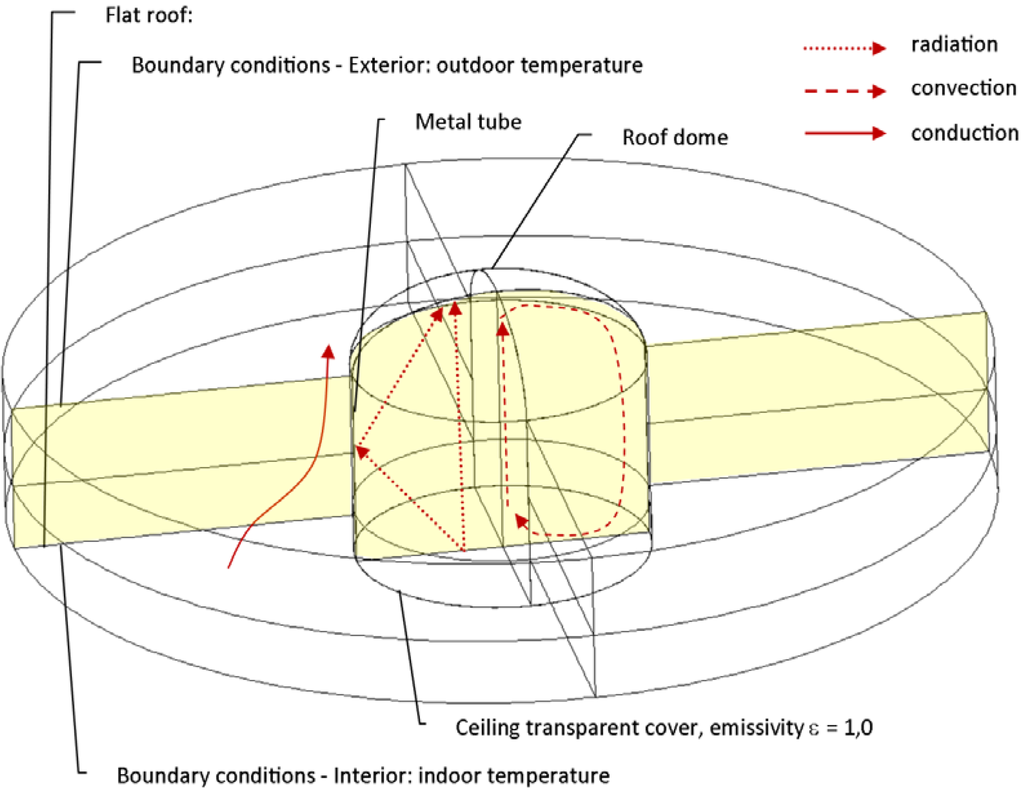
Figure 3. The 3D model, geometry, materials and boundary conditions [23].

Figure 3. The 3D model, geometry, materials and boundary conditions [23].

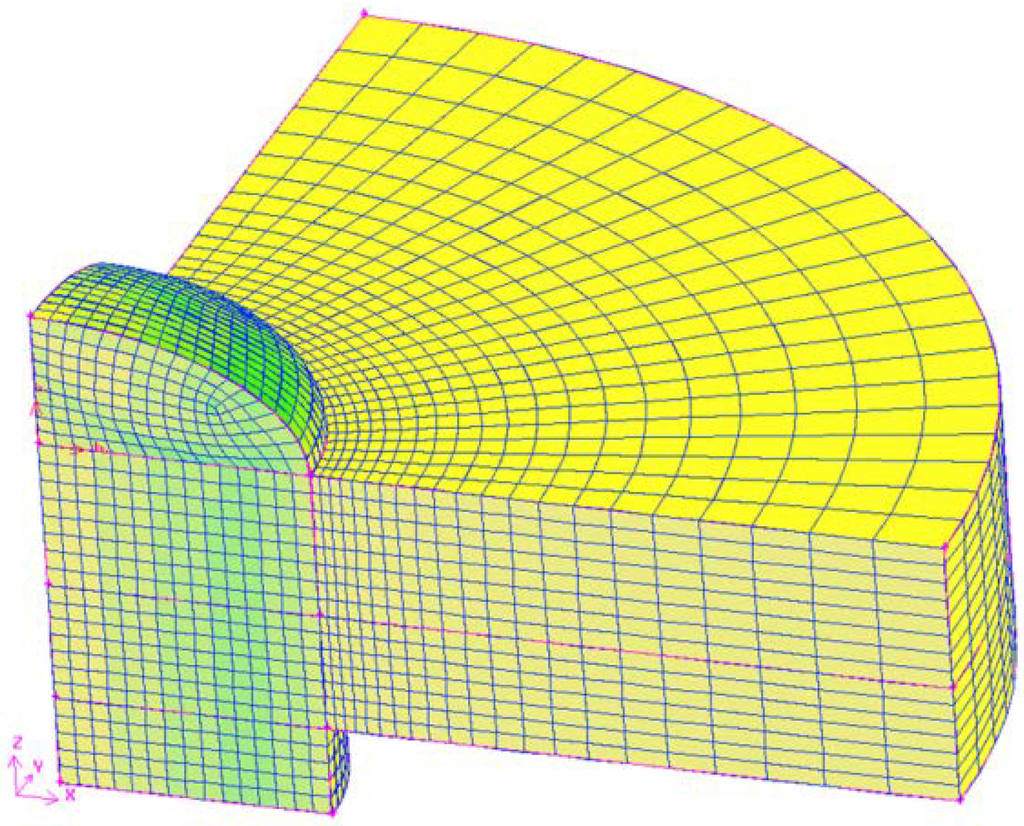
Figure 4. Computational quadrant with 3D meshing.

Figure 4. Computational quadrant with 3D meshing.

The type of meshing was adapted for finer division in the studied segment areas with higher thermal and air flow gradients as shown in Figure 5b. The meshing adaptation together with the widening of horizontal division is supportive of the model accuracy/time optimization. Extremely fine mesh was created to test the aforementioned ways of meshing (Figure 5c). Simulations for the model meshing variations in Figure 5b and Figure 5c give similar computational results. This practically means that the very fine structural meshing, which is computationally expensive, can be substituted with the boundary adapted model, or with a model using prismatic boundary layers, as shown in Figure 5d.

Figure 5. Meshes and geometric types: (a) Initial-structured 3D mesh; (b) boundary adapted 3D mesh; (c) Very fine structural 3D comparative mesh; (d) Non structured 2D rotation symmetrical mesh. Scheme of the geometric models considered; (e) 3D-cylinder; (f) 3D/4-quadrant; (g) 2D rotation symmetrical segment.

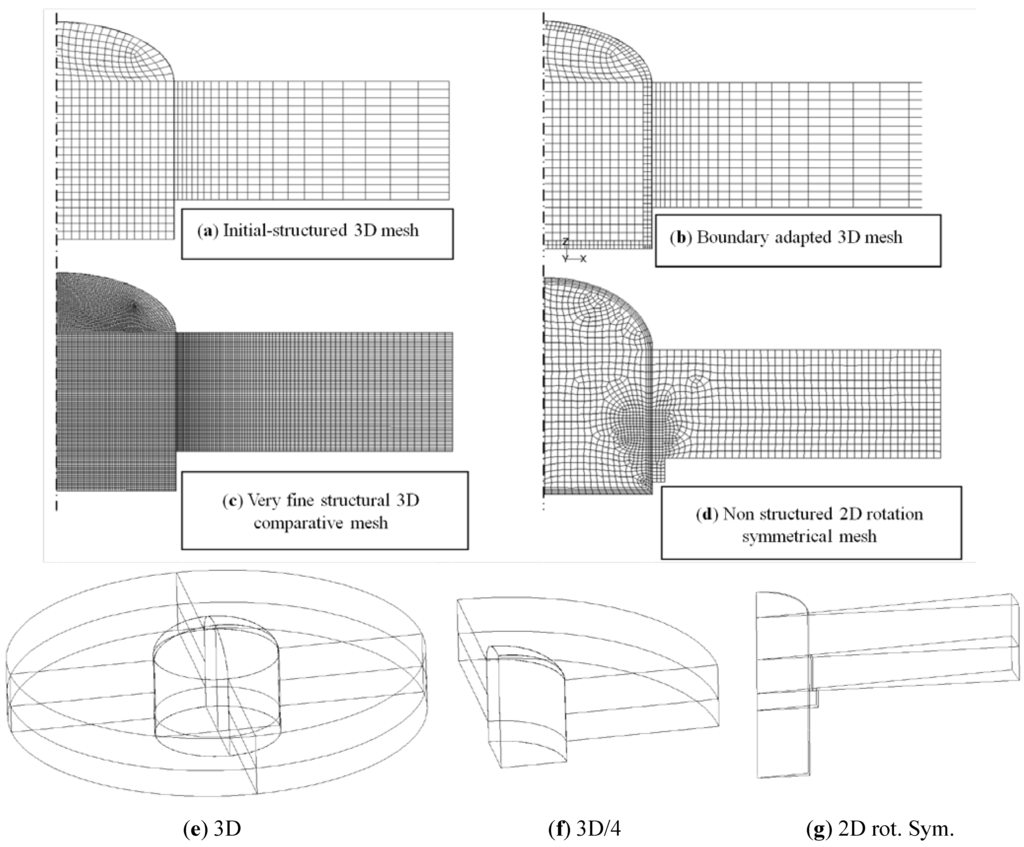
Figure 5. Meshes and geometric types: (a) Initial-structured 3D mesh; (b) boundary adapted 3D mesh; (c) Very fine structural 3D comparative mesh; (d) Non structured 2D rotation symmetrical mesh. Scheme of the geometric models considered; (e) 3D-cylinder; (f) 3D/4-quadrant; (g) 2D rotation symmetrical segment.

An unstructured meshing for 2D rotation symmetrical model as shown in Figure 5d, was found to be adequate compared to the previous ones [23]. The model was finally selected for the tubular light guide simulations. A parametric CFD simulation was used. The simulation enabled the parametric transformation of width and length of the light guide tube. The transformation was followed by automatic computational mesh changes. It makes for the geometric model simplification and computational time reduction. The 2D model simulation results are in compliance with the 3D variations as shown in Figure 5a–c.

Comparative results of the CFD simulation models with the above mentioned several types of meshing can be summarized as follows:

• The mesh adaptation on the internal surfaces of the light guide serves for the fine discretisation of boundary layers. It is essential for the simulation model accuracy;
• Widening of the horizontal mesh distances in the detail of the roof construction connected with the light guide tube is useful for reduction of the simulation time;
• 3D model discretisation of very thin metal tube (thickness 1 mm) needs the discretisation of millimetre fractions in the tube and also in the part of the roof construction that is in contact with the tube. The very fine discretisation extends the simulation time;
• The simplified model was created on the “shell conduction” method. In this model the light guide tube is substituted with a virtual layer of cells for simulation of heat transfer along the model its surface;
• The 2D rotation symmetrical model with unstructured mesh gives results that are comparable to the 3D models. The simple model offers possibility of more calculation results and geometric variations at a given simulation time;
• Performed mesh variants serve to show that the mesh independence of the geometric model is achieved.

2.3. The Final 2D Simplified Model

A simple geometry model of the light guide embedded into a flat roof composition (reinforced concrete slab, thickness 0.2 m and the roof thermal insulation layer, thickness 0.25 m) was completed. Thermal conductivity k (W·m⁻¹·K⁻¹) of the model materials and heat transfer coefficients h (W·m⁻²·K⁻¹) and indoor and outdoor temperatures are defined in accordance with standard values [29].

The 2D model of light guides was studied for thermal and air flow distribution under the defined boundary conditions. Several dimensions of tubular light guides were selected for the simulation: diameters 0.3 m, 0.6 m and 0.9 m and length from 0.56 m to 9 m. The studied 2D model was completed with an additional thermal insulation. The insulation is placed between the light guide metal tube and the roof load bearing construction for elimination of the thermal bridge as shown in Figure 6, and this cross sectional profile was adapted for meshing as shown in Figure 5d.

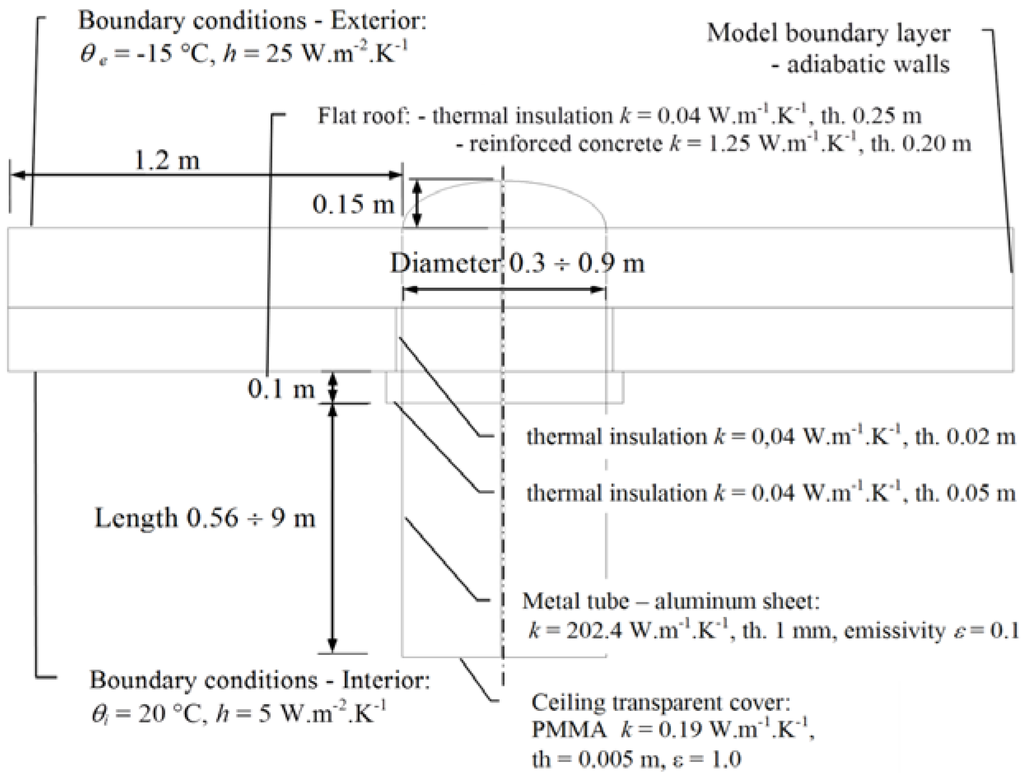
Figure 6. The 2D rotation symmetrical model—thermally insulated roof segment with the studied tubular light guide.

Figure 6. The 2D rotation symmetrical model—thermally insulated roof segment with the studied tubular light guide.

3. Results and Discussion

The results of selected laminar and turbulent models for simulation of heat flux and air flow in the short tubes are very similar. Small differences are in the temperature distribution inside of the light guide air cavity. There is more intensive turbulent flow of air in case of the turbulent model compared to the laminar model, Figure 7.

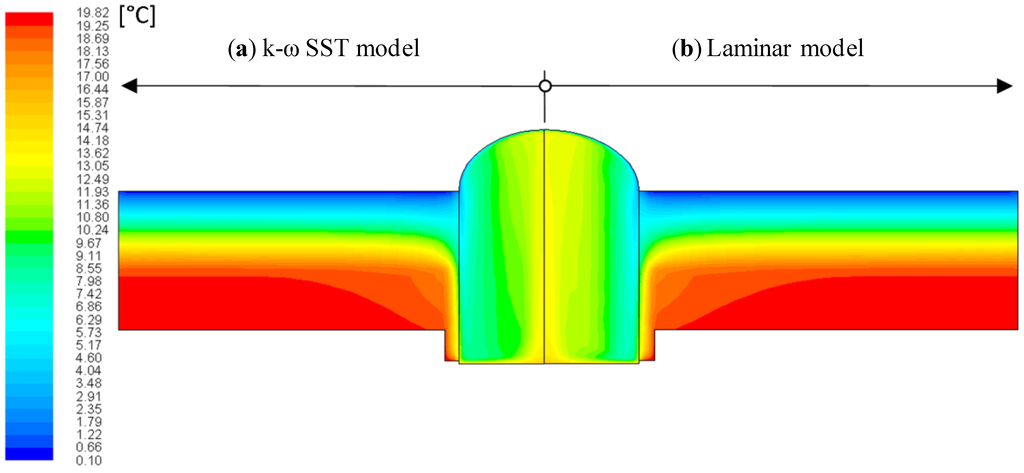
Figure 7. Comparison of temperature distribution profiles in the flat roof segment with the tubular light guide of diameter 0.6 m, length 0.56 m, emissivity of internal surface of the tube ε = 0.1: (a) k-ω SST model; (b) laminar model.

Figure 7. Comparison of temperature distribution profiles in the flat roof segment with the tubular light guide of diameter 0.6 m, length 0.56 m, emissivity of internal surface of the tube ε = 0.1: (a) k-ω SST model; (b) laminar model.

In summary, the CFD simulations have shown following differences between laminar and turbulent models:

• Average temperature in the tubular light guide—difference about 7% (for temperatures in °C) and max difference 0.35% (compared temperatures in K);
• Minimal internal surface temperatures—difference max 6% (compared temperatures in °C) and max difference 0.30% (compared temperatures in K);
• Total heat flux and heat loss—difference to 7%;
• Maximal accessible velocity of air flow in the whole domain—to 50% (max. velocity is lower than 0.15 m·s⁻¹);

The simulation results of selected tubular light guides are presented in temperature and air flow velocity graphs in Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16 and Figure 17.

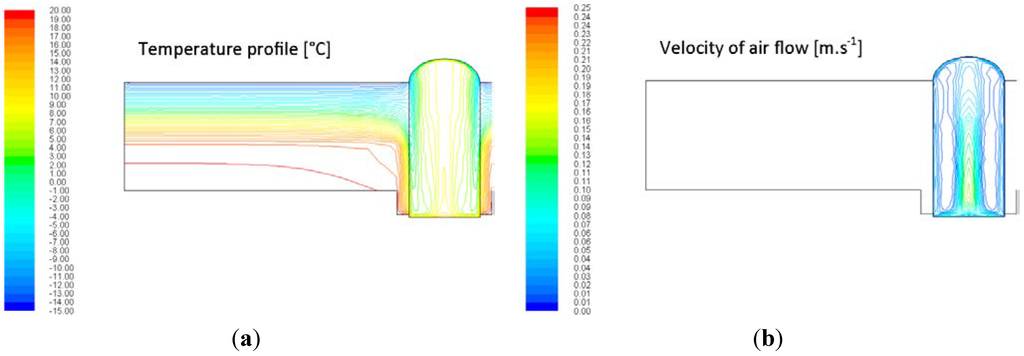
Figure 8. Example of the 2D model of the tubular light guide thermal profile (a) and air flow pattern (b), light guide of diameter d = 0.30 m; length l = 0.56 m, emissivity of internal surface of the pipe ε = 0.10.

Figure 8. Example of the 2D model of the tubular light guide thermal profile (a) and air flow pattern (b), light guide of diameter d = 0.30 m; length l = 0.56 m, emissivity of internal surface of the pipe ε = 0.10.

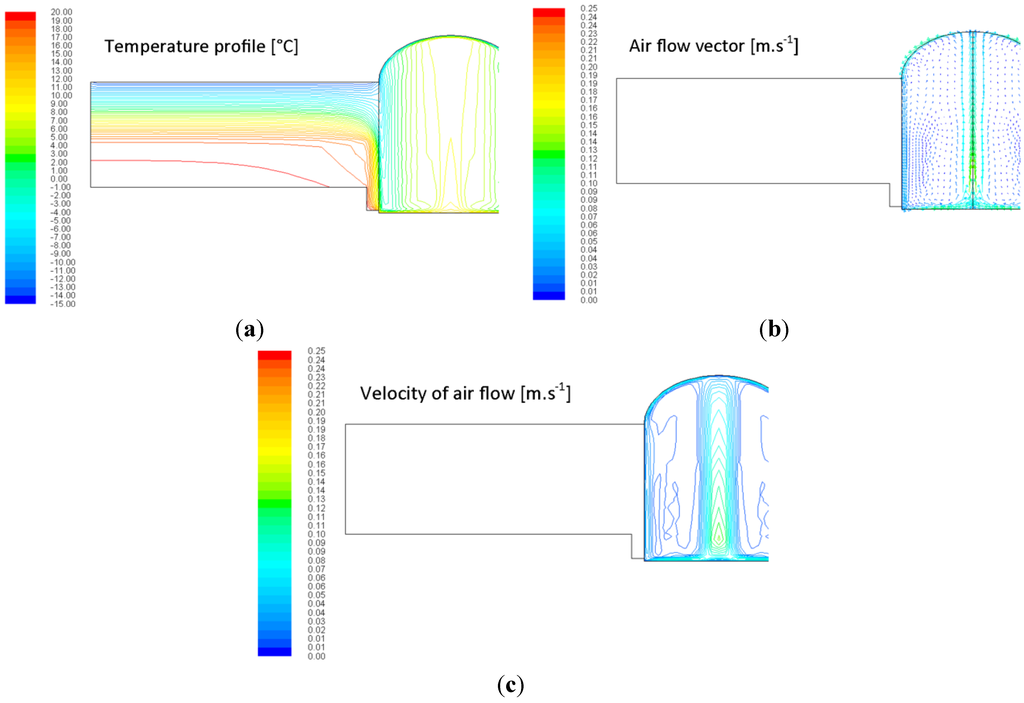
Figure 9. Example of the 2D model of the tubular light guide thermal profile and air flow pattern, light guide of diameter d = 0.60 m; length l = 0.56 m, emissivity of internal surface of the pipe ε = 0.10. (a) Temperature profile; (b) air flow vectors; (c) air flow pattern.

Figure 9. Example of the 2D model of the tubular light guide thermal profile and air flow pattern, light guide of diameter d = 0.60 m; length l = 0.56 m, emissivity of internal surface of the pipe ε = 0.10. (a) Temperature profile; (b) air flow vectors; (c) air flow pattern.

Figure 10. Example of the 2D model of the tubular light guide thermal profile (a) and air flow pattern (b), light guide of diameter d = 0.60 m and length l = 9.0, emissivity of internal surface of the pipe ε = 0.10.

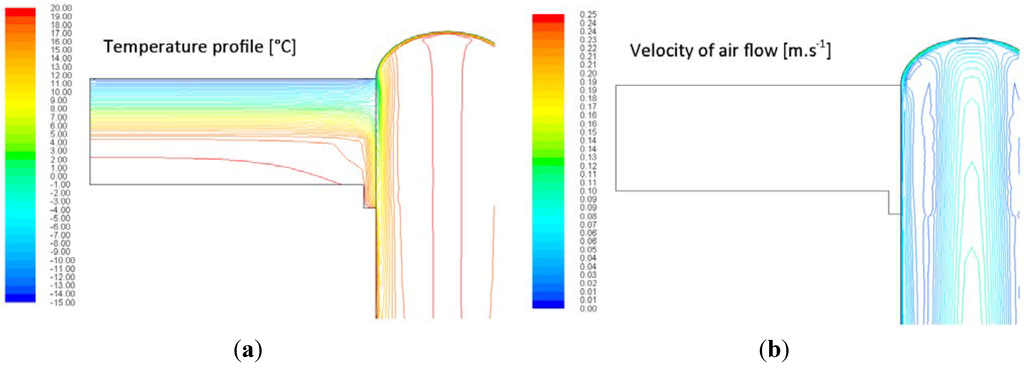
Figure 10. Example of the 2D model of the tubular light guide thermal profile (a) and air flow pattern (b), light guide of diameter d = 0.60 m and length l = 9.0, emissivity of internal surface of the pipe ε = 0.10.

The simulation results show that very short tubular light guides represent weak places in thermally insulated roofs in terms of heat losses and temperature distribution profile. The mean air temperature inside of the shorter tubes is lower as compared with the air temperature within tubular light guides of the same diameter but with longer tubes. This effect is obvious in the following graphs.

Mean temperatures in the light guide tubes of diameters 0.3 m, 0.6 m and 0.9 m and lengths from 0.56 m to 9 m are presented in Figure 11. The mean temperature is higher for light guides of smaller diameters and longer tubes. It means the air temperature in the closed cavity of the tubular light guide increases with length and decreases in wider and shorter profiles.

Figure 11. Mean temperature in tubes of diameters d = 0.3 m (Tmean_0.3), 0.6 m (Tmean_0.6) and 0.9 m (Tmean_0.9) and lengths l = 0.56 m to 9 m.

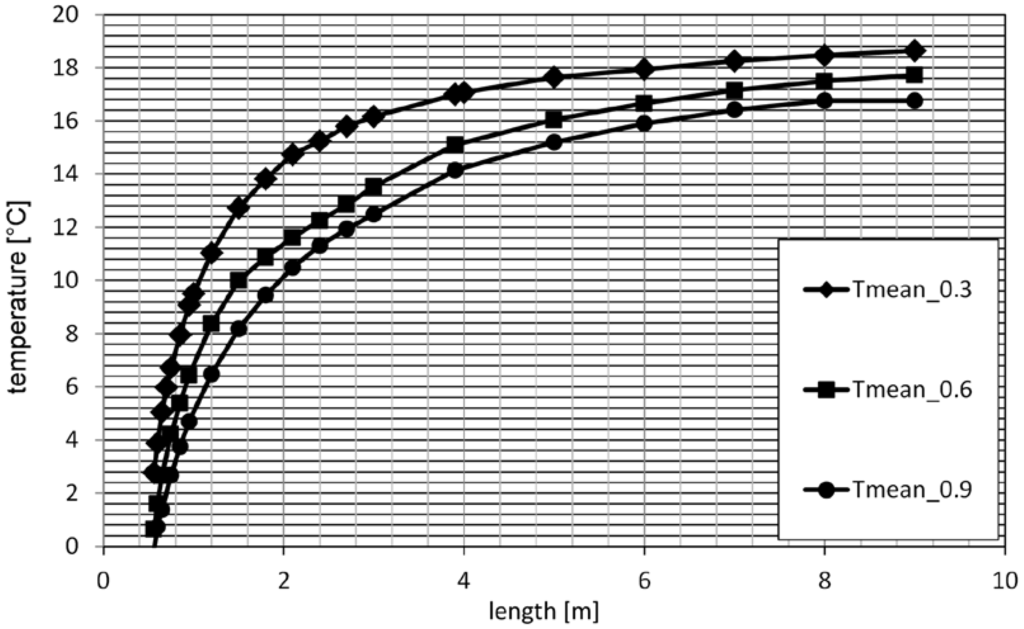
Figure 11. Mean temperature in tubes of diameters d = 0.3 m (Tmean_0.3), 0.6 m (Tmean_0.6) and 0.9 m (Tmean_0.9) and lengths l = 0.56 m to 9 m.

Total heat losses due to conduction, convection and radiation through tubular light guides are compared in Figure 12. The heat losses were calculated for the simulated constructional segment—the quadrant of the tubular light guide with non-ventilated air cavity and the insulated roof segment in the contact with the tube and roof dome. Higher heat losses were estimated for wider light guides. The light guide of diameter 0.9 m increases the heat loss with the length up to 3.0 m of length; the heat loss is nearly constant for longer tubes.

Figure 12. Heat losses of tubes of diameters d = 0.3 m (Q_tot_0.3), 0.6 m (Q_tot_0.6) and 0.9 m (Q_tot_0.9) and lengths l = 0.56 m to 9 m.

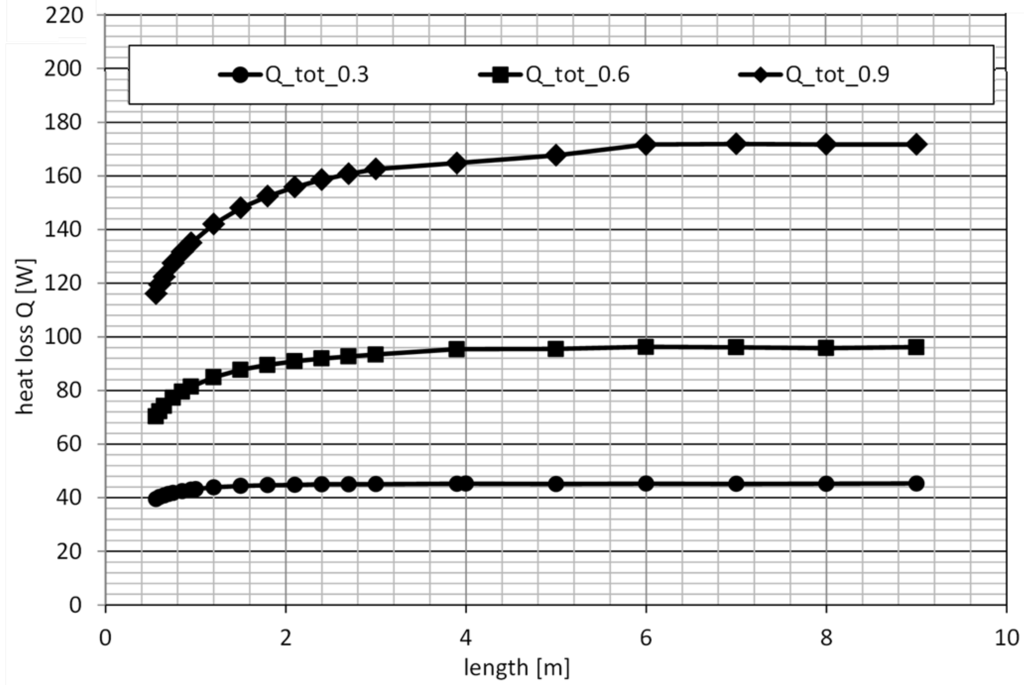
Figure 12. Heat losses of tubes of diameters d = 0.3 m (Q_tot_0.3), 0.6 m (Q_tot_0.6) and 0.9 m (Q_tot_0.9) and lengths l = 0.56 m to 9 m.

The tubular light guides influence on heat losses across the whole area of the roof construction was also studied. The tubular light guides were substituted with point thermal bridges in the study. The point thermal transmittance TT3D (W/K) of the light guides was calculated. The TT3D is defined in standard ISO 10211 [29] for steady state heat transfer and for temperature difference between the environments on either side of a thermal bridge:

$$TT3D=L^{3D}-{\displaystyle \sum _{i=1}^I{U}_i.A_i-}{\displaystyle \sum _{j=1}^J{\Psi }_j.b_j}$$

(1)

where:

• L^3D is thermal coupling coefficient (W·K⁻¹).
• U_j is thermal transmittance of the j element in the studied detail (W·m⁻²·K⁻¹).
• A_j is area of the j element in the studied detail (m²).
• Ψ is linear thermal transmittance (W·m⁻¹·K⁻¹).
• b is length of the linear thermal bridge (m).

The point thermal transmittance calculation result of the studied light guides is presented in Figure 13 in dependence on the tubular light guide aspect ratio (ratio length/diameter).

Figure 13. Point thermal transmittance in dependence on the tubular light guide aspect ratio (length/diameter); the tubular light guides of diameters d = 0.3 m—TT3D (0.3), d = 0.6 m—TT3D (0.6) and d = 0.9 m—TT3D (0.9).

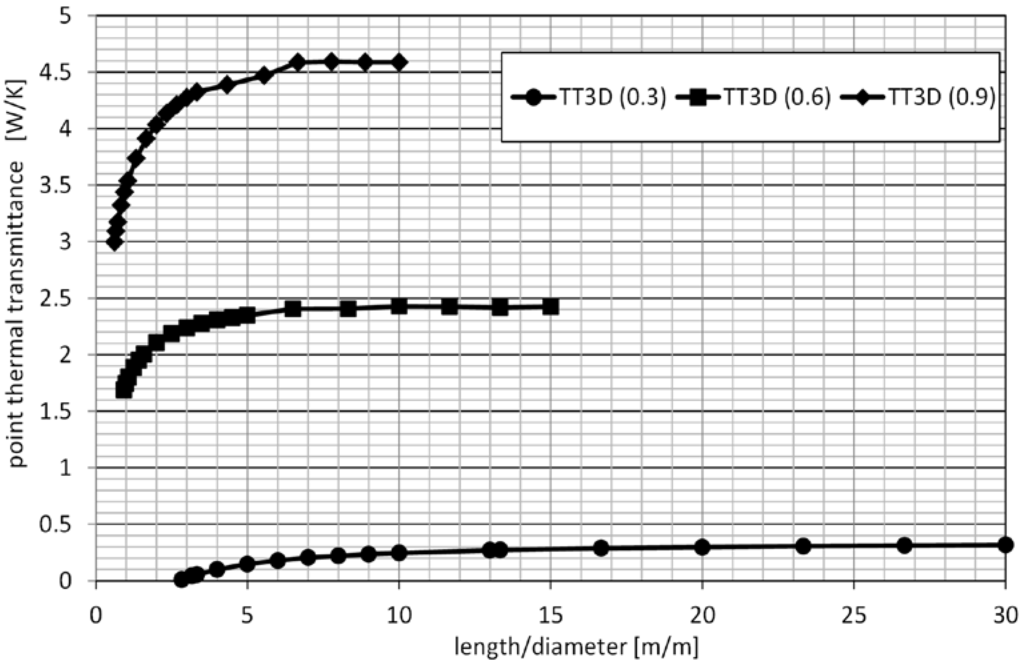
Figure 13. Point thermal transmittance in dependence on the tubular light guide aspect ratio (length/diameter); the tubular light guides of diameters d = 0.3 m—TT3D (0.3), d = 0.6 m—TT3D (0.6) and d = 0.9 m—TT3D (0.9).

The point thermal transmittance was also calculated for different outdoor temperatures within interval −15 °C and +15 °C, Figure 14.

Figure 14. Point thermal transmittance of the tubular light guides of diameter d = 0.6 m, length l = 0.56 m—TT3D (0.56) and length l = 9 m—TT3D (9.0), dependence on outdoor temperature between −15 °C and +15 °C.

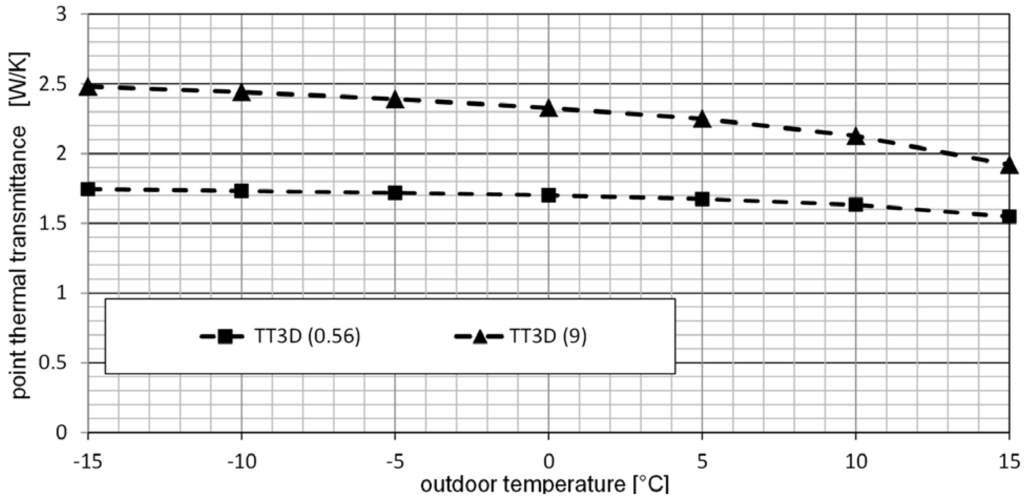
Figure 14. Point thermal transmittance of the tubular light guides of diameter d = 0.6 m, length l = 0.56 m—TT3D (0.56) and length l = 9 m—TT3D (9.0), dependence on outdoor temperature between −15 °C and +15 °C.

The point thermal transmittance decreases more for higher outdoor temperatures and in the case of longer light guides.

The study focused on the air flow distribution and velocity inside non-ventilated tubular light guides gives the following results: a natural ventilation stack is developed in tubes of length up to 3.0 m for light guides of diameter 0.6 m. Velocity of air flow inside of the tube is nearly constant for longer light guides. Maximal velocity of air flow in all studied cases is in the interval between 0.10 m·s⁻¹ and 0.20 m·s⁻¹.

Air flow velocity in the closed cavity of the light guides depends on the outdoor temperature. The indoor temperature is constant (+20 °C) in the model. Minimal surface temperatures in the internal part of the light guide and the mean air temperature within the tube are shown in Figure 15, simulated for the light guides of diameter 0.6 m and length 0.56 m and 9.0 m.

It is interesting that the minimal surface temperature of the shortest light guide is higher than the mean temperature inside its tube (Figure 16). This is caused by the ventilation stack. It is more characteristic for short tubes as compared to the relatively steady conditions within the longer ones.

Figure 15 shows dependence of maximal velocity of air flow within the tubular light guides, under outdoor temperature between −15 °C and +15 °C and constant indoor temperature +20 °C. Results were simulated for tubular light guides of diameters 0.3 m, 0.6 m and 0.9 m and lengths 0.56 m and 9.0 m.

Figure 15. Maximal air flow velocity in tubular light guides d = 0.6 m, l = 9 m (Vel_max_l0.56) and d = 0.6 m, l = 0.56 m (Vel_max_l9), dependence on the outdoor temperature between −15 °C and +15 °C.

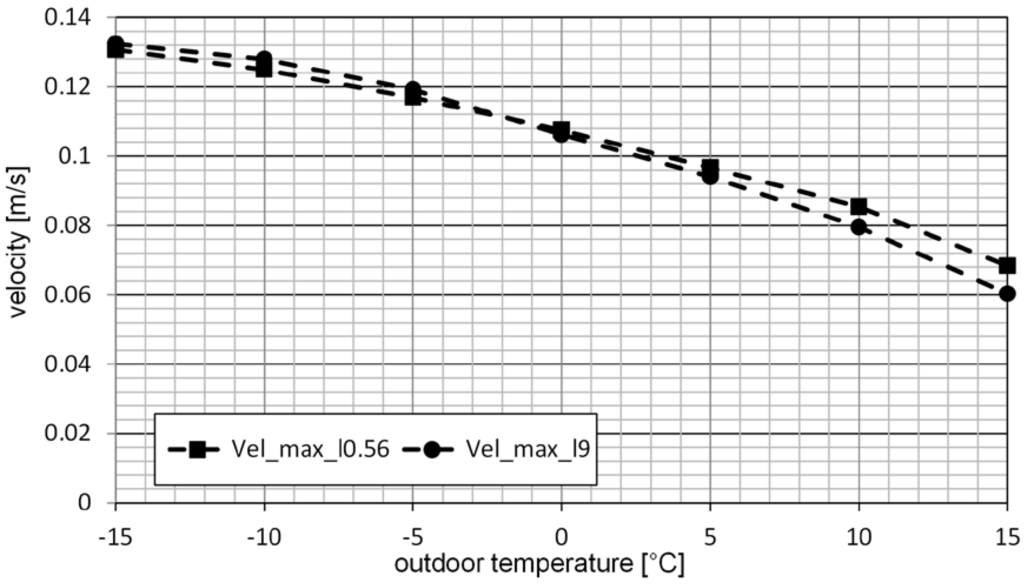
Figure 15. Maximal air flow velocity in tubular light guides d = 0.6 m, l = 9 m (Vel_max_l0.56) and d = 0.6 m, l = 0.56 m (Vel_max_l9), dependence on the outdoor temperature between −15 °C and +15 °C.

The minimal temperature on internal surface of the simulated segment is very important for specification of thermal bridges and places with potential condensation risks (Figure 16 and Figure 17).

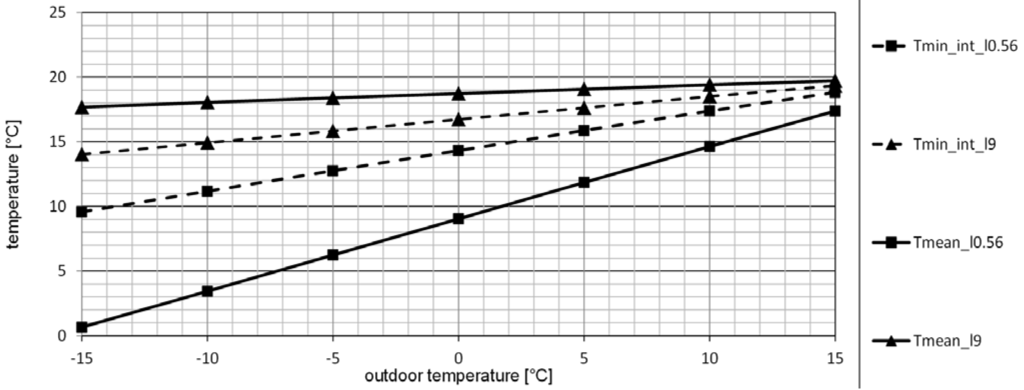
Figure 16. Mean temperatures (Tmean) in the light guides and minimal surface temperatures (Tmin_int), light guides of diameter d = 0.6 m, lengths l = 0.56 m (Tmean_l0.56 and Tmin_int_l0.56) and l = 9 m (Tmean_l9 and Tmin_int_l9).

Figure 16. Mean temperatures (Tmean) in the light guides and minimal surface temperatures (Tmin_int), light guides of diameter d = 0.6 m, lengths l = 0.56 m (Tmean_l0.56 and Tmin_int_l0.56) and l = 9 m (Tmean_l9 and Tmin_int_l9).

Figure 17. Temperature profile—simulation result for outdoor temperature θ_e = +15 °C, length 9 m, diameter 0.6 m.

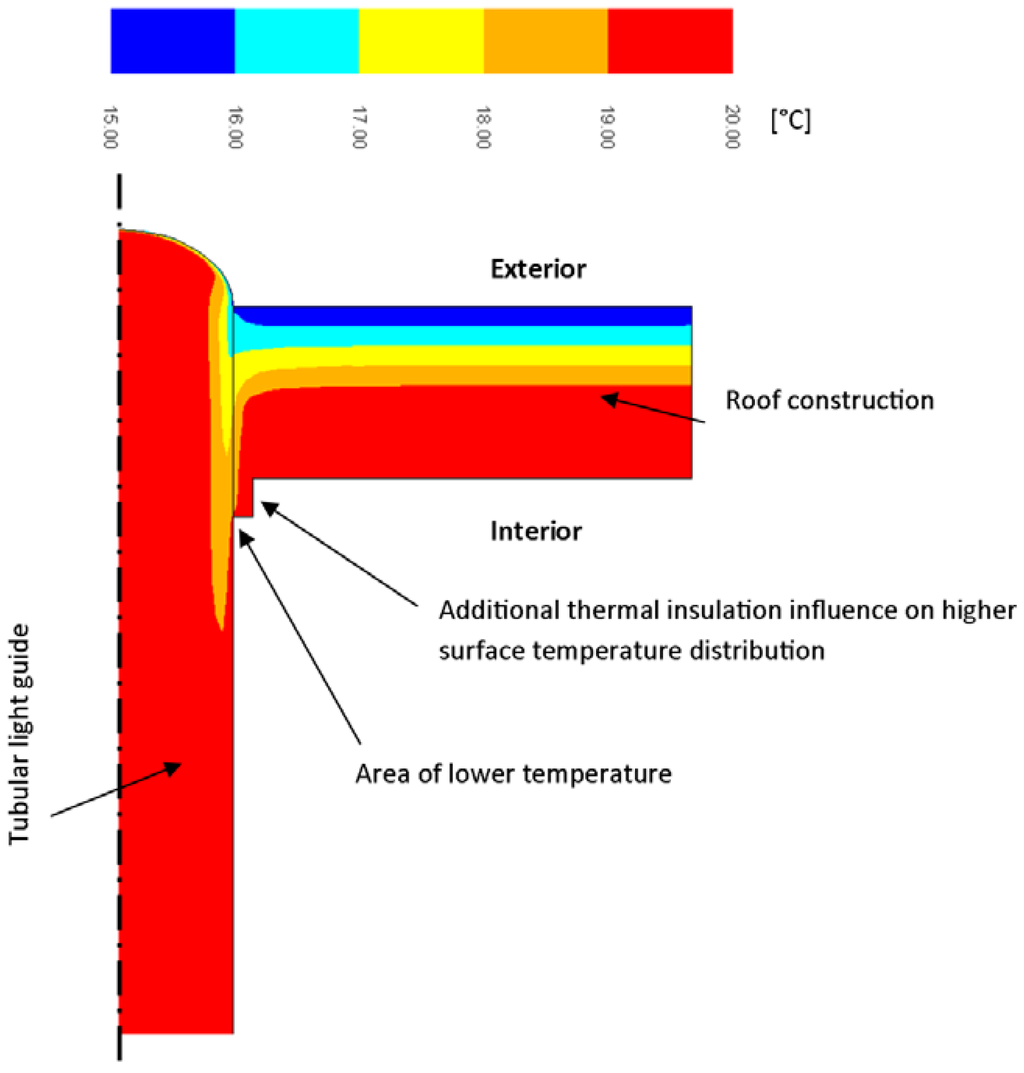
Figure 17. Temperature profile—simulation result for outdoor temperature θ_e = +15 °C, length 9 m, diameter 0.6 m.

The surface temperature on the internal surface of the tube should be sufficiently above the dew point temperature to avoid condensation problems. The simulated segment temperature profiles and their minimal temperatures were compared with the dew point temperature +9.2 °C (indoor temperature +20 °C, relative humidity 50%) [30]. Condensation risk is higher in shorter tubular light guides.

Example of the Real Evaluation of Tubular Light Guides

The daylight guidance systems Tube Transmission Efficiency (TTE) is defined in accordance with [31] as:

$$TTE=\frac{e^t}{{\left(1-t\right)}^{0.5}}$$

(2)

where:

$$t=\frac{l}{d}\cdot \tan (Z)\cdot \log ({\rho }_r)$$

(3)

where l is tubular light guide length (m), d is tubular light guide diameter (m), Z is a portion of the zenithal sky from which illuminance enters to the tubular light guide (for overcast sky Z = 30°), ρ_T is specular reflectance of mirrored inner surface of the tube.

Table 1 summarizes light end energy efficiency of the studied tubular light guides of diameters d = 0.32, 0.6 and 0.9 m and lengths l = 0.56 m, 1.0 m and 9.0 m, TTE calculated for specular reflectance ρ_r = 0.95 (reflectance of internal surface of the light guide).

Table 1. Influence of tubular light guides on point thermal transmittance and heat loss.

Length	Tubular light guide diameter
	d = 0.30 m			d = 0.60 m			d = 0.90 m
L (m)	TTE (-)	TT3D (W/K)	Q (W)	TTE (-)	TT3D (W/K)	Q (W)	TTE (-)	TT3D (W/K)	Q (W)
0.56	0.9648	−0.1391	39.5	0.9822	1.6885	70.3	0.9881	2.9965	116.1
1.00	0.9381	0.0544	43.2	0.9685	2.0055	81.4	0.9788	3.5365	135.0
9.00	0.5775	0.3172	45.3	0.7549	2.4250	96.1	0.8277	4.5864	171.8

Notes: Q (W)—heat transmission loss of the TLG including the surrounding segment of the roof; TTR (-)—Tube transmission efficiency; TT3D (W/K)—Point Thermal Transmittance

Table 1. Influence of tubular light guides on point thermal transmittance and heat loss.

Length	Tubular light guide diameter
	d = 0.30 m			d = 0.60 m			d = 0.90 m
L (m)	TTE (-)	TT3D (W/K)	Q (W)	TTE (-)	TT3D (W/K)	Q (W)	TTE (-)	TT3D (W/K)	Q (W)
0.56	0.9648	−0.1391	39.5	0.9822	1.6885	70.3	0.9881	2.9965	116.1
1.00	0.9381	0.0544	43.2	0.9685	2.0055	81.4	0.9788	3.5365	135.0
9.00	0.5775	0.3172	45.3	0.7549	2.4250	96.1	0.8277	4.5864	171.8

Notes: Q (W)—heat transmission loss of the TLG including the surrounding segment of the roof; TTR (-)—Tube transmission efficiency; TT3D (W/K)—Point Thermal Transmittance

The evaluation of tubular light guides (TLG) as point thermal bridges and their influence on the heat loss of a common room was considered. Results were calculated for an outdoor temperature of −15 °C and indoor temperature +20 °C. The room is located inside a building among other rooms with identical thermal climate; only the heat transmission loss of a roof was considered. The heat loss of the roof without the light guide installation is 94.7 W. The room of floor dimensions 3 m × 6 m is illuminated by the studied tubular light guides in two variations:

• Variation I: 1 × TLG, d = 0.60 m, length 1.0 m: Total heat loss by TLG = 70 W—the tubular light guide increases the heat transmission loss by 74%.
• Variation II: 2 × TLG, d = 0.30 m, length 1.0 m: Total heat loss by TLG = 3.8 W—the tubular light guide increases heat transmission loss by 4%.

The abovementioned results can be summarized as follows: from a thermal protection point of view, it is more convenient to design two light guides of a smaller diameter as compared to a wider one of the comparable length and light efficiency, although the installation of openings for smaller tubular light guides is more demanding on the quality of roof details.

4. Conclusions

CFD simulation results for selected tubular light guides were presented for various thermal and air flow profiles. It has been shown that the application of the 2D rotation symmetrical model is suitable for the geometry simplification. The model meshing variations demonstrate the model optimization for the purposes of the simulation accuracy and reduction of the computational time.

Laminar and turbulent CFD models of the studied light guides were compared. Interesting findings are that simulations show Rayleigh numbers are adequate for turbulent air flow for the light guide of length >0.60 m. This means that laminar as well as turbulent model can be used for shorter light guides of length <0.6 m (the maximum difference between the laminar and turbulent model is 7%). The turbulence model is more suitable for longer light guides.

The simulations have provided thermal profiles which have shown that the air trapped inside the light guide tube has limited space for circulation. The tube is placed inside of the interior space, and for this reason the air in the tube is kept warmer because of high indoor temperature (evaluated for indoor temperature +20 °C). Longer light guides show that warmer air trapped inside the tube and the coldest part is near the roof dome exposed to exterior conditions. Heat radiation losses of the tube are minimal as its highly reflective internal surface coating has very small emissivity. The mirrored internal surface reflects infrared radiation of the opposite parts of the cylindrical tube.

The metal tube represents the main thermal bridge of the light guide system installed in a roof. For this reason it is recommended to add a thermal insulation collar on the interface between the tube and the roof construction. The condensation occurs on the tube metal sheet more frequently in case of shorter tubes without an additional thermal insulation. The potential condensation risks of tubular light guides should be solved in details from early stages of design concept before their practical installation in buildings.