Abstract
In this paper, a double-linear approximation algorithm (DLAA) to achieve maximum-power-point tracking (MPPT) for photovoltaic (PV) arrays is proposed. The DLAA is based on the approximation that the maximum power point varies linearly with irradiation and temperature. With the DLAA, a maximum power point can be determined instantaneously. Moreover, complicated calculations and perturbations about an optimal point can be avoided. The paper also proposes a corresponding circuit to realize the DLAA. The configuration of the DLAA circuit is simple such that it is cost-effective and can be embedded into PV arrays easily. An example of implementation of a PV power supply system with the proposed MPPT is designed and the DLAA is compared with the perturb-and-observe method. Simulated and experimental results have demonstrated the feasibility of the PV power system and verified the advantages of the proposed DLAA.
1. Introduction
Due to the rapid development of industry, the overuse of fossil fuels results in environmental pollution, greenhouse effects and ecological damage. Adopting renewable and clean energy resources to replace fossil fuels is imperative. Among renewable-energy resources, solar energy attracts more interest owing to its noiseless, pollution-free, non-radioactive, and inexhaustible characteristics. Solar energy is converted into electric power through photovoltaic (PV) panels. The output voltage and the output current of a PV panel vary nonlinearly with irradiation, panel temperature and loading condition. There is a maximum power point (MPP) under certain atmospheric conditions. To draw maximum power from PV panel, a large number of researchers have proposed maximum power point tracking (MPPT) algorithms. Current MPPT algorithms include the voltage feedback method (VFM) [1], the power feedback method (PFM) [2,3,4], the perturb-and-observe method (POM) [5,6,7], the incremental conductance method (ICM) [8,9], the three-point weight comparison method (TPWCM) [10,11], the linear approximation method (LAM) [12], the neural-network-based method (NNBM) [13], and the fuzzy-logic-control approach (FLCA) [14,15].
The VFM is the simplest method for MPPT, which regulates PV arrays terminal voltage to a reference, handling the operation point of a PV arrays near the maximum power point. It is only suitable for some fixed irradiations and temperatures. In the power feedback method, the derivative dP/dV is regarded as a control index. While a controlled output voltage and its corresponding output power can lead the derivative to zero, a maximum power point is achieved. However, more parameters and complicated calculations are required, which increase the difficulty of MPPT. The perturb-and-observe method is widely used in maximum PV power tracking because it is easy to carry out and few measured parameters are required. Even though a maximum PV power point is reached, continued perturbing and observing will still oscillate around the point, resulting in PV power losses, especially under constant or slow variation of atmospheric conditions. To overcome the mentioned drawbacks of the POM, the ICM was developed. In the ICM, the output voltage or current of a PV array is adjusted until an incremental conductance dI/dV just reaches the ratio of PV output current to voltage. Owing to detection errors, the determined incremental conductance hardly agrees with the value of I/V. Another solution to avoid fluctuations about the maximum power point is the TPWCM. In the TPWCM, three measured points are compared and weighted. Once a new weighted result matches the preset one, subsequent comparisons stop. Nevertheless, a complicated procedure is also required, which lowers the dynamic response significantly. The LAM tracks the maximum power point according to the straight line which connects all MPPs under different irradiation conditions. It is easy to implement and locates MPP rapidly. However, the influence of temperature is neglected. The NNBM and the FLCA can fulfill MPPT regardless of atmospheric conditions and PV cell parameters, but sophisticated calculation and microprocessor-based implementation are still needed.
In this paper, a double-linear approximation algorithm (DLAA) is proposed, which can track the maximum power point instantaneously and can be implemented easily. The DLAA is based on the approximation that the trajectories of maximum power point vary linearly with irradiation and temperature. According to the DLAA, MPPT can be achieved without any calculation and perturbation about an optimal point can be avoided. In this paper, a corresponding circuit of the DLAA is developed, which determines a reference voltage in order to draw maximum power from PV arrays. Since the configuration of the circuit is simple, it is cost-effective and can be embedded into PV arrays easily. Comparison between the DLAA and the POM is also performed in this paper. The simulations and practical measurements have verified the advantages of the proposed algorithm and the validity of the corresponding MPPT circuit.
2. Characteristics of PV Arrays
In general, PV arrays are composed of a number of PV modules, which are connected in series and/or in parallel. A PV module is made of a group of PV cells, which are wired to each other and encapsulated in a weatherproof flat container. One side of the module is transparent, allowing sunlight to reach the PV cell. Each PV cell is a p-n junction semiconductor converting solar energy into electricity. An equivalent circuit is shown in Figure 1, in which Iph stands for the cell photocurrent source, Dj represents the p-n junction, Rj, Rsh and Rs are the p-n junction nonlinear impedance, intrinsic shunt resistance and intrinsic series resistance, respectively. The series resistance Rs is relatively small and the shunt resistance Rsh is relatively large. Therefore, the equivalent circuit can be simplified by neglecting both resistors.
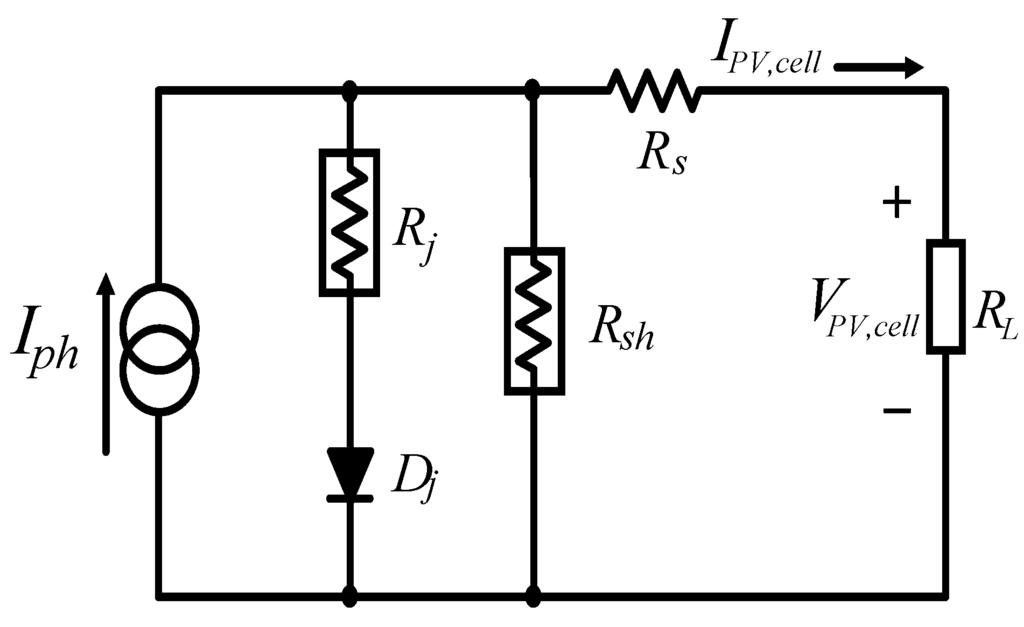
Figure 1.
An equivalent circuit of a PV cell.
From the characteristics of a p-n junction and the equivalent circuit, output current of PV arrays, IPV, can be described as:
where VPV is output voltage of PV arrays, ns is the total number of cells in series, np stands for the total number of cells in parallel, q denotes the charges of an electron (1.6 × 10−19 coulomb), k is the Boltzmann constant (1.38 × 10−23 J/°K), T is temperature of the PV arrays (°K), and A represents ideality factor of the p-n junction (between 1 and 5) [16]. In addition, Isat is the reversed saturation current of the PV cell, which depends on temperature of PV arrays and it can be expressed by the following equation:
where Tr is the cell reference temperature, Irr is the corresponding reversed saturation current at Tr, and Egap stands for band-gap energy of the semiconductor in the PV cell. In (1), the Iph varies with irradiation Si and PV array temperature T, which can be represented as:
where Isso is the short-circuit current while reference irradiation is 100 mW/cm2 and reference temperature is set at Tr, and Ki is the temperature coefficient. Based on (1), output power (PPV) of PV arrays then can be determined as follows:
which reveals that the amount of generated power PPV varies with irradiation Si and PV-array temperature T.
The PV arrays used in this paper are SIEMENS SM55, and the electrical characteristics of each module are listed in Table 1. By solving equations (1)–(4) and with the values listed in Table 1, the relationships of IPV–VPV and PPV–VPV can be plotted. Simulated PPV–VPV curves under various irradiations are shown in Figure 2 for a fixed module temperature (25 °C). In the case of constant irradiation (1000 W/m2), Figure 3 shows the relationship between PPV and VPV under various module temperatures.

Table 1.
Electrical characteristics of the used PV module (SIEMENS SM55).
| Model | SM55 |
|---|---|
| Typical peak power (PP) | 55 W |
| Voltage at peak power (VPP) | 17.4 V |
| Current at peak power (IPP) | 3.15 A |
| Short-circuit current (ISC) | 3.45 A |
| Open-circuit voltage (VOC) | 21.7 V |
| Temperature coefficient of open-circuit voltage | −0.077 V/°C |
| Temperature coefficient of short-circuit current (Ki) | 1.2 mA/°C |
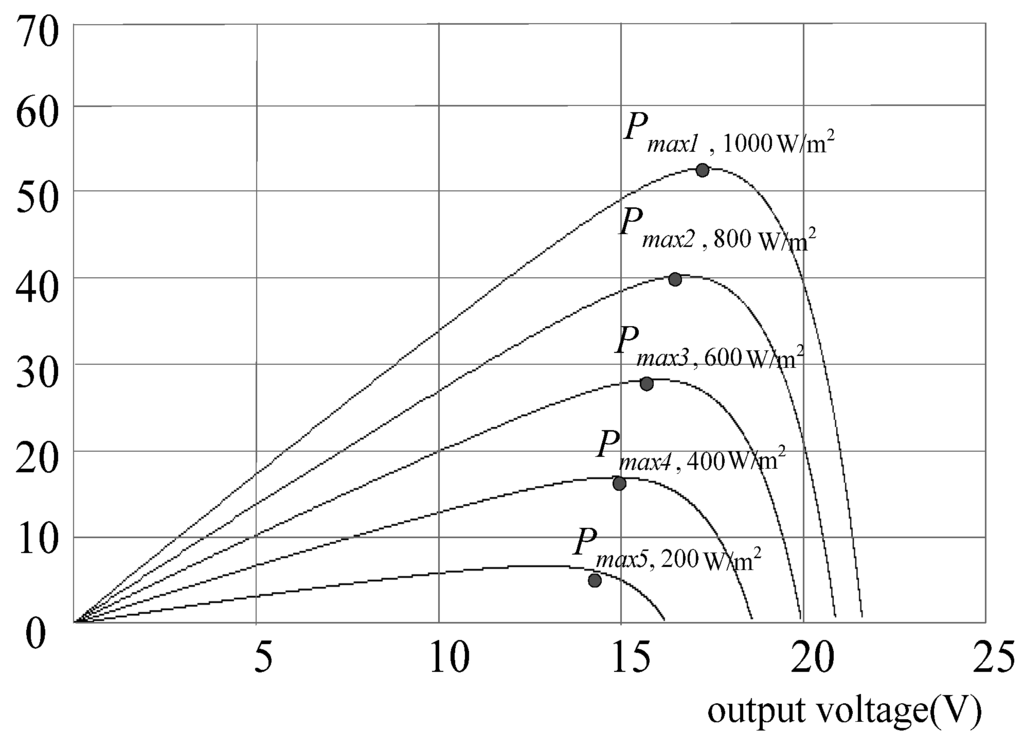
Figure 2.
PPV–VPV curves of the PV module with constant temperature (25 °C).
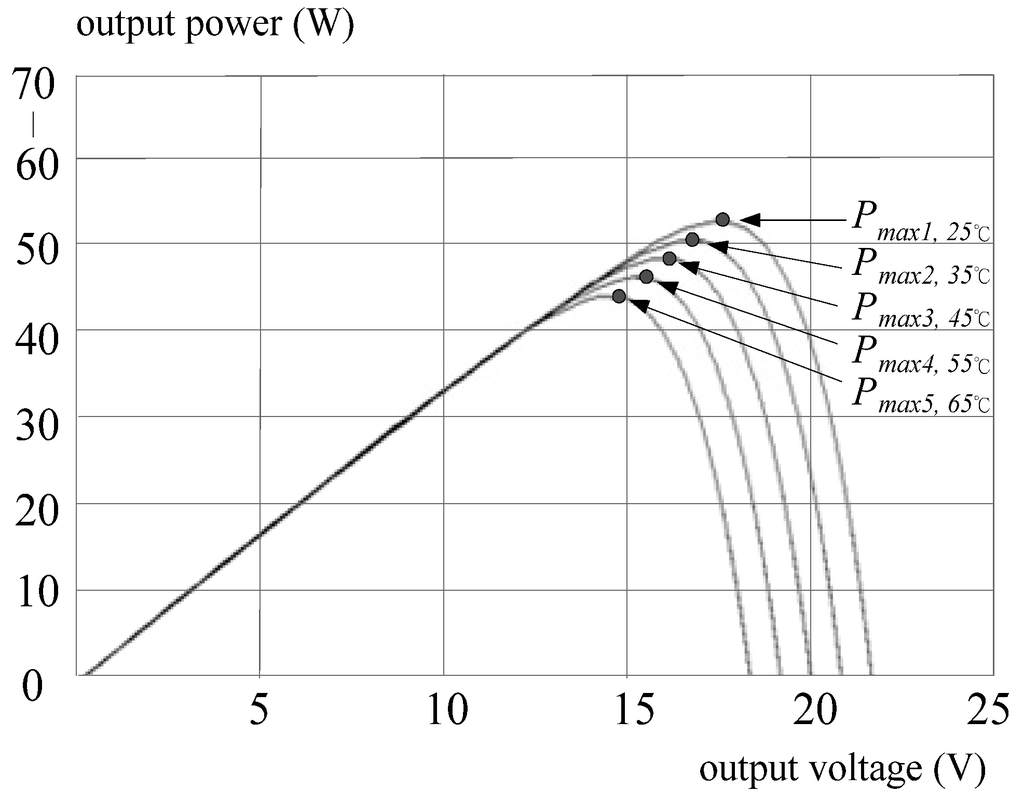
Figure 3.
PPV–VPV curves of the PV module with fixed irradiation (1000 W/m2).
From the above simulations, it is obvious that the two factors, array temperature T and irradiation Si, will affect the generated PV power significantly. To improve system efficiency, an MPPT algorithm has to be adopted to draw maximum power from PV arrays.
3. The Proposed MPPT Algorithm
From Figure 2 and Figure 3, we can find that a maximum power point locates at the point of which the derivative of PV output power with respect to terminal voltage equals zero. Therefore, from (3) and (4), the optimal PV terminal voltage Vref,MPPT to draw maximum power from PV arrays can be obtained:
Suppose that ns and np are one. Then, by substituting (5) into (4), the maximum power PMPPT is expressed as:
Figure 4 shows the relationship between PMPPT and Vref,MPPT under constant module temperature while irradiation varies from 200 to 1000 W/m2. In the case of fixed irradiation, the trajectory of PMPPT–Vref,MPPT with an increase of temperature from 25 to 65 °C is shown in Figure 5. Figure 4 and Figure 5 reveal that PMPPT is linear to Vref,MPPT approximately. In addition, based on Equation (4), the curves of Vref,MPPT–T and Vref,MPPT–Si are shown in Figure 6 and Figure 7, respectively, both of which can be approximated by straight lines. As a result, once a Vref,MPPT is obtained, the MPPT is achieved readily. A corresponding analog circuit to determine Vref,MPPT is designed and shown in Figure 8. We choose a photo-diode (PD) for irradiation sensing to realize the first linear approximation shown in Figure 7 while a negative temperature coefficient of thermal resistor (NTC) is adopted for temperature detecting to practice the second linear approximation shown in Figure 6. In the DLAA circuit, the potential Ei is proportional to the magnitude of irradiation and then, the first approximation is determined by:
To consider the influence of temperature, an MPPT voltage obtained by (7) has to be modified, which is approximated by the following second linear relationship. Thus, one can obtain a reference MPPT voltage:
Based on the simple analog circuit, an optimal voltage achieving MPPT feature can be easily obtained.
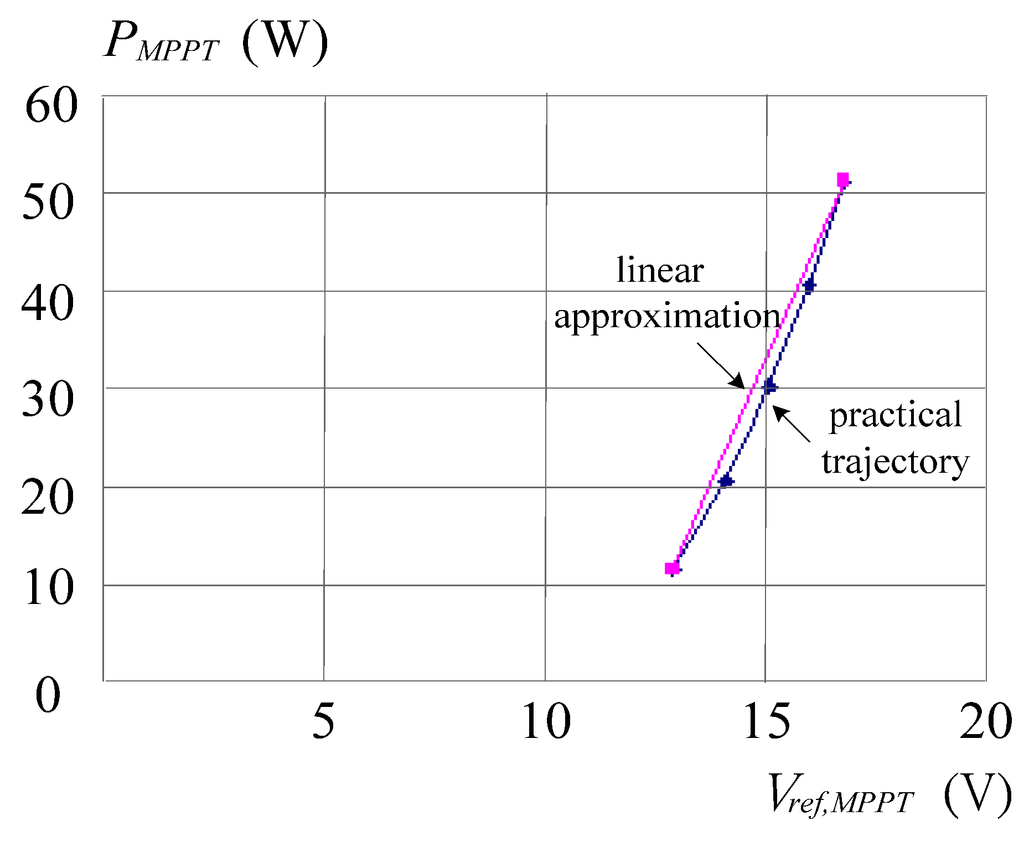
Figure 4.
The relationship between PMPPT and Vref,MPPT while irradiation increases from 200 to 1000 W/m2.
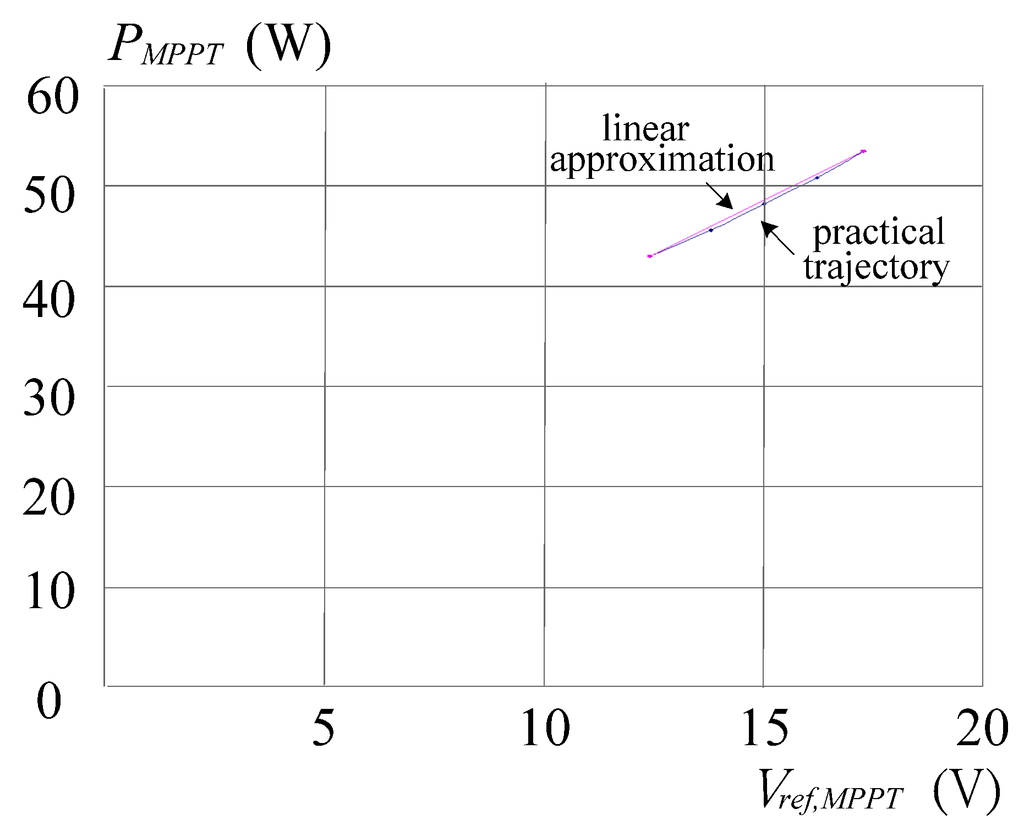
Figure 5.
The relationship between PMPPT and Vref,MPPT while module temperature increases from 25 to 65 °C.
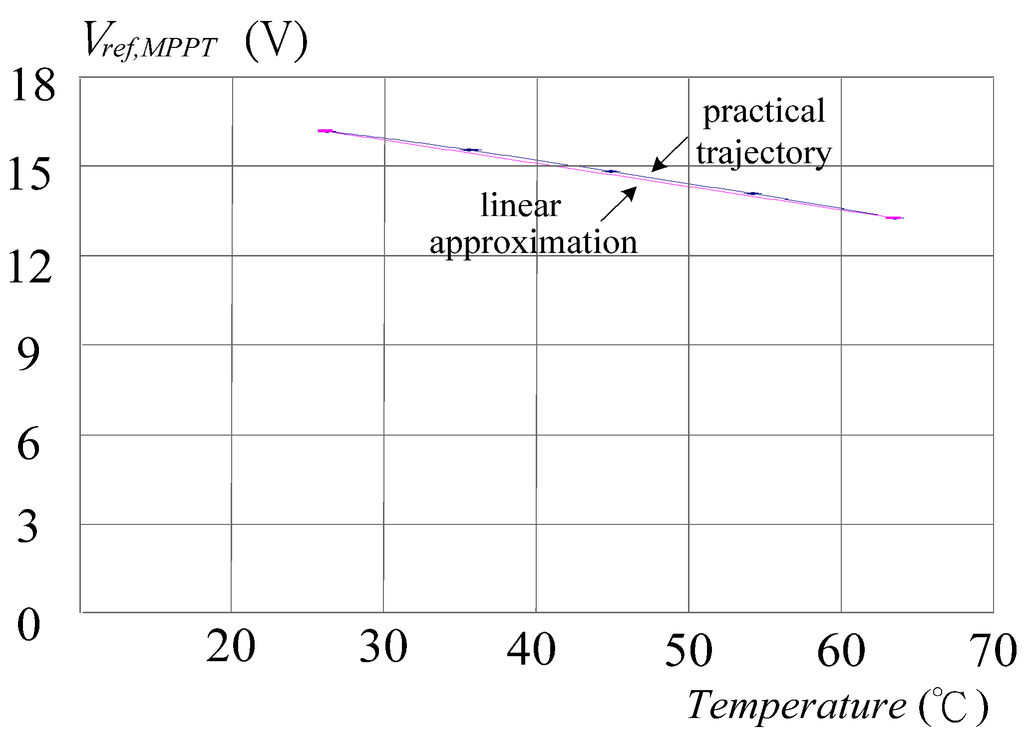
Figure 6.
The trajectory of Vref, MPPT versus temperature T.
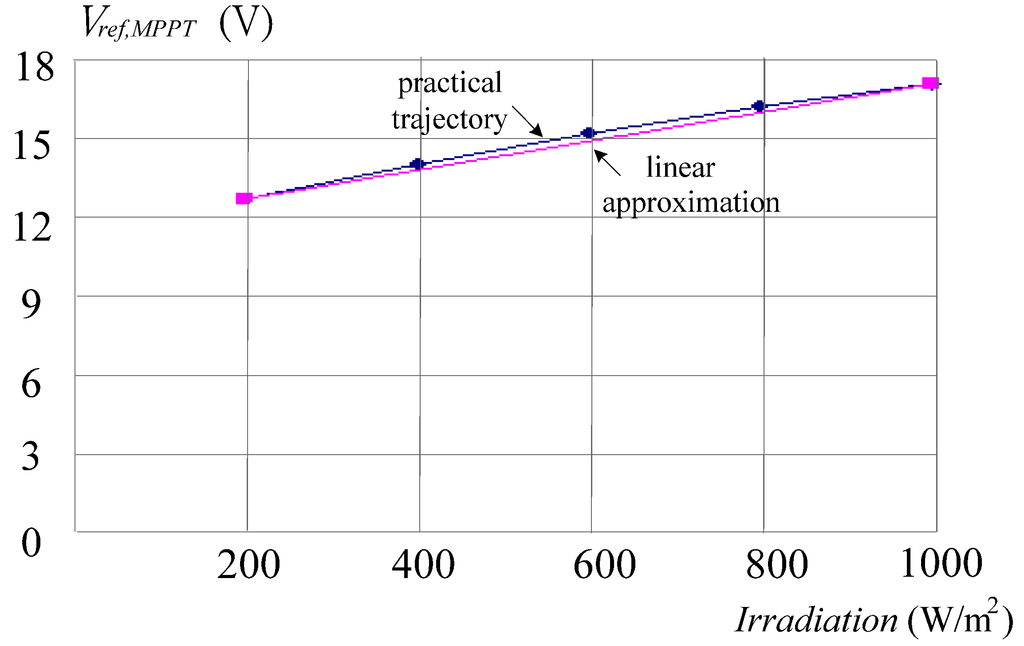
Figure 7.
The trajectory of Vref,MPPT versus irradiation Si.
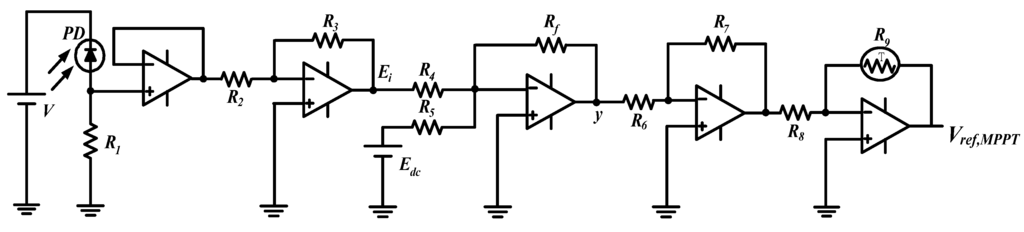
Figure 8.
The proposed DLAA circuit to determine a voltage command achieving MPPT with analog devices.
4. Implementation Example
To verify the proposed MPPT algorithm, a PV DC power supply system is constructed, as shown in Figure 9, which mainly contains PV arrays, a DLAA circuit, and a DC/DC buck converter. The power rating of the converter is 220 W, switching frequency 30 kHz, output voltage 36 V, PV voltage in the range of 45–70 V, and output voltage ripple less than 1%. The converter operates in continuous conduction mode (CCM) while processing power is over 55 W. The minimum inductance Lf,min are computed as:
in which the D denotes duty ratio, Vo is output voltage, Po stands for output power, and T expresses switching period. In addition, the minimum output capacitance Co,min is calculated from:
where L is the inductance of the converter and ΔVo represents the peak-to-peak ripple voltage at the output. Some important parameters of the system are listed as follows:
- PV arrays: SIEMENS SM55 (four units in series),
- Ci = 100 μF, Co = 100 μF,
- Lf = 0.2 mH,
- Kp = 0.0295,
- Ki = 0.0016,
- active power switch: IRF540N, and ultrafast diode: FRF1601CT.
In Figure 9, the DLAA circuit determines a reference voltage Vref,MPPT corresponding to an atmospheric condition. The PV output voltage is sensed and compared with the Vref,MPPT. Through the simple PI controller an appropriate control signal is generated to regulate the PV output voltage so that the DC/DC converter draws maximum power from PV arrays. Then, the DC/DC converter injects the power into DC bus for DC-distribution applications or into utility via a grid-connection DC/AC inverter.
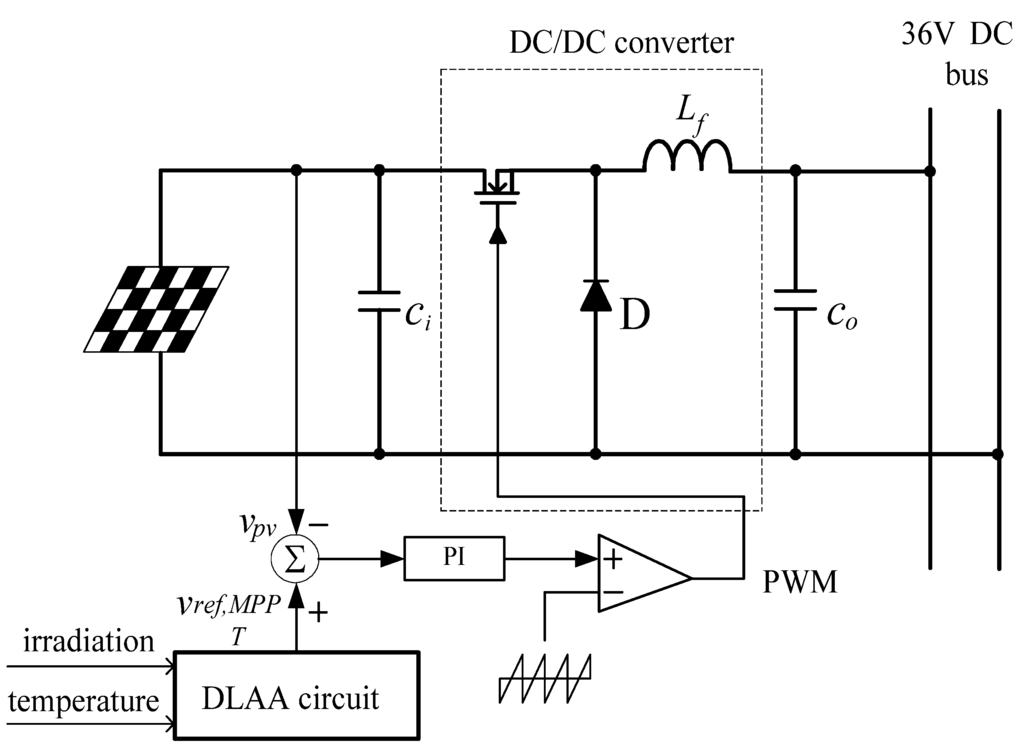
Figure 9.
Illustration of an implementation example which controls PV voltage to fulfill MPPT feature with the proposed DLAA circuit.
The MPPT efficiency is calculated by the ratio of the energy drawn by the converter within a defined measuring period TM to the energy provided by a PV simulator in the MPP. That is:
Theoretical MPPT efficiency of the proposed DLAA can reach 100%. The practical measurement of MPPT efficiency is around 99%.
5. Simulated and Experimental Results
The PV power system mentioned in Section 4 is simulated and implemented to demonstrate the effectiveness of the proposed approach. In simulation and implementation, both algorithms of the DLAA and the POM are adopted and embedded into the PV power system to fulfill MPPT. With fixed temperature Figure 10 and Figure 11 show the simulated MPPT trajectories by the POM and the DLAA, respectively, while Figure 12 and Figure 13 show the MPPT results under constant irradiation.
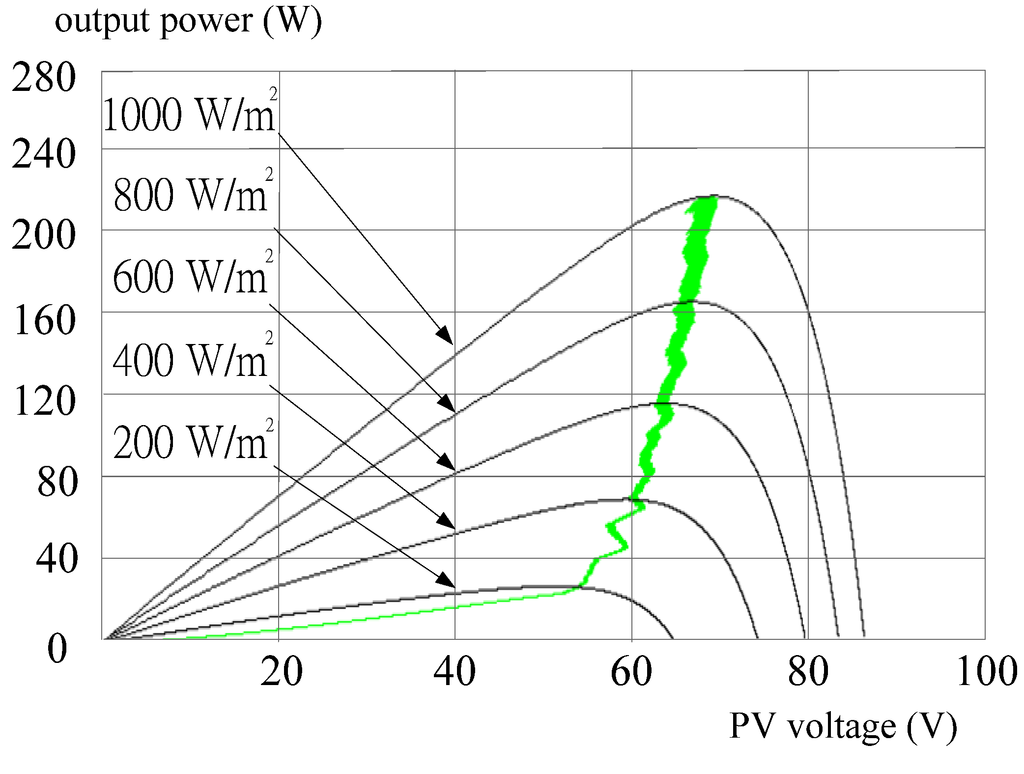
Figure 10.
The MPPT trajectory by the POM under fixed temperature.
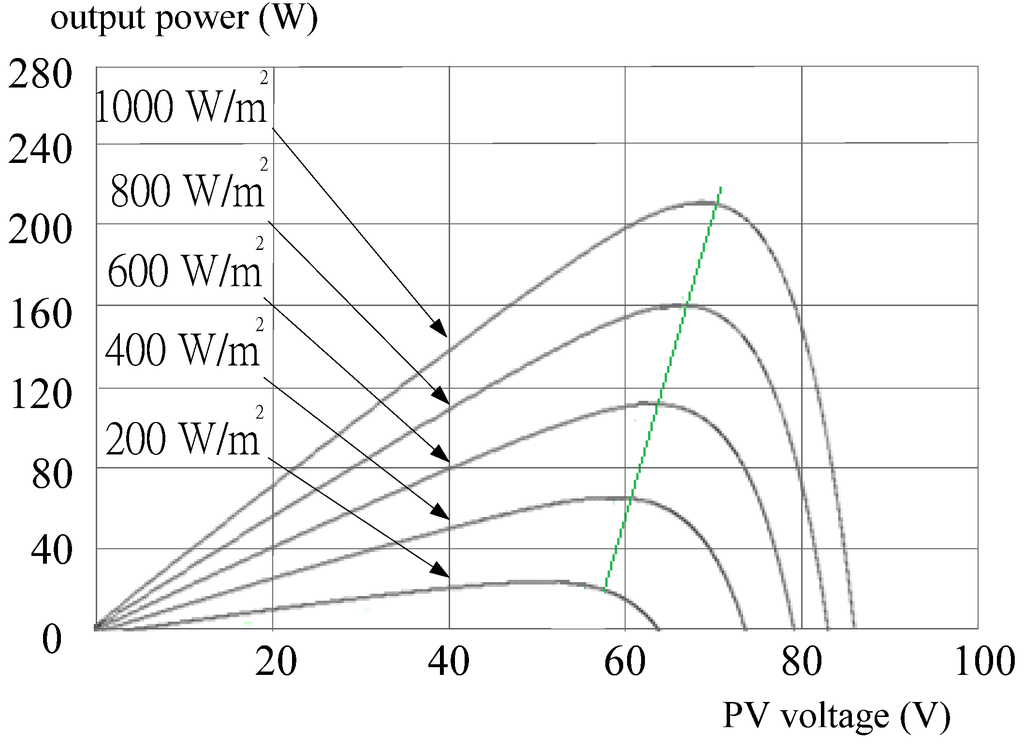
Figure 11.
The MPPT trajectory by the DLAA under fixed temperature.
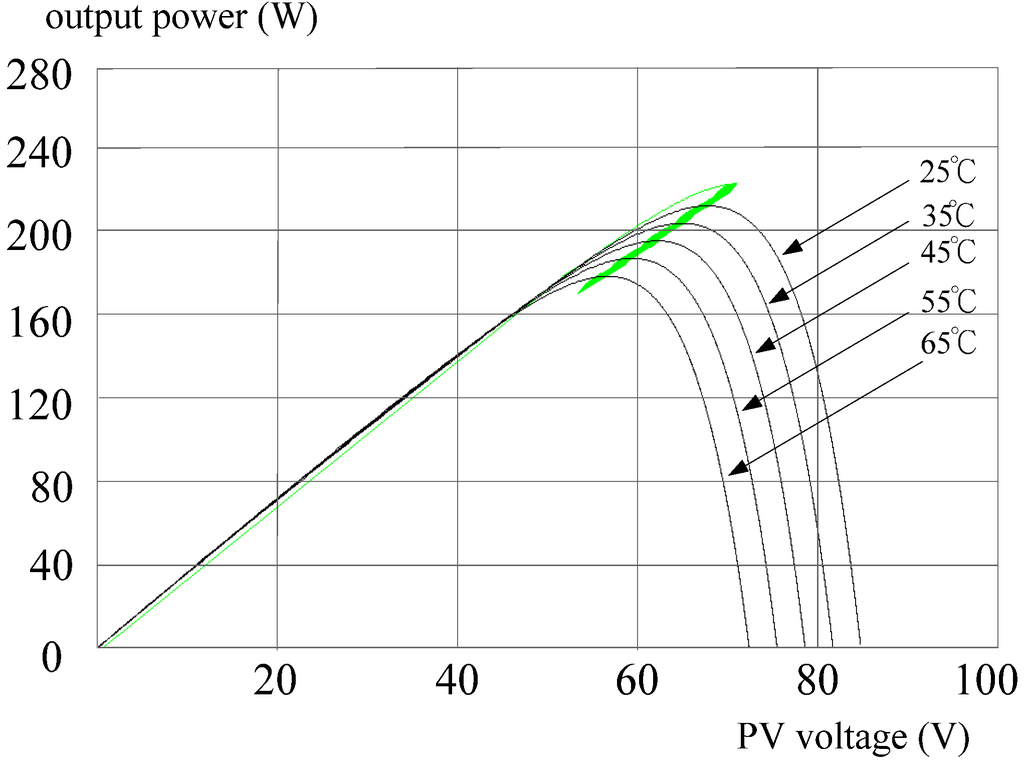
Figure 12.
The MPPT trajectory by the POM under constant irradiation.
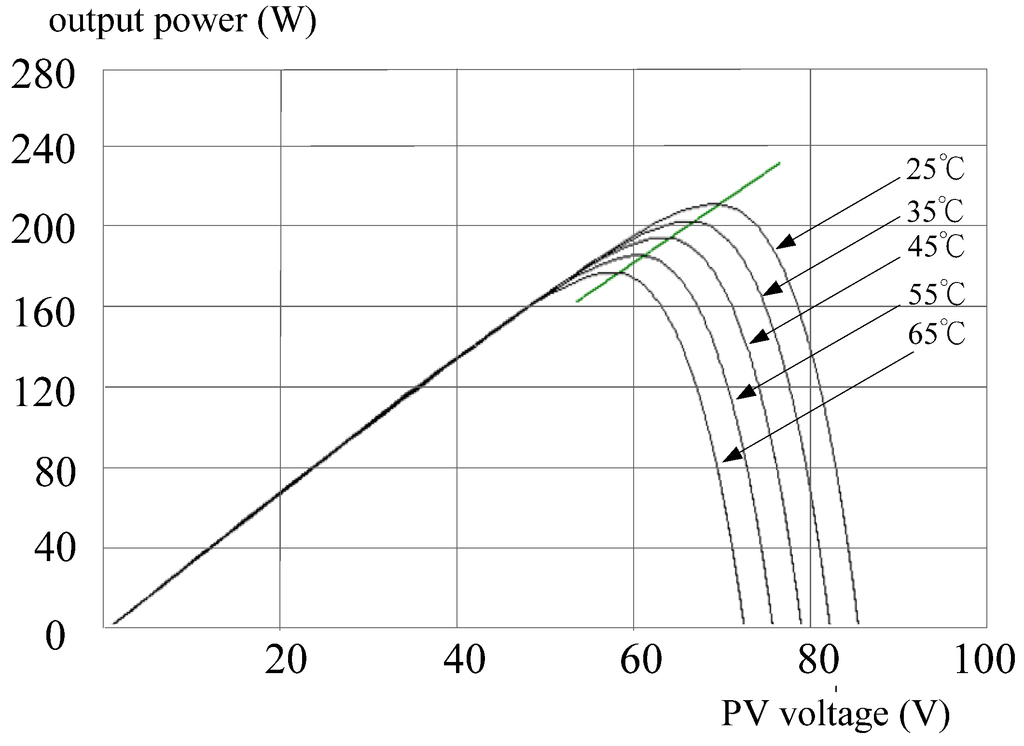
Figure 13.
MPPT trajectory by the DLAA under constant irradiation.
As irradiation and module temperature increase, the trajectories of MPPT by the POM and the DLAA are shown in Figure 14 and Figure 15, in turn.
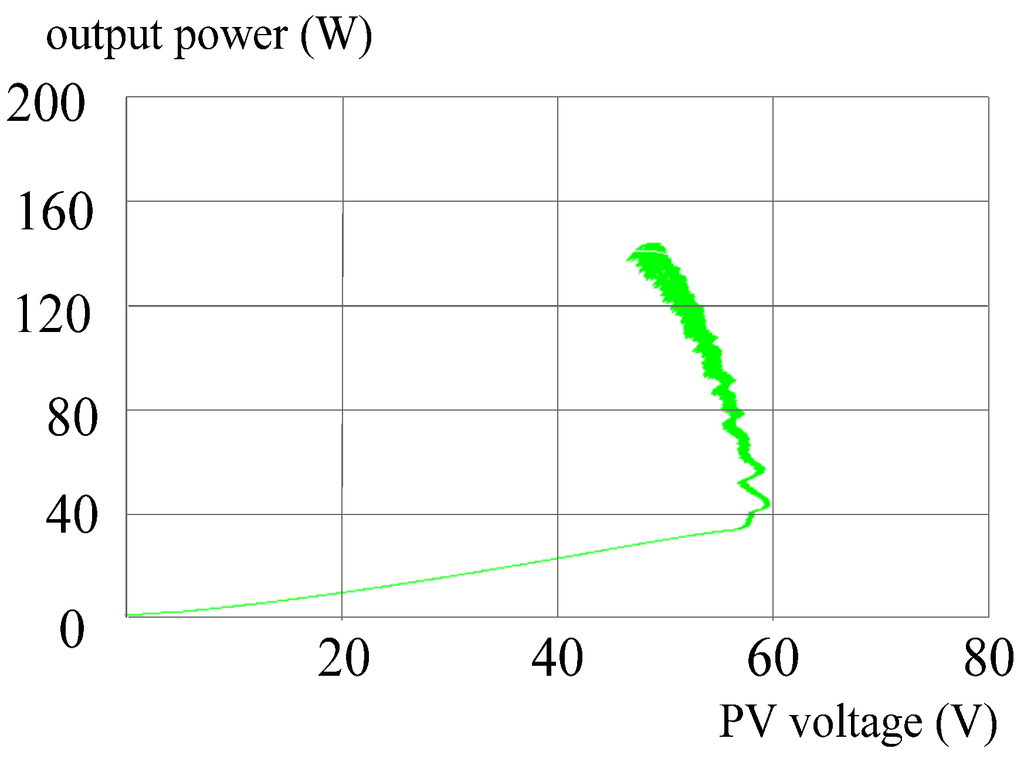
Figure 14.
MPPT trajectory by the POM while irradiation and temperature increase.
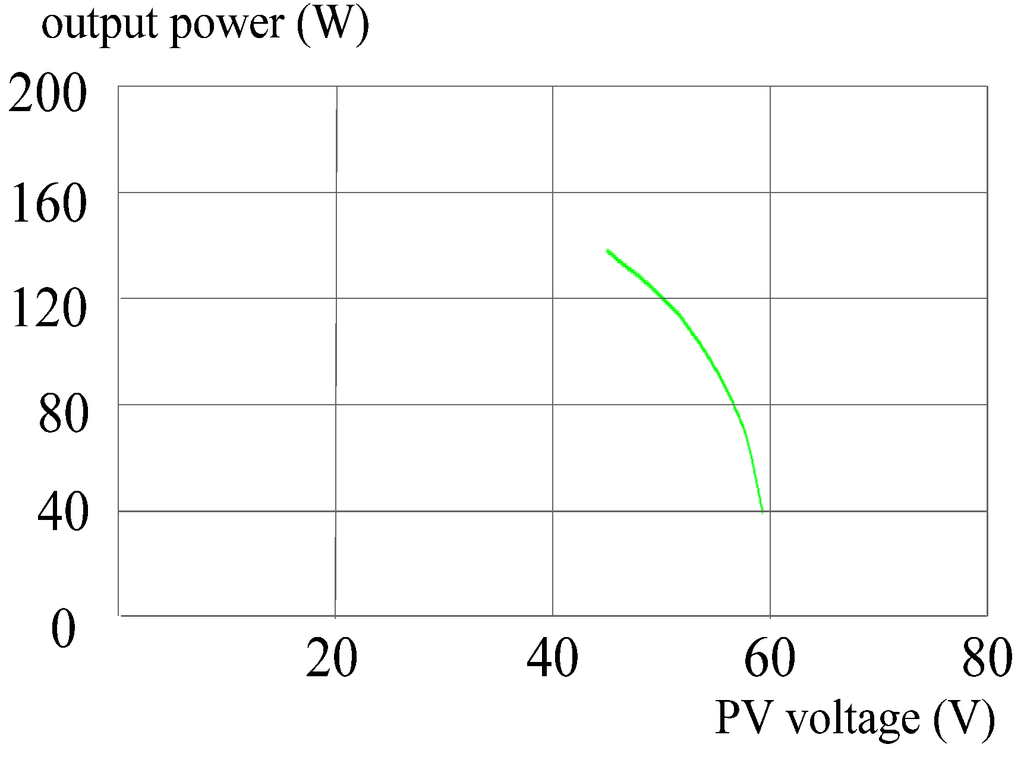
Figure 15.
MPPT trajectory by the DALL while irradiation and temperature increase.
In hardware measurements, Figure 16 is the practical result of the PV power system with the POM and Figure 17 shows MPPT trajectory by the DLAA under the variation of atmospheric condition. From Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16 and Figure 17, it is illustrated that the DLAA can trace MPP effectively and the proposed corresponding circuit is feasible. In addition, a DC/DC converter with the proposed algorithm can obtain better MPPT performance than that with the POM.
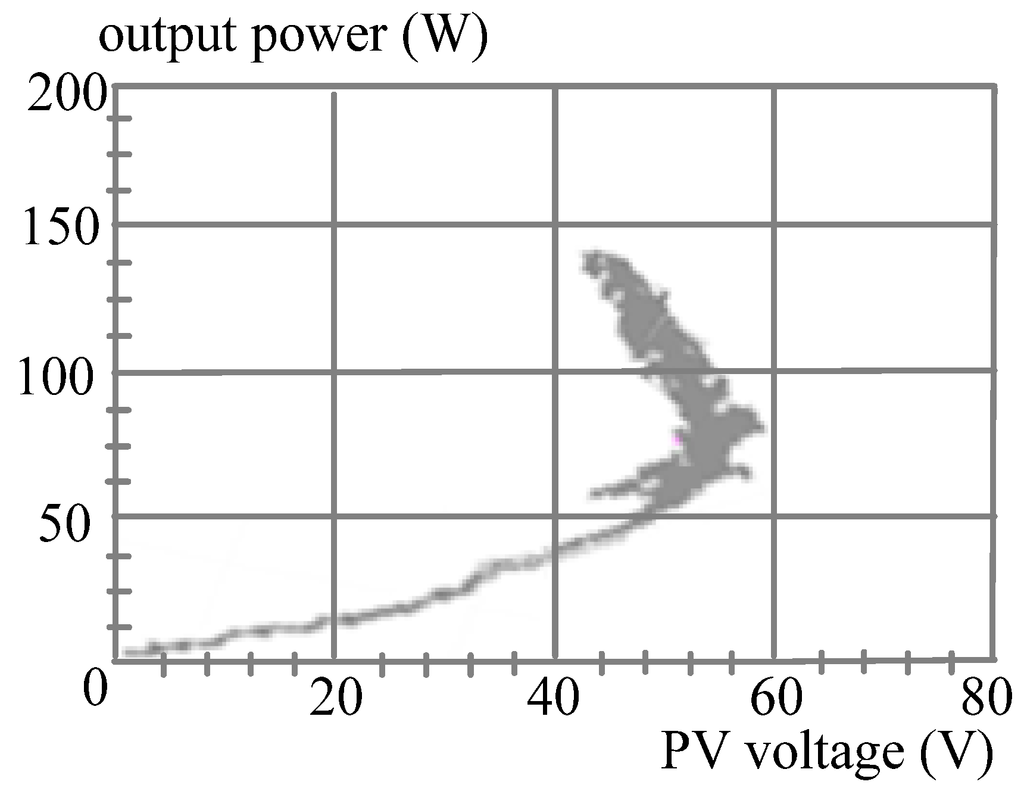
Figure 16.
Practical measurement of the PV power system with the POM.
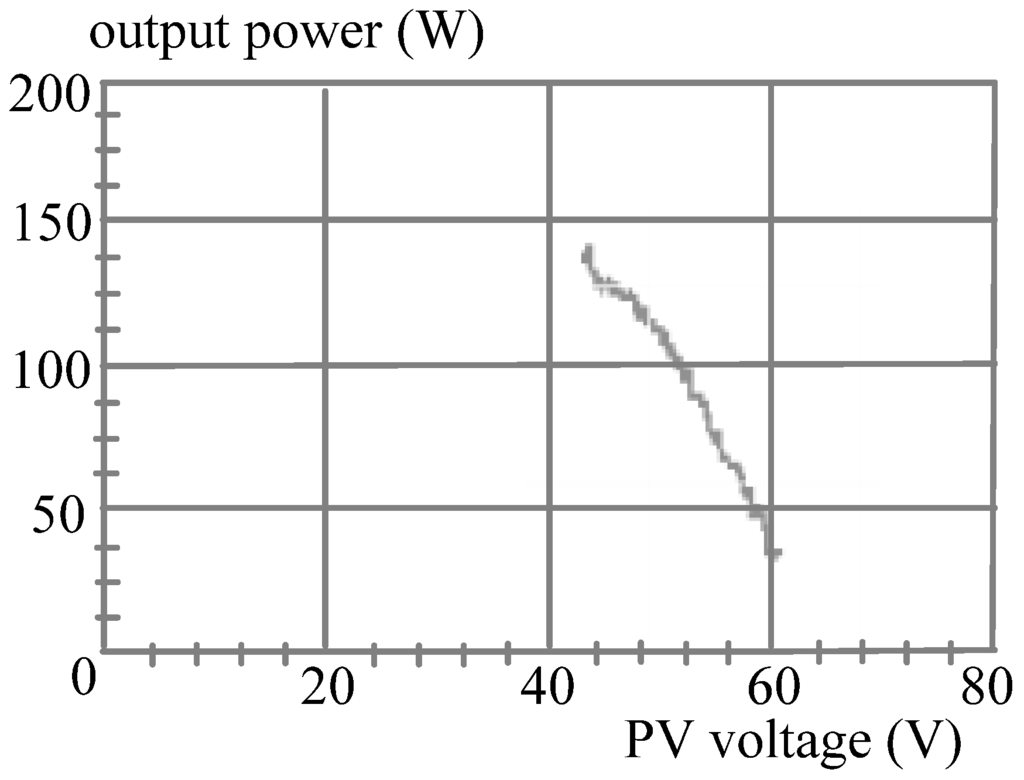
Figure 17.
Practical measurement of the PV power system with the DLAA.
For further comparison between the proposed DLAA and the POM, more simulated results and practical measurements are included in this paper. They are shown in the followings. Figure 18 shows the simulated power tracking trajectory of a PV converter with the POM while maximum PV power steps up from 100 W to 200 W. The power tracking trajectory with the proposed DLAA is shown in Figure 19. From Figure 18, it can be seen that the transition time is up to 4 s. On the other hand, the proposed DLAA catches up with the new PV power status in around 110 ms. Additionally, the proposed DLAA can effectively prevent operation point from fluctuating.
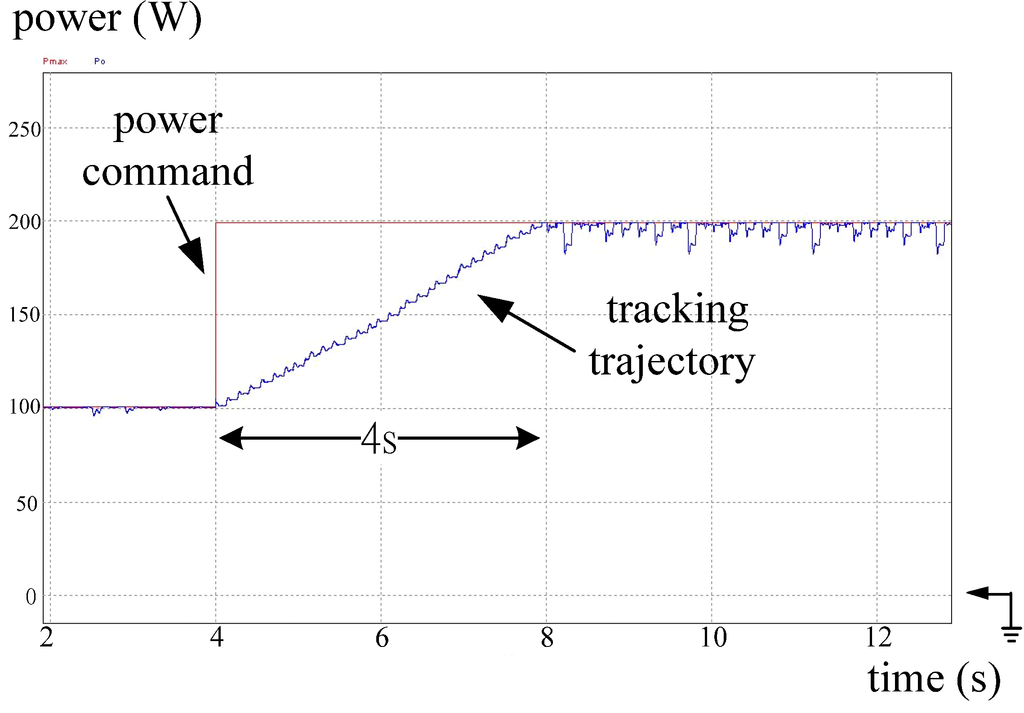
Figure 18.
Simulated result: tracking trajectory of the converter with the POM while PV power steps up from 100 to 200 W. Note: power: 50 W/div; time: 2 s/div.
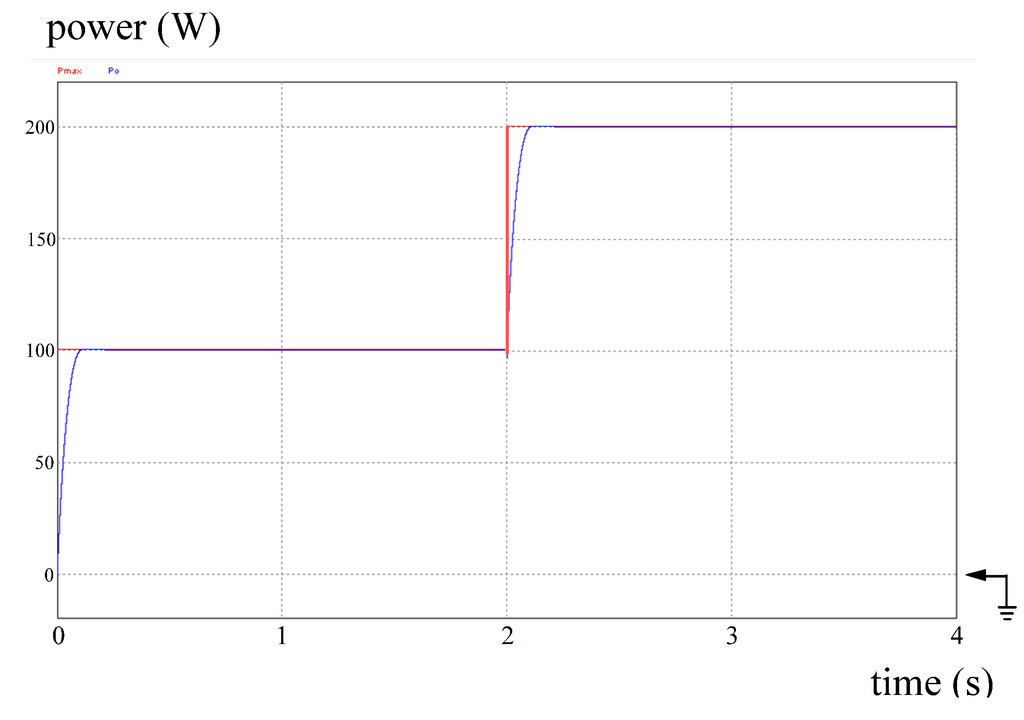
Figure 19.
Simulated result: tracking trajectory of the converter with the DLAA while PV power steps up from 100 to 200 W. Note: power: 50 W/div; time: 1 s/div.
To examine the step-down change, Figure 20 and Figure 21 show the simulated results of the PV converter with the POM and with the DLAA, respectively. The transition time is 6 s in Figure 20 and 50 ms in Figure 21. In hardware illustration, Figure 22 is the output power measurement of the converter with the POM in the case of the PV power changing from 100 W to 200 W while Figure 23 shows the measured result with the DLAA.
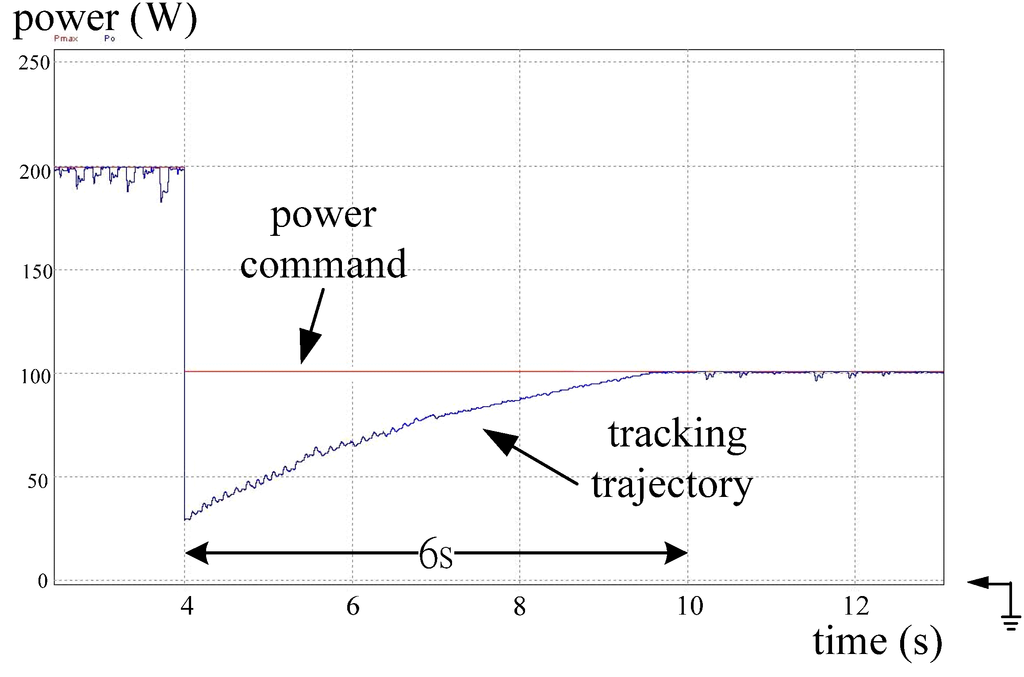
Figure 20.
Simulated result: tracking trajectory of the converter with the POM while PV power steps down from 200 to 100 W. Note: power: 50 W/div; time: 2 s/div.
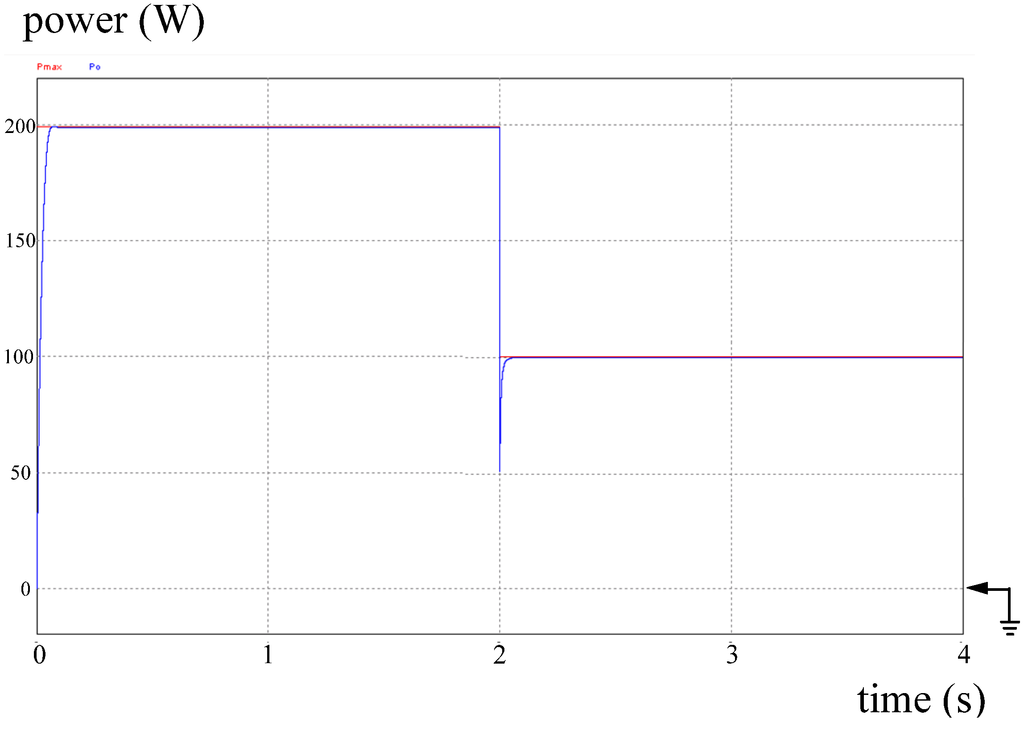
Figure 21.
Simulated result: tracking trajectory of the converter with the DLAA while PV power steps down from 200 to 100 W. Note: power: 50 W/div; time: 1 s/div.
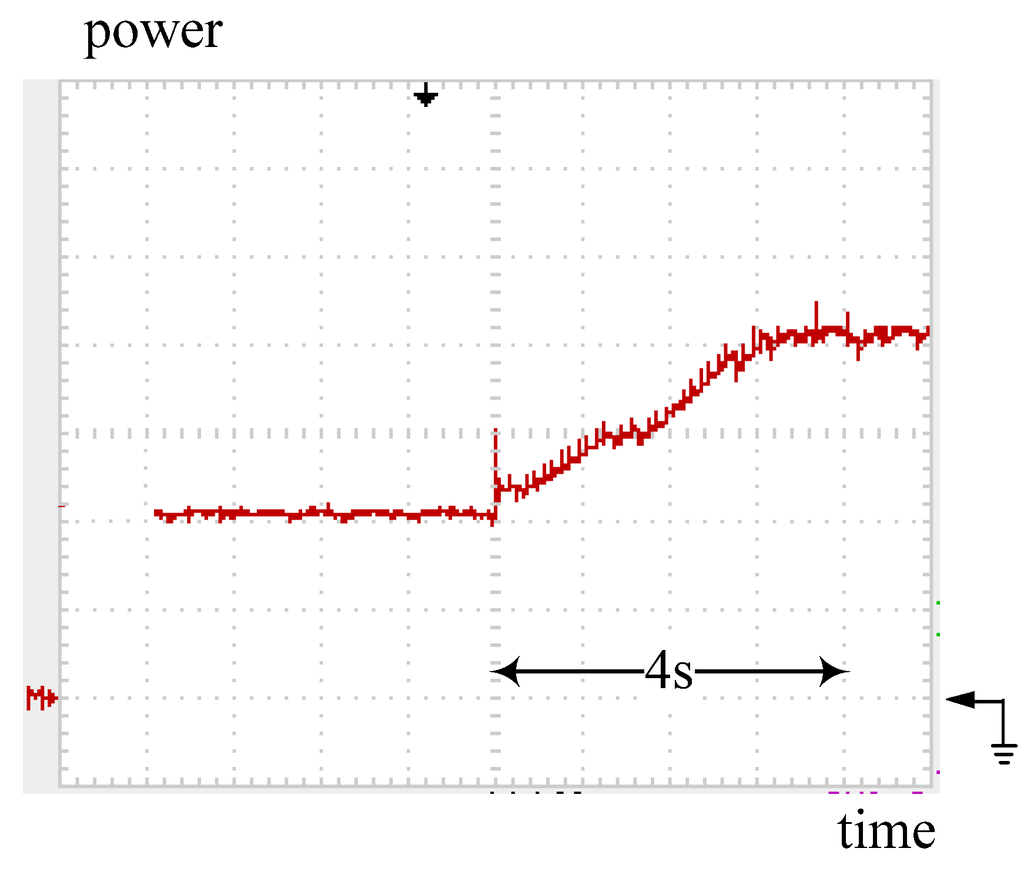
Figure 22.
Practical measurement: tracking trajectory of the converter with the POM while PV power steps up from 100 to 200 W. Note: power: 50 W/div; time: 1 s/div.
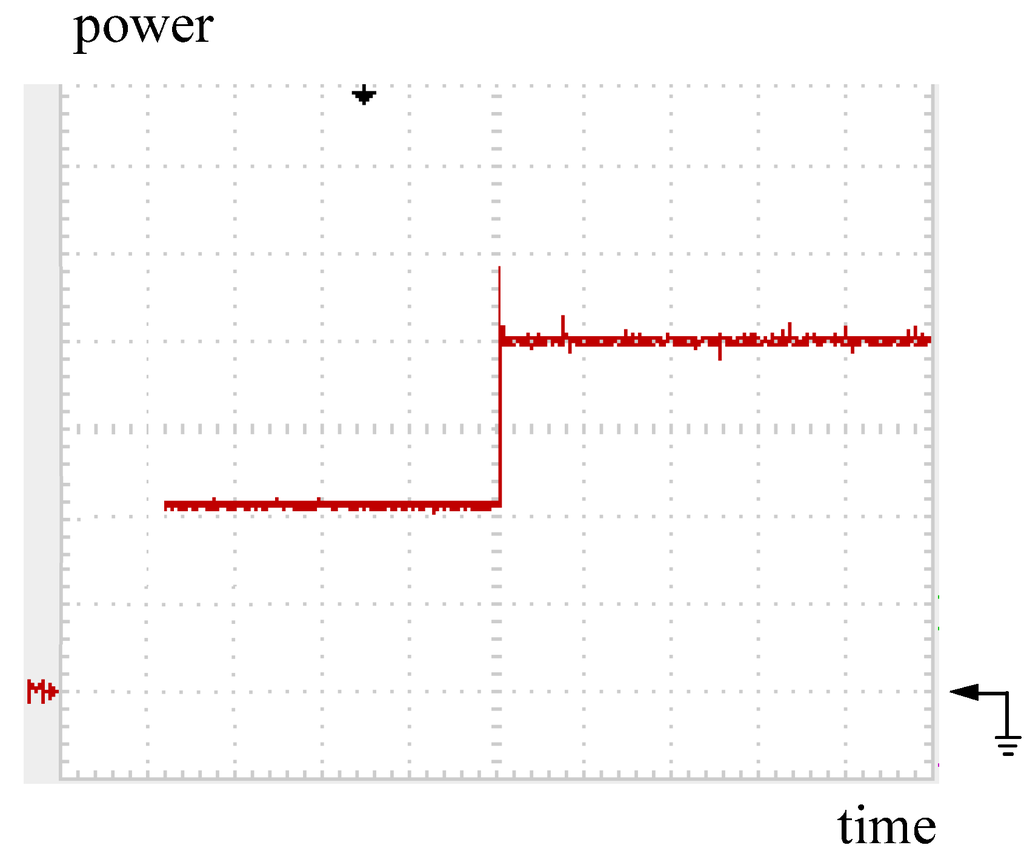
Figure 23.
Practical measurement: tracking trajectory of the converter with the DLAA while PV power steps up from 100 to 200 W. Note: power: 50 W/div; time: 0.5 s/div.
In addition, for 100-to-200 W step-down examination, practical measurements are presented in Figure 24 and Figure 25.
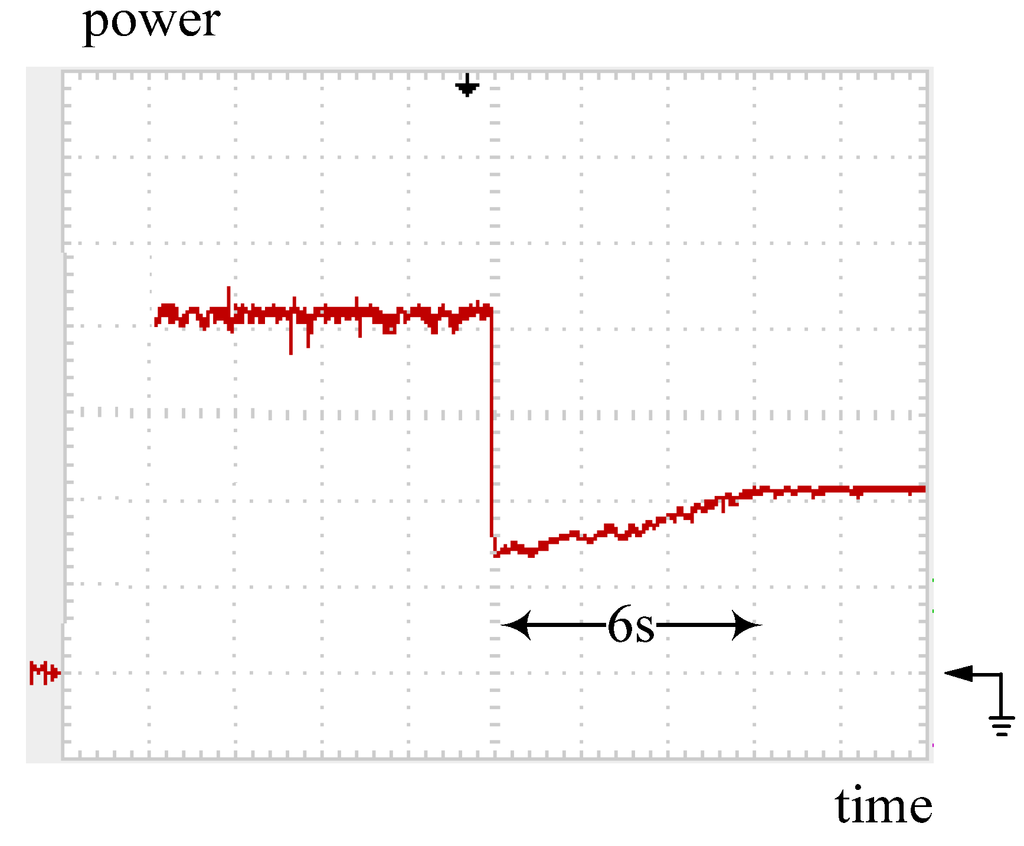
Figure 24.
Practical measurement: tracking trajectory of the converter with the POM while PV power steps down from 200 to 100 W. Note: power: 50 W/div; time: 2 s/div.
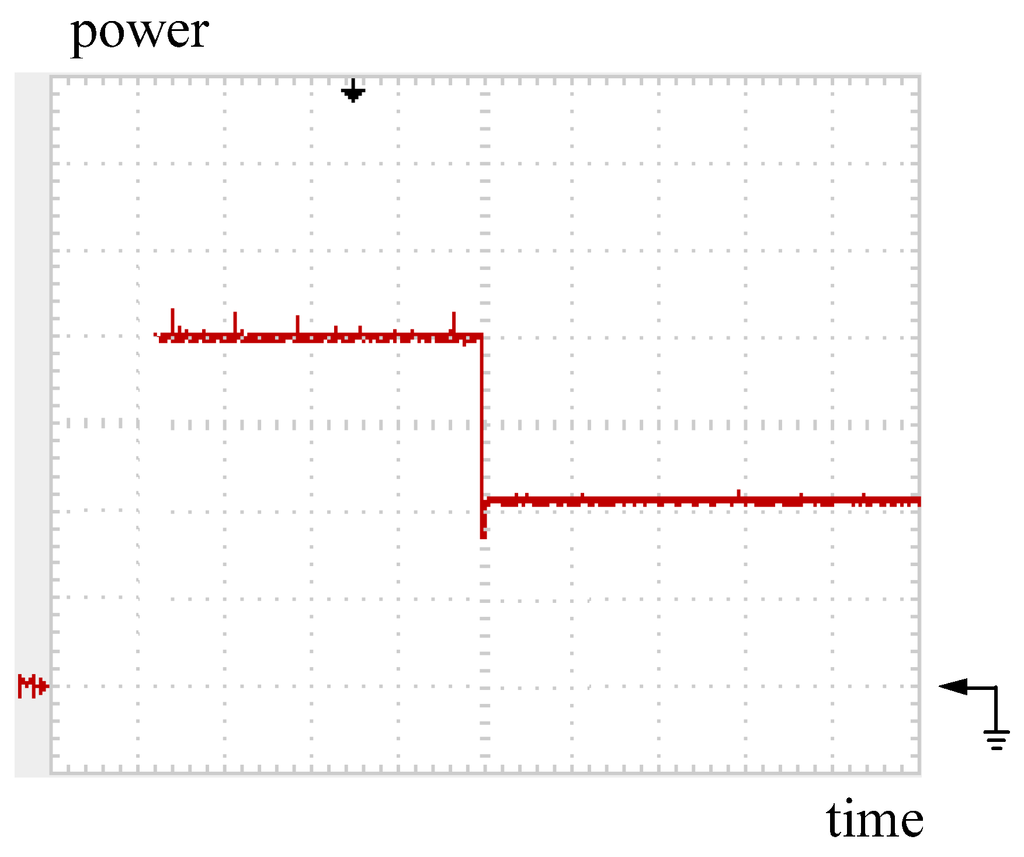
Figure 25.
Practical measurement: tracking trajectory of the converter with the DLAA while PV power steps down from 200 to 100 W. Note: power: 50 W/div; time: 0.5 s/div.
6. Conclusions
In this paper, an MPPT algorithm is proposed, which is based on the notion that an MPP voltage varies linearly with irradiation and temperature. To determine the MPP voltage, a corresponding analog circuit is also proposed. To verify the proposed algorithm and to illustrate the feasibility of the MPPT circuit, a PV power supply system embedding the MPPT circuit is simulated and implemented. Simulations and practical measurements have demonstrated that the proposed DLAA can trace maximum power point effectively and prevent an operation point from oscillating.
References
- Salameh, Z.; Dagher, F.; Lynch, W.A. Step-down maximum power point tracker for photovoltaic system. Sol. Energy 1991, 46, 278–282. [Google Scholar] [CrossRef]
- Harada, K; Zhao, G. Controlled power interface between solar cells and AC source. IEEE Trans. Power Electron. 1993, 8, 654–662. [Google Scholar] [CrossRef]
- Harashima, F; Inaba, H.; Kondo, S.; Takashima, N. Microprocessor-controlled SIT inverter for solar energy system. IEEE Trans. Ind. Electron 1987, IE-34, 50–55. [Google Scholar]
- Wasynezuk, O. Dynamic Behavior of a Class of Photovoltaic Power Systems. IEEE Trans. Power Appar. Syst. 1983, PAS-102, 3031–3037. [Google Scholar]
- Patcharaprakiti, N.; Premrudeepreechacharn, S. Maximum power point tracking using adaptive fuzzy logic control for grid-connected photovoltaic system. In Proceedings of the IEEE Power Engineering Society Winter Meeting, New York, NY, USA, 27–31 January 2002; pp. 372–377.
- Hua, C.C.; Lin, J.R.; Shen, C.M. Implementation of a DSP-controlled photovoltaic system with peak power tracking. IEEE Trans. Ind. Electron. 1998, 45, 99–107. [Google Scholar] [CrossRef]
- Salameh, Z.; Taylor, D. Step-up Maximum power point tracker for photovoltaic arrays. Sol. Energy 1990, 44, 57–61. [Google Scholar] [CrossRef]
- Kuo, Y.C.; Liang, T.J.; Chen, J.F. Novel Maximum-power-point-tracking controller for photovoltaic energy conversion system. IEEE Trans. Ind. Electron. 2001, 48, 594–601. [Google Scholar] [CrossRef]
- Liu, F.R.; Duan, S.X.; Liu, F.; Liu, B.Y.; Kang, Y. A variable step size INC MPPT method for PV Systems. IEEE Trans. Ind. Electron. 2008, 55, 2622–2628. [Google Scholar] [CrossRef]
- Wu, M.C.; Lin, K.J.; Lin, C.R. Analysis and research maximum power point tracking of photovoltaic array. In Proceedings of the International Conference on Computer Communication Control and Automation, Tainan, Taiwan, 5–7 May 2010; pp. 196–200.
- Hsiao, Y.T.; Chen, C.H. Maximum power tracking for photovoltaic power system. In Proceedings of the 2002 IEEE Industry Applications Conference: 37th IAS Annual Meeting, Pittsburgh, PA, USA, 13–18 October 2002; pp. 1035–1040.
- Pan, C.T.; Chen, J.Y.; Chu, C.P.; Huang, Y.S. A fast maximum power point tracker for photovoltaic power systems. In Proceedings of the 25th Annual Conference of the IEEE Industrial Electronics Society, San Jose, CA, USA, 29 November–3 December 1999; pp. 390–393.
- Lin, W.M.; Hong, C.M.; Chen, C.H. Neural-network-based MPPT control of a stand-alone hybrid power generation system. IEEE Trans. Power Electron. 2011, 26, 3571–3581. [Google Scholar]
- Ahmed, K.H.; Finney, S.J.; Williams, B.W. Fuzzy-logic-control approach of a modified hill-climbing method for maximum power point in microgrid standalone photovoltaic system. IEEE Trans. Power Electron. 2011, 26, 1022–1030. [Google Scholar]
- Chiu, C.S. T-S fuzzy maximum power point tracking control of solar power generation systems. IEEE Trans. Energy Convers. 2010, 25, 1123–1132. [Google Scholar] [CrossRef]
- Hussein, K.H.; Muta, I.; Hoshino, T.; Osakada, M. Maximum photovoltaic power tracking: An algorithm for rapidly changing atmospheric conditions. IEE Proc. Gener. Transm. Distrib. 1995, 142, 59–64. [Google Scholar] [CrossRef]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).