The authors wish to make the following corrections to this paper [1]. A modification to the list of authors, contribution section, text, table, figure and references as follows:
List of Authors
Haitao Liu 1,2, Sen Wang 2, Liang Hu 2, Ling Feng 2,* and Yue Wang 2
Author Contributions: Methodology, H.L. and L.F.; software, H.L.; validation, S.W. and L.H.; formal analysis, S.W., L.H. and Y.W.; data curation, L.F.; supervision, Y.W. All authors have read and agreed to the published version of the manuscript.
Text Correction
(1) There was a mistake in the original publication. The mistake lies in the incorrect description of the redundant zero voltage vector in the ANPC.
A correction has been made to the third paragraph of Section 2 (Mathematical Model and Synchronous SVPWM):
In the ANPC three-level topology, each phase bridge arm consists of six power devices, theoretically allowing for 64 possible switching states per phase. However, to ensure the safe operation of the inverter, certain switching combinations must be avoided. Specifically, configurations that result in half-bus or full-bus conduction pose a significant risk, as they can lead to short-circuit conditions or expose devices to voltages exceeding their rated limits. To mitigate these risks, only six permissible switching state combinations are used. For an output voltage of zero, six distinct switching states are available: OU1, OU2, OL1, and OL2. The conduction status of the power devices corresponding to each switching state is detailed in Table 1. These selected states ensure safe and reliable inverter operation while maintaining the necessary output voltage characteristics.
(2) There was a mistake in the original publication. The mistake lies in wrongly expounding the converter mode of ANPC.
A correction has been made to the second to fourth paragraphs of Section 3 (Proposed Active Thermal Control Method):
In Operation Mode I, switching occurs between vectors P1 and OL1 during the positive half-cycle and between vectors N1 and OU2 during the negative half-cycle. In this mode, switches Sx5 (x = a, b, c) and Sx6 operate at a high switching frequency, while switches Sx1, Sx2, Sx3, and Sx4 operate at a lower frequency. As a result, the primary switching losses are concentrated on Sx5 and Sx6.
In Operation Mode II, switching occurs between vectors P and OU2 during the positive half-cycle and between vectors N and OL2 during the negative half-cycle. This configuration ensures that current commutation takes place within a single module, reducing the impact of stray currents. In this mode, switches Sx5 and Sx6 operate at the fundamental frequency, while the remaining switches operate at a higher frequency. Notably, switches Sx2 and Sx3 are switched at a higher frequency than Sx1 and Sx4, which helps to balance the losses across the six switching devices in each phase.
In Operation Mode III, switching occurs between vectors P1 and OU1 during the positive half-cycle and between N1 and OL1 during the negative half-cycle. In this mode, the majority of the commutation losses are concentrated within the high-frequency unit modules Sx1, Sx2, Sx3, and Sx4. Meanwhile, switches Sx5 and Sx6 operate at the industrial frequency only during voltage commutation, effectively avoiding current commutation between different unit modules. This reduces the detrimental effects of parasitic inductance on switching speed. The theoretical loss distribution for this commutation path is more balanced, resulting in improved thermal characteristics compared to the larger commutation loops found in other modes.
Error in Table
In the original publication [1], there is an error in the published Table 1. There is an error of a duplicate definition in the current list of switch states. The corrected Table 1 is as follows:

Table 1.
Switching states of 3L-ANPC Inverters.
Table 1.
Switching states of 3L-ANPC Inverters.
| States | Sx1 | Sx2 | Sx3 | Sx4 | Sx5 | Sx6 | Sx | vxo |
|---|---|---|---|---|---|---|---|---|
| P | 1 | 0 | 1 | 1 | 1 | 0 | 1 | +Vdc/2 |
| P1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | +Vdc/2 |
| OU1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 |
| OU2 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 |
| OL1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 |
| OL2 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 |
| N1 | 1 | 0 | 1 | 1 | 0 | 1 | −1 | −Vdc/2 |
| N | 0 | 1 | 0 | 1 | 1 | 0 | −1 | −Vdc/2 |
0 and 1 represent the closed and open states of the switching transistor, respectively.
Error in Figure 14
In the original publication [1], there was a mistake in Figure 14 as published. A lower-power experiment result is incorrect, instead the traction converter should be used. The corrected Figure 14 and the description has been updated as below.
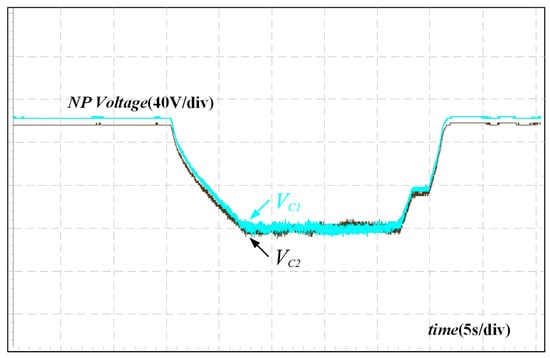
Figure 14.
NP voltage waveform.
The NP voltage control experiments presented in Figure 14 further validate the control performance of the proposed loss equalization strategy. This indicates that the introduction of junction temperature equalization constraints does not interfere with the balancing of the NP voltage. Furthermore, the NP voltage can be well-balanced under full speed conditions.
Newly Added References
The authors realized that several important recently published studies need to be supplemented to further improve the diversity supporting the circulation pathways. These newly added studies are highly relevant to this research, which can more comprehensively reflect the latest progress in the field and enhance the academic rigor of the paper.
Two newly cited references were added on fourth paragraph of Section 2 (Mathematical Model and Synchronous SVPWM):
As illustrated in Figure 2, the synchronous space vector pulse-width modulation (SVPWM) method partitions the space vector plane into six sectors (I–VI), and each sector is divided into six smaller sectors (1–6). To ensure symmetry in the output voltage waveforms, the reference vectors are uniformly distributed within each sector. The distribution of reference vectors in Sector I is depicted in Figure 3 [27,28]. In this scheme, N represents the total number of reference vectors within each sector. When N is odd, the n-th reference vector aligns with the boundary between adjacent sectors, while the remaining reference vectors are positioned entirely within the sector. Conversely, when NNN is even, all reference vectors are confined within the sector. The angular spacing between consecutive reference vectors is consistently maintained at π/(3N), ensuring uniform modulation and high-quality output voltage.
The newly added references appear below:
- 27.
- Novak, M.; Šunde, V.; Čobanov, N.; Jakopović, Ž. Semiconductor loss distribution evaluation for three level ANPC converter using different modulation strategies. In Proceedings of the 19th International Conference on Electrical Drives and Power Electronics (EDPE), Dubrovnik, Croatia, 4–6 October 2017; pp. 170–177.
- 28.
- Wang, Z.; Yang, S.; Feng, L.; Li, Z.; Feng, J. An Optimized Model Predictive Control Method for Hybrid ANPC with Fixed Switching Frequency. IEEE J. Emerg. Sel. Topics. Power Electron. 2025, 13, 2246–2257.
The authors state that the scientific conclusions are unaffected. This correction was approved by the Academic Editor. The original publication has also been updated.
Reference
- Liu, H.; Wang, S.; Hu, L.; Feng, L.; Wang, Y. Junction Temperature Control of a Traction Inverter Based on Three-Level Active Neutral Point-Clamping. Energies 2025, 18, 2241. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license.