Abstract
The rapid development of machine drive systems is closely tied to advancements in signal sampling technology. Accurate measurement results, especially current measurement results, are crucial for high-performance machine drive systems. However, current measurement errors (CME) caused by circuit parameter inconsistencies, aging, and temperature variations can significantly affect the control performance of drive systems, thus necessitating compensation. To better understand the mechanisms of CME in drive systems, this paper reviews existing research on CME analysis and compensation techniques. Based on the source of CME, this paper classifies CME into high-frequency and low-frequency components and discusses their causes and compensation methods, respectively. Additionally, the influence of different types of CME on other control strategies, such as sensorless and model predictive control, is discussed. The characteristics of CME compensation strategies for special current sensor installation positions are also explored. Finally, the paper summarizes the state of the art in CME analysis and compensation and discusses future trends in this field.
1. Introduction
Due to the widespread development of various permanent magnet materials, permanent magnet synchronous machines (PMSM) have received increasing attention in research. Their significant advantages, such as simple structure, high power density, and high efficiency, have led to unprecedented applications in fields such as ship propulsion [1], electric vehicles [2], rail transportation [3], and wind turbines [4]. To meet the diverse demands of various applications, a wide range of PMSMs has been developed, including multi-phase [5], linear [6], and open-winding structures [7]. Meanwhile, diverse control strategies, such as sensorless control [8], model predictive control [9], and direct torque control [10], have been extensively developed.
Regardless of the control strategy used, precise feedback data sampling is essential. In a typical PMSM drive system, rotor position and phase current are the necessary feedback signals for achieving the desired control performance. The rotor position can be indirectly observed through phase current, enabling sensorless algorithms. Therefore, the precise measurement of phase currents is critical for high-performance motor control.
However, due to the existence of non-ideal factors in the current sampling paths, such as device aging, temperature drift, etc., current measurement error (CME) is inevitable [11]. CME refers to the deviation of the sampled current result from the actual values. The presence of CME affects the accuracy of current controllers, which in turn leads to various issues, such as electromagnetic torque pulsation, current ripple, and mechanical vibration. These undesired problems severely threaten the reliable and stable operation of PMSM. Hence, extensive studies have been conducted to clarify the causes, effects, and compensation methods of CME.
This paper reviews previous studies on CME. It should be noted that this paper only focuses on the influence and compensation of low- and high-frequency current harmonic disturbances in the entire current sampling path of the machine drive system. The analysis and improvement of current sensor performance are outside the scope of this paper. Different types of CME have varying effects in different topologies, and the compensation methods also differ. Finally, this article presents future development trends of the studies related to CME, including the influence of CME in different topologies, compensation methods for different types of CME, the interaction of CME with other control algorithms, and current sensor fault diagnosis methods.
The remaining parts of this article are arranged as shown in Figure 1: Section II analyzes the causes of CME and its impact on different drive systems. Section III classifies CME and reviews compensation methods for different types of CME. Section IV reviews the research conducted in the abovementioned areas and provides future trends related to CME. Finally, Section V concludes the article.
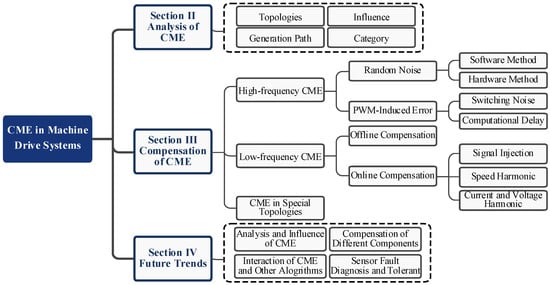
Figure 1.
Arrangements for the subsequent sections of this paper.
2. Analysis of Current Measurement Error
Commonly utilized current sensors include sampling resistors [12], open-loop or closed-loop Hall sensors [13], fluxgate sensors [14], Rogowski coils [15], Giant Magneto Resistive (GMR) sensors [16], and current transformers [17]. Table 1 summarizes the performance characteristics of seven typical current sensors. These sensors exhibit notable variations in bandwidth, accuracy, size, cost, and power loss [17,18,19]. Table 1 provides different types of current sensors and their main parameters in [20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43]. When selecting current sensors, it is essential to consider the specific requirements of different applications, such as temperature tolerance, accuracy, bandwidth, and measurement range. For machine drive systems, shunt resistance (sampling resistance) and Hall sensors are among the most commonly used types.

Table 1.
Performance comparison of typical current sensors.
Figure 2 shows a schematic diagram of the entire current sampling path, where the Hall sensor and sampling resistance are utilized for current sampling. The feedback signal from the sensor first passes through a low-pass filter circuit to eliminate high-frequency interference and noise. The filtered signal is then amplified by a differential operational amplifier circuit to convert the feedback signal range into the desired level range, for example, converting ±5 V to 0–3.3 V. The conditioned signal is then converted into a digital signal by the A/D conversion circuit. Finally, the digital signal is sent to the Digital Signal Processor (DSP) for closed-loop control [44].
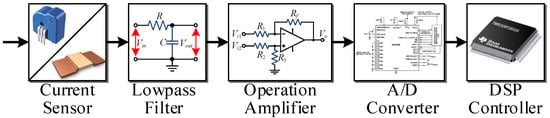
Figure 2.
Schematic diagram of the current sampling path.
It should be noted that the CME discussed in this paper refers not only to the “current measurement error” resulting from the degradation of current sensor performance but also to the cumulative errors arising from the sensor, filtering circuits, operational amplifier circuits, and analog-to-digital (AD) conversion in the overall sampling path shown in Figure 2. Rather than focusing on the specific stages where errors occur, this paper concentrates on the practical influence of the sampling error, specifically the frequency characteristics of the additional disturbance signals. On this basis, this paper explores compensation methods for different types of disturbance signals. According to their harmonic characteristics, these errors can be classified into the following categories:
(1) High-frequency random error: Due to the resolution limitations of the A/D conversion circuit, the analog signals are quantized into 2n digital signals, where n represents the resolution of the A/D conversion circuit. Additionally, the sampled results also involve measurement noise caused by environmental disturbances. Both quantization errors and measurement noise lead to high-frequency random errors in the measurement results [45].
(2) High-frequency PWM-induced error: Due to non-ideal factors such as EMI interference, current oscillation during the device commutation process, sampling, and PWM delay, the measured results may deviate from the average current value within one switching period. This deviation leads to a PWM-induced error between the sampled and desired data, which threatens the current control performance and the stable operation of current controllers [46].
(3) Low-frequency offset error: Due to the deviation of the resistance or other parameters from the pre-designed values in each phase conditioning circuit, a constant or slowly varying low-frequency offset error exists between the measured and desired data. For example, if the expected measured voltage range is 0–3.3 V, the actual measured voltage range could be 0.1–3.4 V [47].
(4) Low-frequency gain error: Due to parameter deviations in the conditioning circuit, the amplification factor in each phase may differ from the pre-designed slope, which leads to low-frequency gain error. For example, if the expected measured voltage slope is 0.1 V/A, the actual measured slope could be 0.09 V/A [48].
Figure 3 shows schematics of different types of CME. Figure 3a,b represent high-frequency random errors and one kind of PWM-induced error, respectively. The current harmonics generated by these high-frequency errors are typically distributed around the switching frequency. Figure 3c,d represent current measurement offset errors (CMOE) and current measurement gain errors (CMGE), respectively. The current harmonics generated by these low-frequency errors are typically DC or at the fundamental frequency. High-frequency errors cause the measured result to deviate from the average current value within this switching period, affecting the stable operation of current controllers [49]. According to the findings of [49], at a switching period of Ts, a one-cycle delay error results in a phase margin reduction of 2πfcTs, where fc denotes the cutoff frequency. However, low-frequency CMGE and CMOE generate additional torque ripples at the fundamental frequency and twice that frequency, resulting in additional loss and vibration [50]. According to reference [44], the typical sources of errors in electric powertrain systems are summarized, highlighting that CMEs can cause problems such as speed fluctuation, torque ripple, phase current mismatch, and additional losses.
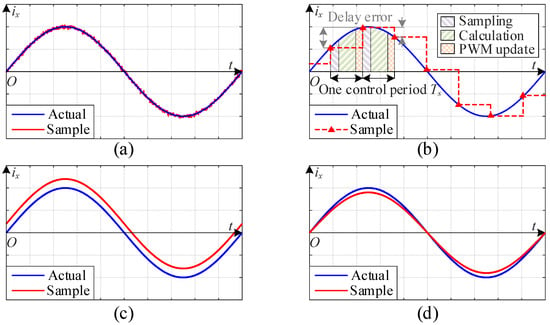
Figure 3.
Schematic diagram of different current sampling errors. (a) High-frequency random error. (b) High frequency PWM-induced error caused by PWM delay. (c) Low-frequency offset error. (d) Low-frequency gain error.
Additionally, the influence of CME on the drive system depends on the sensor installation position. Figure 4 shows several installation positions for current sensors. In driver systems with the installation shown in Figure 4a, CMGE can lead to second torque and speed ripples. However, in driver systems with a single current sensor, as depicted in Figure 4b–d, CMGE does not exist. This is because the additional second torque ripple is caused by the difference in gain coefficients of each phase sensor. Therefore, the problem does not occur in systems that only use a single current sensor [51,52]. Nonetheless, CMGE still causes a deviation in the current limit, which can result in the output current either exceeding the limit or not being fully utilized [53]. This issue is present in drive systems that use either a single current sensor or multiple current sensors.
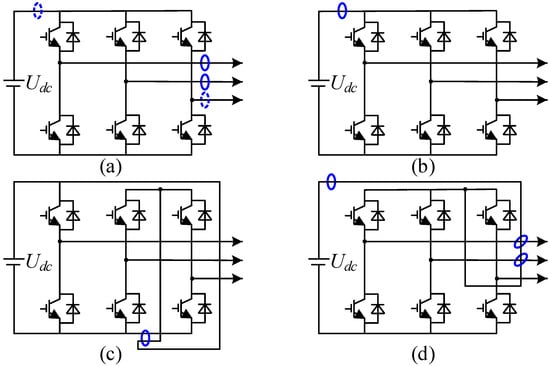
Figure 4.
Schematic diagram of different installation positions for current sensors. (a) Sensors installed on the 2/3 phase output branch or the DC-bus. (b) Sensors installed only on the DC-bus. (c) Sensors installed on the phase-to-phase interleaved branch. (d) Sensors installed on the DC-bus and the interleaved branch between phase output and DC-bus.
For all the topologies in Figure 4, Figure 4a is the most commonly used installation. Sensors are installed on the output branch in each phase or on the DC bus simultaneously. For a Y-connected three-phase PMSM, the sum of the three-phase currents is zero. Thus, only two-phase current sensors are needed to achieve closed-loop current control. However, in applications requiring high safety, such as elevators and cranes, three-phase current sensors are utilized to ensure fault tolerance during current sensor failures [48]. The current sensor installed on the DC bus is commonly implemented in electric vehicles and wind turbines. [47,54]. For low-cost machine drive systems, only one single current sensor is used, as shown in Figure 4b,c. In these cases, currents are sampled multiple times in one switching period, and all phase currents are reconstructed according to different space voltage vectors [51,52,55]. In addition to the installation described in Figure 4a–c, other signal sensor installation positions are studied to improve the performance of the current reconstruction algorithms at all modulation indices, as shown in Figure 4d [56,57,58].
The influence of CME is also related to the implemented control strategy. In drive systems that use disturbance rejection control algorithms, CMEs affect the accurate compensation of disturbances [59]. In multi-phase control systems, CMEs can cause an output power imbalance between different winding sets [60]. In open-wound control systems, CMOE may couple with the zero-sequence circulating current, which leads to non-zero circulating currents [61].
3. Compensation for Current Measurement Error
3.1. High-Frequency Current Measurement Error
According to Figure 3, CME can be divided into high- and low-frequency components. The different spectral distributions result in varying impacts and compensation methods for the two types of CME. In this section, two kinds of high-frequency CME, namely, random noise and PWM-induced error, and their compensation methods are briefly introduced.
(1) Random Noise: Random noise includes measurement noise and quantization noise. In drive systems that use proportional-integral (PI) controllers, reducing the bandwidth of the PI controller can suppress the influence of random noise; however, this will also reduce the dynamic characteristics of the current controller. In drive systems that use model predictive control and direct torque control, random noise directly affects the selection of voltage space vectors, significantly impacting the total harmonic distortion (THD) of the output currents.
(i) Software Method: The compensation of measurement noise can be achieved through software or hardware-based methods. For software compensation, low-pass filters (LPF), moving average filters, recursive least squares (RLS) [62], and Kalman filters [59,63] are effective techniques for pre-filtering the measured currents. In [64], a compensation method based on a Luenberger observer was proposed, which effectively suppresses the influence of measurement noise on the voltage vector selection of MPC. Similarly, a parallel cascaded extended observer was proposed in [65], which effectively suppresses high-frequency measurement noise in direct torque control.
(ii) Hardware Method: Due to the limitation of the switching period, hardware-based techniques are more effective solutions compared to software filtering. Using resistors and capacitors to form a first-order LPF circuit is a widely adopted method in engineering; however, there is a trade-off between noise suppression and transmission delay. A variable-gain ADC conditioning circuit is designed in [66] to achieve full ADC range utilization considering the different amplitudes of the input signals. The enhanced data acquisition system with this circuit significantly suppresses the random noise of the measured signal and enhances the accuracy of online machine state monitoring. In addition, oversampling is also an effective solution [67]. In sensorless drive systems, oversampling significantly improves position estimation and current measurement accuracy [68,69].
Many chips in machine control systems are equipped with oversampling capabilities. For instance, in the TI C2000 digital signal processor (DSP), oversampling can be achieved by modifying the registers of the ADC peripheral [70]. Similarly, in ADI’s AD7606 chip, adjusting the voltage of the OS pin allows for the adjustment of the oversampling mode [71].
However, regardless of the chip used for implementation, the oversampling factor Mos can be utilized to characterize different oversampling levels. A higher Mos results in improved suppression of random noise. The suppression effect of oversampling on random noise can be evaluated using the signal-to-noise ratio (SNR), which can be defined as follows:
where Ps and Pn are the signal and noise power, respectively. Oversampling technology allows ADC circuits to attain higher effective resolution and significantly decrease the SNR of measured results. Theoretically, with each four-fold increase in Mos, the SNR of the input signal is expected to rise by 6 dB, and the ADC’s resolution will also increase by 1 bit [70]. Figure 5 shows the relationship between SNR improvement and Mos for the oversampling operation of the AD7606 chip [71]. It can be seen from Figure 5 that oversampling at different Mos levels improves the low-frequency SNR of the input signals. However, when Mos becomes too large, the improvement in SNR diminishes, and the high-frequency SNR may even decrease. Although oversampling can significantly improve SNR and equivalent resolution, it also entails some performance trade-offs. Higher Mos raises the execution time of the sampling process, thereby decreasing the maximum sampling speed of the ADC. According to the Nyquist sampling theorem, this operation limits the maximum bandwidth of captured signals.
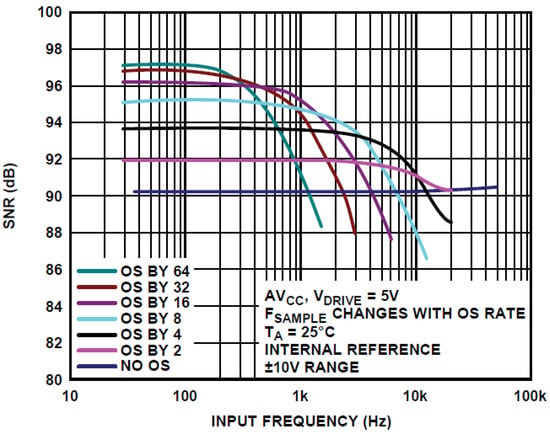
Figure 5.
Signal-to-noise ratio of oversampling operation under different oversampling factor Mos [71].
Figure 6 shows the schematic of the oversampling operation when Mos = 4, where the blue dashed line and the black solid line represent the ideal and noisy signals, respectively, and the red triangles represent the measured points. If a 0–3 V signal is sampled with a 12-bit ADC, the sampled result for a 1.5 V signal should be 2048. However, noise causes a deviation in the sampled result. By using oversampling, four consecutive data points are collected, accumulated, and then down-sampled to obtain the equivalent oversampled result. Compared to single sampling, oversampling effectively suppresses the impact of random noise. The sampled results are closer to the actual values.
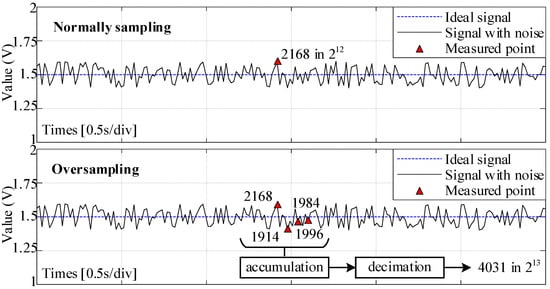
Figure 6.
Schematic diagram of oversampling to suppress the random noise of measurement.
Apart from oversampling techniques, Σ-Δ ADC conversion technology is also an effective method for attenuating high-frequency random noise [72]. This technology was initially used for precise temperature measurements and audio processing. Compared to traditional successive approximation register (SAR) ADCs, Σ-Δ ADCs can achieve 16–18 bits of resolution even without special fine-tuning or calibration [73].
Figure 7 shows the block diagram of the Σ-Δ ADC [74]. The random noise in the input signal is initially mitigated through an oversampling operation, followed by digital filtering and a decimation structure to resample it with fs. Subsequently, the noise is shaped using the Σ-Δ modulator, concentrating the noise energy in the high-frequency band. Finally, the shaped noise is attenuated again by the digital filter and the decimation structure to complete the Σ-Δ conversion process.
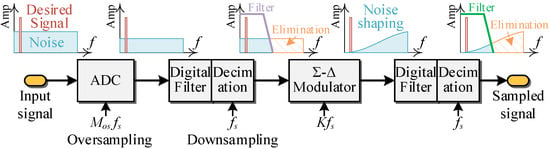
Figure 7.
Block diagram of the Σ-Δ ADC techniques.
The Σ-Δ modulator serves as the central structure in all Σ-Δ conversion processes, facilitating noise shaping to significantly improve noise attenuation effects. Figure 8 shows the block diagram of a first-order Σ-Δ modulator. By employing closed-loop regulation of the integrator and comparator, sinusoidal signals are transformed into PWM signals with amplitudes of ±Vref. A study in [72] compared the noise suppression capabilities of oversampling operations and Σ-Δ-type ADCs. The analysis results validated the remarkable noise suppression capabilities of the Σ-Δ modulator. Compared to oversampling techniques, the Σ-Δ type ADC enhances the SNR by nearly 20 dB.
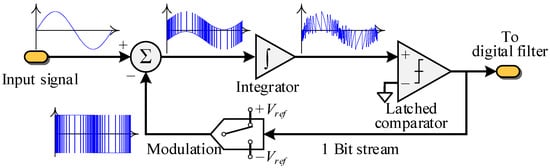
Figure 8.
Block diagram of the Σ-Δ modulator [74].
(2) PWM-Induced Error: Compared to random high-frequency noise, the frequency of PWM-induced error typically aligns near the switching frequency, fs. Notably, switch noise and computational delay are two typical PWM-induced errors.
(i) Switching Noise: Switch noise-induced errors are associated with the use of wide-band gap devices, such as SiC. While SiC devices shorten switching time, they also exacerbate current oscillations during the switching process. If the moment of current sampling closely coincides with the switching process, these current oscillations can lead to deviations in the sampled results from the average current within one switching cycle. Consequently, this phenomenon degrades the current closed-loop control performance and results in output current distortion [75]. Moreover, the rapid switching of SiC devices can result in serious electromagnetic interference (EMI) problems, which may cause the ADC circuits to produce error signals correlated with the PWM frequency. This phenomenon similarly degrades the performance of the drive system [76].
To address these issues, some device drive circuits use fiber optic interfaces instead of traditional isolation transformers to enhance electrical isolation [77]. Furthermore, in [78], both the driving and sampling signals are optically isolated and transmitted to the DSP. These optimized hardware designs effectively address EMI interference issues in the transmission lines. However, the additional fiber optic interfaces increase the cost of the drive system and complicate the design of the system’s auxiliary power supply.
Another solution to PWM-induced error is the use of digital filters. A moving average filter (MAF) is a commonly used solution to suppress random white noise errors. However, for intermittent, non-stationary PWM-induced errors, especially when the number of erroneous sampling points is high compared to the total number of points in the sampling window, the performance of this MAF method is less effective. According to the analysis results in [79], any presence of switching noise can affect the averaged result. Thus, the MAF can only partially mitigate the effect of switching noise.
The median filter (MDF) was proposed to suppress switching noise-induced errors, combined with an amplitude band-pass filter to eliminate sampling points with instantaneous amplitude violations, effectively reducing EMI issues. The MDF can be expressed as follows:
where is[k] represents the sampled stator current at time k, and N is the number of sample points for the MDF window. The “Median” function selects the median value from the sorted set of N samples, averaging the middle two if N is even. It is shown in [79] that if the influence of switching noise does not exceed half the peak-to-peak value of the current ripple, MDF can eliminate the undesired wrong sampling results by sorting the noise-affected points to both sides of the sampling window. When switching noise-induced CME exceeds half the current ripple’s peak-to-peak value, [80] suggests adding a repetitive ripple removal (RR) algorithm to the MDF to solve this problem. The transfer function of the RR controller GRR(s) can be expressed as follows:
where R = 0.125 is used to adjust the time constant of GRR(s) to approximately 10 Ts [81]. The basic principle of the RR controller is to estimate and suppress periodic disturbances using an internal model structure. Figure 9 shows the schematic diagram of the MDF and the combination of MDF and RR. The blue curve represents the real current, the yellow curve represents the average current, and the black discrete stair represents the sampled current. The black and red sampling points represent correct and noise-affected samples, respectively. As shown in Figure 9, when PWM-induced errors exceed half the peak-to-peak ripples, MDF cannot filter out the erroneous sampling points. However, with the help of RR, the bad points are identified and can still be sorted into the two sides of the sampling sequence after MDF, which demonstrates the effectiveness of the RR structure.
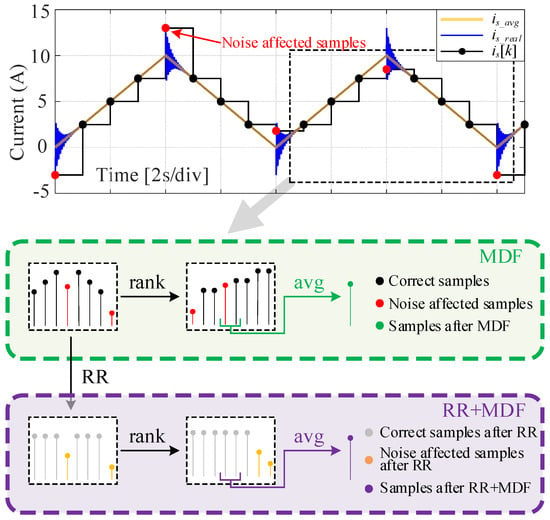
Figure 9.
Schematic diagram of the median filter (MDF) and the MDF with a repetitive ripple removal structure (RR).
(ii) Computational Delays: The second type of PWM-induced CME is caused by computational delays. The delays in PWM updates and ADC sampling lead to the sampled current deviating from the average current during the switching cycle, which reduces the stable operating range of the current controller. Although the sampling process itself is not inherently problematic in this case, the sampled result deviates from the current expected by the controller. Therefore, this paper still reviews the related studies for the sake of generality. Based on the analysis in [82], the delay between the ADC and PWM update in a single-sample, single-update driving system is Ts.
To address this issue, one approach is to perform multiple PWM updates within one switching cycle. Figure 10a,b compare the control frameworks for single-sample single-update and single-sample dual-update, respectively, where the yellow triangular wave represents the carrier, the blue solid line is the modulation wave, and the green curve is the output PWM voltage. The red and blue arrows indicate the time points for triggering the ADC and PWM updates, respectively. The purple Td denotes the delay time between ADC sampling and PWM update. Compared to the single-update algorithm in Figure 10a, the dual-update algorithm significantly reduces the delay from ADC sampling to the duty cycle update. A multi-sample, multi-update structure can further reduce this delay, but it demands higher bandwidth for current sampling and a faster processing speed from the processor. In some algorithms, an FPGA is also required, which increases the complexity of system design and hardware costs [83].
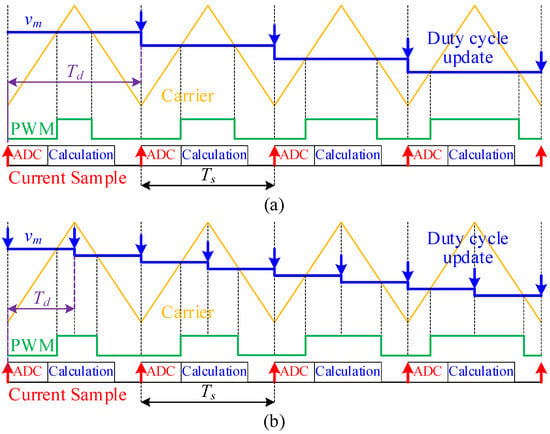
Figure 10.
Comparison of the delay time between the single-sample single-update and single-sample dual-update control algorithms. (a) single-sample single-update control alogrithm; (b) single-sample dual-update control alogorithm.
In addition, adjusting the execution order of each controller task, such as ADC, control computation, and PWM updates, can help reduce the equivalent delay. A method for decreasing PWM updates is proposed in [84], which places time-consuming control computation, such as integration and resonance, outside the ADC sampling and PWM update processes, thereby minimizing the delay between them. Based on this, [49] proposed a control architecture to ensure minimized update delays for all driving systems that use any number of current controllers while maintaining anti-windup characteristics. This algorithm advances the outer loop control program and decomposes the inner loop control program into necessary pre-calculation and post-calculation parts. The addition of more current controllers only increases the post-calculation time and does not affect the pre-calculation part. As a result, this architecture effectively minimizes the delay from ADC sampling to duty cycle update.
3.2. Low-Frequency Current Measurement Error
In this section, two typical types of low-frequency CME, namely, current sampling offset error (CMOE) and current sampling gain error (CMGE), as well as their compensation methods, are briefly introduced. Compared to high-frequency CME, these two low-frequency CMEs lead to additional fundamental and twice-frequency ripples in the output torque. Since these two errors are usually considered and compensated together, the following studies are classified and introduced according to different compensation methods for clarity.
(1) Offline Compensation Method: Offline compensation of CME is the most common method in engineering. These methods are typically used during the initial debugging of the drive system or for pre-correction before factory delivery. In [85], an offline CMGE compensation method is proposed, in which the PMSM operates in standstill mode, and the currents are closed-loop controlled in the stationary frame, and the dq-axis currents, id and iq, and the midpoint current are sampled while ensuring that iq = 0. This method is simple and offers excellent compensation results; however, it requires precise resistance measurements and the use of three current sensors.
An offline CMGE compensation method is proposed that analyzes the compensation ability under resistance asymmetry conditions [48]. However, this method still requires three current sensors, and the rotor of the PMSM must be locked. In [53], an offline compensation method based on elliptical trajectories and sequence signal injection is proposed. By correcting the midpoint current, this algorithm can effectively suppress the influence of resistance offsets and inverter non-linearity on compensation performance, thereby improving the precision of offline compensation. Furthermore, both the deviation and average components of CMGE are analyzed and compensated.
(2) Online Compensation Method: Due to factors such as temperature drift and aging, the CME slowly changes during PMSM operation. These varying errors cannot be addressed by the offline compensation methods mentioned above. Since CMOE and CMGE cause additional fundamental and twice-frequency harmonics, several online compensation methods based on characteristic harmonics suppression have been extensively studied.
(i) Signal Injection-Based Method: By injecting fixed frequency signals into the regulated currents, the magnitude and phase of the feedback signals can be used to indirectly estimate CMOE and CMGE. Zhang et al. [86] proposed a compensation method in which additional CMOE and CMGE are injected. Then, CMEs are estimated by detecting the variation in the speed harmonic magnitude. However, this method is unsuitable for varying speed conditions, and the injected additional CMEs lead to more torque ripples.
Besides injecting additional CME, injecting high-frequency (HF) signals is also an effective means of compensating for CME. With the help of rotational transformation and the amplitude and phase information of high-frequency negative sequence harmonic currents, CME can be reconstructed [87]. Compared to the method in [86], this approach increases the frequency of the injected signal, thereby reducing the negative effect on torque ripples. Further, [60] proposed an HF injection-based CMGE online compensation method for a dual three-phase PMSM. The measured currents are decoupled into the fundamental and harmonic subspaces via vector space transformation (VSD). Since HF signals are injected only into the harmonic subspace, this algorithm has a minimal effect on torque ripple. Additionally, Lu et al. proposed a CME compensation method for electric vehicle drive systems [88]. This algorithm injects reverse voltage vectors to construct additional constraints. The calculation for reconstructing CME is significantly reduced. This method does not require continuous signal injection, further reducing the undesired ripples. However, it necessitates an additional DC-bus current sensor and is unsuitable for systems that only have phase current sensors.
(ii) Speed Harmonic-Based Method: Whether HF or low-frequency (LF) signals are injected, almost all of these methods affect the output torque and vibration noise. However, closed-loop compensation algorithms based on harmonic extraction do not have this issue.
In 1998, Chung et al. proposed a CME compensation method based on speed harmonics [50]. It reveals that CMOE and CMGE can be considered fundamental and as the second load disturbances. The speed harmonics are separated using spectral analysis and extracted through the proportional-integral (PI) controller, thereby enabling closed-loop compensation for CME. However, this algorithm requires the parameters of the mechanical system, such as damping and inertia. In [89,90,91], the authors proposed replacing the PI controller in the speed controller with a proportional-resonant (PR) or repetitive controller, thereby achieving indirect suppression of errors caused by CME. In [92,93], iterative learning or repetitive learning methods were proposed for CME compensation. However, both methods require real-time online learning or fitting, which leads to a significant computational burden. In [94], an improved adaptive selected harmonic elimination algorithm was introduced to compensate for CME. This algorithm extracts the speed harmonics and then achieves compensation for CME with the help of the phase relationship between the d-axis and q-axis harmonic currents.
However, these speed harmonic-based compensation methods in [50,89,90,91,92,93,94] only suppress the additional speed harmonic disturbances caused by CME but do not compensate for the CME itself. This means that these methods are not suitable for conditions with varying loads and speeds. Moreover, these algorithms always need to be executed during the operation of PMSM, which leads to a greater computational burden. Therefore, they also affect the performance of the original control algorithms under low-speed [91] and variable-speed conditions [89,90]. Additionally, the amplitude of torque and speed harmonics at different fundamental frequencies is dependent on the mechanical damping and inertia parameters, which can be expressed as follows [50]:
where J and B are damping and inertia parameters, respectively, and Kps and Kis are the proportional and integral parameters of the speed controller, respectively. The speed harmonic magnitude first increases and then decreases as the fundamental frequency increases [50]. Considering that torque harmonics and current harmonics are approximately proportional, the compensation performance of the speed harmonic-based CME compensation method deteriorates at both low and high frequencies.
(iii) Current and Voltage Harmonic-Based Method: Compared to speed harmonic-based CME compensation methods, current and voltage harmonic-based methods are not affected by mechanical system parameters and have been widely studied.
Figure 11 shows the general block diagram of a CME compensation algorithm based on current and voltage harmonics. The blue part represents the filter used to extract harmonic components from the current and voltage, and in the red part, harmonic voltage and current information are used to reconstruct and compensate for CME.
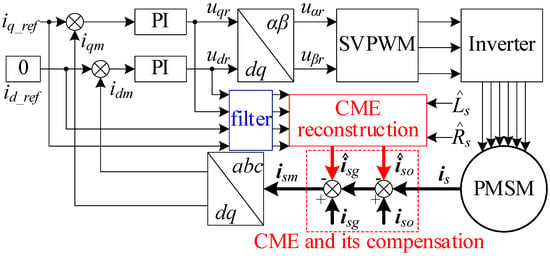
Figure 11.
General block diagram of current sampling error compensation based on voltage and current harmonics.
A CME compensation method using Support Vector Regression (SVR) was proposed in [95], which considers both inverter nonlinearity and parameter uncertainty. The authors of [96] introduced a non-intrusive CMGE compensation method. However, this method requires the tested machine to be controlled to a short-circuit state. Additionally, prior knowledge of the short-circuit current characteristics of each machine is needed, which limits its general applicability.
Considering the machine control system under normal operating conditions with limited computational resources, a CMGE reconstruction approach based on the harmonic spatial effects of CMGE was proposed [97]. However, this method requires three current sensors. To improve applicability, a CME compensation method using two phase current sensors was proposed, in which the effect of the speed controller on CME compensation performance was analyzed [98]. However, this algorithm is not applicable when the current controller is saturated. To address this issue, S.-I. Kim et al. introduced an online compensation algorithm for CMOE, which enables its application under current saturation conditions [99], but the compensation of CMGE has not been considered. To compensate for the CMOE and CMGE simultaneously, a voltage harmonic-based compensation method was proposed [100], but it does not consider the impact of parameter mismatch, and the convergence of the estimated result is relatively slow.
A CME vector reconstruction technique was proposed in [101], in which the fundamental and harmonic components induced by CME are decoupled by a single-frequency suppressor. While this method enables rapid CME compensation, the overall compensation accuracy remains insufficient. The angle-domain definite integral approach is employed to extract current harmonics and reconstruct CME in [102,103]. This method achieves high-precision compensation; however, the performance under varying speed and load conditions has not been thoroughly examined. An online compensation method for CMOEs based on state observers is introduced in [104], which accounts for the influence of load and speed variations, as well as parameter deviations, on compensation performance. M. Hu et al. proposed an LPF-based compensation method for CMOE in [105], in which the effect of transients and saturation are considered. Filter parameters are also designed. However, compensation for CMGE is not provided.
An online CMOE compensation method based on an expanded state observer was introduced in [106], which effectively mitigates the influence of parameter deviations and ensures consistent compensation accuracy at different speeds. Kyung-Rae Cho et al. proposed a structure comprising a resonant observer and a residual compensator in [107], while a compensation method utilizing a virtual winding structure was proposed in [108]. Both methods enable simultaneous compensation for CMOE and CMGE without dependence on motor parameters and provide rapid compensation with high efficiency. Additionally, the modified complex coefficient filter can be used to compensate for CME. Beyond the advantages mentioned above, this method demonstrates satisfactory performance under varying speeds and loads [109].
(iv) Current and Voltage Harmonic-Based Method: Table 2 presents a comparison of the characteristics of various low-frequency CME compensation algorithms in machine drive systems. In addition, to further analyze the performance of different methods based on speed harmonics, high-frequency injection, voltage harmonics, and current harmonics, simulations of the methods in [87,94,100], and [109] were conducted.

Table 2.
Performance comparison of low-frequency CME compensation methods.
Figure 12 illustrates the simulation results of the CME compensation algorithm based on speed harmonics in [94]. The compensation process is divided into three stages: “Normal”, “CME injection”, and “CME compensation”, which are represented by blue, red, and green regions, respectively. The reference values for CMOE are oα_ref = 0 A and oβ_ref = 0.2 A, while the reference value for CMGE is gαβ_ref = 0.2. The amplitude of the fundamental current is 2 A. It can be seen in Figure 12 that the estimated value of CMOE (oαβ) effectively converges to its reference value after enabling CME compensation. However, the negative sequence currents iαβn, rather than CMGE, are compensated. Consequently, this algorithm is not suitable for compensating for the negative sequence disturbance under variable load conditions.
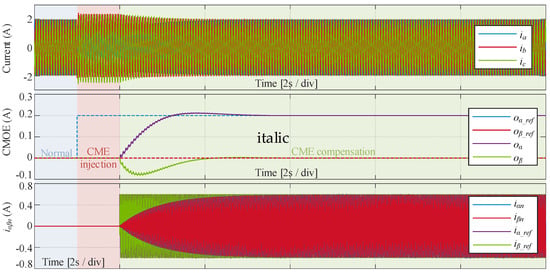
Figure 12.
Simulation results of the CME compensation algorithm based on speed harmonics.
Figure 13 presents the simulation results of the CME compensation algorithm based on HF injection in [87]. The compensation process is divided into four stages: “Normal”, “CME injection”, “HF injection and compensation”, and “Completion of CME compensation”, represented by blue, red, purple, and green regions, respectively, where oα_ref = oβ_ref = 0 A and gαβ_ref = 0.2. It is worth noting that since HF signals do not affect CMOE, this algorithm is only suitable for compensating CMGE. It is evident in Figure 12 that after enabling HF injection, the estimated gαβ rapidly converges to the reference value. Although HF injection introduces additional losses, the estimated results can be locked after convergence, thus preventing the long-term operation of this compensation algorithm.
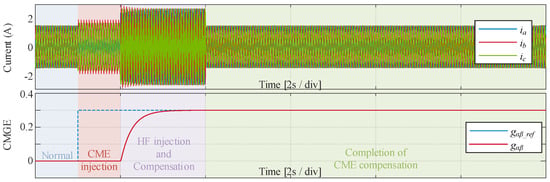
Figure 13.
Simulation results of the CME compensation algorithm based on HF signal injection.
Figure 14 shows the simulation results of the CME compensation algorithm based on voltage harmonics in [100]. The experimental conditions are identical to those in Figure 12, and the compensation process can be divided into the same three stages. It can be seen in Figure 14 that although the estimated results for both CMOE and CMGE gradually converge to their reference values after 2 s, the overall convergence speed is relatively slow. Additionally, there is a noticeable overshoot in the estimated result of CMOE. This indicates that the compensation algorithm, which relies solely on voltage harmonics, requires further improvement to enhance its response performance.
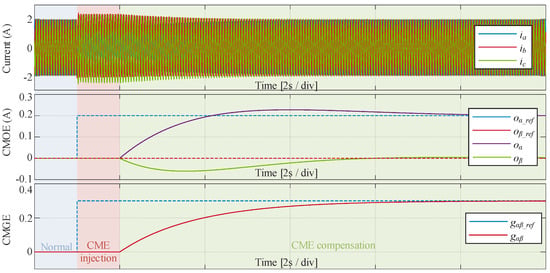
Figure 14.
Simulation results of the CME compensation algorithm based on voltage harmonics.
Figure 15 shows the simulation results of the CME compensation algorithm based on current harmonics in [109]. The experimental conditions are the same as those in Figure 12, and the compensation process follows the same three stages. It can be seen that after enabling the compensation algorithm at 2 s, all estimated results rapidly converge to the reference value within 1 s. Moreover, the estimated results can be locked after stabilization to improve their applicability under varying operating conditions, which demonstrates the excellent performance of this current harmonic-based compensation algorithm.
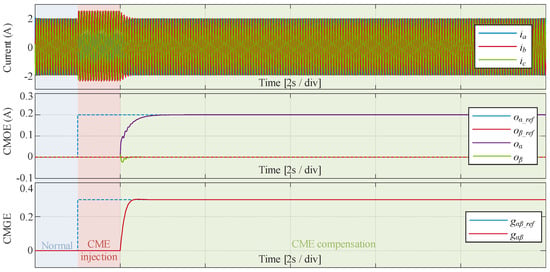
Figure 15.
Simulation results of the CME compensation algorithm based on current harmonics.
3.3. CME in Special Topologies
In addition to the typical online compensation methods mentioned above, there are several specialized CME compensation algorithms with current sensor installations, as shown in Figure 4. For instance, in the three-phase, four-bridge-arm drive system, a current reconstruction technique based on fixed-point sampling was proposed in [56], in which the difference between the positive and negative bus currents is measured by a signal current sensor. By specifying the current during different switching states and predicting the current slope based on each state, compensation for the deviation of the sampled current from the average current within the current period can be achieved.
An all-current-survivable algorithm was proposed in [110] by adding three additional sensors that sample the sum of DC-bus and phase currents. This installation method ensures that errors or faults in any individual sensor do not impact the normal operation of the drive system. Additionally, a CME compensation method with a similar sensor installation was proposed in [57], which significantly reduces the computational burden by avoiding additional filters or observers. For a dual-PMSM-based system, fast calibration can be achieved through a consistency calibration method [111], which enables the simultaneous calibration of two sets of three-phase windings within 1 s. Furthermore, with the help of an additional DC-bus sensor, an orthogonal pulse modulation carrier strategy combined with fixed-point sampling was proposed in [54], which can reconstruct and compensate for CME with some simple algebraic calculations.
4. Future Trends
The high-performance demands in fields such as CNC machine tools and servo drives have posed significant challenges to both hardware and software design. Sensor errors, especially CME, have emerged as crucial factors influencing the control performance of drive systems. The analysis and compensation of CME have been widely studied and developed over the past two decades. Future research trends in this area can be categorized into the following aspects:
(1) Analysis of the Influence of CME under Different Topologies: The effects of CME vary across different topological structures and deserve further investigation. In drive systems utilizing wide-bandgap devices, parasitic capacitances between the inverter and the sensor can result in additional HF switching noise induced by CME [112]. The generation mechanism of this error was carried out by establishing a model of the parasitic parameters of the drive system. Additionally, the influence of this error on HF injection-based sensorless algorithms is analyzed. Similar LF or HF disturbances due to CME can also occur in other types of power electronic converters. For instance, in three-phase grid-connected inverters, errors from additional voltage sensors may couple with CME, thereby affecting fault detection and compensation performance [113,114,115].
Additionally, the compensation algorithms for CME in multi-phase machines [60] and low-carrier ratio scenarios [69] are worth further exploration. In circuit topologies with special current sensor placements, as illustrated in Figure 4, the compensation performance of CME may be improved. However, this also introduces some specific issues. For example, in drive systems with a single current sensor, there exists a region in the space voltage vector where current reconstruction cannot be achieved, leading to current distortion in closed-loop control [56]. Moreover, in systems utilizing position sensors such as resolvers and Hall sensors, measured position signals can also induce errors similar to CME. The combined effects of CME and position errors on the drive system should also be explored further [116].
(2) Compensation for Different Components of CME: CME includes both HF and LF components. For the HF component, existing manufacturing processes have successfully implemented oversampling techniques [70,71] and Σ-Δ ADC technology [73,74] in hardware that significantly enhance the SNR for random noise. Therefore, in applications with fewer cost constraints, suppressing random noise through software algorithms may no longer be a valuable area of research. However, with the use of wide-bandgap semiconductors that have faster switching speeds, the influence of PWM-induced non-random error has become increasingly significant [112]. Especially in cases with high environmental EMI [75] or in which the sensor range is not fully utilized [66], the causes of PWM-induced errors and their compensation strategies still require further investigation. For some special applications, such as those with low inductance and a high carrier ratio, the influence of PWM-induced errors may become more significant.
In the compensation methods for the LF component, offline compensation methods cannot compensate for real-time varying errors caused by temperature drift and aging. Signal injection-based methods introduce additional losses and torque ripples. The performance of methods based on speed harmonic extraction is limited by load, damping, and the fundamental frequency. Therefore, compensation methods based on voltage and current harmonics are expected to be a key area for future development. Moreover, improving the CME compensation performance to achieve satisfactory accuracy at any fundamental frequency is crucial [106]. Furthermore, enhancing the applicability of compensation algorithms under startup, acceleration, deceleration, and load variation conditions is a critical direction for future research [104,105].
(3) Interaction between CME and Other Algorithms: For drive systems with multi-sampling and multi-update PWM, the ADC process is more susceptible to the influence of PWM switching noise, which in turn causes the measured results to deviate from the actual currents. Moreover, CME also depends on the magnitude of overshoot during the device commutation process. For sensorless control algorithms based on observers, the LF components of CME lead to additional negative sequence disturbances in the position estimation results [117]. For sensorless algorithms based on HF injection, PWM-induced errors cause regular deviations in position estimation values [112]. In drive systems using two-phase current sensors, the random noise in CME is significantly higher than in systems using three-phase current sensors, which reduces the SNR of the estimated position [118]. Finally, for fault diagnosis algorithms such as high-resistance connections, inter-turn short circuits, and machine eccentricity, LF CME also affects estimation accuracy and can even lead to fault misdiagnosis in severe cases. Identifying the differences between these faults and CME requires further investigation.
(4) Sensor Fault Diagnosis and Fault-Tolerant Control: In addition to generating HF and LF errors, current sensors can also produce other non-periodic errors due to line damage and power supply loss. Diagnosing different sensor faults and improving the fault tolerance capability of current sensors are crucial research directions. A diagnostic technique for common faults in IPMSM is proposed in [119]. The algorithm injects HF signals and combines current responses to construct multiple fault indicators for identifying inter-turn short circuits, CMOE, and CMGE. However, the application of this algorithm in SPMSM requires further investigation. In [120], for SPMSM, a method is proposed for diagnosing and locating current sensor faults, which can distinguish the number and location of faulty sensors. The authors of [121] present a fault-tolerant algorithm for current sensors in IPMSM, in which state observers are constructed to estimate current results in real time, thereby enabling speed closed-loop control, even with a single-phase sensor or no current sensor. However, mismatched machine parameters can affect control performance. The authors of [122] propose a current sensor fault diagnosis method based on a Multichannel Global Maximum Pooling CNN, which diagnoses not only CMOE and CMGE but also broken-line faults and stuck faults.
5. Conclusions
This paper provides an overview of the existing analysis and compensation methods for CME in PMSM. These studies include the current sampling path and classification of CME, the effects of CME on various topologies and control algorithms, and the different techniques for CME compensation. From a frequency perspective, CME consists of two main components: HF and LF. HF errors include random noise and periodic PWM-induced errors. Some hardware chips equipped with oversampling and Σ-Δ ADC functions can effectively address the issue of random noise. However, PWM-induced errors are related to current oscillations during the device commutation process and ADC delays, necessitating modifications to the control program. LF errors include CMOE and CMGE. Compensation methods based on signal injection introduce additional losses, vibrations, and noise. Methods based on speed harmonic extraction exhibit decreased performance at both low and high speeds. In contrast, voltage and current harmonic-based methods provide relatively superior performance. Finally, trends in the development of CME influence analysis, compensation, and sensor fault-tolerant strategies are discussed.
Author Contributions
Conceptualization, P.S. and T.W.; methodology, P.S.; software, P.S.; validation, P.S., C.L. and X.M.; formal analysis, H.L.; investigation, H.L.; resources, C.L.; data curation, X.M.; writing—original draft preparation, P.S.; writing—review and editing, L.W.; visualization, T.W.; supervision, L.W.; project administration, L.W.; funding acquisition, L.W. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the National Key Research and Development Program of China under Grant 2023YFB4202800; in part by the National Science Fund for Distinguished Young Scholars under Grant 52225703.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Sonandkar, S.; Selvaraj, R.; Chelliah, T.R. Fault Tolerant Capability of Battery Assisted Quasi-Z-Source Inverter Fed Five Phase PMSM Drive for Marine Propulsion Applications. In Proceedings of the 2020 IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES), Jaipur, India, 16–19 December 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Choo, K.-M.; Won, C.-Y. Design and Analysis of Electrical Braking Torque Limit Trajectory for Regenerative Braking in Electric Vehicles With PMSM Drive Systems. IEEE Trans. Power Electron. 2020, 35, 13308–13321. [Google Scholar] [CrossRef]
- Bharatiraja, C.; Vinoth, J. A New Three Phase Twelve Switch Inverter for Three Wheel PMSM Drive Electric Transportation. In Proceedings of the 2024 IEEE 4th International Conference on Sustainable Energy and Future Electric Transportation (SEFET), Hyderabad, India, 31 July–3 August 2024; pp. 1–6. [Google Scholar] [CrossRef]
- Wang, Y.; Meng, J.; Zhang, X.; Xu, L. Control of PMSG-Based Wind Turbines for System Inertial Response and Power Oscillation Damping. IEEE Trans. Sustain. Energy 2015, 6, 565–574. [Google Scholar] [CrossRef]
- Miyama, Y.; Ishizuka, M.; Kometani, H.; Akatsu, K. Vibration Reduction by Applying Carrier Phase-Shift PWM on Dual Three-Phase Winding Permanent Magnet Synchronous Motor. IEEE Trans. Ind. Appl. 2018, 54, 5998–6004. [Google Scholar] [CrossRef]
- Cheema, M.A.M.; Fletcher, J.E.; Xiao, D.; Rahman, M.F. A Linear Quadratic Regulator-Based Optimal Direct Thrust Force Control of Linear Permanent-Magnet Synchronous Motor. IEEE Trans. Ind. Electron. 2016, 63, 2722–2733. [Google Scholar] [CrossRef]
- Jiang, C.; Liu, H.; Wheeler, P.; Wu, F.; Cai, Z.; Huo, J. A Novel Open-Circuit Fault Detection and Location for Open-End Winding PMSM Based on Differential-Mode Components. IEEE Trans. Ind. Electron. 2022, 69, 7776–7786. [Google Scholar] [CrossRef]
- Lee, H.; Lee, J. Design of Iterative Sliding Mode Observer for Sensorless PMSM Control. IEEE Trans. Control. Syst. Technol. 2013, 21, 1394–1399. [Google Scholar] [CrossRef]
- Gao, J.; Gong, C.; Li, W.; Liu, J. Novel Compensation Strategy for Calculation Delay of Finite Control Set Model Predictive Current Control in PMSM. IEEE Trans. Ind. Electron. 2020, 67, 5816–5819. [Google Scholar] [CrossRef]
- Niu, F.; Wang, B.; Babel, A.S.; Li, K.; Strangas, E.G. Comparative Evaluation of Direct Torque Control Strategies for Permanent Magnet Synchronous Machines. IEEE Trans. Power Electron. 2016, 31, 1408–1424. [Google Scholar] [CrossRef]
- Cho, K.-R.; Seok, J.-K. Correction on Current Measurement Errors for Accurate Flux Estimation of AC Drives at Low Stator Frequency. IEEE Trans. Ind. Appl. 2008, 44, 594–603. [Google Scholar] [CrossRef]
- Bourns, Inc. Using Current Sense Resistors for Accurate Current Measurement, Jan. 2017. Available online: https://www.bourns.com/docs/technical-documents/technical-library/current-sense-pulse-power-high-power-resistors/application-notes/bourns_n1702_current_sense_accurate_measurement_appnote.pdf (accessed on 5 March 2025).
- Crescentini, M.; Syeda, S.F.; Gibiino, G.P. Hall-Effect Current Sensors: Principles of Operation and Implementation Techniques. IEEE Sensors J. 2022, 22, 10137–10151. [Google Scholar] [CrossRef]
- Li, J.; Ren, W.; Luo, Y.; Zhang, X.; Liu, X.; Zhang, X. Design of Fluxgate Current Sensor Based on Magnetization Residence Times and Neural Networks. Sensors 2024, 24, 3752. [Google Scholar] [CrossRef] [PubMed]
- Mühlthaler, J.; Lehner, B.; Reeh, A. Detection of Inter-Turn Short-Circuits in Permanent Magnet Machines Based on Rogowski & Search Coil Based Monitoring. In Proceedings of the 2024 International Conference on Electrical Machines (ICEM), Torino, Italy, 1–4 September 2024; pp. 1–8. [Google Scholar] [CrossRef]
- Singh, R.P.; Khambadkone, A.M. Giant Magneto Resistive (GMR) Effect Based Current Sensing Technique for Low Voltage/High Current Voltage Regulator Modules. IEEE Trans. Power Electron. 2008, 23, 915–925. [Google Scholar] [CrossRef]
- Xiao, C.; Zhao, L.; Asada, T.; Odendaal, W.; Van Wyk, J. An overview of integratable current sensor technologies. In Proceedings of the 38th IAS Annual Meeting on Conference Record of the Industry Applications Conference, Salt Lake City, UT, USA, 12–16 October 2003; Volume 2. [Google Scholar] [CrossRef]
- Patel, A. Current Measurement in Power Electronic and Motor Drive Applications—A Comprehensive Study. Master’s Thesis, University of Missouri, Rolla, MO, USA, 2007. Available online: https://scholarsmine.mst.edu/masters_theses/4581 (accessed on 5 March 2025).
- Ziegler, S.; Woodward, R.C.; Iu, H.H.-C.; Borle, L.J. Current Sensing Techniques: A Review. IEEE Sensors J. 2009, 9, 354–376. [Google Scholar] [CrossRef]
- Kawahara, S.; Furuta, Y.; Wada, S.; Taniguchi, S.; Nezuka, T. A 30-nΩ Accuracy Low Power Two-Step Ratiometric Shunt Resistance Measurement System Using a Switching Regulator- Based Current Generator for Shunt-Based Current Sensors. IEEE Sens. J. 2024, 24, 40188–40195. [Google Scholar] [CrossRef]
- Chen, Q.; Li, K.; Ahmed, R. A high-bandwidth current shunt resistor for testing GaN devices. IET Conf. Proc. 2024, 2024, 547–552. [Google Scholar] [CrossRef]
- Zhang, W.; Zhang, Z.; Wang, F.; Brush, E.V.; Forcier, N. High-Bandwidth Low-Inductance Current Shunt for Wide-Bandgap Devices Dynamic Characterization. IEEE Trans. Power Electron. 2021, 36, 4522–4531. [Google Scholar] [CrossRef]
- Moon, J.-S.; Kim, J.-Y.; Lee, J.-S.; Kim, S.-J.; Lee, W.-R. The control strategy of In-wheel motor drive system using inverter leg shunt resistors. In Proceedings of the 2021 24th International Conference on Electrical Machines and Systems (ICEMS), Gyeongju, Republic of Korea, 31 October–3 November 2021; pp. 1742–1746. [Google Scholar]
- Guo, W.; Xiao, G.; Wang, L.; Gao, K. A Current Monitoring Method for Wire-bonding Power Modules based on Magnetoresistance-Planar Rogowski Coil. In Proceedings of the 2024 IEEE 10th International Power Electronics and Motion Control Conference (IPEMC2024-ECCE Asia), Chengdu, China, 17–20 May 2024; pp. 702–706. [Google Scholar]
- Liu, X.; He, Y.; Huang, H.; Xu, Q.; Huang, T. A Method for Increasing the Bandwidth of Rogowski Coils Without Changing Their Size. IEEE Trans. Instrum. Meas. 2022, 71, 1–10. [Google Scholar] [CrossRef]
- Krýsl, P.; Jára, M. Design of Current Measurement Circuit Using PCB Rogowski Coils for Resonant Converters. In Proceedings of the 2024 21st International Conference on Mechatronics-Mechatronika (ME), Brno, Czech Republic, 4–6 December 2024; pp. 1–4. [Google Scholar]
- Moser, S.; Incurvati, M.; Schiestl, M.; Stärz, R. Non-invasive wide-bandwidth current sensor for wide-bandgap devices. In Proceedings of the 2023 25th European Conference on Power Electronics and Applications (EPE’23 ECCE Europe), Aalborg, Denmark, 4–8 September 2023; pp. 1–7. [Google Scholar]
- Chen, B.; Zhang, Z.; Wu, Y.; Tian, C.; Chen, Y. A Novel Anti-DC Bias Energy Meter Based on Magnetic-Valve-Type Current Transformer. IEEE Trans. Instrum. Meas. 2022, 71, 1–9. [Google Scholar] [CrossRef]
- Hu, Y.; Ottoboni, R.; Li, J. A Novel Method for DC Current Measurement Using Current Transformer. IEEE Trans. Instrum. Meas. 2024, 73, 1–9. [Google Scholar] [CrossRef]
- Simonetti, F.; Mohamadian, S.; Buccella, C.; Cecati, C. DC Current Suppression in CHB-STATCOM With Model Predictive Control Employing Current Transformers. IEEE Trans. Ind. Electron. 2024, 71, 13135–13145. [Google Scholar] [CrossRef]
- Bashir, S.; Paul, S.; Chang, J. Novel Core Airgap Profiles Design Scheme for Winding and Thermal Loss Reduction in High-Frequency Current Transformer Sensors. IEEE Sensors J. 2020, 20, 892–898. [Google Scholar] [CrossRef]
- Fritsch, M.; Wolter, M. Saturation of High-Frequency Current Transformers: Challenges and Solutions. IEEE Trans. Instrum. Meas. 2023, 72, 1–10. [Google Scholar] [CrossRef]
- Wang, R.; Du, G.; Xiao, W.; Zhang, B.; Qiu, D. Wide Range Energy Harvesting Technique for Current Transformer Based on Coil Adaptive Switching. IEEE Sensors J. 2024, 24, 41875–41884. [Google Scholar] [CrossRef]
- Kim, K.; Kim, Y.; Han, J.-H.; Hong, S.-K. Analysis and Compensation of Phase Shift Errors of an Open-Loop Current Transducer Considering Eddy Current. IEEE Access 2024, 12, 62730–62737. [Google Scholar] [CrossRef]
- Zapf, F.; Weiss, R.; Itzke, A.; Gordon, R.; Weigel, R. Mechanically Flexible Sensor Array for Current Measurement. IEEE Trans. Instrum. Meas. 2020, 69, 8554–8561. [Google Scholar] [CrossRef]
- Qiu, G.; Ran, L.; Feng, H.; Jiang, H.; Long, T.; Forsyth, A.J.; Shao, W.; Hou, X. A Fluxgate-Based Current Sensor for DC Bias Elimination in a Dual Active Bridge Converter. IEEE Trans. Power Electron. 2022, 37, 3233–3246. [Google Scholar] [CrossRef]
- Sirat, A.P.; Niakan, H.; Gafford, J.; Parkhideh, B. Design and Development of Hybrid Current Sensors for Wide-Bandgap Power Electronics Applications. In Proceedings of the 2024 IEEE Applied Power Electronics Conference and Exposition (APEC), Long Beach, CA, USA, 25–29 February 2024; pp. 260–266. [Google Scholar]
- Wei, Y.; Li, C.; Zhao, W.; Xue, M.; Cao, B.; Chu, X.; Ye, C. Electrical Compensation for Magnetization Distortion of Magnetic Fluxgate Current Sensor. IEEE Trans. Instrum. Meas. 2022, 71, 1–9. [Google Scholar] [CrossRef]
- Tian, X.; Qian, Q.; Fu, W. Fluxgate Current Sensor Based on H-Bridge. In Proceedings of the 2023 6th International Conference on Electronics Technology (ICET), Chengdu, China, 12–15 May 2023; pp. 371–376. [Google Scholar]
- Scherzer, M.; Auer, M.; Valavanoglou, A.; Magnes, W. Implementation of a Fully Differential Low Noise Current Source for Fluxgate Sensors. In Proceedings of the 2022 IEEE 13th Latin America Symposium on Circuits and System (LASCAS), Puerto Varas, Chile, 1–4 March 2022; pp. 1–4. [Google Scholar]
- Yang, X.; Liu, H.; Wang, Y.; Wang, Y.; Dong, G.; Zhao, Z. A Giant Magneto Resistive (GMR) Effect Based Current Sensor with a Toroidal Magnetic Core as Flux Concentrator and Closed-Loop Configuration. IEEE Trans. Appl. Supercond. 2014, 24, 1–5. [Google Scholar] [CrossRef]
- Chen, Y.; Heredia, L.C.C.; Smit, J.J.; Niasar, M.G.; Ross, R. Giant Magneto-Resistive (GMR) Sensors for Non-Contacting Partial Discharge Detection. IEEE Trans. Instrum. Meas. 2023, 72, 1–11. [Google Scholar] [CrossRef]
- Kim, W.; Luo, S.; Lu, G.-Q.; Ngo, K.D.T. Integrated current sensor using giant magneto resistive (GMR) field detector for planar power module. In Proceedings of the 2013 Twenty-Eighth Annual IEEE Applied Power Electronics Conference and Exposition (APEC), Long Beach, CA, USA, 17–21 March 2013; pp. 2498–2505. [Google Scholar]
- Wireko-Brobby, A.; Hu, Y.; Wang, G.; Gong, C.; Lang, W.; Zhang, Z. Analysis of the Sources of Error Within PMSM-Based Electric Powertrains—A Review. IEEE Trans. Transp. Electrif. 2024, 10, 6370–6406. [Google Scholar] [CrossRef]
- Babayomi, O.; Zhang, Z.; Li, Z. Model-Free Predictive Control of DC–DC Boost Converters: Sensor Noise Suppression with Hybrid Extended State Observers. IEEE Trans. Power Electron. 2024, 39, 245–259. [Google Scholar] [CrossRef]
- Yang, D.; Ruan, X.; Wu, H. A Real-Time Computation Method With Dual Sampling Mode to Improve the Current Control Performance of the LCL-Type Grid-Connected Inverter. IEEE Trans. Ind. Electron. 2015, 62, 4563–4572. [Google Scholar] [CrossRef]
- Ding, X.; Zhang, Y.; Ye, Z. Current Sensors Offset Fault Online Estimation in Permanent Magnet Synchronous Generator (PMSG) Drives for Offshore Wind Turbines. IEEE Access 2021, 9, 135996–136003. [Google Scholar] [CrossRef]
- Yoo, M.-S.; Park, S.W.; Choi, Y.-Y.; Han, S.-H.; Yoon, Y.-D. Current-Scaling Gain Compensation of Motor Drives Under Locked-Rotor Condition Considering Inequality of Phase Resistances. IEEE Trans. Ind. Appl. 2020, 56, 4915–4923. [Google Scholar] [CrossRef]
- Hu, M.; Hua, W.; Xiao, H.; Wang, Z.; Liu, K.; Cai, K.; Wang, Y. Fast Current Control Without Computational Delay by Minimizing Update Latency. IEEE Trans. Power Electron. 2021, 36, 12207–12212. [Google Scholar] [CrossRef]
- Chung, D.-W.; Sul, S.-K. Analysis and compensation of current measurement error in vector-controlled AC motor drives. IEEE Trans. Ind. Appl. 1998, 34, 340–345. [Google Scholar] [CrossRef]
- Song, Y.; Lu, J.; Hu, Y.; Zhang, W.; Su, Y.; Wu, X.; Liu, J. Expanding Limit of Minimum Sampling Time Using Auxiliary Vectors for PMSM Drives With Single DC-Link Current Sensor. IEEE Trans. Ind. Electron. 2023, 70, 3437–3448. [Google Scholar] [CrossRef]
- Lu, J.; Zhang, X.; Hu, Y.; Liu, J.; Gan, C.; Wang, Z. Independent Phase Current Reconstruction Strategy for IPMSM Sensorless Control Without Using Null Switching States. IEEE Trans. Ind. Electron. 2018, 65, 4492–4502. [Google Scholar] [CrossRef]
- Retianza, D.V.; Arrozy, J.; Van Duivenbode, J.; Huisman, H.; Vermulst, B. Sequential Error Disentanglement of Three-Phase Current Sensor for AC Machine in Standstill Conditions. IEEE Access 2022, 10, 113902–113914. [Google Scholar] [CrossRef]
- Lu, J.; Hu, Y.; Wang, J.; Song, Y.; Su, Y.; Liu, J. Synergistic Correction of Current Sampling Errors in Dual-Motor Powered Electric Powertrain for High Power Electric Vehicles. IEEE Trans. Ind. Electron. 2022, 69, 225–235. [Google Scholar] [CrossRef]
- Xu, Y.; Yan, H.; Zou, J.; Wang, B.; Li, Y. Zero Voltage Vector Sampling Method for PMSM Three-Phase Current Reconstruction Using Single Current Sensor. IEEE Trans. Power Electron. 2016, 32, 3797–3807. [Google Scholar] [CrossRef]
- Lu, J.; Hu, Y.; Liu, J. Analysis and Compensation of Sampling Errors in TPFS IPMSM Drives With Single Current Sensor. IEEE Trans. Ind. Electron. 2019, 66, 3852–3855. [Google Scholar] [CrossRef]
- Lu, J.; Hu, Y.; Liu, J.; Wen, H. Self-Calibration of Phase Current Sensors With Sampling Errors by Multipoint Sampling of Current Values in a Single PWM Cycle. IEEE Trans. Ind. Electron. 2021, 68, 2942–2951. [Google Scholar] [CrossRef]
- Lu, J.; Hu, Y.; Liu, J.; Wang, J.; Li, P. Fixed-Point Sampling Strategy for Estimation on Current Measurement Errors in IPMSM Drives. IEEE Trans. Power Electron. 2021, 36, 5748–5759. [Google Scholar] [CrossRef]
- Gao, F.; Yin, Z.; Li, L.; Li, T.; Liu, J. Gaussian Noise Suppression in Deadbeat Predictive Current Control of Permanent Magnet Synchronous Motors Based on Augmented Fading Kalman Filter. IEEE Trans. Energy Convers. 2023, 38, 1410–1420. [Google Scholar] [CrossRef]
- Yan, L.; Zhu, Z.Q.; Shao, B. Current Measurement Gain Compensation Using High-Frequency Signal Injection in Dual Three-Phase PMSM Systems. IEEE Trans. Ind. Electron. 2024, 71, 3472–3482. [Google Scholar] [CrossRef]
- Song, Z.; Ma, X.; Yu, Y. Design of Zero-Sequence Current Controller for Open-End Winding PMSMs Considering Current Measurement Errors. IEEE Trans. Power Electron. 2020, 35, 6127–6139. [Google Scholar] [CrossRef]
- Sun, P.; Wu, X.; Ni, R.; Nie, S. A Study of RLS Adaptive Filter Algorithm in Current Loop Noise Suppression of PMSM Vector Control System. In Proceedings of the 2019 22nd International Conference on Electrical Machines and Systems (ICEMS), Harbin, China, 11–14 August 2019; pp. 1–4. [Google Scholar]
- Zhu, H.; Fujimoto, H. Suppression of Current Quantization Effects for Precise Current Control of SPMSM Using Dithering Techniques and Kalman Filter. IEEE Trans. Ind. Inform. 2014, 10, 1361–1371. [Google Scholar] [CrossRef]
- Liu, D.; Wang, Q.; Li, Y.; Gao, J.; Dong, G.; Zhi, W.; Sun, Y.; Wang, Y. An Improved Model Predictive Control method with Luenberger Observer for Measurement Noise Suppression and Reduction of Current Ripples. In Proceedings of the 2023 3rd International Conference on Intelligent Power and Systems (ICIPS), Shenzhen, China, 20–22 October 2023; pp. 326–330. [Google Scholar]
- Babayomi, O.; Li, Z.; Wang, Y.; Li, J.; Zhang, Z. Model-Free Predictive Torque Control of PMSM Drives with Measurement Noise Suppression. In Proceedings of the 2023 IEEE 2nd International Power Electronics and Application Symposium (PEAS), Guangzhou, China, 10–13 November 2023; pp. 912–917. [Google Scholar]
- Dutta, R.; Badajena, H.; Chakraborty, B.; Routray, A.; Jenamani, M. Enhanced Data Acquisition System of Current Signature for Diagnosis of Variable Speed Induction Motor Drives with Full ADC Range Utilization and Noise Cancellation. In Proceedings of the 2023 IEEE 2nd Industrial Electronics Society Annual OnLine Conference (ONCON), Virtual, 8–10 December 2023; pp. 1–6. [Google Scholar]
- Weber, B.; Wiedmann, K.; Mertens, A. Increased signal-to-noise ratio of sensorless control using current oversampling. In Proceedings of the 2015 9th International Conference on Power Electronics and ECCE Asia (ICPE 2015-ECCE Asia), Seoul, Republic of Korea, 1–5 June 2015; pp. 1129–1134. [Google Scholar]
- Landsmann, P.; Paulus, D.; Dotlinger, A.; Kennel, R. Silent injection for saliency based sensorless control by means of current oversampling. In Proceedings of the 2013 IEEE International Conference on Industrial Technology (ICIT 2013), Cape Town, South Africa, 25–28 February 2013; pp. 398–403. [Google Scholar]
- Zhang, H.; Lei, Y.; Zhang, Y. Harmonics Influence Analysis on Current-Oversampling-based Position Estimation under Multi-mode PWM for IPMSM Sensorless Drives in Rail Transit Applications. In Proceedings of the 2024 IEEE 10th International Power Electronics and Motion Control Conference (IPEMC2024-ECCE Asia), Chengdu, China, 17–20 May 2024; pp. 4227–4232. [Google Scholar]
- Texas Instruments, Inc. Application Note: ADC Oversampling, Susmitha Bumadi, August, 2024. Available online: https://www.ti.com/lit/an/sprad55a/sprad55a.pdf (accessed on 5 March 2025).
- Analog Devices, Inc. Datasheet: 8-/6-/4-Channel DAS with 16-Bit, Bipolar Input, Simultaneous Sampling ADC AD7606/AD7606-6/AD7606-4. Available online: https://www.analog.com/media/en/technical-documentation/data-sheets/AD7606_7606-6_7606-4.pdf (accessed on 5 March 2025).
- Li, D.; Liu, Z.; Gui, X. Noise Analysis and Suppression for High Accuracy Current Sampling in Motor Control. In Proceedings of the 2024 IEEE 7th International Electrical and Energy Conference (CIEEC), Harbin, China, 10–12 May 2024; pp. 1123–1128. [Google Scholar]
- Analog Devices, Inc. Technical Articles: Understanding SAR ADCs: Their Architecture and Comparison with Other ADCs, Oct, 2001. Available online: https://www.analog.com/en/resources/technical-articles/successive-approximation-registers-sar-and-flash-adcs.html (accessed on 5 March 2025).
- Analog Devices, Inc. Technical Articles: Fundamental Principles Behind the Sigma-Delta ADC Topology: Part 1, Michael Clifford, Jan, 2016. Available online: https://www.analog.com/en/resources/technical-articles/behind-the-sigma-delta-adc-topology.html (accessed on 5 March 2025).
- Wang, L.; Shi, Y.; Li, H. Anti-EMI Noise Digital Filter Design for a 60-kW Five-Level SiC Inverter Without Fiber Isolation. IEEE Trans. Power Electron. 2018, 33, 13–17. [Google Scholar] [CrossRef]
- Oswald, N.; Anthony, P.; McNeill, N.; Stark, B.H. An Experimental Investigation of the Tradeoff between Switching Losses and EMI Generation With Hard-Switched All-Si, Si-SiC, and All-SiC Device Combinations. IEEE Trans. Power Electron. 2014, 29, 2393–2407. [Google Scholar] [CrossRef]
- Zhang, X.; Li, H.; Brothers, J.A.; Fu, L.; Perales, M.; Wu, J.; Wang, J. A Gate Drive With Power Over Fiber-Based Isolated Power Supply and Comprehensive Protection Functions for 15-kV SiC MOSFET. IEEE J. Emerg. Sel. Top. Power Electron. 2016, 4, 946–955. [Google Scholar] [CrossRef]
- Boroyevich, D. Use of SiC devices in medium-voltage converters. Proc. CPES Workshop WBG Power Electron. Adv. Distrib. Grids, Apr. 2016. Available online: https://www.nist.gov/system/files/documents/pml/high_megawatt/Boroyevich_db-Workshop-on-MV-WBG-PE-for-ADG-2016.pdf (accessed on 5 March 2025).
- Cvetanovic, R.; Petric, I.; Mattavelli, P.; Buso, S. Median Filters for Switching Noise Mitigation in Oversampled Power Electronics Control Systems. In Proceedings of the 2023 IEEE Energy Conversion Congress and Exposition (ECCE), Nashville, TN, USA, 29 October–2 November 2023; pp. 2725–2731. [Google Scholar]
- Cvetanovic, R.; Petric, I.Z.; Mattavelli, P.; Buso, S. Switching Noise Propagation and Suppression in Multisampled Power Electronics Control Systems. IEEE Trans. Power Electron. 2024, 39, 149–163. [Google Scholar] [CrossRef]
- Corradini, L.; Mattavelli, P.; Tedeschi, E.; Trevisan, D. High-Bandwidth Multisampled Digitally Controlled DC–DC Converters Using Ripple Compensation. IEEE Trans. Ind. Electron. 2008, 55, 1501–1508. [Google Scholar] [CrossRef]
- Kim, H.; Degner, M.W.; Guerrero, J.M.; Briz, F.; Lorenz, R.D. Discrete-Time Current Regulator Design for AC Machine Drives. IEEE Trans. Ind. Appl. 2010, 46, 1425–1435. [Google Scholar] [CrossRef]
- Naouar, M.-W.; Monmasson, E.; Naassani, A.A.; Slama-Belkhodja, I.; Patin, N. FPGA-Based Current Controllers for AC Machine Drives—A Review. IEEE Trans. Ind. Electron. 2007, 54, 1907–1925. [Google Scholar] [CrossRef]
- Ke, X.; Buchman, B. Current Control for Passivity of a Power Converter. International Patent Application WO2020048579A1, 12 March 2020. [Google Scholar]
- Yoo, M.-S.; Park, S.-W.; Lee, H.-J.; Yoon, Y.-D. Offline Compensation Method for Current Scaling Gains in AC Motor Drive Systems With Three-Phase Current Sensors. IEEE Trans. Ind. Electron. 2021, 68, 4760–4768. [Google Scholar] [CrossRef]
- Zhang, Q.; Guo, H.; Liu, Y.; Guo, C.; Zhang, F.; Zhang, Z.; Li, G. A Novel Error-Injected Solution for Compensation of Current Measurement Errors in PMSM Drive. IEEE Trans. Ind. Electron. 2023, 70, 4608–4619. [Google Scholar] [CrossRef]
- Harke, M.C.; Guerrero, J.M.; Degner, M.W.; Briz, F.; Lorenz, R.D. Current Measurement Gain Tuning Using High-Frequency Signal Injection. IEEE Trans. Ind. Appl. 2008, 44, 1578–1586. [Google Scholar] [CrossRef]
- Lu, J.; Hu, Y.; Chen, G.; Wang, Z.; Liu, J. Mutual Calibration of Multiple Current Sensors With Accuracy Uncertainties in IPMSM Drives for Electric Vehicles. IEEE Trans. Ind. Electron. 2019, 67, 69–79. [Google Scholar] [CrossRef]
- Zhang, Q.; Guo, H.; Guo, C.; Liu, Y.; Wang, D.; Lu, K.; Zhang, Z.; Zhuang, X.; Chen, D. An adaptive proportional-integral-resonant controller for speed ripple suppression of PMSM drive due to current measurement error. Int. J. Electr. Power Energy Syst. 2021, 129, 106866. [Google Scholar] [CrossRef]
- Zhang, Q.; Guo, H.; Liu, Y.; Guo, C.; Lu, K.; Wang, D.; Zhang, Z.; Sun, J. Robust plug-in repetitive control for speed smoothness of cascaded-PI PMSM drive. Mech. Syst. Signal Process. 2022, 163, 108090. [Google Scholar] [CrossRef]
- Xia, C.; Ji, B.; Yan, Y. Smooth Speed Control for Low-Speed High-Torque Permanent-Magnet Synchronous Motor Using Proportional–Integral–Resonant Controller. IEEE Trans. Ind. Electron. 2015, 62, 2123–2134. [Google Scholar] [CrossRef]
- Qian, W.; Panda, S.; Xu, J. Speed Ripple Minimization in PM Synchronous Motor Using Iterative Learning Control. IEEE Trans. Energy Convers. 2005, 20, 53–61. [Google Scholar] [CrossRef]
- Qian, W.; Panda, S.; Xu, J. Periodic speed ripples minimization in PM synchronous motors using repetitive learning variable structure control. ISA Trans. 2003, 42, 605–613. [Google Scholar] [CrossRef] [PubMed]
- Zhang, K.; Fan, M.; Yang, Y.; Zhu, Z.; Garcia, C.; Rodriguez, J. An Improved Adaptive Selected Harmonic Elimination Algorithm for Current Measurement Error Correction of PMSMs. IEEE Trans. Power Electron. 2021, 36, 13128–13138. [Google Scholar] [CrossRef]
- Choi, C.-H.; Cho, K.-R.; Seok, J.-K. Inverter Nonlinearity Compensation in the Presence of Current Measurement Errors and Switching Device Parameter Uncertainties. IEEE Trans. Power Electron. 2007, 22, 576–583. [Google Scholar] [CrossRef]
- Li, X.; Cheng, S.; Wang, D.; Ji, Z.; Hu, Y.; Lv, Y. A Nonintrusive Current Sensor Gain Tuning Method for Interior Permanent Magnet Synchronous Motor Drives Using Controlled Short-Circuit Tests. IEEE Trans. Transp. Electrif. 2022, 8, 1278–1288. [Google Scholar] [CrossRef]
- Harke, M.C.; Lorenz, R.D. The Spatial Effect and Compensation ofCurrent Sensor Differential Gains for Three-Phase Three-Wire Systems. IEEE Trans. Ind. Appl. 2008, 44, 1181–1189. [Google Scholar] [CrossRef]
- Lee, K.-W.; Kim, S.-I. Dynamic Performance Improvement of a Current Offset Error Compensator in Current Vector-Controlled SPMSM Drives. IEEE Trans. Ind. Electron. 2019, 66, 6727–6736. [Google Scholar] [CrossRef]
- Kim, S.-I.; Kim, J.-Y.; Lee, K.-W. Current Measurement Offset Error Compensation Scheme Considering Saturation of Current Controller in SPMSM Drives. IEEE Access 2023, 11, 17233–17240. [Google Scholar] [CrossRef]
- Kim, M.; Sul, S.-K.; Lee, J. Compensation of Current Measurement Error for Current-Controlled PMSM Drives. IEEE Trans. Ind. Appl. 2014, 50, 3365–3373. [Google Scholar] [CrossRef]
- Bai, Y.; Li, B.; Wang, Q.; Ding, D.; Zhang, G.; Wang, G.; Xu, D. An Adaptive-Frequency Harmonic Suppression Strategy Based on Vector Reconstruction for Current Measurement Error of PMSM Drives. IEEE Trans. Power Electron. 2023, 38, 34–40. [Google Scholar] [CrossRef]
- Jung, H.-S.; Hwang, S.-H.; Kim, J.-M.; Kim, C.-U.; Choi, C. Diminution of Current-Measurement Error for Vector-Controlled AC Motor Drives. IEEE Trans. Ind. Appl. 2006, 42, 1249–1256. [Google Scholar] [CrossRef]
- Park, G.-G.; Hwang, S.-H.; Kim, J.-M.; Lee, K.-B.; Lee, D.-C. Reduction of Current Ripples due to Current Measurement Errors in a Doubly Fed Induction Generator. J. Power Electron. 2010, 10, 313–319. [Google Scholar] [CrossRef]
- Lee, S.; Kim, H.; Lee, K. Current Measurement Offset Error Compensation in Vector-Controlled SPMSM Drive Systems. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 2619–2628. [Google Scholar] [CrossRef]
- Hu, M.; Hua, W.; Wu, Z.; Dai, N.; Xiao, H.; Wang, W. Compensation of Current Measurement Offset Error for Permanent Magnet Synchronous Machines. IEEE Trans. Power Electron. 2020, 35, 11119–11128. [Google Scholar] [CrossRef]
- Zuo, Y.; Wang, H.; Ge, X.; Zuo, Y.; Woldegiorgis, A.T.; Feng, X.; Lee, C.H.T. A Novel Current Measurement Offset Error Compensation Method Based on the Adaptive Extended State Observer for IPMSM Drives. IEEE Trans. Ind. Electron. 2024, 71, 3371–3382. [Google Scholar] [CrossRef]
- Cho, K.-R.; Seok, J.-K. Pure-Integration-Based Flux Acquisition with Drift and Residual Error Compensation at a Low Stator Frequency. IEEE Trans. Ind. Appl. 2009, 45, 1276–1285. [Google Scholar] [CrossRef]
- Song, P.; Ma, E.; Wang, Y.; Wang, T.; Li, H.; Wu, L. Compensation of Current Measurement Error in PMSM Drives Based on Virtual Windings. In Proceedings of the 2024 International Conference on Electrical Machines (ICEM), Torino, Italy, 1–4 September 2024; pp. 1–7. [Google Scholar]
- Song, P.; Wang, Y.; Ma, E.; Wu, L.; Wang, T.; Li, H. Current Measurement Error Compensation Based on Modified Multiple Complex-Coefficient Filters in PMSM Drives. IEEE Trans. Power Electron. 2025, 40, 4067–4079. [Google Scholar] [CrossRef]
- Lu, J.; Hu, Y.; Liu, J.; Wang, Z. All Current Sensor Survivable IPMSM Drive With Reconfigurable Inverter. IEEE Trans. Ind. Electron. 2020, 67, 6331–6341. [Google Scholar] [CrossRef]
- Song, Y.; Lu, J.; Hu, Y.; Wu, X.; Wang, G. Fast Calibration With Raw Data Verification for Current Measurement of Dual-PMSM Drives. IEEE Trans. Ind. Electron. 2024, 71, 6875–6885. [Google Scholar] [CrossRef]
- Lee, Y.-R.; Yoo, J.; Hwang, I.; Sul, S.-K. Analysis of Position Estimation Error in Signal-Injection Sensorless Control Induced by Inverter dv/dt-Based Current Measurement Noise. IEEE Trans. Power Electron. 2023, 38, 839–851. [Google Scholar] [CrossRef]
- Trinh, Q.-N.; Choo, F.H.; Wang, P. Control Strategy to Eliminate Impact of Voltage Measurement Errors on Grid Current Performance of Three-Phase Grid-Connected Inverters. IEEE Trans. Ind. Electron. 2017, 64, 7508–7519. [Google Scholar] [CrossRef]
- Trinh, Q.N.; Wang, P.; Tang, Y.; Koh, L.H.; Choo, F.H. Compensation of DC Offset and Scaling Errors in Voltage and Current Measurements of Three-Phase AC/DC Converters. IEEE Trans. Power Electron. 2018, 33, 5401–5414. [Google Scholar] [CrossRef]
- Trinh, Q.N.; Choo, F.H.; Tang, Y.; Wang, P. Control Strategy to Compensate for Current and Voltage Measurement Errors in Three-Phase PWM Rectifiers. IEEE Trans. Ind. Appl. 2019, 55, 2879–2889. [Google Scholar] [CrossRef]
- Pramod, P. Synchronous Frame Current Estimation Inaccuracies in Permanent Magnet Synchronous Motor Drives. In Proceedings of the 2020 IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 11–15 October 2020; pp. 2379–2386. [Google Scholar]
- Han, J.; Kim, B.-H.; Sul, S.-K. Effect of current measurement error in angle estimation of permanent magnet AC motor sensorless control. In Proceedings of the 2017 IEEE 3rd International Future Energy Electronics Conference and ECCE Asia (IFEEC 2017-ECCE Asia), Kaohsiung, Taiwan, 3–7 June 2017; pp. 2171–2176. [Google Scholar]
- Kang, Y.G.; Reigosa, D.D. Dq-Transformed Error and Current Sensing Error Effects on Self-Sensing Control. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 1935–1945. [Google Scholar] [CrossRef]
- Feng, X.; Wang, B.; Wang, Z.; Hua, W.; Cheng, M. Diagnosis and Identification of Common Electrical Faults in PM Machine Drives. IEEE Trans. Power Electron. 2024, 39, 13686–13695. [Google Scholar] [CrossRef]
- Feng, X.; Wang, B.; Wang, Z.; Hua, W. Investigation and Diagnosis of Current Sensor Fault in Permanent Magnet Machine Drives. IEEE Trans. Ind. Electron. 2024, 72, 1261–1270. [Google Scholar] [CrossRef]
- Jeong, Y.-S.; Sul, S.-K.; Schulz, S.; Patel, N. Fault detection and fault-tolerant control of interior permanent-magnet motor drive system for electric vehicle. IEEE Trans. Ind. Appl. 2005, 41, 46–51. [Google Scholar] [CrossRef]
- Wu, S.; Ma, G.; Yao, C.; Sun, Z.; Xu, S. Current Sensor Fault Detection and Identification for PMSM Drives Using Multichannel Global Maximum Pooling CNN. IEEE Trans. Power Electron. 2024, 39, 10311–10325. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).