Enhancing Reliability Indices in Power Distribution Grids Through the Optimal Placement of Redundant Lines Using a Teaching–Learning-Based Optimization Approach

Abstract

Given the pressing need to strengthen operational reliability in electrical distribution networks, this study proposes an optimization methodology based on the Teaching–Learning-Based Optimization (TLBO) algorithm for the strategic location of redundant lines. The model is validated on the “MV Distribution Network—Base Model” test system, considering the combination of the MTBF (Mean Time Between Failures) and MTTR (Mean Time To Repair) indicators as the objective function. After 500 independent runs, it is determined that the configuration with three redundant lines identified as LN_1011, LN_1058, and LN_0871 offers the most stable solution. Specifically, this topology increases the MTBF from 403.64 h to 409.42 h and reduces the MTTR from 2.351 h to 2.306 h. In addition, significant improvements are observed in the voltage profile and angle, along with a more balanced redistribution of active and reactive power, more efficient use of existing lines, and an overall reduction in energy losses.

1. Introduction

Reliability issues are exacerbated by outages caused by failures or unanticipated occurrences in distribution lines due to lost time and reliability of the electrical system, leading to higher costs and user disruptions. Consequently, identifying backup energy distribution routes in the case of system failures, among other events, is crucial when formulating a plan to ensure the reliability and uninterrupted provision of electrical supply [1,2].

The purpose of an electrical power system is to carry the generated and transformed load from the dispatch points to the end user, taking reliability into account and minimizing costs and losses in the electrical distribution system. The distribution system operates under conditions that affect both the end user and the system’s reliability. Generally, the topology of distribution networks is radial, extending from the substation to the end user [3,4].

One of the most important activities in electrical power system planning is in the distribution stage, as it is expected to improve reliability and reduce losses as the system’s consumer base continues to grow. Improvements to the distribution network are associated with increased reliability, as measured by reduced outage times and fewer hours of outage experienced by the end user in a given year [5].

The goal is to achieve the uninterrupted operation of electrical elements while providing cost-effective, technology-positive solutions which are in line with the performance requirements of distribution systems; accordingly, it will be possible to meet the endpoint cost requirements and meet the demands of cellphone users. In addition, in terms of effectiveness and consistency, the system and its elements are influenced by distribution network topologies and the ever-increasing supply–demand balance [6]. There are numerous other benefits to improving networks, including ensuring network stability, attracting customers, and not being penalized for unreliability. Hence, companies that are liable for electrical energy distribution are trying to improve the reliability of their distribution feeders [7].

Reliability is mostly impacted by component failure, end user interruption, and repair time. These factors are determined by a system’s reliability prediction, due to the rate of response and component failures in an electrical system. To achieve accurate prediction, reliability indices are utilized to help us respond optimally in the shortest possible time when restoring the power supply [8]. A residential user experiences between 70 and 80 min of power outages per year, caused by failures in the distribution system which they are connected to. This is because most distribution systems are radial, with the proximity of the system to the end user being varied [9,10].

This document will analyze two indices based on repair times: MTBF and MTTR. MTBF quantifies the reliability of repairable equipment by dividing the total operating hours by the number of failures. This metric is used in this analysis because components are restored after each failure; in contrast, MTTR corresponds to irreparable units and is therefore not applicable. Decreasing MTBF reduces the frequency of interruptions and improves the system’s overall reliability [11].

The Mean Time To Repair is the time it takes to repair a system. It includes the repair time and the testing time. It is an indicator of the ease of maintenance or repair of a given component, so the objective is to minimize this index to keep repair downtime as low as possible [12,13]. In power systems, the network must be both reliable and efficient. To operate a network effectively, it is essential to manage it centrally to achieve optimal power flow [14].

In distribution, optimization methods are computationally efficient. A very high-speed communication infrastructure is required to optimize its convergence on a solution that has as few interactions as possible [15]. This research employs the TLBO (Teaching–Learning-Based Optimization) algorithm to solve optimization problems. This algorithm can find the optimal point and is ideal for solving problems with large, complex computational loads, as well as for achieving reduced reaction times [16].

The TLBO algorithm employs a mathematical model for teaching and learning [16], but it does not account for the system’s reliability, as it requires a power supply to function. When a failure occurs, the redundant system replaces the non-operating or faulty component. With this redundancy system, power supply interruptions can be avoided. In any electrical system, system continuity must be ensured, and extending the redundant system would reduce failures and repair times [17].

The repair of a defective component is subject to certain restrictions associated with failures, which reveal variables such as the Mean Time To Repair (MTTR). If the element does not meet the MTTR threshold, it is taken out of operation [17]. In parallel redundancy, all components operate simultaneously. This is implemented when the system needs to remain functional without interruption [18,19].

Preliminary work will include analyzing the electrical system, determining key distribution lines, and assessing their reliability. Data will be collected and processed in parallel from two IEEE systems, excluding other electrical power distribution systems, during single-phase faults and for varying outage durations. Reliability measures will be applied to assess the degree and nature of the interruptions.

PowerFactory will be used to construct a model that replicates the EPS function. This will entail partitioning the system components along redundant distribution lines, based on previously stored reliability data. Various fault scenarios will be used to conduct functional testing and simulations to improve and assess the trade-offs of system downtime and reliability during outages.

The analysis will implement downtime mitigation and suitable reliability analyses, i.e., Mean Time Between Failures and Mean Time To Repair. Systems reliability, focusing only on two IEEE systems and not on other electrical power distribution systems, will be quantified based on the specific behavior of the distribution lines, and the system’s ability to cope with failures will be studied. This will serve as the basis for the reliability analysis of this particular system.

2. Related Works

Changing how a distribution network is organized requires minimal investment and provides significant improvements in reliability as already existing resources can be allocated more effectively. System reconfiguration depends on operational states, such as load levels across various nodes. Nonetheless, finding an optimal design requires iterative analysis and calculations [20,21].

Reliability studies utilize a design cycle that can be represented as a bathtub curve. In measuring the slope for each interval and estimating parameters with median-range regression, the standard Weibull distribution is applied, along with other parameters derived from linear regression of the logarithm of useful life, as in the total factor deterioration index (TFDI) [22].

Placing reclosers in a balanced way, which can disconnect faults within a few seconds and prevent downtime for end users, is one technique to improve recloser placement. This is to analyze the SAIFI and SAIDI [23] reliability indices in ETAP. Smart grids offer uninterrupted power and system reliability. The Monte Carlo method is used in a stochastic study of a system with a sequential time structure, in which events are ordered temporally, creating a series of repair cycles that focus on repair and failure times [24].

2.1. Distribution Reliability Indices

When a power failure occurs in the distribution system, the goal is to restore power to end users as quickly as possible, ensuring regular, stable operation. The procedure for managing faults is divided into three levels: first, locate the fault; second, isolate the fault from the distribution network; and third, restore power. Reliability indices help identify fault locations by providing information to restore the power supply as quickly as possible. The main reliability characteristics have been defined as user-based and demand-based [8].

Mean Time Between Failures (MTBF) quantifies the average time between consecutive network outages; its estimate is presented in (1), where the product of the total number of users and the 8760 h per year is divided by the sum of impacted customers. The result, expressed in hours, summarizes the frequency of failures according to the fraction of compromised demand [12,25].

$$MTBF={\displaystyle \frac{N_T·8760}{{\sum }_{i=1}^n{N}_i}}$$

(1)

The Mean Time To Repair (MTTR) indicates the average time required for the system to restore service after each interruption. Equation (2) establishes its calculation. The numerator adds the products, while the denominator accumulates the interrupted users. The result, expressed in hours, evaluates the effectiveness of service restoration efforts [12,25].

$$MTTR={\displaystyle \frac{\sum U_i·N_i}{\sum N_i}}$$

(2)

2.2. Reliability in Redundant Systems

In any electrical or electronic system, system continuity must be ensured, and extending the redundant system would reduce failures and repair times. In the event of a failure, the N + 1 redundant system will replace the failing hot component, thereby avoiding process interruptions [17].

The repair of a defective component is subject to certain restrictions associated with failures, which reveal variables such as the Mean Time To Repair (MTTR). If the element does not meet the MTTR threshold, it is taken out of operation. When performing a reliability analysis on redundant systems, the components are assumed to be independent and to fail simultaneously. Still, in practice, most systems are connected in parallel with another element [26].

In parallel redundancy, all components operate simultaneously. This is implemented when the system needs to remain functional without interruption [18]. Redundancy leads us to consider random variables, such as the useful life of components in a redundant parallel system, which follow a marginal exponential distribution. Then, Tmax (X, Y) has the following reliability function:

$$R\left(t\right)=P\left(min(X,Y)>t\right)={\overline{F}}_{X,Y}(t,t)=e^{-2\lambda t}\left(1+\alpha -2\alpha e^{-\lambda t}+\alpha e^{-2\lambda t}\right)$$

(3)

In this expression, $\alpha$ represents the dependency factor between components in a parallel redundancy arrangement and accounts for the reduction in independence in their joint failure behavior. Values of $\alpha$ are typically obtained from empirical reliability studies or manufacturer data.

Redundant components on standby take over when the system fails. This method is used when component replacement does not require a lengthy process and does not cause further system failure [19]. The convolution of the variables is estimated stochastically, yielding T = X + Y, the system’s useful life, and the following distribution function when they are independent.

The failure and repair times of each component are modeled as exponential random variables with constant rates, and failures are assumed independent across components. This approximation is widely used in reliability assessments of radial medium-voltage distribution systems, where outages are predominantly driven by external random events rather than aging-related mechanisms. Although more sophisticated models could incorporate correlated faults or non-exponential time-to-failure distributions, these require detailed historical datasets that are not available for the present case study. Therefore, the analysis is explicitly framed within a memoryless, independent reliability model, which provides a tractable yet sufficiently accurate representation for evaluating the effect of redundant line placement.

3. Methodology and Problem Statement

The financial losses directly caused by outages and service unavailability resulting from failures in distribution lines highlight the importance of reliability in the distribution of electrical power. A redundancy methodology is utilized as part of a TLBO-focused reliability integration and optimization process presented in this paper.

The proposed process comprises six steps to enhance distribution system reliability. Steps are illustrated in Figure 1. The first step involves reliability assessment of a test system using DigSilent PowerFactory, where fundamental reliability indicators are calculated, and the system’s initial MTBF and MTTR figures are established. Then, the basic indicators, MTBF and MTTR, are downloaded from the repository. To provide data to the mathematical optimizer, the MTBF and MTTR must also be retried, and in turn, the TLBO searches. The search examines a range of systems, and those that do not meet the electrical requirement are eliminated. Subsequently, systems to be considered are those that reduce MTTR, while systems that perform less than optimally from an electrical perspective are excluded. The result is an answer to the question of what is the optimal location and the minimum number of redundant distribution lines required to achieve higher reliability.

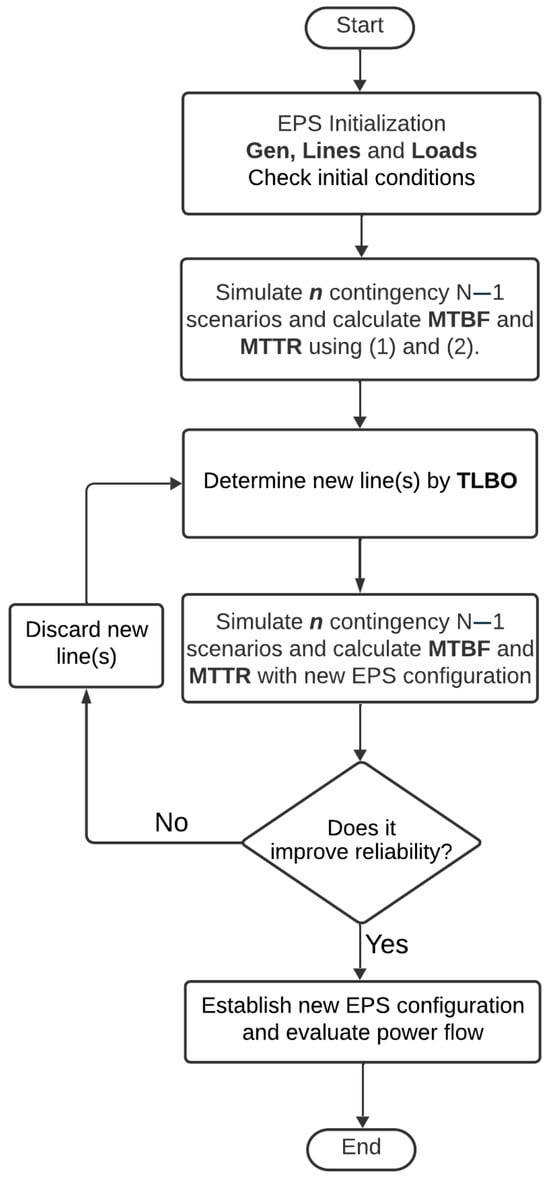
Figure 1. Proposed methodology for improving the reliability of distribution systems.

In the DigSilent model, which has been optimized in previous cycles, the redundant lines identified earlier are integrated, and the critical nodes are connected. In the modified system, a new reliability analysis is conducted, and new MTBF and MTTR parameter values are evaluated to confirm the improvement in the indicators. If the outcomes of the modified system do not meet a satisfactory evidence of improvement, the parameters are altered, and the optimization cycle is repeated.

In the very last stage of the process, the original configuration and the finalized system are reviewed and compared. This process involves analyzing reliability indicators and key electrical parameters, including the nodal voltage profile, active and reactive power, phase angle, technical losses, and, of course, the system’s overall reliability and electrical performance.

3.1. Reliability Analysis

This study examines six reliability cases: the base system with no reinforcements (S0) and five systems with one to five optimal redundant lines (S1–S5). Using the robust TLBO technique, applied 500 times to a 278-bus system with five increasingly complex iterations, the redundant lines are determined. All scenarios are kept with the same historical loads and network topology so that the difference in MTBF and MTTR achieved with the reinforcements is directly comparable.

The historical loads correspond to static representative operating snapshots extracted from the utility database. These values are not time series measurements; instead, they represent typical loading conditions used for reliability assessment. Consequently, no temporal sampling or seasonality modeling is required for the scenarios analyzed.

Algorithm 1 summarizes the procedure for analyzing the reliability of the electrical distribution system in each scenario, organizing the stages developed in the DigSilent PowerFactory simulation environment. This ranges from initial parameterization to the obtaining of final indicators, beginning with the loading of historical operation and maintenance data for each component of the system. Table 1 describes all variables used in Algorithm 1.

Table 1. Description of the variables used in Algorithm 1.

Symbol	Description
${\lambda }_i$	Failure rate of component i (failures/hour)
${\mu }_i$	Repair rate of component i (repairs/hour)
$N_{f,i}$	Number of failures of component i
$T_{\mathrm{operation},i}$	Total operation time of component i
$N_{r,i}$	Number of repairs of component i
$T_{\mathrm{repair},i}$	Total repair time of component i
$T_{f,i}$	Random failure time generated for i
$T_{r,i}$	Random repair time generated for i
$MTB{F}_i$	Mean Time Between Failures of component i
$MTT{R}_i$	Mean Time To Repair of component i
$A_i$	Availability of component i

In lines 2 to 5, for each component i, the failure rate $\lambda$ is calculated by dividing the number of failures $N_{f,i}$ by the total operating time $T_{operation,i}$, similarly determining the repair rate ${\mu }_i$ by dividing the number of repairs $N_{r,i}$ by the total repair time $T_{repair,i}$. Likewise, in lines 6 and 7, the network model is configured in PowerFactory, specifying the analysis time horizon and the number of simulation iterations required to assess the system’s probabilistic behavior under failures.

In lines 8 to 14, the simulation cycle is executed, generating failure and repair events for each component i using exponential distributions with their respective parameters. This allows the system status to be recorded over time and the cumulative duration of unavailability events to be calculated. Once the simulation is complete in lines 15 to 18, the Mean Time Between Failures $MTB{F}_i$, the Mean Time To Repair $MTT{R}_i$, and the availability $A_i$ for each component is determined using the appropriate mathematical expressions. This reveals the individual performance of each element and facilitates the evaluation of its contribution to the overall system reliability.

All candidate redundant lines were modeled as normally open tie switches to ensure the network remains radially operated under normal conditions. This guarantees that no meshed configurations or unintended loops are created after adding redundant links. During contingency evaluations, only one tie switch is closed per event, in accordance with typical switching practices and to prevent conflicts with existing protection coordination. As the focus of this study is on MTBF/MTTR-based reliability improvement, detailed relay modeling and service interruption metrics (e.g., SAIDI and SAIFI) were omitted, and the scope is explicitly restricted to reliability behavior under radial operation.

Algorithm 1 Reliability Evaluation in DigSilent PowerFactory

1: Input: Historical operation and maintenance data   2: for each component i do   3:    Calculate ${\lambda }_i\leftarrow {\displaystyle \frac{N_{f,i}}{T_{\mathrm{operation},i}}}$   4:    Calculate ${\mu }_i\leftarrow {\displaystyle \frac{N_{r,i}}{T_{\mathrm{repair},i}}}$   5: end for   6: Configure the network model and parameters in PowerFactory   7: Define simulation horizon and number of scenarios   8: for each simulation iteration do   9:    for each component i do 10:      Simulate failure with $T_{f,i}\sim \mathrm{Exp}\left({\lambda }_i\right)$ 11:      Simulate repair with $T_{r,i}\sim \mathrm{Exp}\left({\mu }_i\right)$ 12:      Record failure duration and event occurrence 13:    end for 14: end for 15: for each component i do 16:    Calculate $MTB{F}_i\leftarrow {\displaystyle \frac{1}{{\lambda }_i}}$ 17:    Calculate $MTT{R}_i\leftarrow {\displaystyle \frac{1}{{\mu }_i}}$ 18:    Calculate $A_i\leftarrow {\displaystyle \frac{{\mu }_i}{{\lambda }_i+{\mu }_i}}$ 19: end for 20: Output: Indicators $MTBF$, $MTTR$, and system availability

3.2. Data Processing

The export of electrical and reliability data from DigSilent PowerFactory is performed using a DPL routine, as detailed in Algorithm 2, which automates the procedure and transfers results from the simulation environment to Excel spreadsheets. This facilitates the organization of technical information for subsequent analysis and is used as input in the optimization algorithm. Table 2 describes all variables used in Algorithm 2.

Algorithm 2 Export of Electrical and Reliability Data from DigSilent to Excel

1: Input: Network case with executed load flow and reliability study   2: Start Excel connection   3: if Excel does not start then   4:    Show error message and terminate process   5: end if   6: Set Excel visibility and open file at defined path   7: Export of nodal variables (voltage and angle)   8: Create and activate sheet “Nodes”   9: Write headers: Node, $V(p.u.)$, $\varphi {(}^{°})$ 10: Execute load flow (ComLdfExecute()) 11: for each node $O_{bus}$ in ElmTerm do 12:    Read voltage $V_{p.u.}:u$ 13:    Read angle ${\theta }_u-{\theta }_{bus}:{\varphi }_{iu}$ 14:    Write node name, $V_{p.u.}$ and ${\theta }_u$ in sheet “Nodes” 15: end for 16: Export of line variables 17: Create and activate sheet “Lines” 18: Write headers: Line, $L_{ab}$, Long(km), Bus1, Bus2 19: $I_{b1},I_{b2},S_{b1},S_{b2},P_{b1},P_{b2},Q_{b1},Q_{b2},Load(\%)$ 20: Execute load flow (ComLdfExecute()) 21: for each line $O_{line}$ in ElmLine do 22:    Read attributes: name, type, length, buses 23:    Read electrical variables: $I_{b1},I_{b2},S_{b1},S_{b2},P_{b1},P_{b2},Q_{b1},Q_{b2},Load$ 24:    Write line data with all values in sheet “Lines” 25: end for 26: Export of reliability results 27: Create additional sheet for reliability 28: Extract results of MTBF, MTTR and availability from RA module 29: Write results in structured table by component 30: Output: Excel file with sheets: “Nodes”, “Lines” and “Reliability”

Table 2. Description of the variables used in Algorithm 2.

Symbol	Description
$o_{bus}$	Node object of type ElmTerm
$v_{pu}$	Node voltage in per unit (p.u.)
${\varphi }_u$	Phase angle of the node in degrees (°)
$o_{line}$	Line object of type ElmLine
$typ$	Line type (associated object)
$long$	Line length (km)
$bus1,bus2$	Nodes connected at the line ends
$I_{b1},I_{b2}$	Current at each line end (kA)
$S_{b1},S_{b2}$	Apparent power at each line end (MVA)
$P_{b1},P_{b2}$	Active power at each line end (MW)
$Q_{b1},Q_{b2}$	Reactive power at each line end (Mvar)
$Load$	Line load percentage (%)
$MTBF$	Mean Time Between Failures of the component
$MTTR$	Mean Time To Repair of the component
A	Operational availability of the component

Lines 1 to 3 specify the process input, represented by a network case with previously performed load flow and reliability studies. Additionally, the connection between PowerFactory and Excel is established, and an error message is generated, and the procedure is halted if the connection is unsuccessful. Once the connection is complete, line 6 adjusts the visibility of Excel and opens the file located in the specified path, enabling interaction with specific sheets in the workbook to store the data obtained.

Lines 7 to 14 export nodal variables, creating and activating a sheet called “Nodes” where the headers are entered: node name, voltage per unit, and phase angle. Then, the load flow is executed, and each ElmTerm element is scanned, reading the voltage and angle values for each node and recording them in the sheet next to the corresponding identifier.

Lines 16 to 19 export line data, creating a sheet called “Lines” with the following variable headers: line name, type, length, connected nodes, current at both ends, apparent power, active power, reactive power, and load capacity. The load flow is then executed, and each active line in the system (ElmLne) is traversed to record its general attributes and electrical variables in a new row within the respective sheet.

3.3. Optimization with TLBO

The TLBO algorithm identifies the optimal location of redundant distribution lines to increase system reliability, as shown in Algorithm 3. To do this, it uses the MTBF and MTTR vectors, the contingency table T, and the total number of bars n as input. In addition, execution parameters are defined, such as the maximum number of redundant lines to be inserted $M_{max}$, the number of independent repetitions $N_{repetitions}$, the iterations per run $N_{iter}$, and the population size P, generating a population m of solutions for each number of redundant lines $P_{ij}$ where each $L_i$ represents a set of candidate bars for insertion. Table 3 describes all variables used in Algorithm 3.

Table 3. Description of the variables used in Algorithm 3.

Symbol	Description
$MTBF$	Vector of Mean Time Between Failures
$MTTR$	Vector of Mean Time To Repair
T	System contingencyTable
n	Total number of buses
$M_{max}$	Maximum number of redundant lines considered
$N_{\mathrm{repetitions}}$	Number of independent algorithm repetitions
$N_{\mathrm{iter}}$	Number of iterations per run
P	Population size (number of individuals)
k	Index of the independent run
m	Number of redundant lines under evaluation
$P_{i,j}$	Bus value at row i and column j of the population
$VO\left(L\right)$	Objective function value for a solution L
$V{O}_{min}$	Best objective value recorded in a run
t	Iteration index in a run
$L_i$	Solution (individual) i within the population
M	Teacher solution (current best individual)
$Ne{w}_i$	New solution generated for individual i
$diff$	Difference between two selected individuals
$L_{(k,m)}$	Best solution obtained in run k for m lines
$L_m^{\ast }$	Final optimal solution for m redundant lines

The population evolves during execution through the teaching and learning phases, with individuals in the first phase adjusting according to the best current solution, M. In the second phase, new solutions are generated by comparing pairs. The proposed solutions $Ne{w}_i$ are validated and replaced only if they improve the objective value. Finally, once all the runs have been completed, the best $L_m^{\ast }$ solution is selected for each m, representing the most robust locations for installing redundant lines.

Although the scalar index $VO\left(L\right)$ provides a convenient measure for comparing candidate configurations, the ratio (4) combines quantities expressed in hours and may obscure the relative importance assigned to the two underlying criteria (i.e., maximizing MTBF and minimizing MTTR). To avoid these dimensional inconsistencies and to make the trade-off explicit, the problem was reformulated under an actual multi-objective perspective.

$$VO\left(L\right)={\displaystyle \frac{{\sum }_{i}MTB{F}_i}{{\sum }_{i}MTB{F}_i+{\sum }_{i}MTT{R}_i}}$$

(4)

In particular, we introduce the normalized weighted objective function (5), where $MTB{F}_0$ and $MTT{R}_0$ denote the baseline values of the original network (scenario S0). This formulation is dimensionless, allows direct interpretation of improvements relative to the base case, and eliminates the unit-mixing issue.

$$F\left(L\right)=w_1{\displaystyle \frac{MTBF\left(L\right)}{MTB{F}_0}}+w_2{\displaystyle \frac{MTT{R}_0-MTTR\left(L\right)}{MTT{R}_0}},w_1+w_2=1,$$

(5)

Algorithm 3 Robust optimization of redundant line placement using TLBO and normalized weighted objective

1: Input: MTBF and MTTR vectors, baseline indices $MTB{F}_0$ and $MTT{R}_0$, weight pair $(w_1,w_2)$, contingency table T, total number of buses n   2: Define parameters: $M_{max}$, $N_{\mathrm{rep}}$, $N_{\mathrm{iter}}$, population size P   3: Initialize storage matrices $results\_rep$ and $solutions\_rep$   4: for$k=1$ to $N_{\mathrm{rep}}$ do   5:    Set random seed $\mathrm{rng}\left(k\right)$   6:    for $m=1$ to $M_{max}$ do   7:      Initialize random population $\mathcal{P}\in {\mathbb{Z}}^{P\times m}$, each $P_i$ containing m distinct line indices in $[1,n]$   8:      For any placement L, compute $$MTBF\left(L\right)=\sum _{i\in L}MTB{F}_i,MTTR\left(L\right)=\sum _{i\in L}MTT{R}_i$$   9:      Evaluate the normalized weighted objective $F\left(L\right)$ according to (5) 10:      Set $F_{\mathrm{best}}\leftarrow -\infty$ 11:      for $t=1$ to $N_{\mathrm{iter}}$ do 12:         Evaluate each $L_i$ in the population 13:         Identify teacher M as the individual with maximum $F\left(·\right)$ 14:         // Teaching phase 15:         for $i=1$ to P do 16:           $Ne{w}_i\leftarrow P_i+\mathrm{rand}\left(\right)·(M-P_i)$ 17:           Project $Ne{w}_i$ to valid indices in $[1,n]$ without repetition 18:           if $F\left(Ne{w}_i\right)>F\left(P_i\right)$ then 19:              $P_i\leftarrow Ne{w}_i$ 20:           end if 21:         end for 22:         // Learning phase 23:         for $i=1$ to P do 24:           Choose random $j\ne i$ 25:           $diff\leftarrow$ direction toward the better of $\{P_i,P_j\}$ in terms of $F\left(·\right)$ 26:           $Ne{w}_i\leftarrow P_i+\mathrm{rand}\left(\right)·diff$ 27:           Project $Ne{w}_i$ to valid indices in $[1,n]$ 28:           if $F\left(Ne{w}_i\right)>F\left(P_i\right)$ then 29:              $P_i\leftarrow Ne{w}_i$ 30:           end if 31:         end for 32:         Update global best: if ${max}_{i}F\left(P_i\right)$ improves $F_{\mathrm{best}}$, store $(F_{\mathrm{best}},MTB{F}_{\mathrm{best}},MTT{R}_{\mathrm{best}},L_{\mathrm{best}})$ 33:      end for 34:      Save $(F_{\mathrm{best}},MTB{F}_{\mathrm{best}},MTT{R}_{\mathrm{best}},L_{\mathrm{best}})$ into $results\_rep(k,m)$ and $solutions\_rep(k,m)$ 35:    end for 36: end for 37: Selection per m: 38: For each $m\in \{1,\dots ,M_{max}\}$, build the solution set $${\mathcal{S}}_m=\left\{\left(F_{k,m},MTB{F}_{k,m},MTT{R}_{k,m},L_{k,m}\right):k=1,\dots ,N_{\mathrm{rep}}\right\}$$ 39: and select the robust representative $L_m^{\ast }$ (e.g., the one with maximum mean F, low variability, or lying on the empirical Pareto front in the $\{-MTTR,+MTBF\}$ plane). 40: Output: For each m, return robust optimal placement $L_m^{\ast }$ and its performance indicators.

To assess robustness against preference variations, a sensitivity analysis was performed using three representative weight pairs:

$$(w_1,w_2)\in \left\{(0.5,0.5),(0.7,0.3),(0.3,0.7)\right\}.$$

(6)

The obtained iso-utility curves as well as the related MTBF-–MTTR trade-off for the best configuration are shown in Figure 2. Since the same configuration is optimal across these weight combinations, this shows that the final choice is insensitive to the presumed utility structure.

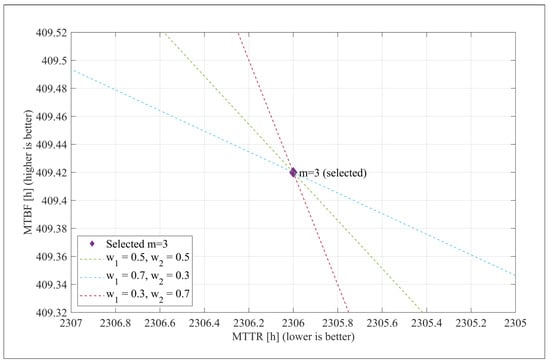
Figure 2. The MTBF–MTTR plane and iso-utility curves of normalized weighted objective $F\left(L\right)$ for the best configuration obtained with $m=3$. The diamond marker corresponds to the best TLBO solution, while the dashed lines are iso-utility curves for weight sets $(w1,w2)=(0.5,0.5),(0.7,0.3),(0.3,0.7)$.

Lastly, in accordance with the reviewer’s request, we added to the Results section a Pareto visualization of the two objectives, in which each candidate solution is assessed in terms of its MTBF–MTTR performance without scalarization.

$$\{-MTTR,+MTBF\}$$

(7)

3.4. Case Study

The proposed methodology has been tested on the MV Distribution Network Base Model within the DigSilent PowerFactory environment. This test system simulates a distribution system at the medium-voltage level with realistic characteristics. It is a model typically used in studies investigating reliability, load flow, and contingency analysis. The model has four primary substations (SUB_01 to SUB_04), and over 270 load connection points and almost 300 primary distribution circuits.

Because of the detail in the network and the limitation of pages in the manuscript, a complete one-line diagram of the network is not presented. However, the network has a radial topology with a primary backbone, multiple lateral branches, and areas with highly concentrated loads. Nested in this topology are the lines LN_1011, LN_1058, and LN_0871, which were repeatedly selected during the optimization and are considered the most advantageous for additional control or standby redundancy. This is because they are located in the topologically central areas where several feeder branches converge or where a load pocket is located.

All failure rates ${\lambda }_i$ and repair times ${\mu }_i$ in this paper are associated with equipment reliability parameters within the DIgSILENT PowerFactory model of the MV feeder. These data were obtained from the utility’s historical reliability database and directly incorporated into the component data of the software. The system contains over 270 nodes and around 300 distribution lines, so the complete database is relatively large and is omitted here.

4. Results Analysis

This portion covers the results from the TLBO algorithm, which optimizes the placement of redundancy lines within the electrical distribution system. Clinching the most optimal solutions for varying tiers of additional line placements was the key focus of the analysis, as was how each line placement optimally influenced the objective function value of the defined problem.

This portion also assesses the impact of the chosen placements on key operational indicators within the system. These indicators are pivotal to the overall functionality of the distribution network. The system’s operational efficiency is then informed by its operational criteria, which analyze the system’s voltage readings at specific nodes, line power flows, and overall system energy loss. The focus here is on how the changes in the system structure, e.g., additional line placements, change the distribution of power in the system.

The results achieved by employing TLBO optimization techniques are displayed in Table 4. The algorithm showed iterative improvement, with the mean, $\mu$, objective function value increasing progressively as redundant lines were added until an optimal value of $m=4$ was reached. It is interesting to note, however, that the selected solution was $m=3$, since the relative dispersion (CV) was the lowest and $\sigma$ was statistically stable over the 500 iterations, independent of the lines selected. This finding indicates that lines LN_1011 and LN_0871 (the selected lines) showed the highest frequency in different configurations, making them valuable to consider strategically for the positioning of additional redundant lines in the electrical distribution system.

Table 4. Result of optimization using TLBO.

m	Mean	$\mathit{\sigma }$	CV	Selected Lines
1	0.06908	0.02583	0.374	LN_0711
2	0.01448	0.01827	1.262	LN_1098 LN_0061
3	0.00429	0.00438	1.021	LN_1011 LN_1058 LN_0871
4	0.00389	0.00443	1.140	LN_0076 LN_0008 LN_1011 LN_0871
5	0.00564	0.00600	1.064	LN_0076 LN_0008 LN_1011 LN_1008 LN_0871

In Table 4, the mean value of the target function is the highest for the configuration with four redundant lines ($m=4$), which is four times larger than that of the configuration with three redundant lines ($m=3$); at the same time, this configuration has a four times larger coefficient of variation (CV) which corresponds to larger dispersion and lower stability of the optimization process, which means that configuration has a four times larger CV. On the other hand, configuration with three redundant lines ($m=3$) also has a mean that is, however, smaller without any minimal additional variation.

Therefore, the choice of m is robust: the foremost configuration provides the most remarkable mean improvement and statistical stability, while the other configuration provides a higher mean improvement but greater instability, making it impractical. $m=3$ is the configuration with the most remarkable mean improvement and that is also statistically stable; hence, this is the configuration recommended for use.

To be able to understand the trade-off concerning reliability improvement versus repair time reduction and the impact of the weighting factors in the normalized objective $F\left(L\right)$, Figure 2 shows the MTBF–-MTTR plane for the best configuration attained with $m=3$. The dashed curves are level sets for $F\left(L\right)$, illustrating three representative weight pairs and demonstrating that the chosen configuration is still optimal for various reliability–repair time preferences.

4.1. Evaluation of Reliability Indicators

As a direct consequence of having a functioning answer accompanied by three spare lines, there were significant changes for the better in the reliability metrics, particularly the average MTBF, which increased from 403.64 to 409.42, and the MTTR, which improved from 2.351 to 2.306 h, as seen in Figure 3. This shows fewer recurrent failures of the system and a quicker return to functionality in every incident, thus validating that the fine-tuned placement of spare lines using the TLBO algorithm significantly improves the electric distribution system’s reliability.

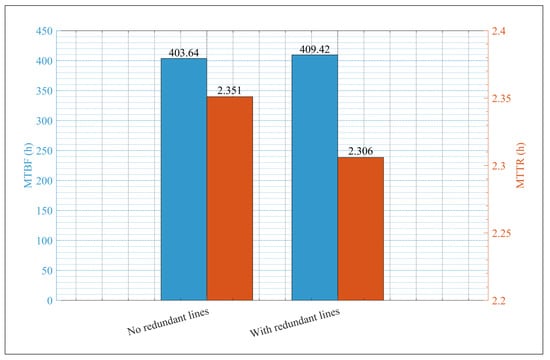
Figure 3. Comparison of MTBF and MTTR reliability indicators.

It should be made clear that the values of MTBF and MTTR used in the study express deterministic MTBF and MTTR and are influenced and defined by the failure and repair rates of the elements in the model. Hence, these quantities should not be viewed as sample statistics from many realizations of the system. Thus, classical forms of uncertainty that would lead to confidence intervals, etc., or paired hypothesis testing do not apply in this case. For pure interpretive value, we analyze the value of MTBF and MTTR deviations concerning the base case, as this indicates the degree of change and value of the improvement.

4.2. Electrical Impact of Redundant Lines

The voltage profile results show that in the simulation without redundant lines (red line), the most significant voltage dips (about 0.94 p.u.) are recorded at nodes 1500 and 2000. When redundant lines are included (blue line), the lowest values (roughly 0.95 p.u.) are positioned around line 2000 and show a smaller spread. The other nodes show a higher voltage in the 0.98 p.u. range. The observations indicate that redundant lines are critical to enhancing the voltage profile (Figure 4).

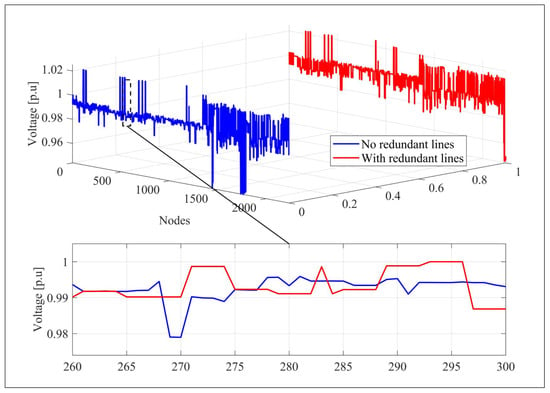
Figure 4. Comparative analysis of voltage profiles with and without redundant lines.

Analysis of the stress angle (Figure 5) reveals that, without redundant lines (blue line), angular variations are significant, reaching a value of approximately −10° in the nodes after 2000. With redundant lines (red line), although variations persist, they are less intense and remain between −4° and −8°.

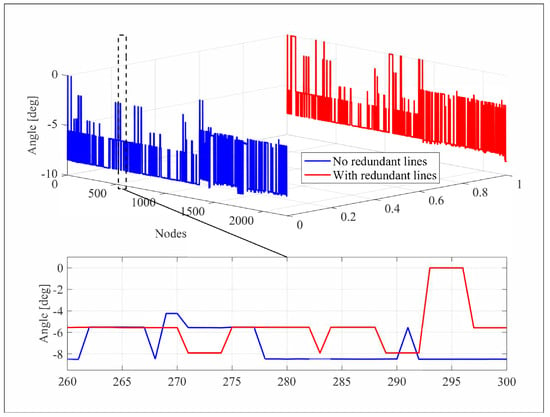
Figure 5. Comparative analysis of the stress angle with and without redundant lines.

In addition to the performance enhancements demonstrated in Figure 4 and Figure 5, the data show that the voltages are in a tighter, more stable operational range than before the addition of lines, with fewer drastic outliers and reduced variability across the nodes. Similarly, it is evident that the voltages are more tightly grouped, and the difference in the upper and lower octave ranges seems to have decreased. These measurable changes suggest an increase in the coherence of voltages and angles throughout the feeder system, which aligns with the more optimized power flow characteristic of the additional pathways.

One of the benefits of the additional redundant lines is the ability to reduce angular dispersion, resulting in better overall synchronization among the nodes. Figure 6 shows how the addition of redundant lines results in a changed distribution of active power per line flowing through the network. In the new configuration, the power flows are within the expected ranges for medium-voltage distribution feeders, with a better power load–flow balance. The system flow pattern changes from one with a high discrepancy in branch counts to one with lower flows and more uniform flows in the network. The overall power transferred is slightly lower in some lines, as additional lines mean power can be more evenly risk-managed, leading to less overall risk in a line. As a result, the less power transferred, the more evenly it is spread over the lines. The additional path presence leads to less localized stress on individual lines. It allows for power to be balanced more freely across the network to be distributed over a greater selection of branches. Ultimately, this leads to a more balanced and reliable operational distribution network.

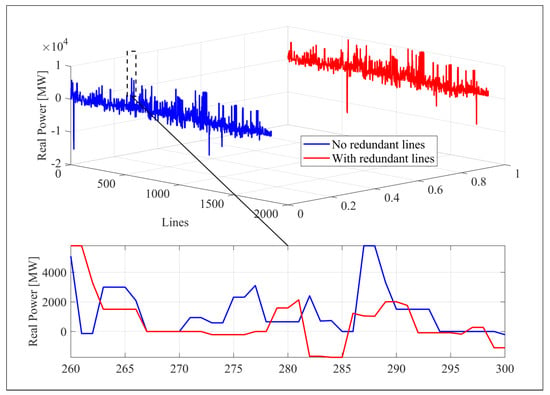
Figure 6. Comparative analysis of real power with and without redundant lines.

For its part, the comparison of reactive power per line reveals a more concentrated distribution with less dispersion in the system with redundant lines, as shown in Figure 7. In the original configuration, reactive flows vary widely, with values exceeding ±3000 Mvar. After the topology modification, the values are grouped in a narrower range, with fewer extreme fluctuations. There is evidence of an attenuation in power peaks, reflecting more uniform behavior between consecutive sections. This redistribution helps to stabilize the reactive power exchange in the network.

Figure 7. Comparative analysis of reactive power with and without redundant lines.

The comparison of load capacity, as shown in Figure 8, reveals that incorporating redundant lines increases the utilization percentage of existing lines. This transforms a system where the original topology has load levels below 40% across virtually the entire network into one where the values increase and are evenly distributed, with multiple lines operating between 40% and 80% of their nominal capacity. This behavior is explained by flow redistribution, which enables previously underutilized lines to participate more actively in energy transport.

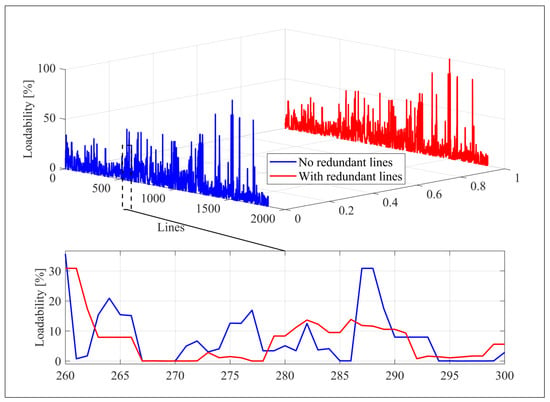
Figure 8. Comparative analysis of loadability y with and without redundant lines.

The comparison of active power losses, shown in Figure 9, demonstrates an overall reduction following the implementation of redundant lines. This is evidenced by a transformation of the system, where the original configuration shows losses peaking at up to 60 MW in specific sections. However, in a modified configuration, the values are distributed more evenly with considerably lower magnitudes.

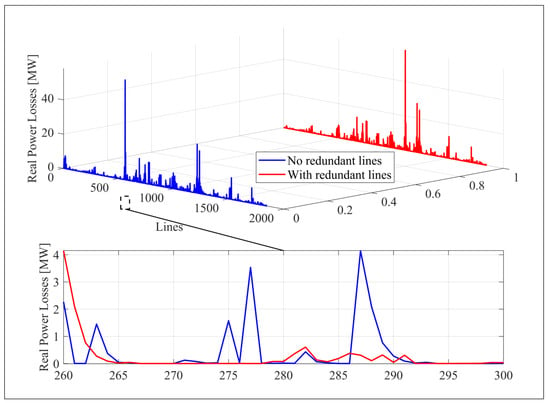
Figure 9. Comparative analysis of real power losses with and without redundant lines.

The reactive power losses per line, shown in Figure 10, experience a general reduction after the incorporation of redundant lines. Since the initial configuration shows pronounced negative values exceeding −40 Mvar in multiple sections, the modified configuration stabilizes the values in a narrower range, with less depth at the extremes.

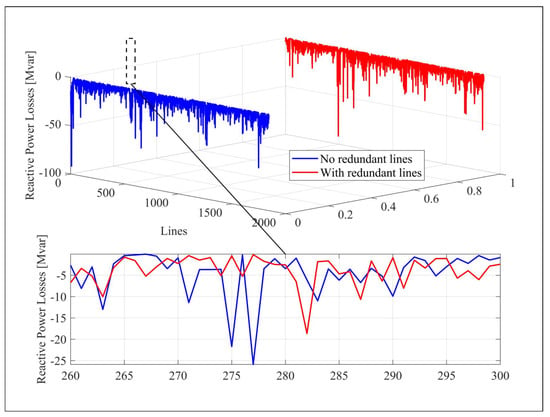
Figure 10. Comparative analysis of reactive power losses with and without redundant lines.

Various factors, such as voltage drops, equipment failures, weather events, or operational interference with power systems, can cause outages of electrical distribution systems. These outages can be random. Given the presence of redundant lines, outages may be longer due to switching interlocks or slow communication. Outages and their durations represent problems utilities are trying to solve, as prolonged outages result in additional operational expenses and less customer dissatisfaction. Similar issues extend to the continuity of operational data as well. The data are also required to support the demand response and intelligent metering systems. Distribution utilities not being able to provide enough redundant lines economically has also been noted as a challenge in [27] operational challenges across the world.

5. Limitations and Future Works

The evaluation of the reliability of the memoryless, independent failure processes is used in this instance, in line with the characteristics of the studied MV feeder. At the same time, future work might employ correlated failures or non-exponential lifetimes to capture complex outage mechanisms better.

This work presents the results of optimizations based on a singular, fully parameterized distribution feeder for which operational and reliability data have been collected in great detail. Although this “Base Model” can provide a realistic insight into the impact of redundant line placement on operational performance, it can cover only a limited set of benchmark scenarios. To enhance the external validity of the methodology, other distribution networks with a variety of structural, operational, and reliability characteristics would need to be assessed, and a comparison of TLBO with other, more popular, meta-heuristic approaches would be conducted. Such approaches are more onerous from a technical perspective, as they would involve reparameterizing failure models, along with the switching constraints and network data to maintain methodological consistency, and are therefore seen as one of the more promising areas of future work.

This analysis poses a small number of operational constraints. It assumes that the system operates radially, with normally open tie switches, and is not detailed to include protection modeling or service interruption indices such as SAIDI or SAIFI. Future developments may provide a more operational evaluation of the model if protection and interruption duration metrics are integrated.

It should be highlighted that the MTBF and MTTR values presented here are model-generated metrics that depend on assumed failure and repair rates. They are not actual values obtained from empirical multiple independent realizations of the system. As a result, there are no formal confidence intervals or hypothesis testing for repeated runs. We consider more detailed uncertainty quantification through, for example, sensitivity or bootstrap analyses to the failure and repair parameters to be an important subject for future research.

6. Conclusions

The application of the TLBO algorithm successfully achieved the specific objectives set out in the research. First, the challenges related to reliability and downtime were clearly identified, highlighting the need for redundant lines to improve the system’s operational performance. Second, through the analysis and evaluation of Mean Time Between Failures (MTBF) and Mean Time To Repair (MTTR), it was determined that the best solution obtained corresponds to the incorporation of three redundant lines (LN-1011, LN-1058, and LN-0871) due to their greater statistical stability and lower variability in results.

Simulation of the distribution system under defined scenarios quantitatively confirmed the improvement in reliability, increasing the MTBF from 403.64 h to 409.42 h and reducing the MTTR from 2.351 h to 2.306 h. In addition, the findings demonstrated specific electrical benefits: the voltage profile showed lower drops and greater stability above 0.98 p.u., angular dispersion decreased significantly, and the distribution of active and reactive power became more uniform, with a considerable reduction in energy losses. Finally, the average line load capacity increased, confirming a more efficient use of the existing electrical infrastructure.

These results clearly validate that the proposed optimal location of redundant lines meets the overall objective of strengthening reliability indicators and improving the electrical performance of the distribution system.

Even though TLBO was chosen because it is parameter-free for implementation and exhibits convergent behaviour, it may have yielded better results if compared with other metaheuristics, such as GA, PSO, and DE. This would involve reparameterizing the search and reliability evaluation for each algorithm and so is recognized as future work.

While this work primarily focuses on the structural aspects of the benefits gained from the placement of redundant lines, other unrelated operational factors affect the practical restoration time, such as crew dispatch, worker availability, and maintenance scheduling. The combination of reliability-oriented optimization with crew management models may improve restoration performance and this indeed is an appealing prospect for future work.