A Bidirectional Multidevice Interleaved SEPIC–ZETA DC–DC Converter for High-Efficiency Electric Mobility

Abstract

This paper presents a high-efficiency bidirectional multidevice interleaved SEPIC–ZETA DC–DC converter for electric mobility applications. The proposed converter offers key advantages, including reduced current and voltage ripple at both the input and output ports, achieved through a port ripple frequency six times higher than the switching frequency. Additionally, the required magnetic and capacitor volume is significantly reduced due to an inductor ripple frequency twice the switching frequency, leading to minimized power losses, reduced stress on power components, and enhanced efficiency. The use of a multidevice structure facilitates more efficient inductor volume optimization and provides improved fault redundancy. The converter is particularly suited for electric vehicle energy management systems, enabling efficient energy management among the various subsystems. It operates in open-loop mode, and this manuscript details the steady-state operating principle under continuous conduction mode. Design guidelines for parameter selection, comprehensive mathematical derivations, and a comparative analysis with existing DC-DC converters are presented. To validate the proposed topology, a 5 kW laboratory prototype was developed and tested across a wide range of load conditions. The experimental results confirm the converter’s high performance, achieving a peak efficiency of 98.6% at rated power.

1. Introduction

The increasing global demand for sustainable energy has positioned renewable energy generation as a viable solution to address energy shortages. A key area of ongoing research involves the integration of renewable sources with energy storage systems and the power grid, aiming to ensure reliability and efficiency. Power electronics, particularly in DC-DC conversion [1], play a pivotal role in this integration and are seeing widespread adoption across high-performance, high-power-density applications such as aircraft systems [2].

Electric vehicles (EVs), Hybrid Electric Vehicles (HEVs) and Fuel Cell Electric Vehicles (FCEVs) have been introduced as a sustainable alternative for transportation and as a means to reduce fossil fuel dependency. These technologies continue to evolve, demanding higher levels of technological maturity [3,4,5]. These systems require power converters capable of handling high power levels with high efficiency [6,7,8,9]. A modern EV propulsion system typically includes an electric machine, power converters, and an energy storage unit. Figure 1 illustrates a representative traction system architecture, in which a DC-DC converter manages the high-power charge and discharge cycles of the battery bank. The ability to support bidirectional power flow is a critical requirement for DC-DC converters in advanced automotive applications, enabling both regenerative braking and battery charging functionality.

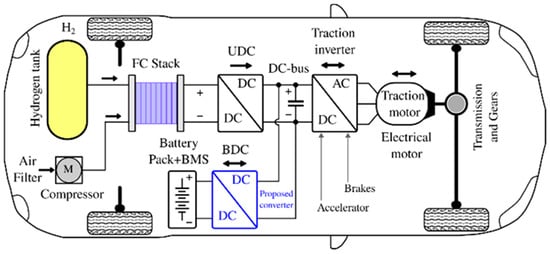
Figure 1. Simplified block diagram of the FCEV application.

DC-DC converters are becoming increasingly essential in EV systems. However, ensuring high-quality current draw from the battery remains a significant challenge across various operating modes, including traction, regenerative braking, and grid-connected charging modes. As discussed in the literature [10], isolated topologies based on the Dual Active Bridge (DAB) have attracted considerable attention. These converters allow for variation in the transformer turns ratio and support series-parallel configurations of the bridges, offering the flexibility required to achieve high voltage gain and efficient power transfer. Due to their galvanic isolation and scalability, isolated topologies have become the architecture of choice for advanced charging applications. However, this flexibility comes at the cost of added design complexity, particularly in the design and optimization of high-frequency magnetic components.

When galvanic isolation is not required, a common approach is to employ a large inductor on the battery-connected side to effectively reduce the ripple current. However, using a large inductor increases the converter’s size, weight and adversely affects its dynamic response. To address these drawbacks, several ripple cancellation techniques have been proposed in the literature [11], aiming to achieve zero ripple current at a specific duty cycle. One widely adopted method involves the use of interleaved converters, in which transistors operate with a defined phase shift [12]. In such topologies, while one inductor is charging, the interleaved counterpart is discharging, effectively canceling the ripple in the source current and yielding a nearly ripple-free waveform. Despite the effectiveness of this technique in ripple mitigation, the converter’s voltage gain presents certain limitations: (a) these include no achievable minimum gain threshold, (b) only a limited portion of the duty cycle range is usable, and (c) although the gain remains relatively constant across a broad duty cycle range, it exhibits a sharp increase near extreme duty cycles.

Several modified converter topologies based on the SEPIC architecture [13] have been proposed to enhance performance in applications such as EV chargers, renewable energy systems (e.g., photovoltaic and wind), LED lighting, power factor correction (PFC) rectifiers, and uninterruptible power supply (UPS) systems. These improvements typically involve one or two active switches and are characterized by reduced conduction losses, increased voltage gain, and higher overall efficiency. In [14], an interleaved SEPIC–Ćuk combination converter is analyzed, demonstrating the capability to generate dual balanced output voltages from a single DC input. The implementation employs four interleaved phases to effectively reduce input and output current ripple, enhance thermal management, and support higher power density. This interleaved architecture is particularly well-suited for applications involving the integration of low- and medium-power hybrid power supplies where space constraints are critical [15].

Interleaved converter topologies have gained significant attention for applications such as DC microgrids, particularly due to their capability to generate a bipolar DC bus while enhancing power quality and reducing losses, as demonstrated in [16]. The adoption of wide-bandgap (WBG) semiconductor devices, as discussed in [17], has further improved the efficiency, power density, and thermal performance of SEPIC converters. Moreover, high voltage gain is often required in these systems, as addressed in [18], where interleaving techniques are employed to reduce ripple current and minimize voltage and current stress on semiconductor devices. SEPIC-derived topologies, especially those featuring interleaving and tapped inductors, offer notable advantages in terms of efficiency, voltage gain, and scalability. However, magnetically coupled designs also introduce challenges, particularly related to leakage inductance, which increases voltage stress on switching devices. To mitigate this, dissipative snubber circuits are often employed, though at the expense of reduced overall efficiency.

Chapparya et al. [19] proposed an interleaved Boost–Zeta converter specifically designed for interfacing renewable energy sources with low-voltage bipolar DC microgrids. The topology demonstrated low current stress on the Zeta-side switch and exhibited excellent steady-state and dynamic performance, resulting in a simpler and more cost-effective solution compared to conventional multiport converter architectures. Nevertheless, the proposed design has certain drawbacks: it is unsuitable for high-voltage or high-power DC applications without modifications, lacks adaptability for systems requiring variable output voltages, and may operate in discontinuous conduction mode (DCM) when the duty cycle D < 0.5, potentially compromising efficiency and control stability. In [20], the analysis and simulation of an interleaved Zeta converter employing fuzzy logic control are presented, demonstrating improved settling time, enhanced output voltage regulation, and higher efficiency compared to conventional PI control methods.

Various interleaved and multistage converter topologies have been proposed in the literature. However, many of these lack bidirectional power flow capability and differ fundamentally from SEPIC and Zeta converters, which are fourth-order circuits. The SEPIC converter is derived from the Boost topology and provides a non-inverting output voltage, while the Zeta converter originates from the Buck–Boost topology and delivers a filtered output current with the same polarity as the input, functionally resembling a Buck converter.

To enhance battery integration across the wide operating range of EV inverters and commercial chargers, enabling unified power management under diverse load conditions, this paper proposes a Bidirectional Interleaved SEPIC-ZETA DC–DC Converter with phase-shifted PWM and parallel switching. The proposed topology is non-isolated, supports efficient bidirectional power flow, and is well-suited for applications involving wide input/output voltage variations, such as battery systems. Compared to conventional interleaved converter designs, the proposed converter offers several key advantages:

(1)

Higher voltage gain can be achieved at lower transistor duty cycles, which is particularly beneficial for sources with a wide voltage range.

(2)

Operates in an interleaved manner, enabling input current ripple cancelation and reducing current stress on individual switching devices through multi-phase current sharing.

(3)

Supports continuous conduction mode (CCM) operation, enhancing versatility under varying load conditions.

(4)

Is easily expandable to an n-arm configuration while maintaining a consistent output voltage setting.

(5)

Presents a comprehensive investigation of a bidirectional interleaved SEPIC-Zeta converter designed for high-performance applications and suitable for operation under varying voltage gain.

(6)

The performance of the converter is validated through experimental results under open-loop control conditions in CCM.

2. Description of the Proposed DC–DC Converter

In Figure 2, the converter consists of six inductors (L₁, L₂, L₃, L₄, L₅, and L₆), twelve switches implemented with MOSFETs, and five capacitors. Capacitors C₁, C₂, and C₃ are used to connect the arm containing switch S to the arm containing switch Q. Additionally, capacitors C₄ and C₅ are connected in parallel with the voltage sources V₂ and V₁, respectively. When power is transferred from the voltage port V₁, typically associated with an energy storage system, to the DC bus (voltage port V₂), the converter operates in step-up mode, delivering energy from V₁ to regulate V₂ at the required voltage. Conversely, in Buck mode, the converter charges the energy storage system. Moreover, it acts as the primary DC bus, supplying power to the load, such as a traction inverter or a high-power battery charger for electric vehicles (EVs).

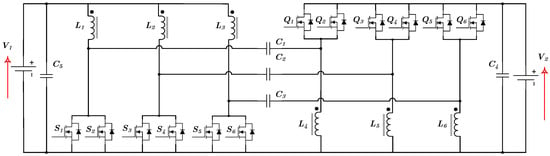
Figure 2. Proposed Three-Arms Bidirectional Interleaved SEPIC-ZETA DC–DC Converter with Interleaved PWM Technique for Parallel-Connected Switches.

The PWM modulation of the power switches is phase-shifted by 360°/6. In step-up mode, switches S₁, S₃, and S₅ are modulated with a phase shift of 120° between each switch. For instance, if S₁ is set as the reference, switches S₃ and S₅ are shifted by 120° and 240°, respectively. Similarly, switches S₂, S₄, and S₆ are phase-shifted by 120° among themselves but with an additional offset of 180° relative to switches S₁, S₃, and S₅. Consequently, if S₂ begins operation with a 180° delay, switches S₄ and S₆ will have their angles shifted by 300° and 60°, respectively. In step-down mode, the modulation strategy remains consistent with that of step-up mode. However, the modulation signals applied to switches S₁, S₃, and S₅ are transferred to switches Q₁, Q₃, and Q₅, respectively. Similarly, the modulation signals assigned to switches S₂, S₄, and S₆ are transferred to switches Q₂, Q₄, and Q₆.

The proposed interleaved PWM technique for parallel-connected switches offers numerous advantages, including the reduction in both the volume and weight of passive components, such as capacitors, and magnetic components, such as inductors [21,22]. Furthermore, the frequency of current and voltage ripples in both ports (V₁ and V₂) is six times higher than the switching frequency, while the frequency of inductor ripple current is three times higher than the switching frequency. The frequency of ripple current in capacitors C₁, C₂, and C₃ is also three times higher than the switching frequency. Additionally, the frequency of current and voltage ripples in C₄ and C₅ is six times higher than the switching frequency.

In each mode of operation, whether power flows from V₁ to V₂ or from V₂ to V₁, the operation of the proposed converter can be divided into three intervals, or regions, denoted as R1, R2, and R3. These regions are classified based on the combination of simultaneously conducting switches and the duty cycle range, as presented in Table 1.

Table 1. Operation regions for the proposed converter.

Regions	Duty Cycle	Simultaneous Conducting
R1	$0<D<1/6$	None
R2	$1/6\le D<1/3$	Two switches
R3	$1/3\le D<1/2$	Three switches

3. Operation and Steady-State Analysis of Power Flow Direction from V₁ to V₂ (SEPIC Mode)

This section provides a comprehensive analysis of the converter operation in Region R2, assuming CCM. It includes the theoretical waveforms of the main components, the derivation of equations for the DC voltage gain, and the mathematical expressions that describe the behavior of the inductors and capacitors.

3.1. Stage Analysis in Region R2

In this mode of operation, the converter consists of twelve operational stages. Due to the symmetry of these stages, a detailed analysis is conducted over half of a switching period.

1st Stage [t₀ − t₁]: At the initial moment t₀, switches S₁ and S₄ are conducting, while all other switches remain off. During this stage, inductors L₁, L₂, L₄, and L₅ store energy, whereas L₃ and L₆ transfer energy. Capacitors C₁ and C₂ discharge, while C₃ charges. The voltage across the inductors (L₁, L₂), as well as across the inductors (L₄, L₅), is represented as V₁ and V_C1, respectively. The voltage across L₃ and L₆ are expressed as V₁ − (V_C1 + V₂) and −V₂, respectively. The voltage across all switches, except S₁ and S₄, is given by V_C1 + V₂. The current i₁(t) is equal to i_L1(t) + i_L2(t) + i_L3(t), where i_S1(t) and i_S4(t) equals i_L1(t) + i_C1(t) and i_L2(t) + i_C2(t), respectively. The currents through body diodes of Q₅ and Q₆, i_QD5(t) and i_QD6(t) are expressed as (i_L6(t) + i_C3(t))/2. This stage concludes at t₁, and the corresponding equivalent circuit is illustrated in Figure 3a. The duration of this operating stage, as well as the instantaneous currents of inductors L₁, L₂, and L₃, switches S₁ and S₄, and the body diodes of switches Q₅ and Q₆, are defined by Equations (1)–(4), respectively.

$${\mathit{∆}t}_1=t_1-t_0={\displaystyle \frac{6 D-1}{6}}·T_S$$

(1)

$$\left\{\begin{array}{c}{i_L}_1(t)=i_{L1}\left(t_0\right)+{\displaystyle \frac{V_1}{L_1}}\left(t-t_0\right) \\ {i_L}_2\left(t\right)=i_{L2}\left(t_0\right)+{\displaystyle \frac{V_1}{L_4}}\left(t-t_0\right) \\ {i_L}_3\left(t\right)=i_{L3}\left(t_0\right)+{\displaystyle \frac{V_1-\left(V_{C1}+V_2\right)}{L_3}} \left(t-t_0\right)\end{array}\right.$$

(2)

$$\left\{\begin{array}{c}{i_S}_1\left(t\right)=i_{L1}\left(t_0\right)+{\displaystyle \frac{V_1}{L_1}}\left(t-t_0\right)+i_{L4}\left(t_0\right)+{\displaystyle \frac{V_{C1}}{L_4}}\left(t-t_0\right)\\ {i_S}_4\left(t\right)=i_{L2}\left(t_0\right)+{\displaystyle \frac{V_1}{L_2}}\left(t-t_0\right)+i_{L5}\left(t_0\right)+{\displaystyle \frac{V_{C1}}{L_5}}\left(t-t_0\right)\end{array}\right.$$

(3)

$${i_{QD}}_{\mathrm{5,6}}\left(t\right)={\displaystyle \frac{i_{L3}\left(t_0\right)+i_{L6}\left(t_0\right)}{2}}+{\displaystyle \frac{V_1-\left(V_{C1}+V_2\right)}{L_3}}\left(t-t_0\right)$$

(4)

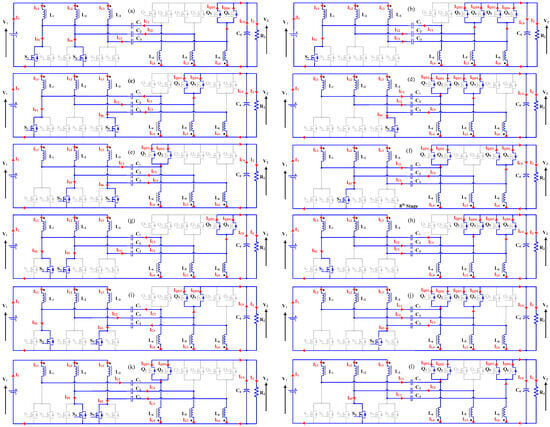
Figure 3. Equivalent circuits of the proposed converter operating in the power flow direction from V₁ to V₂. (a) 1st Stage; (b) 2nd Stage; (c) 3rd Stage; (d) 4th Stage; (e) 5th Stage; (f) 6th Stage; (g) 7th Stage; (h) 8th Stage; (i) 9th Stage; (j) 10th Stage; (k) 11th Stage; (l) 12th Stage.

2nd Stage [t₁ − t₂]: At the initial moment t₁, switch S₁ remains on, and switch S₄ is turned off, while all other switches remain off. During this stage, inductors L₁ and L₄ store energy, whereas inductors L₂, L₃, L₅, and L₆ transfer energy. Capacitor C₁ discharges, while capacitors C₂ and C₃ charge. The voltage across L₁ and L₄ is equal to V₁ and V_C1, respectively. The voltage across the inductors (L₂ and L₃), as well as the inductors (L₅ and L₆) is equal toV₁ − (V_C1 + V₂) and −V₂, respectively. The voltage across all switches, except S₁, is given by V_C1 + V₂. The current i₁(t) is equal to i_L1(t) + i_L2(t) + i_L3(t), where the current through switch S₁, i_S1(t), equals i_L1(t) + i_C1(t), and the currents through body diodes of Q₃, Q₄, Q₅, and Q₆, i_QD3(t), i_QD4(t), i_QD5(t), and i_QD6(t), are expressed as (i_L6(t) + i_C3(t))/2. This stage concludes at t₂, and the corresponding equivalent circuit is illustrated in Figure 3b. The duration of this stage, along with the instantaneous currents of L₁–L₃, S₁, and the body diodes of Q₃–Q₆, are defined by Equations (5)–(8), respectively.

$${∆t}_2=t_2-t_1={\displaystyle \frac{1-3D}{3}}·T_S$$

(5)

$$\left\{\begin{array}{c}{i_L}_1(t)=i_{L1}\left(t_1\right)+{\displaystyle \frac{V_1}{L_1}}\left(t-t_1\right) \\ {i_L}_2\left(t\right)=i_{L2}\left(t_1\right)+{\displaystyle \frac{V_1-\left(V_{C1}+V_2\right)}{L_2}} \left(t-t_1\right)\\ {i_L}_3\left(t\right)=i_{L3}\left(t_1\right)+{\displaystyle \frac{V_1-\left(V_{C1}+V_2\right)}{L_3}} \left(t-t_1\right)\end{array}\right.$$

(6)

$${i_S}_1\left(t\right)=i_{L1}\left(t_1\right)+{\displaystyle \frac{V_1}{L_1}}\left(t-t_1\right)+i_{L4}\left(t_1\right)+{\displaystyle \frac{V_{C1}}{L_4}}\left(t-t_1\right)$$

(7)

$$\left\{\begin{array}{c}{i_{QD}}_{\mathrm{3,4}}\left(t\right)={\displaystyle \frac{i_{L2}\left(t_1\right)+i_{L5}\left(t_1\right)}{2}}+{\displaystyle \frac{V_1-\left(V_{C1}+V_2\right)}{L_2}}\left(t-t_1\right) \\ {i_{QD}}_{\mathrm{5,6}}\left(t\right)={\displaystyle \frac{i_{L3}\left(t_1\right)+i_{L6}\left(t_1\right)}{2}}+{\displaystyle \frac{V_1-\left(V_{C1}+V_2\right)}{L_3}}\left(t-t_1\right) \end{array}\right.$$

(8)

3rd Stage [t₂ − t₃]: At the initial moment t₂, switches S₁ and S₆ are conducting, while all other switches remain off. During this stage, inductors L₁, L₃, L₄, and L₆ store energy, whereas inductors L₂ and L₅ transfer energy. Capacitors C₁ and C₃ discharge, while capacitor C₂ charges. The voltage across the inductors (L₁ and L₃), as well as across the inductors (L₄ and L₆), is defined as V₁ and V_C1, respectively. The voltage across L₂ and L₅ is described by as V₁ − (V_C1 + V₂) and −V₂, respectively. The voltage across all switches, except S₁ and S₆, is equal to V_C1 + V₂. The current i₁(t) is equal to i_L1(t) + i_L2(t) + i_L3(t), where the currents through switches S₁ and S₆, i_S1(t) and i_S6(t), are equal to i_L1(t) + i_C1(t) and i_L3(t) + i_C3(t), respectively. The currents through body diodes of Q₃, Q₄, i_QD3(t) and i_QD4(t), are expressed as (i_L5(t) + i_C2(t))/2. This stage concludes at t₃, and the corresponding equivalent circuit is illustrated in Figure 3c. Stage duration and instantaneous currents of L₁–L₃, S₁ and S₆, and body diodes of Q₃–Q₄ are given by (9)–(12), respectively.

$${∆t}_3=t_3-t_2={\displaystyle \frac{6D-1}{6}}·T_S$$

(9)

$$\left\{\begin{array}{c} {i_L}_1(t)=i_{L1}\left(t_2\right)+{\displaystyle \frac{V_1}{L_1}}\left(t-t_2\right) \\ {i_L}_2\left(t\right)=i_{L3}\left(t_2\right)+{\displaystyle \frac{V_1-\left(V_{C1}+V_2\right)}{L_2}} \left(t-t_2\right)\\ {i_L}_3\left(t\right)=i_{L3}\left(t_2\right)+{\displaystyle \frac{V_1}{L_3}}\left(t-t_2\right) \end{array}\right.$$

(10)

$$\left\{\begin{array}{c}{i_S}_1\left(t\right)=i_{L1}\left(t_2\right)+{\displaystyle \frac{V_1}{L_1}}\left(t-t_2\right)+i_{L4}\left(t_2\right)+{\displaystyle \frac{V_{C1}}{L_4}}\left(t-t_2\right)\\ {i_S}_6\left(t\right)=i_{L3}\left(t_2\right)+{\displaystyle \frac{V_1}{L_3}}\left(t-t_2\right)+i_{L6}\left(t_2\right)+{\displaystyle \frac{V_{C1}}{L_6}}\left(t-t_2\right)\end{array}\right.$$

(11)

$${i_{QD}}_{\mathrm{3,4}}\left(t\right)={\displaystyle \frac{i_{L2}\left(t_2\right)+i_{L5}\left(t_2\right)}{2}}+{\displaystyle \frac{V_1-\left(V_{C1}+V_2\right)}{L_3}}\left(t-t_2\right)$$

(12)

4th Stage [t₃ − t₄]: At the initial moment t₃, switch S₆ remains on, and switch S₁ is turned off, while all other switches remain off. During this stage, inductors L₃ and L₆ store energy, whereas inductors L₁, L₂, L₄, and L₅ transfer energy. Capacitor C₃ discharges, while capacitors C₁ and C₂ charge. The voltage across inductors L₃ and L₆ is equal to V₁ and V_C1, respectively. The voltage across the inductors (L₁ and L₂), as well as the inductors (L₄ and L₅), is equal to V₁ − (V_C1 + V₂) and −V₂, respectively. The current i₁(t) is defined as the sum i_L1(t) + i_L2(t) + i_L3(t), while the current through switch S₆, i_S6(t), is i_L3(t) + i_C3(t). The currents through the body diodes of Q₁, Q₂, Q₃, and Q₄, denoted as i_QD1(t), i_QD2(t), i_QD3(t), and i_QD4(t), are expressed as (i_L4(t) + i_C1(t))/2 and (i_L5(t) + i_C2(t))/2, respectively. This stage concludes at t₄, and the corresponding equivalent circuit is illustrated in Figure 3d. The duration of this stage, along with the instantaneous currents of L₁–L₃, S₆, and the body diodes of Q₁–Q₄, is defined by Equations (13)–(16), respectively.

$${∆t}_4=t_4-t_3={\displaystyle \frac{1-3D}{3}}·T_S$$

(13)

$$\left\{\begin{array}{c}{i_L}_1(t)=i_{L1}\left(t_3\right)+{\displaystyle \frac{V_1-\left(V_{C1}+V_2\right)}{L_1}} \left(t-t_3\right)\\ {i_L}_2\left(t\right)=i_{L2}\left(t_3\right)+{\displaystyle \frac{V_1-\left(V_{C1}+V_2\right)}{L_2}} \left(t-t_3\right)\\ {i_L}_3\left(t\right)=i_{L3}\left(t_3\right)+{\displaystyle \frac{V_1}{L_3}}\left(t-t_3\right) \end{array}\right.$$

(14)

$${i_S}_6\left(t\right)=i_{L3}\left(t_3\right)+{\displaystyle \frac{V_1}{L_3}}\left(t-t_3\right)+i_{L6}\left(t_3\right)+{\displaystyle \frac{V_{C1}}{L_6}}\left(t-t_3\right)$$

(15)

$$\left\{\begin{array}{c}{i_Q}_{\mathrm{1,2}}\left(t\right)={\displaystyle \frac{i_{L4}\left(t_3\right)+i_{L1}\left(t_3\right)}{2}}+{\displaystyle \frac{V_1-\left(V_{C1}+V_2\right)}{L_4}}\left(t-t_3\right) \\ {i_{QD}}_{\mathrm{3,4}}\left(t\right)={\displaystyle \frac{i_{L2}\left(t_3\right)+i_{L5}\left(t_3\right)}{2}}+{\displaystyle \frac{V_1-\left(V_{C1}+V_2\right)}{L_5}}\left(t-t_3\right) \end{array}\right.$$

(16)

5th Stage [t₄ − t₅]: At the initial moment t₄, switches S₃ and S₆ are conducting, while all other switches remain off. During this stage, the inductors L₂, L₃, L₅, and L₆ store energy, whereas the inductors L₁ and L₄ transfer energy. The capacitors C₂ and C₃ discharge, while the capacitor C₁ charges. The voltage across the inductors (L₂ and L₃), as well as across the inductors (L₅ and L₆), is represented as V₁ and V_C1, respectively. The voltage across L₁ and L₄ is expressed as V₁ − (V_C1 + V₂) and −V₂, respectively. The current i₁(t) is defined as i_L1(t) + i_L2(t) + i_L3(t), where the currents through switches S₃ and S₆, i_S3(t) and i_S6(t), are given by i_L2(t) + i_C2(t) and i_L3(t) + i_C3(t), respectively. The currents through the body diodes of Q₁ and Q₂, denoted as i_QD1(t) and i_QD2(t), are expressed as (i_L4(t) + i_C1(t))/2. This stage concludes at t₅, and the corresponding equivalent circuit is illustrated in Figure 3e. The duration of this operating stage, as well as the instantaneous currents of inductors L₁–L₃, switches S₃ and S₆, and the body diodes of switches Q₁ and Q₂, is defined by Equations (17)–(20), respectively.

$${∆t}_5=t_5-t_4={\displaystyle \frac{6D-1}{6}}·T_S$$

(17)

$$\left\{\begin{array}{c}{i_L}_1(t)=i_{L1}\left(t_4\right)+{\displaystyle \frac{V_1-\left(V_{C1}+V_2\right)}{L_1}}\left(t-t_4\right)\\ {i_L}_2\left(t\right)=i_{L2}\left(t_4\right)+{\displaystyle \frac{V_1}{L_2}} \left(t-t_4\right) \\ {i_L}_3\left(t\right)=i_{L3}\left(t_4\right)+{\displaystyle \frac{V_1}{L_3}}\left(t-t_4\right) \end{array}\right.$$

(18)

$$\left\{\begin{array}{c}{i_S}_3\left(t\right)=i_{L2}\left(t_4\right)+{\displaystyle \frac{V_1}{L_2}}\left(t-t_4\right)+i_{L5}\left(t_4\right)+{\displaystyle \frac{V_{C1}}{L_5}}\left(t-t_4\right)\\ {i_S}_6\left(t\right)=i_{L3}\left(t_4\right)+{\displaystyle \frac{V_1}{L_3}}\left(t-t_4\right)+i_{L6}\left(t_4\right)+{\displaystyle \frac{V_{C1}}{L_6}}\left(t-t_4\right)\end{array}\right.$$

(19)

$${i_{QD}}_{\mathrm{1,2}}\left(t\right)={\displaystyle \frac{i_{L4}\left(t_4\right)+i_{L1}\left(t_4\right)}{2}}+{\displaystyle \frac{V_1-\left(V_{C1}+V_2\right)}{L_4}}·\left(t-t_4\right)$$

(20)

6th Stage [t₅ − t₆]: At the initial moment t₅, switch S₃ remains on, while switch S₆ is turned off and all other switches remain off. During this stage, inductors L₂ and L₅ store energy, whereas inductors L₁, L₃, L₄, and L₆ transfer energy. Capacitor C₂ discharges, while capacitors C₁ and C₃ charge. The voltage across inductors L₂ and L₅ corresponds to V₁ and V_C1, respectively. The voltage across the inductors (L₁ and L₃), as well as the inductors (L₄ and L₆), corresponds to V₁ − (V_C1 + V₂) and -V₂, respectively. The voltage across all switches, except S₃, is given by V_C1 + V₂. The current i₁(t) is defined as the sum i_L1(t) + i_L2(t) + i_L3(t), while the current through switch S₃, i_S3(t), is i_L2(t) + i_C2(t). The currents through the body diodes of Q₁, Q₂, Q₅, and Q₆, denoted as i_QD1(t), i_QD2(t), i_QD5(t), and i_QD6(t), are expressed as (i_L4(t) + i_C1(t))/2 and (i_L6(t) + i_C3(t))/2, respectively. This stage concludes at t₆, and the corresponding equivalent circuit is illustrated in Figure 3f. The duration of this stage, along with the instantaneous currents of L₁–L₃, S₃, and the body diodes of Q₁, Q₂, Q₅, and Q₆, is defined by Equations (21)–(24), respectively.

$${∆t}_6=t_6-t_5={\displaystyle \frac{1-3D}{3}}·T_S$$

(21)

$$\left\{\begin{array}{c}{i_L}_1(t)=i_{L1}\left(t_5\right)+{\displaystyle \frac{V_1-\left(V_{C1}+V_2\right)}{L_1}}\left(t-t_5\right)\\ {i_L}_2\left(t\right)=i_{L2}\left(t_5\right)+{\displaystyle \frac{V_1}{L_2}} \left(t-t_5\right) \\ {i_L}_3\left(t\right)=i_{L3}\left(t_5\right)+{\displaystyle \frac{V_1-\left(V_{C1}+V_2\right)}{L_3}}\left(t-t_5\right)\end{array}\right.$$

(22)

$${i_S}_3\left(t\right)=i_{L2}\left(t_5\right)+{\displaystyle \frac{V_1}{L_2}}\left(t-t_5\right)+i_{L5}\left(t_5\right)+{\displaystyle \frac{V_{C1}}{L_5}}\left(t-t_5\right)$$

(23)

$$\left\{\begin{array}{c}{i_{QD}}_{\mathrm{1,2}}\left(t\right)={\displaystyle \frac{i_{L4}\left(t_5\right)+i_{L1}\left(t_5\right)}{2}}+{\displaystyle \frac{V_1-\left(V_{C1}+V_2\right)}{L_4}}\left(t-t_5\right) \\ {i_{QD}}_{\mathrm{5,6}}\left(t\right)={\displaystyle \frac{i_{L3}\left(t_5\right)+i_{L6}\left(t_5\right)}{2}}+{\displaystyle \frac{V_1-\left(V_{C1}+V_2\right)}{L_6}}\left(t-t_5\right) \end{array}\right.$$

(24)

The 7th, 8th, 9th, 10th, 11th, and 12th stages are identical to the 1st, 2nd, 3rd, 4th, 5th, and 6th stages, although they involve different switches from the “S” set engaged. The equivalent circuits for these stages are detailed in Table 2. Figure 4a presents the voltage and current waveforms for the main components in the power flow direction from V₁ to V₂. The theoretical analysis indicates that the current ripple frequency in the inductors (L₁, L₂, L₃, L₄, L₅ and L₆) and capacitors (C₁, C₂, and C₃) is twice the switching frequency, while the ripple current at V₁ and V₂ is six times the switching frequency.

Table 2. Circuits for power flow direction from V₁ to V₂.

	7th Stage	8th Stage	9th Stage	10th Stage	11th Stage	12th Stage
Equivalent circuit	Figure 3g	Figure 3h	Figure 3i	Figure 3j	Figure 3k	Figure 3l

3.2. DC Voltage Gain Expression for Power Flow from V₁ to V₂

The DC voltage gain in CCM for R2 is given by (25). A comprehensive understanding of this behavior is crucial for the accurate sizing of the proposed converter.

$${V_L}_1={\displaystyle \frac{2}{T_S}}·\left[{\int }_0^{{2\mathit{∆}t}_1+{ \mathit{∆}t}_2}{V}_1 dt+{\int }_0^{{\mathit{∆}t}_1+{2 \mathit{∆}t}_2}{V}_1-\left(V_{C1}+V_2\right) dt\right]$$

(25)

The time intervals 2Δt₁ + Δt₂ and Δt₁ + 2Δt₂ is given by (26) and (27).

$${2\mathit{∆}t}_1+{ \mathit{∆}t}_2=D·T_S$$

(26)

$${2\mathit{∆}t}_1+{ \mathit{∆}t}_2={\displaystyle \frac{1-2D}{2}}·T_S$$

(27)

By substituting (26) and (27) into (25), Equation (28) is obtained.

$$0=V_1-V_2-V_{C1}+2 D·V_2+2 D·V_{C1}$$

(28)

The voltage V_C1 is calculated by integrating the average value of the current in inductor L₄, as expressed by:

$${V_L}_4={\displaystyle \frac{2}{T_S}}\left[{\int }_0^{{2\mathit{∆}t}_1+{ \mathit{∆}t}_2}{V}_{C1} dt+{\int }_0^{{\mathit{∆}t}_1+{2 \mathit{∆}t}_2}{-\mathrm{V}}_2 dt\right]$$

(29)

By solving Equation (29), V_C1 is defined by Equation (30).

$$V_{C1}=V_2·{\displaystyle \frac{1-2D}{2D}}$$

(30)

By substituting (30) into (28), the expression for the DC voltage gain in the power flow direction from V₁ to V₂ is derived, as presented in (31).

$${G_{CCM}}_{V_1\to V_2}={\displaystyle \frac{V_2}{V_1}}={\displaystyle \frac{2 D}{1-2 D}}$$

(31)

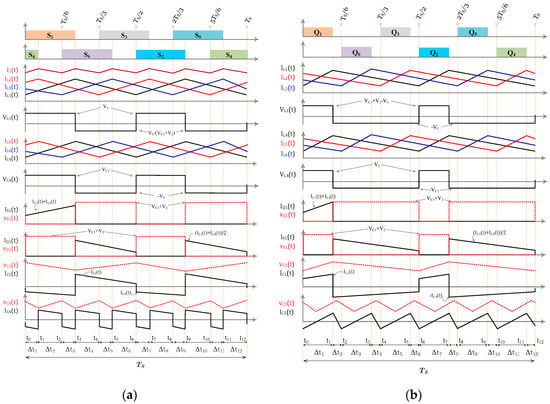
Figure 4. Theoretical waveforms of voltage and current in CCM: (a) for power flow direction from V₁ to V₂; (b) for power flow direction from V₂ to V₁.

Using (31), Figure 5 presents the DC voltage gain of the proposed converter in the power flow direction from V₁ to V₂. The results clearly indicate that the proposed converter exhibits a step-down and step-up characteristic, wherein the gain increases exponentially with the duty cycle D. This behavior demonstrates the converter’s capability to efficiently step up or step down the input voltage, as required by the application. Moreover, the observed gain profile is consistent with the performance of converters studied in [14,17], underscoring the adaptability and efficacy of the proposed topology.

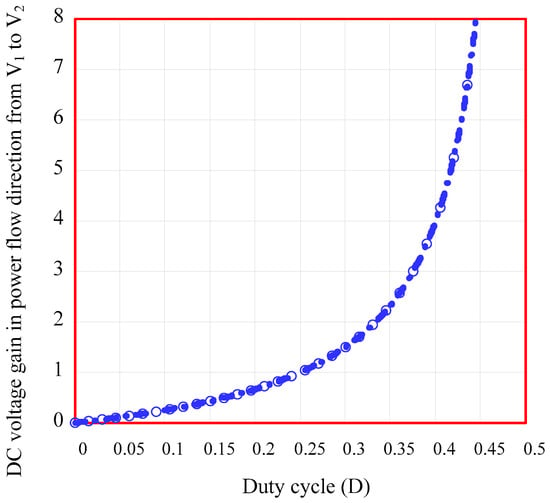
Figure 5. DC voltage gain in power flow direction from V₁ to V₂.

3.3. Sizing of Passive Elements and Calculation of Component Stresses

In this section, the sizing of the inductors and capacitors is presented, including the calculations for the voltage and current stresses of the main components. During the time interval D⋅T_S, the inductors experience a voltage V₁, and their inductance is determined using (32).

$$L_1=L_2=L_3={\displaystyle \frac{V_1}{\Delta i_{L1}\cdot f_S}}\cdot D$$

(32)

By substituting Equation (31) into Equation (32), Equation (33) is derived, which determines the required values of the inductances

L₁, L₂, and L₃ as functions of D, V₂, f_s, and ΔI_L, ensuring the converter operates in CCM.

$$L_1=L_2=L_3={\displaystyle \frac{V_2}{2\Delta i_{L1}\cdot f_S}}\cdot (1-2 D)$$

(33)

Equation (33) is used to determine the inductance values for L₁, L₂, and L₃, as well as for L₄, L₅, and L₆.

The average current through inductors L₁, L₂, and L₃, as a function of the duty cycle (D) and the current I₂, is given by (34).

$${I_{L1}}_{av}={I_{L2}}_{av}={\displaystyle \frac{ 2 I_2 ·D}{3 (1-2 D)}}$$

(34)

The average current through the inductors L₄, L₅, and L₆ is expressed in (35).

$${I_{L4}}_{av}={I_{L5}}_{av}={I_{L6}}_{av}={\displaystyle \frac{I_2}{3}}$$

(35)

The average and RMS current values through the switches S are calculated using (36) and (37), respectively.

$${I_S}_{av}={\displaystyle \frac{I_2·D}{3 \left(1-2 D\right)}}$$

(36)

$${I_S}_{RMS}={\displaystyle \frac{I_2·\sqrt{D}}{3 \left(1-2 D\right)}}$$

(37)

Equations (38) and (39) provide the calculations for the average and RMS currents through the body diode of the switches Q.

$${I_Q}_{av}={\displaystyle \frac{I_2}{6}}$$

(38)

$${I_Q}_{RMS}={\displaystyle \frac{I_2}{6 \sqrt{1-2 D}}}$$

(39)

The maximum voltage across all switches is given by (40).

$$V_S=V_Q={\displaystyle \frac{V_2}{2 D}}$$

(40)

The RMS value of the current through C₁, C₂, and C₃ is determined by analyzing the equivalent circuits shown in Figure 3. When the switches are on, the current through C₁, C₂, and C₃ is given by $i_{C1}(t)={I_{L4}}_{av}$. When the switches are off, the current through C₁, C₂, and C₃ is given by $i_{C1}(t)={I_{L1}}_{av}$. The RMS currents for C₁, C₂, and C₃ are presented in Equation (41).

$${I_{C1}}_{RMS}={I_{C2}}_{RMS}={I_{C3}}_{RMS}={\displaystyle \frac{I_2}{3}}·\sqrt{{\displaystyle \frac{2 D}{1-2 D}}}$$

(41)

From Figure 3 and Figure 4a, it can be seen that capacitors C₁, C₂, and C₃ discharge when the switches S are turned on, and charge when the switches are turned off. Therefore, the capacitance values of the capacitors are given by (42).

$$C_1=C_2=C_3={\displaystyle \frac{I_2·D}{{3 \mathit{∆}V}_{C1}·f_S}}$$

(42)

The maximum voltage values for C₁, C₂ and C₃ are determined by Equation (43).

$$V_{C1}=V_{C2}=V_{C3}=V_2·{\displaystyle \frac{1-2 D}{2 D}}=V_1$$

(43)

From Figure 4a, it can be seen that capacitor C₄ discharges during interval Δt₁ and charges during interval Δt₂. Therefore, applying RMS value integral, Equation (44) is obtained, following which the capacitance of C₄ is given by (45).

$${I_{C4}}_{RMS}=I_2·\sqrt{{\displaystyle \frac{2 (1-3D)·(6D-1)}{3 (1-2 D)}}}$$

(44)

$$C_4={\displaystyle \frac{I_2}{{9 ∆V}_{C4}·f_S}}·{\displaystyle \frac{(1-3D)·(6D-1)}{(1-2 D)}}$$

(45)

4. Operation and Steady-State Analysis of Power Flow Direction from V₂ to V₁ (Zeta Mode)

This section provides a detailed analysis of the power flow direction from V₂ to V₁ over half of a switching period in Region R1. It presents the theoretical waveforms for the main components, alongside the relevant equations for DC voltage gain, component stress, and the sizing of passive elements.

4.1. Stage Analysis in Region R1

1st Stage [t₀ − t₁]: The first stage starts at t₀, when the switch Q₁ is turned on, while all others switches remain off. During this stage, inductors L₄ and L₁ store energy, whereas inductors L₅, L₆, L₂, and L₃ transfer energy. Capacitor C₁ charges, while capacitors C₂ and C₃ discharge. The voltage across L₄ and L₁ is equal to V₂ and (V_C1 + V₂) − V₁, respectively. The voltage across the inductors (L₅ and L₆), as well as the inductors (L₂ and L₃) is equal to −V_C1 and −V₁, respectively. The voltage across all switches, except Q₁, is given by V_C1 + V₂. The current i₂(t) is equal to i_Q1(t), where the current through switch Q₁, i_Q1(t), equals i_L4(t) + i_C1(t), and the currents through body diodes of S₃, S₄, S₅, and S₆, i_SD3(t), i_SD4(t), i_SD5(t), and i_SD6(t), are expressed as (i_L2(t) + i_C2(t))/2. This stage concludes at t₂, and the corresponding equivalent circuit is illustrated in Figure 6a. The duration of this stage, along with the instantaneous currents of inductors L₄–L₆, switch Q₁, and the body diodes of S₃, S₄, S₅, and S₆, is defined by Equations (46)–(49), respectively.

$${\mathit{∆}t}_1=t_1-t_0=D·T_S$$

(46)

$$\left\{\begin{array}{c}{i_L}_4(t)=i_{L4}\left(t_0\right)+{\displaystyle \frac{V_2}{L_4}}\left(t-t_0\right) \\ {i_L}_5\left(t\right)=i_{L5}\left(t_0\right)-{\displaystyle \frac{V_{C1}}{L_5}}\left(t-t_0\right)\\ {i_L}_6\left(t\right)=i_{L6}\left(t_0\right)-{\displaystyle \frac{V_{C1}}{L_6}}\left(t-t_0\right)\end{array}\right.$$

(47)

$${i_Q}_1\left(t\right)=i_{L4}\left(t_0\right)+i_{L1}\left(t_0\right)+\left({\displaystyle \frac{V_2}{L_4}}+{\displaystyle \frac{V_2}{L_1}}\right)·\left(t-t_0\right)$$

(48)

$$\left\{\begin{array}{c}{i_{SD}}_{\mathrm{3,4}}\left(t\right)={\displaystyle \frac{i_{L2}\left(t_0\right)+i_{L5}\left(t_0\right)}{2}}-{\displaystyle \frac{V_1}{L_2}}·\left(t-t_0\right)\\ {i_{SD}}_{\mathrm{5,6}}\left(t\right)={\displaystyle \frac{i_{L3}\left(t_0\right)+i_{L6}\left(t_0\right)}{2}}-{\displaystyle \frac{V_1}{L_6}}·\left(t-t_0\right)\end{array}\right.$$

(49)

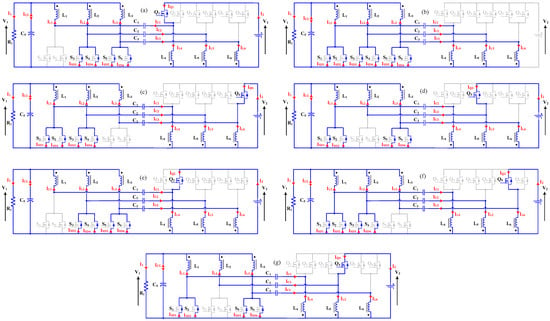
Figure 6. Equivalent circuits of the proposed converter operating in the power flow direction from V₂ to V₁. (a) 1st Stage; (b) 2nd, 4th, 6th, 8th, 10th, 12th Stage; (c) 3rd Stage; (d) 5th Stage; (e) 7th Stage; (f) 9th Stage; (g) 11th Stage.

2nd Stage [t₁ − t₂]: The second stage starts at t₁, when all switches (Q₁–Q₆) remain turned off. During this stage, the inductors L₁, L₂, L₃, L₄, L₅, and L₆ transfer the previously stored energy toward the load and the capacitors. At the same time, capacitors C₁, C₂ and C₃ discharge, providing additional energy to the load and contributing to the current through the inductors. The voltage across inductors L₁, L₂, and L₃ is equal to −V₁, and the voltage across inductors L₄, L₅, and L₆ is equal to −V_C1. The voltage across all switches is determined by V_C1 + V₂. The current i₁(t) corresponds to the sum of i_L1(t), i_L2(t) and i_L3(t), while the current i₂(t) equals i_L4(t) + i_L5(t) + i_L6(t). This stage ends at t₂, and the corresponding equivalent circuit is shown in Figure 6b. Stage duration and instantaneous currents of L₄–L₆ and body diodes of S₁–S₆ are defined by (50)–(52), respectively.

$${\mathit{∆}t}_2=t_2-t_1={\displaystyle \frac{1-6 D}{6}}·T_S$$

(50)

$$\left\{\begin{array}{c} {i_L}_4(t)=i_{L4}\left(t_1\right)-{\displaystyle \frac{V_{C1}}{L_4}}\left(t-t_1\right) \\ {i_L}_5\left(t\right)=i_{L5}\left(t_1\right)-{\displaystyle \frac{V_{C1}}{L_5}}\left(t-t_1\right)\\ {i_L}_6\left(t\right)=i_{L6}\left(t_1\right)-{\displaystyle \frac{V_{C1}}{L_6}}\left(t-t_1\right)\end{array}\right.$$

(51)

$$\left\{\begin{array}{c}{i_{SD}}_{\mathrm{1,2}}\left(t\right)={\displaystyle \frac{i_{L1}\left(t_1\right)+i_{L4}\left(t_1\right)}{2}}-{\displaystyle \frac{V_1}{L_1}}·\left(t-t_1\right)\\ {i_{SD}}_{\mathrm{3,4}}\left(t\right)={\displaystyle \frac{i_{L2}\left(t_1\right)+i_{L5}\left(t_1\right)}{2}}-{\displaystyle \frac{V_1}{L_2}}·\left(t-t_1\right)\\ {i_{SD}}_{\mathrm{5,6}}\left(t\right)={\displaystyle \frac{i_{L3}\left(t_1\right)+i_{L6}\left(t_1\right)}{2}}-{\displaystyle \frac{V_1}{L_6}}·\left(t-t_1\right)\end{array}\right.$$

(52)

3rd Stage [t₂ − t₃]: The third stage begins at t₂, when the switch Q₆ is turned on, while all other switches remain off. During this stage, inductors L₆ and L₃ store energy, whereas inductors L₄, L₅, L₂, and L₁ transfer energy. The capacitor C₃ charges, while capacitors C₁ and C₃ discharge. The voltage across L₆ and L₃ is equal to V₂ and (V_C1 + V₂) − V₁, respectively. The voltage across the inductors (L₅ and L₄), as well as the inductors (L₃ and L₂) is equal to −V_C1 and −V₁, respectively. The voltage across all switches, except Q₆, is given by V_C1 + V₂. The current i₂(t) is equal to i_Q6(t), where the current through switch Q₆, i_Q6(t), equals i_L6(t) + i_C3(t), and the currents through body diodes of S₁, S₂, S₃, and S₄, i_SD1(t), i_SD2(t), i_SD3(t), and i_SD4(t), are expressed as (i_L1(t) + i_C1(t))/2. This stage concludes at t₄, and the corresponding equivalent circuit is presented in Figure 6c. Stage duration and instantaneous currents of L₄–L₆, Q₆, and body diodes of S₁-S₄ are defined by Equations (53)–(56), respectively.

$${\mathit{∆}t}_3=t_3-t_2=D·T_S$$

(53)

$$\left\{\begin{array}{c} {i_L}_4(t)=i_{L4}\left(t_2\right)-{\displaystyle \frac{V_{C1}}{L_4}}\left(t-t_2\right) \\ {i_L}_5\left(t\right)=i_{L5}\left(t_2\right)-{\displaystyle \frac{V_{C1}}{L_5}}\left(t-t_2\right)\\ {i_L}_6\left(t\right)=i_{L6}\left(t_2\right)+{\displaystyle \frac{V_2}{L_6}}\left(t-t_2\right)\end{array}\right.$$

(54)

$${i_Q}_6\left(t\right)=i_{L6}\left(t_2\right)+i_{L3}\left(t_2\right)+\left({\displaystyle \frac{V_2}{L_6}}+{\displaystyle \frac{V_2}{L_3}}\right)·\left(t-t_2\right)$$

(55)

$$\left\{\begin{array}{c}{i_{SD}}_{\mathrm{1,2}}\left(t\right)={\displaystyle \frac{i_{L1}\left(t_2\right)+i_{L4}\left(t_2\right)}{2}}-{\displaystyle \frac{V_1}{L_1}}·\left(t-t_2\right)\\ {i_{SD}}_{\mathrm{3,4}}\left(t\right)={\displaystyle \frac{i_{L2}\left(t_2\right)+i_{L5}\left(t_2\right)}{2}}-{\displaystyle \frac{V_1}{L_2}}·\left(t-t_2\right)\end{array}\right.$$

(56)

4th Stage [t₃ − t₄]: The fourth stage starts at t₃ and is identical to the second stage. All switches remain off, while inductors L₁–L₆ transfer energy and capacitors C₁–C₃ discharge. The voltages across inductors and switches, as well as the current paths, follow the same behavior as in the second stage. This stage ends at t₄, and the corresponding equivalent circuit is shown in Figure 6b. The duration of this stage and the instantaneous currents of L₄–L₆ and the body diodes of S₁–S₆ are given by Equations (57)–(59), respectively,

$${\mathit{∆}t}_4=t_4-t_3={\displaystyle \frac{1-6 D}{6}}·T_S$$

(57)

$$\left\{\begin{array}{c} {i_L}_4(t)=i_{L4}\left(t_3\right)-{\displaystyle \frac{V_{C1}}{L_4}}\left(t-t_3\right) \\ {i_L}_5\left(t\right)=i_{L5}\left(t_3\right)-{\displaystyle \frac{V_{C1}}{L_5}}\left(t-t_3\right)\\ {i_L}_6\left(t\right)=i_{L6}\left(t_3\right)-{\displaystyle \frac{V_{C1}}{L_6}}\left(t-t_3\right)\end{array}\right.$$

(58)

$$\left\{\begin{array}{c}{i_{SD}}_{\mathrm{1,2}}\left(t\right)={\displaystyle \frac{i_{L1}\left(t_3\right)+i_{L4}\left(t_3\right)}{2}}-{\displaystyle \frac{V_1}{L_1}}·\left(t-t_3\right)\\ {i_{SD}}_{\mathrm{3,4}}\left(t\right)={\displaystyle \frac{i_{L2}\left(t_3\right)+i_{L5}\left(t_3\right)}{2}}-{\displaystyle \frac{V_1}{L_2}}·\left(t-t_3\right)\\ {i_{SD}}_{\mathrm{5,6}}\left(t\right)={\displaystyle \frac{i_{L3}\left(t_3\right)+i_{L6}\left(t_3\right)}{2}}-{\displaystyle \frac{V_1}{L_6}}·\left(t-t_3\right)\end{array}\right.$$

(59)

5th Stage [t₃ − t₄]: At the initial time t₅, the switch Q₃ is turned on, while all other switches remain off. During this stage, inductors L₅ and L₂ store energy, whereas inductors L₆, L₄, L₃, and L₁ transfer energy. The capacitor C₂ charges, while capacitors C₁ and C₃ discharge. The voltage across L₅ and L₂ is equal to V₂ and (V_C1 + V₂) − V₁, respectively. The voltage across the inductors L₆ and L₄, as well as the inductors L₃ and L₁ is equal to −V_C1 and −V₁, respectively. The voltage across all switches, except Q₃, is given by V_C1 + V₂. The current i₂(t) is equal to i_Q3(t), where the current through switch Q₃, i_Q3(t), equals i_L5(t) + i_C2(t), and the current through body diodes of S₁, S₂, S₅, and S₆, i_SD1(t), i_SD2(t), i_SD5(t), and i_SD6(t), is expressed as (i_L1(t) + i_C1(t))/2. This stage concludes at t₆, and the corresponding equivalent circuit is presented in Figure 6d. The duration of this stage, as well as the instantaneous currents of inductors L₄–L₆ and the body diodes of S₁, S₂, S₅, and S₆, is characterized by Equations (60)–(62), respectively.

$${\mathit{∆}t}_5=t_5-t_4=D·T_S$$

(60)

$$\left\{\begin{array}{c}{i_L}_4\left(t\right)=i_{L4}\left(t_4\right)-{\displaystyle \frac{V_{C1}}{L_4}}\left(t-t_4\right)\\ {i_L}_5\left(t\right)=i_{L5}\left(t_4\right)+{\displaystyle \frac{V_2}{L_5}}\left(t-t_4\right)\\ {i_L}_6\left(t\right)=i_{L6}\left(t_4\right)-{\displaystyle \frac{V_{C1}}{L_6}}\left(t-t_4\right)\end{array}\right.$$

(61)

$$\left\{\begin{array}{c}{i_{SD}}_{\mathrm{1,2}}\left(t\right)={\displaystyle \frac{i_{L1}\left(t_4\right)+i_{L4}\left(t_4\right)}{2}}-{\displaystyle \frac{V_1}{L_1}}·\left(t-t_4\right)\\ {i_{SD}}_{\mathrm{5,6}}\left(t\right)={\displaystyle \frac{i_{L3}\left(t_4\right)+i_{L6}\left(t_4\right)}{2}}-{\displaystyle \frac{V_1}{L_6}}·\left(t-t_4\right)\end{array}\right.$$

(62)

6th Stage [t₅ − t₆]: The sixth stage is identical to the second and fourth stages. All switches remain off, inductors L₁–L₆ transfer energy, and capacitors C₁, C₂ and C₃ discharge. The equivalent circuit is shown in Figure 6b.

$${∆t}_6=t_6-t_5={\displaystyle \frac{1-6D}{6}}·T_S$$

(63)

$$\left\{\begin{array}{c} {i_L}_4(t)=i_{L4}\left(t_5\right)-{\displaystyle \frac{V_{C1}}{L_4}}\left(t-t_5\right) \\ {i_L}_5\left(t\right)=i_{L5}\left(t_5\right)-{\displaystyle \frac{V_{C1}}{L_5}}\left(t-t_5\right)\\ {i_L}_6\left(t\right)=i_{L6}\left(t_5\right)-{\displaystyle \frac{V_{C1}}{L_6}}\left(t-t_5\right)\end{array}\right.$$

(64)

$$\left\{\begin{array}{c}{i_{SD}}_{\mathrm{1,2}}\left(t\right)={\displaystyle \frac{i_{L1}\left(t_5\right)+i_{L4}\left(t_5\right)}{2}}-{\displaystyle \frac{V_1}{L_1}}·\left(t-t_5\right)\\ {i_{SD}}_{\mathrm{3,4}}\left(t\right)={\displaystyle \frac{i_{L2}\left(t_5\right)+i_{L5}\left(t_5\right)}{2}}-{\displaystyle \frac{V_1}{L_2}}·\left(t-t_5\right)\\ {i_{SD}}_{\mathrm{5,6}}\left(t\right)={\displaystyle \frac{i_{L3}\left(t_5\right)+i_{L6}\left(t_5\right)}{2}}-{\displaystyle \frac{V_1}{L_6}}·\left(t-t_5\right)\end{array}\right.$$

(65)

The 7th, 9th, and 11th stages are similar to the 1st, 3rd, and 5th stages, respectively, with the only difference being the involvement of different switches from the “Q” group. The 8th, 10th, and 12th stages are identical to the 2nd, 4th, and 6th stages. The corresponding equivalent circuits for these stages are provided in Table 3. Figure 4b illustrates the voltage and current waveforms of the main components during the power flow from V₂ to V₁. The theoretical analysis reveals that the ripple current frequency in the inductors (L₁, L₂, L₃, L₄, L₅, and L₆) and capacitors (C₁, C₂, and C₃) is twice the switching frequency. In contrast, the ripple current at V₁ and V₂ occurs at six times the switching frequency.

Table 3. Circuits for power flow direction from V₂ to V₁.

	7th Stage	8th Stage	9th Stage	10th Stage	11th Stage	12th Stage
Equivalent circuit	Figure 6e	Figure 6b	Figure 6f	Figure 6b	Figure 6g	Figure 6b

4.2. DC Voltage Gain Expression for Power Flow from V₂ to V₁

In CCM and for power flow from V₂ to V₁, the expression for the DC voltage gain can be derived by analyzing the average voltage across one of the inductors, as follows:

$${V_L}_1={\displaystyle \frac{2}{T_S}}·\left[{\int }_0^{{\mathit{∆}t}_1}\left(V_{C1}+V_2 - V_1\right) dt+{\int }_0^{{ 2{\mathit{∆}t}_1+3\mathit{∆}t}_2}{ - V}_1 dt\right]$$

(66)

Substituting the time intervals Δt₁ and Δt₂ into Equation (66) yields Equation (67).

$$0=2 D ·V_2-V_1+2 D ·V_{C1}$$

(67)

The voltage V_C1 is determined by integrating the average current through inductor L₄, as given by:

$${V_L}_4={\displaystyle \frac{2}{T_S}}\left[{\int }_0^{{\mathit{∆}t}_1}{V}_2 dt+{\int }_0^{{ 2{\mathit{∆}t}_1+3\mathit{∆}t}_2} - V_{C1} dt\right]$$

(68)

Solving Equation (68) yields the voltage V_C1, as defined in Equation (69).

$$V_{C1}=V_2·{\displaystyle \frac{2D}{1-2D}}$$

(69)

Substituting Equation (69) into Equation (67) yields the expression for the DC voltage gain in the power flow direction from V₂ to V₁, as given in Equation (70).

$${G_{CCM}}_{V_2\to V_1}={\displaystyle \frac{V_1}{V_2}}={\displaystyle \frac{2 D}{1-2 D}}$$

(70)

Using Equation (70), the DC voltage gain of the proposed converter in the power flow direction from V₂ to V₁ is analyzed. It exhibits the same DC voltage gain characteristics as in the power flow direction from V₁ to V₂, with the DC voltage gain increasing exponentially as the duty cycle (D) varies (see Figure 5). This behavior demonstrates the converter’s capability to effectively step up or step down the input voltage, accommodating diverse application requirements.

4.3. Component Stress Determination and Passive Elements Sizing

As the converter handles equal power in both power flow directions, the component stresses remain identical. The only difference lies in the duty cycle values between the power flow from V₁ to V₂ and the power flow from V₂ to V₁. Consequently, the duty cycle for the power flow from V₁ to V₂ is determined as a function of the duty cycle for the power flow from V₂ to V₁. It is important to note that the DC gains for the power flow from V₁ to V₂ and from V₂ to V₁ are determined by Equations (31) and (70). These gains can also be expressed as:

$${G_{CCM}}_{V_1\to V_2}= {\displaystyle \frac{V_2}{V_1}}={\displaystyle \frac{2 D_{V_1\to V_2}}{1-2 D_{V_1\to V_2}}}$$

(71)

$${G_{CCM}}_{V_2\to V_1}={\displaystyle \frac{V_1}{V_2}}={\displaystyle \frac{2 D_{V_2\to V_1}}{1-2 D_{V_2\to V_1}}}$$

(72)

where $D_{V_1\to V_2}$ represents the duty cycle value for power flow from V₁ to V₂, and $D_{V_2\to V_1}$ denotes the duty cycle value for the power flow from V₂ to V₁. The DC gains in both directions are inversely proportional, expressed as ${G_{CCM}}_{V_1\to V_2}=1/{G_{CCM}}_{V_2\to V_1}$. Substituting (71) and (72) into this relationship yields:

$${\displaystyle \frac{2 D_{V_1\to V_2}}{1-2 D_{V_1\to V_2}}}={\displaystyle \frac{1}{\left(\frac{2 D_{V_2\to V_1}}{1-2 D_{V_2\to V_1}}\right)}}$$

(73)

By manipulating Equation (73), the duty cycle in $D_{V_1\to V_2}$ can be expressed as a function of the duty cycle in $D_{V_2\to V_1}$, as shown in Equation (74).

$$D_{V_1\to V_2}={\displaystyle \frac{1-D_{V_2\to V_1}}{2}}$$

(74)

The output capacitance C₅ in the power flow from V₂ to V₁ is directly related to the current ripple in the inductors L₁, L₂, and L₃, as the capacitor functions to smooth out the voltage variations at the output. The output capacitance must be sized to provide the necessary charge to maintain the output voltage stability during the switching cycles. The effective current in the capacitor is determined by the integral of Equation (75), using Figure 4b and Figure 6.

$${I_{C5}}_{RMS}=\sqrt{{\displaystyle \frac{6}{T_S}}\left[{\int }_0^{{\displaystyle \frac{{\mathit{∆}t}_1+{ \mathit{∆}t}_2}{2}}}{\left({\displaystyle \frac{{\mathit{∆}I}_{L1}}{8}}\right)}^{2}dt+{\int }_0^{{\displaystyle \frac{{\mathit{∆}t}_1+{\mathit{∆}t}_2}{2}}}{\left({\displaystyle \frac{{\mathit{∆}I}_{L1}}{8}}\right)}^2 dt\right]}$$

(75)

Substituting the time intervals Δt₁ and Δt₂ into Equation (75) gives rise to Equation (76).

$${I_{C5}}_{RMS}={\displaystyle \frac{{\mathit{∆}I}_{L1}}{8}}$$

(76)

Upon solving the integral of Equation (77), Equation (78) is obtained, which defines the capacitance value C₅.

$${\mathit{∆}V}_{C5}={\int }_0^{{\displaystyle \frac{{\mathit{∆}t}_1+{ \mathit{∆}t}_2}{2}}}{i}_{C5}(t)$$

(77)

$$C_5={\displaystyle \frac{{\mathit{∆}L}_1}{96 { \mathit{∆}V}_{C5}·f_S}}$$

(78)

5. Technical Comparison with Reference Converter Architectures

To assess the performance of the proposed converter, a comprehensive comparison with widely adopted and representative topologies from the literature [14,16,17,23,24,25] is presented in Table 4. This comparison considers operation under CCM, voltage gain, current stresses on the main switch at the low-voltage side, the nature of the current waveform, and the frequency characteristics of current and voltage ripples at both low- and high-voltage ports. While some of the referenced converters are originally unidirectional, their bidirectional counterparts are considered here to ensure a fair and consistent evaluation.

Table 4. Comparison between the proposed architecture and selected literature topologies.

Parameters		[14]	[16]	[17]	[23]	[24]	[25]	Proposed
DC Voltage Gain	${\displaystyle \frac{V_2}{V_1}}$	${\displaystyle \frac{D}{1-D}}$	${\displaystyle \frac{1}{1-D}}$	${\displaystyle \frac{D}{1-D}}$	${\displaystyle \frac{1}{1-2 D}}$	${\displaystyle \frac{1}{1-D}}$	${\displaystyle \frac{3+D}{1-D}}$	${\displaystyle \frac{2 D}{1-2 D}}$
	${\displaystyle \frac{V_1}{V_2}}$	-	-	-	$2D$	$D$	${\displaystyle \frac{D}{4-D}}$	${\displaystyle \frac{2 D}{1-2 D}}$
Switch Voltage Stress		$V_1+V_2$	$V_2$	$V_1+V_2$	$V_1$	$V_2$	${\displaystyle \frac{V_1+V_2}{2}}$	$V_1+V_2$
Switch current Stress		${\displaystyle \frac{I_2}{2}}·{\displaystyle \frac{\sqrt{D}}{1-D}}$	$I_2·{\displaystyle \frac{\sqrt{D}}{1-D}}$	${\displaystyle \frac{I_2}{2}}·{\displaystyle \frac{\sqrt{D}}{1-D}}$	${\displaystyle \frac{I_2}{2}}·\sqrt{D}$	${\displaystyle \frac{I_2}{3}}·{\displaystyle \frac{\sqrt{D}}{1-D}}$	$I_2·{\displaystyle \frac{\sqrt{D}}{1-D}}$	${\displaystyle \frac{I_2}{3}}·{\displaystyle \frac{\sqrt{D}}{1-2 D}}$
Voltage V1/V2 (V)		100/200	27/48	80~120/400	24/10	250~400/800	72/400–800	220/450
Converter Power (W)		3.363	200	600	250	80.000	1.000	5.000
Switching Frequency (fS)		25 kHz	30 kHz	50-250 kHz	20 kHz	50 kHz	50 kHz	20 kHz
Efficiency (%)		88	92	94.6	97.9	97	97.6	98.6
Components Count S/D/L/C		4/8/12/1	4/0/3/4	2/2/4/4	8/0/2/2	6/0/3/2	8/0/4/5	12/0/6/5
Current and voltage ripple frequency at V1/V2		4 × fS	fS	2 × fS	4 × fS	3 × fS	2 × fS	6 × fS
Current ripple frequency of inductors		fS	fS	fS	2 × fS	fS	fS	2 × fS
Bidirectional		no	no	no	yes	yes	yes	yes
Normalized volume comparison	Inductors (PU)	0.3	1	0.67	0.17	0.23	0.33	0.15
	Capacitors (PU)	0.44	1	0.66	0.015	0.32	0.98	0.01

As summarized in Table 4, the converters presented in [14,17] exhibit similar voltage gain and current stress characteristics but do not support bidirectional operation. Specifically, the converter in [14] is limited to bipolar DC network applications and requires a larger number of passive components. Alharbi et al. [17] demonstrate that employing modern WBG devices (SiC/GaN) can improve efficiency. However, this architecture results in significant current stress on the switches when processing medium power levels.

The converter in [16] is tailored for bipolar DC microgrid applications and features asymmetric operation when the duty cycle deviates from 0.5, which limits its voltage gain and operational flexibility. In contrast, the proposed converter offers an extended voltage gain range while operating with lower duty cycles, thereby reducing conduction losses and enhancing efficiency. Conventional solutions such as those in [23,24] either exhibit fixed maximum/minimum gains, impose higher current stresses on the transistors, or rely on multiple conversion stages [25] with complex driving circuits. Across a wide operating range, the proposed converter demonstrates superior performance, including notably reduced current stress and high efficiency. Furthermore, the interleaving effect and phase–shift modulation enable the use of smaller inductance and capacitance values. The main design trade-off is the increased number of transistors and associated gate drivers required to enable interleaved operation.

An important performance aspect highlighted in Table 4 is the frequency of current and voltage ripples at both ports and across the inductors. Conventional converters such as [14,16,23] exhibit relatively low ripple frequencies, typically 2 × f_s or 3 × f_s, which necessitate larger filter components to achieve acceptable ripple attenuation. In contrast, the proposed converter achieves ripple frequencies of 6×fs both at the ports and across the inductors. This higher ripple frequency substantially relaxes the filtering requirements, enabling the use of smaller passive components and contributing to a more compact and lightweight design.

Finally, while many of the topologies considered for comparison produce highly discontinuous or pulsating currents on the high-voltage side, the proposed converter effectively mitigates this drawback. By employing inductors L₄, L₅, and L₆, it ensures low output current ripple, thereby minimizing stress on the output filter capacitor and enhancing overall system reliability

6. Experimental Results and Efficiency Analysis

To validate the feasibility of the proposed 5 kW converter, a laboratory prototype was implemented, as shown in Figure 7. Table 5 summarizes the converter specifications and component parameters. The gating signals for the power switches are generated using a TMS320F28379D digital signal controller and applied to the MOSFET drivers. The experimental waveforms were acquired with a Tektronix DPO3014 oscilloscope. A video demonstrating the real-time operation and dynamic behavior of the prototype under laboratory conditions is available in the Supplementary Materials. This section investigates two operating modes: power flow from V₁ to V₂ and from V₂ to V₁.

Figure 7. Prototype of the proposed converter and main components.

Table 5. Experimental parameters and component specifications.

Specifications/Parameters	Value
Rated power	6 kW
Voltage port (V1)	220 V
Voltage port (V2)	450 V
Switching frequency (fS)	20 kHz
Duty cycle (D1)	0.336
Duty cycle (D2)	0.164
Inductance (L1, L2)	1.5 mH
Capacitors (C1, C2, C3)	MKP1848C71050JY (VISHAY, 100 µF/500 V)
Capacitor (C4, C5)	MKP1848C (VISHAY, 25 µF/800 V)
Power Switches	G3R75MT12D SiC MOSFET
DSP module (For PWM modulation)	TMS320F28379D (Dual-Core Microcontrollers)

6.1. Experimental Results for Power Flow from V₁ to V₂

Figure 8 presents the current and voltage waveforms at the V₁ and V₂ terminals. It can be observed that the voltage at V₁ (Ch1) is 220 V, while the voltage at V₂ (Ch2) reaches 450 V. Additionally, the currents at V₁ and V₂ are shown in Ch3 and Ch4, respectively. These results are consistent with the power flow from V₁ to V₂ and validate Equation (31), which defines the voltage gain in this operating mode. Therefore, the experimental results are in close agreement with the theoretical predictions, confirming the accuracy of the proposed converter.

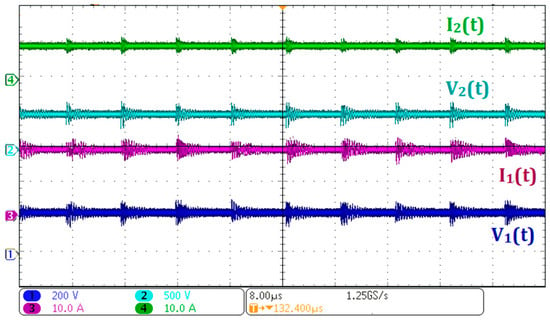
Figure 8. Experimental waveforms for power flow from V₁ to V₂: (Ch1) voltage at V₁; (Ch2) voltage at V2; (Ch3) current at V1 (I₁); (Ch4) current at V₂ (I₂).

Figure 9 shows, in Ch1, the gating signal of S₁, while Ch2, Ch3, and Ch4 display the currents I_L3, I_L2, and I_L1, respectively. It is also observed that the ripple frequency of the inductor currents (L₁, L₂, and L₃) is twice the switching frequency. As a result of the three-phase interleaved operation, the ripple frequency of both the current and voltage at V₁ is six times the switching frequency. This feature enables the use of smaller filter capacitors and represents one of the advantages of the proposed converter compared to conventional interleaved converters.

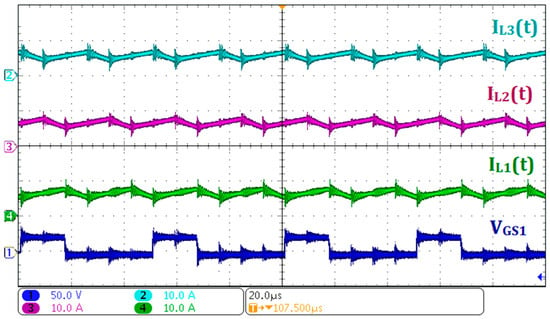
Figure 9. Experimental waveforms for power flow from V₁ to V₂: (Ch1) gating signal of S₁; (Ch2) current I_L3 of inductor L₃; (Ch3) current I_L2 of inductor L₂; (Ch4) current I_L1 of inductor L₁.

Figure 10 presents the voltage and current waveforms of inductors L₁ and L₂, where Ch1 and Ch4 correspond to the voltage across and current through inductor L₁, respectively, while Ch2 and Ch3 display the voltage across and current through inductor L₂. It can be observed that during the energy storage interval, the voltage across the inductors equals V₁, while during the energy transfer interval, it equals V₁ − (V_C1 − V₂). These results are in close agreement with the theoretical analysis previously presented, thereby validating the expected operational behavior of the proposed converter.

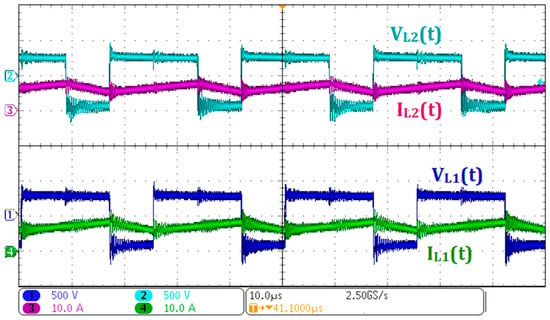
Figure 10. Experimental waveforms for power flow from V₁ to V₂: (Ch1) voltage across L₁ and (Ch4) current through L₁; (Ch2) voltage across L₂ and (Ch3) current through L₂.

Figure 11 shows the voltage waveforms across switches S₁, S₃, and S₅, corresponding to channels Ch3, Ch1, and Ch2, respectively. It can be observed that the peak voltages across these switches reach values close to those predicted by Equation (40).

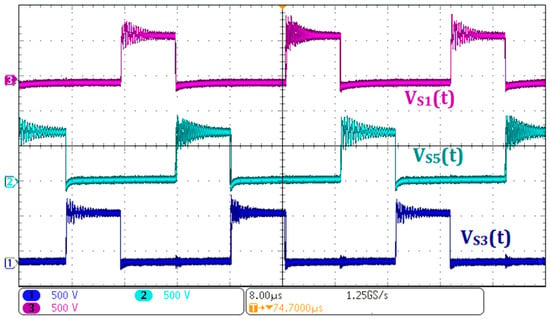
Figure 11. Experimental waveforms for power flow from V₁ to V₂: (Ch1) voltage across S₃; (Ch2) voltage across S₅; (Ch3) voltage across S₁.

Figure 12 shows the voltages across the body diodes of switches Q₁, Q₃, and Q₅, displayed in Ch1, Ch2, and Ch3, respectively. The voltages across the body diodes correspond closely to those measured across switches S, indicating similar voltage stress on these components.

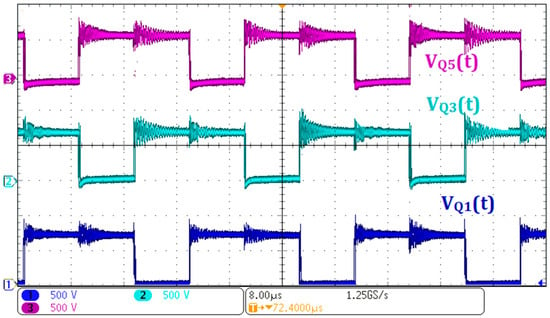
Figure 12. Experimental waveforms for power flow from V₁ to V₂: (Ch1) voltage across the body diode of Q₁; (Ch2) voltage across the body diode of Q₃; (Ch3) voltage across the body diode of Q₅.

Figure 13 presents the current waveforms of inductors L₅, L₆, and L₄, displayed in Ch2, Ch3, and Ch4, respectively. It is observed that the ripple frequency of the inductor currents (L₄, L₅, and L₆) is twice the switching frequency, as also observed in L₁, L₂, and L₃. Due to the three-phase interleaved operation, the ripple frequency of both the current and voltage at V₂ reaches six times the switching frequency. This characteristic allows the use of a smaller filter capacitor C₄, thereby contributing to a more compact and efficient converter design.

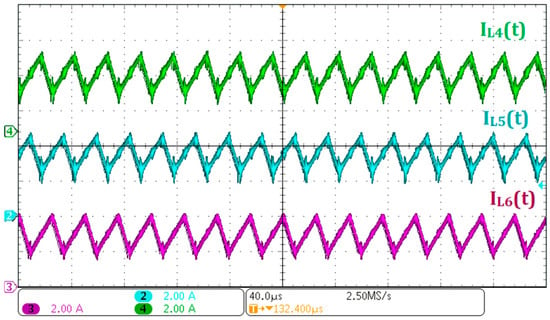
Figure 13. Experimental waveforms for power flow from V₁ to V₂: (Ch2) current I_L5 of inductor L₅; (Ch3) current I_L6 of inductor L₆; (Ch4) current I_L4 of inductor L₄.

6.2. Experimental Results for Power Flow from V₂ to V₁

Figure 14 presents the current and voltage waveforms at the V₂ and V₁ terminals. Ch2 shows the voltage at V₂, approximately 450 V, while Ch1 displays the voltage at V₁, reaching 220 V. The currents at the V₂ and V₁ ports are shown in Ch4 and Ch3, respectively. These values align with the power flow direction from V₂ to V₁ and validate Equation (70), which defines the voltage gain in this operating mode. The experimental results closely match the theoretical predictions, confirming the accuracy of the proposed converter model.

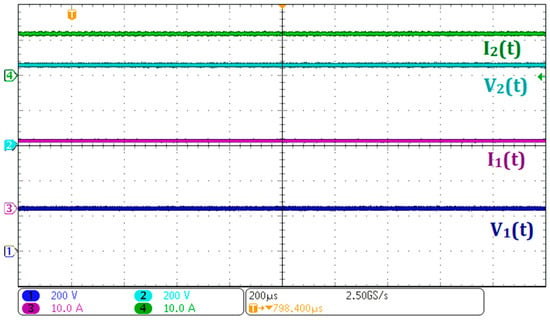
Figure 14. Experimental waveforms for power flow from V₂ to V₁: (Ch1) voltage at V₁; (Ch2) voltage at V₂; (Ch3) current at V₁ (I₁); (Ch4) current at V₂ (I₂).

Figure 15 illustrates the voltage and current waveforms of inductors L₅ and L₆. The voltage across and current through inductor L₆ are shown in Ch1 and Ch3, respectively, while Ch2 and Ch4 display the voltage across and current through inductor L₅. During the energy storage interval, the voltage across the inductors is equal to V₂; during the energy transfer interval, it corresponds to V_C1 + V₂ − V₁. These observed behaviors closely match the theoretical analysis, confirming the expected operation of the converter. Figure 16 presents the voltages across switches Q₁, Q₃, and Q₅, shown in Ch3, Ch2, and Ch1, respectively. The measured voltage across the switches closely matches the theoretical value predicted by (40).

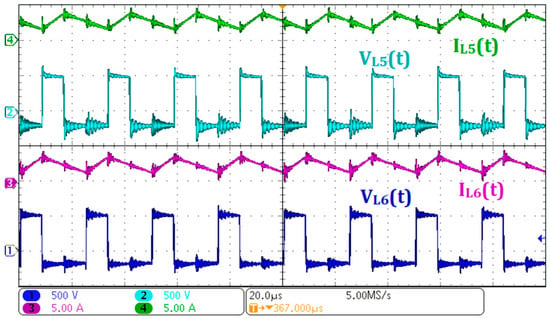
Figure 15. Experimental waveforms for power flow from V₂ to V₁: (Ch1) voltage across L₆ and (Ch3) current through L₆; (Ch2) voltage across L₅ and (Ch4) current through L₅.

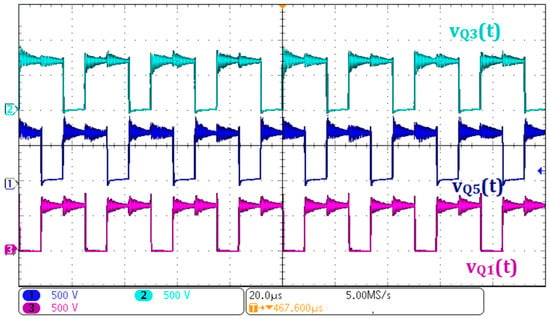
Figure 16. Experimental waveforms for power flow from V₂ to V₁: (Ch1) voltage across Q₅; (Ch2) voltage across Q₃; (Ch3) voltage across Q₁.

Figure 17 presents the current waveforms of inductor L₆ and capacitors C₁ and C₂, shown in Ch2, Ch3, and Ch4, respectively. It is observed that the ripple frequency of both the inductor and the capacitors is twice the switching frequency. Owing to the three-arm interleaved operation, the ripple frequency of both the current and voltage at ports V₂ and V₁ increases to six times the switching frequency. This characteristic enables the use of smaller filter components, including capacitors and inductors, thereby contributing to a more compact and higher-efficiency converter design.

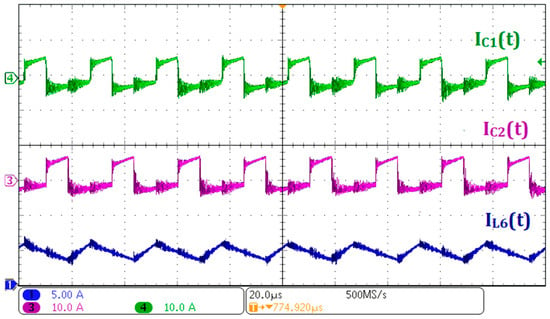
Figure 17. Experimental waveforms for power flow from V₂ to V₁: (Ch1) current I_L6 of inductor L₆; (Ch3) current I_C2 of capacitor C₃; (Ch4) current I_C1 of capacitor C₁.

Figure 18 presents the experimental voltage and current waveforms of the body diodes of switches S₁ and S₃ during power flow from V₂ to V₁. The voltage across the body diodes of S₁ and S₃ is shown in Ch1 and Ch2, respectively, while the corresponding currents are displayed in Ch3 and Ch4. The observed waveforms confirm the correct operation of the body diodes during the commutation intervals, in accordance with the expected behavior of the converter in this mode. These results further validate the theoretical analysis and demonstrate the converter’s capability to handle bidirectional power flow with proper diode conduction.

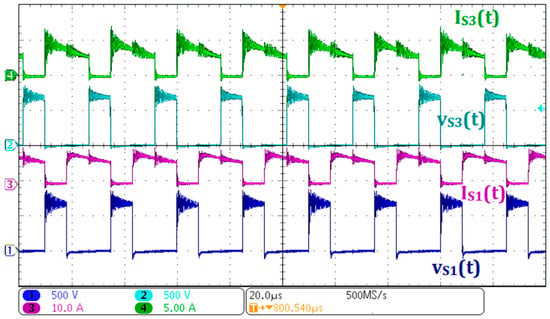
Figure 18. Experimental waveforms for power flow from V₂ to V₁: (Ch1) voltage across the body diode of S₁; (Ch2) voltage across the body diode of S₃; (Ch3) current through the body diode of S₁; (Ch4) current through the body diode of S₃.

Figure 19 presents the experimental efficiency of the converter at two output voltage levels: V₂ = 450 V (red curve) and V₂ = 350 V (blue curve). In both cases, the input voltage is fixed at V₁ = 220 V, and the converter operates with power flow from V₁ to V₂. The converter achieves high efficiency across the entire power range. For V₂ = 350 V, the maximum efficiency reaches 98.60% at 5 kW, while for V₂ = 450 V, the efficiency peaks at 98.10%. In both scenarios, the efficiency increases with output power, approaching its maximum value as power reaches 5 kW. These results demonstrate the converter’s ability to maintain high efficiency under varying voltage conditions and load levels.

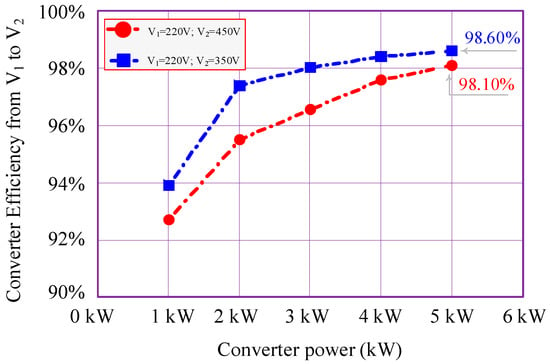
Figure 19. Efficiency of the proposed converter during power flow from V₁ to V₂.

Figure 20 presents the experimental efficiency of the converter for different input voltage levels: V₁ = 220 V (red curve) and V₁ = 350 V (blue curve), with a fixed output voltage of V₂ = 450 V, operating in the power flow direction from V₂ to V₁. The converter maintains high efficiency across the entire power range. At 5 kW, the maximum efficiency reaches 97.60% for V₁ = 350 V and 97.45% for V₁ = 220 V. For both voltage levels, efficiency increases with output power and stabilizes near its maximum at higher power levels. However, in this power flow direction, efficiency shows a slight reduction compared to the power flow from V₁ to V₂, as observed in the previous case. These results confirm the converter’s ability to deliver high efficiency under bidirectional power flow conditions.

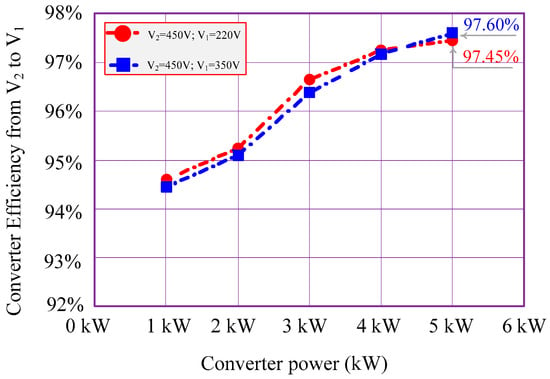
Figure 20. Efficiency of the proposed converter during power flow from V₂ to V₁.

7. Conclusions

This paper presents a high-efficiency bidirectional interleaved SEPIC–ZETA DC–DC converter with a phase-shifted PWM technique and multidevice structure using parallel-connected switches, specifically designed for advanced electric vehicle applications. The proposed topology successfully addresses key challenges in modern bidirectional power conversion, offering significant advantages such as extended voltage gain, reduced current and voltage ripple, and minimized component stress. The three-phase interleaving architecture enables compact and lightweight converter implementation with smaller passive components.

A comprehensive theoretical analysis is provided, covering the steady-state operation in both power flow directions, supported by detailed mathematical modeling and passive element sizing. Experimental validation was performed using a 5 kW prototype, demonstrating excellent performance with a peak efficiency of 98.6% in step-up mode and 97.6% in step-down mode. The results confirm the converter’s ability to efficiently manage energy transfer in bidirectional applications, with high power density and superior ripple mitigation.

Future work will focus on developing a closed-loop control strategy, evaluating dynamic performance, and extending the proposed architecture to multi-arm configurations for higher power and voltage applications.