Short-Term Residential Load Forecasting Based on Generative Diffusion Models and Attention Mechanisms
Abstract
1. Introduction
- A diffusion-based uncertainty modeling strategy is introduced to reconstruct reliable input features from noisy and missing data. The forward diffusion process simulates data degradation, while the reverse process iteratively restores features, enhancing model robustness and adaptability to uncertainty in load patterns.
- A TCN-based sequence encoder is developed to efficiently model high-dimensional, variable-length sequences. Leveraging TCN’s parallelism and stable gradient propagation, the encoder enhances temporal feature extraction while maintaining computational efficiency.
- An attention-augmented GRU decoder is designed to facilitate multi-scale temporal modeling. Integrating attention mechanisms assists the GRU in capturing long-sequence dependencies, thereby improving both prediction accuracy and generalization.
- Extensive experiments on real-world residential load datasets, evaluated using MAE, root mean square error (RMSE), and Pearson correlation coefficient (CORR), demonstrate that the proposed DATeM framework outperforms existing methods in terms of accuracy, robustness, and practical applicability.
2. Related Work
- Traditional statistical methods rely on linear assumptions and manual feature engineering, which are intractable for modeling high-dimensional nonlinear load dynamics.
- Deep learning methods improve the forecasting accuracy but primarily focus on deterministic outputs, lacking the end-to-end probabilistic modeling capability.
- Uncertainty quantification and dynamic adaptation techniques are typically isolated, lacking the effective integration with multi-scale temporal feature extraction.
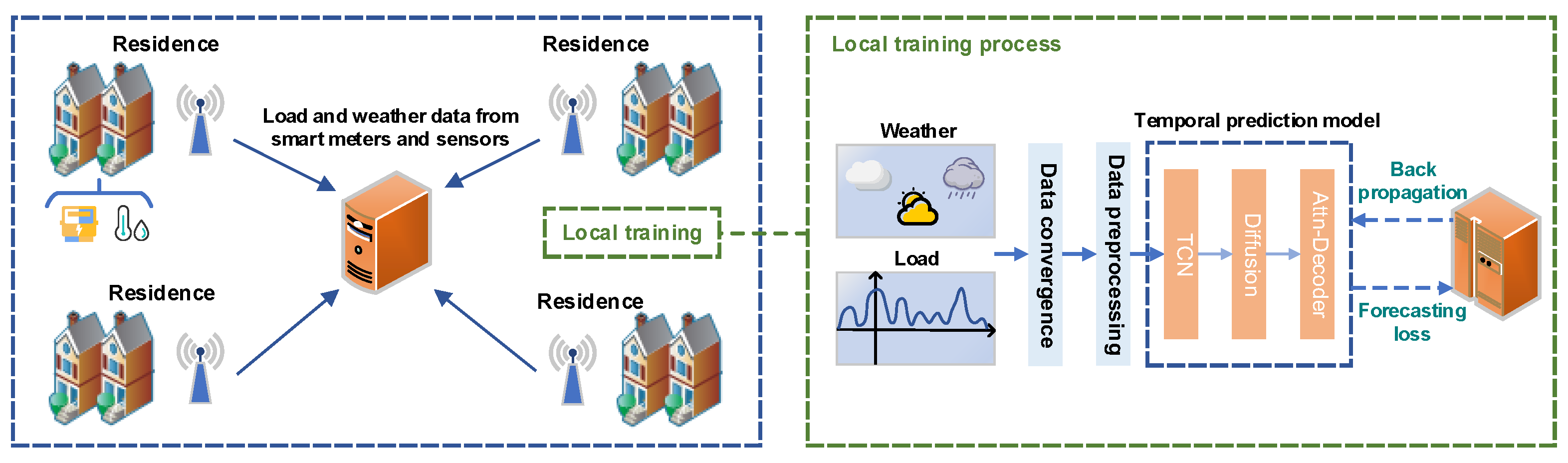
3. Framework Overview
4. Diffusion-Attention Temporal Modeling
- Feature extraction: The latent representation of the input sequence is extracted through the TCN encoder.
- Diffusion enhancement: Noise perturbation is applied to the latent representation, and the denoising process is conducted.
- Dynamic decoding: The prediction result is generated based on the attention mechanism.
- Weight adaptation: An adaptive loss weighting mechanism is integrated to concurrently enhance both the forecasting precision and latent feature discriminability.
| Algorithm 1 DATeM training |
|
4.1. TCN Encoder
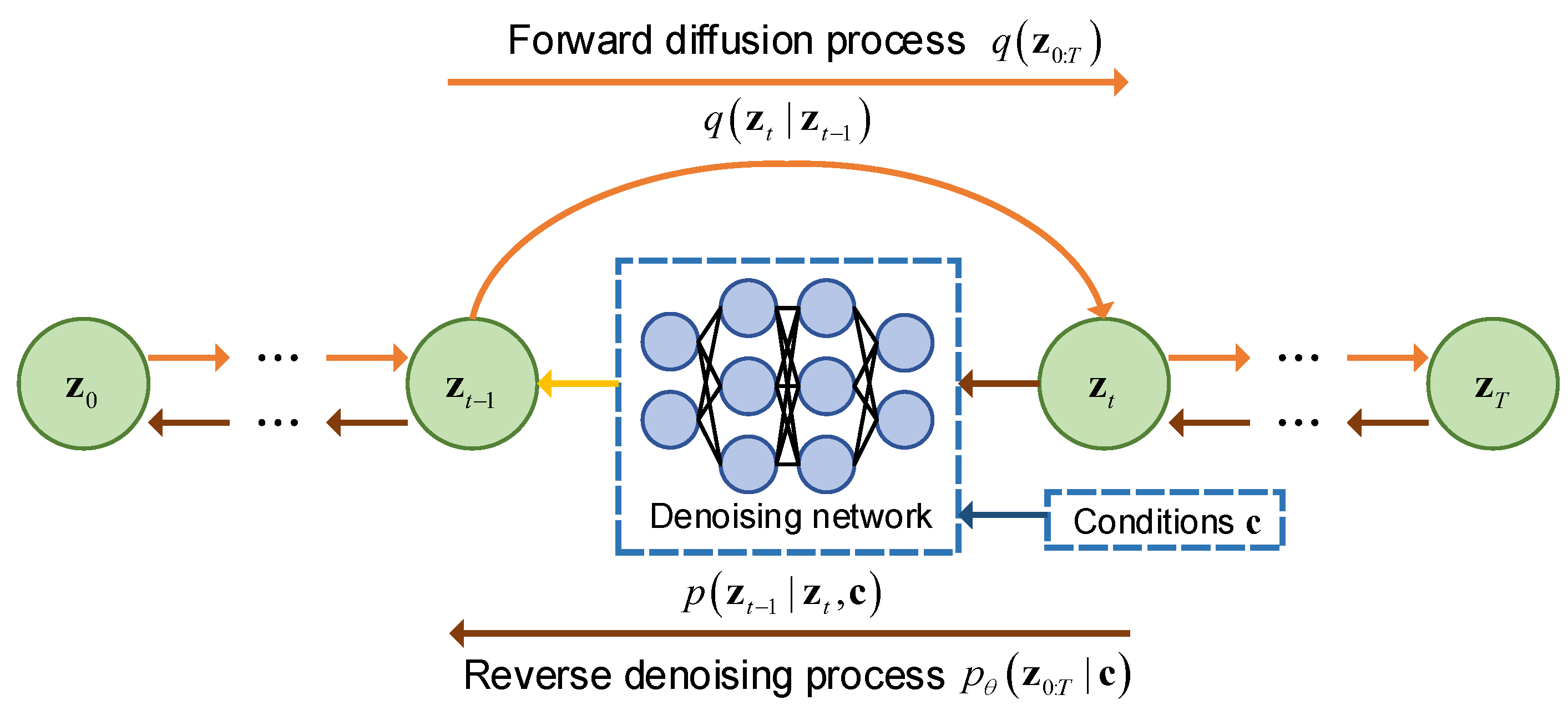
4.2. Latent Space Diffusion Process
- Local volatility: The load may fluctuate sharply over short periods due to sudden weather changes, appliance operations, and other factors.
- External dependence: The load is significantly influenced by external factors such as temperature, humidity and holidays.
- Noise interference: Raw load data often contains measurement errors and outliers, and traditional deterministic models (e.g., RNNs and TCNs) have to struggle with errors and outliers.
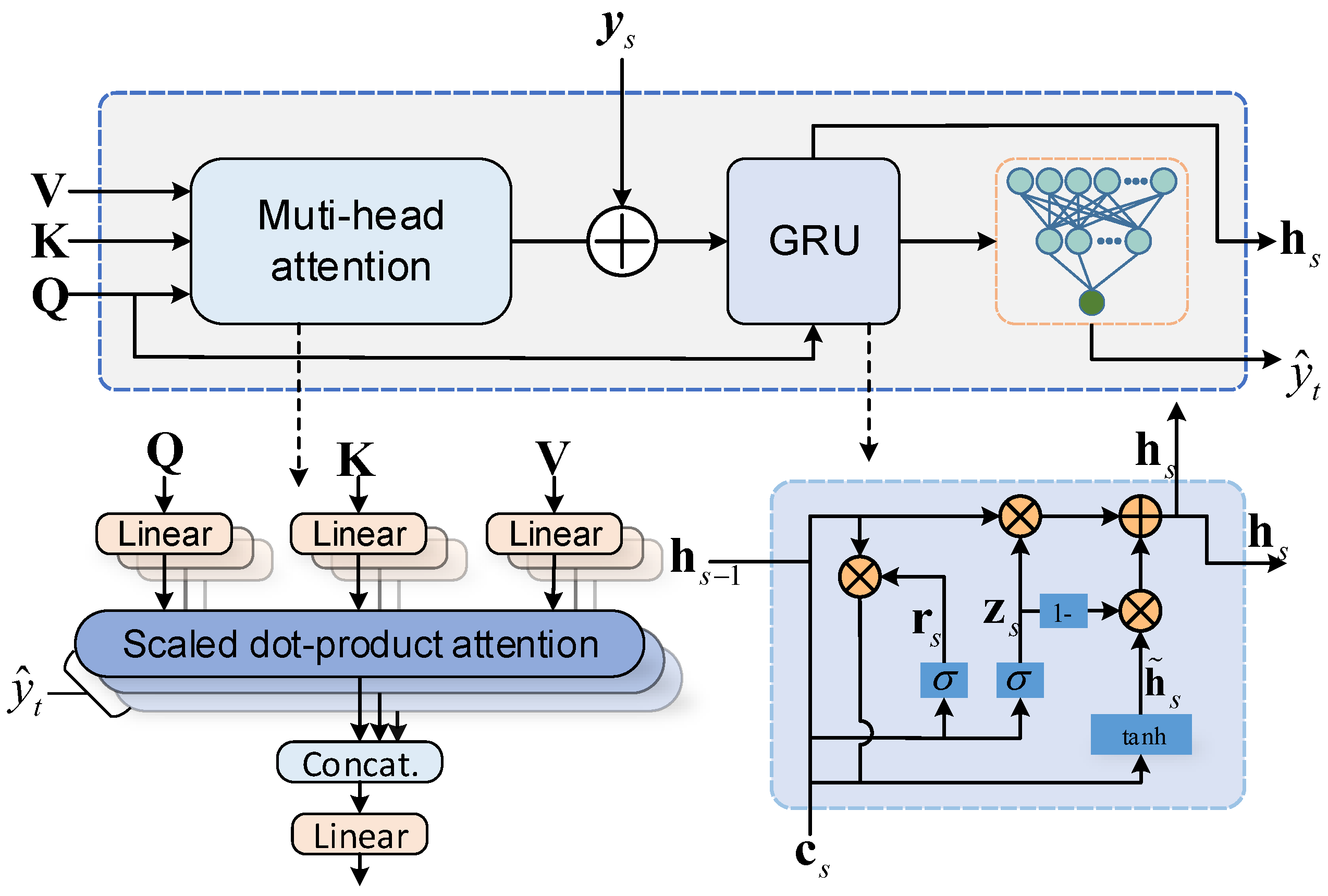
4.3. Attention Decoder
4.3.1. Multi-Head Scaled Dot-Product Attention
4.3.2. State Updating of GRU
4.4. Dynamic Weighted Loss
4.5. Training Convergence Analysis
5. Experiments and Results
5.1. Data
5.2. Evaluation
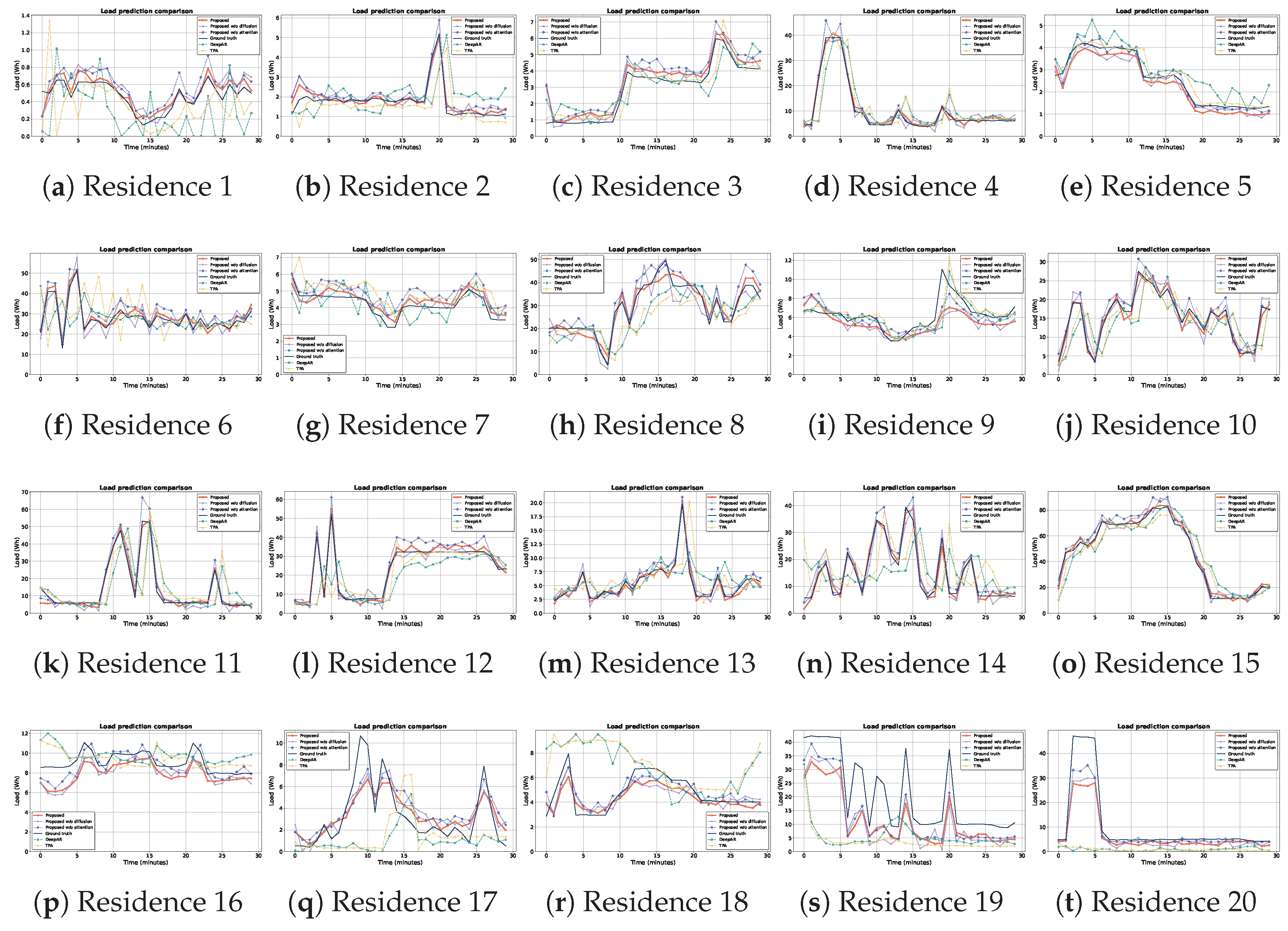
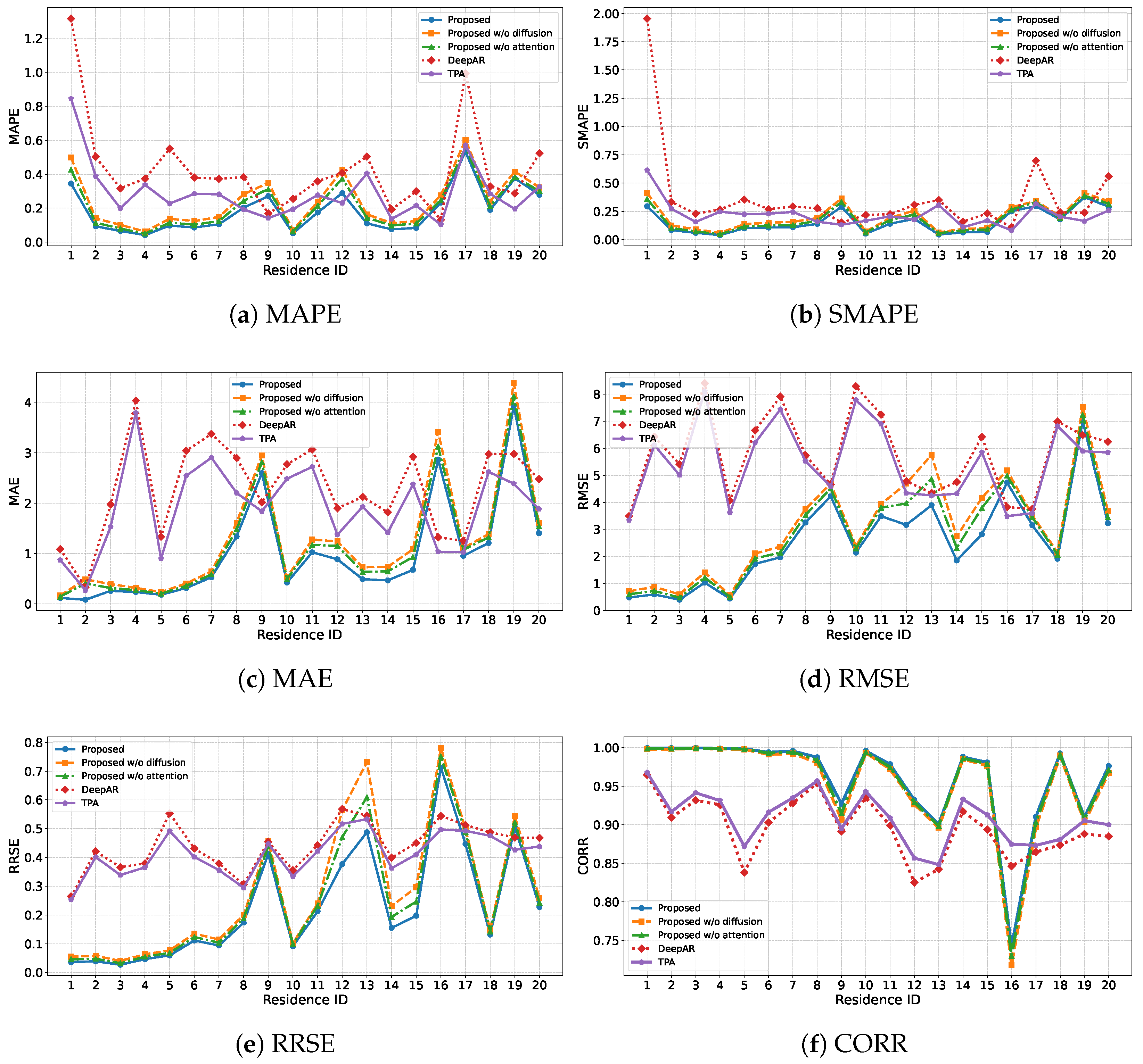
5.3. Comparison
- Experiment setup and dataset partitioning strategy.
- Multi-metric performance comparison with baseline models.
- Statistical significance validation via Friedman test.
- Ablation study analyzing the contributions of key modules.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Seyedeh, F.; Ravinesh, D.; Mohammad, S.; Mauro, C.; Shahaboddin, S. Computational intelligence approaches for energy load forecasting in smart energy management grids: State of the art, future challenges, and research directions. Energies 2018, 11, 596. [Google Scholar] [CrossRef]
- Dong, Q.; Huang, R.; Cui, C.; Towey, D.; Zhou, L.; Tian, J.; Wang, J. Short-term electricity-load forecasting by deep learning: A comprehensive survey. Eng. Appl. Artif. Intell. 2025, 154, 110980. [Google Scholar] [CrossRef]
- Bohara, B.; Fernandez, R.I.; Gollapudi, V.; Li, X. Short-term aggregated residential load forecasting using bilstm and CNN-BiLSTM. In Proceedings of the IEEE International Conference on Innovation and Intelligence for Informatics, Computing, and Technologies (3ICT), Sakheer, Bahrain, 20–21 November 2022; pp. 37–43. [Google Scholar]
- Sousa, J.C.; Bernardo, H. Benchmarking of load forecasting methods using residential smart meter data. Appl. Sci. 2022, 12, 9844. [Google Scholar] [CrossRef]
- Paletta, Q.; Hu, A.; Arbod, G.; Lasenby, J. Eclipse: Envisioning cloud induced perturbations in solar energy. Appl. Energy 2022, 326, 119924. [Google Scholar] [CrossRef]
- Hao, C.H.; Wesseh, P.K.; Wang, J.; Abudu, H.; Dogah, K.E.; Okorie, D.I.; Opoku, E.E.O. Dynamic pricing in consumer-centric electricity markets: A systematic review and thematic analysis. Energy Strateg. Rev. 2024, 52, 101349. [Google Scholar] [CrossRef]
- Jha, N.; Prashar, D.; Rashid, M.; Gupta, S.K.; Saket, R.K. Electricity load forecasting and feature extraction in smart grid using neural networks. Comput. Electr. Eng. 2021, 96, 107479. [Google Scholar] [CrossRef]
- Zhou, H.; Zhang, S.; Peng, J.; Zhanga, S.; Li, J.; Xiong, H.; Zhang, W. Informer: Beyond efficient transformer for long sequence time-series forecasting. In Proceedings of the AAAI Conference on Artificial Intelligence, Vancouver, BC, Canada, 2–9 February 2021; pp. 11106–11115. [Google Scholar]
- Wang, Z.; Wen, Q.; Zhang, C.; Sun, L.; Wang, Y. Diffload: Uncertainty quantification in electrical load forecasting with the diffusion model. IEEE Trans. Power Syst. 2025, 40, 1777–1789. [Google Scholar] [CrossRef]
- Yang, Y.; Jin, M.; Wen, H.; Zhang, C.; Liang, Y.; Ma, L.; Wang, Y.; Liu, C.; Yang, B.; Xu, Z.; et al. A survey on diffusion models for time series and spatio-temporal data. arXiv 2024, arXiv:2404.18886. [Google Scholar] [CrossRef]
- Qian, C.; Xu, D.; Zhang, Y.; Bao, J.; Ma, X.; Wu, Z. Residential customer baseline load estimation based on conditional denoising diffusion probabilistic model. In Proceedings of the IEEE International Conference in Power Engineering Applications (ICPEA), Taiyuan, China, 4–5 March 2024; pp. 59–63. [Google Scholar]
- Zheng, J.; Zhu, J.; Xi, H. Short-term energy consumption prediction of electric vehicle charging station using attentional feature engineering and multi-sequence stacked gated recurrent unit. Comput. Electr. Eng. 2023, 108, 108694. [Google Scholar] [CrossRef]
- Liu, D.; Lin, X.; Liu, H.; Zhu, J.; Chen, H. A coupled framework for power load forecasting with Gaussian implicit spatio temporal block and attention mechanisms network. Comput. Electr. Eng. 2025, 123, 110263. [Google Scholar] [CrossRef]
- Feng, Y.; Zhu, J.; Qiu, P.; Zhang, X.; Shuai, C. Short-term power load forecasting based on TCN-BiLSTM-Attention and multi-feature fusion. Arab. J. Sci. Eng. 2024, 50, 5475–5486. [Google Scholar] [CrossRef]
- Rizi, E.T.; Rastegar, M.; Forootani, A. Power system flexibility analysis using net-load forecasting based on deep learning considering distributed energy sources and electric vehicles. Comput. Electr. Eng. 2024, 117, 109305. [Google Scholar] [CrossRef]
- Yu, C.N.; Mirowski, P.; Ho, T.K. A sparse coding approach to household electricity demand forecasting in smart grids. IEEE Trans. Smart Grid 2017, 8, 738–748. [Google Scholar] [CrossRef]
- Stephen, B.; Tang, X.; Harvey, P.R.; Galloway, S.; Jennett, K.I. Incorporating practice theory in sub-profile models for short term aggregated residential load forecasting. IEEE Trans. Smart Grid 2017, 8, 1591–1598. [Google Scholar] [CrossRef]
- Teeraratkul, T.; O’Neill, D.; Lall, S. Shape-based approach to household electric load curve clustering and prediction. IEEE Trans. Smart Grid 2018, 9, 5196–5206. [Google Scholar] [CrossRef]
- Xie, G.; Chen, X.; Weng, Y. An integrated Gaussian process modeling framework for residential load prediction. IEEE Trans. Power Syst. 2018, 33, 7238–7248. [Google Scholar] [CrossRef]
- van der Meer, D.; Shepero, M.; Svensson, A.; Widén, J.; Munkhammar, J. Probabilistic forecasting of electricity consumption, photovoltaic power generation and net demand of an individual building using Gaussian processes. Appl. Energy 2018, 213, 195–207. [Google Scholar] [CrossRef]
- Lu, J.; Zhang, X.; Sun, W. A real-time adaptive forecasting algorithm for electric power load. In Proceedings of the IEEE/PES Transmission & Distribution Conference & Exposition: Asia and Pacific, Dalian, China, 15–18 August 2005; pp. 1–5. [Google Scholar]
- Kong, W.; Dong, Z.Y.; Jia, Y.; Hill, D.J.; Xu, Y.; Zhang, Y. Short-term residential load forecasting based on LSTM recurrent neural network. IEEE Trans. Smart Grid 2019, 10, 841–851. [Google Scholar] [CrossRef]
- Xu, C.; Chen, G.; Zhou, X. Temporal pattern attention-based sequence to sequence model for multistep individual load forecasting. In Proceedings of the IECON 2020 the 46th Annual Conference of the IEEE Industrial Electronics Society, Singapore, 10–21 October 2020; pp. 1710–1714. [Google Scholar]
- Cheng, L.; Zang, H.; Xu, Y.; Wei, Z.; Sun, G. Probabilistic residential load forecasting based on micrometeorological data and customer consumption pattern. IEEE Trans. Power Syst. 2021, 36, 3762–3775. [Google Scholar] [CrossRef]
- Zuo, C.; Hu, W. Short-term load forecasting for community battery systems based on temporal convolutional networks. In Proceedings of the IEEE 2nd International Conference on Information Technology, Big Data and Artificial Intelligence (ICIBA), Chongqing, China, 17–19 December 2021; pp. 11–16. [Google Scholar]
- Lin, W.; Wu, D.; Boulet, B. Spatial-temporal residential short-term load forecasting via graph neural networks. IEEE Trans. Smart Grid 2021, 12, 5373–5384. [Google Scholar] [CrossRef]
- Tajalli, S.Z.; Kavousi-Fard, A.; Mardaneh, M.; Khosravi, A.; Razavi-Far, R. Uncertainty-aware management of smart grids using cloud-based LSTM-prediction interval. IEEE Trans. Cybern. 2022, 52, 9964–9977. [Google Scholar] [CrossRef] [PubMed]
- Dab, K.; Nagarsheth, S.H.; Amara, F.; Henao, N.; Agbossou, K.; Dubé, Y. Uncertainty quantification in load forecasting for smart grids using non-parametric statistics. IEEE Access 2024, 12, 138000–138017. [Google Scholar] [CrossRef]
- Langevin, A.; Cheriet, M.; Gagnon, G. Efficient deep generative model for short-term household load forecasting using non-intrusive load monitoring. Sustain. Energy Grids Netw. 2023, 34, 101006. [Google Scholar] [CrossRef]
- Khodayar, M.; Wang, J. Probabilistic time-varying parameter identification for load modeling: A deep generative approach. IEEE Trans. Ind. Inform. 2021, 17, 1625–1636. [Google Scholar] [CrossRef]
- Cho, K.; van Merrienboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning phrase representations using RNN encoder-decoder for statistical machine translation. arXiv 2014, arXiv:1406.1078. [Google Scholar] [CrossRef]
- Ho, J.; Jain, A.; Abbeel, P. Denoising diffusion probabilistic models. In Proceedings of the 34th International Conference on Neural Information Processing Systems, Virtual, 6–12 December 2020; pp. 6840–6851. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention is all you need. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Los Angeles, CA, USA, 4–9 December 2017; pp. 6000–6010. [Google Scholar]
- Trivedi, R.; Bahloul, M.; Saif, A.; Patra, S.; Khadem, S. Comprehensive dataset on electrical load profiles for energy community in Ireland. Sci. Data 2024, 11, 621. [Google Scholar] [CrossRef]
- Cai, S.; Qian, J.; Zhang, Z.; Yu, Y.; Gu, X.; Yang, E. Short-term electrical load forecasting based on the DeepAR algorithm and industry-specific electricity consumption characteristics. In Proceedings of the 2023 7th International Conference on Electrical, Mechanical and Computer Engineering (ICEMCE), Xi’an, China, 20–22 October 2023; pp. 384–387. [Google Scholar]
- Zhang, X.; Kong, X.; Yan, R.; Liu, Y.; Xia, P.; Sun, X.; Zeng, R.; Li, H. Data-driven cooling, heating and electrical load prediction for building integrated with electric vehicles considering occupant travel behavior. Energy 2023, 264, 126274. [Google Scholar] [CrossRef]

| Feature | Description |
|---|---|
| Date | Timestamps in 1 min intervals (Year 2020) |
| Production_Wh | Energy generation from PV (Watt-hours) |
| Consumption_Wh | Energy consumption (Watt-hours) |
| Charge_Wh | Battery energy storage charging (Watt-hours) |
| Discharge_Wh | Battery energy storage discharging (Watt-hours) |
| State-of-charge | Battery state of charge (%) |
| From grid_Wh | Energy taken from power grid (Watt-hours) |
| Grid feed_Wh | Energy delivered to power grid (Watt-hours) |
| Feature | Description |
|---|---|
| Date | Timestamps in 1 min intervals (Year 2020) |
| Speed | Wind speed (knots) |
| Dir | Wind direction (degrees) |
| Drybulb | Drybulb temperature (degrees Celsius) |
| Cbl | CBL pressure (hPa) |
| Soltot | Solar radiation (J/cm2) |
| Rain | Rainfall (mm) |
| Hyperparameter | Value |
| Historical window length | 240 |
| Forecasting window length | 30 |
| Batch size | 256 |
| Learning Rate | 0.0005 |
| Epoch | 40 |
| Hidden dimension | 64 |
| Diffusion steps | 5 |
| GRU Layer | 2 |
| Denoising Layer | 6 |
| Model | Average Time |
| Proposed | 55 m 43 s |
| Proposed w/o attention | 54 m 21 s |
| Proposed w/o diffusion | 53 m 17 s |
| DeepAR [35] | 106 m 41 s |
| TPA [36] | 57 m 20 s |
| Model | MAE ↓ | SMAPE ↓ | MAPE ↓ | RMSE ↓ | RRSE ↓ | CORR ↑ |
|---|---|---|---|---|---|---|
| Proposed | 1.0005 | 0.1589 | 0.1850 | 2.5743 | 0.2271 | 0.9602 |
| Proposed w/o diffusion | 1.2362 | 0.2029 | 0.2414 | 3.1392 | 0.2847 | 0.9543 |
| Proposed w/o attention | 1.1413 | 0.1818 | 0.2137 | 2.8925 | 0.2717 | 0.9572 |
| DeepAR [35] | 2.2841 | 0.3730 | 0.4322 | 5.7948 | 0.4394 | 0.8956 |
| TPA [36] | 1.9047 | 0.2220 | 0.2917 | 5.4501 | 0.4123 | 0.9083 |
| MAE ↓ | SMAPE ↓ | MAPE ↓ | RMSE ↓ | RRSE ↓ | CORR ↑ | |
|---|---|---|---|---|---|---|
| Friedman Stat. | 44.960 | 44.120 | 43.680 | 52.680 | 52.680 | 68.040 |
| p-value | < | < | < | < | < | < |
| Proposed | 1.30 | 1.40 | 1.40 | 1.20 | 1.20 | 1.10 |
| Proposed w/o attention | 2.45 | 2.50 | 2.40 | 2.30 | 2.30 | 2.10 |
| Proposed w/o diffusion | 3.45 | 3.55 | 3.50 | 3.45 | 3.50 | 3.15 |
| DeepAR [35] | 4.45 | 4.55 | 4.50 | 4.55 | 4.55 | 4.85 |
| TPA [36] | 3.35 | 3.00 | 3.20 | 3.50 | 3.45 | 3.80 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Y.; Li, J.; Chen, C.; Guan, Q. Short-Term Residential Load Forecasting Based on Generative Diffusion Models and Attention Mechanisms. Energies 2025, 18, 6208. https://doi.org/10.3390/en18236208
Zhao Y, Li J, Chen C, Guan Q. Short-Term Residential Load Forecasting Based on Generative Diffusion Models and Attention Mechanisms. Energies. 2025; 18(23):6208. https://doi.org/10.3390/en18236208
Chicago/Turabian StyleZhao, Yitao, Jiahao Li, Chuanxu Chen, and Quansheng Guan. 2025. "Short-Term Residential Load Forecasting Based on Generative Diffusion Models and Attention Mechanisms" Energies 18, no. 23: 6208. https://doi.org/10.3390/en18236208
APA StyleZhao, Y., Li, J., Chen, C., & Guan, Q. (2025). Short-Term Residential Load Forecasting Based on Generative Diffusion Models and Attention Mechanisms. Energies, 18(23), 6208. https://doi.org/10.3390/en18236208






