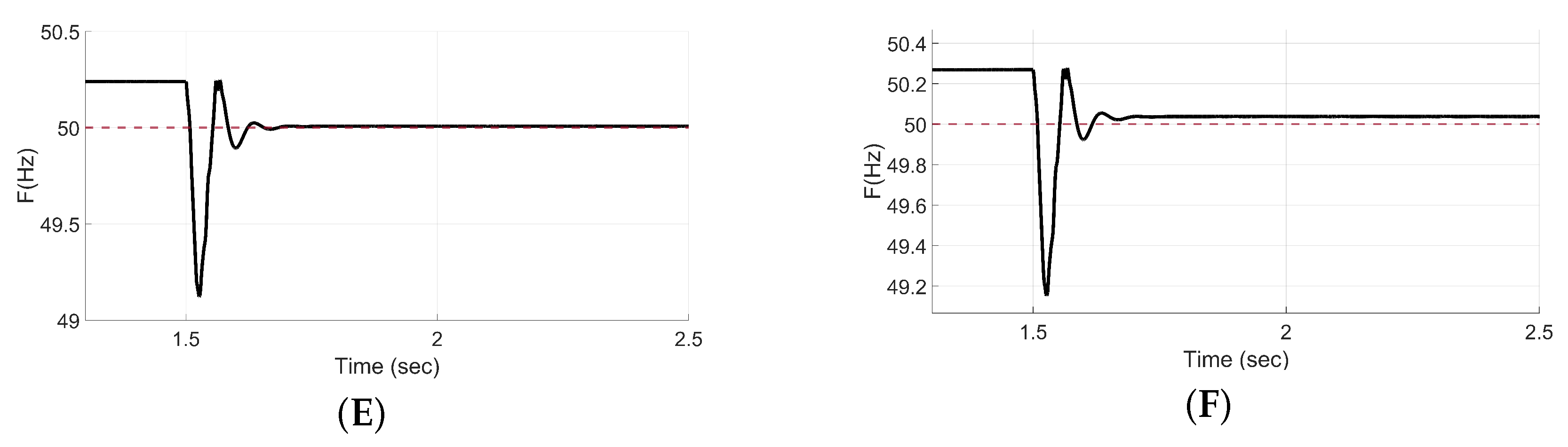PSO-Based Supervisory Adaptive Controller for BESS-VSG Frequency Regulation Under High PV Penetration

Abstract

High photovoltaic (PV) penetration challenges grid frequency stability due to reduced system inertia. Virtual Synchronous Generators (VSGs), particularly when paired with Battery Energy Storage Systems (BESSs), can mitigate this by emulating synchronous machine dynamics. This study focuses on improving frequency response during PV power reductions through the adaptive tuning of an extensive set of VSG parameters. A double-phase Supervisory Controller is developed: in the first phase, Particle Swarm Optimization (PSO) computes multiple sets of optimal VSG parameters for various PV curtailment and load demand change scenarios; in the second phase, the system determines the most appropriate parameters based on current operating conditions to minimize frequency deviations, using the first phase as a foundation for adaptive decision making. The proposed Supervisory Controller reduced the Integral of the Absolute Error (IAE) of 151.55% in the case of a 65% irradiance drop. At 55%, the IAE decreased from 0.4605 to 0.2227, and at 25% from 0.0791 to 0.0546. In the low-disturbance scenario at a 25% drop, the IAE was maintained below 0.06. Supervisory Controller performance led to a reduced settling time and improved frequency recovery. These results demonstrate that the Supervisory Controller improves frequency regulation in both mild and severe irradiance reduction events.

1. Introduction

The increasing penetration of photovoltaic (PV) generation in power systems presents new challenges in ensuring reliable operation under dynamic conditions [1,2]. Among these challenges is the system’s response to sudden variations in power balance, which may result from abrupt changes in PV output—caused by environmental factors, cloud cover, or grid faults—or from rapid fluctuations in load demand. Such disturbances can have a significant impact on grid frequency, particularly in systems that depend on inverter-based resources, which provide little or no rotational inertia [3,4,5]. A notable example of the impact of high PV penetration is the 2016 blackout in South Australia, where a frequency collapse—worsened by low system inertia—led to a major power outage, highlighting the vulnerabilities posed by a high share of renewable energy sources [6].

In contrast to conventional synchronous generators, which naturally contribute inertia through their rotating masses, inverter-based PV systems are decoupled from the mechanical dynamics of the grid and therefore lack this stabilizing feature. As the share of PV generation increases, the overall system inertia declines, reducing the grid’s capacity to absorb and dampen frequency disturbances. This lower inertia makes the power system more susceptible to frequency response issues, especially during sudden mismatches between generation and demand.

Virtual Synchronous Generators (VSGs) have emerged as a promising approach to improve the dynamic behavior of inverter-based systems by emulating the inertia and damping of traditional synchronous machines [7,8,9,10]. Among the technologies suitable for the implementation of VSG control, battery energy storage systems (BESSs) play a key role due to their fast response capabilities and operational flexibility, especially when the VSG operates in a grid-forming mode (GFM), where the inverter actively regulates frequency rather than passively following the grid [11,12,13].

However, the frequency response of a VSG is influenced by the tuning of key parameters, such as the inertia, damping coefficient [14], and control gains in the frequency regulation loop [15,16,17]. The system’s dynamic performance can vary with different parameter settings, making VSG behavior sensitive to controller configuration [14,18]. In systems with high penetration of PV generation, varying severities of PV power reduction or sudden load changes may require distinct sets of VSG parameters to achieve optimal frequency behavior. A controller configuration that is effective under one level of PV curtailment or load fluctuation might prove inadequate—or even destabilizing—under another. This highlights the need for a control strategy whose behavior can be tuned according to changing operating conditions.

This paper explores the design of a Supervisory Controller responsible for selecting the optimal parameter sets for VSGs. The objective is to minimize frequency deviations from the nominal grid frequency and to enhance the dynamic frequency response under varying levels of PV power reduction and changes in load demand. The parameter selection process is carried out over an extended control domain, with particular emphasis on those parameters most influential to frequency dynamics. The methodology is applied in a system configuration that includes a BESS operating under GFM-VSG control. A suite of switching controllers forms the core of the decision-making process, dynamically selecting the most appropriate configuration based on operating conditions. The switching logic is supported by parameter sets previously derived through Particle Swarm Optimization (PSO).

The paper is organized as follows. Section 2 reviews the state of the art in adaptive and optimization-based control of VSGs. Section 3 details the proposed methodology, including the system model, the VSG structure, the PSO algorithm, and the test design. Section 4 presents the simulation results, with a focus on the optimal parameters, the Supervisory Controller performance, and its impact on frequency regulation. Section 5 provides a discussion of the findings, and Section 6 summarizes the main conclusions and suggests future research directions.

2. State of the Art

To address the dynamic nature of the system and ensure good frequency response, adaptive control methods have been developed to tune the VSM parameters in real time or almost real time, with particular emphasis on inertia and damping. One primary area of research focuses on real-time adjustment of inertia and damping parameters in response to system conditions. The method proposed in [19] involves the use of a fuzzy logic controller (FLC), which is responsible for adaptively adjusting the inertia and damping constants of the VSG. These coefficients are modified based on real-time measurements of frequency deviation. The method was simulated in a comprehensive nonlinear analysis using MATLAB/Simulink, which compared the performance of the adaptive VSG with the conventional VSG under various disturbance levels and renewable energy source penetration. It is important to note that the article does not present a specific application of the VSG with an energy storage system. Instead, the VSG is connected to a generic DC energy source, which the authors mention could be a PV system, wind turbine, or energy storage system, but no specific source or condition is modeled in the simulations. In [20] a fuzzy logic-based method is implemented to adaptively change the inertia constant and the damping coefficient. Both MATLAB/Simulink and physical simulations were carried out. A key limitation of the fuzzy logic-based method is that it does not inherently perform a global search for the optimal parameter set, unlike other optimization algorithms. The fuzzy logic algorithm uses a set of predefined rules to adjust the parameters based on input conditions, but it lacks the ability to search the entire parameter space to identify the global optimum. In both [19,20], an evolutionary metaheuristic algorithm is implemented in combination with fuzzy logic. In the first case, a genetic algorithm is used [19], while in the second case, PSO is applied. However, it is important to clarify that the metaheuristic optimization’s goal is not to find the parameters of the VSG, but rather to tune the parameters of the fuzzy logic controller. Even the methods presented in [21,22,23] dynamically adjust the inertia and damping parameters in response to real-time frequency deviations. This is achieved either through mathematical formulations [21,22] or by integrating heuristic optimization with adaptive filters [23]. However, also, these methods do not include a global optimization process to identify the best parameter values for overall system performance. As a result, their effectiveness is constrained by their reactive nature: they adapt to system changes but may not achieve optimal dynamic performance or robustness, especially under highly variable or unforeseen operating conditions.

To overcome these limitations, recent studies have explored more advanced learning-based strategies, among which Reinforcement Learning (RL) has emerged as a promising approach. The RL approach presented in [24] enables a more extensive exploration of the solution space, as it learns through trial-and-error interactions with the environment and continuously adjusts its policy based on feedback, rather than relying on fixed heuristics or predefined models. The use of RL, particularly the twin-delayed deep deterministic policy gradient algorithm (TD3) chosen in this article, may introduce computational challenges, especially when applied in real time to dynamic systems like microgrids with VSGs. Indeed, as said by the authors, the TD3 agent requires extended training durations. Additionally, the VSG is not specifically used to control an energy storage system but rather to control grid-forming inverters in general, which can be connected to various distributed generation sources.

A parallel significant line of research focuses on the use of metaheuristic methods for control parameter optimization. These approaches, inspired by natural or social processes, are particularly valued for their ability to explore complex solution spaces and avoid local optima, making them well-suited for optimizing parameters in dynamic and nonlinear systems. In [25], the optimization of control parameters is achieved through an edge transfer PSO algorithm, specifically targeting the parameters inertia and damping. The droop coefficient is analytically determined based on system characteristics but is not included in the PSO optimization process. Similarly, Refs. [26,27,28] employ evolutionary metaheuristic algorithms for parameter optimization.

An alternative direction in the literature explores the use of multi-stage optimization frameworks under predefined conditions. Ref. [29] employs a two-level optimization framework using the Normal Boundary Intersection to tune inertia. Rather than seeking a globally optimal solution, during the first level the method focuses on optimizing the system for predefined scenarios, particularly those representing worst-case conditions, as outlined by the authors. In the second level, the system makes smaller, real-time adjustments based on the current state, starting from these predefined scenarios. This approach emphasizes robustness and adaptability over pursuing an ideal solution for every possible system state.

It is important to highlight that in all the articles previously referenced [19,20,21,22,23,24,25,26,27,28,29], the only parameters optimized are inertia and damping. Other crucial parameters—particularly the control gains—are not considered in these optimization efforts. Control gains significantly influence the system’s frequency response and dynamic performance. Their appropriate selection is therefore essential, and this has led to a growing interest in research focused on their optimization. Some studies have explored this aspect through static optimization approaches [15,16,17]. The optimization approaches in these do not adapt to varying grid conditions resulting from fluctuations in renewable energy production. Each work typically considers only a single disturbance scenario in power generation, or a limited set of predefined cases. These cases, however, reflect only a narrow portion of the possible operating conditions, rather than aiming to explore a broader and more representative range of scenarios. No methodologies have been developed to dynamically tune the VSG parameters according to intermediate or evolving conditions. For instance, Ref. [16] analyzes only a 50% reduction in solar irradiance. Ref. [17] does not directly address reductions in irradiance or PV output, but instead studies variations in load from 40 kW to 30 kW. Finally, Ref. [15] does not directly consider reductions in wind power generation, but instead introduces unit step changes in load power, along with a single larger disturbance whose exact magnitude is not specified. A static technique may have limitations because the dynamic performance of the system can change significantly with different parameter settings. Since the behavior of the VSG is sensitive to the controller configuration, as highlighted in [14,18], a static approach that does not adjust to real-time variations in system conditions might fail to optimize the VSG’s performance across different operating scenarios. Static methods cannot adapt to fluctuations in frequency response, disturbances, or variations in renewable energy sources, which may result in suboptimal performance or even undesirable dynamic behavior under certain conditions. Therefore, a static control approach, which relies on fixed parameter settings, may not effectively address the ever-changing dynamics of the system, limiting its ability to maintain robust and efficient operation.

To address the limitations of static control strategies, it is essential to consider approaches that can adapt to varying operational conditions. In this regard, only one notable study explores the system’s behavior under different operating scenarios by adjusting control gains accordingly [30]. The analysis incorporates a fixed reduction of 0.006 p.u. in solar power output, alongside stochastic disturbances—modeled as white noise—impacting both solar and wind generation. The work emphasizes optimizing proportional–integral controller parameters within this dynamic context, offering a comprehensive evaluation of control performance under uncertainty.

Table 1. Overview of key articles and their characteristics in the current state of the art.

Article	Inertia	D	${\mathit{K}}_{\mathit{p}}$	${\mathit{K}}_{\mathit{i}}$	${\mathit{K}}_{\mathit{f}}$	Multi-Scenario	Optima Search	ESS Appl.
[19]	✓	✓	X	X	X	✓	X	X
[20]	✓	✓	X	X	X	✓	X	✓
[21]	✓	✓	X	X	X	✓	X	✓
[22]	✓	✓	X	X	X	✓	X	✓
[23]	✓	✓	X	X	X	✓	X	✓
[24]	✓	✓	X	X	X	✓	✓	X
[25]	✓	✓	X	X	X	✓	✓	✓
[26]	✓	✓	X	X	X	✓	✓	✓
[27]	✓	✓	X	X	X	✓	✓	✓
[28]	✓	✓	X	X	X	✓	✓	✓
[16]	X	X	✓	✓	X	X	✓	✓
[17]	X	X	X	X	✓	X	✓	✓
[29]	✓	X	X	X	X	✓	X	✓
[15]	✓	✓	X	X	✓	X	✓	✓
[30]	X	X	✓	✓	X	✓	✓	✓

D: damping coefficient, $K_p$: proportional gain, $K_f$: frequency droop gain, $K_i$: integral gain, Multi-Scenario: optimization is based on multiple scenarios involving renewable energy production variation or on techniques that adaptively update parameters in real time or near real time based on system conditions, Optima Search: the applied algorithm is inherently designed to identify the optimal point, ESS Appl.: Energy Storage System Application of VSG.

provides a summary of the key articles discussed earlier, highlighting their characteristics within the current state of the art. It details the optimized parameters, such as inertia, damping, and/or control gains, and describes the optimization approach—whether it involves considering multiple scenarios of renewable production variability or adaptive real-time updates based on system conditions. Furthermore, the table indicates whether the optimization process seeks to identify the optimal solution and reports whether the VSG is integrated with an energy storage system.

In brief, the current research framework indicates areas where new insights are necessary. The dynamic nature of modern grid systems requires the development of a Supervisory Control system that can adjust its control parameters adaptively. This adaptability is essential for enabling the system to effectively manage grid fluctuations while maintaining the frequency response close to its nominal value. Existing methods primarily focus on adjusting key parameters like inertia and damping. However, these approaches do not fully address the broader range of VSG parameters that influence grid frequency behavior. Consequently, there is an emerging need for a more comprehensive approach that considers not only inertia and damping but also other VSG frequency-related parameters, such as control gains. In addition, any suggested solution should be tailored to GFM-VSGs that handle energy storage systems in settings with PV generation. PV systems are highly variable, with energy production fluctuating based on weather conditions, time of day, and other external factors, while load demand can also change unpredictably due to consumer behavior and operational conditions. This variability presents unique challenges for grid frequency response, and the Supervisory Control system must account for these factors to maintain reliable operation. BESSs improve PV systems by providing crucial frequency support, particularly in GFM configurations. They help stabilize the grid by storing excess energy when solar generation is high and supplying it during low generation. Through effective GFM control strategies, BESSs not only balance energy flow between the grid and the PV system but also support the grid during disturbances, enhancing overall reliability and system robustness [11]. The integration of a VSG with a BESS creates dynamic interactions between the BESS and the grid, necessitating the optimization of system parameters specifically for these scenarios. Thus, the proposed solution should be tailored to address the specific challenges arising from PV generation variability and load demand fluctuations, while optimizing the integration and operation of energy storage systems in such environments.

3. Materials and Methods

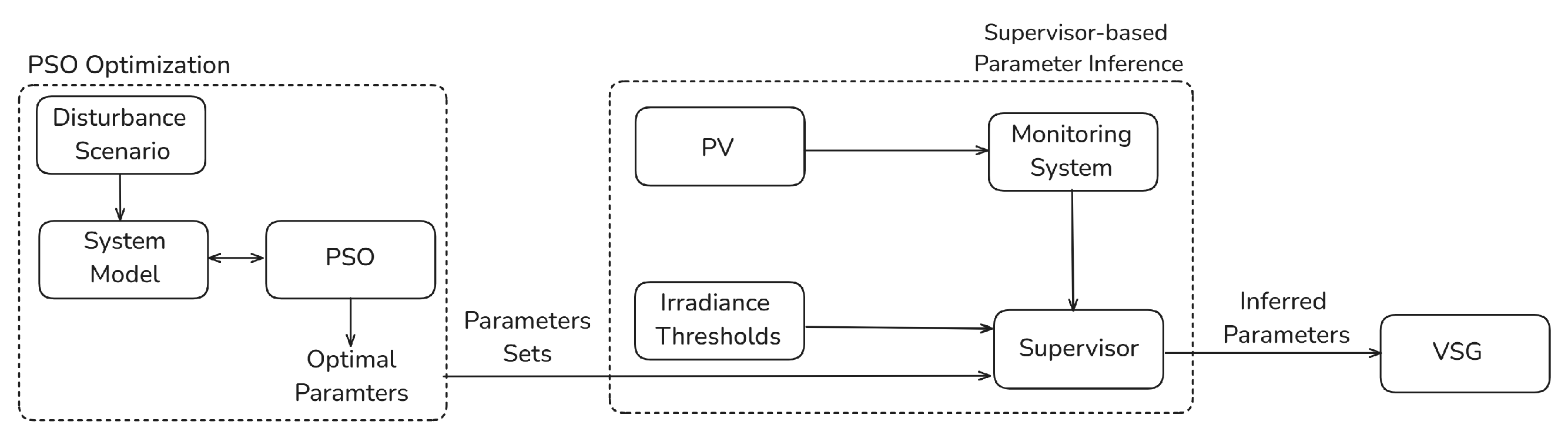
Figure 1 presents an overview of the proposed Supervisory Controller scheme, illustrating two distinct operational phases: a preprocessing optimization phase and a dynamic phase. During the preprocessing phase, optimal parameter sets are computed using a PSO algorithm applied to a system model subjected to various disturbance scenarios. These precomputed parameters are then utilized in the dynamic phase, where the system monitoring drives the decision logic that selects and applies the most appropriate parameter set to the VSG model.

The power system, including the VSG-BESS technology, was modeled by setting up a Simulink model.

The PSO algorithm was implemented in MATLAB to tune five key parameters of the VSG controller used in the BESS inverter: proportional gain ($K_p$), integral gain ($K_i$), droop coefficient ($K_f$), virtual inertia coefficient (H), and damping coefficient (D). The optimization routine was integrated with time-domain simulations carried out in Simulink. For each candidate solution generated by the PSO, the corresponding control parameters were applied to the Simulink power system model, which was then simulated under a PV power drop scenario occurring 1.5 s after the start of each simulation. Four different levels of PV power reduction were analyzed by decreasing the reference array’s solar irradiance (1000 W/m²) by 20%, 40%, 60%, and 80%, respectively. These reductions were simulated using a step-wise reduction approach. Step variations of 10% and 30% (with respect to a nominal load of 60 MW) in load demand were also applied. The PSO algorithm was run independently for each scenario to determine the optimal set of parameters.

Once the optimal parameter sets had been identified, a decision logic was developed to dynamically select the most appropriate parameters based on the system’s condition. Indeed, the Supervisory Controller determined the appropriate parameter set by comparing the actual irradiance reduction (20%, 40%, 60%, 80%) or load change (10%, 30%) with the set of pre-optimized scenarios The scenario that showed the closest correspondence to the current operating condition was then selected. In this way, the controller ensured that the applied parameters were always consistent with the prevailing disturbance level while keeping the decision process computationally lightweight. For example, when the irradiance drop was measured around 55%, the parameter set optimized for the 60% scenario was adopted.

Dedicated tests were carried out to evaluate the Supervisory Controller’s dynamic parameter selection by analyzing the system’s frequency response—measured using the Integral of the Absolute Error (IAE)—under various sudden PV power reduction scenarios. Additionally, tests were conducted to compare the system’s frequency response with the Supervisory Control and with the classical VSG (with fixed parameters).

All tests were conducted using simulations in Simulink/Matlab. Simulations were performed on a PC equipped with an Intel Core i7-1355U processor, 32 GB of RAM, and running Windows 11 Pro. MATLAB R2024b and Simulink R2024b were used throughout the development and simulation process.

3.1. System Model

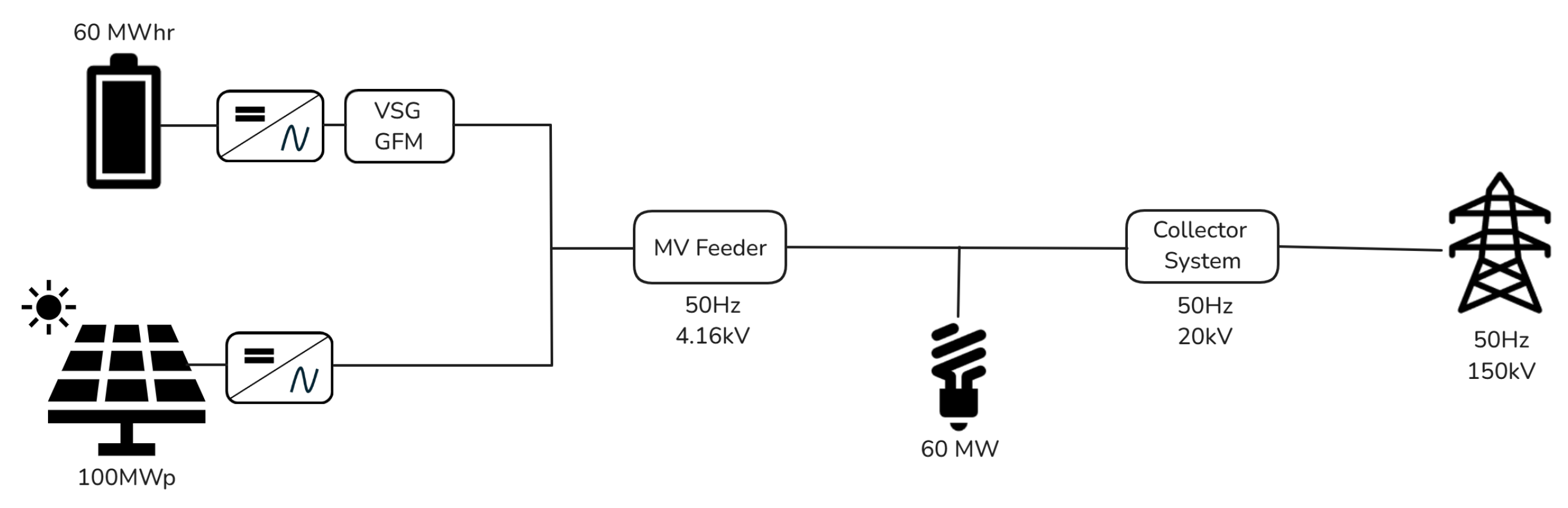
The considered power system (Figure 2) is characterized by high photovoltaic PV penetration and comprises several main components. These include a 100 MWp PV plant, and a BESS with a 60 MWhr capacity with a peak power of 35 MW integrated with a VSM operating in GFM. The system features a 50 Hz medium-voltage grid operating at 20 kV, a high-voltage grid running at 150 kV, and a 60 MW real power load. The PV plant features two three-phase central inverters, each capable of delivering a maximum power of 50 MW at 25 °C and 1000 W/m² solar insolation. These inverters operate at their maximum power point (MPP). A 4.16/20 kV distribution transformer connects the inverters to the medium-voltage power network. The 20 kV to 150 kV transformer links the medium-voltage network to high-voltage transmission lines, which connect to conventional generation units. The VSM is designed with a frequency droop of 0.02 per unit and a voltage droop of 1.6. The VSG-GFM controller employs virtual inertia, with a time constant of 0.25 s.

The power system was modeled in Simulink by adapting the framework presented in [31], with modifications to align its parameters with the characteristics of the Italian and European power grid. An overview of the modified parameters is given in

Table 2. Modified Simulink model parameters.

Parameter	Original Value	Adapted Value
Grid frequency	60 Hz	50 Hz
Grid high voltage	230 kV	150 kV
PV Transformer	24.9 kV	20 kV
Grid low transformer	24.9 kV	20 kV
Grid high transformer	230 kV	150 kV
Battery inverter frequency	60 Hz	50 Hz

PV: photovoltaic. The modifications refer to the model parameters defined in [31].

.

3.2. VSG

The basic equation that governs the VSG’s dynamics is given by:

$$J{\displaystyle \frac{d\omega }{dt}}=P_m-P_e-D(\omega -{\omega }_0)$$

(1)

where:

• J is the moment of inertia of the VSG;
• $\omega$ is the angular velocity of the rotor (related to the grid frequency);
• $P_m$ is the mechanical power reference input (the target power);
• $P_e$ is the electrical power required by the grid;
• D is the damping coefficient;
• ${\omega }_0$ is the nominal frequency (reference angular velocity).

This equation represents the power imbalance between $P_m$ and $P_e$, where the difference $P_m-P_e$ causes the system to either accelerate or decelerate the rotor, adjusting the frequency accordingly. If $P_m>P_e$, the system accelerates, and the grid frequency increases. Conversely, if $P_m<P_e$, the system decelerates, causing a reduction in grid frequency. These responses are divided into two distinct contributions: inertial response and damping response.

The inertial power response is modeled by the term:

$$P_i=J{\displaystyle \frac{d\omega }{dt}}$$

(2)

This term represents the rate of change of the rotor’s angular velocity, and it provides a short-term power response to the grid frequency deviation. The magnitude of the inertial power depends on the moment of inertia J and the rate of frequency change ${\displaystyle \frac{d\omega }{dt}}$.

J is often expressed in terms of H:

$$H={\displaystyle \frac{1}{2}}·{\displaystyle \frac{J{\omega }_0^2}{S_{\mathrm{base}}}}$$

(3)

where:

• $S_{\mathrm{base}}$ is the rated apparent power of the system.

The damping response is modeled by:

$$P_s=D(\omega -{\omega }_0)$$

(4)

The damping term acts as a negative feedback mechanism that opposes large fluctuations in frequency by adjusting the power output based on the deviation of the rotor’s angular velocity ($\omega$) from the nominal value (${\omega }_0$). A larger damping coefficient D leads to a faster response to frequency changes.

The mechanical power reference $P_m$ is controlled through a droop mechanism that dynamically adjusts the reference power in response to grid frequency deviations:

$$P_m=P_{\mathrm{ref}}+K_f(\omega -{\omega }_0)$$

(5)

where:

• $P_{\mathrm{ref}}$ is the nominal mechanical power reference;
• $K_f$ is the droop coefficient that determines how much $P_m$ changes in response to changes in frequency $\omega$.

The reactive power reference $Q_m$ is adjusted using a similar droop control:

$$Q_m=Q_{\mathrm{ref}}+K_v(V-V_0)+Q_{\mathrm{support}}$$

(6)

where:

• $Q_{\mathrm{ref}}$ is the nominal reactive power reference;
• $K_v$ is the droop coefficient for voltage control;
• V is the grid voltage;
• $V_0$ is the nominal voltage reference.

The term $Q_{\mathrm{support}}$ represents additional reactive power support that helps to stabilize voltage during rapid variations:

$$Q_{\mathrm{support}}=\mathrm{VoltageSupport}·(V_0-V)$$

(7)

The VSG employs a proportional–integral (PI) controller that adjusts the reactive current reference $I_q$:

$$I_{q_{\mathrm{ref}}}=K_{qp}{e}_V+K_{qi}\int e_{V}dt$$

(8)

where:

• $e_V=V_0-V$ is the voltage error;
• $K_{qp}$ and $K_{qi}$ are the proportional and integral gains, respectively.

Similarly, the active current reference $I_{\mathrm{ref}}$ is controlled through another PI controller to ensure that the active power is properly managed:

$$I_{\mathrm{ref}}=K_{p}e+K_i\int edt$$

(9)

where $e=P_m-P_e$ is the active power error, and $K_p$ and $K_i$ are the proportional and integral gains for active power control.

3.3. PSO Algorithm

In the PSO algorithm, each particle in the swarm represents a potential solution consisting of a set of control parameters. The particles explore a predefined search space, which specifies the admissible ranges for each parameter (

Table 3. Search space definition for PSO parameters.

Parameter	Lower Bound	Upper Bound
H	0.01 s	3 s
D	0.001	1
$K_p$	0	50
$K_f$	0.001	1
$K_i$	0	50

H: virtual inertia coefficient, D: damping coefficient, $K_p$: proportional gain, $K_f$: frequency droop gain, $K_i$: integral gain.

).

The particles adjust their velocities and positions based on both their personal best position and the best position in the neighborhood. In detail, the velocity is updated according to the following equation:

$$v_{k+1}=W·v_k+y_1·u_1·(p-x_k)+y_2·u_2·(g-x_k),$$

(10)

where:

• $v_{k+1}$ is the updated velocity vector;
• $v_k$ is the velocity vector at iteration k;
• W is the inertia weight that controls the influence of the previous velocity;
• $x_k$ is the current position of the particle at iteration k;
• $y_1$ and $y_2$ are acceleration coefficients that determine the relative influence of the personal best position p and the best position in the neighborhood g;
• $u_1$ and $u_2$ are random vectors uniformly distributed between 0 and 1;
• p is the personal best position of the particle;
• g is the best position in the neighborhood.

The position is then updated as:

$$x_{k+1}=x_k+v_{k+1}$$

(11)

At each iteration, the fitness of the candidate solutions is evaluated based on the system’s performance in Simulink, which reflects how the control parameters influence the system’s frequency response. Specifically, each simulation generates the system’s frequency trajectory in response to PV curtailment or load change. This trajectory is then used to calculate a performance index, based on the IAE, which serves as the fitness function to guide the PSO search process. The IAE is computed over the entire simulation time horizon of 3.5 s after the perturbation occurred with respect to the nominal frequency of 50 Hz. The algorithm iteratively updates the control parameters to minimize this error, with the fitness of each particle being evaluated at each iteration using the results from the Simulink simulations.

The main features of the PSO algorithm implemented in this work are reported in

Table 4. PSO’s key parameters’ values.

Parameter	Value
Swarm size	100
Inertia coefficient	0.5
Function tolerance	$\times {10}^{-6}$
Max iterations	80
Cognitive acceleration coefficient	1.49
Social acceleration coefficient	1.49

.

3.4. Tests

The disturbance in each test case was introduced as a step reduction in irradiance to emulate a sudden drop in PV power. Step variations in load demand were also applied to evaluate the system’s response to demand fluctuations. Dedicated tests were performed to assess the dynamic parameter selection mechanism of the Supervisory Controller in the context of various PV power abrupt reduction cases, specifically, 25%, 35%, 45%, 55%, 65%, and 75% with respect to the nominal irradiance. In addition, tests with load demand variations of 35% (with respect to a nominal load of 60 MW) were performed. The effect of the Supervisory Controller was analyzed by comparing the VSG performance with fixed parameters—set to the optimal values identified for a 40% irradiance drop (VSG without supervision)—to that with dynamic parameter adjustment enabled by the Supervisor (VSG with supervision) in response to various sudden irradiance reductions (25%, 55%, 65%, 75% of nominal irradiance) and load changes (35% nominal load). Each comparison was performed based on the IAE of the frequency response.

4. Results

4.1. Optimal VSG Parameters from PSO

The algorithm successfully converged to an optimal solution in all irradiance drop scenarios.

The Convergence Performance Metrics in

Table 5. Convergence Performance Metrics of the PSO optimization under different irradiance drop and load variation scenarios.

Scenario	Convergence Iterations	Final Variance	Final Stagnation
Irradiance Drop 20%	46	$2.3\times {10}^{-5}$	7
Irradiance Drop 40%	52	$3.1\times {10}^{-5}$	8
Irradiance Drop 60%	58	$4.8\times {10}^{-5}$	9
Irradiance Drop 80%	63	$6.2\times {10}^{-5}$	10
Load Increase 10%	39	$1.9\times {10}^{-5}$	6
Load Increase 30%	47	$2.7\times {10}^{-5}$	7

summarize the overall convergence behavior of the PSO optimization across all analyzed scenarios. In all tested scenarios, the PSO algorithm demonstrated high convergence stability, with the swarm cohesion ranging between 94.3% and 98.4%

The best parameter sets obtained for each scenario are summarized in

Table 6. Optimal VSG parameters and minimum IAE for different disturbance scenarios.

Scenario	Dist.	${\mathit{K}}_{\mathit{p}}$	${\mathit{K}}_{\mathit{i}}$	${\mathit{K}}_{\mathit{f}}$	H	D	Min IAE	c. IAE
Irradiance Drop	20%	0.1855	0.0100	0.0095	3.0000	0.9999	0.0626	0.0845
	40%	0.1837	0.0102	0.0017	2.6886	0.4581	0.0688	0.0688
	60%	0.0001	0.0283	0.0017	2.5346	0.0291	0.2565	0.8933
	80%	0.0000	0.0286	0.0008	1.7492	0.0001	0.3648	1.5434
Load Change	10%	0.0000	0.0000	0.0241	0.2503	0.0232	0.0496	0.7455
	30%	0.0000	0.0000	0.0200	0.2500	0.0200	0.1196	0.7589

D: damping coefficient, $K_p$: proportional gain, $K_f$: frequency droop gain, $K_i$: integral gain; IAE: Integral of Absolute Error; Dist.: disturbance level; c. IAE: IAE corresponding to classical VSG (using as fixed parameters the optimal ones for a 40% irradiance drop).

and the corresponding minimum IAE achieved.

For the PV irradiance drop scenarios, $K_p$ ranges from 0 to 0.1855, showing a decreasing trend as the irradiance drop increases. $K_i$ increases with higher irradiance drop levels, ranging from 0.0100 to 0.0286. $K_f$ varies within a narrow range between 0.0008 and 0.0095, with no clear trend in relation to irradiance drop. H ranges from 1.7492 to 3.0000 and shows a general decrease with increasing irradiance drop. D exhibits a sharp decline from 0.9999 to 0 as the irradiance drop increases. The minimum IAE values range from 0.0626 to 0.3648.

For the load change scenarios, $K_p$ and $K_i$ remain equal to zero, while $K_f$ assumes values between 0.0200 and 0.0241. The virtual inertia coefficient H takes a value of 0.2503 for a 10% load change and 0.2500 for a 30% load change, and D ranges from 0.0200 to 0.0232. The corresponding minimum IAE values range from 0.0496 to 0.1196.

Figure 3 illustrates the grid frequency response for each test case using the corresponding VSG optimal parameter set computed by the Supervisory Controller during the fist phase.

4.2. Supervisory Controller Simulation Test

Table 7. IAE for different test cases.

Test Case	IAE	IAE Classical VSG
Irradiance Drop 25%	0.0546	0.0791
Irradiance Drop 35%	0.0330	0.0330
Irradiance Drop 45%	0.1095	0.1095
Irradiance Drop 55%	0.2227	0.4605
Irradiance Drop 65%	0.2547	0.6407
Irradiance Drop 75%	1.1938	1.5957
Load Change 35%	0.1197	0.6672

IAE: Integral of Absolute Error; classical VSG: (using as fixed parameters the optimal ones for a 40% irradiance drop).

presents the IAE values obtained using the parameter settings determined by the Supervisory Controller for each disturbance scenario in the test. Between 25% and 45% irradiance drop, the IAE remains below 0.1. At 55%, the IAE rises to 0.2227, and then shows an increase, reaching 0.2547 at 65% and 1.1938 at 75%.

Figure 4 illustrates the grid frequency response for each test case using the corresponding VSG optimal parameter set computed by the Supervisory Controller.

Table 8. System frequency response under different conditions.

Scenario	Dist.	Overshoot (Hz)	Undershoot (Hz)	Settling t. (s)
Irradiance Drop	25%	50.20	49.15	0.3
	35%	50.15	49.35	0.3
	45%	50.45	48.60	0.4
	55%	50.34	46.30	0.5
	65%	50.66	45.58	0.3
	75%	51.24	44.40	0.5
Load Change	35%	50.28	49.17	0.4
Irradiance Drop clas. VSG	25%	50.32	49.41	0.3
	35%	50.15	49.35	0.3
	45%	50.45	48.60	0.4
	55%	50.57	47.73	0.9
	65%	50.66	46.97	0.9
	75%	50.64	46.32	1.0
Load Change clas. VSG	35%	50.44	49.66	>1.0

Dist.: Disturbance level; Settling t.: Settling time; clas. VSG: classical VSG (using as fixed parameters the optimal ones for a 40% irradiance drop).

reports the system frequency response for each test case using the corresponding VSG optimal parameter set computed by the Supervisory Controller.

4.3. Supervisory Controller Impact

Table 9. Impact of the Supervisory Controller.

	IAE with Supervised VSG	IAE with Classical VSG	Percentage Difference
PV Irradiance Drop
25%	0.0546	0.0791	44.87
55%	0.2227	0.4605	106.78
65%	0.2547	0.6407	151.55
75%	1.1938	1.5957	33.67
Load Change
35%	0.1197	0.6672	82.07

PV: photovoltaic, VSG: Virtual Synchronous Generator, IAE: Integral of Absolute Error.

presents a comparison of IAE values for scenarios with the Supervisory Controller and with the classical VSG (using as fixed parameters the optimal ones for a 40% irradiance drop), considering different irradiance drop conditions. The Supervised VSG results in a lower IAE. For moderate irradiance drops (25–55%), the percentage difference ranges from 44.87% to 106.78%. At higher drops, the reduction becomes more pronounced, reaching up to 151.55% at 65%. The lowest percentage difference is observed at 75% irradiance drop (33.67%), while the highest improvement is at 65%, where the IAE drops from 0.6407 to 0.2547. When considering a 35% load change, the Supervisory Controller reduces the IAE from 0.6672 (Classical VSG) to 0.1197, corresponding to an 82.07% reduction.

Figure 5 presents a comparison of the grid frequency response for cases with the Supervisory Controller and with the classical VSG (with fixed parameters) considering each irradiance drop scenario. With respect to the nominal reference of 50 Hz, the settling time of the proposed approach is shorter than that of the classical VSG. The difference in settling time between the two approaches is 0.2 s for a 25% irradiance drop, larger than 0.5 s for both the 55% and 65% drops, and exceeds 1.0 s for the 75% drop and for the 35% load change.

5. Discussion

This work proposes a PSO-based Supervisory Control strategy explicitly designed for GFM-VSG-BESS systems implemented in high-PV-penetration networks. PSO is used in a preprocessing phase to compute optimal parameter sets tailored to four representative irradiance drop scenarios. The use of PSO enables comprehensive exploration of the solution space, resulting in tuning not only virtual inertia and damping but also of additional frequency-related control gains. This broader parameter optimization represents an advancement over existing methods, which typically focus on inertia and damping alone.

The computational burden associated with PSO is addressed in a one-time preliminary phase, enabling the adaptive Supervisory Controller to operate with lightweight decision logic. Indeed, this approach eliminates the need to perform PSO optimization every time the system conditions change, thereby reducing computational demands. PSO was chosen for its simplicity, fast convergence, and effectiveness in nonlinear, multidimensional problems. Beyond its use in the VSG context [25,27], PSO has also been applied in power system control and dynamic performance scenarios, as shown in [32,33,34]. It is important to note that the novelty of this work does not lie in the optimization algorithm itself, which is used in its standard form, but in the development of the supervisory switching strategy. PSO was selected as a well-established and reliable method to obtain representative parameter sets. The optimization uses the IAE as the objective function as it captures both the magnitude and duration of frequency deviations [35].

The optimization focuses on parameters that significantly influence frequency response [14,20,36]. Since no standard values exist for these parameters, the bounds were defined based on literature guidelines to ensure a broad yet realistic search space [14,27,37].

The four irradiance drop levels and the two load variation levels were selected to represent a broad range of real-world PV curtailment and demand fluctuation scenarios.

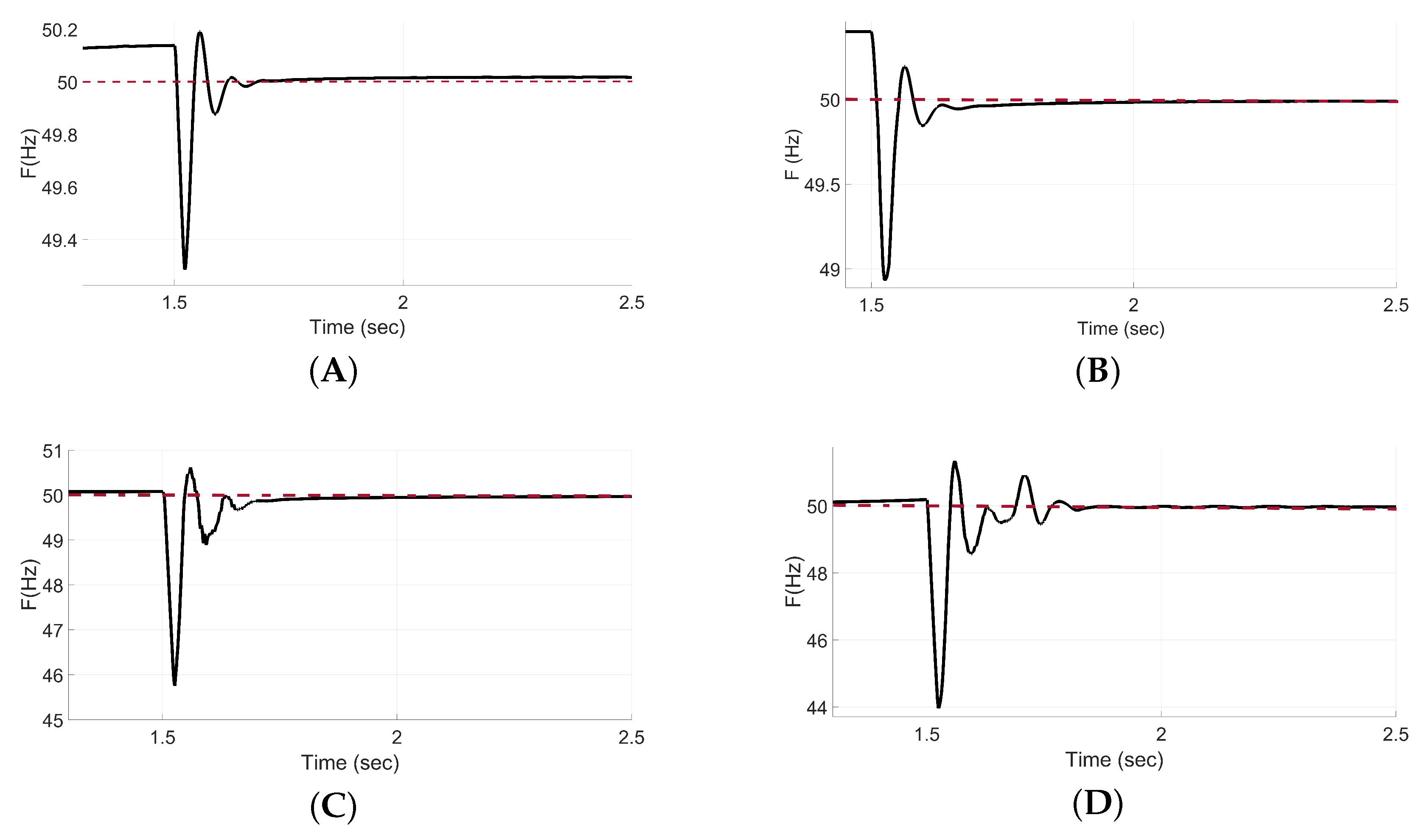
Results show that as the irradiance drop becomes more severe, the control parameters clearly adapt, as visible in Table 6. $K_p$ decreases, reaching zero at an 80% drop, indicating a reduced role of proportional control. Conversely, $K_i$ increases, signaling a shift toward integral-dominant control. This change highlights the system’s need to adjust its dynamic behavior depending on the extent of PV power reduction. D also decreases with larger disturbances, implying that less damping is preferred to maintain system flexibility and responsiveness under low-power conditions. Similarly, $K_f$ decreases, showing that the system relies less on passive frequency regulation as power availability drops. H is reduced as well, reflecting a move toward a more agile system design. In low-power conditions, maintaining high virtual inertia could hinder fast responses to disturbances, so reducing H enables quicker corrections. 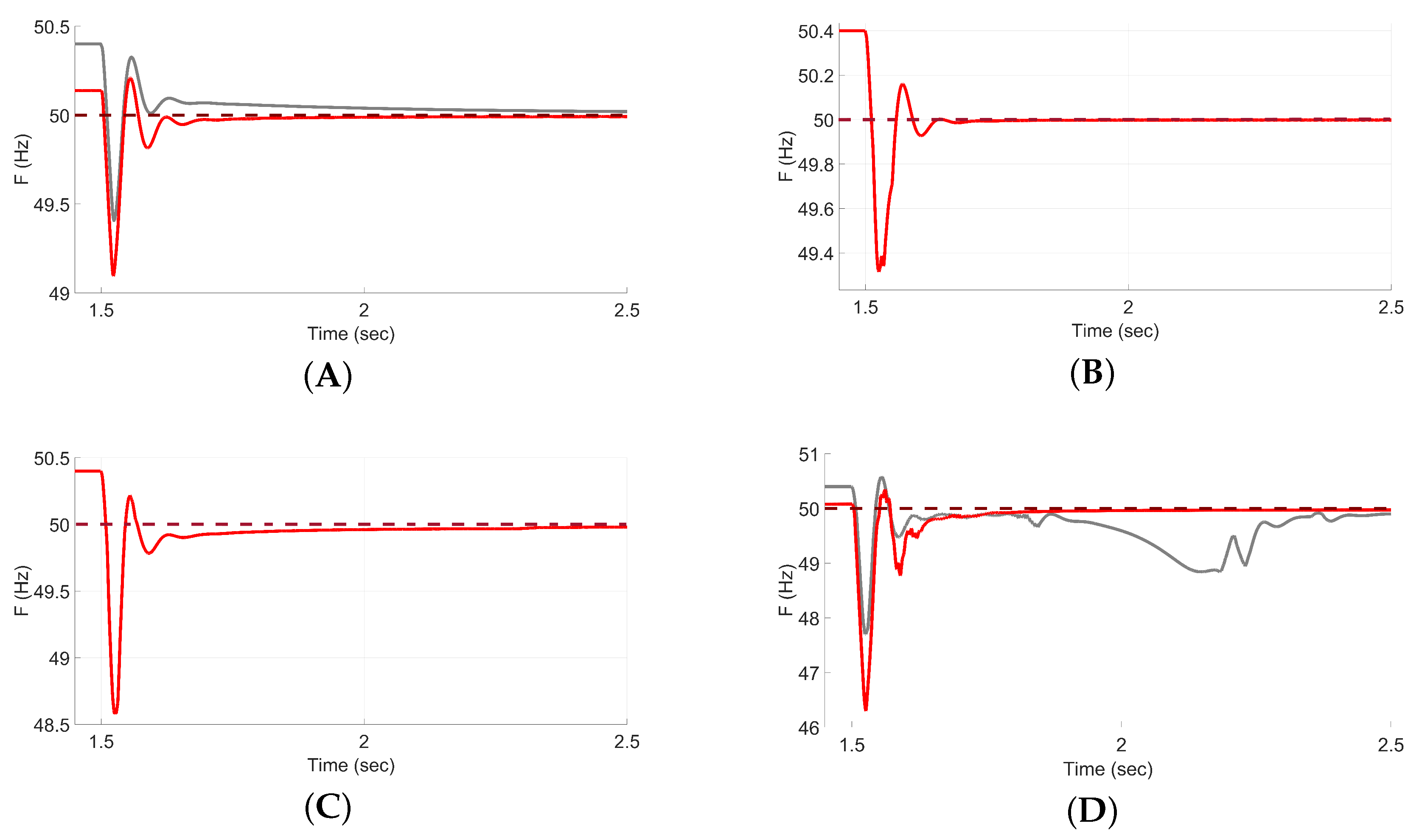As shown in Figure 3 and Table 6, increasing irradiance drops from 20% to 80% lead to larger initial deviations, more pronounced oscillations, and higher IAE values—particularly at 60% and 80%—underscoring the growing difficulty of maintaining frequency stability as PV power reductions become more severe. Despite these challenges, the parameter sets obtained through the PSO enable the system to eventually stabilize, with the frequency returning to its nominal value in all cases.

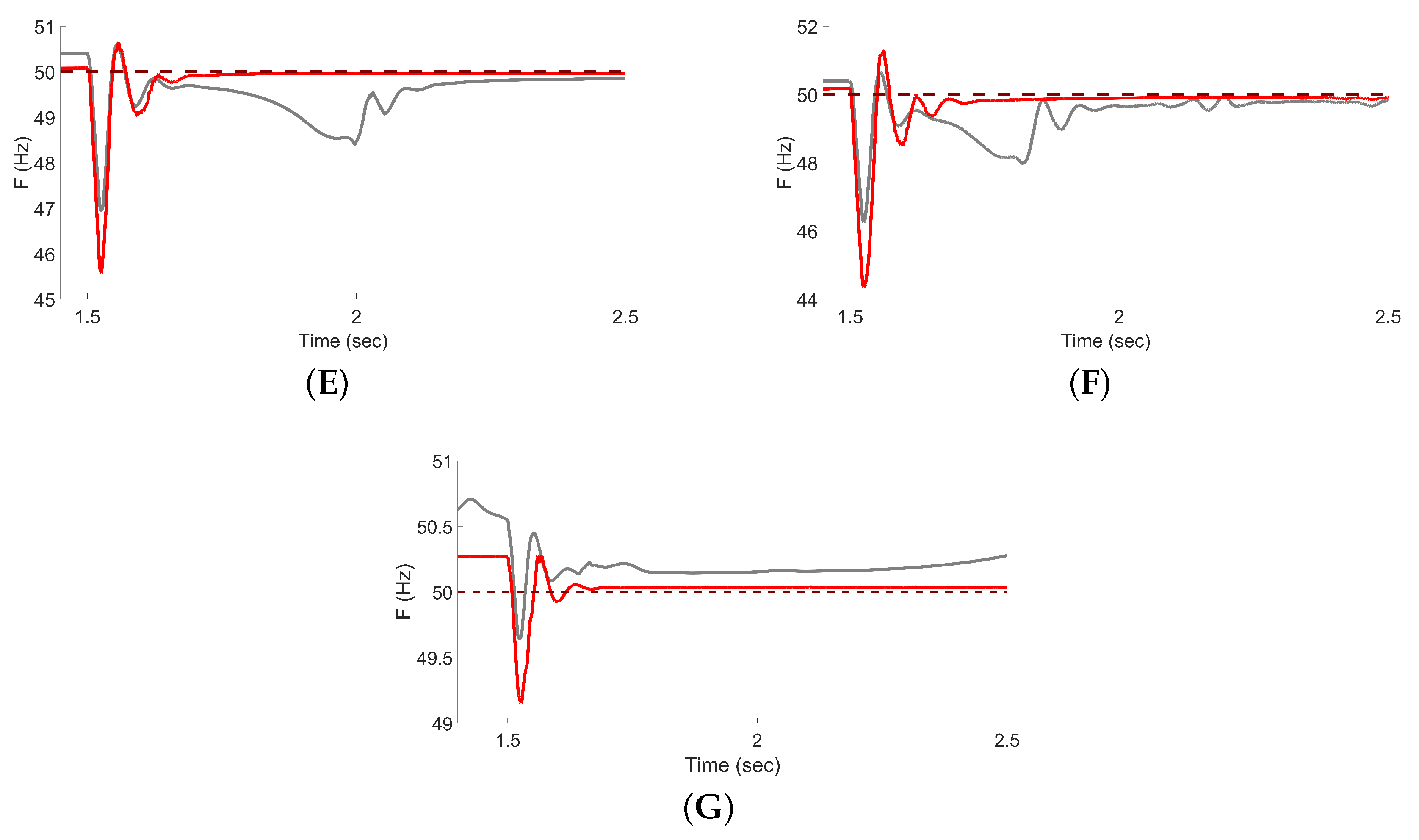
This trend is also evident in Table 7 and Figure 4. The parameter sets selected by the Supervisory Controller show that smaller irradiance drops result in lower IAE values and smoother frequency responses, while larger drops cause a higher IAE and more oscillations. Still, the frequency stabilizes in all cases despite the severity of the disturbances.

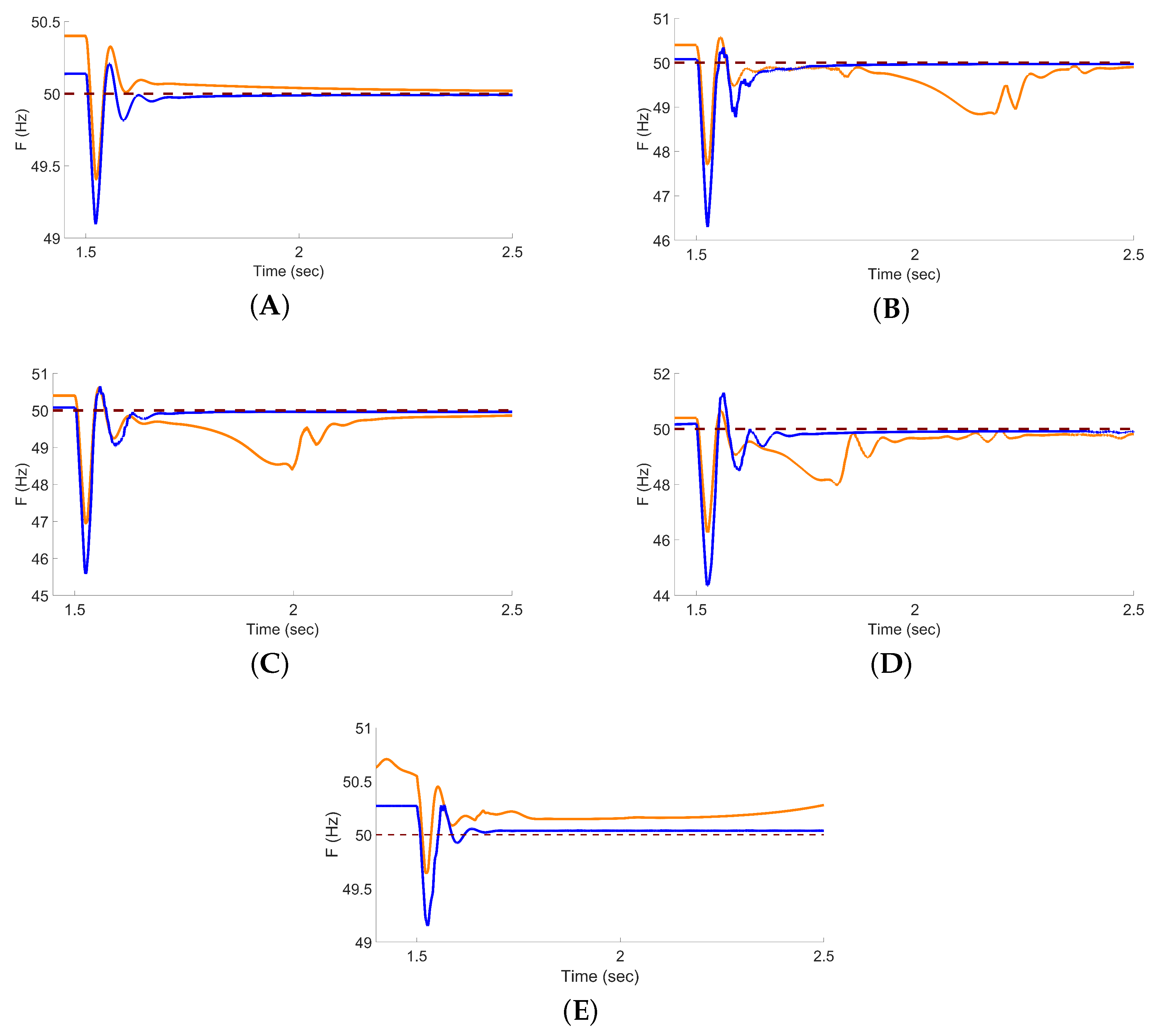
The benefits of the Supervisory Controller are clearly shown in Table 9 and Figure 5. Compared to the traditional VSG with fixed parameters, the supervised VSG improves performance, particularly under severe conditions. For example, at a 65% irradiance drop, the IAE is reduced by more than 150%, from 0.6407 to 0.2547. Frequency response plots confirm these improvements: supervised control results in reduced overshoot, faster settling, and smoother recovery. As irradiance drops become more severe, the differences grow more evident. In high-drop scenarios like 75%, the unsupervised system exhibits prolonged oscillations, whereas the supervised system achieves a quicker and more controlled response.

In addition to irradiance reduction scenarios, the proposed Supervisory Controller was also applied under load variation conditions. For a 10% and 30% increase in load, the PSO algorithm successfully identified optimal parameter sets, with IAE values of 0.0496 and 0.1196, respectively. The tuning trends observed under load variation followed a similar behavior to those seen in irradiance reduction cases, with a progressive decrease in proportional gain and damping, while the integral term and virtual inertia remained within narrow ranges as visible in Table 6. The corresponding frequency responses, illustrated in Figure 3, confirm that the optimized parameters enable fast recovery and limited overshoot even under increased load change. The Supervisor was then tested under a more severe 35% load variation. In this case the supervised VSG achieved an improvement compared to the classical configuration, reducing the IAE from 0.6672 to 0.1197 (an 82.07% reduction). As shown in Figure 5, the supervised system exhibits smoother and faster frequency stabilization. This demonstrates the adaptability of the proposed controller not only to generation-side disturbances but also to load-side variations.

6. Conclusions

This paper proposed a PSO-based Supervisory Control strategy for BESSs under GFM-VSG in high-PV-penetration grids. The approach enables the dynamic selection of well-tuned and comprehensive control parameter sets through a lightweight method.

The results demonstrated that the Supervisory Controller enhances frequency regulation performance compared to the classical VSG configuration. Specifically, it reduces IAE, mitigates oscillations, and shortens settling time, even under severe disturbances such as high irradiance drops or large load variations. However, the present work is limited to simulation-based validation, serving as a first step to demonstrate the feasibility of the proposed approach and to provide a foundation for real-world implementation. The effects of practical aspects have not yet been investigated. Future research will therefore focus on testing the proposed strategy in field applications to confirm its robustness under real operating conditions. In addition, further studies could explore scalability to larger networks and hybrid renewable configurations, as well as the integration of more detailed grid models to assess performance under real operating conditions.