A New Method for Calculating Dynamic Reserves of Fault-Controlled Condensate Gas Reservoir
Abstract
1. Introduction
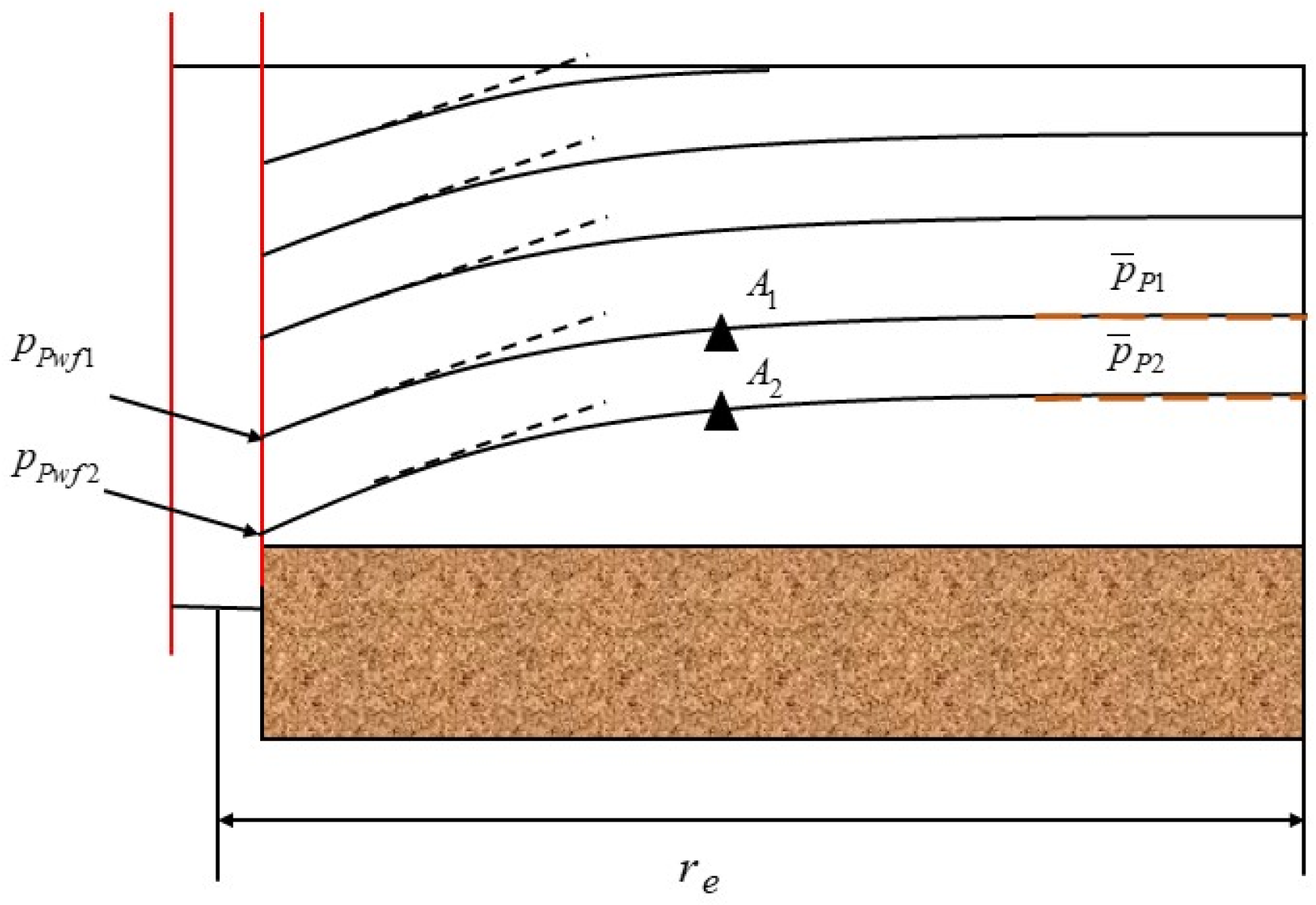
2. A New Method for Calculating the Dynamic Reserves of Single Wells in Fault-Controlled Gas Reservoirs
3. Actual Application Effects
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, X.Z.; Guo, Z.H.; Hu, Y.; Liu, X.; Wan, Y.; Luo, R.; Sun, Y.; Che, M. Challenges, countermeasures and suggestions for high-quality development of super-deep gas fields in China. Gas Ind. 2020, 40, 75–82. [Google Scholar]
- Mattar, L.; McNeil, R. The “flowing” gas material balance. J. Can. Pet. Technol. 1998, 37, 52–55. [Google Scholar] [CrossRef]
- Sun, H.; Cao, W.; Li, J.; Jia, W.; Li, Y.; Wu, Y.; Zhu, S.; Fu, X.; Yang, M.; Meng, G. A new method to improve the reliability of dynamic reserves evaluation of ultra-deep and ultra-high pressure gas reservoirs—Practical material balance analysis method. Gas Ind. 2020, 40, 49–56. [Google Scholar]
- Chen, Y.Q.; Shi, X.M. Derivation and application of new elastic two-phase method. Reserv. Eval. Dev. 2023, 13, 135–140. [Google Scholar] [CrossRef]
- Zhang, Y.Z. Production Decline Analysis Method and Application of Gas Well in Tight Gas Reservoir. Master’s Thesis, China University of Petroleum (Beijing), Beijing, China, 2019. [Google Scholar] [CrossRef]
- Feng, D.; Tang, Y.H.; Li, Y.; Li, X.; Li, D.; Jia, H. Study on calculation method of dynamic reserves of continental shale gas in Yan’an area. Unconv. Oil Gas 2023, 10, 27–31+43. [Google Scholar] [CrossRef]
- Li, Q.; Guo, P.; Huang, Q.H. Study on dynamic reserves method of gas well. J. Chongqing Univ. Sci. Technol. (Nat. Sci. Ed.) 2008, 34–36. [Google Scholar] [CrossRef]
- Mattar, L.; Anderson, D.; Stotts, G. Dynamic material balance: Oil-or gas-in-place without shut-ins. J. Can. Pet. Technol. 2006, 45, 7–10. [Google Scholar] [CrossRef]
- You, X.T.; Jia, C.S.; Liu, J.Y.; Liao, X.; Zheng, A.; Li, J. A new production data analysis method of shale gas: Based on flowing material balance theory and considering the complex flow mechanisms of multiple pressure systems. Energy Procedia 2019, 158, 3626–3632. [Google Scholar] [CrossRef]
- Han, G.F.; Liu, M.; Li, Q. Flowing material balance method with adsorbed phase volumes for unconventional gas reservoirs. Energy Explor. Exploit. 2019, 38, 519–532. [Google Scholar] [CrossRef]
- Xu, Y.M.; Oluwatobi, A.; Hassan, D. A flowing material balance equation for two-phase flowback analysis. J. Pet. Sci. Eng. 2016, 142, 170–185. [Google Scholar] [CrossRef]
- He, L.; Mei, H.Y.; Hu, X.R.; Dejam, M.; Kou, Z.; Zhang, M. Advanced flowing material balance to determine original gas in place of shale gas considering adsorption hysteresis. SPE Reserv. Eval. Eng. 2019, 22, 1282–1292. [Google Scholar] [CrossRef]
- Sun, Z.; Shi, J.T.; Zhang, T.; Wu, K.; Miao, Y.; Feng, D.; Sun, F.; Han, S.; Wang, S.; Hou, C.; et al. The modified gas-water two phase version flowing material balance equation for low permeability CBM reservoirs. J. Pet. Sci. Eng. 2018, 165, 726–735. [Google Scholar] [CrossRef]
- Zhang, C.S.; Han, Z.; Feng, Z.G.; Fan, Z.F.; Xu, A.Z.; He, C.G.; Zhang, D.Y.; Li, J.G.; Wang, F.R.; Ren, J.H.; et al. Calculation method of dissolved gas reinjection reservoir mass balance based on equation of state. Sci. Technol. Eng. 2020, 20, 9851–9855. [Google Scholar]
- Huang, Q.H.; Chen, C.; Pi, J.; Wang, F.; Yang, R.; Wu, J. Research on theoretical basis of “flowing” material balance method. Reserv. Eval. Dev. 2015, 5, 30–33+49. [Google Scholar] [CrossRef]
- Li, D.M.; Li, H.H.; Zhu, S.Y.; Li, T. Flow material balance method of fault solution reservoir. Lithol. Reserv. 2022, 34, 154–162. [Google Scholar]
- Teng, J.W.; Si, X.; Wang, Y.C.H. Exploration, development potential and future of fossil energy in China. Pet. Geophys. Explor. 2021, 60, 1–12. [Google Scholar]
- Sun, H.D.; Cao, W.; Zhu, S.B.; Tang, Y.L.; Wu, Y. Challenges, analysis methods and suggestions for dynamic reserves evaluation of ultra-high pressure gas reservoirs. In Proceedings of the the 32nd National Natural Gas Academic Conference (2020), Chongqing, China, 13–14 November 2020; pp. 603–612. [Google Scholar] [CrossRef]
- Hu, W.G. Development technology and research direction of fracture-vuggy carbonate reservoir in Tahe Basin. Reserv. Eval. Dev. 2020, 10, 1–10. [Google Scholar] [CrossRef]
- Wang, F.P.; Huang, Q.H.; Yang, H.B.; Zhao, C.Z.; Chen, L. Optimization of formation pressure calculation method based on production data. Fault-Block Oil Field 2009, 16, 66–68. [Google Scholar]
- Zhang, Y.; Mao, Q.Y.; Li, H.Y.; Li, Z.; Han, J.; Lin, B. Characteristics and practical application of ultra deep fault controlled fracture cave type oil and gas reservoirs in the central part of Shunbei. China Pet. Explor. 2023, 28, 1–13. [Google Scholar]
- Deng, H.; Feng, X.; Wang, H.; Hu, S.Q.; He, Y.B. A method for calculating dynamic reserves in the early stage of complex gas reservoir development and its applicability analysis. Gas Ind. 2012, 32, 61–63+123. [Google Scholar]
- Liu, R.H. Discussion on calculation method of dynamic reserves in early stage of gas reservoir development. Spec. Oil Gas Reserv. 2012, 19, 69–72+154. [Google Scholar]
- Huang, Q.H.; Li, S.L.; Cao, W.J.; Xu, S. Application of reservoir influence function in gas reservoir. Gas Ind. 2003, 106–109+184. [Google Scholar]

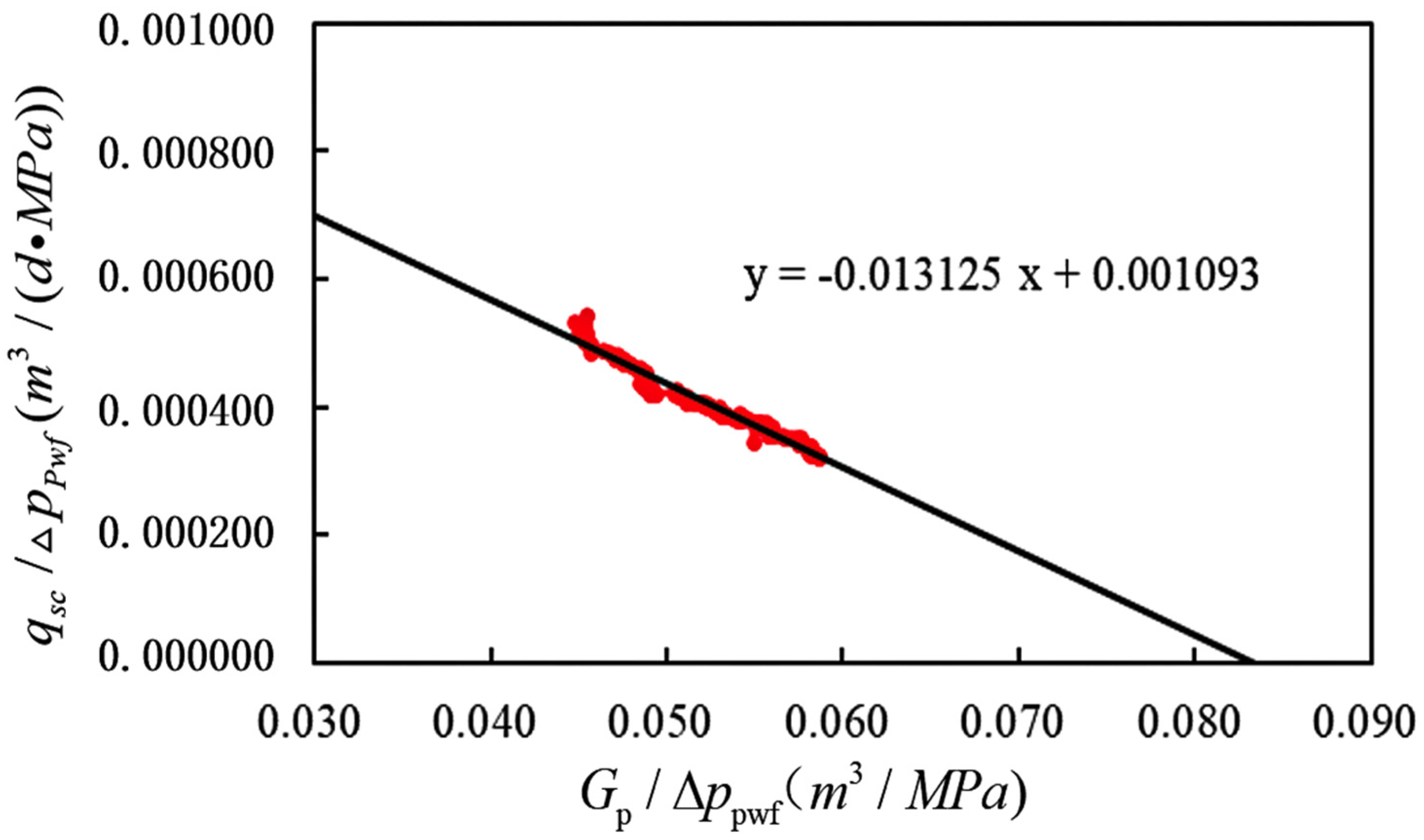
| Well Number | Slope m | Intercept b | Flow Resistance Coefficient | Apparent Original Formation Pressure pi/Zi | Dynamic Reserve G |
|---|---|---|---|---|---|
| SHB4-5H | −0.013125 | 0.001093 | 915 | 47.6 | 4.0 |
| Well Number | Two-Stage Material Balance Method (100 Million Cubic Meters) | Reservoir Influence Function Method (100 Million Cubic Meters) | Gas Production Curve Method (100 Million Cubic Meters) | Sun Hedong’s Empirical Formula (100 Million Cubic Meters) | New Method (100 Million Cubic Meters) |
|---|---|---|---|---|---|
| SHB4-5H | 4.32 | 3.81 | 4.19 | 3.98 | 4.00 |
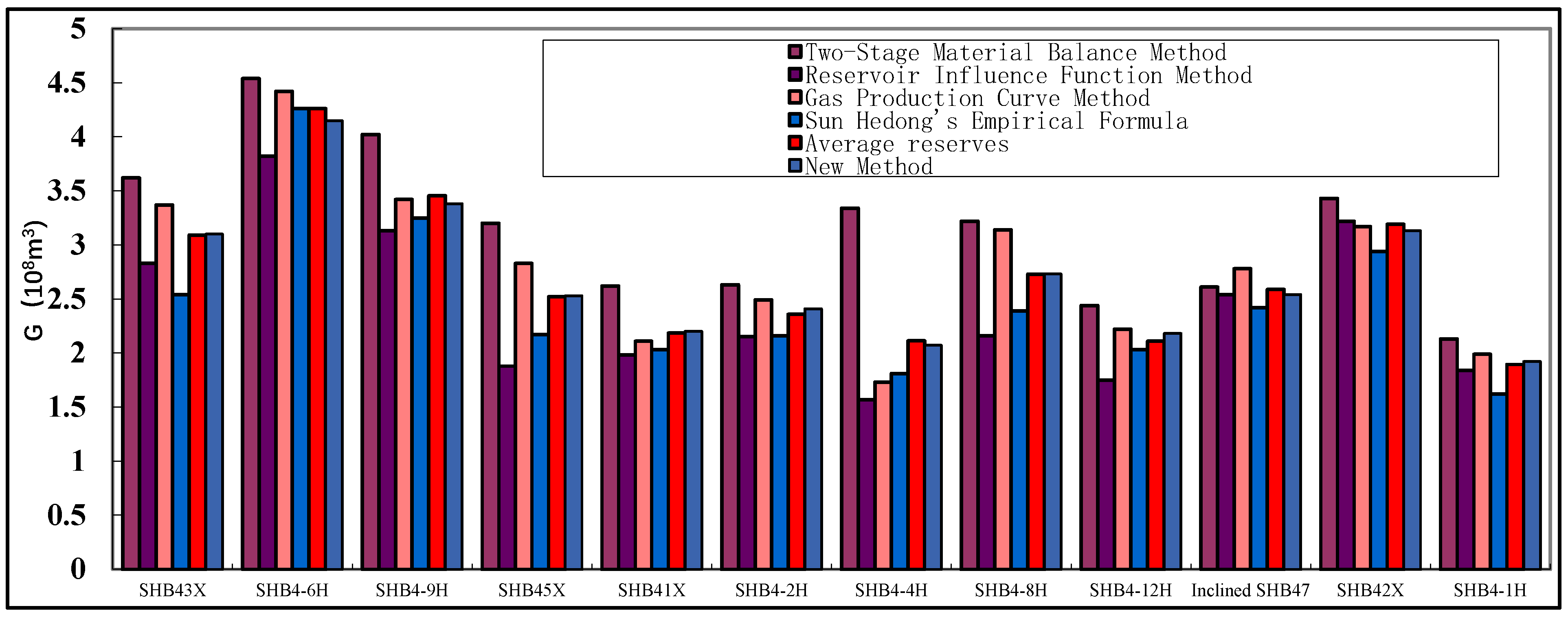
| Well Number | Two-Stage Material Balance Method | Reservoir Influence Function Method | Gas Production Curve Method | Sun Hedong’s Empirical Formula | Average Reserves | New Method |
|---|---|---|---|---|---|---|
| SHB43X | 3.62 | 2.83 | 3.37 | 2.54 | 3.09 | 3.10 |
| SHB4-6H | 4.54 | 3.82 | 4.42 | 4.26 | 4.26 | 4.15 |
| SHB4-9H | 4.02 | 3.13 | 3.42 | 3.25 | 3.46 | 3.38 |
| SHB45X | 3.20 | 1.88 | 2.83 | 2.17 | 2.52 | 2.53 |
| SHB41X | 2.62 | 1.98 | 2.11 | 2.03 | 2.19 | 2.20 |
| SHB4-2H | 2.63 | 2.15 | 2.49 | 2.16 | 2.36 | 2.41 |
| SHB4-4H | 3.34 | 1.57 | 1.73 | 1.81 | 2.11 | 2.07 |
| SHB4-8H | 3.22 | 2.16 | 3.14 | 2.39 | 2.73 | 2.73 |
| SHB4-12H | 2.44 | 1.75 | 2.22 | 2.03 | 2.11 | 2.18 |
| Inclined SHB47 | 2.61 | 2.54 | 2.78 | 2.42 | 2.59 | 2.54 |
| SHB42X | 3.43 | 3.22 | 3.17 | 2.94 | 3.19 | 3.13 |
| SHB4-1H | 2.13 | 1.84 | 1.99 | 1.62 | 1.90 | 1.92 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Q.; Wang, F.; Xiao, H.; Zhang, W.; Liu, J.; Li, W.; Yang, C. A New Method for Calculating Dynamic Reserves of Fault-Controlled Condensate Gas Reservoir. Energies 2025, 18, 5402. https://doi.org/10.3390/en18205402
Huang Q, Wang F, Xiao H, Zhang W, Liu J, Li W, Yang C. A New Method for Calculating Dynamic Reserves of Fault-Controlled Condensate Gas Reservoir. Energies. 2025; 18(20):5402. https://doi.org/10.3390/en18205402
Chicago/Turabian StyleHuang, Quanhua, Fengyuan Wang, Hong Xiao, Wenxue Zhang, Jie Liu, Wenliang Li, and Cong Yang. 2025. "A New Method for Calculating Dynamic Reserves of Fault-Controlled Condensate Gas Reservoir" Energies 18, no. 20: 5402. https://doi.org/10.3390/en18205402
APA StyleHuang, Q., Wang, F., Xiao, H., Zhang, W., Liu, J., Li, W., & Yang, C. (2025). A New Method for Calculating Dynamic Reserves of Fault-Controlled Condensate Gas Reservoir. Energies, 18(20), 5402. https://doi.org/10.3390/en18205402





