Optimization of an Off-Grid PV System with Respect to the Loss of Load Probability Value

Abstract

In this paper, a method for finding the optimal size of an off-grid photovoltaic (PV) system regarding the Loss of Load Probability (LOLP) value is proposed. The proposed method is applied to an off-grid PV system in a scenario where an electricity supply needs to be provided during three summer months. According to the simulation results, 11 PV modules and 11 batteries are required with 0% LOLP. An increase in LOLP to 1% results in 10 PV modules and 7 batteries, and a 24.9% cost reduction. With 5% LOLP, the cost reduction is 39.3%, and with 10% LOLP, it is 49.5%. The use of less expensive batteries also contributes to cost reduction. With the modification of electricity consumption, one combination can be suitable for 4% lower LOLP, and the cost can be reduced to up to 7%. It can be concluded that the required increase in LOLP value leads to a decrease in the number of required PV modules and batteries and to the use of less expensive battery technologies, which then leads to cost reduction. Additionally, with the modification of electricity consumption, the amount of power deficit can be reduced, which makes one combination suitable for lower LOLP and also leads to a further system cost decrease. Lower system costs can encourage more people to invest in an off-grid PV system in locations with occasional consumption or consumption over only a few months. The cost reduction strongly depends on how willing users are to not have all their electricity demands met.

1. Introduction

In a modern world with smart grids, smart appliances, smartphones, and smart TVs, there are still parts of the world without access to electricity. According to the International Energy Agency (IEA), in 2023, there were 745 million people, representing more than 9% of the world’s population, without access to electricity [1]. Of these 745 million people, 706 million, or over 94%, were in countries in sub-Saharan Africa and developing Asia [2]. However, this represents an improvement compared to 2022, when the number of people without access to electricity stood at 760 million. In sub-Saharan Africa, solar home systems contributed to an increase in the number of people with access to electricity from 25 million in 2019 to 45 million in 2022. In sub-Saharan Africa, solar home systems provide access to electricity for 4% of households, and power grids, including microgrids and the utility grid, provide access to electricity for 44% of households, while 52% of households still do not have access to electricity [3].

In order to increase access to electricity, many initiatives and projects have been launched. For example, the World Bank is running a project entitled the “Regional off-grid electrification project” with the objective of increasing electricity access for households and businesses in West Africa using off-grid solar systems [4]. IEEE established the project “IEEE Smart Village”, which takes a unique approach to supporting the world’s energy-impoverished communities by providing a comprehensive solution combining renewable energy, community-based education, and entrepreneurial opportunities [5]. Nationally Appropriate Mitigation Actions (NAMA) established the project “Off-grid rural electrification in Ethiopia” to achieve low-carbon development and reduce poverty [6]. The authors of [7] present a detailed design, analysis, and implementation of off-grid PV microgrid architecture for the electrification of rural parts of developing countries.

According to the previously mentioned projects aimed at increasing access to electricity for people in underdeveloped countries, off-grid PV systems could be a solution. When discussing off-grid PV systems, the main task is to find the optimal configuration of the system. Khatib et al., in [8], provide an overview of methodologies for sizing a PV array and batteries in off-grid PV systems, and they show that there are three main methods for system sizing: 1. intuitive sizing methods, 2. energy planning methods, and 3. real-time power methods. In this paper, the focus will be on energy planning methods. According to [9], energy planning methods are based on steady-state simulations with a typical hourly time step, and objective functions are mostly based on the loss of load probability (LOLP). Khatib et al., in [10], present an iterative method for finding the optimal size of an off-grid PV system regarding the LOLP value. They used simple modeling for optimization, based on three parameters: the battery capacity under a specific load, the PV array capacity under a specific load, and the load. The authors of [11] propose a model for sizing a PV array for off-grid PV systems with a parallel redundant power source for a desired LOLP. This model uses an analytic method with a set of PV/inverter sizing ratios in the iterative loop to find the optimal size of the PV array, taking into consideration the effect of the starting current. The authors of [12] investigated the effect of load profile uncertainty on the optimal size of an off-grid PV system. They propose a novel numerical simulation model that yields an optimal design of the off-grid PV system for achieving the minimum net present cost (NPC) and the maximum value of LOLP set by the designer of the system. The model described in [12] offers a method for formulating different possible daily load profiles for un-electrified rural areas, as well as steady-state simulation for PV/battery techno-economic analysis. Another paper that deals with LOLP analysis for the optimization of off-grid PV systems is presented in [13]. The method proposed in [13] consists of load profile modeling, climate data, and solar module simulation and calculation of the state of charge (SOC) of batteries. The method is applied to three different situations: a household, a school, and a health center. A simplified analytic model for optimal sizing of off-grid PV systems for different values of LOLP set by the designer is presented in [14]. The proposed simplified model gives the optimal size and cost of the off-grid PV system (number of PV modules and batteries) for a defined load curve and different values of LOLP. The results in the [14] show that the cost of the system is 34% lower when LOLP = 3% in comparison to when LOLP = 0%. Golub et al., in [15], used HOMER software to find the optimal configuration of an off-grid PV system with minimum NPC for different values of capacity shortage ranging from 0% to 10%. In [15], the influence of operation and maintenance (O&M) costs is taken into consideration. Another possible application of off-grid PV systems is in enabling residential households to shift from grid-connected to off-grid supply. Goldsworthy and Sethuvenkatraman, in [16], analyzed electricity consumption data for 28 households during 2 years, and based on those data, they performed off-grid PV system sizing and economic assessment using current cost data.

The authors of [17] used elephant herd optimization to minimize LOLP in an off-grid PV system. In the first part of the algorithm, sizing of the PV array, battery bank, charge controller, and inverter is performed. In the second part, the PV system is tested with real solar irradiation to determine the LOLP. Raff et al., in [18], present a model for sizing a hybrid off-grid PV–wind–battery system, considering LOLP, using MATLAB software. LOLPs from 0 to 10% were considered, and based on the results, the system proved to be most profitable with 3% LOLP. In [19], LOLP is calculated according to the reliability of the PV system considering equipment failure and the availability of solar irradiation. With 20 kW of PV, the LOLP is 28%, and with an additional 20 kW of PV, the LOLP is reduced to 26%. With an additional 20 kW of generation from biomass, instead of PV, the LOLP can be reduced to 19%. The authors of [20] investigated the influence of solar irradiation and the operating factor of the PV on LOLP, and determined the optimal size of the PV array for an agricultural load. In the analysis, four different average daily solar radiations and three different PV operating factors were considered.

The different approaches for sizing an off-grid PV system mostly use solar irradiation data with an hourly resolution, or even average daily or monthly solar irradiation data. Such approaches are suitable for estimating the electricity generation of grid-tied PV systems, since exchange of electricity with the main grid is possible with a grid-tied PV system. The use of solar irradiation with a lower resolution provides more insight into solar irradiation variability, because cloud cover is constantly changing. Solar irradiation data with 1 min resolution provide great insight into solar variability when clouds pass. This is important in the case of an off-grid PV system, as there is no possibility of electricity exchange with the main grid. The power difference between the PV output and electricity demand in one minute can be much higher than the hourly average, which makes this approach suitable for the estimation of power deficits and LOLP. It is also suitable for determining the optimal size of an off-grid PV system.

In this paper, a method for sizing an off-grid PV system with respect to the LOLP value using a differential evolution algorithm is presented, which can be classified as an energy planning method. The main contributions of this paper are summarized as follows:

• The proposed method is applied to the scenario of an off-grid PV system with solar irradiation and electricity consumption data at a one-minute resolution.
• In addition to the optimal number of batteries, the algorithm can decide which of two available battery technologies is the most suitable.
• The impact of the initial LOLP value on the use of the installed battery capacity during the simulation period is presented for two different LOLP values.
• The influence of modifications in electricity consumption on the optimal size of an off-grid PV system and the total cost of the system is investigated.

The rest of the paper is organized into four sections. In Section 2, the input data and parameters required for the optimal sizing of the off-grid PV system are presented and explained. The sizing procedure is explained in detail in Section 3. The results are presented and discussed in Section 4 through three subsections. Finally, Section 5 provides the conclusion.

2. Description of Input Data

In this section, the input data required for the off-grid PV battery sizing procedure are described. The proposed input data are as follows:

• The load profile curve;
• Solar irradiation data;
• Component costs;
• The technical specifications of the used components;
• The LOLP value;
• The time period used in the optimization procedure.

The modeling of each input data listed above will be elaborated on in detail in the continuation of this section.

2.1. Load Profile Curve

The determination of the load profile curve is the first step in finding the optimal size of the system. For off-grid PV systems, the load profile can be estimated or measured. The load profile is created based on the measurements stated in [7,14]. The load profile in off-grid PV systems is often determined by the enumeration of the nominal power of the appliances and their estimated working hours. This approach is used in [13,21,22]. In [9], a procedure is developed to formulate daily load profiles based on field research about demand behavior, while in [22], controllable and uncontrollable loads are distinguished.

In this work, the load profile is estimated according to the measured electricity consumption data for one week. The assumption is that the load profile is the same for each week during the simulation period. The load profile for the entire simulation period is presented in Figure 1. Due to the unavailability of 1 min electricity consumption data, the load profile was generated from measured 10 min data using a uniform distribution. The mean value is equal to the measured average 10 min value, and the uniform distribution range is ±100% of the average 10 min value.

2.2. Solar Irradiation Data

For the estimation of electricity generation from grid-connected and off-grid PV systems, solar irradiation data are required. Solar irradiation data can be obtained from on-site measurements or the nearest meteorological station, but in most cases, data are downloaded from online databases. Online databases provide solar irradiation data for any location in the world. Data are derived from satellite measurements, as well as from ground meteorological stations. Online databases usually provide irradiation data with a time interval of 1 h. In this work, solar irradiation data with a time interval of 1 min were obtained from the Meteonorm database [23]. The irradiation data for the location of Osijek, Croatia (45°33′25′′ N, 18°41′44′′ E), are presented in Figure 2 for the entire simulation period.

2.3. Technical Specifications of the Used Components

The off-grid PV system consists of PV modules and batteries with the technical specifications presented in

Table 1. Technical specifications of the used components.

PV Module		Battery
Technology	mono-Si	Technology	LiFePO4	GEL
Rated power	250 W	Rated capacity	50 Ah	50 Ah
Efficiency	15.3%	Rated voltage	12.8 V	12 V
Length	1.649 m	Rated energy	640 Wh	600 Wh
Width	0.991 m	Max. DoD	90%	50%
Area	1.63 m2	Efficiency	92%	80%
		C-rate	1.0C	0.2C

[24,25,26]. Although PV modules with a lower power rating are used due to smaller steps in the sizing procedure, PV modules with a higher rated power can also be used in the proposed model. Two different battery technologies with the technical specifications presented in Table 1 are used, namely lithium iron phosphate (LiFePO₄) and lead acid gel batteries. The rated capacity of the batteries is 50 Ah, and due to their different rated voltages, the amounts of rated energy are different. The maximum battery depth of discharge (DoD) is 90% in the case of the LiFePO₄ battery and 50% in the case of the gel battery. This leads to more available energy for discharging in the LiFePO₄ battery: 576 Wh, compared to 300 Wh in the gel battery. LiFePO₄ is also superior in cycle efficiency, which is 92% in the case of the LiFePO₄ battery compared to 80% in the case of the gel battery.

Technical specifications are required to establish battery limitations. The maximum battery capacity is equal to a fully charged battery, while the minimum capacity depends on the maximum DoD. The maximum battery charging and discharging power is proportional to the maximum battery current, with the assumption of constant voltage. The maximum battery current is defined by the C-rate, which indicates how fast the battery is charged or discharged relative to the maximum battery capacity. In the case of LiFePO₄, the C-rate is 5 times higher than in the case of the gel battery. Although LiFePO₄ is superior in terms of technical parameters, the gel battery has a lower price.

2.4. Component Cost

The input cost data for the proposed algorithm are the cost of the PV modules and the cost of the battery system. The cost of the PV system expressed in EUR/kW is multiplied by the rated power to obtain the cost expressed in EUR/module. To obtain the cost of the battery system expressed in EUR/battery, the cost of the battery system expressed in EUR/kWh is multiplied by the rated energy. The cost of the PV system considered in this work is 1000 EUR/kW [27] and the rated PV module power is 250 W, which leads to the cost of the PV system amounting to 250 EUR/module. The cost of the battery system depends on the battery technology used. The cost of the LiFePO₄ battery considered in this work is 540 EUR/kWh [28], while the cost of the gel battery is 200 EUR/kWh [29]. The cost of a battery with a rated capacity equal to 50 Ah is 345.60 EUR/battery in the case of a LiFePO₄ battery and 120 EUR/battery in the case of a gel battery.

The cost of PV modules and batteries varies depending on the availability of products from different manufacturers on the local market. It should also be noted that component costs change over time, and there is an expected decrease in the future. However, since this work investigates the impact of the LOLP value on the number of components and the system cost, a trend of decreasing system cost with increasing LOLP is expected, regardless of the initial component cost.

2.5. LOLP Value

Grid-connected PV systems, without or with a battery, can cover a power deficit with electricity from the main grid to ensure that a sufficient power supply is available at all times. Off-grid PV systems require a battery to store excess PV generation and ensure power supply when PV generation is not available. Installing enough PV power and battery capacity to meet the electricity consumption of all electrical devices at all times leads to high investment costs, which can be reduced if part of the consumption is not covered. Users can decide what percentage of load demand can be lost without a loss of comfort. LOLP, in this work, is defined as the relationship between the total power deficit and the total load demand during the observed period. In this paper, the maximum LOLP is 20%, and optimization is performed for LOLP values in the range of 0 to 20%, with 1% steps.

2.6. Time Period

The proposed algorithm can be applied to different optimization periods. Optimization can be performed throughout the year, but it is less likely to use the off-grid PV system to meet electricity consumption in properties used for the entire year, due to the high installed PV power and BS capacity required to provide enough electricity in winter months if the electricity grid is available. Off-grid PV systems are more likely to be used for properties used for several months during a year, usually during the summer months, when the lower installed PV power and BS capacity are enough to cover the electricity consumption. In this paper, an algorithm is applied to an off-grid PV system used to cover load demand in cottages used during the three summer months, from 1 June to 31 August, respectively. The period for which the simulation is performed is 92 days.

3. Model Used in Research

A schematic diagram of the off-grid PV system is presented in Figure 3. To find the optimal number of PV modules and batteries, as well as the optimal battery type for the initial LOLP value, the algorithm presented in Figure 4 is used.

The input data required, electricity consumption, and solar irradiation are explained in the previous section. The results of the sizing procedure are the number of PV modules, the number of batteries, the battery technology, and the final LOLP value obtained with the optimal configuration of PV modules and batteries. The size of power converters is not investigated in this work, but DC-DC converters are required to connect the PV array and battery storage (BS) to the same DC bus, and a DC-AC converter is required to connect the PV array and BS with the electricity consumer.

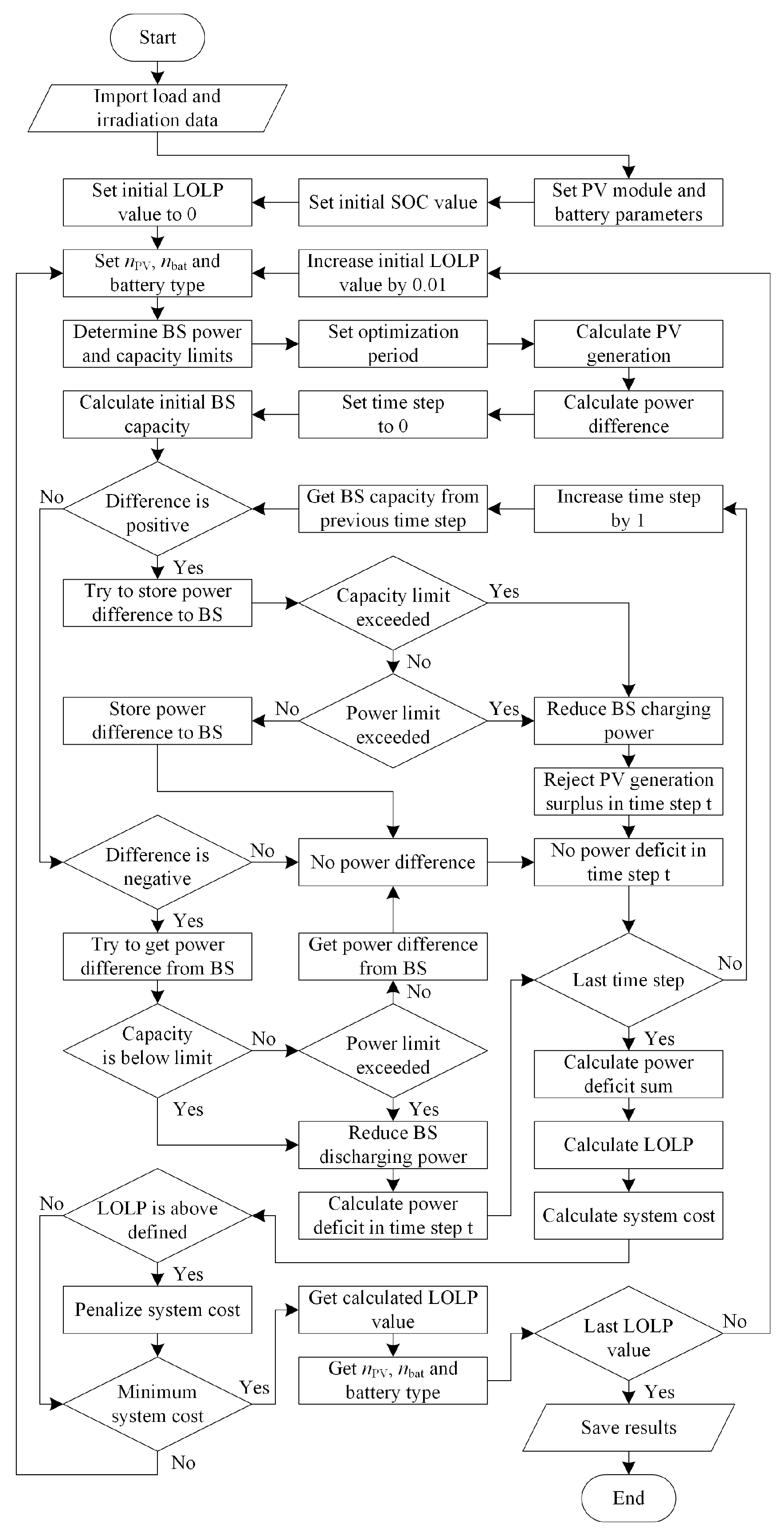
3.1. Description of the Off-Grid PV System Sizing Algorithm

The first step is to define the PV module and battery parameters and the initial state of charge (SoC). Usually, the initial SoC is unknown, with the assumption of a fully charged or discharged battery. In this work, the simulation is performed with the assumption of a fully charged battery, because the maximum DoD is different for the observed technologies. The next step is to define the initial LOLP value.

In the first case, the LOLP is set to 0, and then increased to 0.01. Next, a time period (in minutes) is defined for which optimization is performed. The following step is the calculation of PV generation, representing the amount of electricity generated by the PV system at time step t. The PV generation is first calculated for a single module during the simulation period according to (1). Subsequently, the PV generation for a single module is multiplied by the total number of PV modules to obtain the system’s overall PV generation during the simulation period, according to (2).

$$P_{\mathrm{PV}1,\mathrm{t}}=G_{\mathrm{t}}\ast A_{\mathrm{PV}}\ast {\eta }_{\mathrm{PV}}$$

(1)

where

• P_PV1,t [W] is the PV generation for n_PV = 1 at time step t;
• G_t [W/m²] is the solar irradiation on the horizontal plane at time step t;
• A_PV [m²] is the area of a PV module;
• $\eta$_PV is the PV module efficiency.

$$P_{\mathrm{PV},\mathrm{t}}=P_{\mathrm{PV}1,\mathrm{t}}\ast n_{\mathrm{PV}}$$

(2)

where

• P_PV,t [W] is the PV generation for n_PV at time step t;
• n_PV is the number of PV modules.

The next step is to calculate the power difference between the amount of PV generation and the electricity demand for each time step during the optimization period, according to (3). The power difference indicates the amount of generated electricity that is not consumed in time step t if the value is positive, the amount of generated electricity that is missing to satisfy electricity demand if the value is negative, and the matching of the generated electricity with the electricity demand if the value is equal 0.

$$P_{\mathrm{diff},\mathrm{t}}=P_{\mathrm{PV},\mathrm{t}}-P_{\mathrm{load},\mathrm{t}}$$

(3)

where

• P_diff,t [W] is the power difference between PV generation and load demand in time step t;
• P_load,t [W] is the load demand at time step t.

3.1.1. Positive Power Difference

If the power difference is positive at time step t, there is an excess of generated electricity that the algorithm attempts to store in BS. The battery storage capacity at the time step t, after the algorithm attempts to store the power difference in BS, is calculated according to (4).

$$C_{\mathrm{BS},\mathrm{end},\mathrm{t}}=C_{\mathrm{BS},\mathrm{start},\mathrm{t}}+P_{\mathrm{diff},\mathrm{t}}\ast {\eta }_{\mathrm{charging}}\ast \Delta t$$

(4)

where

• C_BS,end,t [Wh] is the BS capacity at the end of time step t;
• C_BS,start,t [Wh] is the BS capacity at the start of time step t;
• $\eta$_charging is the battery charging efficiency.

BS capacity refers to the amount of energy stored in BS at time step t, and it is limited by two values. The upper or maximum limit is defined by the rated battery capacity, while the lower or minimum limit is defined by the maximum DoD value. The BS capacity at the beginning is equal to the rated BS capacity for n_bat batteries multiplied by the initial SOC, and for the next time steps, the BS capacity at the start of the time step is equal to the BS capacity at the end of the previous time step t − 1. The BS capacity calculated at the time step t is compared with the maximum value. If the calculated capacity is above the maximum capacity limit, the BS charging power is reduced according to (5) in order that it does not exceed the maximum limit at the end of the time step t.

$$P_{\mathrm{charging},\mathrm{t}}={\displaystyle \frac{C_{\mathrm{BS},\max }-C_{\mathrm{BS},\mathrm{start},\mathrm{t}}}{{\eta }_{\mathrm{charging}}\ast \Delta t}}$$

(5)

where

• P_charging,t [W] is the BS charging power at time step t;
• C_BS,max [Wh] is the BS upper capacity limit.

If the calculated BS capacity is below or equal to the maximum capacity limit, the charging power of the BS at time step t is compared to the power limit. If the BS charging power is above the power limit, the BS charging power at time step t is reduced.

If the BS charging power is below or equal to the power limit, the BS charging power at time step t remains unchanged. When the BS charging power at time step t is equal to the power difference, it means that the entire excess generation can be stored in BS. When the BS charging power is reduced, there is an energy excess that is not considered in this algorithm, and it is dismissed. When the BS charging power at time step t is obtained, the BS capacity at the end of time step t is estimated.

3.1.2. Negative Power Difference

If the power difference is negative at time step t, the amount of PV generation is not enough to meet the electricity demand and the algorithm discharges BS if there is enough stored energy. The BS capacity at time step t, after the algorithm discharges the energy required to meet the difference in power, is calculated according to (6).

$$C_{\mathrm{BS},\mathrm{end},\mathrm{t}}=C_{\mathrm{BS},\mathrm{start},\mathrm{t}}+{\displaystyle \frac{P_{\mathrm{diff},\mathrm{t}}\ast \Delta t}{{\eta }_{\mathrm{discharging}}}}$$

(6)

where

• $\eta$_discharging is the battery discharging efficiency.

The calculated BS capacity at time step t is compared to the lower capacity limit. If the BS capacity is below the lower capacity limit, the BS discharging power is reduced according to (7) to ensure that the BS capacity does not fall below the lower capacity limit at time step t.

$$P_{\mathrm{discharging},\mathrm{t}}={\displaystyle \frac{(C_{\mathrm{BS},\mathrm{start},\mathrm{t}}-C_{\mathrm{BS},\min })\ast {\eta }_{\mathrm{discharging}}}{\Delta t}}$$

(7)

where

• P_{discharging,t} [W] is the BS discharging power at time step t;
• C_BS,min [Wh] is the BS lower capacity limit.

If the calculated BS capacity is above or equal to the lower capacity limit, the discharge power of the BS at time step t is compared to the power limit. If the BS discharging power is above the power limit, the BS discharging power at time step t is reduced to the BS power limit. If the discharge power of the BS is below or equal to the power limit, the discharge power of the BS at time step t remains unchanged. When the discharge power of the BS at time step t is equal to the power difference, it means that the electricity demand is satisfied and there is no power deficit at time step t. When the discharge power of the BS is reduced, the load demand is not covered and there is a power deficit at time step t that is calculated according to (8). The power deficit refers to the amount of electricity demand that cannot be supplied by the PV battery system at time step t.

$$P_{\mathrm{deficit},\mathrm{t}}=P_{\mathrm{load},\mathrm{t}}-P_{\mathrm{pv},\mathrm{t}}-P_{\mathrm{discharging},\mathrm{t}}$$

(8)

where

• P_deficit,t [W] is the power deficit at time step t.

3.1.3. No Power Difference

If the power difference in time step t is equal to 0, there is no excess or power deficit, the BS is not charged or discharged, and the BS capacity at time step t remains the same as at the previous time step t − 1.

3.1.4. Obtained LOLP Calculation

The algorithm is then repeated for each time step in the optimization period. When the power difference is compared to 0 for the entire optimization period, the LOLP value is calculated as the ratio between the sum of the power deficit and the sum of load demand in the optimization period, according to (9).

$$LOLP={\displaystyle \frac{{\Sigma }_{t=1}^n{P}_{\mathrm{deficit},\mathrm{t}}}{{\Sigma }_{t=1}^n{P}_{\mathrm{load},\mathrm{t}}}}$$

(9)

where

• LOLP is the calculated value of LOLP;
• n is the total number of time steps.

The total cost of the PV system is calculated as the sum of the number of PV modules multiplied by the cost of the PV module and the number of batteries multiplied by the cost of the battery, according to (10). The cost of the battery depends on the type of battery.

$$Cost=n_{\mathrm{PV}}\ast Cos{t}_{\mathrm{PV}}+n_{\mathrm{bat}}\ast Cos{t}_{\mathrm{bat}}$$

(10)

where

• Cost [EUR] is the total PV battery system cost;
• Cost_PV [EUR/module] is the cost of a PV module;
• n_bat is the number of batteries;
• Cost_bat [EUR/battery] is the cost of a battery.

Two requirements must be met. The first requirement is that the final LOLP achieved must be less than or equal to the defined initial LOLP. If the final LOLP is higher than the initial LOLP defined, the system cost is penalized, and this combination of PV modules and batteries is rejected as a solution. The second requirement is the minimum cost with a selected combination of PV modules and batteries. If the system cost is not minimal, the algorithm sets new combinations until the minimum system cost is achieved.

3.2. Optimization Parameters

The objective function of the proposed optimization model is the minimization of the total cost of the PV system defined by (10). The number of PV modules and the number of batteries are integer variables with bounds defined by (12) and (13). The battery type is a binary variable, as the choice is between only two different battery technologies.

Minimize

$$Cost=f(n_{\mathrm{PV}},n_{\mathrm{bat}},typ{e}_{\mathrm{bat}})$$

(11)

Subject to

$$n_{\mathrm{PV}}>0$$

(12)

$$n_{\mathrm{bat}}>0$$

(13)

$$0\le typ{e}_{\mathrm{bat}}\le 1$$

(14)

The objective function is a sum of products where the number of components is multiplied by the constant price of components, so this is a linear objective function. With two integer decision variables and one binary decision variable, the optimization problem can be classified as a linear integer programming problem. The optimization problem is solved using the Differential Evolution Algorithm in a Python 3.12 environment.

3.3. Modification of Electricity Consumption

The amount of power deficit increases with an increasing LOLP value. During the day, there are periods with a power deficit and also with an excess of PV generation. There is a possibility of moving electricity consumption from periods with a power deficit to periods with power excess, and this will lead to a decrease in the amount of power deficit and to a decrease in the final LOLP value.

Modifying electricity consumption is an additional step in this work, and it is independent of the PV system sizing algorithm. Combinations of PV modules and batteries that do not meet the minimum cost condition before modification may become feasible solutions after modification. The modification is applied to each day during the simulation period. The main condition that must be met is that the sum of the electricity consumption during the day after the modification remains equal to the consumption before the modification.

4. Results

In this section, the results are presented and discussed across three subsections. First, the optimal size of an off-grid PV system with respect to the initial LOLP value is analyzed. Then, the influence of the initial LOLP value on the total system cost is examined. Finally, the results after modification of electricity consumption are compared with those before modification.

4.1. The Optimal Size of the PV Battery Storage System

To cover electricity demand during the entire simulation period, 11 PV modules (Figure 5) and 11 LiFePO₄ batteries (Figure 6) are required. Increasing the initial LOLP to 0.01 reduces the requirement to 10 PV modules and 7 LiFePO₄ batteries, which is 4 batteries fewer than when LOLP = 0. With further increases in the initial LOLP, the number of required components generally decreases, although there are exceptions. When the initial LOLP is 0.04, eight PV modules and six LiFePO₄ batteries are required, and when the initial LOLP is 0.05, nine PV modules and five LiFePO₄ batteries are required, because the cost of an additional PV module is lower than the cost of one LiFePO₄ battery. For initial LOLP values between 0.08 and 0.15, seven PV modules are required, while for values between 0.16 and 0.20, six PV modules are sufficient. The number of batteries decreases to 9 at at LOLP = 0.15, but then increases again to 11 at LOLP = 0.16, because the cost of 2 gel batteries is lower than that of 1 PV module. A high-performance LiFePO₄ battery is the optimal battery type at LOLP values up to 0.08, with the exception of an LOLP value of 0.07, when the gel battery is the optimal solution. At LOLP values above 0.08, a gel battery with lower performance, but also with a much lower price, is a more suitable battery type.

To satisfy electricity consumption during the entire optimization period without load loss, 11 LiFePO₄ batteries are required, which leads to a total installed BS capacity of 7.04 kWh. The use of installed BS capacity during the simulation period for an LOLP equal to 0 is presented in Figure 7. The BS SoC is above 60% during 94.6% of the simulation time, which means that most of the time, five batteries with 2.88 kWh of usable capacity are enough, while only during 5.6% of the simulation time there is a need for more installed battery capacity.

An increase in the LOLP to 0.01 leads to four batteries less, or 4.48 kWh of total installed capacity. In this case, for 92% of the simulation time, the BS SoC is above 40%, which means that five batteries are required most of the time, and 8% of the time, more batteries are required. With an LOLP equal to 0.05, five LiFePO₄ batteries are enough, and in this case, 90.3% of the time, the BS SoC is above 20%, while 9.7% of the time, it is below 20%. The use of installed BS capacity during the simulation period for an LOLP equal to 0.05 is shown in Figure 8. It can be concluded that, in addition to a high initial cost, more installed batteries are not in use during the entire observed time, so the possibility of losing a part of the consumption should be considered during the sizing of an off-grid PV system.

4.2. The Cost of the Off-Grid PV Battery System

The individual costs of PV modules and batteries are presented in Figure 9, while the total cost of the system is presented in Figure 10. With an increase in the LOLP value, the cost of individual components and the total cost of the system decreases, which is expected due to there being fewer PV modules and batteries. The total cost of the system for the case of an LOLP equal to 0 is EUR 6552, according to Figure 10. The cost of batteries is EUR 3802, which is significantly higher than the cost of PV modules, which is equal to EUR 2750, according to Figure 9.

An increase in the initial LOLP value to 0.01 results in the total cost of the PV battery system amounting to EUR 4912, which is a cost reduction of 25%. The battery cost in this case is slightly lower than the cost of the PV modules. As the initial LOLP increases, the share of PV module cost is higher than the share of battery cost in the total cost of the PV battery system. The only exception is in the case of an initial LOLP of 0.04, where the cost of six expensive batteries amounting to EUR 2073 is slightly higher than the cost of eight PV modules amounting to EUR 2000. With an increase in the initial LOLP to 0.02, the total system cost decreases to EUR 4574 or 30%. A cost reduction exceeding 40% is achievable at an initial LOLP of 0.06, while a reduction of more than 50% is observed at an LOLP of 0.11, at which level the total system cost amounts to EUR 3190. A reduction of more than 60% is possible at an initial LOLP of 0.19, when the total system cost amounts to EUR 2580.

4.3. Modification of Electricity Consumption

This subsection presents the impact of modifying electricity consumption on the occurrence of power deficits and the resulting LOLP values. Figure 11 illustrates the electricity consumption and the combined electricity supplied by the PV system and the BS during a typical day in June. The situation after modifying electricity consumption is presented in Figure 12. In both cases, the electricity stored in the BS is subtracted from the sum of electricity generated by the PV system and discharged from the BS.

Prior to modification, power deficits occur during the night until 05:20, in the morning at 09:15, and in the afternoon from 15:00 to 19:00, with the most significant deficit observed between 16:00 and 16:30, as shown in Figure 11. Additionally, an excess of PV generation is observed from 09:00 to 15:00, with the largest surplus occurring after 12:30. After modifying electricity consumption, afternoon power deficits are eliminated, while a surplus of PV generation remains from 13:20 to 15:00, as depicted in Figure 12. The sum of power deficit during the observed day is reduced from 1.997 kWh to 1.049 kWh, while the sum of power excess is reduced from 1.397 kWh to 0.449 kWh.

When electricity consumption is modified, the final LOLP value obtained with one combination of PV modules and batteries can be reduced, making this combination suitable for a lower initial LOLP value. The lower number of PV modules and batteries helps to reduce the total cost of the system. The impact of modifying electricity consumption on the number of PV modules, the number and type of batteries, and the total cost of the system is summarized in

Table 2. The impact of modifying electricity consumption on the size and total cost of the off-grid PV system.

LOLP	Before Modification				After Modification
	npv	nbat	Type	Cost [EUR]	npv	nbat	Type	Cost [EUR]
0.00	11	11	LFP	6552	11	11	LFP	6552
0.01	10	7	LFP	4919	10	7	LFP	4919
0.02	10	6	LFP	4574	9	6	LFP	4324
0.03	9	6	LFP	4324	8	6	LFP	4074
0.04	8	6	LFP	4074	9	5	LFP	3978
0.05	9	5	LFP	3978	8	13	Gel	3560
0.06	8	5	LFP	3728	8	11	Gel	3320
0.07	8	14	Gel	3680	8	10	Gel	3200
0.08	7	5	LFP	3478	8	9	Gel	3080
0.09	7	14	Gel	3430	8	9	Gel	3080
0.10	7	13	Gel	3310	8	8	Gel	2960
0.11	7	12	Gel	3190	7	9	Gel	2830
0.12	7	11	Gel	3070	7	9	Gel	2830
0.13	7	11	Gel	3070	7	9	Gel	2830
0.14	7	10	Gel	2950	6	10	Gel	2700
0.15	7	9	Gel	2830	6	9	Gel	2580
0.16	6	11	Gel	2820	6	8	Gel	2460
0.17	6	10	Gel	2700	6	7	Gel	2340
0.18	6	10	Gel	2700	6	7	Gel	2340
0.19	6	9	Gel	2580	6	6	Gel	2220
0.20	6	9	Gel	2580	6	6	Gel	2220

.

An off-grid PV system consisting of nine PV modules and six LiFePO₄ batteries is suitable for an initial LOLP equal to 0.03 before modifying electricity consumption, and for 0.02 after modification. Similarly, a combination of seven PV modules and nine gel batteries, required for an initial LOLP of 0.15, becomes suitable for an initial LOLP of 0.11 after modification. For the same initial LOLP of 0.15, six PV modules and nine gel batteries are sufficient after modification. This combination, prior to modification, would satisfy an initial LOLP of 0.19, while only six PV modules and six gel batteries are required for an initial LOLP of 0.19 after modification. The most significant cost reduction after modification is for an initial LOLP 0.07, where the total cost of the system is reduced by EUR 480, or 7.5%.

5. Discussion

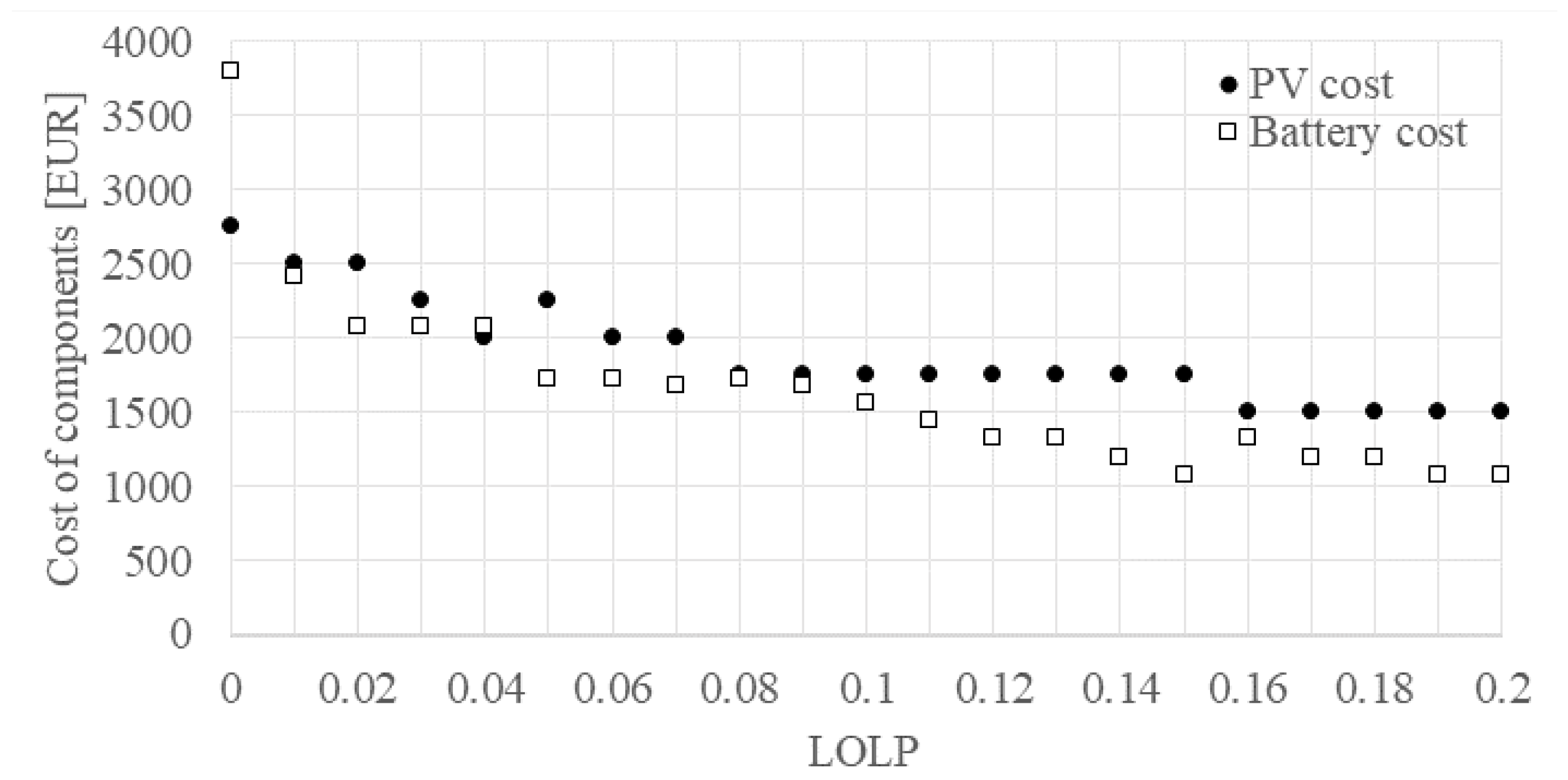
This paper investigates the determination of the optimal number of PV modules and the optimal type and number of batteries required for an off-grid PV system with respect to the LOLP value. To meet electricity consumption requirements over the entire period without any loss of load, 11 PV modules and 11 LiFePO₄ batteries are required. The cost of the PV system in this case is EUR 6552. An increase in the initial LOLP to 0.01 results in 10 PV modules, 7 LiFePO₄ batteries, and a cost decrease to EUR 4919, or 24.9%. With an initial LOLP equal to 0.05, nine PV modules and five LiFePO₄ batteries are required, which leads to a cost of EUR 3978, or a cost reduction of 39.3%. When the initial LOLP is equal to 0.1, with 7 PV modules and 13 GEL batteries, the system cost can be decreased to EUR 3310, or by 49.5%. An additional increase in the initial LOLP value leads to an additional decrease in the cost of the PV system, as fewer PV modules and batteries are required.

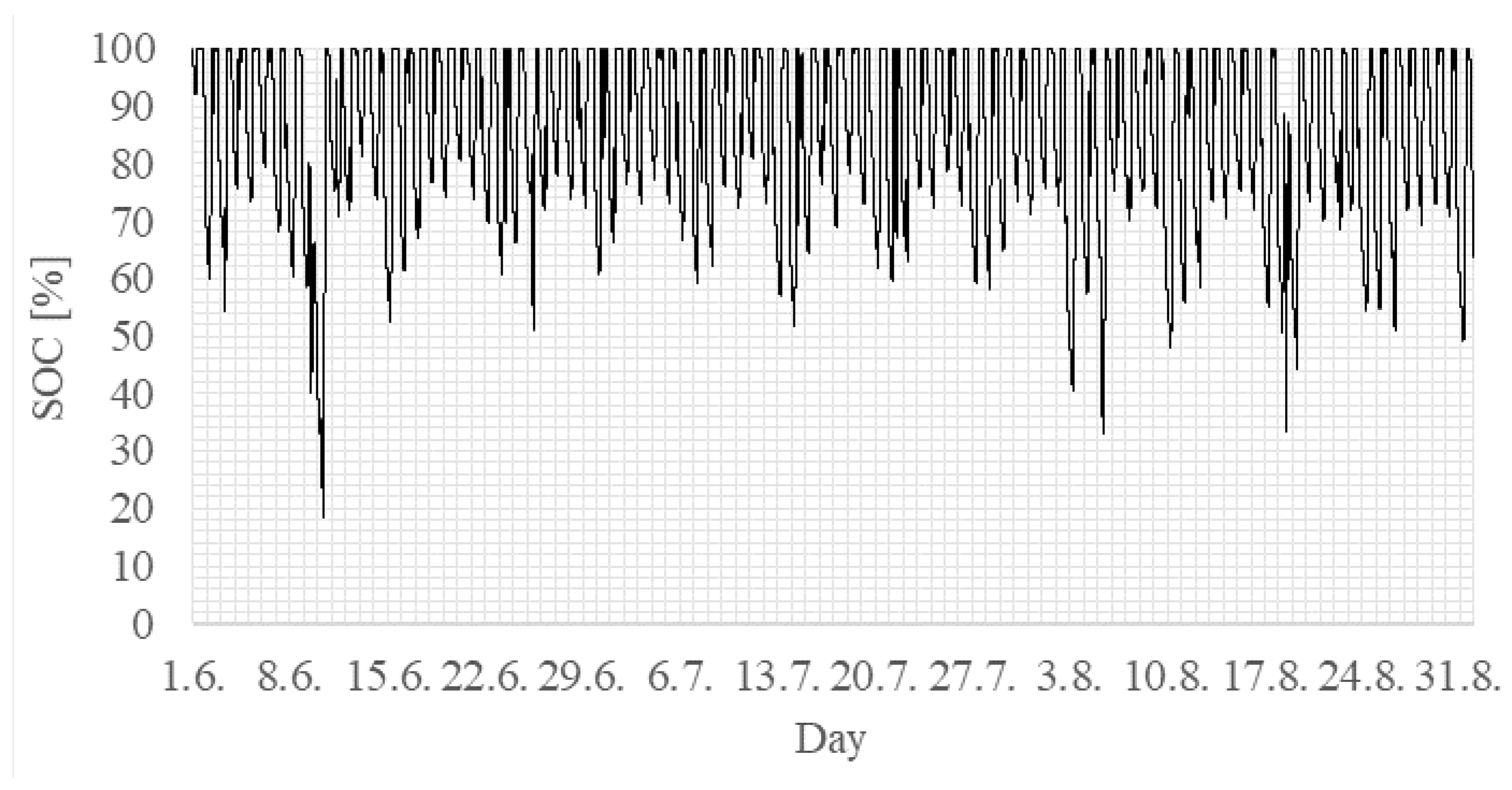
The high installed battery capacity, in addition to the high initial cost, is not fully utilized at all times. Most of the time, a lower battery capacity will suffice, and the probability of partial electricity shortages should be considered during the system sizing procedure. For example, when an LOLP value equal to 0 must be satisfied, 11 LiFePO₄ batteries are required and only 5.6% of the time does the battery capacity fall below 60%. On the other hand, when an LOLP value equal to 0.05 must be satisfied, five LiFePO₄ batteries are required and only 9.7% of the time does the battery capacity fall below 20%. In addition to underutilization, maintaining batteries at a high state of charge (SoC) for significant periods accelerates battery aging. In this study, the batteries are assumed to be new; cycle degradation and aging are not considered, and the system’s ability to meet electricity demand with degraded batteries is not investigated. Future research should incorporate battery degradation to assess system performance over time with respect to the initial LOLP. Cycle degradation can be estimated based on the expected number of charge–discharge cycles associated with the battery DoD. In other words, deeper battery cycling leads to a decrease in battery cycles at the end of battery life. Battery aging is accelerated with a high floating SoC value, as mentioned earlier, and in future work, degradation estimation will be performed according to the expected battery degradation associated with a floating SoC.

Modifying electricity consumption can help to reduce the amount of power deficit that leads to a final reduction in the LOLP value. The combination of n_PV modules and n_bat batteries required for one initial LOLP, after modification of electricity consumption, is applicable for a lower initial LOLP, leading to a reduction in the system cost. At a lower initial LOLP, the final reduction in the LOLP value is around 1%, while for a higher initial LOLP, the reduction is around 4%. The cost of the system can be reduced by up to 7.5%. Electricity consumption is modified without any insight into devices that are turned off or shifted to another time period during a day. Future work should consider disaggregating the total consumption profile into individual device profiles to explore the potential of load shifting in reducing the required size of the PV system and associated investment costs, while maintaining a low LOLP. Consumption should also be divided into critical and noncritical devices, and power supply for critical devices should be provided at all times, regardless of the LOLP value.

The proposed sizing procedure for an off-grid PV system comes with several drawbacks. The algorithm is applied to a single electricity consumption and one solar irradiation dataset, and the influence of variation in the input data on the optimal size of an off-grid PV system is not investigated. In this work, the impact of temperature on the output power and on the optimal number of PV modules is not considered. Additionally, only one PV technology and rated power, as well as a single rated battery capacity, are used in the model. As noted previously, the effects of battery aging and cycle degradation on the system’s ability to meet electricity demand while satisfying defined LOLP values are not examined. A configuration that meets demand when the batteries are new may not be sufficient to meet the electricity demand with respect to the LOLP value as the batteries degrade over time.

6. Conclusions

PV systems provide electricity for consumers without access to the power grid. An off-grid or grid-independent PV system requires a battery to ensure power supply when PV generation is not available, such as at night or on cloudy days. Ensuring a sufficient power supply for all electrical devices all the time in off-grid PV systems requires a high installed battery capacity, which incurs substantial investment costs. Conversely, reducing the installed battery capacity and rated PV power may result in periods of insufficient power supply, although investment costs are reduced. To quantify this trade-off, LOLP is introduced, representing the percentage of electricity consumption that may not be covered.

This paper proposes a method to determine the optimal number of PV modules and the optimal type and number of batteries required for an off-grid PV system with respect to the LOLP value. The method is applied to a scenario where an off-grid PV battery system needs to provide electricity supply during the three summer months, from 1 June to 31 August. To cover electricity consumption during the entire period without any loss, 11 PV modules and 11 LiFePO₄ batteries are required. The cost of the PV system in this case is EUR 6552. Increasing the initial LOLP value allows for fewer PV modules and batteries, thereby reducing the total investment cost.

There is potential for improvement of the presented sizing procedure in future work. The proposed algorithm should be applied to off-grid PV systems in different locations with varying climate conditions and electricity consumption patterns. The proposed methodology should also be extended to cover periods longer than only 3 months, potentially encompassing 6 months or even an entire year. Future work should investigate the potential of load time shifting to reduce the size of the PV system and the associated investment costs while maintaining a low LOLP. There is also a possibility of considering temperature data and the impact of temperature on the output power of PV modules and the size of the PV system. In addition, battery aging and degradation should be incorporated into the analysis, as these factors are closely related to battery replacement. Future studies could include more detailed economic evaluation that accounts for operation and replacement costs. The sizing procedure can also be improved by considering different PV modules and batteries with varying rated capacities.

The potential challenges in real-world implementation of off-grid PV battery systems include additional costs of places to place batteries to protect them from harsh conditions such as extremely high and low temperature, humidity, rain, or dust. Maintenance can also be expensive, particularly in remote locations, where technicians may not be locally available, and unexpected failures could result in several days of system downtime. Tests on larger local solar datasets should be conducted, considering data from more consecutive years to ensure system availability regardless of solar irradiation variability. Furthermore, hardware tests should also be conducted prior to real-world implementation.