Cascade Hydropower Plant Operational Dispatch Control Using Deep Reinforcement Learning on a Digital Twin Environment
Abstract
1. Introduction
- High-Fidelity Data-Driven Simulation Model of the Drava Cascade. We construct a data-driven simulation of all eight hydropower plants on the Drava River—six impoundment and two diversion facilities—with accurate nonlinear head–flow maps, inter-plant hydraulic coupling, and reservoir dynamics, using operational records from DEM d.o.o. and HSE d.o.o. [22,23].
- Model-Free RL Controller. We cast real-time cascade flow control under externally imposed trader schedules as a continuous-state, continuous-action Markov decision process and train actor-critic agents (DDPG, TD3, SAC and PPO) that learn optimal dispatch policies directly from the digital twin, treating uncertain inflows and market targets as exogenous disturbances.
- Empirical Benchmarking Against Human Dispatchers. We perform a head-to-head comparison with historical dispatcher performance on the Drava system, demonstrating that our RL agents achieve an absolute mean error of 7.64 MW—closely approaching the 5.8 MW error of expert operators at a 591.95 MW installed capacity—while fully respecting operational and safety constraints.
- Robustness to Uncertainty. Without relying on explicit probabilistic models for future inflows or schedule deviations, our deterministic RL policies maintain high tracking accuracy and reservoir safety across diverse stochastic scenarios, reducing spillage and preserving system flexibility.
Related Work
2. Methodology
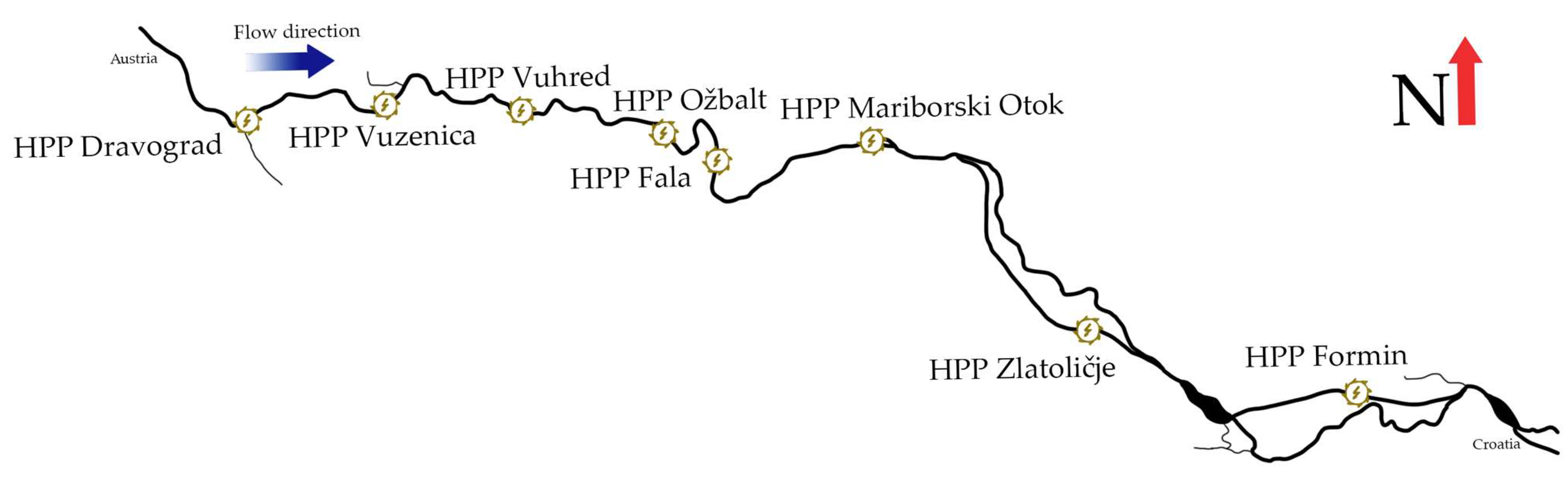
2.1. Cascade Hydropower Plant System
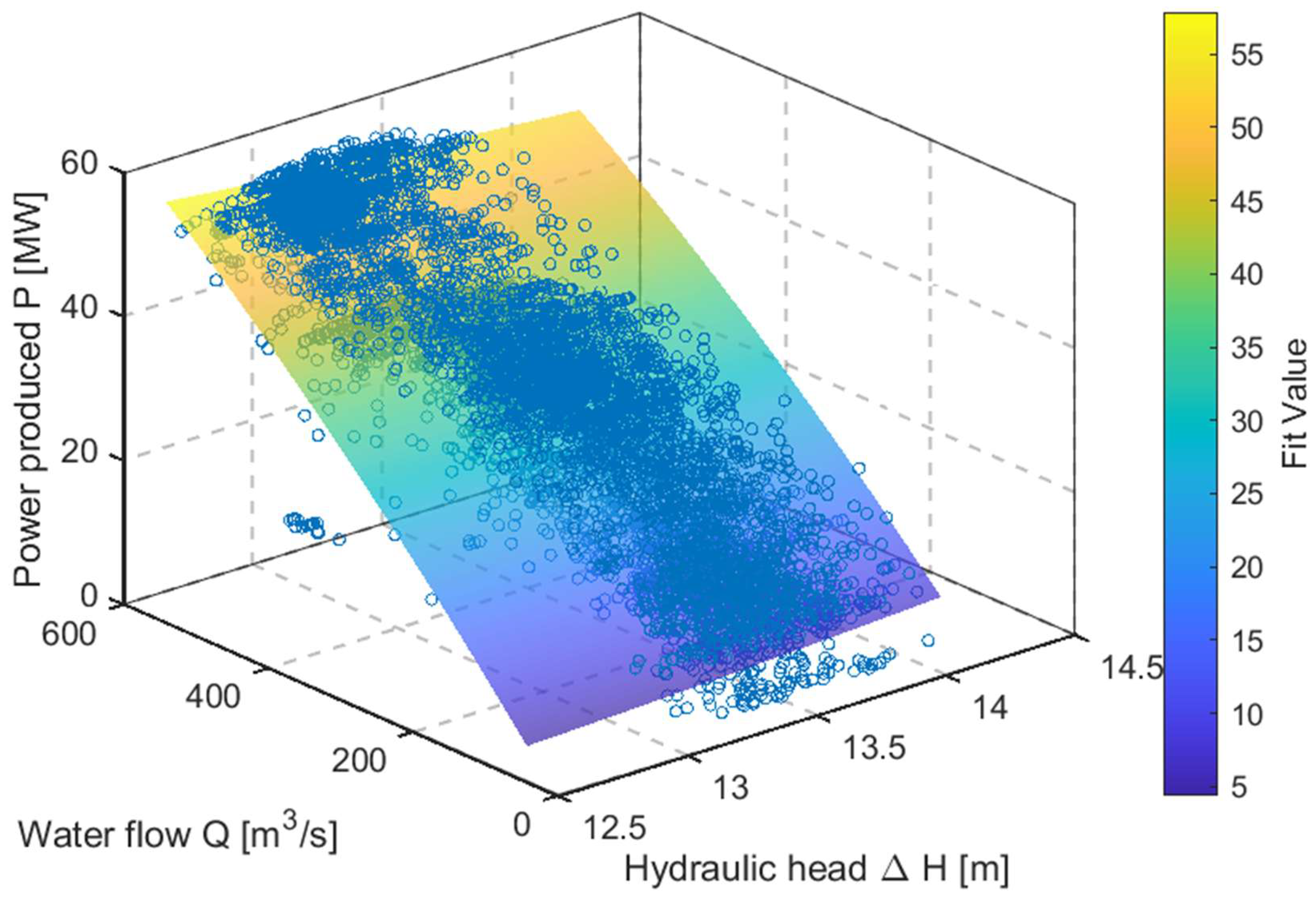
2.2. Digital Twin
- ,
- ,
- .
- ,
- ,
- ,
- ,
- ,
- .
- ,
- ,
- ,
- ,
- ,
- ,
- ,
- ,
- .
2.3. Reinforcement Learning
2.3.1. State Representation
2.3.2. Action Representation
2.3.3. Reward Function
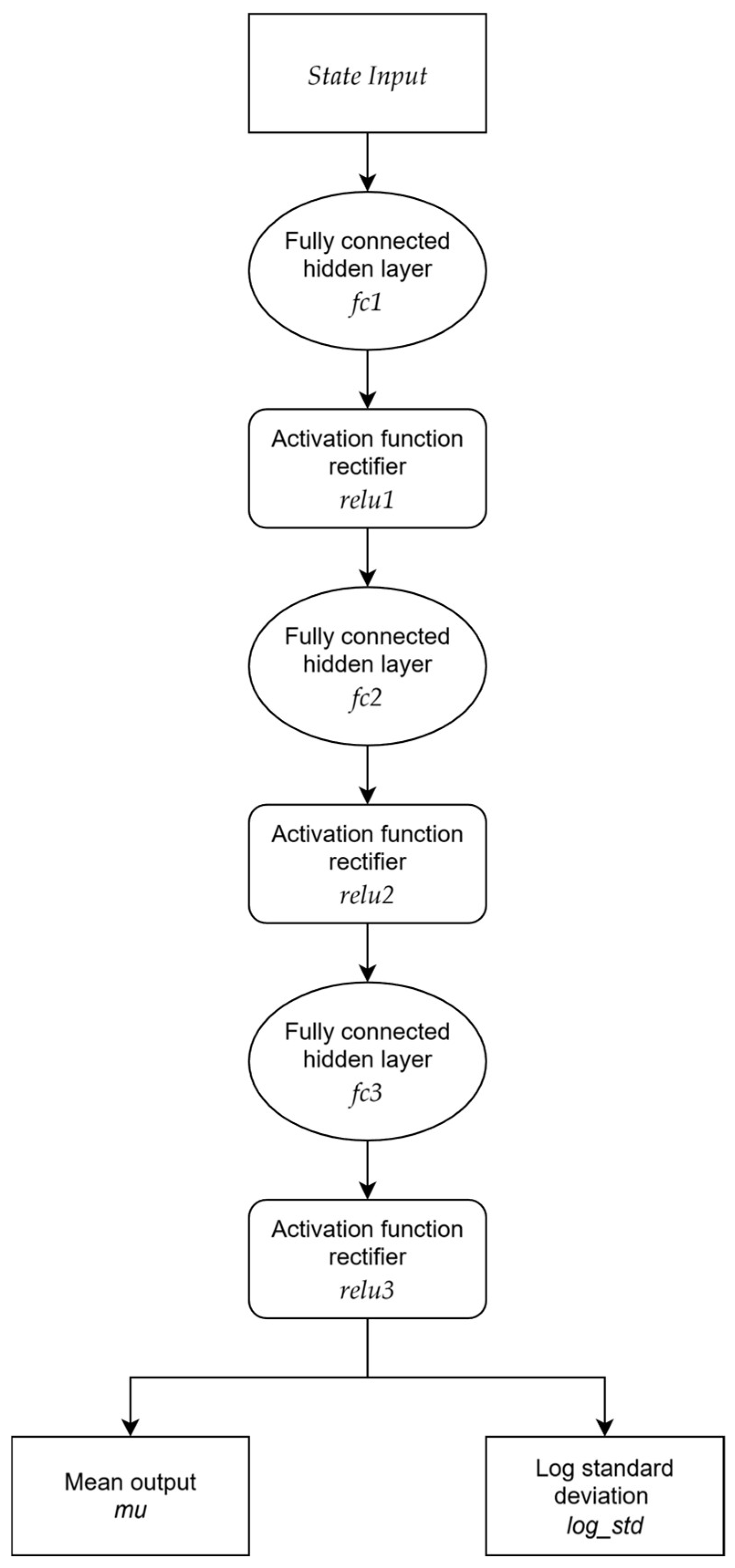
2.3.4. Network Architectures
- Re-parameterisation trick: By expressing the random action as a deterministic function of , , and , you can back-propagate gradients through the stochastic sampling step.
- State-dependent exploration: The spread is scaled by the learned , so the policy controls how much noise is injected in each state.
2.4. Human Dispatcher and Benchmark Method
3. Results
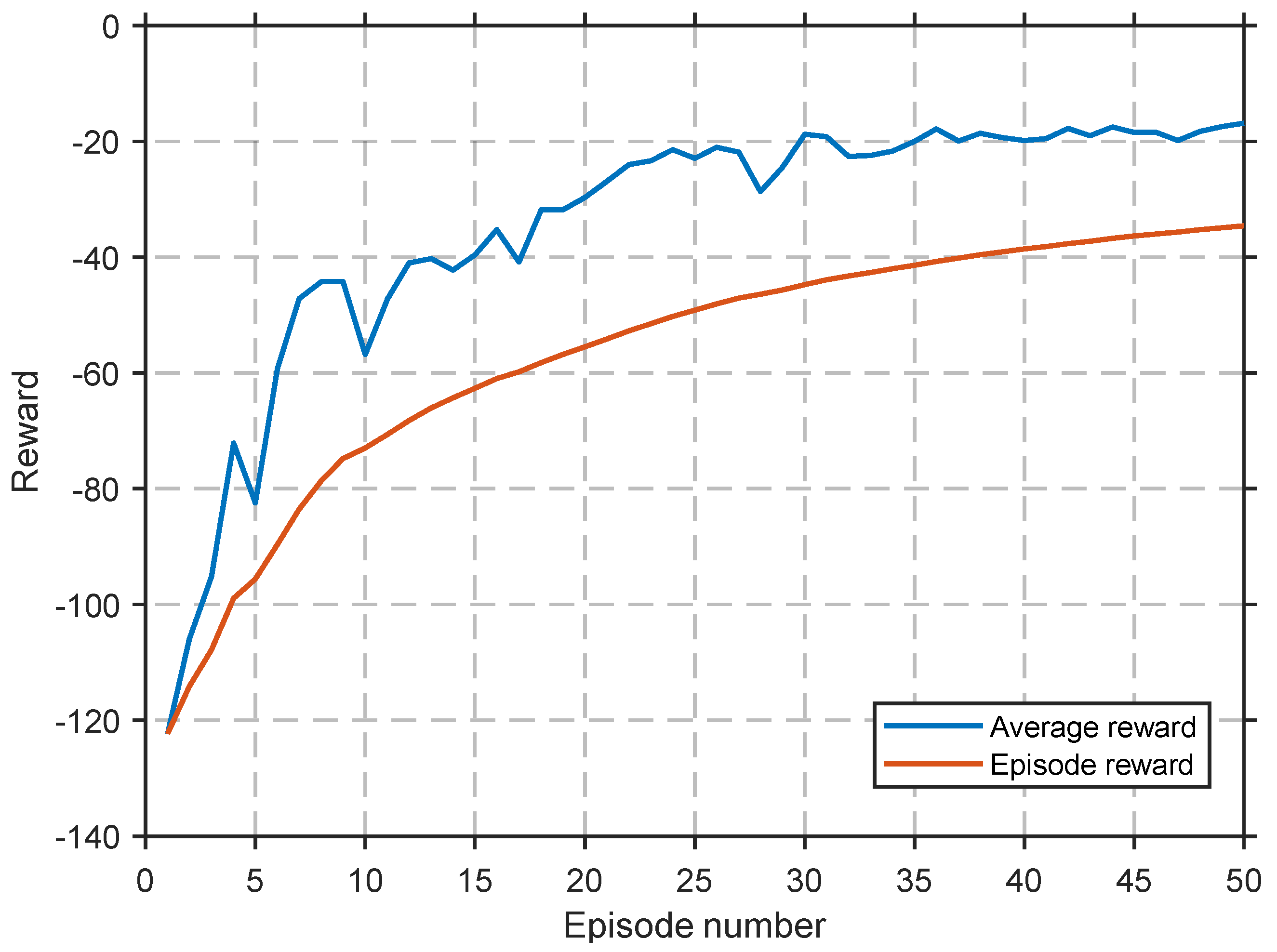
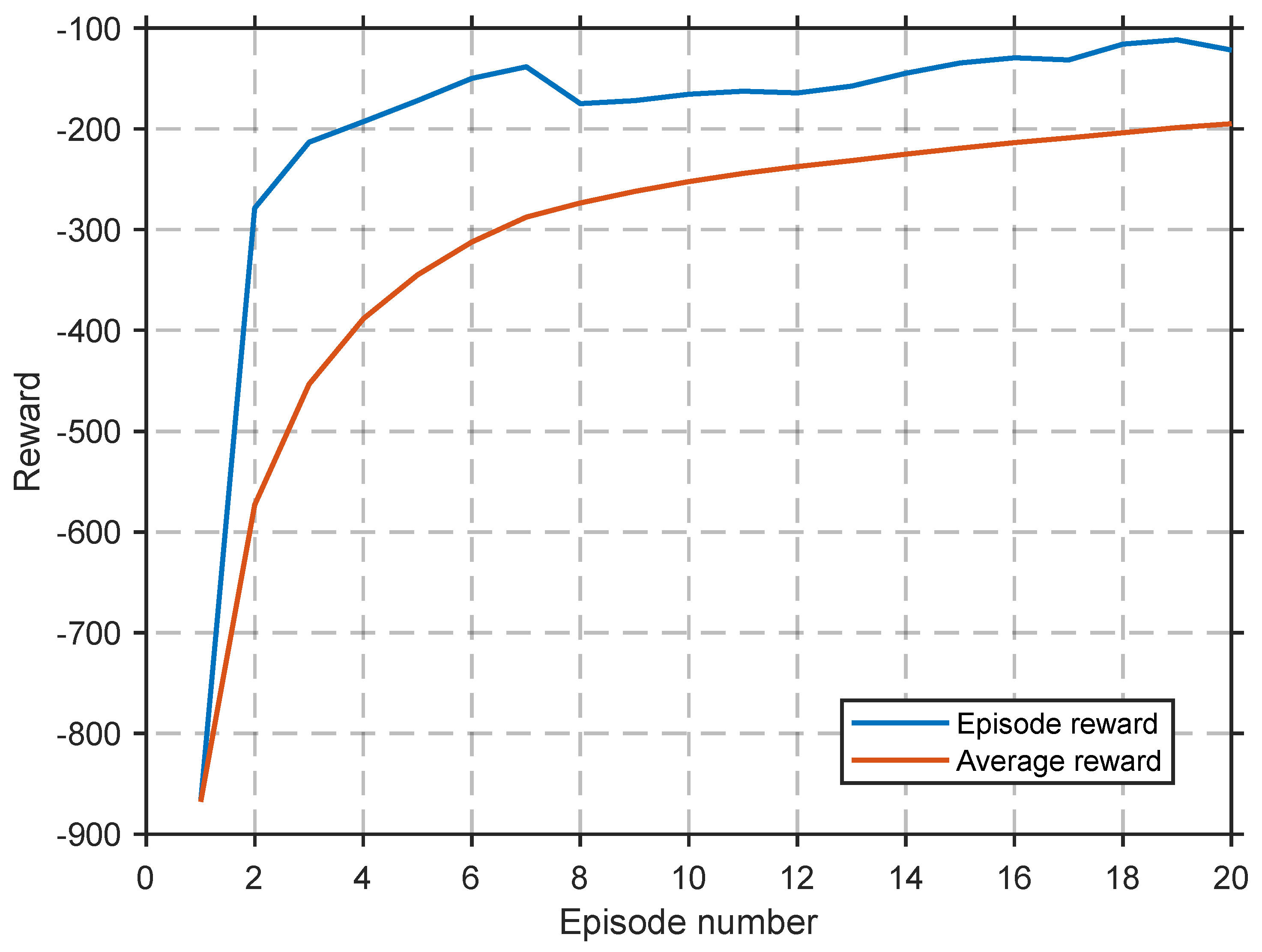
3.1. DDPG Training Results
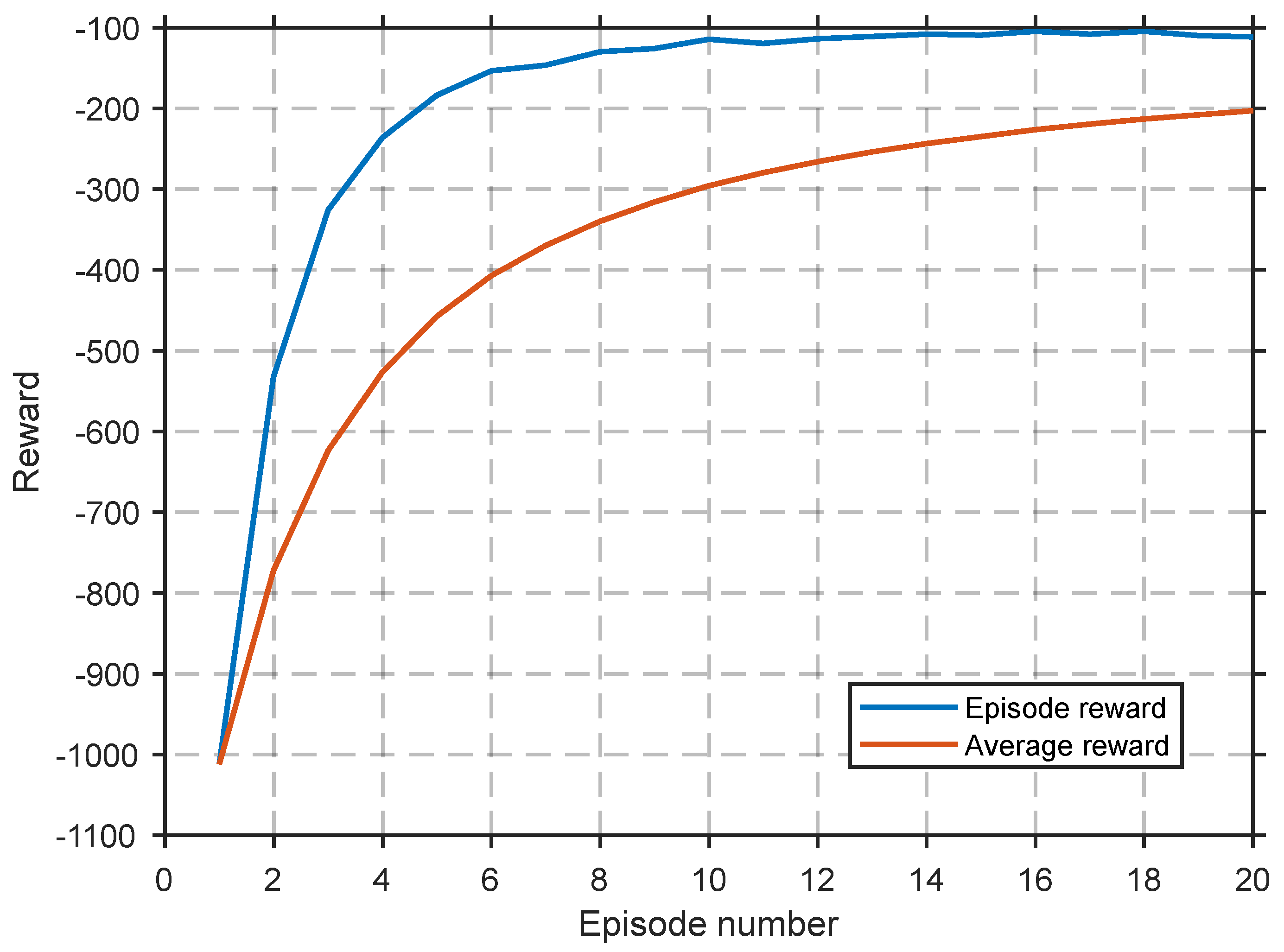
3.2. TD3 Training Results
3.3. SAC Training Results
3.4. PPO Training Results
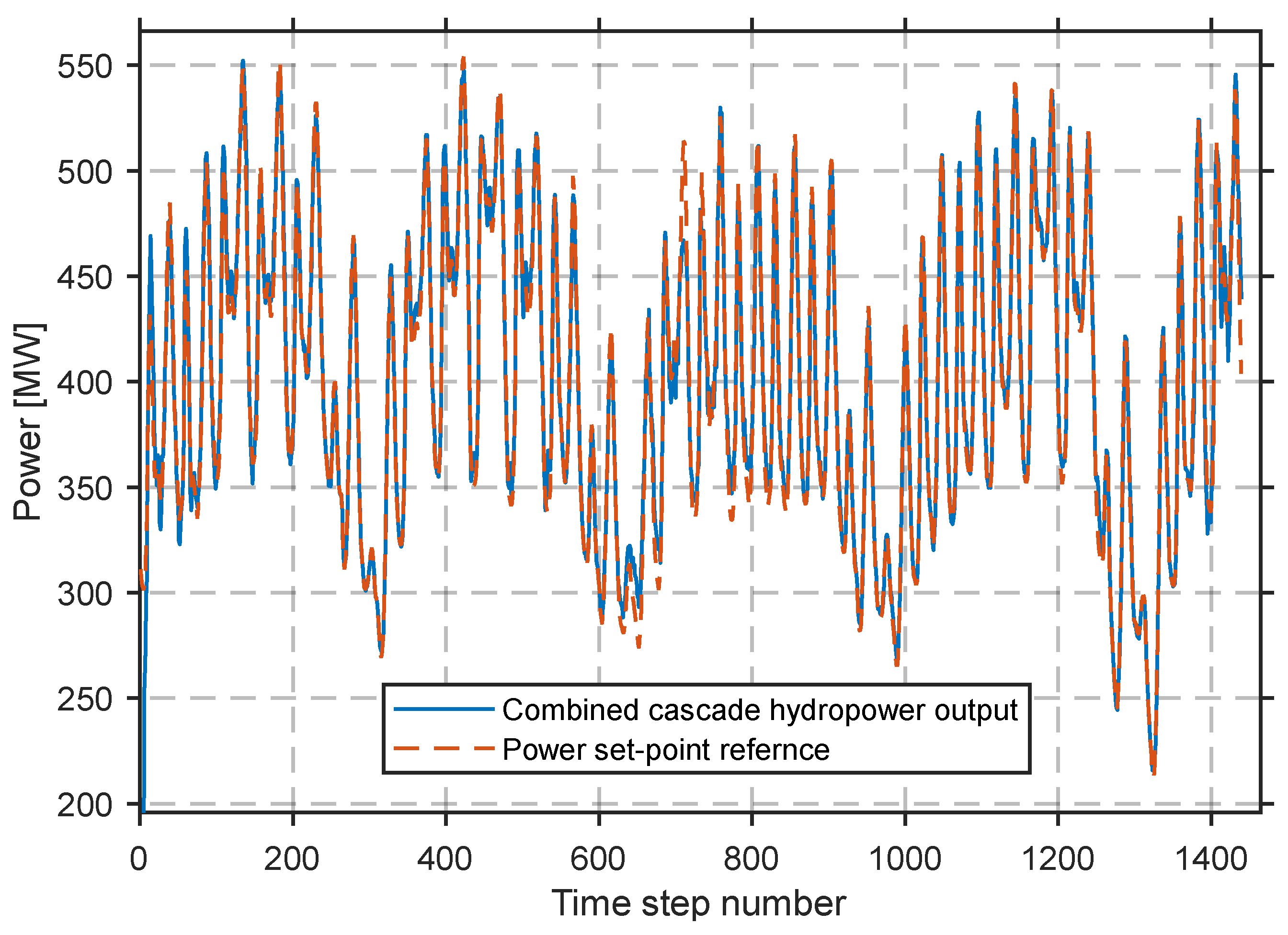
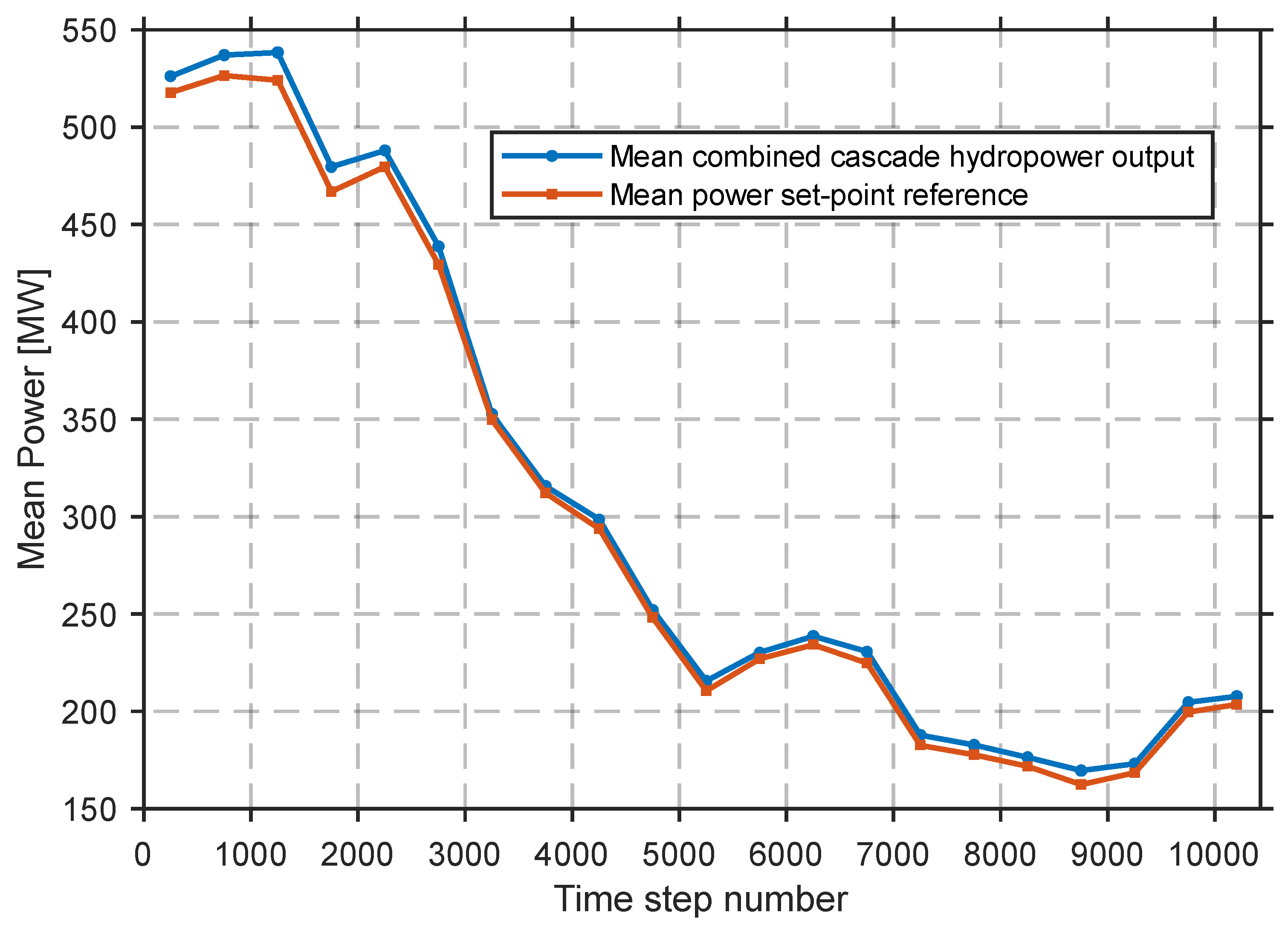
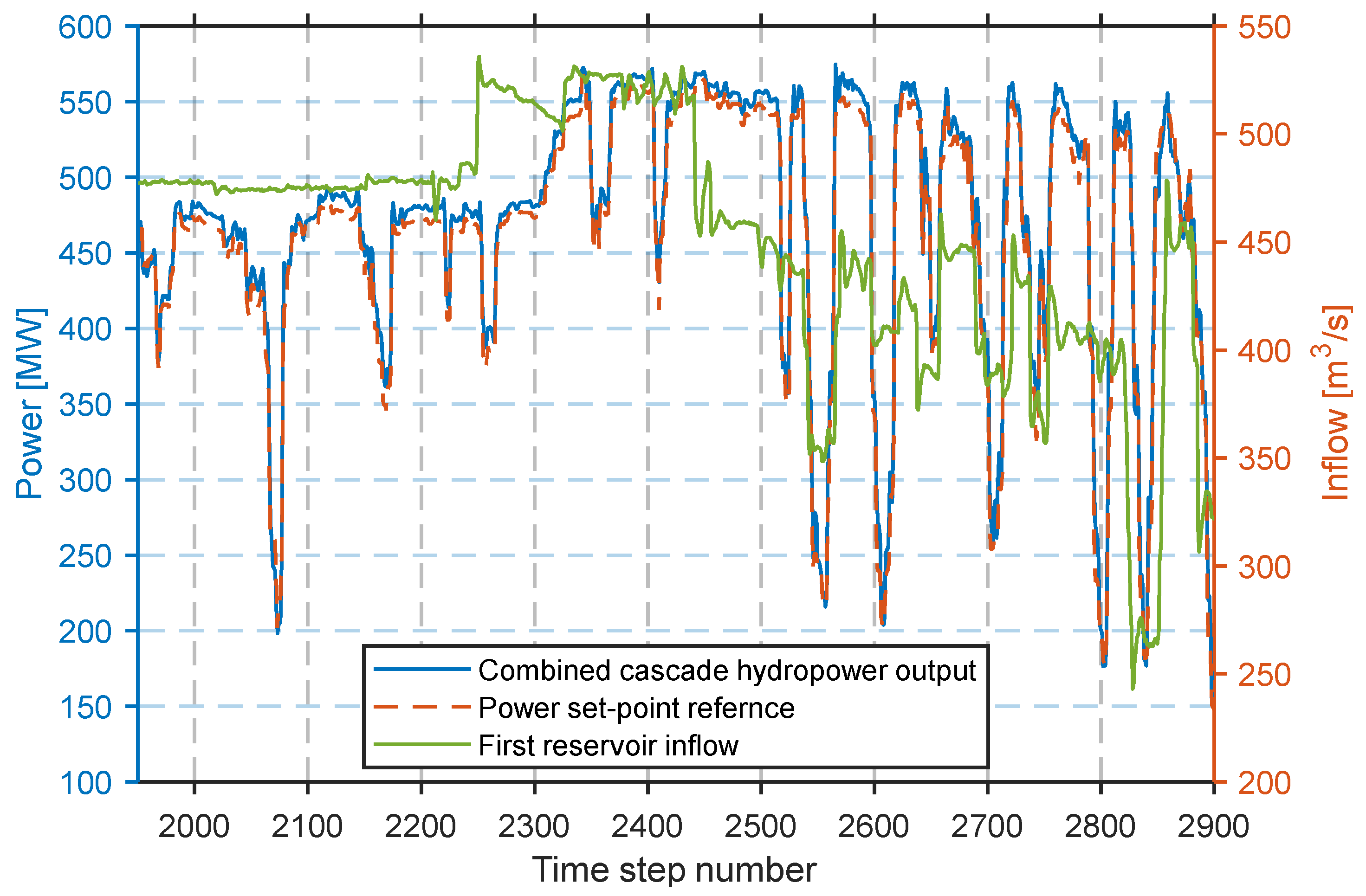
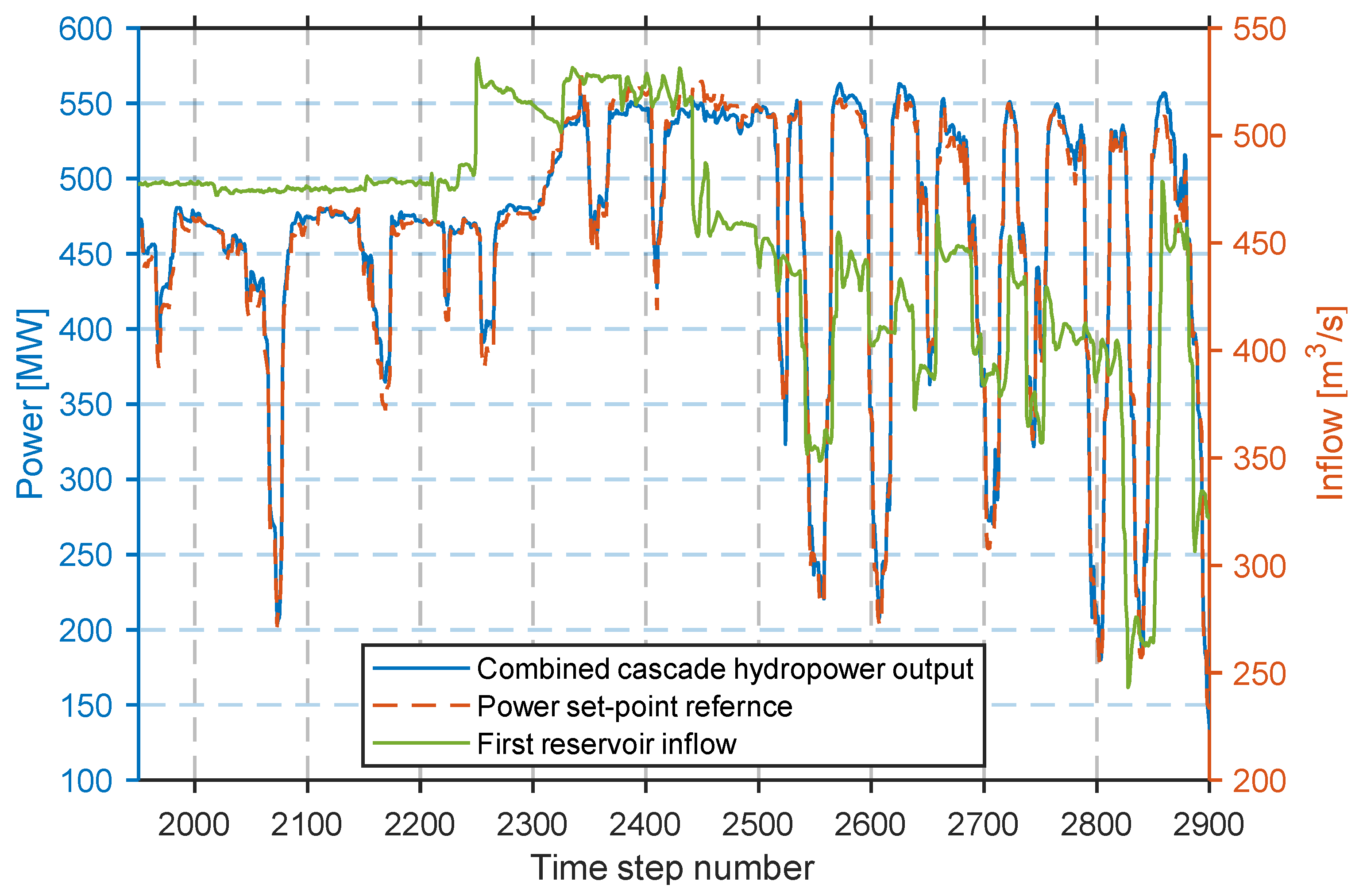
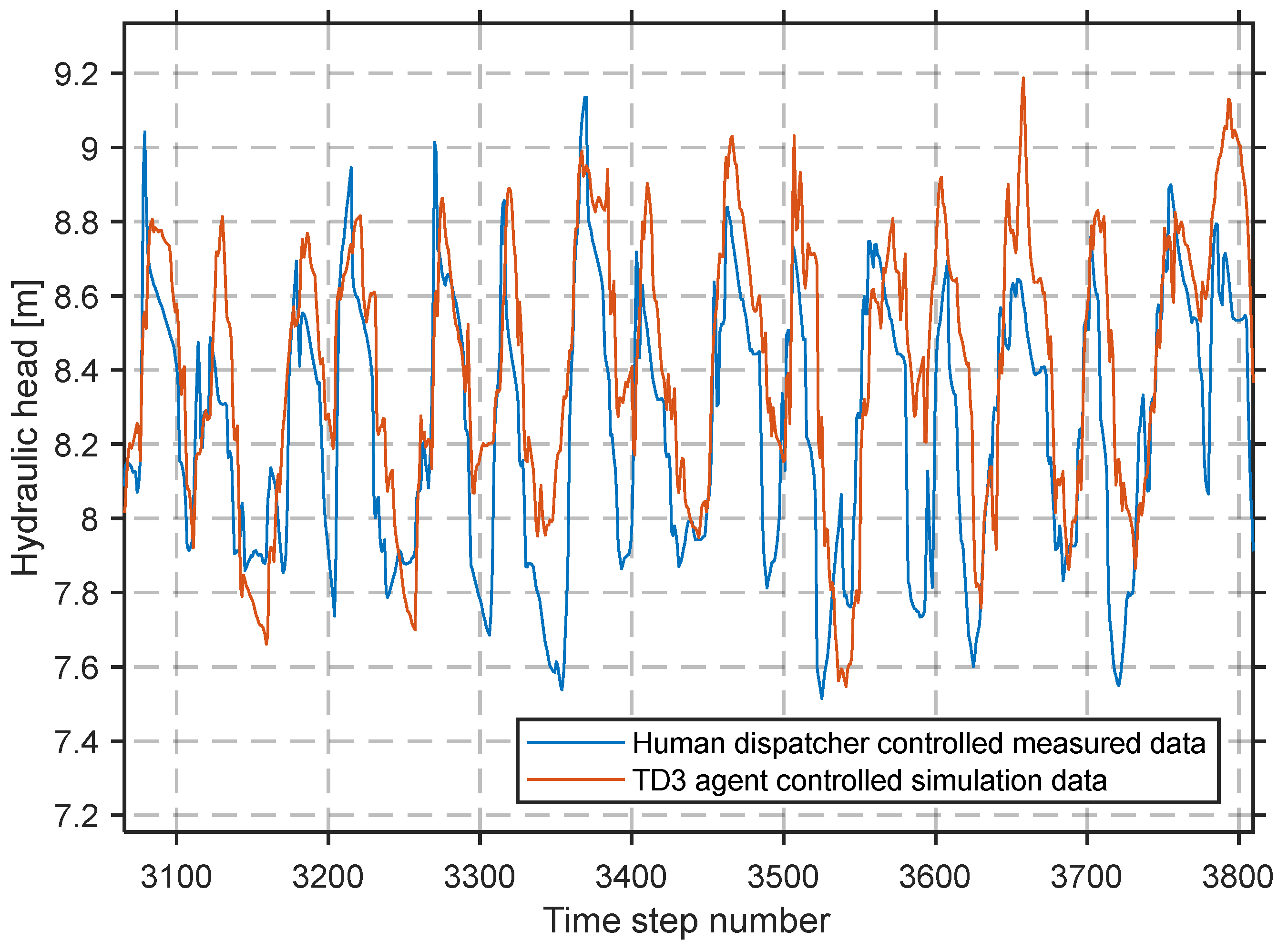
3.5. Comparisons and Benchmarks
- Current and future natural inflows, which give the agent a look-ahead over a chosen horizon. In contrast, we treat original inflows as exogenous.
- Current and future energy prices: This is used to calculate system income.
- Subsystem metrics: Reservoir water volume, turbine flow, power production and number of active turbines. We essentially track very similar metrics in our state representation, except for the number of active turbines.
- Outflow discrepancies: The difference between the agent-chosen outflow and the realized outflow, which exposes the agent to system characteristics. In our work, this is captured implicitly: by including current plant power output in the state, the subsequent state transition informs the agent how its action changed power. These (state, next-state, action, reward) tuples form the basis of RL training.
- Outflow variations: Tracked to flag gate-movement constraint violations. Here, the benefit of a nonlinear formulation is evident, since we enforce hard constraints that the agent cannot violate, making this tracking redundant.
- Past outflows: Similar to our work, they model system delays by recording past outflows and use them as inputs for downstream reservoirs.
- Week number, reservoir storage, weekly inflow, and weekly price: normalized to max storage/price to stabilize learning.
- “Weeks to empty at full capacity”: used to clamp the policy to feasible actions.
4. Discussion
Future Work and Application
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| RL | Reinforcement learning |
| DDPG | Deep deterministic policy gradient |
| TD3 | Twin delayed deep deterministic policy gradient |
| SAC | Soft Actor Critic |
| PPO | Proximal Policy Optimization |
| HPP | Hydropower plants |
| SOP | Standard operating policy |
References
- Statistical Office of the Republic of Slovenia. Energy. SiStat Database. Available online: https://pxweb.stat.si/SiStat/en/Podrocja/index/186/energy#243 (accessed on 28 July 2025).
- Dravske elektrarne Maribor d.o.o. (DEM d.o.o.). Available online: https://www.dem.si/en/ (accessed on 28 July 2025).
- Hamann, A.; Hug, G. Real-time optimization of a hydropower cascade using a linear modeling approach. In Proceedings of the 18th Power Systems Computation Conference (PSCC 2014), Wroclaw, Poland, 18–22 August 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 1–7. [Google Scholar] [CrossRef]
- Catalao, J.P.S.; Mariano, S.J.P.; Mendes, V.M.F.; Ferreira, L.A.F. Scheduling of Head-Sensitive Cascaded Hydro Systems: A Nonlinear Approach. IEEE Trans. Power Syst. 2009, 24, 337–346. [Google Scholar] [CrossRef]
- Arce, A.; Ohishi, T.; Soares, S. Optimal dispatch of generating units of the Itaipu hydroelectric plant. IEEE Trans. Power Syst. 2002, 17, 154–158. [Google Scholar] [CrossRef]
- Resman, M.; Protner, J.; Simic, M.; Herakovic, N. A Five-Step Approach to Planning Data-Driven Digital Twins for Discrete Manufacturing Systems. Appl. Sci. 2021, 11, 3639. [Google Scholar] [CrossRef]
- Faria, R.d.R.; Capron, B.D.O.; Secchi, A.R.; de Souza, M.B., Jr. Where Reinforcement Learning Meets Process Control: Review and Guidelines. Processes 2022, 10, 2311. [Google Scholar] [CrossRef]
- Wu, Y.; Su, C.; Liu, S.; Guo, H.; Sun, Y.; Jiang, Y.; Shao, Q. Optimal Decomposition for the Monthly Contracted Electricity of Cascade Hydropower Plants Considering the Bidding Space in the Day-Ahead Spot Market. Water 2022, 14, 2347. [Google Scholar] [CrossRef]
- Xu, W.; Yin, X.; Zhang, C.; Li, Z. Deep Reinforcement Learning for Cascaded Hydropower Reservoirs Considering Inflow Forecasts. Water Resour. Manag. 2020, 34, 3003–3018. [Google Scholar] [CrossRef]
- Xu, W.; Yin, X.; Li, Z.; Yu, L. Deep Reinforcement Learning for Optimal Hydropower Reservoir Operation. J. Water Resour. Plan. Manag. 2021, 147, 04021045. [Google Scholar] [CrossRef]
- Sadeghi Tabas, S.; Samadi, V. Fill-and-Spill: Deep Reinforcement Learning Policy Gradient Methods for Reservoir Operation Decision and Control. J. Water Resour. Plan. Manag. 2024, 150, 04023034. [Google Scholar] [CrossRef]
- Castro-Freibott, R.; Pereira, M.; Rosa, J.; Pérez-Díaz, J. Deep Reinforcement Learning for Intraday Multireservoir Hydropower Management. Mathematics 2025, 13, 151. [Google Scholar] [CrossRef]
- Tubeuf, C.; Bousquet, Y.; Guillaud, X.; Panciatici, P. Increasing the Flexibility of Hydropower with Reinforcement Learning on a Digital Twin Platform. Energies 2023, 16, 1796. [Google Scholar] [CrossRef]
- Mitjana, F.; Ostfeld, A.; Housh, M. Managing Chance-Constrained Hydropower with Reinforcement Learning and Backoffs. Adv. Water Resour. 2022, 163, 104308. [Google Scholar] [CrossRef]
- Castelletti, A.; Galelli, S.; Restelli, M.; Soncini-Sessa, R. Tree-Based Reinforcement Learning for Optimal Water Reservoir Operation. Water Resour. Res 2010, 46, W09507. [Google Scholar] [CrossRef]
- Riemer-Sørensen, S.; Rosenlund, G.H. Deep Reinforcement Learning for Long Term Hydropower Production Scheduling. arXiv 2020, arXiv:2012.06312. [Google Scholar] [CrossRef]
- Li, X.; Ma, H.; Chen, S.; Xu, Y.; Zeng, X. Improved Reinforcement Learning for Multi-Objective Optimization Operation of Cascade Reservoir System Based on Monotonic Property. Water 2025, 17, 1681. [Google Scholar] [CrossRef]
- Lee, S.; Labadie, J.W. Stochastic Optimization of Multireservoir Systems via Reinforcement Learning. Water Resour. Res. 2007, 43, W11408. [Google Scholar] [CrossRef]
- Ma, X.; Pan, H.; Zheng, Y.; Hang, C.; Wu, X.; Li, L. Short-Term Optimal Scheduling of Pumped-Storage Units via DDPG with AOS-LSTM Flow-Curve Fitting. Water 2025, 17, 1842. [Google Scholar] [CrossRef]
- Rani, D.; Moreira, M.M. Simulation–Optimization Modeling: A Survey and Potential Application in Reservoir Systems Operation. Water Resour. Manag. 2010, 24, 1107–1138. [Google Scholar] [CrossRef]
- Xie, M.; Liu, X.; Cai, H.; Wu, D.; Xu, Y. Research on Typical Market Mode of Regulating Hydropower Stations Participating in Spot Market. Water 2025, 17, 1288. [Google Scholar] [CrossRef]
- Bernardes, J., Jr.; Santos, M.; Abreu, T.; Prado, L., Jr.; Miranda, D.; Julio, R.; Viana, P.; Fonseca, M.; Bortoni, E.; Bastos, G.S. Hydropower Operation Optimization Using Machine Learning: A Systematic Review. AI 2022, 3, 78–99. [Google Scholar] [CrossRef]
- Brezovnik, R. Short Term Optimization of Drava River Hydro Power Plants Operation. Bachelor’s Thesis, University of Maribor, Maribor, Slovenia, 2009. Available online: https://dk.um.si/IzpisGradiva.php?id=9862 (accessed on 2 July 2025).
- Brezovnik, R.; Polajžer, B.; Grčar, B.; Popović, J. Development of a Mathematical Model of a Hydropower-Plant Cascade and Analysis of Production and Power Planning on DEM and SENG: Study Report; Available Upon Request with the Corresponding Author; UM FERI: Maribor, Slovenia, 2011. [Google Scholar]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous Control with Deep Reinforcement Learning. arXiv 2015, arXiv:1509.02971. [Google Scholar] [CrossRef]
- Fujimoto, S.; Hoof, H.; Meger, D. Addressing Function Approximation Error in Actor-Critic Methods. arXiv 2018, arXiv:1802.09477. [Google Scholar] [CrossRef]
- Haarnoja, T.; Zhou, A.; Abbeel, P.; Levine, S. Soft actor-critic: Off-policy maximum entropy deep reinforcement learning with a stochastic actor. arXiv 2018, arXiv:1801.01290. [Google Scholar] [CrossRef]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal Policy Optimization Algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar] [CrossRef]












| Ref. | Authors and Year | Focus Area | RL Method | System Type | Key Contributions/Notes |
|---|---|---|---|---|---|
| [8] | Wu et al. (2022) | Energy market participation optimization | N/A * | Cascaded | Presents a stochastic decomposition model that optimizes monthly contract and day-ahead spot market. |
| [9] | Xu et al. (2020) | Scheduling with inflow forecast | Deep Q-network (DQN) | Cascaded | Uses inflow forecasting for hydropower scheduling; simplified dynamics. |
| [10] | Xu et al. (2021) | Optimal hydropower operation | DQN | Single reservoir | Generalized operation policy learning on simplified discrete models. |
| [11] | Sadeghi Tabas & Samadi (2024) | Fill-and-spill flow control | TD3 + SAC | Single reservoir | Trains policy for flow/spill management on an isolated reservoir. |
| [12] | Castro-Freibott et al. (2025) | Intraday multi-reservoir scheduling | A2C + PPO + SAC | Cascaded | Short-term energy market operation. |
| [13] | Tubeuf et al. (2023) | Enhancing flexibility via Digital Twin | DDPG | Single hydropower plant | Simulation-based control; optimizes for system flexibility, not real dispatch. |
| [14] | Mitjana et al. (2022) | Chance-constrained hydropower operation | Policy gradient method | Multi-reservoir | Addresses uncertainty and safety through backoff margins. |
| [15] | Castelletti et al. (2010) | Optimal water reservoir operation | Fitted Q-iteration | Reservoir | Early fitted Q-iteration method; long-term scheduling focus. |
| [16] | Riemer-Sørensen et al. (2020) | Long-term scheduling of hydropower production—optimizing yearly revenue | SAC | Single reservoir | SAC algorithm can be successfully trained on historical Nordic market data to generate effective long-term release strategies. |
| [17] | Li et al. (2025) | Water availability optimization | Improved reinforcement learning | Multi-reservoir | Increased computation efficiency for optimizing water availability. |
| [18] | Lee & Labadie (2007) | Stochastic multi-reservoir optimization | Q-learning | Multi-reservoir | One of the earliest uses of RL in water systems; focuses on inflow uncertainty. |
| [19] | Ma et al. (2025) | Short-term pumped-storage scheduling | DDPG | Single plant | Uses DDPG for accurate, constraint-aware, water-efficient pumped-storage scheduling. |
| [20] | Rani & Moreira (2010) | Simulation–optimization modelling review | N/A | N/A | Foundational survey; sets the stage for RL and hybrid models. |
| [21] | Xie et al. (2025) | Hydropower plants participation in the spot market | N/A | N/A | Designs spillage management, compensation; separate bidding; long-term supply constraints integrated. |
| [Our work] | Cascade hydropower flow and power operation control | DDPG + TD3 + SAC + PPO | Cascaded | Using RL to approximate the current human dispatcher for simulation and analysis. | |
| Plant | Year Build | Rated Power (Rounded MW) | Reservoir Length (km) | Usable Reservoir Volume m3) | Maximal Turbine Flow |
|---|---|---|---|---|---|
| Dravograd | 1944 | 26 | 10.2 | 1.045 | 420 |
| Vuzenica | 1953 | 56/60 | 11.9 | 1.807 | 550 |
| Vuhred | 1956 | 72 | 13.1 | 2.179 | 297 |
| Ožbalt | 1960 | 73 | 12.7 | 1.400 | 305 |
| Fala | 1918 | 58 | 9.0 | 0.535 | 260 |
| Mariborski Otok | 1948 | 60 | 15.5 | 2.115 | 270 |
| Zlatoličje * | 1969 | 136 | 6.5 + 17 | 0.3600 | 577 |
| Formin * | 1978 | 116 | 7.0 + 8.5 | 4.498 | 548 |
| State Variable | Dimension | Description |
|---|---|---|
| 8 | Usable water volume in each reservoir i at time t. | |
| 8 | Inflow into each reservoir i at time t with inflows for reservoirs 2–8 being delayed to account for water travel time. | |
| 8 | Power output of each powerplant i at time t. | |
| 5 | Dispatch target power set-point for current time step t to time step t + 4. |
| Parameter | Value | Description |
|---|---|---|
| Actor learning rate | 0.00004 | Learning rate of the actor network |
| Critic learning rate | 0.0004 | Learning rate of the critic network |
| Discount factor | 0.99 | Discount factor for future rewards |
| Soft update factor | 0.0002 | Target network update rate |
| Replay buffer size | 1,000,000 | Size of the replay memory buffer |
| Hidden layer 1 (fc1) size | 40 | Number of neurons in the first hidden layer |
| Hidden layer 2 (fc2) size | 40 | Number of neurons in the second hidden layer |
| Hidden layer 3 (fc3) size | 40 | Number of neurons in the third hidden layer |
| Batch size | 64 | Size of mini batches used for training |
| Exploration noise | 0.8 | Added noise for action exploration |
| Exploration decay | 0.999641 | A selected decay of a Gaussian |
| Parameter | Value | Description |
|---|---|---|
| Actor learning rate | 0.00001 | Learning rate of the actor network |
| Critic learning rate | 0.00005 | Learning rate of the critic network |
| Discount factor | 0.99 | Discount factor for future rewards |
| Soft update factor | 0.0004 | Target network update rate |
| Replay buffer size | 1,000,000 | Size of the replay memory buffer |
| Hidden layer 1 (fc1) size | 50 | Number of neurons in the first hidden layer |
| Hidden layer 2 (fc2) size | 50 | Number of neurons in the second hidden layer |
| Hidden layer 3 (fc3) size | 50 | Number of neurons in the third hidden layer |
| Batch size | 254 | Size of mini batches used for training |
| Entropy weight | 2 | Entropy regularization scaling factor |
| Entropy weight learning rate | 0.0003 | Entropy weight parameter update step-size |
| Target entropy | 0 | Desired policy entropy threshold |
| Parameter | Value | Description |
|---|---|---|
| Actor learning rate | 0.0005 | Learning rate of the actor network |
| Critic learning rate | 0.0008 | Learning rate of the critic network |
| Discount factor | 0.99 | Discount factor for future rewards |
| Clip factor | 0.12 | Probability ratio clipping threshold |
| GAE factor | 0.95 | Advantage estimation bias-variance factor |
| Hidden layer 1 (fc1) size | 50 | Number of neurons in the first hidden layer |
| Hidden layer 2 (fc2) size | 50 | Number of neurons in the second hidden layer |
| Hidden layer 3 (fc3) size | 50 | Number of neurons in the third hidden layer |
| Batch size | 548 | Size of mini batches used for training |
| Experience horizon | 10,405 | Rollout length per policy update |
| Number of epochs | 8 | Policy optimization passes per batch |
| Entropy loss weight | 0.02 | Entropy bonus coefficient weight |
| Method | Time Step | Absolute Mean Error | Safety Constraint Violations |
|---|---|---|---|
| Human dispatcher | Real time | 5.8 MW | 14,121 |
| DDPG | 30 min/15 min | 6.38 MW/11.93 MW | 0 |
| TD3 | 15 min | 7.64 MW | 0 |
| SAC | 15 min | 9.06 MW | 0 |
| PPO | 15 min | 8.81 MW | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rot Weiss, E.; Gselman, R.; Polner, R.; Šafarič, R. Cascade Hydropower Plant Operational Dispatch Control Using Deep Reinforcement Learning on a Digital Twin Environment. Energies 2025, 18, 4660. https://doi.org/10.3390/en18174660
Rot Weiss E, Gselman R, Polner R, Šafarič R. Cascade Hydropower Plant Operational Dispatch Control Using Deep Reinforcement Learning on a Digital Twin Environment. Energies. 2025; 18(17):4660. https://doi.org/10.3390/en18174660
Chicago/Turabian StyleRot Weiss, Erik, Robert Gselman, Rudi Polner, and Riko Šafarič. 2025. "Cascade Hydropower Plant Operational Dispatch Control Using Deep Reinforcement Learning on a Digital Twin Environment" Energies 18, no. 17: 4660. https://doi.org/10.3390/en18174660
APA StyleRot Weiss, E., Gselman, R., Polner, R., & Šafarič, R. (2025). Cascade Hydropower Plant Operational Dispatch Control Using Deep Reinforcement Learning on a Digital Twin Environment. Energies, 18(17), 4660. https://doi.org/10.3390/en18174660






