Abstract
As applications like electric vehicles, all-electric ships, and all-electric aircraft continue to evolve, Noise, Vibration, and Harshness (NVH) issues have garnered extensive attention. However, as the core of the power system, permanent magnet synchronous motors (PMSMs) still lack control algorithms that consider vibration problems. Therefore, this paper proposes a model-based predictive vibration suppression algorithm to suppress the PMSM vibration. Firstly, this paper explores the influence of armature currents on vibration by analyzing the vibration characteristics of PMSMs, and proposes a minimum vibration current model. On this basis, according to the torque conditions required for the stable operation of the motor, a model-based predictive vibration suppression algorithm is designed. Finally, the effectiveness of the proposed algorithm is verified through prototype experiments.
1. Introduction
In recent years, with the development of industries such as electric vehicles, society and industry have been placing increasingly higher demands on comfort, reliability, environmental protection, and other aspects. Therefore, the issue of Noise, Vibration and Harshness (NVH) has been raised and has received widespread attention. In systems that primarily rely on electricity as the main energy source, such as electric vehicles or all-electric aircraft, the motor is the most critical source of power. Therefore, the vibration issue of motors, especially the permanent magnet synchronous motors (PMSMs) that are most commonly used in modern servo systems, has become a hot topic of research [1,2,3].
In the field of the PMSM design and manufacturing, there already exist numerous theories and methods for reducing motor vibration. For example, new pole designs were proposed, including the double misaligned pole [4,5], sawtooth skewed pole [6,7], axially varying pole width [8,9], and varying-pole-width structure [10]. However, motor optimization will lead to increased manufacturing costs. Therefore, vibration suppression algorithms suitable for PMSMs have become a hot topic recently.
In PMSM drive systems, the current often contains a large number of harmonics due to various nonlinear factors. These harmonics can easily lead to the increased vibration of the motor. Therefore, many scholars have sought to suppress vibration by mitigating these current harmonics [11,12,13]. Among them, refs. [11,12] effectively suppressed current harmonics and torque ripple using proportional–integral resonant controllers and two-degree-of-freedom resonant controllers, which also reduced motor vibration. Ref. [13] employed a repetitive controller to suppress current harmonics, also contributing to the reduction in motor vibration.
Although harmonics caused by nonlinear factors can increase vibration, injecting specific current harmonics into the motor in accordance with certain patterns can also achieve the effect of vibration suppression [14,15,16]. For example, reference [15] employs a neural network algorithm to calculate in real time the current harmonics required for vibration suppression and injects them into the motor, effectively suppressing the even-order frequency vibrations of the motor. Ref. [16] suppressed the vibration through flux-linkage injection. The aforementioned algorithms all suffer from issues such as system complexity and high computational load. In contrast, ref. [17] proposes a d-axis current injection algorithm that is structurally simple yet effective in vibration suppression. However, during the design process, ref. [17] overlooked the saliency of the PMSM and assumed that the d-axis current had no effect on the torque or that the effect was negligible. In reality, for interior permanent magnet motors, the injection of d-axis current harmonics can cause significant torque ripple. Therefore, this paper proposes a model-based predictive vibration suppression algorithm, which is combined with the torque model. This algorithm suppresses motor vibration while reducing the negative impact on the motor torque.
2. Influence of Armature Current on Vibration
The vibration of PMSMs is mainly caused by radial electromagnetic force (REMF). According to Maxwell stress tensor method, the REMF can be simplified and expressed as
where pr(θm, t) is the electromagnetic force density; Br(θm, t) is the radial air-gap magnetic flux density; μ0 is the air permeability; and θm is the mechanical angle.
The Br(θm, t) consists of the permanent magnet(PM) magnetic flux density BPM(θm, t) and the armature magnetic flux density BAM(θm, t). Its expression is [18]
For PMSMs using field-oriented control (FOC), the armature magnetic flux density can be decomposed into two parts: the magnetic flux density generated by the d-axis current and the magnetic flux density generated by the q-axis current. At this point, Equation (2) can be rewritten as
where the Bad(θm, t) and Baq(θm, t) are the magnetic flux densities generated by the d-axis current and q-axis current.
Only the fundamental current is considered, the terms in (3) can be expressed as [18]
According [18,19], taking a 10-pole, 12-slot PMSM as an example, the REMF generated by the interaction between the 5th and 7th armature field harmonics and the permanent magnet fundamental field has the greatest impact on the vibration of the motor. When considering only these harmonics, (3) can be rewritten as
where the BPM1 is the amplitude of the PM fundamental magnetic field. The Bad5 and Baq5 represent the amplitudes of the 5th armature magnetic fields. The Bad7 and Baq7 represent the amplitudes of the 7th armature magnetic fields.
Substituting (5) into (1) and considering only the alternating components, the following can be obtained:
According to existing research, the influence of REMF on vibration is approximately inversely proportional to its spatial order to the fourth power [17]. The last two terms in (6) have a spatial order of 10, which is much higher than that of the first two terms, and thus can be neglected. At this point, (6) can be rewritten as
Since the REMF generated by the armature is small, it is neglected here. The equation in (13) can be rewritten as
According to (8), to minimum the REMF, the following condition must be met:
Since both Bad7 and Bad7 are magnetic fields generated by current, their amplitudes can be considered proportional to the current amplitudes. Therefore, (9) can be rewritten as
A vibration suppression algorithm based on d-axis current injection can be designed according to (10) [18]. However, the saliency of the PMSM and the coupling between d-axis and q-axis currents can easily lead to increased torque ripple when d-axis current is directly injected into the motor. This affects the torque performance and is often unacceptable in many applications. To address this issue, this paper proposes a model-based predictive vibration suppression algorithm, which integrates the relationships between motor current, vibration, and torque to achieve vibration suppression without negatively affecting the motor torque.
3. Model-Based Predictive Vibration Suppression Algorithm
The core of model predictive control algorithm lies in constructing a dynamic optimization strategy to achieve the precise tracking of system variables to the desired trajectory through real-time decision-making. Its design essence is to predict the dynamic response of the controlled object through mathematical modeling and to select the optimal control input based on the rolling optimization principle, thereby minimizing the deviation between the system output and the desired trajectory. In the control of permanent magnet linear motors, this method discretizes the model to predict the impact of different control strategies on future states.
The drive circuit composed of a three-phase inverter has a total of 8 combinations of stator voltages, and the corresponding inverter switching states are shown in Table 1. Different switching combinations correspond to different voltage vectors. After coordinate transformation, these can be converted into the d-q axis stator voltage output components. At this point, the finite set of d-q axis voltage outputs is
where Vi(n) is the Iinverter switching state.

Table 1.
Inverter switching states.
The voltage equations of a three-phase PMSM in the synchronous rotating coordinate system can be expressed as
where ud and uq represent the d-axis and q-axis voltages, respectively. Ld and Lq represent the d-axis and q-axis inductances, respectively. ψf represents the PM flux linkage. Rs represents the stator resistance.
Rearranging (12), it can be rewritten as
Using first-order Euler discretization on (13), the following can be obtained:
where the Ts is the sample time of current loop. The id(k + 1) and iq(k + 1) represent the d-axis and q-axis currents at time k + 1, respectively. The id(k) and iq(k) represent the d-axis and q-axis currents at time k, respectively.
At the same time, the torque equation of the motor can be expressed as
Substituting (10) into (15), the following can be obtained:
The cost function for constructing the model predictive algorithm is
where Tref represents the desired torque. The λ1 and λ2 are the weighting factors, respectively.
By comparing the cost function for each of the 8 sets of finite d-q axis voltage combinations, the switching state corresponding to the minimum the cost function is selected as the optimal voltage vector switching state.
Combining (10) with (17), the flowchart and the system block diagram of the proposed algorithm are shown in Figure 1 and Figure 2, respectively.

Figure 1.
The flowchart of the proposed model-based predictive vibration suppression algorithm.
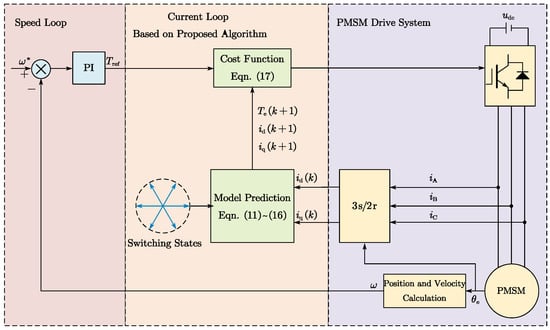
Figure 2.
The system block diagram of the proposed model-based predictive vibration suppression algorithm.
Figure 1 shows the flowchart of the proposed algorithm. It can be seen from Figure 1 that the calculation process of the algorithm is divided into five steps. First, the voltages under different switching states need to be calculated. Second, the current at the next moment is estimated using the obtained voltages. Third, the predicted torque is estimated using this predicted current. Next, the predicted torque is compared with the given torque output by the speed loop to calculate the cost function. Finally, the set of voltage vect. Figure 2 is the system block diagram of the proposed algorithm, which includes three main parts: the speed loop, the current loop, and the drive system. Among them, the proposed algorithm is applied to the current loop to suppress motor vibration by controlling the armature current.
4. Experiment Verification
To verify the proposed algorithm, a 10-pole 12-slot PMSM was used for experiment. Due to the limitations of the experimental conditions, the motor selected in this paper is still a surface-mounted PMSM. However, according to the measured data, the d-axis and q-axis inductances of the prototype motor used are not equal. Specifically, the d-axis inductance is 0.38 mH, while the q-axis inductance is 0.43 mH, resulting in a saliency ratio of 1.13.
The accelerometer is used to measure vibration. The parameters of the PMSM are listed in Table 2, and the test platform is shown in Figure 3.

Table 2.
The motor drive platform parameters.

Figure 3.
Experimental platform.
4.1. Experimental at 600 r·min−1
The experiment was performed at a speed of 600 r·min−1 under rated load conditions. The results of the model-based predictive vibration suppression algorithm are depicted in Figure 4, Figure 5, Figure 6 and Figure 7.
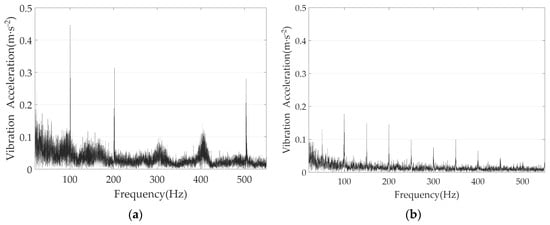
Figure 4.
The vibration acceleration at 600 r·min−1: (a) without and (b) with the proposed algorithm.
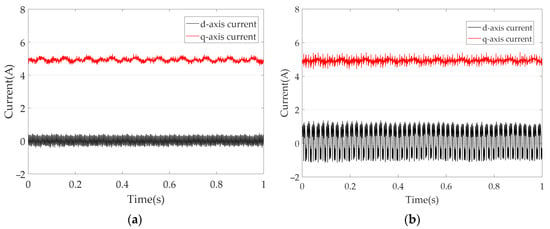
Figure 5.
The currents at 600 r·min−1: (a) without and (b) with the proposed algorithm.
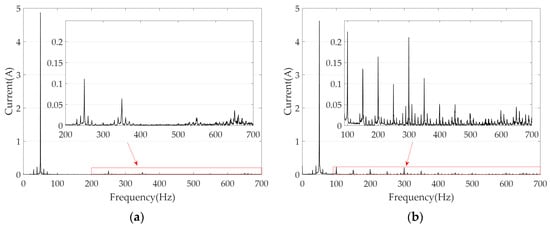
Figure 6.
The A-phase current harmonics at 600 r·min−1: (a) without and (b) with the proposed algorithm.
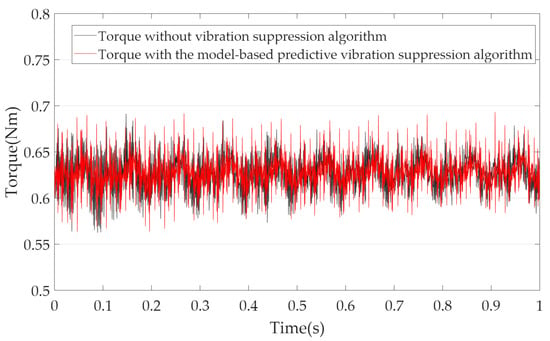
Figure 7.
The torque at 600 r·min−1.
Figure 4 illustrates the comparison of vibration acceleration harmonics. When combined with Table 3, it is evident that without the proposed algorithm, the vibration is predominantly concentrated at even multiples of the fundamental frequency. Specifically, the second harmonic exhibits the highest vibration acceleration, with an amplitude of 0.45 m/s2. In Table 3, the hyphen “–” indicates a amplitude so minimal that it can be disregarded.

Table 3.
The vibration acceleration and A-phase current harmonic, compared for cases with and without the proposed algorithm at 600 r·min−1.
As depicted in Figure 4b, the application of the proposed algorithm results in the emergence of numerous odd-order harmonics in the vibration acceleration. However, the overall amplitude is substantially diminished. The highest vibration acceleration is reduced to 0.18 m/s2, representing a 60.00% decrease.
Without vibration suppression algorithms, the motor current is as shown in Figure 5, where the d-axis current varies between −0.62 A and 0.57 A, and the q-axis current varies between 4.41 A and 5.43 A. In contrast, Figure 5b displays the currents with the proposed algorithm. Here, the d-axis current varies between −1.21 A to 1.35 A, while the q-axis current varies between 4.41 A and 5.40 A. It is clear that the d-axis current transitions from small-range to large-range fluctuations, aligning with the expectation of (10).
The harmonic characteristics of the A phase current are shown in Figure 6. Without the vibration suppression algorithm, the current harmonics are dominated by the 5th, 7th, 11th, and 13th orders. After applying the proposed algorithm, all these harmonics increase; these harmonics serve to suppress vibration.
As seen in Figure 7, the torque ripple remains within the range of 0.56 Nm to 0.69 Nm both before and after the implementation of the proposed algorithm. This suggests that despite introducing current harmonics into the PMSM, the proposed algorithm does not adversely affect the motor torque. The reason is that the algorithm simultaneously injects d-axis current and adjusts the q-axis current, enabling the torque ripple generated by the harmonics to offset each other.
The aforementioned experimental results indicate that the proposed algorithm effectively mitigate even-order vibrations. Although the algorithm still introduces odd-order vibrations into the PMSM, its ability to suppress the vibration acceleration peak remains valuable for enhancing the service life, stability, and safety of the PMSM.
4.2. Experimental Results at 1500 r·min−1
The test was carried out at the rated speed and rated load; Figure 8, Figure 9, Figure 10 and Figure 11 present the results obtained with the proposed algorithm.
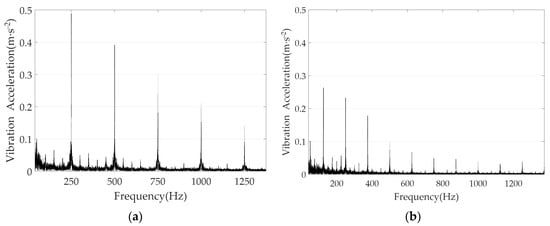
Figure 8.
The vibration acceleration at 1500 r·min−1: (a) without and (b) with the proposed algorithm.
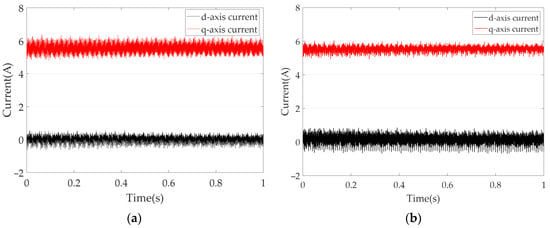
Figure 9.
The d-axis and q-axis currents at 1500 r·min−1: (a) without and (b) with the proposed algorithm.
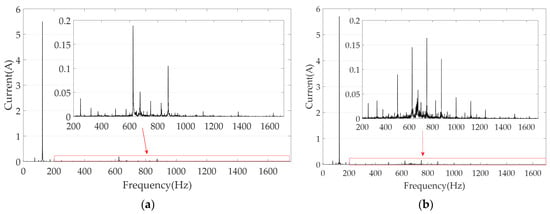
Figure 10.
The amplitudes of A-phase current harmonics at 1500 r·min−1: (a) without and (b) with the proposed algorithm.
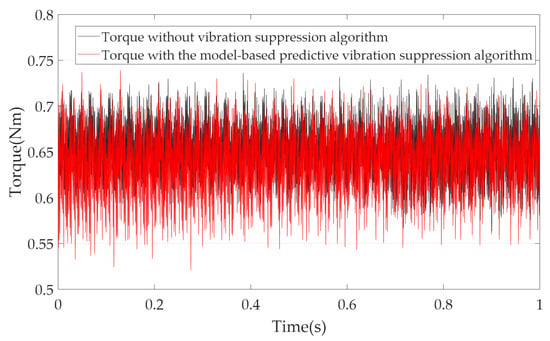
Figure 11.
The torque at 1500 r·min−1.
Figure 8 displays the amplitudes of the vibration acceleration harmonics. When analyzed alongside Table 4, it is evident that without the proposed algorithm, the vibration acceleration is primarily concentrated at even multiples of the fundamental frequency, with the highest amplitude reaching 0.49 m/s2.

Table 4.
The vibration acceleration and A-phase current harmonic, compared for cases with and without the proposed algorithm at 1500 r·min−1.
Upon implementing the proposed algorithm, not only are the even harmonics present, but numerous odd harmonics also emerge. Despite this, the peak amplitude is substantially reduced. The highest vibration acceleration observed is 0.26 m/s2, marking a reduction of 49.94%.
Figure 9 displays the d-axis and q-axis currents. In Figure 9a, the d-axis current fluctuates between −0.66 A and 0.58 A, while the q-axis current spans from 4.80 A to 6.38 A. In Figure 9b, the d-axis current fluctuates between −0.69 A and 0.88 A, and the q-axis current ranges from 4.93 A to 6.04 A. At this stage, the motor operates under rated torque and speed conditions, with the q-axis current nearing its rated value. As indicated by (10), the d-axis current exhibits minimal variation under these conditions. Consequently, its fluctuations do not increase significantly compared to those at 600 r·min−1, which also reduces the effectiveness of vibration suppression.
The harmonics of the A-phase current, obtained through Fourier decomposition, are presented in Figure 10 and Table 4. As Table 4 shows, despite the presence of numerous even-order harmonics, the 5th and 7th harmonics do not increase significantly.
Figure 11 shows that, absent the proposed algorithm, torque oscillates from 0.56 Nm to 0.74 Nm, yielding a torque ripple ratio of 13.8%. When the proposed algorithm is enabled, torque varies between 0.53 Nm and 0.74 Nm, marginally raising the ripple ratio to 16.53%.
Since the rated torque of the prototype motor is only 0.65 Nm, even a small torque ripple may lead to a significant increase in the torque ripple ratio. Although the torque ripple ratio increased by 2.73%, the absolute value of the torque fluctuation only increased by 0.03 Nm.
The experimental outcomes reveal that even though the variation range of the d-axis current is quite limited under the rated operating conditions of the motor, the proposed algorithm is still capable of achieving a certain level of attenuation for even-order vibrations.
5. Conclusions
This paper proposes a model-based predictive vibration suppression algorithm that can effectively suppress even-order frequency vibrations of the PMSM. Experimental results confirm that the proposed algorithm effectively suppresses the peak vibration acceleration across various speeds. Specific reductions of 60.00% and 49.94% were observed at 600 r·min−1 and 1500 r·min−1, respectively.
Despite the introduction of additional current harmonics, the proposed algorithm ensures that the torque ripple remains within acceptable limits. This is achieved by simultaneously injecting d-axis current and adjusting q-axis current, which allows the torque ripple generated by the harmonics to cancel each other out. This feature is particularly important for maintaining the stability and reliability of the motor system.
In conclusion, the proposed model-based predictive vibration suppression algorithm offers a robust and effective solution for reducing vibrations in PMSMs. It enhances the comfort and reliability of the drive systems.
Based on this paper, the proposed model-based predictive vibration suppression algorithm can be further optimized to address its high level of dependency on parameters and computational complexity. Also, exploring its application in various motor types and industrial settings is another valuable research direction.
Author Contributions
Methodology, S.M.; Software, X.H.; Formal analysis, B.Z.; Investigation, G.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by [Liaoning Provincial Education Department] grant number [LJ222411632066]. And The APC was funded by [Liaoning Provincial Education Department].
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zhang, W.; Cheng, S.; Zhu, P.; Liu, Y.; Zou, J. Synchronized Carrier-Wave and High-Frequency Square-Wave Periodic Modulation Strategy for Acoustic Noise Reduction in Sensorless PMSM Drives. Energies 2025, 18, 2729. [Google Scholar] [CrossRef]
- Wang, S.; Hong, J.; Sun, Y.; Zheng, Z.; Cao, H. Filling Force Valley with Interpoles for Pole-Frequency Vibration Reduction in Surface-Mounted PM Synchronous Machines. IEEE Trans. Ind. Electron. 2019, 67, 6709–6720. [Google Scholar] [CrossRef]
- Zhu, Z.; Xia, Z.; Wu, L.; Jewell, G.W. Analytical Modeling and Finite-Element Computation of Radial Vibration Force in Fractional-Slot Permanent-Magnet Brushless Machines. IEEE Trans. Ind. Appl. 2010, 46, 1908–1918. [Google Scholar] [CrossRef]
- Yang, Z.; Wang, S.; Hong, J.; Liu, C. Vibration Reduction by Segmented Continuous Variable Width Pole for Rotating Armature Permanent Magnet Motors. IEEE Trans. Ind. Appl. 2021, 57, 2381–4802. [Google Scholar] [CrossRef]
- Hong, J.; Wang, S.; Sun, Y.; Sun, X.; Cao, H. Piecewise Stagger Poles with Continuous Skew Edge for Vibration Reduction in Surface-Mounted PM Synchronous Machines. IEEE Trans. Ind. Electron. 2020, 68, 8498–8506. [Google Scholar] [CrossRef]
- Wang, S.; Yang, Z.; Liu, C. Vibration Reduction Characteristics of Permanent Magnet DC Motors with Sawtooth Edge Poles. IEEE Trans. Energy Convers. 2021, 36, 737–745. [Google Scholar] [CrossRef]
- Wang, S.; Hong, J.; Sun, Y.; Cao, H. Effect Comparison of Zigzag Skew PM Pole and Straight Skew Slot for Vibration Mitigation of PM Brush DC Motors. IEEE Trans. Ind. Electron. 2019, 67, 4752–4761. [Google Scholar] [CrossRef]
- Yang, Z.; Wang, S.; Sun, Y.; Cao, H. Vibration Reduction by Magnetic Slot Wedge for Rotating Armature Permanent Magnet Motors. IEEE Trans. Ind. Appl. 2020, 56, 4882–4888. [Google Scholar] [CrossRef]
- Wang, S.; Hong, J.; Sun, Y.; Cao, H. Analysis and Reduction of Electromagnetic Vibration of PM Brush DC Motors. IEEE Trans. Ind. Appl. 2019, 55, 4605–4612. [Google Scholar] [CrossRef]
- Hong, J.; Wang, S.; Sun, Y.; Cao, H. An Effective Method with Copper Ring for Vibration Reduction in Permanent Magnet Brush DC Motors. IEEE Trans. Magn. 2018, 54, 1–5. [Google Scholar] [CrossRef]
- Chen, L.; Chen, M.; Li, B.; Sun, X.; Jiang, F. Harmonic Current Suppression of Dual Three-Phase Permanent Magnet Synchronous Motor with Improved Proportional-Integral Resonant Controller. Energies 2025, 18, 1340. [Google Scholar] [CrossRef]
- Huang, M.; Deng, Y.; Li, H.; Liu, J.; Shao, M.; Fei, Q. Torque Ripple Suppression of PMSM Based on Robust Two Degrees-of-Freedom Resonant Controller. Energies 2021, 14, 1015. [Google Scholar] [CrossRef]
- Xu, J.; Wei, Z.; Wang, S. Active Disturbance Rejection Repetitive Control for Current Harmonic Suppression of PMSM. IEEE Trans. Power Electron. 2023, 38, 14423–14437. [Google Scholar] [CrossRef]
- Wu, Z.; Yang, Z.; Ding, K.; He, G. Transfer mechanism analysis of injected voltage harmonic and its effect on current harmonic raegulation in FOC PMSM. IEEE Trans. Power Electron. 2022, 37, 820–829. [Google Scholar] [CrossRef]
- Kang, L.; Xia, J.; Su, H.; Li, Z.; Liu, S. Online Control Strategy for Radial Vibration Suppression of PMSM by Multiharmonic Current Injection Method. IEEE Trans. Ind. Electron. 2022, 69, 8692–8704. [Google Scholar] [CrossRef]
- Harries, M.; Woerndle, A.; De Doncker, R.W. Low Vibrations and Improved NVH in Permanent Magnet Synchronous Machines Due to Injection of Flux-Linkage Harmonics. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 1649–1657. [Google Scholar] [CrossRef]
- Wang, H.; Han, F.; Zhang, B.; Zhao, G. Vibration Suppression Algorithm for Electromechanical Equipment in Distributed Energy Supply Systems. Energies 2025, 18, 3757. [Google Scholar] [CrossRef]
- Wang, S.; Hong, J.; Sun, Y.; Cao, H. Analysis of Zeroth-Mode Slot Frequency Vibration of Integer Slot Permanent-Magnet Synchronous Motors. IEEE Trans. Ind. Electron. 2019, 67, 2954–2964. [Google Scholar] [CrossRef]
- Chen, P.; Wang, D.; Wang, B.; Li, J.; Xu, C.; Wang, X. Torque Ripple and Electromagnetic Vibration Suppression in Permanent Magnet Synchronous Motor Using Segmented Rotor with Different Pole Widths. IEEE transactions on Magnetics 2022, 58, 1–5. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).