Abstract
Within the energy sector, the potential to effectively harness the considerable energy present in gas turbine waste heat via an organic Rankine cycle (ORC) could markedly improve overall energy efficiency. This investigation centers on a printed-circuit heat exchanger (PCHE) utilizing cyclopentane as the working fluid. The study employs a combination of experimental techniques and computational fluid dynamics (CFD) simulations to conduct an in-depth analysis of the PCHE’s performance, leading to the successful development of a highly accurate heat-transfer correlation. A thorough comparison of experimental and simulation data is carried out to examine the temperature and pressure distributions within the heat exchanger. The maximum deviation between experimental and correlation-estimated data is within 20% (hot fluid: 15%; cold fluid: 18%). These findings offer essential theoretical insights and practical guidance for optimizing and ensuring the stable operation of waste-heat recovery systems.
1. Introduction
Amidst the escalating global energy demand and the intensifying emphasis on environmental stewardship, the enhancement of energy utilization efficiency has emerged as a pivotal concern across the international community [1]. A significant proportion of energy within industrial processes is dissipated as waste heat, representing a substantial yet underutilized resource [2]. Notably, high-temperature heat sources, exemplified by gas turbines, often see their waste heat inadequately harnessed. Empirical studies indicate that nearly half of the energy consumed in industrial applications is lost as heat, with the majority of this thermal waste originating from high-temperature machinery such as gas turbines and internal combustion engines. This underscores the critical need for innovative strategies to capture and repurpose this wasted thermal energy, thereby fostering both economic and environmental sustainability [3,4].
A key obstacle in waste-heat recovery lies in the efficient extraction of thermal energy from low-temperature heat sources. Conventional waste-heat recovery methods, including traditional heat exchangers and thermal storage systems, often exhibit limited effectiveness when dealing with low-temperature heat, resulting in suboptimal recovery efficiencies [5]. Given these limitations, there is a pressing need to innovate and develop advanced technologies capable of efficiently capturing and utilizing low-temperature waste heat. In this context, the organic Rankine cycle (ORC) has emerged as a significant technological advancement in recent years. Its ability to effectively manage low-temperature waste heat has positioned it as a vital solution for enhancing waste-heat recovery processes.
The organic Rankine cycle (ORC) technology leverages low-boiling-point organic working fluids to transform low-temperature waste heat into usable mechanical or electrical energy through a series of thermodynamic processes, including evaporation, expansion, and condensation [6,7]. This unique capability allows ORC systems to tap into a broad spectrum of low-temperature heat sources, such as industrial waste heat, geothermal resources, and solar thermal energy [8]. Despite its significant potential for enhancing energy recovery, ORC technology still faces several critical challenges. These include the selection of optimal working fluids, the design of efficient heat exchangers, and the overall optimization of system performance to maximize energy conversion efficiency and economic viability.
The choice of working fluid is a pivotal factor in optimizing the performance of organic Rankine cycle (ORC) systems. Historically, traditional ORC working fluids such as R-245fa and R-134a have been extensively utilized, primarily due to their favorable thermodynamic characteristics. However, these substances are associated with high global warming potential (GWP), prompting researchers to seek more environmentally benign alternatives [9].
Cyclopentane has emerged as a leading contender for waste-heat recovery applications [10]. Its low boiling point of 49 °C, combined with relatively high thermal efficiency and minimal GWP, makes it an attractive option. As an organic working fluid, cyclopentane exhibits robust thermodynamic properties that are particularly well suited to low-temperature waste-heat recovery scenarios [11]. Empirical research indicates that ORC systems utilizing cyclopentane can achieve performance levels comparable to those of traditional working fluids, and in certain low-temperature applications, cyclopentane-driven ORC systems may even outperform their conventional counterparts. This suggests that cyclopentane holds significant promise for advancing sustainable and efficient waste-heat recovery technologies [12,13].
As waste-heat recovery technologies continue to evolve, the printed-circuit heat exchanger (PCHE) has gained widespread adoption in organic Rankine cycle (ORC) systems. This is largely attributed to its compact footprint, superior heat-transfer capabilities, and exceptional high-pressure resistance. The primary strength of the PCHE is its micro-channel architecture, which features a large surface area-to-volume ratio. This design significantly enhances heat exchange efficiency by maximizing the contact area between fluids. Additionally, the compact nature of the PCHE makes it particularly well suited for applications where space is constrained, such as in industrial waste-heat recovery systems [14,15]. In recent years, the integration of PCHEs into ORC systems has garnered significant attention, especially regarding their performance in low-temperature waste-heat recovery scenarios. The ability of the PCHE to efficiently manage heat transfer in these applications has positioned it as a critical component for optimizing the overall efficiency and feasibility of ORC-based waste-heat recovery solutions.
Empirical studies have demonstrated that the heat-exchange performance of printed-circuit heat exchangers (PCHEs) in organic Rankine cycle (ORC) systems markedly surpasses that of conventional shell-and-tube heat exchangers. For instance, research by [16] indicates that PCHEs not only enhance heat-transfer efficiency but also significantly reduce the overall system volume. This is particularly advantageous in gas turbine waste-heat recovery applications, where PCHEs exhibit superior heat recovery efficiency compared to traditional heat exchangers. Furthermore, Zhang et al. [17] highlight that PCHEs excel in high-temperature and high-pressure environments, making them highly suitable for ORC systems utilizing high-pressure working fluids. Their findings suggest that the unique design and material properties of PCHEs enable them to maintain high performance under demanding operating conditions, thereby contributing to the overall effectiveness and reliability of waste-heat recovery systems.
Despite the numerous benefits of printed-circuit heat exchangers (PCHEs), their design and application still encounter certain challenges that need to be addressed. Issues such as non-uniform flow distribution, elevated flow resistance, and the complex interplay between micro-channel design and heat-transfer efficiency are critical areas that require further in-depth research and optimization [18,19]. For instance, Liang et al. [20] conducted a comprehensive study on the micro-channel geometry of PCHEs and elucidated how different design configurations impact heat exchange efficiency and pressure drops. They highlighted that rational optimization of the micro-channel structure can significantly enhance the overall performance of PCHEs in organic Rankine cycle (ORC) systems, thereby improving their applicability and effectiveness in waste-heat recovery applications.
Moreover, the performance of printed-circuit heat exchangers (PCHEs) in organic Rankine cycle (ORC) systems utilizing cyclopentane as the working fluid has emerged as a focal point of contemporary research. Cyclopentane, characterized by its low boiling point and minimal global warming potential (GWP), represents an environmentally benign and thermodynamically efficient choice for ORC applications [14,21]. However, its relatively high viscosity and low thermal conductivity introduce additional complexities in the design of PCHEs. These properties necessitate the use of advanced computational tools, such as computational fluid dynamics (CFD) simulations, to conduct thorough analyses of fluid flow and heat-transfer characteristics within the heat exchanger [18]. Such analyses are crucial for optimizing the design of PCHEs to ensure effective heat recovery and overall system performance when using cyclopentane as the working fluid.
Despite extensive research on the application of printed-circuit heat exchangers (PCHEs) in organic Rankine cycle (ORC) systems, several gaps and limitations remain in the current body of literature. Firstly, the majority of existing studies concentrate on assessing the heat exchange performance and analyzing the thermodynamic properties of PCHEs. However, relatively limited research has been conducted on the long-term performance and stability of PCHEs under real-world operating conditions, particularly in high-pressure and high-flow-rate scenarios [22]. This gap in knowledge restricts the comprehensive understanding of PCHE durability and reliability in practical applications. Secondly, most studies to date have focused on traditional working fluids such as R-245fa and R-134a. The utilization of low-GWP (global warming potential) working fluids like cyclopentane is still in its nascent stages of investigation. Specifically, when cyclopentane is used in conjunction with PCHEs, there is a notable deficiency in detailed analyses of its fluid flow and heat-transfer characteristics [23,24]. This lack of in-depth research hampers the optimization of PCHE design and system performance when employing environmentally friendly working fluids, thereby limiting the full potential of sustainable waste-heat recovery solutions.
The research on the optimized design of printed-circuit heat exchangers (PCHEs) in organic Rankine cycle (ORC) systems also exhibits notable deficiencies. While numerous computational fluid dynamics (CFD)-based simulation studies have explored the impact of various micro-channel geometries on heat-transfer performance, a significant gap persists in practical applications. Specifically, there is a lack of systematic research on how to integrate the design of micro-channel structures with particular working fluids, such as cyclopentane, in order to achieve maximum heat exchange efficiency [25,26]. This gap highlights the need for more comprehensive and application-oriented design strategies. Moreover, optimizing the design of PCHEs under complex operating conditions, particularly in high-temperature and high-pressure environments, remains a crucial area where current research falls short [27]. Addressing this gap is essential for enhancing the overall performance, reliability, and economic viability of ORC systems, especially when employing advanced working fluids with unique thermodynamic properties.
This study is dedicated to an in-depth investigation of the heat exchange performance of printed-circuit heat exchangers (PCHEs) with cyclopentane as the working fluid in organic Rankine cycle (ORC) systems, employing both experimental and computational fluid dynamics (CFD) simulation methodologies. The specific research objectives are outlined as follows.
We conducted experimental studies to assess the heat-exchange efficiency, pressure drops, and flow characteristics of PCHEs when utilizing cyclopentane as the working fluid. This involved setting up a test rig to measure key performance indicators under controlled conditions, providing empirical data on the operational behavior of the PCHE. Utilize the CFD simulation software ANYSIS Fluent 19.2 to model the temperature and pressure fields within the PCHE. This analysis focused on understanding how the flow characteristics of cyclopentane influence the heat-exchange process, offering insights into fluid dynamics and thermal behavior at a detailed level. We integrated experimental and simulation data to develop high-precision heat-transfer correlations tailored to PCHEs. These correlations will serve as a theoretical foundation for the design and optimization of ORC systems, enhancing the accuracy and reliability of performance predictions.
Firstly, this study innovatively combined experimental and CFD simulation approaches to thoroughly examine the heat-transfer performance of PCHEs when using cyclopentane as the working fluid. This integrated methodology addresses the existing research gap in the combined application of low-GWP working fluids and PCHEs, contributing novel insights to the field. Secondly, the derivation of high-precision heat-transfer correlations provides robust theoretical support for optimizing PCHE design in ORC systems. This is particularly significant, given the underexplored potential of PCHEs in high-temperature and high-pressure applications, in which their performance and reliability are critical for maximizing energy recovery efficiency.
2. Theory and Methods
2.1. Thermodynamic Properties of Cyclopentane as a Working Fluid
The thermodynamic characteristics of cyclopentane play a vital role in determining the efficiency and operational performance of the heat exchanger. As depicted in Figure 1, the density, thermal conductivity, viscosity, and specific heat capacity of gaseous cyclopentane exhibit distinct variations across different temperatures. Similarly, Figure 2 illustrates the corresponding changes in these thermodynamic properties for liquid cyclopentane. A notable observation from these figures is the substantial difference in density between the liquid and gaseous phases of cyclopentane. Specifically, at a temperature of 290 K, the density of liquid cyclopentane is approximately 740 kg/m3, whereas the density of gaseous cyclopentane is significantly lower, at around 2.5 kg/m3. Moreover, the viscosity of liquid cyclopentane is markedly higher than that of its gaseous counterpart, with the viscosity of liquid cyclopentane being several orders of magnitude greater than that of gaseous cyclopentane at the same temperature.
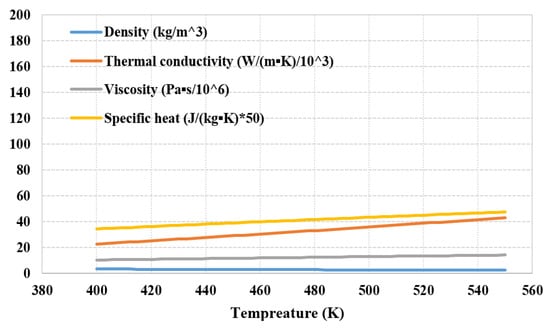
Figure 1.
Physical properties of gaseous cyclopentane.
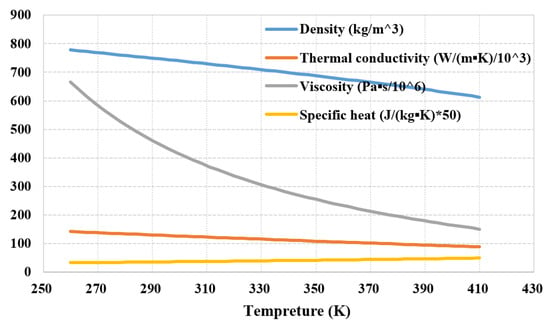
Figure 2.
Physical properties of liquid cyclopentane.
These pronounced disparities in the physical attributes of cyclopentane significantly complicate the fluid dynamics and heat-transfer mechanisms within the heat exchanger. The elevated density and viscosity of liquid cyclopentane notably augment the flow resistance within the channels, thereby necessitating a greater pumping power to sustain the desired flow rates. Conversely, gaseous cyclopentane, characterized by its lower density and viscosity, exhibits superior fluidity and facilitates more rapid heat transfer during the heat-exchange process. Thus, in the design of heat exchangers for cyclopentane-based organic Rankine cycle (ORC) systems, it is imperative to meticulously account for these variations in physical properties [28]. The optimization of the heat-exchanger structure, such as modifying channel dimensions, shape, and configuration, along with the judicious selection of operational parameters like flow rate, temperature, and pressure, are essential strategies to maximize heat-transfer efficiency.
2.2. Design of the Printed-Circuit Heat Exchanger
In this study, the printed-circuit heat exchanger (PCHE) utilizes a cross-flow configuration, as illustrated in the structural schematic diagram (Figure 3). The flow direction of gaseous cyclopentane is indicated with the red arrow, while the flow direction of liquid cyclopentane is denoted with the blue arrow. This cross-flow design effectively enhances the relative velocity between the two fluids and facilitates the development of turbulence. Based on principles of fluid mechanics, the heat-transfer coefficient in turbulent flow can be 2 to 4 times higher than that in laminar flow, thereby significantly improving the overall heat-transfer performance.

Figure 3.
Structural schematic diagram of PCHE: (a) physical diagram; (b) model diagram.
The micro-channel structure of the PCHE serves as the central feature for achieving high-efficiency heat transfer. Typically, these micro-channels have dimensions in the millimeter range. In this particular study, the equivalent diameter of the micro-channels was maintained between 1 and 2 mm. This compact channel design maximizes the heat-transfer area within a limited volume, yielding a unit-volume heat-transfer area of approximately 2000 m2/m3. Additionally, the smaller channel size helps minimize fluid-flow resistance and overall system energy consumption. In terms of structural design, the cross-sectional area of the gaseous flow channel was intentionally made larger to accommodate the high flow rate and low density of gaseous cyclopentane. Conversely, the cross-sectional area of the liquid flow channel is relatively smaller to meet the specific flow requirements of liquid cyclopentane.
Table 1 presents the fundamental characteristics of the PCHE examined in this study. The heat exchanger’s core dimensions are 160 mm in length, 90 mm in width, and 130 mm in height. Its compact design facilitates easy installation and practical engineering applications. The heat-transfer areas for the hot and cold sides are 0.64 m2 and 0.52 m2, respectively, ensuring efficient heat transfer. Figure 4 illustrates the internal micro-channel structure of the PCHE, including a detailed enlargement. By optimizing the geometry, dimensions, and arrangement of the flow channels—such as implementing a gradient channel design and incorporating turbulence-inducing features—the PCHE achieves high heat-transfer efficiency while significantly minimizing pressure drop. Before prototyping, CFD simulations were used to analyze the fluid flow and heat transfer by adjusting the equivalent diameter and flow length. This was done to minimize the volume and pressure drop while meeting the heat-transfer requirements.

Table 1.
Basic parameters of the tested PCHE.
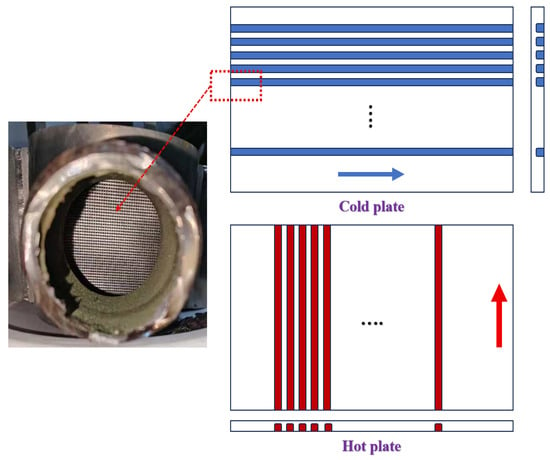
Figure 4.
Internal structural view of PCHE.
2.3. Experimental Method
Ensuring the accuracy and reliability of experimental data is fundamental to robust research. To achieve this, the present study employed a high-precision data acquisition system. For temperature measurement, a Pt100 resistance temperature detector (RTD) was utilized, offering an accuracy of ±0.1 K. This sensor leverages the principle that the electrical resistance of platinum varies with temperature, providing highly accurate and stable measurements. Pressure measurements were obtained using a capacitive pressure sensor, which achieves an accuracy of ±0.5 kPa by detecting changes in capacitance. This sensor is characterized by its rapid response and sufficient accuracy for the experimental requirements. Before the experiment, an uncertainty analysis based on the error propagation formula was carried out, and repeatability tests were conducted. The results showed that the uncertainty met the requirements, and the repeatability of the experiments under the same operating conditions three times was satisfactory, effectively ensuring the robustness and reliability of the experimental results.
In the formula, represents the uncertainty of the indirectly measured value, R. The uncertainty of the pressure is 0.55%, and the uncertainty of the flow rate is 0.73%.
To ensure the stability of experiments during the research, the following protocols were strictly adhered to: After the experimental system was initiated, each operational condition was maintained for a minimum of 20 min to allow the system to reach a steady state. System stability was determined by calculating the heat-transfer rates of the hot and cold fluids; thermal equilibrium was confirmed when the cold-side heat transfer reached at least 95% of the hot-side value. Data collection commenced only after this equilibrium was achieved. At each data point, five replicate measurements were taken under identical conditions, and their average was used as the final data to minimize errors and ensure result reliability.
The experimental design employed the method of controlling variables, where individual operational parameters were systematically altered while others were kept constant. This approach enabled a rigorous investigation of the impact of each variable on the experimental outcomes, facilitating accurate analysis and valid conclusions.
The data acquisition system captures data at a rate of one measurement per second, enabling the detection of minute fluctuations in various parameters throughout the experiment. To enhance the reliability of the results, multiple measurements were taken at each operating condition, with the mean value serving as the definitive experimental outcome. This approach helps mitigate measurement errors. Additionally, all sensors are meticulously calibrated prior to the experiment to ensure the precision of the collected data. Collectively, these measures ensure the high quality of the experimental data, thereby establishing a solid foundation for subsequent analysis.
2.4. CFD Fluent Simulation Method
In this study, the CFD Fluent software was employed to construct a detailed three-dimensional model of the PCHE and perform comprehensive simulation analyses. During the modeling process, the software’s built-in tools are used to create an accurate three-dimensional geometric representation of the PCHE, based on its actual dimensions and structural features. The model meticulously accounts for various factors, including the geometry of the micro-channels, the arrangement of the plates, and the flow direction of the fluids, to ensure that it accurately reflects real-world conditions. For instance, the walls and corners of the micro-channels are precisely modeled to more accurately simulate the fluid dynamics and heat transfer in these regions.
The equations used in the simulation are as follows [28].
Continuity equation:
Momentum equation:
Energy equation:
In the equation, represents the velocity vector, P represents the pressure, and represent the molecular viscosity and turbulent viscosity, respectively, represents the thermal conductivity efficiency, and represents the turbulent thermal conductivity.
Since the shear-stress transport (SST) model can accurately predict the flow separation between the fluid and the wall, it provides the best prediction of the experimental data. Therefore, the SST model is used to simulate the turbulence in this study. The second-order upwind scheme is adopted, and the residual convergence method has a convergence criterion of .
The model is then discretized into a series of small computational units through grid-generation technology, laying the groundwork for subsequent numerical simulations. Table 2 provides the thermal–hydraulic parameters of the PCHE under the designed operating conditions. For example, in Case1, the hot side has a mass flow rate of 0.13 kg/s, an inlet temperature of 453 K, and a pressure of 105 kPa, while the cold side has a mass flow rate of 0.13 kg/s, an inlet temperature of 325 K, and a pressure of 2100 kPa. These boundary conditions serve as the initial flow and thermal field inputs for the simulation. Under the same conditions, the results of models with five different numbers of meshes were obtained through simulation. The simulation results of the models with 7,024,576, 9,119,512, 14,145,985, 25,148,433, and 48,402,502 meshes were compared. With the accuracy and efficiency of the numerical simulation taken into account, the model with 14,145,985 meshes was selected for the simulation. Through the optimization of grid quality—such as maintaining an aspect ratio between 1 and 3 and skewness below 15 K—the accuracy and reliability of the simulation results were ensured.

Table 2.
Thermal-hydraulic parameters of four tested conditions of the PCHE.
Validating the model is crucial to ensuring simulation reliability. When the heat exchanger’s outlet temperature data from experiments and simulations were compared, the maximum error was within 5%, the minimum error was nearly 0%, and the average error was around 2.5%. Regarding the pressure-drop data, the model’s maximum deviation was within 10%. After numerous data points were analyzed, the minimum error was about 1%, and the average error was approximately 5%. As Figure 5 shows, the comparison of experimental and simulation results revealed that the maximum difference in the outlet temperature was within 5%, and the maximum pressure-drop deviation was within 10%. These error values effectively quantify the model’s accuracy. Table 3 presents a detailed comparison of the thermal–hydraulic parameters obtained from both the experiment and simulation under the Case1 operating conditions. The data indicate a close alignment between the experimental and simulation values across various parameters. For instance, the experimental value for the hot-side outlet temperature was 411 K, compared to the simulation value of 408 K; the experimental pressure drop on the hot side was 5 kPa, whereas the simulation result was 4.3 kPa. Overall, the model developed in this study was rigorously validated through experimentation, demonstrating high accuracy and providing a robust foundation for further simulation analysis.
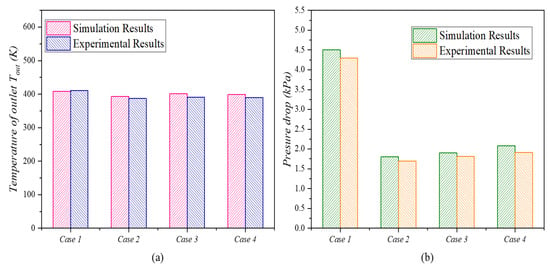
Figure 5.
Comparison between experimental results and simulation results: (a) heat-transfer performance; (b) pressure-drop performance.

Table 3.
The thermal–hydraulic parameters of four tested conditions of the PCHE.
3. Experimental Results and Analysis
3.1. Heat-Transfer Performance Analysis
With the rise in inlet temperature, the heat-transfer capacity of the regenerator exhibits an upward trend. In this context, Q1 denotes the heat released via the hot fluid, while Q2 signifies the heat absorbed via the cold fluid. As illustrated in Figure 6, the difference between Q1 and Q2 was minimal, remaining within a 5% margin across various operating conditions. This suggests that the heat exchanger experiences minimal heat loss during the transfer process, demonstrating excellent heat-transfer and thermal retention capabilities. A closer examination of the experimental data indicates an approximate linear correlation between the heat-transfer capacity and the inlet temperature. Within a specific temperature range, an increase of 10 K in the inlet temperature results in a corresponding rise in the heat-transfer capacity by approximately 10% to 15%.
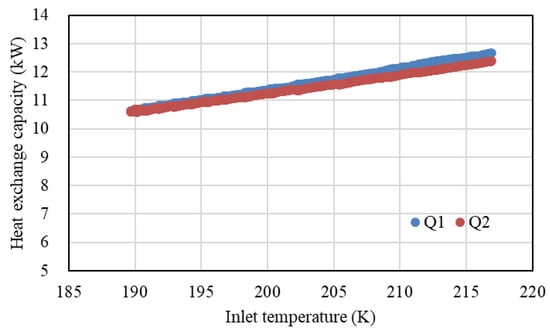
Figure 6.
Heat-Transfer Capacity of Hot and Cold Fluids in PCHE.
Figure 7 illustrates how the heat-transfer efficiency of the PCHE varies with the inlet temperature. The calculation formula for the heat-transfer efficiency of the heat exchanger is as follows:
where represents the heat-transfer efficiency. As observed, the efficiency of heat transfer in the PCHE diminishes with an increase in the inlet temperature. This trend can be attributed to the fact that a higher inlet temperature leads to a greater temperature differential between the hot and cold fluids, thereby enhancing the driving force for heat transfer and consequently increasing the heat-transfer capacity. However, concurrently, heat losses at elevated temperatures also escalate, such as those due to heat dissipation through the walls of the heat exchanger. In accordance with heat-transfer principles, heat loss is proportional to the square of the temperature difference. Thus, as the temperature difference widens, heat loss escalates at a more rapid pace, which, in turn, results in a decline in heat-transfer efficiency. The peak heat-transfer efficiency achieved with this heat exchanger was 72%, which occurred when the inlet temperature was 190 K under operating conditions with a relatively lower inlet temperature. This indicates that the heat exchanger exhibits robust heat-transfer performance within a specific range of operating conditions and is capable of fulfilling the requirements of practical engineering applications. Compared with the research on heat exchangers in the ORC cycle, the PCHE in this study achieved a thermal efficiency of 72%, while the fin-protracted heat exchanger achieved a thermal efficiency of 39.6% [29]. Therefore, this study offers obvious advantages.
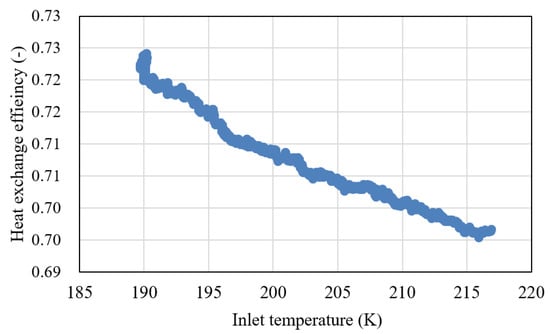
Figure 7.
Heat-transfer efficiency of PCHE.
3.2. Pressure-Drop Performance Analysis
Figure 8 presents the experimental findings regarding the pressure-drop performance of the PCHE. During the actual experiment, the pressure drop across the cold-side fluid was measured at 2.5 kPa, while that of the hot-side fluid was 1.8 kPa. Further analysis revealed that the pressure drop remained relatively stable with an increasing inlet temperature. Within the tested temperature range of 300–450 K, the pressure drop on the cold side fluctuated between 2.3 and 2.7 kPa, and on the hot side, it varied between 1.6 and 2.0 kPa. This indicates that the PCHE can maintain consistent pressure-drop performance across different operating conditions without significant pressure fluctuations due to temperature changes, thereby promoting stable system operation. This stability is attributed to the PCHE’s micro-channel structure and optimized flow channel layout, which effectively minimize fluid-flow resistance.
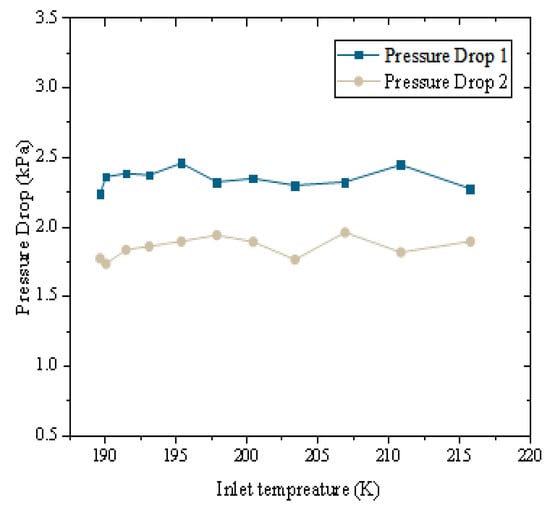
Figure 8.
Pressure-drop performance of PCHE.
4. Simulation Results and Analysis
4.1. Temperature Field and Pressure Field Analysis
The simulation results provide a clear visualization of the temperature and pressure field distributions within the regenerator. The cold fluid flows from top to bottom, while the hot fluid flows from right to left. As shown in Figure 9a, the cold fluid exhibits a temperature gradient across its flow channel, with higher temperatures on the right side (near the inlet of the hot fluid) and lower temperatures on the left side. This gradient is due to the continuous absorption of heat from the hot fluid, causing the cold fluid’s temperature to rise progressively. Near the hot fluid inlet, where the temperature difference between the fluids was significant, the heat-transfer rate was rapid, leading to a substantial increase in the cold fluid’s temperature. Conversely, on the left side, farther from the hot fluid inlet, the heat transfer gradually reached equilibrium, resulting in a smaller temperature increase. The standard deviation of the cold fluid’s temperature was approximately 5–8 K, indicating that improvements in temperature uniformity were still possible.
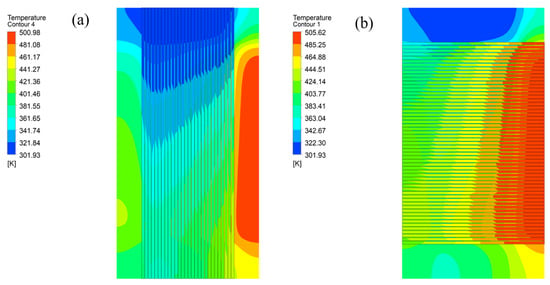
Figure 9.
Temperature-distribution nephograms of PCHE: (a) cold fluid; (b) hot fluid.
Figure 9b illustrates a similar temperature gradient in the hot fluid’s flow channel, with higher temperatures near the lower side (adjacent to the cold fluid inlet) and lower temperatures on the upper side. However, the overall temperature distribution of the hot fluid was relatively uniform, with a standard deviation of about 3–5 K. This suggests that the heat exchanger design effectively maintains temperature uniformity for the hot fluid, reducing the risk of localized overheating or overcooling. Such uniformity is crucial for enhancing the overall performance of the heat exchanger.
As depicted in the pressure-distribution contour in Figure 10, pressure exhibited a gradual decline along the direction of fluid flow, adhering to the fundamental principles of fluid mechanics. A more detailed analysis revealed that the pressure drop of the cold fluid was significantly influenced by temperature variations. As the temperature of the cold fluid rose, its density and viscosity decreased, leading to reduced flow resistance and, consequently, a lower pressure drop. In contrast, the pressure drop of the hot fluid was less sensitive to temperature changes, primarily because the physical properties of the hot fluid remained relatively stable under the experimental conditions employed in this study.
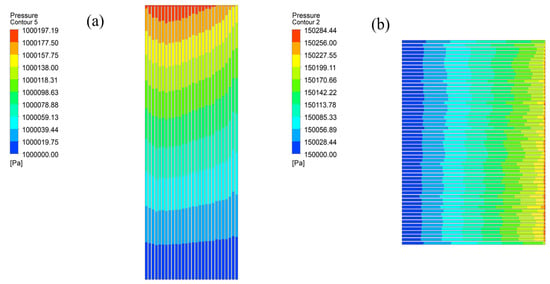
Figure 10.
Pressure-distribution nephograms of PCHE: (a) cold fluid; (b) hot fluid.
Within the operational range examined, the pressure drop losses were maintained within reasonable limits. Specifically, the pressure drop on the cold side ranged from 2 to 3 kPa, while on the hot side, it varied between 1 and 2 kPa. The uniformity of the pressure distribution was evident, indicating that the heat exchanger design effectively manages pressure drop losses, thereby ensuring the reliable and efficient operation of the system.
Figure 11 shows a large velocity difference between hot and cold fluids. This is because of multiple factors. Gases have a lower density than liquids; for instance, gaseous cyclopentane has a density of around 2.5 kg/m3, and liquid cyclopentane has a density of about 740 kg/m3. With the same mass flow rate, the hot gas needs a higher velocity even though it has a larger flow-through area. Viscosity also affects velocity. Liquids have a higher viscosity, creating more internal resistance. So, a cold liquid has a hard time increasing its velocity, while a hot gas with a low viscosity can flow more freely. The heat exchanger’s design and fluid flow patterns matter, too. The larger hot-fluid flow-through area reduces resistance for high-speed flow, and the smaller cold-fluid area suits liquid flow. The hot gas is often in a turbulent state, maintaining high velocity, while the cold liquid in laminar flow has a limited velocity increase. Under Case 1, the hot fluid’s average velocity is about 8 m/s, and the cold fluid’s is only around 0.1 m/s. This velocity difference significantly impacts heat-transfer and pressure drop performance.
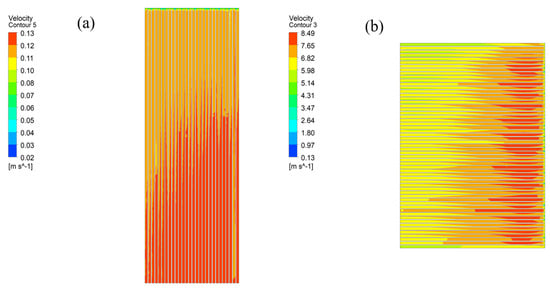
Figure 11.
Velocity-distribution nephograms: (a) cold fluid; (b) hot fluid.
A higher velocity in the hot fluid enhances convective heat transfer, which is beneficial for the heat-exchange process. However, it also increases flow resistance. Conversely, the lower velocity of the cold fluid results in a lower flow resistance but compromises heat-transfer efficiency. Therefore, in the design of the heat exchanger, it is crucial to balance these factors and optimize velocity matching to achieve the best overall performance.
4.2. Heat-Transfer Performance Evaluation
The inlet temperatures and flow rates of both cold and hot fluids are chosen as the operating variables. This selection is based on their significant impact on heat-exchange performance, their adjustability and measurability in practical applications, their mutual independence, and their ability to represent the primary influencing factors in a heat-exchanger operation. The heat-transfer coefficient and Nusselt number derived from the simulation serve as key metrics for assessing the heat exchanger’s performance. The calculation formula for the Nusselt number is as follows:
where K represents the thermal conductivity, and L represents the characteristic length. The characteristic length of the cold side is 0.55 mm, and that of the hot side is 1.152 mm. Dimensional analysis is grounded in the Buckingham Pi theorem [30]. It posits that any physical law can be expressed as a relationship among dimensionless groups. In our study, dimensionless numbers like the Nusselt number (Nu), the Reynolds number (Re), and the Prandtl number (Pr) are crucial. They simplify the complex relationships between heat transfer and fluid flow, allowing for a more generalized understanding across different scales and conditions.
Figure 12 illustrates how these parameters vary with different inlet temperatures. Specifically, Nu1 denotes the Nusselt number for the cold fluid, while Nu2 corresponds to the hot fluid. It is evident that the Nusselt number for the hot fluid exceeds that of the cold fluid. This disparity arises because the higher velocity of the hot fluid intensifies convective heat transfer, thereby yielding a larger Nusselt number.
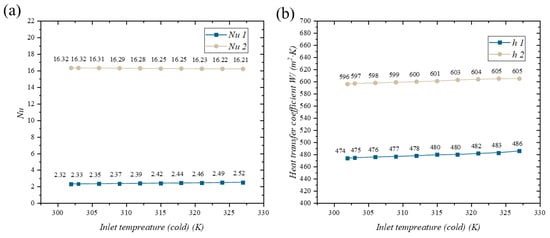
Figure 12.
Heat-transfer performance analysis of CFD model: (a) Nusselt number; (b) heat-transfer coefficient.
As the inlet temperature of the cold fluid rises, both Nusselt numbers exhibit an upward trend. This increase is attributed to changes in the fluid’s physical properties: thermal conductivity improves, and viscosity decreases, enhancing convective heat-transfer capabilities. For instance, when the cold fluid’s inlet temperature increases from 300 K to 350 K, the cold fluid’s Nusselt number rises by approximately 20% to 30%, while the hot fluid’s Nusselt number increases by about 10% to 20%.
Similarly, the convective heat-transfer coefficients (h1 for the cold fluid and h2 for the hot fluid) follow the same trend, with the hot fluid’s coefficient being higher. However, the Nusselt number of the hot side shows a slight decrease as the inlet temperature of the cold side increases. This is because, as shown in Figure 1, the thermal conductivity increases significantly with the increase in temperature.
In practical engineering applications, increasing the cold fluid’s inlet temperature can enhance the heat exchanger’s performance. However, this adjustment must be balanced against considerations of overall system operating costs and safety.
Apart from inlet temperature, flow rate is another crucial factor influencing heat-transfer performance. Figure 13 depicts the trends of the Nusselt number and heat-transfer coefficient under varying flow rate conditions, where the flow rates of both hot and cold fluids are kept equal. As observed, an increase in flow rate leads to a rise in the Nusselt numbers for both fluids. This is attributed to the enhanced convective heat transfer resulting from the higher fluid velocity, which in turn boosts the Nusselt number. The convective heat-transfer coefficient of the hot fluid remains higher than that of the cold fluid, and both coefficients increase progressively with a rising flow rate. For instance, when the flow rate escalates from 0.01 kg/s to 0.03 kg/s, the convective heat-transfer coefficient of the cold fluid surges by approximately 40% to 50%, while that of the hot fluid rises by about 30% to 40%. This underscores the significant impact of flow rate on heat-transfer efficiency, indicating that augmenting the flow rate can markedly enhance the heat-transfer process and overall efficiency of the heat exchanger.
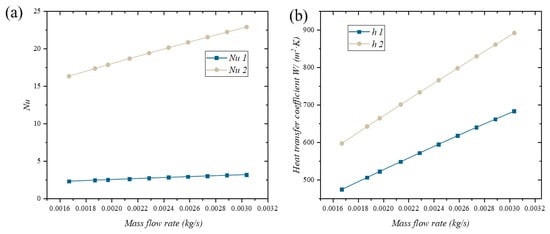
Figure 13.
Variation in heat-transfer performance with mass flow rate: (a) Nusselt number; (b) heat-transfer coefficient.
Through a meticulous analysis of the simulation results, a comprehensive understanding of the heat and mass transfer mechanisms within the heat exchanger was achieved. This knowledge provides robust theoretical support for optimizing the design and operation of the heat exchanger. Moreover, the extensive data obtained from these simulations lay a solid foundation for the subsequent derivation of heat-transfer correlations.
5. Derivation and Verification of Heat-Transfer Correlations
5.1. Derivation of Heat-Transfer Correlations
Leveraging extensive experimental and simulation datasets, this study employed a genetic algorithm to model and derive precise heat-transfer correlations for both the hot and cold sides of the system. The genetic algorithm, inspired by natural evolutionary processes, utilizes mechanisms analogous to biological genetics, crossover events, and mutations to navigate and optimize within complex, multidimensional data landscapes. Within this research framework, heat-transfer data accrued under diverse operational scenarios serve as the foundational input. The overarching objective is to formulate correlations that robustly encapsulate the nuanced interplay between the heat-transfer coefficient and myriad influential variables. Through a meticulous calibration of algorithmic parameters and iterative computational refinement, the study achieves a sophisticated, data-driven elucidation of heat-transfer dynamics.
The correlation for the hot side is as follows:
Here, Nu represents the Nusselt number on the hot side, Re denotes the Reynolds number on the hot side, and Pr signifies the Prandtl number on the hot side. This correlation was derived through the analysis and fitting of extensive simulation data, capturing the heat-transfer behavior of the hot-side fluid across various flow conditions and thermophysical properties.
The Reynolds number on the hot side is indicative of the fluid’s flow state. As Re increases, the fluid’s turbulence intensifies, thereby enhancing convective heat transfer and subsequently raising the Nusselt number. Meanwhile, the Prandtl number reflects how the hot-side fluid’s thermophysical properties influence heat transfer. A higher Pr value implies a greater relative momentum diffusion capacity compared to thermal diffusion, which, in turn, has a notable impact on the overall heat-transfer efficacy.
The correlation for the cold side is as follows:
On the cold side, Nu denotes the Nusselt number, Re represents the Reynolds number, and Pr indicates the Prandtl number. Analogous to the correlation on the hot side, the Reynolds and Prandtl numbers on the cold side significantly influence the Nusselt number. Owing to the distinct physical properties and flow characteristics of the fluids on the cold and hot sides, the coefficients and exponents in the cold-side correlation differ from those on the hot side. Variations in the Reynolds number of the cold-side fluid alter its flow state, thereby impacting the heat-transfer process. Meanwhile, the Prandtl number elucidates how the thermophysical properties of the cold-side fluid affect heat transfer [31].
The genetic algorithm was chosen for its global search capability, suitability for complex nonlinear problems, and parallel processing efficiency. Compared to gradient descent, it offers better global optimization but slower convergence; compared to simulated annealing, it explores a broader solution space but requires more complex parameter tuning.
5.2. Prediction Accuracy of High-Precision Heat-Transfer Correlations for the Hot and Cold Sides
The derived heat-transfer correlations were validated against 34 simulation results. As illustrated in Figure 14a,b, which compares the correlation predictions with the simulation outcomes, the accuracy of the correlations is within a 20% margin of error (red line). For the hot fluid, across various operating conditions, the relative errors between the predicted Nusselt numbers and the simulated values predominantly cluster around 15%. For the cold fluid, these relative errors generally remain within 18%. This level of accuracy demonstrates that the derived correlations can reliably forecast the heat-transfer performance of cyclopentane on both the hot and cold sides of the printed-circuit heat exchanger under diverse operating scenarios. For Nu1 (corresponding to the hot fluid), its values range from a minimum of approximately 11.93 to a maximum of around 22.89. As for Nu2 (associated with the cold fluid), the minimum value is roughly 1.80, and the maximum is about 3.20. The application range of the proposed heat-transfer correlations is as follows: using cyclopentane as the working fluid, with a pressure of 105 kPa, a mass flow rate of 0.036–0.12 kg/s, and a cooling capacity of 8.47–20.27 kW; and with a pressure of 2100 kPa, a mass flow rate of 0.036–0.12 kg/s, and a heating capacity of 8.47–20.27 kW. Consequently, these correlations provide a robust theoretical foundation for the design and performance prediction of heat exchangers in practical engineering applications.
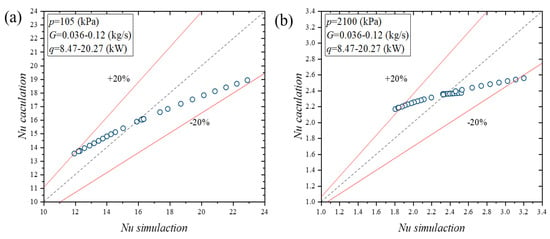
Figure 14.
Comparison between correlation results and simulation results: (a) hot fluid; (b) cold fluid.
Future research: study long-term PCHE-cyclopentane performance under complex conditions and refine correlations for broader use.
6. Conclusions
This investigation has employed a multifaceted approach, integrating both experimental techniques and CFD Fluent simulations, to conduct a comprehensive analysis of the cyclopentane printed-circuit heat exchanger, yielding the following key insights:
- The heat exchanger demonstrates exceptional heat-transfer efficiency and thermal retention capabilities. As the inlet temperature rises, so does the heat-transfer capacity. The heat-transfer discrepancy between the hot and cold fluids is minimal, with peak efficiency reaching 72%. The pressure drop remains stable across varying temperatures, with values of 2.5 kPa and 1.8 kPa for the cold and hot sides, respectively. These characteristics align well with the stringent demands of waste-heat recovery systems.
- Detailed profiles of temperature, pressure, and velocity distributions within the heat exchanger have been elucidated. Both fluids exhibit temperature gradients, though the hot fluid’s temperature distribution is notably more uniform. Pressure decreases progressively along the flow direction, with the cold fluid’s pressure drop being more temperature-sensitive compared to the hot fluid. The hot fluid’s velocity significantly outpaces that of the cold fluid. Additionally, the Nusselt number and convective heat-transfer coefficient for the hot fluid exceed those of the cold fluid, escalating in tandem with increases in the cold fluid’s inlet temperature and flow rate.
- With the utilization of a genetic algorithm, high-precision heat-transfer correlations for both the hot and cold sides were derived from the amalgamation of experimental and simulation data. These correlations boast a prediction accuracy within a 20% margin, thereby furnishing a robust theoretical framework to underpin associated design and application endeavors.
Author Contributions
Methodology, H.X.; Software, X.Q.; Investigation, H.X.; Resources, M.Z., L.S. and X.W.; Data curation, X.Q.; Writing—original draft preparation, X.Q.; Writing—review & editing, M.Z. and L.S.; Visualization, H.Z.; Supervision, H.Z. and X.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
Authors Xiaogang Qin, Haibo Xu and Ming Zhang were employed by the CNOOC Research Institute Co., Ltd.; Authors Lin Sun and Xuan Wang were employed by the CNOOC Enertch Equipment Technology Co., Ltd. The remaining author declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Nomenclature
| Abbreviations | |||
| CFD | Computational fluid dynamics | Q | Heat-transfer rate (kW) |
| PCHE | Printed-circuit heat exchanger | m | Mass flow rate (kg) |
| ORC | Organic Rankine cycle | V | Volume (m3) |
| w | Weight of the whole heat exchanger (kg) | ||
| Symbols | |||
| A | Heat-transfer area | Greek letters | |
| Cp | Specific heat (J/(kg·K)) | Density (kg/m3) | |
| D | Hydraulic diameter, (mm) | Dynamic viscosity (Pa·s) | |
| h | Convective heat-transfer coefficient | Turbulent kinetic energy dissipation rate | |
| Re | Reynolds number | ||
| Nu | Nusselt number | Subscripts | |
| k | Turbulent thermal conductivity | in | Inlet |
| p | Pressure (kPa) | out | Outlet |
| Pressure (kPa) | |||
References
- Narwal, K.; Kempers, R.; O’Brien, P.G. Enhanced energy storage density in thermal energy storage systems simultaneously heated with solar radiation and industrial waste heat. Results Eng. 2024, 25, 103792. [Google Scholar] [CrossRef]
- Du, K.; Calautit, J.; Eames, P.; Wu, Y. A state-of-the-art review of the application of phase change materials (PCM) in Mobilized-Thermal Energy Storage (M-TES) for recovering low-temperature industrial waste heat (IWH) for distributed heat supply. Renew. Energy 2021, 168, 1040–1057. [Google Scholar] [CrossRef]
- Wiśniewska, P.; Wang, S.; Formela, K. Waste tire rubber devulcanization technologies: State-of-the-art, limitations and future perspectives. Waste Manag. 2022, 150, 174–184. [Google Scholar] [CrossRef]
- Chen, T.; Shu, G.; Tian, H.; Zhao, T.; Zhang, H.; Zhang, Z. Performance evaluation of metal-foam baffle exhaust heat exchanger for waste heat recovery. Appl. Energy 2020, 266, 114875. [Google Scholar] [CrossRef]
- Deepak, G.; Sudha, L.; Pauline, S.; Ketaraju, V.D.S.; Aravindan, N.; Neelima, S. Thermodynamic modeling and AI-enhanced optimization of a novel tri-level waste heat recovery system for industrial processes. Therm. Sci. Eng. Prog. 2024, 56, 103098. [Google Scholar]
- Lykas, P.; Atsonios, K.; Gkountas, A.; Bakalis, P.; Manolakos, D.; Grammelis, P.; Itskos, G.; Nikolopoulos, N. Energy, exergy, and economic comparison of ORC with quasi-isothermal expansion with other ORC designs for low-grade waste heat recovery. Therm. Sci. Eng. Prog. 2024, 55, 103010. [Google Scholar] [CrossRef]
- Akbari, S.; Faghiri, S.; Zinjanabi, A.M.; Bijarchi, M.A.; Shafii, M.B.; Hosseinzadeh, K. Thermo-economic investigation and comparative multi-objective optimization of dual-pressure evaporation ORC using binary zeotropic mixtures as working fluids for geothermal energy application. Int. J. Thermofluids 2024, 24, 100899. [Google Scholar] [CrossRef]
- Bellos, E. A detailed analysis of waste heat recovery organic Rankine cycle with partial evaporation and different working fluids. Appl. Therm. Eng. 2025, 263, 125410. [Google Scholar] [CrossRef]
- Shalby, M.; Marachli, A.; Salah, A.A. Working Fluid Selection and Performance Analysis for Subcritical Organic Rankine Cycles. Results Eng. 2025, 25, 104120. [Google Scholar] [CrossRef]
- Ibrahim, O.A.A.-M.; Kadhim, S.A.; Hammoodi, K.A.; Rashid, F.L.; Askar, A.H. Review of hydrocarbon refrigerants as drop-in alternatives to high-GWP refrigerants in VCR systems: The case of R290. Clean. Eng. Technol. 2024, 23, 100825. [Google Scholar] [CrossRef]
- Kittijungjit, T.; Klamrassamee, T.; Laoonual, Y.; Sukjai, Y. Comprehensive study on waste heat recovery from gas turbine exhaust using combined steam Rankine and organic Rankine cycles. Energy Convers. Manag. 2025, 25, 100825. [Google Scholar] [CrossRef]
- Wang, J.; Tian, H.; Sun, R.; Wang, X.; Li, L.; Zhang, X.; Shu, G. Computer-aided molecular design of CO2-based mixture working fluid harvesting engine waste heat. Appl. Therm. Eng. 2023, 227, 120481. [Google Scholar] [CrossRef]
- Feng, X.; Shi, F.; Qiao, G.; Li, Y.; Liu, C. Integrating organic Rankine cycle with thermoelectric generator in various applications utilizing low-grade energy: A review. Sustain. Energy Technol. Assess. 2024, 68, 103882. [Google Scholar] [CrossRef]
- Chowdhury, A.S.; Ehsan, M.M. A Critical Overview of Working Fluids in Organic Rankine, Supercritical Rankine, and Supercritical Brayton Cycles Under Various Heat Grade Sources. Int. J. Thermofluids 2023, 20, 100426. [Google Scholar] [CrossRef]
- Lee, S.W.; Lee, Y.; Lee, Y.; Jo, H. Condensation heat transfer and applicability assessment of a printed circuit heat exchanger as a condenser in a cryogenic CO2 capture and storage system. Appl. Therm. Eng. 2024, 261, 125133. [Google Scholar] [CrossRef]
- Xia, E.; Xie, H.; Sun, L.; Long, X.; Wang, J.; Gao, T.; Li, S.; Li, B.; Li, C.; Gao, M.; et al. Optimal design of a high-performance heat exchanger for modular thermoelectric generator towards low-grade thermal energy recovery. Appl. Therm. Eng. 2024, 258, 124849. [Google Scholar] [CrossRef]
- Zhang, L.; Yang, P.; Li, W.; Klemeš, J.J.; Zeng, M.; Wang, Q. A new structure of PCHE with embedded PCM for attenuating temperature fluctuations and its performance analysis. Energy 2022, 254, 124462. [Google Scholar] [CrossRef]
- Tang, Z.; He, S.; Li, N.; Zeng, M.; Yan, X.; Wang, Q.; Ma, T. Non-equilibrium overlapping grid method with two-phase porous media model for printed circuit heat exchanger based steam generator. Int. J. Heat Mass Transf. 2024, 232, 125960. [Google Scholar] [CrossRef]
- Chen, W.; Ma, Q.; Liu, X.; Cheng, Y.; Wang, Q.; Ma, T. Adaptability analysis of flow and heat transfer multi-scale numerical method for printed circuit heat exchanger. Energy 2024, 311, 133349. [Google Scholar] [CrossRef]
- Liang, Z.; Zheng, G.; Wu, G.; Pan, Z.; Hu, Z.; Xu, M.; Chen, H. Thermodynamic performance of organic rankine cycle based pumped thermal energy storage system with different working fluids. Heliyon 2024, 11, e41052. [Google Scholar] [CrossRef]
- Kim, I.H.; Sun, X. CFD study and PCHE design for secondary heat exchangers with FLiNaK-Helium for SmAHTR. Nucl. Eng. Des. 2014, 270, 325–333. [Google Scholar] [CrossRef]
- Mondejar, M.E.; Andreasen, J.G.; Pierobon, L.; Larsen, U.; Thern, M.; Haglind, F. A review of the use of organic Rankine cycle power systems for maritime applications. Renew. Sustain. Energy Rev. 2018, 91, 126–151. [Google Scholar] [CrossRef]
- Ren, Y.; Jiang, R.; Wang, P.; Wu, W.; Yang, Y.; Yang, Q. Experimental study of a rectangular microchannel printed circuit heat exchanger using supercritical carbon dioxide and water cooling. Appl. Therm. Eng. 2024, 262, 125230. [Google Scholar] [CrossRef]
- Ali, S.; Nohra, C.; Faraj, J.; Dbouk, T.; Khaled, M. Thermo-hydraulic performance of concentric tube heat exchangers with turbulent flow: Predictive correlations and iterative methods for pumping power and heat transfer. Int. J. Thermofluids 2024, 24, 100898. [Google Scholar] [CrossRef]
- Yih, J.; Wang, H. Experimental characterization of thermal-hydraulic performance of a microchannel heat exchanger for waste heat recovery. Energy Convers. Manag. 2020, 204, 112309. [Google Scholar] [CrossRef]
- Zhu, H.; Xie, G.; Berrouk, A.S. Comparative dynamic performance of SCO2 cycle and combined cycle with transiently modelled printed circuit heat exchangers. Appl. Therm. Eng. 2024, 257, 124342. [Google Scholar] [CrossRef]
- Zhang, H.; Shi, L.; Xuan, W.; Chen, T.; Li, Y.; Tian, H.; Shu, G. Analysis of printed circuit heat exchanger (PCHE) potential in exhaust waste heat recovery. Appl. Therm. Eng. 2022, 204, 117863. [Google Scholar] [CrossRef]
- Kazaz, O.; Abu-Nada, E. Innovative high-energy nanocomposite absorbers for superior solar-driven water desalination through broadband solar energy harvesting. Appl. Therm. Eng. 2025, 273, 126531. [Google Scholar] [CrossRef]
- Ravi, R.; Pachamuthu, S.; Kasinathan, P. Computational and experimental investigation on effective utilization of waste heat from diesel engine exhaust using a fin protracted heat exchanger. Energy 2020, 200, 117489. [Google Scholar] [CrossRef]
- Baigh, T.A.; Saif, M.J.; Mustakim, A.; Nanzeeba, F.; Khan, Y.; Ehsan, M.M. Enhancing thermodynamic performance with an advanced combined power and refrigeration cycle with dual LNG cold energy utilization. Heliyon 2024, 10, e35748. [Google Scholar] [CrossRef]
- Huang, Y.; Sarma, B.; Weibel, J.A. A predictive model for fin array boiling heat transfer performance under two-phase immersion cooling. Int. J. Heat Mass Transf. 2025, 239, 126513. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).