Optimizing Lightweight Recurrent Networks for Solar Forecasting in TinyML: Modified Metaheuristics and Legal Implications

Abstract

The limited nature of fossil resources and their unsustainable characteristics have led to increased interest in renewable sources. However, significant work remains to be carried out to fully integrate these systems into existing power distribution networks, both technically and legally. While reliability holds great potential for improving energy production sustainability, the dependence of solar energy production plants on weather conditions can complicate the realization of consistent production without incurring high storage costs. Therefore, the accurate prediction of solar power production is vital for efficient grid management and energy trading. Machine learning models have emerged as a prospective solution, as they are able to handle immense datasets and model complex patterns within the data. This work explores the use of metaheuristic optimization techniques for optimizing recurrent forecasting models to predict power production from solar substations. Additionally, a modified metaheuristic optimizer is introduced to meet the demanding requirements of optimization. Simulations, along with a rigid comparative analysis with other contemporary metaheuristics, are also conducted on a real-world dataset, with the best models achieving a mean squared error (MSE) of just 0.000935 volts and 0.007011 volts on the two datasets, suggesting viability for real-world usage. The best-performing models are further examined for their applicability in embedded tiny machine learning (TinyML) applications. The discussion provided in this manuscript also includes the legal framework for renewable energy forecasting, its integration, and the policy implications of establishing a decentralized and cost-effective forecasting system.

1. Introduction

In recent years, the use of fossil fuels has fallen out of favor for power production. The limited nature of fossil resources, as well as their unsustainable characteristics, has led to increased interest in renewable sources [1]. Nevertheless, the integration of renewable sources is not without challenges [2]. Sources such as wind turbines, solar cells, or electric dams can require a comparatively large upfront investment. Additionally, certain sources, such as solar and wind, rely heavily on external factors like the weather, making them unreliable for certain critical applications [3,4]. Despite these challenges, the integration of renewable sources is essential for sustainability and energy independence. The accurate prediction of solar power generation is crucial for efficient grid management and energy trading. Renewable sources also benefit from being relatively clean and decentralized, which can alleviate many losses caused by power line inefficiencies.

The legal framework for the production and distribution of solar power in Western Balkan countries is increasingly harmonized with European Union (EU) legislation, which issues various legal documents to regulate the development of the energy sector and support the use of renewable energy sources. In policies and directives such as the White and Green Papers on energy policy and renewable energy sources, the EU focuses on supply security, environmental protection, and industry competitiveness. Directive 2018/2001/EU [5] highlights the importance of renewable energy use and sets targets for 2030, including reducing CO₂ emissions by 40%, increasing the share of renewable energy to 32%, and raising the share of renewables in transportation to 14%. To achieve these goals, member states develop national action plans with strategies, legislative frameworks, and incentives. Since the introduction of this directive, the share of renewable energy in the EU’s energy consumption has grown from 12.5% in 2010 to 23% in 2022 [6].

In line with EU policies, the legal framework for solar energy production and distribution in Western Balkan countries is oriented toward alignment with EU requirements. Although there are differences in the legislation of each country, most apply common standards through laws such as the Energy Act and the Renewable Energy Act, as well as through national energy development strategies. All Western Balkan countries have a basic Energy Act that encompasses renewable energy sources (RESs). This law typically defines the rights and obligations of solar energy producers, the obligation of transmission systems to facilitate grid connections for RES producers, procedures for issuing permits for the construction and commissioning of solar power plants, and incentives for investments in RES through subsidies, feed-in tariffs, or favorable loans.

The use of artificial intelligence (AI) has demonstrated impressive capabilities for handling time-series forecasting [7], even in the energy sector. By leveraging the forecasting abilities of AI algorithms to balance production and demand, better utilization of this valuable resource can be attained. Furthermore, by providing a more accurate and reliable estimate of production, better integration can be achieved with existing power distribution systems, reducing transmission losses [8,9].

However, AI algorithms are often computationally demanding, requiring substantial investments to train and execute predictions. Models are usually run on relatively expensive graphics processing units (GPUs) and require supporting system infrastructure. This can lead to relatively high power demands. Optimized models could potentially be compared and executed on significantly cheaper systems, enabling accurate models to run at a fraction of the hardware costs and with significantly lower power demands. Tiny machine learning (TinyML) [10] is a subset of machine learning (ML) that explores the deployment of ML models on microcontroller units (MCUs). Such deployment could significantly reduce the cost of using ML in deployment, especially in remote locations where solar and wind turbines may be installed. Further use of predictive models could help better integrate forecasting models into Internet of Things (IoT) networks [11,12].

This work explores the use of metaheuristic optimization algorithms to select optimal hyperparameters for three types of recurrent neural networks (RNNs) [13]. The goal is to select lightweight architectures that can be ported to MCUs for field use while maintaining suitable performance. As the task of hyperparameter tuning is often considered NP-hard [14], a modified metaheuristic optimizer is proposed, and a comparative analysis is conducted against several contemporary optimizers on two publicly available datasets, resulting in six experiments in total. The best-performing models are further explored for their forecasting potential once deployed on an MCU. The contributions of this work can be summarized as follows:

• An exploration of the legal foundations of energy forecasting in the Western Balkan region;
• The proposal of a lightweight framework for the in situ forecasting of solar energy production using models optimized for MCUs;
• The introduction of a modified metaheuristic optimizer tailored to the optimization needs of this study;
• The selection of lightweight time-series forecasting architectures with suitable accuracy for power systems;
• The implementation of the proposed model on an MCU to evaluate the practical effectiveness of the approach.

The structure of the remaining work is outlined as follows: Section 2 covers preceding works that inspire and support this study. In Section 3, the methodology is discussed in detail. Section 4 and Section 5 discuss the experimental configuration and present the attained results. Section 6 concludes the work and presents proposals for future research in the field.

2. Related Works

Renewable sources play an increasingly important role in maintaining energy sustainability. While full substitution with current technology is not yet possible, it is essential to shift the developmental focus toward improving and better integrating renewable sources into existing grids [15]. The utilization of renewable sources can take several forms; geothermal, wind, and solar energy have all been widely utilized [16], with wind and solar being among the most popular.

An issue with wind and solar energy production is the inherent reliance of this technology on the weather. Changes in production make it difficult to balance supply with demand. While storage solutions exist, they are often not economically viable. Accurately forecasting production can help improve utilization as well as planning for supplemental production from other sources. One potential way of forecasting production is through the use of time-series forecasting techniques [17]. Time-series forecasting has been applied in several fields and demonstrated notably good results. The use of AI algorithms can help improve forecasting accuracy, as AI can learn from observed data, accounting for more subtle relationships between features. Recurrent neural networks are particularly renowned for their capability to handle time series [18,19]; however, other approaches have been used as well, like deep learning models [20,21]. Several research papers outlined long short-term networks [22,23] and gated recurrent units [24,25] as particularly effective for this task.

Much like in situ production, in situ forecasting can help alleviate some of the challenges of operating remote systems [26]. While the training, preparation, and execution of ML forecasting models are undoubtedly very computationally demanding, once a trained model is established, its execution can be sufficiently optimized for relatively modest computational resources. Running predictive models on MCUs, known as TinyML, is a potentially lucrative approach for energy forecasting [12]. Remote production systems could be better tuned to maintain power production, balance stored power usage, and provide warnings when necessary. By operating on edge devices, TinyML minimizes the dependence on centralized infrastructure, effectively reducing the communication cost and improving system robustness. Additionally, it can support real-time data processing, lowering latency and allowing immediate predictions and decision-making. However, it is important to be mindful of the limited capacity of MCUs and design models that are sufficiently accurate yet computationally simple enough to run on economically viable and commercially available MCUs.

Hyperparameter optimization plays an essential role in adapting ML models for both accurate forecasting and execution on TinyML platforms. Hyperparameter selection helps tailor forecasting models to the applied problem, thereby improving overall model performance [27,28]. Optimization can also yield less computationally demanding models, striking a balance between accuracy and efficiency. Nevertheless, optimization in ML environments can be challenging. Given the large search spaces presented by modern algorithm configuration schemes, hyperparameter tuning can be considered NP-hard [29].

Researchers have adapted and utilized several techniques to address NP-hard optimization challenges. A popular approach among these is the use of metaheuristics. Metaheuristic optimizers adopt simulated search strategies to locate promising solutions within a given search space by employing a randomness-guided approach. Several optimizers have emerged over the years, drawing inspiration from various sources. Notable optimization algorithms include particle swarm optimization (PSO) [30] and genetic algorithms (GAs) [31]. More modern examples include the recently proposed reptile search algorithm (RSA) [32] and sinh-cosh optimizer (SCHO) [33]. Metaheuristic optimizers have shown promising outcomes applied to several challenges in the field, including hyperparameter selection. Some notable examples include applications in healthcare [34,35,36] and sentiment analysis [37,38]. Renewable energy forecasting has also been explored [39,40], as well as other time-series forecasting tasks [41,42].

While the use of AI algorithms for forecasting holds great potential in modern research, the incorporation of metaheuristic optimizers could enhance performance while reducing the computational costs of model execution. However, their combination has yet to be explored for deployment on TinyML devices. This work seeks to address this observed gap in the literature by proposing a modified metaheuristic optimizer designed to select optimal hyperparameter settings for solar energy production forecasting using RNN architectures, yielding adequately accurate models while maintaining low computational complexity. Furthermore, few studies have highlighted the difficulties and challenges associated with integration, given the current limitations of the legal framework in the Western Balkan regions.

2.1. Legal Framework for Production and Distribution of Solar Power

The legal framework in Western Balkan countries addressing the impact of solar energy on climate change is increasingly aligned with EU legislation. One of the key measures is the Renewable Energy Directive (RED II), which countries in the region implement through their membership in the Energy Community. The Energy Community, an international organization founded on 25 October 2005 in Athens, aims to extend the EU’s internal energy market to Southeast Europe, including the Montenegrin region.

The current Energy Law in Montenegro, for example, specifies “energy activities, regulates the conditions and manner of their performance to ensure quality and secure energy supply to end consumers, encourages the production of energy from renewable sources and high-efficiency cogeneration, regulates the organization and management of the electricity and gas markets, and other issues relevant to energy” [43]. In 2024, procedures began for adopting a new Energy Law in Montenegro, through which the EU directive will be transposed. It has also been announced that a new law on the cross-border exchange of electricity and natural gas will undergo public consultation. The adoption of this law would be significant for Montenegro, as it would formalize the complete regulatory package of the Energy Community.

In terms of environmental protection, the legal framework in Western Balkan countries is gradually aligning with EU legislation aimed at preserving natural resources, reducing pollution, and ensuring sustainable development. Although specific differences remain, most Western Balkan countries follow similar principles and frameworks. Key elements of environmental protection regulations include the Environmental Protection Law, which sets standards for air, water, and soil quality, environmental impact assessments, and ecological taxes; water resource management, which regulates conservation, pollution control, and river basin planning; biodiversity protection, which outlines strategies for habitat and endangered species preservation; waste management, which promotes recycling and penalizes improper disposal; air pollution control, which sets air quality standards and encourages a transition to cleaner energy sources; and energy efficiency and climate change policies, promoting renewable energy and adaptation to climate change [44].

While the environmental protection framework in the region is improving, implementation challenges remain, including a lack of funding and technical capacity. The international aspects of solar energy exchange and electricity distribution across the Western Balkans are becoming increasingly important due to growing energy demands and the transition to renewable sources. Most Western Balkan countries are connected through energy corridors and networks that enable cross-border energy exchange. However, capacities for solar energy exchange are still under development due to the specific characteristics of solar systems, whose production depends on weather conditions. Efficient solar energy exchange requires storage infrastructure, such as battery systems, which allow energy produced during sunny periods to be stored for later use or exported to neighboring countries during high demand. Solar energy exchange in the region is significant not only environmentally but also geopolitically, as it reduces dependence on fossil fuels and major energy exporters.

The Renewable Energy Directive encourages a greater share of solar and other clean energies in overall energy production, aiming to reduce emissions. The National Energy and Climate Plans (NECPs) of countries like Serbia, North Macedonia, and Albania set targets for renewable energy and CO₂ emission reduction. Before the construction of solar power plants, an environmental impact assessment (EIA) is mandatory to ensure that solar projects do not harm the natural environment. Countries in the region are also introducing financial incentives, such as subsidies and feed-in tariffs, for solar projects, supporting ecological transition. The feed-in tariff (FiT) system is an incentive for renewable energy plants, where the distribution or transmission grid operator contracts with the plant operator to pay a predetermined price for each unit of electricity delivered over an agreed period [45].

According to Montenegro’s Energy Law, the National Energy and Climate Plan specifically includes, under Article 8, paragraph 2, national targets related to greenhouse gas emissions; renewable energy use; energy efficiency; energy security; the internal energy market; and research, innovation, and competitiveness [43]. In addition, regulations are harmonized with EU standards for air quality and pollution control, supporting a sustainable transition to solar energy and reducing the ecological footprint. In May 2021, the International Energy Agency (IEA) published a study [46] analyzing a complete decarbonization scenario by 2050, projecting that, by 2050, 90% of global electricity production could come from wind and solar photovoltaic power plants.

2.2. Recurrent Neural Networks

An RNN [13] is a specialized variant of a neural network designed in such a way as to allow for the handling of sequential data. Many core elements of a neural network are maintained in an RNN, with neurons and connections remaining practically identical. However, the RNN introduces recurrent self-connections for neurons, thus allowing preceding neuron activations to influence future outcomes. Given an input sequence I, an RNN operation for each time step t can be described as follows:

$$\left[\begin{array}{c}{\widehat{o}}_t\\ h_t\end{array}\right]={\varphi }_W(i_t,h_{t-1})$$

(1)

where ${\widehat{o}}_t$ represents the output and $h_t$ denotes the hidden state at time t. A neural network ${\varphi }_W$ is characterized by a weighted network W. While the simple RNN expanded the capabilities available to researchers working with sequential data and neural networks, new issues arose. Specifically, vanishing and exploding gradients tend to disrupt network training and can result in suboptimal overall performance. Thus, mode-refined versions of these models have been developed.

2.3. Long Short-Term Memory Networks

One expanded version of the simple RNN is long short-term memory (LSTM) [47]. The LSTM network expands on the recurrent structure and integrates a complex series of gates to control the flow of information within the network, allowing some information to be retained within the network for later use. A cell state is introduced and used to preserve data. A forget gate $f_t$ can be used to clear a state.

$$f_t=\sigma (W_f{x}_t+U_f{h}_{t-1}+b_f)$$

(2)

where $x_t$ signifies its inputs at time step t, $h_{t-1}$ represents the previous hidden state, and $W_f$ and $U_f$ refer to the weight coefficients linked to these inputs, with $b_f$ representing the bias vector. Incoming data can be introduced to the cell state by using an input gate ($i_t$), as outlined in Equation (3).

$$i_t=\sigma (W_i{x}_t+U_i{h}_{t-1}+b_i)$$

(3)

The weight coefficients relevant to this step are given by $W_i$ and $U_i$, with the bias represented by $b_i$. A series of additional candidate values is computed through a hyperbolic tangent layer, as shown in Equation (4).

$$\widetilde{C_t}=tanh(W_c{x}_t+U_c{h}_{t-1}+b_c)$$

(4)

Here, it is essential to consider the weight coefficients $W_c$ and $U_c$, as well as the bias term $b_c$. To update the cell state, an element-wise product ⊙ is used in combination with the forget gate $f_t$, which clears the prior cell state $C_{t-1}$ to allow the updated cell state $C_t$ to be established with the current data. The newly computed candidate values $\widetilde{C_t}$ are multiplied by the input gate $i_t$ and then combined with this result, as defined by Equation (5).

$$C_t=f_t\odot C_{t-1}+i_t\odot \widetilde{C_t}$$

(5)

The initial sigmoid output, represented by $o_t$, undergoes further processing, as indicated in Equation (6), where the cell state influences this processing. This resulting output is then passed through a $tanh$ layer, as specified in Equation (7), resulting in the updated hidden state. Here, $W_o$ and $U_o$ are the weight coefficients, while $b_o$ represents the bias term.

$$o_t=\sigma (W_o{x}_t+U_o{h}_{t-1}+b_o)$$

(6)

$$h_t=o_t\odot tanh\left(C_t\right)$$

(7)

2.4. Gated Recurrent Units

An additional variation of the simple RNN is the gated recurrent unit (GRU) [48] network. While this network also relies on a series of gates, a significantly simpler system, consisting of only update and reset gates, is utilized. This makes GRU networks less computationally complex then LSTM while still being able to resist some of the obvious drawbacks of the baseline RNN.

In a GRU network, the update gate $z_t$, which controls how much of the hidden state is replaced with new information, is computed at time step t as follows:

$$z_t=\sigma (W_z·[h_{t-1},x_t])$$

(8)

$$r_t=\sigma (W_r·[h_{t-1},x_t])$$

(9)

The candidate hidden state ${\tilde{h}}_t$ is computed as

$${\tilde{h}}_t=tanh(W·[r_t\ast h_{t-1},x_t])$$

(10)

Finally, the hidden state $h_t$ is updated by combining the previous hidden state and the candidate state:

$$h_t=(1-z_t)\ast h_{t-1}+z_t\ast {\tilde{h}}_t$$

(11)

In this context, $\sigma$ denotes the sigmoid function, ⊙ represents element-wise multiplication, and $tanh$ denotes the hyperbolic tangent function. The weights $W_z,W_r,W$ and biases are the learned parameters of the GRU.

3. Methodology

3.1. The Variable Neighborhood Search Optimizer

The variable neighborhood search (VNS) [49] algorithm utilizes a systemic approach to adapt the neighborhood structure during optimization. The idea behind this approach is to focus on exploring more distant locations within the search space and allow the algorithm to avoid local and focus on global optima. The main stages of the optimization strategy are shaking, local search, and neighborhood change.

During shaking procedures, a solution in a simulated neighborhood, different from the current best, is selected. The structure of this neighborhood is then meticulously altered to effectively explore regions. This can be represented as

$$x^{\prime }\in N_k\left(x\right)$$

(12)

where $N_k\left(x\right)$ denotes a neighborhood index in a given iteration K, while x denotes the current solution and $x^{\prime }$ is the output. Once $x^{\prime }$ is determined, a local search is conducted, as described in the following:

$$f\left(x^{″}\right)\le f\left(x^{\prime }\right)$$

(13)

If the local search finds an improved solution, meaning $f\left(x^{″}\right)<f\left(x\right)$, the current solution is updated to $x=x^{″}$, and the neighborhood index is reset to $k=1$. If not, the algorithm explores more distant neighborhoods by increasing k:

$$k\leftarrow k+1$$

(14)

These procedures are repeated until a suitable solution is found or another criterion is met. The VNS algorithm is fairly flexible, and different criteria can be used depending on the goal of optimization.

3.2. The Modified VNS Algorithm

While the original VNS [49] optimizer still showcases admirable performance, extensive testing using congress of evolutionary computing (CEC) benchmarking functions [50] hints that room for improvement exists. Empirical tests also suggest that population diversity improvements can help bolster the outcomes attained by the optimizer. Integrating an adaptive approach could help the modified optimizer strike a better balance between intensification and exploration, further benefiting the attained solution.

Diversification control mechanisms have been proposed in the literature [51] centered on the $L1$ norm. This metric allows for the consideration of diversity on both the agent and population levels. Given a set of agents p for an n-dimensional problem, the $L1$ norm can be computed as follows:

$$\overline{x_j}={\displaystyle \frac{1}{m}}\sum _{i=1}^m{x}_{ij}$$

(15)

$$D_j^p={\displaystyle \frac{1}{m}}\sum _{i=1}^m\mid x_{ij}-{\overline{x}}_j\mid$$

(16)

$$D^p={\displaystyle \frac{1}{n}}\sum _{i=1}^n{D}_j^p,$$

(17)

where $\overline{x}$ denotes the mean vector of agent positions across search space dimensions, with $D_j^p$ denoting an individual diversity vector denoted as the $L1$ norm and $D^p$ signifying the diversity score of the entire population.

Since greater diversity is preferred in the early stages, diversity is dynamically adjusted throughout optimization. The $L1$ norm manages this diversity via a dynamic threshold parameter, $D_t$. If population diversity is found to be inadequate, the worst-performing agents are removed from the population. Diversity is tracked using $D_t$, with an initial diversity value $D_{t0}$ calculated as follows:

$$D_{t0}=\sum _{j=1}^{NP}{\displaystyle \frac{(u{b}_j-l{b}_j)}{2·NP}},$$

(18)

As the algorithm progresses and solutions approach the optimal region, the value of $D_t$ should decrease from the initial value $D_t=D_{t0}$ according to the following rule:

$$D_{t+1}=D_t-D_t·{\displaystyle \frac{t}{T}},$$

(19)

where t and $t+1$ represent the current and next iterations, and T is the total number of iterations per run. In the later stages, as $D_t$ is gradually reduced, this mechanism will no longer be triggered, regardless of the value of $D^P$.

In each optimization iteration, $nrs$ worst-performing agents are removed from the population, and new solutions are generated using techniques inspired by the GA [31]. If $D_t<D_P$, then replacement agents are produced by recombining 2 random agents in the population. If the condition is not met, the two best-performing agents are recombined. By randomly changing the created agent parameters, mutation further alters the obtained solutions. The crossover and mutation mechanisms are depicted in Figure 1.

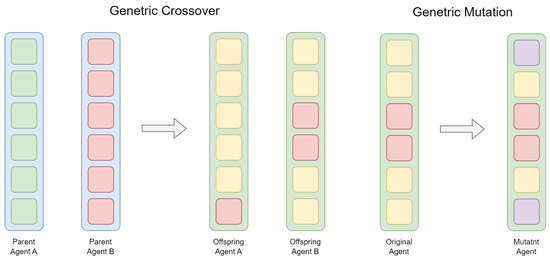
Figure 1. Genetic crossover and mutation mechanisms.

Crossover and mutation are controlled by the crossover and mutational probability parameters $CP$ and $MP$, which have been shown to provide the best results when set to $PC=0.1$ and $MP=0.1$.

The updated metaheuristic incorporates an extra adaptive parameter. To encourage exploration in the early phases of optimization, an adjustable $\psi$ parameter is used. Later phases use the original FA’s [52] remarkably potent intensification plan to encourage exploitation. The following equation presents the search processes for the FA:

$$X_i(t+1)=X_i\left(t\right)+\beta e^{-\gamma r_{ij}^2}(X_j\left(t\right)-X_i\left(t\right))+\alpha {ϵ}_i\left(t\right),$$

(20)

where, as of iteration t, $r_{ij}$ indicates the location of agent j, while $X_i\left(t\right)$ represents the position of the firefly. Depending on their distance from one another, the parameter $\beta$ regulates the attraction between i and j. $\gamma$ represents the light absorption coefficient, $\alpha$ governs the randomness, and ${ϵ}_i\left(t\right)$ represents the stochastic vector.

In order to balance exploration and exploitation and enable both algorithms to participate, the $\psi$ parameter is first set to 1.5 and is changed in each iteration in accordance with

$${\psi }_{t+1}={\psi }_t-t/T$$

(21)

where t is the current optimization iteration, and T is the total. The FA search will be used if a randomly generated value in the range $[0,1]$ at the beginning of each iteration exceeds $\psi$; if not, the VNS search techniques are used. The suggested optimizer is called the diversity-oriented adaptive VNS (DOAVNS) with the included adjustments in mind. Algorithm 1 provides the procedural pseudocode for this optimizer.

Algorithm 1 Proposed DOAVNS optimizer code.

Initialize solutions for a population P Set initial states for $NRS=2$, $\psi =1.5$ while $T>t$ do    for Agent a in P do       Evaluate agent       Assign fitness    end for    Determine $D^p$    Remove worst $NRS$ agents form population    if $DP<Dt$ then       for $NRS$ do          Apply crossover between agents and random agents          Apply mutation to the generated agents       end for    else       for $NRS$ do          Apply crossover between the best agent and a random agent          Apply mutation to the generated agents       end for    end if    Select random value R between $[0, 1]$    if $R>\psi$ then       Leverage FA search for updates    else       Leverage VNS search for updates    end if end while return Best attained solution

3.3. The ESP32 Platform for TinyML Use

The ESP32 [53] is a popular platform for IoT devices. The system-on-a-chip offers many advantages with an affordable, small footprint. The device supports several Bluetooth protocols as well as Wi-Fi functionality. In module form, several standard interfaces are available, including UART, I2C, GPIO, DAC, and ADC, as well as SD card support and motor PWM. This makes the ESP32 a very versatile platform for use in IoT networks [54], especially when considering the low minimum current demands of only 500 mA. The module relies on two low-power Xtensa 32-bit LX6 microprocessors and supports 446 KB of ROM as well as 520 KB of on-chip SRAM. The ESP32 can support a real-time operating system (RTOS). A low-power coprocessor can be utilized if computational resources are not required, such as in the case of monitoring peripherals, allowing for further power reduction.

Several frameworks exist for porting ML models for use on the ESP32, with support from the Arduino community [55]. One such framework allows for TensorFlow Lite models to be compiled, loaded, and run on the ESP32. The best-performing model optimized by metaheuristic optimizers in this work is subjected to compilation and adapted for use on the ESP32 chip. The Arduino IDE is used for programming, TensorFlow Lite is used for model compilation, and Python is used to conduct model training and optimization tasks.

TinyML offers considerable cost benefits in hardware and energy consumption. Microcontrollers compatible with TinyML like STM32 and Arduino Nano 33 BLE Sense cost approximately USD 5–20 per unit, compared to traditional IoT or edge devices such as Raspberry Pi or industrial computers, which range from USD 30 to 150. This results in hardware cost savings of up to 80%. In addition, TinyML devices typically consume just 1–10 milliwatts of power, considerably less than the 1–5 watts consumed by standard edge computing devices, resulting in over 90% reduction in energy usage and leading to lower operational costs and reduced battery maintenance needs.

Deployment and maintenance are also more economical with TinyML. These devices require minimal infrastructure and are simpler for management, resulting in an estimated 50% reduction in deployment and maintenance costs in comparison to the standard edge solutions. Furthermore, by processing data on-device, TinyML drastically reduces the volume of data sent to the cloud, considerably lowering bandwidth and storage costs. This can lead to bandwidth savings of up to 70%, which is particularly beneficial in remote or high-data environments.

3.4. Proposed Framework

The framework proposed in this paper includes three-stage optimization. This encompasses data preparation and time-series encoding. A set of samples is used to create a time series, and data are separated into training, testing, and validation portions. Agent populations are generated, and based on solution parameters, models are generated. The generated models are trained using the training portion of the dataset and evaluated on the validation set. Once a termination criterion is met, the final model is evaluated using the withheld training portion. The best trained model is then compiled for use on an MCU, and performance is simulated using the UART input. In other words, once model optimization is completed (typically using more expensive hardware such as GPUs or TPUs), these optimized models can be efficiently deployed on embedded devices, operating with minimal power consumption. A flowchart explaining the proposed framework is presented in Figure 2.

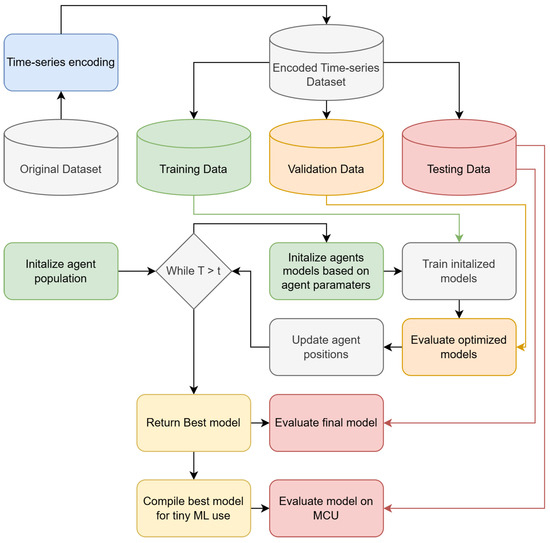
Figure 2. Proposed framework flowchart.

4. Experimental Setup

To evaluate the effectiveness of the proposed method, a publicly available dataset sourced from the real world was used, which can be found on Kaggle (https://www.kaggle.com/datasets/pythonafroz/solar-panel-energy-generation-data, accessed on 25 October 2024). The simulations concentrated on the Elm Crescent and Forest Road segments of the dataset. The data were sequentially divided into training, validation, and testing sets in a 70/10/20 ratio. Simulations were performed with a 12-step lag and 1-step-ahead targets. The dataset divisions are illustrated in Figure 3 for the Elm Crescent and in Figure 4 for the Forest Road portion of the dataset.

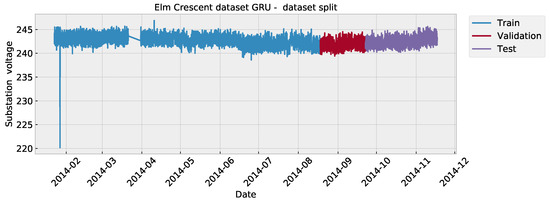
Figure 3. Elm Crescent dataset visualization.

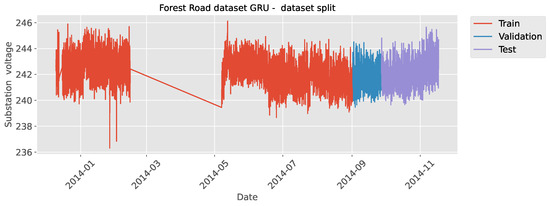
Figure 4. Forest Road dataset visualization.

A comparative simulation was conducted between the proposed algorithm and the baseline VNS [49]. The evaluation also included other algorithms, such as the GA [31], PSO [30], RSA [32], and SCHO [33]. Each optimizer was implemented separately for the simulations using the parameter configurations specified in the original papers for each algorithm. Seven iterations were performed for each optimizer, utilizing a population of five individuals, and the simulations were run independently 30 times due to the high computational cost associated with optimization. The optimizers were responsible for hyperparameter selection for the RNN, LSTM, and GRU models using empirically determined ranges, as detailed in Table 1.

Table 1. Parameter ranges for RNN, LSTM, and GRU networks.

Limit	Learning Rate	Dropout	Number of Epochs	Layers	Neurons in Layer
Lower	0.0001	0.05	300	1	12
Upper	0.0100	0.20	600	4	36

Model performance is assessed using standard regression metrics [56].

$$\mathrm{RMSE}=\sqrt{{\displaystyle \frac{1}{n}}\sum _{i=1}^n{\left(b_i-{\widehat{b}}_i\right)}^2}$$

(22)

$$\mathrm{MAE}={\displaystyle \frac{1}{n}}\sum _{i=1}^n\left|b_i-{\widehat{b}}_i\right|$$

(23)

$$\mathrm{MSE}={\displaystyle \frac{1}{n}}\sum _{i=1}^n{(b_i-{\widehat{b}}_i)}^2$$

(24)

$$R^2=1-{\displaystyle \frac{{\sum }_{i=1}^n{(b_i-{\widehat{b}}_i)}^2}{{\sum }_{i=1}^n{(b_i-\overline{b})}^2}}$$

(25)

An additional metric known as the index of agreement (IoA) [57] was also tracked during optimization to provide a more comprehensive view of the models’ performance. The formula for this metric is provided below:

$$\mathrm{IoA}=1-{\displaystyle \frac{{\sum }_{i=1}^n{(b_i-{\widehat{b}}_i)}^2}{{\sum }_{i=1}^n\left(\right|b_i-\overline{b}| + |b_i-{\widehat{b}}_i{\left|\right)}^2}}$$

(26)

In the given formulas, $b_i$ and ${\widehat{b}}_i$ represent the actual and predicted values for the i-th sample, $\overline{b}$ represents the mean value, and n is the sample size. For the simulations performed, MSE is used as the objective function, while $R^2$ serves as the indicator function.

5. Simulation Outcomes

The simulation outcomes attained in the conducted experiments are presented in three parts. Firstly, the simulation scores of the RNN on the Elm Crescent and Forest Road datasets are presented. In all tables containing simulation outcomes, the best score in every observed category is highlighted in bold. Then, LSTM simulation outcomes are presented in the same order. Finally, simulations with GRU are presented. The best-performing models in each set of simulations are then compared separately in terms of detailed metrics. The outcomes are subjected to statistical validation. Finally, simulations for a model deployed on an ESP32 are reported.

5.1. RNN Simulations

5.1.1. RNN Elm Crescent Simulations

Comparisons in terms of the objective function for Elm Crescent RNN simulation scores are presented in Table 2. The introduced optimizer attained the best-performing model, scoring an objective function result of $0.000943$. The GA showcases impressive performance, achieving the best scores in the worst, mean, and median outcomes, while the PSO showcases the highest rate of stability despite not matching the favorable performance of other optimizers. Further stability comparisons are provided in terms of objective and indicator score distribution diagrams for the objective function in Figure 5 and indicator function in Figure 6. While the modified optimizer showcases a lower rate of stability in comparison to the baseline optimizer, this is to be somewhat expected when boosting algorithm diversification. Furthermore, this drop in stability allowed the optimizer to explore more promising regions of the search space, ultimately attaining the best-performing parameter selections for this test case.

Table 2. Elm Crescent RNN simulations’ objective function outcomes.

Method	Best	Worst	Mean	Median	Std	Var
RNN-DOAVNS	0.000943	0.000986	0.000963	0.000973	$1.71\times {10}^{-5}$	$2.93\times {10}^{-10}$
RNN-VNS	0.000950	0.000979	0.000964	0.000971	$1.05\times {10}^{-5}$	$1.10\times {10}^{-10}$
RNN-GA	0.000949	0.000971	0.000960	0.000959	$1.05\times {10}^{-5}$	$1.09\times {10}^{-10}$
RNN-PSO	0.000961	0.000983	0.000972	0.000972	$\mathbf{7.40}\times {\mathbf{10}}^{-\mathbf{6}}$	$\mathbf{5.47}\times {\mathbf{10}}^{-\mathbf{11}}$
RNN-RSA	0.000960	0.000983	0.000970	0.000967	$7.63\times {10}^{-6}$	$5.83\times {10}^{-11}$
RNN-SCHO	0.000944	0.001017	0.000979	0.000987	$2.56\times {10}^{-5}$	$6.57\times {10}^{-10}$

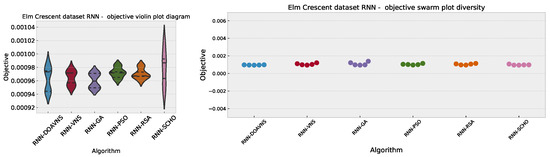
Figure 5. Elm Crescent RNN simulations’ objective function distribution diagrams.

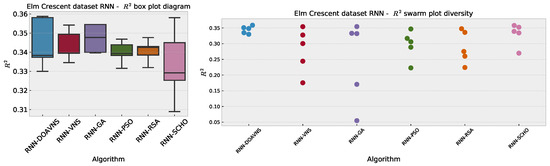
Figure 6. Elm Crescent RNN simulations’ indicator function distribution diagrams.

Further comparisons in terms of detailed metrics are provided in Table 3. The model optimized by the introduced DOAVNS optimizer showcases a definitive advantage over other models, attaining the best scores across all metrics.

Table 3. Elm Crescent RNN simulations’ detailed metrics for the best-performing optimized models.

Method	R2	MAE	MSE	RMSE	IoA
RNN-DOAVNS	0.358764	0.024683	0.000943	0.030712	0.732794
RNN-VNS	0.354170	0.024840	0.000950	0.030822	0.715560
RNN-GA	0.354504	0.024788	0.000949	0.030814	0.711936
RNN-PSO	0.346816	0.024590	0.000961	0.030997	0.742532
RNN-RSA	0.347640	0.024842	0.000960	0.030977	0.734755
RNN-SCHO	0.358032	0.024725	0.000944	0.030729	0.728545

Further insights into the performance of the optimizer and its ability to prevent premature stagnation, as well as avoid being trapped in local optima, are showcased in terms of convergence diagrams. For each of the algorithms included in the comparative analysis, convergence diagrams in terms of objective and indicator functions are provided in Figure 7 and Figure 8. The boost in diversification helps the introduced optimizer converge toward an optimum, while other algorithms struggle with local best solutions.

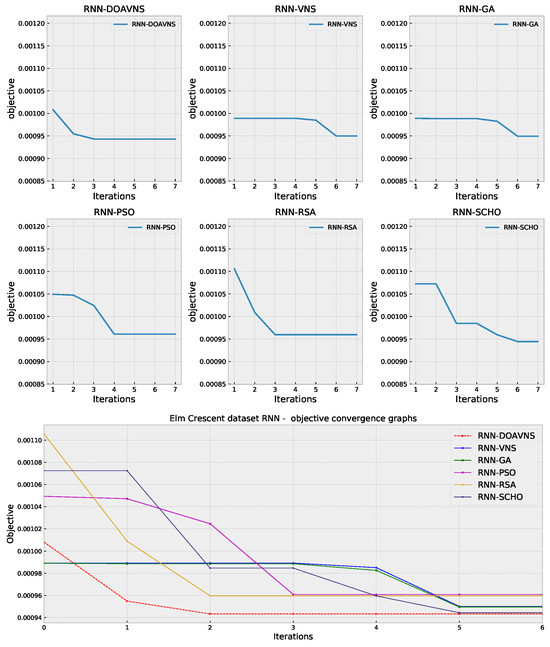
Figure 7. Elm Crescent RNN simulations’ objective function convergence diagrams.

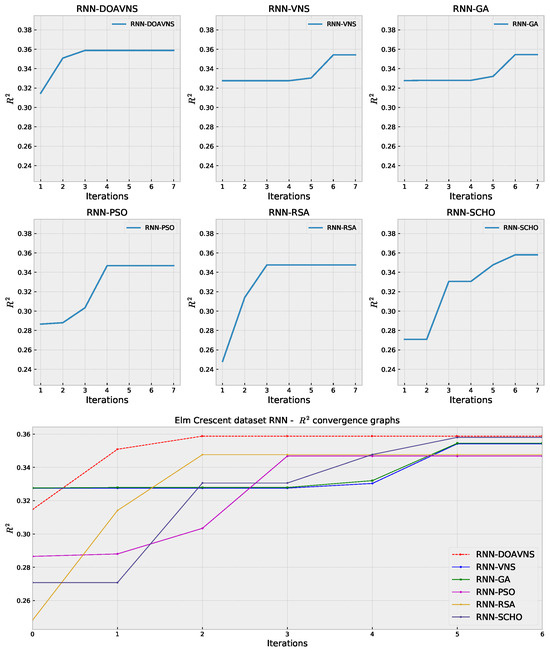
Figure 8. Elm Crescent RNN simulations’ indicator function convergence diagrams.

The parameter selections made by each algorithm for the respective best-performing model are provided in Table 4 to facilitate simulation repeatability. The predictions made by the best-performing model are provided in Figure 9, while the plot of the error over time is presented in Figure 10.

Table 4. Best-performing RNN model parameter selections for Elm Crescent simulations.

	Learning		Training	RNN	L1	L2	L3	L4
Method	Rate	Dropout	Epochs	Layers	Neurons	Neurons	Neurons	Neurons
RNN-DOAVNS	$9.70\times {10}^{-3}$	0.186	427	1	36	N/a	N/a	N/a
RNN-VNS	$7.44\times {10}^{-3}$	0.139	551	1	23	N/a	N/a	N/a
RNN-GA	$7.08\times {10}^{-3}$	0.05	586	1	18	N/a	N/a	N/a
RNN-PSO	$6.52\times {10}^{-3}$	0.2	600	1	36	N/a	N/a	N/a
RNN-RSA	$9.23\times {10}^{-3}$	0.113	600	1	20	N/a	N/a	N/a
RNN-SCHO	$9.66\times {10}^{-3}$	0.2	536	1	36	N/a	N/a	N/a

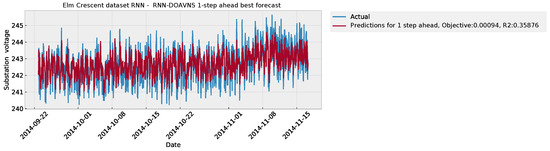
Figure 9. Forecasts of best DOAVNS model from Elm Crescent RNN simulations.

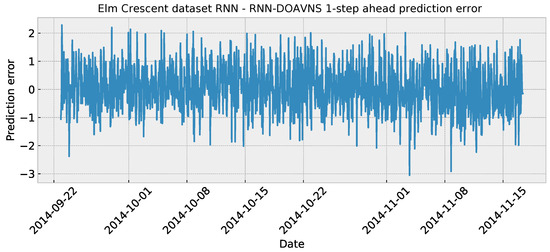
Figure 10. Elm Crescent RNN simulations’ error over time.

5.1.2. RNN Forest Road Simulations

Comparisons in terms of the objective function for Forest Road RNN simulation scores are presented in Table 5. The introduced optimizer attained the best-performing model, scoring an objective function result of $0.000943$. The introduced optimizer showcases superior performance in the mean and median outcomes, with respective scores of $0.007275$ and $0.007275$. The SCHO algorithm attained the best outcomes in terms of worst-case simulations. The highest rate of stability is demonstrated by the SCHO. Further stability comparisons are provided in terms of objective and indicator score distribution diagrams for the objective function in Figure 11 and indicator function in Figure 12. The modified algorithm showcases a slightly reduced stability in this set of simulations, focusing on a more promising region in comparison to all other optimizers, as well as the baseline PSO.

Table 5. Forest Road RNN simulations’ objective function outcomes.

Method	Best	Worst	Mean	Median	Std	Var
RNN-DOAVNS	0.007205	0.007366	0.007275	0.007275	$4.86\times {10}^{-5}$	$2.36\times {10}^{-9}$
RNN-VNS	0.007223	0.007357	0.007293	0.007290	$4.70\times {10}^{-5}$	$2.20\times {10}^{-9}$
RNN-GA	0.007241	0.007354	0.007307	0.007322	$4.15\times {10}^{-5}$	$1.72\times {10}^{-9}$
RNN-PSO	0.007265	0.007376	0.007308	0.007296	$3.74\times {10}^{-5}$	$1.40\times {10}^{-9}$
RNN-RSA	0.007276	0.007385	0.007314	0.007283	$4.59\times {10}^{-5}$	$2.11\times {10}^{-9}$
RNN-SCHO	0.007267	0.007337	0.007313	0.007320	$\mathbf{2.50}\times {\mathbf{10}}^{-\mathbf{5}}$	$\mathbf{6.23}\times {\mathbf{10}}^{-\mathbf{10}}$

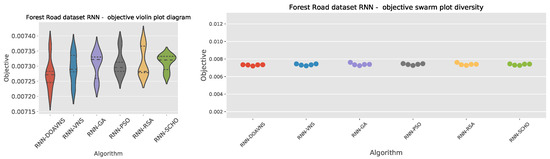
Figure 11. Forest Road RNN simulations’ objective function distribution diagrams.

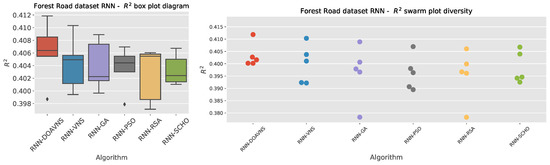
Figure 12. Forest Road RNN simulations’ indicator function distribution diagrams.

Further comparisons in terms of detailed metrics are provided in Table 6. The model optimized by the introduced DOAVNS optimizer showcases the best scores in terms of R², MSE, and RMSE, while the GA showcases a high score in terms of MAE, and the SCHO showcases the best IoA score.

Table 6. Forest Road RNN simulations’ detailed metrics for the best-performing optimized models.

Method	R2	MAE	MSE	RMSE	IoA
RNN-DOAVNS	0.411854	0.067344	0.007205	0.084881	0.758396
RNN-VNS	0.410324	0.067163	0.007223	0.084991	0.757463
RNN-GA	0.408894	0.067151	0.007241	0.085094	0.760513
RNN-PSO	0.406952	0.068032	0.007265	0.085234	0.750386
RNN-RSA	0.406050	0.067403	0.007276	0.085299	0.756161
RNN-SCHO	0.406745	0.067264	0.007267	0.085249	0.759018

Convergence diagrams for each optimizer are provided in Figure 13 and Figure 14 for objective and indicator scores. The introduced optimizer overcomes a local optimum and converges toward a better solution in iteration five, outperforming competing optimizers.

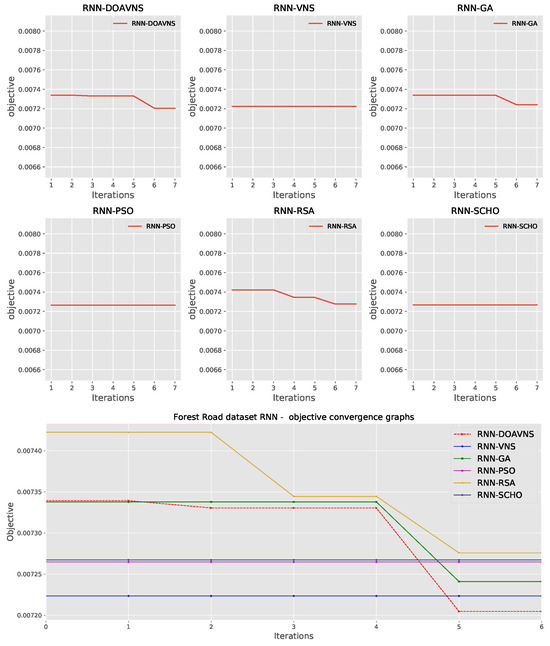
Figure 13. Forest Road RNN simulations’ objective function convergence diagrams.

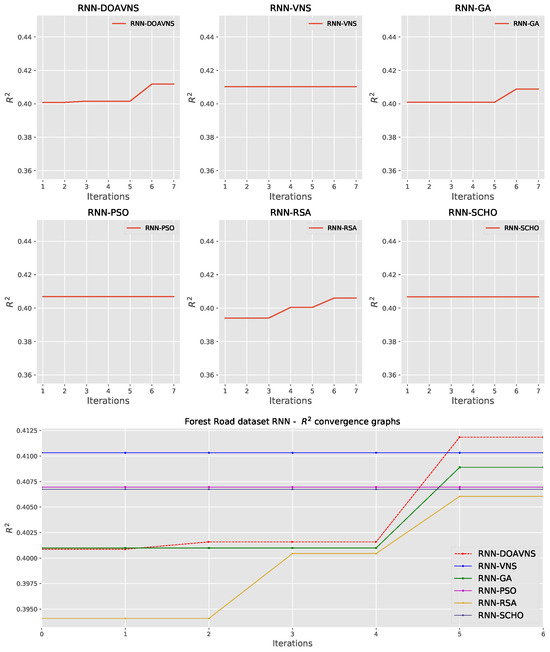
Figure 14. Forest Road RNN simulations’ indicator function convergence diagrams.

The parameter selections made by each algorithm for the respective best-performing model are provided in Table 7 to facilitate simulation repeatability. The predictions made by the best-performing model are provided in Figure 15, while the plot of the error over time is showcased in Figure 16.

Table 7. Best-performing RNN model parameter selections for Forest Road simulations.

	Learning		Training	RNN	L1	L2	L3	L4
Method	Rate	Dropout	Epochs	Layers	Neurons	Neurons	Neurons	Neurons
RNN-DOAVNS	0.1	0.103	521	3	22	32	36	N/a
RNN-VNS	0.01	0.052	555	1	21	N/a	N/a	N/a
RNN-GA	$5.16\times {10}^{-3}$	0.186	541	3	36	34	31	N/a
RNN-PSO	$5.48\times {10}^{-3}$	0.083	349	3	16	24	27	N/a
RNN-RSA	$7.77\times {10}^{-3}$	0.094	308	1	36	N/a	N/a	N/a
RNN-SCHO	$4.67\times {10}^{-3}$	0.133	535	4	18	18	34	14

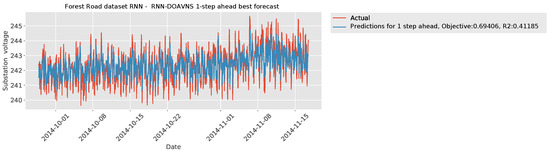
Figure 15. Forecasts of best DOAVNS model from Forest Road RNN simulations.

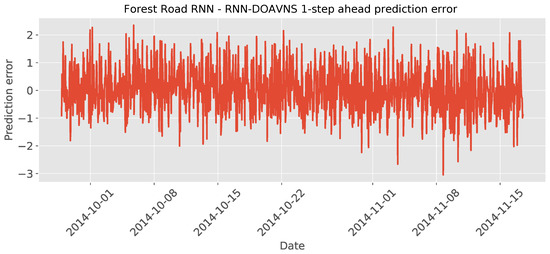
Figure 16. Forest Road RNN simulations’ error over time.

5.2. LSTM Simulations

5.2.1. LSTM Elm Crescent Simulations

Comparisons in terms of the objective function for Elm Crescent LSTM simulation scores are presented in Table 8. The introduced optimizer attained the best-performing model, scoring an objective function result of $0.001054$. The PSO optimizer showcases decent results for the worst and mean scores; however, the introduced optimizer showcases the highest median scores. The VNS showcases the highest rate of stability when compared to other optimizers included in the comparative simulations. Further stability comparisons are provided in terms of objective and indicator score distribution diagrams for the objective function in Figure 17 and indicator function in Figure 18. A notable drop in stability can be observed for the introduced optimizer. This is to be somewhat expected with increasing diversification. However, the introduced modifications help improve performance, allowing the introduced modified algorithm to locate the most promising region and attain the highest objective scores.

Table 8. Elm Crescent LSTM simulations’ objective function outcomes.

Method	Best	Worst	Mean	Median	Std	Var
LSTM-DOAVNS	0.001054	0.001340	0.001181	0.001131	$9.84\times {10}^{-5}$	$9.68\times {10}^{-9}$
LSTM-VNS	0.001157	0.001184	0.001171	0.001171	$\mathbf{8.92}\times {\mathbf{10}}^{-\mathbf{6}}$	$\mathbf{7.96}\times {\mathbf{10}}^{-\mathbf{11}}$
LSTM-GA	0.001062	0.001317	0.001165	0.001146	$7.73\times {10}^{-5}$	$5.97\times {10}^{-9}$
LSTM-PSO	0.001091	0.001174	0.001136	0.001151	$2.96\times {10}^{-5}$	$8.78\times {10}^{-10}$
LSTM-RSA	0.001111	0.001322	0.001174	0.001132	$7.25\times {10}^{-5}$	$5.25\times {10}^{-9}$
LSTM-SCHO	0.001113	0.001295	0.001177	0.001143	$7.10\times {10}^{-5}$	$5.04\times {10}^{-9}$

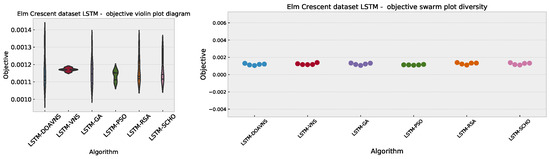
Figure 17. Elm Crescent LSTM simulations’ objective function distribution diagrams.

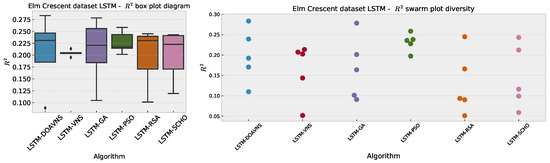
Figure 18. Elm Crescent LSTM simulations’ indicator function distribution diagrams.

Further comparisons in terms of detailed metrics are provided in Table 9. The model optimized by the introduced DOAVNS optimizer showcases the best scores in terms of all metrics except the IoA, where the GA showcases the highest score.

Table 9. Elm Crescent LSTM simulations’ detailed metrics for the best-performing optimized models.

Method	R2	MAE	MSE	RMSE	IoA
LSTM-DOAVNS	0.283279	0.026561	0.001054	0.032469	0.627262
LSTM-VNS	0.213508	0.027945	0.001157	0.034013	0.588553
LSTM-GA	0.278216	0.026651	0.001062	0.032584	0.653422
LSTM-PSO	0.258380	0.027084	0.001091	0.033028	0.644435
LSTM-RSA	0.244873	0.027386	0.001111	0.033328	0.599909
LSTM-SCHO	0.243068	0.027403	0.001113	0.033368	0.612395

Convergence diagrams for each optimizer are provided in Figure 19 and Figure 20 for objective and indicator scores. The introduced optimizer overcomes a local optimum and converges toward a better solution in iteration four, outperforming competing optimizers.

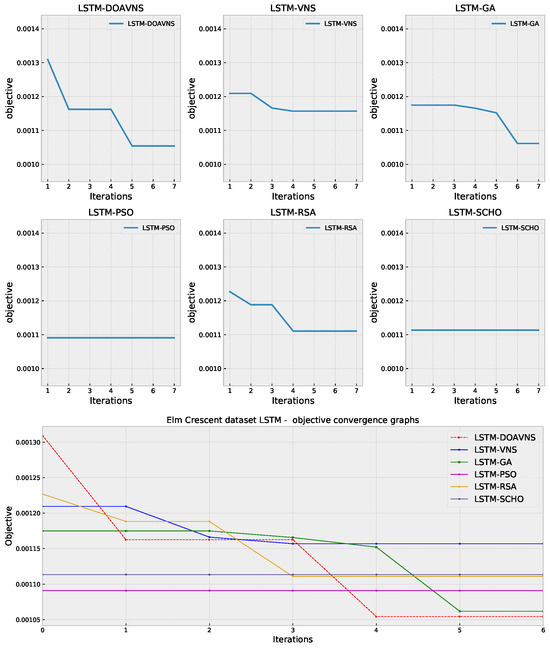
Figure 19. Elm Crescent LSTM simulations’ objective function convergence diagrams.

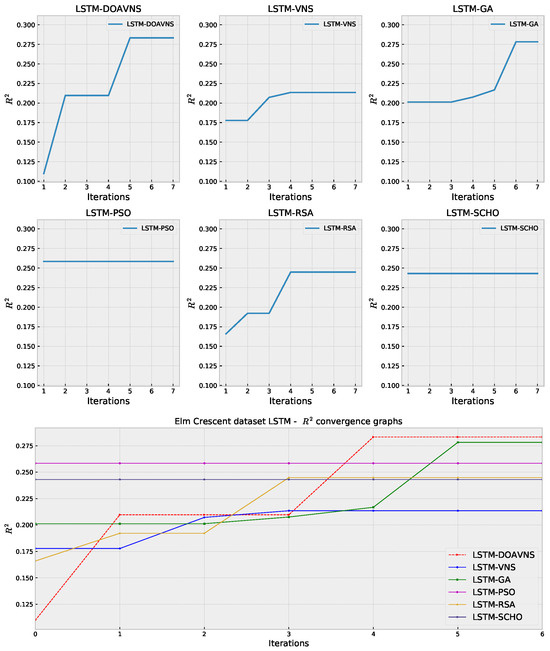
Figure 20. Elm Crescent LSTM simulations’ indicator function convergence diagrams.

The parameter selections made by each algorithm for the respective best-performing model are provided in Table 10 to facilitate simulation repeatability. The predictions made by the best-performing model are provided in Figure 21, while the plot showcasing the error over time is outlined in Figure 22.

Table 10. Best-performing LSTM model parameter selections for Elm Crescent simulations.

	Learning		Training	LSTM	L1	L2	L3	L4
Method	Rate	Dropout	Epochs	Layers	Neurons	Neurons	Neurons	Neurons
LSTM-DOAVNS	$1.00\times {10}^{-2}$	0.05	600	1	36	N/a	N/a	N/a
LSTM-VNS	$5.16\times {10}^{-3}$	0.081	445	1	31	N/a	N/a	N/a
LSTM-GA	$6.92\times {10}^{-3}$	0.136	600	1	25	N/a	N/a	N/a
LSTM-PSO	$1.00\times {10}^{-2}$	0.2	600	1	16	N/a	N/a	N/a
LSTM-RSA	$7.84\times {10}^{-3}$	0.058	600	1	33	N/a	N/a	N/a
LSTM-SCHO	$5.19\times {10}^{-3}$	0.097	598	1	35	N/a	N/a	N/a

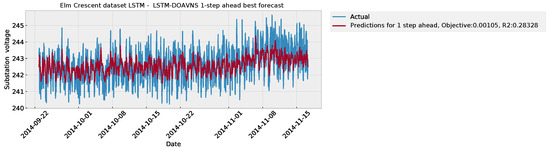
Figure 21. Forecasts of best DOAVNS model from Elm Crescent LSTM simulations.

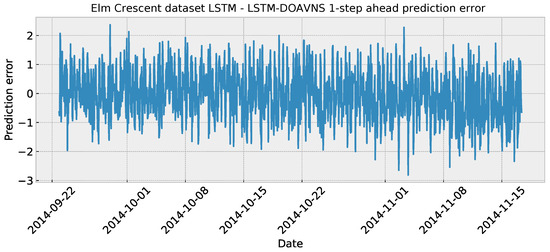
Figure 22. Elm Crescent LSTM simulations’ error over time.

5.2.2. LSTM Forest Road Simulations

Comparisons in terms of the objective function for Forest Road LSTM simulation scores are presented in Table 11. The introduced optimizer attained the best-performing model, scoring an objective function result of $0.007066$. The optimizer also scores highly in terms of the mean and median. However, the RSA attains the best outcome in the worst-case simulation. The GA showcases the highest stability rating. Further stability comparisons are provided in terms of objective and indicator score distribution diagrams for the objective function in Figure 23 and indicator function in Figure 24. A slight drop in stability can be observed for the introduced optimizer. This is to be somewhat expected with increasing diversification. Nevertheless, these modifications also allow the optimizer to avoid local optima, attaining overall better results in comparison to other tested algorithms.

Table 11. Forest Road LSTM simulations’ objective function outcomes.

Method	Best	Worst	Mean	Median	Std	Var
LSTM-DOAVNS	0.007066	0.007250	0.007145	0.007127	$6.58\times {10}^{-5}$	$4.33\times {10}^{-9}$
LSTM-VNS	0.007085	0.007243	0.007166	0.007171	$4.94\times {10}^{-5}$	$2.44\times {10}^{-9}$
LSTM-GA	0.007138	0.007270	0.007193	0.007187	$\mathbf{4.41}\times {\mathbf{10}}^{-\mathbf{5}}$	$\mathbf{1.94}\times {\mathbf{10}}^{-\mathbf{9}}$
LSTM-PSO	0.007110	0.007344	0.007234	0.007215	$6.90\times {10}^{-5}$	$4.76\times {10}^{-9}$
LSTM-RSA	0.007104	0.007241	0.007174	0.007178	$4.91\times {10}^{-5}$	$2.41\times {10}^{-9}$
LSTM-SCHO	0.007084	0.007263	0.007155	0.007134	$6.91\times {10}^{-5}$	$4.77\times {10}^{-9}$

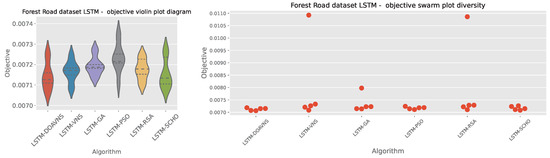
Figure 23. Forest Road LSTM simulations’ objective function distribution diagrams.

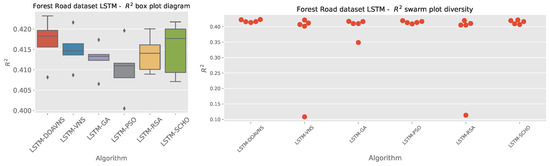
Figure 24. Forest Road LSTM simulations’ indicator function distribution diagrams.

Further comparisons in terms of detailed metrics are provided in Table 12. The model optimized by the introduced DOAVNS optimizer showcases the best scores in terms of all metrics in the conducted tests.

Table 12. Forest Road LSTM simulations’ detailed metrics for the best-performing optimized models.

Method	R2	MAE	MSE	RMSE	IoA
LSTM-DOAVNS	0.423220	0.066313	0.007066	0.084057	0.777800
LSTM-VNS	0.421609	0.066415	0.007085	0.084174	0.779413
LSTM-GA	0.417343	0.066647	0.007138	0.084484	0.770246
LSTM-PSO	0.419611	0.066517	0.007110	0.084319	0.772205
LSTM-RSA	0.420049	0.066523	0.007104	0.084287	0.768804
LSTM-SCHO	0.421743	0.066467	0.007084	0.084164	0.786252

Convergence diagrams for each optimizer are provided in Figure 25 and Figure 26 for objective and indicator scores. The introduced optimizer overcomes a local optimum and converges toward a better solution, outperforming competing optimizers.

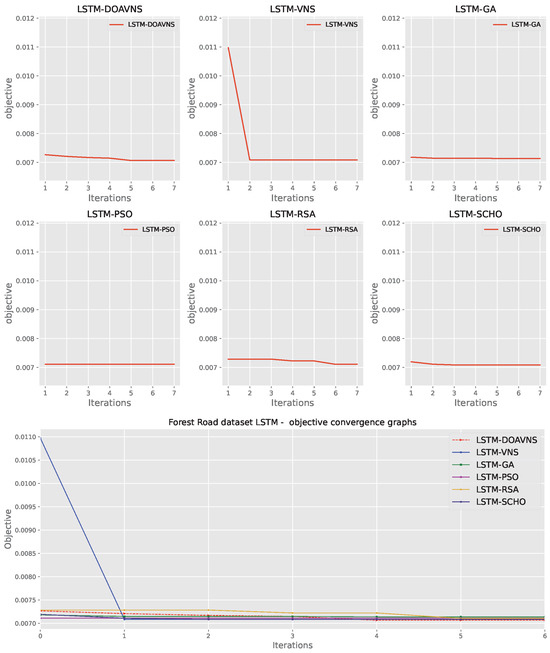
Figure 25. Forest Road LSTM simulations’ objective function convergence diagrams.

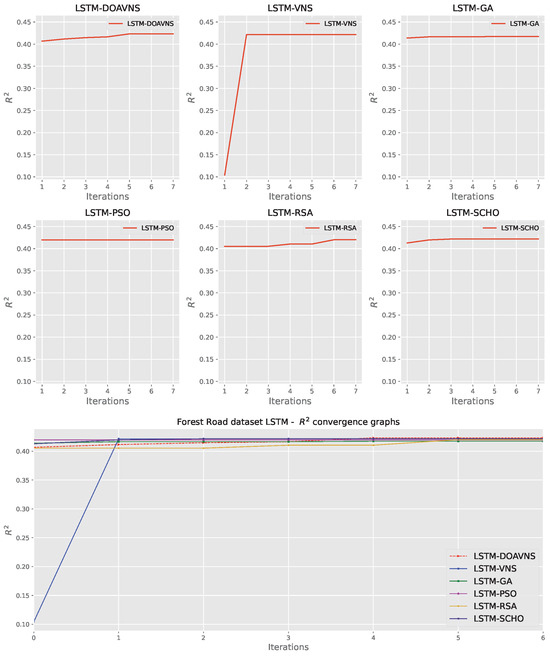
Figure 26. Forest Road LSTM simulations’ indicator function convergence diagrams.

The parameter selections made by each algorithm for the respective best-performing model are provided in Table 13 to facilitate simulation repeatability. The predictions made by the best-performing model are provided in Figure 27, while Figure 28 provides insight into the error over time.

Table 13. Best-performing LSTM model parameter selections for Forest Road simulations.

	Learning		Training	LSTM	L1	L2	L3	L4
Method	Rate	Dropout	Epochs	Layers	Neurons	Neurons	Neurons	Neurons
LSTM-DOAVNS	$6.45\times {10}^{-3}$	0.062	599	3	21	27	26	N/a
LSTM-VNS	$1.00\times {10}^{-2}$	0.2	600	3	36	12	30	N/a
LSTM-GA	$8.96\times {10}^{-3}$	0.05	600	2	35	13	N/a	N/a
LSTM-PSO	$8.73\times {10}^{-3}$	0.094	442	2	36	19	N/a	N/a
LSTM-RSA	$8.47\times {10}^{-3}$	0.198	509	2	20	14	N/a	N/a
LSTM-SCHO	$1.00\times {10}^{-2}$	0.135	600	2	36	29	N/a	N/a

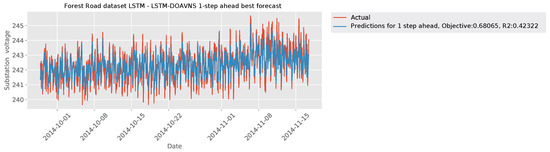
Figure 27. Forecasts of best DOAVNS model from Forest Road LSTM simulations.

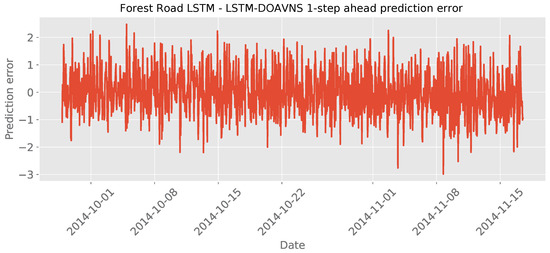
Figure 28. Forest Road LSTM simulations’ error over time.

5.3. GRU Simulations

5.3.1. GRU Elm Crescent Simulations

Comparisons in terms of the objective function for Elm Crescent GRU simulation scores are presented in Table 14. The introduced optimizer attained the best-performing model, scoring an objective function result of $0.000935$, as well as the best worst-case and mean scores. However, the best median performance goes to the GA. Stability rates are best maintained by the VNA algorithm, despite the models not attaining high scores in other metrics. Further stability comparisons are provided in terms of objective and indicator score distribution diagrams for the objective function in Figure 29 and indicator function in Figure 30. A notable drop in stability can be observed for the introduced optimizer. However, as previously stated, this drop can be attributed to the boost in diversification.

Table 14. Elm Crescent GRU simulations’ objective function outcomes.

Method	Best	Worst	Mean	Median	Std	Var
GRU-DOAVNS	0.000935	0.000987	0.000966	0.000972	$1.93\times {10}^{-5}$	$3.71\times {10}^{-10}$
GRU-VNS	0.000953	0.000990	0.000967	0.000967	$\mathbf{1.24}\times {\mathbf{10}}^{-\mathbf{5}}$	$\mathbf{1.53}\times {\mathbf{10}}^{-\mathbf{10}}$
GRU-GA	0.000947	0.001013	0.000969	0.000958	$2.59\times {10}^{-5}$	$6.71\times {10}^{-10}$
GRU-PSO	0.000954	0.001007	0.000978	0.000966	$2.09\times {10}^{-5}$	$4.37\times {10}^{-10}$
GRU-RSA	0.000943	0.001029	0.000981	0.000968	$3.14\times {10}^{-5}$	$9.85\times {10}^{-10}$
GRU-SCHO	0.000946	0.000989	0.000975	0.000980	$1.51\times {10}^{-5}$	$2.28\times {10}^{-10}$

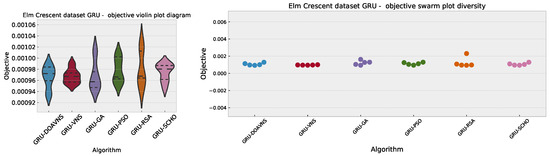
Figure 29. Elm Crescent GRU simulations’ objective function distribution diagrams.

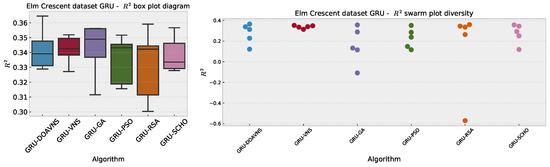
Figure 30. Elm Crescent GRU simulations’ indicator function distribution diagrams.

Further comparisons in terms of detailed metrics are provided in Table 15. The model optimized by the introduced DOAVNS optimizer showcases the best scores in terms of all metrics in the conducted tests.

Table 15. Elm Crescent GRU simulations’ detailed metrics for the best-performing optimized models.

Method	R2	MAE	MSE	RMSE	IoA
GRU-DOAVNS	0.364567	0.024732	0.000935	0.030573	0.714853
GRU-VNS	0.351947	0.024926	0.000953	0.030875	0.699482
GRU-GA	0.356229	0.024853	0.000947	0.030772	0.698655
GRU-PSO	0.351697	0.024939	0.000954	0.030881	0.709874
GRU-RSA	0.359132	0.024496	0.000943	0.030703	0.724398
GRU-SCHO	0.356679	0.024926	0.000946	0.030762	0.695907

Convergence diagrams for each optimizer are provided in Figure 31 and Figure 32 for objective and indicator scores. The introduced optimizer overcomes a local optimum and converges toward a better solution, outperforming competing optimizers.

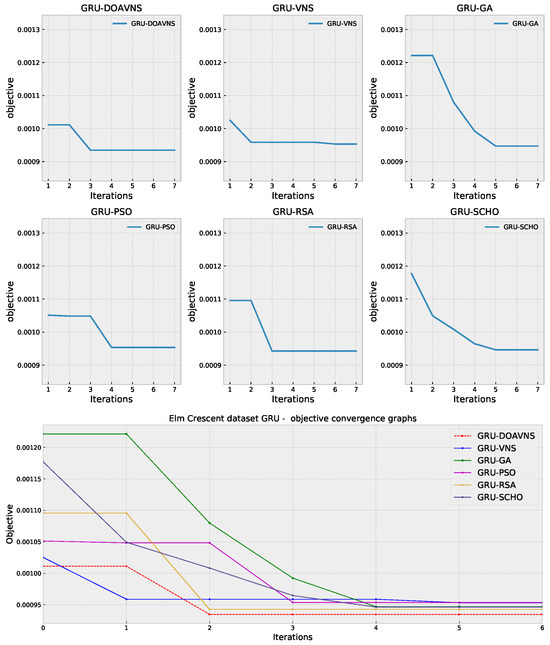
Figure 31. Elm Crescent GRU simulations’ objective function convergence diagrams.

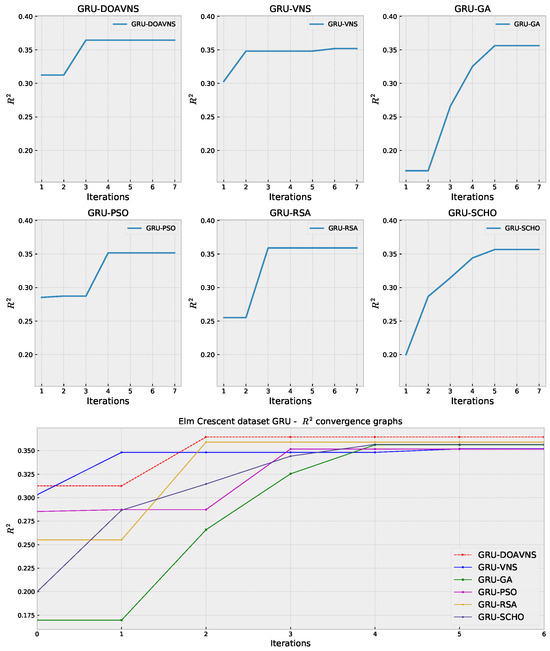
Figure 32. Elm Crescent GRU simulations’ indicator function convergence diagrams.

The parameter selections made by each algorithm for the respective best-performing model are provided in Table 16 to facilitate simulation repeatability. The predictions made by the best-performing model are provided in Figure 33. The plot of the error over time is given in Figure 34.

Table 16. Best-performing GRU model parameter selections for Elm Crescent simulations.

	Learning		Training	GRU	L1	L2	L3	L4
Method	Rate	Dropout	Epochs	Layers	Neurons	Neurons	Neurons	Neurons
GRU-DOAVNS	$1.00\times {10}^{-2}$	0.175	600	1	36	N/a	N/a	N/a
GRU-VNS	$7.79\times {10}^{-3}$	0.0699	600	1	19	N/a	N/a	N/a
GRU-GA	$6.08\times {10}^{-3}$	0.0747	600	1	31	N/a	N/a	N/a
GRU-PSO	$1.00\times {10}^{-2}$	0.05	600	2	32	27	N/a	N/a
GRU-RSA	$8.58\times {10}^{-3}$	0.15	600	3	19	23	35	N/a
GRU-SCHO	$9.45\times {10}^{-3}$	0.125	596	1	13	N/a	N/a	N/a

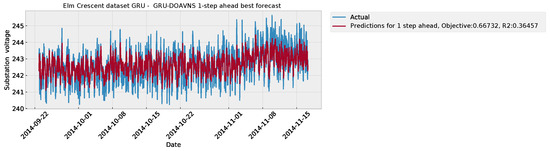
Figure 33. Forecasts of best DOAVNS model from Elm Crescent GRU simulations.

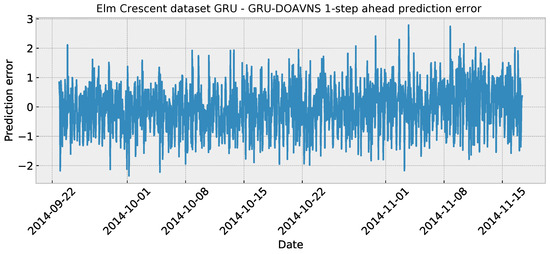
Figure 34. Elm Crescent GRU simulations’ error over time.

5.3.2. GRU Forest Road Simulations

Comparisons in terms of the objective function for Forest Road GRU simulation scores are presented in Table 17. While the introduced optimizer showcases the best outcome in terms of best-case executions with a score of $0.007011$, the other optimizers showcase good performance as well, with the VNS scoring highest in terms of worst-case outcomes, while the PSO has high scores in terms of the median and mean, and the VNS optimizer has the highest rate of stability. Further stability comparisons are provided in terms of objective and indicator score distribution diagrams for the objective function in Figure 35 and indicator function in Figure 36. A notable drop in stability can be observed for the introduced optimizer. However, as previously stated, this drop can be attributed to the boost in diversification.

Table 17. Forest Road GRU simulations’ objective function outcomes.

Method	Best	Worst	Mean	Median	Std	Var
GRU-DOAVNS	0.007011	0.007211	0.007145	0.007171	$7.54\times {10}^{-5}$	$5.68\times {10}^{-9}$
GRU-VNS	0.007131	0.007190	0.007169	0.007179	$\mathbf{2.27}\times {\mathbf{10}}^{-\mathbf{5}}$	$\mathbf{5.15}\times {\mathbf{10}}^{-\mathbf{10}}$
GRU-GA	0.007082	0.007229	0.007143	0.007125	$5.19\times {10}^{-5}$	$2.69\times {10}^{-9}$
GRU-PSO	0.007021	0.007247	0.007128	0.007110	$7.95\times {10}^{-5}$	$6.32\times {10}^{-9}$
GRU-RSA	0.007063	0.007291	0.007167	0.007156	$8.11\times {10}^{-5}$	$6.58\times {10}^{-9}$
GRU-SCHO	0.007018	0.007249	0.007145	0.007187	$9.02\times {10}^{-5}$	$8.14\times {10}^{-9}$

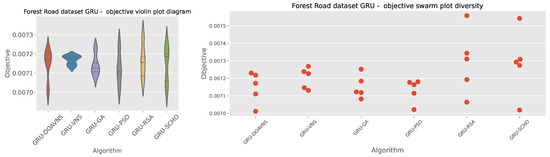
Figure 35. Forest Road GRU simulations’ objective function distribution diagrams.

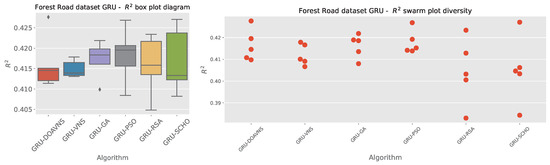
Figure 36. Forest Road GRU simulations’ indicator function distribution diagrams.

Further comparisons in terms of detailed metrics are provided in Table 18. The model optimized by the introduced DOAVNS optimizer showcases the best scores in terms of all metrics in the conducted tests. The introduced optimizer scores the highest in terms of R², MSE, and RMSE. However, the RSA shows admirable performance in terms of MAE as well as the IoA.

Table 18. Forest Road GRU simulations’ detailed metrics for the best-performing optimized models.

Method	R2	MAE	MSE	RMSE	IoA
GRU-DOAVNS	0.427637	0.066774	0.007011	0.083734	0.784870
GRU-VNS	0.417857	0.066844	0.007131	0.084447	0.770818
GRU-GA	0.421873	0.066330	0.007082	0.084155	0.772736
GRU-PSO	0.426849	0.066375	0.007021	0.083792	0.774807
GRU-RSA	0.423387	0.066148	0.007063	0.084044	0.789407
GRU-SCHO	0.427066	0.066585	0.007018	0.083776	0.783809

Convergence diagrams for each optimizer are provided in Figure 37 and Figure 38 for objective and indicator scores. The introduced optimizer overcomes a local optimum and converges toward a better solution, outperforming competing optimizers.

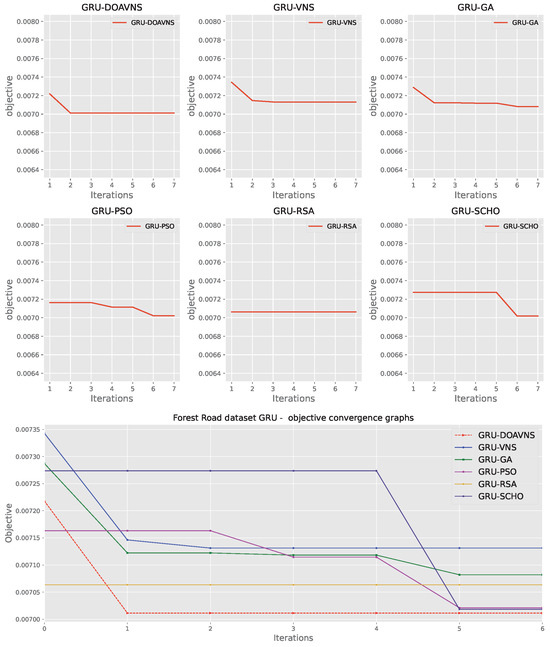
Figure 37. Forest Road GRU simulations’ objective function convergence diagrams.

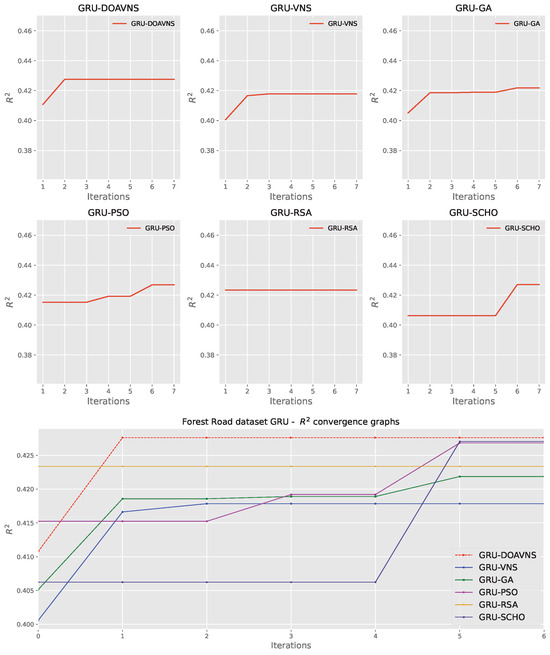
Figure 38. Forest Road GRU simulations’ indicator function convergence diagrams.

The parameter selections made by each algorithm for the respective best-performing model are provided in Table 19 to facilitate simulation repeatability. The predictions made by the best-performing model are provided in Figure 39. Lastly, Figure 40 plots the error over time.

Table 19. Best-performing GRU model parameter selections for Forest Road simulations.

	Learning		Training	LSTM	L1	L2	L3	L4
Method	Rate	Dropout	Epochs	Layers	Neurons	Neurons	Neurons	Neurons
GRU-DOAVNS	$1.00\times {10}^{-2}$	0.2	600	4	12	12	36	12
GRU-VNS	$1.95\times {10}^{-3}$	0.0594	600	4	36	13	12	12
GRU-GA	$5.41\times {10}^{-3}$	0.116	600	4	12	29	35	15
GRU-PSO	$5.37\times {10}^{-3}$	0.128	600	3	30	18	17	N/a
GRU-RSA	$4.57\times {10}^{-3}$	0.160	564	4	33	32	23	14
GRU-SCHO	$8.66\times {10}^{-3}$	0.0838	600	2	23	12	N/a	N/a

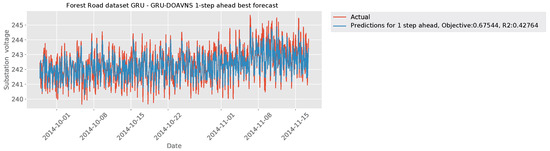
Figure 39. Forecasts of best DOAVNS model from Forest Road GRU simulations.

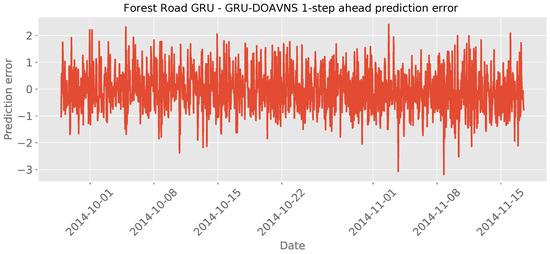
Figure 40. Forest Road GRU simulations’ error over time.

5.4. Comparison Between Best-Performing Models

A comparison between the best-performing optimized models in each simulation is presented in Table 20. The attained outcomes suggest that for the Elm Crescent dataset simulation, the GRU model showcases the best performance, with an R² score of $0.364567$ and an MSE of $0.000935$. In the case of Forest Road simulations, the GRU model also showcases the best scores, with an R² of $0.427637$ and an MSE of $0.007011$. Nevertheless, it is important to consider several factors when deciding on the most suitable model for use. The favorable performance of GRU makes these networks ideal for use in TinyML applications due to their relatively low computational demands in comparison to LSTM modes while still showing higher robustness and resistance to common issues in simple RNNs. For this reason, the GRU models are chosen for simulations with ESP32 devices, developed by Espressif Systems, a Chinese company based in Shanghai, China, and manufactured by TSMC using their 40 nm process.

Table 20. A comparison between the best-performing models in each simulation.

Simulation Method	R2	MAE	MSE	RMSE	IoA
Elm Crescent simulations
RNN-DOAVNS	0.358764	0.024683	0.000943	0.030712	0.732794
LSTM-DOAVNS	0.283279	0.026561	0.001054	0.032469	0.627262
GRU-DOAVNS	0.364567	0.024732	0.000935	0.030573	0.714853
Forest Road simulations
RNN-DOAVNS	0.411854	0.067344	0.007205	0.084881	0.758396
LSTM-DOAVNS	0.423220	0.066313	0.007066	0.084057	0.777800
GRU-DOAVNS	0.427637	0.066774	0.007011	0.083734	0.784870

5.5. Optimization Statistical Validation

To establish a comparison between the evaluated algorithms, statistical validation is necessary, as relying on simple one-time executions can provide misleading conclusions. The conducted simulations need to meet an established set of criteria in order to be eligible for evaluation using parametric testing. Otherwise, non-parametric tests need to be utilized [58]. A sufficient number of simulations is needed to conduct testing; therefore, 30 turns were conducted for each of the conducted experiments, with independent random seeds satisfying the independence criteria. Homoscedasticity was established via Levene’s test [59], where the resulting p values are $0.62$ for each of the simulations, suggesting this criterion is also met. Finally, the normality criterion was tested with the Shapiro–Wilk [60] test. The attained outcomes are presented in Table 21. With the attained values falling below $0.05$, the null hypothesis is rejected, suggesting that the normality assumption is not satisfied, and parametric test usage cannot be justified. Normality observations are further confirmed by the objective function KDE diagrams presented in Figure 41 and Figure 42 for Elm Crescent and Forest Road simulations.

Table 21. Shapiro–Wilk scores for forecasting experiments for normality condition evaluation.

Approach	DOAVNS	VNS	GA	PSO	RSA	SCHO
Elm Crescent
Elm Crescent RNN	0.032	0.029	0.041	0.028	0.024	0.036
Elm Crescent LSTM	0.031	0.034	0.023	0.032	0.027	0.033
Elm Crescent GRU	0.037	0.024	0.029	0.032	0.031	0.029
Forest road
Forest Road RNN	0.035	0.028	0.023	0.034	0.029	0.027
Forest Road LSTM	0.028	0.029	0.033	0.031	0.031	0.029
Forest Road GRU	0.030	0.034	0.024	0.028	0.028	0.031

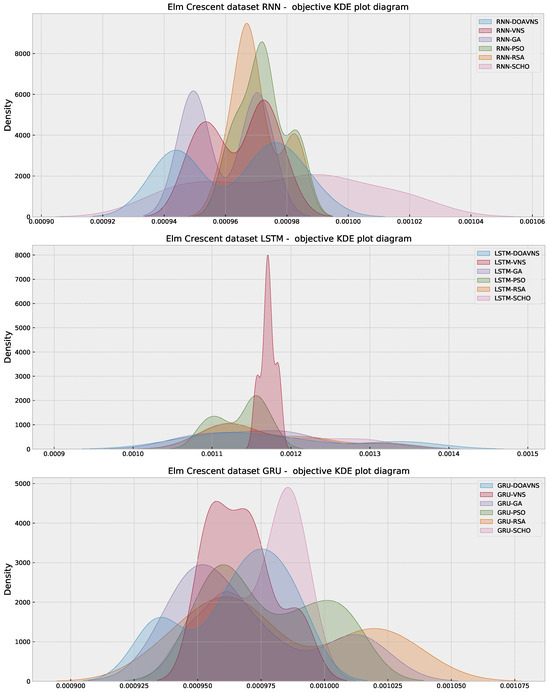
Figure 41. Elm Crescent simulation KDE diagrams.

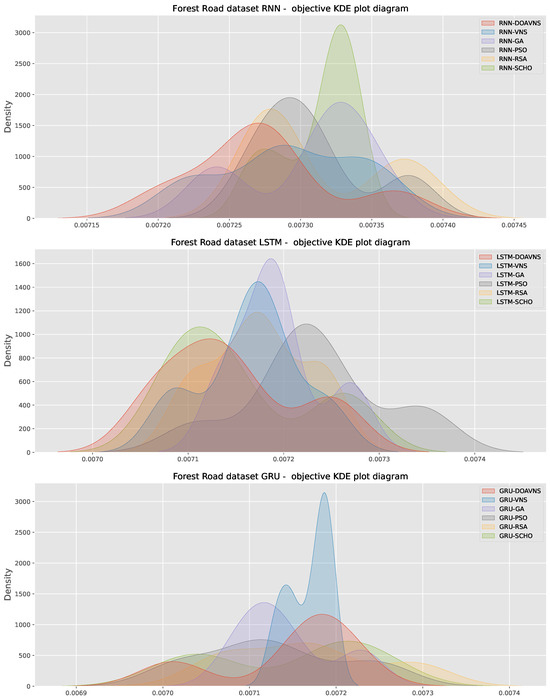
Figure 42. Forest road simulation KDE diagrams.

As the conditions needed for parametric test application were not met, this work resorted to the utilization of the Wilcoxon signed-rank test [61] to establish a comparison between the proposed DOAVNS and other optimizers. The outcomes of this test are outlined in Table 22. As all criteria fall below the threshold limit $\alpha =0.05$, the attained outcomes suggest the statistical significance of the attained comparative analysis scores.

Table 22. Wilcoxon signed-rank test scores in forecasting experiments.

DOAVNS vs. Others	VNS	GA	PSO	RSA	SCHO
Elm Crescent
Elm Crescent RNN	0.034	0.018	0.025	0.029	0.023
Elm Crescent LSTM	0.029	0.031	0.042	0.025	0.036
Elm Crescent GRU	0.039	0.037	0.041	0.039	0.034
Forest road
Forest road RNN	0.025	0.044	0.037	0.028	0.035
Forest road LSTM	0.032	0.038	0.024	0.039	0.037
Forest road GRU	0.031	0.035	0.034	0.028	0.029

5.6. Deployment Simulations

Based on simulation outcomes, GRU models showcase optimal performance once optimized and trained for prediction in both simulation cases. This is favorable, as the lower computational demands of GRUs make them ideal for deployment on MCUs that face challenges with limited computational resources. In this study, the models were re-implemented using TensorFlow Lite, compiled, converted to C, and uploaded to an ESP32 development board using the Arduino IDE. The device is configured to monitor a serial port input and, based on a series of inputs, generates responses accordingly. Simulations using the test portion of the datasets yield results consistent with the scores reported in prior tables, suggesting viability for real-world use.

It is important to note that the ESP32 supports additional configurations, such as a web server and the direct monitoring of voltages using a step-down transformer or external ADC, which could also be integrated with the platform. The proof-of-concept study conducted in this work suggests that an expanded version of this system could significantly aid in the distribution and democratization of IoT devices for energy forecasting, thereby improving renewable energy integration into existing power distribution networks and reducing losses from power overproduction and distribution.

6. Conclusions

With limited fossil resources and their unsustainable impacts, there is an increasing shift toward renewable energy. However, successfully incorporating these new sources into current power grids remains challenging, with both technical and regulatory obstacles to address. Although enhancing reliability could greatly improve energy sustainability, solar energy’s reliance on weather introduces variability that often requires costly storage to ensure stable output.

This study focuses on leveraging metaheuristic optimization to fine-tune recurrent forecasting models aimed at predicting solar power production, designed for TinyML deployment on MCUs in in situ applications. Various recurrent models—RNN, LSTM, and GRU—were tested to identify the most effective model. Additionally, a comparative evaluation on two real-world datasets for separate locations was conducted, encompassing multiple optimizers to validate the approach; a custom optimizer showed promising results, achieving an MSE as low as 0.000935v and 0.007011v in the best-case scenarios on the two evaluated datasets, signaling its potential for real-world implementation. The best models were further assessed on an ESP32 chip, utilizing a UART terminal to simulate execution. Model performance was consistent, with minimal latency for the application’s needs. By deploying models directly on-site, network infrastructure costs are reduced, and local functionalities can be added to help manage demand and supply more effectively, including alerting in critical situations.

One drawback is that, in this setup, models deployed on MCUs cannot be updated in real time; instead, they require retraining on separate hardware and reprogramming MCU firmware for updates. Other limitations include restricted population sizes and optimization times, given the high computational load. Future research aims to extend this methodology, exploring broader applications for the optimized model and developing the experimental framework within the TinyML environment. Specific directions will include the implementation of real-time model updates, the integration of wireless sensor networks, and the development of distributed forecasting systems over different renewable energy sources like wind, hydroelectric, and solar power. The research will also examine a solar power dataset from the Balkans, which is currently being collected; however, it is currently neither openly available nor complete for experiments of this scale. Ultimately, the application of TinyML models will be extended to other application domains, including healthcare, agriculture, IoT security, and industry, where these models may help in image classification, wireless sensor network routing, fault detection, fall prediction for children and elderly persons, etc.

Policy Implications

Precise TinyML-based solar energy forecasting systems can significantly impact legal policies related to grid reliability and renewable energy integration in the Western Balkans. By providing accurate, localized forecasts, these systems enhance compliance with EU regulations, like RED II, which promotes greater renewable energy use and efficient grid integration. Such models support policies aimed at improving grid stability by balancing renewable energy supply and demand, aligning with national energy security and greenhouse gas reduction goals set forth in NECPs. Furthermore, precise in situ forecasts can help reduce reliance on fossil fuel backups during periods of fluctuating solar output, advancing both regional and EU emission reduction targets.

TinyML’s cost-effective, localized deployment enables decentralized monitoring, reducing the need for extensive networking infrastructure and making renewable integration more accessible, particularly for smaller towns and remote areas. Building on incentives like feed-in tariffs, this capability could prompt policymakers to offer financial support for TinyML within larger renewable energy subsidies. Moreover, TinyML supports continuous monitoring and analysis of real-time data coming from sensors, which can aid in the identification of patterns indicating anomalies, like equipment malfunctioning or deviations in electricity output, ensuring fast interventions and reducing system downtime. Continuous monitoring can help in the integration of renewable systems with smart grids, ensuring that energy production matches demand and stabilizing the grid through predictions of energy fluctuations. Improved monitoring and storage capabilities enabled by TinyML could also support cross-border energy exchange regulations. With more accurate forecasting of production surpluses, energy can be stored or traded internationally, aiding regional energy independence, lowering reliance on imports, and achieving the Energy Community’s goal of harmonized market integration across the Western Balkans.

Finally, TinyML’s predictive accuracy aligns with environmental protection regulations by enabling solar projects to anticipate and mitigate environmental impacts more effectively. Accurate production models ensure compliance with air quality and resource conservation standards, expediting environmental impact assessments under regulations like the Environmental Protection Law. By integrating TinyML, regulatory oversight could become more efficient through real-time data that identify inefficiencies or excessive emissions. TinyML thus has the potential to drive policies supporting a resilient and sustainable energy grid across the Western Balkans, equipping decision-makers with improved monitoring and forecasting tools.