Abstract
For breathing humans, the respiratory quotient (RQ = CO2 moles released/O2 mols consumed) ranges from 0.7 to 1.0. In Part I, the literature on the RQ was reviewed and Keeling’s data on atmospheric CO2 and O2 concentrations (1991–2018) were used in the estimation of the global RQ as 0.47. A new interpretation of RQGlob is provided in Part II by treating the planet as a “Hypothetical Biological system (HBS)”. The CO2 and O2 balance equations are adopted for estimating (i) energy-based RQGlob(En) and (ii) the CO2 distribution in GT/year and % of CO2 captured by the atmosphere, land, and ocean. The key findings are as follows: (i) The RQGlob(En) is estimated as 0.35 and is relatively constant from 1991 to 2020. The use of RQGlob(En) enables the estimation of CO2 added to the atmosphere from the knowledge of annual fossil fuel (FF) energy data; (ii) The RQ method for the CO2 budget is validated by comparing the annual CO2 distribution results with results from more detailed models; (iii) Explicit relations are presented for CO2 sink in the atmosphere, land, and ocean biomasses, and storage in ocean water from the knowledge of curve fit constants of Keeling’s curves and the RQ of FF and biomasses; (iv) The rate of global average temperature rise (0.27 °C/decade) is predicted using RQGlob,(En) and the annual energy release rate and compared with the literature data; and (v) Earth’s mass loss in GT and O2 in the atmosphere are predicted by extrapolating the curve fit to the year 3700. The effect of RQGlob and RQFF on the econometry and policy issues is briefly discussed.
1. Introduction
Atmospheric oxygen production on Earth started about 3.2 billion years ago. The total O2 produced was estimated at 5.63 × 105 Peta moles with 0.375 × 105 Peta moles as free oxygen in the atmosphere, 310 Peta moles as dissolved oxygen in the ocean, and the remainder stored in oxidized form (CH2O, SiO2, H2O, CaCO3, etc.) as terrestrial and oceanic compounds [1]. Thanks to abundant oxygen, biological species which consume oxygen evolved on Earth. Generally, the biological systems (BSs) include humans, plants and trees, phytoplankton (PP), etc. The plants, trees and PP are generally referred to as biomasses and perform both (i) respiration, which consumes almost 50% of C(s) produced via the photosynthesis process [2], and (ii) production of oxygen. But humans perform only respiration without the production of oxygen. In biology, the respiratory quotient (RQ) is defined as the ratio of CO2 moles released to the moles of oxygen consumed. The RQ estimated via nasal intake and vented exhaust is called the Apparent Respiration Quotient (ARQ) [3], which could be different from the values of RQ estimated with a chemical formula of nutrients used for metabolism.
The CO2 growth rate in the atmosphere is affected by CO2 released from the combustion of FF and by natural CO2 sinks in the ocean and the land in the carbon cycle. The energy demand is driven by the choice by consumers, level of industrialization and urbanization, climate and environmental policies of the nation, and available technology. There are three reservoirs for storing anthropogenic CO2 over several decades: atmosphere, land (terrestrial biosphere), and oceans {about 93% of C(s)} [4]. The O2 concentration in the atmosphere is affected by the consumption of O2 by FF and O2 production. Hence, Keeling’s data on CO2 and O2 in the atmosphere (1991–2021) are affected by human activities and the distribution of CO2 sink by land and ocean, revealing the inverse relation between CO2 and O2 in a periodic saw tooth pattern within each year.
While part I dealt with review of RQ and estimation of global RQ, the RQ concept, along with CO2 and O2 balance equations, is used in Part II to (i) estimate global CO2 sink and O2 production by land and ocean biomasses, (ii) determine storage of CO2 by the oceans, (iii) establish the control groups that affect the CO2 growth in the atmosphere, and (iv) present the fossil energy-based RQGlob,(En) relation, which enables a ready estimation of CO2 added to the atmosphere from the data on annual fossil energy consumption.
2. Literature Review
The global carbon cycle is affected by the release of CO2 from FF and the exchange of O2 and CO2 between the atmosphere–land and atmosphere–ocean interfaces [5]. A detailed review of CO2 sources and sinks and O2 sinks and sources, and a comparison of terminologies between photosynthesis, engineering, and biology literature are presented in Part I. A brief literature review pertinent to Part II is presented here: (i) effects of CO2 sources other than those from FF and land use (LU) on the estimation of RQ based on annual CO2 and energy data, (ii) controversy on % O2 contribution by ocean biomass to the atmosphere, and (iii) the relation between global warming or “planet fever,” and the Paris agreement to limit temperature rise and the annual energy release rate.
2.1. CO2 Sources and O2 Sinks
The development of modern industrialized nations across the globe resulted in an increase in CO2 from a pre-industrial level of 285 ppm (1850) to 380 ppm in 2006 and 414 ppm in 2020 [6]. In addition to CO2, the greenhouse gases (GHG) include CH4, N2O, O3, etc. Even though the ozone is a GHG, the beneficial effect of stratospheric ozone is more important than its contribution to global warming. An average person in the USA releases 16 tons of CO2e (which includes all GHG), while the global average per person is 4 tons. The US EPA report presents the % GHG distribution from the transportation and energy industry, constituting almost 50% of total GHG (Excel table in [7]). CO2 from land use (LU) accounted for 33% around 1750 [8], while currently, FF: 87%, and LU: 13%. In addition to CO2 sources from the combustion of FF in thermal power systems and LU, cement production results in additional CO2 release. About 50% of cement CO2 is produced by the following process:
while 40% is obtained from the CCP (Coal Combustion Product). The net CO2 released in 2021 for cement is estimated to be 2.4 GT while FF energy is 36.3 GT, and hence, the cement CO2 is about 6.6%. Thus, RQ based on global CO2 and annual energy consumption data yields RQFF+LU++cement due to the addition of cement CO2 [9]. There is no O2 sink in cement manufacturing, while there is an O2 sink in the oxidation of fuels to CO2. Deforestation also causes deoxygenation. The oxygen sinks cause decreasing O2 concentration in the atmosphere [10,11]. Based on the parabolic model [11,12] for O2 concentration in the atmosphere, Martin et al. found that the O2 in the atmosphere will decrease by 50% (i.e., O2 concentration: 10.5%) by the year 3600. The atmospheric hypoxia will result in human extinction. This result is in close agreement with results from Part I which state that the O2 concentration will reach 16.5% by the year 3700 when a quadratic curve fit (also known as a parabolic fit) is used for Keeling’s data on O2 concentration in the atmosphere.
CaCO3 → CaO (lime) + CO2
2.2. CO2 Sinks and O2 Sources
Between 1991 and 2020, CO2 increased by 17% (from 354 ppm in 1991 to 41 ppm in 2020), and photosynthesis grew by 12% from 1982 to 2020 [13] due to CO2 fertilization and is expected to increase by 52% in the 21st century. However, the increased global temperature has a negative effect on photosynthesis. Just like biomass growth requires the consumption of C, growing humans from 3.2 kg (7 lb.) to 34 kg (75 lb.) also requires the storage of C, which becomes fossilized if buried or results in release of CO2 if cremated. Assuming the mass % of C in the human body is at about 18.5% (wet human: 60% moisture and 40% dry mass, dry UCF: CH2.10N0.15O0.48 Ca0.024 P0.021; see Part I) [14], the C storage rate within humans (about 1.5 million tons/year assuming human mass of 75 kg, life span of 75 years and world population of 8 billions) is negligible compared to the C storage in biomass (order of GT/year).
2.3. Ocean CO2 Sinks and Ocean O2 Sources
The oceans occupy 70% of Earth’s area but only 1% of the biomass, whereas land occupies 30% of Earth’s area but contains 86% of the biomass. About 80% of the ocean water biomass is composed of animals, protists, and bacteria [15]. About 78% of global animals live in the ocean. Though the C in phytoplankton in the oceans amounts to only 〜1–2% of the total global biomass carbon, they serve as a C sink of 30–40% of total C [16,17].
The ocean CO2 sink works two ways. The CO2 from high PaCO2 in the atmosphere diffuses to water, dissolves, and is transported to deep water (physical process, shorter time scale). The second way is to use CO2 near the ocean surface to grow PP since sunlight is available (chemical process, longer time scale) [18]. With a net global production of 50 GT of O2/year, RQ = 1, it accounts for 50% of the oxygen, though it is only ~1% of global plant biomass [19]. Blue C populations (seaweed, green, red, and brown algae) are almost nine times that of land plants. Phytoplankton consume about 36.5 GT of CO2 (or 10 GT of C(s)/year) annually. The PP also serves as an aquatic food web (e.g., zooplankton, including bacteria, fungi, etc., along with dead plants and other animal material; they are consumed by fish). The energy needs of marine animals result in the consumption of most O2 produced by ocean biomass and the release of CO2.
However, there is controversy about the net amount of O2 transferred from the ocean to the atmosphere after marine organic matter (MOM) consumption. The oxygen concentration of 0.001% of the current level has existed for almost two billion years. Then, the photosynthesis by phytoplankton (plants and microscopic ocean bacteria) and trees and plants on land resulted in 21% oxygen today. The marine organisms also require oxygen for respiration/metabolism to convert food to energy, so they consume oxygen produced by PP. The dead PP falls like “marine snow” to the sea floor. This “biological carbon pump” transfers about 10 GT of C/year from the atmosphere to the deep ocean [20]. The dead plants are also oxidized due to deep water circulation. Even though the oceans contributed about 50% of oxygen to the atmosphere over hundreds of millions of years, 50% of the oxygen the BS breathes in does not come from the oceans, since most of the oxygen from the oceans is consumed by MOM. Further, the excess nutrients discharged to lakes and rivers (eutrophication) cause excessive algae boom and low oxygen water [21,22]. Thus, only 1.5 GT /year is outgassed from the oceans [23,24]. The global oxygen balance studies by Huang et al. [25] state that only 1.74 GT/year of oxygen enters the atmosphere from the ocean, while the land biomass produces 16.01 GT/year [25]. A detailed report on ocean deoxygenation cites about 0.8 GT/year as of 2017 but −1.8 GT/year as of 2011 [26].
It is noted that the annual ocean CO2 storage in Refs. [27,28] deals only with (i) the formation of bicarbonates without the production of O2 and (ii) dissolved CO2 [29]. The CO2 sink by ocean biomass is omitted in the balance equation (Equation (3) of Ref. [27]), presumably assuming the CO2 sink by phytoplankton is compensated for by CO2 production from the oxidation of dead plants within the oceans.
The PP concentration varies depending on the latitude, time of year [30], and depth where they grow. Thus, CO2, O2, and concentrations are affected by ocean circulation. Table 1 (adopted from [1]) shows that the total distributions of CO2, N2, and O2 differ from the surface distributions.

Table 1.
Fraction of N2, O2, CO2 in air and ocean compartments.
2.4. Global Warming and Temperature
Earth’s atmosphere is increasingly becoming warmer due to activities of “dust to dust” human transients undergoing several cycles of life and death [31]; see Ref. [32]. NASA collected data from more than 32,000 weather stations, land, weather balloons, oceans, ships, and buoys [33]. The rate of global temperature rise was 0.08 °C per decade till 1981, and jumped to 0.19 °C per decade for the period 1981–2014 [34,35] and 0.25 °C per decade from 2014 to 2021. Heating occurs due to the greenhouse effects of human-driven processes and waste heat from the long-term use of fossil energy, called the “deep warming” problem [36]. The global temperature is determined by conducting an energy balance between solar energy transmitted via the atmosphere loaded with GHG, energy absorbed by Earth, and heat loss via radiation and reflection into space. All these processes drive Earth’s heat sources and sinks out of balance. The waste heat from Earth accumulated 381 ZJ with a heating rate of 0.48 W/m2, and 89%, 6%, and 1% of thermal energy is stored in the oceans, land, and the atmosphere, respectively [36]. The imbalance rate has recently increased to 0.76 W/m2. The average temperature is now 0.9 °C (1971–2020) higher, and sea surface temperatures (SST) along the eastern coast of North America were found to be “13.8 °C or 24.8 °F higher than the 1981–2011 average” [37,38].
The Sustainable Development Goals (SDGs) were enacted by the United Nations in 2015 (i) to fill the needs of the present without harming the needs of future generations; (ii) to take actions to protect the environment, planet, and natural resources and end poverty by 2030 [39]; and (iii) to mitigate global warming by following the Paris Agreement, which dictates that global warming temperature rise must be limited to 2 °C, or preferably 1.5 °C [37]. The Intergovernmental Panel on Climate Change (IPCC) reports [40] and the Forbes website with a “cartoonist” depiction of climate explain the difference between the consequences faced by humans as a result of 1.5 °C and 2 °C rises. However, even if the temperature rise is limited to pre-industrial levels, nature may not restore the climate due to the hysteresis effect [41]. The increased global temperature causes plants to mature more quickly, thus reducing the period of photosynthesis and affecting the photosynthesis process in ocean biomasses. The warming effect resulted in the decrease in the phytoplankton population by 30% compared to the 1980s. The rising global temperature of Earth due to increasing CO2 (See Figure 2 of Part I for temperature anomaly, Figure 3 of Part I for global average temperature, [9]) may also reduce the amount of C from the photosynthesis process. Hence, by 2040, CO2 sink due to biomass growth will be reduced by almost 50% [42]. The higher the ocean temperature, more the dissolved CO2 and O2 are released from the ocean, resulting in less oxygen for marine life, the expansion of water, and a higher sea level. It is estimated that the dissolved O2% in the ocean will decrease by 1 to 7% of the current level by 2100 [43].
2.5. Research Gap
While the RQ of humans is important for nutritional therapy on adjusting CO2, the RQ of FFs provides an avenue for “FF” therapy to reduce CO2 release from power plants. The budget analysis using “stand-alone” ocean-biochemical and terrestrial-eco system models for C sink [44] involves extensive computational tools and requires an approximate solution as the initial guess for faster convergence. The RQ-based carbon budget analysis is needed to (i) obtain explicit solutions for CO2 distribution to the atmosphere, land, and ocean biomasses and storage by the oceans in terms of the curve fit constants of Keeling’s data on CO2 and O2, and RQ of FF and biomass, and (ii) present control groups affecting the CO2 budget. Further, there is wide variation in the contribution of oxygen to the atmosphere by ocean biomasses (ranging from 10 to 80%) due to conflicts in the terminology used, for example, total O2 produced by the ocean vs. net O2 contributed by the ocean to the atmosphere. Further, most of the earlier literature data do not present CO2 sink via ocean water biomass (OWBM), but only CO2 storage by ocean water as dissolved gas and carbonate, presuming that there is no net O2 transfer from the ocean to the atmosphere, or CO2 sink by OWBM, while the current work estimates such a contribution. It is desirable to obtain a simple, albeit approximate, relation relating the rate of temperature rise with global RQ obtained from Keeling’s data on CO2 and O2 and the annual energy release rate. Currently there is no such relation, probably due to the complexities involved in Earth’s energy balance.
2.6. Overview of Part I
A brief overview of results from Part I is presented below:
- (i)
- Respiratory Quotient (RQ):
For the CO2 source and O2 sinks, the respiratory quotient (RQ) is defined as
For CO2 sinks and O2 sources, the quotient (RQ) (which is the inverse of the photosynthetic quotient, PQ) is defined as follows:
where represents the CO2 release rate by FF and represents the CO2 release rate by both FF and LU.
- (ii)
- The literature on RQ and its relation to various terminologies in the photosynthesis literature were reviewed.
- (iii)
- RQ values were presented in tabular form for several FFs and BMs in Part I [9]. They are summarized in graphical form in Figure 1 and plotted as a function of the atom ratio H/C with O/H as a parameter.
- (iv)
- The RQ concept was applied to fossil fuels (FFs) fired for power plants [45], and the relation between RQ and CO2 released in GT per Exa J was presented:where HHVO2 = 448 Exa J/Peta mole of O2, and MCO2 = 44.01 g/mole or 44.01 GT per Peta mole of CO2.
- (v)
- The Keeling’s data [46] on CO2 and O2 were used to obtain curve fit constants using linear and quadratic fits and present RQGlob as 0.47 (=d(CO2)/dt) in the atmosphere/ |d(O2)/dt| in the atmosphere), which is similar to ARQ in biology. Planet Earth behaves like a large BS, releasing 0.47 moles of CO2 to the atmosphere for every mole of O2 depleted from the atmosphere. The RQGlob is much less than the RQ of FFs due to CO2 sink by biomass and CO2 storage in the oceans.
- (vi)
- It was shown that the global RQGlob is a measure of the acidity of the oceans [9]. The lower the RQGlob is and the larger the difference between RQFF and RQGlob, the greater the acidity of the oceans.
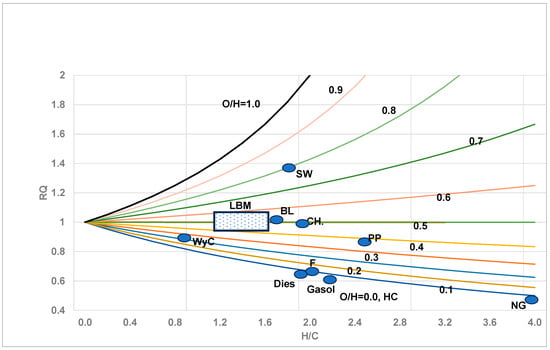
Figure 1.
Variation in RQ (CHhOo fuel or nutrients with (h = H/C, o = O/C), with O/H as parameter. Generally, RQ = 1/ (1 + h/4 − o/2) or 1/ [1 + (h/4) * {1 − 2 * (O/H)}] At O/H = 0.5, RQ = 1. Figure adopted from [47] and modified. Symbols denote RQ estimated from chemical formula of many fuels and nutrients. Most land biomasses have O/H varying from 0.4 (Table A.1 in Appendix of Part I) to 0.57 with an average of 0.49 (see rectangular box labelled LBM), while RQ LBM varies from 0.94 to 1.05 with an average of around 1 due to O/H = 0.5; see horizontal line. It appears as though H2O molecule is chemically attached to C atom in the BM when O/H = 0.5 and hence, during oxidation, H2O is detached, O2 is needed to oxidize only C, and as such, RQ = 1; during growth of biomass, C is separated from CO2 and again RQLBM = 1.
2.7. Objectives of Part II
The objectives of Part II are as follows: (i) Present CO2 (or C) and O2 balance equations, (ii) obtain solutions for global O2 production by land and ocean-based biomasses and CO2 storage by the ocean, (iii) define energy-based RQGlob(En) and estimate it using the curve fit constants for Keeling’s curve (linear and quadratic curve fits), (iv) provide explicit formulae for the CO2 distribution in GT/year and % contribution amongst the atmosphere, land biomass (LBM), and ocean water biomass (OWBM) and the amount stored in ocean water (St, Ocn), (v) validate the results from the RQ method by comparing them with the literature results obtained from more detailed numerical models, which are presented in Global Carbon Project (GCP) reports, and (vi) relate the rate of global temperature rise in terms of RQGlob(En) and annual energy release rate from FFLU.
3. Materials and Methods
3.1. Assumptions
- Humans and land and ocean-based animals consume renewable energy (not coal, oil, or fossil fuels), which presumes that the CO2 produced and O2 consumed by humans and animals is approximately equal to the CO2 sink and O2 production in growing “nutrient-crops”; they operate on “closed C” loop.
- Biomass includes terrestrial (land) and ocean water-based or marine biomass and micro-organisms.
- CO2 is released during calcination (cement making without using oxygen), and CO2 is used in limestone formations in the ocean (without the use of O2). It can be accounted for through the definition of an effective RQOWBM. Note that the C(s) from calcination (cement carbonation) is only 0.2 GT of C/year, while the CO2 storage in the ocean is 90 GT of C/year.
- While CO2 is stored, there is no net O2 storage in the oceans; there was only a 2% drop in ocean’s oxygen levels over the last 50 years [48], and hence, O2 storage in OW is neglected compared to CO2 since O2 in the atmosphere is at much higher concentrations and the ocean is nearly saturated with O2 due to much higher concentrations of O2 in the atmosphere compared to CO2 (note: solubility CO2: 0.0116 mL per L per mm Hg, O2: 0.00565 mL/L per mm Hg; typically, O2 saturation level in OW is about 7–8 mg/L, CO2 0.44–0.66 mg for warm to cold water; O2 saturation level is high due to the high concentration of O2 in the atmosphere}).
- Changes in O2 and CO2 storage due to changes in the temperature of ocean water are ignored in CO2 and O2 balance equations.
Additional assumptions, if any, are stated as the governing equations are presented.
3.2. CO2 and O2 Balance Equations and Solutions for CO2 Distribution amongst Atmosphere, Land, and Ocean
- (i)
- CO2 Balance Equations
The C emissions are from fossil fuels via CO2 (CEFF), and cement production and land use (CELU), and C sinks are in land biomass (CSLBM) due to the fertilization of plants on land and ocean biomasses (CS OWBM), storage of CO2 in the atm [44] (CSATM), and storage in the ocean water (CSSt,Ocn, i.e., without O2 production) as dissolved gas and as carbonate.
The C atom balance equation is written as follows:
which can be equally applied to CO2 since 1 mole of CO2 contains 1 mole of carbon. Replacing C with CO2 in Equation (4) and solving for the CO2 storage rate in the atmosphere yields the following:
where , is the accumulation rate of CO2 in the atmosphere, ppm/year, Nair is the atmosphere air, in Peta moles, and are the annual CO2 release rates by FFs and LU, is the combined CO2 from FFs and LU, is the CO2 sink via land biomass, is the CO2 sink via ocean water-based biomass, is the combined CO2 sink via land and ocean water-based biomasses and is the CO2 storage by the oceans, and all rates are in Peta moles/year. Appendix A shows the conversion from ppm of species per year to GT per year.
- (ii)
- O2 Balance Equation: see Huang et al. [25]:
- (iii)
- CO2 Source/Sink in Atmosphere in terms of RQ
Using the definition of RQ, the CO2 balance Equation (5) becomes
Dividing by , and defining the energy-based RQGlob(En) as
the dimensionless form of Equation (7) is written as
or
where RGlob(en) definition is presented in column 2 and row (6a), of Table 2 and typical values for RQFF, RQLU, etc. are presented in Table 3. The definition for FBal along with their values are presented in Table 4.
Further,
where
where EF, the Energy fraction contribution by FFs, LU, and z, is a measure of the fraction of oxygen contributed by OWBM to the atm. More discussion on the values of “z” will be given later in Section 4.4.1.
Note that soil absorbs roughly 25% of anthropogenic emissions each year and is stored in peatland or permafrost without a well-defined release of O2; this can be accounted for by altering RQLBM and RQOWBM; see Refs. [27,28].
3.3. Solutions for O2 Production, CO2 Storage in Ocean, and Carbon Budget
Solutions for O2 Production and CO2 Storage in Ocean
The CO2 and O2 balance equations indicate that the atmospheric O2 and CO2 in the Keeling curve are affected by O2 consumption and CO2 production via FFLU, O2 production, and CO2 sink by land and ocean biomasses and ocean storage. Thus, the two equations (Equations (6) and (7)) can be solved for two unknowns: O2 production by biomass, , and CO2 storage by ocean, . Appendix B presents the normalization of Equations (9) and (10) and describes the solution procedure. The solutions for the non-dimensional form of O2 production rate (x) and CO2 storage rate (y) are obtained and presented in Rows 7 and 10 of Table 2. It also lists a summary of all the solutions. Note that “y” is not RQ even though both are ratios of CO2 to O2.
Rows 1 and 2: Curve Fit Constants for CO2 and O2.
Rows 3a and 3b: Slopes of CO2 in ppm/year and GT/year.
Rows 4a and 4b: Slopes of O2 in ppm/year and GT/year.
Rows 7 and 10: Solutions for “x” and “y”.
The net O2 moles transferred by ocean and land biomasses to the atmosphere per unit of O2 consumed by FFLU are given as
See Rows 8 and 9 in Table 2 for the O2 contribution by ocean and land biomasses.
3.4. Global RQGlob and Energy-Based RQGlob(En)
Global RQ: Part I [9] defined RQ Glob as follows (Column 2, Row 5 of Table 2):
where d[CO2]/dt is the addition rate of CO2 to the atmosphere. Both CO2 and O2 slopes are known from Keeling’s data and in terms of curve fit constants.
Energy-based RQGlob(En): Definition is given in Equations (8) and (10). If energy data are not available for the year of interest (i.e., 2006) and instead, C data are available in GT/year, then C in Peta Moles per year = {C(s) in GT per year/12.01}, which is the same as CO2 in Peta Moles/year. Then the required O2 in Peta moles is given as {CO2 in Peta moles per year/ RQFFLU}.

Table 2.
List of formulae for estimation of global respiratory quotient of planet, CO2 distribution amongst the atmosphere, land biomass (LBM), ocean water biomass (OWBM), and ocean water storage (St, On). For list of “F” values in many relations, see Table 4. For data on constants a0, a1… j0, j1, see Section 3.4.2. Unless otherwise stated, most of the results on CO2 budget are energy-based. For the year 2006, the quantitative numbers generated by the current method are in curly brackets { }, while the reported data are in square brackets [ ]. Unless otherwise stated, the GT per year denotes GT of CO2 per year.
Table 2.
List of formulae for estimation of global respiratory quotient of planet, CO2 distribution amongst the atmosphere, land biomass (LBM), ocean water biomass (OWBM), and ocean water storage (St, On). For list of “F” values in many relations, see Table 4. For data on constants a0, a1… j0, j1, see Section 3.4.2. Unless otherwise stated, most of the results on CO2 budget are energy-based. For the year 2006, the quantitative numbers generated by the current method are in curly brackets { }, while the reported data are in square brackets [ ]. Unless otherwise stated, the GT per year denotes GT of CO2 per year.
| # | Variable | Linear Fit Numbers for 2006 in Parenthesis {} | Quadratic Fit (Also Called Parabolic Fit) Numbers for 2006 in Parenthesis { } |
|---|---|---|---|
| Curve Fit Constants and Slopes of Keeling’s curves on CO2 and O2 | |||
| 1 | Linear Fit of Keeling’s curve: CO2 in atmosphere, ppm | a1 * years + a0, linear fit {Est. CO2 for year 2006 = 381.7 ppm} [Keeling’s data 382.1 ppm] | c2 * years2 + c1 * years + c0, {CO2 for year 2006 = 380.5 ppm} [Keeling’s data 382.1 ppm] |
| 2 | O2 in atmosphere ppm | b1 * years + b0 {Est O2 for year 2006 = 209421.4 ppm} [Keeling’s data: 209,423 ppm] | d2 * years2 + d1 * years + d0,d2 = −0.0435 ppm/year2, d1 = −3.0332 ppm/year, {Est O2 for year 2006 = 209,424.6 ppm} [Keeling’s data: 209,423] |
| 3a | d[CO2]/d(year) = CO2 change per year, ppm in atmosphere /year | a1 {2.081 ppm/year, constant, independent of year} | 2 * c2 * years + c1 {2.04 ppm/year in 2006} |
| 3b | d (CO2)/d(year), GT/year 1 ppm of CO2 in atmosphere = 7.79 GT | 7.79 * a1 {16.2 in 2006, independent of year} [13.7 in 2006, 7% imbalance] | 7.79 * 2 * c2 * years + c1 {15.9 in 2006} [13.7 in 2006, 7% imbalance] |
| 4a | d[O2]/d(year), ppm/year 1 ppm of O2 in atmosphere = 5.66 GT | b1, negative {−4.44 ppm/year, constant, independent of year} | 2 * d2 * years + d1 {−4.34 ppm/year in 2006} |
| 4b | d(O2)/d(year)dO2/dt, GT removed from atmosphere/year | 5.66 |b1|, b1 in ppm/year {25.12 GT/year, constant and independent of year} | {24.59 GT/year in 2006} |
| Global RQ | |||
| 5 | , constant {0.468 constant, independent of year} | , decreases slightly with years, {0.470 in 2006} | |
| 6a | With Energy data, {d[CO2]/dt}, ppm/year | in Exa J/Year, a1, b1, ppm/year, FBal = 79.3 (see Table 4 for FBal relation) {0.358 in 2006} | in Exa J/Year, a1, b1, ppm/year {0.352 in 2006} |
| 6b | With C data in GT/year, {d[CO2]/dt}, ppm/year | (see Table 4 for FCGt relation) FCGt = 2.13, in GT/Year, a1, b1, ppm/year, {0.36 in 2006} | in GT/Year, a1, b1, ppm/year, {0.36 in 2006} |
| 6c | {d[CO2]/dt}, ppm/year | , | FCO2 = 0.0126 |
| Non-Dimensional Solutions for O2 Production and CO2 Storage in Ocean | |||
| 7a | , FBal = 79.3 {0.24 in year 2006 with FFLU Energy/year =460.1 Exa J/year} | {0.25 in year 2006} | |
| 7b | With C data | , carbon output GT/year by FFLU {0.24 with C data of 9.71 GT/year in 2006} | {0.26 in 2006} |
| 7c | Total O2 prod GT/year, LOWBM Combined Ocean and land biomasses | FO2BM * x * FO2BM = 0.0714 {7.72 GT/year in 2006 with x = 0.235} | FO2BM * x * , FO2BM = 0.0714 {8.25 GT/year in 2006 with x = 0.2516} |
| 8 | Ocean BM Contrib. O2 | z * x, where x for linear fit {0.024 in 2006 with z = 0.1} | z * x, where x for quadratic fit {0.025 in 2006 with z = 0.1} |
| 9 | Land BM Contrib. O2 | (1 − z) * x {0.21 in 2006 with z = 0.1} | (1 − z) * x, where x for quadratic fit {0.23 in 2006 with z = 0.1} |
| 10 | CO2 storage | Or {0.187} | Or {0.178} |
| CO2 Budget Amongst Atmosphere, Land, and Ocean | |||
| 11 | {0.46 in 2006} | {0.45 in 2006 } | |
| 12 | {0.30 in 2006} | {0.32 in 2006 } | |
| 13 | , {0.24 in 2006 with Energy data} | {0.23 in 2006 with Energy data} | |
| 14 | CO2 sink Fr via Ocean Biomass | , {0.030 in 2006} | {0.032 in 2006 with z = −0.1} |
| 15 | CO2 sink Fr Ocean Total | or {0.27 in 2006 with z = 0.1} [0.25 in 2006] | {0.26 in 2006 with z = −0.1} [0.25 in 2006] |
| 16 | CO2 sink Fr LBM | {0.27 in 2006 with z = 0.1} [0.33 in 2006 from data] | {0.29 in 2006 with z = 0.1} [0.33 in 2006 from data] |
| 17 | CO2 sink by land and ocean biomasses, GT/year | {10.5 GT/year in 2006} | {11.2 GT/year in 2006} |
| 18 | CO2 sink by ocean biomass, GT/year | z * CO2 sink by land and ocean biomasses in GT/year {1.05 GT/year in 2006 with z = −0.1} No previous data to compare | z * CO2 sink by land and ocean biomasses in GT/year {1.12 GT/year in 2006 with z = −0.1} No previous data to compare |
| 19 | CO2 sink by land biomass, GT/year | (1 − z) * CO2 sink by land and ocean biomasses in GT/year {9.45 GT/year in 2006 with z = −0.1} [11.06 GT/year in 2006] [28] | (1 − z) * CO2 sink by land and ocean biomasses in GT/year {10.08 GT/year in 2006 with z = −0.1} [11.06 GT/year in 2006] [28] |
| 20 | CO2 storage by ocean, GT/year | FCO2EJ * y * , FCO2EJ = MCO2/HHVO2 = 0.1 {8.63 GT/year in 2006} [8.36 GT/year in 2006] [50] | FCO2EJ * y * , FCO2EJ = MCO2/HHVO2 = 0.1 {8.21 GT/year} [8.36 (GT/year in 2006] [50] |
| Global Temperature and Earth’s Mass Loss | |||
| 21a | Global Temperature, °C vs. year | g1 * (year − 1991) + g0. | - |
| 21b | Global Temperature rise vs. CO2 of atmosphere in ppm. | = 355 ppm in 1991 {2006, T in °C = 12.17; Data 12.06 °C} | |
| 22a | Rate of Temperature rise per year, dT/d(year) in terms of Keeling’s data {d[CO2]/dt}, ppm/year, [CO2,0], ppm | 4 * (a1/a0) {1995 to 2022), dT/year = 0.024 °C /year} | Years = Year of interest—1991 {1995 to 2022, dT/year = 0.023 °C/year } |
| 22b | Rate of Temperature rise per year, dT/d (year) Energy data | ||
| 23 | Earth’s mass Loss Rate, GT/year | FCGTE * RQGlob(En) * , Alternate: FCGT * (d[CO2]/dt)qtm {4.42 GT/year, 2006} | FCGTE * RQGlob(En) * , Alternate: FCGT * (d[CO2]/dt)qtm {4.34 GT/year, 2006} |

Table 3.
RQ values selected for quantitative results.
Table 3.
RQ values selected for quantitative results.
| Source or Sink of Interest | RQ |
|---|---|
| Fossil Fuels, FFs | 0.75 |
| Land Use, LU | 1.0 |
| Combined FFs and LU | EFFF * RQFF + EFLU * RQLU = 0.778 |
| Land Biomass, LBM | 1.0 |
| Ocean water-based biomass, OWBM | 0.87 |
| Com Combined LBM + OWBM; | (1 − z) * RQLBM + (1 − z) * RQOWBM = 0.987 With z = 0.1 |

Table 4.
The constants F: Relations and values. The subscripts for F indicate the “relations” where they were used, e.g., FdTdt represents constants in the relation for dT/dt, etc.
Table 4.
The constants F: Relations and values. The subscripts for F indicate the “relations” where they were used, e.g., FdTdt represents constants in the relation for dT/dt, etc.
| Constants F | Relation | Value |
|---|---|---|
| FBal (item 6a, Table 2) | 10−6 * Nair * HHVO2 | 79.3 |
| FCGT (item 6b, Table 2) | FCGT = 10−6 * Nair * MC | 2.13 |
| FCEJ (item 7c, Table 2) | (MC/HHVO2) | 0.0268 |
| FCO2 | 0.0126 | |
| FCO2EJ (item 20, Table 2) | 0.1 | |
| FO2BM (item 7c, Table 2) | 0.0714 | |
| Fppm (item 17, Table 2) | 10−6 * Nair | 0.177 |
| FdTdt (Equation (36)) | , h1 = 4 |
3.4.1. CO2 Budget amongst Atmosphere, Land, and Ocean Biomasses and Ocean Storage
The solutions for CO2 stored in the atmosphere, CO2 sink by biomass, and CO2 storage are presented in Appendix B. Appendix B provides the details of derivations.
Rows 11, 12, and 13: CO2 stored in the atmosphere, CO2 sink by biomass, and CO2 storage in the ocean.
Rows 14 and 16: CO2 stored in land biomass and ocean biomass.
Row 15: Combined CO2 storage in the ocean and ocean biomass CO2 stored in land biomass, ocean biomass.
Row 16: CO2 fraction by land biomass.
Row 4b, and Rows 17–20 in GT/year for CO2 sink in the atmosphere, combines land and ocean biomasses, ocean biomass, land biomass, and CO2 stored in the ocean.
3.4.2. Data Used in Calculations
Input Data:
Curve fit constants.
Linear Fit [9]: d[CO2]/dt = a1 * years + a0, d[O2]/dt = b1 * years + b0, years = current year − 1991, linear fit a0 = 350.5 ppm, a1 = 2.081 ppm/year, R2 = 0.97, and O2 data, b0 = 209488 ppm, b1 = −4.438 ppm/year R2 = 0.98.
Quadratic Fit [9]: d[CO2]/dt = c2 * years2 + c1 * years + c0, d[O2]/dt = d2 * years2 + d1 * years + d0, c2 = 0.01892, c1 = 1.473, c0 = 354.1, R2 = 0.98: O2 data, d0 = 209,480 ppm, d1 = −3.0332 ppm/year, d2 = −0.0435 ppm/year2, R2 = 0.99.
Global Average Temp vs. year, See Equation (31) and Row 21a of Table 2, g0 = 13.7, g1 = −5.281 * 10−3, g2 = 9.114 * 10−5, R2 = 0.90, years from 1880 to 2023.
Global Temp. See Equation (33) and Row 21b of Table 2, ΔT = T − T0,91 vs. [CO2]/[CO2,0], h1 = 4.0, h0 = −4.10, R2 = 0.86, [CO2,0] = 355 ppm with 1991 data.
Global vs. , See Equation (37) i1 = 4.14, i0 = −3.16, R2 = 0.98.
Global vs. . See Equation (37), j1 = 0.24, j0 = 0.76, R2 = 0.98.
RQ’s: RQOWBM = 0.84, which is close to 0.86, suggested in [51].
RQFFLU = 0.78; compare with values in Ref. [52]: PQ = 1.1 or RQLBM = 0.91 for terrestrial plants [9].
O2 Moles Consumed from FFLU Energy: from energy data =
Atmosphere Properties:
Nair = 1.77 × 105 Peta mol, Oxygen Concentration: 0.21 or 210,000 ppm.
One ppm of CO added to the atmosphere = 0.177 Peta moles of CO2 added, 7.79 GT of CO2 added to the atmosphere, or 2.12 GT of Carbon added to the atmosphere.
One ppm of O2 removed from the atmosphere, 1 ppm = 0.177 Peta moles removed, or 5.66 GT of O2 removed from the atmosphere.
C Imbalance % in literature data: 100 * {CO2 source from FFLU − CO2 sink in (atmosphere + land + ocean)}/FFLU CO2
Adjustable parameter “z” (O2 transferred from ocean to atmosphere/Total O2 produced by LBM and OWBM.
2006 Data
= 408.25 (FF) + 51.96 (LU) = 460.21 Exa J; = 9.71 GT/year
LU energy = 11.3% of total energy from LU or 12.7% of FF energy
C (from FFLU) data in 2006: 9.71 GT/year or CO2 data: 35.6 GT of CO2 /year
= 1.027 Peta moles /year.
3.4.3. Literature Results on CO2 in Atmosphere, Land, and Ocean
Fossil and LU based CO2 and energy data are from Ref. [50]. Atmosphere CO2 data are from [53]. Ocean sink data are estimated from the average of several global ocean biogeochemistry models [44] and the ocean sink uncertainty of ±0.5 GT C/year. Land sink data are from the average of dynamic global vegetation models and uncertainty of ±0.9 GT C/year.
The C or CO2 budget in literature is based on several “stand-alone” land and detailed ocean circulation models. The Global Carbon Budget (GCB) is published by the Global Carbon Project; a summary of various models is provided in [44]. The land sink for C is based on the average of global vegetation models [54]. The estimates on ocean storage are based on global ocean-atmosphere CO2 flux using ocean surface CO2 concentration gradients, satellite data, and an average of several global ocean biochemistry models.
4. Results and Discussion
Table 2 contains all necessary formulae for all the important results required in obtaining CO2 distribution amongst the atmosphere, land, and ocean. The Supplemental Materials titled “Supp Step by Step CO2 budget” describe the step-by-step procedure for obtaining the quantitative results for the year 2006 shown in Table 2 and most of the results presented in Section 4.1, Section 4.2, Section 4.3, Section 4.4 and Section 4.5. An Excel-based program was developed with input data from Section 3.4.2 and an output containing all the results for the variables is listed in Table 2. For 2006, computed numbers generated by the current method are shown in curly brackets {}, while the previous literature data obtained with more detailed models are presented within square brackets [ ] as the last line of each row in the third and fourth columns of Table 2.
(i) The results for the global respiratory quotients (RQGlob, RQGlob(En)), normalized O2 production (“x”) and CO2 storage (“y”), and energy released by FFLU vs. year will be presented first. (ii) The year 2006 was then selected for parametric studies since it was somewhere within the median year for data reported in 1991–2020 (30-year period), for which period the curve fits on Keeling’s data were obtained. (iii) The CO2 in GT/year and % contributed by the atmosphere, land, and ocean storage will be f compared with previous data for 2006 with z as a parameter, and a suitable z value will be selected. For the year 2006, FFLU energy is reported as 460.2 Exa J and CO2 emission is reported as 35.6 GT of CO2 by FFLU. The RQFFLU is estimated at 0.78 (Part I) [9]. Typically, the more oxygen in FFs, the lesser the stoichiometric oxygen, the higher the RQ, and the higher the CO2 emission per Exa J (Equation (3)). (iv) Then, using the selected z value, the annual RQ-based results on CO2 distribution in the atmosphere, land, and ocean storage in GT/year and % vs. year for the years 1991 to 2018 will be compared with the previous data. (v) Based on current analysis, various methods of freezing CO2 growth in atmosphere will be presented followed by presentation of relations between global temperature, rate of heating, Energy, and global CO2 Concentration.
4.1. Global Respiratory Quotients (RQGlob, RQGlob(En))
Part I dealt with RQGlob, estimated as 0.47 using Keeling’s data (Row 5, Table 2) and remaining constant with linear fit. RQGlob decreases from 0.48 to 0.46 (1991–2020) for quadratic fit {part I, [9]} and RQGlob = 0.47 in 2006. It appears that Earth behaves like a large “Hypothetical Biological System (HBS)” (or “barren Earth” without chlorophyll and oceans) to sustain the lifelong activities of humans on Earth with the net effect of increasing CO2 at the cost of decreasing O2 in the atmosphere. For a linear fit on CO2 data, the rate of increase in CO2 is constant at 2.08 ppm/year, and the intercept on the Y-axis, i.e., CO2 concentration in ppm in 1991, is 355 ppm; but for quadratic curve fits, the intercept is 354 ppm (CO2 concentration in 1991), d(CO2/dt) starts at 1.47 ppm/year in 1991, and increases to 2.04 ppm/year in 2006, and 2.57 ppm/year in 2020, indicating the faster growth rate of CO2 concentration in the atmosphere. According to data posted by the Mauna Loa Observatory (MLO), d(CO2)/dt = 2.04 ppm/year and 2.43 ppm/year for 2001–2010 and 2011–2020, respectively [55]. Later, it was shown that the rate of global average temperature is closely coupled to the rate of increase in CO2 concentration in the atmosphere {Section 4.6}.
Figure 2 depicts a large hypothetical biological system (HBS) and the caption has a brief explanation of the figure. This HBS within the dashed boundary includes the land and ocean, while the atmosphere is outside the dashed boundary. The Earth’s RQGlob of 0.47 indicates the release of 0.47 moles of CO2 into the atmosphere (which is outside the dashed boundary) for every 1 mol of O2 depleted from the atmosphere. How does Earth’s RQGlob compare with the RQ of humans? Consider a normal human (NH) born with a mass of 3 kg and grown to a mass of 70 kg with the intake of food, broken down into three components: Carbohydrates (CH), Fats (F), and Protein (P). The oxygen moles breathed in from the atmosphere are used for the oxidation of CH and F for the energy needs of the warm human body and the production of CO2, which is breathed out into the atmosphere. The “P” increases the body mass to almost 70 kg during the period of life. The RQ of NH is about 0.8, indicating that 0.8 moles of CO2 are breathed out into the atmosphere for every mol of O2 used for oxidation. The “fuel” or “nutrient” oxidized is a mix of CH and F, 67% CH and 33% F on a mole basis (or 58% of CH and 42% of F on a mass basis) oxidized to CO2 and H2O at an RQ of NH = 0.8 [56]. The liver stores excess “fuel” as glycogen for delivery between meals. Note that the mass of humans increases during food intake and decreases between the meals due to the transfer of glycogen through the bloodstream and subsequent oxidation to CO2 and H2O. But the average weight of NH increases from birth to death.
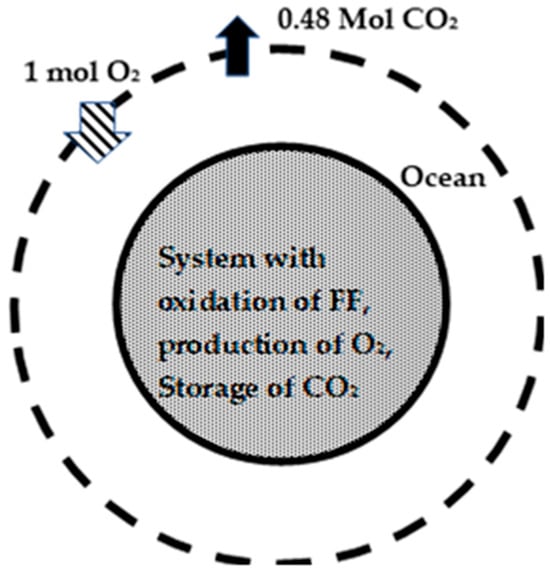
Figure 2.
Hypothetical BS (HBS), within dashed boundary. The HBS includes land (shaded) and ocean (white space between solid and dashed circle). The HBS depletes (or “breathes in”) 1 mole of O2 from atmosphere located outside the dashed boundary and releases 0.47 moles CO2 (or “breathes out” 0.47 moles of CO2) into the atm.
Now consider a hypothetical human (HH) (or HBS), born with a large mass of 5.97 × 1012 GT, which includes a mass of FFs stored within the body along with non-combustible matter, and AI-created “chlorophyll” skin. A part of FFs is stored, (unmined FF) and the remaining part (mined FF) is oxidized to CO2 and H2O annually for energy release to satisfy the energy needs of the HH. As opposed to NH, the HH produces O2 from CO2 using solar energy entering through the skin, which uses a part of the CO2 produced via the oxidation of FFs into C(s), which adds mass to the HH. Thus, O2 for oxidation comes from both the O2 produced and O2 “breathed” in from the atmosphere. Further, the blood of the HH (equivalent to oceans of Earth) has the capability of storing a part of CO2 and, hence, breathing out the remaining CO2 into the atmosphere. The RQGlob of this HH or HBS is 0.47, indicating net CO2 moles of 0.47 (or 0.47 moles of C or 5.84 kg of C) released into the atmosphere for every 1 mol of O2 breathed in from the atmosphere (Figure 2). Unlike an NH with increasing weight during the life cycle, the HH or HBS loses mass during its life cycle. The NH maintains a constant internal temperature (37 °C, called homeostasis), while the HH or HBS is constantly under “fever.”
Figure 2 depicts a thermodynamic description of the HBS of Earth’s mass, which includes the ocean and land (system within the dashed boundary) surrounded by the atmosphere. For planet Earth, the C loss via breathing out is the mass difference between the C mined as FF from the planet and the sum of C deposited for the growth of biomass on land and C(s) stored in the oceans (which adds weight to the land and oceans).
While RQGlob has a better physical meaning, the RQGlob(En) is convenient for obtaining results for the CO2 budget in terms of energy release from FFLU. Figure 3 shows the variations in (i) RQGlob (primary axis), (ii) RQGlob(En) (primary axis), (iii) energy released by FFLU in Exa J/year (secondary axis), and (iv) normalized O2 production (“x”, primary axis) and CO2 storage (“y’’, primary axis) for the years 1991–2020. The RQGlob slightly decreases, revealing the increasing ocean acidity as discussed in Part I [9], but the RQGlob(En) remains almost flat, indicating that the CO2 moles added to the atmosphere per Exa J energy released from FFLU energy remain constant, i.e., almost constant RQFFLU or constant FF mix. Also, RQGlob(En) < RQGlob since the denominator of RQGlob(En) depends on O2 consumption by FFLU , which is a sum of O2 transfer from the atmosphere to power systems and O2 production by LOWBM, while the denominator of RQGlob is .
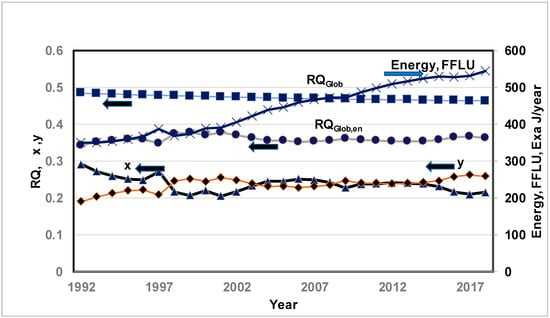
Figure 3.
Predicted Variations in global respiratory quotient (■, RQGlob which is similar to ARQ in biology) and energy-based RQGlob(En) {●}, non-dimensional O2 production (“x”, ▲), and non-dimensional CO2 storage (“y”, ◆) from 1991 to 2020. Arrows ← indicate values on primary axis and → indicate values on secondary axis. “x” < 1, “y” < 1. FFLU energy based on the sum of FF energy consumption and LU energy estimated from LU-CO2 emission quoted in Ref. [50]. Fossil emission data are from [57]. Land use data are from [54,58]. Figures on “x” and “y” are based on Quadratic Curve fit constants of Keeling’s data on CO2 and O\ in atm: (1991–2021).
Recall from Part I that the RQGlob represents the ratio of two slopes of Keeling data on CO2 and O2 and, hence, requires both CO2 and O2 data in the atmosphere. However, RQGlob(En) requires a knowledge of CO2 data in the atmosphere and annual energy consumption. It also enables the following relations for estimating the CO2 mass added to the atmosphere per unit energy release from FFLU.
For the year 2006, RQGlob(En) = 0.36 with reported energy data and with reported C data and CO2 in GT/Exa J ≈ 0.036 (Equation (19)). Both estimations are very close to each other.
The RQGlob(En) of 0.36 is interpreted as the RQ of breathing, barren planet Earth (biomass and ocean free) as though it is breathing with one mole of O2 as intake from the atmosphere for the oxidation of FFLU and releasing 0.36 moles of CO2 into the atmosphere of Earth. See Ref. [59]. With RQGlob(En) ≈ 0.36, and FFLU energy of 460.2 Exa J in the year 2006, the CO2 added to the atmosphere in 2006 was 0.1 * 0.36 * 460.2 = 16.6 GT.
4.2. Normalized O2 Production (“x”) and CO2 Storage (“y”)
Figure 3 shows the variations in dimensionless O2 production (“x”) and O2 storage (“y”) from 1991 to 2020. If the production of O2 by biomass kept up with increased O2 consumption by FFLU, then “x” should have remained constant, but the value of “x” decreased from 0.3 to 0.2 (i.e., 33% decrease), indicating that net O2 from the atmosphere was depleted, indicating that biomass production could not compensate for increased oxygen consumption by FFLU. Hence, decreased “x” indicates net O2 depletion from the atmosphere. Note that the CO2 increased by 17% (from 354 ppm in 1991 to 414 ppm in 2020). There was increased photosynthesis and, hence, the C(s) added to biomass grew by 12% from 1982 to 2020 [13] due to CO2 fertilization and, hence, O2 production must have grown by 12%. In spite of increased photosynthesis, the “x” decreased. The above results of increased photosynthesis with higher CO2 concentration are supported by lab studies at Birmingham which indicated a 33% increase in O2 when CO2 was artificially increased to 565 ppm (current level 415 ppm) [60]. Another avenue of maintaining “x” is to protect existing trees, which have the potential to remove 228 GT of C from the atmosphere [61] and add 607 GT of oxygen {=228 * 32/12.01) (assuming RQBM = 1) to the atmosphere. The increased global temperature has a negative effect on “x” since it causes the plants to mature more quickly, thus reducing the period of photosynthesis.
The FFLU data for 1991–2020 show that energy released (or consumed by FFLU) increased by 60%, and hence, O2 consumption must have increased by 60% due to FFLU, and CO2 released must have increased by 60% at constant RQFFLU. However, the CO2 in the atmosphere increased only by 14% (=(CO2 in 2020 − CO2 in 1991) * 100/CO2 in 1991), indicating that either the biomass growth served as an increased CO2 sink and/or the ocean served as an increased CO2 sink through storage.
Figure 3 shows that “y” has increased from 0.2 to 0.25 but “y” must remain constant if the storage rate of CO2 increases in proportion to the increased O2 consumption or increased CO2 output by FFLU. Increased “y” indicates an increased uptake of CO2 by ocean water, a lowered pH level of the ocean water, or a phenomenon known as ocean acidification. The pre-industrial level of pH was 8.2, and the current level is 8.1. Acidification affects PP, and the micro-organisms that fix carbon are less than efficient at fixing.
In order to understand the effects of CO2 added to the atmosphere and, hence, on RQGlob(En), consider the following cases. The discussions can be clarified by using Equation (9) for the following cases:
Case (I): if there is no biomass which could serve as a CO2 sink, then x = 0.
where RQFFLU = 0.78 (see Data section). Hence, the higher the ocean storage (y), the lower the RQGlob(En); the average y is on the order of 0.23. Thus, RQGlob(En) = 0.55, a reduction of 32% essentially due to storage of CO2 by the ocean.
Case (II): if there is no ocean storage, y = 0 and from Equation (9),
where RQavg = (RQFFLU + RQLOWBM)/2 ≈ 0.9. The more O2 production (i.e., “x”), the less the RQGlob(En). The average x for the period 1991–2020 is 0.25, and hence, RQGlob(En) is on the order of (0.9 * 0.75) = 0.68, indicating a reduction of only 13% from RQFFLU. In addition, the ocean biomass does not add O2 to the atmosphere while it acts, as more CO2 sink as storage. In other words, ocean storage has a stronger effect on RQGlob(En).
4.3. Earth’s Mass Loss, Earth’s Oxygen Concentration in the Future, and Tilt Angle
When FFs are mined in the solid state (e.g., coal) and liquid state (crude oil) and converted into a gaseous state (e.g., CO2, H2O) after oxidation, a part of CO2 is stored by biomass and the oceans, and the remainder enters the atmosphere. Note that H2O is returned to Earth in the form of rain. The mass of C(s) that enter the atmosphere with CO2 gas is responsible for the mass loss from Earth. Using Equation (20), which presents {C(s)} in GT/Exa J released by FFs,
where in Exa J/year. See Row # 23, Table 2. Alternately, one can obtain a similar relation directly by determining the slope of CO2 in Keeling’s curves:
where Nair in Peta moles, (ppm/year), which is known from curve fits. Equation (24) requires knowledge of the slope of CO2 with the year, while Equation (23) relies on the knowledge of RQGlob(En), which is almost constant. Hence, the mass loss rate increases linearly with the annual energy consumption rate. The lower the RQGlob(En), the lower the mass loss of the Earth and the higher the ocean acidity due to increased ocean CO2 storage. With an increasing FFLU energy release rate, from 460 Exa J/year in 2006 to 544 Exa J/year in 2018, there is a rise in Earth’s mass loss rate from 4.4 GT/year in 2006 to 5.2 GT/year in 2018, revealing a total mass loss of about 52 GT within 12 years. Extrapolating the quadratic curve fit of Keeling’s data on CO2 and O2, and estimating the O2 depletion rate from the atmosphere and the CO2 addition rate to the atmosphere for another 2000 years, Table 5 shows the decrease in oxygen %, physiological effects, and predicted hypoxic years with Earth’s corresponding mass loss in GT { = (CO2 in ppm at given year − CO2 in ppm in year 1991) * 2.13}. Under extrapolation of the fit, the rate of decrease of O2 in atm changes from −3.2 ppm/year (i.e. magnitude of depletion 3.2 ppm/year) in 1991 to −113 ppm/year and −186 ppm/year in the year 2900 and 3700 respectively (not shown in Table 5). Note that the Earth’s initial mass is 5.97 × 1012 GT. The first two columns are from data by OSHA [62], and the third column presents average O2 % used in predicting the hypoxic year (within parenthesis); the fourth column on mass loss are estimated values. The estimations of hypoxic year when there is a 50% decrease in atmospheric O2 concentration agree with predictions by Martin et al. [11], who used their extrapolation from parabolic fit to O2 data over Canada. The recent literature on global water pumping {2150 GT, 1993–2010 with a total of 17 years, 126 GT/year} shows that Earth’s tilt of 4.4 cm/year is affected by Earth’s mass re-distribution [63,64]. Thus, the change in the moment of inertia of the Earth due to the mass loss of the Earth due to mining, particularly near the surface, which is far from the axis of rotation, may also affect the tilt angle. I
Even though Table 5 covers O2 concentration from 21 % to 6 %, Ref. [12] warns that the decrease of O2 from 21% to 19% is expected to cause serious health problems for BS including humans.

Table 5.
Deoxygenation in atmosphere, physiological effects for humans, and predicted hypoxic year vs. O2% and Earth’s mass loss based on extrapolation from quadratic fit to Keeling’s data.
Table 5.
Deoxygenation in atmosphere, physiological effects for humans, and predicted hypoxic year vs. O2% and Earth’s mass loss based on extrapolation from quadratic fit to Keeling’s data.
| O2, % (v) | Physiological Effects for Humans | Avg O2% (Predicted Year) | Cumulative Earth’s Mass Loss since 1991, GT (Year) |
|---|---|---|---|
| 21 | Normal | Avg O2% = 21, (1991) | 0 (1991) |
| 19.5 | Adverse effect, Oxygen-deficient | Avg O2% = 19.5, (2600) | 16,800 (2600) |
| 16–19 | Organ function fails, lack of coordination | Avg O2% = 17.5, (2900) | 36,100 (2900) |
| 12–16 | tachypnea (increased breathing rates), tachycardia (accelerated heartbeat), | Avg O2% = 14.0 (3250) | 67,700 (3250) |
| 10–14 | intermittent respiration, vomiting | Avg O2% = 12.0 (3400) | 84,300 (3400) |
| 6–10 | Lethal level of O2 at 62 millibar {called Armstrong limit at 6% sea level pressure}. Loss of consciousness, organ damage | Avg O2% = 8.0 (3700) | 123,000 (3700) |
4.4. CO2 Budget for Year 2006
Readers can skip Section 4.4, which shows the justification for assuming z = 0.1 in presenting the CO2 budget for 2006, and move on to Section 4.5 for comparisons between the annual results for the CO2 budget with results from rigorous models with prescribed z. The CO2 balance via the RQ method yields solutions for CO2 stored in the atmosphere, CO2 sink due to LBM and OWBM, and CO2 stored in the oceans. The relations presented in Table 2 provide the CO2 distribution through data input from Keeling’s data on CO2 and O2 in the atmosphere and annual energy consumption. Only the CO2 sink data by ocean biomass are not reported, while the current results estimate the total CO2 sink due to both biomasses (LBM and OWBM). The CO2 sink by LBM requires a knowledge of a split in O2 added to the atmosphere by LBM and OWBM or a knowledge of the “z” fraction of O2 produced by ocean biomass. A step-by-step procedure for the CO2 budget using the RQ method is indicated in the supplement titled “Supp CO2 budget Supp Step by Step CO2 budget”.
4.4.1. O2 Production by Land and Controversy on O2 Transfer from Ocean to Atmosphere and z Factor
Ref. [65] suggests that upper ocean water is a source of oxygen. Further, there is a periodic outflow of O2 in the atmosphere during warm SS (equivalent to 4.5–5.6 GT of C or 12–14.9 GT of O2) and an inflow from the atmosphere to the ocean in FW [66] But controversy exists about whether the ocean serves as a net oxygen producer or consumer when performing global C and oxygen balance.
Refs. [65,67] suggest that about 50% of oxygen accumulated on Earth originates from ocean PP through photosynthesis in upper 6% of ocean volume. The UN website [68] indicates that 50% of photosynthesis occurs on land, the other 50% in the oceans, and 25% of C is absorbed by the oceans. Others cite that the O2 produced is about 50–70% of the total O2 generated [69]. This statement refers only to oxygen currently in the atmosphere, i.e., O2 stocks (=0.21 * 1.77 × 105 = 37,000 Peta moles of O2), 50% of which originated from biomass in the oceans (i.e., 18,500 Peta moles). The ocean storage is about 220 Peta moles (0.6% of atmospheric O2) of dissolved oxygen. Thus, at first glance, z ≈ 0.5 based on UN data, but this does not mean that all of the O2 produced by OWBM is delivered to the atmosphere or that 50–70% of the air humans currently breathe in comes from the oceans. Skeptics argue [23] that the PP near the ocean surface (data at 20 m and 100 m in Ref. [24]) consumse CO2 and produce O2, but MOM (which includes marine microbes and animals) consumes all of this oxygen, apart from dissolved oxygen, and produces CO2. See also Ref. [70]. So, PP serves as a renewable nutrient or “fuel” for marine life; hence, there is no net O2 delivered to the atmosphere or net CO2 sink due to OWBM. However, the ocean is saturated with O2 near the surface due to a high O2 concentration in the atmosphere (21% O2 or 210,000 ppm; it is much higher than CO2, which is only about 400 ppm). Then, if PP produces O2, it must supersaturate the O2 near the surface, and if so, the extra O2 produced by PP near the ocean surface may enter either the atmosphere or be circulated to deeper parts of the ocean. The global oxygen balance studies by Huang et al. [25] state that only 1.74 GT/year of oxygen enters the atmosphere from the ocean, while land-based biomass generates 16.01 GT/year, indicating about 10% of total O2 from OWBM. See Appendix C, which presents another method of estimating z from the knowledge of C sink via land biomass. For the present study, z is treated as a parameter varying from 0 to 0.5 for comparing the CO2 budget based on the RQ method with results from the literature data generated from more detailed models for 2006 and then selecting an appropriate value for “z”.
4.4.2. Effects of z on CO2 Sink by LBM, OWBM, and Ocean Storage
It is shown that the RQ of the combined RQ for land and ocean biomasses (RQLOWBM) is affected by the value of “z” (Equation (14)) and, hence, depends on the energy (or O2) fraction {z} contributed by ocean-type biomass (Equations (14) and (15)) and (1 − z) contributed by LBM. For the year 2006, the results for CO2 distributions in GT/year and as a % of CO2 emitted from the atmosphere, land, and ocean are shown in Figure 4 and Figure 5 for z = 0, Figure 6 and Figure 7 for z = 0.1, and Figure 8 and Figure 9 for z = 0.5.
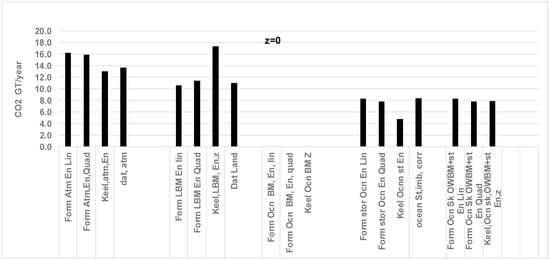
Figure 4.
Comparison of results obtained from the RQ method and literature data for CO2 (GT/year) sink by atmosphere, land, and ocean storage for the year 2006; z = 0.0, i.e., ocean biomass does not add O2 to atmosphere. Data is from Ref. [50]. Atmosphere CO2 data are from [53]. Ocean sink data are estimated from the average of several global ocean biogeochemistry models [44] and the ocean sink uncertainty of ±0.5 GT C/yr. Total CO2 by FFLU = 35.6 GT/year in 2006. Land sink data are from average of dynamic global vegetation models and uncertainty of ±0.9 GT C/yr. Abbreviations in Chart: Form: Formula, ATM: atmosphere, En: Fossil and land use energy; data based on annual energy; Lin: Linear fit for CO2 vs. year in Keeling’s data; Quad: quadratic fit. The “Keel” data are based on 2006 Keeling’s data in ppm for CO2 added to atmosphere [46]; Data atmosphere: reported data from literature for atmosphere. Literature on CO2 distribution is from [44]; LBM: land biomass, Ocn: Ocean, OWBM: ocean water biomass, Sk =Sink. Current results with the RQ method (previous data in parenthesis, Ref. [50]): all in GT of CO2 /year, Atmosphere: 15.9 (13.7), Land 11.4 (11.1), Oceans St: 7.8 (8.4).
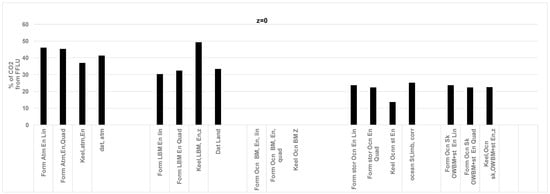
Figure 5.
Comparison of results for the year 2006 obtained from the RQ method and literature data for CO2 (%) sink by atmosphere, land, and ocean storage for the year 2006; z = 0.0, i.e., ocean biomass does not add O2 to atmosphere. Data is from Ref. [50]. Atmosphere CO2 data is from [53]. Z = 0.0, i.e., ocean supplies 0% of total O2 while land supplies 100% of O2. Data from Ref. [50] are for the quadratic fit for CO2 and O2. Abbreviations of terms on “X” axis explained in Figure 4 caption. Current results with the RQ method (previous data in parenthesis, Ref. [50]), in %: Atmosphere: 45.2 (41.3), Land 32.4 (33.4), Ocean St: 22.3 (25.3).
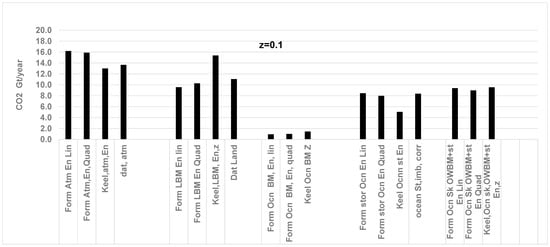
Figure 6.
Comparison of results for the year 2006 obtained from the RQ method and literature data for CO2 (%) sink by atmosphere, land, and ocean storage for the year 2006. Z = 0.1, i.e., ocean supplies 10% of total O2 while land supplies 90% of O2. Data is from Ref. [50]. Abbreviations of terms on “X” axis listed in Figure 4 caption. Keeling’s data on ppm CO2 added to atmosphere [46]. Data atmosphere: reported data from literature for atmosphere. Literature on CO2 distribution is from [44]. RQFFLU = 0.778, RQLBM = 1, RQOWBM = 0.87, RQLOWBM = 0.99 at z = 0.1. Current results with the RQ method (previous data in parenthesis, Ref. [50]): all in GT of CO2 /year, Atmosphere: 15.9 (13.7), Land: 10.3 (11.1), Oceans St: 8.0 (8.4); error % less for ocean storage compared to results for z = 0.0; more error for land biomass compared to z = 0.
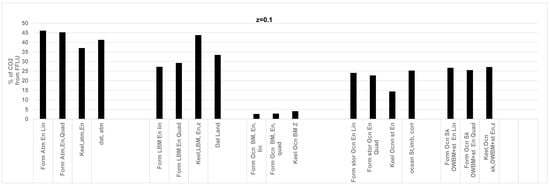
Figure 7.
Comparison between the RQ method and previous data for CO2 (%) sink by atmosphere, land, and ocean storage year 2006. Z = 0.1, i.e., ocean supplies 10% of total O2% while land supplies 90% of O2. Data is from Ref. [50]. Abbreviations are in charts. CO2 by FFLU, year 2006 = 35.6 GT/yr. Abbreviations of terms on X axis explained in Figure 4 caption. RQFFLU = 0.778, RQLBM = 1, RQOWBM = 0.87, RQLOWBM = 0.99 at z = 0.1. Current results with the RQ method (previous data in parenthesis, Ref. [50]): all in %; Atmosphere: 45.2 (41.3), Land 29.2 (33.4), Ocean BM: 2.83, Ocean St: 22.7, (Ocn St + Ocn BM) = 25.53 (25.3).
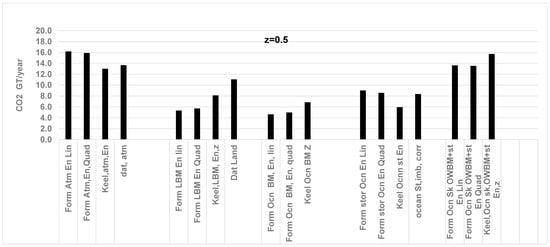
Figure 8.
Comparison between the RQ method and previous data for CO2 (GT/year) sink by atmosphere, land, and ocean storage; z = 0.5, i.e., ocean supplies 50% of total O2 while land supplies 50% of O2. Data is from Ref. [50]. Abbreviations of terms on X axis explained in Figure 4 caption. RQFFLU = 0.778, RQLOWBM = 0.935 at z = 0.5. Current results with the RQ method (previous data in parenthesis, Ref. [54]): all in GT of CO2 /year, Atmosphere: 15.9 (13.7), Land: 8.1 (11.1), Oceans St: 8.6 (8.4). More errors for CO2 capture by land due to high “z”.
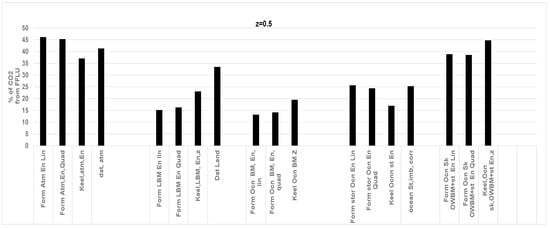
Figure 9.
Comparison of CO2 (%) obtained from the RQ method with the literature data for CO2 (%) sink by atmosphere, land, and ocean storage; z = 0.5, i.e., ocean supplies 50% of total O2 while land supplies 50% of O2. Data areis from Ref. [50]. Abbreviations of terms on X axis explained in Figure 4 caption. RQLOWBM = 0.935 at z = 0.5. All in %; Atmosphere: 45.2 (41.3), Land 16.2 (33.4), Ocean St: 24.4 (25.3). More errors for land due to high z.
Results in these figures are shown for the following methods: (i) Linear fit of Keeling’s data {Form.Lin} and (ii) Quadratic fits {Form.Quad} with constants summarized in data Section 3.4.2. Both of these results fall under the formula {Form} method; (iii) Keeling’s data {Keel.atm} as it is for the year 2005–2006 (no curve fits, year-to-year basis), (iv) the literature data {Dat.atm} on % and GT/year for the atmosphere, land biomass, and ocean sink/storage. The method from (iii) is based on 2005–2006 data only and is subject to more errors due to fluctuating data from year to year. Most discussions are based on curve fit constants from the quadratic method and comparison with reported data. The last two lines in the figure captions give computed GT/year (quadratic method), while previous data are presented in parentheses.
The results from Figure 4, Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9 can be summarized as follows:
- The results for CO2 sink in the atmosphere are not affected by z.
- The ocean CO2 storage is close to the reported data literature for all z (z = 0, 0.1, 0.5) and is a weak function of “z”. The reasons are as follows: the O2 production by biomass is the difference between O2 consumption by FFLU and actual O2 removed from the atmosphere. Thus, once O2 production is determined, the RQLOWBM of combined biomass from the land and ocean determines the amount of CO2 sink, which is O2 production * RQLOWBM. The RQLOWBM of combined biomasses is a weak function of z. The CO2 balance dictates that the CO2 storage (= CO2 produced by FFLU − CO2 sinks via combined land and ocean biomass) is a weak function of z.
- There is a budget imbalance % in the previous literature data on C or CO2, which is given as [(FFLU CO2 source − CO2 added to the atmosphere − CO2 used by both land and ocean biomasses − CO2 stored by ocean water) * 100/ FFLU CO2 source]. The imbalance is about 7% [50]. For example, the CO2 added to the atmosphere is 15.9 GT/year, while data provided by the “stand-alone” atmosphere models indicate only 13.7 GT/year. However, the current formulation with the RQ method is based on the CO2 or C balance method, i.e., the literature data reported on CO2 must be increased by 7%, or data for atmosphere must be increased to 14.7 GT/year when compared with results from the RQ model.
- All the numbers were cross-checked by starting from the end results and back-calculating Keeling’s data (ppm of CO2 added to the atmosphere and ppm O2 removed from the atmosphere) for the following cases. (i) First estimate the ppm of CO2 added to the atmosphere and O2 removed from the atmosphere due to FFLU alone, in case there was no biomass or ocean storage in 2006; (ii) Then, estimate the ppm of CO2 removed and O2 produced by land and ocean biomasses (based on results for CO2% removed by land and ocean biomasses) and re-calculate the ppm of CO2 added to the atmosphere and O2 depleted from the atmosphere. (iii) Finally, estimate the ppm of CO2 removed due to storage by ocean water (based on % CO2 stored by ocean water) and calculate the CO2 added to the atmosphere. (iv) Verify these numbers (ppm/year) to be the same as Keeling’s data on CO2 and O2.
- Using the formula listed Table 2, the CO2 fractions in the atmosphere, land and ocean BM, and ocean storage {Rows 11, 12 and 13} and the CO2 loading in GT/year are estimated {Rows 3b,17 and 20}. The sum of the CO2 fraction in the atmosphere, land and ocean BM, and ocean storage was confirmed to be in unity.
- The RQ method with a quadratic fit for land CO2 sink is estimated as 10.3 GT/year at z = 0.1, while the reported data are 11.1 GT/year. The results from the RQ method agree closely with the literature data on CO2 sink by LBM at low values of z (0 < z < 0.1).
- Since RQOWBM = 0.87, RQLBM = 1, then for z = 0.1, RQLOWBM = 0.987 ≈ RQLBM (since 90% O2 added to atm is assumed to come from LBM).
- When z = 0.5 (50% O2 by ocean biomass or 50% CO2 by land biomass), the RQ method underpredicts the CO2 sink by land biomass since the % of O2 production by land biomass is reduced with a corresponding reduction in CO2 sink at a fixed RQLBM.
- When the explicit formula (Equation (14) to Equation (16)) was used for the year 2006 with z = 0.1, CO2 atmosphere % =45.2 (literature: 41.3), CO2 land BM % = 29.04 (29.2), and (Ocn st + Ocn BM), % = 25.7 (25.3).
4.5. Comparison of Annual CO2 from RQ Method with the Reported Annual Data (1991–2020)
The results for CO2 storage in the atmosphere and ocean are very weak functions of z. Section 4.2 showed that the results on CO2 sink via LBM were a strong function of z and when z = 0.1, the computed results agreed closely with reported data for the year 2006. In this section, RQ-based results for CO2 sink via land, atmosphere, and ocean storage {solid lines Figure 10 (GT/year) and Figure 11 (%)} are compared with previously reported data {dashed line with marker} for atmosphere, land, and ocean storage, assuming z = 0.1. The agreement is very close. The data for the atmosphere fluctuates around the smooth curve due to year-to-year variations in wind conditions, temperature, and gradients of CO2 between land and the atmosphere and ocean and the atmosphere. The predicted results reveal a smooth curve since the prediction is based on curve fit constants. Figure 12 (GT/year) and Figure 13 (%) show a comparison of computed CO2 sink (solid line) by land biomass with previous data (dashed line with marker). The average C sinks from land and ocean sinks from 2000 to 2016 reported in [28] are 9.53 ±2.57 and 5.59 ± 3.30 GT of CO2/year (or 2.6 ± 0.7 and 1.5 ± 0.9 GT of C per year), while the RQ method shows CO2 sink via ocean storage to be 5 to 10 GT /year with an average of 7.5 GT /year and land biomass to be 10.5 GT/year from 1991 to 2018. They are within the error bounds of Tohjima et al.’s work [28]. Ref. [28] also states that their sink estimates are within 1.47 GT/year, as presented by the GCP.
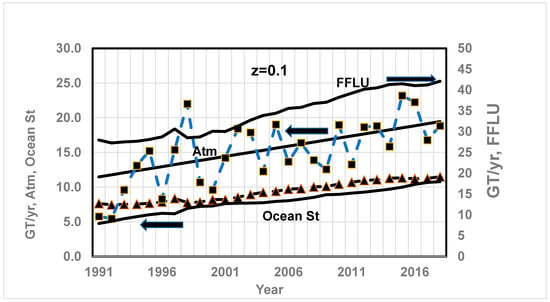
Figure 10.
Comparison of CO2 in GT/year since 1991 based on a quadratic fit of Keeling’s data for CO2 and O2 and the RQ method (solid line) vs. literature results (dashed line with marker, ■ for atm, ▲ for Ocean st) for a; and ocean storage z = 0.1. Arrows ← indicate values on primary axis and → indicate values on secondary axis. Data are from Ref. [50]. See Figure 4 caption for data source. Results are weak function of z. The CO2 stored in atmosphere and ocean storage shows an almost similar gradual increase. They are in proportion to CO2 released in GT of CO2 /year by FFLU. From Ref. [71], average for 1989–1998: CO2 from FFLU = 28.9 GT of CO2 /year; atmosphere: 12.1 and ocean storage = 8.4 GT of CO2 /year.
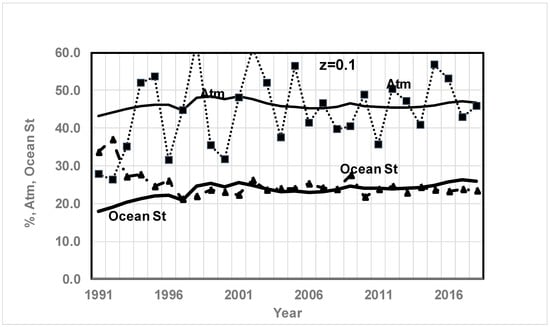
Figure 11.
Comparison of CO2% in atmosphere and ocean since 1991. Results based on quadratic fit of Keeling’s data for CO2 and O2 and the RQ method (solid lines without markers; thin line for atm, thick line for ocean storage) vs. previous results (dashed lines with marker, ■ for atm, ▲ for Ocean Storage) for atmosphere, and ocean storage (z = 0.1). Data is from Ref. [50]. See Figure 4 caption for data source. Results are a weak function of z. Atmospheric storage shows a slight increase in % while ocean storage shows a slight increase in %. From Ref. [71], average % from 1989 to 1998, atmosphere: 41.8%, and ocean storage: 29.1%.
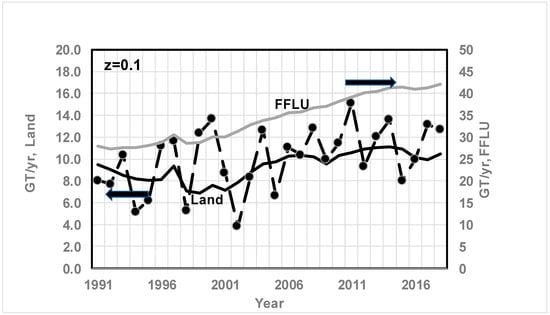
Figure 12.
Comparison of CO2 sink via land biomass (GT/year) since 1991 based on quadratic fit of Keeling’s data for CO2 and O2 and the RQ method (solid line) vs. literature data (dashed line with marker, ● for Land literature data) for atmosphere and ocean storage (z = 0.1). Arrows ← indicate values on primary axis and → indicate values on secondary axis. Data are from Ref. [50]. GT/ of CO2 year seems to increase due to CO2 fertilization. See Figure 4 caption for data source. Results are a strong function of z. From Ref. [71], average for 1989–1998: FFLU = 28.9 GT/year; land 8.4.
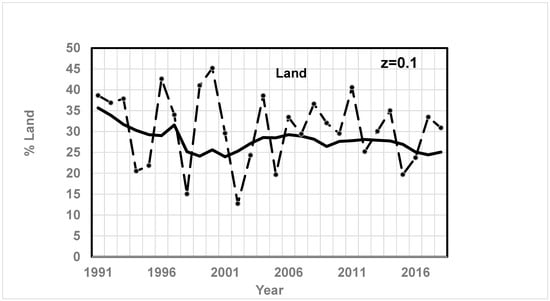
Figure 13.
Comparison of CO2% since 1991 based on quadratic fit of Keeling’s data for CO2 and O2 and the RQ method vs. literature results (dashed line with marker, ● for Land literature data) for land biomass (z = 0.1). Data is from Ref. [50]. See Figure 4 caption for data source. Results are a strong function of z. From Ref. [71], average % from 1989 to 1998 of land: 29.1%. However, Bonan reports 45% of the organic carbon on land in their biomass and soil [72].
4.5.1. Freezing CO2 Growth in Atmosphere Using RQ
One can estimate the desired RQFFLU so that CO2 in the atmosphere remains flat or d(CO2)/dt = 0 in Equation (9). See Appendix B for details.
Required RQFFLU: Solving for RQFFLU from the above equation,
where x is given by Row 7a, Table 2 in terms of annual energy release rate from FFLU, and Row 7b, Table 2 in terms of annual carbon release rate from FFLU and [d(O2)/dt]atm.
It is noted that “y” remains almost flat (Figure 3), indicating increased CO2 storage (hence, ocean acidity) in proportion to O2 consumption rate by FFLU or annual energy release rate from FFLU. Since CO2 remains flat, the coefficients d2, d1, and d0 for quadratic fit of O2 data may be different; hence,
Figure 3 reveals that variations in x and y are mostly flat (x ≈ 0.3 to 0.2, y ≈ 0.2 to 0.25) compared to FFLU energy, which increases by 60%. Assuming x ≈ 0.25, y = 0.23, RQLOWBM = ≈1, the desired RQFFLU = 0.48, y = 0.23 (with ocean acidification), and RQFFLU = 0.25 (with no ocean acidification, y = 0). The low value of 0.25 for RQFFLU is difficult to achieve in practice since the lowest RQ is 0.5 for methane fuel (or natural gas).
Required RQLOWBM: If RQFFLU is fixed, one may solve for the desired RQLOWBM as (Equation (26))
If NG is used as a global fossil fuel, the RQFFLU = 0.5, and assuming x = 0.25, y = 0.23, the desired RQLOWBM = 1.08. Ref. [73] reports an RQ from 1.2 to 2.0 (i.e., PQ as 0.5 to 0.85) for sea weeds. Another avenue for increasing CO2 sink via biomass is to use AI photosynthesis and photoelectrochemical carbon sinks [74].
4.5.2. Freezing CO2 Growth in Atmosphere by CO2 Storage
Carbon Capture and storage: If direct air capture (DAC) technologies are adopted for extracting CO2 directly from the atmosphere, the required underground storage of CO2, , is given as
where in Peta moles/year. The required amount of C(s) to be sequestered in mass units is given as
where are the required amounts to be stored in GT of C(s) and GT of CO2 per year in the underground (UG) storage for maintaining {d[CO2]/dt} in the atmosphere = 0. See Row #3b, Table 2.
Several models exist for underground gas storage [75,76]. One can use depleted oil/gas reservoirs as CO2 underground storage with the additional benefit of reducing Earth’s mass loss rate [9] since CO2 mass, which would have escaped to the atmosphere, is returned to Earth with underground storage.
4.6. Relation between Global Temperature, Rate of Heating, Energy, and Global CO2 Concentration
The authoritative NASA website contains data on land and sea surface temperature (SST) [32]. Most of the data are reported as temperature anomalies, defined as the difference between local temperature and average temperature or base temperature for the specific period of 30 years (1951–1980) at the same location, so the temperature anomaly is location-independent. The global average temperature for 30 years was 13.9 °C or 57 °F [77]. The 2010 global temperature was 14.7 °C, or 0.8 °C was the temperature anomaly in 2010. For additional information, see websites at NASA’s Goddard Institute for Space Studies and NOAA’s National Centers [78].
The quadratic curve fit to the global average temperature since 1880 computed from the temperature anomaly and assuming a global 30-year average (1951–1980) temperature of 13.9 °C (57 F) [79] yields the following relation:
where g2 = 9.114 * 10−5, g1 = −5.281 * 10−3 t, g0 = 13.71, t = Year of interest − 1880,
Based on curve fit constants, the heating rate was 0.15 °C/decade (1981–1991), and now it has jumped to 0.22 °C/decade (2012–2022).
Since data are available for both the global average temperature vs. year and Keeling’s data on CO2 ppm, it is of interest to plot temperature vs. CO2 concentration, which is related to energy from FFLU. Selecting T0 for year 1991, the ΔT was then plotted against ([CO2]/[CO2,0]) where [CO2] was the CO2 concentration in the year of interest and [CO2,0] was the concentration of CO2 in the year 1991 (Figure 14). The curve fits for ΔT vs. [CO2]/ [CO2,0]) for years 1991–2022 (Figure 14) yields
Note that the concentration ratio ([CO2]/[CO2,0]) is the same as the GT ratio of CO2. Differentiating Equation (33), the rate of temperature rise is given as
where {d[CO2]/dt}atm in ppm/year and one may use linear or quadratic fit to obtain the slope .
Row #21a, Table 2 for global temperature rise ΔT vs. year.
Row #21b, Table 2 for global temperature rise ΔT vs. [CO2]/[CO2]0.
Row #22a, Table 2 for rate of temperature rise dT/dt in terms of .
Ref. [1] reports 0.0125 °C/year (or 0.125 °C per decade, around 1994) with a CO2 increase of 2 ppm/year, while Equation (34) with 2.08 ppm/year (Keeling’s data, linear fit) yields 0.023 °C/year or 0.23 °C/decade. The NASA website [77] indicates 0.15–0.20 °C/decade since 1975, while the recent data in 2022 indicates 0.18 °C/decade [80].
In the following, an attempt has been made to relate the rate of heating of Earth to the annual energy release rate {, Exa J/year}, even though the processes governing the relation are complex (see Ref. [36] for balance equations). Using the definition of RQGlob(En), one can express d[CO2]/dt in the atmosphere as
Figure 3 shows that RQGlob(En) is almost constant. Hence, the above equation suggests that the rate of CO2 increase in the atmosphere (ppm/year) is proportional to . Expressing Equation (35) in Equation (34), the rate of heating is given as
which shows that the rate of temperature rise is proportional to the energy release rate in Exa J per year.
Row #22b, Table 2 for the rate of temperature rise dT/dt in terms of RQGlob(En) and energy release rate.
While the relation for dT/dt with d[CO2]/dt has a slope of 4 (Equation (34)), Equation (36) indicates the weaker relation of dT/dt with the annual energy release rate. The cumulative energy release from 1991 to 2018 (total of 27 years) via FFLU was about 12,000 Exa J added to Earth (which is almost 40 times more than FFLU energy in 1991), while 4500 GT of CO2 was added to the atmosphere (which is almost two times the amount present in 1991) during the same period, resulting in the greenhouse effect. Typically, the greenhouse effect is dominant compared to the waste heat/energy release effect.
With 2018 data on = 545 Exa J/year, RQGlob(En) = 0.36 from a quadratic fit, Equation (36) yields dT/dt = 0 0.027 °C/year or 0.27 °C/decade. If a linear fit is adopted, RQGlob(En) = 0.30, dT/dt = 0.023 °C/year or 0.23 °C/decade. The estimate obtained from the RQ method for Keeling’s curves agrees with the heating rates of 0.28 °C/decade (after 2010) and 0.18 °C per decade (1970–2010) [81], which are based on satellite remote sensing data. The same reference cites similar heating rates by the GCP.
Figure 14 yields the following additional relations:
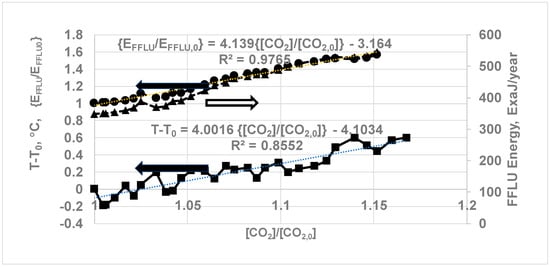
Figure 14.
Variations in global temperature difference (T − T0) {■}, FFLU energy release rate {▲}, and normalized Energy release {Symbol ●}, with normalized CO2 concentration, [CO2]/[CO2,0] (1991–2020); [CO2] atmosphere. Arrows ← indicate values on primary axis and → indicate values on secondary axis. Concentration in ppm in any given year and [CO2,0] atmosphere CO2 concentration in 1991. Energy and CO2 data are from Ref. [50]. Global temperature data are from [82]. See data for temperature of NY City in Ref. [83]. The energy release by FFLU (secondary axis), and normalized energy release (primary axis). There are 18% and 60% increases in energy release rate in the years 2006 and 2018, respectively, compared to year 1991.
The normalized energy release rate and hence the normalized CO2 concentration have the following fits:
4.7. Limitation of Results
The CO2 budget results with the RQ method are based on the presumption that Keeling’s data on CO2 and O2 in the atmosphere are affected by CO2 sources from FFLU and CO2 sinks by biomass and CO2 storage in the oceans. Thus, if there is an increasing global temperature, it would be reflected in less CO2 sink by biomass and less O2 production and vice versa, which are reflected in Keeling’s data. The results do seem to be comparable to the reported literature data, which are based on more detailed fundamental and stand-alone models for the atmosphere, land, and oceans. The results in Table 5 on global O2 concentration and mass of earth vs. year are based upon the extrapolation of quadratic fit to Keeling’s data as though CO2 distributions continue the same trends, and they are independent of global temperature and increasing CO2 concentrations and sea levels.
4.8. Policies and Econometry
Policies: Economic growth measured in terms of a nation’s GDP (gross domestic product) is intricately coupled with the growth of energy consumption. If the source of energy is from the combustion of fossil fuels, the higher the GDP, the higher the energy consumption and the more CO2. The Intergovernmental Panel on Climate Change (IPCC) recommends climate action via policies limiting global warming to 1.5 °C, which requires a quantum leap in policies to reduce the slope of [CO2] vs. year. The benefits of CO2 reduction vs. the cost of policies and the social cost of carbon (SCC), a dollar measure of the “cost” damage to society as a result of CO2 added to the atmosphere, were investigated by Fraas et al. [84]. The cost of promoting clean technology and net zero emissions must be balanced against the SCC.
The policies require changes in the “upstream” and “downstream” of CO2 production.
Upstream: (i) Mandates for utilities to adopt low-carbon FFs in electricity generation by a specified deadline, (ii) recommendation on “layered” tax and increased excise taxes, based on the RQ of FFs (a measure of CO2 emission in tons per unit energy release, e.g., coal with RQ = 1 vs. NG with RQ = 0.5), (iii) use of Ref. [47] in estimating the reduced RQ for a mix of FFs and renewable fuels (RFs) (e.g., gasoline-ethanol blend) and added incentives along with reduced taxes for RFs, and (iv) promotion of solar power.
Downstream: (i) Cap-and-trade regulations, (ii) tax incentives for mitigation, (iii) CO2 per kWH (which involves efficiency and an increase in cost of electricity generation when meeting mandates) and carbon taxes; e.g., Sweden: USD 30 per ton of CO2 in 1991 and increased to USD 132 [85], (iv) carbon capture and storage (CCS) and approximate estimation of C to be sequestered using the relations provided in the current text, (v) emissions trading systems with high USD cost of CO2 per ton, indicating the extent of enforcement of the Paris accord and vice versa, (vi) CO2 tax based on actual CO2 emissions rather than transport vehicle weight estimated from the RQ value of fuels [6] and actual fuel consumed, (vii) residential and industrial non-electricity FFs use (e.g., home use for heating and cooking, shops and offices).
Cost: Cost has been identified as the major barrier to implementing CO2 capture and storage or utilization technologies [86]. Higher adoption of CO2 capture technologies in various heavy industries will be based on the carbon tax credits and policy framework across different countries [87]. It should be noted that the Internal Revenue Code (IRC) Section 45Q of the US tax code provides tax credits for qualified carbon dioxide captured and sequestered. However, additional policies around the transportation of captured carbon, storage, and taxation of unabated carbon dioxide should be enacted for large-scale implementation of the CO2 capture technologies and negative or positive outcomes [88,89].
5. Summary
The power plants breathe in O2 from the atmosphere, oxidize FFs and breathe out CO2. The RQFF varies from 0.5 (NG) to 1.0 (coal). Global RQ is expressed in two forms: (I) RQGlob (= CO2 added to the atmosphere/O2 depleted from the atmosphere), which is at about 0.47, and (II) RQGlob(En) (= CO2 to the atmosphere/O2 consumed by FFLU from the atmosphere), which is about 0.36. The definition of RQGlob(En) leads to an estimation of CO2 in GT in the atmosphere per Exa J released by FFLU = 0.1 * RQGlob(En). If RQGlob or RQGlob(En) decreases, this indicates less CO2 in the atmosphere and higher CO2 storage and, hence, increased acidity of the oceans. The RQGlob(En) of 0.36 implies that 0.36 moles of CO2 are added to the atmosphere for every mole of O2 used by FFLU in releasing energy. The CO2 release by FFLU increased from 27 to 42 GT/year by FFLU for the period 1991–2020.
The simple RQ method of analysis of Keeling’s data leads to explicit formulae for CO2 sinks in the atm, land and ocean biomasses, and storage in the oceans. The computed results with a quadratic curve fit agree with most of the reported data for CO2 sink via land biomass (GT per year and %) for the year 2006 when z (the ratio of O2 contributed by the ocean to the atmosphere/total O2 contributed by both land and ocean biomasses) is selected to be about 0.1. Computed results for CO2 storage in the atmosphere and ocean are weak functions of z and agree closely with the collected data.
The RQ concept Is extended for the period of 1991–2020 for estimating the annual CO2 distribution in GT/year and as a % of CO2 produced by FFLU by assuming z = 0.1. The RQ-based results are then validated with the literature data (1991–2020) generated using a rigorous model, which includes the effects of wind velocity, temperature, and gradients of CO2 (i) between land and the atmosphere and (ii) ocean and the atmosphere, and ocean circulation and temperature; thus, the data fluctuate from year to year. However, the predicted results for CO2 sinks reveal a smooth curve, since the prediction is based on curve fit constants. The RQ method using Keeling’s data shows the variations in CO2 sink by the atmosphere, land, and ocean as follows: 12 to 33 GT/year (atmosphere), 8 to 10 GT/year (land biomass), and 5 to 10 GT/year as storage in the oceans.
If slow, gradual extinction is a part of the evolution of life on Earth, the planet seems to be marching towards slow extinction due to the time lag between the development of human traits and the fast-changing local climate affected by increasing CO2 concentration. Just as in biology where nutritional “therapy” is used to control RQ and reduce acidity in the blood, the FFs “therapy” requires low RQ fuels and high RQ biomasses. The sargassum (seaweed) has an RQ of 1.2 to 2.0 [9,73]. The rate of temperature rise with the change in CO2 concentration is presented, and Keeling’s data seem to suggest a 0.23 °C rise per decade, while NASA’s data indicate a 0.15–0.20 °C rise per decade.
6. Future Work
It was shown that the warming causes an increasing vapor pressure deficit (VPD) {difference between the saturation pressure of H2O in the atmosphere, PsatH2O, which increases with temperature, and actual vapor pressure over land and the oceans (pH2O)} within the globe, creating plant stress, soil drought, and reducing the life span of vegetation [90]. The impact of the VPD on atmospheric pressure, wind velocity, rain, and hurricanes must be studied. Algae (chemical formula: (CH2O)106(NH3)16(H3PO4) or C106H263N16O10P including PP) can serve as a renewable fuel and can minimize the use of FFs for energy.
It is noted that the control of pollutant emissions sometimes results in global warming in addition to CO2. The white reflective clouds formed when SO2, a pollutant, is mixed with water vapor reflect solar energy away from Earth, resulting in more global warming [1]. Thus, future work requires the effects of pollution control on global warming.
There is uncertainty in the literature on the % of O2 contributions by the ocean to the atmosphere and more precise data are required. Data on the relation between the RQ of biomasses and their variation with the increasing concentration of CO2 are required. High RQ values for biomass are desired to provide more CO2 sink by land and ocean biomass. But low RQ values are desired by the same biomasses to provide more O2 production if O2 concentrations need to remain at current level! The ideal scenario is to have a “phytoplankton forest” in the ocean along with seaweed. Botanists must explore the possibility of genetically modifying biomasses (e.g., PP in ocean and plants and trees on the land) and using artificial photosynthesis mimicking the natural photosynthesis for serving as a CO2 sink and O2 source to provide a high RQ and overcome the economic hurdles [91]. The effects of earth’s mass loss due to mining of FF on earth’s tilt angle must be investigated.
Are Keeling’s data an ultimate judgement of what is happening with CO2 sources and sinks, land and ocean biomasses, and ocean storage? Is Earth marching towards “death” without any respiration on the planet? Though it is suggested that the Earth has a life period of another 1700 years, extrapolating Keeling’s data, more detailed modeling is required to predict the decreasing oxygen concentration in the atm and the slow extinction of species on Earth.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/en17081800/s1, The detailed step-by-step procedure for obtaining quantitative results is provided as supplemental materials titled “Supp Step by Step CO2 budget Part II”.
Funding
The author wishes to acknowledge the partial support of research funds, prior to retirement, from the Paul Pepper Professorship, which encouraged research outside of the “loop” and initiation of research on engineering applications of biology’s RQ concept. This research began as a curiosity after looking at Keeling’s saw-tooth pattern curves on CO2 and O2 and their apparent similarity to the data on CO2 and O2 with the RQ concepts used in biology and engineering. There was no funding for the current research on the RQ method for CO2 distribution.
Data Availability Statement
Data are contained within the article and Supplementary materials.
Acknowledgments
The four reviewers for providing critical comments and helping the author in improving the quality of paper. Siva Sankar Thanapal, Texas A&M University Mechanical Engineering graduate, former PhD student of the author and currently Environmental Advisor with an energy company for sharing his thoughts on policy issues and for the addition of a paragraph in the section on the “policy and econometry” of CO2 reduction and sequestration. Megan L. Simison of the J. Mike Walker ’66 Department of Mechanical Engineering, Texas A&M University, English editing of the manuscript.
Conflicts of Interest
The author declares no conflicts of interest.
Nomenclature
| AFFLUE | Annual Fossil and Land Use Energy |
| AI | Artificial Intelligence |
| ARQ | Apparent Respiration Quotient |
| BS | Biological system |
| Carbon release rate, GT/year | |
| CCP | Coal Combustion Project |
| CE | Carbon Emission |
| CH | Carbohydrate |
| CS | Carbon storage |
| CO2eq | CO2 equivalent |
| DAF | Dry ash free |
| Energy release rate from FFLU, Exa J/year | |
| EF | Energy fraction |
| EPA | Environmental Protection Agency |
| EPICA | European Project for Ice Coring in Antarctica |
| Exa g | 1018 g = 1000 Peta g or 1000 Giga tons or 1000 billion tons = 106 Tera g = 109 Giga g = 1012 Mega g = 1015 kg |
| ExR | Exchange ratio = 1/RQ |
| F | Fat |
| Fi | constants used in many relations; Table 4 lists them. |
| FF | Fossil Fuel |
| FFLU | Fossil fuel and Land use |
| GCP | Global Carbon Project |
| GPP | Gross Primary Production |
| GWP | Global warming Potentia-CO2 eq GWP100: GWP over 100 years |
| HBS | Hypothetical biological System |
| HH | Hypothetical Human |
| HHVO2 | Energy released per Peta Mol of O2 = 448 Exa J per Peta mol of O2 |
| IPCC | Inter-government Panel on Climate Change |
| LBM | Land biomass |
| LOWBM | Combined land and ocean water biomasses |
| LU | Land use |
| M | Molecular weight |
| MOM | Marine organic matter |
| Mole rates of CO2, O2 per year | |
| CO2 release rate from FFLU and O2 consumption by FFLU, Peta moles/year | |
| NBS | Non-biological systems |
| NEP | Net Ecosystem Production, NEP = NPP − Loss due to Dead Matter |
| NG | Natural gas |
| NH | Normal Human |
| NOAA | National Oceanic and Atmospheric Administration |
| NPP | Net Primary Product, NPP = GPP − Respiration Rate_ |
| OW | Ocean water |
| OWBM | Ocean water biomass |
| Per meg | 1 molecule out of 1000,000 oxygen molecules, 1 ppm in air = 4.76 per meg |
| PP | Phytoplankton |
| ppb | parts per billion |
| ppm | parts per million or molecules per million molecules 1 ppm in atmosphere = 7.77 GT for CO2, 2.12 GT for C, 1 ppm O2 in atmosphere = 5.65 GT |
| PQ | Photo-synthetic quotient, = 1/RQ |
| Quad BTU | 1015 BTU |
| RQ | Respiratory quotient |
| RQGlob | Global RQ based on Keeling’s data on CO2 and O2, (d[CO2]/dt)/(d[O2]/dt) |
| RQGlob(En) | Energy based Global RQ = Ratio of moles of CO2 release and O2 consumption by FFLU |
| RR | Redfield ratio = 1/RQ |
| SDG | Sustainable development goal |
| SST | Sea surface temperature |
| UCF | Unit carbon formula |
| Yk | mass fraction of element k, g of k/g of mixture |
| ZJ | Zetta joule, 1021 J |
| [k] | Species k in moles or ppm per unit volume |
Appendix A. CO2 Added to Atmosphere and O2 Removed from Atmosphere in GT per Year
- (a)
- CO2 added to the atmosphere.where Nair = 1.77 × 105 Peta moles. Generally for any trace GHG of molecular weight MGHG
- (b)
- O2 Removed from Atmosphere
Appendix B. CO2 and O2 Balance Equations in Non-Dimensional Form and Solutions for O2 Production by Land Ocean Biomasses and CO2 Storage by Ocean
O2 Balance: Dividing the oxygen conservation equation (Equation (6)) by O2 moles consumed by FFLU (combined FF and land use energy), defined as
where x is defined as
where FBal = 10−6 * Nair * HHVO2 = 79.3 (Table 4) with Nair = 1.77 × 105 Peta moles, HHVO2 = 448 Exa J/Peta mole O2, and and in Exa J/year. The left-hand side is known from the curve fit constants term in Keeling’s data on O2 [27] and, hence, “x” can be estimated from Equation (11).
The advantages of normalizing with NO2, FFLU are that (i) the denominator of O2 sink by fossil fuels is known once the annual energy consumption is known and (ii) energy-based global RQGlob(En) can be converted into GT/year by using CO2 in GT/Exa J of energy release by FFLU = 0.1 * RQGlob(En) (Equation (19))
If annual emission data by FFLU (GT/year) are reported instead of energy data, then , Peta mole/year,
where FC = Mc * 10−6 * Nair = 2.13,
CO2 Balance:
Dividing Equation (7) by O2 moles consumed by FFLU () recalling that = RQFFLU * and simplifying,
where
Using x from Equation (A6), “y” is solved as
CO2 Budget
where FBal = 79.3. With definition of RQGlob (En),
CO2 Sink Rate Due to LBM and OWBM: Multiplying by “x” by z, the O2 source due to ocean biomass, and by (1 − z), the O2 source via land biomass are given as as follows:
CO2 Storage Rate in Ocean
Combining with CO2 sink by ocean biomass and using definition of RQGlob (En)
Appendix C. Estimation of “Z” (O2 Transferred from Ocean to Atm /Total O2 Produced) from C Sink on Land and C Emission
When C emission data and C sink on land are available along with Keeling’s data on O2 vs. year, the “z” may be estimated. The procedure is outlined below:
- Estimate the rate of decrease in O2 from the atmosphere from Keeling’s data.
- Use left-hand side of Equation (A8) to determine “x” ratio of O2 produced to O2 used by FFs and LU.
- Since the ratio of O2 production by land to total O2 production is (1 − z) * x and since O2 production is for every mole of C(s) or CO2 sink, then O2 production via land in Peta mole/year = (1 − z) * x * (annual O2 sink in Peta moles due to FFLU) = CO2 or C(s) sink on land in Peta moles on land per year = C(s) sink on land (GT/year) * 1015 (g/GT) /{RQBM * MC (g/mol) * 1015 (mole/Peta mole)} = C(s) sink on land (GT/year)/({RQBM * MC g/mol)}.
- A formula for z can be derived as follows:where O2 sinks due to FFLU, Peta moles/year = (C emission in FFLU in (GT/year)/(RQFFLU * MC), and MC = 12.01.
References
- Duursma, E.K.; Boisson, M.P. Global Oceanic and Atmospheric Oxygen. Oceanol. Acta 1994, 17, 117–141. [Google Scholar]
- Schmiege, S.C.; Heskel, M.; Fan, Y.; Way, D.A. It’s only natural: Plant respiration in unmanaged systems. Plant Physiol. 2023, 192, 710–727. [Google Scholar] [CrossRef]
- Pries, H.C.P.; Angert, A.; Castanha, C.; Hilman, B.; Torn, M.S. Using respiration quotients to track changing sources of soil respiration seasonally and with experimental warming. J. Biogeoscience 2020, 17, 3045–3055. Available online: https://bg.copernicus.org/articles (accessed on 28 January 2024). [CrossRef]
- Feely, R.A.; Sabine, C.L.; Takahashi, T.; Wanninkhof, R. Uptake and Storage of Carbon Dioxide in the Ocean: The Global CO2 Survey. JGOFS Oceanogr. 2001, 14, 18–32. [Google Scholar] [CrossRef]
- Gruber, N.; Gloor, M.; Fan, S.-M.; Sarmiento, J.L. Air-sea flux of oxygen estimated from bulk data: Implications for the marine and atmospheric oxygen cycles. Glob. Biogeochem. Cycles 2001, 15, 783–803. [Google Scholar] [CrossRef]
- Mehmood, T.; Hassan, M.A.; Li, X.; Ashraf, A.; Rehman, S.; Bilal, M.; Obodo, R.M.; Mustafa, B.; Shaz, M.; Bibi, S.; et al. Mechanism behind Sources and Sinks of Major Anthropogenic Greenhouse Gases, Climate Change Alleviation for Sustainable Progression; CRC Press: Boca Raton, FL, USA, 2022; Chapter 8; ISBN 9781003106982. [Google Scholar]
- U.S. EPA. 2020 Common Reporting Format (CRF); U.S. EPA Environmental Protection Agency: Washington, DC, USA, 2020.
- Gasser, T.; Crepin, L.; Quilcaille, Y.; Houghton, R.A.; Ciais, P.; Obersteiner, M. Historical CO2 emissions from land use and land cover change and their uncertainty. Biogeosciences 2020, 17, 4075–4101. [Google Scholar] [CrossRef]
- Annamalai, K. Breathing Planet Earth: Global Respiratory Quotient (RQGlob) from Keeling’s Data and CO2-Budget among the Atmosphere, Land and Oceans, Part I: Brief Review on RQ and Global Respiratory Quotient of Earth. J. Energy 2023, 17, 299. [Google Scholar]
- Available online: https://www.theguardian.com/commentisfree/2008/aug/13/carbonemissions.climatechange (accessed on 1 January 2024).
- Martin, D.; McKenna, H.; Livina, V. The human physiological impact of global deoxygenation. J. Physiol. Sci. 2017, 67, 97–106. [Google Scholar] [CrossRef]
- Livina, V.N.; Martins, T.M.; Forbes, A.B. Tipping point analysis of atmospheric oxygen concentration. Chaos 2015, 25, 036403. [Google Scholar] [CrossRef]
- Available online: https://news.climate.columbia.edu/2022/01/27/how-climate-change-will-affect-plants/ (accessed on 7 December 2023).
- Available online: https://en.wikipedia.org/wiki/Composition_of_the_human_body (accessed on 25 August 2023).
- Available online: https://ourworldindata.org/life-by-environment (accessed on 14 January 2023).
- Gruber, N.; Clement, D.; Carter, B.R.; Feely, R.A.; van Heuven, S.; Hoppema, M.; Ishii, M.; Key, R.M.; Kozyr, A.; Lauvset, S.K.; et al. The oceanic sink for anthropogenic CO2 from 1994 to 2007. Science 2019, 363, 1193–1199. [Google Scholar] [CrossRef]
- Falkowski, P.G. The role of phytoplankton photosynthesis in global biogeochemical cycles. Photosynth. Res. 1994, 39, 235–258. [Google Scholar] [CrossRef]
- Available online: https://socratic.org/questions/55c2531d581e2a136c45b148 (accessed on 28 January 2024).
- Behrenfeld, M.J. Climate-mediated dance of the plankton. Nat. Clim. Chang. 2014, 4, 880–887. [Google Scholar] [CrossRef]
- Available online: https://mynasadata.larc.nasa.gov/basic-page/global-phytoplankton-distribution (accessed on 15 April 2023).
- Available online: https://ugc.berkeley.edu/background-content/oxygen-levels/ (accessed on 15 January 2024).
- Zhao, R.; Zhang, I.H.; Jayakumar, A.; Ward, B.B.; Babbin, A.R. Origin, age, and metabolisms of dominant anammox bacteria in the global oxygen deficient zones. bioRxiv 2023. [Google Scholar] [CrossRef]
- Available online: https://theconversation.com/humans-will-always-have-oxygen-to-breathe-but-we-cant-say-the-same-for-ocean-life-165148 (accessed on 6 February 2023).
- Balkanski, Y.; Monfray, P.; Battle, M.; Heimann, M. Ocean primary production derived from satellite data: An evaluation with atmospheric oxygen measurements. Glob. Biogeochem. Cycles 1999, 13, 257–271. [Google Scholar] [CrossRef]
- Huang, J.; Huang, J.; Liu, X.; Li, C.; Ding, L.; Yu, H. The global oxygen budget and its future projection. Sci. Bull. 2018, 63, 1180–1186. [Google Scholar] [CrossRef]
- Long, M.C.; Ito, T.; Deutsch, C. Oxygen projections for the future. In Ocean Deoxygenation: Everyone’s Problem—Causes, Impacts, Consequences and Solutions; Laffoley, D., Baxter, J.M., Eds.; IUCN: Gland, Switzerland, 2019; Chapter 4; pp. 171–211, xxii+56. [Google Scholar]
- Keeling, R.F.; Manning, A.C. Studies of Recent Changes in Studies of Recent Changes in Atmospheric O2 Content. In Treatise on Geochemistry, 2nd ed.; Holland, H.D., Turekian, K.K., Eds.; Elsevier: Amsterdam, The Netherlands, 2014; pp. 385–404. [Google Scholar] [CrossRef]
- Tohjima, Y.; Mukai, H.; Machida, T.; Hoshina, Y.; Nakaoka, S. Global carbon budgets estimated from atmospheric O2/N2 and CO2 observations in the western Pacific region over a 15-year period. Atmos. Chem. Phys. 2019, 19, 9269–9285. [Google Scholar] [CrossRef]
- Webb, P. Introduction to Oceanography; Chapter 5, Digital Book; Rebus Community: Montreal, Quebec, Canada. Available online: https://rwu.pressbooks.pub/webboceanography (accessed on 28 January 2024).
- Available online: https://newportbay.org/ask-a-naturalist-do-phytoplankton-produce-more-oxygen-than-a-rainforest-if-so-does-the-oxygen-they-produce-go-into-the-atmosphere-or-does-it-just-remain-dissolved-in-the-ocean/ (accessed on 26 February 2023).
- Lenssen, N.; Schmidt, G.; Hansen, J.; Menne, M.; Persin, A.; Ruedy, R.; Zyss, D. Improvements in the GISTEMP uncertainty model. J. Geophys. Res. Atmos. 2018, 124, 6307–6326. [Google Scholar] [CrossRef]
- Available online: https://climatedataguide.ucar.edu/climate-data/global-temperature-data-sets-overview-comparison-table (accessed on 31 July 2023).
- Hansen, J.; Ruedy, R.; Sato, M.; Lo, K. Global surface temperature change. Rev. Geophys. 2010, 48, RG4004. [Google Scholar] [CrossRef]
- NOAA; National Centers for Environmental Information. State of the Climate: Global Climate Report for 2022. 2023. Available online: https://www.ncei.noaa.gov/access/monitoring/monthly-report/global/202213 (accessed on 28 January 2024).
- Available online: https://www.climate.gov/news-features/understanding-climate/international-report-2021-climate-record-high-greenhouse-gases (accessed on 12 September 2023).
- Chaisson, E.J. Long-Term Global Heating from Energy Usage. Eos Trans. AGU 2008, 89, 253–254. [Google Scholar] [CrossRef]
- Schuckmann, K.; Minère, A.; Gues, F.; Cuesta-Valero, F.J.; Kirchengast, G.; Adusumilli, S.; Straneo, F.; Ablain, M.; Allan, R.P.; Barker, P.M.; et al. Heat stored in the Earth system 1960–2020: Where does the energy go? J. Earth Syst. Sci. Data 2023, 15, 1675–1709. [Google Scholar] [CrossRef]
- Available online: https://www.ncei.noaa.gov/access/monitoring/monthly-report/global/202303 (accessed on 7 June 2023).
- Available online: https://www.un.org/development/desa/jpo/wp-content/uploads/sites/55/2017/02/2030-Agenda-for-Sustainable-Development-KCSD-Primer-new.pdf (accessed on 15 February 2024).
- Available online: https://www.ipcc.ch/sr15/ (accessed on 1 February 2024).
- Kim, S.K.; Shin, J.; An, S.I.; Kim, H.J.; Im, N.; Xie, S.P.; Kug, J.S.; Yeh, S.W. Widespread irreversible changes in surface temperature and precipitation in response to CO2 forcing. Nat. Clim. Chang. 2022, 12, 834–840. [Google Scholar] [CrossRef]
- Duffy, K.A.; Schwalm, C.R.; Arcus, V.L.; Koch, G.W.; Liang, L.L.; Schipper, L.A. How close are we to the temperature tipping point of the terrestrial biosphere? Sci. Adv. 2021, 7, eaay1052. [Google Scholar] [CrossRef]
- Available online: https://climate.mit.edu/ask-mit/how-will-future-warming-and-co2-emissions-affect-oxygen-concentrations (accessed on 15 January 2024).
- Friedlingstein, P.; O’sullivan, M.; Jones, M.W.; Andrew, R.M.; Gregor, L.; Hauck, J.; Quéré, C.L.; Luijkx, I.T.; Olsen, A.; Peters, G.P.; et al. Global Carbon Budget 2022. Earth Syst. Sci. Data 2022, 14, 4811–4900. [Google Scholar] [CrossRef]
- Thanapal, S.S.; Annamalai, K.; Lawrence, B.; Sweeten, J.M. Biomass Co-Combustion with Coal. In Reference Module in Earth Systems and Environmental Sciences; Elsevier: Amsterdam, The Netherlands, 2023; ISBN 9780124095489. [Google Scholar] [CrossRef]
- Keeling, C.D.; Piper, S.C.; Bacastow, R.B.; Wahlen, M.; Whorf, T.P.; Heimann, M.; Meijer, H.A. Atmospheric CO2 and 13CO2 Exchange with the Terrestrial Biosphere and Oceans from 1978 to 2000: Observations and Carbon Cycle Implications. In A History of Atmospheric CO2 and Its Effects on Plants, Animals, and Ecosystems; Ecological Studies; Springer: New York, NY, USA, 2005; Volume 177, pp. 83–113. [Google Scholar] [CrossRef]
- Annamalai, K.; Thanapal, S.; Ranjan, D. Ranking renewable and fossil fuels on global warming potential using respiratory quotient (RQ) Concept. J. Combust. 2018, 2018, 1270708. [Google Scholar] [CrossRef]
- Schmidtko, S.; Stramma, L.; Visbeck, M. Decline in global oxygen content during the past five decades. Nature 2017, 542, 335–339. [Google Scholar] [CrossRef]
- Energy Institute. Energy Institute—Statistical Review of World Energy-with Major Processing by Our World in Data. Other Renewables (Including Geothermal and Biomass). 2023. Available online: https://ourworldindata.org/energy-mix (accessed on 21 February 2024).
- Available online: https://github.com/openclimatedata/global-carbon-budget/blob/main/data/global-carbon-budget.csv#L2 (accessed on 21 February 2024).
- Moreno, A.R.; Larkin, A.A.; Lee, J.A.; Gerace, S.D.; Tarran, G.A.; Martiny, A.C. Regulation of the respiration quotient across ocean basins. AGU Adv. 2022, 3, e2022AV000679. [Google Scholar] [CrossRef]
- Severinghaus, J.P. Studies of the Terrestrial O2 and Carbon Cycles in Sand Dune Gases and in Biosphere 2. Ph.D. Dissertation, Columbia University, New York, NY, USA, 1995. [Google Scholar]
- Dlugokencky, E.; Tans, P. Trends in atmospheric carbon dioxide, National Oceanic & Atmospheric Administration. Earth System Research Laboratory (NOAA/ESRL). Available online: http://www.esrl.noaa.gov/gmd/ccgg/trends/global.html (accessed on 21 February 2024).
- Hansis, E.; Davis, S.J.; Pongratz, J. Relevance of methodological choices for accounting of land use change carbon fluxes. Glob. Biogeochem. Cycles 2015, 29, 1230–1246. [Google Scholar] [CrossRef]
- Available online: https://www.co2.earth/co2-acceleration (accessed on 12 September 2023).
- Annamalai, K.; Nanda, A. Biological aging and life span based on entropy stress via organ and mitochondrial metabolic loading. Entropy 2017, 19, 566. [Google Scholar] [CrossRef]
- Gilfillan, D.; Marland, G.; Boden, T.; Andres, R. Global, Regional, and National Fossil-Fuel CO2 Emissions. Available online: https://energy.appstate.edu/CDIAC (accessed on 2 May 2023).
- Houghton, R.A.; Nassikas, A.A.; Hansis, E.; Davis, S.J.; Pongratz, J. Releva average of two bookkeeping models: Global and regional fluxes of carbon from land use and land cover change 1850–2015. Glob. Biogeochem. Cycles 2017, 31, 456–472. [Google Scholar] [CrossRef]
- Available online: https://ourworldindata.org/fossil-fuels#global-fossil-fuel-consumption (accessed on 28 January 2024).
- Gardner, A.; Ellsworth, D.S.; Crous, K.Y.; Pritchard, J.; MacKenzie, A.R. Is photosynthetic enhancement sustained through three years of elevated CO2 exposure in 175-year-old Quercus robur? Tree Physiol. 2022, 42, 130–144. [Google Scholar] [CrossRef]
- Mo, L.; Zohner, C.M.; Reich, P.B.; Liang, J.; de Miguel, S.; Nabuurs, G.-J.; Renner, S.S.; Hoogen, J.v.D.; Araza, A.; Herold, M.; et al. Integrated global assessment of the natural forest carbon potential. Nature 2023, 624, 92–101. [Google Scholar] [CrossRef]
- Available online: https://www.osha.gov/laws-regs/standardinterpretations/2007-04-02-0#:~:text=Paragraph%20(d)(2)(,dangerous%20to%20life%20or%20health (accessed on 14 February 2024).
- Seo, K.; Ryu, D.; Eom, J.; Jeon, T.; Kim, J.; Youm, K.; Chen, J.; Wilson, C.R. Drift of Earth’s Pole Confirms Groundwater Depletion as a Significant Contributor to Global Sea Level Rise 1993–2010. Geophys. Res. Lett. 2023, 50, 1215. [Google Scholar] [CrossRef]
- Available online: https://www.space.com/earth-tilt-changed-by-groundwater-pumping (accessed on 11 August 2023).
- Karl, D.M.; Laws, E.A.; Morris, P.; Williams, P.J.; Le, B.; Emerson, S. Metabolic balance in the open sea. Nature 2003, 426, 32. [Google Scholar] [CrossRef]
- Najjar, R.G.; Keeling, R.F. Mean annual cycle of the air-sea oxygen flux: A global view. Glob. Biogeochem. Cycles 2000, 14, 573–584. [Google Scholar] [CrossRef]
- del Giorgio, P.A.; Duarte, C.M. Respiration in the open ocean. Nature 2002, 420, 379–384. [Google Scholar] [CrossRef]
- Available online: https://www.un.org/en/climatechange/science/climate-issues/ocean#:~:text=The%20ocean%20generates%2050%20percent,the%20impacts%20of%20climate%20change (accessed on 15 February 2023).
- Lindsey, R.; Scott, M. What are Phytoplankton? 2010. Available online: https://earthobservatory.nasa.gov/features/Phytoplankton (accessed on 6 February 2023).
- Available online: https://oceanservice.noaa.gov/facts/ocean-oxygen.html (accessed on 24 February 2024).
- Land Use, Land-Use Change, and Forestry, A Special Report of the Intergovernmental Panel on Climate Change; IPCC Special Report, Summary for Policy Makers Secretary; General World Meteorological Organization: Montreal, QC, Canada, 2000; ISBN 92-9169-114-3.
- Bonan, G.B. Forests and climate change: Forcings, feedback, and the climate benefits of forests. Science 2008, 320, 1444–1449. [Google Scholar] [CrossRef]
- Rosenberg, G.; Littler, D.S.; Littler, M.M.; Oliveira, E.C. Primary production and photosynthetic quotients of seaweeds from Sao Paulo State, Brazil. Bot. Mar. 1995, 39, 369–377. [Google Scholar] [CrossRef]
- May, M.; Rehfeld, K. Negative Emissions as the New Frontier of Photoelectrochemical CO2 Reduction. Adv. Energy Mater. 2022, 12, 2103801. [Google Scholar] [CrossRef]
- Urych, T.; Chećko, J.; Magdziarczyk, M.; Smoliński, A. Numerical Simulations of Carbon Dioxide Storage in Selected Geological Structures in North-Western Poland. Carbon Capture, Utilization and Storage. Front. Energy Res. 2022, 10, 827794. [Google Scholar] [CrossRef]
- Xue, W.; Wang, Y.; Chen, Z.; Liu, H. An integrated model with stable numerical methods for fractured underground gas storage. J. Clean. Prod. 2023, 393, 136268. [Google Scholar] [CrossRef]
- Available online: https://earthobservatory.nasa.gov/world-of-change/global-temperatures (accessed on 12 September 2023).
- Available online: https://earthobservatory.nasa.gov/world-of-change/decadaltemp.php (accessed on 20 January 2024).
- Available online: https://earthobservatory.nasa.gov/world-of-change/global-temperatures#:~:text=The%20data%20reflect%20how%20much,several%20tenths%20of%20a%20degree (accessed on 2 January 2024).
- Samset, B.H.; Zhou, C.; Fuglestvedt, J.S.; Lund, M.T.; Marotzke, J.; Zelinka, M.D. Steady global surface warming from 1973 to 2022 but increased warming rate after 1990. Commun. Earth Environ. 2023, 4, 400. [Google Scholar] [CrossRef]
- Hansen, J.; Sato, M. Global Temperature in 2021, July Temperature Update: Faustian Payment Comes Due. Available online: https://www.columbia.edu/jeh1 (accessed on 13 August 2021).
- Available online: https://www.weather.gov/media/slc/ClimateBook/Annual%20Average%20Temperature%20By%20Year.pdf (accessed on 28 January 2024).
- Available online: https://www.chegg.com/homework-help/questions-and-answers/536-511-ear-nyc-temperature-1870-1871-1872-1873-1874-1875-1876-1877-1878-1879-1880-1881-18-q73111012 (accessed on 28 January 2024).
- Fraas, A.G.; Graham, J.D.; Krutilla, K.M.; Lutter, R.; Shogren, J.F.; Thunström, L.; Viscusi, W.K. Seven Recommendations for Pricing Greenhouse Gas Emissions. J. Benefit-Cost Anal. 2023, 14, 191–204. [Google Scholar] [CrossRef]
- Andersson, J.J. Carbon Taxes and CO2 Emissions: Sweden as a Case Study. Am. Econ. J. Econ. Policy 2019, 11, 1–30. [Google Scholar] [CrossRef]
- Gowd, S.C.; Ganeshan, P.; Vigneswaran, V.S.; Hossain, M.S.; Kumar, D.; Rajendran, K.; Ngo, H.H.; Pugazhendhi, A. Economic perspectives and policy insights on carbon capture, storage, and utilization for sustainable development. Sci. Total Environ. 2023, 883, 163656. [Google Scholar] [CrossRef]
- Available online: https://sgp.fas.org/crs/misc/IF11455.pdf (accessed on 14 January 2024).
- Dindi, A.; Coddington, K.; Garofalo, J.F.; Wu, W.; Zhai, H. Policy-Driven Potential for Deploying Carbon Capture and Sequestration in a Fossil-Rich Power Sector. Environ. Sci. Technol. 2022, 56, 9872–9881. [Google Scholar] [CrossRef]
- Thanapal, S. (Former Texas A&M PhD student and with Energy Company). Personal communication, 2023.
- Treydte, K.; Liu, L.; Padrón, R.S.; Martínez-Sancho, E.; Babst, F.; Frank, D.C.; Gessler, A.; Kahmen, A.; Poulter, B.; Seneviratne, S.I.; et al. Recent human-induced atmospheric drying across Europe has been unprecedented in the last 400 years. Nat. Geosci. 2023, 17, 58–65. [Google Scholar] [CrossRef]
- Van Noorden, R. “Artificial Leaf” faces economic hurdle. Nature 2012, S2CID 211729746, 10703. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).