A Comprehensive Approach to Load Frequency Control in Hybrid Power Systems Incorporating Renewable and Conventional Sources with Electric Vehicles and Superconducting Magnetic Energy Storage

Abstract

This study addresses the load frequency control (LFC) within a multiarea power system characterized by diverse generation sources across three distinct power system areas. area 1 comprises thermal, geothermal, and electric vehicle (EV) generation with superconducting magnetic energy storage (SMES) support; area 2 encompasses thermal and EV generation; and area 3 includes hydro, gas, and EV generation. The objective is to minimize the area control error (ACE) under various scenarios, including parameter variations and random load changes, using different control strategies: proportional-integral-derivative (PID), two-degree-of-freedom PID (PID-2DF), fractional-order PID (FOPID), fractional-order integral (FOPID-FOI), and fractional-order integral and derivative (FOPID-FOID) controllers. The result analysis under various conditions (normal, random, and parameter variations) evidences the superior performance of the FOPID-FOID control scheme over the others in terms of time-domain specifications like oscillations and settling time. The FOPID-FOID control scheme provides advantages like adaptability/flexibility to system parameter changes and better response time for the current power system. This research is novel because it shows that the FOPID-FOID is an excellent control scheme that can integrate these diverse/renewable sources with modern systems.

1. Introduction

Load frequency control (LFC) is an important part of a power system to maintain the balance between supply and load demand by keeping continuous track of generation and demand.

1.1. Research Background

Load frequency control (LFC) maintains the supply and demand in power systems to ensure stable system frequency and reliable delivery. LFC plays a vital role in compensating for deviations in load/generation. The world is demanding more clean energy; therefore, renewable energy sources (RESs) have become more important to incorporate into power systems. RESs, i.e., solar and wind, lead to inconsistency and uncertainties due to their intermittent nature. Integrating RES in multiarea power systems consisting of conventional sources (thermal, hydro), electric vehicles, and energy storage leads to challenges for the task of LFC. Therefore, these modern challenges require more advanced control schemes that can manage the frequency and power exchange of interconnected power systems. To handle these issues, control techniques have changed from PID controllers to more sophisticated methods, including fractional-order controllers.

1.2. Literature Review

Since electric energy cannot be stored, LFC adjusts both the supply and demand in order to provide reliable power to consumers [1,2]. LFC works as a control scheme that keeps the system frequency within specified limits by regulating the generator’s output in response to load changes to restore balance. LFC’s main aim is to minimize (reduce) frequency deviations by instantly adjusting the generator output as per load requirements [3]. Additionally, LFC is used to keep tie-line power in limits by regulating the power flow between areas to keep a power system in balance. To achieve this, LFC requires a controller. In the literature, several control schemes have been reported. Some of the most well-liked schemes are conventional (PID), robust, modern, and intelligent ones [4]. As a whole, it can be concluded that LFC is essential for maintaining the stability of a power system. Furthermore, to guarantee the reliable supply of electricity, nowadays, the integration of renewable energy sources (RESs) is in demand, which makes LFC’s role more crucial due to the changes in dynamic loads and generation uncertainties [5]. Since the controller is like the brain of the LFC scheme, it must be used efficiently (utilizing a control algorithm) to regulate the generator response [6]. The PID control scheme is a widely used scheme in LFC because of its simplicity and effectiveness and provides generator outputs to maintain system frequency within limits [7]. It also faces challenges in the implementation of control strategies in modern systems. Authors [8] suggested PID tuning using metaheuristic optimization algorithms and demonstrated the effectiveness of the proposed approach. A study [9] investigated the use of fractional-order PID controllers for robust load frequency control in multiarea power systems. It conducted a theoretical analysis, with simulation results highlighting the advantages of fractional-order control in enhancing system stability and performance. In [10], an adaptive LFC scheme for power systems with high RES integration using PID neural networks was proposed. The results evidenced that the proposed control scheme is effective in minimizing the deviations in frequency. In [11], the impact of communication delays/dropout was reported with PID controllers. Furthermore, in [12], a PID-fuzzy logic controller in deregulated LFC was proposed to achieve improved time-domain specifications. Though PID is a good control scheme, it suffers from lagging behavior in nonlinear systems and large settling times; therefore, researchers are looking for alternate control schemes like the PID-2DF controller, which outperforms PID and provides more reliable/accurate control, as given in [13]. It is seen that PID-2DF can dampen system frequency effectively. In [14], an optimal tuning for multiarea PID-2DF is presented so that the system can be settled more accurately. A robust fractional-order PID-2DF is proposed in [15]. It is seen that fractional-order techniques can improve robustness than PID controllers. Authors of [10], also proposed a PID-2DF neural controller for the RES-LFC scheme in [16], and it was found that this control scheme can control a system with high stability and reliability. LFC using communication delays employing PID-2DF controllers is reported in [17]. It shows that PID-2DF compensate communication constraints, and maintain stability. A PID-2DF controller in decentralized LFC scheme in deregulated scenario is reported in [18], to enables and ensure robust frequency regulation. Later, fractional calculus opened a new window in controller’s design. The FOPID (Fractional-order PID) controller proposals improved flexibility and accuracy over PID by using fractional-orders integral-derivative. A two-area interconnected system with various RESs + hydrogen energy storage using FOPID controller is given in [19]. The optimal parameters have been obtained using gradient-based optimizer (IGBO) techniques in order to provide the frequency stabilization. A multiarea–multisource power system utilizing improved gravitational search algorithm binary particle swarm optimization (IGSA-BPSO) optimized FOPID is given in [20], which reported the robustness dynamics of the used control scheme for various load scenarios. A cascaded fractional controller having a 3DOF-FOPID and FOPI is presented in [21]. The controller performance was checked for LFC utilizing doubly fed induction generators. In [22], a [FOPID/(1 + PI)] controller utilizing the equilibrium optimizer (EO) algorithm was reported for the LFC of interconnected microgrids. Ref. [23] reported a fractional-order multistage controller for interconnected microgrids to determine exploitation and exploration competencies. In [24], a 3DOF-FOPID utilizing mountain gazelle optimization (MGO) was applied in low-inertia microgrids to enhance stability under fluctuating conditions. In the literature, other variants of the FOPID control scheme are also available in order to improve the performance of the FO system. Ref. [25] reported a FOPID controller for an automatic generation control (AGC) scheme utilizing the big bang-big crunch algorithm. It is seen that this approach can provide resilience against load variations and random fluctuations. A 1 + PD/FOPID controller utilizing the moth flame optimization (MRFO) technique was given in [26]. It achieved better performance and reduces frequency deviations with shorter settling times as compared to the PID, FOPID, and PD/FOPID control schemes. An adaptive model predictive FOPID controller was investigated in [27], which makes the power system more stable against load variations. A FOPID control scheme utilizing various optimization algorithms was reported in [28]; the scheme was employed in renewable energy systems to optimize frequency regulation and system stability. Ref. [29] reported the application of FOPID controllers in hybrid (thermal, hydro, and EV) systems including RESs and showed better performance against perturbations. Ref. [30] reported an LFC scheme incorporating a microgrid, and EVs were used in order to check the performance of the PID-2DF controller.

The optimization algorithm plays an important role in obtaining the parameters of a control scheme. In the literature, many algorithms have been reported. In Ref. [31] algorithms like firefly (FA), particle swarm optimization (PSO), and gravitational search (GSA) have been used to obtain the parameters in order to improve the LFC. In [32], PSO- and GA-based H-infinity LFC schemes are reported. Similarly, in [33], various optimization techniques to address LFC issues in deregulated hybrid systems were reported. A new technique known as JAYA was utilized in adaptive LFC for thermal, PV, and wind systems [34]. An LFC scheme for a two-area multisource system utilizing a GA-PSO control structure was presented in [35]. Ref. [36] investigated a hybrid PSO and gravitational search (GSA) model to improve the LFC scheme in hybrid power systems, which consisted of electric vehicles, achieving an improvement in convergence speed, leading to better stability. An LFC scheme utilizing GA to improve the response and stability of a deregulated power system integrating electric vehicles was given in [37]. An LFC scheme consisting of JAYA optimization for interconnected RES with EVs to provide less complexity, increased robustness, and better frequency under diverse conditions was given in [38]. A big bang-big crunch (BBBC)-based adaptive LFC scheme to improve frequency regulation in multiarea power systems with EVs was reported in [39]. The results show that the designed control scheme performed better in settling the deviations quickly.

A variety of optimization methods and advanced control schemes have been studied recently, with the aim of enhancing the efficiency of power systems integrating RESs. These studies have achieved considerable improvements in system efficiency and stability under various operational scenarios. The use of innovative control methods for energy management in hybrid energy systems was reported in [40]. The global transition to renewable energy sources has been further pushed by international climate agreements and carbon emission reduction programs. The COP26 summit was essential in establishing challenging goals for the clean energy transition in order to encourage sustainable energy practices around the world. These commitments are essential for driving development in renewable energy technologies and incorporating them into modern power systems [41,42,43].

1.3. State-of-the-Art Research

Previous studies have demonstrated that because of their simplicity and ease of use, PID controllers are suitable for load frequency control (LFC) tasks in conventional power systems. However, nonlinearities, parameter variations, load fluctuations, intermittency, and variability are the common limitations of these controllers. To overcome these limitations, PID-2DF controllers have been employed for LFC, allowing independent tuning for set point tracking and disturbance rejection, which enhances system performance under dynamic scenarios. However, the performance of these controllers is not effective in scenarios with substantial communication delays and complex system dynamics. Since fractional calculus enables more flexible tuning, controllers like fractional-order PID (FOPID) offer improved adaptation to nonlinear behaviors and parameter uncertainty.

Further developments in fractional-order controllers like FOPID-FOI and FOPID-FOID offer enhanced robustness, superior oscillation suppression, and faster settling times. The current study addresses gaps in the existing research, particularly the integration of superconducting magnetic energy storage (SMES) and thyristor-controlled phase shifters (TCPSs) in LFC schemes. This study also distinguishes itself by employing the JAYA optimization algorithm, which provides better computational efficiency and robustness compared to conventional techniques. The comparative analysis under various conditions, including step load changes, parameter variations, and random load, offers important insights into the best LFC strategies for hybrid power systems with renewable energy integration.

1.4. Motivation, Novelty (Innovation), and Contributions of the Current Study

The decision regarding which controller to use for a specific LFC scheme is never easy. Selecting the appropriate controller becomes more challenging when RESs are integrated with a conventional power system. As a result, one must select the controller that offers the best performance. PID control has long been the best scheme that provides a simple and effective solution. However, as systems became complex, nonlinear, and dynamic, other techniques, such as PID with two degrees of freedom (PID-2DF), FOPID, and its variations, have drawn attention.

This study distinguishes itself by exploring the application of PID, PID-2DF, and FOPID and variants of FOPID control schemes in a multiarea power system configuration that includes diverse energy sources:

• area 1: Thermal, geothermal (GTP), and EVs.
• area 2: Thermal and EVs.
• area 3: Hydro, gas, and EVs.

Tie lines are used to connect each area. The novelty lies in integrating thyristor-controlled phase shifters (TCPSs) and superconducting magnetic energy storage (SMES), which have not been frequently considered together in LFC studies. To determine the best control parameters, this study used the JAYA algorithm focusing on step load changes, parameter variations, and random load disturbances.

The novelties include the following:

• A comparative analysis of different control schemes (PID, PID-2DF, FOPID, FOPID-FOI, FOPID-FOID) under various scenarios, including high RES integration and diverse generation sources, demonstrates the advantages of advanced control strategies in complex power systems.
• The use of JAYA optimization for tuning shows better computational efficiency and robustness compared to conventional methods.
• System oscillation (overshoot/undershoot) is evaluated and settling time is reduced, providing insights into the most effective control method for dynamic system conditions.

1.5. Paper Structure

• Section 2: Modeling of the power system and control schemes.
• Section 3: Different controller structures.
• Section 4: Optimization algorithm used for tuning controller parameters.
• Section 5: Simulation results and discussion.
• Section 6: Conclusions and future research directions.

The diagram shown in Figure 1a depicts the research structure carried out in this study. A comparative study of all the references in terms of optimization techniques, applications, limitations, and highlights of the work reported is given in Table 1.

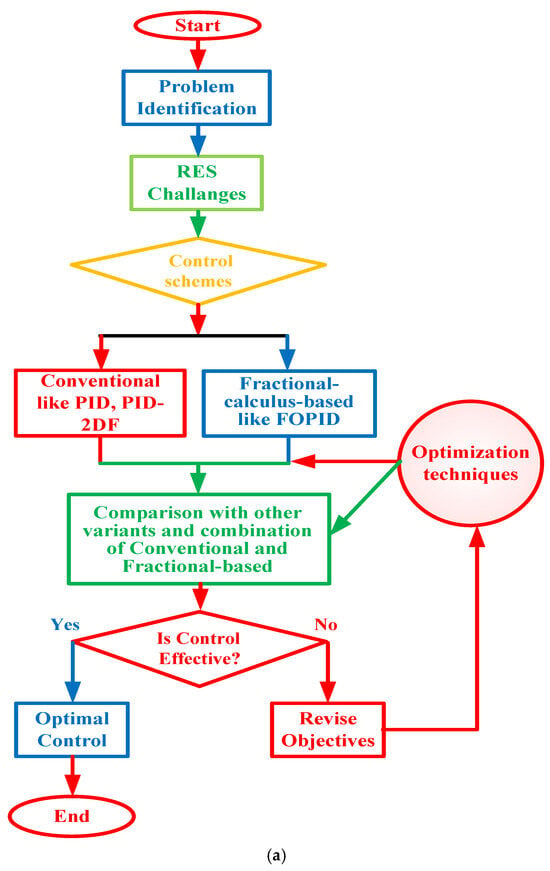
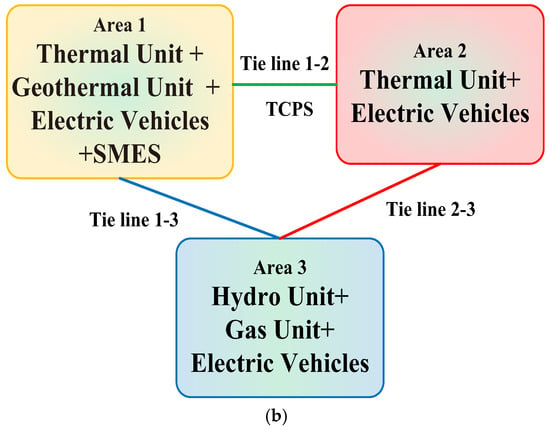
Figure 1. (a) Research flowchart. (b) An overall diagram of the three areas of power studied.

Table 1. Comparative analysis of control strategies for power systems: optimization techniques, applications, limitations, and highlights of this work.

Author(s)	Year	Power System	Controller	Optimization	Areas	RES/Type	ES/Type	Limitation	Highlights of the Work
S. Zhu, Y. Zhang and P. Chang [1]	2021	Two-area interconnected power system	Distributed Model Predictive Control (DMPC)	Not Specified	2-area	Wind Power, Photovoltaic (PV)	Thermal Power	Limited to traditional power systems	Focused on the DMPC and traditional PID control strategies
M. Wadi, A. Shobole, W. Elmasry, and I. Kucuk [2]	2024	Multi-area interconnected power systems	Fuzzy control, robust, optimal, self-tuning, adaptive controllers	Classical control, optimization algorithms, machine learning, reinforcement learning	Multi-area interconnected power systems	Wind, Photovoltaic (PV), EVs, Storage Devices	No	System complexity	Implemented LFC with RES Integration
M. Ranjan and R. Shankar [3]	2022	Modern power system	Various Controllers	Classical, Modern, and soft computing	Interconnected power systems	Wind, solar	Yes, Energy storage, FACTS	Voltage instability, reliability issues with RES	Studied the challenges and solutions in LFC with RES
X.-C. ShangGuan, Y. He, C.-K. Zhang, L. Jin, L. Jiang, M. Wu, and J. W. Spencer [4]	2021	Modern power system	Traditional controller	Stability analysis control gain	Multiarea	NA	NA	Instability, Vulnerability to DoS	Investigated stability against DoS for interconnected and deregulated system
B. Kroposki [5]	2017	Electric Power System with variable renewable energy	Not discussed	Not discussed	various	Solar and wind	Not discussed	Integration challenges	Explored review of operational examples of VRE and their integration
D. D. Rasolomampionona, M. Połecki, K. Zagrajek, W. Wróblewski, and M. Januszewski [6]	2024	Various Power System models	Classical, Robust, Optimal, Fuzzy, ANN	Not Specified	Multi	Yes/RES	FACTS	DC link, cyberattacks, RES complexity	Explored various control techniques in LFC and RES
A. K. Maurya, D. Singh, H. Khan and P. Kumar [7]	2024	Conventional	PI, PID	Classical	2-area	No	No	Limited to Two area	Examined classical controllers in two area systems
S. B. Joseph, E.G. Dada, A. Abidemi, D. O. Oyewola, B. M. Khammas [8]	2022	Not Specified	PID	Metaheuristic	Not specified	No	No	Limited to tuning of PID	Focused on metaheuristics algorithms, their implementation and applications.
A. Fathy, D. Yousri, H. Rezk, S. B. Thanikanti, and H. M. Hasanien [9]	2022	Interconnected	Fractional Order PID	Modified Hunger Games search	Two	PV, Wind turbine	Not specified	Limited to simulation study	Analyzed tuning challenges in fractional-order PID controllers using MHGS algorithm
F. Bano, M. Ayaz, D.-e.-Z. Baig, and S. M. H. Rizvi [10]	2024	Single and interconnected	PID	GA, PSO	Single and multi	Not	Not	Stability issues	Studied GA, PSO and integration of neural networks with PID control
G. Cao, X. Zhang, P. Li, F. Li, Y. Liu, and Z. Wu [11]	2023	Modern Power System	ADRC	Classical	Multiarea	Wind	Not Specified	Communication delays, RES Challenges	Addressed that ADRC can handles delay and robust against disturbances.
M. Barakat [12]	2022	Multiarea Hybrid	PID-Fuzzy Logic	Water cycle Algorithm, Fuzzy Logic	2-area	Reheat Hydro, Gas	No	Implementation complexity	Combined fuzzy logic with PID control to enhance performance.
N.K. Gupta, M.K. Kar, and A.K. Singh [13]	2022	Conventional	PID-2DF	Sin-cosine algorithm	3 or more	No	No	Limited application to modern grids	Examined the limitations of traditional control methods in disturbance rejection
N.K. Gupta, A.k. Singh, and R.N. Mahanty [14]	2023	Three area	PID-2DF	Moth flame optimizer	3 area	No	No	Limited handling of non-linearity	Proposed solutions to enhance tuning in multi-area PID control using MFO
S. Sondhi and Y. V. Hote [15]	2014	Conventional	Fractional Order PID	Classical	Single area	No	No	Parameter uncertainty	Explored fractional-order control strategy for disturbance rejection
J. Singh, K. Chattterjee, and C.B. Vishwakarma [16]	2018	Single and Two area	PID-2DF with IMC	Logarithmic Based	Single and Two	No	No	Designed for reduced order model	Investigated IMC-PID-2DF for stability in systems.
R. K. Sahu, S. Panda, and U. K. Rout [17]	2013	Conventional	PID-2DF	Differential Evolution (DE)	2 area	No	No	Sensitivity to parameter variation	Analyzed the Robust performance for wide range of conditions.
M. Sariki, and R. Shankar [18]	2022	Deregulated	PID-2DF	Opposition-based Volleyball Premier League Algorithm (OVPLA)	2-area	Hydro, Gas	No	Implementation complexity	Effective control strategies tailored for deregulated environments.
P. Wang, X. Chen, Y. Zhang, L. Zhang, and Y. Huang [19]	2024	Interconnected	Fractional-Order	Improved Gradient-Based Optimizer (IGBO)	2 area	Hydro, wind, solar	Hydrogen based energy storage	Challenges of frequency stability	Investigated the role of fractional-order control in interconnected hydrogen energy systems.
A. Kumar, D. K. Gupta, and S. R. Ghatak, B. Appasani, N.Bizon and P. Thounthong [20]	2022	Restructured	PID	IGSA-BPSO	2 area	No	No	High computational cost	Developed IGSA-BPSO driven PID controller for multi-area deregulated power systems
S. Xie, Y. Zeng, J. Qian, F. Yang, and Y. Li [21]	2023	Interconnected	Cascaded Fractional-Order Controller (CC-FOC)	CPSOGSA	2 area	Wind, hydro, diesel	No	High complexity	Explored 3DOF-FOPID and a FOPI controller optimizing using CPSOGSA.
S. Das, P.C. Nayak, R.C. Prusty, and S. Panda [22]	2024	Microgrids	Fractional Order Multistage	Equilibrium Optimizer (EO)	2-area	Wind, PV, Diesel	Various	complexity	Addressed effective performance of fractional-order control for microgrid systems.
D. Murugesan, K. Jagatheesan, P. Shah, and R. Sekhar [23]	2023	Microgrid	PIλDμ	Cohort Intelligence (CI)	2-area	Distributed Energy systems	No	Load variations	Introduced a new control strategy (PIλDμ) and compared with conventional PID for microgrid applications.
S. Santra, and M. De [24]	2023	Low Inertia Microgrid	3DOF-FOPID-Virtual Inertia	Mountain Gazelle Optimization	2-area	Inverter based RES	No	Implementation complexity	Proposed a virtual inertia controller based on fractional-order PID to enhance frequency stability in low inertia microgrids, demonstrating improved performance over conventional methods.
N.Kumar, B. Tyagi, V. Kumar [25]	2017	Deregulated multi-area AGC	BBBC-FOPID	Big Bang-Big Crunch	2-area	No	No	High tuning complexity	BBBC-FOPID controller for AGC in deregulated multi-area systems,
F.F.M. El-Sousy, M.H. Alqahtani, A.S. Aljumah, M. Aly, S.Z. Almutairi, and E.A. Mohamed [26]	2023	Electrical Power Grids with EVs	Fractional-Order Cascaded	Manta Ray Foraging Optimization (MRFO)	3 or more	Yes/Various	Yes/Electric Vehicles	High complexity	optimized fractional-order controllers for frequency regulation in electric vehicles and power grids, emphasizing the integration of renewable energy sources.
A. Ragab, D. Allam, and H.A. Attia [27]	2024	Power system with RES	Fractional-Order PID	Artificial Rabbits Heuristic Algorithm (ARHA)	Interconnected	Wind, Solar	No	High computational of tuning	Implemented FOPID with ARHA control to enhance performance.
A. Latif, S.M. S. Hussain, D.C. Das, T.S. Ustun, and A. Iqbal [28]	2021	Single and multi-area	Fractional-Order	Various Optimization Techniques	Single and multi-area	Yes/Various	EV, Energy storage	Integration and complexity challenges	Explored FOPID control schemes and integration challenges in Power energy systems.
D. Mohanty and S. Panda [29]	2019	Hybrid Energy Systems	Fractional-Order PID	Moth Flame Optimization (MFO)	Single area	Yes/Various	Yes	Limited exploration of multiarea	Studied fractional-order PID controllers in hybrid renewable energy systems for improved performance.
H. Shayeghi, A. Rahnama, R. Mohajery, N. Bizon, A.G. Mazare, and L.M. Ionescu [30]	2022	Microgrids	Master Slave configuration	JAYA	2-area	Yes	Yes/Electric Vehicles	Evaluated Only for two area system	Enhanced PID control strategies for microgrid applications
D.K. Gupta, A.V. Jha, B. Appasani, A. Srinivasulu, N. Bizon, and P. Thounthong [31]	2021	Multi-source	PID	Hybrid Optimization	2 area	Yes	No	Lacking of detailed robustness testing	Investigated hybrid optimization methods for multi-source power systems.
V.P. Singh, S.R. Mohanty, N. Kishor, and P.K. Ray [32]	2013	Distributed Generation Systems	H-infinity	PSO and GA	Single area	Yes/Various	Yes	High complexity	Proposed a robust control strategy using PSO and GA for distributed generation systems.
A. Pappachen, and A.P. Fathima [33]	2017	Deregulated-Hybrid	Hybrid	General survey	Multiarea	No	Yes/Various	Limited to deregulated systems	Examined hybrid control mechanisms in deregulated environments to enhance stability.
M. I. A. E. Ali, A. A. Z. Diab and A. A. Hassan [34]	2019	Conventional	Adaptive	Jaya Optimization	Single areas	PV, Wind	No	Focus on LFC for single area	Developed an adaptive control utilizing Jaya optimization for conventional systems.
A. Dogan [35]	2019	Two area interconnected	PID	Grey Wolf Optimization (GWO)	2 area	No	No	Not included RES	Focused on GWO based optimization strategies for efficiency in power system stability.
R.K. Sahu, S.Panda, and S. Padhan [36]	2015	Hybrid Power Systems	PI	Hybrid Gravitational Search Algorithm	2 area	No	No	Not included RES	Introduced a hybrid GSA-PS optimization technique for enhancing performance in hybrid system
R. Kumar, and L.B. Prasad [37]	2024	Deregulated	Conventional PI and PID	Genetic, PSO and TLBO Algorithms	2-area	No	Yes/Electric Vehicles	Lack detailed on diverse RESintegration	Proposed EV role in frequency control in interconnected system
A. Annamraju and S. Nandiraju [38]	2019	Japanese power system	PID Controller	Jaya based LFC	Single area	PHEV	Yes/Electric Vehicles	Single area system	Developed Jaya based control strategy for load frequency utilizing PHEV.
N. Kumar, P. Datta, K. Sharma, R. Mehrotra, and J. Singh [39]	2023	Hybrid system with EV	PID Controller	BBBC based LFC	2 area/Multi area	Yes/ various	Yes/BESS, UC	Complexity in tuning	Demonstrated role of EVs in frequency control.
S. Praveenkumar, E. B. Agyekum, J. D. Ampah, et al. [40]	2022	Hydrogen production and EV charging	Not specified	Techno-economic optimization	5 different climates in India	PV (Photovoltaic)	Hydrogen Storage	Climate variability affecting system performance	Optimization of PV system for hydrogen production and EV charging under various climatic conditions
S. P. Kumar, E. B. Agyekum, A. Kumar, V. I. Velkin [41]	2023	Solar PV modules	Not specified	Experimental investigation	Single-area	PV (Photovoltaic)	Phase Change Material	Performance impacted by natural air convection limitations	Evaluation of aluminium reflectors and phase change material integration to improve solar PV module efficiency

2. Modeling of Power System Elements

Figure 1b shows a general schematic of the interconnected electrical power system utilizing tie lines. The description of the figure is as follows: thermal, EV, and geo and SMES (area 1); thermal and EV (area 2); and hydro, gas, and EV generation (area 3). Tie lines (1–2) have TCPS support. To keep the balance between load and generation among all three areas, different control schemes were designed and compared in this study.

Below are the main points used in this study:

-

Experimental (Simulation) Design

• System configuration:
  • area 1: Thermal, geothermal, and electric vehicle (EV) generation with superconducting magnetic energy storage (SMES).
  • area 2: Thermal and EV generation.
  • area 3: Hydro, gas, and EV generation.

-

Simulation Platform: MATLAB/Simulink, R2023b.

-

Testing Cases:

• Normal conditions with step load changes.
• Parameter variations, i.e., change in system parameters.
• Random load disturbances.

-

Performance metrics included settling time, overshoot, undershoot, frequency deviations, area control error (ACE), and tie-line power deviations.

2.1. EV Modeling

Electric vehicles (EVs) play a crucial role in load frequency control (LFC) by acting as both dynamic loads and distributed storage resources. EVs can respond to frequency deviations by modulating their charging and discharging rates, thereby providing a rapid and flexible means of balancing supply and demand fluctuations in the power grid. This capability enhances the stability and reliability of power systems, especially those integrating variable renewable energy sources. A precise dynamic model of an electric vehicle (EV) is shown in Figure 2, and its comprehensive electrical equivalent circuit is shown in [36,37,38,39].

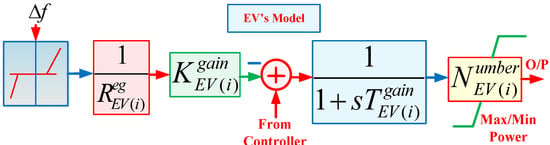
Figure 2. Modeling of EV LFC studies.

Figure 2 shows an EV that comprises a battery charger, a primary, and LFC in order to transfer power between the battery and power system. A dead band (+/−10 Mhz) is incorporated to prevent the undesirable cut-off of EVs from the grid.

The droop coefficient (R_ev) = 2.4 Hz/pu MW. The values of K_gev (EV gain) and T_gev (time constant of the battery) are given in Appendix A. The max./min. power of the EV is determined as

$$\Delta P_{aggregate(i)}^{\max }=+\left[{\displaystyle \frac{1}{number\_ EV}}\ast \left({\Delta Power}_{ev(i)}\right)\right]$$

$$\Delta P_{aggregate(i)}^{\min }=-\left[{\displaystyle \frac{1}{number \_ EV}}\ast \left(\Delta Powe{r}_{ev(i)}\right)\right]$$

where $N_{ev(i)}^{umber}$ represents the number of electric vehicles. In this study, 500 EVs were considered in area 1, 1000 in area 2, and 1500 in area 3. The charging and discharging capacity of an EV was considered within ±5 kW.

2.2. Modeling of Various Generating Systems

The block diagram was generated of the simulated test system comprising various power generation sources (thermal, geothermal, and EV (area 1), thermal and EV (area 2), hydro, gas, EV (area 3) and load demand modules, along with the models of SMES and TCPS. In this section, a brief over of the above-mentioned models is given.

2.2.1. Thermal Power Model

Thermal power systems have been in service for energy generation for a very long time and, still, they are suitable. In fact, they are providing the maximum share in power production. Figure 3 shows the transfer function model of a reheat thermal power system, where K_reheater is the reheat system gain, and R_eg represents droop control. T_Gov-Therm., T_turbine, and T_reheater are the time constants of the governor, turbine, and reheat system, respectively.

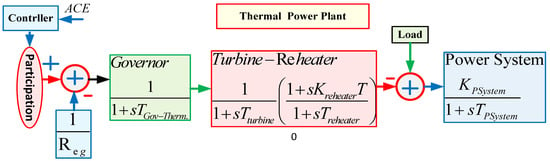
Figure 3. The transfer function of reheat thermal plant model.

2.2.2. Hydro Power Model

After thermal, hydropower systems are the second most important for generating electricity. The transfer function model of a hydropower system is given in Figure 4, where T_Hydro is the transient droop time constant, T is the reset time constant, T_Gov-Hydro is the governor time constant, and Tw represents water starting time.

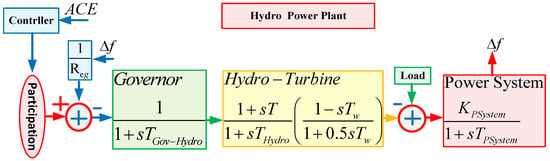
Figure 4. The transfer function of the hydropower plant model.

2.2.3. Gas Power Model

Figure 5 represents a gas power generator, where c_gas represents valve position, b_gas is the valve positioner constant, x_gov/y_gov represents the speed governor lead-lag time constant, and T_FC-gas, T_comp, and T_f represent compressor discharge volume, combustion reaction time delay, and fuel time constant, respectively.

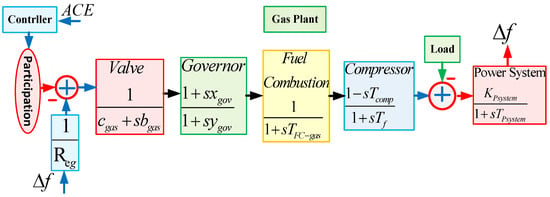
Figure 5. The transfer function of the G=gas plant model.

2.2.4. Super Magnetic Energy Storage Device (SMES) Model

SMES is used to inject/receive the power to/from the power system in order to minimize deviations. Figure 6 shows that the SMES model consists of lead time constants (T₁–T₄), K_SMES (gain), and T_SMES (time constant).

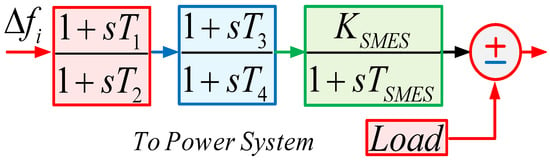
Figure 6. The transfer function of the SMES model.

2.2.5. Thyristor-Controlled Phase Shifter (TCPS) Model

A TCPS is used to dampen the power fluctuations and increase the power transfer capabilities of the line utilizing changing the phase angle. Figure 7 presents a model of TCPS, placed near area 1 and connected to the ΔPtie12 tie line in series, where T_TCPS is the time constant of the TCPS.

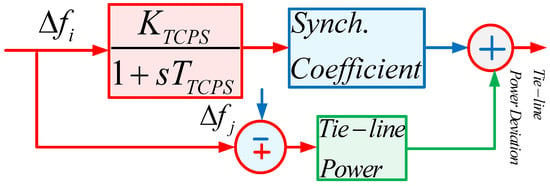
Figure 7. The transfer function of the TCPS model.

2.2.6. Geothermal Plant (GTP) Model

The GTP model is given in Figure 8. The geothermal plant is used to produce electricity and falls in the RES category. The power produced is almost similar to that of the thermal stations, but it does not have a boiler. Here, T_geo-t is the governor, and T_s-geo is the turbine time constant of the GTP.

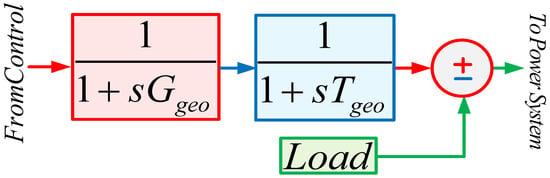
Figure 8. The transfer function of the GTP model.

The overall diagram of the interconnected test system is given in Figure 9.

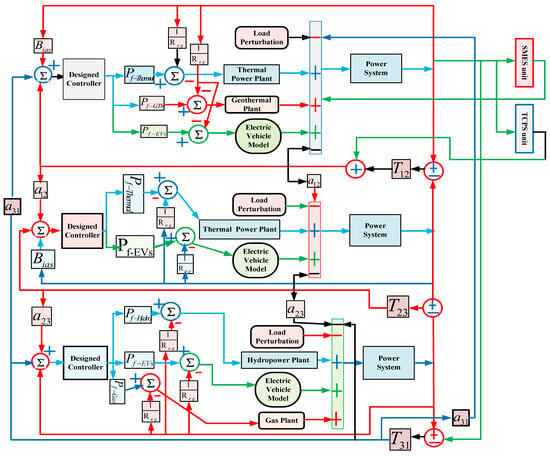
Figure 9. Block diagram of the tested interconnected three-area power system.

3. The Control Scheme

The controller is known as the brain of an LFC scheme. Many control schemes have been tried in LFC schemes so far, i.e., from conventional to modern ones. Each control scheme has its own merits and limitations. In this study, PID, PID-2DF, FOPID, FOPID-FOI, and FOPID-FOID controllers were constructed and tested for the system given in this article.

In this section, different control schemes, their mathematical models, and the algorithm used to obtain their parameters are studied. Let us start with the basic one, i.e., the PID control scheme.

PID control scheme: PID is the conventional and very popular control scheme, with the structure given in (1) and (2) and represented in Figure 10.

$${\mathrm{U}\left(\mathrm{t}\right)=\mathrm{K}}_{\mathrm{P}}.\mathrm{E}\left(\mathrm{t}\right)+{\displaystyle \frac{{\mathrm{K}}_{\mathrm{I}}}{s}}{.\mathrm{E}\left(\mathrm{t}\right)+\mathrm{K}}_{\mathrm{D}}\mathrm{s} .\mathrm{E}\left(\mathrm{t}\right)$$

(1)

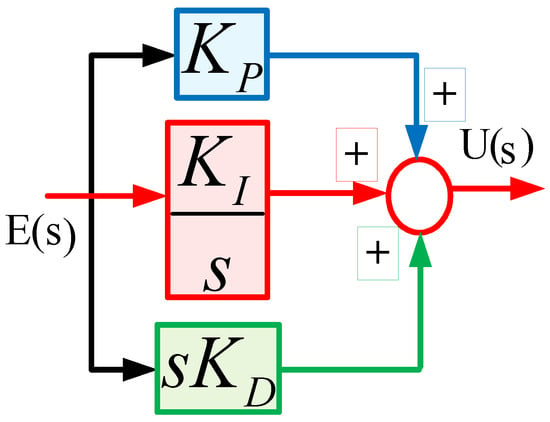
Figure 10. Structure of PID control scheme.

The Laplace form of (1) is given in (2).

$${\mathrm{G}}_{\mathrm{PID}}{\left(\mathrm{s}\right)=\mathrm{K}}_{\mathrm{P}}{+\mathrm{K}}_{\mathrm{I}}{\mathrm{s}}^{-1}{+\mathrm{K}}_{\mathrm{D}}\mathrm{s}$$

(2)

where K_P, K_I, and K_D are PID parameters, E(t) is the error signal, U(t) is the response of the controller, and G_PID is the transfer function of the PID controller.

PID-2DF control scheme: PID-2DF (two degrees of freedom, as shown in Figure 11) controllers offer advantages over traditional PID controllers by allowing the independent tuning of set point tracking and disturbance rejection, leading to improved control performance. They provide better transient response, reduce overshoot, and enhance system stability, making them ideal for applications requiring precise and adaptable control. A well-known form of the PID-2DF controller is given as

$${\mathrm{U}\left(\mathrm{s}\right)=\mathrm{K}}_{\mathrm{P}}(\mathrm{b}.\mathrm{r}-{\mathrm{y})+\mathrm{K}}_{\mathrm{I}}({\displaystyle \frac{1}{s}}(\mathrm{r}-{\mathrm{y}))+\mathrm{K}}_{\mathrm{D}}{\displaystyle \frac{N}{1+\frac{N}{s}}}(\mathrm{c}.\mathrm{r}-\mathrm{y})$$

(3)

where K_P, K_I, and K_D are PID-2DF parameters, b is a weighting factor for K_P, r is the reference input, y is the measured variable, c is the weighting factor for the derivative term, U(s) is Laplacian response of the controller, and N is the derivative filter coefficient.

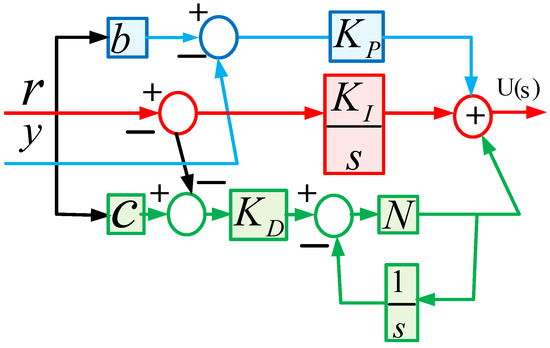
Figure 11. Structure of PID-2DF control scheme.

FOPID control scheme: The implementation of the FO transfer function was proposed by Oustaloup, which is reported in [25,26,27,28,29,30]. The FOPID controller shown in Figure 12 can be represented as given in (4).

$${\mathrm{U}\left(\mathrm{t}\right)=\mathrm{K}}_{\mathrm{P}}.\mathrm{E}\left(\mathrm{t}\right)+{\displaystyle \frac{{\mathrm{K}}_{\mathrm{I}}}{s^L}}{.\mathrm{E}\left(\mathrm{t}\right)+\mathrm{K}}_{\mathrm{D}}{\mathrm{s}}^M .\mathrm{E}\left(\mathrm{t}\right)$$

(4)

where D = ${\displaystyle \frac{\mathrm{d}}{\mathrm{dt}}}$. The FOPID controller can also be represented as (5).

$${\mathrm{G}}_{\mathrm{FOPID}}\left(\mathrm{s}\right)=\left[{\mathrm{K}}_{\mathrm{P}}+{\displaystyle \frac{{\mathrm{K}}_{\mathrm{I}}}{{\mathrm{s}}^L}}{+\mathrm{K}}_{\mathrm{D}}{\mathrm{s}}^M\right]$$

(5)

where ${\mathrm{K}}_{\mathrm{P}},$ ${\mathrm{K}}_{\mathrm{I}},$ ${\mathrm{K}}_{\mathrm{D}}$ are FOPID gains, and $L$ and $\mathrm{M}$ are the fractional integrator and differentiator.

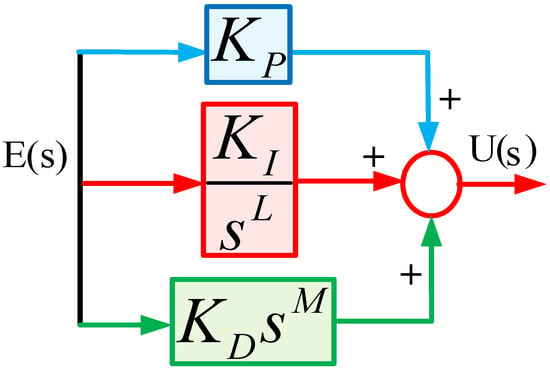
Figure 12. Structure of FOPID scheme.

The authors used the other variants of the FOPID control structure in order to determine the best control scheme for the tested system.

FOPID-FOI control scheme: FOPID-FOI controllers, shown in Figure 13, offer improved stability and better handling of nonlinearities due to the additional fractional-order integral component that provides small steady-state errors and smoother control.

$${\mathrm{U}\left(\mathrm{t}\right)=\mathrm{K}}_{\mathrm{P}}.\mathrm{E}\left(\mathrm{t}\right)+{\displaystyle \frac{{\mathrm{K}}_{\mathrm{I}1}}{s^{L1}}}{.\mathrm{E}\left(\mathrm{t}\right)+\mathrm{K}}_{\mathrm{D}}{\mathrm{s}}^M .\mathrm{E}\left(\mathrm{t}\right)+{\displaystyle \frac{{\mathrm{K}}_{\mathrm{I}2}}{s^{L2}}}.\mathrm{E}\left(\mathrm{t}\right)$$

(6)

$${\mathrm{G}}_{\text{FOPID-FOI}}\left(\mathrm{s}\right)=\left[{\mathrm{K}}_{\mathrm{P}}+{\displaystyle \frac{{\mathrm{K}}_{\mathrm{I}1}}{{\mathrm{s}}^{L1}}}{+\mathrm{K}}_{\mathrm{D}}{\mathrm{s}}^M+{\displaystyle \frac{{\mathrm{K}}_{\mathrm{I}2}}{{\mathrm{s}}^{L2}}}\right]$$

(7)

where K_P, K_I1, K_D, K_I2 = FOPID-FOI parameters; S^L1, S^L2 = fractional terms of the integra; S^M = fractional term of the derivative.

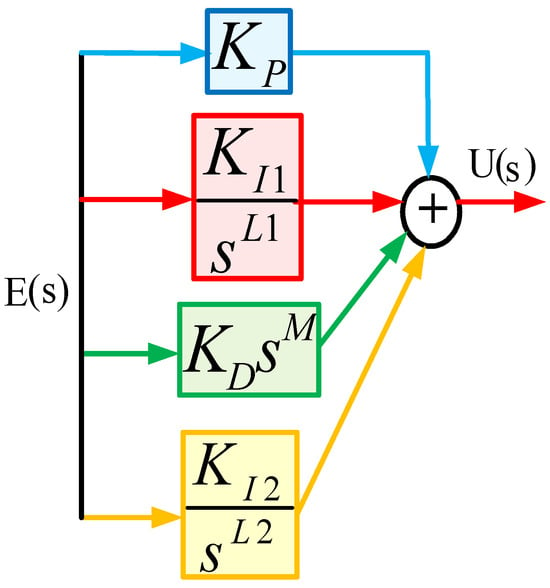
Figure 13. Structure of FOPID-FOI scheme.

FOPID-FOID control scheme: FOPID-FOID controllers, shown in Figure 14, offer improved stability and better handling of nonlinearities, as well as enhanced robustness over FOPID and FOPID-FOI control schemes. It has an additional fractional-order integral-derivative component in order to provide small steady-state errors, better control, and improved overall stability.

$${\mathrm{U}\left(\mathrm{t}\right)=\mathrm{K}}_{\mathrm{P}}.\mathrm{E}\left(\mathrm{t}\right)+{\displaystyle \frac{{\mathrm{K}}_{\mathrm{I}1}}{s^{L1}}}{.\mathrm{E}\left(\mathrm{t}\right)+\mathrm{K}}_{\mathrm{D}1}{\mathrm{s}}^{M1} .\mathrm{E}\left(\mathrm{t}\right)+{\displaystyle \frac{{\mathrm{K}}_{\mathrm{I}2}}{s^{L2}}}{.\mathrm{E}\left(\mathrm{t}\right)+\mathrm{K}}_{\mathrm{D}2}{\mathrm{s}}^{M2} .\mathrm{E}\left(\mathrm{t}\right)$$

(8)

$${\mathrm{G}}_{\text{FOPID-FOID}}\left(\mathrm{s}\right)=\left[{\mathrm{K}}_{\mathrm{P}}+{\displaystyle \frac{{\mathrm{K}}_{\mathrm{I}1}}{{\mathrm{s}}^{L1}}}{+\mathrm{K}}_{\mathrm{D}1}{\mathrm{s}}^{M1}+{\displaystyle \frac{{\mathrm{K}}_{\mathrm{I}2}}{{\mathrm{s}}^{L2}}}+{\mathrm{K}}_{\mathrm{D}2}{\mathrm{s}}^{M2}\right]$$

(9)

where, K_P, K_I1, K_D1, K_I2, K_D2 = FOPID-FOID parameters; S^L1, S^L2 = fractional terms of the integral; S^M1, S^M2 = fractional term of the derivative.

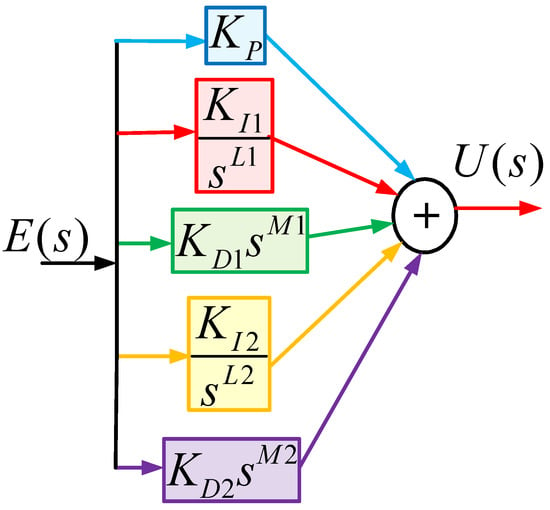
Figure 14. Structure of FOPID-FOID scheme.

4. The Optimization Algorithm

A controller is as only as good as its parameters. In the literature, several optimization algorithms have been used in order to design the parameters of the control scheme. Some of the popular algorithms are big bang-big crunch (BBBC), particle swarm optimization (PSO), harmony search (HS), and JAYA. In this work, the authors obtained the parameters using all the given algorithms; however, the parameters obtained using JAYA were used due to its fast convergence. The comparative convergence curve is shown in Figure 15.

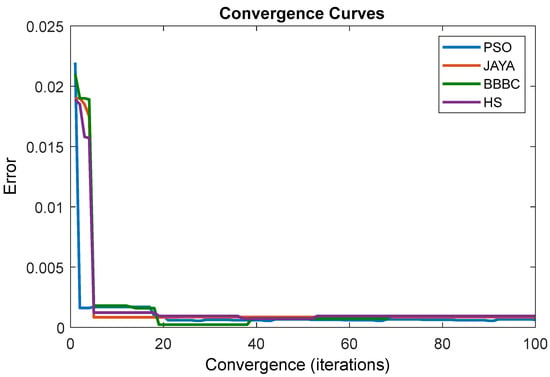
Figure 15. The comparative convergence curve.

JAYA Algorithm

The JAYA algorithm is a simple method for optimizing controller settings in load frequency control (LFC) systems. It performs better than traditional methods like genetic algorithms (GA) and particle swarm optimization (PSO), making it suitable for real-time applications. It is characterized by ease of implementation and convergence assurance, and works well for multiarea power system. It is more computationally efficient and has faster convergence than GA and PSO, as well as low computational complexity. Regarding the quality of the solution, JAYA has global optimization capability.

The features of JAYA are as given below:

• Feature 1: JAYA is a simple and straightforward algorithm to implement that does not require parameters like crossover/mutation rates.
• Feature 2: It modifies its approach using exploration to obtain an understanding, and it uses exploitation in order to maximize the finest solutions (exploration—exploitation).
• Feature 3: It converges quickly in order to perform efficiently.

The steps for designing a controller using JAYA are as follows:

Step 1: JAYA is used to minimize the objective function given below in order to obtain the parameters of the designed controllers.

$$\begin{array}{ll}& J_{opt\_fun}={\displaystyle \frac{1}{k}}{\displaystyle \sum _{i=1}^k[{(AC{E}_i)}^2}]\\ \mathrm{Objective} \mathrm{function}=\mathrm{minimization} \mathrm{of} & J_{opt\_fun}={\displaystyle \frac{1}{k}}{\displaystyle \sum _{i=1}^k[{(B_i\Delta f_i+{\Delta Ptie}_{i\_error})}^2}]\end{array}$$

where k = areas, ACE = area control error, ∆f = deviation in frequency, B_i = bias factor, and ∆Ptie = tie-line deviations.

Step 2: This step involves the initialization of the population of the solution parameters (gains) for each control scheme, i.e., PID, PID-2DF, FOPID, FOPID-FOI, and FOPID-FOID (initialization).

Step 3: In this step, the objective function given in step 1 is calculated for each parameter to check the fitness of the solution (evaluation).

Step 4: This step involves the update of the parameters based on best or worst solutions (update).

$$x_{i,j}^{new}=x_{i,j}^{current}+ran{d}_1(x_{i,j}^{BEST}-\left|x_{i,j}^{current}\right|)-ran{d}_2(x_{i,j}^{WORST}-\left|x_{i,j}^{current}\right|)$$

where

$$\begin{array}{l}{x}_{i,j}^{current}=current value of x_{i,j}^{WORST}{j}^{th}parameter, i^{th} solution \\ x_{i,j}^{BEST}=value of j^{th}parameter of best solution\\ x_{i,j}^{WORST}=value of j^{th}parameter of worst solution\end{array}$$

$$ran{d}_1,ran{d}_2=random number (0,1)$$

Step 5: This step involves comparing the current and new solutions, and, if new solutions have better fitness, the current ones are replaced with new ones (selection).

Step 6: This step involves determining the optimal parameters or stopping the algorithm if the threshold is achieved. In that event, repeat steps 1–4 again in order to obtain the optimal parameters (termination).

5. Results and Discussion

The overall system was modeled in the SIMULINK/MATLAB ver. R2018a environment to investigate the performance of the designed control schemes. As mentioned, area 1 consisted of thermal, geothermal, and EV generation systems. area 2 consisted of EV and thermal generation systems, and area 3 had gas, EV, and hydro systems. Apart from this, an SMES device was also incorporated in area 1 and a TCPS system was inserted between areas 1 and 2. The following cases were considered in order to check the controller’s performance.

Case 1: Case 1 deals with normal system parameters and a step load of 0.15 pu, 0.13 pu, and 0.15 pu in area 1, area 2, and area 3, respectively.

Frequency Deviation: The step load in all three areas is presented in Figure 16. From the comparative analysis of the frequency deviation results (Figure 17) for various controllers, it is evident that the FOPID-FOID controller exhibits superior performance, particularly in terms of settling time. While the traditional PID controllers and their variant PID-2DF demonstrate competent control over frequency deviations, their settling times are relatively longer. The FOPID and FOPID-FOI controllers offer improvements by incorporating fractional calculus, leading to enhanced adaptability and precision. However, the FOPID-FOID controller achieves the most significant reduction in settling time.

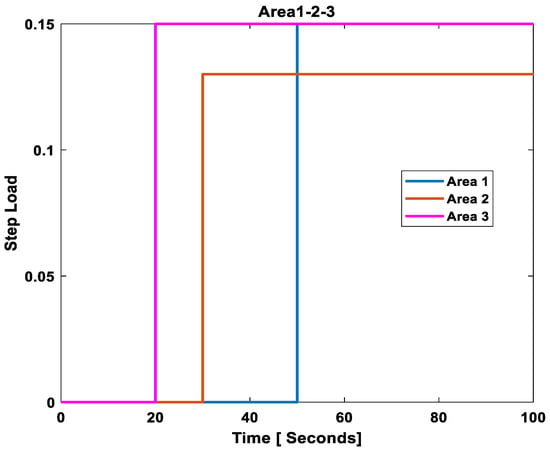
Figure 16. Step load in all areas.

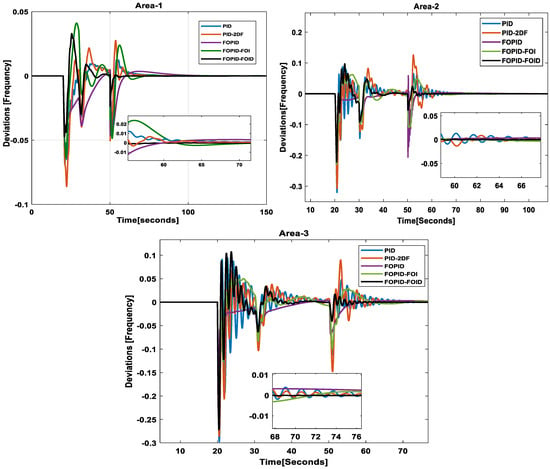
Figure 17. Frequency deviations in all areas.

Change in generation/(area 1): In evaluating the change in generation using the applied control schemes, as shown in Figure 18, it becomes clear that the FOPID-FOID controller delivers superior performance. PID controllers, while effective in managing generation changes, often struggle with overshoot and longer stabilization periods. It can be seen that the generators in area 1 respond to load perturbation and change their generation as per the requirements. The thermal generators provide 0.1179 pu, the geothermal plant provides 0.1964 pu, and the EVs change their generation and settling to 0.125 pu in order to keep a balance between generation and demand of 0.15 pu in area 1.

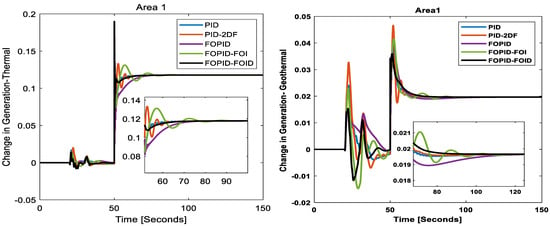
Figure 18. Change in generation in area 1.

The PID-2DF controller offers some improvement, leading to better control and quicker response. The FOPID and FOPID-FOI controllers enhance control accuracy and response times. However, the FOPID-FOID controller excels and significantly refines the control process. This control scheme results in more precise and quicker adjustments in generation, minimizing overshoot and achieving desired power output levels more rapidly and with greater stability than the other control methods.

In the assessment of the change in the electric vehicle (EV) response (Figure 19), the FOPID-FOID controller stands out for its superior performance. PID controllers, while competent in managing EV response changes, exhibit longer response times. The PID-2DF controller leads to better response times. The FOPID and FOPID-FOI controllers deliver more precise control and faster response times, outperforming their integer-order counterparts. Nevertheless, the FOPID-FOID controller surpasses all others in significantly reducing response time and minimizing overshoot in the EV response.

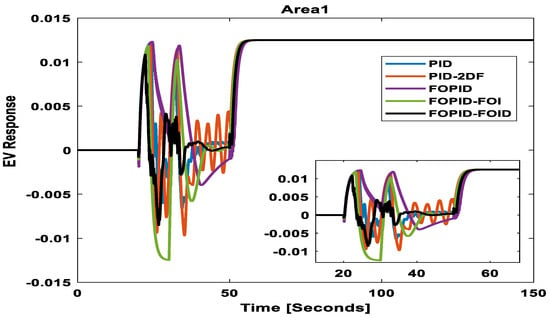
Figure 19. EV response in area 1.

Change in generation/(area 2): The change in generation for thermal and electric vehicle (EV) generation in area 2, using various control schemes, is given in Figure 20. The FOPID-FOID controller demonstrates superior performance. PID controllers, although effective in managing generation changes, deliver it with a prolonged stabilization time. The PID-2DF controller provides some improvement over PID. The FOPID and FOPID-FOI controllers offer more accurate control and faster response times, ensuring rapid and stable adjustments to generation changes. The results show that the thermal plant in area 2 regulates its generation and settles to 0.105 pu, whereas the EVs settle to 0.025 pu in order to take care of the load demand of 0.13 pu in area 2.

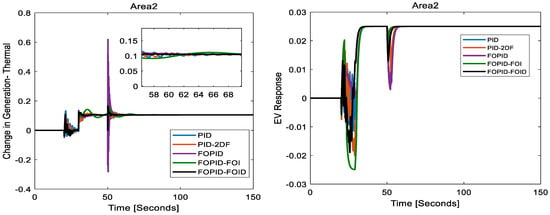
Figure 20. Change in generation and EV response in area 2.

Change in generation/(area 3): We analyzed the control performance for changes in generation, thermal, electric vehicle (EV), and gas generation in area 3. The results given in Figure 21 clearly indicate that the FOPID-FOID controller delivers the most effective performance. It is also seen that the hydropower plant in area 3 regulates its generation and settles to 0.08036 pu, the gas plant settles to 0.03214 pu, whereas the EVs settle to 0.0375 pu in order to meet the load demand of 0.15 pu in area 3. PID controllers, though capable, often face difficulties with overshoot and settling times in multisource, multiarea systems. The PID-2DF controller enhances performance by introducing an additional degree of freedom. But, controllers utilizing fractional calculus, such as FOPID and FOPID-FOI, provide improved precision and faster response times.

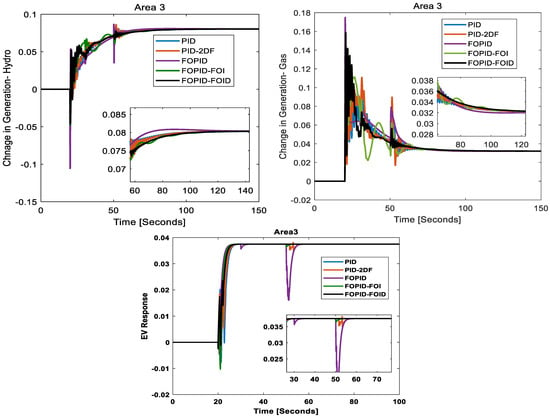
Figure 21. Change in generation (hydro, gas) and EV response in area 3.

However, the FOPID-FOID controller stands out and offers significant advantages in handling the dynamic changes in thermal, EV, and gas generation in area 3. This advanced controller significantly reduces response times and minimizes overshoot, achieving rapid and stable generation adjustments.

Area control error (ACE): When analyzing the area control error (ACE) across all three areas using the different control schemes—PID, PID-2DF, FOPID, FOPID-FOI, and FOPID-FOID—it is evident that the FOPID-FOID controller produces the best performance. The results shown in Figure 22 evidence that FOPID-FOID performs better than the other used control approaches. This advanced control strategy effectively minimizes the ACE in all three areas by reducing response time and overshooting, ensuring more stable and accurate control.

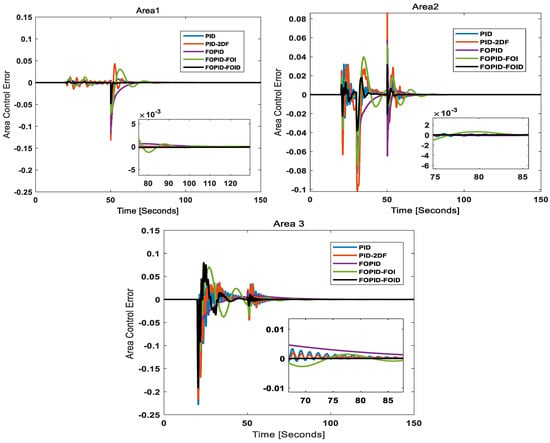
Figure 22. Area control error in all areas.

Tie-line power: The results of the tie-line power deviations in all areas are given in Figure 23. Tie-line power faces deviations with the occurrence of load perturbations, and it is seen that among all the control approaches, the FOPID-FOID scheme works better and reduces tie-line power oscillations and minimizes overshoot, more rapidly than other schemes. Areas 1–2 also have a TCPS to overcome the deviations’ oscillations and slower settling times.

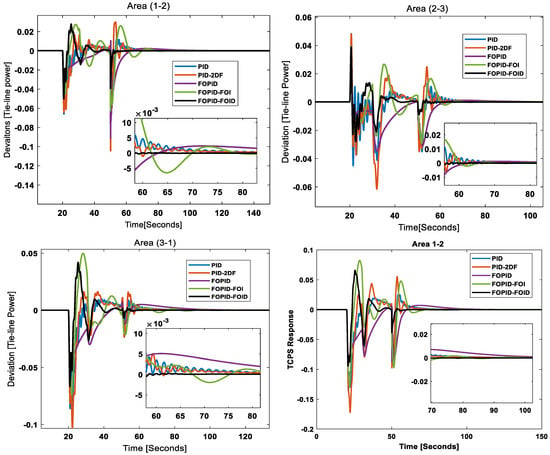
Figure 23. Tie-line power deviations (all areas) and TCPS response (areas 1–2).

Case 2: Case 2 deals with changes in system parameters and a step load of 0.2 pu, 0.15 pu, and 0.15 pu in area 1, area 2, and area 3, respectively.

The performance of the designed control schemes was checked for parameter variation in order to verify whether controllers can handle the parameter uncertainty or not. In all areas, the power system gain and time constant were modified as given in Table 2.

Table 2. Parameters changes in all areas.

Area	Parameter	Change in Parameter
Area 1	KP1	10% Reduction
	TP1	20% Increase
Area 2	KP2	20% Increase
	TP2	50% Increase
Area 3	KP3	25% Reduction
	TP3	15% Reduction

Though the results for this case were obtained for generation, ACE, and tie-line power, only the frequency deviation results are given here, as shown in Figure 24. Upon analysis, it was found that though all control schemes are able to handle this parameter variation, they exhibit oscillations in magnitude (generally increasing the magnitude of undershoot and overshoot) and have a longer settling time; however, the FOPID-ID control scheme still performs better the all others and provides the results with the shortest settling time with no or very little change in oscillations. It manages parameter variations more effectively, resulting in fewer oscillations and faster settling times.

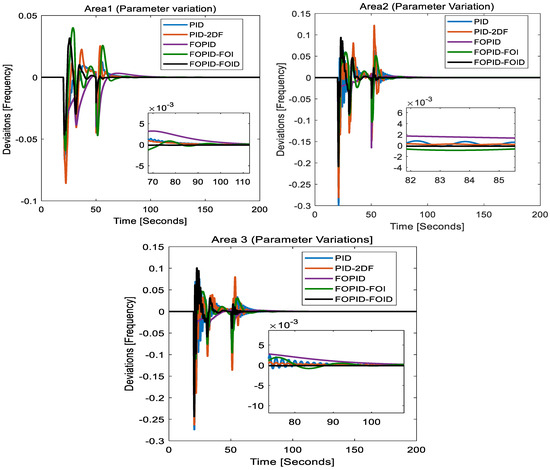
Figure 24. Frequency deviations in all areas.

Case 3: Case 3 deals with normal system parameters and a random load in area 1, area 2, and area 3.

The performance of the designed control schemes was checked for random load disturbance applied in all areas in order to verify the behavior of the designed controller behavior if a sudden load of random nature occurs. The nature of the load is given in Figure 25. The frequency deviations in all areas for this load perturbation are given in Figure 26. The analysis reveals that the FOPID-FOID control scheme is superior in handling the random load disturbance and exhibits smaller oscillations. It consistently maintains more stable and accurate frequency control under random load changes, outperforming all other control methods. PID controllers, although effective, show increased deviations and longer settling times. These controllers struggle to stabilize quickly under random load disturbances, leading to less-consistent frequency control.

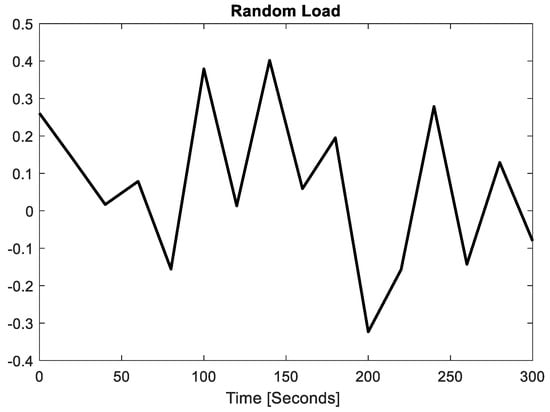
Figure 25. Random load profile.

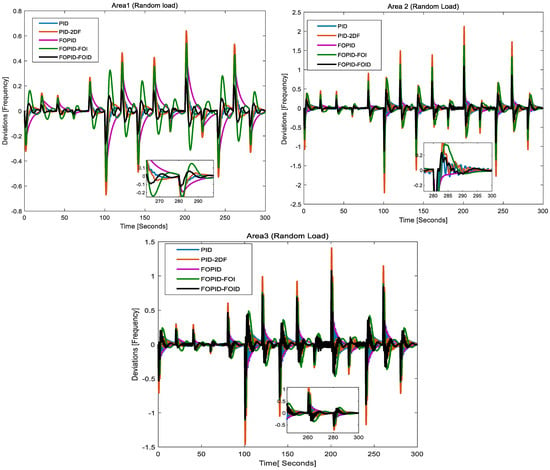
Figure 26. Frequency deviations in all areas.

Case 4: Case 4 deals with normal system parameters and a step load in area 1, area 2, and area 3 (without SMES or TCPS).

Frequency deviation (with and without SMES): The frequency deviation in area 1 typically shows larger and more persistent oscillations due to the lack of rapid energy exchange capability. The presence of SMES reduces the settling time considerably. The fast response tune of SMES allows it to quickly counteract deviations by injecting or absorbing power almost instantaneously. As a result, the system returns to its nominal frequency much faster compared to scenarios without SMES, as given in Figure 27.

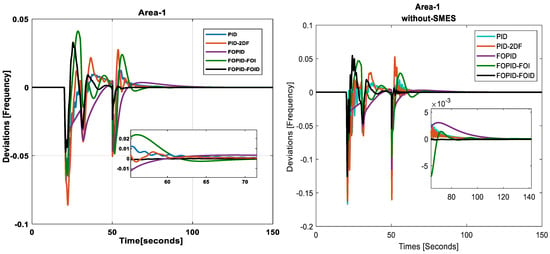
Figure 27. Frequency deviation (without SMES).

Tie-line power deviations (with and without TCPS): The thyristor-controlled phase shifter (TCPS) can lead to significant improvements in tie-line power deviation in area 1 which demonstrates smaller oscillations and reduced settling time when TCPS is integrated. The tie-line power deviation in area 1 typically shows larger and more persistent oscillations. This is because conventional control methods cannot rapidly adjust the phase angle of the power flow, leading to less-efficient power exchange between areas. TCPS effectively mitigates these oscillations, as given in Figure 28. As a result, the system achieves the desired tie-line power level much faster and with smaller oscillations compared to scenarios without TCPSs. Table 3. Shows the Optimal coefficients for various controllers.

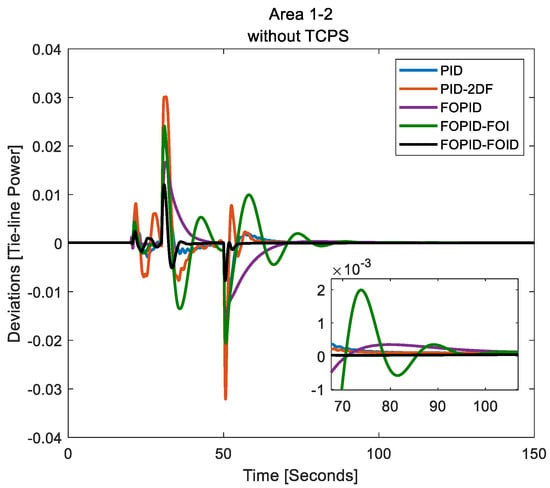
Figure 28. Tie-line power deviations (without TCPS).

Table 3. Optimal coefficients for various controllers.

Controller	Area	Coefficients
PID	area 1	−1.5/−2.5/−1.9	KP/KI/KD
	area 2	−1.8/−1.6/−1.7
	area 3	−1.2/−1.1/−1.15
PID-2DF	area 1	−0.15/4.32/1.25/0.95/0.85	KP/KI/KD/b/c
	area 2	−0.235/1.25/1.36/0.9/0.7
	area 3	−0.685/1.23/1.68/0.8/0.89
FOPID	area 1	−1.5/−1.53/−1.9/1.2/1.1	KP/KI/KD/L/M
	area 2	−1.8/−1.86/−1.7/1.6/1.7
	area 3	−1.2/−1.86/−1.15/1.8/1.9
FOPID-FOI	area 1	−3.65/−1.35/−1.68/1.56/1.32/−0.098/1.56	KP/KI1/KD/L1/M-KI2/L2
	area 2	−2.35/−1.35/−1.21/1.56/1.32/−0.098/1.56
	area 3	−1.98/−1.27/1.96/1.56/1.32/−0.098/1.56
FOPID-FOID	area 1	−7.35/−8.65/−3.62/0.365/1.32/−9.65/0.556/−0.25/0.8	KP/KI1/KD1/L1/M1-KI2/L2/KD2/M2
	area 2	−5.3/−6.85/−2.56/1.12/1.32/−0.098/1.62/−1.2/0.8
	area 3	−2.32/−3.21/−1.23/1.39/1.32/−0.098/1.56/−1.2/0.8

Table 4 shows the performance analysis of PID, PID-2DF, and fractional controllers for multiarea LFC. The analysis in Table 5 and Table 6 shows that fractional-order controllers (especially FOPID-FOID) exhibit better stability and reduced frequency deviations across different areas and provide better adaptability to system dynamics.

Table 4. Performance analysis of PID, PID-2DF, and fractional controllers for multiarea LFC.

Parameter	Controller	Overshoot	Undershoot	Settling Time (Ts)	Parameter	Controller	Overshoot	Undershoot	Settling Time (Ts)
Frequency (area 1)	PID	0.0125	−0.0682	105 or Ts > 100	Tie-line (1–2)	PID	0.0122	−0.9308	115 or Ts > 110
	PID-2DF	0.0276	−0.0863	100 or Ts > 100		PID-2DF	0.02999	−0.1044	110 or Ts > 100
	FOPID	0.0044	−0.0465	110 or Ts > 110		FOPID	0.0102	−0.9107	120 or Ts > 110
	FOPID-FOI	0.041	−0.0640	105 or Ts > 100		FOPID-FOI	0.02723	−0.4899	100 or Ts > 90
	FOPID-FOID	0.033	−0.0473	80		FOPID-FOID	0.02757	−0.500	80
Frequency (area 2)	PID	0.08754	−0.3204	125 or Ts > 120	Tie-line (2–3)	PID	0.04832	−0.4500	115 or Ts > 110
	PID-2DF	0.1258	−0.3071	125 or Ts > 120		PID-2DF	0.04815	−0.6140	110 or Ts > 100
	FOPID	0.05814	−0.2057	120 or Ts > 110		FOPID	0.00123	−0.3073	120 or Ts > 110
	FOPID-FOI	0.06215	−0.2295	120 or Ts > 110		FOPID-FOI	0.03946	−0.2904	110 or Ts > 100
	FOPID-FOID	0.0969	−0.2212	75		FOPID-FOID	0.03879	−0.2756	65
Frequency (area 3)	PID	0.0942	−0.2974	140 or Ts > 135	Tie-line (1–3)	PID	0.01001	−0.8547	110 or Ts > 100
	PID-2DF	0.08951	−0.2859	140 or Ts > 135		PID-2DF	0.01619	−0.1036	105 or Ts > 100
	FOPID	0.0035	−0.2358	140 or Ts > 140		FOPID	0.00521	−0.4931	120 or Ts > 110
	FOPID-FOI	0.0501	−0.2586	130 or Ts > 120		FOPID-FOI	0.04981	−0.7378	110 or Ts > 100
	FOPID-FOID	0.1074	−0.2715	80		FOPID-FOID	0.04110	−0.6667	75

Table 5. Statistical parameters of frequency deviation (all areas).

	Controllers	Mean	Peak	Valley	Standard Deviation
F1 (area 1)	PID	−0.0095	0.0125	−0.686	0.0180
	PID-2DF	−0.0118	0.0276	−0.861	0.0256
	FOPID	−0.0173	0.0044	−0.465	0.0149
	FOPID-FOI	−0.0028	0.0411	−0.641	0.0211
	FOPID-FOID	−0.0055	0.0329	−0.473	0.0135
F2 (area 2)	PID	−0.0126	0.0879	−0.3204	0.0540
	PID-2DF	−0.0123	0.1259	−0.3072	0.0624
	FOPID	−0.0211	0.0587	−0.2058	0.0331
	FOPID-FOI	−0.0174	0.0622	−0.2296	0.0467
	FOPID-FOID	6.2639 × 10−4	0.0971	−0.2214	0.0371
F3 (area 3)	PID	−0.0093	0.0942	−0.2975	0.0473
	PID-2DF	−0.0086	0.0899	−0.2859	0.0523
	FOPID	−0.0184	0.0035	−0.2358	0.0264
	FOPID-FOI	−0.0104	0.0501	−0.2588	0.0449
	FOPID-FOID	−9.8933 × 10−4	0.1075	−0.2716	0.0338

Table 6. Statistical parameters of tie-line power deviation (all areas).

	Controllers	Mean	Peak	Valley	Standard Deviation
T1-2	PID	−0.0077	0.0123	−0.0931	0.0183
	PID-2DF	−0.0085	0.0300	−0.1044	0.0236
	FOPID	−0.0134	0.0102	−0.0911	0.0148
	FOPID-FOI	−0.0015	0.0278	−0.0501	0.0105
	FOPID-FOID	−0.0077	0.0275	−0.0627	0.0226
T2-3	PID	−0.0047	0.0483	−0.0450	0.0129
	PID-2DF	−0.0051	0.0482	−0.0615	0.0155
	FOPID	−0.0062	0.0284	−0.0347	0.0083
	FOPID-FOI	−2.2573 × 10−4	0.0395	−0.0290	0.0103
	FOPID-FOID	−0.0027	0.0388	−0.0281	0.0076
T3-1	PID	−0.0061	0.0101	−0.0860	0.0185
	PID-2DF	−0.0093	0.0164	−0.1036	0.0272
	FOPID	−0.0145	0.0069	−0.0493	0.0159
	FOPID-FOI	−0.0024	0.0499	−0.0739	0.0214
	FOPID-FOID	−0.0010	0.0420	−0.0667	0.0149

The findings are provided in Table 7.

Table 7. Percentage improvement in settling time, overshoot, and undershoot.

Parameter	Controller	Settling Time (PID)	Settling Time (Controller)	% Improvement in Settling Time	Overshoot (PID)	Overshoot (Controller)	% Improvement in Overshoot	Undershoot (PID)	Undershoot (Controller)	% Improvement in Undershoot
Frequency (area 1)	PID	105	-	-	0.0125	-	-	−0.0682	-	-
	PID-2DF	105	100	4.76%	0.0125	0.0276	−120.8%	−0.0682	−0.0863	−26.0%
	FOPID	105	110	−4.76%	0.0125	0.0044	64.8%	−0.0682	−0.0465	31.2%
	FOPID-FOI	105	105	0.00%	0.0125	0.041	−228%	−0.0682	−0.0640	6.6%
	FOPID-FOID	105	80	23.81%	0.0125	0.033	18.4%	−0.0682	−0.0473	30.5%
Frequency (area 2)	PID	125	-	-	0.08754	-	-	−0.3204	-	-
	PID-2DF	125	125	0.00%	0.08754	0.1258	−43.5%	−0.3204	−0.3071	4.9%
	FOPID	125	120	4.00%	0.08754	0.05814	33.6%	−0.3204	−0.2057	35.6%
	FOPID-FOI	125	120	4.00%	0.08754	0.06215	29.1%	−0.3204	−0.2295	28.4%
	FOPID-FOID	125	75	40.00%	0.08754	0.0969	−10.7%	−0.3204	−0.2212	30.9%
Frequency (area 3)	PID	140	-	-	0.0942	-	-	−0.2974	-	-
	PID-2DF	140	140	0.00%	0.0942	0.08951	0.7%	−0.2974	−0.2859	4.8%
	FOPID	140	140	0.00%	0.0942	0.0035	96.3%	−0.2974	−0.2358	20.7%
	FOPID-FOI	140	130	7.14%	0.0942	0.0501	46.7%	−0.2974	−0.2586	13.0%
	FOPID-FOID	140	80	42.86%	0.0942	0.1074	−14.0%	−0.2974	−0.2715	8.7%

Settling time improvements: The FOPID-FOID controller demonstrates the best improvement in settling time for area 1 (23.81%) and area 2 (40.00%).

Overshoot reductions: The FOPID controller in area 3 shows the highest improvement in overshoot (96.3%).

Undershoot improvements: The FOPID-FOID controller improves undershoot in area 1 by 30.5% compared to the PID controller.

The result and discussion can be summarized in the following manner:

(a) 

Main Findings of this Study

This study revealed that the FOPID-FOID controller outperforms other control techniques when it comes to controlling frequency deviations and generation changes in the studied multisource hybrid power system. The key findings include the following:

• The FOPID-FOID controller considerably reduces settling time and overshoot compared to the PID, PID-2DF, FOPID, and FOPID-FOI controllers.
• The integration of energy storage devices like SMES and TCPS enhances system performance, reduces deviations, and increases response times.
• All controllers effectively handle parameter variations, but the FOPID-FOID consistently exhibits superior performance, especially for settling time.

(b) 

Comparison with Other Studies

When compared to previous research, this study reveals that advanced control techniques perform better in multiarea power systems. Although many studies emphasize the efficiency of PID controllers, this study shows that fractional-order controllers, specifically the FOPID-FOID, offer greater adaptability and precision. Additionally, the inclusion of SMES and TCPS has not been frequently examined in earlier research; thus, this study focused on their relevance too.

(c) 

Implication and Explanation of Findings

The results show that employing advanced/sophisticated control techniques can greatly improve power system performance. The FOPID-FOID controller may offer a strong foundation for control design in complex and dynamic environments. This study also shows the importance of the SMES and TCPS in reducing oscillations and enhancing settling times, which are critical for reliable power delivery following varying demands.

(d) 

Strengths and Limitations

Strengths:

• We comprehensively evaluated several control strategies for various operational scenarios like parameter variations and random load disturbances.
• We integrated advanced control schemes like FOPID-FOID with energy storage (SMES) and phase control technologies (TCPS).
• The detailed simulation results support the claims regarding performance improvements.

Limitations:

• This study mainly relied on simulations, which may not fully model the uncertainties in real-world applications.
• The result’s applicability to various power system operating conditions may be limited by different power systems’ operational conditions.
• Future research could focus on experimental validation to enhance the reliability of the proposed control strategies.

6. Conclusions

In conclusion, this study contributes significantly to the understanding of control strategies for load management in energy systems, particularly through the application of various controllers, including PID, FOPID, PID-2DF, FOPID-FOI, and FOPID-FOID. The theoretical contributions of this research include a detailed comparative analysis of these controllers across different load types—thermal, electric vehicle (EV), geothermal, hydropower, and gas—highlighting the unique advantages of fractional-order control techniques in enhancing system performance. The results provided in the various figures demonstrate that the FOPID-FOID controller consistently outperforms traditional control strategies, achieving shorter settling times and minimizing oscillations in all three areas studied. In area 1, the FOPID-FOID controller shows remarkable effectiveness in suppressing oscillations and responding to load changes under varying conditions. In area 2, it facilitates quicker stabilization of thermal and EV load management, while in area 3, it adeptly manages the complexities of hydropower and gas generation, reinforcing its applicability to real-world scenarios where rapid response and precision are critical. Form the analysis of Table 5, Table 6 and Table 7, it is seen that the FOPID-FOID controller provides significant reductions in oscillations and settling times in order to improve system dynamics. Therefore, this control scheme is suitable for LFC schemes of multiarea hybrid power system. Despite these strengths, this study has limitations, primarily its reliance on simulation data, which may not fully capture the dynamics of actual power systems. Additionally, the specific configurations and parameters used may limit the generalizability of the findings.

7. Future Research

Future research should focus on the experimental validation of these control strategies in real-world/practical applications. In order to further improve control schemes, FOPID-FOID may be used with machine learning and predictive analytics. In energy management systems, FOPID-FOID is a promising control scheme. These findings not only advance the theoretical knowledge but also pave the way for practical applications that can successfully meet the changing demands of modern power systems.