The Sharing Energy Storage Mechanism for Demand Side Energy Communities

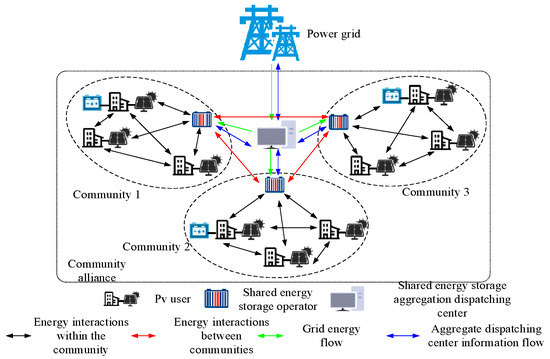
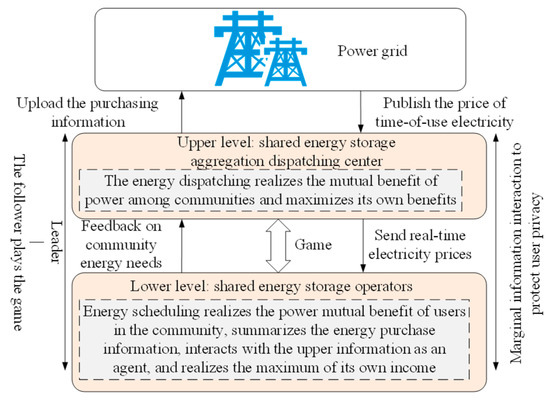
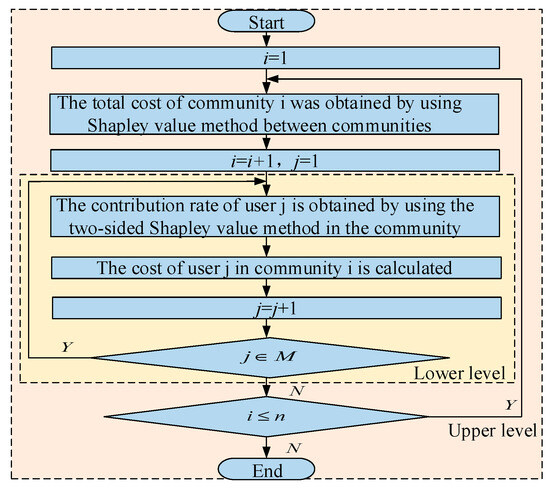
Abstract

Energy storage (ES) units are vital for the reliable and economical operation of the power system with a high penetration of renewable distributed generators (DGs). Due to ES’s high investment costs and long payback period, energy management with shared ESs becomes a suitable choice for the demand side. This work investigates the sharing mechanism of ES units for low-voltage (LV) energy prosumer (EP) communities, in which energy interactions of multiple styles among the EPs are enabled, and the aggregated ES dispatch center (AESDC) is established as a special energy service provider to facilitate the scheduling and marketing mechanism. A shared ES operation framework considering multiple EP communities is established, in which both the energy scheduling and cost allocation methods are studied. Then a shared ES model and energy marketing scheme for multiple communities based on the leader–follower game is proposed. The Karush–Kuhn–Tucker (KKT) condition is used to transform the double-layer model into a single-layer model, and then the large M method and PSO-HS algorithm are used to solve it, which improves convergence features in both speed and performance. On this basis, a cost allocation strategy based on the Owen value method is proposed to resolve the issues of benefit distribution fairness and user privacy under current situations. A case study simulation is carried out, and the results show that, with the ES scheduling strategy shared by multiple renewable communities in the leader–follower game, the energy cost is reduced significantly, and all communities acquire benefits from shared ES operators and aggregated ES dispatch centers, which verifies the advantageous and economical features of the proposed framework and strategy. With the cost allocation strategy based on the Owen value method, the distribution results are rational and equitable both for the groups and individuals among the multiple EP communities. Comparing it with other algorithms, the presented PSO-HS algorithm demonstrates better features in computing speed and convergence. Therefore, the proposed mechanism can be implemented in multiple scenarios on the demand side.

1. Introduction

Multiple types of energy sources, including large amounts of renewable distributed generators (DGs) and energy storage (ES) units are intensively interacting in the new power system [1]. Among them, the integrated energy system (IES) on the demand side can provide flexible energy services by considering various features of the multiple energy sources (such as electric and thermal sources) and taking full advantage of their complementary properties [2]. A high penetration of renewable energies can pose a severe challenge to the power system, and their outputs may have to be cut due to their fluctuating and intermittent nature [3]. ES units can be used to smooth the fluctuations, but their implementations could be limited due to high investment and maintenance costs [4]. Therefore, flexible and diversified energy-sharing mechanisms like a “clouded ES system” [5] or “ES leasing” [6,7] have been proposed to improve the economic benefits of ESs through cost sharing and economies of scale [8,9] and promote “self-consumption” for local DGs [10].

A microgrid with an optimized ES sharing configuration is proposed to participate in demand response services [11]. The ES sharing framework must be built considering the complementarity of power generation and consumption behavior among different prosumers [12]. A real-time joint system of ES sharing and load management is developed to meet household needs and reduce energy costs [13]. Blockchain can be used to enhance trust in energy marketing within the community [14,15]. In [16,17], a two-stage credit-sharing model is proposed between the coordinator who manages the shared ES system (ESS) and the producers who purchase energy from the former. A shared hybrid ES framework, which consists of private ES units from energy suppliers and independent ES operators, is capable of providing ES services for the whole community [18].

Numerous energy prosumers (EPs) will be the major players in future energy markets, and game theory is an effective method to coordinate their interests [19]. At present, most of the game theory implementations for a shared ES system are based on the master-slave scheme [20,21,22], but they require participants to determine the identity of buyers/sellers in advance, which may limit the flexibility of participants. On the other hand, a multiple-agent cooperative game for a shared ES model is often difficult to achieve due to the conflict of interests among agents [23]. The multiple-timescale rolling optimization of the IES with a hybrid ES system is investigated, in which the uncertainty of price, renewable energies, and loads are considered [24]. An optimal scheduling model is proposed for an integrated energy microgrid system considering electric and thermal ES units [25,26]. A combined hybrid ESS containing electric, thermal, hydrogen, and natural gas storage devices can be scheduled by a hybrid ES operator (IHESO) to provide energy marketing services [27]. Algorithms like adaptive wavelet decomposition and fuzzy control theory are proposed for hybrid ES units [28]. In [29], the IES planning optimization model is proposed, considering the mixed storage differentiation characteristics.

For one single energy community, the effects of load scheduling or any other interaction with the power grid may not be evident. However, clustered communities can operate in coordination through sophisticated scheduling, thus greatly improving the potential of the whole “source–load–storage” system [30]. A double-layered energy optimization framework can coordinate the benefits for all participants and reduce operating costs for multiple communities [31]. Non-cooperative aggregate game theory is used in a double-layer energy management scheme in which day-ahead optimal scheduling and dynamic electricity prices are introduced for multiple-community systems [32,33]. For the demand side (or microgrids), an advanced stochastic optimization method based on deep reinforcement learning can provide the optimal redistribution of active power between subsystems by minimizing network losses [34]. Bilevel programming and reinforcement learning, for constructing and solving the internal local market of community microgrids, makes it possible to enable the interaction of the local control systems for microgrids with the community microgrid operator [35].

For these secondary energy markets, the normalization of energy interacting procedures and the fairness of energy marketing profits still need to be improved. Meanwhile, privacy protection for energy market participants also needs to be considered [36,37]. Therefore, it is essential to develop a new sharing mechanism to promote renewable utilization, enhance ES operation flexibility, and improve social welfare. In the meantime, how to evaluate the effects of the sharing business on the energy system is another key issue to be focused on. A suitable energy trading mechanism is needed for the sharing market, while protecting the privacy of individual users is also an important issue.

In this work, the shared ES-based energy scheduling and trading mechanism for multiple energy communities on the demand side are developed. First, in Section 2, a shared ES operation framework considering multi-new energy communities is proposed, and the operation strategies of each participant under this framework are analyzed. In Section 2.1, the ES model is introduced, and its physical form and mathematical model are analyzed. In Section 2.2 and Section 2.3, a shared ES model of multi-new energy communities based on a leader–follower game is proposed. Then, in Section 2.4, an ES-sharing cost allocation strategy based on the Owen value method is proposed. Finally, in Section 3, the advanced nature and fairness of the proposed framework and strategy are verified by simulation cases.

2. Optimal Collaboration of Shared ES in Multiple Energy Communities

The ES sharing mechanism is developed for the multiple energy communities with renewable DGs, in order to make full use of the distributed ES units, promote energy interactions at the demand side, improve renewable utilization, reduce energy costs, and maintain cost allocation fairly. The optimal collaboration shall be conducted at the community level and user level as well.

2.1. Energy Storage (ES) Model

For the whole EP community, if the total power generation is less than the total load demand, the operator will purchase energy from the main grid. If the total power generation is greater than the total load demand, the ES units will be given instructions to store charge. The peak of PV generation is mostly during the noon, while the peaks of the load demand often appear in the morning, noon, and evening, so the operation status of the ES battery may be different in each time period. For ES units, there are three operation modes: charging, discharging, and standby, respectively. The ES energy storage is indicated by the state of charge (SOC), which is a time variable related to the charging and discharging operation, charging and discharging efficiency of the system, and the charging and discharging status of the previous period, as shown in (1) and (2).

The charging status of the ES is as follows:

$$SO{C}_e(t)=SO{C}_e(t-1)+{\eta }_c{\displaystyle \frac{P_{c,t}^c\Delta t}{E_c}}$$

(1)

The discharging status of the ES is as follows:

$$SO{C}_e(t)=SO{C}_e(t-1)-{\displaystyle \frac{P_{c,t}^d\Delta t}{E_c{\eta }_d}}$$

(2)

where $SO{C}_e(t)$ and $SO{C}_e(t-1)$ are the ES charging state at time t and time (t − 1), respectively; $P_{c,t}^c$ and $P_{c,t}^d$ are the charging and discharging power of ES at time t, respectively; $\Delta t$ is the charging and discharging time; $E_c$ is the rated capacity of ES; ${\eta }_c$ and ${\eta }_d$, respectively, represent the charging efficiency and discharge efficiency of ES. There are upper and lower limit constraints on the ES charging status, as shown in the following formula. The status variable (0–1 variable) is introduced to represent the charging and discharging status of the ES. The status of charging or discharging is represented by 1, and the standby status is represented when both are 0, as shown in (3)–(6).

$$SO{C}_{e,\min }\le SO{C}_e(t)\le SO{C}_{e,\max }$$

(3)

$$P_{c,\min }^c{\tau }_c^c\le P_{c,t}^c\le P_{c,\max }^c{\tau }_c^c$$

(4)

$$P_{c,\min }^d{\tau }_c^d\le P_{c,t}^d\le P_{c,\max }^d{\tau }_c^d$$

(5)

$$0\le {\tau }_c^c+{\tau }_c^d\le 1$$

(6)

where $SO{C}_{e,\max }$ and $SO{C}_{e,\min }$, respectively, represent the upper and lower limits of the charging status, ${\tau }_c^c$ and ${\tau }_c^d$ are the charging and discharging status variables, $P_{c,\max }^c$ and $P_{c,\min }^c$ are the maximum and minimum amounts of the charging power, while $P_{c,\max }^d$ and $P_{c,\max }^d$ are the maximum and minimum amounts of the discharging power.

2.2. ES Sharing Mechanism for Clustered Energy Communities with Renewable DGs

The ES-sharing mechanism for clustered energy communities is shown in Figure 1, in which an aggregated ES dispatch center (AESDC) is responsible for collecting energy generation and consumption data, formulating energy-sharing plans, and facilitating energy interactions among communities and the main grid. Each community has a shared ES operator (SESO) in charge of aggregating loads, DG generators, and ES scheduling within the community to meet load demands, guarantee benefits, and promote renewable consumption.

Figure 1. The framework of the ES sharing mechanism for clustered energy communities.

The AESDC guarantees energy equilibrium for the community alliance in such a way that, if energy interactions within the lower layer do not meet their load demands, the SESO of each community and the AESDC determine the optimal real-time electricity price through the leader–follower game and then conduct energy trading. The AESDC purchases energy from the power grid, and real-time electricity prices can be optimized according to its own interests and issued to each SESO, which adjusts each community’s demand according to the real-time electricity prices. Then the process iterates until both sides reach agreements on the energy strategies, so as to formulate a day-before scheduling contract.

The specific procedure is shown in Figure 2, which includes the following: (1) the power grid issues the time-of-use (TOU) price to the AESDC; (2) the AESDC issues the energy purchase information to the power grid according to the TOU price and the load demand of each community and establishes the real-time energy price to the SESOs; (3) the SESO adjusts the energy consumption plan of the community according to the real-time electricity price and uploads it to the AESDC; (4) the AESDC updates the real-time electricity price according to the new energy demands and reissues it to the SESOs; (5) then the 2nd to 4th steps are iterated until the SESO and the AESDC have reached agreement on the energy marketing price and strategy. Then the updated energy purchase plan is uploaded to the grid for energy purchase.

Figure 2. Multiple-community energy interaction scheme based on leader–follower game.

After achieving the energy scheduling plan at the community level, it is necessary to share the energy consumption costs rationally within the energy community. This issue is solved through the following two levels:

(1)

Cost allocation among users within the community

At the lower layer, the user carries out energy transactions with each other within the community through the internal power line. Users need to sign an energy marketing and data sharing contract with the SESO and other users in the community, and they can pay their costs in time on the execution of the energy interacting and ES sharing plans.

(2)

Cost sharing among communities

The SESO is responsible for integrating energy consumption and generation data within the community to supervise the energy sharing situation and internal cost allocation and for communicating with the AESDC and SESOs from other communities to represent the overall interests of its own community for energy marketing and ES cost allocation at the upper layer.

2.3. Energy Scheduling Model Between Multiple Communities Based on Leader–Follower Game

(1)

Profit model of the SESO

Electric loads are classified into two categories: transferable and non-transferable. According to the electric and thermal characteristics of phase-change ES units, the heat load in the community is equivalent to that of the transferable loads for scheduling within the community. Then the initial loads of a single community are composed of the following:

$$p_{i,t}^0=p_{i,t}^{flex,0}+p_{i,t}^{fix,0}$$

(7)

where $p_{i,t}^0$ is the total initial load demand of community i at time slot t, $p_{i,t}^{flex,0}$ is the initial total demand of the translatable electric load of community i at time slot t, and $p_{i,t}^{fix,0}$ is the initial total demand of the non-translatable electric load of community i at time slot t.

On receiving the real-time electricity price from the AESDC, the SESO issues the electricity price to each user in the community, and the latter can adjust the electricity demand profile through load shifting under the guidance of the electricity price signal, to reduce energy costs. The load demands and related constraints of the users in each community after adjustment are as follows:

$$p_{i,t}^L=p_{i,t}^{flex,0}+p_{i,t}^{flex}+p_{i,t}^{fix,0}$$

(8)

$${\displaystyle \sum _{t\in T}{p}_{i,t}^{flex}}=0$$

(9)

$$p_{i,t}^{flex}\ge -p_{i,t}^{flex,0}$$

(10)

$$p_{i,t}^{L,\min }\le p_{i,t}^L\le p_{i,t}^{L,\max }$$

(11)

In (8), $p_{i,t}^L$ is the total load demand of community i after the internal load shift at time t and $p_{i,t}^{flex}$ is the load of community i shift at time t; (9) indicates the shiftable load constraint, and the operation period of the shiftable load can be adjusted, but the total load remains unchanged; (10) indicates that the total shifted load $p_{i,t}^{flex}$ should not exceed the maximum shift load threshold $-p_{i,t}^{flex,0}$ of the period; (11) indicates the load adjusting range in the community, which shall not exceed the upper and lower limits.

The non-negative power purchase and sale constraint of community i at time slot t are shown in (12) and (13), while (14) is the power balance constraint of the community alliance:

$$p_{i,sell}^t\ge 0$$

(12)

$$p_{i,buy}^t\ge 0$$

(13)

$${\displaystyle \sum _{i=1}^I{p}_{i,t}^L}+p_{sell}^t={\displaystyle \sum _{i=1}^I{p}_{i,t}^{PV}+p_{buy}^t}$$

(14)

where I is the total number of communities in the alliance, and $p_{i,t}^{PV}$ is the total photovoltaic (PV) power of community i at time slot t.

The willingness of users to use shared ES energy is mainly affected by the real-time electricity price. The more sensitive the users are to the electricity price change, the more willing they are to load shift. The model of the user’s response to the load transfer can be expressed by (15):

$$p_{i,t}^{j,flex}={\alpha }_i{\displaystyle \frac{r_{dc,t}-r_{b,t}}{r_{b,t}}}{p}_{i,t}^{j,flex,0}$$

(15)

where $p_{i,t}^{j,flex}$ is the shifting load power of user j in community i at time t, $p_{i,t}^{j,flex,0}$ is the initial amount of load shifting of user j in community i at time t, ${\alpha }_i$ is the sensitivity coefficient of community i to electricity price changes, $r_{dc,t}$ is the real-time electricity price issued by the AESDC, and $r_{b,t}$ is the TOU price issued by the power grid.

Based on the above analysis, the SESO’s income model in one single community is as follows:

$$I_{i,ES}=I_{i,E2U}+I_{i,E2C}-C_{i,loss}$$

(16)

$$I_{i,E2U}={\displaystyle \sum _{t=1}^T(p_{i,buy}^t{r}_{dc,t}}-p_{i,sell}^t{r}_{c,t})$$

(17)

$$I_{i,E2C}={\displaystyle \sum _{t=1}^T(p_{i,sfC}^t{r}_{sfC,t}}-p_{i,bfC}^t{r}_{bfC,t})$$

(18)

$$C_{i,loss}=\beta {(p_{i,t}^L-p_{i,t}^0)}^2$$

(19)

where $I_{i,ES}$ is the total revenue of the SESO in community i in one scheduling cycle, $I_{i,E2U}$ is the revenue of SESOs through shared ES charging and discharging, $I_{i,E2C}$ is the revenue of energy interacting with the AESDC, which is also the revenue of selling surplus energy to other communities, $C_{i,loss}$ is the cost due to load shifting in the community, and $\beta$ is the power utility loss coefficient. $r_{dc,t}$ and $r_{c,t}$ are the charging and discharging price of the SESO at time t, $p_{i,bfC}^t$ and $p_{i,sfC}^t$ are the energy purchased by the SESO from the AESDC and the power dispatching among other communities under AESDC’s permission, $r_{bfC,t}$ and $r_{sfC,t}$ are the unit power prices of the transactions with the AESDC.

The above income model needs to meet multiple constraints, including power balance constraints and state of charge (SOC) constraints. To encourage the SESOs to actively participate in the ES sharing business, the following price difference between charging and discharging is set to ensure their profits:

$$\begin{array}{l}{r}_{dc,t}-r_{c,t}\ge r_0\\ r_0\ge 0\end{array}$$

(20)

From the above analysis, it can be seen that SESOs provide ES resources and services for community users, so their optimization goals to obtain benefits are as follows:

$$\max I_{ES}=\max {\displaystyle \sum _{i=1}^I{I}_{i,ES}}$$

(21)

(2)

Profit model of the AESD

The AESDC is mainly responsible for the following two tasks: (1) it aggregates the load demands from lower-layer communities, formulates energy interaction plans among communities, and announces the energy purchase plan to the power grid when the community alliance has a power shortage; (2) it issues the real-time electricity price to the SESOs according to the load demand and TOU price. Then the total energy cost C of each community can be obtained at the AESDC, as shown in (16), and the profit of the AESDC of community i can be expressed as follows in (23):

$$C={\displaystyle \sum _{t=1}^T{\displaystyle \sum _{i=1}^I[(r_{b,t}{p}_{i,bfg}^t-r_{sfC,t}{p}_{i,sfc}^t)+C_{i,loss}]}}$$

(22)

$$I_{i,C}={\displaystyle \sum _{t=1}^T(r_{bfC,t}{p}_{i,bfC}^t-r_{b,t}{p}_{i,bfg}^t)}$$

(23)

where $p_{i,bfg}^t$ is the total power purchased from the grid.

To prevent the AESDC from maliciously raising electricity prices, the pricing is constrained by setting the upper limit of average price, as shown in (24):

$${\displaystyle \sum _{t=1}^T\frac{r_{bfC,t}}{T}}\le r_{bfC,av}$$

(24)

where $r_{bfC,av}$ is the upper limit of the average electricity price. Since SESOs have no right to change pricing, the users purchase energy from their SESO at the real-time electricity price, that is, $r_{bfC,t}=r_{dc,t}$ and $r_{sfC,t}=r_{c,t}$.

As an intermediary between the power grid and multiple communities, the AESDC obtains profits from price differences, so its optimization goal is to maximize the return, as shown in (25):

$$\max I_C=\max {\displaystyle \sum _{i=1}^I{I}_{i,C}}$$

(25)

(3)

Model of the leader–follower game between the AESDC and the SESOs

The AESDC and the SESOs have independent decision-making schemes, in which the AESDC maximizes its own benefits, mainly from the differences between the TOU price of the grid and the real-time price of the alliance. The SESOs optimize load profiles in each community based on the real-time electricity price and carry out energy exchange with other communities. Therefore, the income of the AESDC is also affected by each SESO’s decision-making. Then a leader–follower game is played between two sides, which can be defined as follows:

$$G_S=\{N_S;\{r_{dc,t},p_{i,bfC}^t,p_{i,stC}^t,p_{i,bfg}^t;p_{i,buy}^t,p_{i,sell}^t,p_{i,t}^L,p_{i,t}^{flex}\};\{I_{ES},I_C\left\}\right\}$$

(26)

The elements of the game are described as follows:

(1)

Player set: including the AESDC and multiple SESOs, in which the AESDC is the leader and the SESOs are followers.

(2)

Action set: also known as strategy set. The upper-layer strategy of the AESDC includes the unit power price (real-time price) that is traded with the AESDC and the energy that interacts with the SESOs. The strategy of each SESO at the lower layer includes the load demands of the community and the amount of load to be shifted.

(3)

Utility function: including the target income function of the SESOs and the target income function of the AESDC.

(4)

Solution of the double-layered optimization model.

The presented leader–follower game model is a double-layered optimization problem, which cannot be solved directly. Therefore, it is necessary to convert the lower-layer model into the upper layer’s constraints by using KKT optimal conditions, so the game model is transformed into a single-layer optimization model. Then the large M method is used to relax the nonlinear model and transform the double-layered model into a mixed integer linear programming (MILP) model for solving.

The linearization of complementary relaxation conditions in KKT conditions is as follows: let $\mu$ and $\lambda$ be the dual variables of inequality and equality constraints of the lower-layer optimization, and complementary constraints exist in the lower-layer optimization problem, as shown in (27):

$$0\le \mu \perp h(x)\ge 0$$

(27)

where $h(x)\ge 0$ is an inequality constraint for the lower-layer optimization, $x\perp y$ means that at most one of the scalars that is strictly not less than zero can exist.

Then, the large M method is used to transform the above equation into linear constraints. The purpose of the specific process is to introduce Boolean variables $\kappa$ to transform the above equation into linear inequalities, as shown in (28) and (29):

$$0\le \mu \le M\kappa$$

(28)

$$0\le h(x)\le M(1-\kappa )$$

(29)

where M is a sufficiently large positive number.

Following the above steps, the KKT condition of the lower layer is taken as the constraint condition of the upper layer, then the double-layered model is transformed into a single-layer model and can be solved by particle swarm optimization (PSO) or other heuristic algorithms.

To enhance the global optimal convergence rate of structural reliability analysis, an improved particle swarm optimization algorithm is presented. The particle swarm optimization-based harmony search algorithm (PSO-HS) is developed to increase the convergence speed and enhance global converging ability [38]. The algorithm uses dynamic adaptive terms to perform a local adjustment process and has good robustness and efficiency in solving high-dimensional problems.

2.4. Cost Allocation Strategy and Model of Multiple Participants

Profit distribution fairness is the key issue for the multiple-community alliance with shared ESs, in which the cost allocation within the community must be fair and reasonable. Existing cost allocation methods include the nucleolar method, the Shapley value method, the Nash solution, etc. These methods directly apportion the cost to single energy users, but it is hard for participants from different communities to share fairly, which will lead to unreasonable cost allocation and affect the willingness of each user to participate in the ES sharing scheme.

This section will consider the natural alliance structure of the community and consider the SESO as the community agent to carry out cost allocations with other communities at the upper layer. Then it will focus on each community and carry out a second cost allocation according to the results obtained at the upper layer, so as to achieve a reasonable benefit distribution. The Owen value method is an extension of the Shapley value method consisting of two aspects: first, the cost allocation among priority alliances; second, the further allocation of costs payable by members within the alliance according to the upper-layer allocation results [39]. Therefore, the Owen value method is essentially a successive application of the Shapley value method on both layers, suitable for this scenario in which users from different communities cannot directly cooperate with each other. It can achieve fair and reasonable cost allocations, with a fast calculation speed and good protection for user privacy.

(1)

Cost sharing among communities

Since the total number of communities is small, the conventional Shapley value method is used at the upper layer. The basic rule is to allocate the total cost after the coordinated operation of multiple communities according to the expected marginal cost brought by the SESOs of each community. Then the SESO of community i should share the cost as follows:

$${\phi }_i={\displaystyle \sum _{S\in S_i}\omega (\left|S\right|)[c(S)-c(S/i)]}$$

(30)

$$\omega (\left|S\right|)={\displaystyle \frac{(n-\left|S\right|)!(\left|S\right|-1)!}{n!}}$$

(31)

where ${\phi }_i$ is the cost to be paid by the SESO in community i, $S_i$ is all alliance subsets containing community i, $\left|S\right|$ is the number of subset S, $\omega (\left|S\right|)$ is the probability of S appearing in all possible alliances, $c(S)-c(S/i)$ is the marginal cost contribution of community i to alliance S, c is the characteristic function, which is the total energy cost function in this paper, S/i is the alliance without community i, and n is the total number of SESOs participating in the cooperation.

At the upper layer, communities should maintain “group rationality”, which means the cost after cooperation should not be greater than the cost before cooperation, as expressed in (32):

$$\forall {\phi }_i\le {\phi }_{i0}$$

(32)

where ${\phi }_{i0}$ is the cost for community i before collaboration.

(2)

Cost sharing between community users at the lower layers

When the total cost of energy consumption has been distributed to each community at the upper layer, the cost needs to be distributed again within the community at the lower layer. To eliminate the complexity of the calculation due to the increase in the number of users, this paper uses the bilateral Shapley value method to replace the traditional Shapley value method for cost allocation. The bilateral Shapley value method divides all community users into two subjects: $\left\{j\right\}$ and $\left\{M/j\right\}$. Then it determines the cost of user j. The complexity of the calculation is greatly reduced, though there is a little sacrifice in accuracy. The cost shared by user j is as follows:

$${\phi }_j={\displaystyle \frac{1}{2}}(C_M-C_{M-j}+C_{\left\{j\right\}})$$

(33)

where ${\phi }_j$ is the cost of user j, M is the scenario where all community users participate in cooperation, $C_M-C_{M-j}$ is the marginal cost contribution of user j to M, and $C_{\left\{j\right\}}$ is the cost of j not participating in cooperation.

Through the above allocation, the total cost allocation rate of user j for multiple-community cooperation is as follows:

$$I_j={\displaystyle \frac{{\phi }_j}{C_M}}$$

(34)

where I_j is the apportionment rate of the total cost.

Similar to the upper layer, each user also needs to meet the “individual rationality”, which means the cost after cooperation should not be greater than the cost before cooperation, as shown in (29):

$$\forall {\phi }_j\le {\phi }_{j0}$$

(35)

where ${\phi }_{j0}$ is the cost of user j before cooperation.

According to the above analysis, the specific cost of user j in community i is derived as follows:

$${\phi }_{ij}=I_j{\phi }_i$$

(36)

where ${\phi }_{ij}$ is the specific cost shared for user j in community i.

(3)

Cost sharing process

From the above analysis, it can be seen that the cost allocation based on the Owen value method includes cost allocation among communities at the upper layer and the cost allocation among the community users at the lower layer. The specific process is shown in Figure 3.

Figure 3. Double-layered cost sharing flowchart.

3. Case Study

Three energy communities are selected for analysis, and the DG (such as PV) resources in each community are sufficient. We assume that the users are typical commercial users of domestic EPs, with the DG units rated at around 30 kw. Each community had nine users equipped with PV devices, and the load data of each user in the three communities are shown in Figure 4.

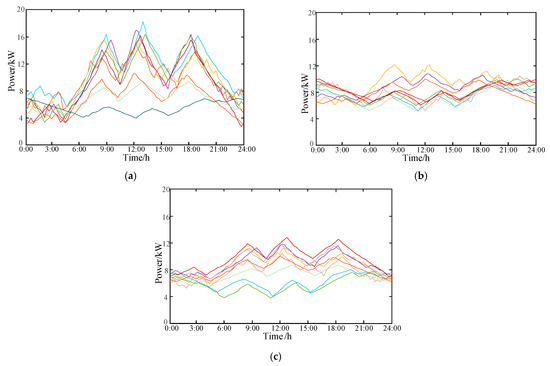
Figure 4. Load profiles of Community 1, Community 2, and Community 3 (each has 9 users). (a) Community 1. (b) Community 2. (c) Community 3.

A time of 24 h is taken as a scheduling cycle, with each step length being 1 h. The PV output is predicted at each sampling point based on historical data for the current period.

$$P_n\left(s+r\left|s\right.\right)=P_n^0\left(s\right)+{\displaystyle \sum _{t=1}^r\Delta {\upsilon }_n\left(s+t\left|s\right.\right)}$$

(37)

where $P_n\left(s+r\left|s\right.\right)$ is the uncertain prediction of user n for the s + r period in period s; $P_n^0\left(s\right)$ is the initial value of the uncertainty in period s; $\Delta {\upsilon }_n\left(s+t\left|s\right.\right)$ is the prediction increment of uncertainty in the period of s + t; r is the length of the prediction domain. In the intra-day stage, the influence of the prediction error is reduced by ES scheduling, so as to improve users’ trading income and relieve the operating pressure of the power grid.

Three typical days are selected, namely, a typical summer day (6 August), a typical transitional season day (2 October), and a typical winter day (31 December). Next, the transitional season typical day is taken as an example for discussion. The total predicted PV output of each community and the total initial load demand are shown in Figure 5, and the PV output of each user in a single community is the same. The ratio of shiftable load to non-shiftable load in each community is 0.5 to 0.2, so each community has the potential to achieve economic optimization through a load profile adjustment, and the capacity of the ES unit in each community is about 500 kWh. The upper limit of allowable trading power between the AESDC and the power grid at each step is 500 kW, the coefficient of power consumption loss $\beta$ is 0.2, and the lower and upper limits of real-time electricity price of the AESDC are $r_{bfC,\min }=0.8r_{stG}$ and $r_{bfC,\max }=1.2r_{bfG}$.

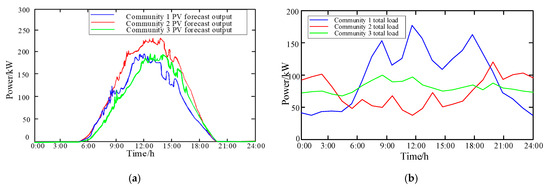
Figure 5. Forecasted PV output and total load profiles of each community. (a) Forecasted PV output. (b) Total load.

On this basis, three scenarios are studied to verify the proposed strategy:

Scenario 1: Community users do not use shared ES equipment, no SESOs involved, and only configured PV equipment is used.

Scenario 2: There are no cooperation and energy interactions among communities, the SESOs within each community directly deal with the power grid for day-ahead scheduling, and cost sharing is only among community users at the lower layer.

Scenario 3: Communities cooperate as an alliance for ES sharing, using the leader–follower game for day-ahead scheduling and the Owen value method for the double-layer cost allocation strategy. Cost sharing is conducted on both the upper and the lower layers.

(1)

Revenue analysis of the SESOS

Taking Community 1 as an example, the load shift in scenario 2 and scenario 3 is shown in Figure 6. The total load from 00–14:00 is larger than the original load demand, while the total load from 9:00–10:00 and 16:00–20:00 is smaller, which is due to load shifting to reduce energy consumption costs. We can also find that, to reduce the cost of electricity, a small amount of load shifting will be carried out at night, but the maximum amount of shift will be carried out at around 9:00–14:00 and 16:00–20:00, because they are the peak load time periods and the electricity price is also high. In order to reduce the energy consumption cost, this part of the load will be shifted as the first choice.

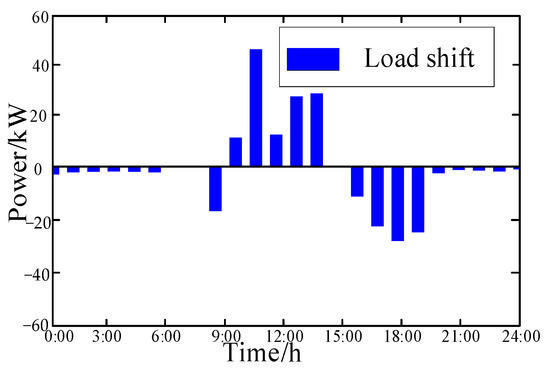
Figure 6. Load shift in Community 1.

The net load profile of each community obtained in scenario 1 is shown in Figure 7a, and the net load of each community in scenario 2 is shown in Figure 7b. With the presented optimal scheduling strategy, the net load profile of each community in scenario 3 is shown in Figure 7c. The positive value in the figure indicates that there is an overall power shortage in the community, and the negative value indicates that there is a surplus of power generation in the community.

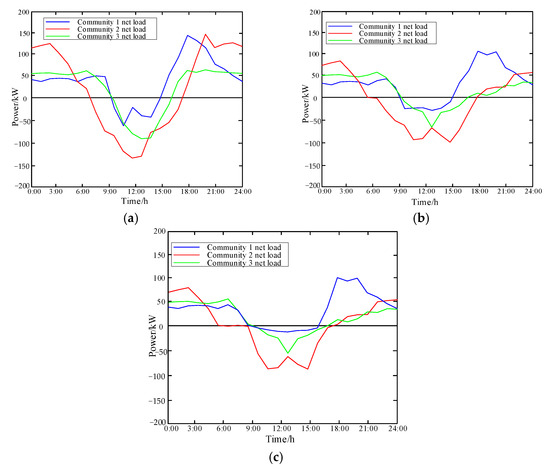
Figure 7. The net load of each community in each scenario. (a) Scenario 1. (b) Scenario 2. (c) Scenario 3.

As seen from Figure 7a, when there are no Ess equipped, the PV output in each community only supplies its own load, and there is no SESO to guide users to respond to the demand. When PV generation exceeds the load demand, a large amount of it has to be discarded. As seen from Figure 7b, with the shared ES units, SESOs can guide users to actively participate in demand response, and users in various communities carry out load shifting to promote renewable consumption and obtain extra benefits. However, there are no energy Interactions among communities, and purchasing energy from the power grid is required, which increases total costs. In Figure 7c, it can be concluded that, under the ES sharing mechanism established in this paper, there are energy interactions among communities. Because the electricity price for inter-community interaction is lower than the TOU price of the grid, the energy consumption costs of each community are further reduced.

Since there is no SESO involved in scenario 1, its income is not analyzed. In other scenarios, the SESO income of the three communities is shown in Table 1. In scenario 2, the SESO earns profits mainly by adequate planning of its charging and discharging operation according to the energy consumption habits of each user and the TOU price of the grid. In scenario 3, with the scheduling of the AESDC at the upper layer, there exists a mutual benefit among the communities. When there is an energy surplus in one community, it can earn profits by selling it to SESOs in other communities. Through comparison, it can be seen that, under the trading mechanism based on the leader–follower game, the revenue of the SESO in Community 1 has increased by 26.69%, and that of Community 3’s SESO has increased by 13.69%. However, the income of the SESO in Community 2 has decreased, because the daytime load of Community 2 is low during the PV peak period. After participating in the community alliance, the surplus power needs to be preferentially sold to communities with a power shortage at a lower price than the PV on-grid price, which reduces the SESO’s income, but this result is in line with the group rationality of cost allocation. This will be explained in detail later.

Table 1. Benefit analysis of the SESOs in each community.

	Community 1 SESO Benefits (USD)	Community 2 SESO Benefits (USD)	Community 3 SESO Benefits (USD)
Scenario 2	9.21	8.01	8.35
Scenario 3	11.95	7.37	9.50
Revenue increment	26.69%	−8.02%	13.69%

(2)

Profit analysis of the AESDC at the upper layers

In scenario 3, the AESDC schedules the charging and discharging of the shared ES units in each community, issues the real-time electricity price of the alliance, and makes the power transaction plan with the grid at the same time. Taking the charge and discharge scheduling decision of the SESO in Community 1 as an example, the amount of power purchased and sold for each SESO is shown in Figure 8. The SESO stores energy between 10:00 and 15:00 when the PV generation is greater than load demands, and the SESO trades with each PV owner for energy storage. From 24:00 to 7:00, the SESO also instructs the ESs for charging, and the trading object at this time is the AESDC, because of the low electricity price during that period. Then the SESO instructs the ES to discharge when the PV output is low and the electricity price is at its peak (8:00–10:00, 17:00–21:00).

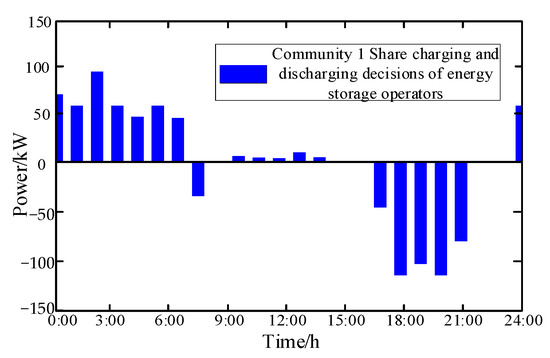
Figure 8. Share ES charging and discharging instructions of the SESO in Community 1.

The real-time price of purchasing and selling electricity formulated by the AESDC is shown in Figure 9. The issued purchasing and selling price must be between the upper and lower limits of the benchmark electricity price, and the SESOs can reduce their energy consumption costs through energy transactions with the AESDC. The income of the AESDC in the whole dispatch cycle is CNY 98.46.

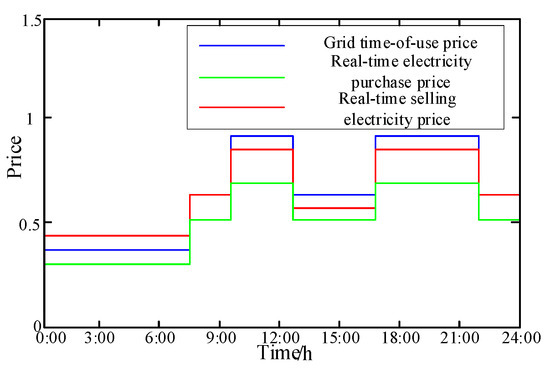
Figure 9. AESDC purchasing and selling electricity price decision.

At peak load time, the TOU price of the grid is also at the peak. The AESDC reduces its own real-time electricity price to encourage the communities to purchase electricity. However, during the low electricity price period, the AESDC’s electricity price is higher than the TOU price in order to ensure its benefits. Since user loads are also in the low period at this time, the willingness of all communities to participate in the sharing mechanism will not be weakened. According to Figure 8, the real-time electricity price of the SESO is higher when discharging, while the real-time electricity price of the charging period is lower. It is also a reasonable measure from the AESDC’s perspective, because it can issue energy prices independently, and the pricing decision is more inclined to for its own profits. The AESDC is in the leading position in the leader–follower game, and the SESOs as followers will bear a certain loss of market efficiency when participating in the leader–follower game. However, the pricing of the AESDC also takes into account the influence of various SESOs in such a way that at noon when the PV power is abundant, the communities have more surplus power, and the demand for electricity purchased from the AESDC is greatly reduced, so the real-time electricity price is relatively low at this time, reflecting the original intention of the AESDC to guide the community SESOs for energy purchases.

(3)

Cost sharing results and analysis

As there are multiple communities and users in this framework, the traditional Shapley value method will fall into a dimensional disaster and cannot achieve feasible solutions. Then the cost was allocated based on Owen’s value method. Table 2 shows the cost sharing results among communities.

Table 2. Results of cost sharing among communities.

	Community 1 Shared Cost (USD)	Community 2 Shared Cost (USD)	Community 3 Shared Cost (USD)
Scenario 1	102.39	77.01	76.08
Scenario 2	90.05	34.06	42.49
Scenario 3	79.00	21.47	32.89

As seen from Table 2, according to the results of scenario 1 and scenario 2, the cost of each community in the shared ES mode is lower than that without the shared ES mechanism, due to ES’s flexibility in promoting renewable utilization and maintaining a power balance. According to the results of scenario 2 and scenario 3, the cost allocated to each community under the shared ES framework is better than that without cooperation. The cost allocation among communities is rational and is conducive to the stable operation of the ES sharing mechanism.

Taking Community 1 as an example and combining it with the results of scenario 2 and scenario 3 in Table 2, the cost redistribution scheme of community users at the lower layer is further analyzed. Table 3 shows the cost allocation results of the community users.

Table 3. Cost sharing results for users within Community 1.

Cost (USD)	Scenario 2	Scenario 3	Cost Reduction Rate
User 1	11.53	10.32	10.53%
User 2	11.73	10.53	10.20%
User 3	11.37	10.44	8.20%
User 4	8.99	7.88	12.40%
User 5	12.13	10.92	9.94%
User 6	12.41	11.09	10.63%
User 7	8.47	7.37	12.99%
User 8	1.50	−0.26	117.67%
User 9	11.87	10.44	12.04%
Total cost	90.05	79.00	12.28%

As seen from Table 3, although the PV output of each user is similar, the cost reduction degree of each user is different, which is because the load profile of each user is different, so the contribution to the community is different. Therefore, the cost allocation among users satisfies individual rationality and is also conducive to the practical application of the ES sharing mechanism.

(4)

Cost sharing analysis under scenarios of different typical days

An analysis is carried out under scenarios of typical days in the transition season, in summer and in winter. Table 4 and Table 5 show the cost sharing results among communities under the scenarios of typical days in summer and winter, respectively.

Table 4. Cost sharing results among communities (typical day in summer).

	Community 1 Shared Cost (USD)	Community 2 Shared Cost (USD)	Community 3 Shared Cost (USD)
Scenario 1	118.46	89.10	88.02
Scenario 2	100.14	39.41	49.16
Scenario 3	90.22	24.84	38.05

Table 5. Cost sharing results among communities (typical day in winter).

	Community 1 Shared Cost (USD)	Community 2 Shared Cost (USD)	Community 3 Shared Cost (USD)
Scenario 1	150.72	113.36	111.99
Scenario 2	132.55	50.14	62.55
Scenario 3	100.73	31.60	48.41

Under the scenarios of typical days in summer and winter, taking Community 1 as an example, the cost redistribution scheme of community users in the lower layer is further analyzed. Table 6 and Table 7 show the cost allocation results for users in the community during summer and winter.

Table 6. Cost sharing results for users within Community 1 (a typical day in summer).

Cost (USD)	Scenario 2	Scenario 3	Cost Reduction Rate
User 1	12.82	11.79	8.08%
User 2	13.04	12.03	7.81%
User 3	12.64	11.92	5.70%
User 4	10.00	9.00	9.98%
User 5	13.49	12.47	7.55%
User 6	13.80	12.66	8.23%
User 7	9.42	8.42	10.64%
User 8	1.67	−0.30	117.80%
User 9	13.20	11.92	9.67%
Total cost	100.14	90.22	9.90%

Table 7. Cost sharing results for users within Community 1 (a typical day in winter).

Cost (USD)	Scenario 2	Scenario 3	Cost Reduction Rate
User 1	16.97	13.16	22.45%
User 2	17.27	13.43	22.24%
User 3	16.74	13.31	20.49%
User 4	13.23	10.05	24.04%
User 5	17.86	13.92	22.06%
User 6	18.27	14.14	22.61%
User 7	12.47	9.40	24.62%
User 8	2.21	−0.33	114.93%
User 9	17.47	13.31	23.81%
Total cost	132.55	100.73	24.01%

Table 6 and Table 7 show that, under scenarios of typical days in winter and summer, the cost of each community with the shared ES mechanism is apparently lower than the cost of each community without ES sharing, and the cost allocated to each community is more reasonable and fairer than the cost without cooperating. The cost allocation among users is reasonable, and the cost for each user has been reduced. Therefore, it is concluded that the presented cost allocation method is practical in different scenarios.

(5)

Cost sharing analysis under different heuristic algorithms

Different heuristic algorithms are used to solve this optimization problem. Table 8 shows the cost sharing results of Community 1 under different algorithms.

Table 8. The cost sharing results of Community 1 under different algorithms.

Community 1 Shared Cost (USD)	GA	PSO	PSO-HS
Scenario 1	110.66	110.38	102.39
Scenario 2	97.86	97.21	90.05
Scenario 3	85.74	85.47	79.00

From Table 8, the presented PSO-HS algorithm results in the lowest costs in all scenarios. Moreover, the PSO-HS algorithm shows better performances in global convergence and robustness.

4. Conclusions

To enhance the operational stability of the power system with high renewable penetrations and further explore the economic benefits on the demand side, this paper proposes an ES-sharing mechanism with energy scheduling, trading, and cost allocation for multiple energy communities of EPs. The AESDC serves as the energy service provider of the multiple-community alliance and the SESOs serve as agents for communities of EPs who are responsible for the ES sharing mechanism. A double-layer optimal energy scheduling model based on leader–follower game is established, which is transformed into a single-layer model by using the KKT condition and then resolved by using the large M method and the PSO-HS algorithm. On this basis, the cost allocation model of alliance and community based on the Owen value method is established to solve the fairness of the benefit distribution and the privacy of users. Through case studies, the economy of the proposed ES sharing mechanism as well as the fairness and feasibility of the cost allocation strategy are verified. The features of the adaptation and robustness of the proposed strategy are verified by comparing the results under multiple scenarios of different seasons. The solution results of multiple algorithms show that the PSO-HS algorithm adopted in this paper is satisfactory in both computing speed and converging features.

In future works, the following will be focused on: (1) For the leader–follower game, the bidding game among various communities will be further considered. (2) For energy scheduling case studies in this paper, only the renewable output on sunny days is considered; in future works, fluctuations of the renewable DGs due to weather changes will be considered, which will bring more challenges to the scheduling strategies but will be more useful for justifying the functionality of the ES sharing mechanism.