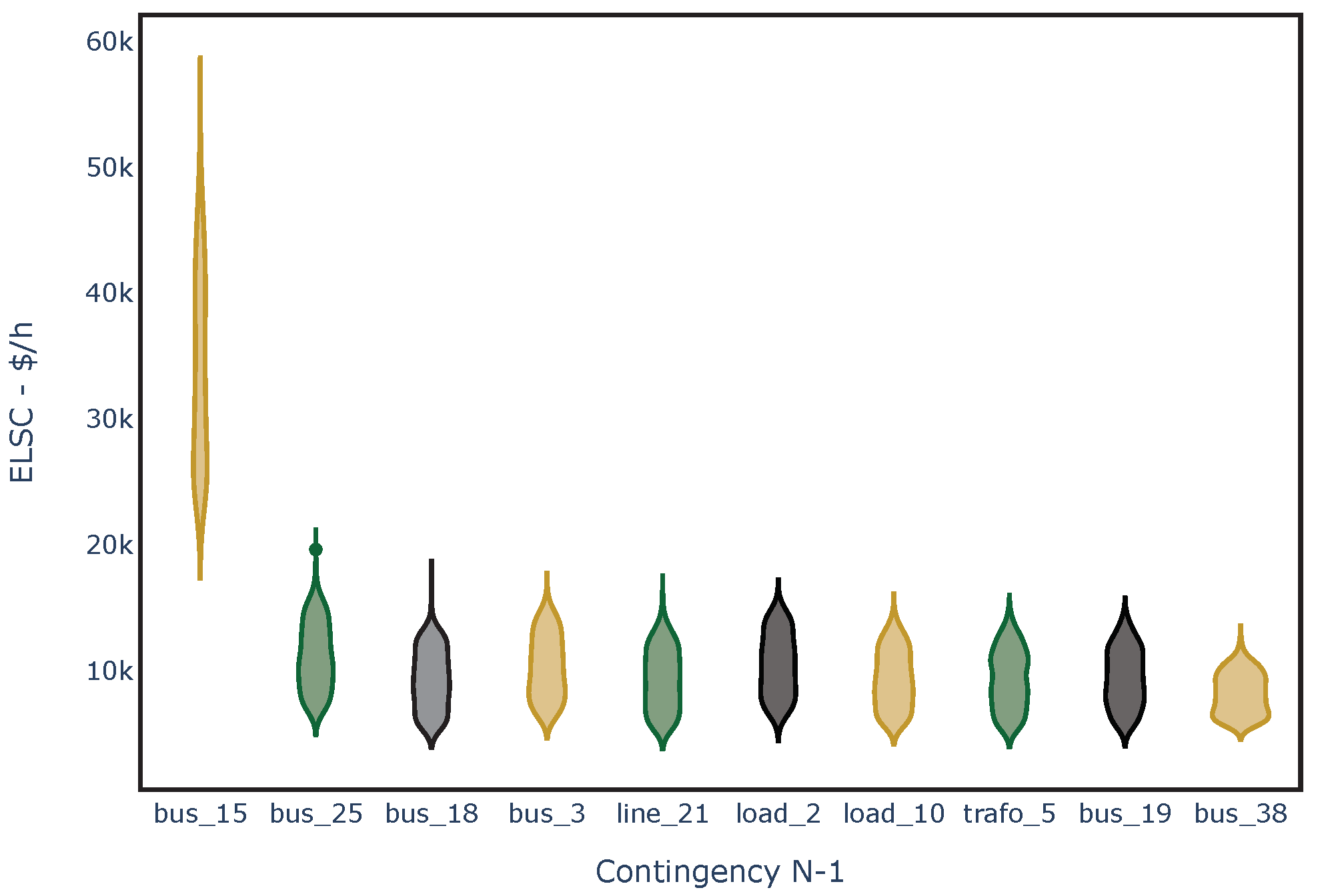N − k Static Security Assessment for Power Transmission System Planning Using Machine Learning

Abstract

This paper presents a methodology for static security assessment of transmission network planning using machine learning (ML). The objective is to accelerate the probabilistic risk assessment of the Hydro-Quebec (HQ) TransÉnergie transmission grid. The model takes the expected power supply and the status of the elements in a $N-k$ contingency scenario as inputs. The output is the reliability metric Expecting Load Shedding Cost ($ELSC$). To train and test the regression model, stochastic data are performed, resulting in a set of $N-k$ and $k=\left\{1,2,3\right\}$ contingency scenarios used as inputs. Subsequently, the output is computed for each scenario by performing load shedding using an optimal power flow algorithm, with the objective function of minimizing $ELSC$. Experimental results on the well-known IEEE-39 bus test system and PEGASE-1354 system demonstrate the potential of the proposed methodology in generalizing $ELSC$ during an $N-k$ contingency. For up to $k=3$ the coefficient of determination $\left(R^2\right)$ obtained was close to 98% for both case studies, achieving a speed-up of over four orders of magnitude with the use of a Multilayer Perceptron ($MLP$). This approach and its results have not been addressed in the literature, making this methodology a contribution to the state of the art.

1. Introduction

Modern Power Systems (PSs) seek to supply energy with certain economic, sustainable, reliable and secure levels. According to Singh et al. [1], security studies usually focus on generation, transmission, protection, distribution, interconnection and, industrial and commercial systems. Power transmission systems are widely regarded as the backbone of PS and their security assessment determines the system’s capacity to supply uninterrupted power from generation to the demand in a secure manner [2]. Nevertheless, performing power transmission planning of large networks to guarantee reliability is a challenging task if multiple scenarios and a high penetration of renewable power sources are considered, primarily due to the size and complexity of modern grids.

Lumbreras et al. [3] proposed a methodology to simplify large networks for expansion planning considering a set of scenarios for minimizing investments, operation costs and penalties for non-served power. The cost and penalties are computed using DC power flow. The control actions such as load shedding or generator response, as well as reactive power and voltages issues, are not considered. The definition of critical branches is labeled in a deterministic way.

Ideally, security assessment analysis should be performed under $N-k$ criterion, where N is a set of equipment and k the number of disconnected elements simultaneously during a contingency. If corrective actions are required the well-known Security Constrain Optimal Power Flow (SCOPF) algorithm is usually employed [4] as extension of the Optimal Power Flow algorithm (OPF). SCOPF takes into account operational constraints for a set of $N-k$ contingencies while minimizing impact of the contingency. However, this problem is a nonlinear, non-convex, mixed variable and large scale, being their solution a changeling task and time consuming. Therefore, different approximations, methods and assumptions such as $k=1$, DC power flows, contingency screening [5] and high-performance computing [6], among others, are used to solve SCOPF in a reasonable time. More advanced methods suggest quantum computation to deal with the computational complexity of the $N-k$ contingency analysis problem [7]. However, with the existing quantum computation technology, their application is not possible.

Nowadays, PSs are operating in more stressed conditions, because both the demand and the generation are increasing while the capacity of the transmission system is reaching their limits. This condition, along with the penetration of renewable generation, increases the uncertainty in the planning being necessary to refine the security assessment. Probabilistic risk assessment for $N-k$ [8,9] has emerged as an option to face this challenge; however, this method is time demand. Recently, the use of Machine Learning (ML) to generalize security assessment seeking increased computational speed [10] has gained popularity.

Table 1 presents a literature review of recent proposed methods for reliability assessment, where ENS, AC, AI, PF, and Plan. are energy not supplied, alternating current power flow, artificial intelligence, power flow, and planning application, respectively. In the table, the following characteristics of each method are identified: numerical analysis model, objective function, consideration of $N-k$ contingencies and if was developed for system planning. The main differences between models used for operation or operation planning and system planning involves the consideration of unit comment, generation costs, and generator ramp for the first one, while for system planning, the impact on the demand as last remedial action is commonly the main issue to evaluate.

Table 1. Methodologies for security constraint assessment proposed in the literature.

Author	Model	Objective	AC	$\mathit{N}-\mathit{k}$	Plan.	Year
Sundar et al. [8]	SCOPF	Inve, Ope and VoLL		✓	✓	2018
Karangelos et al. [11]	SCOPF	Socio-econ		✓		2020
Majidi-Qadikolai and Baldick [12]	SCOPF	Socio-econ			✓	2016
Karangelos and Whenkel [13]	SCOPF	Socio-econ		✓		2016
Heylen et al. [14]	SCOPF	Socio-econ		✓		2016
Moreira et al. [15]	SCOPF	Socio-econ		✓	✓	2015
Karangelos and Wehenkel [16]	SCOPF	Socio-econ	✓			2019
Perkin et al. [17]	SCOPF	ENS	✓			2019
Delavari et al. [18]	SCOPF	ENS		✓	✓	2021
Duchesne et al. [19]	AI-SCOPF	Socio-econ				2017
Duchesne et al. [20]	AI-SCOPF	Socio-econ				2017
Donnot et al. [21]	AI-PF	Ranking	✓	✓	✓	2018

In recent years, Hydro-Quebec (HQ) has been developing a global methodology for Risk-Informed decision making [22]. That methodology integrates a power grid reliability simulator to estimate the Value of Lost Load ($VoLL$) when a $N-k$ contingency occurs. However, conducting this assessment for the HQ’s entire transmission network is a time-demanding task, because the AC-SCOPF algorithm is required to minimize $VoLL$ for a set of $N-k$ contingency scenarios. Implementing the simulator with the entire set of equipment poses a bottleneck. According to Table 1, a comparable model to address this challenge is currently unavailable in the existing literature. Moreover, there is a need for accelerating the method for large power networks. To meet this challenge, we present in this paper a reliability security $N-k$ assessment using ML, focusing on the static operation [2] of PS. Our objective is to accelerate the evaluation of contingencies to support decision making processes within an asset management framework. Our approach incorporates constraints such as the voltage limits of buses, generator capabilities and the thermal limits of branches. The objective function is the minimization of $VoLL$ when disturbances occur under different operating scenarios.

The main contributions addressed in this paper are as follows:

• We propose a ML methodology for generalizing $AC-SCOPF$ for different time scopes and scenarios, allowing to reduce the computational cost;
• We describe the procedure to fit the ML model executing $LS-OPF$ for multiple $N-k$ contingency scenarios;
• We present a real-size case study base on European Union transmission system PEGASE-1354 case to evaluate the performance in the generalization of $ELSC$ for large networks. Our approach achieves high accuracy compared to traditional AC-OPF formulations.

This paper is structured as follows: a comprehensive review of ML for PF, OPF, SCOPF is presented in Section 2. Our proposed methodology for generalization of LS-OPF under $N-k$ scenarios using ML is addressed in Section 3. Section 4 presents the case studies where the application of the methodology is performed. Lastly, this paper is concluded in Section 5.

2. Related Work

ML for security assessment of power systems is a well-known application given its versatility to generalize complex phenomena [23]. For static security assessment, ML applications are related to reduce computational burden during contingency analysis, allowing to perform probabilistic risk assessment. Duchesne et al. [24] presents a complete review for ML for PS reliability management, addressing applications in the field of PF, OPF and SC-OPF.

2.1. Power Flow—PF

Donnot et al. [25] present a method to rank N-1 and N-2 contingencies using ANN. The ranking is performed using a probabilistic risk assessment that considers thermal limits of OHLs. Oliveira et al. [26] propose to assess power system operation security under multiple contingencies using decision tree (DT). The security criterion involves the computation of bus voltage through load flow simulation.

2.2. Optimal Power Flow—OPF

Zhang et al. [27] propose solving DCOPF using a convex neuronal network to guarantee its generalization. Recent efforts have focused on extending the use of ML to ACOPF problems considering the majority of constraints. Pan et al. [28] used ANN for solving ACOPF, considering the feasibility and optimality during generation of solutions. The objective function is to minimize the total cost of generation. The inputs are the active and reactive power of each load. The outputs are the voltage magnitude of the slack bus, the active power by generator, and the voltage magnitude of the PV-V buses. The feasibility in the solutions obtained was greater than 99%, with a speed-up of 123×. Jia et al. [29] propose a ML approach using Convolutional Neural Networks (CNN), where the load and network topology are labeled as inputs, and the state variables bus voltage magnitude and angle are labeled as outputs for training the ML model. A 350× speed-up with a prediction accuracy $R^2$ close to 100% was reached compared with Matpower for a 2000 bus system. At a distribution level, Liu and Wu [30] proposed a Reinforced Learning algorithm to minimize active power loss through voltage control, considering both voltage and reactive power constraints. A similar optimization problem is addressed by Liao et al. [31] using capsule networks. While these proposed methods exhibit high performance, their formulation is limited to distribution networks.

2.3. Security Constrained Optimal Power Flow—SCOPF

The use of ML for OPF has extended their variant SCOPF. Pan et al. [32] develop an approach for solving SC-DCOPF problems using DNN. The objective function is to minimize the generation cost. The inputs and outputs of the DNN are the power load and power generation, respectively. A 328× speed-up with a prediction error less than 0.1% was reached compared with the Gurobi solver for a 300 bus system. Zhou et al. [33] extend the OPF problem formulation to Load Shedding SCOPF (LS-SCOPF) using an AC model for emergency operations. The objective function consists only of cost of load reduction. The inputs and outputs were the PF data and load shedding, respectively. For the IEEE 14-bus systems, the errors obtained were between 8% and 98% for a single line outage.

Table 2 compares recent studies of application of ML for security assessment with the method addressed in this work. The column Bus is the system with maximum number of bus where the model was tested, limits describe the security criteria, where full denotes thermal, voltage and generators limits. The columns Method, Inputs, Outputs are the ML algorithm employed, the ML inputs and the ML outputs, respectively.

Table 2. Summary of recent studies on machine learning to accelerate the solution of PF problems.

Paper	Prob.	Model	$\mathit{N}-\mathit{k}$	Bus	Limits	Method	Inputs	Architecture	Ouputs	Year	Accuracy	Speed-Up
Donnot et al. [25]	LF	AC	k = 1, 2	118	Therm.	ANN	PF in lines	layers 2, Neurons: 200	Therm. violation	2018	≈100%	>2000×
Oliveira et al. [26]	LF	DC	k = 1	136	Vol.	DT	Topology, PF results	73 nodes	Volt. violation	2017	≈99%
Zhang et al. [27]	OPF	DC	k = 0	118	Therm.	ANN	Gen and Load	5 layers	OPF variables	2022	≈89%
Jia et al. [29]	OPF	AC	k = 0	30	Full	CNN	Topology and Load	layers: 1 Conv., 1 max-pool, 1 flatten, 2 dense	Bus Voltage	2023	$\approx 100\%$	>350×
Pan et al. [28]	OPF	AC	k = 0	2000	Full	ANN	Load	2 layers, Neurons: 2048/1024	Power and Volt. of PV buses	2023	≈99%	>100×
Pan et al. [32]	OPF	DC	k = 1	300	Therm., Gen	ANN	Load	3 Layers, Neurons: 256/128/64	Volt.	2021	≈99.8%	>300×
Zhou et al. [33]	OPF	AC	k = 1, 2, 3	14	Full	ANN	PF data	2 Layers, Neurons: 12/15	Load Reduction	2022
This Work	OPF	AC	k = 1, 2, 3	1354	Full	ANN	Topology, Total Load	3 Layers, Neurons: 400/200/100	ELSC		≈98%	>$10,000\times$

In this work, we generalize by ML the estimation of $ELSC$ using as inputs the $N-k$ topology and the expected load to supply. As the scope of this approach is grid planning, the estimation the state variables are not required avoid post-processing or reconstruction of system, as required in [29,32]. Hence, according to Huang et al. [34], who present a review of recent progress in grid dispatch using deep learning, alongside the findings from the review [24] and Table 1 and Table 2, this paper introduces a novel method to accelerate static security assessment. The method achieves this by generalizing the $AC-LSOPF$ to obtain the $ESLC$ for multiple contingencies in large power networks with high accuracy.

3. Machine Learning Approach for LS-OPF

This section addressees the formulation of the Load Shedding Optimal Power Flow (LS-OPF) problem for load shedding under contingency. This formulation enables the generation of the raw data set used for training the ML model. Lastly, the background of the employed ML algorithm is provided.

3.1. Load Shedding Security Constrained Optimal Power Flow

In order to perform a static security assessment for power systems planning, a grid power flow model is necessary. The DC power flow model focuses on active power flow calculations, while the AC load flow (ACLF) model considers both active and reactive power flows. The evaluation of reactive capability of generation, the security voltage limits of buses and reactive compensation necessities the inclusion of reactive power flow.

The mathematical formulation of ACLF requires the specification of one or a set of reference buses $\left(R\right)$. Typically, the phase angle $\left(\theta \right)$ of these reference buses is constraint to 0, as shown below:

$${\theta }_r=0,\forall r\in R$$

(1)

To model the power flow in the set of branches $\left(\mathcal{E}\right)$, the Ohm’s Law is described by the following equations that must be satisfied:

$$P_{ij}=\Re \left({\left(Y_{ij}+Y_{ij}^c\right)}^{*}{V}_i^2-Y_{ij}^{*}{V}_i{V}_j^{*}\right)\forall \left(i,j\right)\in \mathcal{E}$$

(2)

$$Q_{ij}=\Im \left({\left(Y_{ij}+Y_{ij}^c\right)}^{*}{V}_i^2-Y_{ij}^{*}{V}_i{V}_j^{*}\right)\forall \left(i,j\right)\in \mathcal{E}$$

(3)

$$P_{ji}=\Re \left({\left(Y_{ij}+Y_{ji}^c\right)}^{*}{V}_j^2-Y_{ij}^{*}{V}_i^{*}{V}_j\right)\forall \left(i,j\right)\in \mathcal{E}$$

(4)

$$Q_{ji}=\Im \left({\left(Y_{ij}+Y_{ji}^c\right)}^{*}{V}_j^2-Y_{ij}^{*}{V}_i^{*}{V}_j\right)\forall \left(i,j\right)\in \mathcal{E}$$

(5)

where P and Q represent the active and reactive branch power flow, V the bus voltage and Y and $Y^c$ refers to he $\pi$-section parameters. Branches consist of transmission lines and power transformers. To ensure the active and reactive power equilibrium between load, losses and generation, the following equalities must be satisfied for each bus:

$$\sum _{k\in {\mathcal{G}}_i}{P}_k^g-\sum _{k\in {\mathcal{L}}_i}{P}_k^l-V_i^2\sum _{k\in {\mathcal{S}}_i}G{s}_k-\sum _{\left(i,j\right)\in {\mathcal{E}}_i}{P}_{ij}=0\forall i\in \mathcal{N}$$

(6)

$$\sum _{k\in {\mathcal{G}}_i}{Q}_k^g-\sum _{k\in {\mathcal{L}}_i}{Q}_k^l+V_i^2\sum _{k\in {\mathcal{S}}_i}B{s}_k-\sum _{\left(i,j\right)\in {\mathcal{E}}_i}{Q}_{ij}=0\forall i\in \mathcal{N}$$

(7)

where $\mathcal{G},\mathcal{L},{\mathcal{S}}_i$ and $\mathcal{N}$ are the set of generators, loads, shunt and buses, respectively. $P^g,P^l,Q^g,Q^l$ denote active and reactive power generation, and active and reactive power demand. Finally, $Gs$ and $Bs$ are the conductance and susceptance of branch.

The PF model allows the assessment of the impact of a contingency on the secure operation of the system. Security violation encompass the limits the buses, branches and generators. Regarding buses, the voltage magnitude is bound by $v_l$ and $v_u$ as follows:

$$v_i^l\le V_i\le v_i^u,\forall i\in \mathcal{N}$$

(8)

To prevent branch overloading, the following inequality constraints for the maximum allowable power flow must be satisfied for all power transformers and lines:

$$P_{ij}^2+Q_{ij}^2\le {\left(S_{ij}^u\right)}^2\forall \left(i,j\right)\in \mathcal{E}$$

(9)

Lastly, the active and reactive power for generators are bounded by the following limits:

$$P_k^{g_l}\le P_k^g\le P_k^{g_u}\forall k\in \mathcal{G}$$

(10)

$$Q_k^{g_l}\le Q_k^g\le Q_k^{g_u}\forall k\in \mathcal{G}$$

(11)

Since the objective in this approach is static security assessment during system planning, factors such as generator power ramps, unit comment and line switching are not considered in the aforementioned formulation.

In the event of security violations, remedial actions such as redispatch and/or load shedding become necessary. Therefore, to ensure secure system operation and minimize the impact of these remedial actions, an optimization problem must be formulated. The optimization problem takes the following general form:

$$\begin{array}{cc}\hfill \underset{\mathbf{x}}{min}& f\left(\mathbf{x}\right),\hfill \\ \hfill \mathrm{s}.\mathrm{t}.& c^E\left(\mathbf{x}\right)=0,\hfill \\ \hfill & c^I\left(\mathbf{x}\right)\ge 0.\hfill \end{array}$$

(12)

where f and $\mathbf{x}$ are the objective function and optimization variables $\left(P^g,P^l,Q^g\right)$, respectively. The optimization problem is subjected to equality $c^E$ (Equations (1)–(7)) and inequality $c^I$ (Equations (8)–(11)) constraints in order to guarantee power balance and secure operation. The objective function can take various forms, such as minimizing generation cost, maximizing market surplus, or minimizing expected load shedding cost $\left(ELSC\right)$, among others. In long term planning for PS, $ELSC$ is commonly considered as a reliability index to minimize. The minimization of $ELSC$ can be formulated as the maximization (negative minimization) of the value of the supply load. Hence, $ELSC$ is calculated as the expected supply load cost $\left(ESLC\right)$ in pre-contingency minus the supply load cost $\left(SLC\right)$ in post-contingency, as shown below:

$$ELSC=ESLC-SLC$$

(13)

Therefore, to consider load curtailment as remedial action, the objective function is formulated by minimizing the negative $SLC$, as follows:

$$\min -\sum _{k\in \mathcal{L}}{c}_{k_1}{P}_k^l$$

(14)

where P and c represent the supplied load and the unitary cost of the energy not supplied, respectively. If load shedding is not required, the $LSC$ will be zero, as indicated by Equations (13) and (14). Finally, if LS is assumed with a constant power factor, the load can be modeled as generator with negative power injection as shown below:

$$Q_i-P_{i}r=0\forall i\in \mathcal{L}$$

(15)

$$0\le P_i\le P_i^p\forall i\in \mathcal{L}$$

(16)

where r is the ratio $Q^p/P^p$ where the index p denotes the pre-contingency value. In summary, each contingency is assessed by minimizing load shedding (LS-OPF) through the adjustment of generator and load capabilities to achieve an optimal and secure operating point.

3.2. ML Algorithm—ANN

The idea we proposed involves generalizing the relation between an $N-k$ contingency with $ELSC$. Hence, given a set of features $\mathbf{x}=\left[x_1,x_2,\cdots ,x_m\right]$, the target is to predict $\widehat{y}$ by a function f as follows:

$$\widehat{y}\left(\mathbf{x}\right)=f\left(\mathbf{x},\omega \right)$$

(17)

where $\omega$ represents a set of parameters that fit the function f. The goal is to find the values of $\omega$ that minimize the loss function L for a set of known samples $\left\{\mathbf{X},\mathbf{Y}\right\}$ as illustrated below:

$$\underset{\omega }{min}\sum _{i=1}^{p}L\left(f\left({\mathbf{x}}_{\mathbf{i}},\omega \right),y_i\right)$$

(18)

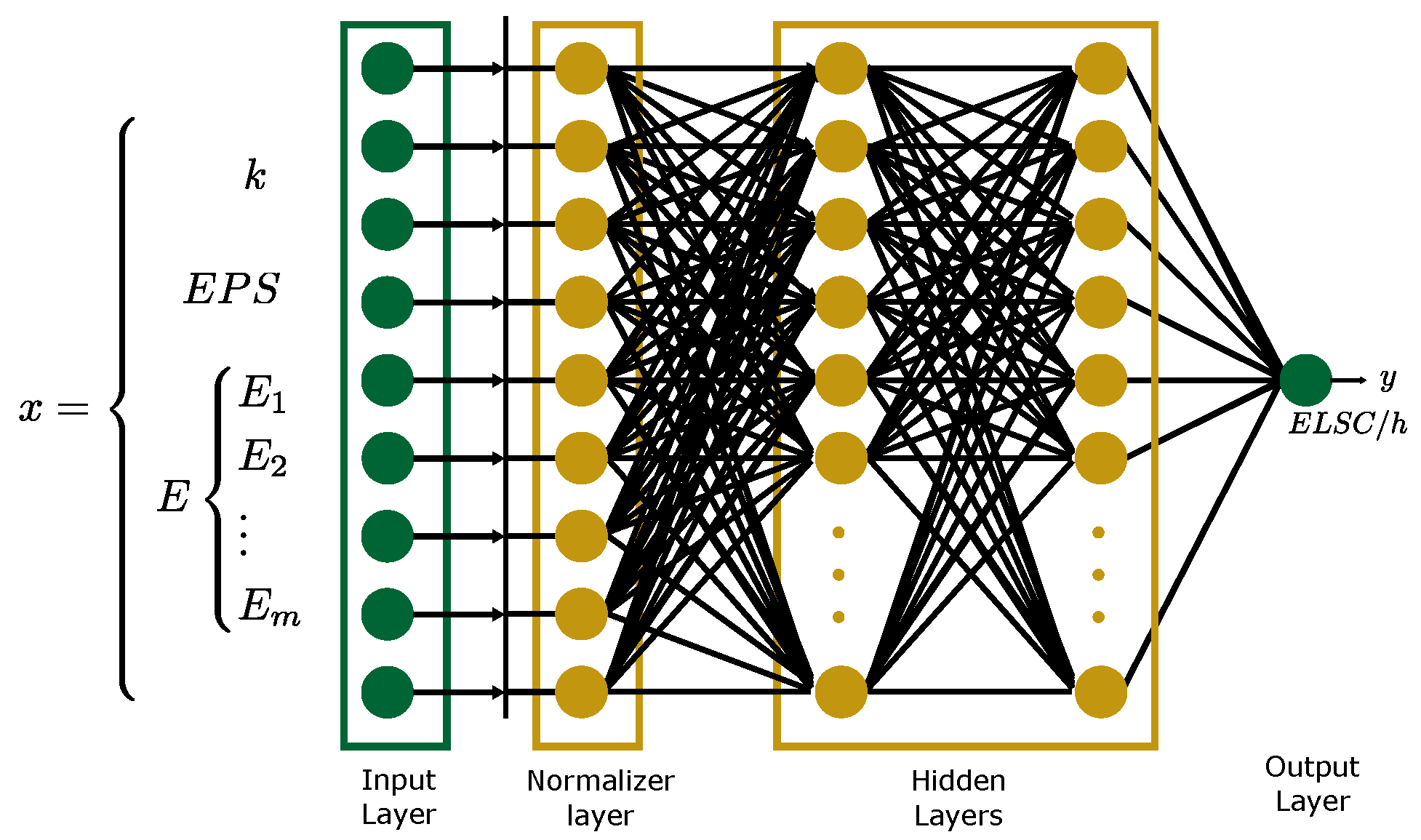
where $\mathbf{X}=\left[{\mathbf{x}}_1,{\mathbf{x}}_2,\cdots ,{\mathbf{x}}_p\right]$ and $\mathbf{Y}=\left[y_1,y_2,\cdots ,y_p\right]$. The optimization problem in the form of Equation (18) can be solved using regression ML algorithms, with ANN widely adopted for its high performance [24]. For the prediction of $ELSC$ with ML in this paper, the selected set of features are $\mathbf{x}=\left[k,EPS,E_1,E_2,\cdots E_m\right]$ and $y=ELSC/h$, where $EPS$ and $E_i$ represent the expected power to supply and a binary value indicating if element i is connected, respectively. The training data set is obtained using the methodology addressed in Section 3.1 for multiple contingency scenarios. Figure 1 illustrates the generic architecture of an $MLP$ for the generalization of $ELSC$, where the number of inputs must be adjusted to each network.

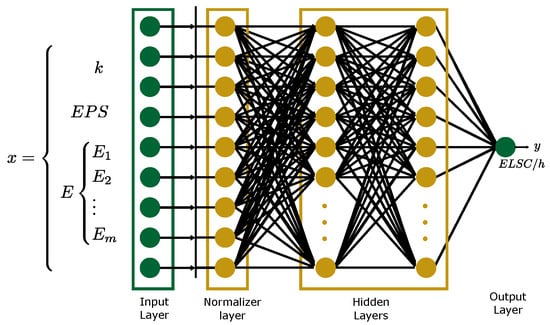
Figure 1. Proposed ANN architecture for generalization of $ELSC$ given an $N-k$ contingency.

4. Numerical Analysis

To assess the performance of the proposed approach, two case studies are evaluated by comparing the results obtained with the proposed method against the well-known interior point algorithm (IP) for an $AC-LSOPF$ formulation. The results of the IP algorithm are considered as true values and are used for both fitting and evaluating the ML model.

4.1. Case Studies Description

The IEEE-39 bus and the PEGASE-1354 cases are used to demonstrate the practical applicability of the proposed ML model. The IEEE-39 case serves didactic purposes, providing a detailed illustration of the model’s performance, while the PEGASE-1354 model is employed to evaluate the ML performance in large power grids. The raw data for both networks was taken from matpower cases [35] and is summarized in Table 3.

Table 3. Network data of the two case studies.

No.	IEEE-39	PEGASE-1354
Buses	39	1354
Gen	10	260
Branches	35	1991
Transformers	11	234

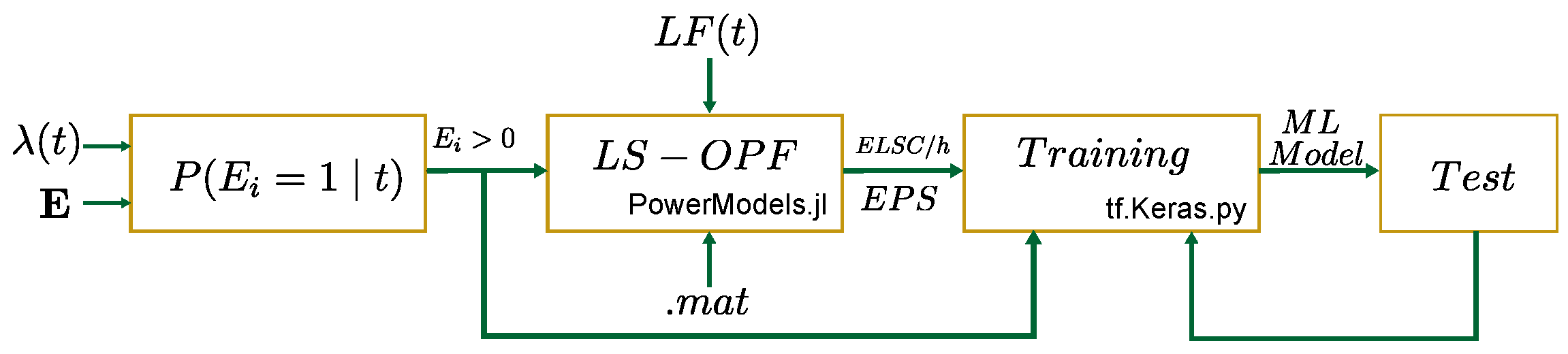
Figure 2 summarized the procedure employed to generate the raw data, train the ML and test the fit. A detailed explanation is presented in the following subsections.

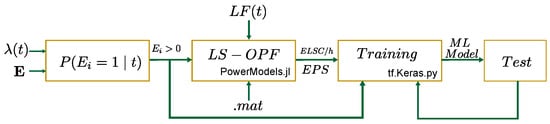
Figure 2. Procedure used in case studies for estimation of $VoLL$ using ML.

4.2. Raw Data

The set of contingencies was generated stochastically, assuming a failure rate $\lambda =5\times {10}^{-4}$ failures/h (approx. 99.8% availability per year) for each element ($E_i$) over a one-year period, $P\left(E_i=1|t\right))$. Thus, the set of contingencies is selected from scenarios where a least one element fails $\left(E_i\ne 0\right)$. Table 4 shows the number of scenarios for each $N-k$ contingency used for training and testing in each case study. A total of $p=268.5\times {10}^3$ and $p=502.5\times {10}^3$ scenarios were used for IEEE-39 and PEGASE-1354, respectively. In the IEEE-39 bus system, m = 115 elements, including circuit breakers (CB) associated with loads, buses, generators, power transformers and lines were considered as equipment to fail. For the PEGASE-1354 network, equipment considered for failure included CBs of loads greater than 1 $\mathrm{M}$$\mathrm{W}$, generators, power transformers, and lines, totaling m = 2528 equipment. The selection of power limits in the chosen loads was made to enhance the robustness of the LS-OPF algorithm. Only synchronous machines are considered, as they currently constitute the majority in HQ’s transmission grid. However, Inverted-Based Resources will be addressed in future research.

Table 4. Number of $N-k$ contingencies used to train the ANN.

$\mathit{N}-\mathit{k}$ Scenarios	IEEE-39, m = 115	PEGASE-1354, m = 2528
N-1	65.4 × 103	73.2 × 103
N-2	188.5 × 103	285.5 × 103
N-3	14.6 × 103	143.8 × 103

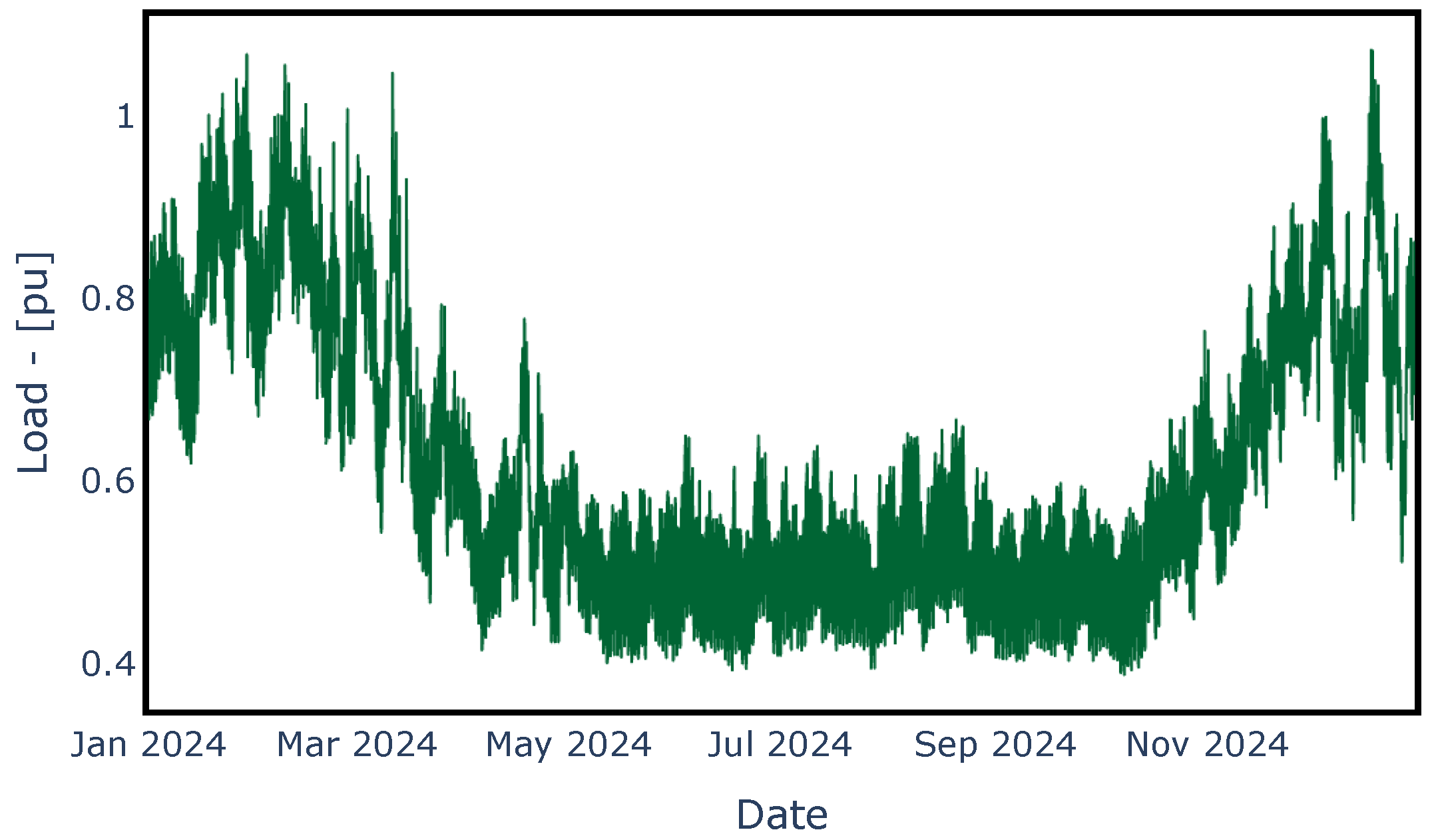
Before executing the LS-OPF algorithm, a load update is performed for each scenario, assuming the HQ’s demand pattern shown in Figure 3. This is performed to simulate the load changes over the course of 1 year. Lastly, LS-OPF was executed for each contingency scenario.

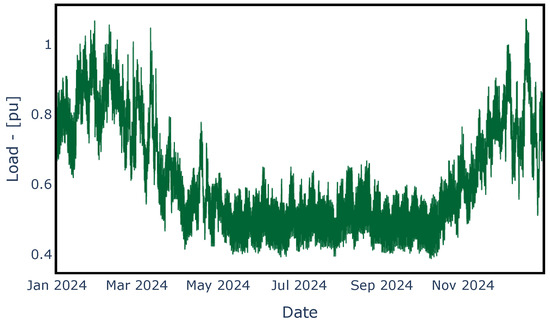
Figure 3. HQ’s demand pattern used in the different contingency scenarios.

4.3. LS-OPF Using PowerModels.jl

The LS-OPF algorithm was implemented using the open-source platform PowerModels.jl [36]. The abstract model shows in Listing 1 was written in the Julia Programming Language to evaluate $ELSC$ for each contingency scenario, based on the formulation addressed in Section 3.1. The load shedding model was implemented in the Julia function as shown Listing 2. The loads are treated as generators and are labeled as “Load”.

The LS-OPF problem was solved using the non-linear solver IPOPT [37], which was restricted to a maximum of 200 iterations and 150 $\mathrm{s}$ for each scenario. As linear solver, the MA57 library was used with a tolerance of 1 × 10⁻⁶. The evaluation of the entire set of contingencies was performed using a 2.2 GHz Intel Core i5-9500T CPU with 16 GB of RAM. On average, each LS-OPF simulation took approx. in $0.5$ $\mathrm{s}$ for the IEEE-39 case study and around 5 $\mathrm{s}$ for the PEGASE-1354 case study.

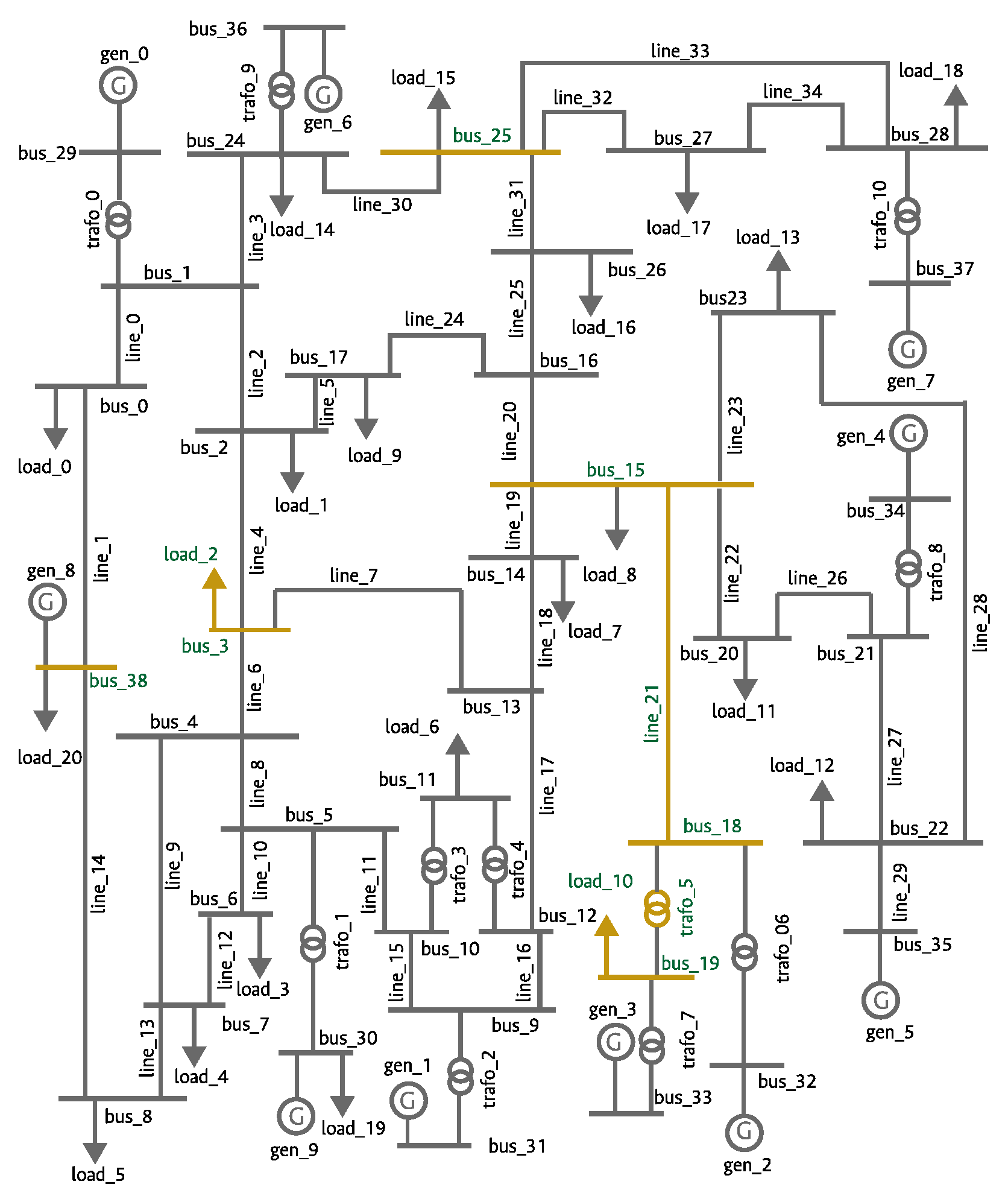
To verify the LS-OPF results and procedure, a visual assessment is performed. Figure 4 shows the distribution of $N-1$ contingencies with the highest $ELSC$. These results are further explained using Figure 5, where the top $N-1$ contingencies are highlighted. The disconnection of bus 15 leads to the isolation of a part of the network, including five loads and four generators. Since the simulation did not permit operation in islanding mode, bus 15 emerges as the most critical failure in the system.

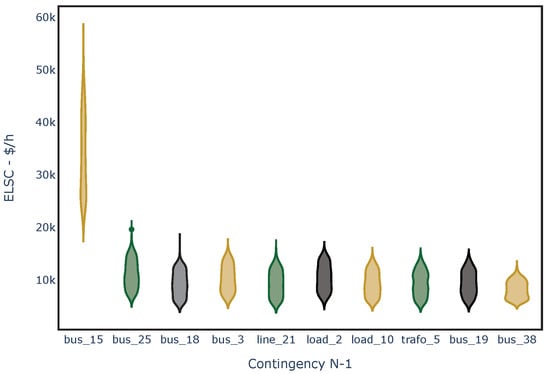
Figure 4. Violin plot ranking of $N-k_{k=1}$ contingencies with the highest $ELSC$ for the IEEE-39 bus system.

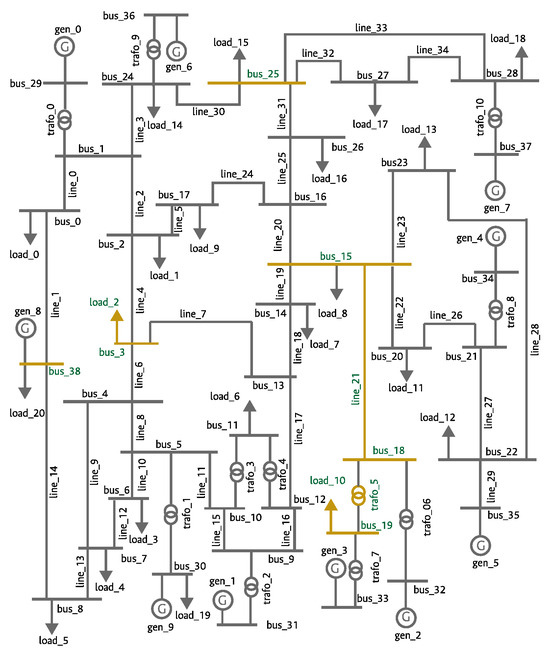
Figure 5. Location of $N-k_{k=1}$ contingencies in the network with the highest $ELSC$ for the IEEE-39 bus system.

Listing 1. Implemented PowerModels Abstract LS-OPF Model.

Listing 2. Function implemented in PowerModels.jl for modeling load shedding.

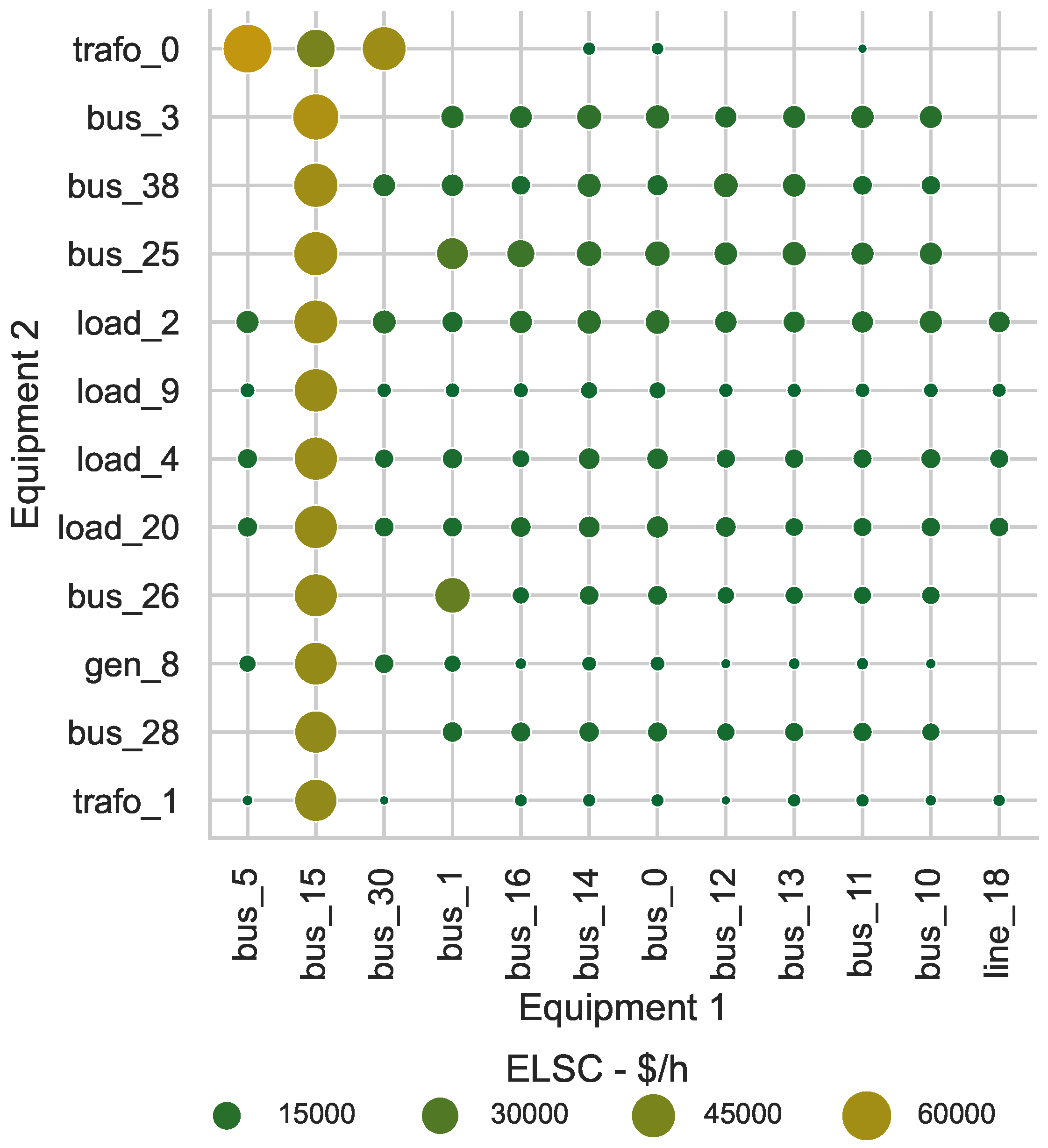
Figure 6 shows the top $N-k$ with $k=2$ contingencies, reaffirming that scenarios involving bus 15 have the highest $ELSC$, except for the situation when bus 16 and line 18 fail. As shown in Figure 5, a simultaneous failure of these two elements would have a similar impact as the disconnection of bus 15 with the disconnection of load 7.

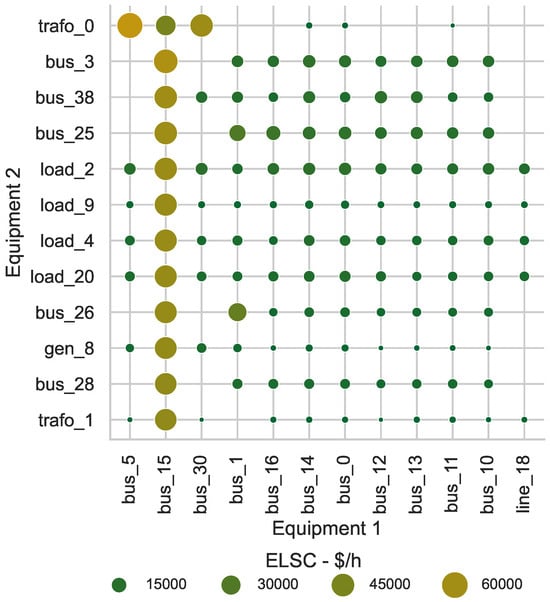
Figure 6. $N-k_{k=2}$ contingencies with the highest $ELSC$ for the IEEE-39 bus system.

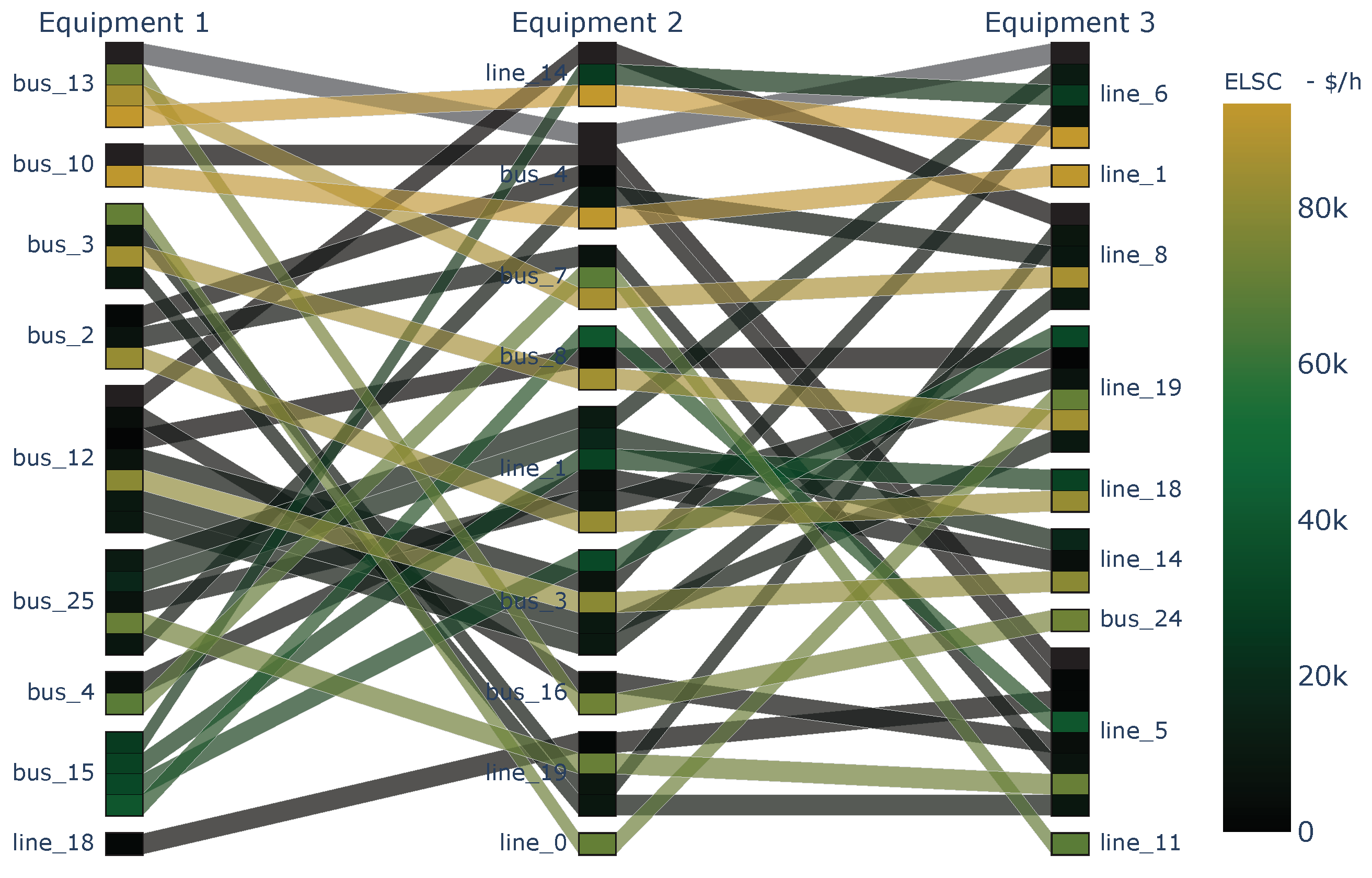
Lastly, Figure 7 shows the top N-3 contingencies, with those related to bus to bus 15 presenting the highest impacts. Based on the previous visual assessment, the results obtained during the raw data generation align with the expected outcomes.

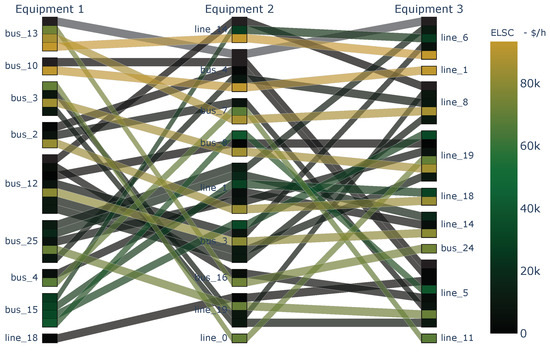
Figure 7. $N-k_{k=3}$ contingencies with the highest $ELSC$ for the IEEE-39 bus system.

4.4. ELSC Regression

The proposed ML algorithm, as illustrated in Figure 1, was implemented using the TensorFlow-Keras API in Python. The number of inputs is 117 for IEEE-39 and 2530 for PEGASE-1354, respectively. These quantities result from the number of equipment to fail, the consideration of contingency level (k), and the $EPS$ as inputs. The output was the $ELSC$. The optimization solver used was the ADAM algorithm, set with a learning rate of 1 × 10⁻⁴. For the loss function, the Mean Square Error was selected. Among the various architectures evaluated, an ANN with three hidden layers consisting of 400, 200 and 100 neurons, each using the Relu activation functions was chosen for both the IEEE-39 System and the PEGASE-1354 network. Additionally, a normalization layer was included to improve the model’s fit. To prevent negative values of $ELSC$, a Relu activation function was added to the output layer. Listing 3 provides the Python script with the implemented ANN architecture.

Listing 3. TensorFlow-Keras ANN Model for STLF.

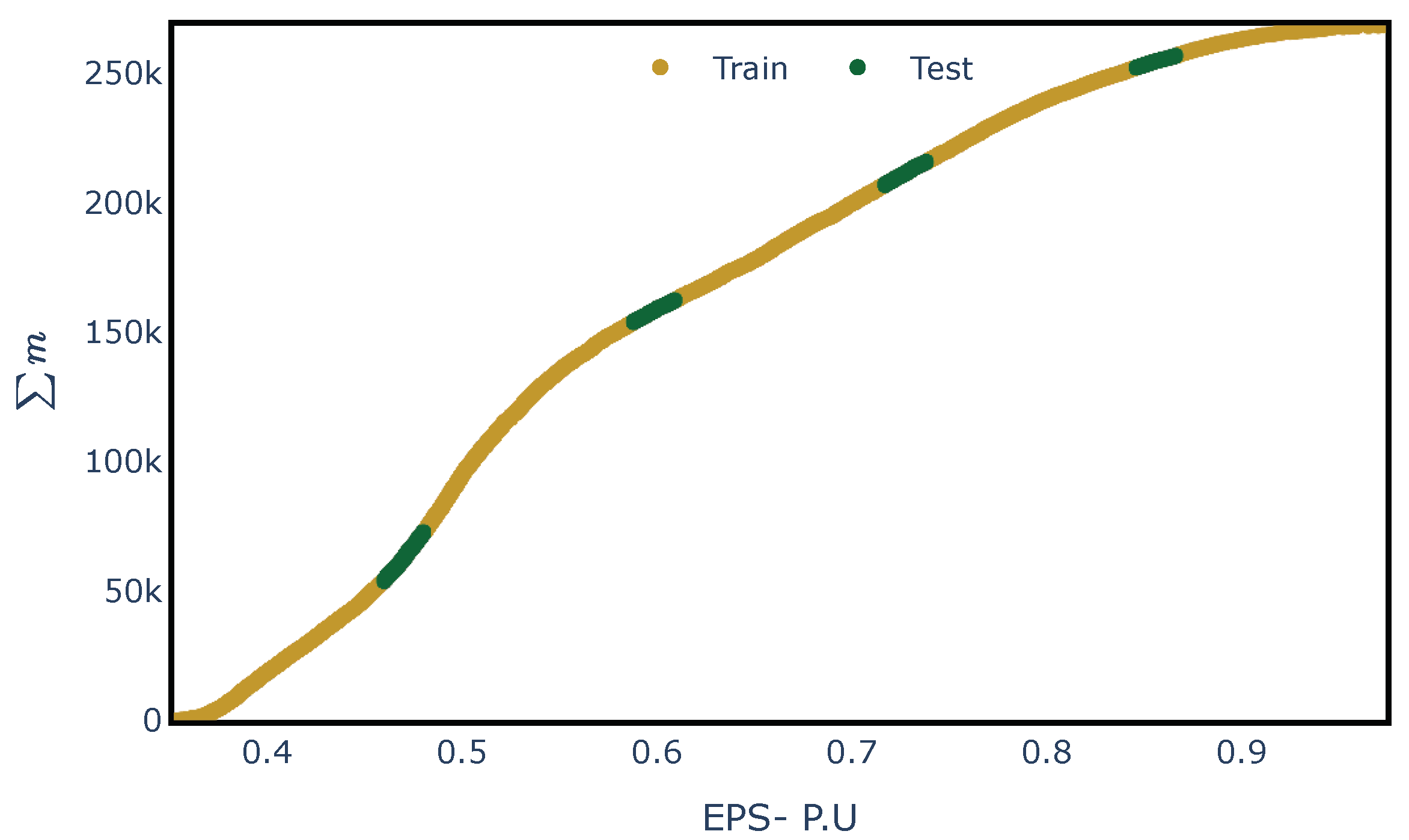
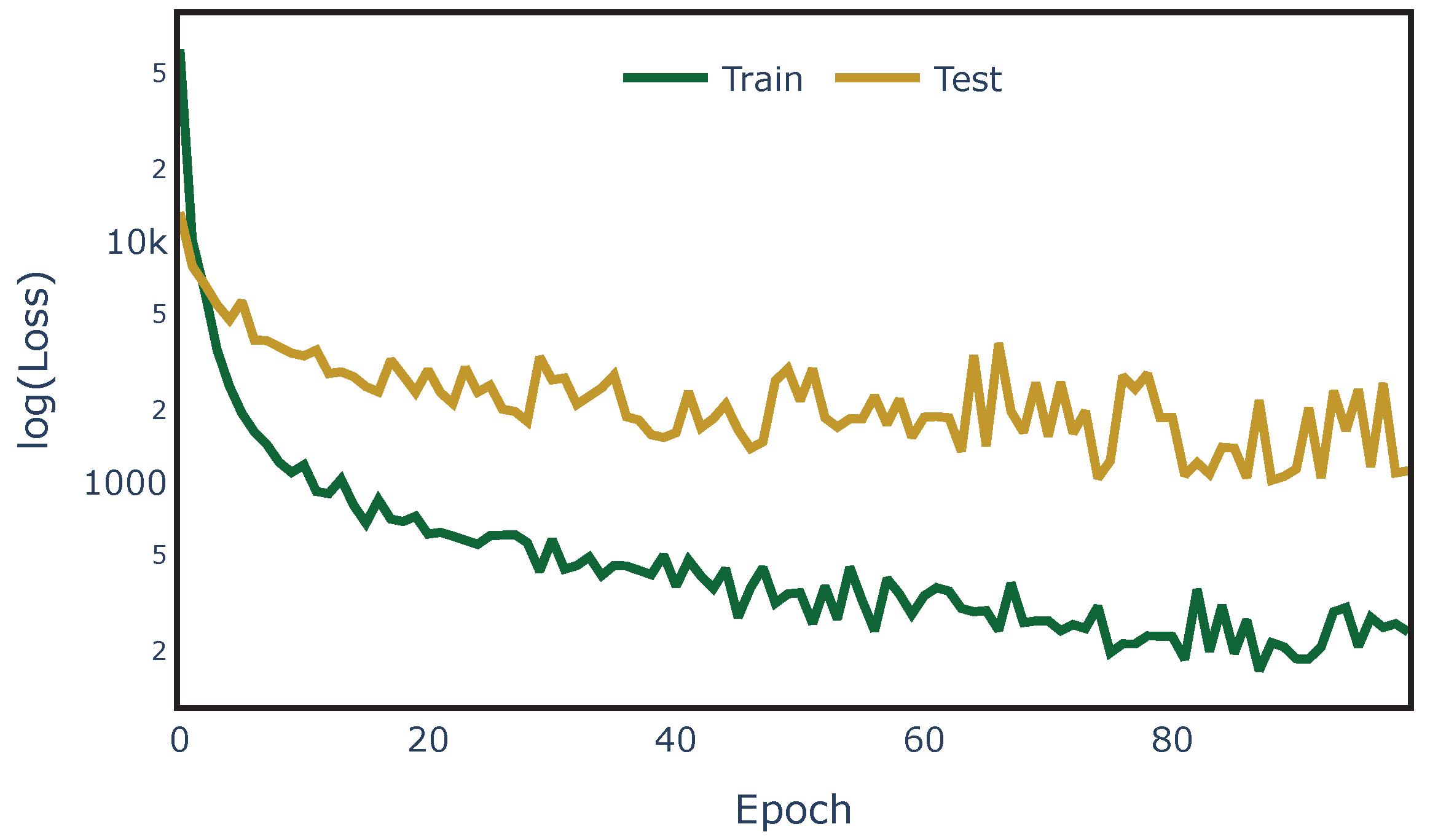
With the established architecture, the model for each network was fitted and tested. Listing 4 provides the Python code developed to fit the proposed ANN model. To assess the learning capacity of the ML model, unknown load conditions and contingencies were used for testing. Hence, the training and test datasets were split as shown in Figure 8, with 85% of the samples used for training and 15% for testing, using the raw data generated in Section 4.2. Figure 9 shows the testing and training loss obtained during the fitting processes for PEGASE-1354.

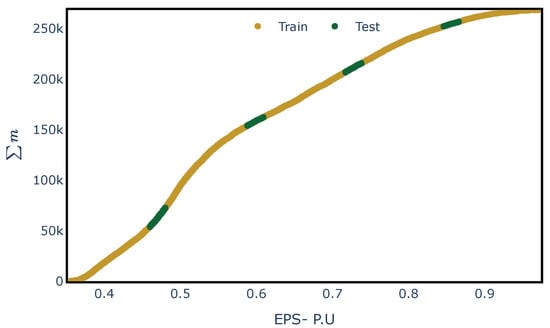
Figure 8. Split of the dataset to assess the ANN model’s learning capability under unknown Expected Power to Supply (EPS).

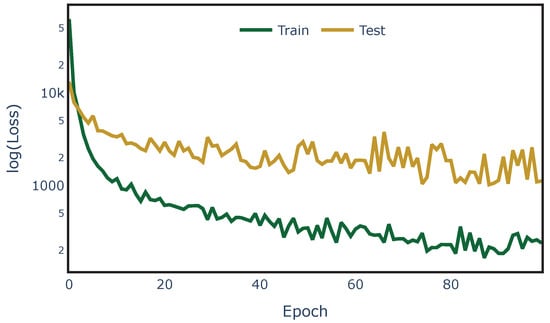
Figure 9. Convergence analysis for $ELSC$ on the PEGASE-1354 network.

Listing 4. Python Code to fit the ANN-model.

4.5. Regression Assessment

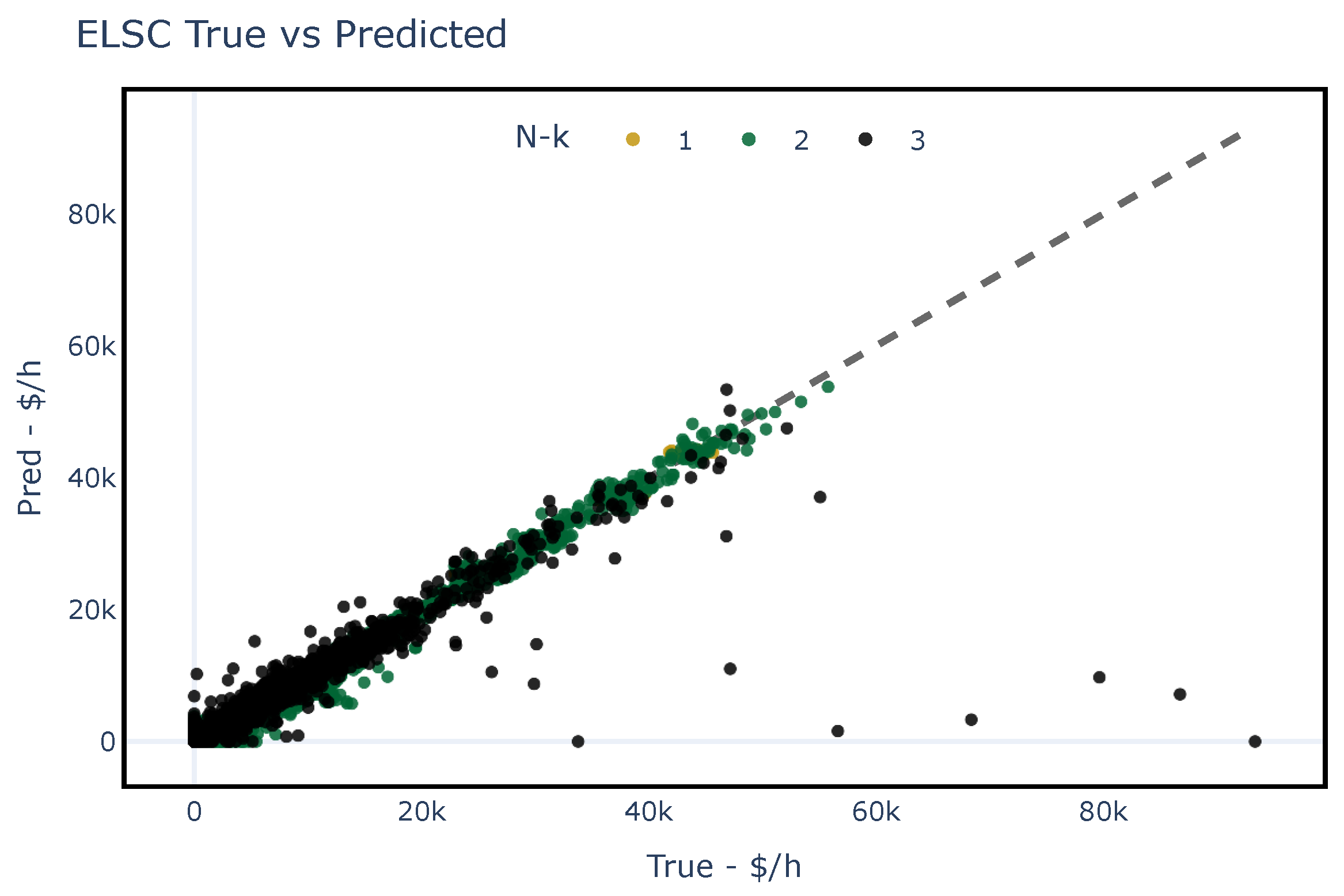
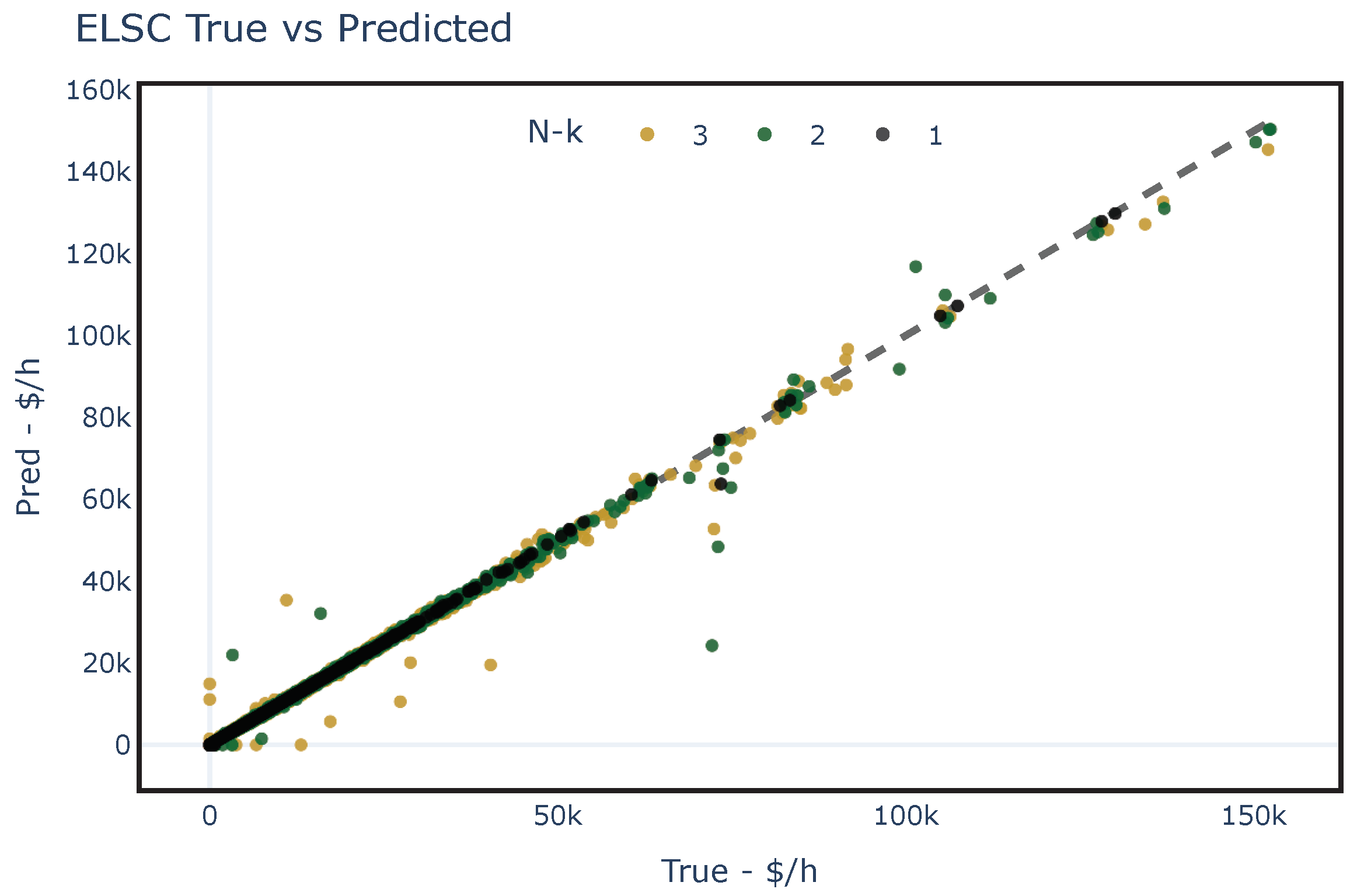
Figure 10 and Figure 11 show the predicted and the true values of $ELSC$ using the testing dataset for each studied network. These figures illustrate the model’s capability to generalize $ELSC$ accurately when the status of the elements is known. It should be noted that two outliers were obtained for the PEGASE-1354 case and were subsequently excluded from the assessment.

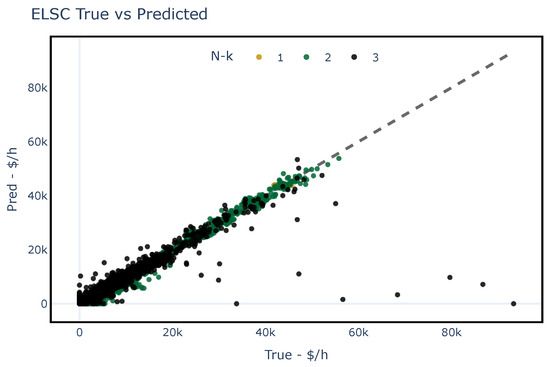
Figure 10. Predicted values obtained by assessing the fit of the proposed $ELSC$ regression ML model for the IEEE-39 bus system with different $N-k$ contingencies. The dashed line represents an assumed perfect fit.

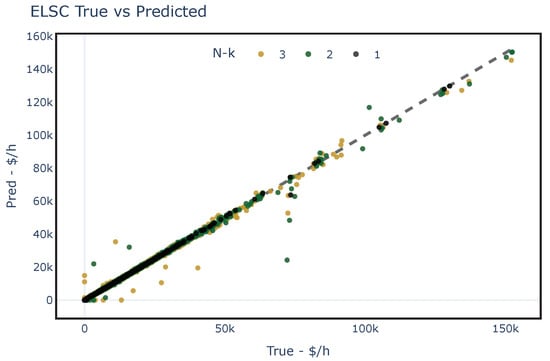
Figure 11. Predicted values obtained by assessing the fit of the proposed $ELSC$ regression ML model for the PEGASE-1354 network with different $N-k$ contingencies. The dashed line represents an assumed perfect fit.

To evaluate the overall performance of the fit, four regression metrics were used: R-Squared coefficient of determination ($R^2$), Mean Absolute Error (MAE), Root Mean Square Error (rMSE) and Relative Root Mean Square Error (rrMSE). These metrics were computed comparing the LS-OPF results with the ML fit. Table 5 presents the results of these metrics for both case studies. Notice that, based on the dimensionless metric $R^2$ and rrMSE, the fit demonstrates high performance in generalizing $ELSC$ when a contingency occurs.

Table 5. Regression performance metrics obtained to generalize the $ELSC$ for IEEE-39 bus and PEGASE-1354 network.

Indicator	IEEE-39	PEGASE-1354
$R^2$	96.7%	99.8%
MAE	$233.0$ $/$\mathrm{h}$	$61.7$ $/$\mathrm{h}$
rMSE	$1000.7$ $/$\mathrm{h}$	$334.8$ $/$\mathrm{h}$
rrMSE	14.9%	4.1%

The average time for predicting $ELSC$ was $0.04$ $\mathrm{m}$$\mathrm{s}$ and $0.11$ $\mathrm{m}$$\mathrm{s}$ for the IEEE-39 and PEGASE-1354 networks, respectively. This significant reduction in execution time demonstrates the substantial speed-up achieved when using ANN compared to LS-OPF, resulting in speed-up factors of 12,500× and 45,000× for each case, respectively.

Table 6 shows the rrMSE for each $N-k$ set of contingencies. As expected, the error increases as k increases. This consequence is attributed to the exponential growth in the number of combinations when k increases, given that $N-k$ criterion involves $\left(\genfrac{}{}{0pt}{}{N}{k}\right)=\frac{N!}{k!\left(N-k\right)!}$ contingency scenarios. In other words, as k increases, more training scenarios are required. This can be observed by comparing the size of $N-3$ scenarios used to train the ANN in Table 4 with the performance results provided in Table 5. For instance, the IEEE-39 case, which has fewer scenarios, also has the lower performance.

Table 6. rrMSE between test and predicted values of $ELSC$ for different k $(N-k)$ contingencies.

	${\mathit{R}}^2$		rrMSE
$\mathit{N}-\mathit{k}$	IEEE-39	PEGASE-1354	IEEE-39	PEGASE-1354
$N-1$	99.6%	99.9%	5.5%	1.7%
$N-2$	99.4%	99.8%	6.4%	4.4%
$N-3$	70.1%	99.8%	37.2%	4.1%

4.6. Discussion

Based on the assessment of LS-OPF simulations, it is observed that in the majority of cases with a contingency $k>1$, the expected load shedding is the summation of $ELSC$ under $N-1$ contingencies; in other words, $ELS{C}_{N-k_C}={\sum }_{c\in C}ELS{C}_{N-1_c},\left|C\right|=k$, where C is the set of elements that fails. To illustrate, considering the case $k=2$, the aforementioned expression is valid for 75% of 188,452 scenarios for the IEEE-39 bus system, and for 99% of 982 scenarios for PEGASE-1354. The reduced number of N-2 scenarios, compared to those shown in Table 4, is attributed to the limited number of $N-2$ contingencies, which corresponds $N-1$ for specific EPS (Figure 3). This implies that only a small subset of the entire dataset can be used to compute $ELS{C}_{N-k}$ as the sum of $N-1$ contingencies. This could explain the fast convergence of the ANN shown in Figure 9. Despite the presence of a strong linear dependence of $N-1$ for higher-order contingencies $(k>1)$, the ANNs shows the ability to generalize the $ELS{C}_{N-k}$ for unknown training values of $ELS{C}_{N-1}$.

The proposed approach is limited to static topologies with synchronous generation at transmission level, and outlier detection techniques should be implemented to identify abnormal contingencies. Additionally, uncertainties in generation, dynamic stability limits, and demand response, among others, are beyond the scope of this work. Future research should aim to address these limitations by exploring new approaches, such as graph neural networks.

5. Conclusions

In this paper, we propose an approach for fast $N-k$ security assessment in power transmission planning using ANN to accelerate contingency evaluation. The training is performed by executing Load Shedding Optimal Power Flow (LS-OPF), which minimizes the $ELSC$ for a set of $N-k$ contingencies generated stochastically. The ANN predicts $ELSC$ using the connection status of elements such as lines, generators, and power transformers, among others, as features. As a result, an accuracy close to 98% and acceleration gains of 12,500× and 45,000× were obtained for the IEEE-39 bus system and PEGASE-1354 system, respectively, demonstrating great effectiveness. These results highlight the high accuracy and efficiency of our proposal, making it an attractive option for probabilistic grid planning using $N-k$ criterion within a reasonable execution time. A similar approach and its results have not addressed in the literature. As potential areas for future research, we suggest extending this method to distribution networks with distributed generation, the classification of problematic contingencies, and applying the approach to resilience assessment.