Abstract
Accurately calculating winding losses has always been a significant challenge in the design of large-capacity medium-frequency transformers. This paper presents an accurate design algorithm for calculating the winding losses of a large-capacity medium-frequency distribution transformer. First, the peculiarities of winding losses in medium-frequency distribution transformers are analyzed. Various commonly used winding conductor types for medium-frequency transformers are introduced. The mechanisms of and differences between AC and DC winding losses in medium-frequency transformers are explained, and an effective analytical method for calculating the AC-to-DC resistance ratio is provided. Finally, the analytical calculation results of different types of winding losses are compared with those obtained through finite element simulations and experimental methods applied to a real transformer prototype. The discrepancies between the analytical results and those obtained using the other two methods were found to be within acceptable error margins, thereby validating the accuracy and effectiveness of the proposed algorithm.
1. Introduction
With the establishment of China’s goals for “carbon peaking and carbon neutrality,” the proportions of renewable energy generation and power electronic devices are expected to increase significantly [1]. Medium-frequency transformers, in combination with power electronic conversion devices, play a crucial role in scenarios involving the flexible regulation of power and voltage; energy interconnection and mutual support; fault management; the integration of high-proportion distributed energy resources; large-capacity energy storage access; flexible interaction between sources, grids, loads, and storage; and AC-DC grid interconnection [2,3,4]. These transformers are essential for realizing the functions of new power distribution systems.
In the context of introducing power electronic conversion devices into new distribution systems, the operating frequencies of transformers can be increased [5]. Compared to power-frequency distribution transformers with the same operational capacity, medium-frequency distribution transformers operating at frequencies between 400 Hz and 2000 Hz exhibit significant reductions in design volume and weight as the operating frequency increases [6,7,8]. Consequently, medium-frequency transformers are more cost-effective, occupy less space, and are applicable in a broader range of scenarios [9,10,11]. However, an increase in operating frequency substantially affects the characteristics of transformers, and traditional transformer design algorithms are no longer suitable for the design and development of medium-frequency distribution transformers.
In many application scenarios, power electronic distribution systems also introduce a significant quantity of harmonic currents to medium-frequency distribution transformers, complicating their operational conditions and making loss design more challenging [12,13]. Accurately calculating the losses of large-capacity medium-frequency distribution transformer windings under harmonic operating conditions is one of the critical challenges in their design.
In this paper, we not only conduct an in-depth study on the analytical calculation of winding losses in large-capacity medium-frequency distribution transformers but also verify the accuracy of this analytical algorithm through finite element simulation and experimental tests conducted on a prototype. This analytical algorithm will significantly enhance the design efficiency of similar medium-frequency transformers in engineering applications, thereby contributing to the development of new distribution systems.
In this paper, the calculation of winding losses in distribution transformers under medium-frequency excitation, rather than the typical power-frequency excitation, is investigated. Meanwhile, the capacity of the distribution transformer is up to the MW level. Through derivation and calculation, it is demonstrated that the AC resistance losses of Litz wire windings in medium-frequency transformers can be equivalently represented by DC resistance losses. Additionally, special consideration is given to the practical engineering scenario where the height of the copper foil winding often does not match the height of the core window. By using the porosity factor algorithm, the winding height is equivalently adjusted to match the height of the core window, making the algorithm more applicable to engineering practices.
2. Specificity of Winding Losses in Medium-Frequency Distribution Transformers
Winding losses in transformers, also known as copper losses, are caused by the working resistance of winding conductors when alternating current flows through them [14,15]. In power-frequency transformers, copper losses are equivalent to the losses caused by the resistance of the copper material in the windings, known as DC resistance losses [16]. This is because, at a 50 Hz operating current, the skin effect and proximity effect in the conductor are weak, resulting in minimal difference between the AC resistance and DC resistance of the windings [17]. Consequently, the DC resistance losses and AC resistance losses are nearly identical [18].
The resistance exhibited by a conductor under direct current (DC) excitation is referred to as DC resistance, while the resistance under alternating current (AC) excitation is known as AC resistance [19]. In an AC environment, the skin effect and proximity effect influence the conductor, causing a change in resistance. As a result, the AC resistance of the conductor varies with the operating frequency [20].
For medium-frequency transformers used in power electronic transformers, the operating frequency is relatively high. The operating current is often non-sinusoidal, and the operating voltage is typically a square waveform (as shown in Figure 1). This results in a significant amount of higher-order harmonic currents entering the windings. In such cases, the influence of the skin effect and proximity effect on the winding conductors cannot be ignored, as they lead to AC resistance losses that are greater than DC resistance losses [21,22]. Therefore, it is necessary to study the impact of operating frequency and harmonic composition on transformer winding losses.
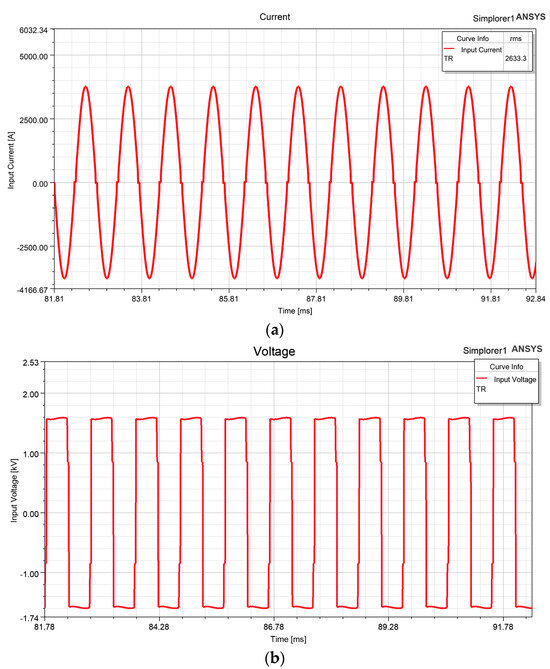
Figure 1.
Medium-frequency transformers’ operating conditions. (a) Operating current. (b) Operating voltage.
3. Introduction to Winding Conductor Types for Medium-Frequency Distribution Transformers
The selection of winding conductors is of paramount importance in the design of medium-frequency distribution transformers [23]. The type of conductor significantly influences the winding losses, and the calculation of these losses varies depending on the conductor type.
Currently, copper foil, Litz wire, and flat copper wire are the commonly used conductor types in medium-frequency transformers to better suppress eddy current effects [24]. The most suitable type should be selected based on the transformer’s specific characteristics.
Flat copper wire windings have a sizeable current-carrying capacity and exhibit good thermal performance, and their manufacturing process is simple. However, due to their relatively large thickness, their ability to suppress the skin effect and proximity effect is weak [25,26]. Therefore, flat copper wire windings are suitable only for transformers operating at relatively low frequencies (several hundred Hz).
Litz wire windings can mitigate the skin effect and proximity effect, bringing the AC resistance of the Litz wire close to its DC resistance. This makes Litz wire advantageous in medium- to high-frequency transformers [27]. However, due to manufacturing limitations, Litz wire windings have a lower current-carrying capacity and poor heat dissipation. Thus, Litz wire windings are typically used in medium- to high-frequency transformers with small currents.
Copper foil windings offer a large current-carrying area and small thickness, effectively weakening the skin effect and proximity effect. They also have good thermal conductivity and can be simply manufactured, making them suitable for large-current medium-frequency transformers.
4. Methods for Analyzing Winding Losses in Medium-Frequency Distribution Transformers
In designing medium-frequency distribution transformers, the theoretically calculated winding losses must not significantly deviate from the measured losses of the actual product. However, the calculation of transformer winding losses is inherently a complex electromagnetic field problem [28]. The structural composition of actual transformers is highly intricate, and the internal magnetic field distribution is equally complex, making it extremely challenging to analytically compute winding losses [29]. Typically, simplified calculation models are used to approximate winding losses in transformers. These models must ensure that the calculated results closely approximate the measured results for the actual product.
A medium-frequency distribution transformer (the parameters of which are shown in Table 1) is used as a prototype to analyze and validate the analytical calculation method for winding losses under harmonic current excitation (the parameters of which are shown in Table 2). Flowcharts for the two analytical methods of winding loss calculation introduced in this chapter are shown in Figure 2.

Table 1.
Parameters of the medium-frequency distribution transformer.

Table 2.
Parameters of excitation current containing harmonics.
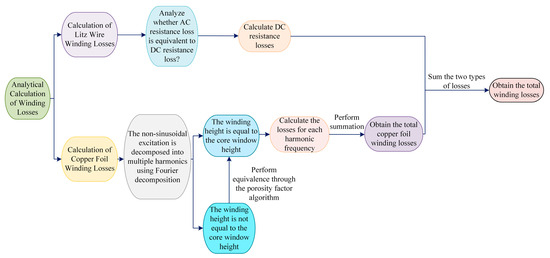
Figure 2.
Flowchart of analytical calculation of winding losses.
4.1. Calculation of Litz Wire Winding Losses
In this case study, the secondary winding is composed of Litz wire, with the specific parameters detailed in Table 1. Due to the structural characteristics of Litz wire, the skin effect and proximity effect are significantly weakened. Historically, in medium-frequency transformer design, the AC resistance losses of Litz wire windings have been considered equivalent to the DC resistance losses.
This study calculates the AC resistance losses of the Litz wire winding and verifies whether they can indeed be equated to the DC resistance losses.
4.1.1. Analysis of Deviation between AC and DC Resistance
The complex structure of Litz wire makes the analysis of AC resistance particularly challenging. Numerous studies have proposed methods for calculating the AC resistance of Litz wire [30,31,32,33]. In this case study, the employed method leverages the orthogonal relationship between the skin effect and proximity effect to perform the calculations. The formula is as follows:
where is the AC resistance of the Litz wire, is the DC resistance of the Litz wire, is the AC-to-DC resistance ratio for a single strand (generally equal to 1), is the diameter of a single strand, is the diameter of the Litz wire, is the eddy current factor, and is the operating frequency.
The constant related to the number of strands in the Litz wire has specific values provided in Table 3.

Table 3.
Correspondence between the constants K and N.
By substituting the parameters of the transformer from Table 1 into Equation (1), the following result can be obtained:
The resulting calculation shows that the ratio of the AC resistance to the DC resistance of the Litz wire winding is approximately equal to 1 in this case. This demonstrates that the AC resistance losses in the Litz wire winding of medium-frequency transformers can be effectively approximated using the DC resistance losses.
4.1.2. Calculation of Secondary Litz Wire Winding Losses
The losses in the secondary Litz wire winding can be calculated as follows:
where is the secondary winding loss; is the RMS value of the rated current for the secondary winding; is the DC resistance of the secondary winding; is the resistivity of copper, taken to be 0.02135 Ω·mm2/m (at 75 °C); is the length of the conductor; and is the total cross-sectional area of the conductor.
By substituting the parameters of the medium-frequency distribution transformer from Table 1 into Equation (3), the value of can be obtained:
4.2. Calculation of Copper Foil Winding Losses
The losses in copper foil windings are primarily AC resistance losses, which entail solving a three-dimensional electromagnetic field problem within the transformer [34]. This scenario is highly complex, making it challenging to use analytical methods. To facilitate the calculations, the three-dimensional model is simplified to an ideal two-dimensional model, as shown in Figure 2, for analysis.
4.2.1. Winding and Core Window of Equal Height
In Figure 3, it is assumed that the height of the winding equals the height of the core window . The thickness of the copper foil is significantly smaller than the height , and the interlayer spacing is relatively small. Thus, the magnetic field component in the -direction is negligible compared to that in the -direction. Therefore, the magnetic field intensity within the core window can be approximated as being distributed only in the -direction. The electromagnetic field within the copper foil windings, being the internal magnetic field of a conductor, is a typical quasi-static magnetic field.
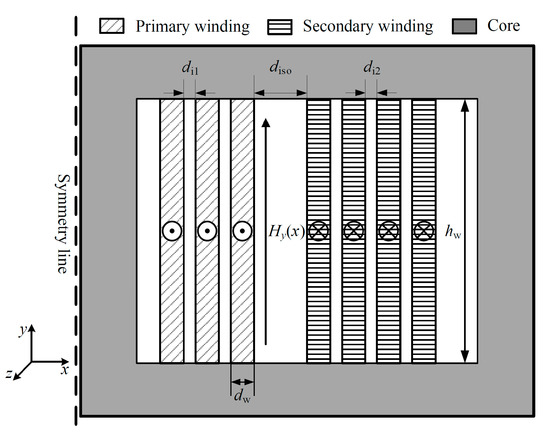
Figure 3.
Cross-sectional view of the ideal transformer winding model.
The windings of the medium-frequency transformer studied in this paper are good conductors, wherein the conduction current component significantly outweighs the displacement current component, allowing the displacement current to be neglected. Therefore, the electromagnetic field within the windings of the medium-frequency transformer is a typical quasi-static magnetic field. The excitation of this medium-frequency transformer is not of a single frequency, and thus the resulting electromagnetic field is also not of a single frequency. However, since the winding conductor material is linear and isotropic, Fourier decomposition can be used to equivalently represent the excitation as a series of harmonic sources at different frequencies [35]. Each equivalent harmonic source can then be analyzed using Maxwell’s equations.
The variables above are explained below:
- is the electric displacement vector;
- is the electric field intensity vector;
- is the magnetic flux density vector;
- is the magnetic field intensity vector;
- is the current density vector;
- is the charge density.
Through complex electromagnetic derivations, the final analytical formula for the AC-DC resistance coefficient can be obtained as follows:
The variables above are explained below:
- is the skin effect coefficient;
- is the proximity effect coefficient;
- is the number of layers in the copper foil winding;
- is the conductor penetration ratio;
- is the skin depth;
- is the angular frequency;
- is the magnetic permeability of the conductor material;
- is the electrical conductivity of the conductor material.
4.2.2. Winding and Core Window of Unequal Height
In practice, the height of the copper foil winding often varies with respect to the height of the core window. Additionally, other types of windings cannot be directly calculated using the above method. To equate the winding height to the core window height, the porosity factor algorithm is used to convert the winding equivalently. As shown in Figure 4, the winding on the far left is a segmented conductor, the height of each conductor segment is . Using the porosity factor , the winding can be converted into a copper foil winding with the same geometric height (as shown in the middle winding in Figure 4). Then, using the porosity factor , the winding can be further converted into a copper foil winding with a height equal to the core window height (as shown in the far-right winding in Figure 4, and its height is ).
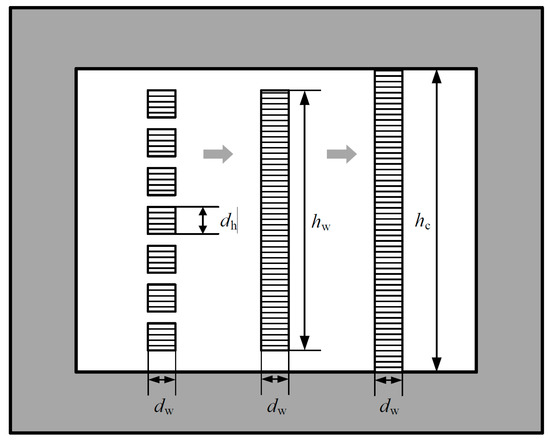
Figure 4.
Schematic diagram of winding equivalence.
The calculation formulas for and are as follows:
where is the number of segments in one layer of the winding.
After two equivalent transformations, the cross-sectional area of the winding changes compared to the actual area. To ensure the DC resistance remains constant, the porosity factor is used to adjust the conductivity and the conductor penetration ratio .
where is the adjusted conductivity, is the total porosity factor, and is the adjusted conductor penetration ratio.
The excitation current from Table 2, including the fundamental and harmonic currents, was substituted into the formula to calculate the AC-DC resistance ratio and the resulting losses. The results are shown in Table 4.

Table 4.
AC-DC resistance ratio and loss calculation results.
As shown in Table 4, the total winding loss is 3953.8 W.
5. Simulation Validation of Winding Losses in Medium-Frequency Transformers
As shown in Figure 5, a three-dimensional model of the medium-frequency transformer (whose parameters are in Table 1) was created. The transformer has an inner copper foil winding and an outer Litz wire winding.

Figure 5.
A 3D model of the medium-frequency transformer.
Transient field simulations were conducted using Ansys Maxwell, with the excitation circuit established, as shown in Figure 6. The primary winding was subjected to an excitation current containing harmonics, with multiple parallel current sources set according to Table 2. The secondary winding was set to be short-circuited. The specific simulation process is illustrated in Figure 7a. Additionally, the core of the transformer employed in this study consists of an amorphous material, 1K101. According to the laboratory measurements, the B-H curve of this material is shown in Figure 7b, and the B-P curves under various frequency excitations are presented in Figure 7c.
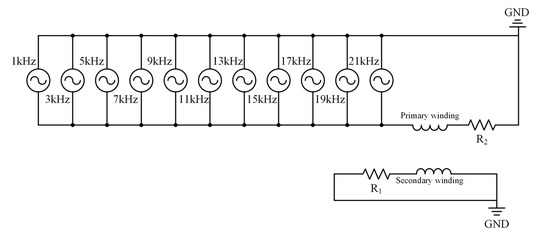
Figure 6.
Excitation circuit model.
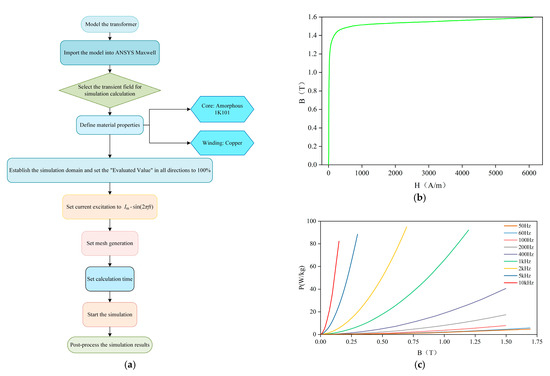
Figure 7.
Detailed description of the finite element simulation. (a) Simulation process flowchart; (b) B-H curve of the amorphous material 1K101; (c) B-P curves of the amorphous material 1K101 at various frequencies.
The prototype has a standard symmetrical structure. To reduce computational complexity, one-quarter of the prototype was simulated. The simulated copper foil winding loss curve and actual copper foil winding loss curve are shown in Figure 8. The average copper foil winding loss and Litz wire winding loss for the quarter model were 987 W and 478.45 W, respectively. Therefore, the average copper foil winding loss and Litz wire winding loss for the entire prototype were 3948 W and 1913.8 W, respectively.
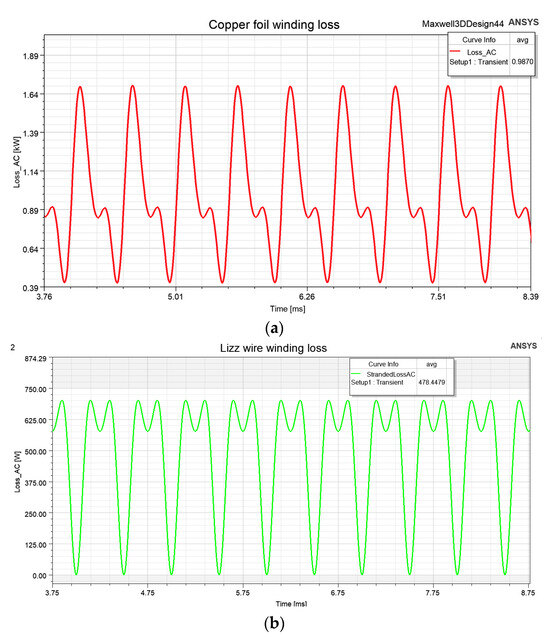
Figure 8.
One-quarter of the prototype’s winding loss simulation waveforms. (a) Copper foil winding loss waveform. (b) Litz wire winding loss waveform.
6. Experimental Validation
The equipment used to measure load losses includes a variable frequency power supply, a power analyzer (WT3000), a voltage transformer, and a current transformer.
Before conducting the experimental measurements, the following connections needed to be made: As shown in Figure 9, the high-voltage side windings of the transformer are connected in series, and the low-voltage windings are connected to the variable frequency power supply. A voltage transformer and a current transformer are installed on the low-voltage side, and their signals are fed into the power analyzer.

Figure 9.
Experimental site photograph.
The steps of the experimental measurement process are as follows: Activate the variable frequency power supply, and adjust the voltage and current to reach the rated voltage and current on the low-voltage side of the transformer. Once the data stabilize, record the losses from the power analyzer and convert the losses to 75 °C as required.
The experimental data indicated that the total winding loss, after adjustment to 75 °C, was 6239.8 W.
7. Conclusions
This paper demonstrates that the AC resistance losses in the Litz wire windings of medium-frequency transformers can be effectively approximated using the DC resistance losses. This significantly reduces the workload and complexity involved in calculating the winding losses for Litz wires in medium-frequency transformers. For copper foil windings, this study accounts for the practical scenario where the winding height often does not match the height of the core window. The porosity factor algorithm was employed to achieve equivalence, transforming the calculation into the more established method used when the winding height equals the core window height. Additionally, the changes in the cross-sectional area of the winding after equivalence were considered, and the conductivity was accordingly adjusted.
For the large-capacity medium-frequency distribution transformer prototype used in this study, the analytical calculation results, simulation results, and experimental results for winding losses are shown in Figure 10. It can be observed that the values of different types of winding losses obtained from the three different methods are very close. The discrepancy between the total winding losses calculated using the analytical algorithm and the results from the other two methods is within 6%, which is acceptable. Therefore, it can be concluded that the design algorithm for winding loss proposed in this paper is accurate and effective. This design algorithm can be widely applied in the design of large-capacity medium-frequency transformers, promoting the development of accurate winding loss calculations within this industry.
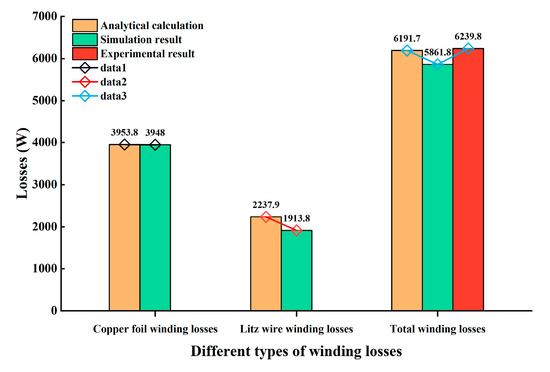
Figure 10.
Parametrical curves of winding losses obtained via the three methods.
Author Contributions
Conceptualization, Z.Y.; formal analysis, T.J.; investigation, T.J. and Z.Y.; methodology, T.J. and Z.Y.; writing—original draft, T.J.; writing—review and editing, T.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data presented in this study are available from the corresponding authors upon reasonable request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Zhang, X.; Qu, Z.; Zhang, Y.; Cai, X.; Han, X.; Chai, Y. Research on carbon emission reduction and carbon peaking strategies for power grid enterprises. In Proceedings of the 2023 4th International Conference on Advanced Electrical and Energy Systems (AEES), Shanghai, China, 1–3 December 2023; pp. 944–949. [Google Scholar] [CrossRef]
- Figueroa-Barrera, A.C.I.; Venegas-Rebollar, V.; Ruiz-Robles, D.; Moreno-Goytia, E.L.; Granados-Liberman, D. Medium frequency transformers for DC-DC converters applied to renewable energies. In Proceedings of the 2019 IEEE International Autumn Meeting on Power, Electronics and Computing (ROPEC), Ixtapa, Mexico, 13–15 November 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Ma, D.; Chen, W.; Shu, L.; Qu, X.; Zhan, X.; Liu, Z. A multiport power electronic transformer based on modular multilevel converter and mixed-frequency modulation. IEEE Trans. Circuits Syst. II Express Briefs 2020, 67, 1284–1288. [Google Scholar] [CrossRef]
- Ma, D.; Chen, W.; Shu, L.; Qu, X.; Hou, K. A MMC-based multiport power electronic transformer with shared medium-frequency transformer. IEEE Trans. Circuits Syst. II Express Briefs 2021, 68, 727–731. [Google Scholar] [CrossRef]
- Wu, W.; Li, P.; Wang, B.; Liu, Y.; Xu, T.; Du, H.; He, Y. Integrated distribution management system: Architecture, functions, and application in China. J. Mod. Power Syst. Clean Energy 2022, 10, 245–258. [Google Scholar] [CrossRef]
- Zhang, J.; Du, Y.; Li, Z.; Wang, P. Design of a medium frequency, high voltage transformer for power electronic transformer. In Proceedings of the 2014 IEEE Conference and Expo Transportation Electrification Asia-Pacific (ITEC Asia-Pacific), Beijing, China, 31 August–3 September 2014; pp. 1–5. [Google Scholar] [CrossRef]
- Guo, Z.; Rajendran, S.; Tangudu, J.; Khakpour, Y.; Taylor, S.; Xing, L.; Xu, Y.; Feng, X.; Huang, A.Q. A novel high insulation 100 kW medium frequency transformer. IEEE Trans. Power Electron. 2023, 38, 112–117. [Google Scholar] [CrossRef]
- Pourkeivannour, S.; Curti, M.; Drofenik, U.; Cremasco, A.; Lomonova, E.A. Mitigation of circulating currents in parallel foil windings for medium frequency transformers. IEEE Trans. Magn. 2022, 58, 8401904. [Google Scholar] [CrossRef]
- Gautam, S.P.; Kedia, S.; Bahirat, H.J.; Shukla, A. Design considerations for medium frequency high power transformer. In Proceedings of the 2018 IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES), Chennai, India, 18–21 December 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Kiran, M.R.; Islam, M.R.; Muttaqi, K.M.; Sutanto, D. Characterization of amorphous soft magnetic materials for toroidal core multi-winding medium frequency transformers. In Proceedings of the 2017 IEEE Region 10 Humanitarian Technology Conference (R10-HTC), Dhaka, Bangladesh, 21–23 December 2017; pp. 470–473. [Google Scholar] [CrossRef]
- Leibl, M.; Ortiz, G.; Kolar, J.W. Design and experimental analysis of a medium-frequency transformer for solid-state transformer applications. IEEE J. Emerging Sel. Top. Power Electron. 2017, 5, 110–123. [Google Scholar] [CrossRef]
- Zheng, L.; Marellapudi, A.; Chowdhury, V.R.; Bilakanti, N.; Kandula, R.P.; Saeedifard, M.; Grijalva, S.; Divan, D. Solid-state transformer and hybrid transformer with integrated energy storage in active distribution grids: Technical and economic comparison, dispatch, and control. IEEE J. Emerging Sel. Top. Power Electron. 2022, 10, 3771–3787. [Google Scholar] [CrossRef]
- Zhang, X.; Li, C.; Li, D.; Jiang, S. Study on operation parameter characteristics of induction filter distribution transformer in low-voltage distribution network. IEEE Access 2021, 9, 78764–78773. [Google Scholar] [CrossRef]
- Li, B.; Zhang, P.; Li, P.; Liu, Z.; Li, W.; Zhang, J. Research on magnetic-thermal-force multi-physical field coupling of a high-frequency transformer with different winding arrangements. Electronics 2023, 12, 5008. [Google Scholar] [CrossRef]
- Smajic, J.; Hughes, J.; Steinmetz, T.; Pusch, D.; Monig, W.; Carlen, M. Numerical computation of ohmic and eddy-current winding losses of converter transformers including higher harmonics of load current. IEEE Trans. Magn. 2012, 48, 827–830. [Google Scholar] [CrossRef]
- Arifin, Z.; Adi, N.; Ardiansah, M.H.; Aziz, H. Life assessment of aluminium and copper winding distribution transformers using loss of life analysis. In Proceedings of the 2020 2nd International Conference on Industrial Electrical and Electronics (ICIEE), Lombok, Indonesia, 20–21 October 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Zhang, W. Winding Losses in High-Speed Machines using Form-Wound Windings. Ph.D. Thesis, University of Wisconsin-Madison, Madison, WI, USA, 17 August 2015. [Google Scholar]
- Jiao, S.; Liu, X.; Zeng, Z. Intensive study of skin effect in eddy current testing with pancake coil. IEEE Trans. Magn. 2017, 53, 6201608. [Google Scholar] [CrossRef]
- Li, B.; Guo, Y.; Zhao, S. Feasibility analysis of transformer winding DC resistance measuring on-line. In Proceedings of the 2012 International Conference on Systems and Informatics (ICSAI2012), Yantai, China, 19–20 May 2012; pp. 568–571. [Google Scholar] [CrossRef]
- Wang, R.; Xiao, F.; Zhao, Z.; Shen, Y.; Yang, G. Effects of asymmetric coupling on winding AC resistance in medium-frequency high-power transformer. IEEE Trans. Magn. 2014, 50, 8402304. [Google Scholar] [CrossRef]
- Zaręba, M.; Szczegielniak, T.; Jabłoński, P. Influence of the skin and proximity effects on the thermal field in a system of two parallel round conductors. Energies 2023, 16, 6341. [Google Scholar] [CrossRef]
- Awat, A.; Arafat, O.B.; Ouzer, N.A.; Capraro, S.; Ahamat, C.; Chatelon, J.P.; Pietroy, D.; Rousseau, J.J. Determination of winding losses in magnetic integrated inductors and separate skin and proximity effects, magnetic and copper losses and study of evolution of the losses. In Proceedings of the 2021 International Conference on Electrical, Computer and Energy Technologies (ICECET), Cape Town, South Africa, 9–10 December 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Pourkeivannour, S.; Drofenik, U.; Curti, M.; Lomonova, E.A. Design trade-off analysis of dry-type medium frequency transformers with parallel foil windings. In Proceedings of the 2022 International Conference on Electrical Machines (ICEM), Valencia, Spain, 5–8 September 2022; pp. 2149–2154. [Google Scholar] [CrossRef]
- Chen, T.; Zhao, Z.; Shen, Z.; Jia, H.; Ji, J.; Wang, H. Litz-wire winding loss calculation method for optimal design of high-frequency transformers. IEEE J. Emerging Sel. Top. Power Electron. 2024, 12, 2027–2040. [Google Scholar] [CrossRef]
- Soloot, A.H.; Høidalen, H.K.; Gustavsen, B. Influence of the winding design of wind turbine transformers for resonant overvoltage vulnerability. IEEE Trans. Dielectr. Electron. Insul. 2015, 22, 1250–1257. [Google Scholar] [CrossRef]
- Wojda, R.P.; Kazimierczuk, M.K. Winding resistance of Litz-wire and multi-strand inductors. IET Power Electron. 2012, 5, 257–268. [Google Scholar] [CrossRef]
- Chen, T.; Zhao, Z.; Shen, Z.; Ming, L.; Wang, H. A homogenized FEM data-driven model for calculating leakage inductance of high-frequency transformer with Litz-wire winding. IEEE J. Emerging Sel. Top. Power Electron. 2024, 12, 2067–2081. [Google Scholar] [CrossRef]
- Li, W.; Zhou, L.; Chen, J.; Liu, B.; Gao, S.; Zhang, C.; Wang, D. Numerical model for eddy-current loss of wound core in single-phase transformer. IEEE Trans. Transp. Electrif. 2024, 10, 150–162. [Google Scholar] [CrossRef]
- Li, Y.; Yan, X.; Wang, C.; Yang, Q.; Zhang, C. Eddy current loss effect in foil winding of transformer based on magneto-fluid-thermal simulation. IEEE Trans. Magn. 2019, 55, 8401705. [Google Scholar] [CrossRef]
- Kawahara, S.; Umetani, K.; Hiraki, E. Analysis and prediction of AC resistance of Litz wire with rectangular cross-section. In Proceedings of the 2020 IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 11–15 October 2020; pp. 3273–3279. [Google Scholar] [CrossRef]
- Patel, R.; Premkumar, S.; Ambade, A.; Mangalvedhekar, H.A.; Rajan, R.N.; Bakhtsingh, R.I. AC resistance calculation of Litz wire and its modeling with FEMM. In Proceedings of the 2016 IEEE International Conference on Recent Trends in Electronics, Information & Communication Technology (RTEICT), Bangalore, India, 20–21 May 2016; pp. 692–696. [Google Scholar] [CrossRef]
- Väisänen, V.; Hiltunen, J.; Nerg, J.; Silventoinen, P. AC resistance calculation methods and practical design considerations when using Litz wire. In Proceedings of the IECON 2013—39th Annual Conference of the IEEE Industrial Electronics Society, Vienna, Austria, 10–13 November 2013; pp. 368–375. [Google Scholar] [CrossRef]
- Peng, C.; Chen, G.; Wang, B.; Song, J. Semi-analytical AC resistance prediction model for Litz wire winding in high-frequency transformer. IEEE Trans. Power Electron. 2023, 38, 12730–12742. [Google Scholar] [CrossRef]
- Wang, T.; Yuan, W.; Yuan, J. A novel semi-analytical method for foil winding losses calculation considering edge effect in medium frequency transformers. IEEE Trans. Magn. 2022, 58, 8401009. [Google Scholar] [CrossRef]
- Zhurkin, A.; Matyunina, Y.; Rashevskaya, M. Application of the short time Fourier transform for calculating electric energy losses under the conditions of a non-sinusoidal voltage. In Proceedings of the 2020 International Ural Conference on Electrical Power Engineering (UralCon), Chelyabinsk, Russia, 22–24 September 2020; pp. 230–234. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).