Brief Analysis of the Location and Determination of Maximum Capacity of Distributed Generation in Electrical Systems Considering Demand Scenarios in Ecuador

Abstract

This research focuses on evaluating the importance of the use of renewable sources through distributed generation and its implication in the operation of electrical systems given that its incorporation has a direct impact on the expansion of the capacity of the networks, the minimization losses, and the impact on end users, all supported by the growth of demand. Under this context, the study focuses on incorporating distributed generation (DG), taking scenarios of base, medium, and peak demand and the modeling of the network, and subsequently evaluating the service quality indices and operating costs in addition to the electrical variables of the system. For this purpose, the present work proposes an optimization model to be solved using the Matlab (2021b) computational program together with GAMS (37.1.0 Major release (11 November 2021)) and mixed-integer nonlinear programming, determining the optimal insertion and determination of the maximum capacity of distributed generators while complying with the technical restrictions of the system and applying optimal AC power flows. Localizing and determining maximum capacity for distributed generation (DG) in electrical systems are critical aspects of modern grid planning and operation. With the increasing penetration of renewable energy sources and the growing complexity of energy demand patterns, efficient integration of DG has become paramount for ensuring grid reliability and sustainability. In this context, the analysis of DG localization and capacity determination considering demand scenarios emerges as a critical area of research in electrical engineering. By employing advanced optimization techniques such as mixed-integer nonlinear programming (MINP), this research addresses the multidimensional challenges associated with DG deployment, including technical constraints, economic considerations, and environmental impacts. Understanding the contribution of this optimization approach to electrical engineering is fundamental for optimizing grid performance, enhancing renewable energy integration, and supporting the transition towards more resilient and sustainable energy systems. Consequently, investigating this optimization model represents a crucial step towards advancing the state-of-the-art in grid planning and facilitating the transition to a cleaner and more efficient energy future.

1. Introduction

For more than seventy years, most of the electricity generated has been produced by large-scale centralized plants owned by public utilities regulated by state standards. This has been the case in Europe, the United States, and other countries; however, in the last twenty years, private companies—also supported by public shareholders—have become increasingly important in energy markets [1]. Parallel to this, research has been carried out worldwide on new models related to the architecture of future electricity systems. In this context, analysis arises regarding the implementation of Distributed Generation (DG) plants; these projects include a variety of technologies with different characteristics in terms of efficiency, demand compatibility, capital and operating costs, emission levels, land occupation, and social acceptability [2,3]. Distributed generation (DG) of larger and smaller scales can be referred to as “Taking Power To the Load” (TPTL), which ensures electricity generation with high efficiency and low pollution. The DG ratings range from 5 kW to 100 MW worldwide [4,5]. Additionally, implementing a distributed generation unit has a low cost investment with respect to the investment required by conventional power generation plants that are centralized; this is complementary to the indicated maintenance cost of the DG, which, like that of certain renewable energies, is low due to the absence of moving parts [6]. Several research developments have encouraged the entry of distributed generation and energy storage at the distribution level; among these, Ref. [7] can be cited, which mentions the following:

Retail competition. Options for supplying customers demanding customized power supplies that suit their needs; alternatives to defer capital investments in the construction of new power plants and transmission lines. Emergence of various technologies with reduced environmental impacts and high conversion efficiencies.

On the other hand, traditional distribution networks are designed to supply radially arranged consumption whose power flow is unidirectional; in this sense, conventional electrical networks are not designed for the connection of distributed generators, which would lead to the creation of bidirectional flows of power flow, thus affecting the operation of the electrical system, particularly in elements such as primary feeders, compensators, and transformers, among others [4]. Complementing the above, the link of the DG to the grid could also cause problems in the coordination of insulation and protections of the network, given its contribution to the short circuit, and can cause disturbances in the voltage profiles since the injection of active and reactive power of the DGs will force a modification in the operation of the system [8]. Despite the problems of incorporating DG, the integration of this type of generator in the power system, as visualized in Figure 1, could create several benefits, with the main ones including the reduction of power loss in the grid; a decrease in environmental impacts; a decline of peaks; higher overall energy efficiency; reduction of transmission and distribution congestion; and voltage support and deferred investments to improve the existing generation, transmission, and distribution systems [9]. For the development of this work, several theoretical contributions focused on the location and capacity of DG must be made. The optimal determination of the location and capacity of distributed generation (DG) in power systems is a crucial research topic for the transition to more efficient and sustainable grids. A recent study by [10] addressed the importance of considering both active and reactive load power when siting DG in power systems, highlighting that joint optimization can significantly improve system stability and efficiency. This holistic approach is critical because distributed generation must meet active power demand and maintain adequate voltage and reactive power levels to ensure power quality [4]. In contrast to other recently used methods that focus only on the load’s active power, the approach proposed in the article offers a significant improvement by also considering reactive power. Previous research, such as the study by [11], has shown that failure to consider reactive power can lead to imbalances in the power grid, resulting in voltage problems, energy losses, and lower operating efficiency. Therefore, the proposed article stands out in the current landscape by providing a more comprehensive and robust approach to the location and determination of DG capacity in power systems, making it a significant contribution to the field [12]. Moreover, this research is theoretically significant, highly relevant, and beneficial in real scenarios. Unlike many methods proposed in the literature, which often lack practical implementations or specific considerations of the challenges faced by power grids in specific environments, the proposed article offers a clear and applicable methodological framework. Power grid operators and energy planners can use this framework to enhance decision-making in DG siting and sizing, making it particularly valuable and impactful compared to other theoretical approaches. In summary, the proposed paper stands out from other recently used methods by offering a comprehensive approach that considers both the active and reactive power of the load in the siting and determination of distributed generation capacity in power systems. This research contributes to the field’s theoretical advancement and provides practical and applicable tools to improve the planning and operation of power grids.

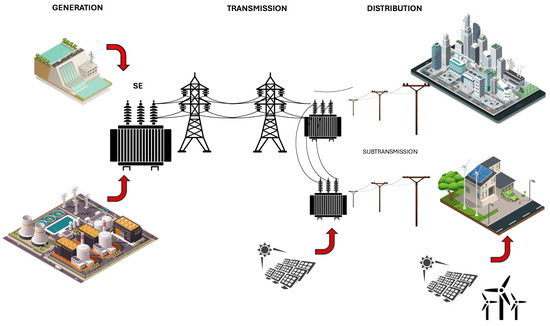
Figure 1. Distributed generation in electric power systems.

2. Background and Related Works

The necessity of accurately dimensioning and locating distributed generation (DG) within the framework of optimal dispatch strategies arises from its pivotal role in modernizing and enhancing the resilience of electrical grids. The efficient operation of power systems requires a delicate balance between generation, transmission, and distribution assets to meet demand while ensuring grid stability and reliability. In this context, the integration of DG introduces additional complexity due to its decentralized nature and variability. Optimal dispatch strategies must account for DG capacity, location, and grid constraints to effectively leverage its potential benefits while mitigating potential drawbacks such as voltage fluctuations and congestion. Precise dimensioning and placement of DG assets enable grid operators to strategically deploy generation resources where they are most needed strategically, reducing transmission losses, enhancing voltage support, and improving overall system efficiency. Moreover, optimal dispatch incorporating DG localization helps to maximize renewable energy utilization, contributing to sustainability goals and fostering energy independence. Accurately determining DG capacity and location is critical to modern grid management strategies, facilitating the transition toward a more resilient, efficient, and sustainable energy infrastructure.

2.1. Distributed Generation in Electric Power Systems

Safety and reliability levels throughout the power system must be preserved, and its structure must evolve to meet the growth in consumer demand, which is why the inclusion of DGs is used to provide energy efficiently, which are placed at points close to the load [2,12]. The main benefits for the electricity system with DG over large generators are the investment costs involved in the generation and transmission of large generation units, with this being a determining factor in modifying the system topology and including this new technology to supply the demand using small generation units [5]. The inclusion of distributed generation provides efficiency, flexibility, and optimal economy; so, it is necessary to study and include it in the planning considering financial, environmental, technical, and technological aspects to determine its capacity and optimal location of the DG units. The general elements considered for the incorporation of DG are as follows [5]:

a.

Technical: the systems to be connected must be adapted to the connection network in terms of the technical characteristics of the equipment and their quality factors for the service.

b.

Technological: innovation in the development of smaller-scale technology equipment connected to the power system, with higher efficiency and capacity, as well as the development of modular equipment that has the advantage of being able to be added to and removed from the system according to the required configuration and adjusting to the demand, thus acting as cogenerators.

c.

Environmental: energy policies give preferential treatment to renewable energies, reducing dependence on units that use polluting fuels for generation.

d.

Economic: unlike large power plants that are far from the distribution networks where transmission generates losses and production must be higher to meet demand, high prices are the result of the process; therefore, it is essential to highlight the difference between the DG that supplies the local load by joining the distribution network directly, thus eliminating transportation costs, and also reduces network congestion.

The solution to the dynamic growth of demand and the disturbances that can cause electrical energy losses due to the lack of response of centralized generation is decentralized generation in a determined framework based on planning studies and for strategic sectors. However, the use of DG causes certain inconveniences to the grid due to its insertion. In Figure 2, the advantages and disadvantages of implementing DG are detailed.

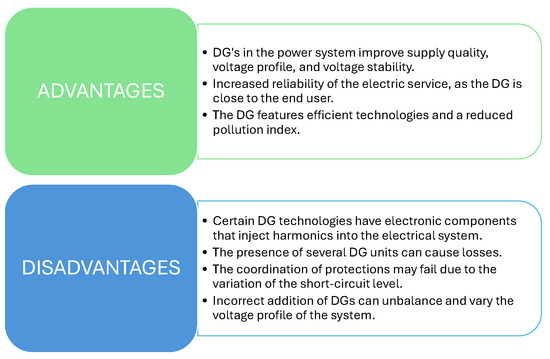
Figure 2. Advantages and disadvantages of distributed generation.

Considering the above points, sizing and location should be variables considered in the optimal dispatch to meet the needs of the system and users; an example of the optimization process with DG considering economic aspects is to achieve reduced prices by delivering energy at peak hours [13]; an example of the optimization process with DG considering economic elements is to achieve reduced prices by providing energy at peak hours. Typically, the generation units incorporated in an electrical system are large-scale and involve high power and voltage; with the connection of DG, the voltage levels available in the different stages of the system are taken advantage of, making it more dynamic so that users deliver and receive energy to and from the grid. The connection of distributed generation to the electric grids depends on the type of technology and the voltage level to be connected. For example, according to [14], the transmission system in Ecuador, where the voltage level is higher than 138 kV, is located in the traditional centralized energy systems, while in the sub-transmission stage it can be integrated-grade hydraulic generation units and photovoltaic, wind farms, geothermal, tidal, and geothermal generation. In the medium-voltage distribution stage, between 13.8 to 69 kV, medium-sized wind, photovoltaic and solar thermal projects, biomass, hydroelectric, and combined cycle plants are incorporated. Then, for the low-voltage distribution network between 120 and 220 kV, small- and micro-generation systems such as internal combustion systems, micro-hydro turbines, and solar panels can be incorporated. Figure 3 shows how the subset of distributed resources is located in the power electric system depending on the voltage and capacity level, and it is visualized that the location is undefined in the distribution or sub-transmission network [13].

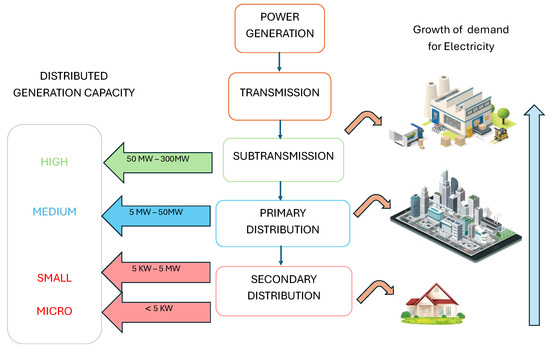
Figure 3. Capacity and location of the DG in the electric power system.

There are several energy sources used in distributed generation due to the technological development that exists, but due to the need to safeguard safety and reduce the environmental impact, the consumption of energy—preferably originating from renewable energy sources—is increasing. The existing technologies based on energy conversion are as follows [8,9,10,11]:

a.

Internal combustion thermal machines;

b.

Hydroelectric plants;

c.

Fuel cells;

d.

Wind power generation;

e.

Solar power generation;

f.

Tidal power generation;

g.

Biomass resource;

h.

Geothermal energy.

Efforts are being made to develop the best technology to take advantage of renewable resources in electricity generation because these sources have high potential in distributed and large-scale generation systems [15].

2.2. Impact of the DG on Distribution Planning

The increasing growth in demand mainly affects the distribution network, forcing it to operate at its maximum capacity, thus generating losses and altering voltage levels. Added to the losses that occur in the transmission from the immense power plants to the consumption points, this becomes a problem that does not allow the main objective of supplying quality electricity to the user to be met; therefore, arduous studies are carried out in distribution planning, projecting future demand and adding the incorporation of distributed generation on a larger scale, considering the great benefits of its integration [16]. The combination of the DG in the distribution system is profitable as long as the sizing and location are optimal, as well as the energy costs. Concerning costs of sale, these must be maximized for the owner of the unit by setting the price to proceed to the determination of the location and capacity of the DG units, to consequently lead to the minimization of the cost for the purchase of energy for the consumer by determining the proportion of energy taken from the centralized generators and the amount of energy absorbed from the distributed generation. This model is included in the planning of the distribution system according to the demand growth forecast. According to [16], the methodologies to address this problem can be analytical, genetic algorithms, multiobjective optimization, and mathematical programming. Based on the above, this work develops an optimization model that minimizes operating costs, locating and determining the maximum capacity of distributed generation units to analyze their impact on the distribution system. This analysis allows the modeling of a traditional electricity market and one with the insertion of distributed generation to study the importance of its inclusion in distribution expansion planning and how it improves the reliability of the electric power system [17]. The influence of distributed generation on distribution has been described in technological, economic, and environmental terms; now, the technical problems caused by DG, how existing networks are affected, and what should be considered in the operation and expansion planning [3,13] are technically specified.

2.2.1. Losses Related to the DG

The topology of the distribution network is the path through which electrical energy is transported, where the most significant amount of losses occur due to conductor resistance, which is why the location of the DG is mainly related to the structure of the grid, as this type of generation is usually located at points close to the loads without considering geographical spatial components, among others; thus, the energy path is smaller and the losses are proportionally reduced, improving transmission and reducing the load ability of the system equipment that make it up. Given that the greater penetration of distributed resources leads to a decrease in losses as opposed to the scenario without DG, considering the constant growth of demand and also depending on the technology to be inserted [18].

2.2.2. Voltage Profile with DG

In power flows, the elements of the electrical system are represented by an impedance that directly links a relationship with the voltage at each node or connection point in the network, and the voltage profile varies depending on how far the load node is from the substation depending on the power flow and the impedance of the substation as illustrated in Figure 4.

$$V_C=V_S-I(R+jX)\to V_C=V_S-\left[\frac{P-jQ}{V_s}\right](R+jX)$$

(1)

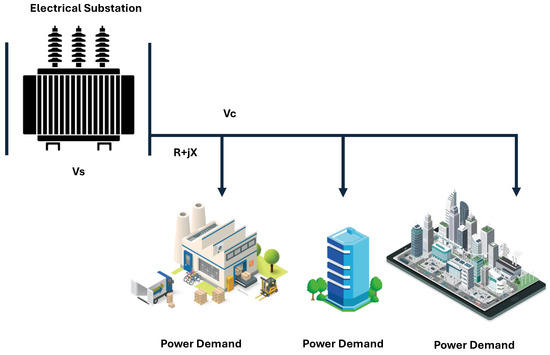
Figure 4. Power flow to the demand side of the distribution section.

The voltage measured at the load connection node, as can be seen in Figure 4 and Equation (1), depends on the power flows, taking the substation voltage as a reference; the same happens for each demand point along the section. If DG is incorporated, the impact on the voltage profile is positive because it acts as a voltage regulator as long as the location is adequate and the network design is considered in the study; in traditional systems, transformers with taps, capacitors, and regulators are used to control the voltage and, thus, ensure a voltage limit in the network for the consumption of users and equipment [1]. Therefore, the correct location is ideal; for example, when the DG is at the end of a section of the network, the power flow through the same decreases; thus, the voltage drops, resulting in a higher voltage profile, allowing the demand to have higher consumption without loading the network or significantly affecting the voltage level. On the contrary, the adverse effects of the installation of distributed generation occur when it is placed on the low voltage side of a transformer with taps because the injection of generation reduces the load and causes the transformer to reduce the voltage as an effect of the more significant voltage drop [19].

2.2.3. Flows in the Distribution Network with DG

The direction of the load flows in energy transport is changing; with the DG, benefiting the network by reducing the congestion of the lines according to different scenarios is possible. The first scenario occurs when the capacity of the DG unit connected near the load is lower than the demand’s capacity requirement. In this case, the demand is supplied with what is available and the network provides the remainder; this reduces the congestion of the network, but the flow’s direction toward the load remains unchanged. If the losses are reduced, the next scenario happens when the power of the distributed resource exceeds the demand requirement. The load is supplied and the distribution network also delivers the surplus to the power system as a reserve, i.e., the flow’s direction in the network changes, but energy transportation continues with losses that, depending on the surplus, either increase or decrease. Based on these events, it is necessary to consider the network elements’ capacity limits due to the thermal effects that overload in energy absorption and delivery might cause to ensure the system performs adequately.

2.2.4. System Protections with DG

The planners and designers of the distribution system must anticipate the impact of DG, considering the bidirectional flow. DG technologies possess a fault level that falls within the current limit of the protection elements for producing a response. The distribution stage varies according to the behavior of the demand. Typically, the incorporated generation units are small and their impact is insignificant. However, adding several units can affect the short-circuit rates and the coordination of the protection elements [10].

2.2.5. Power Quality with the DG

Distributed generators mainly build the composition with power electronics, such as power converters of photovoltaic systems or wind turbines, and other technologies that contribute to nonlinear loads whose effect is to distort current waves, voltage, and harmonic pollution to the network; however, specifically, the DG harms the system due to flickers in the voltage at the input and output of the DG units generating intermittency in the voltage by the control equipment and DC units that interact in the event; inevitably, the harmonics in large quantities due to the power electronics involved in this equipment affect the operation of the distribution system and, consequently, the power system [5]. Despite these negative aspects, DG can also improve power quality. When the load-parallel power grid is large, use DG quickly and as much as possible to reduce system failures and improve the stability of the entire power grid, thereby ensuring power quality [2].

3. Optimization Model

The following section develops the optimization model that allows locating and establishing the maximum capacity of the distributed generation plants to be implemented in electrical systems to minimize the operating costs associated with demand and supply, which will be solved using the GAMS software. This model allows defining the quantity and capacity of the distributed generators to be incorporated in the electrical systems at medium voltage levels, considering the active and reactive power balance restrictions, voltage limits at the nodes, binary restrictions, and the maximum capacity of the electrical system links.

3.1. General Considerations

We will consider the following for resolving the optimization model.

i.

Application of the optimization model for the 13-node IEEE system.

ii.

Supply of the load corresponding to that established in the 13-node IEEE system.

iii.

Modeling three load scenarios corresponding to a 7% increase in initial demand; therefore, each scenario is called base, average, and peak demand.

iv.

Determine the number and capacity of distributed generators for each of the demands.

v.

To assess the operational cost, the price of DG corresponds to the average price for promoting renewable energy through distributed generation, which amounts to 50 USD/MWh. Meanwhile, the cost of energy supplied by the power system is valued using the end-user tariff, which for the analysis will amount to (9.017 ¢/kWh, approx. 90 USD/MWh) [20].

vi.

To technically and economically assess the supply costs of the demand, evaluate the voltage quality indices for each loading scenario, and analyze the various electrical variables.

As previously mentioned, the study considers the IEEE 13-node system, which comprises twelve (12) links, a load of approximately 48 MW, and 34 MVAr distributed across 10 of the 13 nodes. In this context, the study considers different load scenarios with a 7% growth compared to the initial scenario. For each scenario, the quantity and capacity of distributed generators are determined, with a maximum capacity of 10 MW. Additionally, the electrical parameters of the system will be evaluated as a result of the optimization model, and the voltage quality index will be determined according to the regulations of the Ecuadorian electricity sector.

In this regard, the optimization model considers the operational constraints imposed and incorporates binary and continuous variables that determine the location of the DG and their maximum capacity, which interact to supply the demand under economic conditions and technical criteria.

3.2. Mathematical Formulation

The mathematical model considers a mixed-integer nonlinear optimization composed of an objective function and constraints, the details of which are presented below.

3.2.1. Objective Function

The optimization model will establish an objective function that minimizes the operational costs of meeting the demand.

$$FO=P_s{P}_m+\sum _{i=1}^{n}LCOE\left(u_i\right)P_{D{G}_i}$$

(2)

where the variables are defined as follows:

• $P_s$—System Active Power;
• $P_m$—Price applied to the final consumer (USD/MWh);
• $LCOE$—Average price for the promotion of renewable energy through DG (USD/MWh);
• $u_i$—Binary variable of selection of the DG at each i-node;
• $P_{D{G}_i}$—DG power dispatched at each i-node (MWh).

3.2.2. Constraints

The mathematical model will use optimal power flows to minimize the objective function, modeling constraints associated with the stable operation of the electrical system and the technical conditions of the DG. Consequently, we will specify these constraints below.

(a)

Nodal balance of active and reactive power

To model power flow, we proceed with the nodal balance of active and reactive power, which models the powers injected and withdrawn at each node of the electrical system. This includes distributed generation and its contribution. The mathematical formulation is as follows:

$$\sum P_{gi}-\sum P_{di}+PD{G}_i=\sum _{k=1}^n{V}_i{V}_k[g_{ik}cos\left({\delta }_{ik}\right)+b_{ik}sin\left({\delta }_{ik}\right)]$$

(3)

$$\sum Q_{gi}-\sum Q_{di}+QD{G}_i=\sum _{k=1}^n{V}_i{V}_k[g_{ik}sin\left({\delta }_{ik}\right)-b_{ik}cos\left({\delta }_{ik}\right)]$$

(4)

where the variables are as follows:

• $P_{gi}$—Active power of the generator located at i-node;
• $P_{di}$—Active power of the load located at i-node;
• $Q_{gi}$—Reactive power of the generator located at i-node;
• $Q_{di}$—Reactive power of the load located at i-node;
• $V_i,V_k$—Magnitude of the voltage at i-node and node k, respectively;
• ${\delta }_i,{\delta }_k$—Voltage angle at i-node and node k;
• $g_{ik}$—ik-th element of the mutual conductance matrix;
• $b_{ik}$—ik-th element of the mutual susceptance matrix;
• $PD{G}_i$—Active power of the DG located at i-node;
• $QD{G}_i$—Reactive power of the DG located at i-node.

(b)

Restriction on Voltage Limits

This constraint ensures that the voltage magnitude variable remains within the permissible limit, providing the operational stability of the electrical system. The mathematical formulation is as follows:

$$V_{mi{n}_i}\le V_i\le V_{ma{x}_i}$$

(5)

where the variables are defined as follows:

• $V_{mi{n}_i}$—Minimum voltage at i-node in the electrical system;
• $V_{ma{x}_i}$—Maximum voltage at i-node in the electrical system.

(c)

Angular constraint at each bus of the system

This constraint sets the limits of the voltage phasor angle at each node, ensuring the operation of the electrical system. The constraint is described as follows:

$${\delta }_{mi{n}_i}\le {\delta }_i\le {\delta }_{ma{x}_i}$$

(6)

where the variables are as follows:

• ${\delta }_{mi{n}_i}$—Minimum angle at i-node of the system;
• ${\delta }_{ma{x}_i}$—Maximum angle at i-node of the system.

(d)

Constraint for link limits

The restriction models the active power capacities to be carried by each link, corresponding to the thermal limit that must not be exceeded, and depends on the physical laws regarding optimal power flow. The mathematical modeling is as follows:

$$F_{mi{n}_{i,j}}\le V_i^2\left(g_{ii}\right)+V_i{V}_k[g_{ik}sin\left({\delta }_{ik}\right)-b_{ik}cos\left({\delta }_{ik}\right)]\le F_{ma{x}_{i,j}}$$

(7)

where the variables are as follows:

• $F_{mi{n}_{i,j}}$—Minimum active power flow between i-node and k-node;
• $F_{ma{x}_{i,j}}$—Minimum active power flow between i-nodes and k-nodes.

(e)

Constraint on system power limits

The system, through the interconnection substation, enables the supply to meet the demand of the medium-voltage distribution system. Operational constraints adjust the limits in this regard. The following restrictions impose that the dispatched active and reactive power does not exceed the established constitutive limits.

$$P_{sy{s}_{min}}\le P_{sys}\le P_{sy{s}_{max}}$$

(8)

$$Q_{sy{s}_{min}}\le Q_{sys}\le Q_{sy{s}_{max}}$$

(9)

where the variables are defined as follows:

• $P_{sy{s}_{min}}$—Minimum active power of the system;
• $P_{sy{s}_{max}}$—Maximum active power of the system;
• $P_{sys}$—Active power to be dispatched by the system;
• $Q_{sy{s}_{min}}$—Minimum reactive power of the system;
• $Q_{sy{s}_{max}}$—Maximum reactive power of the system;
• $Q_{sys}$—Reactive power of the system to be dispatched.

(f)

Constraint on distributed generation capacity limits

The constraint allows setting the capacity limits of DG to be implemented at each node, considering international standards, with the following mathematical formulation:

$$CAPD{G}_{min}\le CAPD{G}_i\le CAPD{G}_{max}$$

(10)

where the variables are the following:

• $CAPD{G}_{min}$—Minimum capacity of the DG to be incorporated at i-node;
• $CAPD{G}_{max}$—Maximum capacity of the DG to be incorporated at i-node;
• $CAPD{G}_i$—Maximum capacity of the DG to be incorporated at i-node.

(g)

Constraint for limits of DG

Based on their physical constitution, the distributed generators to be implemented maintain operational constraints regarding the power to be delivered. In this regard, the following constraints impose that the dispatched active and reactive power does not exceed the established constitutive limits.

$$0\le PD{G}_i\le \left(u_i\right)CAPD{G}_i$$

(11)

$$QD{G}_i=PD{G}_i\left[tan\left(acos\left(f{p}_i\right)\right)\right]$$

(12)

where the variables are as follows:

• $PD{G}_i$—Active power of DG located at i-node;
• $QD{G}_i$—Reactive power of DG located at i-node;
• $f{p}_i$—Power factor of DG;
• $u_i$—Binary selection variable of DG at each i-node.

(h)

Constraint for the placement of DG generation

This constraint models the limitation on the number of distributed generators to be implemented in the electrical network, as expressed mathematically below:

$$\sum _{i=1}^G{u}_i\le N_{max}$$

(13)

where the variables are as follows:

• $u_i$—Each distributed generator located at i-node has a binary variable for selection;
• $N_{max}$—Maximum number of DG units to be implemented in the system.

4. To Implement the Mathematical Model

To evaluate the proposed optimization model, the IEEE 13-node test model, which includes a power supply, ten electrical loads, and twelve lines modeling the network, will be utilized. The electrical system data are systematically acquired; the optimization model will be applied and solved using the GAMS software. The results will assist in evaluating the voltage quality indicators of the system and its electrical parameters, as well as in establishing the quantity and capacity of distributed generators.

4.1. Parameters

The electrical system parameters that will enable the applicability of the optimization model are detailed below in Table 1.

Table 1. Network data—IEEE 13 nodes.

Link	${\mathbf{NC}}_{\mathit{i}}$	${\mathbf{NC}}_{\mathit{f}}$	Rpu	Xpu
L1	1	2	0.016	0.0129
L2	2	3	0.0652	0.0123
L3	3	4	0.1149	0.1171
L4	2	5	0.12	0.3579
L5	5	6	0.12	0.3579
L6	2	7	0.0018	0.032
L7	7	8	0.0689	0.0702
L8	8	9	0.0689	0.0702
L9	8	10	0.0599	0.1786
L10	7	11	0.0704	0.0714
L11	11	12	0.1896	0.0724
L12	7	13	0.0728	0.0381

$Link$—Corresponds to the links of the network to be modeled; $N{C}_i$—Initial node of the link; $N{C}_f$—Final node of the link; $Rpu$—Resistance per unit of the link; $Xpu$—Reactance per unit of the link.

Similarly, the IEEE 13-node electrical system model contains the following loads, whose active and reactive power values are shown in Table 2.

Table 2. Technical data of the system load.

Node	${\mathit{N}}_{\mathit{c}}$	${\mathit{P}}_{\mathit{car}}$	${\mathit{Q}}_{\mathit{car}}$
n1	1	0.00	0.00
n2	2	2.00	1.60
n3	3	0.00	0.00
n4	4	4.00	3.0
n5	5	3.90	1.4
n6	6	3.40	2.55
n7	7	3.35	2.51
n8	8	0.00	0.00
n9	9	5.10	3.83
n10	10	5.60	4.20
n11	11	2.00	1.50
n12	12	4.50	3.83
n13	13	5.70	4.28

$Nc$—Connection node; $P_{car}$—Active power for each load in MW; $Q_{car}$—Reactive power for each load in MVAR.

On the other hand, the energy source corresponds to the power delivered by the grid to the distribution system. For this purpose, this source will be modeled as the slack generator, and its data are as follows in Table 3.

Table 3. Technical specifications of the power source.

${\mathit{P}}_{\mathit{m}\mathit{a}\mathit{x}}$ [MW]	${\mathit{P}}_{\mathit{m}\mathit{i}\mathit{n}}$ [MW]	${\mathit{Q}}_{\mathit{m}\mathit{a}\mathit{x}}$ [MVAR]	${\mathit{Q}}_{\mathit{m}\mathit{i}\mathit{n}}$ [MVAR]	Price [USD/MWh]
100	0	60	−60	90

$P_{max}$—The maximum active power of the system to supply the total load of the distribution system; $P_{min}$—The minimum active power of the system to supply the total load of the distribution system; $Q_{max}$—The maximum reactive power of the system to supply the total load of the distribution system; $Q_{min}$—The minimum reactive power of the system to supply the total load of the distribution system. $Price$—Price to end-users concerning the distribution system.

Finally, the potential distributed generators to be used will have a maximum capacity of 10 MW, as established in Regulation No. ARCERNNR 002/21, “Regulatory framework for the participation in the distributed generation of companies authorized to carry out the generation activity”. Considering the objective function and the related restrictions, the optimization problem can be solved using mixed-integer nonlinear integer programming, known as MINLP, which uses the GAMS (General Algebraic Modeling System) optimizer.

4.2. Resolution Procedure

For the optimization problem resolution, we will first acquire data associated with the technical characteristics of the IEEE 13-node system network, demand values at each node, and link capacities; additionally, we include the connection substation of the distribution system with the transmission system, considering this node as the slack of the system. Valuing the energy delivery from this node at the average end-user tariff, we will proceed with the corresponding modeling, considering the constraints and objective function described earlier. Algorithm 1 details the algorithm, showing the process of solving the optimization model.

Algorithm 1. Application of GA to Optimally Locate and Size DGFs
Step 1:	Definition of the models, in which the GA will be applied.
Step 2:	Determination of the demand at each node.
Step 3:	Establishment of system energy prices and distributed generation.
Step 4:	Determination of the capacity limits of potential distributed generators.
Step 5:	Set maximum transfer capacities on each link.
Step 6:	Set the Y bus of the system to be modeled.
Step 7:	Optimization Problem
	Set initial conditions
	Set electrical grid and Y-bar modeling.
	Set continuous variables.
	$P_g,Q_g,V_i,{\delta }_i,P_{i,k},PD{G}_i,QD{G}_i,CAPD{G}_i$
	Set binary variables
	$u_i$
	Set the restrictions
	$\sum P{g}_i-\sum P{d}_i+PD{G}_i={\sum }_{k=1}^n{V}_i{V}_k{g}_{ik}cos\left({\delta }_{ik}\right)+b_{ik}sin\left({\delta }_{ik}\right)$
	$\sum Q{g}_i-\sum Q{d}_i+QD{G}_i={\sum }_{k=1}^n{V}_i{V}_k{g}_{ik}sin\left({\delta }_{ik}\right)-b_{ik}cos\left({\delta }_{ik}\right)$
	$V_{mi{n}_i}\le V_i\le V_{ma{x}_i}$
	${\delta }_{mi{n}_i}\le {\delta }_i\le V{\delta }_{ma{x}_i}$
	$Fmi{n}_{i,j}\le V_i^2{g}_{ii}+V_i{V}_k[g_{ik}sin\left({\delta }_{ik}\right)-b_{ik}cos\left({\delta }_{ik}\right)]\le Fma{x}_{i,j}$
	$Psy{s}_{min}\le Psys\le Psy{s}_{max}$
	$Qsy{s}_{min}\le Qsys\le Qsy{s}_{max}$
	$CAPD{G}_{min}\le CAPD{G}_i\le CAPD{G}_{max}$
	$0\le PD{G}_i\le \left(u_i\right)CAPD{G}_i$
	$QD{G}_i=PD{G}_i\left[tan\left(acos\left(fp\right)\right)\right]$
	${\sum }_{i=1}^G\left(u_i\right)\le Nmax$
	Objective Function
	$Fo=P_{sys}{P}_m+{\sum }_{i=1}^{N}LCOE\left(u_i\right)PD{G}_i$
Step 8:	Analysis of results by case studies.
Step 9:	End.

4.3. Study Case

We will simulate two cases to establish relevant aspects of the study and the modeling itself. In the first case, the electrical system does not consider incorporating distributed generation, meaning that the 13-node IEEE electrical system is solely supplied by the connection substation with the transmission system, adhering to the respective constraints. Meanwhile, the second case study will consider incorporating distributed generation, through which the capacity and dispatch of such generation will be determined while adhering to the constraints. By comparing both cases, we will validate the benefits of this option. For this purpose, we will analyze the system costs, electrical variables, and voltage quality indices according to the applicable regulations for Ecuador. The resolution process will begin by acquiring data associated with the following:

i.

Characteristics and technical parameters of the network to be modeled;

ii.

The demand for active and reactive power at each node;

iii.

We assess system costs using parameters of distributed generation and economic parameters;

iv.

The maximum capacity parameters of the links are determined, followed by the resolution of the optimization model.

Electricity demand growth considers the 7% value due to historical projections and growth trends in electricity consumption. We consider two scenarios for the proposed case studies involving a 7% increase in demand, with the values shown in Table 4.

Table 4. Nodal demand and increment scenarios.

Node	Base Scenario		Scenario 1		Scenario 2
	MW	MVAR	MW	MVAR	MW	MVAR
n1	0.00	0.00	0.00	0.00	0.00	0.00
n2	2.40	1.92	2.57	2.05	2.75	2.20
n3	0.00	0.00	0.00	0.00	0.00	0.00
n4	4.80	3.60	5.14	3.85	5.50	4.12
n5	4.68	1.68	5.01	1.80	5.36	1.92
n6	4.08	3.06	4.37	3.27	4.67	3.50
n7	4.02	3.01	4.30	3.22	4.60	3.45
n8	0.00	0.00	0.00	0.00	0.00	0.00
n9	6.12	4.60	6.55	4.92	7.01	5.27
n10	6.72	5.04	7.19	5.39	7.69	5.77
n11	2.40	2.80	2.57	1.93	2.75	2.06
n12	5.40	4.06	5.78	4.34	6.18	4.65
n13	6.84	5.14	7.32	5.50	7.83	5.88

Figure 5 displays the electrical schematic of the system.

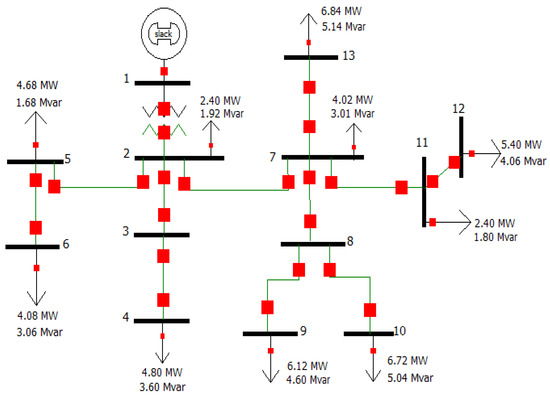
Figure 5. IEEE 13-node system one-line diagram.

The previous presentation includes the electrical parameters used to model the system depicted in Figure 5, tabulated in Table 5.

Table 5. Parameters of the IEEE 13-node system network.

Link	${\mathit{N}}_{\mathit{start}}$	${\mathit{N}}_{\mathit{end}}$	${\mathit{R}}_{\mathit{pu}}$	${\mathit{X}}_{\mathit{pu}}$
L1	1	2	0.016	0.0129
L2	2	3	0.0652	0.1023
L3	3	4	0.1149	0.1171
L4	2	5	0.12	0.3579
L5	5	6	0.12	0.3579
L6	2	7	0.018	0.0032
L7	7	8	0.0689	0.0702
L8	8	9	0.0689	0.0702
L9	8	10	0.0599	0.1786
L10	7	11	0.0704	0.0714
L11	11	12	0.1896	0.0724
L12	7	13	0.0728	0.0381

In addition to the indicated information, the capacity of the links corresponds to the data presented in Table 6.

Table 6. Link capacity of the IEEE 13 system.

Link	${\mathit{N}}_{\mathit{start}}$	${\mathit{N}}_{\mathit{end}}$	${\mathit{Cap}}_{\mathit{max}}$[MW]
L1	1	2	60
L2	2	3	10
L3	3	4	10
L4	2	5	15
L5	5	6	10
L6	2	7	40
L7	7	8	20
L8	8	9	10
L9	8	10	10
L10	7	11	15
L11	11	12	10
L12	7	13	10

With the displayed data and parameters, we analyze the case studies and simulate the scenarios described earlier.

5. Analysis of Results

We will consider each case study for the analysis of results. We will evaluate the system without distributed generation, considering the demand growth for the two scenarios. Subsequently, we will analyze the second case based on incorporating DG and its implications for the electrical variables. Before examining the cases, we simulate the initial case using the DIgSilent software (DIgSILENT Power Factory 15.1.7). Subsequently, we compare the voltage variable obtained with GAMS and the simulator with the values presented in Table 7.

Table 7. Comparison of electrical variables between GAMS and DIgSilent.

Node	Gams	DIgSilent	%Error
n1	1.0000	1.0000	0.0000
n2	0.9947	0.99467	0.0003
n3	0.9877	0.98767	0.0002
n4	0.9777	0.97765	0.0005
n5	0.9654	0.96539	0.0001
n6	0.9486	0.9487	0.0004
n7	0.9933	0.99329	0.0005
n8	0.9771	0.97709	0.0001
n9	0.9695	0.9695	0.0000
n10	0.9636	0.963598	0.0002
n11	0.9834	0.983396	0.0004
n12	0.9698	0.969797	0.0003
n13	0.9863	0.9863	0.0000

The results indicate that the error obtained is minimal for the voltage variable, which leads to the conclusion that the optimization model functions correctly. Therefore, it proceeded to use it to evaluate the case studies.

5.1. Initial Case: Meeting Demand without DG

Acquiring the described data and considering the absence of DG incorporation into the system, we solve the proposed optimization model, obtaining the generation dispatch, the optimal power flow (and thus, the electrical variables), as well as the system’s operating cost. The results for each load scenario are displayed in Figure 6, illustrating the voltage profile for each demand scenario, indicating a decrease in voltages with increasing load.

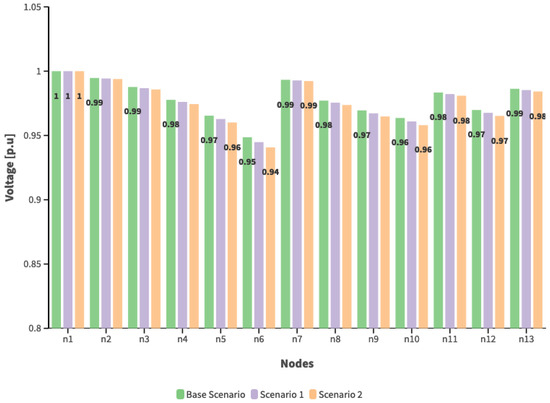
Figure 6. Voltage profile for each demand scenario without DG.

Considering the voltage values obtained, the voltage quality index is calculated for each demand scenario, as shown in Figure 6.

Table 8 presents the voltage quality index, and the highlighted results correspond to the nodes located at the end of each branch of the modeled electrical system, which will serve to evaluate the impact of DG when incorporated into the network. Additionally, Figure 7 illustrates the amount of active and reactive power the system delivers through the substation, with values tabulated according to the demand scenario. An increase in demand leads to an increase in the energy supplied by the system through the interconnection substation.

Table 8. Voltage level quality index by demand scenario.

Node	Base Scenario [%]	Scenario 1 [%]	Scenario 2 [%]
n1	0.000	0.000	0.000
n2	−0.534	−0.5730	−0.615
n3	−1.231	−1.320	−1.416
n4	−2.227	−2.387	−2.560
n5	−3.458	−3.717	−3.993
n6	−5.135	−5.518	−5.930
n7	−0.670	−0.718	−0.771
n8	−2.287	−2.453	−2.633
n9	−3.055	−3.277	−3.517
n10	−3.643	−3.908	−4.195
n11	−1.663	−1.783	−1.912
n12	−3.022	−3.241	−3.476
n13	−1.373	−1.472	−1.578

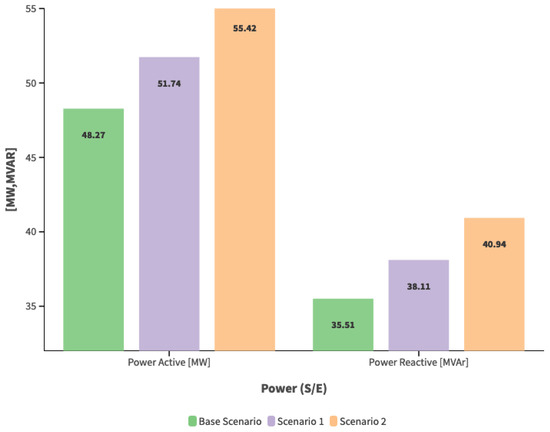
Figure 7. Dispatch of the substation to supply the demand of the IEEE 13-node system.

In line with the preceding, an increase in demand will also increase losses when the system does not consider the inclusion of DG. Figure 8 depicts this aspect.

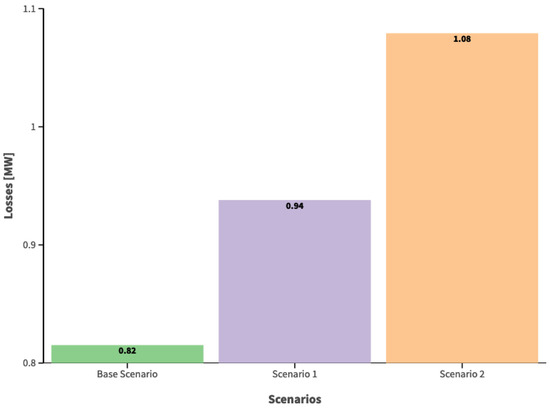
Figure 8. System losses without DG by load scenario.

Finally, we obtain the operating cost results for each demand scenario, and Figure 9 depicts their values.

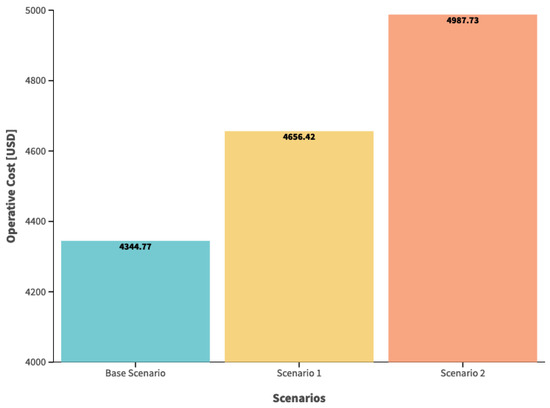
Figure 9. Operating cost as a function of the demand scenario.

The results associated with costs indicate that an increase in demand leads to an increase in operating expenses, provided that the incorporation of DG does not exist.

5.2. Case 2: Supplying Demand with DG

Given the three load scenarios, we proceed to integrate a quantity of two, four, and six distributed generators for each of these scenarios. This aspect will allow for evaluating the modeled system’s technical and economic parameters, considering the results obtained in the initial case, where no distributed generation exists. Initially, the results of the DG placement for each load scenario will be presented and tabulated in Table 9.

Table 9. DG location by load scenario.

Number of DG	Node	Base Scenario	Scenario 1	Scenario 2
	n3	-	1.00	1.00
With 2 DGs	n5	-	1.00	1.00
	n7	1.00	-	-
	n11	1.00	-	-
	n4	1.00	1.00	1.00
	n5	1.00	1.00	1.00
With 4 DGs	n7	1.00	-	-
	n9	1.00	1.00	1.00
	n12	-	1.00	1.00
	n2	-	1.00	-
	n3	-	1.00	1.00
	n4	1.00	1.00	-
	n5	-	1.00	1.00
With 6 DGs	n6	1.00	1.00	1.00
	n9	1.00	-	1.00
	n10	1.00	-	1.00
	n11	-	-	-
	n12	1.00	-	1.00
	n13	1.00	-	-

Table 9 indicates that the location of DGs varies depending on the amount of active and reactive power of the load at each system node. Therefore, despite the system having the same number of distributed generators, the amount of load and the links’ limits will determine the DGs’ placement. Consequently, the optimizer chooses the nodes where the DGs should be placed, resulting in different DG locations across various load scenarios. In addition to the above, the following table presents the capacity and dispatched power of the selected DGs.

Analyzing Table 10 reveals that the capacity and dispatch of the selected DG depend on the fulfillment of constraints associated with the DG’s network and the minimization of the system’s operating costs. Consequently, in the base scenario and scenario 1, when two and four DG units integrate into the system, their capacity and dispatched power match and approach the maximum value of the DG’s capacity. However, examination of the scenario with six DG units indicates that while a capacity lower than the maximum is determined, the dispatched power is also lower. This adherence to network constraints underscores the distribution system’s ability to supply power to the transmission system. These factors will be evaluated when assessing the electrical variables linked to the substation linking the distribution and transmission systems. Figure 10, Figure 11 and Figure 12 exhibit the voltage module outcomes for each load scenario, considering the location and capacity of the selected DG units and the quantity of incorporated DG units.

Table 10. Capacity and power of selected DG by load scenario.

Number of DG	Node	Base Scenario		Scenario 1		Scenario 2
		CAP [MW]	PDG [MW]	CAP [MW]	PDG [MW]	CAP [MW]	PDG [MW]
	n7	10.00	10.00	-	-	-	-
With 2 DGs	n11	10.00	10.00	-	-	-	-
	n3	-	-	10.00	10.00	10.00	10.00
	n5	-	-	10.00	10.00	10.00	10.00
	n4	10.00	10.00	10.00	10.00	10.00	10.00
	n5	10.00	10.00	10.00	10.00	10.00	10.00
With 4 DGs	n7	10.00	10.00	-	-	-	-
	n9	10.00	10.00	10.00	10.00	10.00	10.00
	n12	-	-	10.00	10.00	10.00	10.00
	n2	-	-	10.00	10.00	-	-
	n3	-	-	10.00	10.00	10.00	10.00
	n4	9.08	8.08	8.95	7.16	-	-
	n5	-	-	10.00	10.00	10.00	10.00
With 6 DGs	n6	10.00	10.00	10.00	10.00	10.00	10.00
	n9	8.82	7.49	-	-	10.00	10.00
	n10	10.00	10.00	-	-	10.00	10.00
	n11	-	-	10.00	10.00	-	-
	n12	8.52	6.74	-	-	9.86	9.70
	n13	10.00	10.00	-	-	-	-

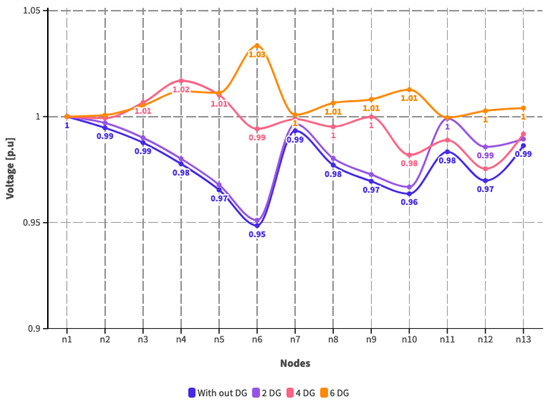
Figure 10. Voltage profile with DG incorporation—Scenario Base.

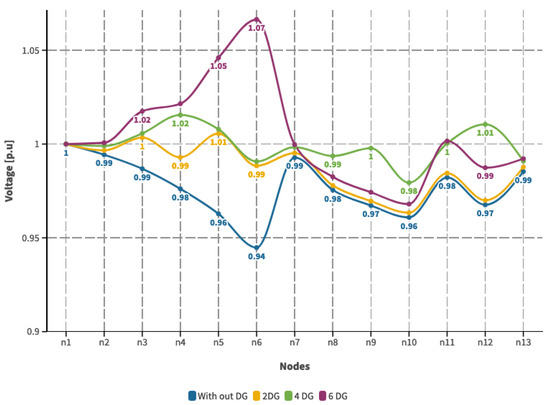
Figure 11. Voltage profile with DG incorporation—Scenario 1.

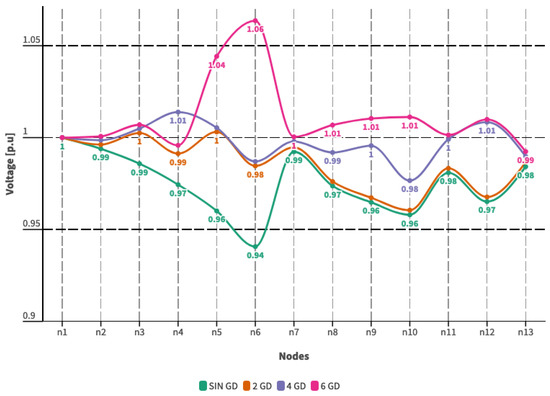
Figure 12. Voltage profile with DG incorporation—Scenario 2.

The previous graph presentation indicates that incorporating DG into the distribution system enhances the voltage profile regardless of the load scenario. Additionally, we can observe a significant improvement in the voltage profile with a more optimally incorporated DG in the system. In this context, it is crucial to emphasize that the optimizer defines the placement of the DG units, ensuring the proper injection of active and reactive power. This interaction with the system’s power flows enables the system to operate adequately, ensuring that voltage levels meet the voltage level quality index and improve compared to the initial scenario, as shown in Figure 13.

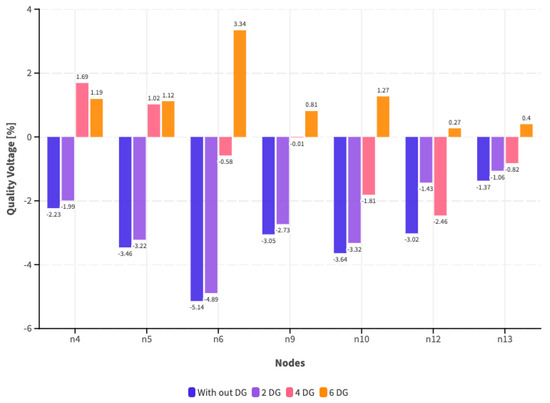
Figure 13. Voltage level quality index—Base Scenario.

Figure 13, Figure 14 and Figure 15 show that the voltage level quality index initially evaluated in the initial case without DG improves compared to that with the incorporation of DG. It remains within the permitted limits according to Regulation No. ARCONEL 005/18. This is related to the improvement of the voltage profile. In this context, a higher optimal incorporation of DG enhances the quality above the index, resulting in a substantial increase, as demonstrated when six DG units are incorporated into the system regardless of the demand scenario. Corresponding to the analysis of the voltage profile and the voltage level quality index, we analyze the system losses based on the demand scenarios and the quantity of incorporated DG, with the results shown in Figure 16.

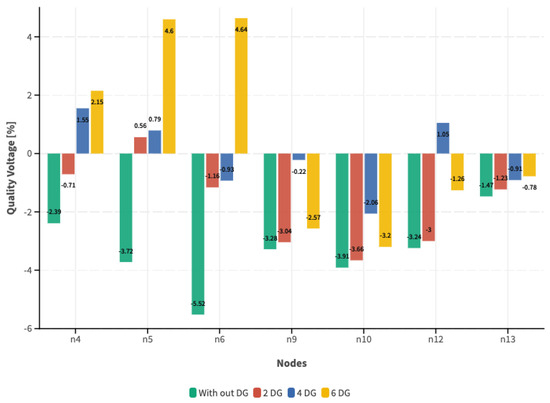
Figure 14. Voltage level quality index—Scenario 1.

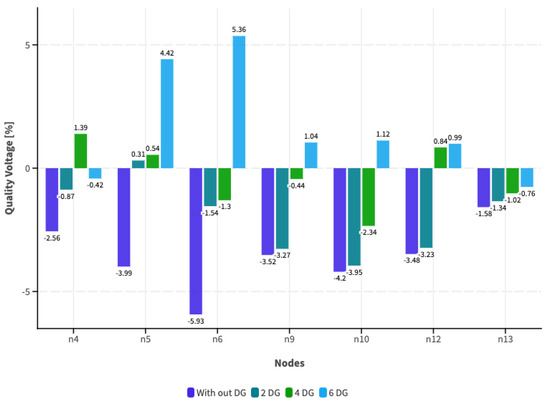
Figure 15. Voltage level quality index—Scenario 2.

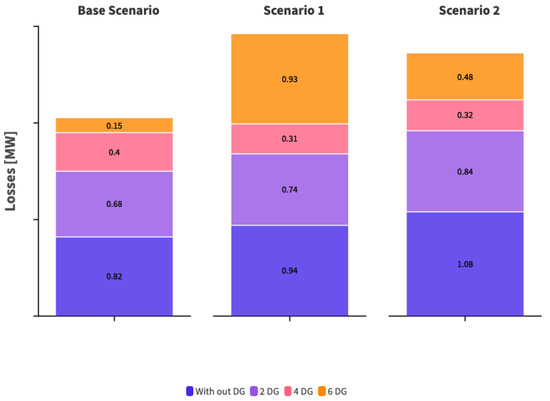
Figure 16. Losses by load scenario and by quantity of DG.

From the results obtained regarding losses, including DG in the system initially tends to reduce losses. However, with a more significant increase in DG, they begin to deliver sufficient energy to supply the load of the distribution system. This leads to an increase in losses in the distribution system and may even provide energy to the transmission system, as shown in Figure 17.

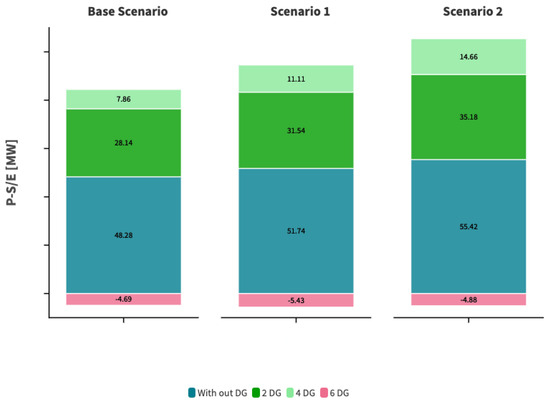
Figure 17. Losses per load scenario and by quantity of DG.

The results obtained for the substation power by load scenario and by the quantity of DGs imply that a higher number of DGs requires less energy from the power system. In the case of intensive DG penetration, the distribution system supplies energy to the power system, as shown in Figure 17, with the implementation of six DG units regardless of the load scenario. Finally, in evaluating the system’s operating cost, we assess the energy delivered by the power system to the distribution system at the final user tariff. Conversely, we consider the power supplied by the DG using the average price of the levelized Cost of Energy (LCOE). We obtained the results and present them accordingly in Figure 18.

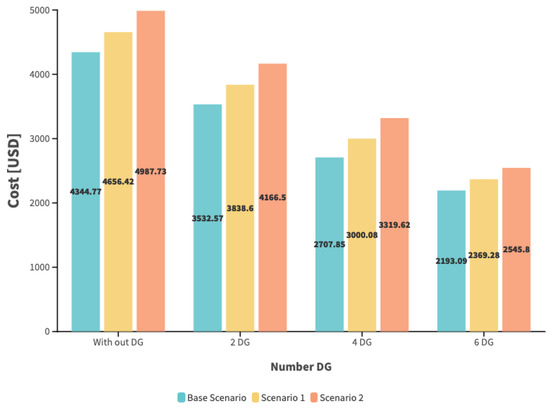
Figure 18. Operating cost per load scenario and by quantity of DG.

The model considers the operating cost as its objective function. As expected, it tends to minimize, as confirmed by the presented results. Therefore, we note that the operating cost minimizes in any load scenarios, regardless of the quantity of incorporated DGs. In general terms of the electricity market, this benefits the demand. It receives more economical generation resources not influenced by additional tariffs associated with network tolls or other supplementary charges.

6. Conclusions

After analyzing the results obtained from this study, we can present the following conclusions. The results obtained regarding the electrical variables for the load scenarios indicate that implementing DG improves the voltage profile and enhances the voltage level quality indicator, evaluated according to Regulation No. ARCONEL 005/18, remaining within the medium voltage limit of +/−6%. For the cases under analysis, we can note that in any demand scenario without considering DG, the value of the indices averages at 3.37%. In contrast, when DG is implemented, these values are reduced on average to 0.43%, demonstrating a significant reduction and ensuring an adequate voltage level at the buses.

Based on the results, when evaluating the cost without DG in any of the scenarios and cases studied, the average value amounts to USD 4662.97. However, when assessing the average price in any of the scenarios, including DG, it amounts to USD 3074.82, representing a decrease of 34.06%. Therefore, we confirm that the model fulfills the function of minimizing costs.

The analyzed economic results show a reduction in system operating costs, which depend on the quantity of DG. In this regard, incorporating six DG units achieves the maximum decrease in operating expenses for the initial case, resulting in a 50% reduction. Consequently, this cost reduction leads to savings for the demand, thereby translating into a minimization of tariffs for end-users.

Regarding the assessment of losses, we can observe that when evaluating them without DG in any of the scenarios and cases studied, the average value amounts to 0.9466 MW. However, when we assess an average value of losses in any of the scenarios, including DG, they amount to 0.5388 MW, representing a decrease of 43.07%. Therefore, DG, in addition to providing the benefits mentioned above, also reduces losses in the system due to its bidirectional flow in the networks.

When integrating DG, one must consider the associated costs and technical aspects. Within the theoretical framework reviewed, most studies focus on technical issues of the network, regardless of the cost related to the integration of DG and the economic incentives provided; therefore, the two contexts described above are relevant when evaluating the rate of return, which in many cases can define the viability of a generation project.

In conclusion, the localization and determination of maximum capacity for distributed generation represent pivotal steps in enhancing interconnected electrical systems’ reliability and economic viability. Significant improvements in system performance can be achieved by leveraging optimization models, such as mixed-integer nonlinear programming (MINP). These models facilitate the strategic placement and sizing of distributed energy resources, optimizing their integration into the grid while maximizing reliability and minimizing costs. This approach underscores the importance of rigorous optimization methodologies in effectively managing distributed energy resources within the electrical grid, ensuring their seamless integration and contribution to a sustainable energy future.

Future research stemming from investigations into the location and determination of maximum distributed generation capacity in electrical systems considering demand scenarios may include the following:

• Optimizing operational costs by improving the distribution scheduling.
• Optimizing distributed generation in electrical engineering—a methodological framework for integrating renewable energies, leveraging tools such as Distribution System Modeling and Simulation (DSMS) and employing algorithms tailored for the efficient integration of distributed renewable energy sources.
• Modeling future scenarios is an approach leveraging advanced computational tools such as Monte Carlo simulation and employing algorithms tailored for predictive analysis and scenario planning.
• Examining smart grid implementations in distributed generation, employing methodological tools such as Power World Simulator, and utilizing algorithms specifically designed for analyzing smart grid performance and optimization like grey wolf optimization and others.

Through inquiry, it aims to enhance electrical systems’ efficiency, reliability, and sustainability while accommodating evolving demand patterns and technological advancements.